A hybrid stochastic–deterministic mechanochemical model of cell polarization

Abstract

Polarization is a crucial component in cell differentiation, development, and motility, but its details are not yet well understood. At the onset of cell locomotion, cells break symmetry to form well-defined cell fronts and rears. This polarity establishment varies across cell types: in Dictyostelium discoideum cells, it is mediated by biochemical signaling pathways and can function in the absence of a cytoskeleton, while in keratocytes, it is tightly connected to cytoskeletal dynamics and mechanics. Theoretical models that have been developed to understand the onset of polarization have explored either signaling or mechanical pathways, yet few have explored mechanochemical mechanisms. However, many motile cells rely on both signaling modules and actin cytoskeleton to break symmetry and achieve a stable polarized state. We propose a general mechanochemical polarization model based on coupling between a stochastic model for the segregation of signaling molecules and a simplified mechanical model for actin cytoskeleton network competition. We find that local linear coupling between minimally nonlinear signaling and cytoskeletal systems, separately not supporting stable polarization, yields a robustly polarized cell state. The model captures the essence of spontaneous polarization of neutrophils, which has been proposed to emerge due to the competition between frontness and backness pathways.

INTRODUCTION

The ability to break symmetry spontaneously is fundamental to most eukaryotic cells and plays an important role in embryogenesis, cell differentiation, cell division, and migration. Intrinsically motile cells can switch spontaneously to a migratory polarized phenotype (Parent and Devreotes, 1999). Understanding complex molecular circuits employed by a cell to establish polarization has been studied both theoretically (Levchenko and Iglesias, 2002; Maree et al., 2006; Mori et al., 2008; Altschuler et al., 2008; Lomakin et al., 2015; Goryachev and Leda, 2017) and experimentally (Burridge and Wennerberg, 2004; Wong et al., 2006; Nguyen et al., 2016; Peglion and Goehring, 2019).

Polarity establishment arises primarily through the localization of particular proteins and lipids in the cell to specific regions of the plasma membrane, and often precedes motility. Experiments have identified a few conserved sets of proteins involved in polarization including the PAR system (Munro et al., 2004; McCaffrey and Macara, 2012), the Wnt system (Ip and Gridley, 2002), the Scribble complex (Assemat et al., 2008; Su et al., 2012), and the Rho system (Burridge and Wennerberg, 2004; Schwartz, 2004). Here, we focus on the Rho molecular circuit whose dynamics can lead to cell polarization at the onset of cell motility. The Rho family of GTPases is a family of small proteins that act as molecular switches (Hall, 1998; Schwartz, 2004). Three important members of the family have been studied in detail: Cdc42, Rac1, and RhoA (Schwartz, 2004). These proteins cycle between an inactive (GDP) cytosolic form and an active (GTP) membrane-bound form that signals to the actin cytoskeleton and other downstream targets. Mutually antagonistic interactions between Rac1 (Rac) and RhoA (Rho) were identified, as well as spatial and/or temporal exclusions that produce a tendency for them to segregate to the front versus rear of a polarized cell (van Leeuwen et al., 1997; Xu et al., 2003; Burridge and Wennerberg, 2004; Byrne et al., 2016). From previous theoretical work, it is well known that mutually inhibitory circuits, such as those in Rac/Rho, could yield a robustly polarized system (Jilkine and Edelstein-Keshet, 2011; Edelstein-Keshet et al., 2013).

Cell polarization is also associated with the rearrangement of the actin cytoskeleton during polarization, in which branched actin filaments form at the cell front while actomyosin contractile bundles segregate to the cell rear (Wong et al., 2006; Yam et al., 2007; Svitkina, 2018). Just as diffusible chemical activators and inhibitors trigger biochemical instabilities, mechanical instabilities can arise due to stochastic fluctuations in actin filament densities or mechanical feedback between motor proteins and cytoskeletal elements (Vekhovsky et al., 1999). In mechanically driven polarity systems, cells polarize due to mechanical forces and actin flow generated by these forces (Yam et al., 2007; Mullins, 2010; Goehring et al., 2011; Barnhart et al., 2015; Lomakin et al., 2015). Two classic cases involving cytoskeleton-driven polarization are the formation of actin comet tails by intracellular pathogens (Dayel et al., 2009; Haglund and Welch, 2011) and the directional locomotion of keratocytes (Barnhart et al., 2015; Lomakin et al., 2015; Yam et al., 2007). In both cases, the mechanical properties of the actin cytoskeletal network appear sufficient for polarization, which can be triggered by stochastic or induced asymmetries in the mechanical network.

Mathematical models have been used to explain spontaneous pattern formation in cells since the 1950s (Turing, 1952; Meinhardt and Gierer, 1974). Initial approaches were based on Turing patterns and focused on biochemical signaling pathways for polarity. In Turing-like models, chemical patterns emerge from stochastic fluctuations combined with interactions between chemical species that diffuse at different rates; these models often require elaborate nonlinearities for stable polarized distributions of chemicals (Howard et al., 2011; Jilkine and Edelstein-Keshet, 2011).

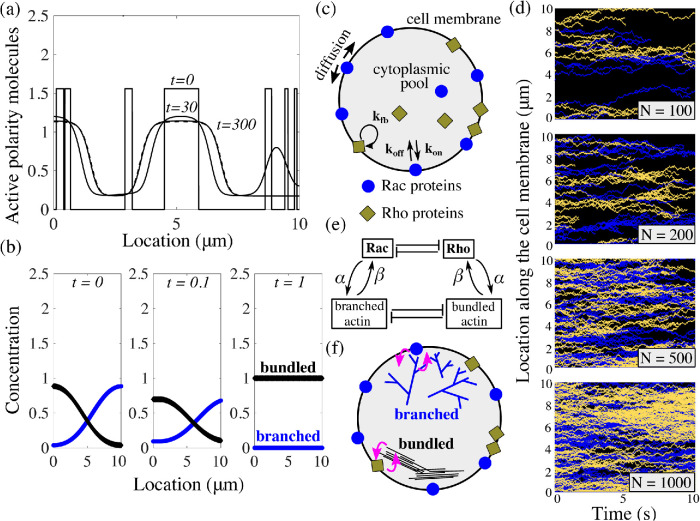
Recently, many models for cell polarization have been proposed based on reaction–diffusion (not necessarily Turing-like) equations (Jilkine and Edelstein-Keshet, 2011). In one of the most popular models, the “wave-pinning” model (Figure 1a), a minimal bistable reaction–diffusion system gives rise to polarization of active/inactive chemicals (Mori et al., 2008). In the model, the active form of the chemical diffuses slowly on the membrane and autocatalytically activates the inactive form of the chemical, which diffuses fast in the cytoplasm. Conservation of the total chemical and the fast diffusion of its inactive form act as global inhibitors and pin or “arrest” the active chemical in space into a stable polarized distribution. The model reproduces a number of observed features shared by many eukaryotic cells: (a) spontaneous (self-) polarization, (b) maintenance of the polarized state after a stimulus is removed, and (c) sensitivity to new incoming signals and ability to repolarize in a new direction.

FIGURE 1:

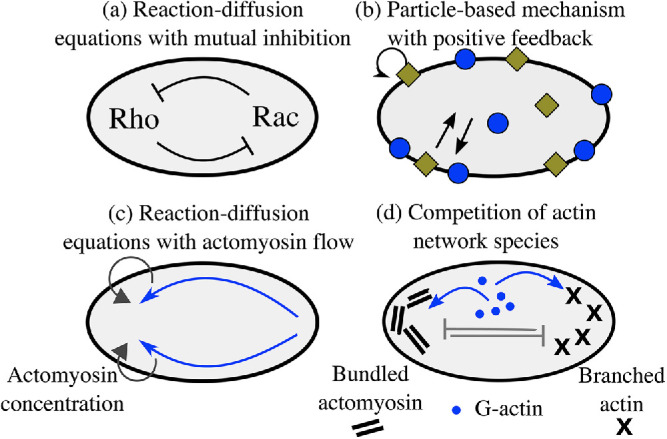
Simple models of cell polarization. Biochemical (a, b) and mechanical (c, d) approaches for polarity establishment. (a) Reaction–diffusion model of Rho GTPase signaling pathways are based on mutual antagonism between signaling molecules. (b) Stochastic model of the cycling of active–inactive states of signaling molecules with autocatalytic feedback. (c) Polarization can also emerge due to positive feedback between myosin concentration gradients and myosin transport by the flow, which generates actomyosin flow up the gradient. (d) In an advection-free model, polarization emerges due to the competition between the branched protrusive actin network and contractile bundles of the actomyosin network caused by competition for a conserved number of molecular resources.

Besides reaction–diffusion models, stochastic polarization models have also been proposed (Figure 1b; Altschuler et al., 2008; Walther et al., 2012; Wu et al., 2015; Pablo et al., 2018). For example, Altschuler et al. (2008) found that clusters of active membrane-associated molecules can form and persist in time if there is a positive feedback loop in which active molecules recruit additional copies of themselves from a cytoplasmic pool, provided the system is operating within a stochastic regime and the molecule number is limited. A stochastic version of the wave-pinning model was introduced by Walther et al. (2012). The authors found that when the molecule number is lowered, the wave front collapses predominantly due to the fluctuations in the pinning position of a traveling wave. The result of loss of polarization at low cellular concentration is in contrast to the work of Altschuler et al. (2008).

A much smaller body of literature exists for actin-driven models for cell polarization (van der Gucht et al., 2005; Goehring et al., 2011; Barnhart et al., 2015; Lomakin et al., 2015). Most of these models focus on the fast-moving fish epithelial keratocytes, which do not require the stereotypical signaling cascades to polarize (Ridley, 2001). A combined experimental and theoretical effort showed that the mechanical feedback between actin network flow, myosin, and adhesion is sufficient to amplify stochastic fluctuations in actin flow and trigger polarization (Figure 1c); aggregation of myosin at the cell rear generates rearward actin flow and forward cell movement, which both amplify the myosin concentration at the rear (Barnhart et al., 2015). An actin flow–free mechanical mechanism for cell polarization was proposed by Lomakin et al. (2015; Figure 1d). The authors demonstrated that competition between branched and bundled actin networks around the cell periphery leads to segregation of the actin cytoskeleton into branched filaments at the cell front and actomyosin bundles at the rear. A key assumption in this model is that protrusion of the boundary favors the branched network, while boundary retraction favors the contractile bundles.

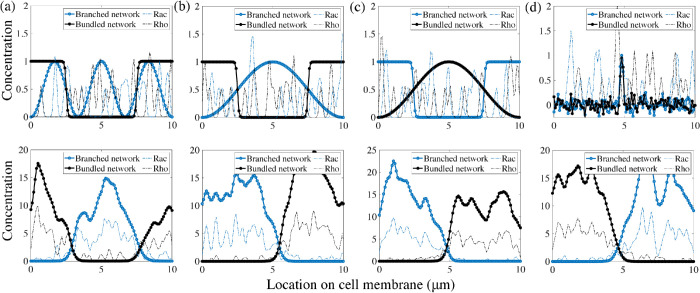
Deterministic models for biochemical polarization mechanisms have limitations. For example, in the wave-pinning model, the stability of the polar distribution of the active chemical requires highly nonlinear reaction terms (Mori et al., 2008). Furthermore, when the initial condition in the wave-pinning model consists of multiple localized patches of active chemicals, and when the diffusion constant is very small, these initial patches persist in time, corresponding to formation of not one but multiple zones of activity on the plasma membrane (Figure 2a). Stochastic models for polarity molecules require very simple kinetics, but also require additional assumptions to constrain the number and location of emergent clusters into a single one (Figure 2d, N = 100; Altschuler et al., 2008).

FIGURE 2:

Neither model produces a stable polarized cell state. (a) Given patchy initial conditions and low diffusion on the membrane, the wave-pinning model (Mori et al., 2008) cannot yield a polar distribution of the membrane-bound active polarity molecules. (b) In the mechanical cytoskeleton model for polarization of keratocytes without movement (Lomakin et al., 2015), perturbations to the polar distributions of the branched and bundled actin networks lead to annihilation of one of the networks. (c) Schematic of the stochastic polarization model modified from Altschuler et al. (Altschuler et al., 2008) describes the cycling of active–inactive states of two species of signaling molecules: Rac and Rho. (d) Results of model simulations from (c) with varying total number of species N. With a small number of particles, long-lasting patches of active form of Rac and Rho appear; however, there is no control on the number of emergent patches or their merging into single protrusive and contractile fronts. Decreasing the number of signaling molecules leads to increasing levels of spatial segregation between the two signaling species. (e) In our coupled model, we link the nonpolarizing mechanical model for the cytoskeleton to the nonpolarizing simple kinetics model for Rac/Rho dynamics. (f) Schematic of the coupled model: Rac proteins and the branched actin network engage in mutual local feedback and similarly; so do Rho proteins and the bundled actin network.

Although cell polarity can emerge from systems that are either chemical or mechanical, in many cases cell polarity depends on the interplay between the two (Bois et al., 2011; Dawes and Munro, 2011; Howard et al., 2011; Prager-Khoutorsky et al., 2011). One such example of mechanochemical polarization is the establishment of the anterior–posterior axis in Caenorhabditis elegans embryos, which depends on both actomyosin flow and the biochemistry of PAR polarity proteins (Munro et al., 2004; Dawes and Munro, 2011; Goehring et al., 2011). In this system, asymmetrical cell contractility and cortical actin flow are essential for polarity establishment (Dawes and Munro, 2011; Munro et al., 2004). By coupling an advective transport of the flowing cell cortex to a reaction–diffusion system for PAR protein segregation, Goehring et al. (2011) showed that advection could serve as a mechanical trigger and would be sufficient to form stable asymmetric PAR distribution. Similar experimental observations of the feedback between mechanics and biochemical signaling in polarity of other organisms continue to appear (Graziano et al., 2018).

Here, we set out to uncover a minimal coupling between the simplest biochemical signaling and cytoskeletal circuits that supports robust cell polarization. The competition between two actin networks (branched and protruding vs. bundled and contracting) is one such minimal cytoskeletal mechanism not requiring advective actin flow (Lomakin et al., 2015). However, to generate stable polarization, this mechanism requires coupling to physical cell movement. Most cells move slowly and break symmetry before initiating locomotion (Prager-Khoutorsky et al., 2011). Here, we show that the simplest feedback between two-network competition and the simplest stochastic model of biochemical polarization with minimal nonlinearities leads to robust cell polarization. The model is applicable to neutrophils, in which a competition between frontness and backness pathways, each built from a mutually beneficial actin network and a signaling circuit, is essential for the spontaneous polarization of cells (Xu et al., 2003). Separately, neither competition between the leading-edge actin and the rear-edge actomyosin networks nor feedback between Rac-and Rho-related pathways can polarize these cells, but when they are coupled, the polarization emerges, as our model will demonstrate.

MODEL FORMULATION

Minimal biochemical signaling model

The biochemical part of our model is a simplification of well-studied Rho GTPase kinetics (Moissoglu and Schwartz, 2014). Each Rho GTPase molecule cycles between two states: an active GTP-bound form, bound to the plasma membrane, and an inactive GDP-bound form, diffusing in the cell cytosol (Burridge and Wennerberg, 2004; Hall, 1998). The conformational changes between these two states are facilitated by a class of regulatory proteins such as GEFs, GAPs, or GDIs (Burridge and Wennerberg, 2004; Hall, 1998). Rac and Rho pathways cross-talk with one another, and previous research has revealed evidence of mutual inhibition of Rac and Rho signaling (Burridge and Wennerberg, 2004; Byrne et al., 2016; van Leeuwen et al., 1997; Xu et al., 2003). Furthermore, this mutual antagonism is believed to promote spatial and/or temporal exclusions that produce a tendency for Rac and Rho segregation (Yamada and Nelson, 2007).

At the onset of polarity, nascent polar sites appear along the plasma membrane and their presence is believed to be sustained by local positive feedback that depends on the assembly of branched actin filaments (Inoue and Meyer, 2008; Ma et al., 2018). These initial polar sites are thought to be sustained through local positive feedback loops that depend both on the presence of polarity molecules (Nguyen et al., 2016) and on actin assembly (Inoue and Meyer, 2008; Srinivasan et al., 2003; Weiner, 2002). Specifically, in their active state, Rho GTPase can bind to downstream effector proteins that control the actin cytoskeleton rearrangements (Heasman and Ridley, 2008; Ridley, 2006). Rac polarity sites mediate the formation of a branching actin filament network at the leading edge (Weiner et al., 1999). Interaction between Rac and branched actin network appears to be mutual—Rac activates nucleation-promoting factors such as WAVE and WASP, which activate Arp2/3 branching complexes (Higgs and Pollard, 2001; Machesky and Insall, 1998), while recruitment of additional Rac in nascent polarity zones in highly protrusive regions is also reported (Das et al., 2015; Nguyen et al., 2016; Weiner et al., 2007). Rho is believed to stimulate the formation of a bundled actomyosin network through recruitment of myosin II molecular motors at the opposing end (Hall, 1998; Pertz et al., 2006). While less is known about the interaction from actomyosin bundles to Rho, recent work seems to indicate that localization of Rho activators is actin-dependent (Segal et al., 2018).

Our signaling kinetics model is formulated on a one-dimensional circular domain representing polarity molecules on the plasma membrane and a thin volume of cytoplasm adjacent to the membrane on the circular edge of a disk-like cell spread on a flat surface. Position of the molecules is represented by the arc length s on a circle. We track coordinates of activated Rac and Rho molecules on the membrane along the cell edge, 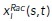and 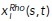, where i is the index of the specific molecule. Cytoplasmic concentrations of Rac and Rho are assumed to be homogeneous due to the fast diffusion in the cytoplasm. For the dynamics of these proteins, we extend the theory of Altschuler et al. (2008) to include two species of signaling molecules. The redistribution of signaling molecules is determined by the rates of four mechanisms (Figure 2c): 1) positive feedback–induced activation and recruitment of cytoplasmic molecules to the locations of membrane-bound active signaling molecules with rate k_fb; 2) spontaneous activation and association of cytoplasmic molecules to random locations on the plasma membrane with rate k_on; 3) lateral diffusion (with coefficient d) of active molecules along the membrane; and 4) deactivation and disassociation of signaling molecules from the membrane with rate k_off. For simplicity, we use the same kinetic rates for both Rac and Rho.

We first describe the simple case where the signaling molecules’ kinetic rates are constant in space. At initialization, 10% of the signaling molecules of each type, N, are randomly placed along the cell membrane, while it is ensured that there is no spatial overlap between particles of different types. Based on the dynamics described above, the number of Rac (or Rho) molecules on the membrane, n(t), evolves by a continuous-time Markov-chain process where the transitions in the numbers of membrane-bound particles are jumps by +1 or 1. Because the kinetic rates governing the Poisson process will be spatially dependent (see Mechanochemical coupling), we consider individual transition rates: the time and location of the next biochemical reaction event is computed discretely based on the locations of the already membrane-bound particles. For each membrane-bound particle j, we compute the time to its next reaction, which is exponentially distributed with rate:

1

The rate 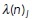should be interpreted as a reaction rate per membrane-bound particle—hence, the unbinding rate per particle is a constant k_off, while the binding rate is proportional to the remaining fraction of available binding spots on the cell membrane with a constant of proportionality 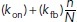. The spontaneous association rate per particle is constant but the enhanced association per particle due to its implicit dynamics of enhanced recruitment is proportional to the fraction of molecules that are still in the cytosol. After n random times based on these rates are generated, the time for the next reaction in the system is chosen as the minimum time across all active particles. Then, for each respective particle, either a disassociation event with probability 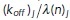, a spontaneous association event with probability 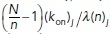, or an induced association event with probability 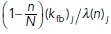is generated. If a disassociation event has occurred, the particle is removed from the membrane and added to the well-mixed homogeneous cytoplasmic pool of inactive particles. If a positive feedback–induced recruitment association event has occurred, a particle is added to the membrane from the cytoplasmic pool and its position is chosen to coincide with the position of the already membrane-bound particle. Last, for a spontaneous association event, the new particle is added from the cytoplasmic pool of inactive particles to the membrane at a randomly chosen location within the spatial segment centered at particle j. The endpoints of the spatial segment associated with particle j are at the halfway location between the nearest neighboring membrane-bound particles of the same type. Independently, this process is repeated for both Rac and Rho particles. Between Markov events, the number of membrane-bound Rac (or Rho) particles is constant and the particles diffuse freely on the membrane. A steric repulsion is enforced between Rac and Rho polarity molecules so that the two chemicals cannot cross paths at any moment in time. The rates of transition (Zhang and Zheng, 1998; Moissoglu et al., 2006; Altschuler et al., 2008; Mori et al., 2008; Falkenberg and Loew, 2013; Das et al., 2015), relative rates of diffusion (Mogilner and Keren, 2009), and concentrations of active and inactive states (Altschuler et al., 2008; Das et al., 2015) are readily biologically interpretable and estimated from experimental data (see Supplemental Table S1). In the Supplemental Material, we explain in detail how the diffusive random walk of the molecules on the membrane is simulated, as well as the numerical implementation of the modified spatial Gillespie first reaction algorithm for chemical reactions (Gillespie, 1977, 2007). We also note that the above description only considers a model for the signaling pathway in the absence of the actin dynamics. The modified model that incorporates actin dynamics will follow in the next subsection.

Minimal actin network model

Two different actin structures are characteristic of polarized cell migration: a branched, protrusive actin network at the cell front, and a contractile network made up of actomyosin bundles at the cell rear (Lomakin et al., 2015). These two actin networks compete mechanically (Lomakin et al., 2015): protrusion of the branched network leaves the bundled network behind the cell edge, while the contractile bundles collapse the branched filaments into bundles. The networks also compete for the same pool of actin monomers and other molecular resources in the cytosol (Rotty and Bear, 2014). Thus, our model has the features of a system with two competing species (Edelstein-Keshet, 1988). The spatiotemporal distributions of the two species of actin networks along the plasma membrane arc length are A(s, t) for the protrusive network and B(s, t) for the contractile actin–myosin meshwork. We assume that the branched network is protrusive and devoid of myosin II motors, while the bundled network contains contractile actomyosin bundles that generate contractile forces and retract the cell’s posterior. Their dynamics are given by the following nondimensionalized coupled system of equations adapted from Lomakin et al. (Lomakin et al., 2015):

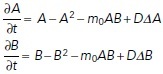2

Full model assumptions and details are explained in the Supplemental Material. The rate of network growth is proportional to their density, but it is limited at high densities by the finite amounts of molecular resources (e.g., depletion of monomers or branching complexes or myosin II motors). The model assumes that the competition terms, proportional to the product AB, stem from either mechanical competition or competition for limited molecular resources. Parameter m₀ is the magnitude of competition between the networks. Last, the diffusive terms describe the action of myosin II motors that slide and shuffle bundled filaments in the contractile actomyosin network, as well as the random lateral displacements of the growing ends of the barbed filaments along the cell membrane (Lomakin et al., 2015).

Mechanochemical coupling

To couple the cytoskeleton meshwork dynamics to the cycling of signaling molecules, we assume, based on the experimental evidence described above, the simplest possible local feedback loops between 1) Rac and the branched actin network, and 2) Rho and the bundled actin network (Figure 2f). Specifically, we posit that the chemical rates in the signaling module are no longer constant but rather are linear functions of the local concentration of each respective actin network, which evolves in space and time. On the other hand, the growth rate of each actin network is linearly proportional to the respective local densities of active polarity proteins. We use the following mathematical expressions for the modified rates of Rac and Rho kinetics (Figure 2e):

3

Here, the expressions for on and off rates are for either Rac or Rho chemical kinetics. For Rac/Rho kinetics, C denotes branched/bundled actin network density, A or B, respectively. Thus, the induced on rate for Rac increases with the local branched actin density, while the Rho induced on rate increases with the local bundled actin–myosin density. The off rates are constant. The maximum function in the expressions for k_fb and k_on is a pointwise maximum function and serves to ensure that the association rates do not exceed a threshold value. In principle, all kinetic rates could depend on the spatial distribution of actin. Additionally, introducing spatial dependence into the disassociation rate produced no qualitative changes from the results presented here (unpublished data). Similarly, not all kinetic rates need to depend on actin concentration, and as an example, we found that in order to reproduce the results presented here, only the enhanced association rate should vary spatially with actin concentration. The coupling constant β is the measure of this feedback strength. The growth term in the actin networks equations is altered as follows:

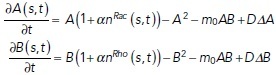4

The coupling constant is a measure of the feedback from Rac/Rho to the branched/bundled actin, respectively. In these expressions, 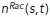and 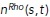are the densities of Rac and Rho, respectively. Numerically, these densities are computed from the discrete locations of the respective molecules by computing at each time step a superposition of Gaussian peaks with variance and centers at their molecular locations.

Importantly, in the presence of the feedback from actin networks to the signaling molecules, their on/off rates depend on the spatial positions on the cell edge due to varying actin densities. In this case, the numerical implementation of the chemical kinetics becomes more complex; because the kinetic rates vary spatially, the individual time between events in the number of membrane-bound molecules is determined for every individual molecule according to the rates

5

and the minimum time is chosen as the first event in the Poisson process. Then, the dissociation, spontaneous association, and induced association events take place with probabilities given above for the spatially independent model; however, the rates now depend on the positions of the active signaling molecules. The numerical implementation of this modified stochastic model is provided in the Supplemental Material. The codes used are accessible online on a public repository (link provided in Supplemental Material). The values for the coupling constants range between 0 (uncoupled) and 2 (strongly coupled).

RESULTS

Neither the mechanical nor the biochemical model leads to stable polarization

A deterministic formulation of the polarity signaling model in Figure 1b with only one chemical species results in a reaction–diffusion equation with stably nonpolar distributions (Altschuler et al., 2008). On the other hand, a stochastic formulation of the same kinetics leads to the emergence of clusters of Rac and Rho that persist in time (Figure 2b). However, we find that neither Rac nor Rho clusters localize into a single cluster; Rac and Rho do not concentrate to opposite sides of the polarized cell, as observed at the onset of motility. As the total number of signaling molecules is increased, the number of clusters of Rho GTPase activity also increases, resulting in a patchy distribution. We varied the biochemical kinetic rates and found that these results hold over a wide range of model parameters. The actin competition model is based on the classical Lotka–Volterra model of the population dynamics of two species competing for a common resource (Edelstein-Keshet, 1988). If the competition parameter m₀ is small, two networks can coexist in space, and both of their densities are spatially constant. However, if the competition parameter m₀ is large, the situation becomes “winner take all,” and one network dominates, while the other goes extinct. We examined if polarized actin distributions are possible: one of the networks occupies one region in space, while the other occupies the remaining space (Figure 2b). Such a polarized state exists only when the initial distributions are exactly symmetric. Any small perturbation of the initial polarized distribution results in one network (the one with slightly greater spatial support) taking over and displacing the other network (Figure 2b). Rigorous mathematical analysis showed that this nontrivial spatial segregation of competing species in Lotka–Volterra models is not stable (Cosner and Lazer, 1984; Kan-On, 1998; Takeuchi, 1989).

These simulations led us to wonder if coupling between the chemical and mechanical modules could stabilize cell polarization. The idea is that the slow destabilization of the polar state of actin networks could bias the signaling molecules into segregating into two opposite parts of the cell; this bias is caused by the up-regulation of Rac on the membrane by the branched network and simultaneously the up-regulation of Rho by the bundled network. Then patches of Rac and Rho, whose positions are arbitrary without feedback, could drift to opposing cell regions. In turn, feedback from Rho GTPase to the respective actin networks ensures that one network does not invade another’s territory, since each network dominates in a specific region due to the presence of its supporting chemical.

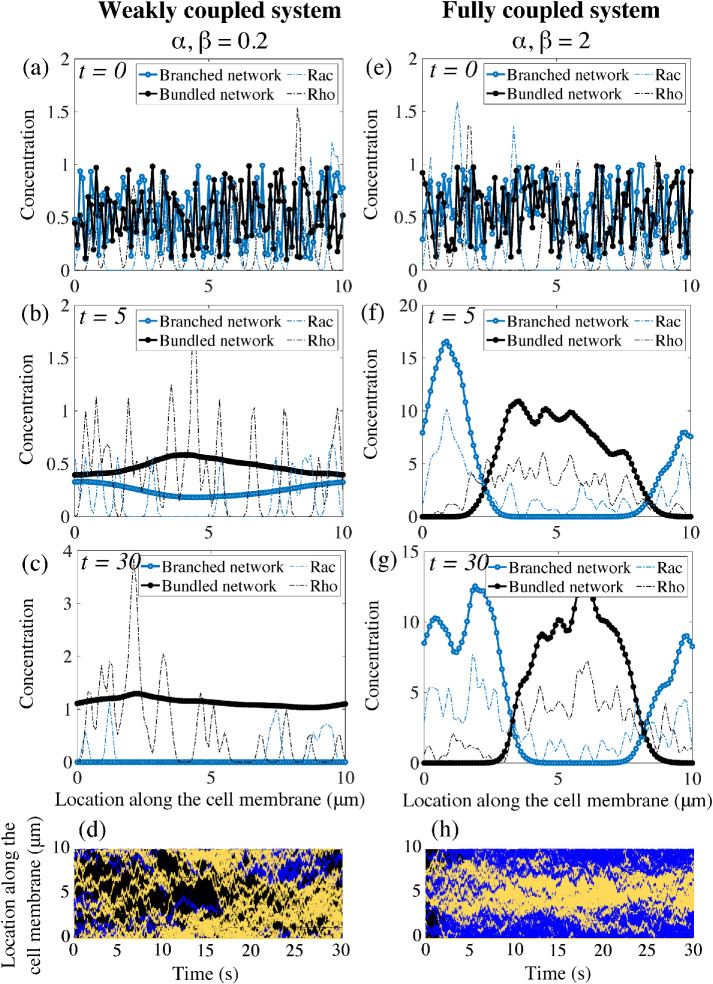
The coupled mechanochemical model produces symmetry breaking depending on coupling strength

To assess whether this model with positive feedback between protrusive actin and Rac, and contractile actin and Rho, can account for symmetry breaking, we run simulations with two choices for the coupling constants (Figure 3). The numerical simulations assume random initial distributions and equal total conserved amounts of Rac and Rho, and of two types of actin network (Figure 3, a and e). We define a polarized cell state when two spatially separated well-defined peaks emerge, one for the branched actin and another for the bundled actomyosin network, and simultaneously, peaks for the chemical concentrations, Rac and Rho, form in the same locations as the peaks of their respective actin networks. For low coupling constants, the polarity proteins segregated into many nonoverlapping Rac and Rho clusters (Figure 3d). The mechanical model was unable to achieve a polar distribution: either the actomyosin bundles or the branched actin meshwork went extinct (Figure 3c). In this particular instance of the simulation, the protrusive branching network died out while the bundled actomyosin network survived and took over the entire plasma membrane (Figure 3c). Tens of instances for this set of parameters were considered and a probability of polarization establishment of 5% was computed as a fraction of the number of simulations with stable polar distributions of both actin and polarity chemicals over the total number of runs.

FIGURE 3:

Emergence of polarity in the coupled mechanochemical system. (a–c) With weak feedback between the polarity molecules and the actin networks, the underlying chemicals do not segregate into a polar distribution but remain in a patchy distribution around the cell membrane. In this particular simulation, the bundled actin persists and eliminates the branched actin meshwork in the system. (e–g) For strong coupling constants, both the mechanical and signaling system polarize. The polarity proteins completely segregate and each actin network separates into a peak of activity in complementary regions of the cell membrane. (d, h) Kymographs of the molecular locations of Rac and Rho around the cell edge. Rac/Rho trajectories are blue/yellow, respectively. The weak/strong coupling systems are d/h, respectively.

Next, we considered a strongly coupled system and observed that the polarity molecules segregated into two clusters on the membrane: a Rac-dominated front and a Rho-dominated rear (Figure 3h). Simultaneously, the same spatial pattern is adopted by the actin networks: in the Rac-dominated region, a branched actin network is assembled, while in the Rho-dominated patch, bundled actomyosin is present (Figure 3g). Initial patches of Rac enhance local recruitment of the branched actin network, while at the same time, in different regions, Rho patches promote the formation of actomyosin bundles. This initial feedback-based recruitment leads to the formation of peaks in the concentration of each actin network, which ultimately increases the association and feedback rates in the signaling system. This transient behavior ultimately gives rise to a well-formed and stable peak in each actin species and a corresponding peak in its associated polarity molecule concentration. While these peaks are dynamic, their locations in space remain fixed, given no external stimulus. Furthermore, perturbations of the spatial profiles of the actin networks quickly return to equilibrium.

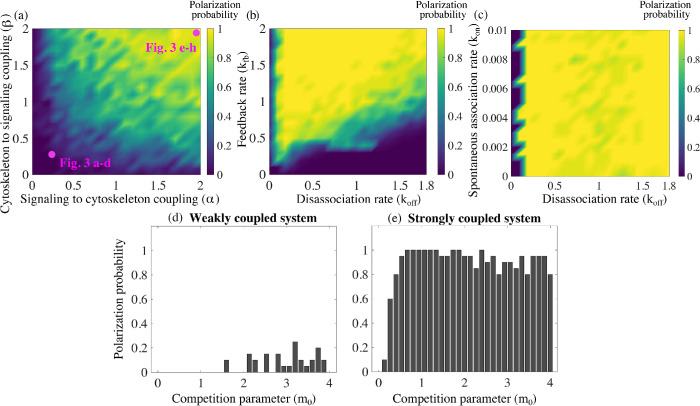
To characterize the parameter dependence on establishing polarity in the model, we performed simulations where all biochemical signaling and mechanical parameters were held constant but the coupling constants were varied. By simultaneously changing these two coupling strengths, we obtained heat maps of the polarization probability (Figure 4a), defined as the fraction of simulations with stable polar distributions of the actin networks and polarity molecules over the total number of runs. Based on Figure 4, the system is more likely to polarize in the presence of higher coupling constants. Importantly, both feedback directions—from actin to Rho GTPase and from Rho GTPase to actin—are needed for the polarization.

FIGURE 4:

Stronger mutual coupling between the actin networks and the signaling system improves cell polarization. Twenty simulations are considered for each set of parameters. Based on the outcome, the probability of a stable polarized solution is reported as the fraction of polarized solutions out of the total number of simulations for that specific choice of parameters. (a) Polarization probability is reported as a function of the two coupling parameters in the mechanochemical positive feedback loop, α and β. The parameters that were used to produce the simulations shown in Figure 3 are indicated. (b) Polarization probability as a function of two signaling kinetic rates: induced recruitment to the membrane rate k_fb and disassociation rate k_off. (c) Polarization probability as a function of two signaling kinetic rates: spontaneous association rate k_on and disassociation rate k_off. For subplots (a–c), a strongly coupled system is considered with α = β = 2. Effect of the actin competition parameter m₀ on polarization probability is reported for (d) a weakly coupled system, α = β = 0.2, and (e) a strongly coupled system, α = β = 2.

The effect of biochemical and other mechanical rates on polarity establishment

We performed a series of simulations varying the competition parameter in the mechanical model and obtained the corresponding polarization probability. For a strongly coupled system, the competition parameter has little to no effect on the likeliness of establishing polarity (Figure 4d). For a system with weaker coupling, the ability to establish a polar distribution of the actin networks is diminished even further with a lower competition parameter (Figure 4c). In the absence of competition, the equations are well known to exhibit coexistence with uniform spatial distribution (Edelstein-Keshet, 1988). We find that in the absence of competition, but coupled to the signaling module, the two actin networks can coexist on the entire domain, but, due to the randomness of the signaling module, two actin densities exhibit arbitrarily positioned small-amplitude peaks. We also varied the relative initial amounts of branched and bundled actin networks and found that even in the case where 90% of the F-actin was initially assembled into actomyosin bundles, the cell was able to polarize roughly 80% of the time, with half of the actin in one type of network and half in the other (Supplemental Figure S2a).

Next, we varied the kinetic rates in the biochemical signaling module. The mechanical parameters and coupling constants were held constant, while two chemical rates for both Rac and Rho were varied: the induced association rate, k_fb, and the disassociation rate, k_off . We obtained a heat map of the polarization probability (Figure 4b). For the majority of the heat map, the probability to polarize is largely unaffected by variations in these parameters. However, the model is sensitive to high disassociation rates and simultaneously low enhanced recruitment rates (bottom right corner of Figure 4b). In this situation of high disassociation and low feedback rates, there are too few polarity molecules on the cell membrane. Hence the chemical system is not able to influence the mechanical module, and the system gravitates toward the stable “winner takes all” state; one of the actin meshworks completely annihilates another. To comment on the effect of the third kinetic rate, we varied the spontaneous association rate, k_on, and the disassociation rate, k_off, while the other constants were held constant. The model is largely insensitive to variations of the on rate, due to the compensatory effect of the induced association rate. We find that for a very low disassociation rate, the random initial distribution of actin and polarity molecules is enhanced everywhere through recruitment to the membrane, thus corrupting the process of polarization.

The total number of polarity molecules in the system was also varied. Altschuler et al. (2008) reported that for a large number of polarity molecules, the active molecules are spread over the membrane, and polarity is lost. By contrast, our coupled model does not exhibit the same response—the probability of polarization is largely unaffected by the total number of polarity molecules (Supplemental Figure S2b). Last, we report on the response to lowering the diffusion constant by an order of magnitude for a strongly coupled system with baseline parameter values. We find that two actin density peaks do emerge, one corresponding to a protrusive zone with Rac and branched actin present, and a second peak with Rho and bundled actomyosin (Supplemental Figure S3). The width of these peaks is notably narrower than that of those reported in our other results, due to the lower diffusivity. These peaks are also closer to each other. While the cell is, formally speaking, polarized, it does not have a well-defined front and rear at opposite ends. Instead, the protrusive and retractive regions could be close to each other on the cell edge.

Polarization direction is responsive to the orientation of the external signal

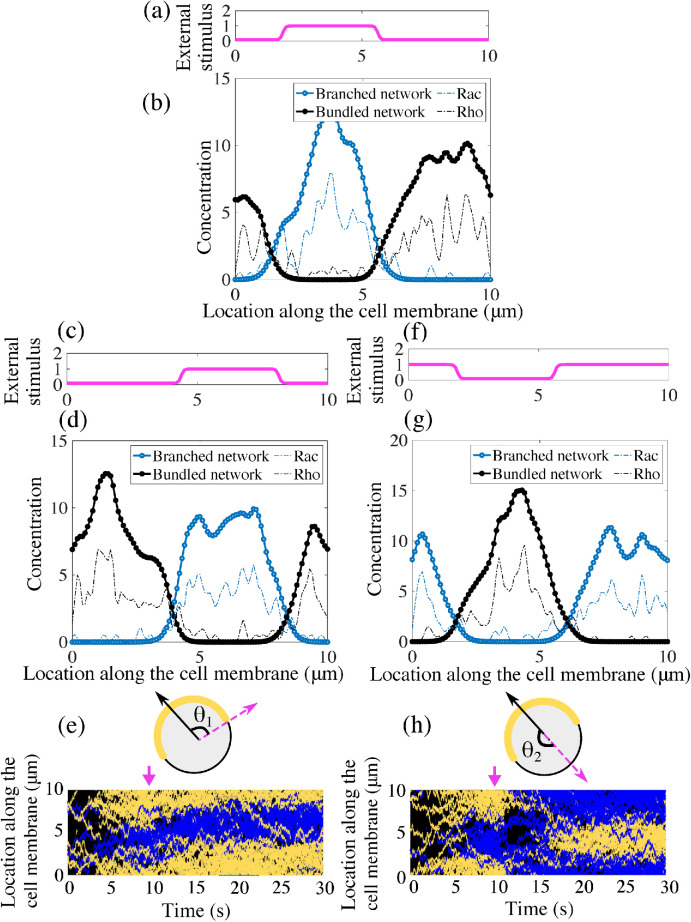
Thus far, our model simulations suggest that spontaneous polymerization in an arbitrary direction can arise from the coupling between the cytoskeletal mechanics and chemical kinetics. To determine whether our model exhibits sensitivity and adaptation to external signals, we simulated polarization in the presence of directional bias (Figure 5, a and b). We assumed that the association/dissociation rates for Rac molecules vary along the cell edge, which is equivalent to a directional bias, as shown in Figure 5a (the dissociation rate varied oppositely to the association rate, as the spatial complement of the curve in Figure 5a: the sum of the association and disassociation rates is constant). The kinetic rates for Rho molecules vary oppositely to those of Rac: where Rac rates were low, Rho rates were high and vice versa. We observed that a polarized state evolved from random initial conditions, with Rac and Rho peaks with the same orientation as the external bias (Figure 5b). The actin networks peaks also colocalized with the respective chemicals and the external bias (Figure 5b).

FIGURE 5:

Polarization direction responds to changes in the external signal. (a) An external stimulus imposes a directional bias on the kinetic rates of both polarity proteins Rac and Rho. Rac association and Rho disassociation rates have the profile around the cell edge shown in this plot. (b) With the biased chemical kinetics, polarized distributions of both signaling chemical concentrations and actin networks are oriented in the direction of this external stimulus. (c) After the polarized distributions shown in b evolve, the peak of the external stimulus is shifted by θ₁ = 90°. (d) In response to the shift of the external signal, the cell reestablishes polarity in the new direction. (e) Schematic of the change in external stimulus and resulting kymograph of the membrane-bound polarity proteins Rac/Rho (blue/yellow) along the cell membrane. (f) The peak of the external stimulus is now shifted by θ₂ = 180°, corresponding to a reversal of the incoming signal. (g) In response to the shift of the external stimulus, the cell reestablishes polarity in the opposite direction. (h) Schematic of the change in external stimulus and kymograph of the membrane-bound polarity proteins along the cell membrane in response to reversal of the external stimulus. Blue indicates Rac chemicals, while yellow indicates Rho chemicals. The arrows in the bottom plots indicate the temporal location of a new stimulus.

Next, we assessed how an already polarized cell responds to changes in the external signal direction. To achieve this, after the oriented polarized state established, we abruptly shifted the signal direction by 90° (Figure 5, c and e). After a transient reorganization of the signaling chemicals, the actin networks rearrange as well and the polarization direction turns to the new direction (Figure 5, d and e). If this was a motile cell, it would execute a smooth turn: at no time was the polarization lost, just its orientation changed smoothly. Last, we reversed the direction of the external signal by 180° (Figure 5, f and h), and observed that the cell repolarized in the new direction (Figure 5, g and h). Note that in this case, polarization was momentarily lost but emerged in a new direction.

The model is robust to changes in initial and boundary conditions

To investigate the sensitivity to initial conditions, we explore the model’s response to different initial distributions of the actin networks. A feature of robust polarity establishment is the ability to coalesce multiple protrusions, or peaks in the branched actin concentration, into a single protrusive front. Thus, we considered an initiation of the system where branched actin concentration has three evenly spaced peaks, bundled actin density has one square peak, but active signaling molecule concentrations are randomly distributed along the plasma membrane (Figure 6a). All 10 instances of this simulation setup showed the formation of a single protruding front (Figure 6a). The location of this front along the cell membrane will vary based on the initiation.

FIGURE 6:

Polarity establishment is robust to variations of the initial distributions of the cytoskeletal meshworks and of the boundary conditions. Initial (top row) and evolved (bottom row) distributions of the actin networks and polarity molecules. In all initial conditions, the Rac and Rho molecular distributions are random. (a) Periodic boundary conditions are used to represent the circular cell edge. Initially, there is one peak of the bundled network density but three peaks of the branched network density, two of which colocalized with the bundled network. (b–d) The model on the 1D segment with no-flux boundary conditions representing the anterior–posterior cross-section of an elongated cell. (b) Initially, the ends of the cell are contractile, while the middle is protrusive. (c) Initially, the cell ends are protrusive, while the middle is contractile. (d) Initially, both protrusive and contractile networks are concentrated at the cell center. In all cases, the same polarized state with segregated protrusive and contractile networks evolve. Notably, for the segment-like cell, the networks segregate to the opposite ends of the cell, making the cell robustly motile.

Next, the model geometry was changed: instead of the circular edge of a disklike cell, we considered the anterior–posterior cross-section of an elongated cell. The model remains 1D, but the boundary condition becomes no-flux, as actin, myosin, and signaling molecules do not enter or exit the cell. All previously described results in this case qualitatively match those obtained by solving the same set of equations on the 1D segment with periodic boundary conditions (see Supplemental Figures S4 and S5). We show that three possible different initial spatial distributions of actin networks all evolve to a stable polarized state with a protrusive network at one end of the 1D cell, and a contractile network at the other end (Figure 6, b–d).

DISCUSSION

The initiation of cell migration involves a complex web of signaling and cytoskeletal modules. While in certain cellular systems polarity can arise from only signaling or mechanical pathways, many cells rely on the interplay between the two to robustly break symmetry to initiate locomotion. We have presented a mechanochemical model for cell polarization based on two minimal submodels, one describing signaling molecular dynamics, the other mechanics of cytoskeletal networks. The first submodel is for two types of signaling molecules, such as Rac and Rho, which can diffuse on the cell membrane, dissociate from the membrane, or move from the cytoplasm to the membrane spontaneously, or can be recruited to the membrane by other molecules of the same type. This induced recruitment is the simplest autocatalytic feedback and corresponds to the only nonlinear (quadratic) term in the mathematical model. One species of molecules with these dynamics aggregates into a finite number of clusters (Altschuler et al., 2008). Steric interaction is the only relation between two different types of molecules in the model. We show that this interaction leads to the emergence of multiple interspersed clusters across the cell. While the Altschuler model is appropriate for capturing Cdc42 cluster emergence in budding yeast, the signaling system does not polarize the cell globally: different types of molecules segregate locally, but the clusters of the two kinds do not aggregate in the respective halves of the cell, as required for establishment of a polarity axis for migration. More generally, we find that our model resolves patchy initial conditions better than the Altschuler et al. model (Altschuler et al., 2008) and the wave-pinning model (Mori et al., 2008; Figure 2a) separately.

The second submodel is for two types of dynamic actin networks at the cell edge, branched protruding meshwork and actin–myosin contractile bundled network. These networks spread slowly and randomly around the cell edge, due to physical movements and treadmilling of actin filaments, and turn over while maintaining a certain equilibrium density. The nontrivial interaction between these networks is competition, such that the local density of one tends to diminish the density of another. This interaction stems both from mechanical effects and from competition for molecular resources. Mathematically, it is described by the simplest quadratic nonlinear term, which makes this submodel equivalent to the Lotka–Volterra equations for two competing populations (Edelstein-Keshet, 1988). It was shown in Lomakin et al. (2015) that this competition between two actin networks is an important part of the spontaneous polarization process, but without cell movement, the model is not able to polarize the cell, as one network will always win.

Thus, neither model is capable of producing cell polarization on its own. Here, we have demonstrated that the simplest coupling between the chemical and mechanical models—local, linear positive feedback loops between signaling molecules and actin cytoskeletal networks—is sufficient for spontaneous polarity. The model works if the strength of the mechanochemical coupling is above a certain threshold. The qualitative mechanism suggested by the model is simple: branched/bundled actin networks support recruitment of Rac/Rho to the membrane, respectively, so Rac and Rho tend to segregate into separate parts of the cell. In turn, neither network can now invade the other’s territory, because Rac/Rho enhance branched/bundled networks, respectively; for example, when the bundled network tries to encroach into the part of the cell occupied by the branched actin, Rac colocalizing with branched actin gives its advantage over bundled actin and prevents the invasion.

The competition between the actin networks has to be strong enough for stable polarization, so that the networks do not coexist locally, but not so strong as to overcome the effect of the mechanochemical coupling and enable one network to win the cell from the other. Effective diffusion also has to be neither too slow nor too fast for the model to work. If the diffusion coefficients in the model are too small, then the different networks with their supporting signal molecules localize into peaks that are too narrow and arbitrarily positioned. If the diffusion coefficients are too large, no pattern forms. However, overall the model is robust: a fewfold variations of any other parameters do not change the stable separation of branched actin and Rac in one half of the cell, and of bundled actomyosin and Rho to another half. The polarized pattern is not sensitive to the initial or boundary conditions. It is very likely that the model performs in 2D and 3D as well as in 1D. Interestingly, the model works even if the total number of signaling molecules becomes too large, while in this regime, the signaling submodel without mechanochemical coupling fails to produce clustering (Altschuler et al., 2008). Likely, this means that a strongly continuous variant of the mechanochemical model also supports stable polarization.

Our simulations showed that the model cell can polarize spontaneously, without any signal from the environment, but the direction of polarization adapts to an external signal. For example, if the kinetics of the polarity molecules is biased in a certain direction by an external signal, then the cell polarizes in that specific direction. If the cell is already polarized, and the signal is applied in a different direction, this causes a reorientation of the entire mechanochemical polarity machinery in the new direction. If the signals direction is close to that of the cell orientation, then the mechanochemical pattern turns smoothly; otherwise, the cell first momentarily loses polarity and then repolarizes in the new direction. This response is similar to experimental observations: motile cells execute a smooth turn when the external signal is applied normal to the direction of locomotion (Allen et al., 2019) but repolarize when the signal is opposite to the movement direction (Sun et al., 2013).

The first conceptual biological implication of our model is a mathematical demonstration that a signaling module coupled to a cytoskeletal module leads to robust spontaneous polarization and reorientation in the presence of incoming signals; this occurs despite the fact that each module separately can segregate chemical networks in space but cannot stably polarize the cell. Second, there are a number of solely chemical and solely mechanical polarization models, but for these to work, significantly nonlinear terms, supporting cooperative or switchlike behavior, are required. We show that a linear local coupling of two minimally nonlinear models (only quadratic nonlinearity in actin growth) can achieve robust cell symmetry breaking.

Our model relates conceptually to a number of cell types. The first and foremost example is neutrophils, which polarize spontaneously when chemoattractant concentration is spatially uniform (Xu et al., 2003). This polarization was shown to depend on the competition of the frontness and backness pathways (Xu et al., 2003) and to require intimate involvement of both actin dynamics and signaling systems. More specifically, Xu et al. (2003) proposed that the competition between the protrusive actin network and the contractile actomyosin network, assisted by feedback between these networks and frontness and backness signaling circuits, stably segregate and maintain the protrusive cell front and the contractile rear. Experimental studies have shown that Rac/Rho knockout neutrophil cells have severely impacted chemotaxis (Roberts et al., 1999; Glogauer et al., 2003; Sun et al., 2004), and similarly when actin dynamics is arrested (Dandekar et al., 2013). In fact, Xu et al. found that when Rho is overexpressed, neutrophils fail to polarize, and when Rho is inhibited, protrusions are observed everywhere along the cell periphery. Similarly, in our model, we demonstrate that blocking either the backness or the frontness pathway gives similar results (Figure 7, a and b). More recent experimental findings also support the coupled action of actin networks and Rho GTPase pathway in spontaneous neutrophil polarization (Dandekar et al., 2013; Graziano et al., 2018). Previous theoretical studies (Narang, 2005; Onsum and Rao, 2007) proposed models for the frontness/backness competition that were either too abstract (Narang, 2005), or loaded with too many unverified details (Onsum and Rao, 2007), and not including the actin dynamics explicitly. In the case of neutrophils, three out of the four directions in our coupling model between actin and Rac/Rho dynamics have been reported previously. The study in Xu et al. (2003) posits an indirect positive feedback from branched actin to Rac. The positive feedback from Rac to actin polymerization is also well established (Wang et al., 2002; Weiner et al., 2002; Srinivasan et al., 2003; Hoeller and Kay, 2007; Inoue and Meyer, 2008). Less is known about the interaction between Rho activation and actomyosin bundle formation, although a mechanosensitive factor in Rho activation has been implicated previously (Wang et al., 2017; Boyle et al., 2018). Similarly, polarization of fibroblasts, macrophages, and astrocytes is certainly a mechanochemical, not a purely chemical process, with cytoskeletal dynamics intimately intertwined with the Rho GTPase signaling pathway in the symmetry breaking process before migration (reviewed in Etienne-Manneville, 2006).

FIGURE 7:

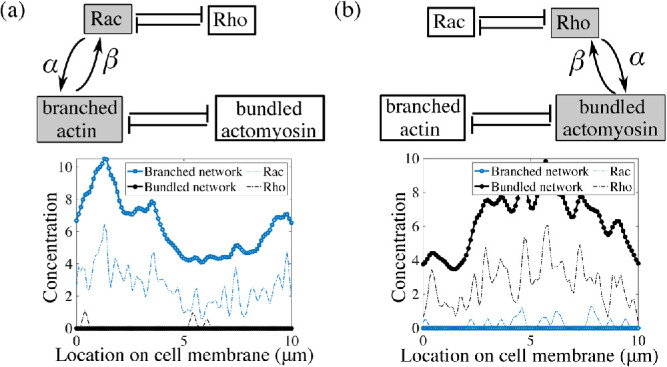
If either frontness or backness pathways are inhibited, then cell polarity cannot be established. (a) When Rho/actomyosin is inhibited (α, β = 0 for Rho and bundled actomyosin), protrusions are all around the periphery, while (b) if Rac/branching actin is inhibited (α, β = 0 for Rac and branched actin), cells fail to form protrusive areas. Only the coupling rates, α and β, were changed in the simulations; all other parameters were kept fixed to their baseline values provided in Supplemental Table S1.

We do not claim that our model can predict the biological details of polarity for these cell types. In general, polarization involves not only actin, but also microtubules, as well as more complex cytoskeletal networks, such as stress fibers, multiple pseudopods, and adhesion complexes. Signaling circuits other than Rho could also be implicated in cell polarization. The model does not include many molecular players—PIP, PI3K, PTEN, G-proteins, actin regulators—but simply conceptually captures their lumped effect on the cross-talk between Rac/Rho and actin/actomyosin. Thus, our model posits one of the simplest quantitative frameworks for understanding a possible mechanism for spontaneous mechanochemical cell polarization.

It is possible for our model to rely on other forms of feedback between the biochemical and mechanical circuits. For example, negative, instead of positive, feedback between Rac and branched actin and Rho and actomyosin, respectively, could do the job (Wong et al, 2006; Xu et al., 2003). We also limited the dynamics of the model to the local chemical and mechanical processes, but global mechanical effects, for example, membrane tension, could play an important role in polarization of some cell types (Houk et al., 2012). Another paradigm for mechanochemical polarization requires transport of chemicals in the signaling framework. The key to such models is that myosin-driven flow assists the polarization of signaling proteins by mechanically triggering the formation of a stable asymmetric chemical distribution (Goehring et al., 2011; Maiuri et al., 2015; Tostevin and Howard, 2008). Our model is simpler because it does not have directional movement—either in the form of a flow, as in these models, or in the form of whole cell movement as in Lomakin et al. (2015). More detailed and complex models have included the cell-surface adhesion dynamics as a mechanical component in the biochemical polarization pathway (Park et al., 2017). Finally, one of the models of gradient sensing (Gamba et al., 2007) is based on an idea similar to that of our model: when signaling dynamics is such that clusters of polarity molecules appear on the cell membrane, the clusters’ location can be biased to one side of the cell by an external signal. Our model adds a novel and simple potential polarization mechanism to these theoretical paradigms.

Abbreviations used:

GDP

guanosine diphosphate

GTP

guanosine triphosphate.