Abstract
Cells precisely control their mechanical properties to organize and differentiate into tissues. The architecture and connectivity of cytoskeletal filaments change in response to mechanical and biochemical cues, allowing the cell to rapidly tune its mechanics from highly cross-linked, elastic networks to weakly cross-linked viscous networks. While the role of actin cross-linking in controlling actin network mechanics is well-characterized in purified actin networks, its mechanical role in the cytoplasm of living cells remains unknown. Here, we probe the frequency-dependent intracellular viscoelastic properties of living cells using multifrequency excitation and in situ optical trap calibration. At long timescales in the intracellular environment, we observe that the cytoskeleton becomes fluid-like. The mechanics are well-captured by a model in which actin filaments are dynamically connected by a single dominant cross-linker. A disease-causing point mutation (K255E) of the actin cross-linker α-actinin 4 (ACTN4) causes its binding kinetics to be insensitive to tension. Under normal conditions, the viscoelastic properties of wild-type (WT) and K255E+/– cells are similar. However, when tension is reduced through myosin II inhibition, WT cells relax 3× faster to the fluid-like regime while K255E+/– cells are not affected. These results indicate that dynamic actin cross-linking enables the cytoplasm to flow at long timescales.
INTRODUCTION
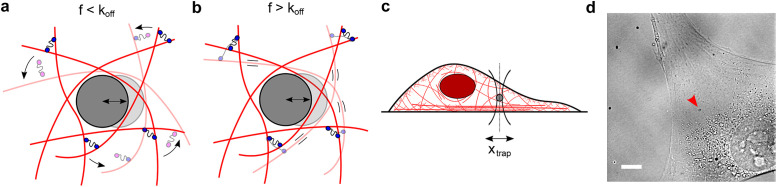
The actin cytoskeleton is a network of filaments cross-linked by actin-binding proteins. The cytoskeleton provides mechanical support and drives cell motility and morphological changes (Fletcher and Mullins, 2010). Cross-linking proteins undergo continuous cycles of binding and unbinding, enabling the cell to act as an elastic solid at short timescales and as a viscous fluid at long timescales (Kole et al., 2005; Fischer-Friedrich et al., 2016). To characterize the mechanics of the active, viscoelastic cellular environment, we developed methods to probe cytoplasmic mechanics in living cells over timescales ranging from 0.02 to 500 Hz using an optical trap (OT). Active microrheology as applied here is insensitive to nonequilibrium active cellular processes like motor protein–based transport and cytoskeletal dynamics because only the response that is coherent with the applied displacement is analyzed (Hoffman et al., 2006; Guo et al., 2014). OTs can apply a local deformation directly in the cytoplasm of living cells, while other commonly used active methods such as atomic force microscopy (AFM) and magnetic twisting cytometry apply a local deformation at the cell surface. The viscoelastic response is described by the frequency-dependent complex shear modulus G*(f) = G’(f) + G’’(f), where the real part G’(f) and the imaginary part G’’(f) correspond to the elastic (storage) and viscous (loss) modulus, respectively. While the magnitudes of G’(f) and G’’(f) reported in the literature vary greatly between different measurements, their frequency dependence is well conserved across different cell types and experimental conditions (Hoffman et al., 2006). G’(f) and G’’(f) increase with frequency following a weak power law G*(f) ∼ fα with α = 0.05–0.35 from ∼1 to ∼100 Hz (Fabry et al., 2001, 2003; Alcaraz et al., 2003; Balland et al., 2004; Puig-de-Morales et al., 2004; Stamenović et al., 2004; Deng et al., 2006; Hoffman et al., 2006; Wei et al., 2008; Zhou et al., 2009; Guo et al., 2013, 2014; Gupta and Guo, 2017; Gupta et al., 2019; Rigato et al., 2017) and a stronger power law G*(f) ∼ fβ with β = 0.5–1.0 for frequencies above ∼100 Hz (Deng et al., 2006; Hoffman et al., 2006; Mas et al., 2013; Rigato et al., 2017; Ahmed et al., 2018). The weak power law has been attributed phenomenologically to the soft glassy material (SGM) theory (Fabry et al., 2001; Bursac et al., 2005; Deng et al., 2006) while the strong power law has been explained by entropic filament-bending fluctuations (Gittes et al., 1997; Gardel et al., 2004; Deng et al., 2006). However, at timescales longer than 1 s (i.e., at frequencies below ∼1 Hz) corresponding to cell division and motility and morphological changes, active microrheological data are scarce especially in the cytoplasm of living cells. Microrheology using thermally driven particles is prone to errors at these timescales from the contribution of active processes in the cell (Hoffman et al., 2006; Guo et al., 2014). In purified actin networks, transient cross-linking by actin-binding proteins governs the viscoelastic properties at long timescales (Wachsstock et al., 1994; Tharmann et al., 2007; Lieleg et al., 2008, 2009, 2011; Ward et al., 2008; Broedersz et al., 2010; Yao et al., 2011). When these networks are deformed at frequencies slower than the cross-linker’s unbinding rate (koff), the cross-linkers have enough time to unbind, allowing the filaments to freely slide past one another, resulting in a more fluid-like, viscous network (Figure 1a). At deformation frequencies faster than koff, the actin filaments remain highly interconnected, resulting in filament bending and a more solid-like, elastic network (Figure 1b). We hypothesize that this role of dynamic actin cross-linking may allow the actin cytoskeleton to become fluid-like during movement and morphological changes, while also maintaining structural integrity. While active microrheological studies on the cell surface have reported weak power law scaling of mechanics at timescales down to ∼0.1 Hz (Fabry et al., 2001, 2003; Alcaraz et al., 2003; Balland et al., 2004; Puig-de-Morales et al., 2004; Stamenovic´ et al., 2004, 2007; Deng et al., 2006; Zhou et al., 2009), the distinct mechanical properties in the interior of the cell (Hoffman et al., 2006) at these long timescales remain largely unexplored. OTs are well-suited to measure these mechanical properties, and while several studies have reported intracellular viscoelasticity (Wei et al., 2008; Guo et al., 2013, 2014; Mas et al., 2013; Bergeron-Sandoval et al., 2017; Gupta and Guo, 2017; Gupta et al., 2019; Ahmed et al., 2018), the mechanics at ∼0.01–1 Hz have not been quantified in detail. Experimental measurements of slow dynamics are challenging due to the long observations required, and while in situ OT calibration provides more accurate measurements (Fischer and Berg-Sorensen, 2007; Hendricks et al., 2012; Blehm et al., 2013), it has often been neglected.
FIGURE 1:
The cytoplasm is a crowded viscoelastic matrix of cross-linked polymers and proteins. (a) Schematic of the actin network being deformed by a microbead at frequencies (f) slower than the unbinding rate of the cross-linkers (koff), before (opaque) and after deformation (transparent). Previously bound cross-linkers (blue heads) detach (magenta heads), and the filaments are free to slide past one another and rearrange (curved arrows), resulting in a more viscous, fluid-like network. (b) At frequencies faster than koff, the cross-linkers stay bound and interlock the filaments, resulting in filament bending and a more solid-like, elastic response. (c) Schematic of the experimental setup showing the active oscillation of bead in the intracellular environment by the OT (xtrap). Not to scale. (d) Representative brightfield image of a live cell showing the optically trapped bead (arrow). Scale bar is 10 µm.
RESULTS AND DISCUSSION
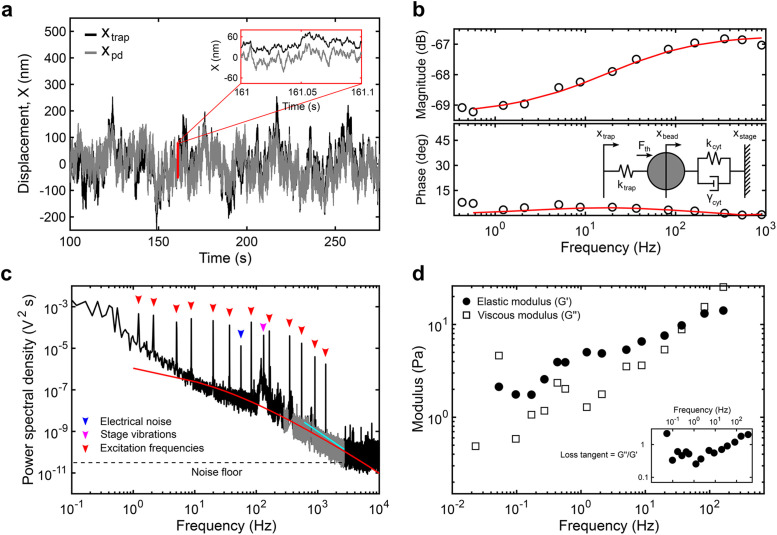
To perform simultaneous measurements over a wide frequency range, we optically trap a 500-nm polyethylene glycol (PEG)-coated bead located in the cytoplasm (Figure 1, c and d; Materials and Methods) and apply a multifrequency excitation input to the trap position using an acousto-optic deflector (AOD). Because there are significant elastic contributions from the cytoplasm and nonequilibrium active processes, the trap stiffness, ktrap, and the photodiode constant, βpd, cannot be calibrated using traditional methods relying on thermal fluctuations. Here, we fitted a simple viscoelastic model to the measured response to calibrate the optical trap in situ (Hendricks et al., 2012). The frequency response function (FRF) is obtained from the time domain signal of the photodetector and the trap position (Figure 2, a and b). The magnitude and phase of the FRF, as well as the power spectrum, are simultaneously fitted to the model to estimate ktrap and βpd. The magnitude response at frequencies above ∼1 Hz is well-captured by this simple viscoelastic model, with a first inflection point at ∼4 Hz representing the stiffness of the cytoplasm and a second inflection point at ∼200 Hz representing the combined stiffnesses of the cytoplasm and the OT (Figure 2b; Supplemental Information). The resulting ktrap and βpd vary between cells and between experiments due to variable optical properties (Supplemental Figure S2), reinforcing the necessity for in situ calibration. Despite variability among cells, the product of ktrap and βpd falls within the same constant range, as reported previously (Farre et al., 2012) (Supplemental Figure S2). The viscoelastic response measured in entangled purified actin networks (Supplemental Figure S3) using this method agrees well with the literature (Gittes et al., 1997; Mizuno et al., 2008; Broedersz et al., 2010; Atakhorrami et al., 2014; Gurmessa et al., 2019), and the response measured in a 20% PEG water solution agrees well with data obtained from a rheometer (Supplemental Figure S4). Once calibrated, ktrap and βpd are used, along with the FRF, to obtain the complex shear modulus G*(f) (Mizuno et al., 2008). Combined with multifrequency excitation, this calibration method allows ktrap, βpd, and G*(f) to be obtained in a single continuous measurement, thereby minimizing sources of error (see the Supplemental Information). This approach has advantages over other methods used to calibrate the OT in active, viscoelastic media. Methods based on light momentum changes rely on capturing most of the diffracted and scattered light (Farre et al., 2012). However, organelles and other structures result in substantial refraction. An alternative method uses the active response to sinusoidal inputs combined with the passive response for in situ calibration in viscoelastic medium (Fischer and Berg-Sorensen, 2007; Fischer et al., 2010; Hendricks et al., 2012; Blehm et al., 2013, 2016; Mas et al., 2013; Bergeron-Sandoval et al., 2017; Staunton et al., 2017; Ahmed et al., 2018). ktrap can be obtained from the average ktrap values at each input frequency based on the ratio of the real part of the active spectrum to the passive thermal spectrum at the same frequency (Fisher and Berg-Sorensen, 2007; Fischer et al., 2010; Blehm et al., 2013, 2016; Mas et al., 2013; Staunton et al., 2017; Ahmed et al., 2018). βpd can be calibrated separately using an active oscillation of the stage or the laser combined with the position readings from the camera or photodiode. However, both ktrap and βpd are sensitive to sources of error as they are derived from a single frequency point.
FIGURE 2:
Analytical methods to obtain the viscoelastic properties of the cytoplasm from optical trapping data. (a) Sample trace of the trap position (xtrap, black) and photodiode position (xpd, gray) in the time domain. Note that the photodiode signal is acquired in volts and converted to nanometers after in situ calibration. (b) The magnitude and phase of the response of the photodiode output signal to movements of the trap at each input frequency is captured by the transfer function. The transfer function above 1 Hz is fitted (red) to the active part of a simple viscoelastic model (inset) to obtain the trap stiffness ktrap (pN/nm) and photodiode constant βpd (nm/V). The mechanical circuit (inset) depicts the forces experienced by the bead from the OT and the viscoelastic environment. (c) The power spectrum of the output between 250 and 2500 Hz (gray) resulting from thermal fluctuations is simultaneously fitted (red) to the passive part of the model. Below 250 Hz, nonequilibrium active cellular processes, electrical noise (blue arrowhead), and stage vibrations (magenta arrowhead) contribute to the response while above ∼2500 Hz, the noise floor (dashed line) is reached. The active response from the multifrequency excitation (red arrowheads) is visible. A slope smaller than 2 (cyan) indicates constrained diffusion. (d) The elastic (G’, solid circles) and viscous (G’’, open squares) moduli are obtained for each experiment (see the Supplemental Information).
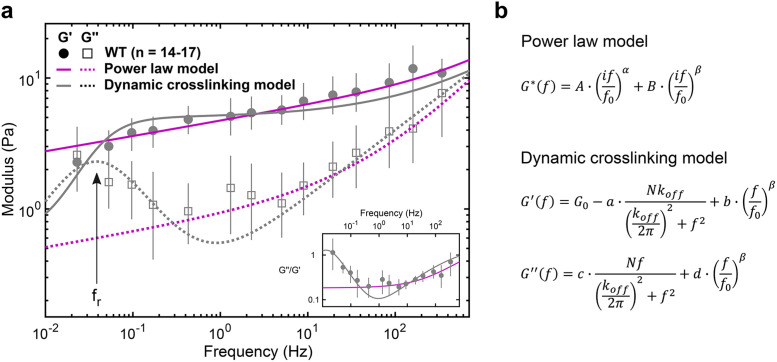
Using multifrequency excitation and in situ calibration, we characterize the viscoelastic properties of the cytoplasm of living cells at frequencies ranging from 0.02 to 500 Hz. In wild-type (WT) fibroblasts, the measured moduli can be described by a double power law (Figure 3a, magenta), yielding a weak power law (α = 0.116 ± 0.021) at frequencies between ∼1 and ∼20 Hz and a stronger power law above ∼20 Hz (β = 0.717 ± 0.062), in excellent agreement with previous observations (Deng et al., 2006; Mas et al., 2013; Guo et al., 2014; Gupta and Guo, 2017). However, at frequencies below ∼1 Hz, we observe a pronounced transition to a fluid-like response, apparent in the loss tangent (G’’/G’), which reaches a minimum at ∼1 Hz and increases steadily with decreasing frequencies. This transition to a more fluid-like regime occurs at timescales relevant to slower processes such as cell migration (Kole et al., 2005; Lautenschlager et al., 2009) and cell division (Murthy and Wadsworth, 2005; Fischer-Friedrich et al., 2016) but is not well captured by the power law model (Figure 3a, inset). A transition to fluid-like behavior has been observed in mixtures of actin filaments and actin cross-linkers in vitro, where the timescale is determined by the cross-linker unbinding kinetics (Tharmann et al., 2007; Lieleg et al., 2008, 2009, 2011; Broedersz et al., 2010). The observation of a similar fluid-like transition in cells is surprising as many cross-linking proteins with different binding kinetics likely contribute to the viscoelastic response. Several possible mechanisms might explain the single dominant timescale for relaxation: 1) the slowest cross-linker dominates the mechanical response, 2) α-actinin 4 is the dominant cross-linker in the interior of the cells examined here, or 3) many cross-linking proteins have similar binding kinetics.
FIGURE 3:
The viscoelastic properties of the cytoplasm show relaxation dynamics at lower frequencies. (a) Elastic (G’) and viscous (G’’) moduli of WT fibroblasts (mean and 95% confidence interval from 1000 bootstrap samples; see Materials and Methods). The fluid-like transition (i.e., relaxation) is visible at frequencies below ∼1 Hz: reading from right to left, there is a local G’’ minimum followed by a local G’’ maximum along with a drop in G’, also evident in the loss tangent (inset), with a minimum at ∼1 Hz and a steady rise with decreasing frequency. The dynamic cross-linking model (gray) captures the dynamics at lower frequencies better than the power law model (magenta; see Supplemental Figure S5), with the local G’’ maximum corresponding to the relaxation frequency, fr = koff/2π (arrow). (b) Analytical expressions of the models. From the power law model fit, α = 0.116 ± 0.021 (mean and SD of the means) and β = 0.717 ± 0.062. From the dynamic cross-linking model fit, koff = 0.24 Hz (see Figure 4b, gray) and β = 0.509 ± 0.0
The first term of the double power law model describes a SGM at longer timescales, and the second term describes frequency scaling from entropic filament fluctuations at shorter timescales (Deng et al., 2006) (Figure 3b, top). The rheology of a SGM has been empirically observed as elastically dominant and weakly scaling with frequency with a constant loss tangent of ∼0.1 (Sollich et al., 1997). In contrast, our data indicate that the loss tangent of the cytoplasm varies at frequencies below ∼1 Hz and reaches 1.0, indicating an equal viscous and elastic contribution at low frequencies (Figure 3a, inset). A study using magnetic twisting cytometry of beads attached to the cell cortex also observed a deviation from the SGM model at these low frequencies (Stamenović et al., 2007), suggesting that despite the differences in mechanical properties between the cell cortex and intracellular environment, a different rheological model must be considered at these long timescales. A model that assumes that mechanics are governed by the unbinding kinetics of a dominant cross-linker (Lieleg et al., 2008) captures the data well (Figure 3a, gray). The first term of the dynamic cross-linking model is derived from the Fourier transform of the exponentially decaying lifetime of cross-linked points. The first term decreases the plateau elastic modulus G0 and increases the amount of viscous dissipation in isotropically cross-linked actin networks (Lieleg et al., 2008). The second term describes filament-bending fluctuations at shorter timescales as before. The dominant cross-linker’s characteristic timescale, koff, appears as a local maximum in the viscous modulus (Figure 3a) at the frequency of relaxation (fr = koff/2π). Fitting this model to the measured moduli yields an estimate of koff = 0.24/s (Figure 4b) for WT fibroblasts. This estimate is in agreement with unbinding rates measured for several passive actin cross-linkers including α-actinin, filamen, and fascin (Goldmann and Isenberg, 1993; Aratyn et al., 2007). The dynamic cross-linking model was derived from bulk rheology of actin polymer gels where the unbinding of cross-linkers was related to bulk properties through the assumption that G0 ∼ Nx with x = 1 (where N is the number of cross-linked points) in a homogeneous and isotropically cross-linked network (Lieleg et al., 2008). However, the cytoplasm is likely a composite network with the coexistence of bundled, branched, and isotropically cross-linked actin filaments, despite our efforts to probe the most homogeneous region of the cytoplasm (Figure 1, c and d). Additionally, cell orientation and deformation axis also result in anisotropic mechanical properties (Gupta et al., 2019). The same model with G0 ∼ Nx and x not equal to 1 may account for some of this anisotropy. In addition, in bulk rheology, the shear stresses are assumed to be evenly distributed at the microscale. Thus, the resulting mechanical response is a summation of the contributions of individual cross-linkers across the sample. However, in microrheology, an increased viscous dissipation from the depletion of cross-linked points in the vicinity of the probe is expected, causing a cross-over of elastic and viscous moduli at lower frequencies (Lieleg et al., 2008). Thus, it may be possible to further improve the fit to the model by including a stronger frequency-dependent loss of cross-linking points.
FIGURE 4:
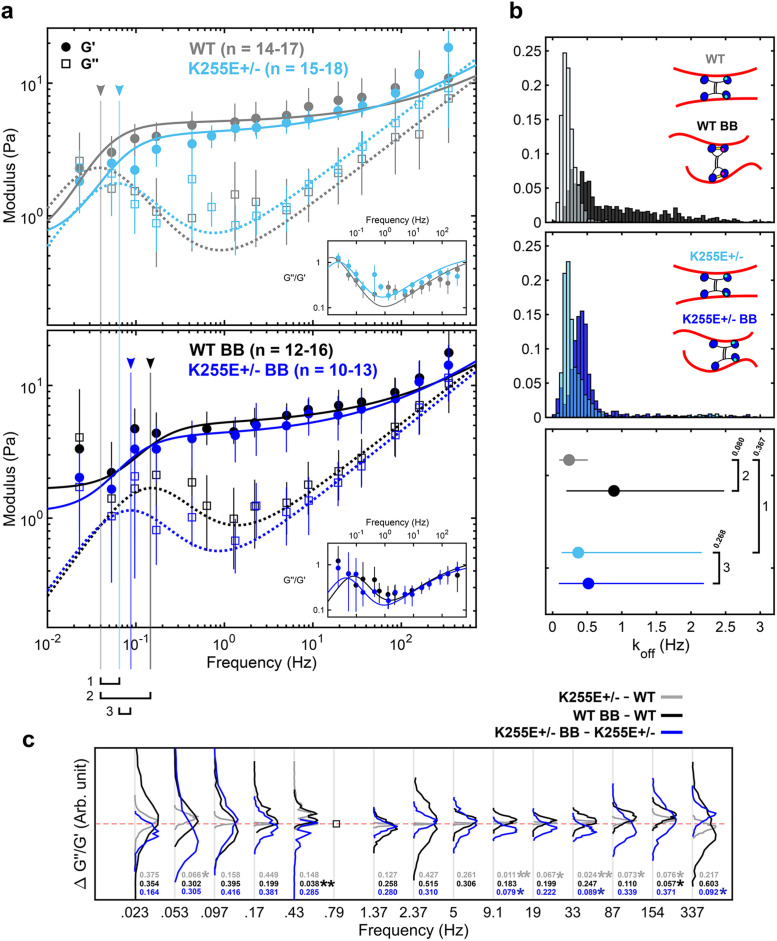
Relaxation dynamics after alteration of α-actinin 4 binding kinetics and myosin II disruption. (a) Elastic (G’) and viscous (G’’) moduli of WT cells and ACTN4 K255E+/– mutant cells under control (top) and 50 µM BB-treated (bottom) conditions (mean and 95% confidence intervals from 1000 bootstrap samples), along with the best fit to the dynamic cross-linking model. Untreated WT cells (gray) and K255E+/– cells (light blue) show similar dynamics, with little shift (1) in fr (arrowhead and vertical line). The fr shift to the right from WT to WT BB (black) is very apparent (2), indicating faster relaxation. The fr shift from K255E+/– to K255E+/– BB (blue) is less apparent (3). (b) Unbinding rate (koff) distributions (top and middle) and mean with 95% confidence interval (bottom) obtained from the bootstrap fits. The untreated WT and BB-treated WT cells show different koff distributions (p = 0.08). ACTN4 has two principal actin-binding sites (inset schematic, blue heads) and a third putative actin-binding site (cyan) that is exposed upon tension. Under reduced tension, the WT ACTN4 is in its closed conformation due to the presence of a cross-bridge (yellow). The untreated K255E+/– and BB-treated K255E+/– cells show similar koff distributions (p = 0.268). The untreated WT and K255E cells also show similar koff distributions (p = 0.367). koff WT = 0.24 Hz, koff WT BB = 0.89 Hz, koff K255E = 0.37 Hz, and koff K255E BB = 0.52 Hz (mean and 95% confidence interval) are obtained (bottom). The difference between these unbinding rates are proportional to the differences in fr numbered in panel a. (c) The difference between loss tangents (∆G’’/G’) indicates that the mechanics of WT cells are tension sensitive while the K255E mutation reduces sensitivity to tension. The empty square at 0.79 Hz indicates a frequency point that is present for only one of the two conditions, resulting in no quantifiable difference. Distributions shifted above zero (red dashed line) indicate an increase in the loss tangent, i.e., an increase in fluid-like mechanics (p values indicated above). Distributions shifted below zero indicate a decrease in the loss tangent (p value indicated below). ∆G’’/G’ between untreated K255E+/– and untreated WT cells (gray) show narrow distributions about zero. ∆G’’/G’ between BB-treated WT and untreated WT cells (black) show a general upward shift, indicating that the BB-treated WT cells are more viscous compared with untreated WT cells. ∆G’’/G’ between BB-treated K255E+/– and untreated K255E+/– cells (blue) show a slight but consistent downward shift, indicating that the BB-treated cells are slightly less viscous compared with untreated K255E cells. At 0.43 Hz, the black curve is shifted upward while the blue remains slightly below zero. This indicates an earlier transition to the fluid-like regime when WT cells are treated with BB compared with when K255E+/– cells are treated with BB. This upward shift is consistent below 1 Hz, except at 0.097 Hz, indicating an overall increased fluid-like behavior at long timescales upon BB treatment in WT cells compared with K255E+/– cells.
Together, our data along with the fit to the model suggest that dynamic cross-linking of the cytoskeleton results in a fluid-like transition of the cytoplasm. By modulating the cross-linking dynamics of key cross-linkers, the cell could tune its viscoelastic properties in response to biochemical or mechanical cues. Correspondingly, dysregulation of cytoskeletal cross-linking may contribute to disease (Ehrlicher et al., 2015). To investigate the role of actin cross-linker binding kinetics in governing cytoplasmic mechanics, we probe the viscoelastic properties of cells heterozygous for an ACTN4 mutation. ACTN4 is a ubiquitous cross-linker that dynamically cross-links actin filaments with koff ∼ 0.4 Hz (Goldmann and Isenberg, 1993) and is involved in the formation of actin bundles (Weins et al., 2007). The K255E mutation has been associated with focal segmental glomerulosclerosis (FSGS) (Kaplan et al., 2000). In FSGS, podocytes are less able to resist cyclic loading, suggesting a dysregulation of the mechanical properties of the cytoskeleton (Feng et al., 2018). Indeed, this mutation alone reduces cell motility while increasing cellular forces in heterozygous cell lines through an interplay with tension-generating myosin II motors (Ehrlicher et al., 2015). Increased contractility is believed to be due to the exposure of a cryptic actin-binding site in the K255E mutant, resulting in its increased affinity for actin (i.e., slower koff) (Weins et al., 2007). In WT ACTN4, the cryptic actin-binding site is thought to be exposed only when the cross-linker is under tension, resulting in a catch-bond behavior (Yao et al., 2011) (Figure 4b, top inset). The difference in the unbinding rates of the WT ACTN4 and the K255E mutant results in a shift of fr in purified networks (Ward et al., 2008; Broedersz et al., 2010; Yao et al., 2011). In contrast, our results show no significant difference in the mechanical properties of WT and K255E+/– cells under normal conditions (Figure 4a), possibly due to lower expression of K255E mutant and other mechanical anisotropies in the region probed. Overall, with koff WT = 0.24 Hz and koff K255E = 0.37 Hz (Figure 4b) from the average best fit, our results suggest similar cross-linking dynamics in the WT and K255E+/– cells under normal conditions (Figure 4b, top and bottom insets).
To investigate the role of tension on ACTN4-binding kinetics, we treat the cells with 50 µM blebbistatin (BB). BB reversibly locks myosin II in the low-affinity ADP-Pi state, reducing tension in the actin cytoskeleton (Kovacs et al., 2004). With 50 µM BB, a sufficient number of cells (Supplemental Figure S7) do not exhibit gross morphological changes and remain viable for mechanical measurements. Surprisingly, we do not observe significant softening of the cytoplasm (Figure 4b) as reported previously (Guo et al., 2014). This may be due to differences in BB treatment response levels inducing more local heterogeneity, as depicted by the greater variability in the data (Figure 4a, bottom) and the wider distribution of koff (Figure 4b, top), or differences in the in situ calibrated trap and βpd values (Supplemental Figure S2). It is also likely that the local cytoplasmic microenvironment is less sensitive to actomyosin activity, and thus BB treatment, compared with on the cortex where a much more dramatic effect on magnitude is expected (Balland et al., 2004; Van Citters et al., 2006). While the mechanics at fast timescales are not affected, at long timescales we observe an approximately threefold faster transition to fluid-like behavior in BB-treated WT cells, with koff increasing from 0.24 to 0.89 Hz in the presence of BB (Figure 4a, bottom). Interestingly, koff in K255E+/– cells remained similar, with koff K255E = 0.37 Hz and koff K255E BB = 0.52 Hz. The results suggest that with reduced tension (through myosin II inhibition), actin-binding kinetics differ in a manner that is consistent with the differences between the binding kinetics of WT and K255E ACTN4 (Figure 4b, top and bottom insets). While tension levels vary between cells and within a single cell (Grashoff et al., 2010), it is expected that, on average, the tension levels are reduced with BB treatment. The active cross-linker myosin II may also directly play a role in regulating the observed mechanics as shown previously in purified networks (Humphrey et al., 2002; Koenderink et al., 2009) at intermediate and long timescales. The effect of cross-linking dynamics on relaxation is also readily apparent in the differences in loss tangent (Figure 4c). Latrunculin A (Lat A) depolymerizes actin filaments by sequestering free actin monomers (Yarmola et al., 2000). Interestingly, treating WT cells with Lat A shifts the relaxation to faster timescales (Supplemental Figure S6), suggesting that actin filament disruption plays a similar role in relaxation as the inhibition of intracellular tension (Rigato et al., 2017). In Lat A–treated cells, the presence of fewer, shorter actin filaments is expected to reduce the ability of ACTN4 and myosin II to interact with and cross-link actin filaments, reducing the tension generated and stored in the network (Koenderink et al., 2009). This reduced number of cross-linked points does not alter the frequency of relaxation in purified networks (Lieleg et al., 2008, 2009; Ward et al., 2008), suggesting that the shift in relaxation that we observe in Lat A–treated WT cells results from changes in binding kinetics, similar to what is observed with BB treatment. In both BB- and Lat A–treated cells (Figure 4 and Supplemental Figure S6), the loss tangent indicates that the network is more fluid-like at lower frequencies, consistent with previous observations using AFM (Rigato et al., 2017). However, similar to BB treatment, and in contrast to previous studies (Zhou et al., 2009; Rigato et al., 2017), we observe negligible differences in the magnitudes of G* with Lat A treatment (Van Citters et al., 2006). Intermediate filaments, another component of the cytoskeletal network, contribute approximatively half of the mechanical resistance in the intracellular environment (Guo et al., 2013) and thus help maintain mechanical integrity even when the actin cytoskeleton is disrupted. Furthermore, cells that show severe signs of actin cytoskeleton disruption are not viable for mechanical measurements. Consequently, healthier cells (Supplemental Figure S7) were chosen preferentially to yield more consistent and quantifiable results, which may partly explain the similar magnitudes observed under BB and Lat A treatment. Overall, our results show a shift in relaxation to faster timescales when myosin II is inhibited, particularly in the case of WT cells, suggesting an earlier transition to the fluid-like regime consistent with the tension-dependent differences in binding kinetics between WT and K255E ACTN4.
While perturbations to the cross-linked actin network modulate the transition to fluid-like behavior, the mechanics at timescales >1 Hz are largely unaffected. Intermediate filaments (Guo et al., 2013) and microtubules (Brangwynne et al., 2006; Robison et al., 2016) also contribute to the mechanical response of the cytoplasm, particular in the cell interior (Hoffman et al., 2006; Van Citters et al., 2006). Further studies are needed to dissect the relative roles of actin, microtubules, and intermediate filaments in governing cell mechanics.
Mechanical properties play an important role in the regulation of many cellular functions and allow the cell to be solid enough to provide structural support but also fluid enough to reorganize and perform dynamic functions. By developing a novel method to measure intracellular mechanics, our measurements reveal relaxation of the cytoskeleton at long timescales across all conditions, pointing to a fundamental mechanical property of the cytoplasm. In addition, a model that includes the binding kinetics of a dominant actin cross-linker captures these relaxation dynamics well. However, while our data suggest a relationship between mechanical relaxation and the cross-linking dynamics of ACTN4, many other cross-linkers and motor proteins contribute, and it is unlikely that ACTN4 alone governs the viscoelasticity at these timescales. Other cytoskeletal components with their associated proteins may also contribute to cytoplasmic relaxation through mechanisms that are yet to be identified. Overall, we performed calibrated mechanical measurements in the cytoplasm of living cells using optical tweezers and related the relaxation dynamics observed to the binding kinetics of ACTN4. Future work focusing on other cross-linkers and other components of the cytoskeleton, as well as on simplified in vitro systems, will add to the results reported here and provide a more complete understanding of the mechanisms governing the fluid-like transition of the cytoplasm.
MATERIALS AND METHODS
Cell culture and preparation
Two immortalized dermal fibroblast cell lines are used (Ehrlicher et al., 2015). Cells are cultured in DMEM (Thermo Fisher Scientific), supplemented with 10% fetal bovine serum (Thermo Fisher Scientific) and 1% Glutamax (Thermo Fisher Scientific). Cells are passaged at 80% confluency and seeded on glass coverslips 24 h before the experiment at low enough confluency to minimize cell–cell contacts. Fluorescent latex beads (500 nm diameter) (Thermo Fisher Scientific) are PEG-coated following previously published protocols (Valentine et al., 2004). Prior to the experiment, the beads are washed and resuspended in hypertonic media (∼109 beads/ml in 10% PEG 35000, 0.25 M sucrose in complete DMEM). The cells are incubated for 1 h with the hypertonic media to allow the beads to be phagocytosed. A gentle osmotic shock is administered to the cells to burst endogenous membranes formed around the internalized beads, minimizing further interactions of the bead with proteins of the endocytic pathway (Nelson, 2009; Pierobon et al., 2009; Bergeron-Sandoval et al., 2017). This shock is applied by incubating the cells with a hypotonic solution for 3 min. The cells are then left in the incubator in regular complete media for 1 h to recover from the shock. Tracking the difference in mechanics over time of cells hypotonically shocked at the same time shows no significant changes (Supplemental Figure S8), suggesting that the 1-h recovery period is enough. The coverslips are mounted on microscope slides using double-sided tape to form a flow chamber. In some experiments, media is replaced with complete media supplemented with 50 µM BB or 100 nM Lat A. Measurements start 15 min after treatment, and cells are kept at 37°C using a heater (World Precision Instruments) in a custom-built environmental chamber during all optical trapping experiments.
Optical trap
The OT is installed on an inverted microscope (Eclipse Ti-E: Nikon; 1.49 NA oil-immersion 100×-objective). The near-IR 1064-nm laser beam (10 W; IPG Photonics) is expanded to overfill the back aperture of the objective. The bead position relative to the laser center is measured using a lateral effect photodiode (Thorlabs) positioned conjugate to the objective’s back focal plane. The laser is steered using two-axis AODs (AA Optoelectronic) controlled through a field-programmable gate array and custom LabVIEW programs (National Instruments). A multifrequency (∼18 frequencies) excitation input wave is applied to a single intracellularly located bead per cell. The frequencies range from 0.02 to 1300 Hz (moduli obtained from 0.02 to 500 Hz), with corresponding amplitudes ranging from ∼50 to ∼1 nm. The frequencies of oscillation are selected to avoid harmonics. The amplitudes are empirically chosen to yield a linear response from the cytoplasm. No significant harmonic generation was observed from the amplitudes applied, indicating that the measurements were performed in the linear regime (Wilhelm et al., 2011). Measurement are performed on beads located in the most mechanically homogeneous region of the cell, midway between the cell periphery and perinuclear region where distinct actin cytoskeleton organization exists.
Optical trap data analysis
Data are acquired at 200 kHz downsampled to 20 kHz or directly acquired at 20 kHz (Supplemental Figure S1). ktrap and βpd are obtained for each individual measurement as previously described (Hendricks et al., 2012). In brief, the FRF (Supplemental Figure S9) is obtained from the cross-spectral density of the bead displacement and AOD using Welch’s method in MATLAB. The window length is chosen at each individual frequency to be an integer multiple of the period of the input frequency to avoid leakage (Fischer and Berg-Sorensen, 2007). The integer multiple is chosen to obtain the best trade-off between frequency resolution and averaging. A simplified viscoelastic model is simultaneously fitted to the FRF and the power spectrum of the thermal response to obtain ktrap and βpd (Hendricks et al., 2012). The elastic and viscous moduli are directly obtained from the FRF knowing ktrap and βpd (Mizuno et al., 2008). See Figure 2 and the Supplemental Information for more details.
Statistics and fits
One thousand bootstrap samples (random samples of the measurements) are drawn from the data, and each bootstrap sample is fitted to either the dynamic cross-linking model or the power law model, providing distributions of fit parameters to be obtained for each condition. The power law model consists of two frequency terms raised to the power of α and β, respectively (see Figure 2b), added together and scaled with constants A, B, and f0. The real and imaginary parts yield the elastic and viscous modulus, respectively. The dynamic cross-linking model includes a koff-dependent term. G0 is the plateau elastic modulus, N is the number of cross-linked points, a, b, c, d, and f0 are scaling constants. The fits are done using the nonlinear least-squares MATLAB function. Owing to differences in excitation inputs applied across experiments, the number of experiments (n) used to compute the mean bootstrap moduli at each frequency varies slightly. To compare the two model fits, Bayesian information criteria (BIC) are used. Fitting bootstrap samples allows statistics to be directly obtained and also allows a more representative comparison of the fit parameters between conditions, as opposed to directly fitting the mean of the data. See the Supplemental Information for more details.
Supplementary Material
Acknowledgments
We thank Gary Tom and Giancarlo Szymborski for their work on the control software for the optical trap, Chris Sitaras for helpful discussions and assistance in PEG coating of the beads, and both Chris Sitaras and Ajinkya Ghagre for bulk rheology data. We also thank Malina K. Iwanski and Linda Balabanian for helpful discussions and valuable feedback on the manuscript. A.G.H. acknowledges support from the NSERC (RGPIN-2014-06380) and the Canadian Foundation for Innovation. A.J.E. acknowledges support from the Natural Sciences and Engineering Research Council of Canada (RGPIN/05843-2014, EQPEQ/472339-2015, RTI/00348-2018), the Canadian Institutes of Health Research (Grant #143327), and the Canadian Foundation for Innovation (Project #32749).
Abbreviations used:
- ACTN4
α-actinin 4
- AFM
atomic force microscopy
- FSGS
focal segmental glomerulosclerosis
- Lat A
latrunculin A
- OT
optical trap
- SGM
soft glassy material
- WT
wild-type.
Footnotes
This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E19-09-0504) on June 24, 2020.
REFERENCES
- Ahmed WW, Fodor E, Almonacid M, Bussonnier M, Verlhac MH, Gov N, Visco P, Wijland F, Betz T. (2018). Active mechanics reveal molecular-scale force kinetics in living oocytes. Biophys J , 1667–1679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alcaraz J, Buscemi L, Grabulosa M, Trepat X, Fabry B, Farré R, Navajas D. (2003). Microrheology of human lung epithelial cells measured by atomic force microscopy. Biophys J , 2071–2079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aratyn Y, Schaus T, Taylor E, Borisy G. (2007). Intrinsic dynamic behavior of fascin in filopodia. Mol Biol Cell , 3928–3940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atakhorrami M, Koenderink G, Palierne J, MacKintosh F, Schmidt C. (2014). Scale-dependent nonaffine elasticity of semiflexible polymer networks. Phys Rev Lett , 088101. [DOI] [PubMed] [Google Scholar]
- Balland M, Richert A, Gallet F. (2004). The dissipative contribution of myosin II in the cytoskeleton dynamics of myoblasts. Eur Biophys J , 255–261. [DOI] [PubMed] [Google Scholar]
- Bergeron-Sandoval LP, Heris HK, Chang C, Cornell CE, Keller SL, François P, Hendricks AG, Ehrlicher AJ, Pappu RV, Michnick SW. (2017). Endocytosis caused by liquid-liquid phase separation of proteins. bioRxiv. 10.1101/145664 [DOI]
- Blehm B, Devine A, Staunton J, Tanner K. (2016). In vivo tissue has non-linear rheological behavior distinct from 3D biomimetic hydrogels, as determined by AMOTIV microscopy. Biomaterials , 66–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blehm B, Schroer T, Trybus K, Chemla Y, Selvin P. (2013). In vivo optical trapping indicates kinesin’s stall force is reduced by dynein during intracellular transport. Proc Natl Acad Sci USA , 3381–3386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brangwynne C, MacKintosh F, Kumar S, Geisse N, Talbot J, Mahadevan L, Parker K, Ingber D, Weitz D. (2006). Microtubules can bear enhanced compressive loads in living cells because of lateral reinforcement. J Cell Biol , 733–741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Broedersz C, Depken M, Yao N, Pollak M, Weitz D, MacKintosh F. (2010). Cross-link-governed dynamics of biopolymer networks. Phys Rev Lett , 238101. [DOI] [PubMed] [Google Scholar]
- Bursac P, Lenormand G, Fabry B, Oliver M, Weitz D, Viasnoff V, Butler J, Fredberg J. (2005). Cytoskeletal remodelling and slow dynamics in the living cell. Nat Mater , 557–561. [DOI] [PubMed] [Google Scholar]
- Deng L, Trepat X, Butler J, Millet E, Morgan K, Weitz D, Fredberg J. (2006). Fast and slow dynamics of the cytoskeleton. Nat Mater , 636–640. [DOI] [PubMed] [Google Scholar]
- Ehrlicher A, Krishnan R, Guo M, Bidan C, Weitz D, Pollak M. (2015). Alpha-actinin binding kinetics modulate cellular dynamics and force generation. Proc Natl Acad Sci USA , 6619–6624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fabry B, Maksym G, Butler J, Glogauer M, Navajas D, Fredberg J. (2001). Scaling the microrheology of living cells. Phys Rev Lett , 148102. [DOI] [PubMed] [Google Scholar]
- Fabry B, Maksym G, Butler J, Glogauer M, Navajas D, Taback N, Millet E, Fredberg J. (2003). Time scale and other invariants of integrative mechanical behavior in living cells. Phys Rev E , 041914. [DOI] [PubMed] [Google Scholar]
- Farre A, Marsa F, Montes-Usategui M. (2012). Optimized back-focal-plane interferometry directly measures forces of optically trapped particles. Opt Express , 12270–12291. [DOI] [PubMed] [Google Scholar]
- Feng D, Notbohm J, Benjamin A, He S, Wang M, Ang LH, Bantawa M, Bouzid M, Del Gado E, Krishnan R, Pollak MR. (2018). Disease-causing mutation in alpha-actinin-4 promotes podocyte detachment through maladaptation to periodic stretch. Proc Natl Acad Sci USA , 1517–1522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischer M, Berg-Sorensen K. (2007). Calibration of trapping force and response function of optical tweezers in viscoelastic media. J Opt A: Pure Appl Opt , 239. [Google Scholar]
- Fischer M, Richardson AC, Reihani SN, Oddershede LB, Berg-Sorensen K. (2010). Active-passive calibration of optical tweezers in viscoelastic media. Rev Sci Instrum , 015103. [DOI] [PubMed] [Google Scholar]
- Fischer-Friedrich E, Toyoda Y, Cattin C, Müller D, Hyman A, Jülicher F. (2016). Rheology of the active cell cortex in mitosis. Biophys J , 589–600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fletcher DA, Mullins RD. (2010). Cell mechanics and the cytoskeleton. Nature , 485–492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardel ML, Shin JH, MacKintosh FC, Mahadevan L, Matsudaira P Weitz DA. (2004). Elastic behavior of cross-linked and bundled actin networks. Science , 1301–1305. [DOI] [PubMed] [Google Scholar]
- Gittes F, Schnurr B, Olmsted P, MacKintosh F, Schmidt C. (1997). Microscopic viscoelasticity: shear moduli of soft materials determined from thermal fluctuations. Phys Rev Lett , 3286–3289. [Google Scholar]
- Goldmann WH, Isenberg G. (1993). Analysis of filamin and alpha-actinin binding to actin by the stopped flow method. FEBS Lett , 408–410. [DOI] [PubMed] [Google Scholar]
- Grashoff C, Hoffman BD, Brenner MD, Zhou R, Parsons M, Yang MT, McLean MA, Sligar SG, Chen CS, HA T, Schwartz MA. (2010). Measuring mechanical tension across vinculin reveals regulation of focal adhesion dynamics. Nature , 263–266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo M, Ehrlicher A, Jensen M, Renz M, Moore J, Goldman R, Lippincott-Schwartz J, Mackintosh F, Weitz D. (2014). Probing the stochastic, motor-driven properties of the cytoplasm using force spectrum microscopy. Cell , 822–832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo M, Ehrlicher A, Mahammad S, Fabich H, Jensen M, Moore J, Fredberg J, Goldman R, Weitz D. (2013). The role of vimentin intermediate filaments in cortical and cytoplasmic mechanics. Biophys J , 1562–1568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta SK, Guo M. (2017). Equilibrium and out-of-equilibrium mechanics of living mammalian cytoplasm. J Mech Phys Solids , 284–293. [Google Scholar]
- Gupta SK, Li Y, Guo M. (2019). Anisotropic mechanics and dynamics of a living mammalian cytoplasm. Soft Matter , 190–199. [DOI] [PubMed] [Google Scholar]
- Gurmessa B, Francis M, Rust M, Das M, Ross J, Robertson-Anderson R. (2019). Counterion crossbridges enable robust multiscale elasticity in actin networks. Phys Rev Res , 013016. [Google Scholar]
- Hendricks AG, Holzbaur EL, Goldman YE. (2012). Force measurements on cargoes in living cells reveal collective dynamics of microtubule motors. Proc Natl Acad Sci USA , 18447–18452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffman BD, Massiera G, Van Citters KM, Crocker JC. (2006). The consensus mechanics of cultured mammalian cells. Proc Natl Acad Sci USA , 10259–10264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humphrey D, Duggan C, Saha D, Smith D, Kas J. (2002). Active fluidization of polymer networks through molecular motors. Nature , 413–416. [DOI] [PubMed] [Google Scholar]
- Kaplan JM, Kim SH, North KN, Rennke H, Correia LA, Tong HQ, Mathis BJ, Rodríguez-Pérez JC, Allen PG, Beggs AH, Pollak MR. (2000). Mutations in ACTN4, encoding alpha-actinin-4, cause familial focal segmental glomerulosclerosis. Nat Genet , 251–256. [DOI] [PubMed] [Google Scholar]
- Koenderink G, Dogic Z, Nakamura F, Bendix P, MacKintosh F, Hartwig J, Stossel T, Weitz D. (2009). An active biopolymer network controlled by molecular motors. Proc Natl Acad Sci USA , 15192–15197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kole TP, Tseng Y, Jiang I, Katz JL, Wirtz D. (2005). Intracellular mechanics of migrating fibroblasts. Mol Biol Cell , 328–338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kovacs M, Toth J, Hetenyi C, Malnasi-Csizmadia A, Sellers JR. (2004). Mechanism of blebbistatin inhibition of myosin II. J Biol Chem , 35557–35563. [DOI] [PubMed] [Google Scholar]
- Lautenschläger F, Paschke S, Schinkinger S, Bruel A, Beil M, Guck J. (2009). The regulatory role of cell mechanics for migration of differentiating myeloid cells. Proc Natl Acad Sci USA , 15696–15701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lieleg O, Claessens MM, Luan Y, Bausch AR. (2008). Transient binding and dissipation in cross-linked actin networks. Phys Rev Lett , 108101. [DOI] [PubMed] [Google Scholar]
- Lieleg O, Kayser J, Brambilla G, Cipelletti L, Bausch AR. (2011). Slow dynamics and internal stress relaxation in bundled cytoskeletal networks. Nat Mater , 236–242. [DOI] [PubMed] [Google Scholar]
- Lieleg O, Schmoller KM, Claessens MM, Bausch AR. (2009). Cytoskeletal polymer networks: viscoelastic properties are determined by the microscopic interaction potential of cross-links. Biophys J , 4725–4732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mas J, Richardson AC, Reihani SN, Oddershede LB, Berg-Sorensen K. (2013). Quantitative determination of optical trapping strength and viscoelastic moduli inside living cells. Phys Biol , 046006. [DOI] [PubMed] [Google Scholar]
- Mizuno D, Head DA, MacKintosh FC, Schmidt CF. (2008). Active and passive microrheology in equilibrium and nonequilibrium systems. Macromolecules , 7194–7202. [Google Scholar]
- Murthy K, Wadsworth P. (2005). Myosin-II-dependent localization and dynamics of F-actin during cytokinesis. Curr Biol , 724–731. [DOI] [PubMed] [Google Scholar]
- Nelson WJ. (2009). Remodeling epithelial cell organization: transitions between front-rear and apical-basal polarity. Cold Spring Harb Perspect Biol , a000513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pierobon P, Achouri S, Courty S, Dunn A, Spudich J, Dahan M, Cappello G. (2009). Velocity, processivity, and individual steps of single myosin V molecules in live cells. Biophys J , 4268–4275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Puig-de-Morales M, Millet E, Fabry B, Navajas D, Wang N, Butler J, Fredberg J. (2004). Cytoskeletal mechanics in adherent human airway smooth muscle cells: probe specificity and scaling of protein-protein dynamics. Am J Physiol Cell Physiol , C643-C654. [DOI] [PubMed] [Google Scholar]
- Rigato A, Miyagi A, Scheuring S, Rico F. (2017). High-frequency microrheology reveals cytoskeleton dynamics in living cells. Nat Phys , 771–775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robison P, Caporizzo M, Bogush A, Margulies K, Prosser B. (2016). Detyrosinated microtubules bear load and transmit mechanical force in cardiomyocytes. Biophys J , 185a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sollich P, Lequeux F, Hébraud P, Cates M. (1997). Rheology of soft glassy materials. Phys Rev Lett , 2020–2023. [Google Scholar]
- Stamenović D, Rosenblatt N, Montoya-Zavala M, Matthews B, Hu S, Suki B, Wang N, Ingber D. (2007). Rheological behavior of living cells is timescale-dependent. Biophys J , L39-L41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stamenović D, Suki B, Fabry B, Wang N, Fredberg J, Buy J. (2004). Rheology of airway smooth muscle cells is associated with cytoskeletal contractile stress. J Appl Physiol , 1600–1605. [DOI] [PubMed] [Google Scholar]
- Staunton JR, Blehm B, Devine A, Tanner K. (2017). In situ calibration of position detection in an optical trap for active microrheology in viscous materials. Optic Express , 1746–1761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tharmann R, Claessens MM, Bausch AR. (2007). Viscoelasticity of isotropically cross-linked actin networks. Phys Rev Lett , 088103. [DOI] [PubMed] [Google Scholar]
- Valentine M, Perlman Z, Gardel M, Shin J, Matsudaira P, Mitchison T, Weitz D. (2004). Colloid surface chemistry critically affects multiple particle tracking measurements of biomaterials. Biophys J , 4004–4014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Citters KM, Hoffman BD, Massiera G, Crocker JC. (2006). The role of F-actin and myosin in epithelial cell rheology. Biophys J , 3946–3956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wachsstock DH, Schwarz WH, Pollard TD. (1994). Cross-linker dynamics determine the mechanical properties of actin gels. Biophys J , 801–809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ward SM, Weins A, Pollak MR, Weitz DA. (2008). Dynamic viscoelasticity of actin cross-linked with wild-type and disease-causing mutant alpha-actinin-4. Biophys J , 4915–4923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei M, Zaorski A, Yalcin H, Wang J, Hallow M, Ghadiali S, Chiou A, Ou-Yang H. (2008). A comparative study of living cell micromechanical properties by oscillatory optical tweezers. Opt Express , 8594. [DOI] [PubMed] [Google Scholar]
- Weins A, Schlondorff J, Nakamura F, Denker B, Hartwig J, Stossel T, Pollak M. (2007). Disease-associated mutant alpha-actinin-4 reveals a mechanism for regulating its F-actin-binding affinity. Proc Natl Acad Sci USA , 16080–16085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilhelm M, Maring D, Spiess H-W. (2011). Fourier-transform rheology. Rheol Acta , 399–405. [Google Scholar]
- Yao N, Becker D, Broedersz C, Depken M, MacKintosh F, Pollak M, Weitz D. (2011). Nonlinear viscoelasticity of actin transiently cross-linked with mutant α-actinin-4. J Mol Biol , 1062–1071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yarmola EG, Somasundaram T, Boring TA, Spector I, Bubb MR. (2000). Actin-latrunculin A structure and function. Differential modulation of actin-binding protein function by latrunculin A. J Biol Chem , 28120–28127. [DOI] [PubMed] [Google Scholar]
- Zhou E, Trepat X, Park C, Lenormand G, Oliver M, Mijailovich S, Hardin C, Weitz D, Butler J, Fredberg J. (2009). Universal behavior of the osmotically compressed cell and its analogy to the colloidal glass transition. Proc Natl Acad Sci USA , 10632–10637. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.