Skip to main content
PMC home page
Molecular Biology of the Cell logoLink to Molecular Biology of the Cell
. 2020 Jul 21;31(16):1726–1734. doi: 10.1091/mbc.E19-10-0588

Direct evidence that tumor cells soften when navigating confined spaces

Carmela Rianna a,b, Manfred Radmacher a, Sanjay Kumar b,c,*
Editor: Dennis Discherd
PMCID: PMC7521845  PMID: 31995446

Abstract

The mechanical properties of cells strongly regulate many physiological and pathological processes. For example, in cancer, invasive and metastatic tumor cells have often been reported to be softer than nontumor cells, raising speculation that cancer cells might adaptively soften to facilitate migration through narrow tissue spaces. Despite growing interest in targeting cell softening to impede invasion and metastasis, it remains to be directly demonstrated that tumor cells soften as they migrate through confined spaces. Here, we address this open question by combining topographically patterned substrates with atomic force microscopy (AFM). Using a polydimethylsiloxane open-roof microdevice featuring tapered, fibronectin-coated channels, we followed the migration of U2OS cells through various stages of confinement while simultaneously performing AFM indentation. As cells progress from unconfined migration to fully confined migration, cells soften and exclude Yes-associated protein from the nucleus. Superresolution imaging reveals that confinement induces remodeling of actomyosin stress fiber architecture. Companion studies with flat one-dimensional microlines indicate that the changes in cytoarchitecture and mechanics are intrinsically driven by topographical confinement rather than changes in cellular aspect ratio. Our studies represent among the most direct evidence to date that tumor cells soften during confined migration and support cell softening as a mechanoadaptive mechanism during invasion.

INTRODUCTION

The mechanical properties of cells deeply underlie many physiological functions, such as adhesion, migration, and differentiation. Alterations in cellular mechanics are strongly associated with a number of disease processes; for example, many of the classically described hallmarks of cancer (Hanahan and Weinberg, 2000, 2011) are predicated on dramatic changes in cellular mechanical properties. In particular, the ability of tumor cells to invade tissues and metastasize to distant sites requires tumor cells to overcome mechanical barriers posed by migration through confined spaces within the extracellular matrix and between cells (Fidler, 2003; Talmadge and Fidler, 2010; Lambert et al., 2017). The growing appreciation that tumor cells may need to adaptively change their mechanics to drive disease has motivated significant efforts to explore altered cellular mechanics as a physical biomarker and the mechanotransductive machinery as a therapeutic target. Many of these studies have focused on identifying differences in mechanical properties between tumor cells and their nontumorigenic counterparts (Lekka et al., 1999; Zhang et al., 2002; Cross et al., 2008; Faria et al., 2008; Li et al., 2008; Kumar and Weaver, 2009; Swaminathan et al., 2011; Rebelo et al., 2013; Alibert et al., 2017; Rianna and Radmacher, 2017a). Tumor cells are frequently found to be softer than normal cells, which has raised the attractive idea that tumor cells adaptively soften during invasion and metastasis (Guck et al., 2005; Xu et al., 2012).

Despite its intuitive appeal, the adaptive-softening hypothesis is primarily based on population-level comparisons between normal and tumor cells (Guck et al., 2001, 2005; Hou et al., 2009; Lekka and Laidler, 2009; Byun et al., 2013; Lee and Liu, 2014; Pachenari et al., 2014). For example, atomic force microscopy (AFM) studies have indicated that cancerous human bladder cells are an order of magnitude softer than healthy bladder cells (Lekka et al., 1999). High-throughput optical stretching measurements similarly indicate that human breast cancer cells deform more than mammary epithelial cells and that deformability increases with metastatic potential (Guck et al., 2005). However, these population-based studies paint a somewhat mixed picture. For example, AFM measurements have revealed that leukemia cells are stiffer than leukocytes (Lam et al., 2008), and micropipette aspiration studies show that hepatocellular carcinoma cells are stiffer than normal hepatocytes (Zhang et al., 2002). A variety of other studies employing a range of mechanical modalities provide evidence that tumor cells are either stiffer than their normal counterpart or stiffen during tumor progression, complicating the adaptive-softening hypothesis (Baker et al., 2010; Lopez et al., 2011; Staunton et al., 2016). The lack of clarity in the evolution of cell stiffness during invasion fundamentally derives from a lack of direct measurements of cellular mechanics during the invasion process. This gap has undoubtedly arisen in part from the technical challenge of longitudinally measuring the mechanical properties of a cell during confined migration.

To address this challenge, we engineered a microscale culture platform that allows us to measure changes in cellular mechanical properties during confined migration. Our system is based on an open-roof polydimethylsiloxane (PDMS) microdevice with tapered, extracellular matrix (ECM)–functionalized channels. We observed tumor cells spontaneously migrating from flat to confined spaces while simultaneously measuring elastic properties by AFM. We find that cells soften substantially during channel traversal (Young’s modulus values reduce from 5.6 to 2.1 kPa), which is accompanied by the presence of increased actomyosin density at the side walls as well as exclusion of Yes-associated protein (YAP) from the nucleus. Notably, when cells were confined through culture on narrow, one-dimensional (1D) ECM microlines, cells elongated but did not soften, indicating that softening is an intrinsic feature of three-dimensional (3D) geometries.

RESULTS

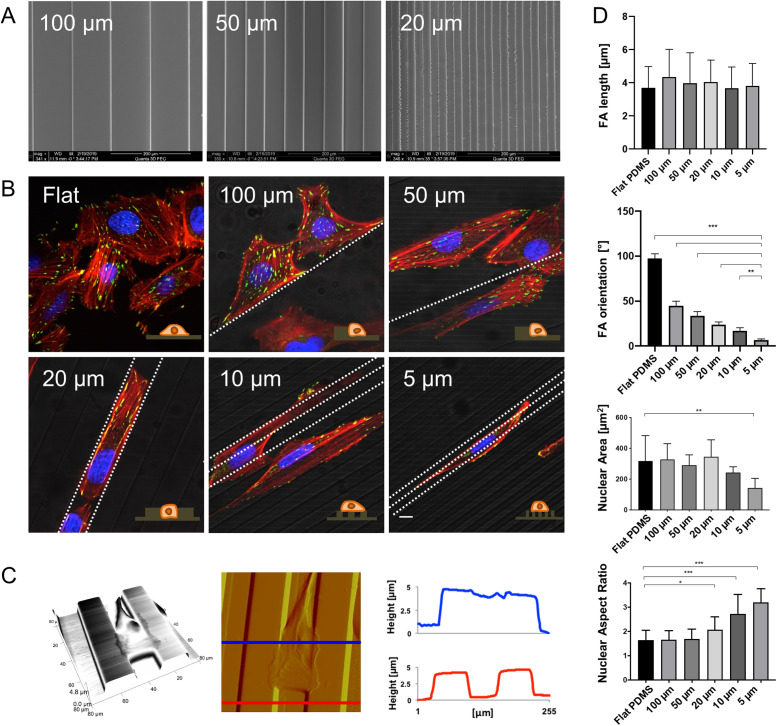
To determine how tumor cells adapt their mechanics as they migrate through confined spaces, we sought to design a culture paradigm that places cells in confined migration while allowing longitudinal live-cell optical imaging and AFM indentation measurements. As a starting point, we employed open PDMS microchannels, which have been used to model confined migration (Cha et al., 2015; Smith et al., 2016). Our first challenge was to identify geometric conditions under which cells experience lateral cell confinement and begin to physically engage the channel walls. We therefore fabricated individual devices featuring linear, fibronectin-coated PDMS channels with widths ranging from 5 to 100 µm (Figure 1A). When we cultured U2OS human osteosarcoma cells within these devices, we found that the morphology varied strongly with channel width (Figure 1B). On flat PDMS surfaces, cells adopted a highly spread morphology with random orientations, as expected. As the channel width was reduced to 50–100 µm, cells tended to adhere to a single channel wall and assemble stress fibers (SFs) along that wall. When the channel width was further reduced to 20 µm, cells were fully confined within the channel, with elongated morphologies and extensive contacts with both walls (see Supplemental Figure S1 for additional confocal images). Further reduction of channel width to 5–10 µm did not produce confinement, with cells spanning multiple channels and the adjoining mesas (plateaus). AFM imaging confirmed that cells occupy a 3D morphology within the channels, with engagement of the walls through their entire height (Figure 1C; see Supplemental Figure S2 for AFM images of the other channel widths). We also quantified focal adhesion (FA) and nuclear morphology (Figure 1D). While FA length was indistinguishable across conditions, FA orientation varied significantly relative to the channel axis (calculated as θFAs−θpattern). Specifically, increasingly narrow channels increased the alignment of FAs with the channel. Nuclear area was indistinguishable from flat PDMS across all channel widths, save for a moderate decrease in the narrowest channel (5 µm). Nuclear aspect ratio began to increase relative to flat PDMS for 20-µm-wide channels and progressively increased with further channel narrowing.

FIGURE 1:

FIGURE 1:

Open in a new tab

U2OS cell morphology varies strongly with PDMS channel width, achieving cell confinement within 20-µm spaced channels. (A) Scanning electron microscopy (SEM) images of linear PDMS channels with widths of 20 µm, 50 µm, and 100 µm, and lateral wall heights of ∼5 µm. (B) Confocal immunofluorescence images of U2OS cells on flat surfaces and in 5–100-µm-wide channels showing actin (red), vinculin (green), and nuclei (blue). The fluorescence images are superimposed on grayscale phase contrast images to show the underlying substrate; white dotted lines indicate the pattern direction. Scale bar is 10 µm. (C) Left to right, AFM 3D projection, deflection image, and cross-sectional profiles of U2OS cell confined within 20-µm-spaced PDMS channels. As displayed in the deflection image, the cross-section images are measured on the top of the cell (blue) and on bare channels (red). (D) Quantification of FA length and orientation (top two plots) and nuclear area and aspect ratio (bottom two plots) on flat PDMS and channels of 5–100 µm width. All error bars depict standard deviations (n = 10 across three independent experiments; ***, p < 0.0001; **, p < 0.001; *, p < 0.01, as calculated by the Mann-Whitney test between each pair of categories).

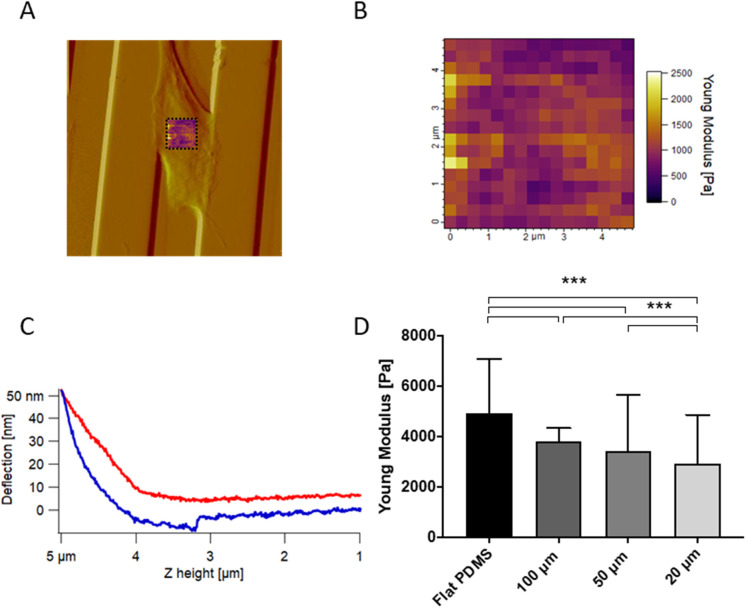
To determine whether channel confinement influenced cellular mechanics, we obtained arrays of AFM indentation measurements on cells within 100, 50, and 20 µm channels, performing force maps on the supranuclear regions of each cell (Figure 2, A and B). Each map was made of 256 (16 × 16) force curves and each force curve (Figure 2C) was fitted with the Hertzian model for pyramidal probes to yield a Young’s modulus. Young’s modulus values were highest on the flat, unconfined surfaces and fell with decreasing channel width (Figure 2D and Supplemental Figure S3). To explore the generality of this relationship in a distinct tumor cell–matrix system, we repeated these measurements with U87 human glioblastoma cells on patterned hyaluronic surfaces and found the same trend, with cells getting softer when laterally confined and squeezed within channels (Supplemental Figure S4).

FIGURE 2:

FIGURE 2:

Open in a new tab

Microchannel confinement regulates cell mechanics. (A) AFM deflection image showing that force maps were measured over the central, supranuclear portion of the cell. (B) AFM force map made of 16 × 16 force curves over a 5 µm × 5 µm area; each pixel of the force map represents a force curve. (C) Representative force curve with approach in red and retraction in blue. Each curve within the force volume was fit with the Hertz model to extract the Young’s modulus, with the median value across all curves reported in the bar plot. (D) Young’s modulus values of U2OS cells seeded on flat PDMS and 20–100 µm channels. As above, each bar represents the median value of all the Young’s modulus values collected on all the cells for each category, plotted with interquartile range as error bars. Statistical significance was determined using the Mann-Whitney test between each pair of categories (***, p < 0.0001; n = 2560, 2304, 3072, and 3328 force curves on 10, 9, 12, and 13 cells across three independent experiments. For each cell, one 16 × 16 force map was recorded on the supranuclear region of the cell body).

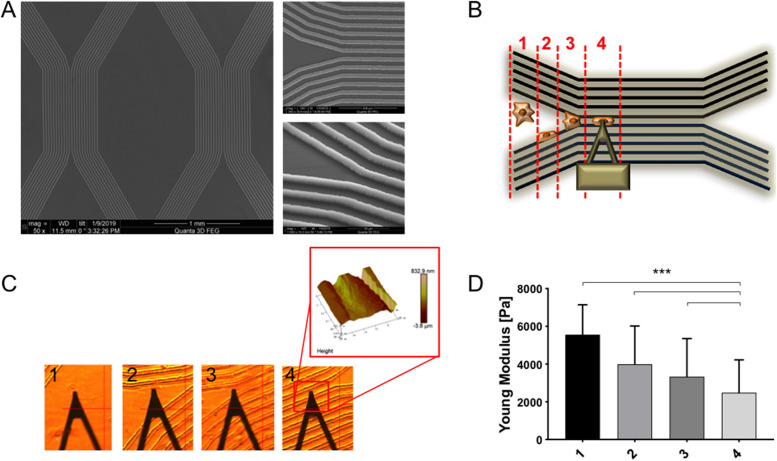
Having established 20 µm as a critical channel width to induce confinement in U2OS cells, we introduced a new PDMS device with a tapered, Y-shaped channel to allow observation of cell migration from an unconfined to a confined geometry (Figure 3A). An important advantage of the Y-shaped channel design is that it allowed us to capture, on a single surface, “snapshots” of many cells at different stages of confined migration, ranging from fully unconfined to partially confined to fully confined. To better restrict cells to the channels we passivated the mesas between the channels by microcontact-printing polyethylene glycol (PEG) before fibronectin-coating the device. Time-lapse imaging of U2OS cells within these devices revealed successful confined migration, with cells entering the channels from one end and traversing the entire length of the channel (Supplemental Movie S1).

FIGURE 3:

FIGURE 3:

Open in a new tab

U2OS cells progressively soften as they progress from unconfined to fully confined migration. (A) SEM images of Y-shaped PDMS devices with different magnification and tilted angle. (B) Schematic of cells traversing Y-shaped channels, showing different cell categories: 1) unconfined, 2) associated with one wall, 3) associated with two walls but not fully confined, and 4) fully confined. (C) Optical images of AFM cantilever in contact with different cells and (D) AFM Young’s modulus values of U2OS cells sorted in the four different categories. Each bar represents the median value of all the Young’s modulus values collected on all the cells for each category, plotted with interquartile range as error bars. Statistical significance was determined using the Mann-Whitney test between each pair of categories (***, p < 0.0001; n = 2560, 3072, 3072, and 3840 force curves on 10, 12, 12, and 15 cells across three independent experiments. For each cell, a 16 × 16 force map was recorded on the supranuclear region of the cell body).

Movie S1.

Download video file (3.5MB, mov)
Open in a new tab

Time-lapse movie of U2OS cells migrating within Y-shaped PDMS channels. Confined migration was achieved passivating the mesas between the channels by microcontact-printing PEG prior to fibronectin-coating the device. Cells were observed for 12 h with optical microscope, recording one image every 15 minutes.

We then used AFM indentation to follow changes in cellular mechanics before and after confinement (Figure 3, B–D). To simplify interpretation, we sorted each cell into one of four categories: 1) unconfined; 2) associated with one wall; 3) associated with two walls but not fully confined; and 4) fully confined. Comparison of cells in each category revealed that U2OS cells progressively soften as they transition from unconfined migration to partially confined migration to fully confined migration (Young’s modulus value decreases from 5.6 to 2.1 kPa). These findings are consistent with our measurements in straight channels (Figure 2) and indicate that cells adaptively soften as they encounter increasingly confined geometries. Interestingly, time-lapse imaging failed to yield significant differences in migration speed or directionality as a function of confinement stage, at least over this limited time window (Supplemental Figure S5 and Movie S2).

Movie S2.

Download video file (3.5MB, mov)
Open in a new tab

U2OS cell migration within Y-shaped PDMS channels. A U2OS cell is seen migrating into the central channel of the device, going from unconfined to confined spaces. Cells were observed for 12 h with optical microscope, recording one image every 15 minutes.

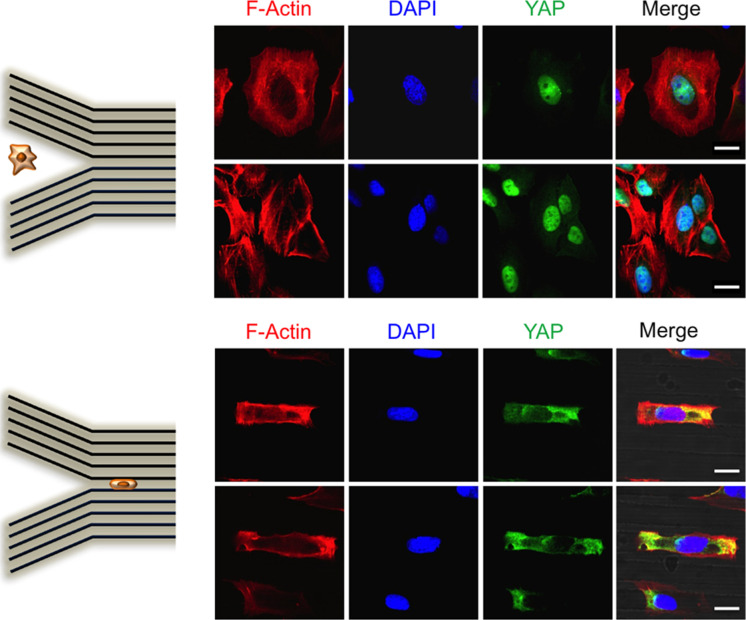
To gain additional insight into cytoarchitecture during the transition to confined migration, we performed confocal imaging of the actin cytoskeleton within this device. As expected, cells in unconfined geometries primarily assembled SFs at their basal surface, with the expected distribution of dorsal fibers, transverse arcs, and ventral fibers (Lee et al., 2018). However, cells in confined geometries mainly positioned SFs adjacent to the channel walls, creating two parallel arrays of actin bundles and few SFs adjacent to the device floor (Supplemental Movies S3 and S4). To determine whether these changes in mechanics and cytoarchitecure were accompanied by functionally relevant mechanotransductive signaling events, we examined localization of YAP, which has been observed to traffic to the nucleus under conditions of high cellular contractility (Dupont et al., 2011; Elosegui-Artola et al., 2017). Confocal imaging revealed strong YAP nuclear localization for cells in unconfined geometries and strong cytoplasmatic localization for cells confined within channels (Figure 4). However, when cells were either associated with one channel wall or incompletely confined (categories 2 and 3 in Figure 3B), YAP mainly localized to the nuclei. This result aligns with our AFM measurements, which show that cells soften as they traverse narrow channels (Figure 3D). In other words, cells on unconfined regions of the substrate are stiff, have well-developed basal SF networks, and show strong YAP nuclear localization. As cells experience increasing confinement, they soften, increase actin density at the channel walls, and partition YAP from the nucleus into the cytoplasm.

FIGURE 4:

FIGURE 4:

Open in a new tab

YAP localization is influenced by topographical cell confinement. Confocal images of U2OS cells fixed and stained for actin (red), nuclei (blue), and YAP (green). The top panel shows cells seeded on unconfined regions and the bottom panel shows cells in confined channels. Scale bars are 20 µm.

Movie S3.

Download video file (79.4KB, mov)
Open in a new tab

Confocal z-stack movie of a U2OS cell confined in channels. Staining is for actin (red); vinculin (green) and nuclei (blue). Movie starts at the bottom of the cell and ends at the top.

Movie S4.

Download video file (66.4KB, mov)
Open in a new tab

Confocal z-stack movie of a U2OS cell confined in channels. Staining is for actin (red); vinculin (green) and nuclei (blue). Movie starts at the bottom of the cell and ends at the top.

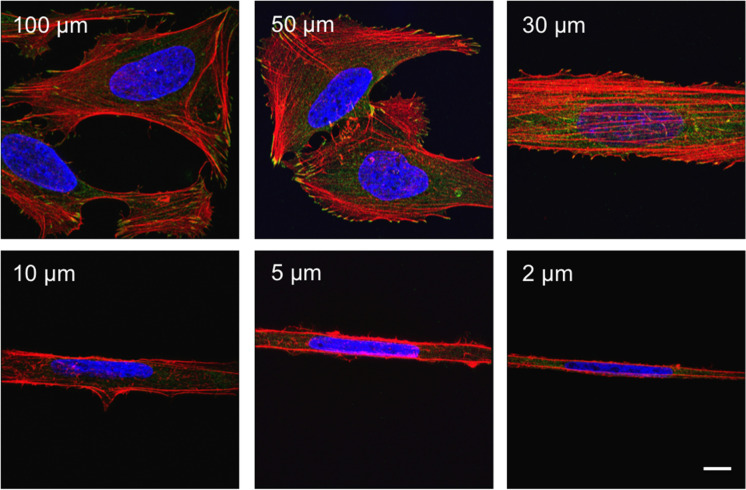
The confocal images illustrate that confinement leads to dramatic changes in cell shape, in addition to changes in mechanics and YAP localization. Importantly, cellular elongation has been reported to alter cytoarchitecture and YAP localization independent of topographical confinement (Bao et al., 2017; Gegenfurtner et al., 2018). This raises the possibility that narrow channels might induce softening and YAP localization by altering cell shape rather than by introducing mechanical constrictions (Bao et al., 2017; Gegenfurtner et al., 2018). To experimentally separate elongation and mechanical confinement, we conducted a parallel set of studies in which we cultured cells on fibronectin (FN) 1D microlines of widths ranging from 2 to 100 µm (Supplemental Figures S6 and S7). Structured illumination microscopy (SIM) imaging revealed that cells closely adhere to the geometry of the microline, with greater aspect ratios observed on narrower microlines (Figure 5).

FIGURE 5:

FIGURE 5:

Open in a new tab

1D microlines strongly affect U2OS morphology. SIM images of U2OS cells seeded on FN microlines ranging from 2 to 100 µm width. Cells were fixed and stained for actin (red), vinculin (green), and nuclei (blue). Scale bar is 10 µm.

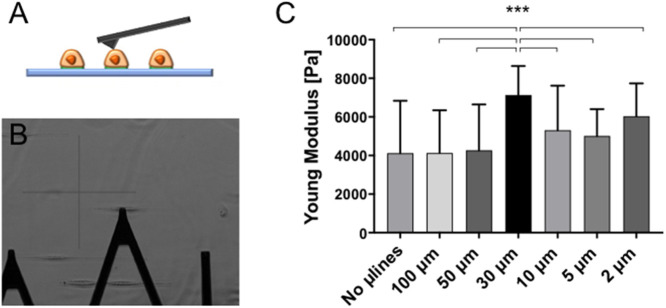
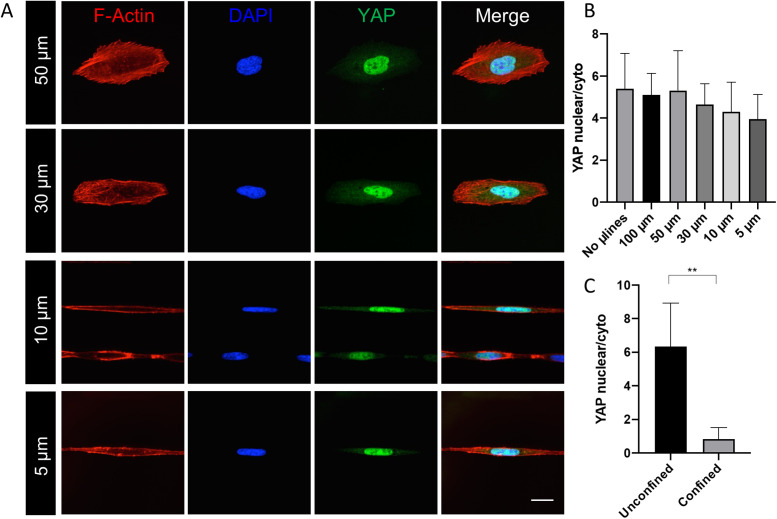
However, unlike in 3D-like topographical channels, AFM measurements indicated that cells do not appreciably soften on increasingly narrow microlines (Figure 6). Instead, cell stiffness reached a peak of 30-µm-wide lines (Young’s modulus values increase from 4.1 to 7.2 kPa), where SIM images revealed prominent thick and parallel bundles of SF (Figure 5). Consistent with this result, YAP localized robustly to the nucleus for all microline widths (Figure 7A). The YAP nuclear/cytoplasmic (N/C) ratio fell only during topographical confinement, with no statistically significant width-dependent variation of the YAP N/C ratio for cells cultured on 1D microlines (Figure 7, B and C). This effect did not strictly correlate with nuclear elongation (Supplemental Figure S8). Thus, confinement-induced softening is an intrinsic effect of a 3D-like geometry and cannot be solely attributed to changes in cell or nuclear shape.

FIGURE 6:

FIGURE 6:

Open in a new tab

U2OS mechanics are only modestly affected by 1D microline width. (A) Schematic representation of an AFM cantilever engaging a cell seeded on 1D microlines of fibronectin. (B) MLCT-Bio cantilever (lever C) indenting living cells. (C) Young’s modulus values of U2OS cells seeded on microlines with widths ranging from 5 to 100 µm. Each bar represents the median value of all the Young’s modulus values collected on all the cells for each category, plotted with interquartile range as error bars. Statistical significance was determined using the Mann-Whitney test between each pair of categories (***, p < 0.0001; n = 2048, 2560, 2048, 2816, 3072, and 3072 force curves on 8, 10, 8, 11, 12, and 12 cells across six independent experiments. For each cell, a 16 × 16 force map was recorded on the supranuclear region of the cell body).

FIGURE 7:

FIGURE 7:

Open in a new tab

YAP localization is not affected by 1D microline width. (A) Confocal images of U2OS cells seeded on FN microlines with different widths (5–50 µm). Cells were fixed and stained for actin (red), nuclei (blue), and YAP (green); merged colors are shown on the rightmost micrographs. Scale bar is 30 µm. (B) Quantification of YAP nuclear/cytoplasmic ratio in cells cultured on FN microlines and (C) on unconfined and confined regions of a Y-shaped PDMS device. Error bars are SD of mean values (n = 10 across two independent experiments; **, p < 0.001, calculated with the Mann-Whitney test).

DISCUSSION

We have explored how tumor cells adapt their mechanical properties as they migrate through confined spaces, processes key to invasion and metastasis. Previous efforts to address this question have often focused on mechanical comparisons between cancer and normal cells (Lekka et al., 1999; Cross et al., 2008; Faria et al., 2008; Li et al., 2008; Rebelo et al., 2013). These studies have yielded tremendous insight into the role of cellular mechanics during invasion and metastasis and raised the notion that tumor cells must be highly deformable to navigate tight tissue spaces (Guck et al., 2005; Xu et al., 2012). While many studies have indeed shown that cancer cells are softer than normal cells (Lekka et al., 1999; Cross et al., 2008; Faria et al., 2008; Li et al., 2008; Rebelo et al., 2013), the result is far from universal, with some studies indicating that tumor cells are stiffer than normal cells (Zhang et al., 2002; Lam et al., 2008), especially when they are in contact with an ECM (Pickup et al., 2014; Acerbi et al., 2015; Rianna and Radmacher, 2017a,b; Abidine et al., 2018). Moreover, the interpretation of many of these studies is complicated by the differences in genetic background between the normal and tumorigenic culture models, such that it is difficult to know whether measured differences in cell stiffness are intrinsically associated with differences in tumorigenic potential. In fact, when mechanical comparisons have been made within an isogenic tumor progression series, cell stiffness has been observed to increase with tumorigenic potential (Baker et al., 2010). Our study brings additional insights to this question by characterizing tumor cells in various stages of confinement and invasion. As tumor cells experience increasing confinement, they markedly soften, consistent with the idea that deformability supports invasion and metastasis. Our results broadly agree with two recent studies. The first investigated cell traction forces in confined microenvironments and found that 3D confinement reduces cell traction forces (Raman et al., 2013). The second examined migration of breast tumor cells within collagen “microtracks” and found that this confined geometry reduces basal FAs and SFs. Notably, the latter study found that confinement also increases matrix strain, which both complements and contrasts with our AFM stiffness measurements and implies that stiffness and contractility are not fully coupled (Mosier et al., 2019).

A central enabling technology in our work is our open microchannel-based paradigm that allows AFM access for mechanical measurements during confined migration. This innovation addresses the technical challenge of obtaining contact-based mechanical measurements in a 3D-like environment. Our open-roof Y-shaped PDMS device combines the features of confined migration in 3D matrices, with the accessibility of two-dimensional supports to perform longitudinal mechanical measurements. By combining this device with AFM, we were able to follow cell migration from unconfined to confined spaces, while simultaneously measuring mechanical properties on the supernuclear region of the cell. The design of the platform also proved highly amenable to high-resolution optical imaging, including superresolution imaging. Through these studies, we found that cells in unconfined geometries adopt a highly spread morphology with classical SF networks at the cell base and above the nucleus. As cells experience increasing confinement, they become increasingly elongated and exhibit increased actin density at the lateral device walls. Such cytoskeletal rearrangements have been observed in past microchannel studies (Balzer et al., 2012) but without a clear function. Our study suggests that confinement induces the assembly of SFs at the channel walls, which could facilitate confined migration by exploiting the walls as “handholds” to build traction force and migrate, while simultaneously reducing their cortical stiffness. As a result, our work may eventually help reconcile conflicting views of how stiffness changes in tumorigenesis—namely, cells may become more deformable and generate greater contractile forces during confinement, thus simultaneously appearing to be both more and less stiff, depending on the measurement. Nonetheless, higher-resolution imaging and/or a modified channel system is still needed to definitively demonstrate that confinement induces SF assembly along the channel walls. It is also important to note that measures of cortical stiffness (e.g., AFM) are not equivalent to measures of traction force or contractility, even though the two are often strongly correlated (Wang et al., 2002; Schierbaum et al., 2019). Coupling our platform with finer intracellular mechanical measurements should help refine our conceptual model.

Another important outcome from our work is the direct correlation of mechanical changes during confined migration with functionally significant signaling events. In particular, for cells on flat, unconfined regions, cell stiffening is accompanied by strong nuclear YAP localization. With increasing confinement, cells soften, and YAP localizes to the cytoplasm. These results are consistent with previous work in which YAP nuclear localization closely tracks actomyosin assembly and contractility (Elosegui-Artola et al., 2017) and confirm the role of YAP in mechanotransduction (Dupont et al., 2011; Raghunathan et al., 2014; Nardone et al., 2017). Previous studies observed that cellular elongation has a role in altering cytoarchitecture and YAP localization independently of topographical confinement (Bao et al., 2017; Gegenfurtner et al., 2018). Notably, YAP remained in the nucleus for cells on 1D microlines, indicating that cell softening and YAP function intrinsically depends on topographical confinement and is not simply being driven by changes in cellular elongation. In the future, it will be informative to quantify traction forces at the channel walls and investigate how SF distribution is related to YAP localization. Another interesting open question raised by our studies is which YAP-dependent genes are most strongly affected by confinement geometry and the extent to which the resulting gene products contribute to confined motility.

Our study also suggests a number of other interesting future directions. For example, it would be valuable to quantify changes in cell viscous (loss) modulus during confinement, in addition to the elastic properties measured here. It would also be informative to learn whether confinement-induced softening tracks in some interesting way with malignant potential, for example, using a progression series with well-matched genetic backgrounds. Finally, it will be important to ask whether our observations also hold in more tissue-like systems, including both organotypic culture models and animal models.

MATERIALS AND METHODS

Fabrication of patterned PDMS substrates

PDMS channels were created with photolithography and replica molding techniques (Xia et al., 1997; Gates et al., 2005). Photolithography masks were designed with AutoCAD and produced from Artnet Pro (San Jose, CA). A clean silicon wafer (WaferNet, CA) was spin-coated with SU-8 3005 photoresist (MicroChem, MA) to create a 5-µm-thick film. After soft baking at 95°C for 3 min, the film was exposed to UV light for 15 s through the mask, postbaked at 65°C (1 min) and 95°C (2 min). Finally, the wafer was developed and hard-baked at 200°C for 15 min. PDMS monomer and cross-linker were mixed (ratio 10:1; Sylgard 184 Silicone Elastomer Kit; Dow Corning, Midland, MI) and the prepolymer solution was poured onto the wafer. The wafer was degassed in vacuum and then prepolymer was cured for 2 h at 80°C (or overnight at room temperature [RT]). Finally, the PDMS was gently peeled off the wafer. Before proceeding with cell culture, PDMS substrates were extensively washed with ethanol, dried, and subjected to plasma treatment for 3 min to reduce hydrophobicity. Finally, substrates were incubated with fibronectin (FN) for 3 h before proceeding with cell seeding. U2OS cells were then seeded on PDMS substrates for 24 h, after which cells were either maintained as live cultures for AFM measurements or fixed and processed for fluorescence imaging.

PEG passivation

To restrict cell adhesion to the channels, we passivated the surrounding mesas with PEG. A cover glass was coated with poly-l-lysine grafted to polyethylene glycol (PLL-g-PEG, Surface Solutions) for 1 h and then brought into close contact with the patterned PDMS for 15 min to allow PEG adsorption onto the mesas. The PEG-coated PDMS substrates were incubated with FN for 3 h, during which time FN adsorption was expected to be restricted to the channels due to the PEG passivation of the mesas.

Deep UV-based fabrication of FN microlines

Microlines were produced as previously reported (Lee et al., 2018). Briefly, 18 × 18 mm cover glasses (Fisher Scientific) were incubated with 0.01 mg/ml PLL-g-PEG (Surface Solutions) in 10 mM HEPES for 1 h. After washing twice with phosphate-buffered saline (PBS) and deionized (DI) water (2 min each), PLL-g-PEG–coated glasses were illuminated for 15 min with deep UV light (UVO cleaner; Jelight) through a chrome–quartz photomask encoding multiple microlines ranging from 2 to 100 µm width. After illumination, cover glasses were left in DI water until use in cell culture. Before cell culture, cover glasses were incubated in fibronectin for 3 h at 37°C and then extensively washed with PBS.

Cell culture

U2OS human osteosarcoma cells and U87 human glioblastoma cells were cultured in DMEM supplemented with 10% fetal bovine serum (FBS) and 1% penicillin–streptomycin. Cells were incubated at 37°C in a humidified atmosphere of 95% air and 5% CO2. All substrates used in this study were incubated with fibronectin for 3 h and then with DMEM medium for 20 min before proceeding with cell seeding. Cells were tested for mycoplasma every 3 mo and authenticated via short tandem repeat profiling.

Immunofluorescence staining

Cell were fixed in 4% (vol/vol) paraformaldehyde (Alfa-Aeser) for 15 min at RT, permeabilized with 0.1% (vol/vol) Triton X-100 (EMD Millipore) for 3 min, and blocked with 1% (vol/vol) bovine serum albumin (BSA; Thermo Fisher) for 30 min in a humid chamber. Cells were incubated with primary antibodies for 2 h, rinsed with 1% BSA in PBS, and then incubated with secondary antibodies and phalloidin (3:500; Thermo Fisher Scientific) for 30 min in a humid chamber. The following primary antibodies were used for immunostaining: mouse anti-vinculin hVin-1 (1:1000; Sigma) and YAP (D8H1X) XP Rabbit mAb (1:1000; Cell Signaling). As secondary antibodies we used Alexa Fluor 488 goat anti-mouse (1:500) and Alexa Fluor 488 goat anti-rabbit (1:500), both from Life Technologies. Finally, cells were incubated with NucBlue Live ReadyProbes Reagent (Thermo Fisher Scientific) for 20 min in PBS to stain nuclei. Samples were rinsed in PBS and stored in PBS at 4°C in the dark.

Confocal and structured illumination microscopy

Samples were imaged with a Prairie Technologies swept field confocal microscope using an Olympus LUMPlanFL N 60×/1.0 water dipping objective and a Zeiss Elyra PS.1 structured illumination microscope (Zeiss) with a DIC M27 63×/1.4 oil objective (Zeiss).

Image analysis

Quantification analysis of FAs, nuclei, and YAP nuclear/cytoplasmic ratio was performed using the open source software Fiji (Schindelin et al., 2012). Morphometric analysis of FAs was performed after processing images with a brightness/contrast tool, followed by the threshold command to obtain binarized images, and finally subjected to particle analysis. The orientation of FAs was calculated with (θFAs−θpattern), such that a smaller value indicates a stronger orientation to the pattern axis. Nuclear area and aspect ratio were calculated after processing the images with the threshold and particle analyzed, measuring area and shape descriptors. Finally, YAP nuclear/cytoplasmic ratio was calculated as the ratio between the intensity values for the pixels in the nuclear and in the cytoplasmatic regions of each cell. Both intensity values were divided by the area of the corresponding regions.

Scanning electron microscopy (SEM)

Samples were sputter-coated with Au-Pa for 50 s (85 Å thickness). A FIB-SEM (Zeiss) was used to image surface topography of patterned PDMS substrates.

AFM measurements

AFM measurements on living cells were performed with a Bruker Catalyst (CA, USA) with Bruker MLCT-Bio cantilevers (lever C). To acquire AFM images, MLCT-Bio tips were used in contact mode with a scan rate of 0.5–1 Hz. For cell mechanics measurements, cantilevers were calibrated with the thermal tune method (Hutter and Bechhoefer, 1993) before each experiment, and force volumes were obtained using a 50 nm (0.5 nN) trigger threshold to limit indentations. Arrays of force curves (force maps) were recorded at the central and highest part of the cell body to avoid any thin peripheral regions, which are more susceptible to contributions from the underlying substrate (Domke et al., 2000). Force maps were recorded on 5 µm × 5 µm areas and obtained in a 16 × 16 grid (256 force curves). More than 4000 force curves were obtained for each cell category.

AFM data analysis

The data analysis package IGOR (Wavemetrics, Lake Oswego, OR) was used to analyze AFM data and to extract the Young’s or elastic modulus (E). Force-indentation curves were fit to the Hertzian model for pyramidal probes for every force curve within a force map. For each 16 × 16 force map, 256 Young’s modulus values were calculated. Finally, the median of E values, calculated from all the force curves, were considered representative of each cell category. Every graph reporting AFM data is presented as a bar graph, reporting the median values of all force curves with interquartile range as error bars.

Statistical analysis

Statistical analysis and graphing were performed in Graph-Pad Prism (v 7.00). The Mann-Whitney test, a nonparametric test for non-Gaussian distributions, was used to assess statistical differences. For AFM mechanical data, two categories at a time were compared with each other, to study statistical differences between all of them. For each category, a range of 8–15 cells were studied, for each of which one force map (made of 256 force curves) was recorded, yielding 2048–3840 force curves per category. Experiments were independently repeated three to six times, with measurements obtained across multiple samples. Additional statistical details are specified in the figure captions.

Supplementary Material

Click here for additional data file. (4.2MB, pdf)

Acknowledgments

This work was supported by a German Academic Exchange Service (DAAD) Fellowship (C.R.) with funds from the German Federal Ministry of Education and Research (BMBF) and the European Union (FP7-PEOPLE-2013-COFUND, Grant agreement no. 605728), and the National Institutes of Health (NIH; Grant no. R01GM122375 to S.K.). Micropatterns and patterned silicon masters were fabricated at the QB3 Biomolecular Nanotechnology Center. Confocal images were obtained at the CIRM/QB3 Shared Stem Cell Facility (University of California, Berkeley). Structured illumination microscopy was performed at the UC Berkeley Biological Imaging Facility, which was supported in part by the NIH S10 program under award no. 1S10OD018136-01. The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH. We thank Mary West, Tram Do, Paul Lum, Naima Azgui, Denise Schichnes, Stacey Lee, and Kelsey Springer for training and/or assistance.

Abbreviations used:

AFM

atomic force microscopy

ECM

extracellular matrix

FA

focal adhesion

FN

fibronectin

PDMS

polydimethylsiloxane

SEM

scanning electron microscopy

SF

stress fiber

SIM

structured illumination microscopy

YAP

Yes-associated protein.

Footnotes

This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E19-10-0588) on June 29, 2020.

REFERENCES

  1. Abidine Y, Constantinescu A, Laurent VM, Rajan VS, Michel R, Laplaud V, Duperray A, Verdier C. (2018). Mechanosensitivity of cancer cells in contact with soft substrates using AFM. Biophys J , 1165–1175. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Acerbi I, Cassereau L, Dean I, Shi Q, Au A, Park C, Chen Y, Liphardt J, Hwang E, Weaver V. (2015). Human breast cancer invasion and aggression correlates with ECM stiffening and immune cell infiltration. Integr Biol , 1120–1134. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Alibert C, Goud B, Manneville JB. (2017). Are cancer cells really softer than normal cells? Biol Cell , 167–189. [DOI] [PubMed] [Google Scholar]
  4. Baker EL, Lu J, Yu D, Bonnecaze RT, Zaman MH. (2010). Cancer cell stiffness: integrated roles of three-dimensional matrix stiffness and transforming potential. Biophys J , 2048–2057. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Balzer EM, Tong Z, Paul CD, Hung W-C, Stroka KM, Boggs AE, Martin SS, Konstantopoulos K. (2012). Physical confinement alters tumor cell adhesion and migration phenotypes. FASEB J , 4045–4056. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bao M, Xie J, Piruska A, Huck WT. (2017). 3D microniches reveal the importance of cell size and shape. Nat Commun , 1962. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Byun S, Son S, Amodei D, Cermak N, Shaw J, Kang JH, Hecht VC, Winslow MM, Jacks T, Mallick P. (2013). Characterizing deformability and surface friction of cancer cells. Proc Natl Acad Sci USA , 7580–7585. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Cha J, Koh I, Choi Y, Lee J, Choi C, Kim P. (2015). Tapered microtract array platform for antimigratory drug screening of human glioblastoma multiforme. Adv Healthcare Mater , 405–411. [DOI] [PubMed] [Google Scholar]
  9. Cross SE, Jin Y-S, Tondre J, Wong R, Rao J, Gimzewski JK. (2008). AFM-based analysis of human metastatic cancer cells. Nanotechnology , 384003. [DOI] [PubMed] [Google Scholar]
  10. Domke J, Dannöhl S, Parak WJ, Müller O, Aicher WK, Radmacher M. (2000). Substrate dependent differences in morphology and elasticity of living osteoblasts investigated by atomic force microscopy. Colloids Surf B , 367–379. [DOI] [PubMed] [Google Scholar]
  11. Dupont S, Morsut L, Aragona M, Enzo E, Giulitti S, Cordenonsi M, Zanconato F, Le Digabel J, Forcato M, Bicciato S. (2011). Role of YAP/TAZ in mechanotransduction. Nature , 179. [DOI] [PubMed] [Google Scholar]
  12. Elosegui-Artola A, Andreu I, Beedle AE, Lezamiz A, Uroz M, Kosmalska AJ, Oria R, Kechagia JZ, Rico-Lastres P, Le Roux A-L. (2017). Force triggers YAP nuclear entry by regulating transport across nuclear pores. Cell , 1397–1410. [DOI] [PubMed] [Google Scholar]
  13. Faria EC, Ma N, Gazi E, Gardner P, Brown M, Clarke NW, Snook RD. (2008). Measurement of elastic properties of prostate cancer cells using AFM. Analyst , 1498–1500. [DOI] [PubMed] [Google Scholar]
  14. Fidler IJ. (2003). The pathogenesis of cancer metastasis: the ‘seed and soil’ hypothesis revisited. Nat Rev Cancer , 453–458. [DOI] [PubMed] [Google Scholar]
  15. Gates BD, Xu Q, Stewart M, Ryan D, Willson CG, Whitesides GM. (2005). New approaches to nanofabrication: molding, printing, and other techniques. Chem Rev , 1171–1196. [DOI] [PubMed] [Google Scholar]
  16. Gegenfurtner FA, Jahn B, Wagner H, Ziegenhain C, Enard W, Geistlinger L, Rädler JO, Vollmar AM, Zahler S. (2018). Micropatterning as a tool to identify regulatory triggers and kinetics of actin-mediated endothelial mechanosensing. J Cell Sci , jcs212886. [DOI] [PubMed] [Google Scholar]
  17. Guck J, Ananthakrishnan R, Mahmood H, Moon TJ, Cunningham CC, Käs JA. (2001). The optical stretcher: a novel laser tool to micromanipulate cells. Biophys J , 767–784. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Guck J, Schinkinger S, Lincoln B, Wottawah F, Ebert S, Romeyke M, Lenz D, Erickson HM, Ananthakrishnan R, Mitchell D. (2005). Optical deformability as an inherent cell marker for testing malignant transformation and metastatic competence. Biophys J , 3689–3698. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Hanahan D, Weinberg RA. (2000). The hallmarks of cancer. Cell , 57–70. [DOI] [PubMed] [Google Scholar]
  20. Hanahan D, Weinberg RA. (2011). Hallmarks of cancer: the next generation. Cell , 646–674. [DOI] [PubMed] [Google Scholar]
  21. Hou HW, Li Q, Lee G, Kumar A, Ong C, Lim CT. (2009). Deformability study of breast cancer cells using microfluidics. Biomed Microdevices , 557–564. [DOI] [PubMed] [Google Scholar]
  22. Hutter JL, Bechhoefer J. (1993). Calibration of atomic-force microscope tips. Rev Sci Instrum , 1868–1873. [Google Scholar]
  23. Kumar S, Weaver VM. (2009). Mechanics, malignancy, and metastasis: the force journey of a tumor cell. Cancer Metast Rev , 113–127. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Lam WA, Rosenbluth MJ, Fletcher DA. (2008). Increased leukaemia cell stiffness is associated with symptoms of leucostasis in paediatric acute lymphoblastic leukaemia. Brit J Haematol , 497–501. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Lambert AW, Pattabiraman DR, Weinberg RA. (2017). Emerging biological principles of metastasis. Cell , 670–691. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Lee LM, Liu AP. (2014). The application of micropipette aspiration in molecular mechanics of single cells. J Nanotechnol Eng Med , 040902. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Lee S, Kassianidou E, Kumar S. (2018). Actomyosin stress fiber subtypes have unique viscoelastic properties and roles in tension generation. Mol Biol Cell , 1992–2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Lekka M, Laidler P. (2009). Applicability of AFM in cancer detection. Nat Nanotechnol , 72. [DOI] [PubMed] [Google Scholar]
  29. Lekka M, Laidler P, Gil D, Lekki J, Stachura Z, Hrynmiewicz AZ. (1999). Elasticity of normal and cancerous human bladder cells studied by scanning force microscopy. Eur Biophys J , 312–316. [DOI] [PubMed] [Google Scholar]
  30. Li Q, Lee G, Ong C, Lim C. (2008). AFM indentation study of breast cancer cells. Biochem Biophys Res Commun , 609–613. [DOI] [PubMed] [Google Scholar]
  31. Lopez JI, Kang I, You W-K, McDonald DM, Weaver VM. (2011). In situ force mapping of mammary gland transformation. Integr Biol , 910–921. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Mosier J, Rahman-Zaman A, Zanotelli M, VanderBurgh J, Bordeleau F, Hoffman B, Reinhart-King C. (2019). Extent of cell confinement in microtracks affects speed and results in differential matrix strains. Biophys J , 1692–1701. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Nardone G, Oliver-De La Cruz J, Vrbsky J, Martini C, Pribyl J, Skládal P, Pešl M, Caluori G, Pagliari S, Martino F. (2017). YAP regulates cell mechanics by controlling focal adhesion assembly. Nat Commun , 15321. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Pachenari M, Seyedpour SM, Janmaleki M, Shayan SB, Taranejoo S, Hosseinkhani H. (2014). Mechanical properties of cancer cytoskeleton depend on actin filaments to microtubules content: investigating different grades of colon cancer cell lines. J Biomech , 373–379. [DOI] [PubMed] [Google Scholar]
  35. Pickup MW, Mouw JK, Weaver VM. (2014). The extracellular matrix modulates the hallmarks of cancer. EMBO Rep , 1243–1253. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Raghunathan VK, Dreier B, Morgan JT, Tuyen BC, Rose BW, Reilly CM, Russell P, Murphy CJ. (2014). Involvement of YAP, TAZ and HSP90 in contact guidance and intercellular junction formation in corneal epithelial cells. PLoS One , e109811. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Raman PS, Paul CD, Stroka KM, Konstantopoulos K. (2013). Probing cell traction forces in confined microenvironments. Lab Chip , 4599–4607. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Rebelo LM, de Sousa JS, Mendes Filho J, Radmacher M. (2013). Comparison of the viscoelastic properties of cells from different kidney cancer phenotypes measured with atomic force microscopy. Nanotechnology , 055102. [DOI] [PubMed] [Google Scholar]
  39. Rianna C, Radmacher M. (2017a). Comparison of viscoelastic properties of cancer and normal thyroid cells on different stiffness substrates. Eur Biophys J , 309–324. [DOI] [PubMed] [Google Scholar]
  40. Rianna C, Radmacher M. (2017b). Influence of microenvironment topography and stiffness on the mechanics and motility of normal and cancer renal cells. Nanoscale , 11222–11230. [DOI] [PubMed] [Google Scholar]
  41. Schierbaum N, Rheinlaender J, Schäffer TE. (2019). Combined atomic force microscopy (AFM) and traction force microscopy (TFM) reveals a correlation between viscoelastic material properties and contractile prestress of living cells. Soft Matter , 1721–1729. [DOI] [PubMed] [Google Scholar]
  42. Schindelin J, Arganda-Carreras I, Frise E, Kaynig V, Longair M, Pietzsch T, Preibisch S, Rueden C, Saalfeld S, Schmid B. (2012). Fiji: an open-source platform for biological-image analysis. Nat Methods , 676–682. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Smith CL, Kilic O, Schiapparelli P, Guerrero-Cazares H, Kim D-H, Sedora-Roman NI, Gupta S, O’Donnell T, Chaichana KL, Rodriguez FJ. (2016). Migration phenotype of brain-cancer cells predicts patient outcomes. Cell Rep , 2616–2624. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Staunton JR, Doss BL, Lindsay S, Ros R. (2016). Correlating confocal microscopy and atomic force indentation reveals metastatic cancer cells stiffen during invasion into collagen I matrices. Sci Rep , 19686. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Swaminathan V, Mythreye K, O’Brien ET, Berchuck A, Blobe GC, Superfine R. (2011). Mechanical stiffness grades metastatic potential in patient tumor cells and in cancer cell lines. Cancer Res , 5075–5080. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Talmadge JE, Fidler IJ. (2010). AACR centennial series: the biology of cancer metastasis: historical perspective. Cancer Res , 5649–5669. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Wang N, Tolic-Nørrelykke IM, Chen J, Mijailovich SM, Butler JP, Fredberg JJ, Stamenovic D. (2002). Cell prestress. I. Stiffness and prestress are closely associated in adherent contractile cells. Am J Physiol , C606–C616. [DOI] [PubMed] [Google Scholar]
  48. Xia Y, McClelland JJ, Gupta R, Qin D, Zhao XM, Sohn LL, Celotta RJ, Whitesides GM. (1997). Replica molding using polymeric materials: a practical step toward nanomanufacturing. Adv Mater , 147–149. [Google Scholar]
  49. Xu W, Mezencev R, Kim B, Wang L, McDonald J, Sulchek T. (2012). Cell stiffness is a biomarker of the metastatic potential of ovarian cancer cells. PLoS One , e46609. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Zhang G, Long M, Wu Z-Z, Yu W-Q. (2002). Mechanical properties of hepatocellular carcinoma cells. World J Gastroenterol , 243. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Click here for additional data file. (4.2MB, pdf)

Articles from Molecular Biology of the Cell are provided here courtesy of American Society for Cell Biology

RESOURCES