Characterizing the cellular architecture of dynamically remodeling vascular tissue using 3-D image analysis and virtual reconstruction

Abstract

Epithelial tubules form critical structures in lung, kidney, and vascular tissues. However, the processes that control their morphogenesis and physiological expansion and contraction are not well understood. Here we examine the dynamic remodeling of epithelial tubes in vivo using a novel model system: the extracorporeal vasculature of Botryllus schlosseri, in which the disruption of the basement membrane triggers rapid, massive vascular retraction without loss of barrier function. We developed and implemented 3-D image analysis and virtual reconstruction tools to characterize the cellular morphology of the vascular wall in unmanipulated vessels and during retraction. In both control and regressed conditions, cells within the vascular wall were planar polarized, with an integrin- and curvature-dependent axial elongation of cells and a robust circumferential alignment of actin bundles. Surprisingly, we found no measurable differences in morphology between normal and retracting vessels under extracellular matrix (ECM) disruption. However, inhibition of integrin signaling through focal adhesion kinase inhibition caused disruption of cellular actin organization. Our results demonstrate that epithelial tubes can maintain tissue organization even during extreme remodeling events, but that the robust response to mechanical signals—such as the response to loss of vascular tension after ECM disruption—requires functional force sensing machinery via integrin signaling.

INTRODUCTION

Epithelial sheets in living organisms are highly dynamic and must be able to remodel sheet geometry–through addition, removal, or migration of cells within the sheet—while simultaneously maintaining barrier function through stable cell–cell adhesion. This balance places high demands on epithelial cells, requiring them to both generate and respond to forces through integration of mechanical and biochemical pathways. Thus, understanding epithelial organization and dynamics provides fundamental insights into biomechanical signaling pathways that are applicable to a wide range of biological processes, including embryonic development, angiogenesis, wound healing, and metastasis.

Some of the most tractable experimental model systems for epithelial dynamics are variations of cultured epithelial cells grown on glass coverslips; these can be imaged with high spatial and temporal resolution and have the advantage of a well-controlled chemical environment through use of perfusion systems. For example, cultured monolayer models have enabled investigations of how vascular cells respond to various chemical and physical stimuli (Dewey et al., 1981; Galbraith et al., 1998; Kaunas et al., 2005; Gu et al., 2011; Kutys and Chen, 2016). One major drawback of these assays, however, is that glass or plastic substrates are much stiffer than the natural tissue environment of the cells, and in the case of vascular cells, the planar geometry is not physiological. Thus, it is unclear how relevant the insights gained in these artificial conditions ultimately are in vivo. Conversely, high-resolution imaging of epithelial sheets in their natural mechanical environment in vivo is not always feasible, since many epithelial and vascular tissues of interest are found deep within organisms—this constraint limits the available imaging approaches and leads to significant signal extinction and scattering, fundamentally limiting any optical analysis.

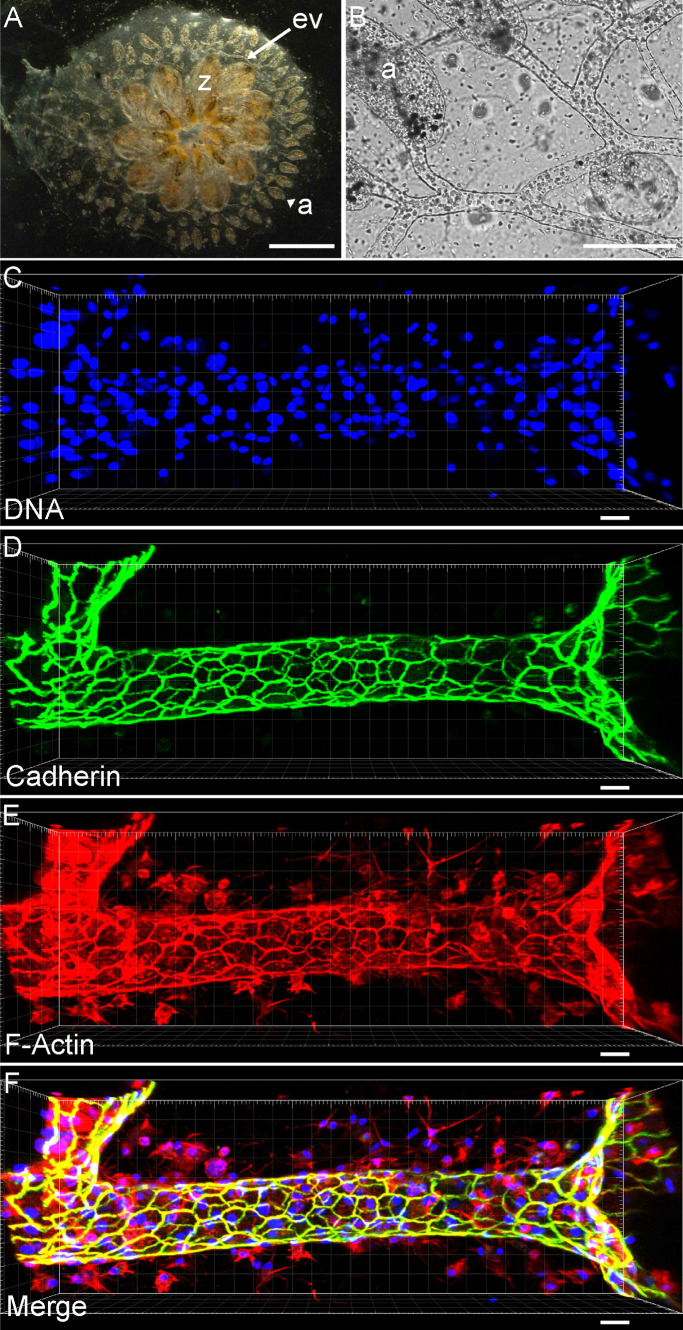
Here we address this challenge using a unique model system: the extracorporeal vasculature of the ascidian (sea squirt) Botryllus schlosseri. Botryllus is an invertebrate chordate closely related to vertebrates (Gasparini et al., 2015; Holland, 2016; Kassmer et al., 2016) and has a large, transparent extracorporeal vascular network that allows unparalleled accessibility to study vascular biology in vivo (Tiozzo et al., 2008; Rodriguez, Braden, et al., 2017). These blood vessels are large (with an average diameter of ∼50 μm) and consist of a single tubular monolayer of myoepithelial cells that create a massive branching vascular network encompassing areas greater than 10 cm². These vessels are embedded in a transparent, extracellular matrix (ECM) called the tunic, can be directly manipulated, and are uniquely amenable to high-resolution imaging (Figure 1 and Supplemental Figure S1). At the periphery of the vascular bed, the vessels terminate in structures called ampullae, which are bulbous, blind-ended extensions of the vessels themselves. The vascular cells are contractile, and the Botryllus vasculature consists of a single tube, without layers of smooth muscle or pericytes. Finally, the vessel architecture is inverted in comparison to mammals: the vascular cells are not endothelial; rather the basal side of the vessel epithelium faces the lumen, with the basement membrane forming the inner layer of the vessel.

FIGURE 1:

The extracorporeal vasculature of B. schlosseri. (A) Ventral view of a single colony of Botryllus, showing all individuals (zooid = z) at the center that are interconnected by an extracorporeal vasculature (ev) that extends out to blind end protrusions (ampulla = a). (Scale bar = 2 mm.) (B) Bright field micrograph showing blood vessels and ampullae. (Scale bar = 1 mm.) (C–F) Maximal projection of a confocal micrograph of a single blood vessel stained for DNA in blue (Scale bar = 25 μm) (C), pan-cadherin in green (D), and F-actin in red (E). (F) Merged maximal projections.

Under normal conditions, the Botryllus vasculature is highly dynamic, with individual vessels undergoing expansion and retraction on the order of millimeters on a daily basis, and during high-growth periods the entire vascular bed can double in size every week. Angiogenesis can also be triggered experimentally: the extracorporeal vasculature can be surgically ablated; the vessels will clot, remodel, and begin proliferating, resulting in regeneration of the entire bed within 72 h (Tiozzo et al., 2008; Braden et al., 2014). Finally, we have recently demonstrated that we can also induce regression of the vasculature via direct manipulation of the stiffness of the basement membrane: Specifically, exposing the vasculature to β-aminopropionitrile fumarate (BAPN), which blocks collagen cross-linking, and which within a few hours of treatment completely changes the structure of collagen fibers in the basement membrane (Supplemental Videos 1 and 2). We have shown that the corresponding change of ECM stiffness is sensed through integrin-dependent pathways and causes anoikis of a subset of cells, which are then extruded basally and removed by phagocytic cells in circulation (Rodriguez, Braden, et al., 2017). This loss and removal of individual cells induces a rapid macroscopic regression of blood vessels on the order of millimeters in a time period of 16 h.

Movie S1.

Download video file ^{(1.1MB, mov)}

3D reconstruction of the blood vessel. Movie of 3D reconstruction of the blood vessel with each cell represented by a different color and each face of the cell highlighted.

Movie S2.

Download video file ^{(9.6MB, avi)}

Time-lapse video of BAPN induced regression of the extracorporeal vasculature. Bright field dorsal view of Botryllus schlosseri colony with BAPN treatment for 16 hours incubated in 400 μM BAPN.

Importantly, while this regression constitutes a massive macroscopic morphological change, it produces no pathological damage to the organism—regression progresses without bleeding or plasma leakage, indicating that the vessels maintain barrier function. Regression is also fully reversible: following removal of BAPN, the vessels begin proliferating and regenerate the entire vascular bed. As vessels are dynamic and regress even under normal conditions, we hypothesize that BAPN treatment induces normal physiological responses to changes in the mechanical environment. One interpretation is that the collapse of ECM tonus is interpreted mechanically by the epithelial sheet as cellular overcrowding, to which it responds with a homeostatic cell density reduction (Eisenhoffer et al., 2012; Marinari et al., 2012). This suggests that under normal conditions, changes in the structure of the basement membrane and other mechanosensation events precede and trigger vascular regression or branching, as has been shown for epithelial remodeling events in other model systems (Ingber and Folkman, 1988). Finally, a number of small molecule inhibitors of the integrin pathway (e.g., inhibition of focal adhesion kinase [FAK]) can also induce vascular regression in a manner similar to the disruption of the basement membrane (Rodriguez, Braden, et al., 2017) (Supplemental Videos 3 and 4). This suggests that cells sense loss of anchorage to the ECM due to collagen network disruption via an integrin-signaling pathway and that loss of this tonic signal induces cell death (Ives et al., 1986).

Movie S3.

Download video file ^{(1.5MB, mov)}

Close-up video of fluorescently labeled blood vessels during regression induced by BAPN treatment. Time-lapse of a subset of blood vessels from a colony injected with BSA-594 which labels vascular cells, the colony was incubated in FSW containing the BAPN (400 μM) treatment for 16 hours.

Movie S4.

Download video file ^{(220.1KB, mov)}

Time-lapse video of FAKI induced regression of the extracorporeal vasculature. Bright field dorsal view of Botryllus schlosseri colony with FAKI treatment for 10 hours incubated in 50 μM FAKI.

The ability to experimentally induce growth and regression of the Botryllus vasculature provides a unique model system in which to study morphogenesis and maintenance of epithelial tubes in an in vivo vascular network. In this study, we focus on the induced regression event, which allows us to examine large-scale remodeling of epithelial sheets under physiological conditions. To capitalize fully on the strengths of this system, we aim to develop quantitative approaches to examine tissue morphology and multiscale organization to provide insight into the mechanical and molecular mechanisms that underlie dynamic remodeling of the vasculature at both tissue and cellular resolution. To achieve this, we developed and implemented a procedure for a detailed reconstruction of the cellular architecture and morphology using high-resolution 3-D confocal image stacks of immunostained samples of Botryllus vasculature. Using this approach, we examined changes in cellular organization and cytoskeletal structure under conditions of normal growth and chemically induced vascular regression. We found no stark differences in morphology between normal and retracting vessels under ECM disruption; however, inhibition of integrin signaling caused significant disruption of cellular actin organization. Our results provide insight into the organization and properties of cells within a dynamic remodeling tissue while demonstrating the remarkable ability of organisms to maintain barrier function and structure in extreme conditions.

RESULTS

Three-dimensional reconstruction of the epithelial sheet

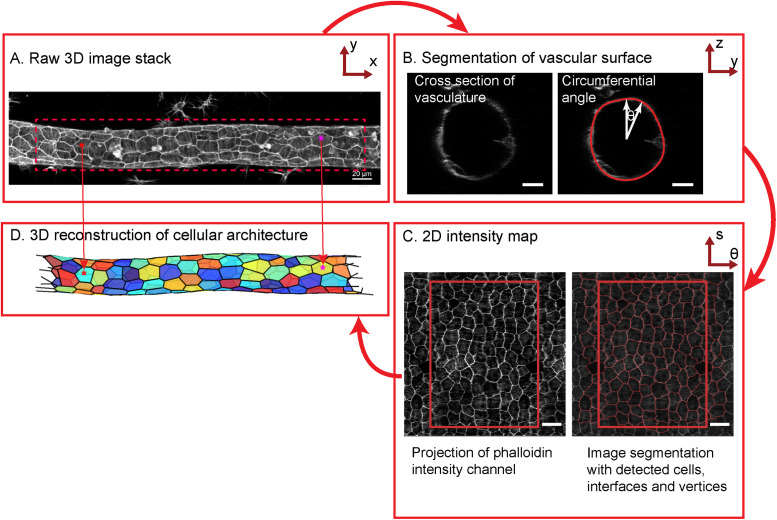
Our reconstruction of the cellular architecture and morphology is based on high-resolution 3-D confocal image stacks of immunostained samples of Botryllus vasculature (Figure 2A). The surface of the cylindrical epithelial sheet was defined via staining with a cadherin antibody, followed by segmenting the 2-D cross-sectional profile, while stepping this cross-section along the long axis of the blood vessel (the “vascular axis”) (Figure 2B) and attaching cylindrical coordinates to each surface point in the process (axial distance s, radial distance r from the center, and angle θ). Using that segmented surface, raw fluorescence intensities in the available color channels were interpolated into 2-D intensity maps using regular-spaced bins of the axial distance s and of the circumferential angle θ. The resulting intensity maps thus conceptually represent the “unwrapped” epithelial sheets in the different color channels (Figure 2C, left panel, showing the example of the “unwrapped” map for rhodamine-labeled phalloidin; scale bar 10 μm; also see Supplemental Figure S2, A–C). We subsequently performed standard 2-D image analysis on these 2-D maps of the unwrapped sheets, using watershed segmentation to segment the cell–cell interfaces and then calculate the position of vertices and cell centroids (Figure 2C right panel). Importantly, we retain the inherently 3-dimensional structure of the sheet by using the surface points’ radial distance information from the original surface segmentation, such that every point on the 2-D intensity map can be mapped back to its true position on the 3-D curved surface. We used this approach to create a triangulated reconstruction of the complete vascular architecture, using the 3-D positions of the cell vertices and cell centroids that were identified in the 2-D intensity map (Figure 2D; see Materials and Methods for additional details).

FIGURE 2:

Overview of image analysis workflow. (A) Mean projection of the raw 3-D image stack along the z-axis. (Scale bar = 20 µm.) (B) Raw resized axial section of the vessel with the detected surface overlaid in red. (Scale bar = 10 µm.) (C) Left panel: 2-D projection of the vessel obtained by unwrapping the intensities along each axial section. Right panel: Intensity projection with cell outlines detected by watershed segmentation overlaid in red. Rectangular boxes correspond to nonrepeat regions. (Scale bar = 10 µm.) (D) 3-D reconstruction of the blood vessel with each cell represented by a different color.

Actin bundles are preferentially oriented into circumferential direction

We first used this quantitative analysis approach to characterize the organization and properties of cells within the normal Botryllus vasculature, and then to compare the wild-type features to those of cells in regressing vessels in animals treated with BAPN to disrupt ECM organization, or the FAK inhibitor 14 (FAKI) to disrupt integrin signaling. Supplemental Figure S3 shows partial maximum projections of the blood vessels in homeostasis in wild-type, BAPN-treated, and FAKI-treated animals. In all cases, fixation of BAPN-treated animals was performed 8 h after the drug was applied, and 6 h after FAKI application, which for both drugs constitutes the time point where vessels are regressing at maximum velocity (Rodriguez, Braden, et al., 2017). Our sample size of analyzed images consisted of n = 30 blood vessels in control conditions (from 10 unique animals), with a range of 26–219 cells per blood vessel for a total of k = 2990 cells; in BAPN-treated conditions, n = 20 blood vessels (from nine unique animals) with a range of 28–185 cells per blood vessel for a total of k = 1660 cells; in FAKI-treated conditions, n = 13 blood vessels (from five unique animals) with a range of 23–257 cells per blood vessel for a total of k = 1391 cells. The same data sample was used for all the analyses shown in Figures 3 – 5.

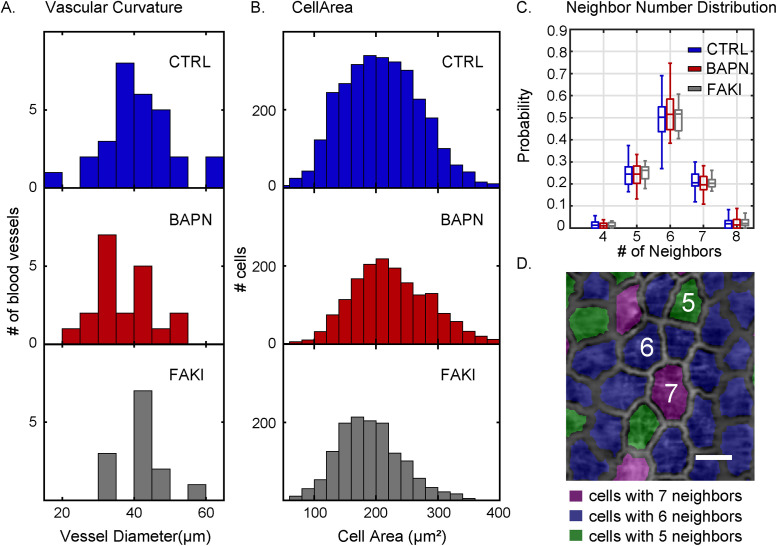
FIGURE 3:

Cell morphometrics show no significant difference between control and BAPN-treated vessels. (A) Distribution of vascular curvature, as assessed by the distribution of mean blood vessel diameters, analyzed under control (CTRL, top, blue), BAPN-treatment (middle, red), and FAKI-treatment (bottom, gray) conditions. (B) Distribution of cell areas for control (top, blue), BAPN-treated (middle, red), and FAKI-treated (bottom, gray) animals. (C) Distribution of the number of nearest cellular neighbors of control (blue), BAPN-treated (red) and FAKI-treated (gray) animals. Box plots show the central median, where edges of the boxes represent the 25th and 75th percentiles (q₁ and q₃, respectively); whiskers correspond to q₁-1.5 (IQR) and q₃+1.5 (IQR). (D) 2-D projection of the blood vessel with cells colored based on their neighbor number. (Scale bar = 20 µm.) For all the panels, the number of vessels (n) and number of cells (k) used were n = 30, k = 2990 (CTRL); n = 20, k = 1660 (BAPN-treated); and n = 13, k = 1391 (FAKI-treated).

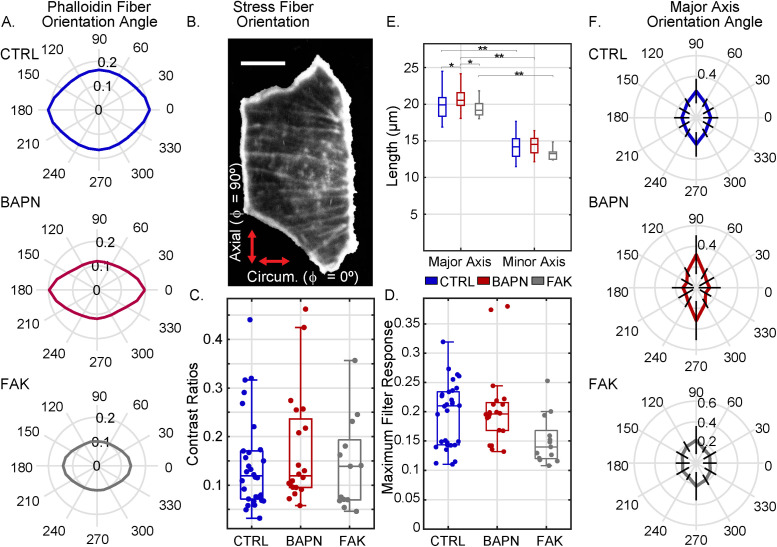
FIGURE 4:

Both cell morphology and actin fiber orientation are planar polarized in the axial versus circumferential direction. (A) Quantification of preferred actin fiber orientation, as determined by the response of a rotating line filter. The radial amplitude in the polar plot in each panel represents the line filter response in that direction (averaged over the entire 2-D map) in one representative blood vessel in each condition (specifically, the vessel with the median response intensity for that condition). Control, CTRL = blue (top plot), BAPN-treated = red (middle plot), and FAKI-treated = gray (bottom plot). (B) Image of one representative control cell (with background masked out) with actin filaments stained with phalloidin. (Scale bar = 10 µm.) (C) Directional preference, defined as the contrast ratio of maximum vs. minimum line filter responses like those shown in panel A, with c = (max – min)/(max + min) of all vessels in control, BAPN-treatment, and FAKI-treatment conditions. (D) Absolute value of the maximum line filter response (like those shown in panel A) for each vessel for control and BAPN- and FAKI-treated vessels. (E) Mean cellular major and minor axis lengths (averaged over all cells in each individual vessel) in control, BAPN-treatment, and FAKI-treatment conditions (*p < 0.05 and **p < 10^–8, two-sample t test). (F) Preferred major axis orientation angle of the cells. The radial amplitude in the polar plot represents the mean normalized probability—averaged over all vessels in that condition—where the radial lines are error bars representing SD. For all the panels in this figure, number of vessels (n) and number of cells (k) were n = 30, k = 2990 (CTRL); n = 20, k = 1660 (BAPN treated); and n = 13, k = 1391 (FAKI treated). Box plots show the central median, and edges of the boxes represent 25th and 75th percentiles (q₁ and q₃, respectively); whiskers correspond to q₁-1.5 (IQR) and q₃+1.5 (IQR).

FIGURE 5:

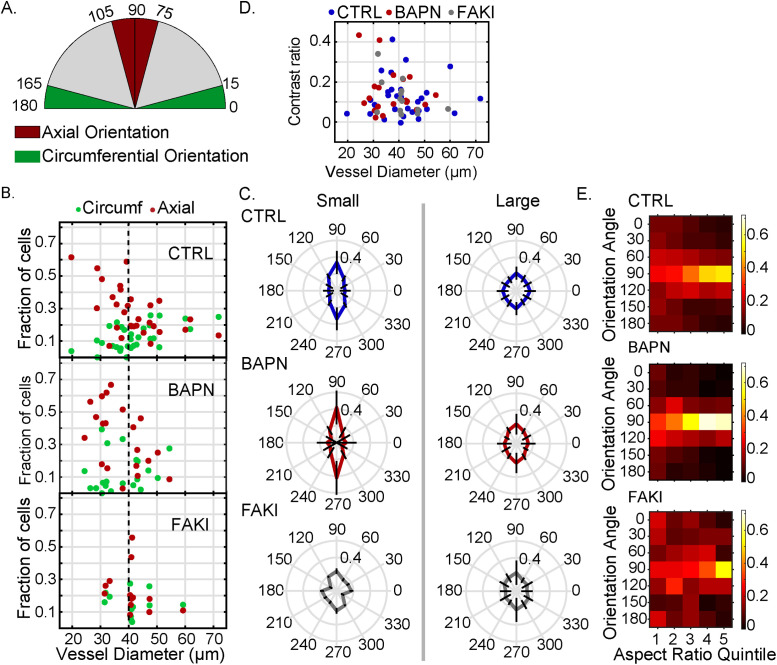
Planar polarity is enhanced in smaller diameters. (A) Schematic showing categorization of cells into axial (75°–105°), circumferential (0°–15° and 165°–180°), and other (15°–75° and 105°–165°) categories based on their major axis orientation angle. (B) Fraction of cells with major axis oriented along axial (red) or circumferential (green) direction as a function of bood vessel diameter. (C) Polar histogram of the major axis orientation angle of the cells in small (diameter ≤ 40 µm) and large (diameter > 40 µm) vessels; the radial amplitude represents the mean probability distribution, and the thick black lines pointing radially along different polar angles represent the SD. (D) Mean contrast ratio of filtered phalloidin intensity of cells as a function of blood vessel diameter. Contrast ratio = (circumferential response – axial response)/(circumferential response + axial response). (E) Heat maps of the normalized probability density as a function of major axis orientation angle (in angle bins of 30°) and of cell aspect ratio quintile for predominantly axially oriented blood vessels. Control = blue, BAPN treatment = red, and FAKI treatment = gray. For all the panels number of vessels (n) and number of cells (k) used were n = 30, k = 2990 (CTRL); n = 20, k = 1660 (BAPN treated), and n = 13, k = 1391 (FAKI treated).

We found that most blood vessels in our sample ranged in dia­meter from approximately 25 to 55 µm (Figure 3A), where vessel diameter was calculated as the average diameter along each vessel’s axis. The cell area (weighted mean ± weighted SD) was 211 ± 40 μm² in control, 227 ± 35 μm² in BAPN-treated animals (difference from control not significant, two-sample t test), and 190 ± 26 μm² in FAKI-treated animals (difference from control not significant, difference from BAPN significant at p = 0.005, two-sample t test) (Figure 3B). In all three cases, the tissue had a primarily hexagonal morphology (Figures 2C and 3, C and D). Thus, somewhat surprisingly, for these specific metrics (cell area and number of nearest neighbors) we found no drastic differences in basic tissue morphology, despite the presence of significant macroscopic tissue remodeling of blood vessels (Supplemental Videos 1, 3 and 5).

Movie S5.

Download video file ^{(345.4KB, mov)}

Close-up video of fluorescently labeled blood vessels during regression induced by FAKI treatment. Time-lapse of a subset of blood vessels from a colony injected with BSA-594 which labels vascular cells, the colony was incubated in filtered sea water containing the FAKI (50 μM) treatment for 10 hours.

To test whether the cells responded to the anisotropies in their mechanical environment—since they experience lowest curvature within the tubular sheet into the axial direction and highest curvature into the circumferential direction—we next probed for morphological anisotropies within the plane of the sheet.

The myoepithelial cells that form the lining of Botryllus blood vessels contain actin-rich bundles that are brightly labeled with the actin-binding dye phalloidin, and resemble the cross-linked, contractile actin bundles called stress fibers in mammalian cells (Chazotte, 2010; Rodriguez, Braden, et al., 2017). We examined the preferential orientation of these actin bundles in the 2-D intensity maps of phalloidin intensity by performing line filtering with a variable filter orientation (i.e., variable spatial angle ϕ within the sheet) (see Material and Methods; Supplemental Figure S4, A–H). The filter response—which we calculate as the mean of the absolute image intensity after line filtering —is maximized when the orientation of the line filter element is aligned with the predominant orientation of any fiber-like features in the image. We observed that the line-filtered intensity was significantly increased for a filter orientation into the circumferential direction (representative sample plots in Figure 4A), indicating that the phalloidin-stained actin bundles have a predominantly circumferential orientation; this directional preference was extremely robust across all vessels and conditions (Supplemental Figure S4, I–L). This quantitative finding is consistent with visual inspection of the phalloidin-stained images, which often show a distinct visible horizontal orientation of fiber-like structures (Figure 4B and Supplemental Figure S4C). On the basis of these results, we calculated directional preference mathematically as the contrast c between the maximum and minimum filter responses (i.e., the filtered intensities into those directions that either maximize or minimize signal), c = (I_max – I_min)/(I_max + I_min). This directional preference is conceptually similar to the eccentricity of the polar plot in Figure 4A; thus, this metric designates relative directional preference without regard to absolute filter response magnitude. Numerically, this contrast metric will have a value of 0.2 if the maximum is 50% larger than the minimum and ∼0.1 if the maximum is 25% larger than the minimum. This directional preference value was not normally distributed (Figure 4C), with median (IQR = interquartile range) being 0.12 (IQR = 0.10) in control, 0.12 (IQR = 0.14) for BAPN-, and 0.14 (IQR = 0.12) for FAK-inhibited animals (with the differences between control versus BAPN and control versus FAKI not statistically significant, two-sided Kolmogorov–Smirnov test). This suggests that the directional preference of the actin bundle architecture is mostly conserved in BAPN and in FAKI.

In addition, we examined the absolute magnitude of the maximum line filter response, which reflects the degree to which the image structures are fiber-like in appearance (as opposed to punctate, or homogeneous). This maximum line filter intensity was also not normally distributed (Figure 4D), with the median being 0.21 (IQR = 0.09) in control, 0.20 (IQR = 0.05) for BAPN, and 0.14 (IQR = 0.05) for FAKI animals. In this case, the difference between control versus BAPN treatment was not statistically significant, but the difference between control versus FAKI-treated animals was statistically significant at p = 0.016 (both two-sided Kolmogorov–Smirnov test). This indicates that while the FAKI-treated animals do preserve the overall directional preference for circumferential orientation in the existing fibers, there is a substantial disruption of actin bundle organization overall, reflected in a reduction of the density and contrast of fiber-like features in the image (Supplemental Figure S4, I–K). This quantitative result is consistent with the visual impression of actin fiber organization being disrupted or even entirely absent in some FAKI-treated animals (Supplemental Figure S4C).

Vascular epithelial cells are net axially elongated in homeostasis and induced regression

In examining the cells’ major and minor axis lengths and orientations, we found that the major and minor axis lengths were (weighted mean ± weighted SD) 19.7 ± 1.7 μm versus 14.0 ± 0.5 μm for control, 20.8 ± 1.7 μm versus 14.4 ± 1.3 μm for BAPN treatment, and 19.2 ± 1.4 μm versus 13.1 ± 0.9 μm for FAKI treatment (Figure 4E). The resulting aspect ratio was (weighted mean ± weighted SD) 1.41 ± 0.08 for control, 1.44 ± 0.10 for BAPN (difference from control not significant, two-sample t test), and 1.46 ± 0.04 for FAKI (difference from control significant at p = 0.02, two-sample t test).

Importantly, the orientation of the cells’ major axis significantly favored the axial direction over the circumferential direction (Figure 4F) by roughly a factor of two (calculated by dividing axial frequency by circumferential frequency). This axial preference was increased relative to control in BAPN-treated animals and decreased relative to control in FAKI animals. Specifically, the fractions of cells oriented into a 30° axial angle window versus a 30° circumferential angle window were (weighted mean ± weighted SD) 25.7 ± 11.8% versus 14.0 ± 7.3% in control conditions (significance of axial–circumferential difference p = 7.65 × 10^–5, two-sample t test), 31.8 ± 18.7% versus 12.9 ± 10.6% in BAPN-treated animals (significance of axial–circumferential difference p = 9.0 × 10^–4, two-sample t test), and 22.3 ± 13.5% versus 13.2 ± 6.6% in FAKI-treated animals (significance of axial–circumferential difference p = 0.049, two-sample t test), with the differences between conditions being not statistically significant. Thus, the vascular morphology is planar polarized (anisotropic within the plane of the sheet) in all measured conditions, with a net preference for elongation of cells into the axial direction, and the strength of this preference varies slightly between conditions. In addition, we also found an axial preference in the orientation of cell–cell interfaces (Supplemental Figure S5A), which is consistent with a “ladder-like” morphology of the tissue, with almost rectangular cells in many cases (Supplemental Figure S5, B and C).

Planar polarity depends on vascular curvature

We have now established that the epithelial architecture within the blood vessels is typically planar polarized, where actin bundles within cells are net preferentially aligned into the circumferential direction, while the cells themselves are net preferentially elongated into the axial direction. To gain further insight into the relationship of these observations to curvature, we asked the following: 1) Does this observed polarity depend on epithelial sheet curvature, i.e., does polarity increase in highly curved vessels? 2) Does a cell’s orientation depend on its relative elongation?

To answer these questions, we performed further directionally resolved analyses on cell properties. First, to address whether the degree of cellular polarization depends on vascular curvature, we measured the distribution of cells’ orientation angles as a function of vascular diameter. We designated the angular range of 90 ± 15° as representing cells with “axial” orientation and the range of 0 ± 15° as “circumferential” orientation (Figure 5A and Supplemental Figure S5D). Thus, the total range for axial and circumferential categories was 30° each; this means that for a perfectly isotropic case—in which cells have no directional preference whatsoever—we would expect to see (30°/180°) = 16.7% of cells fall into either the “axial” or the “circumferential” categories.

For blood vessels with diameters >40 μm, we observed that the proportions of “axial” and “circumferential” cell orientations were close to the reference values for an isotropic distribution in all conditions (Figure 5, B and C); while all conditions had a net systematic axial directional preference, the differences were not statistically significant (see Table 1). However, as the vascular diameter decreased below 40 μm, both in control conditions and in BAPN-treated animals, cells showed a growing preference for axial orientation at the expense of the circumferential one, reaching a fraction of >50% axially oriented cells in some individual blood vessels (Figure 5, B and C), which constitutes a threefold increase over an isotropic distribution; these differences were significant at p < 10^–3 (see Table 1). In FAKI cells, this increase of the axial preference for small vessel diameters was absent, and the observed small axial preference was similar to the baseline of large vessel diameters (Figure 5C).

TABLE 1:

Fraction of cells oriented into different planar directions.

	Control fraction				BAPN fraction				FAK fraction
	n	Axial	Circumferential	p	n	Axial	Circumferential	p	n	Axial	Circumferential	p
d < 40	14	0.34 ± 0.14	0.10 ±0.06	4.8 × 10–5	12	0.42 ± 0.20	0.11 ± 0.12	8.9 × 10–4	3	0.24 ± 0.03	0.18 ± 0.02	0.11
d > 40	16	0.21 ± 0.08	0.16 ±0.07	0.07	8	0.23 ± 0.12	0.14 ± 0.09	0.13	10	0.22 ± 0.14	0.13 ± 0.06	0.08

n = number of blood vessels, p = p value of two-sample t test performed on weighted mean of axial and circumferential fractions. Significant p values (p < 0.05) are shown in bold font. Fractions are shown as (weighted mean ± weighted SD).

Interestingly, in all observed blood vessels—both in control and in BAPN-treated animals, and even in the FAKI-treated animals that experience a strong loss of overall fiber content and organization—the existing actin fibers retained their preference for circumferential orientation (Figure 5D), regardless of whether cell orientation was isotropic or axially polarized, and across a wide range of vascular diameters. Thus, we conclude that the observation of planar polarity has two independent components: 1) the preferentially circumferential orientation of actin bundles, which is extremely robust; and 2) the preferentially axial orientation of cell axes, which is fairly weak for large vascular diameters (i.e., >40 μm), but which becomes more pronounced for vascular diameters below 40 μm in a FAK-dependent manner.

In addition, we observed visually that in some blood vessels with a strong axial orientation preference, the cells also appeared to be more elongated overall (e.g., Supplemental Figure S5B). We speculated that this correlation might arise from a tendency of cells to change shape in order to reduce their net circumferential “exposure” in the blood vessel. If this were the case, we would expect that, within the population of cells from a given blood vessel, the more elongated cells should have a stronger preference for being axially oriented than the round cells. We tested this hypothesis in those blood vessels that showed a polarized phenotype—defined as those in which the fraction of axially oriented cells exceeded 30%. For each blood vessel of this phenotype, we divided the cell population into quintiles according to their elongation (as measured by cells’ major-to-minor axis aspect ratio) and determined the relative probability density as a function of orientation angle in bins of 30° (Figure 5E). We found that cells indeed show a progressive axial orientation preference with increasing elongation: there was almost no observable preference for axial orientation in the least elongated quintile of cells, but the preference increased with increasing aspect ratio and reached its maximum in the most elongated quintile, for all conditions. Specifically, in control cells, the probability for axial orientation (mean ± SD) in the least elongated group of cells was only 24.0 ± 4.4% (which is only a mild increase over the isotropic probability of 16.7%), compared with a 57.9 ± 4.7% probability for axial orientation among the most elongated group of cells (two-sided Kolmogorov–Smirnov test of the probabilities in these two quintiles against each other p < 10^–3). This result is consistent with the notion that within this polarized phenotype, cell morphology minimizes the cells’ circumferential width. This effect—where the cells’ probability of axial orientation increased from the least to the most elongated quintile—was also present for BAPN treatment, where the probability (mean ± SD) increased from 25.5 ± 11.3% to 68.7 ± 13.4% (p < 10^–5), but was somewhat less pronounced in FAKI, where the probability increased from 24.6 ± 13.5% to 53.2 ± 25.2% (p = 0.08). In contrast, in blood vessels of the isotropic phenotype (where the fraction of axially oriented cells was <30%), we found no strong relationship between cell elongation and orientation, suggesting that these cells show no strong systematic avoidance of circumferential exposure (Supplemental Figure S5E).

DISCUSSION

In this paper, we perform quantitative and high-resolution reconstruction of the epithelial architecture of the Botryllus vasculature by “unwrapping” the 3-D vascular tube into a 2-D epithelial sheet; our method complements recent demonstrations of ‘unrolled’ tubular epithelia to enable analysis of developmental and other tissue systems (Heemskerk and Streichan, 2015; Yang et al., 2019). We observed that cells within the vascular wall were planar polarized, with robust preference for actin stress fiber orientation into the circumferential direction and a preference for cell elongation into the axial direction that appears to minimize cells’ circumferential dimension, which is both FAK-dependent and curvature-dependent.

A key motivator for this study was to understand the dynamic and dramatic tissue remodeling that could be triggered by collagen disruption in the Botryllus vasculature. Yet, strikingly, none of our measured morphological features (number of nearest neighbors, cell size, and elongation) was significantly disrupted in BAPN treatment relative to control conditions, even though we know that the vasculature is undergoing rapid cellular remodeling and macroscopic regression at this time point. There could be several possible explanations for this phenomenon: On the one hand, it is theoretically possible that not all regions of the vasculature are equally dynamic. If the bulk of BAPN-induced tissue remodeling were to be localized to regions outside of those “linear” stretches of the vasculature that we typically select for imaging (e.g., instead of vascular junctions, or ampullae, or vessels close to the bodies), then our measurements could represent a population of less dynamic cells. However, we consider this scenario to be unlikely, since live-imaging data (Rodriguez, Braden, et al., 2017) show that apoptosis (followed by cell extrusion) is distributed fairly randomly across the entire vasculature, and no specialized extrusion zones have been observed thus far. Thus, we propose that apoptosis/extrusion most likely does occur in these linear stretches, and that our findings—that is, the lack of obvious morphological defects—suggest that there must be a nearly immediate resealing of the epithelium after an individual cell is removed. We believe that these extrusion and recovery events happen so quickly that the fixed specimens examined here do not capture a sufficient number of active extrusion events to cause measurable defects in the morphology. Such fast resealing would have tremendous benefit for the organism since the vascular epithelium would be capable of maintaining homeostasis and barrier function even in the presence of large-scale dynamic rearrangement. This is consistent with the observation that the animals do not bleed during BAPN-induced regression and are capable of full regeneration after the drug is removed, and is in line with the idea that the dramatic regression in BAPN falls on a continuum of homeostatic (as opposed to catastrophic) responses to mechanical signaling. We hypothesize that the extrusion and resealing events that define the dynamic remodeling contribute to the considerable spread of the measured nearest-neighbor number distribution (Figure 3C), which indicates some degree of topological disorder. While the precise topology of epithelial tissue of course depends on many factors—including tension and cell–cell adhesion—and is difficult to compare between different model organisms, we have observed similar features in the early germ band epithelium in Drosophila melanogaster. In particular, there is a significant increase in the number of cells with five or seven nearest neighbors and corresponding decrease in the number of cells with six nearest neighbors after the onset of germ band extension (Supplemental Figure S6), in which the tissue begins to remodel and transitions from a static to a highly dynamic state.

In addition, we found a system of planar polarity within the epithelial sheet, which was robust not just against regression but also partially against FAKI; one component of this polarity is cell orientation, and the other is actin fiber orientation. With respect to cell orientation, larger-diameter blood vessels with less wall curvature (curvature radius >40 μm) are generally more isotropic in terms of cell shape and orientation; while there is still a small degree of axial polarity, in our sample sizes it is not statistically significant. Strikingly, in smaller-diameter blood vessels with more wall curvature (curvature radius <40 μm) this axially oriented phenotype becomes more pronounced in both control and BAPN-treated tissues, with axial orientation of cells preferred over circumferential orientation at a ratio of up to 3:1. Since within a given cell population, the preference for axial orientation increases with cell aspect ratio, we interpret this strongly polarized phenotype as an attempt to minimize the individual cell’s circumferential “exposure,” by sensing cell bending or other force asymmetries. The features of this phenotype, however, are weakened or absent in FAKI-treated animals, suggesting that the mechanical sensing directing the morphological response requires integrin signaling. We note that our approach to the quantitative measurement of cell morphometrics in fact likely underestimates the disruption under FAKI, since our watershed-based segmentation method requires somewhat regular cell boundaries in order to produce meaningful results, and we occasionally have to exclude an image stack when the fluorescence signal of the cell boundaries is too irregular (e.g., due to incomplete or irregular staining; see Supplemental Figure S7). We observed that the fraction of excluded image stacks was significantly higher under FAK disruption conditions; in addition to a stronger degradation of intensities, we also observed the appearance of “rippling” in the shape of cell–cell boundaries, which suggests loss of tension across the cell–cell junctions. While our current analysis tools do not yet fully capture these differences, they will be a focus of future work.

Previous studies of in vitro cultures of endothelial cells, which have an isotropic orientation at rest, have shown that cells become elongated and reorient in the direction of the fluid force when shear stress is applied (Dewey et al., 1981; Franke et al., 1984; Wechezak et al., 1985; Ives et al., 1986; Iba and Sumpio, 1991). In vivo, local hemodynamic forces dictate the shape of endothelial cells; the greater the force, the flatter and more elongated the cells become, and the more they align with the direction of blood flow (Flaherty et al., 1972; Gotlieb et al., 1981; White and Fujiwara, 1986). Thus, the preferential elongation and orientation of cells into the axial direction that we observed in Botryllus could be related to the mechanical shear effects of blood flow (Hellbach et al., 2011). Unlike mammalian models, in Botryllus, individuals have a tubular heart that beats bidirectionally, where the direction of blood flow reverts every 2–3 min; thus, the shear force vectors should almost always point axially, along the vessel length, while the magnitude of the shear forces likely depends on the wall curvature of the vessel, producing stronger effects in smaller blood vessels.

In the majority of prior in vitro studies, however, the observed cytoskeletal structures (e.g., actin-rich stress fibers) were also aligned along the elongated cell axis, into the direction of fluid flow, which has been used as evidence to suggest that the stress fibers play a role in protection against fluid shear stress (Wong et al., 1983; Sato and Ohashi, 2005). This is a notable difference from our study—which is the first to measure actin fiber orientation in intact vasculature in Botryllus. We found a strong and robust preference for circumferential alignment of actin bundles, which are thus oriented perpendicular to the direction of fluid flow and perpendicular to the direction of net cell elongation, both in control and in BAPN-treated animals and regardless of cell size and shape. Not surprisingly, this polarized architecture was also integrin-dependent, as it was massively disrupted in FAKI-treated animals. Circumferential orientation of both actin fibers and cells was previously noted in the smooth muscle cells of rat blood vessel vein grafts (Liu, 1998) and was linked to the presence of significant circumferential stress (i.e., “hoop” stress) within the vessel wall arising from the applied arterial blood pressure. It is possible that a similar circumferential stress develops within the Botryllus vessel wall, but that the substantially different anatomy of the invertebrate system allows the decoupling of the actin orientation (which may be more sensitive to vessel contraction and blood pressure) and the cell elongation axis (which may be more sensitive to fluid flow).

Cell and actin orientation on curved surfaces has also been investigated in the past with in vitro model systems in the absence of fluid flow using microfabricated tubes or rods made from a variety of substrates including polydimethylsiloxane (PDMS), hydrogels and collagen (Shin et al., 2004; Fidkowski et al., 2005; Chrobak et al., 2006; Fernandez et al., 2007; Song et al., 2009). Cells on such rigid cylindrical substrates have shown a wide range of responses. On rod diameters ranging from 10 to 500 μm (a range that spans the diameters of capillaries to large blood vessels in the brain), human brain microvasculature endothelial cells (HBMEC) presented circumferentially oriented stress fibers, whereas human umbilical vein endothelial cells (HUVEC) presented axially aligned stress fibers (Ye et al., 2014). Epithelial cells (both Madin–Darby canine kidney [MDCK] and retinal pigmented epithelial [RPE1] cells) showed strong circumferential alignment of both the cells and actin stress fibers on highly curved rods (radius < 40 μm), whereas 3T3 fibroblasts tended to align axially (Yevick et al., 2015). In a separate study, it was shown that both mouse embryonic fibroblasts and human vascular smooth muscle cells aligned axially on highly curved rods (radius of ∼40 μm) and that their actin stress fibers were polarized, with apical fibers aligned axially and basal fibers aligned circumferentially (Bade et al., 2017). Activation of Rho enhanced the circumferential alignment, particularly in confluent monolayers.

The results of these studies, in which cells are adhered to a rigid, solid cylinder, are difficult to compare to our results due to their relatively artificial environment and our limited understanding of the role of geometry and boundary conditions in cellular structure, organization, and remodeling dynamics. However, these prior in vitro results have generally been interpreted by considering an energy balance between stress fiber bending, which would bias toward axial orientation, and contraction, which would favor a circumferential orientation (Biton and Safran, 2009). It is not clear that fiber bending would be penalized within a naturally curved surface, as found within the vessel wall, or in the absence of strong cell–substrate adhesions. Furthermore, a recent study of cells attached to regions of positive and negative Gaussian curvature demonstrated that at the unbounded apical surface, cells could minimize stress fiber bending by lifting away from the substrate and forming a straight chord between two distant focal adhesion sites within the 3-D volume (Bade et al., 2018). This suggests that when able to occupy a 3-D volume, cells can adapt their overall shape and cytoskeletal organization to minimize fiber bending. It is possible that similar mechanisms are at play in Botryllus blood vessels, which are naturally suspended in the tunic. Finally, it is not established that the phalloidin-stained actin bundles that we observed in the Botryllus vasculature are identical in form and function to contractile actin stress fibers (or actomyosin bundles) in mammalian cells. If their orientation is not motivated by minimizing or resisting curvature, then they may fulfill an entirely different mechanical function, for example, to resist variable hoop stress caused by changes in blood pressure during pulsatile beating.

Indeed, there is evidence that the actin-rich bundles we observe in Botryllus are not typical stress fibers. In mammalian cells, stress fibers are composed of complexes of actin filaments and the motor protein myosin II; these fibers are usually thick and very stable (Livne and Geiger, 2016) and typically are anchored to focal adhesions that in turn connect to the ECM (Tojkander et al., 2012). In Botryllus we found no significant disruption or loss of planar polarity of actin bundles between control and BAPN-treated animals, despite the fact that BAPN treatment leads to collagen disruption and disassembly on the timescales of hours (Rodriguez, Braden, et al., 2017). In fact, this massive disruption to the ECM is what we believe triggers the vessel retraction in the first place, via an integrin-dependent cell death pathway (i.e., anoikis). Such systemic disruption of collagen and the ECM would be expected to disrupt stress fiber formation as well, but we see no disruption of the actin bundles under BAPN treatment. It is possible that the focal adhesion complex in Botryllus has distinct mechanisms for regulating actin binding and ECM anchorage. Alternatively, it is also possible that in addition to ECM adhesion, the Botryllus vascular epithelium is mechanically supported by the external cellulose-rich tunic and that this support provides additional pathways for cytoskeletal regulation, and perhaps even promotes the rapid resealing of the sheet. The latter case raises interesting possibilities for mechanically supported vascular grafts using biocompatible hydrogel materials to create an artificial scaffold that stimulates cell dynamics and promotes organization into stable tubular structures.

MATERIALS AND METHODS

Botryllus mariculture and induced vascular regression

Botryllus schlosseri colonies were retrieved from the harbor in Santa Barbara, California, and allowed to spawn on 3 × 2 inch glass slides. The progeny were subsequently grown in a mariculture system according to established protocols (Boyd et al., 1986), with circulating 0.5-mm filtered seawater (FSW) at 18–21°C and daily feedings with live algae for a period of 1–2 mo, until they reached 5–8 zooids in size, as described (Rodriguez, Braden, et al., 2017). Pharmacological inhibition of lysyl oxidase (LOX) activity with the specific small molecule inhibitor BAPN disrupts the basement membrane, which in turn induces vascular regression of the entire extracorporeal vasculature within 16 h (Rodriguez, Braden, et al., 2017) (Supplemental Figure S1, A and B). Induced vascular regression was obtained by incubating colonies of a single system 4–5 zooids 2–3 mo old, in 400 µM BAPN for 8 h (full regression is obtained in 16 h) or in 50 µM FAKI 14 (FAKI) 6 h (Supplemental Figure S1, C and D) (full regression is obtained in 10 h); colonies were then fixed and processed for immunostaining. Note that both BAPN and FAKI were resuspended in molecular biology grade water and therefore this water is used as a carrier control. Control colonies were treated with molecular biology grade water using the exact same volume as used in BAPN (512.8 µl in 500 ml of FSW), and they were incubated for 8 h; colonies were then fixed and processed for immunostaining.

Live imaging

Live imaging of colonies treated with either BAPN or FAKI was carried out using motorized fluorescence stereomicroscope MZ16FA (Leica, Germany) as previously described (Braden et al., 2014; Rodriguez, Braden, et al., 2017). For live imaging of fluorescently labeled vasculature of Botryllus colonies labeled with BSA-Alexa 594 (A13101; Thermo Fisher Scientific, Waltham, MA), 2 μl of the dye was microinjected directly into the vasculature of each colony and incubated for 24 h before imaging using motorized fluorescence stereomicroscope M205FCA (Leica, Germany).

Staining

For each round of staining, colonies were transferred to glass coverslip-bottom dishes (0.17 mm Delta TPG Dishes) (Bioptechs; 0420041500C) to enable high-resolution imaging while preserving the structure of the blood vessels throughout the staining process. After plating, the colonies were left undisturbed for 1 wk to allow them to strongly adhere to the glass portion of the dish. Twenty colonies were incubated in 400 µM BAPN (MP Biomedicals, Santa Ana, CA; 150105) in seawater for 8 h, 23 colonies were incubated in 50 µM FAKI 14 (Santa Cruz Biotechnology; sc-203950) in seawater for 6 h, and 25 colonies remained in seawater for control conditions. For the whole-mount immunofluorescence staining, the animals were first anesthetized using 790 µM Trichane (TCI, Tokyo; T0941) in seawater for 10 min and then fixed for 3 h using 4% paraformaldehyde (Fisher Scientific; 50-00-0) in 0.1 M MOPS buffer and 0.5 M NaCl. After three 10-min washes in phosphate-buffered saline with 0.05% Tween (Fisher Scientific; BP337) (PBST), the specimens were incubated in a blocking buffer of 2% Bovine Serum Albumin including 4’,6-diamino-2phenylindole (DAPI) (Invitrogen; H3570) and 1:100 rhodamine-phalloidin (Invitrogen; R415) (Phalloidin) in PBST overnight and then washed with three 10-min washes with PBST. We observed no obvious macroscopic differences in morphologies between live and fixed and stained cells.

Imaging

Imaging of the vasculature of B. schlosseri triple labeled with anti–pan-cadherin Hoechst 33342 and rhodamine-phalloidin was obtained using an SP8-TCS resonant scanning confocal microscope (Leica, Germany). 3-D images were collected as z-stacks using a 40 × water immersion objective with motorized correction collar, a numerical aperture (N.A.) of 1.1, and a digital 0.75 × zoom. Laser excitation wavelength ranges were 350–461, 496–519, and 540–565 nm for visualization of Hoechst-labeled cell nuclei, immunolabeled cadherin, and phalloidin-labeled actin, respectively. Each x–y image within the z-stack had a size of 6704 × 2302 pixels, and all images were taken at a speed of 600 Hz.

Image analysis

All the image and data analysis was performed using MATLAB (Mathworks); our custom code written for the image analysis procedures described in sections 1–4 below was also written in MATLAB and is available from the Loerke lab on request. Figures were edited using Adobe Illustrator and Adobe Photoshop

1) Mapping the surface of the epithelial sheet.

From projections of the raw confocal z-stacks (with separate color channels for Hoechst dye, immunolabeled cadherin, and phalloidin-labeled actin), we selected “straight” regions of the blood vessels, defined as stretches without branching points or overlap with other vessels (Figure 2A). First, raw 3-D stacks (x–y–z pixel sizes 75 × 75 × 600 nm) of each channel (Figure 2A) were resized through interpolation to create image voxels of equal size into x–y–z direction. Subsequently, the vascular surface was identified through a watershed transformation on the individual axial sections of the vessel (i.e., sections into the y–z dimension) (Figure 2B), using the images collected in the phalloidin/actin channel. The seeds for the watershed segmentation were propagated to subsequent axial sections after being manually initialized for the first axial section. After watershed segmentation, the resultant single-pixel-width segmentation lines were smoothed using a Savitzky–Golay filter with a polynomial of order 3 and a frame length of 23 μm. For every axial cross-section, each point on the segmentation line of the vascular surface is assigned to an angle θ and a distance r with respect to the center of mass of the cross-sectional profile (Figure 2B); these values are retained for subsequent analysis.

2) Construction of “unwrapped” 2-D intensity maps.

After this segmentation step, each pixel on the vascular surface was uniquely identifiable by its circumferential angle θ (and distance r) with respect to the center of the cross-sectional profile, as well as its distance s along the length of the vascular axis. Using these parameters, the intensities (in each color channel) on the vascular surface were interpolated as 2-D maps as a function of θ and s (Figure 2C, Supplemental Figure S2, A–C). These 2-D intensity maps correspond to the mantle of the cylinder, that is, what the epithelial sheets would look like if they were cut along the length of the cylinder and then “unwrapped” and flattened from their cylindrical shape. The bin size of the circumferential angle for the interpolation was chosen as Δθ = 360°/(mean circumference of the blood vessel) so that the pixels in the resulting 2-D intensity maps have approximately the same size in the (circumferential) x-direction as in the (axial) y-direction, with some size compressions and rarefactions into the circumferential direction depending on variations in radius (see further below). The resultant 2-D intensity map (Figure 2C) was then segmented using a standard 2-D seeded watershed segmentation algorithm. The initial segmentation seeds were extracted from cell nucleus positions in the 2-D map of the DAPI channel (Supplemental Figure S2A). Postprocessing of the watershed segmentation (Vanderleest et al., 2018) yielded cell and vertex positions, as well as cell/vertex/interface connectivity.

3) 3-D reconstruction.

While this unwrapping technique of the tubular sheet is a powerful means of data reduction for 2-D (as opposed to 3-D) data analysis, it creates some challenges for quantitative analysis. The pixels in the unwrapped intensity maps (Figure 2C) have the physical dimension of microns into the axial direction (representing the axial distance s) but the physical dimension of radians into the circumferential direction (representing the circumferential angle θ). As a result, quantitative distance measurements within the sheet must first dimensionally convert the circumferential distances from angles into the lengths of the corresponding circumferential arc segments. In perfectly cylindrical tubes—with constant tube radius—the circumferential arc distance and the radial angle are conveniently related by a constant linear factor, but in practice, the vasculature shows variations of the radial distance both in the axial direction (as vessels gradually widen along their length) and in the circumferential direction (as some vessels have slightly elliptical cross-sectional profiles).

We retained these radial variations for all experimental samples in corresponding maps of the true circumferential arc length (Supplemental Figure S2E) and used them for pixel-by-pixel length correction for all 2-D morphological measurements. Thus, the position of any feature that is detected in the 2-D intensity map—for example, the vertex between three specific cells—can be directly mapped back to a specific location on the 3-D surface of the blood vessel, since any location on the 2-D map is associated with axial length and the circumferential angle information; in addition, the original segmentation of the vascular surface retains the information where the center point of each axial cross-section was located, and at what distance from the center point the surface is located at any angular bin. In this way, we can reconstruct the “true” 3-D locations of all cell centroids and cell vertices from the 2-D segmentation results and visualize the meshwork of connected points with standard 3-D plotting tools (in our case using the trisurf function in MATLAB) (Figure 2D). Triangulation is performed on each cell by connecting the centroid of the cell with two of its connected vertices at a time.

To test the effectiveness of this strategy, we compared cell areas calculated using this 2-D approach and a “true” 3-D approach (in which we directly measured cell area in the 3-D triangulated surface), intentionally choosing as a test sample a blood vessel with some deviation from a perfect cylindrical shape (Supplemental Figure S2, D and E). While the values produced using 2-D morphometrics with arc length correction (Supplemental Figure S2D, right panel) aligned well with “true” 3-D measurements, the 2-D morphometrics without arc length correction (Supplemental Figure S2D, left panel) introduced a significant level of scatter, representing measurement “compressions” and “rarefactions” of the true circumferential distances due to arc length variations. Thus, we conclude that when using the convenient and computationally straightforward morphometric analysis on the “unwrapped” 2-D epithelial sheet, it is necessary to correct for nonuniform circumferential arc distance variation in order to obtain accurate morphometric measurements, and this approach was used for all quantitative analyses.

4) Line filtering.

To eliminate any confounding effects due to the potentially polarized orientation of cell–cell interfaces (which are also efficiently stained with phalloidin), the interfaces were removed from the image for this analysis by masking off a dilated mask of the interface segmentation map, thereby isolating the image of the phalloidin signal only from the cell interiors. Line filtering was then performed by convolving the “masked” raw image with a 2-D Ricker wavelet kernel of variable spatial angle.

The basic 2-D wavelet profile is given by Eq. 1, where ψ (x, y) is the probability:

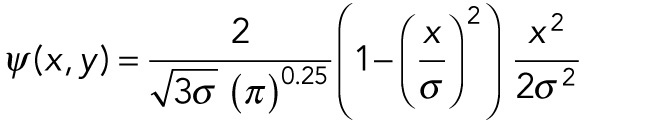1

The length of the kernel matrix in the y-direction was 5 µm. The value of σ was selected to match the thickness of the fibers (0.32 µm) in the raw image, slightly above the width of the point spread function (PSF) (Supplemental Figure S4, A and B), and the total width of the kernel matrix in the x-direction was chosen to be 6σ (ranging from –3σ to +3σ), so as to encompass the first zero crossing (which occurs at ±σ) while also making sure the kernel is not too large (which would significantly increase the computation time). Through the above equation, the filter kernel is already normalized in the x-direction; to also normalize it in the y-direction, each element was divided by the y-length of the kernel (in units of pixels). The spatial angle of the kernel with respect to the image coordinates was then varied using the MATLAB function imrotate.

The raw images were first normalized by subtraction of image mean and dividing by image SD before performing line filtering; subsequently, convolution of the image with the normalized and rotated kernel was performed using the MATLAB function imfilter.

5) Quantitative morphometric and data analysis.

Major and minor axes of a cell are determined in MATLAB’s regionprops function by fitting an ellipse to the cell perimeter.

Statistical analysis

In Figures 3–5, unless explicitly stated otherwise, the plots show mean ± SD, where the mean and SD are calculated across the values from all unique blood vessels. Our sample size of analyzed images consisted of n = 30 blood vessels in control conditions (from 10 unique animals), with a range of 26–219 cells per blood vessel for a total of k = 2990 cells; in BAPN-treated conditions, n = 20 blood vessels (from nine unique animals) with a range of 28–185 cells per blood vessel for a total of k = 1660 cells; in FAKI-treated conditions, n = 13 blood vessels (from five unique animals) with a range of 23–257 cells per blood vessel for a total of k = 1391 cells. Thus, the error bars in the figures represent the typical variation of the parameter between individual blood vessels (not between individual cells).

If the parameter of choice is cell-based (such as cell major axis), the parameter is first averaged within each blood vessel across the available cells in that vessel, before we then calculate the mean across blood vessels. Since each blood vessel contains a different number of cells (ranging from 23 to 257 cells per blood vessel), a weight corresponding to the number of cells is assigned to each blood vessel. Unless specified otherwise, p values were calculated using a two-sample t test on these weighted means (e.g., control vs. BAPN, or circumferential vs. axial), with the number of observations in the t test being n = the number of vessels (and not k = total number of cells). In cases where the value distributions were clearly nonnormal, Kolmogorov–Smirnov tests were used as significance tests.

Abbreviations used:

BAPN

b-aminopropionitrile

DAPI

4’,6-diamidino-2-phenylindole

ECM

extracellular matrix

FAK

focal adhesion kinase

FAKI

FAK inhibitor

LOX

lysyl oxidase.