Abstract
Air Transportation is a major contributor to international mobility and has high requirements to ensure safe and secure operations. Aircraft ground operations are impacted significantly by the current pandemic situation so that standard operating procedures need a redesign to incorporate the upcoming sanitation requirements. In particular, the passenger boarding process is challenged with requirements for physical distances between passengers, while in addition to standard cleaning, the cabin has to be disinfected after each flight. We evaluate potential alterations of these two aircraft cabin processes with respect to a pre-pandemic reference aircraft turnaround. The implementation of microscopic approaches allows to consider individual interactions and a step-wise process adaptation aiming for an efficient operational design. We find a significant extension of boarding times (more than doubled) if the physical distance rule is applied. The new disinfection process further extends the critical path of the turnaround, so we see a high impact on airport and airline operations. To compensate for the increased workload and process times, we provide an integrated cleaning and disinfection procedure with additional personnel. Our results indicate that the pre-pandemic turnaround times cannot be maintained for the same seat load, even if the process adaptations are being implemented. However, a seat allocation scheme with empty middle-seats (seat load of 67%) and the use of an apron position (additional use of rear aircraft door for boarding) enable pre-pandemic turnaround times without additional cleaning personnel. Aircraft turnarounds at terminal positions require between 10% (with additional personnel) and 20% (without additional personnel) more ground time.
Keywords: Aircraft ground operations, Aircraft turnaround, Airport management, COVID-19, Operational changes, Passenger boarding, Aircraft cabin disinfection
1. Introduction
Air transportation offers mobility at national/international levels and faces numerous challenges ranging from safety, security, and operational efficiency to the call for zero environmental impact. The current worldwide pandemic situation demands significant changes in the aviation industry, which starts with a nearly full stop of air travel to avoid spreading of the coronavirus disease (COVID-19). After each major air traffic incident/accident or attack, the operational processes were significantly changed to prevent a recurrence. Thus, the multi-crew coordination concept to reduce authority gradients in the cockpit was introduced as a consequence of the Tenerife accident (1977) similar as hand luggage restrictions with regards to liquids were implemented after critical security events in 2006. From a passenger and operational point of view, process changes often result in longer service times and interrupt the idea of seamless transport. Besides safety and security constraints, we believe that the current pandemic situation will also sustainably change both aircraft ground operations and passenger handling.
The processes of aircraft ground handling at the airport apron are summarized as aircraft turnaround. For years, airlines have pursued to enhance the efficiency of their turnaround operations to increase flight times of their aircraft and thereby resource utilization. Pushed by the groundbreaking innovations of low-cost carriers, turnaround processes across the entire industry have been shortened, redesigned, or rationalized in the course of the last three decades. Especially cleaning and catering processes have seen the most substantial cut-backs, either being reduced to every second or third turnaround over the day or being operated cursory by cabin crew personnel, leaving full and thorough executions to overnight periods.
The current pandemic situation demands specific changes to the standard operating procedures for several turnaround sub-processes: (a) during aircraft deboarding and boarding, passengers have to comply to a minimum physical distance and (b) in addition to the standard cleaning, the cabin has to be disinfected. We expect that these changes will significantly impact also the total turnaround time, given that the related processes are typically part of the critical path. To ensure a minimum transmission risk during boarding and flight, new operational concepts and structural changes in the aircraft cabin could be applied.
There are several approaches for infrastructural changes to the aircraft cabin, but most of these ideas are far away from being a flexible and standardized solution for the aviation industry. Wearing a mask and ensuring low transmission risk during de-/boarding by using appropriate strategies (Schultz and Fuchte, 2020) is more likely to be implemented in actual airline and airport operations than altered cabin layouts. To limit the transmission via surfaces, the aircraft cabin needs to be disinfected before boarding starts. The disinfection process is currently tested by several airlines in mock-up and real environments to derive an appropriate process design.
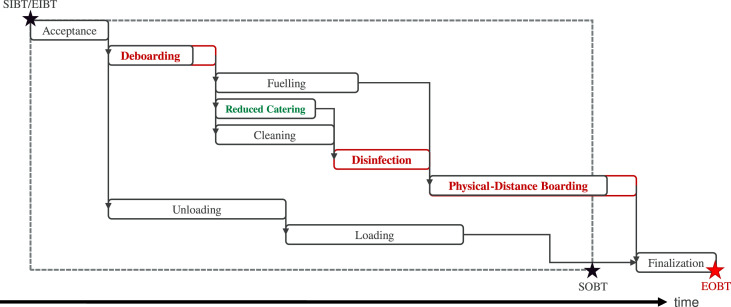
If currently required passenger de-/boarding and new disinfection procedures are implemented into a turnaround reference model, as shown in Fig. 1 , it is obvious that an extended ground time needs to be considered for airline and airport operations. As a result, aircraft rotations may be significantly affected along the entire day of operations, especially in-between flights that have no schedule buffers assigned in excess to the aircraft's minimum ground times. While current research approaches are more aimed at finding out to what extent ground times need to be reduced in order to increase aircraft utilization, the question now is how much additional ground time can be tolerated without endangering the operational efficiency of the entire airline network.
Fig. 1.
Adapted turnaround reference model with cabin disinfection, reduced catering and physical-distancing of passengers during deboarding and boarding. Because of the altered process layouts, the total turnaround time is likely to extend required ground times so that estimated off-block times (EOBT) overrun former scheduled off-block times (SOBT).
1.1. State-of-art
Comprehensive overviews are provided for aircraft ground operations, passenger boarding, and their corresponding economic impact (Schmidt, 2017; Jaehn and Neumann, 2015; Nyquist and McFadden, 2008; Mirza, 2008; Cook, 2015; Delcea et al., 2018).
Research on ground operations is divided in strategic and tactical approaches. From a strategic perspective, it is a long-term research objective to allocate schedule buffers efficiently throughout daily airline schedules to eliminate critical resource dependencies and improve network robustness (Beatty et al., 1999; AhmadBeygi et al., 2010; Wu, 2006; Wu and Law, 2019). For a better tactical situational awareness in the course of Airport-Collaborative Decision Making (A-CDM), several studies aim at the accurate prediction of turnaround target times by incorporating stochastic process time distributions (Wu and Caves, 2004; Fricke and Schultz, 2009; Oreschko et al., 2012). A microscopic turnaround model was introduced which applies flight-specific trigger parameters and process variations for cleaning and boarding to actively manage delayed turnaround operations (Schultz et al., 2013). Further turnaround control options are proposed in (Kuster et al., 2009), while several analytical approaches target the optimal allocation of airport resources, such as ground handling equipment (Andreatta et al., 2014; Padrón et al., 2016), pushback trucks (Du et al., 2014), de-icing slots (Norin et al., 2012), and aircraft stands (Dorndorf et al., 2017; Dijk et al., 2019). Future research will concentrate more on an integrated view of aircraft handling, which evaluates delays also concerning self-connecting passengers (Ali et al., 2019) or coupled ground and flight operations (Rosenow and Schultz, 2018) to include them into the optimization of ground procedures.
A common goal of simulation-based approaches for passenger boarding is to minimize boarding time. Thus, the efficiency of different boarding strategies was the focus of several research activities (Marelli et al., 1998; Van Landeghem and Beuselinck, 2002; Ferrari and Nagel, 2005; van den Briel et al., 2005; Bachmat and Elkin, 2008; Schultz et al., 2008; Bachmat et al., 2013). The developed models are based on cellular automaton (Burstedde et al., 2001; Schultz, 2010) or analytical approaches, but also other methods were applied to the passenger boarding challenge: mixed integer linear programs (Bazargan, 2007), statistical mechanics (Steffen, 2008a), power law rule (Frette and Hemmer, 2012; Bernstein, 2012), cellular discrete-event system specification (Jafer and Mi, 2017), and stochastic approach covering individual passenger behavior and aircraft/airline operational constraints (Schultz, 2018a). Focus at current research is set on seat assigned passengers with regards to hand luggage (Qiang et al., 2014; Milne and Salari, 2016; Steffen, 2008; Milne and Kelly, 2014), boarding of groups (Zeineddine, 2017; Schultz, 2018a), consideration of passenger expectations (Wittmann, 2019), use of apron busses (Milne et al., 2019), real-time seat allocation (Schultz, 2018b; Yazdani et al., 2019), or the assessment of new technologies in the aircraft cabin (Schultz, 2017).
There are two new research contributions available, which set a focus on behaviors during pandemic situations and their impact on the aircraft boarding procedures. The first research addresses the quantity and quality of passenger interactions (Cotfas et al., 2020) and the second research additionally develops and implements a transmission model to provide a more detailed evaluation (Schultz and Fuchte, 2020). With a focus on airport operations, the impact of physical distances on the performance of security control lanes was analyzed to provide a reliable basis for appropriate layout adaptations (Kierzkowski and Kisiel, 2020).
1.2. Focus and structure of the document
Within our contribution, we evaluate the impact of operational process changes for the aircraft turnaround, which are mainly triggered by restrictions from a pandemic scenario. In particular, we will focus on the cabin cleaning process (i.e, integrating disinfection activities) and the passenger boarding (i.e., respecting minimum distance requirements). We implement the altered operating procedures into a turnaround reference model as we expect that the studied processes will be situated on the critical path and, thus, have a significant impact on the required ground time.
Sec. 2 introduces the turnaround reference model and presents post-pandemic process adaptations made by airlines around the world as they currently ramp-up their operations after the shut-down. Sec. 3 presents two microscopic cabin models - one for the stochastic simulation of boarding times and another for the resource-constrained optimization of the cabin cleaning duration. Sec. 4 describes the implementation of both process models into various resource-constrained scenarios, which analyze different seat allocation schemes. The results of both microscopic models are presented in Sec. 5, which furthermore incorporates them into the turnaround reference model. Sec. 6 discusses the results in the context of efficient post-pandemic airline operations and draws conclusions for future research and long-term consequences.
2. Aircraft turnaround
The turnaround is defined as the ground times of aircraft in-between two flight legs, starting with scheduled in-block time (SIBT) of the inbound leg and finishing with the scheduled off-block time (SOBT) of the outbound leg. The turnaround consists of up to twelve interdependent sub-processes which contain more than 150 individual activities and involve up to 30 different actors (IATA, 2018). The most critical sub-processes are those which are part of the critical path of the turnaround and, thus, directly influence the total turnaround time (see Fig. 1). Given that sub-process durations are stochastically distributed and depend on different trigger parameters (Fricke and Schultz, 2009), the critical path can differentiate between individual turnarounds (Evler et al., 2018).
2.1. Reference model
After aircraft acceptance, which includes the positioning of ground handling equipment and passenger stairs/bridges, two process paths are operated in parallel - cabin processes and cargo processes (Wu and Caves, 2004) (see Fig. 1). Fueling is associated with cabin processes, given that local safety regulations may define that during fueling no passengers should be on-board (deboarding and boarding). Thus, cleaning, catering, and fueling processes are operated in parallel, whereby all these processes have been omitted from time to time by some carriers in recent years to reduce total turnaround times. E.g., Lufthansa has switched to a so-called “return-catering” concept, so that the catering process is only executed at the aircraft's home base and includes items for both upcoming flight legs. Ryanair caters aircraft only once at the beginning of the day for all scheduled flights, while the cleaning process is typically performed cursory by cabin crew members. For cleaning, Lufthansa still uses an external cleaning provider but has defined several procedures, such as “reduced-cleaning”, “standard-cleaning” and “extended cleaning”, the latter one typically being operated during night-stops. To spare the fueling process, some airlines have even implemented so-called “tankering” for some flight cycles, so that the tanked fuel suffices for both upcoming flight legs, which extends the process at one airport but omits it at another one. Boarding starts only after all previous sub-processes have been completed. In the case of fueling, boarding could start earlier but needs to be authorized by the captain and the local fire brigade (so-called tank-protection procedure).
2.2. Post-pandemic process adaptations
With the ramp-up of flight operations following the pandemic shut-down, many airlines have implemented increased hygienic precautions and redesigned their standard operating procedures for the turnaround to adhere to more strict official regulations regarding sanitary conditions at the airport and inside the cabin. In cooperation with Dubai Health Authority, Emirates has been the first airline to introduce rapid result blood tests at the airport. On flights that exceed 90 min turnaround time, a dedicated cabin service assistant complements the crew to ensure frequent disinfection of central touch-points, such as lavatories. Furthermore, Emirates has decided to reduce the seat load to respect distance requirements during the entire flight. Also, other airlines, such as Air France and American Airlines, have decided to employ seat allocation restrictions so that passengers are evenly allocated in the aircraft cabin. Delta Airlines follows a similar approach and applies the back-to-front boarding strategy to reduce contacts in the cabin. Air Canada has adapted arrival rates during boarding to guarantee enough physical distance between passenger groups and performs an infra-red screening at the gate to measure the individual body temperature of a passenger, considering that fever is a major indicator of a COVID-19 infection. All airlines require their employees and passengers to wear masks for the entire journey, while many additionally provide hand sanitizers in lavatories and at cabin doors. Catering is reduced to few packaged items and water bottles, reducing the number of trolleys which needs to be loaded onto the aircraft during the turnaround (Puckett, 2020).
Almost all airlines advertise that high efficiency particulate air (HEPA) filters for the cabin are exchanged frequently and that the cabin is disinfected. In the initial process layout, disinfection is performed by a dedicated unit after the standard cleaning process has been finished. Assuming this process design within the turnaround reference model would mean that both processes are on the critical path and extend the turnaround time (see Fig. 1). Furthermore, the consideration of physical distances between passengers during boarding (and deboarding) would jeopardize the turnaround performance, which would ultimately impact the available block hours per day and thereby decrease aircraft utilization.
3. Microscopic cabin model
In our contribution, we focus on two major turnaround sub-processes in the aircraft cabin, which require a redesign to maintain pre-pandemic ground times: passenger boarding and disinfection as part of the adapted cabin cleaning. Whereas cabin cleaning is done by trained personnel, boarding mainly depends on the willingness and ability of the individual passenger to follow the proposed boarding procedures (e.g. late arrival at the gate, family groups).
3.1. Aircraft boarding
In the following sections, we introduce the aircraft boarding model and briefly describe the virus transmission model. This microscopic model is applied to standard boarding scenarios to exhibit the consequences of physical distances to the aircraft boarding time.
3.1.1. Passenger movement model
To reflect operational conditions of aircraft and airlines (e.g. seat load factor, conformance to the boarding procedure) as well as the non-deterministic nature of the underlying processes (e.g. amount and distribution of hand luggage) a stochastic model was developed (Schultz, 2018a) and calibrated (see Schultz, 2018c). Herein, the passenger boarding is defined as an agent-based, stochastic, forward-directed, one-dimensional, and discrete (time and space) process, which is mapped to a regular grid. An appropriate mapping of the aircraft seat layout is shown in Fig. 2 (Airbus A320, 29 rows, 174 seats). This regular grid consists of equal cells with a size of 0.4 × 0.4 m, whereas a cell can either be empty or contain exactly one passenger.
Fig. 2.
Grid-based simulation environment - Airbus A320 as reference.
The boarding progress consists of a simple set of rules for the passenger movement: a) enter the aircraft at the assigned door (based on the current boarding scenario), b) move forward from cell to cell along the aisle until reaching the assigned seat row, and c) store the baggage (aisle is blocked for other passengers) and take the seat. The storage time for the hand luggage depends on the individual number of hand luggage items. The seating process depends on the constellation of already used seats in the corresponding row. To reflect the narrow space in the cabin, the corridor is modeled with a width of one cell, and passengers are not allowed to pass each other.
An evaluation scenario for passenger boarding is mainly defined by the underlying seat layout, the number of passengers to board (seat load factor, default: 85%), the arrival frequency of the passengers at the aircraft, the number of available doors (default left front door), the specific boarding strategy (default: random boarding) and the conformance of passengers in following the current boarding strategy (default: 85%). Further details regarding the model, the simulation environment and a comprehensive comparison of several boarding scenarios are provided at (Schultz, 2018a).
The actual model for passenger boarding was adapted for considering different approaches addressing a reduced transmission risk during boarding. These approaches primarily focus on the two major concepts of distance keeping and reduction of contact times, where both concepts result in a lower chance to get in close contact with a probably infected passenger. As already introduced and analyzed in detail (Burstedde et al., 2001; Schultz, 2010; Schultz, 2013; Nishinari et al., 2003), social and long-range interaction could be reliably modeled by using a floor field. This field contains information about preceding passengers, which allows for a long-range interaction even considering adjacent cells around the actual position. So each passenger will leave a trace with a given length during movement phase, which blocks the corresponding cells and indicate the minimum distance required.
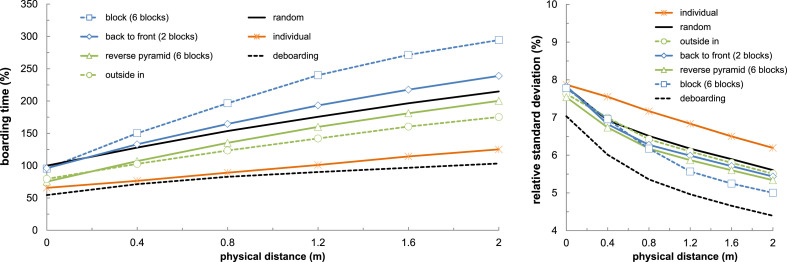
As Fig. 3 exhibits, an increasing physical distance results in a longer boarding time accompanied by a decreased standard deviation. Assuming a minimum distance of 1.6 m, which corresponds to 4 grid cells in the stochastic model, the boarding time is nearly doubled for random boarding. The effect of physical distance superimposes advantages by a significantly reduced arrival rate and the completely coupling of the individual passenger movements. This is also indicated by the reduced relative standard deviations (, standard deviation divided by average value) (Fig. 3, right).
Fig. 3.
Progress of boarding time (left) and relative standard deviation (right) time with increasing physical distance between passengers.
Furthermore, the increased distance between passengers results in a worse performance of standard block-based boarding strategies. This would be also true for the individual boarding, which follows the idea that each row is a block and this block should be boarded with window seat first and aisle seat last (outside-in). The distance of subsequently following blocks has to be adapted according to the required distance of the passengers. Finally, each (optimized) block-based strategy will converge to this individual approach with an increasing number of blocks.
3.1.2. Transmission model
The stochastic model for the passenger movements is extended by an approach to evaluate the risk of a virus transmission during the boarding process. In this approach, face masks are not considered. The transmission risk is defined by two major input factors: distance to the index case and reduction of contact time. A straight forward approach is to count both the individual interactions (passengers located in adjacent cells) and the duration these contacts in aisle and during the seating process. However, counting the individual contacts will only provide a first indication about potential ways of infections. We used a more comprehensive approach, which is based on the transmission model (Smieszek, 2009) defining the spread of SARS-CoV2 as a function of different public distancing measures (Müller et al., 2020). The probability of a person n to become infected in a time step t is described in Equation (1).
| (1) |
defined by:
the probability of the person n to receive an infectious dose. This shall not be understood as “infection probability”, because this strongly depends on the immune response by the affected person.
θ the calibration factor for the specific disease.
the shedding rate, the amount of virus the person m spreads during the time step t.
the intensity of the contact between n and m, which corresponds to their distance.
the time the person n interacts with person m during the time step t.
In our approach, we define the shedding rate as a normalized bell-shaped function (Eq. (2)) with for both longitudinal and lateral dimensions, respectively (see (Schultz and Fuchte, 2020)).
| (2) |
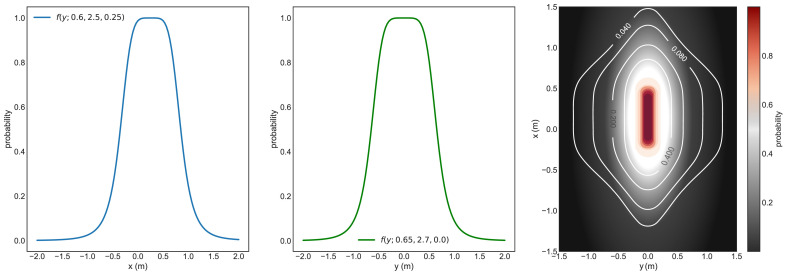
The parameters are a (scaling factor), b (slope of leading and falling edge), and c (offset) to determine the shape of the curve. The parameters have been initially set to , , , , , and . This provides the spread in y-direction (lateral to moving direction) a slightly smaller footprint than in x-direction (longitudinal to moving direction). The spread in x-direction is higher in front of the index case than behind it (see Fig. 4 ). When the passenger arrives his corresponding seat row, the moving direction is changed by 90°.
Fig. 4.
Transmission probability for longitudinal (x) and lateral (y) components and as two-dimensional probability field (right).
Finally, the individual probability for virus transmission corresponds to , the specific intensity (dose) per time step (Eq. (3)). We set to , which means a passenger reaches a probability of after standing 20 s in closest distance in front of an infected passenger (SRxy = 1). The parameter is 1 and changed to 2 when the passenger stores the luggage or enters the seat row. This doubled shedding rate reflects the higher physical activities within a short distance to surrounding passengers.
| (3) |
3.1.3. Simulation results
Table 1 shows the comprehensive evaluation of transmissions around one infected passenger, which is randomly seated in the aircraft cabin. Two different scenarios are evaluated against the reference implementation (R) of the boarding strategies: (A) applying a minimum physical distance between two passengers of 1.6 m, and (B) additionally to the physical distance the amount of hand luggage items are reduced by 50%. Furthermore, the use of two aircraft doors in the front and at the rear is evaluated (A2 and B2) using the transmission risk and boarding time as indicators. In particular, the back-to-front strategy (2 blocks: front block with rows 1–15, rear block with rows 16–29) exhibits lower values for the transmission risk than the optimized block strategy (using 6 blocks of aggregated seat rows) (see Schultz (2018a)). When passengers are boarded (block-wise) from the back to the front, the chance to pass an infected person is reduced to a minimum, which is confirmed by the reduced transmission probability exhibited in Table 1. This effect is also a root cause of the low transmission probabilities of outside-in, reverse pyramid, and individual boarding strategies. The reference case of random boarding initially shows an average value of 5.9 possible transmissions, which could be reduced by operational changes (less hand luggage) to 1.1 using one aircraft door and 1.0 if two doors are used. With a focus to the corresponding boarding times, it may be noticed that a back to front approach is favorable for a reduced transmission risk, but on a cost of increased boarding times in comparison to the random boarding case .
Table 1.
Evaluation of transmissions risk assuming one SARS-CoV2 passenger in the cabin. The simulated scenarios are: (R) reference implementation (Schultz, 2018a), (A) 1.6 m minimum physical distance between two passengers, (B) additional reduction of hand luggage by 50%, (A2) and (B2) use of two door configuration.
| transmission risk |
boarding time (%) |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| boarding strategy | R | A | B | A2 | B2 | R | A | B | A2 | B2 |
| random | 5.9 | 1.6 | 1.1 | 1.4 | 1.0 | 100 | 198 | 154 | 133 | 103 |
| back-to-front (2 blocks) | 5.6 | 1.4 | 1.0 | 1.2 | 0.8 | 96 | 220 | 169 | 153 | 116 |
| optimized block (6 blocks) |
6.5 |
2.3 |
1.5 |
1.5 |
1.0 |
95 |
279 |
210 |
166 |
125 |
| outside-in | 3.5 | 0.4 | 0.2 | 0.3 | 0.1 | 80 | 161 | 116 | 107 | 77 |
| reverse pyramid | 3.0 | 0.2 | 0.1 | 0.2 | 0.1 | 75 | 185 | 128 | 119 | 82 |
| individual |
2.0 |
0.2 |
0.1 |
0.2 |
0.1 |
66 |
114 |
104 |
103 |
74 |
| deboarding | 10.0 | 9.7 | 7.8 | 7.6 | 6.0 | 55 | 97 | 68 | 52 | 36 |
The use of two aircraft doors for boarding will provide an appropriate solution for a reduced transmission risk inside and outside the cabin, if near apron stands could be used and passengers could walk from the terminal to the aircraft. This kind of walk boarding also prevents passengers from standing in the badly ventilated jetway during the boarding. Deboarding is difficult to control by specific procedures given that passengers demonstrated little discipline and high eagerness to leave the aircraft. More attention should be paid to this process and consideration should also be given to procedural or technical solutions to provide passengers better guidance and control.
3.2. Cabin cleaning
To avoid that cleaning becomes a critical process for the entire aircraft turnaround, this subsection introduces an analytical approach for the optimal allocation of cleaning personnel so that standard cleaning and disinfection can be performed mostly in parallel. The aim is to estimate the process duration for different cleaning schemes using a constrained number of cleaning agents.
3.2.1. Problem description
Cabin cleaning activities (ALL) include a number of specific activities () which need to be performed at various points inside the aircraft, such as galley preparation (GAL) , lavatory cleaning (LAV) , cockpit cleaning (COC) , vacuuming (VAC) and seat preparation (SEA) . As already mentioned, some airlines (e.g. Ryanair) have totally omitted the cleaning process or use cabin crew members instead of dedicated personnel to perform it in order to reduce required ground times. However, given the increased requirements for thorough cabin sanitation, we assume that such procedures are deferred for the near future.
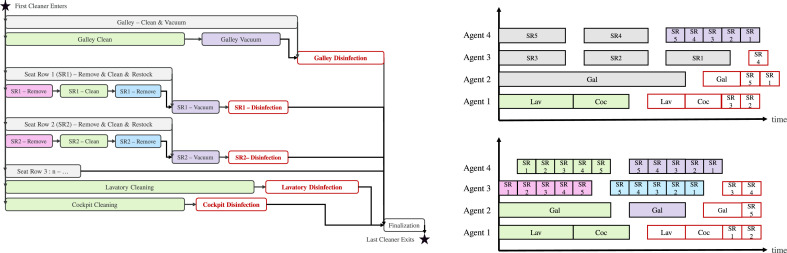
Thus, our resource-constrained cabin cleaning scheduling model includes the full set of standard cleaning activities plus disinfection (DIS) of all cabin areas. Within the initial version of the model, all cleaning agents k are qualified to perform all activities, so that there is no extra unit for disinfection. All activities are associated with flexible starting times s so that task allocation is mainly influenced by activity duration D irk, as well as setup and transition times T in-between activities. Note that setup times are zero between two activities of the same kind. For each part of the cabin, the respective activities in that particular area have predecessor and successor relationships, which are defined within the precedence matrix (see Fig. 5 ). While for some cabin areas (i.e., lavatories and cockpit) there is only one operating procedure (i.e., process sequence) which is to be performed at once by one agent, others are more flexible and can either be operated at once by one agent or split into the individual sub-activities cleaned by separate agents (i.e., galleys and seat rows - see Fig. 5).
Fig. 5.
Microscopic resource scheduling model for cabin cleaning with precedence constraints (left) and two potential resource allocation schemes (right). Note the setup periods when an agent changes between two activities of a different kind.
A decision variable defines whether the respective activity i of the chosen procedure are part of the overall working scheme and need to performed by an agent k, 0 otherwise. Flexible operating procedures exist for galley and seat preparation. Galley preparation can be split into sub-activities galley cleaning (GCL) and galley vacuuming (GVA). Seat preparation can be subdivided into removing trash from seat-pockets (REM), cleaning seat-surfaces and tray tables (CLE), and restocking seat-pockets and head-rests (RES). Task durations were retrieved from field measurements (Schultz et al., 2013) and are adapted with their mean values as exhibited in Table 2. Given the lack of field data for disinfection procedures, we estimate the duration according to the size of the respective application area.
Table 2.
Task durations for cleaning sub-activities (adapted from Schultz et al. (2013a)).
| (Sub-)Activity | Duration (Sec.) |
|---|---|
| Galley cleaning + vacuuming | 149 |
| Galley cleaning | 100 |
| Galley vacuuming | 40 |
| Galley disinfection |
40 |
| Seat row preparation | 30 |
| Seat row item removal | 3 |
| Seat row cleaning | 12 |
| Seat row restocking | 6 |
| Seat row vacuuming | 10 |
| Seat row disinfection |
20 |
| Lavatory cleaning | 120 |
| Lavatory disinfection |
20 |
| Cockpit cleaning | 60 |
| Cockpit disinfection | 40 |
Our model considers that not all seats might have been occupied on the inbound flight, so that seat preparation may be reduced or omitted for these areas. The number and location of such unnecessary cleaning tasks follows different seat allocation scenarios, which are detailed in Sec. 4. Note, however, that disinfection needs to be performed in all cases, given that passengers from adjacent seats may have contaminated surfaces in the vicinity of their allocated seats.
3.2.2. Mathematical formulation
In this part a mathematical optimization model is developed based on the Resource-Constrained Project Scheduling Problem (RCPSP) with considering sequencing constraints for each cleaning agent between the activities in cleaning process.
| Sets: | |
|---|---|
| ALL | Set of all cabin cleaning activities |
| GAL | Sub-set of all galley preparation activities |
| GCL | Sub-set of all galley cleaning activities |
| GVA | Sub-set of all galley vacuuming activities. |
| SEA | Sub-set of all seat row preparation activities |
| REM | Sub-set of all seat row item removal activities |
| CLE | Sub-set of all seat row cleaning activities |
| RES | Sub-set of all seat row restocking activities |
| VAC | Sub-set of all seat row vacuuming activities |
| LAV | Sub-set of all lavatory cleaning activities |
| COC | Sub-set of cockpit cleaning activities |
| DIS | Sub-set of all disinfection activities |
| AR | Start and end node |
| CDP | Set of cleaning depot |
| AGT | Set of available cleaning agents |
| ROW | Set of seat rows (left- and right-side) |
| Parameters: | |
| Transfer and setup time between nodes i and j, in seat rows r and l respectively when both are performed by agent k | |
| N | Total number of cleaning agents |
| M | Parameter specific big M |
| PMij | precedence matrix - equal to 1, if activities j can only be performed after activity i has been finished, and 0 otherwise |
| Duration of activity i performed by agent k | |
| Variables: | |
| Binary variable – equal to 1, if activity i in seat row r is performed by agent k, and 0 otherwise | |
| Binary variable – equal to 1, if activity j in seat row r and directly succeeds activity i in seat row l and both are performed by agent k, and 0 otherwise | |
| Scheduled starting time of activity i in sear row r performed by agent k | |
| Earliest finishing time of cleaning process | |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
The objective function (4) minimizes the overall cleaning duration. Scheduling constraints (5) ensure that all selected activities are performed in a sequence which corresponds to the underlying precedence relationships in the respective area of the cabin. Constraints (6–7) define that galley preparation is either performed entirely by one agent or is split up into its individual processes, which can be performed by different agents. Equally, constraints (8–10) determine that the preparation of a seat row is either performed by one agent entirely or is subdivided among different agents. Flow balance constraints (11–12) consider that one cleaning agent can only perform one activity at a time, whereby the number of available cleaning agents is bounded by (13) and setup and transition times between activities are considered by (14).
4. Scenarios and application
As mentioned above, the stochastic boarding simulation and the resource-constrained cleaning scheduling model are implemented for an Airbus A320 aircraft. This single-aisle, narrow-body aircraft configuration represents the dominating cabin layout for more than 70% of worldwide operated flights. Also, narrow-body aircraft fly more legs per day and therefore have shorter ground times, which leads to greater time pressure in turnaround activities.
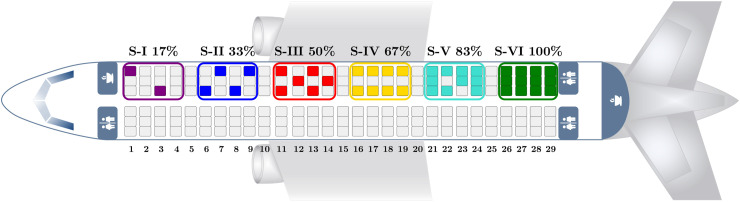
Taking into consideration that several airlines are purposely reducing the seat load to guarantee minimum distance requirements during the flight (see Sec. 2.2), we study the impact of various seat allocation schemes and a different amount of available cleaning agents onto the respective sub-process duration and, thus, the total turnaround time. Six different scenarios are generated which resemble potential allocation schemes as depicted in Fig. 6 and include seat load factors (SLFs) in the range between 17% (i.e., every sixth seat is occupied) to 100% (i.e., all seats are occupied). For each scenario, the number of available cleaning agents ranges from 1 to 6, so that a total number of 36 sub-scenarios is analyzed against a baseline instance, which contains a standard cabin cleaning process (i.e., without disinfection activities) with three cleaning agents and random boarding via the front-door at a terminal position. All scenario instances are summarized in Table 3.
Fig. 6.
Scenarios consider different seat load and allocation schemes.
Table 3.
Post-pandemic turnaround scenarios considering various seat allocation schemes and a different amount of available cleaning agents.
| Scenario ID | Scenario Description | |
|---|---|---|
| Baseline |
83% SLF |
3 agents - standard cleaning with no disinfection |
| S–I | 17% SLF | only one in six seats needs to be cleaned by x agents |
| S-II | 33% SLF | only two in six seats need to be cleaned by x agents |
| S-III | 50% SLF | only three in six seats need to be cleaned by x agents |
| S-IV | 67% SLF | only four in six seats need to be cleaned by x agents |
| S–V | 83% SLF | only five in six seats need to be cleaned by x agents |
| S-VI | 100% SLF | all seats need to be cleaned by x agents |
For each scenario instance, the stochastic boarding simulation presented in Sec. 3.1 is run with the number of passengers which corresponds to the respective seat load, while the resource-constrained cleaning scheduling model presented in Sec. 3.2 assumes preparation times according to the number of occupied seats per row. Results from both models are transferred into the turnaround reference model so that the total turnaround time can be calculated under consideration of all precedence constraints.
5. Results
This section presents the individual results from the stochastic boarding simulation and the resource-constrained cabin cleaning scheduling model for all scenarios. Afterwards, both are incorporated into the turnaround reference model to study the impact on total turnaround time.
5.1. Results of boarding simulation considering physical distances
Table 4 exhibits the results from the stochastic boarding simulation considering the SLF of the respective scenario instances and the available number of doors. With similar SLF, transmission risk can be reduced by more than two-thirds in the post-pandemic scenarios (from 5.9 to 1.8/1.5) compared to the reference case. The risk can be reduced to an average below 1 transmission per flight if SLF is lowered to 50% or less. The transmission risk is effectively zero when only one in six seats are occupied (scenario S–I). Analyzing the relative changes in boarding time, the results in Table 4 indicate that a SLF of 50% with a one door boarding configuration and a SLF of 67% with a two-door configuration would be required so that pre-pandemic boarding duration could be maintained with the random boarding strategy. The frequently-referenced seat allocation scheme which leaves middle-seats unoccupied (i.e., scenario S-IV) would require a two-door boarding configuration so that the duration remains below the reference case (boarding time of 100%). Otherwise, the boarding time would be extended by roughly 40%. With similar SLF as in the reference instance, the duration of one door boarding would be almost doubled, while simultaneous boarding via front and rear doors would still take 29% more time.
Table 4.
Simulation of seat configurations defined by scenarios S–I to S-VI using a random boarding sequence. The simulated scenarios are: (P) pre-pandemic situation with one door as reference implementation (Schultz, 2018a), (1D) post-pandemic situation (1.6 m physical distance) with one door and (2D) post-pandemic situation with two door configuration.
| transmission risk |
boarding time (%) |
||||||
|---|---|---|---|---|---|---|---|
| Scenario | P | 1D | 2D | P | 1D | 2D | |
| S–I | 17% SLF | – | 0.0 | 0.0 | – | 33 | 23 |
| S-II | 33% SLF | – | 0.3 | 0.2 | – | 60 | 40 |
| S-III | 50% SLF | – | 0.6 | 0.5 | – | 101 | 68 |
| S-IV | 67% SLF | – | 1.4 | 1.2 | – | 141 | 94 |
| S–V | 83% SLF | 5.9 | 1.8 | 1.5 | 100 | 192 | 129 |
| S-VI | 100% SLF | – | 2.1 | 1.7 | – | 240 | 160 |
5.2. Results for resource-constrained cabin cleaning
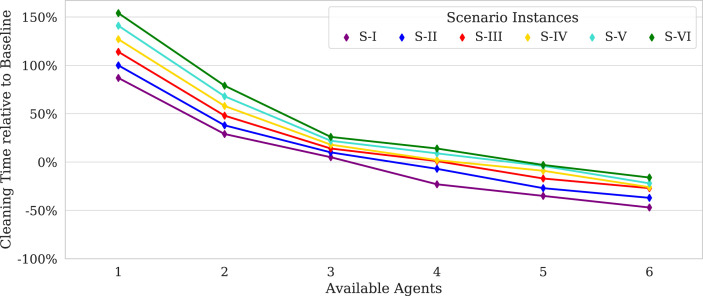
Fig. 7 exhibits the performance difference between the baseline instance and the minimal cleaning duration for all of the six seat allocation scenarios considering the available cleaning agents. Note that with the same amount of cleaning agents as in the baseline (i.e., three), all instances comprise an increased process duration of up to 25%, which is still less than if cleaning and disinfection would be operated sequentially. Contrarily, at least five agents are required to maintain or outperform the baseline duration regardless of the seat allocation scheme. Typically for closed systems with increasing interactions, process times are not linked proportionally to the number of assigned resources, so that the marginal benefit of another agent decreases and causes the hyperbolic shape towards a saturation limit visible in Fig. 7. The saturation limit for the cleaning process is estimated at 40% of the pre-pandemic process duration, given that two exemplary calculations with 12 and 18 agents produced no additional time benefits. Thus, the negative time impact of less available agents is higher than the benefit of additional agents. This effect should be considered when the overall number of cleaning agents available across multiple turnarounds does not increase in a post-pandemic scenario so that resources would need to be prioritized between aircraft. An assignment of additional agents to one aircraft would mean a reduced availability for parallel operated turnarounds, which might lead to substantially extended cleaning and ground times for these aircraft.
Fig. 7.
Resulting cleaning times corresponding to scenario instances and number of available cleaning agents.
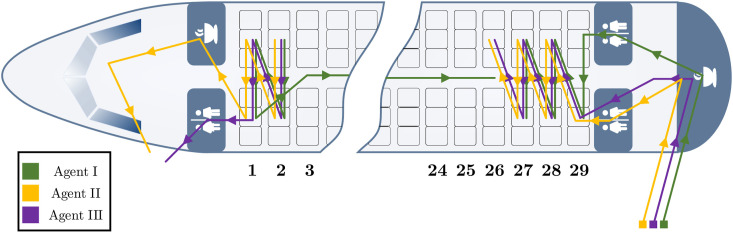
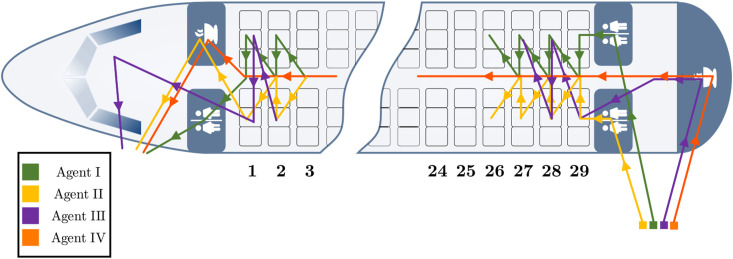
Fig. 8, Fig. 9 depict two optimal cleaning schemes calculated with the resource-constrained cleaning scheduling model. In the prior instance, three cleaning agents need to clean the aircraft in which the middle seat in each row was not assigned, whereas in the latter instance four agents are available. Analyzing the working schemes of all three agents in Fig. 8, it can be recognized that galley and seat preparations are split among all agents. Thus, after the cleaning of rear galleys and lavatories, the first agent performs the removing of items for each seat row, the second one cleans seats, before the third agent restocks all items and headrests and vacuums the aisle. Once all seats are prepared, one agent performs all disinfection activities, while the others clean the front galley, lavatory, and cockpit. Contrarily, the working schemes in Fig. 9 display that after cleaning the rear lavatory, one agent removes items and cleans the seats for all rows right of the aisle, while another one prepares all rows on the left side of the cabin. A third agent restocks all seats and vacuums the aisle before moving to the cockpit. As soon as the respective areas are finished, the fourth agent disinfects the cabin from rear to front.
Fig. 8.
Optimal cleaning scheme with 67% SLF and three available cleaning agents (scenario instance S-4-3).
Fig. 9.
Optimal cleaning scheme with 67% SLF and four available cleaning agents (scenario instance S-4-4.
5.3. Impact on total turnaround time
For the estimation of the total turnaround time in the reference case, pre-pandemic process time distributions for all turnaround sub-processes are adopted (Fricke and Schultz, 2009; Schultz, 2018a) and convoluted with each other (Evler et al., 2018). The 90% quantile of the resulting distribution is compared with the post-pandemic turnaround model (see Fig. 1), which incorporates the results from Sec. 5.1 and 5.2. Given the lack of a sophisticated deboarding model, results from the boarding simulation are equally adapted for the changes of deboarding times under post-pandemic circumstances. The duration of catering is assumed to be 30% less than in pre-pandemic operations, given that fewer items are loaded onto the aircraft. The fueling process remains unchanged.
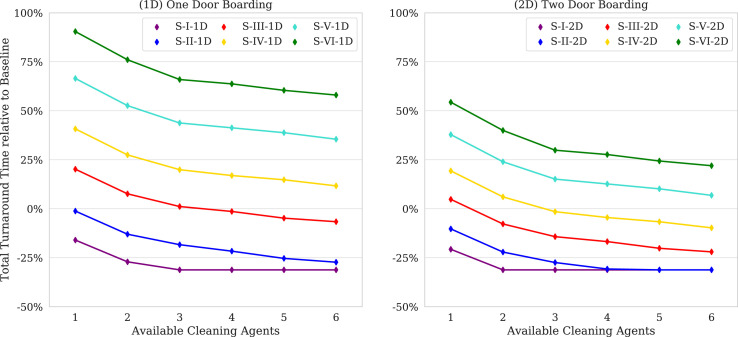
Fig. 10 shows the relative changes of the total turnaround time in the post-pandemic scenario considering different seat allocation schemes, a different amount of available cleaning agents, and the application of one-door or two-door boarding strategy. The graphs indicate that with the pre-pandemic amount of cleaning agents (i.e., three) and aircraft allocation to a terminal contact stand (i.e., one door boarding), former ground times can only be maintained when the SLF is reduced to 50% (i.e., scenario instance S-III-1D). Given that this scenario guarantees minimum distance requirements and reduced interactions during boarding and the disinfection of the cabin, transmission risk can be reduced by almost 90%. With an allocation to remote- or walk-boarding stands, which would enable a two-door boarding strategy, the completion of the turnaround with a SLF of 67% (i.e., scenario instance S-IV-2D) would become feasible without extending scheduled ground times. This corresponds to the seat allocation scheme which applies free middle-seats. This procedure still ensures a reduction of the transmission risk by at least 75% compared to the standard boarding. If airlines aim at maintaining pre-pandemic SLFs, scheduled ground times should be extended by at least 20% (e.g., 60 instead of 50 min for an A320 turnaround) when aircraft are positioned remotely, whereas turnarounds at terminal contact stands require a 40% time extension (e.g., 70 instead of 50 min for an A320 turnaround). If the availability of cleaning agents would be doubled (i.e., six agents instead of three per turnaround), new scheduled ground times could be reduced by 5 min in both cases (e.g., 55 min with two-door boarding, 65 min with one door boarding). Note that even with six cleaning agents and remote stands, former scheduled ground times cannot be achieved with higher SLFs (scenarios S–V and S-VI). Further note that with very low SLFs (scenario S–I and S-II) the relative time benefit is bounded at −30%, given that in these cases the critical path of the turnaround would go via the cargo processes unloading and loading (see Fig. 1).
Fig. 10.
Post-Pandemic Total Turnaround Time relative to Pre-Pandemic Total Turnaround Time at 90% Quantile for all considered Scenario Instances.
6. Discussion and outlook
Our contribution has highlighted that required adaptations to the aircraft turnaround standard operating procedure in a post-pandemic scenario can be incorporated while guaranteeing low level of virus transmissions. However, these adaptations involve additional cost for airlines at three different strategic levels: (1) opportunity cost caused by a reduced seat load and extended scheduled ground times, (2) more cleaning personnel leads to higher costs for ground handling, and (3) investments into altered gate infrastructure and walk-boarding positions.
The analysis of six different seat allocation schemes has revealed that it is impossible to maintain previously scheduled ground times while aiming for an equal seat load and low transmission risk during the boarding process. Thus, trade-offs need to be made between reduced seat load per flight and longer scheduled ground times. Given the fact that airlines generally have very low profit margins, a lower seat load challenges the economic efficiency of many flights. However, considering that demand is only slowly picking up after the shut-down, reduced seat loads seem more feasible than fewer flights per day (might result in reduced connectivity in the network), which would make the product even more unattractive. Nowadays, the option of leaving the middle seats in each row unoccupied seems to be a favored solution. Future research could focus on how ticket prices can be adjusted to ensure efficient operations with fewer tickets sold per flight, or how modified aircraft rotations can include longer ground segments for parts of the fleet.
Our results show that a seat load factor of 67%, which corresponds to the “empty middle-seat” scenario, would require an extension of the minimum ground time by 20% at terminal positions when a one-door, physical distance strategy for boarding is applied and the same amount of cleaning agents is available as before the pandemic. At apron stands (enabling walk-boarding), previously scheduled ground times could be maintained given that front and rear aircraft doors can be used for deboarding and boarding processes. In both cases, transmission risks are reduced by more than 75% compared to the reference boarding. Also, an increase in cleaning personnel can help to keep overall turnaround times low, even if additional disinfection activities have to be carried out after standard cleaning. Assuming 67% SLF and a one-door, physical distance strategy for boarding is applied, only 10% more ground time would be required compared to pre-pandemic operation if the number of available cleaning agents were doubled from 3 to 6 per turnaround. In a parallel study, further seat allocation schemes are analyzed, taking into account the fact that members of the same group do not require physical distances during boarding and can sit together during the flight (Schultz and Soolaki, 2020). Future research should cover the same ground for the deboarding process and provide ideas for this rather uncontrolled aircraft cabin process.
Taking into consideration that airport and ground handling resources are constrained, not all turnarounds can be operated on walk-boarding positions with increased cleaning personnel. Thus, airlines will need to prioritize between aircraft more than ever before. Especially walk-boarding positions are limited, given that they were requested solely by low-cost carriers in pre-pandemic operations, while full-service network carriers transported their passengers via apron busses to remote positions and parked their aircraft at terminal contact stands whenever available. Thus, walk-boarding positions and the related pre-boarding areas in the terminal have been built predominantly at secondary airports or low-cost terminals of primary airports. Given that badly-ventilated jetway bridges (and apron busses) offset the reduced transmission risks from physical-distance boarding, more stands in the vicinity of the terminal should be established at primary airports, so that passengers can board the aircraft via two doors in open space. Otherwise, airlines will need to pre-assign certain flights to walk-boarding stands to enable two-door boarding strategies. All other aircraft will require extended scheduled ground times when they are allocated to terminal positions. Future research should analyze the impact of additional airport and ground handling resources on multiple parallel turnarounds when they all adhere to the proposed process adaptations. With this, airlines can sustainably rebuild their schedules by considering that increased sanitation requirements might remain permanently and require extended ground times for at least a part of their fleet.
Acknowledgements
This project has received funding from the German Federal Ministry of Economic Affairs and Energy (BMWI) within the LUFO-V project OPsTIMAL (grant number 20X1711M).
References
- AhmadBeygi S., Cohn A., Lapp M. Decreasing airline delay propagation by re-allocating scheduled slack. IIE Trans. 2010;42:478–489. doi: 10.1080/07408170903468605. [DOI] [Google Scholar]
- Ali H., Guleria Y., Alam S., Schultz M. A passenger-centric model for reducing missed connections at low cost airports with gates reassignment. IEEE Access. 2019;7:179429–179444. doi: 10.1109/ACCESS.2019.2953769. [DOI] [Google Scholar]
- Andreatta G., De Giovanni L., Monaci M. A fast heuristic for airport ground-service equipment–and–staff allocation. Procedia - Soc. Behav. Sci. 2014;108:26–36. doi: 10.1016/j.sbspro.2013.12.817. [DOI] [Google Scholar]
- Bachmat E., Elkin M. Bounds on the performance of back-to-front airplane boarding policies. Oper. Res. Lett. 2008;36:597–601. doi: 10.1016/j.orl.2008.03.008. [DOI] [Google Scholar]
- Bachmat E., Khachaturov V., Kuperman R. Optimal back-to-front airplane boarding. Phys. Rev. E, Statist. Nonlinear Soft Matter Phys. 2013;87 doi: 10.1103/PhysRevE.87.062805. [DOI] [PubMed] [Google Scholar]
- Bazargan M. A linear programming approach for aircraft boarding strategy. Eur. J. Oper. Res. 2007;183:394–411. doi: 10.1016/j.ejor.2006.09.071. [DOI] [Google Scholar]
- Beatty R., Hsu R., Berry L., Rome J. Preliminary evaluation of flight delay propagation through an airline schedule. Air Traffic Contr. Q. 1999;7:259–270. doi: 10.2514/atcq.7.4.259. [DOI] [Google Scholar]
- Bernstein N. Comment on ”Time needed to board an airplane: a power law and the structure behind it”. Phys. Rev. E, Statist. Nonlinear Soft Matter Phys. 2012;86 doi: 10.1103/PhysRevE.86.023101. [DOI] [PubMed] [Google Scholar]
- Burstedde C., Klauck K., Schadschneider A., Zittartz J. Simulation of pedestrian dynamics using a two-dimensional cellular automaton. Phys. Stat. Mech. Appl. 2001;295:507–525. doi: 10.1016/S0378-4371(01)00141-8. [DOI] [Google Scholar]
- Cook A. University of Westminster; London: 2015. European Airline Delay Cost Reference Values - Updated and Extended Values. Technical Report 4.1. [Google Scholar]
- Cotfas L.A., Delcea C., Milne R.J., Salari M. Evaluating classical airplane boarding methods considering COVID-19 flying restrictions. Symmetry. 2020;12:1087. doi: 10.3390/sym12071087. [DOI] [Google Scholar]
- Delcea C., Cotfas L.A., Paun R. Agent-based evaluation of the airplane boarding strategies– efficiency and sustainability. Sustainability. 2018;10:1879. doi: 10.3390/su10061879. [DOI] [Google Scholar]
- Dijk B., Santos B.F., Pita J.P. The recoverable robust stand allocation problem: a GRU airport case study. OR Spectrum. 2019;41:615–639. doi: 10.1007/s00291-018-0525-3. [DOI] [Google Scholar]
- Dorndorf U., Jaehn F., Pesch E. Flight gate assignment and recovery strategies with stochastic arrival and departure times. OR Spectrum. 2017;39:65–93. doi: 10.1007/s00291-016-0443-1. [DOI] [Google Scholar]
- Du J.Y., Brunner J.O., Kolisch R. Planning towing processes at airports more efficiently. Transport. Res. E Logist. Transport. Rev. 2014;70:293–304. doi: 10.1016/j.tre.2014.07.008. [DOI] [Google Scholar]
- Evler J., Asadi E., Preis H., Fricke H. 8th SESAR Innovation Days. 2018. Stochastic Control of Turnarounds at HUB-Airports. [Google Scholar]
- Ferrari P., Nagel K. vol. 1915. SAGE Publications Inc; Publisher: 2005. Robustness of efficient passenger boarding strategies for airplanes; pp. 44–54. (Transportation Research Record). [DOI] [Google Scholar]
- Frette V., Hemmer P.C. Time needed to board an airplane: a power law and the structure behind it. Phys. Rev. E, Statist. Nonlinear Soft Matter Phys. 2012;85 doi: 10.1103/PhysRevE.85.011130. [DOI] [PubMed] [Google Scholar]
- Fricke H., Schultz M. 8th USA/Europe Air Traffic Management Research and Development Seminar. 2009. Delay Impacts onto Turnaround Performance. [Google Scholar]
- IATA . International Air Transport Association; 2018. IATA Ground Operations Manual. [Google Scholar]
- Jaehn F., Neumann S. Airplane boarding. Eur. J. Oper. Res. 2015;244:339–359. doi: 10.1016/j.ejor.2014.12.008. [DOI] [Google Scholar]
- Jafer S., Mi W. Comparative study of aircraft boarding strategies using cellular discrete event simulation. Aerospace. 2017;4(4) doi: 10.3390/aerospace4040057. [DOI] [Google Scholar]
- Kierzkowski A., Kisiel T. Simulation model of security control lane operation in the state of the COVID-19 epidemic. J. Air Transport. Manag. 2020;88:101868. doi: 10.1016/j.jairtraman.2020.101868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuster J., Jannach D., Friedrich G. Extending the RCPSP for modeling and solving disruption management problems. Appl. Intell. 2009;31:234–253. doi: 10.1007/s10489-008-0119-x. [DOI] [Google Scholar]
- Marelli S., Mattocks G., Merry R. The role of computer simulation in reducing airplane turn time. Boeing AERO Magazine. 1998 [Google Scholar]
- Milne R.J., Kelly A.R. A new method for boarding passengers onto an airplane. J. Air Transport. Manag. 2014;34:93–100. doi: 10.1016/j.jairtraman.2013.08.006. [DOI] [Google Scholar]
- Milne R.J., Salari M. Optimization of assigning passengers to seats on airplanes based on their carry-on luggage. J. Air Transport. Manag. 2016;54:104–110. doi: 10.1016/j.jairtraman.2016.03.022. [DOI] [Google Scholar]
- Milne R.J., Delcea C., Cotfas L.A., Salari M. New methods for two-door airplane boarding using apron buses. J. Air Transport. Manag. 2019;80:101705. doi: 10.1016/j.jairtraman.2019.101705. [DOI] [Google Scholar]
- Mirza M. Economic impact of airplane turn-times. Aero Quarterly. 2008;4 [Google Scholar]
- Müller S.A., Balmer M., Neumann A., Nagel K. Mobility traces and spreading of COVID-19. medRxiv. 2020 doi: 10.1101/2020.03.27.20045302. [DOI] [Google Scholar]
- Nishinari, K.; Kirchner, A.; Namazi, A.; Schadschneider, A. Extended Floor Field CA Model for Evacuation Dynamics. arXiv:cond-mat/0306262, 2003.
- Norin A., Yuan D., Granberg T.A., Värbrand P. Scheduling de-icing vehicles within airport logistics: a heuristic algorithm and performance evaluation. J. Oper. Res. Soc. 2012;63:1116–1125. doi: 10.1057/jors.2011.100. [DOI] [Google Scholar]
- Nyquist D.C., McFadden K.L. A study of the airline boarding problem. J. Air Transport. Manag. 2008;14:197–204. doi: 10.1016/j.jairtraman.2008.04.004. [DOI] [Google Scholar]
- Oreschko B., Kunze T., Schultz M., Fricke H., Kumar V., Sherry L. 5th International Conference on Research in Airport Transportation. 2012. Turnaround prediction with stochastic process times and airport specific delay pattern. [Google Scholar]
- Padrón S., Guimarans D., Ramos J.J., Fitouri-Trabelsi S. A bi-objective approach for scheduling ground-handling vehicles in airports. Comput. Oper. Res. 2016;71:34–53. doi: 10.1016/j.cor.2015.12.010. [DOI] [Google Scholar]
- Puckett J. Library Catalog; 2020. How Airlines Are Changing Their In-Flight Rules for Coronavirus.www.cntraveler.com [Google Scholar]
- Qiang S.J., Jia B., Xie D.F., Gao Z.Y. Reducing airplane boarding time by accounting for passengers' individual properties: a simulation based on cellular automaton. J. Air Transport. Manag. 2014;40:42–47. doi: 10.1016/j.jairtraman.2014.05.007. [DOI] [Google Scholar]
- Rosenow J., Schultz M. Coupling of turnaround and trajectory optimization based on delay cost. In: Winter Simulation Conference (WSC), pp. 2018:2273–2284. doi: 10.5555/3320516.3320788. [DOI] [Google Scholar]
- Schmidt M. A review of aircraft turnaround operations and simulations. Prog. Aero. Sci. 2017;92:25–38. doi: 10.1016/j.paerosci.2017.05.002. [DOI] [Google Scholar]
- Schultz M. Technische Universität Dresden, Faculty of Transport and Traffic Sciences “Friedrich List”; Dresden: 2010. Entwicklung eines individuenbasierten Modells zur Abbildung des Bewegungsverhaltens von Passagieren im Flughafenterminal. PhD thesis. [Google Scholar]
- Schultz M. Springer International Publishing; 2013. Stochastic transition model for pedestrian dynamics; pp. 971–985. (Pedestrian and Evacuation Dynamics 2012). [DOI] [Google Scholar]
- Schultz M. Dynamic change of aircraft seat condition for fast boarding. Transport. Res. C Emerg. Technol. 2017;85:131–147. doi: 10.1016/j.trc.2017.09.014. [DOI] [Google Scholar]
- Schultz M. Implementation and application of a stochastic aircraft boarding model. Transport. Res. C Emerg. Technol. 2018;90:334–349. doi: 10.1016/j.trc.2018.03.016. [DOI] [Google Scholar]
- Schultz M. Fast aircraft turnaround enabled by reliable passenger boarding. Aerospace. 2018;5:8. doi: 10.3390/aerospace5010008. [DOI] [Google Scholar]
- Schultz M. Field trial measurements to validate a stochastic aircraft boarding model. Aerospace. 2018 doi: 10.3390/aerospace5010027. [DOI] [Google Scholar]
- Schultz M., Fuchte J. Evaluation of aircraft boarding scenarios considering reduced transmissions risks. Sustainability. 2020;12:5329. doi: 10.3390/su12135329. [DOI] [Google Scholar]
- Schultz M., Kunze T., Oreschko B., Fricke H. Microscopic process modelling for efficient aircraft turnaround management. 4th International Air Transport and Operations Symposium. 2013 [Google Scholar]
- Schultz M., Schulz C., Fricke H. 3rd International Conference on Research in Airport Transportation. 2008. Efficiency of aircraft boarding procedures; pp. 371–377. [Google Scholar]
- Schultz Michael, Soolaki Majid. Analytical and Simulation Method for Aircraft Passenger Boarding Problem during the Coronavirus Pandemic. arXiv:2007.16021. 2020 doi: 10.1016/j.trc.2020.102931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smieszek T. A mechanistic model of infection: why duration and intensity of contacts should be included in models of disease spread. Theor. Biol. Med. Model. 2009;6 doi: 10.1186/1742-4682-6-25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steffen J.H. vol. 76. Publisher: American Association of Physics Teachers; 2008. A statistical mechanics model for free-for-all airplane passenger boarding; pp. 1114–1119. (American Journal of Physics). [DOI] [Google Scholar]
- Steffen J.H. Optimal boarding method for airline passengers. J. Air Transport. Manag. 2008;14:146–150. doi: 10.1016/j.jairtraman.2008.03.003. [DOI] [Google Scholar]
- van den Briel M.H.L., Villalobos J.R., Hogg G.L., Lindemann T., Mulé A.V. vol. 35. Publisher; INFORMS: 2005. America west airlines develops efficient boarding strategies; pp. 191–201. (INFORMS Journal on Applied Analytics). [Google Scholar]
- Van Landeghem H., Beuselinck A. Reducing passenger boarding time in airplanes: a simulation based approach. Eur. J. Oper. Res. 2002;142:294–308. doi: 10.1016/S0377-2217(01)00294-6. [DOI] [Google Scholar]
- Wittmann J. Customer-oriented optimization of the airplane boarding process. J. Air Transport. Manag. 2019;76:31–39. doi: 10.1016/j.jairtraman.2019.02.002. [DOI] [Google Scholar]
- Wu C.L. Improving airline network robustness and operational reliability by sequential optimisation algorithms. Network. Spatial Econ. 2006;6:235–251. doi: 10.1007/s11067-006-9282-y. [DOI] [Google Scholar]
- Wu C., Caves R.E. Modelling and simulation of aircraft turnaround operations at airports. Transport. Plann. Technol. 2004;27:25–46. doi: 10.1080/0308106042000184445. [DOI] [Google Scholar]
- Wu C.L., Law K. Modelling the delay propagation effects of multiple resource connections in an airline network using a Bayesian network model. Transport. Res. E Logist. Transport. Rev. 2019;122:62–77. doi: 10.1016/j.tre.2018.11.004. [DOI] [Google Scholar]
- Yazdani D., Omidvar M.N., Deplano I., Lersteau C., Makki A., Wang J., Nguyen T.T. Real-time seat allocation for minimizing boarding/alighting time and improving quality of service and safety for passengers. Transport. Res. C Emerg. Technol. 2019;103:158–173. doi: 10.1016/j.trc.2019.03.014. [DOI] [Google Scholar]
- Zeineddine H. A dynamically optimized aircraft boarding strategy. J. Air Transport. Manag. 2017;58:144–151. doi: 10.1016/j.jairtraman.2016.10.010. [DOI] [Google Scholar]