MRI Radiomics for the Prediction of Fuhrman Grade in Clear Cell Renal Cell Carcinoma: a Machine Learning Exploratory Study

Abstract

The Fuhrman nuclear grade is a recognized prognostic factor for patients with clear cell renal cell carcinoma (CCRCC) and its pre-treatment evaluation significantly affects decision-making in terms of management. In this study, we aimed to assess the feasibility of a combined approach of radiomics and machine learning based on MR images for a non-invasive prediction of Fuhrman grade, specifically differentiation of high- from low-grade tumor and grade assessment. Images acquired on a 3-Tesla scanner (T2-weighted and post-contrast) from 32 patients (20 with low-grade and 12 with high-grade tumor) were annotated to generate volumes of interest enclosing CCRCC lesions. After image resampling, normalization, and filtering, 2438 features were extracted. A two-step feature reduction process was used to between 1 and 7 features depending on the algorithm employed. A J48 decision tree alone and in combination with ensemble learning methods were used. In the differentiation between high- and low-grade tumors, all the ensemble methods achieved an accuracy greater than 90%. On the other end, the best results in terms of accuracy (84.4%) in the assessment of tumor grade were achieved by the random forest. These evidences support the hypothesis that a combined radiomic and machine learning approach based on MR images could represent a feasible tool for the prediction of Fuhrman grade in patients affected by CCRCC.

Introduction

Despite being relatively rare, renal cancer is estimated to cause almost 15.000 deaths during 2019 in the USA alone [1]. The most common primary kidney malignancy is the renal cell carcinoma (RCC), with the clear cell subtype (CCRCC) accounting for the large majority of cases [2]. While characterization of these lesions using imaging modalities such as CT and MRI still represents a complex and challenging task, the increasing number of management strategies endorses the need for a more informative pre-treatment assessment to allow treatment tailoring [3]. Fuhrman grade is a histological predictive factor based on nuclear characteristics which is highly regarded as an independent prognostic factor in patients with CCRCC [4]. It allows to stratify patients into four groups (I, II, III, IV) with progressively worse prognosis, although the first two grades are generally considered as low grades having a better cancer-specific survival compared with high-grade tumors (III and IV) [5, 6]. While Fuhrman grade can be obtained prior to treatment by means of percutaneous biopsy, this invasive technique suffers from serious limitations [7, 8]. As a result, attempts have been made to identify imaging parameters predictive of nuclear grade at histopathology with many investigating texture analysis (TA) approaches [9–16]. Indeed, TA might hold the key to reach a deeper insight into RCC biology through medical imaging [17–19]. This advanced post-processing technique is based on the quantification of tumor heterogeneity with the extraction of numerous parameters differing in terms of significance and complexity, with interesting results in other fields of radiology [20–22]. Recently, machine learning (ML) has been successfully coupled to TA for both oncologic and non-oncologic imaging applications [23–26]. ML is a branch of artificial intelligence focused on the development of algorithms capable of learning and improving by analyzing datasets, without prior explicit programming. With specific regard to CCRCC and prediction of nuclear grade, to the best of our knowledge, TA has been exclusively explored on CT images [10–13], recently in combination with ML too [14–16]. Therefore, the aim of the present study was to evaluate the feasibility of a combined TA and ML approach on MR images for the prediction of Fuhrman grade in CCRCC.

Methods and Materials

This retrospective study was approved by the local IRB and the need for informed consent was waived.

Patient Population

MRI scans of patients referred to our institution between 01 January 2017 and 01 January 2019 for the evaluation of renal lesions were retrieved from the department radiology information system’s database. The following inclusion criteria were applied: (1) MRI protocol including at least a T2-weighted and a dynamic contrast-enhanced sequence on the axial plane; (2) patients who underwent surgical treatment no more than 1 month after the MRI scan was performed; (3) final histopathologic diagnosis of CCRCC with Fuhrman grading was available. Finally, patients were excluded if artifacts were present on MR images.

MRI Acquisition

All MR images were acquired on a 3-Tesla scanner (Magnetom Trio, Siemens Healthcare, Erlangen, Germany) equipped with surface multichannel body coils and embedded spinal coils. The imaging protocol included, among others, the following sequences that were used for the analysis: (1) HASTE T2 on the axial plane without fat suppression (TE, 95; TR, 2000; slice thickness, 4 mm; FOV, 328 × 350; matrix, 192 × 256) and (2) T1 VIBE on the axial plane (TE, 1.1; TR, 3.3; slice thickness, 2 mm; FOV, 393 × 450; matrix, 179 × 256) acquired before and after the injection of contrast agent (0.1 mmol/kg Gd-DTPA Magnevist, Bayer Pharma, Germany).

Image Segmentation and Texture Analysis

Two readers reviewed the entire protocol in consensus to identify the renal tumor. Similarly, image segmentation was performed in consensus. In particular, using a dedicated segmentation software (ITK-Snap, v3.6.0) [27], regions of interest were manually drawn on every slice containing the renal tumor on T2-w and arterial phase DCE images while excluding macroscopic necrotic and cystic areas when present (Fig. 1). Therefore, a whole-lesion volumetric region of interest (VOI) was obtained for each patient. Subsequently, an open-source Python software (PyRadiomics, v2.2.0) [28] was employed for feature extraction.

Fig. 1.

Images from a patient with a Fuhrman grade III clear cell renal cell carcinoma of the left kidney. T1-weighted post-contrast (a, b) and T2-weigthed (c, d) images are shown before (a, c) and after (b, d) lesion segmentation

The image pre-processing pipeline follows the recommendations of PyRadiomics’ developers and previously published studies [29]. First of all, images and corresponding VOIs were resampled to an isotropic 1 × 1 × 1 mm. Then, image normalization was performed. In detail, mean intensity was subtracted on a voxel-by-voxel basis followed by division by the standard deviation and scaling by a factor of 100, resulting in an expected range of [− 300, 300]. The resulting intensity array was shifted by 300, as suggested by the developers, to avoid negative values that may alter the calculation of some first-order texture parameters. Image discretization was performed by applying a fixed bin width of 5 and finally, additional filtered images were obtained by applying Laplacian of Gaussian filters with sigma values ranging from 1 (finest texture) to 5 mm (coarsest), with 1 mm increments, and Wavelet decomposition, yielding 8 derived images. These filters were used in addition to the original images for feature extraction as they can highlight different aspects of tissue texture. From the resulting images, first-order statistics, 3D shape–based, and Gray Level Co-occurrence (GLCM), Run Length (GLRLM), Size Zone (GLSZM) and Dependence (GLDM) Matrices–derived features together with Neighboring Gray Tone Difference Matrix ones were computed.

Machine Learning

The Konstanz Information Miner analytics platform (KNIME, v 3.7.1) was employed for the ML analyses as it was already proved to be useful in similar settings [30–32]. Patient data were divided in a binary fashion in high (III and IV) and low (I and II) tumor grade classes; then, a multiclass assessment was performed using all available tumor grades as classes.

Prior to the analysis, the Synthetic Minority Over-sampling Technique (SMOTE) was applied. It generates synthetic data points (patients in this study) by extrapolating an object between two nearest neighbors belonging to the same class. Successively, a point along the line connecting these two objects is randomly selected, determining the new object’s attributes [33]. In this study, the extra data created using SMOTE, consisting of 90 completely artificial patients, was not employed for model training or testing but only for validation.

After the application of the hold-out method to divide the dataset in training (75% of the total sample) and testing sets (the remaining 25%) on the data obtained from real patients, a two-step feature selection was applied to the training set [34]. First of all, the correlation matrix was computed among all variables and a correlation threshold of 0.5 was selected to exclude highly intercorrelated ones as to eliminate redundant data (Fig. 2). Secondly, the Wrapper method was applied for each algorithm. This searches for the best combination of features based on a heuristic function optimization and a tenfold cross-validation. It splits the dataset into k folds and the model is trained k times on k-1 folds and tested on the remaining fold.

Fig. 2.

Feature correlation matrix represented as a hierarchically clustered heatmap. The resulting data was employed in the first step of the feature selection process

Subsequently, evaluation metrics (i.e., accuracy, recall, precision, sensitivity, specificity, and AUCROC) were obtained by assessing the performance of the resulting models on the test and validation sets, composed respectively by real patient data and artificial data [35].

Algorithms

In this study, a J48 decision tree alone and in combination with ensemble learning methods were used. Decision trees perform predictions by comparing test observations to predictor space segmentations made on the training data. The rules on which training data stratification is obtained can be represented graphically in a tree-like structure, to which the name of the algorithm class is owed [36].

Bagging and boosting (ADA-B) are among the most famous ensemble learning methods. While the first one needs an unstable learner to achieve the best performances, the second one keeps a group of weights over the original training set and updates them after each classifier is learned by the base learning algorithm [37]. On the other hand, random forest (RF) employs a large number of decision trees, based on bagging, resampling data repeatedly, and training a new classifier for each sample. Each tree is trained on a diverse set of records and attributes. The row sets for each decision tree are created by bootstrapping and have the same size as the original input table. For each node of a decision tree, a new set of attributes is determined by taking a random sample of size square root of m, where m is the total number of attributes [38]. Decorate generates an ensemble by training a classifier on a given training data set. In successive iterations, some artificial data are created from the training set in a way that their classes differ maximally from the predicted classes by the current ensemble. These data are added to the first training set and a new classifier is made on this new data set. This procedure increases the diversity of the ensemble. The artificial data are created by using the mean and the standard deviation of the training set together with its Gaussian distribution [39].

Results

Patient Population

The final population included 32 patients, 15 males and 17 females, with a median age of 59.5 years (interquartile range = 23.5). Overall, lesion grouping based on Fuhrman grade was the following: 8 grade I lesions, 12 grade II lesions, and 12 grade III lesions. No grade IV lesions were found in our population. Therefore, the low-grade group was composed of 20 patients while the high-grade group of 12 patients.

Feature Selection

Since the number of features was too high (2438 features) related to the number of patients (30 real patients in the first test, 90 patients in the extra validation), the correlation matrix–based feature selection allowed us to reduce the number of non-redundant features to 53. The Wrapper method further reduced the number of employed features to between 1 and 7 according to algorithm and number of classes (Tables 1 and 2).

Table 1.

Algorithms and features selected for the binary classification (high- vs. low-grade tumors)

Algorithms	Features
J48	1. t2_log-sigma-2-0-mm-3D_glcm_Correlation
Bagging	1. dce_wavelet-LLH_glcm_SumEntropy 2. dce_wavelet-HHH_firstorder_Kurtosis 3. t2_log-sigma-1-0-mm-3D_gldm_LargeDependenceLowGrayLevelEmphasis
RF	1. dce_wavelet-LLH_glcm_InverseVariance 2. dce_wavelet-LHH_glcm_Imc2 3. t2_wavelet-HHH_glrlm_GrayLevelVariance
ADA-B	1. dce_wavelet-LHL_firstorder_Mean 2. dce_wavelet-HHH_firstorder_Kurtosis 3. t2_wavelet-HHH_glszm_SizeZoneNonUniformityNormalized
Decorate	1. dce_wavelet-LLH_glcm_InverseVariance 2. dce_wavelet-LLH_glcm_SumEntropy 3. t2_wavelet-HLH_glszm_LargeAreaHighGrayLevelEmphasis 4. t2_wavelet-HLH_glszm_SizeZoneNonUniformityNormalized

RF, random forest; ADA-B, bagging and boosting

Table 2.

Algorithms and features selected for the multiclass assessment

Algorithms	Features
J48	1. dce_wavelet-LHH_glcm_Imc2 2. dce_wavelet-HHH_firstorder_Maximum 3. dce_wavelet-HHH_glcm_SumEntropy 4. t2_wavelet-HLH_glcm_InverseVariance 5. t2_wavelet-HHH_glcm_SumSquares
Bagging	1. dce_original_glrlm_LongRunHighGrayLevelEmphasis 2. t2_log-sigma-1-0-mm-3D_gldm_LargeDependenceLowGrayLevelEmphasis 3. dce_wavelet-HHH_glcm_SumEntropy 4. 2_wavelet-HLH_glszm_LargeAreaHighGrayLevelEmphasis 5. t2_wavelet-HHH_firstorder_Uniformity 6. t2_wavelet-HHH_glrlm_GrayLevelNonUniformityNormalized
RF	1. dce_wavelet-HLL_firstorder_Skewness 2. t2_wavelet-HHL_gldm_DependenceNonUniformityNormalized 3. dce_wavelet-LLH_glcm_SumEntropy 4. dce_wavelet-LLH_glcm_InverseVariance 5. t2_wavelet-HHH_glrlm_GrayLevelNonUniformityNormalized 6. t2_wavelet-HHH_glrlm_GrayLevelVariance
ADA-B	1. dce_log-sigma-2-0-mm-3D_glcm_Imc2 2. dce_wavelet-HHH_glcm_SumEntropy 3. dce_wavelet-LLH_glcm_SumEntropy 4. t2_wavelet-HLL_glszm_LargeAreaLowGrayLevelEmphasis 5. t2_wavelet-HLH_glszm_LargeAreaHighGrayLevelEmphasis 6. t2_wavelet-HHL_firstorder_Median 7. t2_wavelet-HHH_glrlm_GrayLevelNonUniformityNormalized
Decorate	1. dce_wavelet-HLL_firstorder_Kurtosis 2. dce_wavelet-HHH_glcm_SumEntropy 3. dce_original_glrlm_LongRunHighGrayLevelEmphasis

RF, random forest; ADA-B, bagging and boosting

Machine Learning Analysis

For each model in the binary classification, the results of learning and testing on real data as well as testing on the artificial data are shown in Table 3. All the ensemble methods achieved an accuracy greater than 90%: ADA-B obtained the best accuracy (92.7%), recall, and sensitivity (91.7%); bagging showed the highest AUCROC, being an indicator of a good quality of binary prediction; decorate reached out the greatest precision (91.2%) and specificity (95.0%).

Table 3.

Accuracy parameters for each model in the binary classification

	Test on real data		Test on artificial data
	Accuracy (%)	AUCROC	Accuracy (%)	Recall (%)	Precision (%)	Sensitivity (%)	Specificity (%)	AUCROC
J48	87.5	0.900	74.0	55.5	69.0	55.5	85.0	76.6
Bagging	62.5	73.3	90.6	88.9	86.5	88.9	91.7	0.952
RF	75.0	0.633	91.7	88.9	88.9	88.9	93.3	0.918
ADA-B	75.0	0.733	92.7	91.7	89.2	91.7	93.3	0.933
Decorate	62.5	0.700	91.7	86.1	91.2	86.1	95.0	0.903

RF, random forest; ADA-B, bagging and boosting

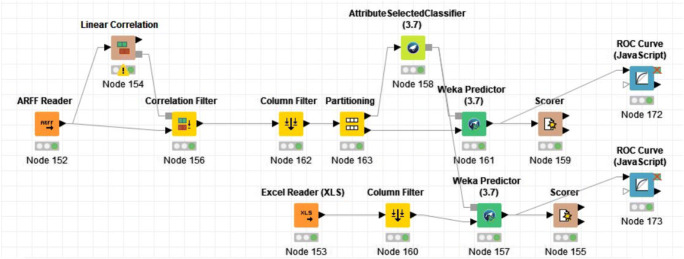
As aforementioned, after the binary analysis on both real and artificial data in order to distinguish a low and a high grade of tumor, the multiclass assessment according to tumors’ grading was performed. All the results according to this classification are summarized in Table 4. In this case, the best results were achieved by RF in terms of accuracy (84.4%), decorate in terms of recall and sensitivity (100%), and ADA-B in terms of precision (94.1%) and specificity (96.7%) (Fig. 3). Figure 4 represents the complete analysis workflow on KNIME.

Table 4.

Accuracy parameters for each model in the multiclass assessment

	Test on real data	Test on artificial data
	Accuracy (%)	Accuracy (%)	Recall (%)	Precision (%)	Sensitivity (%)	Specificity (%)
J48	37.5	75.0	69.4	80.6	69.4	90.0
Bagging	50.0	81.2	83.3	88.2	83.3	93.3
RF	62.5	84.4	94.4	91.9	94.4	95.0
ADA-B	50.0	83.3	88.9	94.1	88.9	96.7
Decorate	62.5	83.3	100	81.8	100	86.7

RF, random forest; ADA-B, bagging and boosting

Fig. 3.

Bar plot comparison of the accuracy obtained on artificial data by each algorithm in both binary and multiclass classifications

Fig. 4.

Schematic representation of the KNIME analysis workflow employed in the analysis

Discussion

In recent years, there has been a growing interest towards radiomic applications in medical imaging and in particular in their potential role in the evaluation of renal tumors. Many publications focused on differential diagnosis of renal lesions, based either on CT [25, 40–43] or MRI-derived [44–46] textural features. Other authors also focused their attention on tumor staging [47] or prediction of survival [48]. While CT radiomic features have been used to predict CCRCC Fuhrman grade, we aimed to expand the available literature by combining radiomic TA and ML on MR images for this purpose. As reported above, the model with the best performance reached a diagnostic accuracy of 92.7% on the test dataset in discriminating low- and high-grade CCRCC. On the hand, the 3-class assessment performance was relatively lower (84.4%). This difference in accuracy is somewhat expected as ML algorithms usually benefit from a lower number of output classes, especially when available data is limited [49]. Similarly, the improved performance of ensemble methods compared with the J48 decision tree alone could be anticipated [37].

It is interesting to note that Lin et al. also employed a gradient-boosted decision tree from the CatBoost library to classify CCRCC grade on CT images, obtaining an AUC of 0.87 [16]. This approach is similar to that employed in our study as we confirm the good performance of decision tree ensembles in this setting, even on MRI radiomic data. Recently, Kocak also tested the usefulness of SMOTE in CT ML of CCRCC [15]. In his study, a more complex algorithm (a neural network) was employed, but no difference was found in its accuracy when balancing the data with this over-sampling technique. Similarly, we chose not to employ SMOTE for data balancing, but to create a new artificial data set that allowed us to perform classifier external validation, a known approach in ML [50, 51]. Other families of classifiers were tested in literature for Fuhrman grade prediction from CT images [14]. In his study, Bektas reports that the best performing model was based on a support-vector machine. It should be noted that the cited studies obtained overall lower accuracy for the classification of low and high CCRCC grade (reported AUC range = 0.71–0.87) when compared with our results (AUC = 0.93). It could be hypothesized that MRI TA provides more useful information than CT for the training of ML models. This is further supported by the good accuracy also demonstrated in the 3-class prediction.

The present work might contribute in the laying of foundations for a non-invasive pre-operatory assessment of CCRCC nuclear grade. As aforementioned, the Fuhrman grade is an independent predictor of prognosis for patients. However, while percutaneous biopsy is currently accepted as the diagnostic tool to predict nuclear grade, it is an invasive procedure prone to limitations highlighted by previous study sharing a similar clinical implication to ours [15]. If our preliminary results were to be confirmed, this approach might allow multiple assessments of Fuhrman grade in patients during follow-up without the need for ionizing radiation exposure [15].

This study suffers from some limitations that should be acknowledged and discussed. Firstly, the retrospective nature of the study and the relatively small sample size, which is also accountable for the absence of grade IV lesions in our population, might undermine the value of our results. Secondly, a reproducibility analysis to test the reliability of manual segmentation and therefore feature stability was not performed in the present study. Indeed, it has been reported that two-dimensional segmentations of CT images for CCRCC patients are sensitive to inter- and intra-operator variability [52] and that segmentations’ margins can significantly affect the ML workflow and output [53]. However, the abovementioned limitations are intrinsically related to the exploratory nature of this study, specifically aimed to test the feasibility of a methodology that will need further and more robust validations to achieve its promising clinical potential.

Conclusion

With this study, we provided evidences to support the feasibility of a combined TA and ML approach on MR images for the prediction of Fuhrman grade in patients affected by CCRCC. Further studies are advocated to assess whether this methodology could play a role in the management of these patients in clinical practice.

Compliance with Ethical Standards

This retrospective study was approved by the local IRB and the need for informed consent was waived.