Abstract
NEMA characterization of PET systems is generally based on 18F because it is the most relevant radioisotope for the clinical use of PET. 18F has a half-life of 109.7 min and decays into stable 18O via β+ emission with a probability of over 96% and a maximum positron energy of 0.633 MeV. Other commercially available PET radioisotopes, such as 82Rb and 68Ga have more complex decay schemes with a variety of prompt gammas, which can directly fall into the energy window and induce false coincidence detections by the PET scanner.
Methods
Aim of this work was three-fold: (A) Develop a GATE model of the GE Signa PET/MR to perform realistic and relevant Monte Carlo simulations (B) Validate this model with published sensitivity and Noise Equivalent Count Rate (NECR) data for 18F and 68Ga (C) Use the validated GATE-model to predict the system performance for other PET isotopes including 11C, 15O, 13N, 82Rb, and 68Ga and to evaluate the effect of a 3T magnetic field on the positron range.
Results
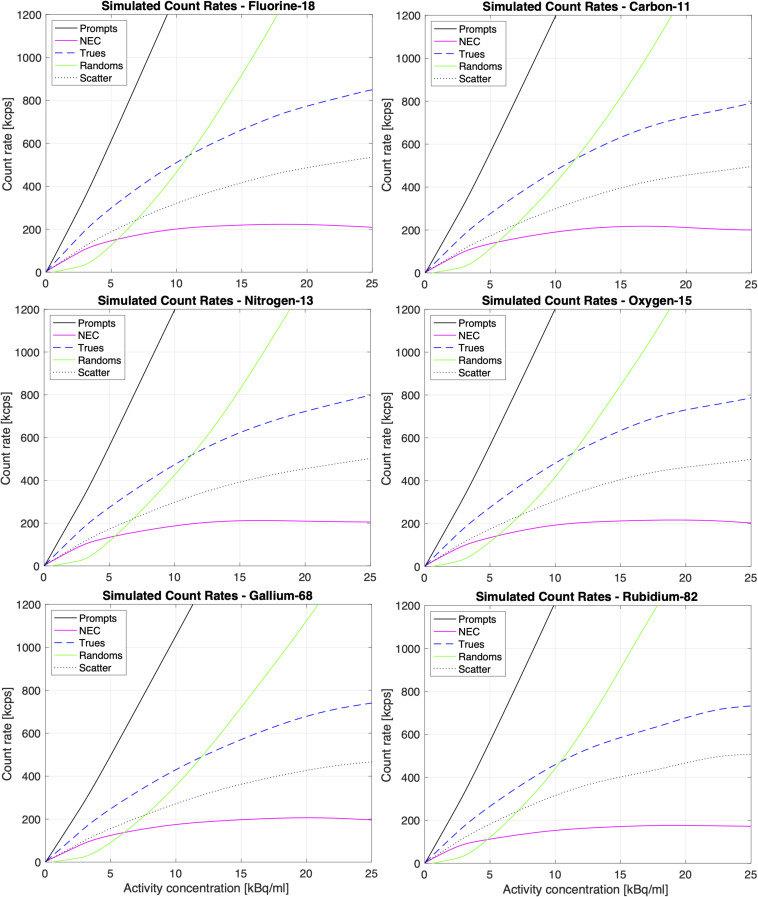
Simulated sensitivity and NECR tests performed with the GATE-model for different radioisotopes were in line with literature values. Simulated sensitivities for 18F and 68Ga were 21.2 and 19.0/kBq, respectively, for the center position and 21.1 and 19.0 cps/kBq, respectively, for the 10 cm off-center position compared to the corresponding measured values of 21.8 and 20.0 cps/kBq for the center position and 21.1 and 19.6 cps/kBq for the 10 cm off-center position. In terms of NECR, the simulated peak NECR was 216.8 kcps at 17.40 kBq/ml for 18F and 207.1 kcps at 20.10 kBq/ml for 68Ga compared to the measured peak NECR of 216.8 kcps at 18.60 kBq/ml and 205.6 kcps at 20.40 kBq/ml for18F and 68Ga, respectively. For 11C, 13N, and 15O, results confirmed a peak NECR similar to 18F with the effective activity concentration scaled by the inverse of the positron fraction. For 82Rb, and 68Ga, the peak NECR was lower than for 18F while the corresponding activity concentrations were higher. For the higher energy positron emitters, the positron range was confirmed to be tissue-dependent with a reduction of the positron range by a factor of 3 to 4 in the plane perpendicular to the magnetic field and an increased positron range along the direction of the magnetic field.
Conclusion
Monte-Carlo simulations were used to predict sensitivity and NECR performance of GE Signa PET/MR for 18F, 15O, 13N, 11C, 82Rb, and 68Ga radioisotopes and were in line with literature data. Simulations confirmed that sensitivity and NECR were influenced by the particular decay scheme of each isotope. As expected, the positron range decreased in the direction perpendicular to the 3T magnetic field. However, this will be only partially improving the resolution properties of a clinical PET/MR system due to the limiting spatial resolution of the PET detector.
Keywords: nuclear medicine, PET/MR, NEMA NU 2–2012, high energy positron emitters, positron range
Introduction
The simultaneous acquisition of both PET and MRI was first developed for small animal imaging (Shao et al., 1997) whereas the development of an integrated PET/MR system for human studies only dated from a decade ago (Catana et al., 2010). The development of solid-state detectors such as avalanche photodiodes (APDs) and silicon photomultipliers (SiPMs) made it possible to integrate a PET detector ring into the bore of an MR scanner and to develop fully integrated PET/MR systems. The main advantage of using SiPMs over APDs is the faster detector response, therefore enabling simultaneous Time-of-Flight (TOF) PET and MR scanning, as demonstrated with the GE Signa PET/MR system (Yamamoto et al., 2003; Levin et al., 2016b; Vandenberghe et al., 2016; Efthimiou et al., 2019).
In terms of resolution, the PET spatial resolution is mainly limited by the detector size of discrete detector elements, the positron range, non-collinearity of the gamma rays resulting from an annihilation event and the decoding scheme of the PET scanner (Levin and Hoffman, 1999; Moses, 2011). The positron range, that is the distance the positron travels from the emitting nucleus to the location where the annihilation occurs, is the main non-detector related factor that limits the PET resolution (Moses, 1994; Palmer et al., 2005; Park et al., 2007; Peng and Levin, 2012) and the use of a magnetic field to limit its impact has already been proposed in the nineties (Iida et al., 1986; Rickey et al., 1992; Hammer et al., 1994; Laforest and Liu, 2008; Vallabhajosula et al., 2011). Because of the Lorentz force, a moving charged particle such as a positron describes a helical path along the direction of a magnetic field. As such, the positron range is reduced in the plane perpendicular to the magnetic field, while it remains unaltered or becomes slightly enlarged in the direction of the magnetic field (Eleftheriou et al., 2014; Kolb et al., 2015). Furthermore, the positron range relates directly to the energy of the positron (Kemerink et al., 2011; Emond et al., 2019). Studies with various PET radioisotopes have reported a larger reduction of the positron range for isotopes emitting positrons with a higher energy such as 120I (Herzog et al., 2010), 82Rb (Rahmim et al., 2008); or 68Rb (Wirrwar et al., 1997; Cal-González et al., 2009; Soultanidis et al., 2011; Alva-Sánchez et al., 2016; Li et al., 2017). In order to reduce the blurring effect of the positron range, it can be modeled as part of Point Spread Function (PSF), used in the reconstruction algorithm to model the PET system response. However, as stated in Jodal et al. (2012), different values for the positron range of different PET isotopes have been reported in literature, probably because of the limited accuracy of the experimental setup used in some of these studies such that the intrinsic detector resolution might be comparable to the positron range. As reference values for this study, we used the positron range values reported in Cal-González et al. (2009), Jodal et al. (2012) for the most relevant PET isotopes and various surrounding tissues.
Generally, the evaluation of the performance of a PET system is done for 18F because it is the most widely used PET isotope in a clinical setting to evaluate the glucose metabolism in mainly oncological but also specific cerebral (Phelps et al., 1979) and cardiac diseases (Marshall et al., 1983). However, with the increasing clinical relevance of other radioisotopes, such as 15O, 13N, 11C, 82Rb, and especially 68Ga (Hoffend et al., 2005), the need to evaluate the PET system performance for these isotopes is increasing because of their different decay scheme and physical properties. 18F almost exclusively decays via positron emission with a branching ratio of 96.8% and has a relatively low maximum positron energy (0.6335 MeV). Properties of 15O, 13N, and 11C, are in line with 18F properties and are considered pure β+ emitters, with the probability of positron emission being close to 100% and with a maximum positron energy of 1.735, 1.198, and 0.960 MeV, respectively. On the other hand, 82Rb and 68Ga have more complex decay schemes with multiple positron emission branches with different energies and with a significant contribution of prompt gamma emissions (Banerjee and Pomper, 2013; Afshar-Oromieh et al., 2014; Conti and Eriksson, 2016; Papp et al., 2018; Mayerhoefer et al., 2020). In addition, these PET radioisotopes emit positrons with a higher maximum energy of 3.381 and 1.8991 MeV, respectively (energy of the most abundant positron). In the context of simultaneous PET/MR imaging, the impact of a high magnetic field on positron range during PET scanning still needs extensive evaluation, especially for high-energy positron emitters.
Among the NEMA acceptance tests, the sensitivity and Noise Equivalent Count Rate (NECR) tests are essential to evaluate the PET system performance. Sensitivity expresses the fraction of coincidences resulting from β+ decay that is registered by the PET system for low activity concentrations. NECR is related to signal-to-noise ratio (SNR) and evaluates the impact of an increased activity concentration on the PET signal. It determines the interplay between true events, scatter and randoms to estimate which increase of activity concentration is still beneficial to improve the SNR.
The aim of this work was three-fold and can be summarized as follows: (A) Develop a realistic GATE model for the GE Signa PET/MR (B) Validate this model with sensitivity and NECR measurements performed on the 3T GE Signa PET/MR for 18F and 68Ga according to the NEMA NU 2–2012 protocol (National Electrical Manufacturers Association [NEMA], 2012; Caribé et al., 2019) (C) Use the validated GATE-model to predict the PET/MR system performance for other isotopes including 18F, 11C, 15O, 13N, 82Rb, and 68Ga and to evaluate the effect of the 3T magnetic field on the positron range.
Materials and Methods
GATE Model for the GE Signa PET/MR
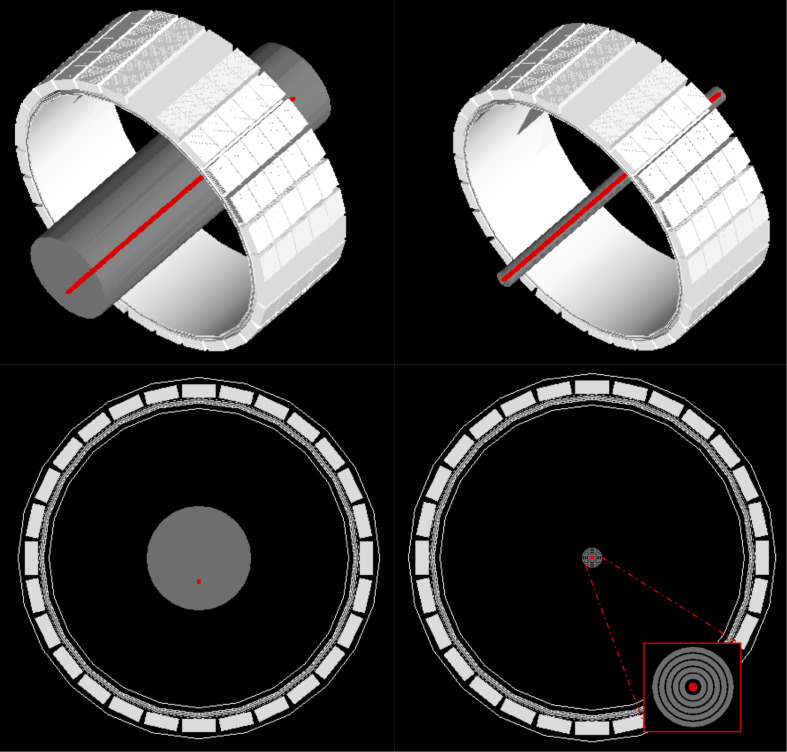
GATE is a toolbox for Monte Carlo (MC) simulations based on GEANT4 and adapted for nuclear medicine applications (Jan et al., 2004). GATE Monte Carlo (MC) simulations were performed on a high-performance computer installed at Ghent University (Vlaams Supercomputer Centrum – VSC). The GATE model was implemented to mimic the PET hardware configuration of the integrated GE Signa PET/MR system consisting of five rings of 28 detector blocks each, covering an axial Field Of View (FOV) of 25 cm while the transaxial FOV is 60 cm. Each detector element consisted of a lutetium-yttrium-oxyorthosilicate (LYSO) scintillator with crystal elements of 25 mm × 4.0 mm × 5.3 mm and MR-compatible SiPM technology (Levin et al., 2016a). In addition, an energy window of 425–650 keV was used while the coincidence window was set to 4.57 ns (±2.29 ns). The geometry was modeled using the cylindrical PET system model in GATE, which also takes into account the foam, plastic and copper shielding between the bore and the detectors. This model was used to simulate the annihilation distribution of positrons for different tissue types and included the following physical processes: positron decay, multiple scattering, ionization, bremsstrahlung and electron annihilation. To evaluate the effect of a magnetic field on the positron range, a magnetic field with a field strength of 3.0 Tesla was in the axial direction to model the MR component of the GE Signa PET/MR system which has a static magnetic field of 3.0 Tesla with a maximum radiofrequency amplitude of 44 mT/m and a maximum slew rate of 200 T/m/s.
Validation of the GATE Model for the GE Signa PET/MR
To validate the GATE model for the GE Signa PET/MR, we compared the sensitivity and NECR results of the NEMA NU 2–2012 acceptance measurements of the GE Signa PET/MR system using 18F and 68Ga with simulated sensitivity and NECR for 18F and 68Ga using GATE and the appropriate model for the GE Signa PET/MR and the hardware phantoms.
Sensitivity Measurements
Sensitivity measurements were performed at two different locations in the FOV according to the NEMA NU 2–2012 protocol (National Electrical Manufacturers Association [NEMA], 2012). At each location, multiple measurements were performed of a 700 mm long source filled with low levels of activity. The line source was surrounded by an aluminum cylinder of initially 2.5 mm thickness with successively adding four 2.5 mm thick aluminum sleeves. Low activity levels were used to minimize random events and dead time effects while the dense aluminum surroundings of the line source ensured sufficient annihilation events to measure the PET signal. To obtain sufficient count statistics, sensitivity data were measured as long as it took to have at least 10.000 true events collected per slice. The sensitivity was calculated by extrapolating the sensitivity values for the line source surrounded by an aluminum sleeve with varying thickness to the sensitivity value corresponding to the attenuation-free measurement of the line source via the following equation:
| (1) |
where Si is the sensitivity corresponding to the ith measurement, Xi the thickness of the aluminum sleeve for the ith measurement, μAl the linear attenuation coefficient of aluminum and S0 actual sensitivity corresponding to a measurement with no aluminum surrounding the line source.
Sensitivity Simulations Using GATE
The simulations consisted of modeling a low activity line source filled with 5 MBq, positioned first in the center of the FOV and then at a radial distance of 10 cm from the center. To measure the sensitivity, simulations were performed of the line source surrounded by an aluminum sleeve with five different thicknesses ranging from 2.5 to 12.5 cm in steps of 2.5 cm. For each simulation, the count rate of true events only was obtained ROOT’s “Coincidences” tree which stores pairs of single events that meet the conditions specified in the digitizer. Each pair is identified by an eventID for each of the two single events (eventID1 and eventID2), which identifies the radioactive decay generating the singles. Furthermore, the entire history of interactions, including Compton or Rayleigh scattering, occurring from their location of origin till they reach the detector, is recorded for each event of a pair. A coincidence detection is considered to be random when the eventID between the two single events of one pair is different. When they are identical, a coincidence event can still be either a scattered or true event. True coincidences are obtained by excluding paired events with a history of compton or rayleigh scattering. Corresponding sensitivity values were determined as described for the sensitivity measurements and the final sensitivity was reported as the average of both positions in the FOV.
NECR Measurements
Noise Equivalent Count Rate was measured with a 700 mm long and 203 mm wide polyethylene cylinder containing a 700 mm long plastic tube line source (3.2 mm inner diameter) filled with high activity. To evaluate the impact of random counts and dead time effects for different activity levels, the measurements were repeated to take advantage of the physical decay and cover different levels of activity. Through a sinogram-based analysis, as described below, the peak NECR, corresponding activity concentration and scatter fraction were extracted from these measurements (National Electrical Manufacturers Association [NEMA], 2012).
NECR Simulations Using GATE
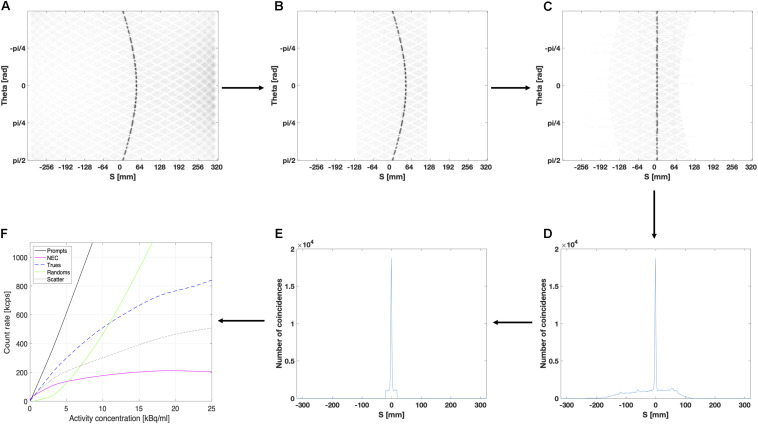
For NECR simulations, the activity in the line source was varied from 1 to 800 MBq using a total of 11 different levels in order to reduce the computation time. In order to estimate the rate at which the scanner acquires coincidence data, that is true, random, or scattered coincidences, a sinogram based analysis was performed. For each slice, the sinogram stores the LOR as function of the projection angle and the distance from the center of the FOV. The GATE output file containing the sinogram data were imported as a 2D matrix and transformed into a 2D histogram with 320 bins for the vertical axis, representing the projection angle from 0 to π, and 640 projection bins for the horizontal axis, representing the distance from the center of the FOV ranging from −300 to 300 mm for the GE Signa PET/MR. All processing steps are shown in Figure 4.
FIGURE 4.
Simulated count rates and NECR for 18F, 15O, 11C, 13N, 82Rb, and 68Ga according to NEMA, as a function of the activity concentration.
According to the NEMA protocol, an alignment of the sinogram data was performed by finding the maximum value for each projection angle and shifting the projection data such that the maximum value for each projection angle is at the center of the sinogram, as shown in Figures 1A–C. After alignment, the corresponding projection bins of all projection angles are summed to obtain a summed projection profile, as shown in Figure 1D. Next, a 40 mm wide strip (see Figure 1E) was centralized around the peak of the summed projection profile in order to estimate the background counts according to NEMA procedures. The values of the projection bins at left and right edge of this central 40 mm wide strip were averaged and multiplied by the number of projection bins within the strip. This value was considered as a representative estimate for the fraction of random and scattered events detected within the strip and used to estimate the corresponding fraction of true events. Once the fractions of random, scattered and true events are estimated for different activity levels, the corresponding count rate curves as well as NECR can be extracted (Figure 1F).
FIGURE 1.
Extraction of NECR data: (A) Extract in ROOT the sinogram data for each slice, (B) Set all pixels located more than 12 cm from the center of the FOV to 0, (C) Align the projection bins of each projection angle according to the maximum values, (D) Sum all projection angles of the sinogram, (E) Select a 40 mm wide strip to estimate random and scattered events, (F) Compute the scatter fraction and different count rate curves as well as the NECR.
Simulated Sensitivity and NECR of the GE Signa PET/MR for Other Isotopes Using GATE
The GATE-model for the GE Signa PET/MR was used to simulate the sensitivity and NECR of the PET/MR system for isotopes other than 18F and 68Ga including 11C, 15O, 13N, and 82Rb. In terms of sensitivity, the simulated values were compared with the theoretical sensitivities based the branching ratio of each isotope and the average sensitivity of 21.5 cps/kBq measured for 18F (Caribé et al., 2019).
Positron Range Evaluation Using the GATE Model for the GE Signa PET/MR
The GATE-model for the GE Signa PET/MR was used to simulate the presence of the magnetic field and evaluate its impact on the positron range in different tissue media. To characterize the effect of the 3T magnetic field on the positron range, we simulated point sources of positron-emitting radionuclides including 18F, 11C, 15O, 13N, 68Ga, and 82Rb positioned in the middle of a homogeneous 20 cm × 20 cm × 20 cm cube with different tissue media: lung (mass density of 0.3 g/cm3), soft tissue (mass density of 1.0 g/cm3), bone (mass density of 1.42 g/cm3). To evaluate the tissue-dependence, we simulated the spatial distribution of positron annihilation for 68Ga in an inhomogeneous region. The region comprises two adjacent cubes of 20 cm × 20 cm × 20 cm filled with lung and soft tissue. For each isotope, 5 million events were simulated with and without 3T magnetic field applied in the axial direction. As output, the spatial coordinates of the location of the annihilation end point were saved to a file for each recorded positron.
Results
GATE Model for the GE Signa PET/MR
The GATE model for the GE Signa PET/MR including the MR-body (gray) is presented in Figure 2 together with the phantom configurations for the sensitivity and NECR simulations according to the NEMA NU 2-2012 protocols.
FIGURE 2.
Visualization of the GATE model of the GE Signa PET/MR system including the NEMA NECR (right) and sensitivity (left) phantom with a 70-cm-line activity source (red). The PET system consists of 5 rings of 28 detector blocks (25 mm × 4.0 mm × 5.3 mm) based on lutetium-yttrium-oxyorthosilicate (LYSO) crystals with MR-compatible SiPM technology (Alva-Sánchez et al., 2016). This results in an axial and transaxial FOV of 25 and 60 cm, respectively.
Validation of the GATE Model for the GE Signa PET/MR
The simulated and measured sensitivity values for 18F and 68Ga at the center of the FOV and 10 cm off-center are presented in Table 1 while the simulated and measured peak NECR with the corresponding activity concentration and scatter fraction at peak NECR are presented for 18F and 68Ga in Table 2.
TABLE 1.
Sensitivity for 18F and 68Ga in the center of the FOV and 10 cm off center in the presence of 3T MR field.
|
Measured (cps/kBq) |
Simulated (cps/kBq) |
|||
| 0 cm | 10 cm | 0 cm | 10 cm | |
| 18F | 21.831 | 21.173 | 21.205 | 21.112 |
| 68Ga | 20.063 | 19.689 | 19.098 | 19.017 |
These results are compared to the measured 18F and 68Ga-values (Caribé et al., 2019).
TABLE 2.
Measured and simulated scatter fraction, peak NECR and the corresponding activity concentration for different isotopes in the presence of 3T magnetic field.
| Scatter fraction at peak (%) | Peak NECR (kcps) | Activity concentration at peak NECR (kBq/ml) | |
| Measured | |||
| 18F (Caribé et al., 2019) | 43.3 | 216.8 | 18.60 |
| 18Ga (Caribé et al., 2019) | 42.9 | 205.6 | 20.40 |
| Simulated | |||
| 18F | 38.8 | 216.8 | 17.4 |
| 15O | 38.8 | 216.4 | 18.2 |
| 13N | 38.2 | 212.0 | 16.5 |
| 011C | 38.5 | 217.6 | 16.7 |
| 82Rb | 39.1 | 173.5 | 19.6 |
| 68Ga | 38.7 | 207.1 | 20.1 |
Simulated Sensitivity and NECR of the GE Signa PET/MR for Other Isotopes Using GATE
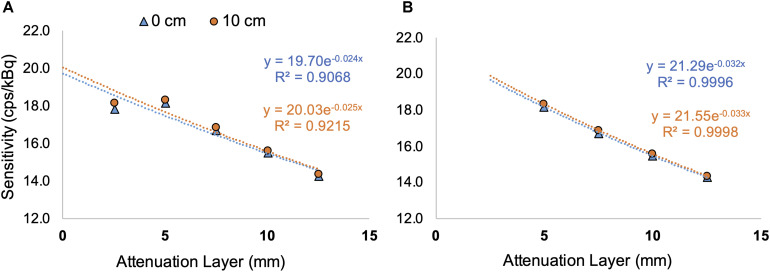
Table 3 shows the simulated NEMA sensitivity for 18F, 15O, 13N, 82Rb, and 68Ga as the average value of the sensitivity at the center of the FOV and 10 cm off-center. Figure 3A shows the underestimation of the simulated sensitivity for 82Rb when only one aluminum sleeve is surrounding the line source while Figure 3B presents the estimated sensitivity without taken into account the sensitivity values using only one aluminum sleeve. As such, the sensitivity value averaged over the center and 10 cm off center position in the FOV is increased to 21.4 cps/kBq (Figure 3B), compared to 19.9 cps/kBq when taken into account all five sleeve thicknesses (Figure 3A).
TABLE 3.
Sensitivity for different isotopes in the presence of 3T magnetic field, presented as the average value of the sensitivity at the center of the FOV and the sensitivity at 10 cm off center.
| Branching ratio (%) | Measured (cps/kBq) (Caribé et al., 2019) | Simulated (cps/kBq) | Theoretical values (cps/kBq) | R2 at the center values | |
| 18F | 96.76 | 21.5 | 21.2 | 1.00 | |
| 15O | 99.89 | 20.9 | 22.20 | 1.00 | |
| 13N | 99.82 | 21.5 | 22.18 | 1.00 | |
| 11C | 99.75 | 21.1 | 22.16 | 1.00 | |
| 82Rb | 95.45 | 19.9 | 21.21 | 0.91 | |
| 68Ga | 87.90 | 19.9 | 19.2 | 19.53 | 1.00 |
FIGURE 3.
Sensitivity data for 82Rb with the sensitivity plotted against the thickness of the attenuation layer together with the exponential regression. Graphs show the fitted equation and coefficient of determination for the simulations at the center of the FOV (0 cm, blue) and for 10 cm radially off center (10 cm, orange) with, respectively, 5 (A) and 4 (B) different thicknesses for the attenuation layers.
The results for the simulated peak NECR, the corresponding activity concentration and the scatter fraction at peak NECR for 18F, 11C, 15O, 13N, 68Ga, and 82Rb are presented in Table 2 while Figure 4 shows the simulated true, random and scattered coincidence rates as well as NECR curves for these isotopes as a function of the activity concentration.
Positron Range Evaluation Using the GATE Model for the GE Signa PET/MR
Table 4 shows the comparison of the simulated positron range in soft tissue for different radioisotopes with and without 3T magnetic field with measured values taken from literature (Li et al., 2017; Soultanidis et al., 2011). The simulated mean positron range values for different isotopes in soft tissue, lung and bone are presented on Tables 5, 6 with and without the presence of a 3T magnetic field, with the mean positron range averaged over all directions (Table 5) and the mean positron range calculated for the transversal plane perpendicular to the magnetic field and axial plane parallel to the magnetic field (Table 6). The impact of the magnetic field on the positron range is also visually shown in Figures 5, 6.
TABLE 4.
Comparison of positron range in soft tissue for different radioisotopes with and without 3T magnetic field.
| Max energy (keV) |
Mean 3D positron range (mm) |
||||||
| GATE | Ref. | Ref. | |||||
| (Li et al., 2017) | (Soultanidis et al., 2011) | ||||||
| None | 3T | None | 3T | None | 3T | ||
| 18F | 633.5 | 0.50 | 0.52 | 0.64 | 0.45 | 0.56 | 0.54 |
| 15O | 1732.0 | 1.87 | 1.66 | 2.01 | 1.74 | 2.44 | 2.00 |
| 13N | 1198.5 | 1.08 | 1.01 | 1.32 | 1.26 | ||
| 11C | 960.2 | 1.02 | 0.96 | 1.03 | 0.82 | 1.05 | 0.96 |
| 82Rb | 3378.0 | 4.85 | 3.82 | 4.29 | 3.65 | 5.21 | 3.90 |
| 68Ga | 1899.0 | 2.32 | 2.04 | 2.24 | 2.02 | 2.62 | 2.07 |
TABLE 5.
Mean 3D positron range for different tissues and radioisotopes with and without 3T magnetic field.
|
Mean 3D positron range (mm) |
||||||
| Soft tissue | Lung | Bone | ||||
| None | 3T | None | 3T | None | 3T | |
| 18F | 0.50 | 0.52 | 2.23 | 1.70 | 0.34 | 0.34 |
| 15O | 1.87 | 1.66 | 7.74 | 4.28 | 1.22 | 1.17 |
| 13N | 1.08 | 1.01 | 4.30 | 2.63 | 0.71 | 0.69 |
| 11C | 1.02 | 0.96 | 3.05 | 1.97 | 0.51 | 0.51 |
| 82Rb | 4.85 | 3.82 | 18.2 | 10.1 | 3.09 | 2.74 |
| 68Ga | 2.32 | 2.04 | 8.09 | 4.59 | 1.33 | 1.26 |
TABLE 6.
Mean positron range in the transversal (perpendicular to the magnetic field) and axial direction (parallel to the magnetic field) for different tissue types and radioisotopes with and without 3T magnetic field.
| Mean transversal positron | Mean axial positron | |||||||||||
|
range (mm) |
range (mm) |
|||||||||||
| Soft tissue | Lung | Bone | Soft tissue | Lung | Bone | |||||||
| None | 3T | None | 3T | None | 3T | None | 3T | None | 3T | None | 3T | |
| 18F | 0.27 | 0.26 | 0.95 | 0.73 | 0.17 | 0.17 | 0.27 | 0.27 | 0.95 | 1.08 | 0.17 | 0.17 |
| 15O | 0.93 | 0.77 | 3.74 | 0.97 | 0.61 | 0.57 | 0.93 | 0.93 | 3.75 | 3.74 | 0.61 | 0.61 |
| 13N | 0.54 | 0.49 | 2.15 | 0.74 | 0.35 | 0.34 | 0.54 | 0.54 | 2.15 | 2.15 | 0.35 | 0.35 |
| 11C | 0.48 | 0.48 | 1.52 | 0.63 | 0.26 | 0.25 | 0.48 | 0.51 | 1.52 | 1.52 | 0.26 | 0.26 |
| 82Rb | 2.42 | 1.62 | 9.10 | 2.25 | 1.54 | 1.28 | 2.42 | 2.42 | 8.95 | 8.96 | 1.54 | 1.55 |
| 68Ga | 1.01 | 0.95 | 4.04 | 1.00 | 0.66 | 0.61 | 1.01 | 1.16 | 4.05 | 4.04 | 0.66 | 0.66 |
FIGURE 5.
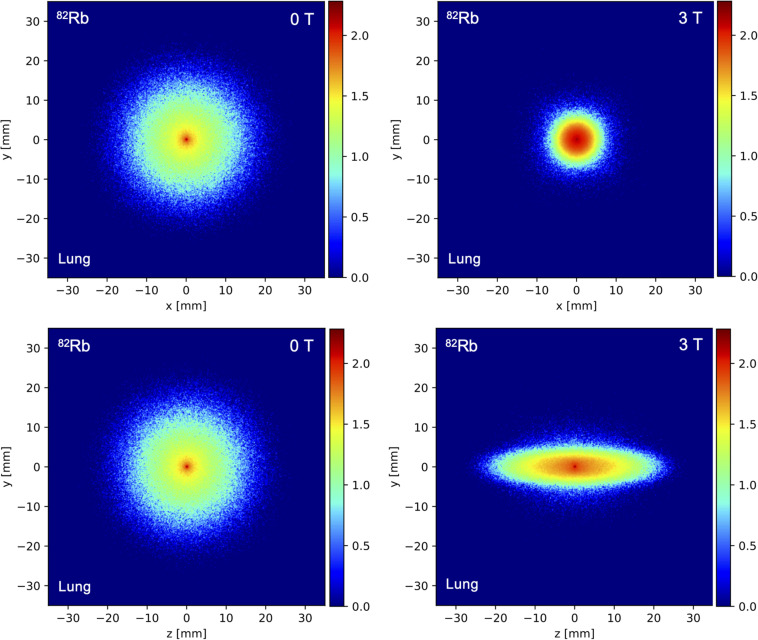
Spatial distribution of the simulated annihilation endpoints in the x/y plane perpendicular to the magnetic field and the z/y plane parallel to the magnetic field for a 82Rb point source positioned in homogeneous lung tissue for a field strength of 0 T (left) and 3 T (right).
FIGURE 6.
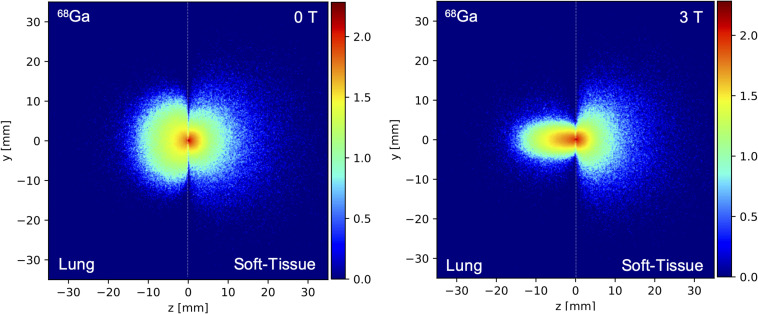
Spatial distribution of the simulated annihilation endpoints in the z/y plane parallel to the magnetic field for a 68Ga point source positioned at the interface between lung and soft tissue (dashed black line) for a field strength of 0 T (left) and 3 T (right).
Discussion
In this work we have developed and evaluated a model for the GE Signa PET/MR to run realistic Monte Carlo simulations using GATE. The model was validated by comparing simulated sensitivity and NECR data 18F and 68Ga with corresponding measurements performed on a GE Signa PET/MR system (Caribé et al., 2019). Once validated, these simulations allowed us to evaluate the system characteristics in terms of sensitivity and NECR for different, less conventional PET isotopes such as 15O, 13N, 11C, and 82Rb. In addition, the effect of the 3T magnetic field on positron range was investigated for different PET isotopes in different tissue types (lung tissue, soft tissue, and bone).
In terms of validating the GATE MC simulations, the simulated NEMA sensitivity values, presented in Tables 1, 3, were in line with the expected, theoretical values for all simulated PET radioisotopes, These theoretical values were based on the measured GE Signa PET/MR sensitivity for 18F while accounting for the differences in branching ratio between each isotope and 18F. These sensitivity values confirmed the higher count rate and increased sensitivity (Iagaru et al., 2019) of the GE Signa PET system due several design factors including Compton scatter recovery, longer axial FOV and reduced ring diameter (Lubberink and Herzog, 2011; Wagadarikar et al., 2014; Hsu et al., 2017).
For the pure β+ emitters such as 11C, 13N, and 15O, the sensitivity was comparable to that of 18F. However, 68Ga and 82Rb showed considerable differences. For 68Ga, this was expected as literature data already reported a sensitivity of about 2 cps/kBq lower than 18F (Peng and Levin, 2012), which was confirmed by the simulations. However, for 82Rb with a positron branching ratio very similar to 18F (less than 2% difference), the sensitivity is much lower than expected. This could be explained by the high energy of 3.381 MeV of the emitted positrons such that only one aluminum sleeve surrounding the line source is not adequate enough to generate sufficient annihilations. Therefore, sensitivity measurements with only one attenuating layer of aluminum surrounding the line source should be discarded for 82Rb or material with a higher density than aluminum should be considered (see Figure 3 and Table 3). In addition, and specifically for 82Rb, a significant portion of the coincidences were detected outside of the scanner bore, which, in theory, is not be possible since the LOR corresponding to two annihilation photons detected by the scanner can be positioned outside of the scanner. However, due to the additional 777 keV prompt-gamma emission, two gamma photons originating from a decaying 82Rb source, can be registered as a pair of annihilation photons by the scanner, even when the source is situated outside of the scanner bore.
The results of the simulated NEMA count rate performance tests of the GE Signa PET/MR are summarized in Figure 4 and Table 2 and showed good agreement with previous count rate data for 18F (Levin et al., 2016a). These results confirmed that GATE MC simulations can be used to study the count rate performance of the GE Signa PET/MR. For positron emitters with high branching ratios for β+ decay such as 11C, 13N, and 15O, the simulation results confirmed a peak NECR similar to 18F with the corresponding activity concentration scaled by the inverse of the positron fraction.
For the higher energy positron emitters such as 68Ga and 82Rb, the simulated count rates were slightly lower than the measured values for 18F, as shown in Figure 4 and Table 2. These lower values are primarily due to the respective 1.2% (1.883 MeV) and 13.1% (2.604 MeV) fraction of β+ decay for 68Ga and 82Rb, which also results in prompt gamma emissions. These prompt gammas contaminate the PET signal by generating additional random, scattered and detection events which, in turn, increases the deadtime effects. The third gamma effect was also reported by different research groups (Martin et al., 1995; Converse et al., 2003).
In terms of the positron range, the 3T magnetic field clearly reduced the positron range by a factor up to 3–4 in the direction perpendicular to the magnetic field, especially for the higher energy positron emitters such as 15O, 68Ga, and 82Rb and for low-density tissues such as lung tissue. While changes in positron range could clearly be observed in the perpendicular direction, the magnetic field does not have a clear impact on the positron range in the direction of the magnetic field, as was shown in Figure 5 and Tables 4–6. The impact of the magnetic field on the positron range is highly dependent on the positron energy and tissue type as shown in Tables 5, 6. The latter is known to be related to the tissue electron density such that the mean free path of the positron is larger for tissues with lower electron density (Cal-González et al., 2013). This dependency is clearly demonstrated at the interface between different tissues as shown in Figure 6. These findings are in agreement with previous studies on the positron range (Rickey et al., 1992; Cal-González et al., 2009; Shah et al., 2014; Alva-Sánchez et al., 2016; Huang et al., 2016; Caribé et al., 2017), and confirm a reduced positron range in the perpendicular direction of a magnetic field. Moreover, studies have also indicated (Iida et al., 1986; Wirrwar et al., 1997; Soultanidis et al., 2011; Kraus et al., 2012) that a higher magnetic field will also induce a greater reduction of the positron range. However, it has to be noted that this effect was negligible for low energy positron emitters, such as 18F. Moreover, the expected improvement of the PET image resolution, resulting from a reduced positron range by the presence of a 3T magnetic field, will only partially be observed in the resolution properties of the GE Signa PET/MR system due to the limited resolution of the PET detectors. Indeed, detector-dependent factors, such as crystal size and crystal penetration during detection, and inherent limitations such as the non-collinearity of the annihilation photons are also present and can explain why a reduced positron range with an increasing magnetic field does not translate directly into improved image quality (Herzog et al., 2010; Bertolli et al., 2016; Caribé et al., 2019; Wadhwa et al., 2020). However, in a preclinical setting with small diameter detector rings and crystal sizes, the impact of a reduced positron range on the PET image quality is expected to be much higher while the use of monolithic crystals or recordings of the depth of interaction in clinical PET systems can further enhance the PET resolution such that it becomes more sensitive to positron range effects (Hammer et al., 1994; Stockhoff et al., 2019).
However, there are also limitations to be considered for this study. The dead time digitizer settings have a certain degree of uncertainty since these values were not provide by the manufacturer. This could affect the NEMA sensitivity estimates via the exponential regression of the simulated data (Khalif et al., 2016) and could explain the slightly lower simulated sensitivity values compared to theoretical values. Due to the uncertainty of the dead time digitizer settings, the deadtime was heuristically tuned to match measured data, and then applied to other simulations. These settings could also have lowered the scatter count rate (∼500 kcps scatter at 20 kBq/ml as shown in Figure 4), compared to ∼700 kcps (Levin et al., 2016a) and ∼600 kcps (Caribé et al., 2019) scatter (at the same activity concentration) reported values for the Signa PET/MR with 18F. Moreover, it should be noted that the count rates and NECRs for each simulation in this study were estimated using the NEMA approach which does not require an estimate for the number of random events (National Electrical Manufacturers Association [NEMA], 2012). This could explain the slight underestimation of the scatter fraction which was determined directly from the count events in the ROOT file. Indeed, for all of isotopes, the simulated scatter fractions were around 38 to 40%, which is slightly lower compared to reported, measured scatter fraction of 43.3% for 18F. Finally, this study only evaluated the impact of a 3T magnetic field on the positron range, as this is a field strength which is clinically relevant and in line with the magnetic field of GE Signa PET/MR.
Conclusion
GATE Monte-Carlo simulations were validated for simulating the GE Signa PET/MR system and used to predict sensitivity and NECR performance for 18F, 15O, 13N, 11C, 82Rb, and 68Ga. The GATE based predicted sensitivity and NECR data were in line with expected and previously published sensitivity and NECR values for all simulated PET isotopes and confirmed the impact of deadtime effects and increased random events on NECR for 68Ga and 82Rb because of the additional prompt gamma emissions. In addition, we have investigated the impact of the magnetic field on the positron range for different tissue types and PET isotopes. The improvement of image resolution resulting from a decreased positron range in the plane perpendicular to a 3T magnetic field, especially for high energy positron emitters, is only partially observed in the resolution properties of the GE Signa PET/MR system due to the limited spatial resolution of the PET detectors.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
PC performed the conceptualization. PC, AD, NE, and CT contributed to the simulations of the study. PC and AD performed the data collection. PC, AD, and DP-B completed the data analysis. All authors discussed the results and commented on the manuscript, contributed to the design of the study, and read and approved the final manuscript.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was partially published at EANM’19 in Barcelona, Spain as a short 400-word abstract (Congress and October, 2019).
Footnotes
Funding. This present study was conducted with a grant support to the first author from CNPq, the National Council of Technological and Scientific Development – Brazil (process number 235040/2014-2).
References
- Afshar-Oromieh A., Zechmann C. M., Malcher A., Eder M., Eisenhut M., Linhart H. G. (2014). Comparison of PET imaging with a 68Ga-labelled PSMA ligand and 18F-choline-based PET/CT for the diagnosis of recurrent prostate cancer. Eur. J. Nucl. Med. Mol. Imaging 41 11–20. 10.1007/s00259-013-2525-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alva-Sánchez H., Quintana-Bautista C., Martínez-Dávalos A., Ávila-Rodríguez M. A., Rodríguez-Villafuerte A. (2016). Positron range in tissue-equivalent materials: experimental microPET studies. Phys. Med. Biol. 61 6307–6321. 10.1088/0031-9155/61/17/6307 [DOI] [PubMed] [Google Scholar]
- Banerjee S. R., Pomper M. G. (2013). Clinical applications of Gallium-68. Appl. Radiat. Isot. 76 2–13. 10.1016/j.apradiso.2013.01.039 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertolli O., Eleftheriou A., Cecchetti M., Camarlinghi N., Belcari N., Tsoumpas C. (2016). PET iterative reconstruction incorporating an efficient positron range correction method. Phys. Med. 32 323–330. 10.1016/j.ejmp.2015.11.005 [DOI] [PubMed] [Google Scholar]
- Cal-González J., Herraiz J. L., España S., Desco M., Vaquero J. J., Udías J. M. (2009). “Positron range effects in high resolution 3D pet imaging,” inProceedings of the IEEE Nuclear Science Symposium Conference Record (Orlando, FL: IEEE; ) 2788–2791. [Google Scholar]
- Cal-González J., Herraiz J. L., Espana S., Garcia Corzo P. M., Vaquero J. J., Desco M. (2013). Positron range estimations with PeneloPET. Phys. Med. Biol. 58 5127–5152. 10.1088/0031-9155/58/15/5127 [DOI] [PubMed] [Google Scholar]
- Caribé P., Koole M., Deller T., Van Laere K., Vandenberghe S. (2017). NEMA NU 2-2007 Performance Characteristics of GE Signa Integrated PET/MR: impact of using different PET Isotopes. Eur. J. Nucl. Med. Mol. Imaging 44 119–956.28894880 [Google Scholar]
- Caribé P. R. R. V., Koole M. D., Asseler Y., Deller T. W., Van Laere K., Vandenberghe S. (2019). NEMA NU 2–2007 performance characteistics of GE Signa integrated PET/MR for different PET isotopes. EJNMMI Phys. 6:11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Catana C., van der Kouwe A., Benner T., Michel C. J., Hamm M., Fenchel M. (2010). Toward implementing an MRI-based PET attenuation-correction method for neurologic studies on the MR-PET brain prototype. J. Nucl. Med. 51 1431–1438. 10.2967/jnumed.109.069112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Congress A., October N. M. (2019). Annual Congress of the European Association of Nuclear Medicine, Vol. 46 Barcelona: Barcelona International Convention Centre. [Google Scholar]
- Conti M., Eriksson L. (2016). Physics of pure and non-pure positron emitters for PET: a review and a discussion. EJNMMI Phys. 3:8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Converse A. K., Nye J., Barnhart T. E., Dick D. W., Avila-Rodriguez M. A., Sundaresan R. (2003). MicroPET performance in the presence of the third gamma. IEEE Nucl. Sci. Symp. Conf. Rec. 3 1797–1799. [Google Scholar]
- Efthimiou N., Emond E., Wadhwa P., Cawthorne C., Tsoumpas C., Thielemans K. (2019). Implementation and validation of time-of-flight PET image reconstruction module for listmode and sinogram projection data in the STIR library. Phys. Med. Biol. 64:aaf9b9. [DOI] [PubMed] [Google Scholar]
- Eleftheriou A., Tsoumpas C., Bertolli O., Stiliaris E. (2014). Effect of the magnetic field on positron range using GATE for PET-MR. EJNMMI Phys. 1 49–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Emond E. C., Groves A. M., Hutton B. F., Thielemans K. (2019). Effect of positron range on PET quantification in diseased and normal lungs. Phys. Med. Biol. 64:205010. 10.1088/1361-6560/ab469d [DOI] [PubMed] [Google Scholar]
- Hammer B. E., Christensen N. L., Heil B. G. (1994). Use of a magnetic field to increase the spatial resolution of positron emission tomography. Med. Phys. 21 1917–1920. 10.1118/1.597178 [DOI] [PubMed] [Google Scholar]
- Herzog H., Lida H., Weirich C., Tellmann L., Kaffanke J., Spelleberg S. (2010). “Influence from high and ultra-high magnetic field on positron range measured with a 9.4TMR-BrainPET,” in Proceedings of the IEEE Nuclear Science Symposuim & Medical Imaging Conference, (Knoxville, TN: IEEE; ), 3410–3413. [Google Scholar]
- Hoffend J., Mier W., Schumacher J., Schmidt K., Dimitrakopoulou-Strauss A., Strauss L. G. (2005). Gallium-68-DOTA-albumin as a PET blood-pool marker: experimental evaluation in vivo. Nucl. Med. Biol. 32 287–292. 10.1016/j.nucmedbio.2005.01.002 [DOI] [PubMed] [Google Scholar]
- Hsu D. F. C., Ilan E., Peterson W. T., Uribe J., Lubberink M., Levin C. S. (2017). Studies of a next-generation silicon-photomultiplier–based time-of-flight PET/CT system. J. Nucl. Med. 58 1511–1518. 10.2967/jnumed.117.189514 [DOI] [PubMed] [Google Scholar]
- Huang S. Y., Savic D., Yang J., Shrestha U., Seo Y. (2016). “The effect of magnetic field on positron range and spatial resolution in an integrated whole-body time-of-flight PET/MRI system,” in Proceedings of the 2014 IEEE Nuclear Science Symposium and Medical Imaging Conference (Seattle, WA: IEEE; ), 3–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iagaru A., Mittra E., Minamimoto R., Jamali M., Levin C., Quon A. (2019). Simultaneous whole-body time-of-flight 18F-FDG PET/MRI. Clin. Nucl. Med. 40 1–8. 10.1097/rlu.0000000000000611 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iida H., Kanno I., Miura S., Murakami M., Takahashi K., Uemura K. (1986). A simulation study of a method to reduce positron annihilation spread distributions using a string magnetic field in positron emission tomography. IEEE Trans. Nucl. Sci. 33 118–122. [Google Scholar]
- Jan S., Santin G., Strul D., Staelens S., Assié K., Autret D. (2004). GATE: a simulation toolkit for PET and SPECT. Phys. Med. Biol. 49 4543–4561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jodal L., Le Loirec C., Champion C. (2012). Positron range in PET imaging: an alternative approach for assessing and correcting the blurring. Phys. Med. Biol. 57 3931–3943. 10.1088/0031-9155/57/12/3931 [DOI] [PubMed] [Google Scholar]
- Kemerink G. J., Visser M. G., Franssen R., Beijer E., Zamburlini M., Halders S. G. (2011). Effect of the positron range of 18F, 68Ga and 124I on PET/CT in lung-equivalent materials. Eur. J. Nucl. Med. Mol. Imaging 38 940–948. 10.1007/s00259-011-1732-1 [DOI] [PubMed] [Google Scholar]
- Khalif M., Stute S., Wagadarikar A., Comtat C. (2016). “Modeling the GE Signa PET-MR with monte-carlo simulations using GATE,” in Proceedings of the IEEE Nuclear Science Symposium and Medical Imaging Conference (San Diego, CA: IEEE; ). [Google Scholar]
- Kolb A., Sauter A. W., Eriksson L., Vandenbrouke A., Liu C. C., Levin C. (2015). Shine-through in PET/MR imaging: effects of the magnetic field on positron range and subsequent image artifacts. J. Nucl. Med. 56 951–954. 10.2967/jnumed.114.147637 [DOI] [PubMed] [Google Scholar]
- Kraus R., Delso G., Ziegler S. I. (2012). Simulation study of tissue-specific positron range correction for the new biograph mMR whole-body PET/MR system. IEEE Trans. Nucl. Sci. 59(5 Pt. 1), 1900–1909. 10.1109/tns.2012.2207436 [DOI] [Google Scholar]
- Laforest R., Liu X. (2008). Image quality with non-standard nuclides in PET. Q. J. Nucl. Med. Mol. Imaging 52 151–158. [PubMed] [Google Scholar]
- Levin C. S., Deller T. W., Delso G., Khalighi M. M., Maramraju S. H., Grant A. M. (2016a). NEMA NU 2-2012 performance studies for the SiPM-based ToF-PET component of the GE SIGNA PET/MR system. Med. Phys. 43 2334–2343. 10.1118/1.4945416 [DOI] [PubMed] [Google Scholar]
- Levin C. S., Hoffman E. J. (1999). Calculation of positron range and its effect on the fundamental limit of positron emission tomography system spatial resolution. Phys. Med. Biol. 44 781–799. 10.1088/0031-9155/44/3/019 [DOI] [PubMed] [Google Scholar]
- Levin C. S., Maramraju S. H., Khalighi M. M., Deller T. W., Delso G., Jansen F. (2016b). Design features and mutual compatibility studies of the time-of-flight PET capable GE SIGNA PET/MR system. IEEE Trans. Med. Imaging 35 1907–1914. 10.1109/tmi.2016.2537811 [DOI] [PubMed] [Google Scholar]
- Li C., Cao X., Liu F., Tang H., Zhang Z., Wang B. (2017). Compressive effect of the magnetic field on the positron range in commonly used positron emitters simulated using Geant4. Eur. Phys. J. Plus 132:484. [Google Scholar]
- Lubberink M., Herzog H. (2011). Quantitative imaging of 124I and 86Y with PET. Eur. J. Nucl. Med. Mol. Imaging 38(Suppl. 1), 10–18. 10.1007/s00259-011-1768-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marshall R. C., Huang S. C., Nash W. W., Phelps M. E. (1983). Assessment of the [18F]fluorodeoxyglucose kinetic model in calculations of myocardial glucose metabolism during ischemia. J. Nucl. Med. 24 1060–1064. [PubMed] [Google Scholar]
- Martin C. C., Christian B. T., Satter M. R., Nickerson L. D. H., Nickles R. J. (1995). Quantitative PET with positron emitters that emit prompt gamma rays. IEEE Trans. Med. Imaging 14 681–687. 10.1109/42.476109 [DOI] [PubMed] [Google Scholar]
- Mayerhoefer M. E., Prosch H., Beer L., Tamandl D., Beyer T., Hoeller C. (2020). PET/MRI versus PET/CT in oncology: a prospective single-center study of 330 examinations focusing on implications for patient management and cost considerations. Eur. J. Nucl. Med. Mol. Imaging 47 51–60. 10.1007/s00259-019-04452-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moses W. W. (1994). Empirical observation of resolution degradation in positron emission tomographs utilizing block detectors. J. Nucl. Med. 34:101. [Google Scholar]
- Moses W. W. (2011). Fundamental limits of spatial resolution in PET. Nucl. Instrum. Methods Phys. Res. A. 648(Suppl. 1), 1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- National Electrical Manufacturers Association [NEMA] (2012). NEMA NU 2-2007: Performance Measurements of Positron Emission Tomographs. Rosslyn, VA: National Electrical Manufacturers Association. [Google Scholar]
- Palmer M. R., Zhu X., Parker J. A. (2005). Modeling and simulation of positron range effects for high resolution PET imaging. IEEE Trans. Nucl. Sci. 52 1391–1395. 10.1109/tns.2005.858264 [DOI] [Google Scholar]
- Papp L., Spielvogel C. P., Rausch I., Hacker M., Beyer T. (2018). Personalizing medicine through hybrid imaging and medical big data analysis. Front. Phys. 6:19 10.3389/fphy.2018.00051 [DOI] [Google Scholar]
- Park S. J., Rogers W. L., Clinthorne N. H. (2007). Effects of positron range and annihilation photon acolinearity on image resolution of a compton PET. IEEE Trans. Nucl. Sci. 54 1543–1552. 10.1109/tns.2007.902358 [DOI] [Google Scholar]
- Peng H., Levin C. S. (2012). Study of PET intrinsic spatial resolution and contrast recovery improvement for PET/MRI systems. Phys. Med. Biol. 57 N101–N115. [DOI] [PubMed] [Google Scholar]
- Phelps M. E., Huang S. C., Hoffman E. J., Selin C., Sokoloff L., Kuhl D. E. (1979). Tomographic measurement of local cerebral glucose metabolic rate in humans with (F-18)2-fluoro-2-deoxy-D-glucose: validation of method. Ann. Neurol. 6 371–388. 10.1002/ana.410060502 [DOI] [PubMed] [Google Scholar]
- Rahmim A., Tang J., Lodge M. A., Lashkari S., Mohammad R. A., Bengel F. M. (2008). “Resolution modeled PET image reconstruction incorporating space-variance of positron range: Rubidium-82 cardiac PET imaging,” in Proceedings of the IEEE Nuclear Science Symposium Conference Record (Dresden: IEEE; ), 3643–3650. [Google Scholar]
- Rickey D. W., Gordon R., Huda W. (1992). On lifting the inherent limitations of Positron Emission Tomography by using using magnetic fields (MagPET). Automedica 14 355–369. [Google Scholar]
- Shah N. J., Herzog H., Weirich C., Tellmann L., Kaffanke J., Caldeira L. (2014). Effects of magnetic fields of up to 9.4 T on resolution and contrast of PET images as measured with an MR-BrainPET. PLoS One 9:e95250. 10.1371/journal.pone.0095250 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shao Y., Cherry S. R., Farahani K., Meadors K., Siegel S., Silverman R. W. (1997). Simultaneous PET and MR imaging. Phys. Med. Biol. 42 1965–1970. [DOI] [PubMed] [Google Scholar]
- Soultanidis G., Karakatsanis N., Nikiforidis G., Loudos G. (2011). Study of the effect of magnetic field in positron range using GATE simulation toolkit. J. Phys. Conf. Ser. 317:012021 10.1088/1742-6596/317/1/012021 [DOI] [Google Scholar]
- Stockhoff M., Van Holen R., Vandenberghe S. (2019). Optical simulation study on the spatial resolution of a thick monolithic PET detector. Phys. Med. Biol. 64:195003. 10.1088/1361-6560/ab3b83 [DOI] [PubMed] [Google Scholar]
- Vallabhajosula S., Solnes L., Vallabhajosula B. (2011). A broad overview of positron emission tomography radiopharmaceuticals and clinical applications: what is new? Semin. Nucl. Med. 41 246–264. 10.1053/j.semnuclmed.2011.02.003 [DOI] [PubMed] [Google Scholar]
- Vandenberghe S., Mikhaylova E. D., Hoe E., Mollet P., Karp J. S. (2016). Recent developments in time-of-flight PET. EJNMMI Physics. 3:3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wadhwa P., Thielemans K., Efthimiou N., Wangerin K., Keat N., Emond E. (2020). PET image reconstruction using physical and mathematical modelling for time of flight PET-MR scanners in the STIR library. Methods 10.1016/j.ymeth.2020.01.005 [Epub ahead of print]. [DOI] [PubMed] [Google Scholar]
- Wagadarikar A. A., Ivan A., Dolinsky S., McDaniel D. L. (2014). Sensitivity improvement of time-of-flight (ToF) PET detector through recovery of compton scattered annihilation photons. IEEE Trans. Nucl. Sci. 61 121–125. 10.1109/tns.2013.2282119 [DOI] [Google Scholar]
- Wirrwar A., Vosberg H., Herzog H., Halling H., Weber S., Muller-Gartner H.-W. (1997). 4.5 tesla magnetic field reduces range of high-energy positrons-potential implications for positron emission tomography. IEEE Trans. Nucl. Sci. 44 184–189. 10.1109/23.568801 [DOI] [Google Scholar]
- Yamamoto S., Kuroda K., Senda M. (2003). Scintillator selection for MR compatible gamma detectors. 2002 IEEE Nucl. Sci. Symp. Conf. Rec. 3 1632–1635. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.