Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2019 Aug 8;36(3):751–757. doi: 10.1093/bioinformatics/btz623

Integrating ab initio and template-based algorithms for protein–protein complex structure prediction

Sweta Vangaveti 1, Thom Vreven 1, Yang Zhang 2, Zhiping Weng 1,✉
Editor: Jan Gorodkin
PMCID: PMC7523679  PMID: 31393558

Abstract

Motivation

Template-based and template-free methods have both been widely used in predicting the structures of protein–protein complexes. Template-based modeling is effective when a reliable template is available, while template-free methods are required for predicting the binding modes or interfaces that have not been previously observed. Our goal is to combine the two methods to improve computational protein–protein complex structure prediction.

Results

Here, we present a method to identify and combine high-confidence predictions of a template-based method (SPRING) with a template-free method (ZDOCK). Cross-validated using the protein–protein docking benchmark version 5.0, our method (ZING) achieved a success rate of 68.2%, outperforming SPRING and ZDOCK, with success rates of 52.1% and 35.9% respectively, when the top 10 predictions were considered per test case. In conclusion, a statistics-based method that evaluates and integrates predictions from template-based and template-free methods is more successful than either method independently.

Availability and implementation

ZING is available for download as a Github repository (https://github.com/weng-lab/ZING.git).

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Protein–protein interactions (PPIs) are integral to cellular functions (Bruce, 1998). Through PPIs, cells control and regulate numerous biological processes, e.g. signal transduction, transcription regulation and metabolism. Experimental approaches such as yeast two-hybrid (Brückner et al., 2009) and affinity purification-mass spectrometry (Huttlin et al., 2015) can identify interacting proteins on a large scale. However, these methods do not provide the three-dimensional (3D) structures of the complexes, which are essential for a complete understanding of the interaction mechanisms. Approaches such as X-ray crystallography, nuclear magnetic resonance (NMR) spectroscopy and cryogenic electron microscopy (cryoEM) can provide this structural information, but they are resource and time intensive and they do not succeed for many complexes. Therefore, experimentally determined structures are available only for a small fraction of the cellular interactome, making computational approaches an important alternative for structural characterization of PPIs.

The computational methods for predicting the quaternary structure of proteins can be broadly classified into two categories—template-free (ab initio) (Dominguez et al., 2003; Lyskov and Gray, 2008; Ritchie et al., 2008; Chen et al., 2003) and template-based (Aytuna et al., 2005; Chen and Skolnick, 2008; Guerler et al., 2013; Günther et al., 2007; Kundrotas and Vakser, 2010; Lu et al., 2002; Mukherjee and Zhang, 2011; Tuncbag et al., 2011). Given the unbound structures of the component proteins, template-free methods use statistical or thermodynamic energy potentials to find the most likely binding mode and predict the complex structure. In contrast, template-based approaches use known structures of homologous protein–protein complexes, assuming that homologous proteins adopt the same binding modes.

It has been shown that just like the limited set of protein folds, there exists a limited set of structurally unique protein–protein interfaces despite the large number of possible complexes (Patrick and Robert, 2004; Zhang et al., 2012). Thus, template-based methods could potentially outperform template-free methods since they involve identifying the best fit from a database of observed PPIs. However, the collection of experimentally determined, structurally unique protein–protein interfaces is still incomplete (Kundrotas et al., 2012; Skolnick and Gao, 2010). Therefore, in the cases where a reliable template cannot be identified, template-free methods are preferred. Even when a template is available, template-free methods may still produce more accurate complex structures than template-based methods.

Because template-based and template-free methods fundamentally focus on different information, they complement each other if each can be utilized to its full strength (Vreven et al., 2014). As an example, the predictions of the two types of methods have been combined with simple pooling. A prediction list comprising the top two predictions from the template-based algorithm SPRING (Guerler et al., 2013) and the top three predictions from the template-free algorithm ZDOCK (Chen et al., 2003) performed better than using the top five predictions from either method (Guerler et al., 2013). Alternatively, some template-based prediction algorithms incorporate template-free features like de-solvation energies and steric clash penalties in their scoring functions (Guerler et al., 2013; Kundrotas et al., 2017). Xue et al. (Xue et al., 2016) used the restraints predicted by their template-based interface prediction algorithm PS-HomPPI (Xue et al., 2011) to guide their template-free algorithm HADDOCK (Dominguez et al., 2003). The resulting HADDOCK predictions had better interface root mean square deviations (I-RMSDs), fewer clashes and more native contacts than the predictions produced without these restraints. Thus, by combining the results of ab initio and template-based methods, an improvement in PPI structure prediction can be achieved.

Here, we explored a new approach for combining a template-based algorithm (SPRING) and a template-free algorithm (ZDOCK). We started by running the two methods independently to retain their respective strengths. We then assigned a confidence score to each SPRING and ZDOCK prediction that represents the probability of the prediction being correct. Thereafter, instead of selecting a fixed number of SPRING and ZDOCK predictions as in a previous work (Guerler et al., 2013), we used the confidence scores to assemble an optimally combined list of predictions from the two algorithms. Cross-validated using the protein–protein docking benchmark version 5.0, our new method, ZING, achieved a success rate higher than that of SPRING or ZDOCK.

2 Materials and methods

2.1 Dataset

For training and testing our method, ZING, we used the protein–protein docking benchmark 5.0 (Vreven et al., 2015), which contains high-quality X-ray crystal structures of 230 protein–protein complexes and X-ray crystal or NMR structures of their unbound components. The benchmark is non-redundant at the SCOP (Murzin et al., 1995) family-family pair level, which ensures that the sequence identity between two proteins is never more than 30%, and even lower when they also have similar function and structure. The resulting set includes 88 enzyme-substrate/inhibitor, 40 antibody-antigen and 102 other complexes. Split by expected docking difficulty, the benchmark contains 151 rigid-body, 45 medium-difficulty and 34 difficult complexes. SPRING cannot handle multi-chain proteins; thus, we excluded the 88 entries with multi-chain component proteins. The docking difficulty distribution was approximately retained in the remaining 142 cases (91, 28 and 23 rigid-body, medium-difficulty and difficult complexes, respectively). Only two antibody-antigen complexes remained, whose antibodies had just the heavy chain, along with 72 enzyme-substrate/inhibitor and 68 other complexes.

2.2 Performance evaluation

2.2.1. Interface root mean square deviation (I-RMSD)

An interface residue is defined as a residue with any of its atoms within 10 Å of the partner protein in the bound structure. The I-RMSD of a prediction is the RMSD of the Cα atoms of its interface residues calculated after superposition of the Cα atoms in the prediction onto the bound structure. We consider a prediction to be correct when its I-RMSD is less than 5 Å.

2.2.2. Integrated success rate

The success rate of an algorithm for a given number of predictions per test case (N) is defined as the percentage of test cases in the dataset with at least one correct prediction (also called a hit). The integrated success rate (ISR) is the normalized area-under-the-curve of the success rate plotted against the log10(N). The ISR ranges between 0 and 1, with a higher value indicating a more successful method (Vreven et al., 2011).

2.3 SPRING

We used the downloadable version of SPRING (Guerler et al., 2013), which comes with its own template library and uses the same algorithm as the server version but makes more predictions and provides more detailed log files. Given the sequences of the two component proteins, SPRING first employs the threading algorithm HH-search (Söding, 2005) to find single-chain template structures for the sequences separately, and constructs a model for each protein using the top-ranking template. SPRING then searches all the single-chain templates from HH-search against a library of complex templates constructed using the Protein Data Bank (PDB). Finally, the models of the component proteins are superposed onto the identified complex templates, using interface residues only, to obtain the complex models, which are then scored. The SPRING score (SSP), is a linear combination of three terms—an interface contact potential (E), a template modeling score (TMscore) and a Z-score for threading the input sequence to the template—which it uses to rank its predictions. The total number of complex models is capped at 50, but could be fewer when templates are limited.

2.3.1. Confidence score for SPRING predictions

We needed a confidence score for evaluating SPRING predictions so that they could be compared with ZDOCK predictions. Thus, we defined the confidence score for SPRING using a logistic regression model. To train the model, we used a binary response variable—a prediction was classified as correct if its I-RMSD was less than 5.0 Å or incorrect otherwise. We tested five features derived from quantities computed by SPRING—minTM (the smaller of the TMscores, TMscoreA and TMscoreB), minZ (the smaller of the Z-scores for threading, Z-scoreA and Z-scoreB), Coverage (fraction of the input sequences that are aligned with the template structures), E (an interface contact potential) and minS (the smaller of the sequence identities between the input sequences and their templates, SeqidA and SeqidB), where subscripts A and B refer to the two query proteins, respectively. We performed feature selection on all 25–1 possible combinations of the five features with 4-fold cross-validation while ensuring that all predictions from a test case were assigned to the same fold. Brier’s score, the mean squared error of predicted probabilities, was used to evaluate the logistic regression models. Among the models with Brier’s scores within one standard error of the minimum score, we selected the model with the smallest number of features.

We intended to train the model using the 142 test cases in the docking benchmark 5.0 that contained only single-chain component proteins (described above). However, since SPRING’s template database was derived from the PDB, the complex structures in the docking benchmark could also be present in SPRING’s template database. To prevent SPRING from using known complex structures as the templates, we required all SPRING predictions to have <95% sequence identity (using global alignment) to both query proteins. We note that even though the sequence identity threshold was set at 95%, most of the top-ranked templates identified by SPRING were not close homologs—in the majority (78%) of the cases, one of the proteins of the top ranked templates from SPRING had a sequence identity less than 50% (Supplementary Fig. S1a). There were 21 cases where all SPRING predictions had ≥95% sequence identity to the query proteins. Thus, we restricted our training of the logistic regression model to the 121 (85%) test cases which had at least one prediction that cleared the sequence identity filter. Furthermore, the number of predictions per test case varied depending on template availability (capped at 50), and we did not want template availability to bias our choice of features. So, we performed bootstrapping to reduce the bias against test cases with fewer than 50 predictions—a bootstrapped dataset was generated by adding predictions via sampling with replacement from available predictions for each test case, yielding 50 predictions per test case. We generated 100 such bootstrapped datasets.

The feature selection process for the logistic regression model, as described above, was repeated for each of the 100 bootstrapped datasets, and the feature set selected most frequently among the 100 trials was then deemed the final feature set and used for computing the SPRING confidence score.

2.4 ZDOCK

For template-free predictions, we used ZDOCK version 3.0.2 (Mintseris et al., 2007; Pierce et al., 2011; Chen and Weng, 2003; Chen et al., 2003), which was developed in our lab. ZDOCK is a grid-based docking algorithm that uses fast Fourier transforms to accelerate an exhaustive search in the 6D rotational and translational space, sampling the three Euler angles with a 6° or 15° spacing and the three translational degrees of freedom with a 1.2 Å spacing. For each set of rotational angles, only the best-scoring translation is retained, which results in 3600 or 54 000 predictions for 15° or 6° rotational sampling, respectively. The predictions are ranked according to the ZDOCK scoring function, which combines shape complementarity, electrostatics and de-solvation. In the current work, we used the 15° sampling, resulting in a total of 3600 docking decoys per test case.

2.4.1. Confidence score for ZDOCK predictions

To be able to compare SPRING and ZDOCK predictions, we needed to assign a confidence score to ZDOCK predictions, analogous to that of SPRING. The ZDOCK score could not be used directly because its scoring function was optimized to discriminate between different binding modes of the same pair of proteins, but we required a score that could evaluate the likelihood of a prediction being correct across different pairs of proteins. Therefore, we determined the probability of a correct prediction at each ZDOCK rank, across the 142 cases of our dataset and then used this probability to convert a rank into a confidence score.

2.5 Combining SPRING and ZDOCK predictions

The confidence scores for SPRING and ZDOCK predictions can be directly compared; hence, we combined these predictions, sorted by the confidence score (Fig. 1). For test cases without any SPRING predictions, the final list consisted of ZDOCK predictions only. When comparing the success rate of the combined method ZING with ZDOCK and SPRING, we performed another round of 4-fold cross-validation to obtain SPRING confidence scores. ZDOCK does not require training; hence, it was run only once. To assess the robustness of the results, we performed the 4-fold cross-validation for SPRING five times by randomly partitioning the test cases each time. We did not use bootstrapping in this step (i.e. generate 50 models per test case, as was employed for the feature selection), because we wanted the performance of SPRING (and hence ZING) to reflect the actual template availability.

Fig. 1.

Fig. 1.

Open in a new tab

Workflow for combining predictions from SPRING and ZDOCK. Different intensities of blue and pink are used to represent the confidence scores for the ZDOCK and SPRING predictions respectively (deep shades representing high confidence). (Color version of this figure is available at Bioinformatics online.)

3 Results

3.1 Testing SPRING and ZDOCK individually

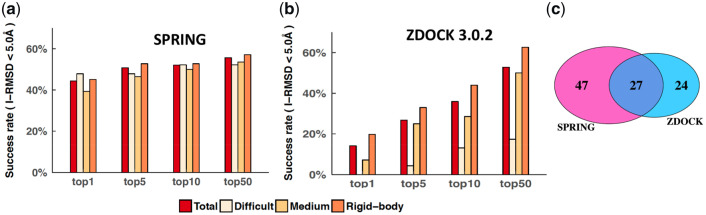
We tested the performance of SPRING on a subset of the protein–protein docking benchmark 5.0 (Vreven et al., 2015) consisting of 142 complexes with single-chain component proteins. For 21 cases SPRING did not find appropriate templates (Section 2). Figure 2a shows that the success rate of SPRING was 44.4% with only the top-ranking prediction, and increased to 55.6% when all models from SPRING were included (up to 50 per test case). For only five test cases (PDB IDs: 1J2J, 1QA9, 2OZA, 1PPE, 1CLV), the best hit was ranked after 10 (Supplementary Fig. S1b), corresponding to a mere 3% improvement in the success rate when predictions ranked after 10 were included. This shows that if SPRING found a correct template, it typically ranked the template at the top. The success rate was 50.7% when the top five predictions were considered, which was similar to that reported earlier (Guerler et al., 2013) on version 3.0 of the docking benchmark.

Fig. 2.

Fig. 2.

Open in a new tab

Performance of SPRING and ZDOCK on the docking benchmark. Success rates for SPRING (a) and ZDOCK (b), respectively. The success rate was calculated as the percentage of test cases with at least one hit (I-RMSD < 5.0 Å) when the top N predictions were considered for each test case, where N = 1, 5, 10, or 50. (c) Number of unique and shared test cases that ZDOCK and SPRING succeeded in producing at least one hit at N = 10

The success rate for ZDOCK was 14.1%, 35.9% and 52.8% for the top one, top 10 and top 50 predictions, respectively. These values are similar to those reported earlier (Vreven et al., 2015). As expected, ZDOCK performed better on the rigid-body cases than the medium-difficulty and difficult cases. ZDOCK’s success rates for the 21 test cases that SPRING did not find appropriate templates were comparable with its success rates for the remaining 121 test cases (19.1%, 28.6% and 38.1% versus 13.2%, 37.2%, 55.4% for N = 1, 10 and 50, respectively).

Out of the 142 test cases, ZDOCK and SPRING yielded a hit in the top 10 predictions for 51 and 74 cases, respectively. ZDOCK’s performance for rigid-body cases was close to that of SPRING (N = 10), while SPRING outperformed ZDOCK in the medium-difficulty and difficult categories. This is expected because template-based methods like SPRING are not affected by the flexibility of the interfacial residues upon complex formation. Overall, the two methods are highly complementary: at least one method ranked a hit in the top 10 for 98 test cases, while both methods succeeded for only 27 cases (Fig. 2c). Thus, if we combine the results such that the best predictions from both methods are ranked near the top, we could potentially achieve a better success rate than that for either method independently.

3.2 Logistic regression model for SPRING: feature selection

To formulate a method for combining ZDOCK and SPRING, we needed to determine the confidence in each prediction. For SPRING we performed logistic regression modeling using five features that relate the input sequence to the template (Section 2): minTM (a template modeling score), minZ (a threading Z-score), Coverage (fraction of the input sequence that is aligned), E (an interface contact potential) and minS (sequence identity between input and template). Among these five features, E is slightly anti-correlated with the other four features, which are positively correlated with one another; especially, Coverage and minTM are highly correlated (correlation coefficient = 0.96; Supplementary Fig. S2).

The goal of the logistic regression model was to produce a normalized output PLR (between 0 and 1) to estimate the probability that a SPRING prediction was correct. For training and testing of logistic regression models, we used the 2405 predictions that SPRING generated for the aforementioned subset of 121 test cases in the docking benchmark (Section 2). We performed an exhaustive search of the feature space using 100 bootstrapped datasets. Figure 3a shows the results for one such dataset, and an interesting observation is that although E is the worst single feature, it is included in all the multi-feature models with the lowest errors. Besides E, other features present in such models include Coverage and minTM. Notably, the five models with lowest errors all contained E and Coverage (Fig. 3a).

Fig. 3.

Fig. 3.

Open in a new tab

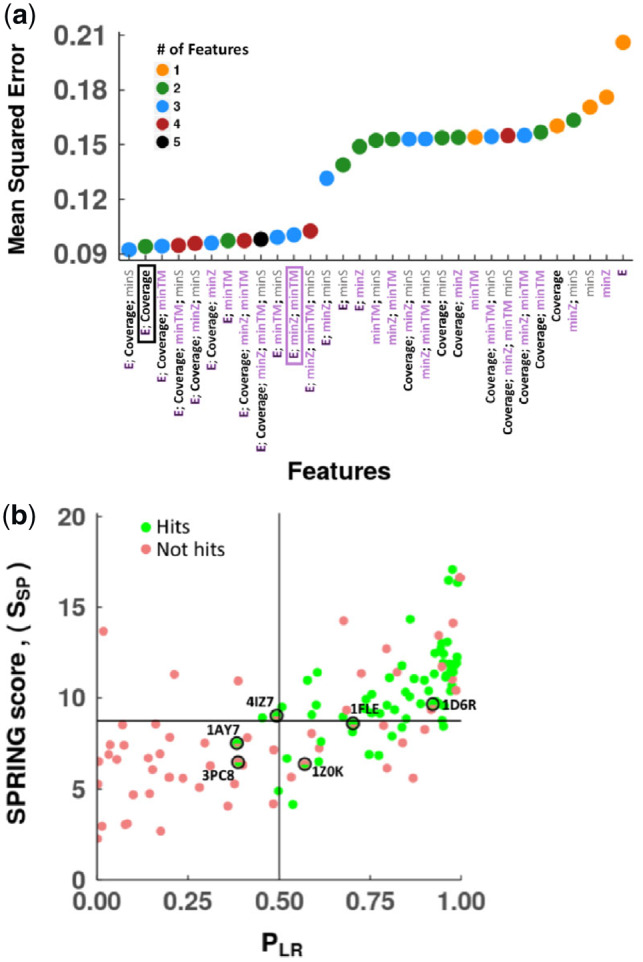
Logistic regression modeling of SPRING predictions. (a) The mean squared errors for the 31 possible combinations of the five features (E, Coverage, minTM, minZ, minS) tested for logistic regression modeling, colored by the number of features in the model. E; minTM; minZ (enclosed in pink) and E; Coverage (enclosed in black) are feature sets, used by SPRING and selected by our model selection process, respectively. (b) Each point represents a test case (121 cases in total), with the scores of the top-ranked predictions by the two scoring metrics (SSP versus PLR) on the test set during cross-validation. A point is colored green if the top-ranked prediction by SSP is a hit and the top-ranked prediction by PLR is also a hit; a point is colored red if the top-ranked prediction by SSP is not a hit and the top-ranked prediction by PLR is not a hit either. For four test cases (1AY7, 4IZ7, 1FLE, 1D6R; represented by a top-green and bottom-red point with a black outline), the top-ranked prediction by PLR is a hit but the top-ranked prediction by SSP is not a hit. For two other cases (3PC8 and 1Z0K; represented by two top-green and bottom-red points with a black outline), the top-ranked prediction by SSP is not a hit but the top-ranked prediction by PLR is a hit. Two lines indicate the cutoffs that separate positive and negative predictions: 0.5 for PLR and 8.75 for SSP. (Color version of this figure is available at Bioinformatics online.)

To account for model complexity, we selected the model for each dataset to be the one with the smallest number of features among the models that had mean squared errors within one standard error of the minimum mean squared error (Section 2). In 94 of the 100 trials of cross-validation, the selected model combined two features, E and Coverage (both with a higher value implying a more stable complex), to calculate the SPRING logistic regression score (SLR):

SLR=k0 + k1*Coverage + k2*E (1)
PLR= 11+e-SLR (2)

where k0 = –14.23, k1 = 12.48 and k2 = 0.18 when computed using the entire dataset. k1 and k2 are both positive, indicating that E and Coverage both positively contribute to SLR and hence to PLR.

We then compared our confidence score (PLR) with the score computed by SPRING. The default SPRING score (SSP) is a linear sum of three terms: E, minTM and minZ, while E and Coverage were identified as key features by our feature selection process for logistic regression modeling (Fig. 3a). PLR is correlated with SSP (correlation coefficient = 0.68; P-value < 0.0001; Fig. 3b). When only the top-ranked prediction was considered for each test case, PLR predicted hits for two more test cases than SSP (65 versus 63 out of 121). Furthermore, when a SSP score cutoff was used to decide whether the top-ranked prediction was a hit (i.e. prediction with a SSP score higher than the cutoff), the maximal accuracy of SSP was 75.2% with the cutoff set at 8.75 to maximize the accuracy (the horizontal line in Fig. 3b). For PLR, the maximal accuracy cutoff was 0.5 (the vertical line in Fig. 3b), and its accuracy at this cutoff was 79.3%, higher than SSP. A logistic model with the same three features as SSP had slightly higher mean squared error than our final two-feature model (Fig. 3a); however, a two-feature model is simpler than and thus more likely to outperform a three-feature model on future test cases. Thus, we decided on the two-feature model with E and Coverage.

3.3 Combining SPRING and ZDOCK predictions

The complementarity between template-based and template-free methods (Vreven et al., 2014) suggests that a combined approach could lead to better results, and Guerler et al. pooled ZDOCK and SPRING predictions (top 3 predictions from ZDOCK and top 2 from SPRING) to achieve a better performance than either method independently (Guerler et al., 2013). Instead of using a fixed ratio of predictions from the two methods, in this study, we combined predictions from both methods and ranked them by their confidence scores, which we have designed to be comparable. For SPRING, we used the probability predicted by our logistic regression model [PLR, Eq. (2)] as the confidence score. For ZDOCK, we used the frequency that the prediction at a specific ZDOCK rank is correct across the 142 test cases, as the confidence score (Supplementary Fig. S3). We named this combined approach ZING.

To evaluate the performance of ZING, we partitioned the test cases randomly into 4-folds and then trained and tested using 4-fold cross-validation. To assess the consistency of the success rate and estimate associated errors, we performed the 4-fold cross-validation five times, each time with a different random partitioning of the dataset.

Figure 4 shows the success rate curves for ZDOCK, SPRING and our new approach ZING. While the success rate of ZDOCK kept growing with the number of predictions per test case (N), that of SPRING was constant after it had made the maximum of N = 50 predictions per test case. The success rate of the methods for N = 10 is often cited because the CAPRI experiment (Lensink et al., 2018) uses 10 predictions in the assessments of its participants’ performance, and it is also a reasonable number for follow-up experiments or more accurate computational modeling. At N = 10, the success rate of ZING was 68.2%, better than that of both ZDOCK and SPRING, at 35.9% and 52.1%, respectively (Fig. 4a). We then compared the overall performance of the methods, using the ISR (ISR, Section 2) for values of N between 1 and 100. ZING, with an ISR of 0.66 performed better than ZDOCK and SPRING with ISRs of 0.37 and 0.52, respectively. For the results shown in Figure 4, we used a query-template sequence identity threshold of 95% to filter predictions from SPRING (Section 2). However, the results in Figure 4 also extend to using lower levels (70%, 50% and 30%) of query-template sequence identity thresholds (Supplementary Fig. S4). Furthermore, the improvement of ZING is robust to random partitioning of the data, as it yielded higher success rates than ZDOCK and SPRING across all five random partitionings of the data for 4-fold cross-validation. We also looked at the number of unique and shared cases between the three methods. Considering the top 10 predictions, we observed two cases for which ZING succeeded but neither ZDOCK nor SPRING. ZING also succeeded for 94 of the 98 cases where at least one of the methods was successful (Fig. 4b).

Fig. 4.

Fig. 4.

Open in a new tab

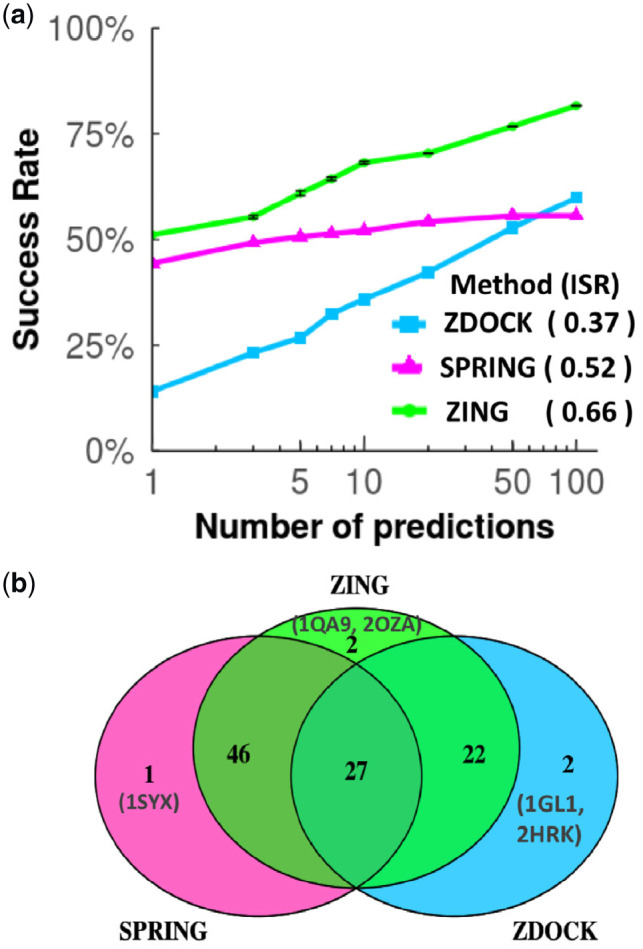
Comparing the performance of ZDOCK, SPRING and ZING. (a) The success-rate curves for ZDOCK, SPRING and ZING. The error bars indicate the SD calculated from five different random partitions of the dataset into 4-fold training and test sets. The ISRs for the corresponding methods are shown in parentheses. (b) The number of unique and overlapping test cases that ZDOCK, SPRING and ZING succeeded in predicting one or more hits at N = 10. The unique cases for each method are identified by their PDB IDs

3.4 Detailed analysis of individual test cases

We inspected the performance of ZING, ZDOCK and SPRING on a case-by-case basis, at N = 10, shown in Figure 5. The columns in the figure correspond to the five random partitionings of the data, each used for one round of cross-validation. The effect of data partitioning on the results is small as indicated by the consistent results across the five different runs for each case. There were 27 cases where both ZDOCK and SPRING had a hit in the top 10 predictions and ZING retained the hit(s) as well, indicated by zs-labeled grid squares (Fig. 5). There are also 42 cases where neither SPRING nor ZDOCK yielded a hit (entirely-red rows). In contrast, there were 71 cases for which only one of the methods provides a hit(s) and ZING succeeded in picking up 68 of those cases (green grid squares with either z or s only), attesting to the power of combining template-based and template-free methods.

Fig. 5.

Fig. 5.

Open in a new tab

Evaluation of ZING on a case-by-case basis across five random partitionings of the dataset, each used for one round of cross-validation. Green and red grid squares indicate at least one hit or no hits, respectively, in the top 10 predictions of the ZING prediction list. The labels show which method contributed towards the hit(s) in the ZING prediction list–z: ZDOCK; s: SPRING; p: ZING prediction list includes a hit because of PLR or PZD re-ranking (not included in the top 10 predictions from either of the parent methods), *: a hit from ZDOCK or SPRING not retained in the top 10 ZING predictions. (Color version of this figure is available at Bioinformatics online.)

Five test cases (labeled z*, s* or p, in Fig. 5) deviated from expected behavior due to the re-ranking of predictions using PLR or PZD. For two test cases (1QA9 and 2OZA; labeled p in Fig. 5), high PLR values pushed a hit to the top 10 predictions in ZING. In both these cases, the hits had high Coverage values, a feature included in our PLR but not in the original SPRING score. For three other cases, the hit(s) identified by SPRING (1SYX; labeled s* in Fig. 5) or ZDOCK (2HRK and 1GL1; labeled z* in Fig. 5) were not included in the top 10 predictions of ZING. We examine these three cases below.

1SYX (Nielsen et al., 2007) involves the interaction between two proteins—U5-52K and U5-15K in the spliceosomal complex. SPRING generated only one prediction that was a hit (I-RMSD = 3.8 Å), for which the complex template (PDB ID: 4J3C) is a homodimer of a 16S ribosomal RNA methyltransferase. However, the complex template only partially matches the query complex, as shown in Figure 6a, which leads to a low Coverage value (which is one of the features for PLR) and hence a low PLR. As a result, ZING did not include the prediction in its top 10 predictions.

Fig. 6.

Fig. 6.

Open in a new tab

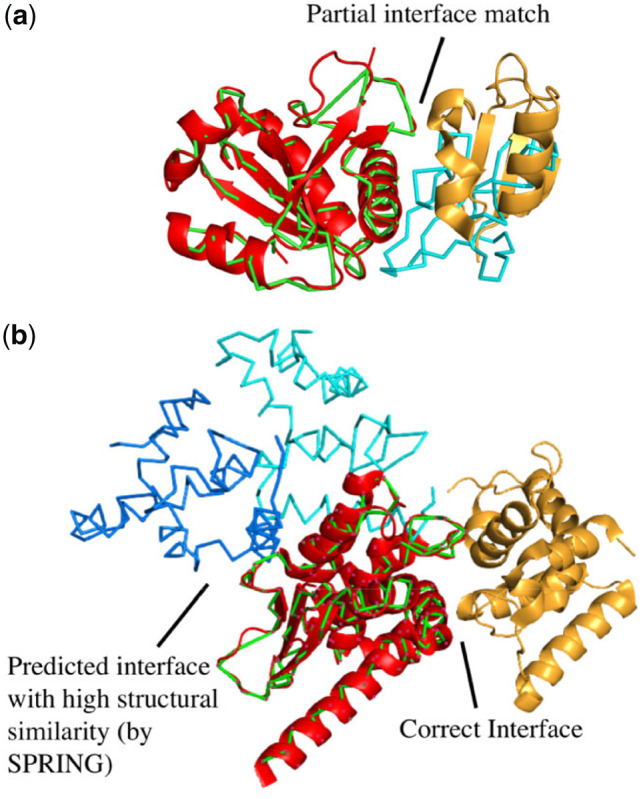
Structures of two complexes (PDB ID: 1SYX and 2HRK) (a) 1SYX (U5-15K in red and U5-52K in yellow ribbons) superposed on the SPRING prediction (green and cyan wire-frame structures), which is classified as a hit. (b) 2HRK (GluRS in red and Arc1-p in yellow ribbons) superposed on the SPRING prediction (GluRS in green and two predicted positions of Arc1-p in blue and cyan wire-frame structures). Only Cα atoms are shown in the wire-frame structures. The top 10 ZING predictions for these cases do not have a hit(s), that was present in the top 10 predictions of one of the parent methods––SPRING/ZDOCK. (Color version of this figure is available at Bioinformatics online.)

1GL1 is an enzyme inhibitor complex with bovine α-chymotrypsin and a protease inhibitor LCM II (Roussel et al., 2001). There were four predictions (none of them were hits) by SPRING with higher confidence scores than the top-ranked ZDOCK prediction (which was not a hit either). ZDOCK did produce a hit but ranked it seventh. This ZDOCK hit was ranked 11 by ZING and hence not included in ZING’s top 10 predictions.

Finally, we examined 2HRK, the complex of Glutamyl-tRNA synthetase (GluRS) and tRNA aminoacylation factor 1 (Arc1-p) in yeast (Simader et al., 2006). ZDOCK made a correct prediction (ranked 2) in the top 10, but it was ranked 50 by ZING as 48 incorrect SPRING predictions had higher confidence scores. This case exemplifies the failures that violate the premise of template-based docking (and our combined approach), due to the existence of homologous protein–protein complexes with different binding modes. GluRS contains a GST-like fold, which is commonly found in many different proteins (Dulhunty et al., 2001; Morris et al., 2011) and as a result, SPRING identified many templates with high confidence. However, in 2HRK, GluRS shows an alternative, unique binding mode for the GST fold that is not observed in any other PDB entry. The incorrect templates overwhelmed ZING predictions and pushed the correct ZDOCK prediction outside the top 10.

4 Discussion

We presented a method that combines results from a template-based algorithm (SPRING) and a template-free algorithm (ZDOCK) to predict protein–protein complexes. Our combined method ZING achieved a higher success rate than either SPRING or ZDOCK. The strength of ZING is that it ranks SPRING and ZDOCK predictions with confidence scores that are directly comparable, such that high confidence predictions from both methods are ranked higher up in the final list of predictions for ZING, leading to a consolidation of the successes of the individual methods.

Our logistic regression only used two features (E and Coverage) to classify the predictions from SPRING as hits or non-hits for test cases in the docking benchmark. Guerler et al. used three features in the SPRING score—E, minTM and minZ—with their weights trained from 200 randomly selected protein complexes (Guerler et al., 2013). The difference between the feature sets of the two approaches is minimal because Coverage and minTM are highly correlated with each other (Supplementary Fig. S2) and the inclusion of the minZ feature led to only a small increase in the error of our logistic regression model (Fig. 3a). If a single feature were to be considered, minTM on its own is the most informative feature, although less accurate than our two-feature (E and Coverage) model (Fig. 3a). A value of 0.7 or higher for minTM generally indicates a good chance for the SPRING prediction to be correct.

The maximum probability (PZD) calculated for ZDOCK predictions is 0.104 across all test cases; on average, 17% of the SPRING predictions per case have PLR values higher than 0.1. Thus, the top ZING predictions often rely on the template-based method (for 74% of the test cases). The remainder of the ZING prediction list is populated by both template-free and template-based methods depending on template availability and the confidence scores. Given that homologous proteins often have conserved binding modes, it is reasonable for most top-ranking predictions in the combined list to come from the template-based method. Such a scenario may lead to cases as 2HRK discussed above where a high-scoring, incorrect binding mode gains precedence over a correctly identified structure using the template-free method. However, we identified only three cases out of 142 where the top 10 combined predictions did not include a hit that was included in the top 10 predictions of either ZDOCK or SPRING. This shows that our method is robust in getting the best of both the template-based and template-free methods.

Ideally, we would like to compare our approach with other template-based methods. However, such a comparison would be difficult to carry out because the performance of template-based methods depends on their template libraries. For biological applications, users are expected to use SPRING’s template library inclusive of all template structures regardless of their sequence similarity to the target. The library will be updated to keep up with growth of the PDB.

We will continue to evaluate the performance of ZING by making predictions in the CAPRI (Lensink et al., 2018) and CASP-CAPRI (Lensink et al., 2017) challenges. Until now, we have manually combined homology-modeled and ab initio predictions; we will use ZING to select the predictions from the two approaches in future challenges. This automation will also allow us to participate more effectively as a server, which requires automated selection of predictions.

Supplementary Material

btz623_Supplementary_Data
Click here for additional data file. (694.4KB, pdf)

Acknowledgements

The authors thank Dr Brandon Govindaraju, as well as our lab members for helpful discussions.

Funding

This work was supported by the National Institutes of Health grant R01 GM116960.

Conflict of Interest: none declared.

References

  1. Aytuna A.S. et al. (2005) Prediction of protein-protein interactions by combining structure and sequence conservation in protein interfaces. Bioinformatics, 21, 2850–2855. [DOI] [PubMed] [Google Scholar]
  2. Bruce A. (1998) The cell as a collection overview of protein machines: preparing the next generation of molecular biologists. Cell, 92, 291–294. [DOI] [PubMed] [Google Scholar]
  3. Brückner A. et al. (2009) Yeast two-hybrid, a powerful tool for systems biology. Int. J. Mol. Sci., 10, 2763–2788. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Chen R., Weng Z. (2003) A novel shape complementarity scoring function for protein-protein docking. Proteins, 51, 397–408. [DOI] [PubMed] [Google Scholar]
  5. Chen H., Skolnick J. (2008) M-TASSER: an algorithm for protein quaternary structure prediction. Biophys. J., 94, 918–928. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Chen R. et al. (2003) ZDOCK: an initial-stage protein-docking algorithm. 52, 80–87. [DOI] [PubMed] [Google Scholar]
  7. Dominguez C. et al. (2003) HADDOCK: a protein−protein docking approach based on biochemical or biophysical information. J. Am. Chem. Soc., 125, 1731–1737. [DOI] [PubMed] [Google Scholar]
  8. Dulhunty A. et al. (2001) The glutathione transferase structural family includes a nuclear chloride channel and a ryanodine receptor calcium release channel modulator. J. Biol. Chem., 276, 3319–3323. [DOI] [PubMed] [Google Scholar]
  9. Guerler A. et al. (2013) Mapping monomeric threading to protein–protein structure prediction. J. Chem. Inform. Model, 53, 717–725. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Günther S. et al. (2007) Docking without docking: ISEARCH-prediction of interactions using known interfaces. Prot. Struct. Funct. Genet., 69, 839–844. [DOI] [PubMed] [Google Scholar]
  11. Huttlin E.L. et al. (2015) The BioPlex network: a systematic exploration of the human interactome. Cell, 162, 425–440. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Kundrotas P.J., Vakser I.A. (2010) Accuracy of protein-protein binding sites in high-throughput template-based modeling. PLoS Comput. Biol., 6, e1000727. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Kundrotas P.J. et al. (2017) Modeling CAPRI targets 110-120 by template-based and free docking using contact potential and combined scoring function. Prot. Struct. Funct. Genet., 107, 1785–1789. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Kundrotas P.J. et al. (2012) Templates are available to model nearly all complexes of structurally characterized proteins. Proc. Natl. Acad. Sci. USA, 109, 9438–9441. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Lensink M.F. et al. (2017) Modeling protein-protein and protein-peptide complexes: CAPRI 6th edition. Prot. Struct. Funct. Genet., 85, 359–377. [DOI] [PubMed] [Google Scholar]
  16. Lensink M.F. et al. (2018) The challenge of modeling protein assemblies: the CASP12-CAPRI experiment. Prot. Struct. Funct. Genet., 86, 257–273. [DOI] [PubMed] [Google Scholar]
  17. Lu L. et al. (2002) MULTIPROSPECTOR: an algorithm for the prediction of protein-protein interactions by multimeric threading. Prot. Struct. Funct. Genet., 49, 350–364. [DOI] [PubMed] [Google Scholar]
  18. Lyskov S., Gray J.J. (2008) The RosettaDock server for local protein-protein docking. Nucleic Acids Res., 36, W233–W238. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Mintseris J. et al. (2007) Integrating statistical pair potentials into protein complex prediction. Prot. Struct. Funct. Genet., 69, 511–520. [DOI] [PubMed] [Google Scholar]
  20. Morris M.J. et al. (2011) A structural basis for cellular uptake of GST-fold proteins. PLoS One, 6, e17864. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Mukherjee S., Zhang Y. (2011) Protein-protein complex structure predictions by multimeric threading and template recombination. Structure, 19, 955–966. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Murzin A.G. et al. (1995) SCOP: a structural classification of proteins database for the investigation of sequences and structures. J. Mol. Biol., 247, 536–540. [DOI] [PubMed] [Google Scholar]
  23. Nielsen T.K. et al. (2007) Structural basis for the bifunctionality of the U5 snRNP 52K protein (CD2BP2). J. Mol. Biol., 369, 902–908. [DOI] [PubMed] [Google Scholar]
  24. Patrick A., Robert R.B. (2004) Ten thousand interactions for the molecular biologist. Nat. Biotechnol., 22, 1193–1193. [DOI] [PubMed] [Google Scholar]
  25. Pierce B.G. et al. (2011) Accelerating protein docking in ZDOCK using an advanced 3D convolution library. PLoS One, 6, e24657.. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Ritchie D.W. et al. (2008) Accelerating and focusing protein-protein docking correlations using multi-dimensional rotational FFT generating functions. Bioinformatics, 24, 1865–1873. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Roussel A. et al. (2001) Complexation of two proteic insect inhibitors to the active site of chymotrypsin suggests decoupled roles for binding and selectivity. J. Biol. Chem., 276, 38893–38898. [DOI] [PubMed] [Google Scholar]
  28. Simader H. et al. (2006) Structural basis of yeast aminoacyl-tRNA synthetase complex formation revealed by crystal structures of two binary sub-complexes. Nucleic Acids Res., 34, 3968–3979. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Skolnick J., Gao M. (2010) Structural space of proteinprotein interfaces is degenerate, close to complete, and highly connected. PNAS, 107, 22517–22522. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Söding J. (2005) Protein homology detection by HMM-HMM comparison. Bioinformatics, 21, 951–960. [DOI] [PubMed] [Google Scholar]
  31. Tuncbag N. et al. (2011) Predicting protein-protein interactions on a proteome scale by matching evolutionary and structural similarities at interfaces using PRISM. Nat. Protocols, 6, 1341–1354. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Vreven T. et al. (2014) Evaluating template-based and template-free protein-protein complex structure prediction. Brief. Bioinform., 15, 169–176. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Vreven T. et al. (2011) Integrating atom-based and residue-based scoring functions for protein-protein docking. Prot. Sci., 20, 1576–1586. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Vreven T. et al. (2015) Updates to the integrated protein–protein interaction benchmarks: docking benchmark version 5 and affinity benchmark version 2. J. Mol. Biol., 427, 3031–3041. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Xue L.C. et al. (2011) HomPPI: a class of sequence homology based proteinprotein interface prediction methods. BMC Bioinformatics, 12, 1–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Xue L.C. et al. (2016) Template-based protein–protein docking exploiting pairwise interfacial residue restraints. Brief. Bioinform., 7, 458–466. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Zhang Y. et al. (2012) How many protein-protein interactions types exist in nature? PLoS One, 7, e38913. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

btz623_Supplementary_Data
Click here for additional data file. (694.4KB, pdf)

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES