Variable selection for recurrent event data with broken adaptive ridge regression

Abstract

Recurrent event data occur in many areas such as medical studies and social sciences and a great deal of literature has been established for their analysis. On the other hand, only limited research exists on the variable selection for recurrent event data, and the existing methods can be seen as direct generalizations of the available penalized procedures for linear models and may not perform as well as expected. This article discusses simultaneous parameter estimation and variable selection and presents a new method with a new penalty function, which will be referred to as the broken adaptive ridge regression approach. In addition to the establishment of the oracle property, we also show that the proposed method has the clustering or grouping effect when covariates are highly correlated. Furthermore, a numerical study is performed and indicates that the method works well for practical situations and can outperform existing methods. An application is provided.

1. INTRODUCTION

This article discusses regression analysis of recurrent event data with the focus on simultaneous parameter estimation and variable selection. By recurrent event data, we mean that in an event history study concerning the occurrence rate of a recurrent event, the observed data on each subject include all occurrence times of the event during the follow up (Andersen etal., 1993;Cook & Lawless, 2007). An example is the study of the hospitalization rate for certain patient groups. Another example is given by investigating the occurrence rate of some disease symptoms or infections, as discussed in Section 5. For recurrent event data, it is assumed that each study subject is observed over a continuous time interval or window. In contrast, sometimes study subjects may be observed only at discrete time points, and thus only incomplete data, often referred to as panel count data, are available (Sun & Zhao, 2013).

Recurrent event data occur in many areas such as medical studies and social sciences and a great deal of literature has been established for their analysis (Andersen etal., 1993; Lawless & Nadeau, 1995; Lin etal., 2000; Cai & Schaubel, 2004; Schaubel, Zeng, & Cai, 2006; Cook & Lawless, 2007). In particular, Cook & Lawless (2007) gave a comprehensive review of the literature on the analysis of such data. However, there exists little research on the variable selection in the context of recurrent event data except Tong, Zhu, & Sun (2009) and Chen & Wang (2013). Tong, Zhu, & Sun (2009) considered the data arising from a multiplicative rate model and proposed a penalized estimating equation-based procedure with the focus on the smoothly clipped absolute derivation (SCAD) penalty function (Fan & Li, 2001). In contrast, Chen & Wang (2013) considered the additive rate model and developed a penalized least square loss function-based method with the use of the SCAD penalty function and the adaptive least absolute shrinkage and selection operator (ALASSO) proposed by Zou (2006). As seen in this article, the two methods may perform poorly sometimes and do not have the grouping effect, which is especially important when variables are highly correlated.

Variable selection is an important topic and has been discussed in many areas such as regression analysis. For this analysis, it is well known that a natural approach is the L₀-penalized regression that directly penalizes the cardinality of the variables in the model and seeks the most parsimonious model explaining the data. However, solving an exact L₀-penalized nonconvex optimization problem involves an exhaustive combinatorial best subset search, which is NP-hard and computationally infeasible, especially for high-dimensional data. To overcome this, a popular approach is to replace the nonconvex L₀-norm by the L₁-norm, which is known as the closest convex relaxation of the L₀-norm. In addition, the L₁-penalized optimization problem can be solved exactly with efficient algorithms and the method became popular since the introduction of the least LASSO method (Tibshirani, 1996). However, it is known that LASSO does not have the oracle property as it tends to select too many small noise features and is biased for large parameters. In addition, it cannot accommodate the grouping effect when covariates are highly correlated. To address these, several approaches have been proposed including the ALASSO and SCAD. In this article, we propose a broken adaptive ridge (BAR) regression approach that approximates the L₀-penalized regression using an iteratively reweighted L₂-penalized algorithm for variable selection for recurrent event data.

To describe the BAR regression approach, we will first introduce some notation and the model to be used throughout the article and also briefly describe the existing estimation procedure in Section 2. The proposed method is presented in Section 3 and as mentioned above, it approximates the L₀-penalized regression using an iteratively reweighted L₂-penalized algorithm and takes the limit of the algorithm as the BAR estimator. The approach has the advantages of performing simultaneous variable selection and parameter estimation and accommodating clustering effects, and the BAR iterative algorithm is fast and converges to a unique global optimal solution. Also in Section 3, the asymptotic properties of the proposed BAR estimator including the oracle property are established. Section 4 presents the results of extensive simulation studies to assess the performance of the proposed methodology, and they suggest that the proposed method works well and can outperform the existing method for practical situations. An application is provided in Section 5, and Section 6 contains some discussion and concluding remarks.

2. MODEL AND THE EXISTING ESTIMATION PROCEDURE

Consider an event history study consisting of n independent subjects which concerns the occurrence of a recurrent event of interest. For subject i, let $N_i^{*}(t)$ denote the underlying recurrent event process indicating the total number of the occurrences of the event over the time interval [0, t]. Let C_i denote the follow-up time on subject i and let $N_i(t)=N_i^{*}\left(t\wedge C_i\right)$ be the observed recurrent event process. Suppose that there exists a p-dimensional vector of external covariate process, denoted by ${\mathit{Z}}_i(t)={(Z_{i1}(t),\dots ,Z_{ip}(t))}^{\prime }$ (Kalbfleisch & Prentice, 2002), the main objective is to perform regression analysis with the focus on parameter estimation and covariate selection.

To describe the covariate effect, we assume that given ${\mathit{Z}}_i(t),N_i^{*}(t)$ satisfies the model

$$E\left[d{N}_i^{*}(t)|{\mathit{Z}}_i(t)\right]=d{\mu }_0(t)+{\mathit{\beta }}^{\prime }{\mathit{Z}}_i(t)dt,$$ (1)

where ${\mu }_0(t)$ denotes an unspecified increasing function and $\mathit{\beta }={\left({\beta }_1,\dots ,{\beta }_p\right)}^{\prime }$ is a p-dimensional vector of regression parameters. Model (1) is usually referred to as the additive rate model and has been studied by many authors for analyzing recurrent event data. Lin et al. (2000), and Schaubel, Zeng, & Cai (2006), and Cook & Lawless (2007) discussed the validity and usefulness of the model and Schaubel, Zeng, & Cai (2006) provided an approach to measure the validity of the model given the observed recurrent event data. But there does not seem to exist an established method that can be used for covariate selection except that of Chen & Wang (2013). As opposed to its commonly used alternative, the proportional rate model, where the regression coefficient reflects relative effects, model (1) characterizes the absolute covariate effects which are often of direct interest in epidemiological and clinical studies.

In the following, we will use boldface to denote vectors or matrices. For the time being, we are only interested in estimation of the regression parameter β. For this, define

$$d{M}_i(t;\mathit{\beta })=d{N}_i(t)-I\left(C_i>t\right)\left\{d{\mu }_0(t)+{\mathit{\beta }}^{\prime }{\mathit{Z}}_i(t)dt\right\}.$$

One can easily show that M_i(t; β) is a zero-mean stochastic process at the true value, say β₀, of the regression parameter, and this motivates the estimating equations

$$\sum _{i=1}^n{\int }_0^{t}d{M}_i(s;\mathit{\beta })=0$$ (2)

and

$$\sum _{i=1}^n{\int }_0^{\tau }{\mathit{Z}}_i(s)d{M}_i(s;\mathit{\beta })=0$$ (3)

for estimation of β₀ and μ₀(t), where τ is a prespecified constant such that $P\left(C_i\ge \tau \right)>$ 0 for i = 1,..., n. Solving Equation (2) for μ₀(t) with β fixed and plugging the solution into Equation (3), we obtain the estimating equation

$$U_n(\mathit{\beta })=\sum _{i=1}^n{\int }_0^{\tau }\{{\mathit{Z}}_i(s)-\overline{\mathit{Z}}(s)\}d{M}_i(t;\mathit{\beta })=0.$$ (4)

Here $\overline{\mathit{Z}}(t)={\mathit{S}}^{(1)}(t)/S^{(0)}(t)$ and ${\mathit{S}}^{(k)}(t)=n^{-1}{\sum }_{i=1}^{n}I\left(C_i\ge s\right){\mathit{Z}}_i^{\otimes k}(t)$ with ${\mathit{a}}^{\otimes 0}=1,{\mathit{a}}^{\otimes 1}=\mathit{a},{\mathit{a}}^{\otimes 2}=\mathit{a}{\mathit{a}}^{\prime }$ for a vector a, k = 0, 1, 2. Such equations were also given by Schaubel, Zeng, & Cai (2006). Solving Equation (4) gives an explicit estimator of β as

$$\widehat{\mathit{b}}={\left[\sum _{i=1}^n{\int }_0^{\tau }I\left(C_i\ge s\right){\{{\mathit{Z}}_i(s)-\overline{\mathit{Z}}(s)\}}^{\otimes 2}ds\right]}^{-1}\left[\sum _{i=1}^n{\int }_0^{\tau }\{{\mathit{Z}}_i(s)-\overline{\mathit{Z}}(s)\}d{N}_i(s)\right].$$

Schaubel, Zeng, & Cai (2006) showed that under some regularity conditions, $\widehat{\mathit{b}}$ is a consistent estimator of β and $\sqrt{n}(\widehat{\mathit{b}}-\mathit{\beta })$ has an asymptotic normal distribution.

3. BAR REGRESSION ESTIMATION PROCEDURE

Now we discuss the covariate selection problem and for this, let

$${\mathit{P}}_n=\sum _{i=1}^n{\int }_0^{\tau }\{{\mathit{Z}}_i(s)-\overline{\mathit{Z}}(s)\}d{N}_i(s)$$

and

$${\mathrm{\Omega }}_n=\sum _{i=1}^n{\int }_0^{\tau }I\left(C_i\ge s\right){\{{\mathit{Z}}_i(s)-\overline{\mathit{Z}}(s)\}}^{\otimes 2}ds,$$

and define the loss function

$$l(\mathit{\beta })=\frac{1}{2}{\mathit{\beta }}^{\prime }{\mathrm{\Omega }}_n\mathit{\beta }-{\mathit{\beta }}^{\prime }{\mathit{P}}_n.$$

One can easily show that $\widehat{\mathit{b}}$ is the minimizer of l(β). Also let X denote the p × p upper triangular matrix given by the Cholesky decomposition of ${\mathrm{\Omega }}_n$ in ${\mathrm{\Omega }}_n={\mathit{X}}^{\prime }\mathit{X},$ and $\mathit{y}={\left({\mathit{X}}^{\prime }\right)}^{-1}{\mathit{P}}_n.$ Then we can see that the minimization of l(β) is equivalent to minimizing the least squares loss function $\Vert \mathit{y}-\mathit{X}\mathit{\beta }{\Vert }^2$ up to a constant. This suggests that by borrowing the idea behind the penalized least squares, we define the L₀-penalized least squares estimator of β as

$$\widehat{\mathit{\beta }}\left(L_0\right)=\arg \underset{\mathit{\beta }}{\min }\left\{\Vert \mathit{y}-\mathit{X}\mathit{\beta }{\Vert }^2+{\lambda }_n\sum _{j=1}^{p}I\left({\beta }_j\ne 0\right)\right\},$$ (5)

where ${\lambda }_n>0$ is a tuning parameter.

Although with some good properties, the determination of $\widehat{\mathit{\beta }}\left(L_0\right)$ is very difficult or computationally infeasible. To deal with this, we propose to approximate Equation (5) by

$$g(\tilde{\mathit{\beta }})\equiv \arg \underset{\mathit{\beta }}{\min }\left\{\Vert \mathit{y}-\mathit{X}\mathit{\beta }{\Vert }^2+{\lambda }_n\sum _{j=1}^p\frac{{\beta }_j^2}{{\tilde{\beta }}_j^2}\right\},$$

which can be rewritten as $g(\tilde{\mathit{\beta }})={\left\{{\mathit{X}}^{\prime }\mathit{X}+{\lambda }_n\mathit{D}(\mathit{\beta })\right\}}^{-1}{\mathit{X}}^{\prime }\mathit{y},\text{or}$

$$g(\tilde{\mathit{\beta }})={\left\{{\mathrm{\Omega }}_n+{\lambda }_n\mathit{D}(\mathit{\beta })\right\}}^{-1}{\mathit{P}}_n,$$

where $\mathit{D}(\tilde{\mathit{\beta }})=\text{diag}\left\{{\tilde{\beta }}_1^{-2},\dots ,{\tilde{\beta }}_p^{-2}\right\}\text{with}\tilde{\mathit{\beta }}={\left({\tilde{\beta }}_1,\dots ,{\tilde{\beta }}_p\right)}^{\prime }$ denoting a reasonable or consistent estimator of β₀ such that there are no zero components in $\tilde{\mathit{\beta }}$ More discussion on this follows.

To see why the proposed idea works, we note that the quadratic function is an approximation to the L₀ penalized regression defined in (5) and that the L₀ penalty is a good tool for variable selection except for its difficult computation feature. Also note that the approximation idea of iteratively reweighted quadratic penalization actually has its roots in the well-known Lawsons algorithm in the classical approximation theory and sparse signal reconstruction theory (Lawson, 1961; Gorodnitsky & Rao, 1997). In the approximation above, the weighted penalty for a zero component will iteratively become large and as the consequence, a zero-coefficient estimate is expected to decrease and converge to zero. In contrast, the weighted penalty for a non-zero component is expected to converge to a constant.

We define the BAR estimator of β as

$${\widehat{\mathit{\beta }}}^{*}=\underset{k\to \infty }{\lim }{\widehat{\mathit{\beta }}}^{(k)}$$

based on the iterative formula ${\widehat{\mathit{\beta }}}^{(k)}=g({\widehat{\mathit{\beta }}}^{(k-1)}).$ For the selection of the initial values for the iteration procedure above, we suggest ${\widehat{\mathit{\beta }}}^{(0)}={\left({\mathrm{\Omega }}_n+{\xi }_n\mathit{I}\right)}^{-1}{\mathit{P}}_n,$ where ${\xi }_n\ge 0.$ When ${\xi }_n>0,{\widehat{\mathit{\beta }}}^{(0)}$ is the ridge estimator; if ${\xi }_n=0,$ then ${\widehat{\mathit{\beta }}}^{(0)}$ reduces to the unpenalized estimator $\widehat{\mathit{b}}={\mathrm{\Omega }}_n^{-1}{\mathit{P}}_n.$ The idea discussed above has been considered under different contexts by Frommlet & Nuel (2016) and Liu & Li (2016), who demonstrated empirically that as an automatic variable selection and parameter estimation procedure, the BAR method can provide substantial improvements over some existing methods. However, no theoretical justification was provided.

To establish the asymptotic properties of ${\widehat{\mathit{\beta }}}^{*},$ we write ${\mathit{\beta }}_0={\left({\mathit{\beta }}_{01}^{\prime },{\mathit{\beta }}_{02}^{\prime }\right)}^{\prime }$ with β₀₁ and β₀₂ being the first q and remaining p − q components of β₀, respectively, and without loss of generality assume that ${\mathit{\beta }}_{02}=0.\text{Let}{\widehat{\mathit{\beta }}}^{(k)}={\left({\widehat{\mathit{\beta }}}_1^{{(k)}^{\prime }},{\widehat{\gamma }}^{\left(k^{{}^{\prime }}\right)}\right)}^{\prime }\text{and}{\widehat{\mathit{\beta }}}^{*}={\left({\widehat{\mathit{\beta }}}_1^{{*}^{\prime }},{\widehat{\mathit{\beta }}}_2^{{*}^{\prime }}\right)}^{\prime }$ denote the corresponding decomposition of ${\widehat{\mathit{\beta }}}^{(k)}\text{and}{\widehat{\mathit{\beta }}}^{*},$ respectively. $\text{Let}\overline{\mathit{z}}(t)={\lim }_{n\to \infty }\overline{\mathit{Z}}(t),\mathrm{\Omega }=E[{\int }_0^{\tau }I(C_i\ge t){\left\{{\mathit{Z}}_i(t)-\overline{\mathit{z}}(t)\right\}}^{\otimes 2}ds]$ and $\Sigma (\mathit{\beta })=E[{\int }_0^{\tau }\left\{{\mathit{Z}}_i(t)-\overline{\mathit{z}}(t)\right\}d{M}_i(t;\mathit{\beta })]{}^{\otimes 2},$ and let ${\mathrm{\Omega }}_{(1)},{\Sigma }_{(1)},{\mathit{P}}_n^{(1)}\text{and}{\mathrm{\Omega }}_n^{(1)}$ be the leading q × q submatrix of $\mathrm{\Omega },\Sigma \left({\mathit{\beta }}_0\right),{\mathit{P}}_n$ and ${\mathrm{\Omega }}_n,$ respectively.

Theorem 1.

Assume that the regularity conditions (C1)–(C7) given in the Appendix hold. Suppose that the initial estimator satisfies ${\widehat{\mathit{\beta }}}^{(0)}={\mathit{\beta }}_0+O_p\left(n^{-1/2}\right).$ Then with probability tending to 1, the BAR estimator ${\widehat{\mathit{\beta }}}^{*}={\left({\widehat{\mathit{\beta }}}_1^{{*}^{\prime }},{\widehat{\mathit{\beta }}}_2^{{*}^{\prime }}\right)}^{\prime }$ has the following properties:

1. ${\widehat{\mathit{\beta }}}_1^{*}$ exists and is the unique fixed point of the equation ${\mathit{\beta }}_1={\left({\mathrm{\Omega }}_n^{(1)}+{\lambda }_n{\mathit{D}}_1\left({\mathit{\beta }}_1\right)\right)}^{-1}{\mathit{P}}_n^{(1)},$ where ${\mathit{D}}_1\left({\mathit{\beta }}_1\right)=\text{diag}\left\{{\beta }_1^{-2},\dots ,{\beta }_q^{-2}\right\};$

2. ${\widehat{\mathit{\beta }}}_2^{*}=0;$

3. $\sqrt{n}\left({\widehat{\mathit{\beta }}}_1^{*}-{\mathit{\beta }}_{01}\right)\stackrel{D}{\to }N\left(0,{\mathrm{\Omega }}_{(1)}^{-1}{\Sigma }_{(1)}{\mathrm{\Omega }}_{(1)}^{-1}\right)\mathit{\text{as}}n\to \infty .$

For a variable selection procedure, in addition to the oracle property, another property that is often desired is the grouping effect, meaning that the highly correlated covariates should have similar regression coefficients and be selected or deleted simultaneously. For the proposed BAR approach, it follows from ${\mathrm{\Omega }}_n={\mathit{X}}^{\prime }\mathit{X}$ that the (j, k) elements of the two matrices are equal, giving

$$\sum _{i=1}^n{\int }_0^{\tau }I\left(C_i\ge s\right)\left\{Z_{ij}(s)-{\overline{Z}}_j(s)\right\}\left\{Z_{ik}(s)-{\overline{Z}}_k(s)\right\}ds={\mathit{x}}_j^{\prime }{\mathit{x}}_k,$$

where x_j denotes the jth p-dimensional column vector of $\mathit{X}=\left({\mathit{x}}_1,\dots ,{\mathit{x}}_p\right),j,k=1,\dots ,p.$ This implies that the correlation between the original covariates Z_j and Z_k can be described by that between x_j and x_k and leads to the following grouping effect property.

Theorem 2.

Assume that X is standardized in the sense that ${\sum }_{j=1}^n{x}_{ij}=0and{\sum }_{j=1}^n{x}_{ij}^2=1.$ Then with probability tending to unity, the BAR estimator ${\widehat{\mathit{\beta }}}^{*}={\left({\widehat{\beta }}_1^{*},\dots ,{\widehat{\beta }}_p^{*}\right)}^{\prime }$ satisfies

$$\left|\frac{1}{{\widehat{\beta }}_i^{*}}-\frac{1}{{\widehat{\beta }}_j^{*}}\right|\le \frac{1}{{\lambda }_n}\Vert \mathit{y}\Vert \sqrt{2\left(1-{\rho }_{ij}\right)}$$

for those non-zero components ${\widehat{\beta }}_i^{*}\mathit{\text{and}}{\widehat{\beta }}_j^{*},$ where ρ_ij denotes the sample correlation coefficient of x_i and x_j.

The proofs of Theorems 1 and 2 are sketched in the Supporting Information Materials. To implement the procedure, one needs to choose the tuning parameter λ_n as well as ξ_n. To reduce the computational burden, we suggest employing the K-fold cross-validation, where K is a positive integer.

4. A SIMULATION STUDY

An extensive simulation study was conducted to investigate the performance of the proposed BAR regression estimation procedure. In the study, recurrent event data were generated from the mixed Poisson processes with the rate function given in (1) multiplied by gamma random variables with mean 1 and variance σ². The follow-up times C_i were generated from the uniform distribution over [0,4.5]. For the covariate Z, we considered several settings with different P-values, different locations for non-zero components, and different types of distributions, continuous or discrete, with the components being independent or correlated. For each scenario, we considered the sample size n = 100, 300, or 500 with 500 replications.

As comparisons, we also considered the approach of Chen & Wang (2013) with LASSO, ALASSO, and SCAD penalty functions. The LASSO and ALASSO were implemented by using the R package glmnet and the SCAD was realized by the R package ncvreg. For the selection of the tuning parameter, both packages use similar methods to select 50 candidates, and the largest candidates are max ${}_l\left|{\mathit{x}}_l^{\prime }\mathit{y}\right|,{\max }_l\left|w_l{\mathit{x}}_l^{\prime }\mathit{y}\right|,\text{and}{\max }_l\left|{\mathit{x}}_l^{\prime }\mathit{y}\right|$ for the LASSO, ALASSO, and SCAD, respectively. For the ALASSO, the weights $w_i=1/\left|{\beta }_i^{ols}\right|$ and γ = 1 were used as suggested by Zou (2006), where β^ols denotes the ordinary least squares estimator of β For the selection of the tuning parameter λ_n as well as ξ_n, we used the fivefold cross-validation and considered five candidate values for ξ_n chosen to be the equally spaced points over [0.01,10] in a logarithmic scale. For each ξ_n, 50 candidate values were considered for λ_n that are equally spaced over [ελ_max, λ_max] also in a logarithmic scale, where ε was set to be 0.001 and λ_max = ${\max }_{l}4{\left({\mathit{x}}_l^{\prime }\mathit{y}\right)}^2/\left({\mathit{x}}_l^{\prime }{\mathit{x}}_l\right)$ with x_l being the lth column of X.

Table 1 presents the covariate selection results with p = 9, where the true value of β₀ is (1,0,−1,0,0,0,0,0,0)′, μ₀(t) = 0.45t, and σ² = 0.5 or 1. Here the covariates were generated from the normal distribution and the correlation between Z_i and Z_j was set as ${\rho }^{|j-i|}$ with ρ = 0.1, 0.5, or 0.95. The table includes the average of the empirical values of the mean squared error (MSE) defined as ${\left(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0\right)}^{\prime }E\left(\mathit{Z}{\mathit{Z}}^{\prime }\right)\left(\widehat{\mathit{\beta }}-{\tilde{\mathit{\beta }}}_0\right),$ the average of the numbers of correctly selected zero coefficients (Corr), and the average of the numbers of incorrectly selected zero coefficients (Inco). It is seen that with respect to the correctly selected zero coefficients, the BAR always gave the best performance and the BAR and SCAD seemed to significantly outperform LASSO and ALASSO. On the incorrectly selected zero coefficients, no method gave overall better performance than the others. With respect to the MSE, the BAR yielded the least MSE and as expected, all methods gave better performance as the sample size increased.

TABLE 1:

Result on the selection of the normal covariates with p=9.

			n = 100			n = 300			n = 500
σ2	ρ	Method	MSE	Corr	Inco	MSE	Corr.	Inco.	MSE	Corr.	Inco.
0.5	0.1	BAR	0.586	0.829	0.084	0.136	0.922	0.000	0.082	0.919	0.000
		LASSO	0.722	0.545	0.071	0.230	0.518	0.000	0.149	0.531	0.000
		ALASSO	0.557	0.771	0.040	0.157	0.819	0.000	0.096	0.826	0.000
		SCAD	0.723	0.563	0.072	0.124	0.667	0.000	0.072	0.789	0.000
	0.5	BAR	0.493	0.823	0.098	0.125	0.913	0.001	0.070	0.909	0.000
		LASSO	0.594	0.557	0.104	0.195	0.525	0.000	0.117	0.539	0.000
		ALASSO	0.464	0.734	0.060	0.140	0.827	0.000	0.079	0.827	0.000
		SCAD	0.600	0.617	0.117	0.111	0.750	0.000	0.060	0.830	0.000
	0.9	BAR	0.196	0.759	0.179	0.051	0.869	0.012	0.030	0.881	0.000
		LASSO	0.202	0.615	0.176	0.071	0.535	0.000	0.047	0.561	0.000
		ALASSO	0.187	0.701	0.136	0.059	0.743	0.003	0.035	0.789	0.000
		SCAD	0.225	0.722	0.236	0.049	0.804	0.010	0.027	0.870	0.001
1	0.1	BAR	0.564	0.797	0.078	0.147	0.908	0.000	0.088	0.923	0.000
		LASSO	0.704	0.523	0.070	0.241	0.482	0.000	0.152	0.504	0.000
		ALASSO	0.547	0.758	0.041	0.167	0.797	0.000	0.100	0.836	0.000
		SCAD	0.715	0.550	0.075	0.136	0.651	0.000	0.076	0.787	0.000
	0.5	BAR	0.443	0.803	0.069	0.125	0.895	0.000	0.071	0.900	0.000
		LASSO	0.539	0.524	0.072	0.201	0.501	0.000	0.125	0.503	0.000
		ALASSO	0.430	0.736	0.042	0.144	0.790	0.001	0.085	0.791	0.000
		SCAD	0.558	0.602	0.085	0.113	0.739	0.001	0.064	0.812	0.000
	0.9	BAR	0.207	0.771	0.209	0.053	0.843	0.016	0.027	0.893	0.002
		LASSO	0.209	0.610	0.188	0.072	0.566	0.004	0.045	0.568	0.000
		ALASSO	0.190	0.697	0.144	0.059	0.749	0.005	0.033	0.796	0.000
		SCAD	0.234	0.718	0.241	0.050	0.797	0.020	0.023	0.886	0.000

Tables 2 and 3 give the results for the same setup as Table 1 but with different values for p and β₀. In Table 2, p = 50 and the first six components of β₀ were (1,0, −1,1,0, −1)′ with the other components being zero, while in Table 3, p = 100 and the first 30 components of β₀ were replicators of (1,0, −1)′ with the other components being zero. The results in Table 4 were obtained for the covariates whose first 3 components of Z followed the Bernoulli distribution with the probability of success being 0.5 and the other components were generated from the standard normal distribution with n = 100 and β₀ = (1,1,1,0,0,0,0,0,0)′. Also all components were assumed to be independent of each other and the other setup is the same as Table 1 except that the recurrent event processes followed either the homogeneous Poisson process (σ² = 0) or the mixed Poisson process with the variance of the gamma random variables being 1(σ² = 1). It is apparent that all tables gave similar conclusions to those given by Table 1 and again suggest that the proposed BAR procedure seems to give better performance than the other procedures on the covariate selection in general.

TABLE 2:

Result on the selection of the normal covariates with p=50.

0.5	0.1	BAR	3.199	0.947	0.540	0.559	0.966	0.020	0.279	0.981	0.001
		LASSO	3.299	0.843	0.516	1.132	0.693	0.014	0.701	0.679	0.000
		ALASSO	3.309	0.747	0.219	0.680	0.817	0.003	0.384	0.834	0.000
		SCAD	3.347	0.857	0.519	0.652	0.685	0.013	0.240	0.752	0.000
	0.5	BAR	2.059	0.949	0.576	0.403	0.965	0.031	0.184	0.982	0.001
		LASSO	2.135	0.858	0.597	0.863	0.660	0.046	0.481	0.636	0.001
		ALASSO	2.198	0.759	0.281	0.500	0.804	0.005	0.265	0.829	0.000
		SCAD	2.146	0.874	0.607	0.441	0.728	0.037	0.141	0.813	0.000
	0.9	BAR	0.682	0.950	0.660	0.212	0.965	0.253	0.098	0.970	0.060
		LASSO	0.638	0.883	0.691	0.316	0.763	0.262	0.193	0.679	0.070
		ALASSO	0.908	0.758	0.462	0.251	0.771	0.093	0.138	0.779	0.014
		SCAD	0.658	0.918	0.737	0.262	0.865	0.295	0.127	0.853	0.113
1	0.1	BAR	3.119	0.945	0.501	0.575	0.967	0.017	0.285	0.980	0.001
		LASSO	3.294	0.839	0.492	1.152	0.675	0.009	0.714	0.690	0.000
		ALASSO	3.226	0.739	0.197	0.715	0.802	0.001	0.385	0.837	0.000
		SCAD	3.305	0.850	0.493	0.653	0.677	0.010	0.250	0.758	0.000
	0.5	BAR	2.025	0.942	0.522	0.379	0.964	0.017	0.201	0.981	0.002
		LASSO	2.130	0.838	0.565	0.819	0.648	0.033	0.502	0.638	0.001
		ALASSO	2.206	0.744	0.262	0.490	0.799	0.001	0.272	0.831	0.000
		SCAD	2.134	0.860	0.572	0.390	0.719	0.020	0.153	0.806	0.000
	0.9	BAR	0.691	0.950	0.687	0.216	0.961	0.253	0.100	0.965	0.056
		LASSO	0.645	0.891	0.711	0.311	0.751	0.240	0.191	0.679	0.079
		ALASSO	0.883	0.759	0.474	0.249	0.766	0.092	0.135	0.770	0.013
		SCAD	0.664	0.926	0.766	0.270	0.864	0.300	0.126	0.851	0.118

TABLE 3:

Result on the selection of the normal covariates with p=100.

			n = 100			n = 300			n = 500
σ2	ρ	Method	MSE	Corr	Inco	MSE	Corr.	Inco.	MSE	Corr.	Inco.
0.5	0.1	BAR	22.903	0.970	0.931	16.480	0.954	0.713	7.110	0.889	0.182
		LASSO	20.336	0.917	0.867	16.222	0.813	0.584	8.877	0.541	0.124
		ALASSO	63.584	0.569	0.493	11.013	0.704	0.172	5.469	0.691	0.022
		SCAD	19.821	0.936	0.887	16.626	0.847	0.610	7.493	0.606	0.131
	0.5	BAR	10.771	0.979	0.957	8.305	0.960	0.755	3.307	0.900	0.153
		LASSO	9.660	0.941	0.917	8.678	0.877	0.765	5.325	0.567	0.261
		ALASSO	27.797	0.620	0.556	5.748	0.704	0.180	2.804	0.686	0.017
		SCAD	9.518	0.947	0.922	8.609	0.893	0.754	3.509	0.666	0.175
	0.9	BAR	2.566	0.973	0.946	1.848	0.971	0.850	1.307	0.934	0.551
		LASSO	2.282	0.940	0.912	1.899	0.896	0.800	1.492	0.739	0.513
		ALASSO	5.791	0.679	0.611	1.703	0.722	0.378	1.003	0.665	0.121
		SCAD	2.205	0.957	0.934	1.929	0.935	0.851	1.616	0.876	0.652
1	0.1	BAR	23.857	0.969	0.935	16.213	0.953	0.699	7.618	0.899	0.214
		LASSO	20.412	0.928	0.880	16.051	0.810	0.580	9.441	0.567	0.156
		ALASSO	63.446	0.578	0.500	10.684	0.705	0.160	5.585	0.698	0.025
		SCAD	19.897	0.939	0.891	16.395	0.848	0.606	8.117	0.625	0.159
	0.5	BAR	10.768	0.976	0.955	8.225	0.943	0.719	3.489	0.902	0.172
		LASSO	9.611	0.942	0.918	8.667	0.864	0.753	5.536	0.575	0.280
		ALASSO	26.281	0.651	0.581	5.724	0.680	0.164	2.919	0.681	0.019
		SCAD	9.470	0.951	0.928	8.614	0.894	0.762	3.611	0.666	0.180
	0.9	BAR	2.571	0.973	0.951	1.846	0.974	0.859	1.324	0.936	0.571
		LASSO	2.262	0.944	0.918	1.895	0.900	0.802	1.505	0.743	0.519
		ALASSO	5.757	0.692	0.640	1.695	0.736	0.394	0.993	0.663	0.121
		SCAD	2.232	0.958	0.933	1.938	0.939	0.859	1.643	0.884	0.681

TABLE 4:

Results on the selection of the Bernoulli covariates with p=9.

σ2		n = 100			n = 200			n = 300
		MSE	Corr	Inco	MSE	Corr	Inco	MSE	Corr	Inco
0	BAR	0.081	5.510	0.004	0.037	5.674	0.000	0.023	5.738	0.000
	LASSO	0.152	3.166	0.002	0.072	3.306	0.000	0.050	3.238	0.000
	ALASSO	0.143	4.252	0.002	0.059	4.700	0.000	0.040	4.724	0.000
	SCAD	0.101	5.330	0.004	0.041	5.546	0.000	0.031	5.488	0.000
1	BAR	0.786	5.108	0.974	0.427	5.054	0.372	0.264	5.104	0.158
	LASSO	0.780	4.186	0.916	0.515	3.392	0.256	0.353	3.050	0.060
	ALASSO	1.042	4.096	1.048	0.606	3.764	0.358	0.380	3.892	0.140
	SCAD	0.955	5.078	0.770	0.500	5.228	0.362	0.268	5.460	0.172

To assess the grouping ability of the methods discussed above, we performed a simulation study with p = 12, β₀ = (1,1,1,0.5,0.5,0.5,0,0,0,0,0,0), and n = 10,000; other settings are the same as before. A large sample size was used in order to reveal the grouping effect. For the covariate generation, we assumed that

$$Z_j=x_1+{\epsilon }_j,x_1~N\left(0,{50}^2\right),j=1,2,3;$$

$$Z_j=x_2+{\epsilon }_j,x_2~N\left(0,{50}^2\right),j=4,5,6;$$

$$Z_j~N\left(0,{50}^2\right),\text{independent with each other},j=7,\dots ,12;$$

where the ε_j are i.i.d. N(0, 0.025²). That is, the 12 covariates were from three different groups with the within-group correlations being nearly 1 and the between-group correlations being close to 0. Figure 1 shows the solution paths of the estimates given by the four methods. One can see the obvious grouping effect of the proposed BAR estimator when the tuning parameters are in the proper range. The method clearly selected the six relevant covariates and organized them into their two separate groups with almost the same coefficients within each group when log(λ_n) is roughly between 0.7 and 5.6. Although the estimate paths were unstable when λ is small, the cross-validation criterion can successfully find the tuning parameters inducing the grouping effect. In contrast, all three other methods showed little grouping effects as they selected only β₁ and β₄.

FIGURE 1:

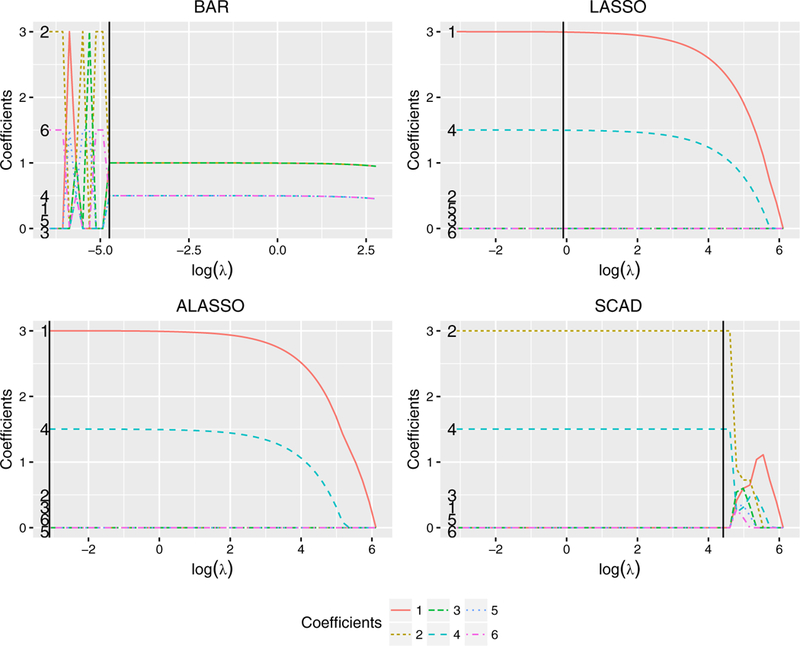
Path plots of the four estimates with the black solid vertical lines corresponding to the optimal tuning parameters based on the 5-fold cross-validation.

5. AN APPLICATION

We apply the proposed BAR regression estimation procedure to the recurrent event data arising from the chronic granulomatous disease (CGD) study discussed by Fleming & Harrington (1991), and Tong, Zhu, & Sun (2009), and Chen & Wang (2013) among others. This disease is a group of inherited rare disorders of the immune function characterized by recurrent pyogenic infections which are usually present in early life and may lead to death in childhood. The CGD study consists of 128 patients with CGD between October 1988 and March 1989. For each subject, the collected information includes the occurrence times of all recurrent serious infections during the study period. The study involves two treatments, a placebo (65) and gamma interferon (63). During the study period, 20 placebo patients and 7 treated patients had experienced at least one serious infection. A goal of the study is to investigate the ability of gamma interferon to reduce the occurrence rate of serious infections.

We use Z₁ to denote the treatment with Z₁ = 0 for the patients on gamma interferon and Z₁ = 1 otherwise. In addition to the treatment, the data set includes information on eight other covariates. Other variables considered include the pattern of inheritance (Z₂ = 0 for X-linked patients and Z₂ = 1 for autosomal recessive patients), the age, height, and weight of the patient (Z₃, Z₄, Z₅), the use of corticosteroids at time of study entry (Z₆ = 0 if yes and Z₆ = 1 if no), the use of prophylactics at time of study entry (Z₇ = 0 if yes and Z₇ = 1 if no), the patient’s gender (Z₈ = 1 if female and Z₈ = 0 if male), and the hospital category (US-NIH, US-other, Europe-Amsterdam, and Europe-other). For the last covariate, following Tong, Zhu, & Sun (2009) and Chen & Wang (2013), we describe it using three dummy variables as Z₉ = 1 for US-NIH and Z₉ = 0 otherwise, Z₁₀ = 1 for US-other and Z₁₀ = 0 otherwise, Z₁₁ = 1 for Europe-Amsterdam and Z₁₁ = 0 otherwise.

For the analysis, we consider both the selection of covariates or predictive factors and the estimation of their effects simultaneously. The results are given in Table 5 and here for comparison, we also included the results given by LASSO, ALASSO, SCAD, and the ordinary least squares procedure. Table 5 includes the selected covariates with their estimated effects and the estimated standard errors (in parentheses) for each method. It is seen that all procedures selected the treatment indicator, indicating that gamma interferon had significant effect on reducing the rate of serious infections. In addition, the BAR procedure suggested that the pattern of inheritance and the use of prophylactics at time of study entry seem to have some effects on the rate of serious infections, and also the infection rate appears to be different between the patients in the hospitals in the US-other group and other types of hospitals. Based on the ALASSO procedure, the patient’s age and the use of corticosteroids at the time of study entry could affect the infection rate. It is interesting to note that as LASSO and SCAD, the method given by Chen & Wang (2013) selected only the treatment indicator Z₁, while the results obtained here are similar to those given by Tong, Zhu, & Sun (2009) under the proportional rate model.

TABLE 5:

Results on covariate selection and their estimated effects for the CGD study.

	BAR	LASSO	ALASSO	SCAD	OLS
Z1	0.127 (0.043)	0.080 (0.038)	0.104 (0.016)	0.088 (0.036)	0.170 (0.050)
Z2	0.018 (0.004)	0	0	0	0.152(0.113)
Z3	0	0	−0.138 (0.020)	0	−0.409 (0.152)
Z4	0	0	0	0	0.081 (0.397)
Z5	0	0	0	0	0.105 (0.266)
Z6	0	0	−0.105 (0.016)	0	−0.343 (0.269)
Z7	0.027 (0.007)	0	0	0	0.140 (0.087)
Z8	0	0	0	0	−0.134 (0.111)
Z9	0	0	0	0	0.059 (0.065)
Z10	0.018 (0.004)	0	0	0	0.094 (0.069)
Z11	0	0	0	0	−0.051 (0.076)

To assess the appropriateness of the selected models by each of the four methods given above, as suggested by a reviewer, we performed model checking by using the statistic

$$D={\left\{\sum _{l=1}^L\sum _{i=1}^n{I}_i\left(t_l<C_i\right)\right\}}^{-1}\sum _{l=1}^L\sum _{i=1}^n{\left\{{\widehat{M}}_i\left(t_l\right)\right\}}^2$$

based on the sum of the mean squared residuals. Here ${\widehat{M}}_i(t)$ is defined as $M_i(t,\mathit{\beta })$ with the unknowns replaced by their estimates and the values ${\left\{t_l\right\}}_{l=1}^L$ denote all time points where the N_t(t) have jumps. Lin, Wei, & Ying (2001) employed a similar statistic for checking transformation models with the focus on estimation. The application of this statistic to the data yielded D = 0.4598, 0.4670, 0.4588, and 0.4662 for the models selected by the four methods in Table 5, respectively, and indicates that the four models are not significantly different.

6. DISCUSSION AND CONCLUDING REMARKS

This article discussed simultaneous covariate selection and estimation of covariate effects for the event history study that yields recurrent event data. As mentioned above, only limited research exists for covariate selection in Tong, Zhu, & Sun (2009) and Chen & Wang (2013) due to the special data structures and the difficulties involved. We presented a BAR regression estimation procedure that can not only allow for estimation and variable selection simultaneously but also accommodate the clustering effect when covariates are highly correlated. The oracle property of the proposed approach was established, and the simulation study indicated that the proposed method can have better performance than the existing procedures.

There exist several directions for future research. Here we have focused on the underlying recurrent event process that follows the additive rate model (1). It would be useful to generalize the proposed method to the situation where the event process may follow other models such as the proportional rate model or the semiparametric transformation model. Another extension is to consider a terminal event, which corresponds to the situation where the follow-up time C_i may be related to $N_i^{*}(t).$ In this case, it is clear that the proposed method may not be valid and could give biased results (Cook & Lawless, 2007).

Our discussion assumes that the dimension of covariates p is fixed. It would be interesting to consider the case where p is larger than the sample size n. Although the idea described here may still apply, the implementation procedure would not work due to the irregularity of some needed matrices.

APPENDIX: Regularity conditions

The following are the regularity conditions needed for the asymptotic properties of ${\widehat{\mathit{\beta }}}^{*}$.

(C1) $\{N_i^{*}(\cdot ),C_i,{\mathit{Z}}_{{}^i}\},\text{i=1,}\mathrm{...}\text{,}n\text{,}$ are independent and identically distributed.

(C2) $P(Ci\ge \tau )>0$, for i = 1,..., n.

(C3) $N_i(\tau )$ is bounded by a constant.

(C4) The matrix Ώ is positive definite.

(C5) The Z_i(·)’s have bounded total variations, that is, $\{\parallel {\mathit{Z}}_i(0)\parallel \}+{\int }_0^{\tau }\parallel d{\mathit{Z}}_i(t)\parallel \}$ is bounded for all i, where ||Z_i(·)|| is the Euclidean metric of the vector Z_i(·).

(C6) $c^{-1}<{\lambda }_{\min }(\mathrm{\Omega })\le {\lambda }_{\max }(\mathrm{\Omega })<c$, for all n > 0 and some large constant c > 1, where λ(Q) stands for the eigenvalues of the matrix Q.

(C7) ${\lambda }_n\to \infty \text{and}{\lambda }_n/\sqrt{n}\to 0\text{as}n\to \infty$