Accuracy of Commonly Used Age-Predicted Maximal Heart Rate Equations

Abstract

Age-predicted maximal heart rate (APMHR) is an essential measure for healthcare professionals in determining cardiovascular response to exercise testing, exertion, and prescription. Although multiple APMHR prediction equations have been validated for specific populations, the accuracy of each within a general population requires testing. We aimed to determine which APMHR equation (Fox, Gellish, Gulati, Tanaka, Arena, Astrand, Nes, Fairbarn) most accurately predicts max heart rate (HR_max) in a general population. HR_max from 99 graded treadmill exercise tests (GXT) were measured. GXTs ended upon volitional fatigue and were only included for analysis if RER > 1.10. Individual paired t-test were performed to determine if significant differences existed between measured and predicted HR_max, along with root mean square errors for each equation. Bland-Altman plots were constructed to determine agreement between equations and measured HR_max. Significant differences between measured and predicted HRmax were found for the Gulati, Astrand, Nes, and Fairbarn (male) equations (p < 0.05). Bland-Altman plots revealed wide limits of agreement for all nine APMHR equations, suggesting poor agreement between measured and predicted HR_max. Proportional bias indicates that prediction equations under and overestimated HR_max in individuals with lower and higher measured HR_max, respectively, with the exception of the Fox equation. All equations used in this study show poor agreement between measured HR_max and APMHR. The Fox equation may represent the best option for a general population as it is less likely to under or overestimate based on individual HR_max. Individuals should use data from GXTs to determine HR_max when applicable to ensure accuracy.

INTRODUCTION

Maximal heart rate (HR_max) is an essential measure for health care professionals in determining cardiovascular compliance to exercise testing (7), exertion during exercise (10), and exercise prescription (2,5,16,33). Graded exercise testing (GXT) involving gas exchange analysis and ventilation measurements is recognized as the gold standard for measuring (HR_max) (1); however, access to this equipment is not always available and may be contraindicated due to individuals age, functional capabilities, or health status. An alternative approach to estimate HR_max is to utilize age predicted maximal heart rate (APMHR) using the equation HR_max = 220-Age. This is the most commonly used APMHR and was proposed by Fox et al. in 1971 (14). This equation, however, has been reported to have a standard deviation of between 10 and 12 bpm (15), as well as significantly over and underestimating HR_max in younger and older adults, respectively (17, 29). Although the limited predictive accuracy of this equation has been documented (11, 24, 26, 27, 31, 34, 35) it is still used in clinical settings and published in resources by well-established organizations in the field (13).

In recent years, additional age-based regression equations have been proposed; however, each from specific populations (3, 4, 12, 17, 18, 23, 29). These studies have either been completed using meta-analyses in conjunction with laboratory studies (29), or with retrospective designs (3, 17, 18, 23) to include larger sample sizes and improve the accuracy of their prediction equations. At present, five prediction equations (4, 14, 17, 18, 29) are presented in the American College of Sports Medicine’s Guidelines for Exercise Testing and Prescription (2) and are regarded as valid for their respective populations (16). Alternative equations exist, including those by Arena et al. (3), Nes et al. (23), and Fairbarn et al. sex specific equations (12), all of which utilized gas analysis to ensure effort. Not all equations used in this study were derived using gas analysis (17, 18), which may influence the predictive accuracy of these equations when used in a sample with documented exhaustion.

Despite this, it remains unclear which of these proposed equations is most robust to predict HR_max in a diverse population. Many clinicians work with a wide variety of patients on a daily basis, and therefore, it is important to test which equation can most accurately predict HR_max in a diverse range of individuals. Therefore, the purpose of this study is to assess the agreement between HR_max as measured by nine previously studied APMHR equations and HR_max measured during a GXT.

METHODS

Participants

Data was collected from 134 participants who completed GXTs from May 2017, to October 2019 at a sports performance clinic. All participants were apparently healthy and free of any medical condition that would prevent them from completing the GXT safely and signed an informed consent prior to testing approved by the institution’s IRB. This research was carried out fully in accordance to the ethical standards of the International Journal of Exercise Science (20).

Protocol

The tests were administered according to a custom protocol used to assess maximal oxygen uptake during a treadmill (Desmo, Woodway) GXT. Gas exchange was analyzed using a metabolic cart (TrueOne® 2400, Parvo Medics, USA), and heart rate was continuously monitored using a wearable chest monitor (Polar H10, Polar Electro, Kempele, Finland). Participants were asked to refrain from consuming caffeine the day prior to the test in pre-test instructions sent by email. Each participant performed an incremental incline protocol, lasting 8–12 minutes. Before starting, the test protocol was explained to each participant, after which they completed a brief warmup of 3–5 minutes. During testing, participants ran at a comfortable pace (equivalent to their 5K running pace). Starting at a 0% incline, the gradient was increased 2% every two minutes until volitional exhaustion. At the end of each stage, participants were asked to rate their perception of effort (RPE) using 10-level perceived exertional scale (30). Maximal heart rate, maximal oxygen uptake (VO_2max), and respiratory exchange ratio (RER) were determined as the maximum value achieved during the GXT. Individuals who did not achieve a RER >1.10 were excluded from the analysis to ensure maximal exertion was achieved (6, 19). This left a final sample of ninety-nine participants (male: n = 67, age = 37.3 ± 11.8 yrs, female: n = 32, age = 39.9 ± 13.5).

Statistical Analysis

The mean and standard deviation (SD) of participants’ demographics and GXT measures (VO_2max, HR_max, and RER achieved during testing) were calculated. Individual paired t-test were performed to determine if significant differences existed between HRmax as measured during GXT and calculated using prediction equations (prediction equations are presented in Table 2). Respective subgroups were compared only with each other. For example, the Gulati equation designed for females was only compared with GXT HR_max from female subjects etc. To assess agreement, Bland-Altman plots were constructed between GXT measured and predicted HR_max from each APMHR equation to detect systematic bias and error (8). Confidence intervals for bias and limits of agreements were also calculated to determine the precision of estimated limits of agreement (9). Proportional bias was assessed by linear regression between the averages and the differences in the results obtained with each APMHR method. Furthermore, typical measurement error was assessed with root mean square error (RMSE). Alpha was set at 0.05 for statistical significance. All statistical analysis was performed using R (25) (R Core Team; Vienna, Austria).

Table 2.

Mean and 95% confidence intervals for maximal heart rate, bias, and lower (LLOA) and upper limits of agreement (ULOA, and root mean square error (RMSE).

		Max Heart Rate	Prediction Equation	Bias	LLOA	ULOA	RMSE
GXT	All	181.67 (179.03, 184.30)
	Male	182.93 (179.89, 185.96)
	Female	179.03 (173.77, 184.30)
Fox	All	181.82 (179.35, 184.28)	HRmax = 220 – Age	−0.15 (−2.49, 2.18)	−23.11 (−27.15, −19.06)	22.80 (18.76, 26.85)	11.65
Gellish	All	181.32 (179.67, 182.97)	HRmax = 207 – 0.7 ·Age	0.35 (−1.80, 2.50)	−20.74 (−24.46, −17.03)	21.44 (17.72, 25.16)	10.71
Gulati	Female	170.86* (166.58, 175.13)	HRmax = 206 – 0.88 · Age	8.18 (3.67, 12.68)	−16.33 (−24.14, −8.52)	32.68 (24.87, 40.49)	14.77
Tanaka	All	181.27 (179.55, 183.00)	HRmax = 208 – 0.7 · Age	0.39 (−1.76, 2.55)	−20.75 (−24.48, −17.02)	21.54 (17.81, 25.26)	10.74
Arena	All	181.81 (180.03, 183.58)	HRmax = 209.3 – 0.72 · Age	−0.14 (−2.30, 2.01)	−21.33 (−25.07, −17.60)	21.05 (17.31, 24.78)	10.75
Astrand	All	184.53* (182.46, 186.6)	HRmax = 216.6 – 0.84 · Age	−2.86 (−5.07, −0.65)	−24.57 (−28.39, −20.74)	18.85 (15.02, 22.67)	11.38
Nes	All	186.56* (184.99, 188.14)	HRmax = 211 – 0.64 · Age	−4.90 (−7.04, −2.75)	−25.96 (−29.66, −22.25)	16.17 (12.46, 19.88)	11.76
Fairbarn	Male	177.45* (175.48, 179.43)	HRmax = 208 – 0.8 · Age	4.80 (2.28, 7.32)	−15.48 (−19.85, −11.11)	25.08 (20.71, 29.45)	11.34
	Female	176.95 (175.39, 178.50)	HRmax = 201 – 0.63 · Age	3.19 (−1.13, 7.52)	−20.32 (−27.81, −12.83)	26.70 (19.21, 34.20)	12.23

Note.

^*Indicates significant difference (p < 0.05) from maximal heart rate in respective subgroup (i.e. GXT female, and Gulati female).

Units of bias, LLOA, ULOA and RMSE are beats per minute.

RESULTS

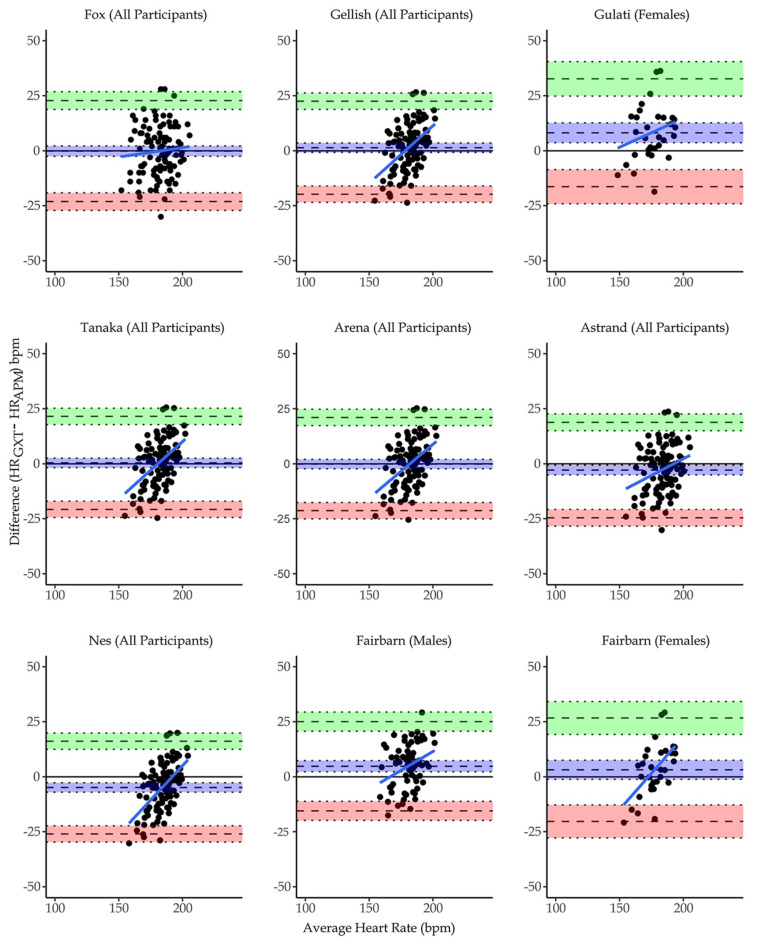
Descriptive measures of participants’ demographics and GXT outcomes are presented in Table 1. Significant differences between measured and predicted HRmax were found for the Gulati, Astrand, Nes, and Fairbarn (male) equations (p < 0.05). Analysis of Bland-Altman plots revealed minimal bias with similar limits of agreement for the Fox, Gellish, Arena, and Tanaka equations while the remainder showed much greater bias (Table 2). The range between upper and lower limits of agreement (mean: 43.88 ± 2.79 bpm) and confidence intervals of the limits of agreement (9.43 ± 3.36 bpm) were large for all APMHRs. Additionally, the slope of the plots show that prediction equations underestimated HR_max in individuals with lower measured HR_max and vice versa, with the Fox equation showing the smallest amount of proportional bias. Root mean square error showed similar results to bias, in that the Gulati equation showed much greater RMSE compared to all other prediction equations.

Table 1.

Descriptive measures (mean ± standard deviation) of participants. Range (min, max) included for maximal heart rate.

	Male	Female	Total
n	67	32	99
Age (years)	37.3 ± 11.8	39.9 ± 13.5	38.2 ± 12.4
BMI (kg/m2)	26.4 ± 3.9	24.0 ± 3.2	25.6 ± 3.9
VO2max (mL/kg/min)	48.6 ± 10.2	42.1 ± 8.9	46.5 ± 10.3
Maximal RER	1.2 ± 01	1.2 ± 0.1	1.2 ± 0.1

DISCUSSION

This study examined the predictive accuracy of nine commonly used APMHR equations in a diverse sample of individuals. Our interest was to assess which formula most accurately predicted HR_max in a diverse sample of individuals as a medical or exercise professional may encounter a wide variety of patients or clients in many healthcare and/or fitness settings. The Gulati (206–0.88*age), Astrand (216.6-0.84*age), Nes (211-0.64*age), and Fairbarn male (208-0.8*age) equations all produced results that were significantly different from HR_max measured during GXT (p < .001). Each showed a large bias and wide ranges between limits of agreement suggesting poor agreement with HR_max measured during GXT. We also wanted to assess the accuracy of each formula for its intended population. The Gulati (18) and Fairbarn (12) equations were derived for use only in females, as sex differences have been shown to influence the predictive accuracy of APMHR equations (18, 28, 35). Interestingly, the Gulati formula showed the greatest bias and RMSE of all nine equations.

Our results suggest that the other formulas, Fox (220-age), Gellish (207–0.7*age), Tanaka (208 – 0.7*age), Arena (209.3–0.72*age), and Fairbarn female (201-0.63*age) have similar limits of agreement with HR_max measured during GXT (Figure 1). Although each formula showed minimal bias (with the exception of the female Fairbarn equation), wide limits of agreement suggest that all nine APMHR equations have poor agreement with HRmax measured with the metabolic cart. Additionally, limits of agreement had wide confidence intervals suggesting the possibility of even greater disagreement between measures. High RMSE values for all equations also support the lack of agreement between predicted and measured HR_max regardless of equation. Therefore, these equations all produce poor predictions with unsatisfactory limits of agreement. All equation plots reveal non-zero slopes, suggesting each proportional bias is present in each, however, the Fox equation may be the best APMHR for a diverse population as the trendline shows it is less likely to under or overestimate based on individual HR_max. In comparison, the proportional bias evident in the other equations show that those with lower fitness and/or elderly individuals will have HR_max consistently underestimated, and fitter and/or younger individuals will have HR_max consistently overestimated.

Figure 1.

Bland-Altman plots showing agreement between measured and predicted HRmax. The vertical axes represent the difference in heart rate (bpm) between HR_max during GXT and HR_max as predicted by each equation. The horizontal axes represent the mathematical average for each participants HR_max measurements. The middle dashed line represents bias, while the upper and lower dashed lines represent the upper (+2SD) and lower (−2SD) limits of agreement. The dotted lines surrounding each dashed line represent the confidence intervals of the bias (middle), upper, and lower levels of agreement.

The strength of this study is the use of a diverse sample that better represents the range of individuals a medical or exercise professional may encounter on a daily basis, as opposed to narrowly defined populations. Additionally, RER was directly measured, which has not always been the case in prior studies used to construct APMHR equations (17, 18). Possible limitations include sample size and fitness level. Our sample only contained data from 99 subjects aged 17–67, with the majority between 26–51 years old. Fitness level may also affect HR_max when comparing individuals of the same age and sex (35). This could stem from cardiac remodeling commonly seen in aerobically trained individuals (22, 32). The average VO_2max of all subjects was 46.5 ± 10.3mL/kg/min, showing our sample was made of individuals with above average cardiorespiratory fitness (21).

This study demonstrates that these nine APMHR equations all have poor agreement between measured HR_max and APMHR, and produce poor HR_max predictions. Of the available APMHR equations, the Fox equation may represent the best option for a general population as it is less likely to under or overestimate based on individual HR_max. It also demonstrates that the Gulati equation should only be used on the population was derived from (i.e., asymptomatic women). Based on these results, clinicians should use professional judgement when prescribing exercise or rehabilitation programs based on these HR_max values. Future research should be done with stringent populations that include large samples to prevent the influence of covariates when developing APMHR equations.