Efficiency of the Wilks and IPF Formulas at Comparing Maximal Strength Regardless of Bodyweight through Analysis of the Open Powerlifting Database

Abstract

The purpose of this study was to measure the efficiency of the Wilks and International Powerlifting Federation (IPF) Formulas at comparing powerlifting performance (total) between weight classes of the same sex (men and women) and division (classic and equipped) in order to determine the champion of champions. The Open Powerlifting database was downloaded (June 21st, 2019), filtered (Python) and analyzed (IBM SPSS). Single factor ANOVA revealed that the total (kg) was able to compare 3 out of the 98 weight class comparison possibilities (3.1%), the total ratio was able to compare 5 of the 98 weight class comparison possibilities (5.1%), the Wilks Formula was able to compare 53 of the 98 weight class comparison possibilities (54.1%) and that the IPF formula was able to compare 51 of the 98 weight class comparison possibilities (52%). Making the Wilks slightly more efficient than the IPF Formula (54.1% > 52%) at determining the champion of champions. Results also show that the IPF Formula is more efficient at comparing women’s weight classes and that the Wilks Formula is more efficient at comparing men’s weight classes, for both divisions. Results could not validate the IPF’s decision to replace the Wilks by the IPF Formula. Subjects’ performances (kg, ratio, % of the event on the total, Wilks and IPF points) presented for each weight class per sex and division coming from a total of 26,472 open powerlifters could be utilized by practitioners. Further research should be directed towards updating the constants of both formulas.

INTRODUCTION

Powerlifting is a sport where competitors test their maximal strength through three events: the back squat, the bench press and the deadlift (6). Since 2012, the International Powerlifting Federation (IPF) and its affiliated federations offer powerlifters to compete in two divisions: classic and equipped (8, 10). Both divisions can be distinguished through the supportive equipment allowed in competition. The additional supportive equipment permitted in the equipped division are supportive lifting suits for the squat and the deadlift, as well as knee wraps for the squat and a bench shirt for the bench press (10). Unsurprisingly, the extra supportive equipment permitted in the equipped division helps competitors lift more weight (14).

In all of the powerlifting events, participants from each of the federated weight classes have three attempts to lift the heaviest weight possible while respecting judging criteria. The winner of each weight class is determined by the total of the best completed attempt of each event. As of January 1st, 2019, the validated Wilks Formula (16), which had been utilized for many years to determine the winner between weight classes of the same sex and division (champion of champions), was replaced by the new IPF Formula within the IPF and all of its underlying federations (9).

These formulas were created to compensate the curvilinear relationship between body weight and maximal strength (16). The Wilks formula was introduced in 1995 at a time where, there was no differentiation between classic and equipped lifting and was created through regression analysis of a 5,000 ranked powerlifters sample, then converted into a quadratic and spliced into coefficients (18) The new IPF Formula was designed to differentiate “classic and equipped” lifters and was based on a larger sample that consisted of 20,000 individual best performances that included a higher number of female performances and competitors of modern-day powerlifting (9).

At the time the present study was conducted, various studies had already attempted to develop systems to be able to compare powerlifters’ performances, whether it was according to their Z-score (2), to their differences in body mass (3), to their allometrics (4) or body size (11). Furthermore, the Wilks Formula has been validated (16) by examination of systemic and residual bias through observation of the trends of the curvilinear relationship between weight lifted and body weight presented in scatterplots. In contrast, to the best of our knowledge, no study has been published validating the IPF Formula. Lastly, the largest powerlifting database analysis published in the scientific literature was conducted by Ball and Weidman on June 11, 2016 USA Powerlifting (15) database including competition results of over 20,000 subjects (1).

Thus, the purpose of this study was to analyze the recently updated Open Powerlifting (13) database in order to compare the efficiency of the already established Wilks Formula to the new IPF Formula in determining the champion of champions for powerlifters of the same sex and division. Consequently, the hypothesis of this study was that the new IPF Formula would be more efficient than the Wilks Formula at comparing results between weight classes of the same sex and division to determine the champion of champions. The results presented in this study could help validate the decision taken by the IPF committee, which was to replace the Wilks by the IPF Formula and also present which of the official weight classes are advantaged by each of the formulas. Furthermore, this study was conducted immediately following the 2019 World Classic Powerlifting Championships that took place from June 3rd to June 15th in Helsingborg, Sweden, which was the first Classic World Championships to utilize the new IPF formula, in order to include results from the competition in the sample utilized for the analysis (8–10).

METHODS

Participants

This research was carried out fully in accordance to the ethical standards of the International Journal of Exercise Science (12). No ethical certificate was obtained through the institutional review board as all the information analyzed in this study was publicly accessible through the open Powerlifting website (13) as well as on the powerlifting federations’ websites. Subject’s characteristics from this article present maximum, minimum, means and standard deviations in kg, as well as ratios (weight lifted/body weight), percentage of each event on the total, Wilks and IPF points for all three powerlifting events and the total, for each weight class per sex and their respective division coming from 26,472 powerlifters’ best performance (view supplemental material). Sample characteristics are presented in tables 1 to 3.

Table 1.

Sample Distribution by Sex and Division

Sex	Division		Total
	Classic	Single-Ply
Women	7867	1182	9049
Men	14479	2944	17423
Total	22346	4126	26472

Table 2.

Sample Age Distribution and Mean

Age	Frequency	Percent
24	3394	12.8
25	2825	10.7
26	2596	9.8
27	2429	9.2
28	2271	8.6
29	2004	7.6
30	1722	6.5
31	1617	6.1
32	1411	5.3
33	1314	5.0
34	1137	4.3
35	984	3.7
36	885	3.3
37	843	3.2
38	1040	3.9
Total	26472	100.0

Table 3.

Sample Distribution by Powerlifting Federation

Federation	Database String	n	Percent
Asociación Española de Powerlifting	AEP	392	1.5
African Powerlifting Federation	AfricanPF	42	0.2
Australian Powerlifting Union	APU	182	0.7
Asian Powerlifting Federation	AsianPF	309	1.2
British Powerlifting	BP	122	0.5
Bundesverband Deutscher Kraftdreikämpf	BVDK	931	3.5
Confederação Brasileira de Levantamentos Básicos	CBLB	6	0.0
Commonwealth Powerlifting Federation	CommonwealthPF	72	0.3
Canadian Powerlifting Union	CPU	436	1.6
Český svaz silového trojboje	CSST	353	1.3
Danish IPF affiliate	DSF	419	1.6
English Powerlifting Association	EPA	342	1.3
European Powerlifting Federation	EPF	520	2.0
Federación Argentina de Levantamiento de Potencia	FALPO	36	0.1
Federación Mexicana de Powerlifting	FEMEPO	20	0.1
Federación Sudamericana de Powerlifting	FESUPO	159	0.6
Federation Francaise de Force	FFForce	114	0.4
Powerlifting Federation of Russia	FPR	1654	6.2
Croatian IPF affiliate	HPLS	80	0.3
International Powerlifting Federation	IPF	638	2.4
Irish Powerlifting Federation	IrishPF	74	0.3
Japan Powerlifting Federation	JPA	606	2.3
Kazakhstan IPF affiliate	KPF	462	1.7
Icelandic IPF affiliate	KRAFT	109	0.4
North American Powerlifting Federation	NAPF	182	0.7
Nauru Powerlifting Federation	NauruPF	45	0.2
Northern Ireland Powerlifting Federation	NIPF	87	0.3
Nordic Powerlifting Federation	NordicPF	13	0.0
National Powerlifting Association of the Netherlands	NPB	27	0.1
Norwegian IPF affiliate	NSF	86	0.3
New Zealand Powerlifting Federation	NZPF	702	2.7
Oceania Regional Powerlifting Federation	ORPF	56	0.2
Powerlifting Association of the Philippines	PAP	10	0.0
Powerlifting zveza Slovenije	PLZS	63	0.2
Polish IPF affiliate	PZKFiTS	37	0.1
South African Powerlifting Federation	SAPF	133	0.5
Scottish Powerlifting	ScottishPL	80	0.3
Swedish IPF affiliate	SSF	86	0.3
Finnish IPF affiliate	SVNL	570	2.2
Swiss IPF affiliate	SwissPL	70	0.3
Thai IPF affiliate	ThaiPF	47	0.2
Ukrainian Powerlifting Federation	UkrainePF	445	1.7
USA Powerlifting	USAPL	15645	59.1
Welsh Powerlifting Association	WelshPA	10	0.0
Total		26472	100.0

Protocol

The study design of this descriptive quantitative applied research consisted of analyzing the results from all Open powerlifters (24 to 38 yo) competing in the IPF (8) affiliated federations present (44 out of 97) in the Open Powerlifting (13) database in order to compare the Wilks and the IPF formulas as well as to present the strength (kg, ratios, percentage of each event on the total, Wilks and IPF pts) per weight classes, specific to their gender and division.

The Open Powerlifting raw database was downloaded as a Comma Separated Values (CSV) file on June 21st by a qualified software developer graduated in software engineering from the École de Technologie Supérieure (ÉTS), Montreal, Quebec, Canada as he was mandated to filter the database. Many volunteers gathered the Open Powerlifting database manually from the included individual federations over the years (5 years at the time the analysis was conducted). The database is presented through the Open Powerlifting Website (13) and its content is verified through a validation program. Both, the database and the validation program, were developed by the volunteer contributors.

A data filtering script was written in Python (version 3.6.8 for Linux) to create a My Structured Query Language (MySQL) (version 8.0.16 for Linux on x86_64 MySQL Community Server – GPL) database in which it will store all the raw data contained in the provided CSV file. All software were updated on June 21st prior to filtering data.

The first part of the Python script validated all entries (row) in the CSV file. For every row, the script verified that there was a valid total (Total > 0). If there was no total presented for a row, a total was calculated with the powerlifter’s highest successful attempt in each event. The script inserted a valid weight class based on the provided bodyweight column. Once all the data was saved in the database (1,489,461 entries), the script filtered the database using SQL queries in the following specific order.

All entries that were not coming from an IPF affiliated federation (964,965) were removed from the database. All entries presenting competition result prior to January 1st, 2012 (217,550) were removed from the database. All entries presenting non-full-meet competition results (71,477) were removed from the database. All entries presenting powerlifters aged under 24 and over 38 years old (170,761) were removed from the database.; retaining only the powerlifters competing in the Open age category. Additionally, all entries that did not present the powerlifter’s age were removed. All entries presenting an incomplete powerlifting performance (2,949) were removed (meaning the powerlifter had to complete at least one attempt in each of the 3 events). All entries not specifying the division in which the total was completed (7) were removed from the database. All entries not presenting the powerlifter’s body weight (43) were removed from the database. All entries not presenting the Wilks or IPF points (105) were removed from the database. If a powerlifter presented multiple (more than one) competition results, the retained entry was the one presenting the highest total in kg (35,222 entries were removed). If two entries presented the same total for the same powerlifter, the script retained the first one occurring in the dataset. After all the following steps were completed, the script extracted the resulting database into a new CSV file that would then be imported into SPSS for the statistical analysis.

The database filtration process was strict in order to eliminate erroneous or incomplete competition results. For example, a powerlifter entered in the Open category could have been discarded because his age wasn’t present. This measure was taken because of a preliminary examination that presented that the age category column did not follow the IPF’s age category rule and was stated to not be reliable by the contacted Open Powerlifting Contributor. A true Open powerlifter will start competing in the Open category January 1st of the year he turns 24 and will compete until he is 39 (Masters 1 will start January 1st of the year he turns 40) (10). Therefore, 23 years of age entries were discarded due to the possibility of the lifter still being a Junior competitor and 39 years of age entries were discarded due to the possibility of the lifter being a Master 1 competitor. Furthermore, utilizing only powerlifters from the Open age category would make the sample most representative of well-developed competitive powerlifters and increase its homogeneity. As well, utilizing only IPF affiliated federation results would permit to increase competition results reliability by decreasing between-subjects standard error of measurement (7) as the IPF and its underlying federations are considered to have higher judging standards in all of the three powerlifting events (10). Not to mention, the IPF is also affiliated to the World Anti-Doping Agency (19) and these results would help compare athletes competing under drug-tested federations (5), which also increases results reliability.

The individual’s best performance was considered the one presenting the highest total in kg as authors could not utilize the Wilks or IPF points to measure performance as these were going to get reviewed through the statistical analysis. Then again, the IPF Formula document available on the IPF website states that the dataset utilized to create the formula was based on 20,000 individual best performances, but does not specify how the best performance was determined and does not present any detail about their sample distribution (9).

Statistical Analysis

Statistical analysis was executed using IBM SPSS Statistics for Windows version 25 on a total of 26,472 entries (powerlifters). Mean, standard deviation, maximum and minimum for each weight class per sex and division are presented for the performance scores expressed in kg, ratio (weight lifted/body weight), percentage of the event on the total, Wilks and IPF points.

A single factor (weight class) ANOVA was utilized to compare between weight classes scores (kg, ratios, Wilks and IPF points) of the same sex and division. When a significant within difference was detected, a post-hoc analysis was performed by using the least significant difference (LSD) for pairwise comparisons. This analysis was conducted to verify if group (weight classes) scores from the same sex and division were significantly different from one another. This was done to validate which of the four methods (weight lifted, ratio, Wilks and IPF points) was the most efficient to compare results between weight classes of the same sex and division (men’s classic, men’s equipped, women’s classic, women’s equipped) in order to determine the champion of champions. Therefore, the method with the least significant differences between weight classes of the same sex and division would be considered the most efficient. Presenting 21 weight class comparison possibilities between women of the same division and 28 weight class comparison possibilities between men of the same division, which makes it a total of 98 weight class comparison possibilities for each method (Classic + Equipped).

One could criticize that conducting that many post-hoc analyses could lead to a type one error, and would normally recommend decreasing the statistical significance (alpha) with an appropriate correction (ex: p < 0.01), however, since the goal of the analysis was to compile the comparisons that were not statistically different, increasing the statistical significance (p < 0.05) made this approach more conservative.

The unpaired Student’s t test was utilized to compare scores between classic and equipped lifters (division) of the same sex and weight class. No comparisons in between sexes were performed. Statistical significance was set at p < 0.05.

Here are the two formulas:

$$\text{Wilks\hspace{0.17em}Points}=\text{Weight\hspace{0.17em}lifted\hspace{0.17em}in\hspace{0.17em}kg}*(\frac{500}{\text{a}+\text{bx}+{\text{cx}}^2+{\text{dx}}^3+{\text{ex}}^4+{\text{fx}}^5})$$

x: Bodyweight in kg

$$\text{IPF\hspace{0.17em}Points}=500+100*\frac{(\text{Total}-(\text{C}1*\text{LN}(\text{Bodyweight})-\text{C}2))}{(\text{C}3*\text{LN}(\text{Bodyweight})-\text{C}4)}$$

Constants for the Wilks formula are nowhere to be found other than on the Wikipedia website (18) but were confirmed through personal communication with Robert Wilks (19). Constants for the IPF Formula can be found in the IPF Formula document from the IPF website (8, 9).

RESULTS

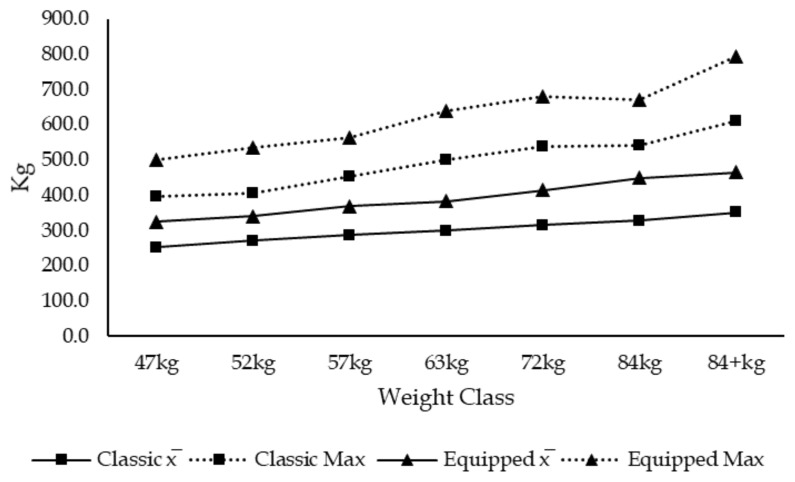
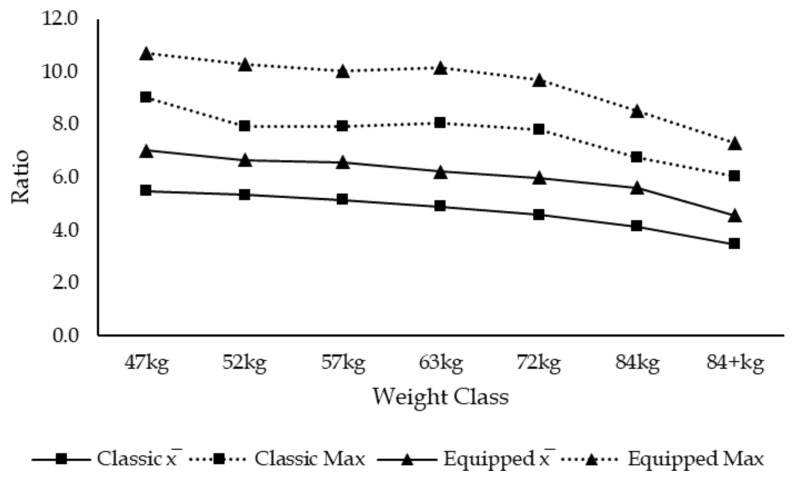
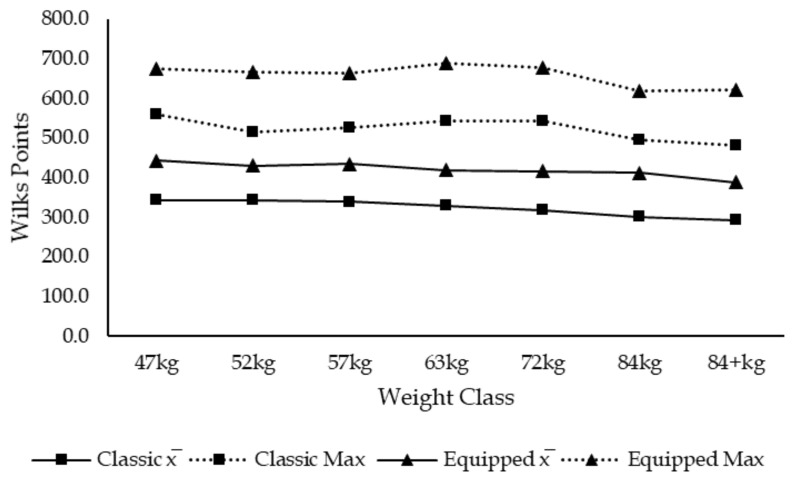
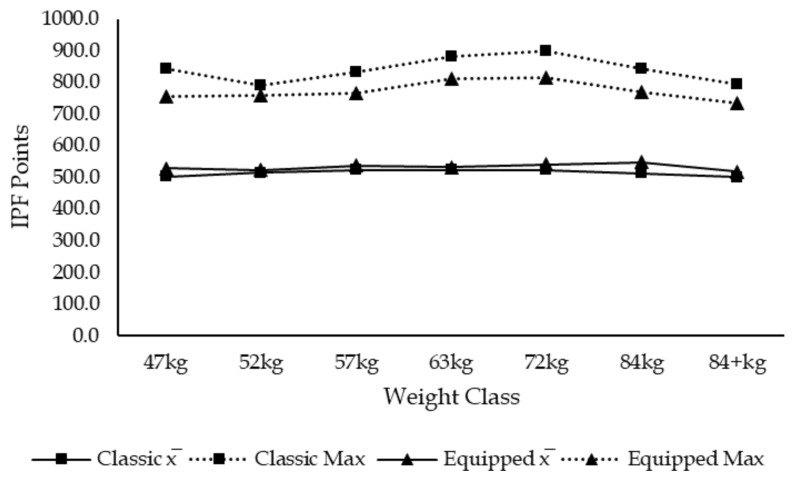
Results from the single factor ANOVA revealed significant differences between groups of the same sex and division. Results from the Post hoc analysis revealed that the total in absolute weight lifted (kg) was able to compare 3 out of the 98 weight class comparison possibilities (3.1%), that the total ratio was able to compare 5 out of the 98 weight class comparison possibilities (5.1%), that the Wilks Formula was able to compare 53 out of the 98 weight class comparison possibilities (54.1%) and that the new IPF Formula was able to compare 51 out of the 98 weight class comparison possibilities (52%) (view tables 4 and 5). Ultimately, making the Wilks formula the most efficient at determining the champion of champions as it was able to compare more weight classes of the same sex and division. Furthermore, results show that the IPF Formula is more appropriate to determine women’s champion of champions as it was able to compare the most weight classes of the same division for both divisions (classic and equipped) and that the Wilks formula is more appropriate to determine men’s champion of champions as it was able to compare the most weight classes of the same division for both divisions (view figures 1 to 8 which present means and maximums for each weight class of their respective sex and division as comparing means helps illustrate which weight classes are advantaged by each formula and the maximum determines the winner for each respective weight class).

Table 4.

Women’s Post-Hoc ANOVA p-Values on total

		Kg		Ratios		Wilks Points		IPF Points
		Classic	Equipped	Classic	Equipped	Classic	Equipped	Classic	Equipped
−47kg	−52kg	0.000	0.289	0.039	0.100	0.941	0.434	0.114	0.789
	−57kg	0.000	0.002	0.000	0.036	0.342	0.568	0.005	0.558
	−63kg	0.000	0.000	0.000	0.000	0.001	0.093	0.005	0.809
	−72kg	0.000	0.000	0.000	0.000	0.000	0.056	0.003	0.363
	−84kg	0.000	0.000	0.000	0.000	0.000	0.039	0.141	0.203
	84+kg	0.000	0.000	0.000	0.000	0.000	0.000	0.893	0.566
−52kg	−57kg	0.000	0.011	0.000	0.637	0.200	0.746	0.099	0.267
	−63kg	0.000	0.000	0.000	0.005	0.000	0.277	0.105	0.493
	−72kg	0.000	0.000	0.000	0.000	0.000	0.166	0.064	0.116
	−84kg	0.000	0.000	0.000	0.000	0.000	0.111	0.697	0.051
	84+kg	0.000	0.000	0.000	0.000	0.000	0.001	0.007	0.701
−57kg	−63kg	0.000	0.158	0.000	0.010	0.000	0.114	0.856	0.609
	−72kg	0.000	0.000	0.000	0.000	0.000	0.053	0.964	0.656
	−84kg	0.000	0.000	0.000	0.000	0.000	0.037	0.008	0.333
	84+kg	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.139
−63kg	−72kg	0.000	0.000	0.000	0.078	0.000	0.753	0.785	0.310
	−84kg	0.000	0.000	0.000	0.000	0.000	0.511	0.005	0.137
	84+kg	0.000	0.000	0.000	0.000	0.000	0.007	0.000	0.279
−72kg	−84kg	0.000	0.000	0.000	0.013	0.000	0.696	0.001	0.542
	84+kg	0.000	0.000	0.000	0.000	0.000	0.013	0.000	0.053
−84kg	84+kg	0.000	0.167	0.000	0.000	0.000	0.050	0.002	0.023
Total		0	3	0	3	3	14	10	20
Percentage (%)		0	14.3	0	14.3	14.3	66.7	47.6	95.2

Note: Statistical Significance was set a p < 0.05 meaning that if p-value coming from group comparison is p < 0.05, groups were statistically significantly different and therefore could not be compared

Table 5.

Men’s Post-Hoc ANOVA p-Values on total

		KG		Ratios		Wilks		IPF
		Classic	Equipped	Classic	Equipped	Classic	Equipped	Classic	Equipped
−59kg	−66kg	0.000	0.035	0.990	0.033	0.318	0.185	0.009	0.344
	−74kg	0.000	0.000	0.000	0.000	0.680	0.146	0.014	0.413
	−83kg	0.000	0.000	0.000	0.000	0.362	0.010	0.014	0.042
	−93kg	0.000	0.000	0.000	0.000	0.136	0.022	0.121	0.033
	−105kg	0.000	0.000	0.000	0.000	0.619	0.067	0.189	0.012
	−120kg	0.000	0.000	0.000	0.000	0.961	0.652	0.628	0.015
	120+kg	0.000	0.000	0.000	0.000	0.084	0.622	0.001	0.000
−66kg	−74kg	0.000	0.000	0.000	0.117	0.023	0.987	0.536	0.778
	−83kg	0.000	0.000	0.000	0.000	0.001	0.181	0.452	0.235
	−93kg	0.000	0.000	0.000	0.000	0.000	0.352	0.028	0.194
	−105kg	0.000	0.000	0.000	0.000	0.012	0.717	0.012	0.076
	−120kg	0.000	0.000	0.000	0.000	0.091	0.194	0.000	0.092
	120+kg	0.000	0.000	0.000	0.000	0.328	0.245	0.000	0.000
−74kg	−83kg	0.000	0.001	0.000	0.000	0.275	0.087	0.894	0.061
	−93kg	0.000	0.000	0.000	0.000	0.015	0.221	0.026	0.039
	−105kg	0.000	0.000	0.000	0.000	0.867	0.624	0.008	0.007
	−120kg	0.000	0.000	0.000	0.000	0.474	0.108	0.000	0.013
	120+kg	0.000	0.000	0.000	0.000	0.000	0.163	0.000	0.000
−83kg	−93kg	0.000	0.000	0.000	0.000	0.118	0.519	0.013	0.921
	−105kg	0.000	0.000	0.000	0.000	0.288	0.149	0.003	0.438
	−120kg	0.000	0.000	0.000	0.000	0.065	0.000	0.000	0.485
	120+kg	0.000	0.000	0.000	0.000	0.000	0.002	0.000	0.000
−93kg	−105kg	0.000	0.000	0.000	0.000	0.008	0.387	0.548	0.465
	−120kg	0.000	0.000	0.000	0.000	0.002	0.002	0.000	0.518
	120+kg	0.000	0.000	0.000	0.000	0.000	0.006	0.000	0.000
−120kg	−120kg	0.000	0.000	0.000	0.000	0.341	0.018	0.000	0.990
	120+kg	0.000	0.000	0.000	0.000	0.000	0.041	0.000	0.000
120+kg	120+kg	0.000	0.005	0.000	0.000	0.002	0.928	0.000	0.000
Total		0	0	1	1	16	20	7	14
Percentage (%)		0	0	3.6	3.6	57.1	71.4	25	50

Note: Statistical Significance was set a p < 0.05 meaning that if p-value coming from group comparison is p < 0.05, groups were statistically significantly different and therefore could not be compared

Figure 1.

Women’s Total in Kg

Figure 2.

Women’s Total in Ratio

Figure 3.

Women’s Total in Wilks Points

Figure 4.

Women’s Total in IPF Points

Figure 5.

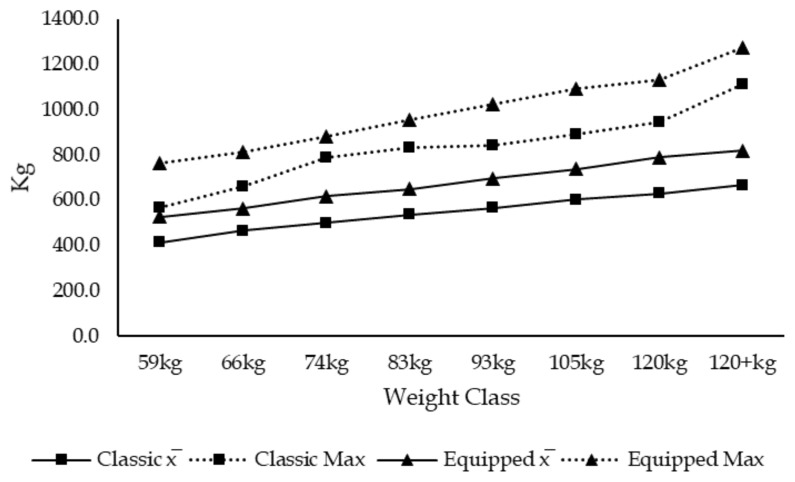
Men’s Total in Kg

Figure 6.

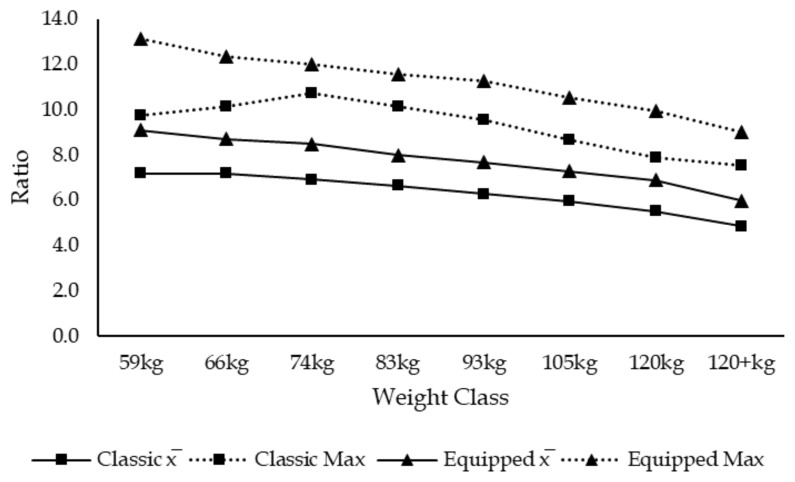
Men’s Total in Ratio

Figure 7.

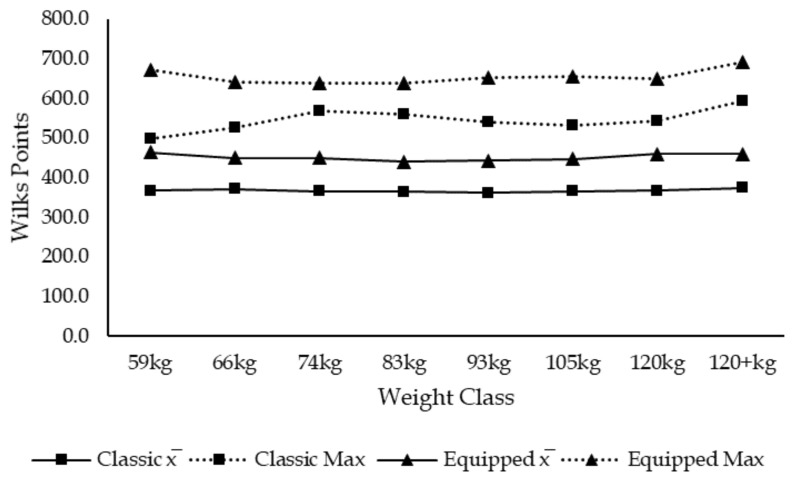
Men’s Total in Wilks points

Figure 8.

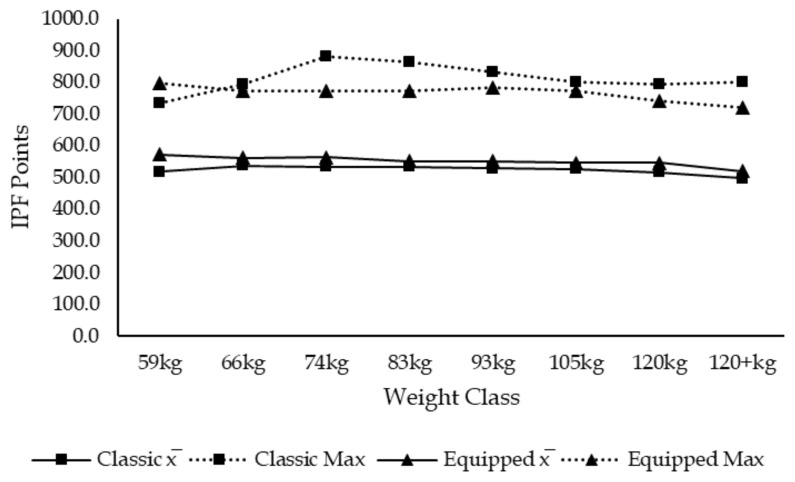
Men’s Total in IPF Points

Results from the unpaired Student’s t-test revealed that weight lifted in kg, ratio, percentage of the lift on the total, Wilks and IPF points for each event and the total was statistically significantly different (p < 0.05) when comparing classic and single-ply to their respective weight class except for women’s deadlift ratio (p = 0.276), deadlift Wilks points (p = 0.544), total Wilks points (p = 0.094), squat IPF points, deadlift IPF points (0.96) and total IPF points (p = 0.282) and for men’s deadlift ratio (p = 0.198), deadlift Wilks points (p = 0.523), deadlift IPF points (p = 0.645) and total IPF points (p = 0.071). Therefore, single-ply powerlifters significantly lift more weight than classic powerlifters in the squat and bench press (view figures 1 to 8 and supplemental material).

DISCUSSION

The main finding of the present analysis shows that the Wilks is slightly more efficient than the IPF Formula (54.1% > 52%) at determining the champion of champions of the same sex and division. Despite the IPF Formula document (9) available on the IPF website (8) supporting that Wilks formula had been developed over 25 years ago with data gathered between 1988 and 1994 and that at the time there was not a big sample size for women present in the dataset utilized, supportive equipment and training techniques have evolved, the weight classes have changed in 2011 and athletes have on average changed body weight and body composition.

Results also show that the IPF formula is more adequate to compare women’s classic and equipped weight classes of their respective division. These results could be explained by the fact that the Wilks Formula had been developed with a much smaller women sample size than the IPF Formula (9). Ultimately, updating the constants present in the women’s Wilks Formula could have been performed by utilizing a, now available, bigger sample size. This update could have hypothetically made the results from the present analysis favorable for the Wilks Formula for both sexes. Furthermore, the Wilks Formula’s coefficients could have been updated for both sexes with a more recent and more representative of modern-day powerlifting sample like the one utilized in this study and this could have improved the precision of the current Wilks formula.

One could hypothesize that the change of formula emerged from a political decision as Robert Wilks is now board director of the recently founded World Powerlifting Federation (WPF), which is a direct competitor to the IPF (20). Authors also believe that during the selection process of the new IPF Formula both formulas efficiency should have been compared to ensure that the change would improve the accuracy of the champion of champions point system. Updating the already established Wilks Formula could perhaps have been more appreciated by the powerlifting community as the Wilks’ points system was already well known from powerlifters and by the non-IPF-affiliated federations that are still using the Wilks Formula to this day.

A factor that could explain why the IPF Formula is less precise than the Wilks Formula is that it only contains 4 constants compared to 6 for the Wilks. A second factor that could explain why the IPF Formula is less precise than the Wilks Formula, is that the IPF Formula was designed to make all subcategories comparable (classic vs equipped vs single lifts); normalizing absolute score for that many sub-groups may have affected the precision of the formula and receded from the ultimate goal of the formula which is to determine four champions of champions (women’s classic, women’s equipped, men’s classic, men’s equipped).

Other results showing that equipped powerlifters lift significantly more weight than their fellow classic competitors for the same weight class confirms similar statements coming from other studies (1, 14) and could help powerlifters understand how much more weight the extra/different supportive equipment permits to lift in each event (view supplemental material). The descriptive results presented herein could also be utilized by powerlifting coaches, as they could position their athletes within the current IPF population, strength wise, but also according to the percentage of their lifts on their total.

A limit to this study is that the analysis presented was only performed on open powerlifters aged from 24 to 38 years old and could have been directed on a broader sample as the IPF formula claims to be valid for bodyweights of 40 kg or more and athletes aged of 14 years old or more (9). Further analyses should be directed at a sample that includes all age categories (Sub-Junior, Junior, Master 1, 2, 3 and 4 powerlifters of both sexes and division).

In conclusion, this research was able to analyze the Open Powerlifting database in order to compare the efficiency of the already established Wilks Formula to the new IPF Formula in determining the champion of champions for powerlifters of the same sex and division.

Ultimately, the hypothesis of this study was that the new IPF Formula would be more efficient than the Wilks Formula at comparing results between weight classes of the same sex and division to determine the champion of champions. Therefore, the hypothesis is rejected.

From the results of the present analysis, it seems that the International Powerlifting Federation has replaced a formula that does not improve the efficiency in determining the champion of champions, as it appears that there is very little difference in efficiency between both points systems. Unfortunately, authors could not validate the decision made by the IPF committee to replace the Wilks by the IPF Formula. Results support the decision of the other non-IPF-affiliated federations to still utilize the Wilks Formula.

Descriptive results presented in this article, which present maximum, minimum, means and standard deviations in kg, as well as ratios (weight lifted/body weight), percentage of each event on the total, Wilks and IPF points for all three powerlifting events and the total, for each weight class per sex and their respective division coming from 26,472 powerlifters could be utilized by powerlifting coaches to position their athletes within the current IPF standards. Further research should be directed towards updating the constants of both formulas.