An Assessment of Earth's Climate Sensitivity Using Multiple Lines of Evidence

Abstract

We assess evidence relevant to Earth's equilibrium climate sensitivity per doubling of atmospheric CO₂, characterized by an effective sensitivity S. This evidence includes feedback process understanding, the historical climate record, and the paleoclimate record. An S value lower than 2 K is difficult to reconcile with any of the three lines of evidence. The amount of cooling during the Last Glacial Maximum provides strong evidence against values of S greater than 4.5 K. Other lines of evidence in combination also show that this is relatively unlikely. We use a Bayesian approach to produce a probability density function (PDF) for S given all the evidence, including tests of robustness to difficult‐to‐quantify uncertainties and different priors. The 66% range is 2.6–3.9 K for our Baseline calculation and remains within 2.3–4.5 K under the robustness tests; corresponding 5–95% ranges are 2.3–4.7 K, bounded by 2.0–5.7 K (although such high‐confidence ranges should be regarded more cautiously). This indicates a stronger constraint on S than reported in past assessments, by lifting the low end of the range. This narrowing occurs because the three lines of evidence agree and are judged to be largely independent and because of greater confidence in understanding feedback processes and in combining evidence. We identify promising avenues for further narrowing the range in S, in particular using comprehensive models and process understanding to address limitations in the traditional forcing‐feedback paradigm for interpreting past changes.

Key Points

• We assess evidence relevant to Earth's climate sensitivity S: feedback process understanding and the historical and paleoclimate records

• All three lines of evidence are difficult to reconcile with S < 2 K, while paleo evidence provides the strongest case against S > 4.5 K

• A Bayesian calculation finds a 66% range of 2.6–3.9 K, which remains within the bounds 2.3–4.5 K under plausible robustness tests

1. Introduction

Earth's equilibrium climate sensitivity (ECS), defined generally as the steady‐state global temperature increase for a doubling of CO₂, has long been taken as the starting point for understanding global climate changes. It was quantified specifically by Charney et al. (National Research Council, 1979) as the equilibrium warming as seen in a model with ice sheets and vegetation fixed at present‐day values. Those authors proposed a range of 1.5–4.5 K based on the information at the time but did not attempt to quantify the probability that the sensitivity was inside or outside this range. The most recent report by the Intergovernmental Panel on Climate Change (IPCC) (2013) asserted the same now‐familiar range but more precisely dubbed it a >66% (“likely”) credible interval, implying an up to one in three chances of being outside that range. It has been estimated that—in an ideal world where the information would lead to optimal policy responses—halving the uncertainty in a measure of climate sensitivity would lead to an average savings of US$10 trillion in today's dollars (Hope, 2015). Apart from this, the sensitivity of the world's climate to external influence is a key piece of knowledge that humanity should have at its fingertips. So how can we narrow this range?

Quantifying ECS is challenging because the available evidence consists of diverse strands, none of which is conclusive by itself. This requires that the strands be combined in some way. Yet, because the underlying science spans many disciplines within the Earth Sciences, individual scientists generally only fully understand one or a few of the strands. Moreover, the interpretation of each strand requires structural assumptions that cannot be proven, and sometimes ECS measures have been estimated from each strand that are not fully equivalent. This complexity and uncertainty thwarts rigorous, definitive calculations and gives expert judgment and assumptions a potentially large role.

Our assessment was undertaken under the auspices of the World Climate Research Programme's Grand Science Challenge on Clouds, Circulation and Climate Sensitivity following a 2015 workshop at Ringberg Castle in Germany. It tackles the above issues, addressing three questions:

1. Given all the information we now have, acknowledging and respecting the uncertainties, how likely are very high or very low climate sensitivities, that is, outside the presently accepted likely range of 1.5–4.5 K (IPCC, 2013)?

2. What is the strongest evidence against very high or very low values?

3. Where is there potential to reduce the uncertainty?

In addressing these questions, we broadly follow the example of Stevens et al. (2016, hereafter SSBW16) who laid out a strategy for combining lines of evidence and transparently considering uncertainties. The lines of evidence we consider, as in SSBW16, are modern observations and models of system variability and feedback processes, the rate and trajectory of historical warming, and the paleoclimate record. The core of the combination strategy is to lay out all the circumstances that would have to hold for the climate sensitivity to be very low or high given all the evidence (which SSBW16 call “storylines”). A formal assessment enables quantitative probability statements given all evidence and a prior distribution, but the “storyline” approach allows readers to draw their own conclusions about how likely the storylines are and points naturally to areas with greatest potential for further progress. Recognizing that expert judgment is unavoidable, we attempt to incorporate it in a transparent and consistent way (e.g., Oppenheimer et al., 2016).

Combining multiple lines of evidence will increase our confidence and tighten the range of likely ECS if the lines of evidence are broadly consistent. If uncertainty is underestimated in any individual line of evidence—inappropriately ruling out or discounting part of the ECS range—this will make an important difference to the final outcome (see example in Knutti et al., 2017). Therefore, it is vital to seek a comprehensive estimate of the uncertainty of each line of evidence that accounts for the risk of unexpected errors or influences on the evidence. This must ultimately be done subjectively. We will therefore explore the uncertainty via sensitivity tests and by considering “what if” cases in the sense of SSBW16, including what happens if an entire line of evidence is dismissed.

The most recent reviews (Collins et al., 2013; Knutti et al., 2017) have considered the same three main lines of evidence considered here and have noted that they are broadly consistent with one another but did not attempt a formal quantification of the probability density function (PDF) of ECS. Formal Bayesian quantifications have been done based on the historical warming record (see Bodman & Jones, 2016, for a recent review), the paleoclimate record (PALAEOSENS, 2012), a combination of historical and last millennium records (Hegerl et al., 2006), and multiple lines of evidence from instrumental and paleorecords (Annan & Hargreaves, 2006). An assessment based only on a subset of the evidence will yield too wide a range if the excluded evidence is consistent (e.g., Annan & Hargreaves, 2006), but if both subsets rely on similar information or assumptions, this codependence must be considered when combining them (Knutti & Hegerl, 2008). Therefore, an important aspect of our assessment is to explicitly assess how uncertainties could affect more than one line of evidence (cf. section 6) and to assess the sensitivity of calculated PDFs to reasonable allowance for interdependencies of the evidence.

Another key aspect of our assessment is that we explicitly consider process understanding via modern observations and process models as a newly robust line of evidence (section 3). Such knowledge has occasionally been incorporated implicitly (via the prior on ECS) based on the sample distribution of ECS in available climate models (Annan & Hargreaves, 2006) or expert judgments (Forest et al., 2002), but climate models and expert judgments do not fully represent existing knowledge or uncertainty relevant to climate feedbacks nor are they fully independent of other evidence (in particular that from the historical temperature record, see Kiehl, 2007). Process understanding has recently blossomed, however, to the point where substantial statements can be made without simply relying on climate model representations of feedback processes, creating a new opportunity exploited here.

Climate models (specifically general circulation models, or GCMs) nonetheless play an increasing role in calculating what our observational data would look like under various hypothetical ECS values—in effect translating from evidence to ECS. Their use in this role is now challenging long‐held assumptions, for example, showing that twentieth century warming could have been relatively weak even if ECS were high (section 4), that paleoclimate changes are strongly affected by factors other than CO₂, and that climate may become more sensitive to greenhouse gases (GHGs) in warmer states (section 5). GCMs are also crucial for confirming how modern observations of feedback processes are related to ECS (section 3). Accordingly, another novel feature of this assessment will be to use GCMs to refine our expectations of what observations should accompany any given value of ECS and thereby avoid biases now evident in some estimates of ECS based on the historical record using simple energy budget or energy balance model arguments. GCMs are also used to link global feedback strengths to observable phenomena. However, for reasons noted above, we avoid relying on GCMs to tell us what values to expect for key feedbacks except where the feedback mechanisms can be calibrated against other evidence. Since we use GCMs in some way to help interpret all lines of evidence, we must be mindful that any errors in doing this could reinforce across lines (see section 6.2).

We emphasize that this assessment begins with the evidence on which previous studies were based, including new evidence not used previously, and aims to comprehensively synthesize the implications for climate sensitivity both by drawing on key literature and by doing new calculations. In doing this, we will identify structural uncertainties that have caused previous studies to report different ranges of ECS from (essentially) the same evidence and account for this when assessing what that underlying evidence can tell us.

An issue with past studies is that different or vague definitions of ECS may have led to perceived, unphysical discrepancies in estimates of ECS that hampered abilities to constrain its range and progress understanding. Bringing all the evidence to bear in a consistent way requires using a specific measure of ECS, so that all lines of evidence are linked to the same underlying quantity. We denote this quantity S (see section 2.1). The implications for S of the three strands of evidence are examined separately in sections 3, 5, and anticipated dependencies between them are discussed in section 6. To obtain a quantitative PDF of S, we follow SSBW16 and many other studies by adopting a Bayesian formalism, which is outlined in sections 2.3–2.4. The results of applying this to the evidence are presented in section 7, along with the implications of our results for other measures of climate sensitivity and for future warming. The overall conclusions of our assessment are presented in section 8. We note that no single metric such as S can fully describe or predict climate responses, and we discuss its limitations in section 8.2, as well as implications of our work for future research.

While we endeavor to write for a broad audience, it is necessary to dip into technical detail in order to support the reasoning and conclusions, and some of the methods used are novel and require explanation. We have therefore structured this assessment so that the discussions of the three lines of evidence (sections 3, 5) are quasi‐independent, with separate introductions, detailed analyses, and conclusions. Readers who are not interested in the details can gain an overview of the key points from the concluding portions of these sections. Likewise, readers not interested in details of the statistical method could skip most of section 2 and focus on the “storylines” presented in sections 3, 5. The probabilities given in section 7 derive from the statistical method, but the independence issues discussed in section 6 are important for either quantitative or qualitative assessment of the evidence.

2. Methods

This section first explains the measure of ECS we will use and how it relates to others (section 2.1) then presents the simple physical model used to interpret evidence (section 2.2). Section 2.3 summarizes the overall methodology, and section 2.4 goes over this in more detail, beginning with a basic review of Bayesian inference intended mainly for those new to the topic while focusing on concepts relevant to the ECS problem (section 2.4.1), then working through the solution of the model and sampling approach (sections 2.4.2, 2.4.4). For other basic introductions to Bayesian inference, see Stone (2012) or Gelman et al. (2013).

2.1. Measures of Climate Sensitivity

Climate sensitivity is typically quantified as warming per doubling of CO₂, but this is by tradition. One could also consider the warming per unit radiative forcing or the increment of additional net power exported to space per unit warming (the feedback parameter, i.e., energetic “spring constant” of the system) denoted λ. Indeed (see section 2.2 and later), we will find it easier to write our evidence in terms of λ rather than warming‐per‐doubling (ECS), making the definition of an ECS optional. One can imagine a range of CO₂ forcing scenarios, each yielding its own value for the ECS; each such scenario also implies a matching value for λ. Our approach simultaneously constrains both λ and S (see section 2.3).

In choosing the reference scenario to define sensitivity for this assessment, for practical reasons we depart from the traditional Charney ECS definition (equilibrium response with ice sheets and vegetation assumed fixed) in favor of a comparable and widely used, so‐called “effective climate sensitivity” S derived from system behavior during the first 150 years following a (hypothetical) sudden quadrupling of CO₂. During this time the system is not in equilibrium, but regression of global mean top‐of‐atmosphere (TOA) energy imbalance onto global mean near‐surface air temperature (SAT), extrapolated to 0 imbalance, yields an estimate of the long‐term warming valid if the average feedbacks active during the first 150 years persisted to equilibrium (Gregory et al., 2004). This quantity therefore approximates the long‐term Charney ECS (e.g., Danabasoglu & Gent, 2009), though how well it does so is a matter of active investigation addressed below. Our reference scenario does not formally exclude any feedback process, but the 150‐year time frame minimizes slow feedbacks (especially ice sheet changes).

This choice involves weighing competing issues. Crucially, effective sensitivity (or other measures based on behavior within a century or two of applying the forcing) is more relevant to the time scales of greatest interest (i.e., the next century) than is equilibrium sensitivity, and effective sensitivity has been found to be strongly correlated (r = 0.95) with the magnitude of model‐simulated 21st century warming under a high‐emission scenario (Gregory et al., 2015; Grose et al., 2017, 2018). It is also widely available from climate models (e.g., Andrews, Gregory, Webb, et al., 2012), which facilitates many steps in our analysis. All candidate climate sensitivity measures are based on an outcome of a hypothetical scenario never realized on Earth. Ultimately, models or theory are required to relate the outcome of any one scenario to that of any other. The ideal measure S is one that is as closely related as possible to scenarios of practical interest: those which produced evidence (e.g., the historical CO₂ rise) or which might occur in the future. Effective sensitivity is a compromise that is relatively well related to both the available past evidence and projected future warmings.

The transient climate response (TCR, or warming at the time of CO₂ doubling in an idealized 1% per year increase scenario), has been proposed as a better measure of warming over the near to medium term; it may be more generally related to peak warming and better constrained (in absolute terms) by historical warming, than S (Frame et al., 2005; Frolicher et al., 2013). It may also be better at predicting high‐latitude warming (Grose et al., 2017). But as mentioned above, 21st century global mean trends under high emissions are better predicted by S than by TCR, perhaps because of nonlinearities in forcing or response (Gregory et al., 2015) or because TCR estimates are affected by noise (Sanderson, 2020). TCR is also less directly related to the other lines of evidence than is S. In this study we will briefly address TCR in sections 4 and 7.4 but will not undertake a detailed assessment.

The IPCC (at least through AR5) formally retains a definition of ECS based on long‐term equilibrium. Much of the information they use to quantify ECS, however, exploits GCM calculations of effective (e.g., Andrews, Gregory, Webb, et al., 2012), not equilibrium, sensitivity, and it appears that the distinction is often overlooked. In this report, we will use “long term” to describe processes and responses involved in the effective sensitivity S and “equilibrium” for the fully equilibrated ECS. The ECS differs from S due to responses involving the deep ocean, atmospheric composition, and land surface that emerge on centennial time scales (e.g., Frey & Kay, 2018; see section 5), though calculations here (following Charney and past IPCC reports) do not include ice sheet changes.

To calculate the ECS in a fully coupled climate model requires very long integrations (>1,000 years). Fortunately, a recent intercomparison project (LongrunMIP; Rugenstein, Bloch‐Johnson, Abe‐Ouchi, et al., 2019) has organized long simulations from enough models to now give a reasonable idea of how ECS and S are likely to be related.

Relationships between S and several other quantities are shown in Figure 1 from available models. Predicted S is reasonably well correlated with the other sensitivity measures (Figure 1a), indicating that S is a useful measure and also that the conclusions of this assessment would still hold if another measure were used. Note that we do not consider here all possible measures; see Rugenstein, Bloch‐Johnson, Gregory, et al. (2019) for a discussion of some additional ones, which also generally correlate well with S. S is less well correlated to TCR (r = 0.81) than to ECS (r = 0.94), as expected since the TCR is sensitive to ocean heat uptake efficiency as well as to λ.

Figure 1.

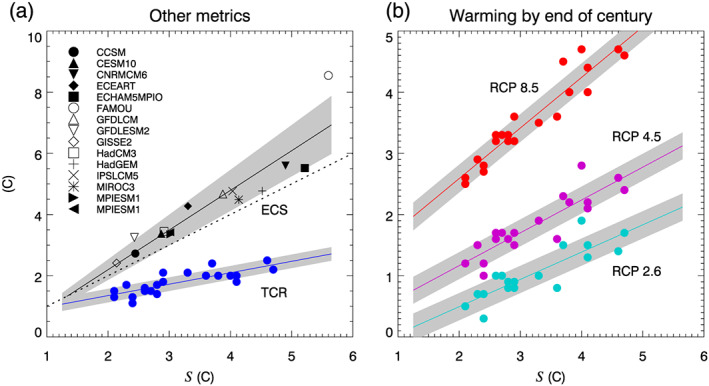
Relation of (a) other climate sensitivity metrics and (b) predicted warming by late this century, to S as defined in section 2.1. In (a), symbols show 15 LongRunMIP model estimates of the equilibrium warming per doubling of CO₂ (Rugenstein, Bloch‐Johnson, Gregory, et al., 2019), with small purple symbols showing equilibria in 4xCO₂ simulations and large black symbols equilibria in 2xCO₂ simulations. Blue filled circles show TCR from CMIP5 models. In (b), projected change in global mean temperature in 2079–2099 relative to 1986–2005, under the RCP8.5 (red), RCP4.5 (magenta), and RCP2.6 (cyan) scenarios, from 24 CMIP5 models. CMIP5 data are from Grose et al. (2018). For each set of points, a best linear fit is shown, with one standard deviation shown in gray shading (assumed homogeneous except for ECS where it is assumed to scale linearly with S); see section 7.4 for further details on fits.

Although the measures correlate well, all available LongRunMIP models equilibrate to a higher warming at 4xCO₂ than S from the same simulation (Figure 1a, small symbols); details of how the equilibrium is estimated are given in Rugenstein, Bloch‐Johnson, Abe‐Ouchi, et al. (2019) and Rugenstein, Bloch‐Johnson, Gregory, et al. (2019). The median equilibrium warming per doubling at 4xCO₂ is 17% higher than the median S, suggesting a robust amplifying impact of processes too slow to emerge in the first 150 years. This occurs due to responses of the climate system on multidecadal to millennial time scales, including “pattern effects” from differences between ocean surface warming patterns that have not fully equilibrated within the first century or two (sections 3.3.2 and 4.2), slow responses of vegetation, and temperature dependence of feedbacks. Evidence also shows, however (section 5.2.3), that sensitivity to two doublings (as assumed for S) is somewhat greater than that to one doubling. This state dependence partly cancels out the low bias in the 150‐year regression, leading to an ECS (for one doubling) that averages only 6% greater than S over the simulations, although the ratio of the two is uncertain so we assign an uncertainty of ±20% (about 50% wider than the sample standard deviation in the available GCMs). Thus, statements about S in this assessment can also be interpreted, to relatively good approximation, as statements about ECS for one doubling of CO₂. (We use the symbol ζ to represent this difference, with 1 + ζ therefore being the ratio of our target S to the long‐term equilibrium.)

Figure 1b shows the relationships of S to future warming. The warming trend over the 21st century (Figure 1b) is also well correlated with S, especially for the highest‐emission scenario Representative Concentration Pathway 8.5 (RCP8.5). The correlations are not quite as strong for the weaker‐forcing cases, suggesting that global temperature changes are harder to predict (in a relative sense) in more highly mitigated scenarios. This is mostly due to a weaker warming signal, but there is also a slightly greater model spread, reasons for which are not currently understood.

To conclude, the effective sensitivity S that we will use—a linear approximation to the equilibrium warming based on the first 150 years after an abrupt CO₂ quadrupling—is a practical option for measuring sensitivity, based on climate system behavior over the most relevant time frame while still approximating the traditional ECS. Moreover, the quantitative difference between this and the traditional equilibrium measure based on a CO₂ doubling (with fixed ice sheets) appears to be small, albeit uncertain. This uncertainty is skewed, in the sense that long‐term ECS could be substantially higher than S but is very unlikely to be substantially lower. Further work is needed to better understand and constrain this uncertainty.

2.2. Physical Model

Here we review the equations that will be used to relate the evidence to the key unknowns. According to the conventional forcing‐feedback theory of the climate system, the net downward radiation imbalance ∆N at the TOA can be decomposed into a radiative forcing ∆F, a radiative response ∆R due directly or indirectly to forced changes in temperature which is the feedback, and variability V unrelated to the forcing or feedback:

$$∆N=∆F+\mathrm{\Delta R}+V$$ (1)

Variability V can arise due to unforced variations in upwelling of cold water to the surface, cloud cover, albedo, and so forth. The net radiation balance ∆N consists of the net absorbed shortwave (SW) solar radiation minus the planet's emission of longwave (LW) radiation. Taking the radiative response ∆R as proportional to first order to the forced change in global mean SAT ∆T, Equation 1 becomes

$$∆N=∆F+\lambda ∆T+V$$ (2)

where the climate feedback parameter λ is defined as the sensitivity of the net TOA downward radiation N to T, dN/dt, (at fixed F). If this feedback parameter is negative, the system is stable.

In equilibrium over sufficiently long time scales (assuming λ < 0) the net radiation imbalance ∆N and mean unforced variability V will each be negligible, leaving a balance between the (constant) forcing ∆F and radiative response ∆R. In this case Equation 2 can be written as

$$\mathrm{\Delta T}=-\mathrm{\Delta F}/\lambda$$ (3)

The case of a doubling of CO₂ defines the climate sensitivity:

$$S=-\frac{∆F_{2\mathrm{xCO}2}}{\lambda },$$ (4)

where ∆F _2xCO2 is defined as the radiative forcing per CO₂ doubling (noting that since our reference scenario involves two doublings, ∆F _2xCO2 is defined as half the effective forcing in that scenario). Estimation of this quantity is discussed in section 3.2.1. Note that while the above equations assume equilibrium, our reference scenario (section 2.1) is not an equilibrium scenario; however, because in this scenario ∆N is 0 (by construction) at the time of the projected equilibrium warming ∆T, these equations still hold.

Finally, we note that the total system feedback λ can be decomposed into the additive effect of multiple feedbacks in the system of strengths λ _i:

$$\lambda =\mathrm{\Sigma }{\lambda }_i.$$ (5)

These feedbacks represent how the TOA radiation balance is altered as the climate warms by forced changes in identified radiatively active constituents of the climate system. In this study these are represented as six feedback components: the Planck feedback, combined water vapor and lapse rate feedback, total cloud feedback, surface albedo feedback, stratospheric feedback, and an additional atmospheric composition feedback. These individual feedback components are elaborated in section 3, where evidence is presented to constrain each of them (sections 3.3 and 3.4). Other process evidence is presented (section 3.5), which constrains the total, λ. Finally, so‐called “emergent‐constraint” studies are discussed (section 3.6), which tie S to some observable in the present‐day climate, thereby constraining λ and S. For reasons discussed later, however, they are not used in our Baseline calculation but are explored via a sensitivity test.

The other evidence used (sections 4 and 5) comes from past climate changes and typically is interpreted via Equations 2 and 3 in previous climate sensitivity studies. These have typically assumed that the equations apply to any relevant climate change with universal values of λ and S, provided that the same feedbacks are counted therein (cf. Equation 5). We will likewise apply these equations simultaneously to different past climate change scenarios, leading to a set of relationships shown graphically in Figure 2 (which offers a picture of our overall model, in particular its dependence structure; see section 2.4.2 for more information).

Figure 2.

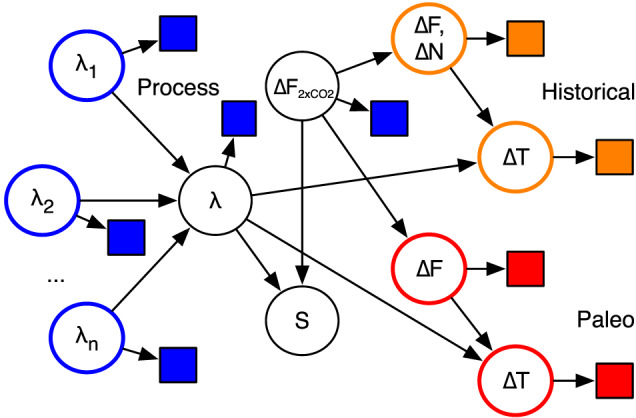
A Bayesian network diagram showing the dependence relationships between main variables in the inference model. Circles show uncertain variables, whose PDFs are estimated; squares show evidence (random effects on the evidence would appear as a second “parent” variable for each square and are omitted for simplicity). Colors distinguish the three main lines of evidence and associated variables (blue = process, orange = historical, and red = paleoclimate). For paleoclimate, only one ∆F/∆T climate change pair is shown but two independent ones are considered (see section 5).

Recent work, however, has shown that effective λ (the value that satisfies Equation 2 for some climate change scenario) can vary significantly across scenarios even when the same feedbacks are nominally operating. All measurements relevant to climate sensitivity come from the recent historical period (during which internal variability may play a large role and the climate is far out of equilibrium; section 4) or from proxy reconstructions of past climate equilibria (during which the climate may have been quite different to that of the reference scenario; section 5). Thus, possible variations in the apparent λ during those time periods must be accounted for. Two particular issues are recognized. First, feedbacks can change strength in different climate states due to direct dependence on global temperature or indirect dependence (e.g., via snow or ice cover) or other differences in the Earth system (e.g., topography). Second, the net outgoing radiation ∆N can depend not only on the global mean surface temperature but also on its geographic pattern ∆T′, leading to an apparent dependence of λ on ∆T′ when applying Equation 2. Such pattern variations can arise either because of heterogeneous radiative forcings, lag‐dependent responses to forcings, or unforced variability. To use such observations to constrain our S and λ, it is important to account for these effects. Note that these effects are distinct from atmospheric “adjustments” to applied radiative forcings (Sherwood et al., 2015), which scale with the forcing and are included as part of the effective radiative forcing (ERF) ∆F.

We account for impacts on λ by defining an additive correction ∆λ for each past climate change representing the difference between its apparent λ and the “true” λ defined by our reference scenario. For simplicity we define these corrections to subsume both forcing‐related and unforced variations, so that henceforth V = 0. Equation 2 then becomes

$$∆N=∆F+\left(\lambda -\mathrm{\Delta }\lambda \right)\mathrm{\Delta }T$$ (6)

where λ is the “true” value we want to estimate. From the chain rule, having assigned to ∆λ two components, we obtain

$$\mathrm{\Delta }\lambda =\frac{\partial \lambda }{\partial T}\mathrm{\Delta }T+\frac{\partial \lambda }{\partial T\prime \left(x\right)}\mathrm{\Delta }T\prime \left(x\right)={∆\lambda }_{\mathit{\text{state}}}+{∆\lambda }_{\mathit{\text{pattern}}}$$ (7)

State dependence. The first term represents state dependence: The concept that the feedbacks in a glacial climate, for example, might not remain the same strength over the next century. Ice‐albedo feedback, for example, has long been expected to be climate sensitive (Budyko, 1969; Sellers, 1969), and some studies have found strong sensitivity of cloud feedbacks (Caballero & Huber, 2013). The simplest parameterization of this is to add a quadratic dependence of net outgoing radiation on ∆T, which yields a linear dependence of total feedback λ:

$$∆{\lambda }_{\text{state}}=2\alpha ∆T$$

There are, however, reasons to expect changes could be nonlinear (e.g., discontinuous changes in cloud feedbacks when ice sheets disappear) so this formulation will not always be used (see section 5). State dependence corrections are made only for paleoclimate evidence, and state dependence of ∆F _2xCO2 is subsumed into that of λ.

Pattern effects. The second term represents the “pattern effect” and expresses the possibility that different patterns of warming will trigger different radiative responses. The pattern effect is significant whenever (a) the pattern of temperature change differs from that in the reference scenario and (b) this difference in pattern is radiatively significant, that is, alters the global mean TOA net radiation. Such patterns can arise either due to non‐CO₂ forcings, lags in response, or unforced variability. In section 4.2, the possible existence of a pattern effect arising from transient warming patterns that do not resemble the eventual equilibrium response is discussed further. Pattern effects may also complicate the comparison of estimates derived from proxy reconstructions of past equilibria, if the resulting sea surface temperature (SST) patterns differ from those of the reference scenario. However, in the absence of reliable reconstructions of past warming patterns and a dearth of existing literature addressing this, here we do not explicitly consider paleoclimate pattern effects. We note that the concept of forcing “efficacy” (i.e., Hansen et al., 2005; Marvel et al., 2016; Stap et al., 2019; Winton et al., 2010), in which one unit of radiative forcing produces a different temperature response depending on where, geographically, it is applied, can be attributed to a pattern effect (e.g., Rose et al., 2014) or to a forcing adjustment. Our estimated historical and paleoforcings ∆F will include uncertainties from adjustment/efficacy effects.

Time scale. Finally, we note that any definition of planetary sensitivity depends on the time scale considered. Our S incorporates only feedbacks acting on time scales of order a century. Traditional ECS allows for more complete equilibration of the system, albeit with some feedbacks explicitly excluded (see section 2.1). In this report we assume that ECS and S are related via

$$\mathit{ECS}=\left(1+\zeta \right)S.$$ (8)

See section 5.2.3 for more information. Earth system sensitivity (ESS), by contrast, reflects the slower feedback processes such as changes to the carbon cycle and land ice. Due to the lack of information on short temporal scales, most paleoclimate reconstructions necessarily incorporate the effects of these slow feedbacks. The difference between ESS and S or ECS is not relevant to the analyses in sections 3 and 4 but is discussed further in section 5.3.

2.3. Statistical Method: Summary

To obtain probability distributions of the various quantities introduced and mathematically linked in section 2.2, we adopt the Bayesian interpretation of probability, which describes our uncertain beliefs concerning facts that are not intrinsically random but about which our knowledge is uncertain (e.g., Bernardo & Smith, 1994). The Bayesian approach has been adopted in many past studies inferring climate sensitivity from historical or paleoclimate data (see sections 4 and 5) and is used for other climate‐relevant problems such as data assimilation (Law & Stuart, 2012), remote sensing (Evans et al., 1995), and reconstruction of past temperatures (Tingley & Huybers, 2010), among others.

The basic expression of Bayes's rule for the case of unknown variables is

$$p\left(\mathrm{\Phi }|E\right)=\frac{p\left(E|\mathrm{\Phi }\right)p\left(\mathrm{\Phi }\right)}{p\left(E\right)}$$ (9)

where Φ is a vector of variables (in our case feedbacks λ _i and total λ, forcings, temperature changes, parameters representing ∆λ's, and S) and E represents some evidence about these variables. p(Φ|E) is our sought‐for posterior probability density of Φ given (conditional on) E, that is, the joint PDF of all the variables considering the evidence. On the right‐hand side, p(E|Φ), the likelihood, measures the probability of the evidence E for any given Φ and is what quantifies the constraint offered by the evidence. p(Φ) is our prior for Φ, that is, the PDF we would assign to Φ in the absence of E. p(E), the overall probability of E, is essentially a normalization constant. A key insight is that a PDF can never be determined by evidence alone but begins with one's prior expectations p(Φ), which are then modified by the evidence. The PDF is small for Φ that are judged implausible at the outset (small prior) or unlikely to have led to the observed evidence (small likelihood). If the evidence is strong enough to restrict values to a sufficiently narrow range, the prior becomes practically irrelevant; this is typical for standard scientific measurements, and the prior is usually unexamined. It is unfortunately not the case for climate sensitivity, so we need to pay attention to the prior.

Because of the structure of our problem (in particular that ∆F _2xCO2 is relatively well known and many conditional independencies are expected among the variables, see section 2.4.2), the Bayes result 9 can approximately be written in terms of λ alone:

$$p\left(\lambda |E\right)\propto p\left(\lambda |E_{\text{proc}}\right)p\left(E_{\text{hist}}|\lambda \right)p\left(E_{\text{paleo}}|\lambda \right)$$ (10)

and a similar equation can be written for S. Thus, the PDF of either sensitivity measure is approximately proportional to the product of three components, one for each of our lines of evidence, where E _proc is the process evidence and so on. The first term on the right‐hand side of Equation 10 is the PDF given only our process understanding and an assumed prior on the feedbacks; this is estimated in section 3. The second and third terms are marginal likelihoods of the historical and paleo evidence as functions of the sensitivity measure, worked out (sections 4 and 5) by directly computing the probability of our best‐estimate warming as a function of all variables using the equations given in section 2.2. The posterior PDFs will be shown in section 7 (and employ a fully accurate calculation, viz., Equation 9 with full likelihoods rather than marginal ones; see section 2.4). Although Equation 10 is not exact, it is a very good approximation helpful in understanding results.

Importantly, each term in Equation 10 is computed using a model (cf. section 2.2) and involves judgments about structural uncertainty including limitations of the model. Our goal is for each term to represent fully educated and reasonable beliefs. In sections 3, 5 we will sometimes present a range of calculations and evidence and then assert a quantitative likelihood informed by the totality of this evidence and background knowledge. This will to some extent be unavoidably subjective.

A key assumption behind the multiplication in Equation 10 (also made in the fully accurate calculation) is that the lines of evidence are independent, which we assume for our Baseline calculation. For example, this means that learning the true historical aerosol radiative forcing would not alter our interpretation of the paleo or process evidence, and so on for other uncertainties. The plausibility of this assumption and consequences of relaxing it are explored in different ways in sections 6 and 7.

Many past studies (see sections 3, 5) have produced PDFs of S based on a single line of evidence represented by one likelihood term in Equation 10. One might think that if two such likelihoods from different evidence look different, it means there is some inconsistency or problem in the way evidence is being interpreted. This is a misconception. Suppose one line of evidence demonstrates S is above 3 K and the other that it is between 0 and 4 K; each by itself would yield a very different PDF, but together, they simply say S must be between 3 and 4 K. This is embodied in Equation 10. The difference in ranges is no reason to question either line of evidence so long as there is reasonable overlap. This point will be revisited in section 8 when discussing what turns out to be strong similarity among our lines of evidence.

In general, as discussed above, posterior PDFs depend on a (multivariate) prior. This prior is placed on all variables in the system and must obey the model equations (section 2.2), which force the beliefs it expresses about different variables to be consistent. In practice one begins with independent variables (in our case the individual feedbacks λ _i, ∆F _2xCO2, and for each past climate change the forcing ∆F, observational error for ∆T, and parameters for ∆λ; see sections 4 and 5). A prior on the dependent variables (i.e., the so‐called prior predictive distribution, PPD), such as λ and S, is then determined by the independent‐variable prior and the model. In cases where one has prior knowledge about a dependent variable X, the prior on the independent variables can be adjusted so that the PPD of X reflects this (see, e.g., Wang et al., 2018).

For each independent variable except the λ _i, we specify a marginal prior PDF by expert judgment using available evidence, discussed in the relevant sections 3, 5. This is typical of past Bayesian studies. The knowledge used to specify the prior for each variable is specific to that variable and not used elsewhere (this is important for the historical forcing PDF, section 4.1.1). For the λ _i, we explicitly consider a likelihood of each feedback's evidence E _i and a separate prior; that is, the PDF of λ _i is p (λ _i)p (E _i|λ _i). All of these prior PDFs adjust when the evidence is considered, resulting in posterior PDFs.

Our baseline choice for the prior p(λ _i), which is consistent with past work on estimating feedbacks components with which we are familiar, is uniform (over negative and positive values) and independent between feedbacks (i.e., learning information about one feedback would not alter our beliefs about others in the absence of other information on S; see section 7.2 for more discussion). From Equation 5, this implies a prior on λ that is also uniform across positive and negative values. Thus, we do not rule out an unstable climate a priori. An unstable climate is however ruled out by nonprocess evidence (i.e., the length and stability of Earth's geologic record). For efficiency, at the outset we eliminate from our numerical calculations individual λ _i for which the process likelihood is less than 10⁻¹⁰. Note that if the λ _i priors are restricted—for example, a broad Gaussian rather than uniform—results are essentially unaffected, since values far away from 0 are ruled out by evidence.

We also consider a different multivariate prior PDF, specified in such a way as to induce a PPD on S (via Equation 4) that is uniform from near 0 up to 20 K. This assigns high prior belief to combinations of λ _i that happen to sum to small negative λ and 0 belief to combinations summing to positive λ (for which S is undefined). Implementation of priors is further discussed in section 2.4.3, and issues concerning the choice of prior are discussed in section 7.2.

2.4. Statistical Method: Further Information

2.4.1. Introduction to Bayesian Inference Modeling

Bayes's theorem arises as a consequence of the laws of probability. Considering all possible Φ and all E that could have eventuated, the joint density (or probability, or PDF) of E and Φ of the real world, p(E,Φ), can be decomposed in two different ways via

$$p\left(E,\mathrm{\Phi }\right)=p\left(\mathrm{\Phi }|E\right)p\left(E\right)=p\left(E|\mathrm{\Phi }\right)p\left(\mathrm{\Phi }\right),$$

which immediately leads to Equation 9.

The likelihood p(E|Φ) is determined by the inference model, which takes the variables as an input and predicts what would be observed as a consequence of these variables. It is often a source of confusion. Although expressed as a probability (of E), once E is known, p(E|Φ) is best thought of as a relative measure of the consistency of the evidence with each value of Φ, according to our inference model. Low likelihoods indicate a Φ that would be unlikely to give rise to the evidence that was seen, and if the likelihood is low enough, we would say this Φ is inconsistent with that evidence. Bayes's theorem says that the probability of Φ given evidence is determined by two things: the a priori plausibility of Φ and the consistency of Φ with the evidence. Strictly speaking, “evidence” E should be observations of the real world. However, in this assessment (section 3 in particular) we will also selectively consider as evidence the emergent behavior of numerical simulations of processes (e.g., large‐eddy simulations [LESs] of cloud systems), where the numerical model is informed by, and tested against, observations not used elsewhere in the assessment.

The roles of the prior and likelihood are most simply illustrated by an example of a test for a rare disease. If the test correctly identifies both diseased and nondiseased patients 95% of the time, but only 1% of people tested carry the disease, then a patient who tests positive still only has ~16% probability of carrying the disease. This is because even though the likelihood p(E|Φ) of the positive test result is high (0.95) under the hypothesis that the patient is diseased (Φ = 1) and low (5%) under no‐disease (Φ = 0), the very low prior p(Φ = 1) = 0.01 due to the rarity of the disease renders a low 0.16 posterior p(Φ = 1|E) of disease. This may be obtained from Equation 9 noting that p(E positive) = 0.01 × 0.95 + 0.99 × 0.05 (equivalently one can reason that out of 10,000 patients, 100 would have the disease, 95 of whom would test positive; but of the 9,900 who do not have the disease, 5% or 495 would wrongly test positive, such that only 16% of those testing positive are actually diseased). This example illustrates that prior information or beliefs can have a powerful influence on outcomes, a point that has been emphasized in the context of inferring ECS from the historical record (see Bindoff et al., 2013; Lewis, 2014).

While the above example is based on discrete (binary) Φ, in this assessment all variables are continuous. Hence, probabilities are expressed as densities or continuous distributions in a real space. To illustrate this case, consider that one has a thermometer with a Gaussian‐distributed error of standard deviation 2°C and measures the temperature T of some fresh water and obtains 1.5°C. Now since we know the water is liquid, the temperature must a priori lie between 0°C and 100°C. If our prior p(T) is uniform (all unit intervals of Celsius temperature equally likely) within that range and 0 outside, our likelihood p(obs|T) is normally distributed about 1.5°C, but the posterior PDF is truncated with no weight on negative temperatures. Thus, the maximum‐likelihood temperature (the one most consistent with the evidence) is 1.5°C—but the expectation value (the mean of the PDF, or the average true temperature if this situation occurred many times) is higher at 2.27°C. One could also imagine a highly nonuniform prior within 0–100°C, for instance, if the water were known to be in the Arctic region. In this case T would be highly likely a priori to be near the freezing point, and its expectation value given the measurement might even be lower than the measurement. Other priors could also be possible, based on analogous past experience or any other line of reasoning.

The role of multiple lines of evidence, important for our assessment, is also clarified by a Bayesian approach. If, in the above example, we had two independent measurements with the same Gaussian uncertainty each returning 1.5°C, we would multiply the two likelihoods and renormalize, obtaining a new likelihood with a standard deviation of 1.4°C (which could be combined with the same prior to get a new PDF). This independence assumption would be justified if the second observation came from a different technology, for example, infrared radiometry. But if it came from the same thermometer used again, we would expect the same error both times and the new likelihood and PDF would be unchanged. If the second observation came from another thermometer by the same manufacturer, we would have to delve into the reasons for thermometer error to decide how independent we expect the two measurements to be. These issues are highly relevant to this assessment and are discussed in section 6.

The final generalization required is that our problem is multivariate. In section 2.4.2 we describe in more detail the multivariate problem solved in this assessment.

2.4.2. Description of Methods and Calculations

Following Equation 9, the most general approach for a multivariate system, after specifying a prior, would be to calculate the likelihood of the entirety of evidence E, as a function of the full set of model variables Φ (of which there are 15 if we treat six distinct feedbacks, λ, ∆F _2xCO2, S, and three pairs of ∆T and ∆F—one historical and two paleoclimate—see sections 3 and 5). Calculating a 15‐dimensional likelihood function in this way is computationally inefficient and moreover is not very helpful conceptually. Fortunately, we can simplify and better understand the problem by considering more carefully the relationships between variables.

These relationships are illustrated graphically in Figure 2, separated into three broad lines of evidence. All quantities in Equations 3–5 are unknown (random) variables characterized by PDFs, shown as circles in this figure. So the only things “known” before priors are placed on the variables are the evidence (shown by boxes), the equations linking the variables, and the relationships between these variables and the evidence. Note that while many previous ECS studies have taken ∆F _2xCO2 as a known constant, we consider it as uncertain, and therefore, λ and S are not uniquely related—though in practice the uncertainty in ∆F _2xCO2 is relatively small and λ and S are nearly reciprocal.

Figure 2 shows the dependence in the inference model, in which individual feedbacks combine to determine λ, which then determines (together with ∆F _2xCO2) S and (together with forcings) the magnitude of forced responses. The arrows indicate direct causality, where a (“child”) node value is determined by the (“parent”) variables upstream that point to it. This has strict implications for the conditional independence of variables inherent in the joint distribution p(Φ)—most importantly, that any variable is conditionally independent of all others that are not its descendants, given its parents (see, e.g., Pearl, 1988). The Bayesian inference process can work backward, where information on a child tells us about its parent(s), and information from multiple children is independent if there are no direct links in the diagram between the children.

A first simplification therefore is that the evidence consists of a set of components (boxes in Figure 2), which we supposed to be conditionally independent given Φ. In general, we suppose the remaining uncertainties in E, once Φ is known, arise from instrumental and other errors that are unrelated between lines of evidence; possible violations of independence will be revisited later in the assessment. The likelihood components can be collected into lines of evidence (e.g., the three shown by colors in Figure 2), and, based on this independence ansatz, the likelihood of all evidence E can be written as follows:

$$p\left(E|\mathrm{\Phi }\right)=p\left(E_{\text{proc}}|\mathrm{\Phi }\right)p\left(E_{\text{hist}}|\mathrm{\Phi }\right)p\left(E_{\text{paleo}}|\mathrm{\Phi }\right),$$ (11)

where p(E _proc|Φ) is termed the “process likelihood,” which isolates the impact of process evidence, and so on for the other two. The multivariate PDF of Φ follows from inserting Equation 11 into Equation 9; to obtain the marginal posterior PDF of S, p(S|E) (or any other particular variable) would require integrating that multivariate PDF over all variables in Φ other than S.

A further simplification, however, is that in our inference model, each evidence line directly depends only on the most immediate model variable(s), not the entire Φ. For example, once λ and historical ∆F are specified, the historical warming ∆T does not depend on paleoclimate changes or individual feedbacks, a further statement of conditional independence. This means that the historical likelihood p(E _hist|Φ) can be written as a function of λ and ∆F _2xCO2 alone, for example, p(E _hist|λ,∆F _2xCO2). The same can be done for the paleo evidence. This motivates an expression analogous to Equation 9 for the total likelihood or PDF of just the variables of interest, λ or S, which we develop here for better understanding of the approach.

It is not possible, however, to simplify the entire process likelihood in a similar way to the historical and paleo likelihoods as above. This is because the primary part of this evidence consists of multiple pieces E _i pertaining to individual feedbacks i, and these cannot be written as a function of λ; hence, we cannot directly write p(E _proc|λ,∆F _2xCO2). Each E _i can, however, be written as a function of its parent feedback value λ _i alone which is again a great simplification. These feedback values are the independent variables in our inference model (those with no parent variables). Starting from these, the PDF of each feedback, given its direct evidence E _i only, is

$$p\left({\lambda }_i|E_i\right)=p\left(E_i|{\lambda }_i\right)p\left({\lambda }_i\right)/p\left(E_i\right).$$ (12)

where p(λ _i) is a prior PDF for λ _i. The posterior PDF of the total λ given all individual‐feedback evidence E _i is an integral over these component feedbacks:

$$p\left(\lambda |E_i,\dots ,E_n\right)\propto \int \prod p\left({\lambda }_i|E_i\right)\delta \left(\lambda -\mathrm{\Sigma }{\lambda }_i\right)\mathrm{d}{\lambda }_1\mathrm{d}{\lambda }_2\dots \mathrm{d}{\lambda }_{\mathrm{n}},$$ (13)

where hereafter, for clarity, we omit normalization constants. In the special case of Gaussian distributions, which result from the priors and likelihoods employed in section 3, this integral produces another Gaussian whose mean and variance are simply the sums of those of the components (see, e.g., Ross, 2019).

There is additional process evidence E _λ, from “emergent constraint” approaches, that depends on the total λ; that is, E _proc = {E _i, …, E _n, E _λ}. The PDF of λ given all process evidence, if both types are independent, is the product of the component‐derived PDF (Equation 13) and the likelihood of this additional evidence:

$$p\left(\lambda |E_{\text{proc}}\right)\propto p\left(\lambda |E_i,\dots ,E_n\right)p\left(E_{\lambda }|\lambda \right).$$ (14)

(However, in part because of dependence concerns, this evidence is only used in a sensitivity test, see section 3.) The historical and paleo evidence depends on λ and ∆F _2xCO2 (denoted F in Equations 15–17 for brevity). We assume (see section 3.4) that λ and F are independent a priori, so that

$$p\left(\lambda ,F|E_{\text{proc}}\right)=p\left(\lambda |E_{\text{proc}}\right)p\left(F\right).$$ (15)

This can be combined with the other lines of evidence to yield

$$p\left(\lambda ,F|E\right)\propto p\left(\lambda ,F|E_{\text{proc}}\right)p\left(E_{\text{hist}}|\lambda ,F\right)p\left(E_{\text{paleo}}|\lambda ,F\right)$$ (16)

Integrating Equation 16 over F yields a marginal PDF of λ. Also, using Equation 4, the marginal PDF of S could be obtained by integrating over λ and F:

$$p\left(S|E\right)\propto \int p\left(F\prime \right)p\left(\lambda \prime ,F\prime |E\right)\delta \left(S-F\prime /\lambda \prime \right){\left(\partial S/\partial F\right)}^{-1}{\left(\partial S/\partial \lambda \right)}^{-1}\mathrm{d}F\prime \mathrm{d}\lambda \prime ,$$ (17)

where primes denote integration variables. In practice, ∆F _2xCO2 contributes very little to the uncertainty in historical or paleo forcings and therefore plays a weak role in those likelihoods. If the interdependence among likelihoods arising from this small role is neglected, the above integrals over ∆F _2xCO2 could be performed separately for each line of evidence rather than over the entirety, yielding Equation 10 given earlier or an equivalent equation for S. Note that calculations shown in this assessment do not make this approximation. Equation 10 or its S equivalent resemble the basic equation used in past ECS studies on the historical and/or paleo records, except that the process PDF p(λ|E _proc) or p(S|E _proc) takes the place usually occupied by the prior on ECS or λ.

So far Equation 16 shows likelihoods for historical and paleo evidence only. The process PDF (Equation 14) can be written as the product of a process marginal likelihood p(E _proc|λ) and a PPD, p(λ), which is the prior PDF on λ induced by those placed on the independent variables upstream. An analogous product can be written for S. Either PPD can be calculated from Equations 12–17 by setting the likelihoods to unity, since it is just the predicted distribution of λ and S with no evidence. The marginal process likelihood is then the ratio of the process PDF to this PPD. Calculating this likelihood thus requires integrating over all possible combinations of the λ _i (i.e., their joint distribution) weighted by their prior probabilities. This is because an individual feedback value/evidence E _i cannot be predicted from the sum λ alone; its likelihood of occurrence for a given total depends on the probabilities (hence priors) of all of the feedbacks. Hence, the marginal process likelihood versus λ or S is not independent of the prior the way the other likelihoods are: It changes each time the prior is changed.

There is in general no closed form solution to Equations 13–17 and therefore we use a Monte Carlo sampling approach to compute the solution. This is described further in section 2.4.4. This approach is fully consistent with Equations 13–17 but approaches the problem more directly via Equation 11.

2.4.3. Specification of Priors and Novel Aspects of Our Approach

As mentioned in section 2.3, prior PDFs must be placed on all independent variables and are propagated to the dependent variables (such as λ and S) via the model equations. For each of the independent variables except the λ _i, the prior PDF is specified by expert judgment using the available evidence about that quantity, without considering any other lines of evidence. These expert priors are given in the appropriate sections and are crucial in determining the historical and paleo likelihoods. Note that PDFs of these and other variables change once all the evidence is propagated through the model. For example, if historical warming turns out to be weaker than would be expected based on the other lines of evidence, then our posterior PDF of S shifts downward from what it would have been with only the other evidence—but at the same time, our posterior PDF of the historical ∆F also shifts downward relative to what we expected a priori. These revised, posterior PDFs will not be presented except those of S and the historical forcing ∆F.

Many previous studies have used past climate changes to constrain climate sensitivity using Bayesian methods (e.g., Aldrin et al., 2012; Johansson et al., 2015; Skeie et al., 2014, 2018) and so had to specify priors. Such studies mostly aimed to constrain S without incorporating the process knowledge exploited here, instead fitting inference models formulated with S or λ as an independent variable. As such, they required prior PDFs for S (which were typically uniform in S or peaked at S values somewhere within the 1.5‐ to 4.5‐K range). Due to the use of a different inference model, the prior on S in this assessment is nominally based on less information and hence not fully equivalent to those in the past Bayesian ECS studies. This and other issues of how to interpret the priors are taken up in section 7.2.

2.4.4. Calculation of Likelihoods and Sampling Method

Implementation of the Bayesian updating generally follows the principles described in Liu (2004), in which we sample from our prior over Φ and weight each instance in the sample according to the likelihood p(E|Φ). The weighted ensemble is then an approximation to the posterior PDF and can be analyzed and presented as desired (e.g., in terms of the mean/expectation and credible intervals) via relationships such as expectation E[Φ|E] = Σ (w _j Φ_j)/Σ (w _j), where Σ denotes a sum over all instances Φ_j from Φ and w _j is the weight. This approach can also be viewed as a specific form of importance sampling (Gelman et al., 2013) in which the prior is used as an initial “proposal” distribution from which samples are drawn and subsequently weighted to estimate the target distribution.

To create the sample, we begin by sampling the independent variables according to their priors (e.g., uniform sample distribution for a uniform prior) and then use the inference model equations to calculate the values of each dependent variable (such as S) and the model outputs for each instance in the sample. This yields a sample population approximating the PPD for all variables in Φ. Next, a weight w _j for each instance j is computed from the global likelihood function (which is a product of local likelihoods, cf. Equation 11). Finally, the posterior PDF is approximated by the histogram of the weighted sample (see below).

For the individual‐feedback process evidence (see section 3), the likelihood for each feedback component i is represented as a Gaussian function with mean μ _i and standard deviation σ _i. Each sample instance j is accordingly given a likelihood weight for λ _ij equal to G(λ_ij, μ _i, σ _i) where λ _ij is the i _th feedback value of the j _th instance in the sample and G(x, μ, σ) is defined as the Gaussian N(μ, σ) function evaluated at x. The weights for the six feedbacks are multiplied to give the total likelihood weight for the individual‐feedback evidence. In the baseline case with a prior uniform in λ _i, the posterior after updating by this likelihood thus approximates the anticipated Gaussian N(μ _i, σ _i), although we do not explicitly take advantage of this relationship within the algorithm, in order to allow full generality. Similarly, an “emergent constraint” likelihood is specified in terms of a Gaussian in total λ, evaluated G(λ _j, μ _λ, σ _λ).

For the observed temperature change evidence (see sections 4 and 5), we consider a forward model in the basic form (cf. Equation 3):

$$\mathrm{\Delta }T=f\left(\mathrm{\Phi }\prime \right),$$

where the predicted temperature change ΔT is a function of the other model variables Φ′. The observed temperature change ΔT _obs, which includes an uncertainty σ _e due to measurement error and unforced variability, is interpreted as giving rise to a likelihood which takes the Gaussian form N(ΔT, σ _e) (Annan & Hargreaves, 2020). Thus, the likelihood assigned to any Φ′ is G(ΔT, ΔT _obs, σ _e), which is the probability of the observed warming for a given ΔT = f(Φ′). This value is maximized when ΔT is equal to ΔT _obs and drops off rapidly as the difference between ΔT and ΔT _obs becomes large compared to σ _e. The exact forward models used will differ from 3 due to additional terms as previously mentioned and are given in sections 4 and 5.

Likelihood weights for process (excluding emergent‐constraint), emergent‐constraint, historical, and paleoclimate evidence (separately for cold and warm periods) are calculated for each instance. These weights (or a subset thereof) are then multiplied together to give a single likelihood weight w for each member of the sample.

The posterior PDF for Φ can be calculated from the weighted sample distribution; marginal PDFs for variable subsets are calculated from the marginal sample distributions. For example, a posterior PDF for S is calculated as the histogram of S in the sample (i.e., the PPD), weighted by the corresponding likelihood weights—that is, p(S|E) ∝ Σ_j∈Q w _j, where the set Q contains all instances j whose S _j falls within a histogram bin centered on S—with normalization. Posterior PDFs for any other variable in Φ are calculated similarly. The marginal likelihood function for any variable (e.g., S) is just the average weight w from the same histogram. Hence, the marginal likelihood is equal to the PDF divided by the PPD.

Various approximations are made in the sampling calculations to make them less computationally expensive. The Baseline calculation initially samples each feedback component uniformly and independently over the range U(−10,10). We also use an alternative prior, which is calculated by weighting samples from the Baseline prior to give a PPD for S which is uniform from near 0 to 20 K. This does not include 0 because the Baseline prior covers a finite range U(−10,10). When calculating the posterior, to avoid wasted computational effort, we restrict the initial sample to absolute values for each feedback λ _i within a six standard deviation range of the likelihood function for that feedback. This does not affect the posterior PDF because the likelihood is effectively 0 outside this range. The posterior calculation in section 7.2 with a uniform‐S PPD uses a weighted version of an equivalent sample (and so also makes this approximation). This approximation enabled us to produce stable 5–95% ranges with a Monte Carlo sample size of 2 × 10¹⁰. We also used kernel smoothing to produce satisfactorily smooth posterior PDFs. (We applied a Gaussian kernel smoother to the posterior PDFs with a standard deviation of 0.1 K and found that this affected the 5–95% ranges by at most 0.02 K.) Since in the Baseline calculation the feedback evidence yields a process PDF, which is Gaussian in λ (cf. Equations 13 and 14), this can be reused as a feedback‐based prior on total lambda and combined with the prior on ∆F _2xCO2 via Equation 15 and the downstream likelihoods via Equations 14 and 16, thus avoiding the need to sample from a prior on the λ _i feedbacks each time the calculation is repeated. This more streamlined calculation requires only a 2 × 10⁸ sample size and is used as the baseline for most of the sensitivity tests with a uniform‐λ prior in section 7. In calculations that use a uniform‐S prior and omit process evidence (in sections 4 and 7), we speed up the calculations by sampling from uniform independent distributions for S and ∆F _2xCO2, calculating λ from Equation 4.

3. Constraints From Process Understanding

3.1. Introductory Concepts

From Equation 4, climate sensitivity is the amount of surface temperature increase necessary to induce a radiative response ∆R whose energy loss to space cancels the energy trapped by a CO₂ doubling (the CO₂'s radiative forcing ∆F _2xCO2). The radiative response ∆R is achieved through changes in the various climate system constituents that influence Earth's radiation balance. The goals of “Process” research into climate sensitivity are to determine (a) the magnitude of CO₂ radiative forcing and (b) the mix of changes in various climate system constituents that produces the necessary radiative response ∆R. The responses of these constituents to warming are termed feedback. The constituents, including atmospheric temperature, water vapor, clouds, and surface ice and snow, are controlled by processes such as radiation, turbulence, condensation, and others. The CO₂ radiative forcing and climate feedback may also depend on chemical and biological processes.

3.1.1. Definitions of CO₂ Radiative Forcing and Climate Feedbacks

CO₂ radiative forcing ∆F _2xCO2, with units W m⁻², includes both the direct radiative impact of doubling of atmospheric CO₂ and the indirect radiative impacts arising from adjustments of the atmosphere and surface that happen without the surface temperature T having appreciably risen.

For climate feedbacks, we expand upon Equation 5 to express the total climate feedback parameter λ, with units W m⁻² K⁻¹, as the sum of the sensitivities of TOA radiation to factors x _i multiplied by how those factors x _i change with surface warming:

$$\lambda ={\sum }_i{\lambda }_i={\sum }_i\frac{\partial N}{\partial x_i}\frac{d{x}_i}{\partial T}={\lambda }_{\mathit{\text{Planck}}}+{\lambda }_{\mathit{\text{water vapor}}}+{\lambda }_{\mathit{\text{lapse rate}}}+{\lambda }_{\mathit{\text{surface}}}+{\lambda }_{\mathit{\text{clouds}}}+{\lambda }_{\mathit{\text{other}}}$$ (18)

where x _i conventionally includes the changes in temperature (Planck), water vapor, lapse rate, surface albedo, and clouds. Each of the terms on the right‐hand side of Equation 18 is known as a “feedback,” for example, the Planck feedback, water vapor feedback, and lapse rate feedback. Since ∆F _2xCO2 is defined per a prescribed atmospheric CO₂ concentration, carbon cycle feedback on CO₂ is excluded here. However, we also consider feedbacks λ_other from other changes in atmospheric composition such as those associated with atmospheric ozone and aerosol‐cloud interactions and from changes in stratospheric temperature and water vapor not normally quantified. Readers interested in this conventional forcing‐feedback theory may consult Hansen et al. (1984), Dessler and Zelinka (2015), Sherwood et al. (2015), and Hartmann (2016).

3.1.2. Lines of Evidence for Process Understanding

Process evidence focuses on the current climate and its internal variability, excluding evidence considered in the historical and paleoclimatic sections (sections 4 and 5, respectively). There are four primary sources for process evidence for S,∆ F _2xCO2 and climate feedbacks:

1. Global climate models (GCMs). Their strength is that they are a globally complete representation of the climate system approximately satisfying known conservation laws of energy, mass, and momentum. They can be used to estimate feedback and forcing from idealized experiments, such as the simulation following an abrupt quadrupling of CO₂ or an atmosphere‐model‐only integration with quadrupled CO₂ but fixed SST and sea ice. One weakness is that they account for subgrid processes, particularly of clouds and convection, with approximate parameterizations whose varying representations contribute to a large intermodel spread in the cloud feedback. Archives of many GCM simulations, particularly those collected for the Coupled Model Intercomparison Projects (CMIPs, Eyring et al., 2016; Meehl et al., 2005; Taylor et al., 2012), have been used to determine the robust and nonrobust aspects of GCM‐simulated CO₂ forcing and feedbacks.

2. Observations. Short‐term responses at global and regional scales can be quantified from satellite observations of the covariation of TOA radiation with temperature, particularly from interannual variability. These observable responses likely differ from those associated with CO₂‐induced long‐term warming, creating uncertainty as to the interpretation of short‐term feedback‐like responses. GCMs can be used to test the correspondence between short‐term responses and the longer‐term ones determining λ and S.

3. Process‐resolving models. High‐resolution atmospheric simulations, such as LESs, explicitly calculate the turbulence associated with clouds. These models have increasingly been used to understand cloud feedbacks, primarily for tropical marine low‐level clouds, by forcing them with the environmental changes associated with climate warming. Their simulated cloud responses are likely more realistic than those of GCMs because LES resolves the main cloud‐forming motions, which GCMs must parameterize. LES does, however, still contain parameterizations of cloud microphysics and the motions that are smaller than the resolution of their grids, which is typically ~10 m for boundary layer clouds or ~100 m for deep convection clouds. LES also cannot simulate all important cloud conditions, must be forced by uncertain environmental changes from GCMs, and, for the case of boundary layer clouds, may be missing the effects of mesoscale motions occurring at scales larger than their domain size. A very different type of process model used to estimate the clear‐sky direct component of ∆F _2xCO2 is the observationally verified line‐by‐line radiative transfer model, which is more accurate than the radiative transfer models used in GCMs.

4. Theory. Although limited in precision, theory can provide critical assurance regarding feedbacks inferred from the other sources. For example, basic thermodynamics supports the lapse rate and water vapor feedbacks. Also, the understanding that tropical tropospheric overturning circulations are governed by the balance between subsidence warming and clear‐sky radiative cooling underlies the fixed‐anvil temperature hypothesis relating to the high‐cloud altitude feedback.

A new type of reasoning called emergent constraints arises by combining two of these primary sources—GCMs and observations (Hall et al., 2019). Emergent constraints are empirical relationships between a present‐day climate system variable and a future climate change that emerge in an ensemble of simulations by structurally diverse GCMs. (More generally, emergent constraints also exist using variables from other periods in the past but these are not discussed in this section.) If the constraint is valid, one may infer a more likely estimate of the future change when given an observation of the present‐day variable. Using emergent constraints in this way can be viewed as a kind of model weighting. Confidence in this inference depends on the strength of the present‐to‐future relationship, the relative observational uncertainty of the present‐day variable, and how well the relationship is understood. Emergent constraints exist for S as well as individual feedbacks and are used to inform our assessment.

3.1.3. Methodology for Assessing Process Understanding

As discussed in section 2.4, we use two approaches to assess the constraints on S. We do not assess S directly but rather assess ∆F _2xCO2, λ and λ _i, which are related to S via Equations 4 and 18.

In the primary approach, we use all sources of evidence to determine a prior for ∆F _2xCO2 (section 3.2.1) and likelihood functions for each individual feedback component λ _i in Equation 18. Consistent with our target definition of S, we characterize the feedbacks λ _i acting over the 150 years following an increase of CO₂. The relatively certain Planck, water vapor, lapse rate, surface albedo, and other feedbacks are assessed in sections 3.2.2, 3.2.5, and in section 3.3 we assess the cloud feedback that is much more uncertain than the other feedbacks. For the cloud feedback we assume that the total cloud feedback is a linear sum of feedbacks from individual cloud types, each of which we consider separately. Such an approach is necessary to fully exploit our current understanding, much of which pertains to specific cloud types. In section 3.4, we combine the results from individual feedbacks to derive PDFs for the total cloud feedback and total climate feedback parameter λ. Finally, in section 3.5 we examine observations of global interannual radiation variability to address the concern that we might have missed some important feedbacks through our method of combining individual feedbacks.

In the secondary approach, we consider emergent constraints that have been used to directly infer S based upon the relationships between S and present‐day climate system variables exhibited in GCM ensembles. This evidence is given its own distinct likelihood function in section 3.6, where we also discuss the relative independence of this evidence from that used in the primary approach and why greater caution in the use of this evidence is required.

A summary of all assessed process understanding of S then follows in section 3.7.

3.1.4. Further Considerations

Both approaches are consistent with the effective climate sensitivity S definition used (section 2.1). Thus, when considered, GCM feedback estimates are generally calculated from the linear regression of associated anomalies on global mean SAT during the first 150 years of the abrupt 4xCO₂ experiment simulations. One problem with this approach is that GCM feedback estimates calculated in this manner when combined with a CO₂ forcing that uses surface albedo and tropospheric adjustments from fixed‐SST GCM experiments (section 3.2.1) would overestimate our target definition of S by ~15%. (This is because the CO₂ forcing estimated from fixed‐SST experiments is ~15% larger than that estimated via ordinary linear regression from abrupt 4xCO₂ experiments.) However, because this error only affects feedback estimates from GCMs and not the feedback estimates from theory, LES, or observations of interannual variability, the overall impact on the feedback values estimated with the primary approach would be much less (<5%) and is accordingly neglected.

Mathematically, Gaussian likelihoods are assigned for each individual feedback component λ _i. This means that we assume that the likelihood is a Gaussian function of the variable being assessed, requiring that we specify two parameters—the mean and standard deviation. Note that if a Gaussian likelihood function is applied to a variable with a broad (e.g., uniform) prior PDF in that variable, the implied posterior PDF will also be Gaussian with the same mean and standard deviation. Broad priors are appropriate for feedback components for which we do not have an a priori expectation of their value, and which can be positive or negative (our Baseline prior case). Hence, the likelihood functions for λ _i determined below can be considered equivalent to PDFs for this case.

3.2. Process Understanding of CO₂ Radiative Forcing and Noncloud Feedbacks

3.2.1. CO₂ Radiative Forcing

Increases in CO₂ lead, all other things unchanged, to a decrease in LW emission to space (i.e., the CO₂ “greenhouse effect”). This instantaneous radiative forcing for a doubling of CO₂ can be obtained from very accurate line‐by‐line radiative transfer models (W. D. Collins et al., 2006; Etminan et al., 2016; Pincus et al., 2015); these are in very good agreement and provide a global mean estimate of 2.9 W m⁻² at the TOA (Figure 3). The instantaneous CO₂ radiative forcing varies with location due to variations in temperature, water vapor, clouds, and tropopause position (Huang, Tan, & Xia, 2016). The traditionally defined forcing also includes a contribution from the perturbed stratosphere because the stratosphere is dynamically isolated from the surface (Hansen et al., 1981). Within a few months, the stratosphere cools in response to increased CO₂ causing an additional reduction in the emission to space of LW radiation. This “stratospheric adjustment” is well understood and is estimated to add 0.9 W m⁻² at the TOA (Figure 3).

Figure 3.

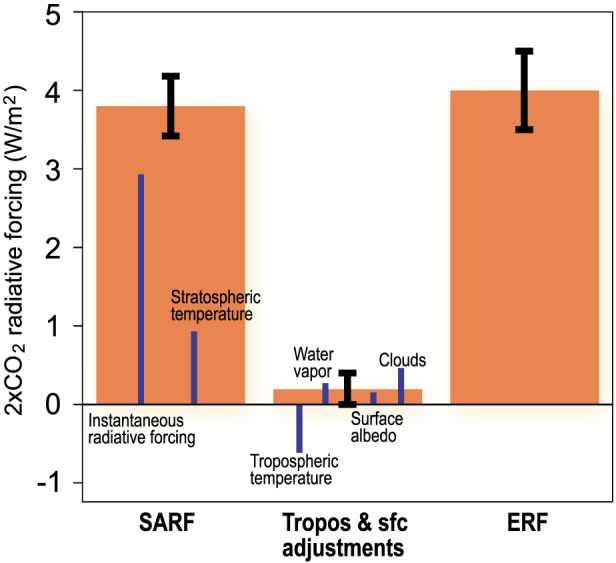
Assessed values of the 2xCO₂ effective radiative forcing (ERF) at the TOA. Orange bars represent stratospheric‐adjusted radiative forcing (SARF), tropospheric and surface albedo adjustments, and their sum (i.e., ERF). The error bar indicates the 5–95% ranges of the respective terms. Further decomposed components are presented for reference by blue bars based on Etminan et al. (2016) and Smith et al. (2018). The contribution from land surface warming has been excluded in the surface adjustment.

Using an updated line‐by‐line radiative transfer model that also includes the SW absorption bands of CO₂ as well as the spectral overlap with N₂O absorption bands, Etminan et al. (2016) estimate the sum of the instantaneous radiative forcing and the stratospheric adjustment, often called the stratospheric‐adjusted radiative forcing (SARF), to be 3.8 W m⁻² for a doubling of CO₂, using the equation in their Table 1. They also show that the radiative forcing increases slightly more than logarithmically with CO₂ concentration. The 5th to 95th percentile uncertainty range for the SARF is estimated to be ±10% (i.e., ±0.38 W m⁻²), with major components of the uncertainty due to the radiative transfer code, the method of calculating the stratospheric adjustment, and the specification of temperature, clouds, and tropopause position (Etminan et al., 2016; Hodnebrog et al., 2013). Uncertainties due to spectroscopic data themselves are considered to be much smaller (<1%) (Mlynczak et al., 2016).

Table 1.

Assessed Values for ∆F_2xCO2 and Climate Feedbacks λ_i Based Upon the Various Lines of Process Evidence

Term	Value	Source
		GCMs	Observations	Process‐resolving models	Theory
Effective radiative forcing from a CO2 doubling ∆F 2xCO2	N(+4.00, 0.30)	✓✓	✓	✓✓	✓
Planck feedback	N(−3.20, 0.10)	✓✓	✓✓		✓✓
Water vapor + lapse rate feedback	N(+1.15, 0.15)	✓✓	✓✓	✓	✓
Surface albedo feedback	N(+0.30, 0.15)	✓✓	✓✓		✓
Individual cloud feedbacks
High‐cloud altitude	N(+0.20, 0.10)	✓✓	✓	✓	✓
Tropical marine low cloud	N(+0.25, 0.16)		✓✓	✓✓	✓
Tropical anvil cloud area	N(−0.20, 0.20)		✓✓		✓
Land cloud amount	N(+0.08, 0.08)	✓✓	✓		✓
Middle‐latitude marine low‐cloud amount	N(+0.12, 0.12)	✓✓	✓✓		✓
High‐latitude low‐cloud optical depth	N(+0.00, 0.10)		✓✓		✓
Total cloud feedback λ clouds	N(+0.45, 0.33)
Stratospheric feedback	N(+0.00, 0.10)	✓✓	✓
Feedbacks induced by atmospheric composition changes	N(+0.00, 0.15)	✓✓
Climate feedback parameter λ	N(−1.30, 0.44)

Note. The “Source” column identifies which lines of process evidence support the assessed value. If the source column has a double check mark (✓✓), then it signifies that the line of evidence provided a usable quantitative estimate. If the source column has a single check mark (✓), then it signifies that the line of evidence provided qualitative support for mechanisms involved or the sign of the feedback but does not provide a usable quantitative estimate. If the source column is without a check mark, then it signifies that the line of evidence was not used in the assessment of that term. The reason for not using a line of evidence for a given term varies but typically was because a line of evidence is absent or not applicable for that term or because it provided inconsistent or untrustworthy results. Values are reported as Gaussians in the format N(x, y), where x is the mean and y is the standard deviation. Means and standard deviations have units of W m⁻² for ∆F _2xCO2 and W m⁻² K⁻¹ for feedbacks. ∆F _2xCO2 is specified as a prior, λ and λ _clouds as a PDF, and the remaining λ _i as likelihood functions.

Components of the surface and troposphere also adjust in response to the increase in CO₂, independent of the rise in surface temperature (Boucher et al., 2013; Gregory & Webb, 2008). They are fundamentally the same as the stratospheric adjustment in a sense that they occur rapidly to modulate the TOA radiative flux (Sherwood et al., 2015), but their estimates are methodologically distinct as currently these tropospheric and surface adjustments can be estimated globally only from GCMs (M. H. Zhang & Huang, 2013; Smith et al., 2018; Vial et al., 2013). Clouds are one component with reductions of low and middle‐level clouds producing a positive radiative adjustment of ~0.4 W m⁻² (Andrews, Gregory, Forster, et al., 2012; Kamae et al., 2015; Sherwood et al., 2015; Smith et al., 2018). Several mechanisms for these cloud reductions have been identified. First, the increase in CO₂ causes the vertical profile of radiative cooling to shift to higher levels. This results in less radiative cooling at low levels, a shoaling of the marine boundary layer, and a reduction of low clouds (Kamae & Watanabe, 2013). LES also simulates boundary layer shoaling and low‐cloud reductions (Blossey et al., 2016; Bretherton & Blossey, 2014; Bretherton et al., 2013), lending credence to the GCM results. Second, the increase in CO₂ also causes a reduction in the vertically integrated tropospheric radiative cooling, which reduces the strength of the overall hydrologic cycle and hence the overall amount of cloud produced (Dinh & Fueglistaler, 2020). Finally, plant physiological processes cause the stomatal resistance to increase with increasing CO₂ (Doutriaux‐Boucher & Webb, 2009). The resulting reduction in surface evaporation and concomitant increase in sensible heat flux to the atmospheric boundary layer dries and warms the near surface air. This reduces the low‐level relative humidity and clouds over land (Andrews & Ringer, 2014; Arellano et al., 2012).

Other adjustments include negative ones from increased LW emission to space from a warmer troposphere and increased land surface temperatures and positive ones from increased water vapor and reduced surface albedo (Figure 3; Andrews, Gregory, Forster, et al., 2012; Kamae & Watanabe, 2012; Smith et al., 2018; Vial et al., 2013). The increase in land surface temperature in these GCM experiments results from the increase in surface downward LW radiation (itself the direct consequence of the increased CO₂ concentration) and happens despite the simulations being performed with fixed SSTs. The land surface warming slightly increases the global mean surface temperature, and its inclusion would be inconsistent with a definition of radiative forcing, which counts only those adjustments that occur without change in the global mean surface temperature. Thus, we exclude the land surface warming component, yielding a total of +0.2 W m⁻² as the sum of surface albedo and tropospheric adjustments, as calculated from the data in Smith et al. (2018). (In reality, a portion of the other surface and tropospheric adjustments are the consequence of the land surface warming and also should be excluded. However, current research has not isolated the portion of these adjustments that results from the land surface warming from the portion that directly responds to the CO₂ concentration.)

The sum of the instantaneous radiative forcing and the stratospheric, tropospheric, and surface albedo adjustments is known as the ERF and for a doubling of CO₂ will be denoted with the symbol ∆F _2xCO2. From the above arguments and Figure 3, we estimate the Gaussian prior of ∆F _2xCO2 to have a mean of 2.9 + 0.9 + 0.2 = 4.0 W m⁻². As for uncertainty in the ERF, we assign its 5th to 95th percentile uncertainty range to ±0.5 W m⁻², where the increase in uncertainty above that of the SARF is attributed to the additional source of uncertainty from the surface and tropospheric adjustments (dominated by the clouds) (Smith et al., 2018). Interpreting this uncertainty as being Gaussian distributed, we determine the standard deviation to be 0.3 W m⁻². Altogether, we assess the prior of ∆F _2xCO2 to be N(+4.0, 0.3), where we use the notation N(x, y) to indicate a Gaussian distribution with mean x and standard deviation y.

To estimate the CO₂ ERF for perturbations other than a doubling, different approaches are used in the paper. To estimate a CO₂ ERF time series over the historical period, section 4 uses the equation for SARF in Table 1 of Etminan et al. (2016) scaled by the ratio of ERF to SARF for CO₂ doubling which is 4.0/3.8 (an increase of 5%). The scaling factor is applied under the assumption that the sum of tropospheric and surface albedo adjustments is linearly proportional to the SARF. Section 5 follows the same approach and also adjusts the forcing of CH₄ and N₂O by the same 5% factor, based upon the assumption that the adjustments behave similarly for these other well‐mixed GHGs.

3.2.2. Planck Feedback

The Planck feedback represents the extra emission to space of LW radiation arising from a vertically uniform warming of the surface and the atmosphere with no change in composition. Physical expectation for this feedback is that λ_Planck ≈  − 4εσT³ ≈  − 3.3 W m⁻² K⁻¹ for present‐day conditions, and the values shown in Figure 4 from GCMs of −3.2 ± 0.04 W m⁻² K⁻¹ (1‐sigma) (Caldwell et al., 2016; Colman & Hanson, 2017; Vial et al., 2013) and those from observations of interannual variability (Dessler, 2013) are both in general agreement with this physical expectation. Uncertainties in modeled λ_Planck arise from differences in the spatial pattern of surface warming, and the climatological distributions of clouds and water vapor that determine the planetary emissivity (ε). In particular, the latter impacts the radiative temperature kernel, which is often held fixed in studies of inter model spread, thus leading to slight underestimates of structural uncertainty in λ_Planck within individual studies. Accounting for these issues, we assign the likelihood function for the Planck feedback to be N(−3.2, 0.1).

Figure 4.

Estimates of global mean climate feedbacks from observations of interannual variability (blue triangles), from CMIP5 and CMIP6 model simulations of global warming in response to an abrupt CO₂ quadrupling (colored circles—orange: Vial et al., 2013; green: Caldwell et al., 2016; red: Colman & Hanson, 2017; and purple: Zelinka et al., 2020) and from this assessment (black squares). Error bars on climate model feedback estimates span the one standard deviation range across models. Observational estimates are derived using a combination of ERA‐Interim meteorological fields and CERES TOA radiative fluxes (Loeb et al., 2009) covering the period March 2000 to December 2010 (Dessler, 2013). Error bars on the observational estimates are 1‐sigma uncertainties, accounting for autocorrelation. Individual feedbacks are computed by multiplying temperature‐mediated changes in relevant fields by radiative kernels (Huang et al., 2017; Shell et al., 2008; Soden et al., 2008). Error bars on values from this assessment correspond to 1‐sigma uncertainties. Note that Planck feedback estimates are offset by 2.5 W m⁻² K⁻¹ from their actual values in order that they appear within the plot range.

3.2.3. Water Vapor and Lapse Rate Feedbacks

The water vapor feedback quantifies the change in outgoing LW and absorbed SW radiation at the top of the atmosphere due to changes in atmospheric water vapor concentration associated with a change in global mean surface temperature. It arises because water vapor absorbs both LW and SW radiation and its concentration is expected to increase exponentially with temperature. The equilibrium (saturation) concentration increases following fundamental thermodynamic theory of the Clausius‐Clapeyron relationship. Although concentrations are usually below saturation (relative humidity less than 100%), this difference is well understood (Sherwood, Roca, et al., 2010) and well captured by GCMs with adequate resolution (Sherwood, Ingram, et al., 2010). Increases in specific humidity in response to 1 K of warming at constant relative humidity in the middle and upper troposphere result in a greater reduction in outgoing LW radiation than similar increases in the lower troposphere due to the masking effects of overlying water vapor and clouds (Soden et al., 2008; Vial et al., 2013). A given increase in specific humidity generally has a larger impact on LW than on SW radiation. GCM simulations and observations of the seasonal cycle, interannual variability, and climate trends all exhibit relatively small changes in relative humidity with warming, and therefore large increases in specific humidity with warming (Boucher et al., 2013; Dessler & Sherwood, 2009). The agreement of observations and GCMs with expectations from basic thermodynamic theory (Romps, 2014) leads to high confidence in robustly positive water vapor feedback.

The lapse rate feedback is the change in LW radiation emitted to space resulting from any nonuniformity of the change in temperature in the vertical. The LW emission to space depends on both surface and atmospheric temperatures. The more the atmosphere warms per degree of surface warming, the greater the increase in LW emission to space, and hence the greater the LW radiative damping of surface warming. Low‐latitude warming occurs along a moist adiabat such that free‐tropospheric warming exceeds that at the surface, causing a negative lapse rate feedback. At higher latitudes with greater stability and reduced coupling between the surface and free troposphere, warming is generally largest near the surface, leading to a positive lapse rate feedback (Manabe & Wetherald, 1975). Though consistently negative in the global mean, the strength of the lapse rate feedback varies among models and between observational estimates.

The impact of the separate uncertainties in these feedbacks on the climate feedback parameter λ is limited, however, because GCMs and physical reasoning suggest that these two feedbacks are strongly anticorrelated (M. H. Zhang et al., 1994; Held & Shell, 2012; Soden & Held, 2006). This is fundamentally because radiation to space depends to good approximation on the relative humidity, which changes little overall with warming as mentioned above, and the near‐surface temperature (Ingram, 2010). Although the anticorrelated spread of the two feedbacks in models was thought to arise because models experiencing greater upper tropospheric warming also experience greater moistening of the upper troposphere, it is now clear that the varying partitioning of surface warming between the tropics and extratropics is responsible. Specifically, models with warming concentrated at low latitudes have larger negative extratropical lapse rate feedbacks and stronger positive extratropical water vapor feedbacks (Po‐Chedley et al., 2018). As a result of this anticorrelation, it is useful to consider the sum of the lapse rate plus water vapor feedback, which is much less uncertain than the individual components. Still, there remains structural or methodological uncertainty with studies coming up with ensemble mean estimates of 0.9–1.4 W m⁻² K⁻¹ (Figure 4), which exceeds the intermodel spread. This could partly be due to the use of different radiative kernels, and likely related to SW absorption by water vapor (Pincus et al., 2015). These central estimates are in quantitative agreement, though, with estimates based on reanalysis (Dessler, 2013) (Figure 4). From this agreement and with consideration of the uncertainty in both reanalysis and GCM estimates, we therefore assess the likelihood function for the lapse rate plus water vapor feedback to be N(+1.15, 0.15).

3.2.4. Surface Albedo Feedback

The surface albedo feedback mostly arises from warming‐induced shrinkage of the cryosphere, which exposes less reflective surfaces that absorb more sunlight. It is dominated by snow and sea ice at high latitudes. Its strength is determined primarily by how snow and ice vary with global mean temperature, the contrast in albedo between frozen and nonfrozen surfaces, and the SW transmissivity of the atmosphere as the photons have to traverse the atmosphere at least twice to be reflected to space by the surface. Quantitative estimates from GCMs and observations based on interannual variability generally agree, with a feedback value near 0.3 W m⁻² K⁻¹ (Figure 4), and GCMs suggest that the feedback value implied by interannual variability is near that in response to long‐term CO₂ warming (section 3.5). The relevance of internal climate variability to global warming is also supported by an emergent constraint from the seasonal cycle for the surface albedo feedback which is very strong on Northern Hemisphere land and is mostly caused by snow cover changes (Hall et al., 2006; Qu & Hall, 2007, 2014). Early attempts to form an emergent constraint on sea ice feedbacks were less encouraging (Colman, 2013; Crook & Forster, 2014); however, recent progress has been achieved by taking advantage of the seasonal cycle in Arctic sea ice to constrain its contribution to global feedback (Thackeray & Hall, 2019). Mostly, this progress arises from a focus on surface albedo feedback in near‐term global warming, well before Arctic sea ice vanishes.

However, uncertainties can be larger than apparent in these comparisons for various reasons. Observed trends in surface albedo for the period 1979 to 2008, driven mostly by Northern Hemisphere sea ice loss, suggest a larger value of surface albedo feedback (Cao et al., 2015; Flanner et al., 2011; Pistone et al., 2014), although internal decadal variability may also be contributing to the diagnosed feedback in this period. Atmospheric transmissivity largely depends on liquid or mixed phase clouds in the Arctic summer season, and since many GCMs fail to simulate these clouds (Karlsson & Svensson, 2013; Pithan et al., 2014), GCMs likely overestimate the surface albedo feedback. The surface albedo feedback is also state dependent such that reduced cryospheric extent will reduce its magnitude in a warmer climate (Block & Mauritsen, 2013; Jonko et al., 2012; Thackeray & Hall, 2019). Separately, some GCMs exaggerate snow albedo feedback on land because they do not account for vegetation masking (Qu & Hall, 2007, 2014; Thackeray et al., 2018).

Based upon the good agreement between the observed estimate from interannual variability and the GCM values for both interannual variability and long‐term warming, we assign a central estimate of surface albedo feedback as 0.3 W m⁻² K⁻¹. As the just‐discussed uncertainties do not have a consistent sign, we do not alter the central estimate but double the quantitative uncertainties diagnosed from observations (Dessler, 2013) and GCM intermodel spread. Thus, we assess the likelihood function for the surface albedo feedback to be N(+0.3, 0.15).

Apart from the cryosphere, a small positive surface albedo feedback comes from the inundation of coastal lands by sea level rise which thus replaces land with a less reflective ocean surface. For the Last Glacial Maximum (LGM), the estimated radiative effect is of order 1 W m⁻² (Köhler et al., 2010; see section 5.1). But because sea level rise realized during 150 years and several K of warming would be limited to at most a few meters compared to the LGM change of over 100 m, the resulting effective feedback is only of order 0.01 W m⁻² K⁻¹. Other surface albedo feedbacks can occur as a function of changing precipitation patterns affecting soil moisture, vegetation changes in response to moisture and/or temperature changes, and changes in surface chlorophyll in response to ocean circulation changes. Calculations suggest that these feedbacks are also negligible on global mean temperature, although they can significantly affect regional climate changes (Levis et al., 1999).

3.2.5. Stratospheric Feedback

The feedback estimates shown in Figure 4 do not include those from the response of stratospheric temperature and water vapor to climate warming. Banarjee et al. (2019) calculate a stratospheric water vapor feedback of +0.15 ± 0.04 W m⁻² K⁻¹ (1‐sigma) from 27 CMIP5 model simulations of the abrupt 4xCO₂ experiment, resulting from the robust increase in stratospheric water vapor in each model. Climate warming, however, increases the strength of the Brewer‐Dobson circulation; this forces temperature anomalies that compensate for those induced by water vapor, with the result that the net feedback is smaller. From 11 CMIP5 models, Huang, Zhang, et al. (2016) quantify the total feedback from changes in stratospheric temperature and water vapor to be 0.00 ± 0.04 W m⁻² K⁻¹ (1‐sigma).

Based upon this study, we assess the likelihood function for this total stratospheric physical feedback to be N(+0.0, 0.10), where the increased standard deviation is justified by a lack of confidence in the fidelity with which the CMIP5 GCMs used by Huang, Zhang, et al. (2016) simulate stratospheric processes. Increased standard deviation is also justified by the lack of quantitative confirmation from observations. However, qualitative observational support for our assessment exists. Specifically, observations show that increases in lower stratospheric water vapor in interannual variability are correlated to increases in tropospheric temperature (Dessler et al., 2013) and observations support the notion that the Brewer‐Dobson circulation has strengthened over the most recent four decades (Fu et al., 2015, 2019).

3.2.6. Feedbacks From Other Atmospheric Composition Changes

In this assessment we consider well‐mixed gases (CO₂, CH₄, and N₂O) to be specified forcers, since in the modern era, they are effectively under human control. Thus, we do not include climate‐driven variations of these gases (e.g., carbon cycle feedbacks). However, this still leaves several possible sources of feedback apart from the traditional ones discussed so far.

One example is ozone, an absorber of both SW and LW radiation whose chemistry responds to temperature and temperature‐mediated circulation changes. The direct feedback from climate‐driven tropospheric ozone changes appears negligible (Dietmuller et al., 2014). However, the indirect effects of ozone changes could be considerable with one study suggesting that interactive ozone chemistry induces a substantial negative feedback averaging 0.13 W m⁻² K⁻¹ (Nowack et al., 2015). In their study, the robust strengthening of the Brewer‐Dobson circulation in a warmer climate causes a reduction of tropical lower stratospheric ozone, and because this region is particularly cold this leads to a reduction of the greenhouse effect. Follow‐up studies with other models found similar ozone concentration changes but similar or smaller impacts on the climate feedback parameter λ in response to CO₂‐induced climate change (Chiodi & Polvani, 2017; Dacie et al., 2019; Marsh et al., 2016). In contrast, a larger impact has been identified in response to solar forcing (Chiodi & Polvani, 2016) and with stronger impacts on atmosphere and ocean circulations (Chiodi & Polvani, 2017; Muthers et al., 2016; Nowack et al., 2017). Simulations with fully interactive atmospheric chemistry in the GISS CMIP5 models had an ~10% increased S compared to noninteractive versions (Schmidt et al., 2014), and this change was influenced in part by the ozone changes, but also the direct and indirect aerosol responses to a higher CO₂ world.

A warmer climate could also affect the production and/or lifetime of aerosols, in particular, dust, sea salt, natural sources of SO₂/SO₄ and reactive nitrogen species, and natural fires. Besides changes to the direct aerosol radiative effect (Paulot et al., 2020), this could lead to additional indirect aerosol effects on clouds (Gettelman et al., 2016; Gettelman & Sherwood, 2016) and fire‐induced effects on surface albedo. For example, one recent study showed that the increase in Southern Ocean emissions of primary organic matter and gaseous dimethyl sulfide with climate warming could impact the climate feedback parameter λ by 0.2 W m⁻² K⁻¹ depending on how the aerosol change affected cloud droplet number (Bodas‐Salcedo et al., 2019). Another recent study showed that the increase with warming of sea‐salt emissions altered λ by 0.13 W m⁻² K⁻¹ (Paulot et al., 2020). A review of possible mechanisms (Carslaw et al., 2010) suggested high uncertainty but a possible total effect of up to ±0.2 W m⁻² K⁻¹ over the 21st century. A direct CO₂ effect to the biophysical change in stomatal conductance over land has been accounted for in many GCMs and has been discussed in section 3.2.1.

In the absence of evidence for a systematic effect, we assess these processes have no expected net effect and assign the mean of the likelihood function for λ_otherto 0. For the standard deviation, we base our quantitative estimate on the Nowack et al. (2015), Schmidt et al. (2014), and Carslaw et al. (2010) studies, and assign a value of 0.15 W m⁻² K⁻¹.

3.3. Process Understanding of Cloud Feedbacks

Because both observations and GCMs indicate that the largest uncertainty resides with the cloud feedback (Figure 4), it has been the main focus of climate feedback research for the past three decades. The cloud feedback is particularly difficult since there are diverse cloud formation processes, most of which are challenging to represent in GCMs, and we must add up the response to warming of all cloud types capable of making a significant radiative contribution.

Given this complexity, it is logical to start by considering the mean and range of GCM simulations of both present‐day zonal mean cloud fraction and its response to global warming (Figures 5a and 5b) and the corresponding radiative impact (Figures 5c–5e), noting the simulated roles of various cloud types. (Note that these GCM cloud feedbacks are presented only to orient the reader for the following sections, which will assess specific cloud feedbacks based upon all of the evidence from observations, process‐resolving models, theory, and GCMs.)

Figure 5.

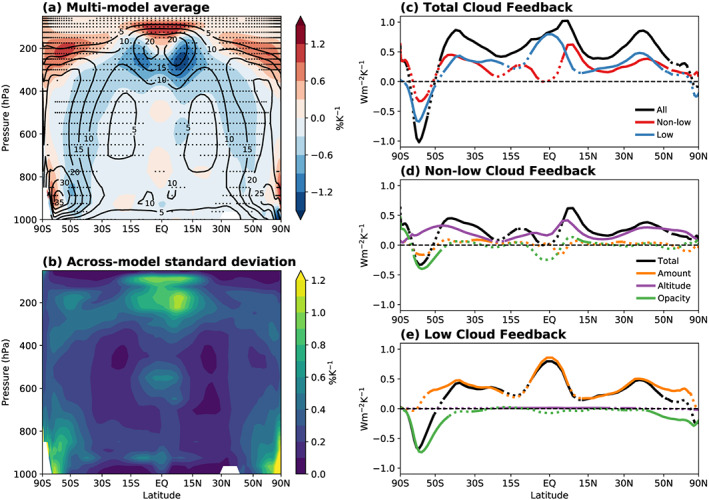
Multimodel and zonal mean cloud diagnostics: (a) Mean cloud fraction (contours, every 5%) and warming response (shading), with stippling where at least 20 of the 25 contributing CMIP5 models agree on the sign of the response. (b) Intermodel standard deviation of cloud fraction response. (c) Total cloud feedback from all clouds and also partitioned into contributions from low (cloud top pressures >680 hPa) and other (“nonlow,” cloud top pressures <680 hPa) clouds. (d) Non‐low‐ and (e) low‐cloud feedback partitioned into amount, altitude, and optical‐depth responses to warming. Latitudes where at least 14 of the 18 contributing models agree on the sign of the feedback are plotted with a solid line. Feedbacks in (c)–(e) are calculated from abrupt4xCO₂ simulations of seven CMIP5 models and from equilibrium 2xCO2 simulations of 11 CMIP3 slab‐ocean models (see Zelinka et al., 2016, for details). Note that all plots use an area‐weighted latitude scale. Figure based upon Zelinka et al. (2016).

Even though GCMs disagree significantly on the value of the total cloud feedback, at least 80% of 25 CMIP5 models agree on the direction of change in cloud cover over 80% of the atmosphere (see stippling in Figure 5a). This indicates that GCMs broadly agree on many large‐scale responses including an upward shift of clouds near the tropopause, a poleward shift of clouds in midlatitudes, and a decrease in clouds of 0.5–1% K⁻¹ in most of the troposphere. The intermodel standard deviation of cloud fraction response to warming (Figure 5b) can be considered an internal measure of model uncertainty. It tends to be greatest in regions where the multimodel mean cloud fraction is large, more so for tropical boundary layer and deep convective clouds.

Figure 5c shows the corresponding zonally averaged cloud feedbacks, with a solid line shown at latitudes where at least 14 of the 18 GCMs providing the needed data agree on the feedback sign. Equatorward of 50° latitude, GCMs robustly predict positive feedback, of which more than half is due to low cloud. Most of the positive nonlow (i.e., high and middle level) cloud feedback is due to cloud altitude shifts (Figure 5d), whereas most of the positive low‐cloud feedback is due to cloud fraction reductions (Figure 5e). Negative cloud feedbacks near 60°S are primarily due to an increase in cloud optical depth (opacity), particularly in low cloud.

Our level of understanding of the physical processes responsible for these patterns of cloud response and radiative feedback varies. We begin with cloud feedbacks that are considered more certain (high‐cloud altitude) or important (tropical low cloud) before discussing less certain feedbacks associated with other cloud types.

3.3.1. High‐Cloud Altitude Feedback

The altitude of high‐cloud tops is expected to increase with global warming, a response that arises from relatively basic physics. Convective mixing in the tropics occurs only at altitude ranges experiencing substantial radiative cooling by water vapor (Manabe & Strickler, 1964), which expand upward as the atmosphere warms if relative humidity does not change substantially. Because anvil clouds form from detrainment near the top of the convecting layer, they too are expected to rise with warming, roughly isothermally (Hartmann & Larson, 2002). Because cloud‐top temperature and hence LW emission to space from high‐cloud tops does not increase in step with the warming atmosphere and surface below, this response impedes the planet's ability to radiate away extra energy—a positive radiative feedback (Yoshimori et al., 2020). This notion can be traced back at least as far as Cess (1974), who showed that the empirical relationship between temperature and outgoing LW flux (Budyko, 1969) was better explained by cloud top temperature rather than altitude staying constant with surface warming.

Observations of interannual variability confirm that tropical high clouds rise with surface warming (Eitzen et al., 2009; Y. Li et al., 2012; Vaillant de Guélis et al., 2018; Xu et al., 2005, 2007; Zelinka & Hartmann, 2011; Zhou et al., 2014). Using interannual variability in cloud properties observed by CALIPSO over 2008–2014, Vaillant de Guélis et al. (2018) estimate a global mean short‐term LW cloud altitude feedback of 0.86 ± 0.48 W m⁻² K⁻¹ (1‐sigma). Scaling this short‐term value by the ratio of short‐ to long‐term altitude feedbacks in a single GCM computed using the same methodology implies a long‐term value of 0.35 ± 0.20 W m⁻² K⁻¹. Further observational analyses for longer periods and examination of the relationship between short‐ and long‐term altitude feedbacks in more GCMs are needed. At longer time scales, the climate change‐induced upward shift of high clouds is expected to be detectable and distinct from the noise of internal variability sooner than for other cloud properties (Chepfer et al., 2014; Marvel et al., 2015). Indeed, 25‐year trends from artifact‐corrected ISCCP and PATMOS‐x satellite data sets (Norris & Evan, 2015) indicate an upward shift of high clouds, suggesting that this signal may already be emerging from the noise (Norris et al., 2016).

An increasing altitude of high clouds with warming has been simulated ever since GCMs began predicting cloud distributions (Hansen et al., 1984; Wetherald & Manabe, 1988) and is clearly seen in Figure 5a. All current climate models simulate a positive feedback from increases in the altitude of high‐cloud tops with global warming (Zelinka & Hartmann, 2010; Zelinka et al., 2012, 2013). This feedback has a mean and one standard deviation of 0.20 and 0.10 W m⁻² K⁻¹ across all GCMs (including some CMIP6 models) that have provided the necessary diagnostics to perform the calculations in Zelinka et al. (2016). The purple curve in Figure 5d shows the multimodel mean latitudinal dependence of this LW cloud radiative feedback. The simulated increase in altitude is a global phenomenon, but its strength is modulated regionally by the mean‐state high‐cloud distribution. In model simulations, a slight warming of cloud tops occurs rather than the purely isothermal response anticipated by Hartmann and Larson (2002). This has been attributed to increases in upper tropospheric stability (Bony et al., 2016; Zelinka & Hartmann, 2010) but can be modulated by changes in humidity (Kluft et al., 2019), ozone and stratospheric upwelling (Dacie et al., 2019), and additional processes (Seeley et al., 2019). The same principles have been shown to apply in the extratropics, providing support for the positive extratropical cloud altitude feedback (Thompson et al., 2017), which GCMs suggest is comparable in magnitude to the tropical cloud altitude feedback. Depletion of condensate by mixing with the drier environment is also relevant for high‐cloud coverage and its vertical shifts with warming (Seeley et al., 2019) but should not affect the basic result that warming increases high‐cloud altitude.

Tropical clouds also shift upward nearly isothermally with warming in cloud‐resolving models and LESs (Harrop & Hartmann, 2012; Khairoutdinov & Emanuel, 2013; Kuang & Hartmann, 2007; Narenpitak et al., 2017; Tompkins & Craig, 1999). Global cloud‐resolving model simulations further support this upward shift, including in the extratropics (Bretherton et al., 2014; Satoh et al., 2012; Tsushima et al., 2014). The cloud altitude feedback diagnosed in Bretherton et al. (2014) falls within the range of conventional GCMs quoted above, providing an important confirmation of its sign and magnitude in a model that explicitly simulates cumulus convection.

In summary, theoretical, observational, high‐resolution modeling and GCM studies all support a positive high‐cloud altitude feedback. Given that GCMs appear to represent the relevant physics and have a mean feedback within the uncertainty estimate of a limited first observational estimate, we assess the likelihood function of the high‐cloud altitude feedback to be N(+0.20, 0.10), where the mean and standard deviation corresponds to that of GCMs. This assumes that GCMs well sample the uncertainty in the effective high‐cloud amount and the rate at which the high‐cloud altitude will rise with warming.

3.3.2. Tropical Marine Low‐Cloud Feedback

Uncertainties in the response to climate change of low‐latitude marine boundary layer clouds (cumulus and stratocumulus) in subsiding regions remain a central challenge. The GCM intermodel spread in the tropical low‐cloud feedback is large and well correlated with intermodel spread in S (Bony & Dufresne, 2005; Vial et al., 2013). However, a combination of process‐resolving modeling and new observational analysis is leading to a better understanding and quantification of the most important cloud response mechanisms, leading to increasing confidence that this regime contributes to positive global cloud feedback.

The feedback of low clouds is almost exclusively via SW radiation because they have a small effect on TOA LW radiation. Figure 5e shows that most GCMs simulate positive low‐cloud feedbacks throughout low latitudes (30°S to 30°N), which are especially strong in the deep tropics (10°S to 10°N) and are almost exclusively due to reduced cloud amount in a warmer climate. As will be discussed in section 3.3.5, GCMs also simulate positive low‐cloud feedback in midlatitudes (30–50° latitude), where the mechanisms controlling low cloud are likely similar but quantitatively less well constrained. Despite the general agreement among GCMs in the sign of the feedback, the large intermodel spread has motivated major efforts to use other lines of evidence, namely, process‐resolving models and observations, to infer the tropical low‐cloud feedback.

Bretherton (2015) reviews results from LES of low‐latitude marine cloud‐topped boundary layers in present‐day versus perturbed climates. This work suggests that four main mechanisms affect the cloud response on climate time scales. These are (1) cloud reduction due to thermodynamic effects of overall warming of the atmosphere‐ocean column, including the associated increase in specific humidity; (2) stratocumulus cloud reduction due to the direct effect of CO₂ increases on boundary layer radiative cooling, an important process for stirring up cloud‐forming turbulence (note this contributes to rapid adjustment to CO₂ (section 3.2.1), and not the temperature‐mediated feedback that we are trying to determine here); (3) increases in the stratification between the boundary layer and overlying free troposphere, favoring more cloud; and (4) reductions in the mean subsidence rate, which favor more cloud by keeping the cloud layer from shoaling. Other possible forcings, such as changes in free‐tropospheric relative humidity and surface wind speed, may be important for regional cloud response to climate change but seem to be secondary to global cloud feedback. LES for the expected global warming environment typically predicts less low cloud, hence positive cloud feedback. This happens because the warming‐induced reduction in low cloud (Mechanism [1]) overwhelms the increases from the small changes in expected stratification and subsidence (Mechanisms [3] and [4]).

The cloudy boundary layer responds within hours to days to changes in the overlying atmosphere or underlying ocean. Klein et al. (2017) review a series of observational analyses that have tried to quantify the sensitivity of clouds to each of the “cloud‐controlling factors” associated with the mechanisms above using satellite observations of natural space‐time variability on weekly to interannual time scales (Brient & Schneider, 2016; McCoy et al., 2017; Myers & Norris, 2016; Qu et al., 2015; Zhai et al., 2015). These studies also establish that in GCMs sensitivities to these factors are similar for the century time scale climate warming as for present‐day climate variability. Using the GCM predictions of how the controlling factors change with climate warming, Klein et al. (2017) find positive thermodynamic feedback and a smaller, partially compensating contribution from negative stability feedback; the effects of other possible cloud‐controlling factors are either small or difficult to observationally separate from these. They estimate a 90% confidence interval for the local radiative feedback of low‐latitude marine low clouds of 0.3–1.7 W m⁻² K⁻¹ (Figure 6). They also compare their observational results to the LES studies reviewed by Bretherton (2015), finding that LES estimate a similar range of positive cloud feedback, with trade cumulus regimes in the lower half of this range and stratocumulus regimes in the upper half of this range. Observations from Cesana et al. (2019) also support the notion that the positive feedback from trade cumulus regimes will be smaller than those from stratocumulus regimes.

Figure 6.

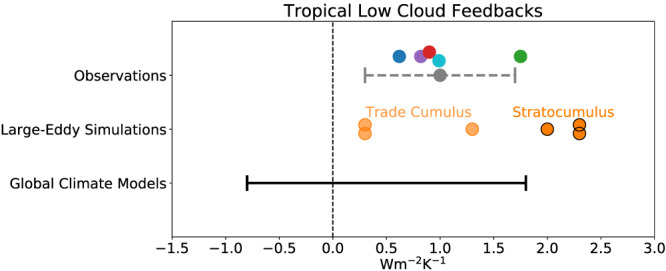
Local tropical low‐cloud feedbacks from observations, large‐eddy simulations, and global climate models from Klein et al. (2017). Each dot represents the feedback from an individual research study. The upper horizontal bar indicates the central estimate and 90% confidence interval for the feedback inferred in that study from the observations. The lower bar indicates the range of feedbacks simulated by global climate models. Note that our assessment reinterprets the upper horizontal bar into a likelihood statement assuming a uniform prior and with considering additional evidence (section 3.3.2).

Given the agreement between observations and LES shown in Figure 6, we base our assessed tropical low‐cloud feedback on these two lines of evidence. Since 25% of the globe is covered by marine tropical subsidence regimes, the local feedbacks shown in Figure 6 are multiplied by 0.25 leading to the Klein et al. (2017) estimate that the tropical low‐cloud contribution to the global cloud feedback is 0.25 ± 0.11 W m⁻² K⁻¹ (1‐sigma). Thus, we assign the mean value of the likelihood function of the tropical low‐cloud feedback to +0.25 W m⁻² K⁻¹. However, we have subjectively chosen to increase the standard deviation of likelihood function from 0.11 to 0.16 W m⁻² K⁻¹, reflecting methodological uncertainties in the direct use of LES and current climate observations to infer climate change.

It is important to recognize that these estimates rely on the environmental conditions applied to LES and the observations. These boundary conditions were taken from GCM climate change simulations dominated by CO₂ warming. If future changes in boundary conditions differ from those predicted, this would imply a different response of low clouds. In particular, over the historical period from 1980–2015, the tropical western Pacific SST increased markedly with little or no change of tropical eastern Pacific SST. This pattern of SST change caused an increase in the strength of the capping inversion in tropical subsidence regions (Zhou et al., 2016). The net result was increased low cloud in tropical subsidence regions, which can be understood to result from the combination of very little warming‐induced reduction of low cloud (Mechanism [1]) and strong stratification‐induced increase in low cloud (Mechanism [3]) (Seethala et al., 2015; Zhou et al., 2016). Thus, due to the dependence of low cloud on the pattern of SST change, tropical low clouds increased even as the planet as a whole warmed over the period 1980–2015. This is the physical explanation underlying the low‐cloud contribution to the “pattern effect,” which significantly affects interpretation of the historical record and is discussed in section 4.2.

3.3.3. Tropical Anvil Cloud Area Feedback

In addition to the positive feedback from high‐level clouds rising in a warmer climate (section 3.3.1), a change in the areal coverage of these clouds in a warmer climate may exert a feedback. Of particular interest is the response of “anvil” high clouds found in tropical deep convection regions in conditions of high SST and large‐scale ascent. These clouds are highly reflective of solar radiation and at the same time greatly reduce the outgoing LW radiation to space (Kiehl, 1994). Small changes in the balance between these large cooling and warming effects may cause a significant radiative feedback on climate warming.

A reduction in the area coverage of tropical anvil clouds with warming was first suggested to be a strongly negative feedback by Lindzen et al. (2001) and is sometimes referred to as the “iris” effect. Lindzen et al. (2001) hypothesized that the microphysical processes in convective updrafts that provide much of the condensate for high‐level clouds become more efficient with climate warming causing a decrease in anvil cloud area. While GCMs show that the simulation of tropical high clouds and their climate response are highly sensitivity to convective updraft microphysics (Clement & Soden, 2005; Mauritsen & Stevens, 2015; Zhao, 2014; Zhao et al., 2016), there is no clear evidence that precipitation efficiency would increase in a warmer climate.

Another mechanism that could cause a decrease in anvil cloud area would be a tendency in a warmer world toward increased convective organization—the propensity for clouds to cluster or aggregate (Khairoutdinov & Emanuel, 2010; Mauritsen & Stevens, 2015). In both observations (Stein et al., 2017; Tobin et al., 2012) and convection resolving models (Bretherton et al., 2005), aggregated convective cases are considerably drier and have less upper‐level clouds. However, there is no clear evidence from cloud‐resolving models that aggregation systematically increases with temperature (Wing, 2019). Even if aggregation does not systematically vary with temperature, the degree of aggregation in the base climate may affect climate feedbacks. This is because the dryness and less upper‐level cloud of aggregated states may cause smaller water vapor and high‐cloud altitude feedbacks (Wing, 2019), or increase the sensitivity to feedbacks from exposed low clouds (Bony et al., 2016).

Bony et al. (2016) proposed another mechanism for a decrease in anvil cloud area with warming called a “stability iris.” Specifically, in a warmer world there is increased static stability at the levels where convective updrafts detrain and form high‐level clouds. This increased stability is associated with a weaker radiatively driven divergence at these heights, which results in less detrained mass and hence less anvil cloud.

While these proposed mechanisms generally suggest reduced anvil cloud area with warming, they do not determine the net cloud radiative effect that would impact S. A separate theoretical argument by Hartmann et al. (2001) posits that large‐scale circulations act to keep net cloud radiative effects of tropical deep convection regions close to the small net cloud radiative effects of nearby nonconvective regions. If such considerations apply to a warmer world, this would predict small net cloud feedbacks from clouds in tropical deep convective regions.

As for GCMs, they are not deemed trustworthy for the simulation of anvil cloud area because they lack sufficient cloud microphysics and convective organization processes, among other reasons. GCMs also largely fail to reproduce the observed increase in outgoing LW radiation that accompanies warming on interannual time scales (Mauritsen & Stevens, 2015) despite simulating some decrease in anvil cloud area with warming at least in some models (Bony et al., 2016). Thus, little confidence is placed in the small GCM response of tropical high‐cloud area with warming (Figure 5d).

One might place greater confidence in convection‐resolving models, but results are varied. While cloud‐resolving models run in limited area or tropical channel domains tend to simulate decreases in high‐cloud area with warming (Bony et al., 2016; Cronin & Wing, 2017), global or near‐global models with convection permitting resolution simulate little change (Bretherton et al., 2014; Narenpitak et al., 2017) or even increases (Chen et al., 2016; Tsushima et al., 2014). The one simulation with increased high cloud was very sensitive to the representation of ice cloud microphysics and sub‐grid‐scale turbulence, suggesting that the current generation of convection‐resolving models may not provide definitive answers about the response of tropical high clouds to warming (Bretherton, 2015).

This leaves observed variability as the primary guide to tropical high‐cloud feedbacks, particularly for the net radiative impact of high‐cloud changes. Observational analyses focus on the response of tropical high clouds to interannual variability, under the idea that short‐term feedbacks in tropical high clouds are relevant to their long‐term climate feedbacks, an idea partially supported by GCM analyses (Mauritsen & Stevens, 2015). Using CERES radiation budget measurements, I. N. Williams and Pierrehumbert (2017) found that under warming, the large reduction in SW reflection by fewer tropical deep convective clouds was a little bit smaller than the large reduction in the LW trapping by tropical deep convective clouds. The net result, seen in their Figure 3, is a local cooling of 1–5 W m⁻² K⁻¹. We convert their estimate of a tropical feedback to a global feedback by accounting for differences in area fraction and local versus global temperature changes and by removing an estimate of the positive cloud feedback from increased cloud altitude (this is done so as not to double count the altitude feedback estimated in section 3.3.1). This yields an estimate of the tropical anvil cloud area feedback of −0.23 ± 0.08 W m⁻² K⁻¹ (1‐sigma) from their study (note this uncertainty only includes sampling errors).

Other observational studies have tried to estimate the net radiative effect of changing anvil clouds. While a negative feedback was also found in Choi et al. (2017), some studies have found tropical high clouds produce neutral (Zelinka & Hartmann, 2011) or even slightly positive cloud radiative feedbacks (B. Lin et al., 2002; Chambers et al., 2002). While the results from I. N. Williams and Pierrehumbert (2017) are given more weight because they use the most accurate radiation budget measurements covering the most recent analysis period, we also recognize the considerable uncertainties associated with the observational estimates, the differing quantities measured in various studies, and the correspondence between short‐term observed and long‐term climate feedbacks. Accordingly we assign a maximum likelihood value of −0.20 W m⁻² K⁻¹, with a large standard deviation of 0.20 W m⁻² K⁻¹. Our assessment would be consistent with the moderately stabilizing negative cloud feedbacks found in I. N. Williams and Pierrehumbert (2017) but does not rule out neutral cloud feedbacks, since a value of 0 is within one standard deviation of our maximum likelihood value. Note that the effect we find based on recent observational analyses is an order of magnitude smaller than the strongly stabilizing cloud feedbacks once suggested by Lindzen et al. (2001) and Lindzen and Choi (2011).

3.3.4. Land Cloud Feedback

Preferential warming of land surfaces is expected to lead to relative humidity reductions, particularly where the climatological temperatures are warm, that is, the tropics, subtropics, and midlatitudes in summer (Findell & Delworth, 2001; Manabe et al., 1981; Sherwood & Fu, 2014). The primary explanation for this relative humidity reduction is that the combination of surface evaporation and horizontal water vapor transport from oceans does not increase as fast with warming as Clausius‐Clapeyron requires to keep local relative humidity constant (Byrne & O'Gorman, 2016; Scheff & Frierson, 2015; Sherwood & Fu, 2014). This is mainly because the surface temperature warms considerably more over land compared with the ocean (Byrne & O'Gorman, 2013a; Joshi et al., 2008), a robust result of GCM warming simulations. Theoretically, the greater warming over land may result in large part from atmospheric dynamics (Sobel & Bretherton, 2000) maintaining constant convective instabilities between ocean and land leading to nearly the same changes in surface moist static energy (Byrne & O'Gorman, 2013b; Sherwood & Fu, 2014). Secondary contributions to relative humidity reductions with warming may come from reductions in soil moisture (Berg et al., 2016; Manabe & Wetherald, 1987) or regional circulation changes such as the poleward expansion of subtropical dry zones (Scheff & Frierson, 2012). (Note that effects on relative humidity and clouds from the response of plant stomata to CO₂ increases contribute to rapid radiative adjustment to CO₂ (section 3.2.1) and not the temperature‐mediated changes discussed here).

The consequence of the relative humidity reductions is a widespread reduction of cloudiness over warm land regions that are very robustly simulated by GCMs (Bretherton et al., 2014; Kamae et al., 2016). Decreasing cloudiness due to decreases in relative humidity is also theoretically expected and supported by observations of low clouds over land (Del Genio & Wolf, 2000; Y. Zhang & Klein, 2013). In GCMs, the contribution from cloud amount reductions over land to the global mean cloud feedback is +0.08 W m⁻² K⁻¹ with standard deviation 0.03 W m⁻² K⁻¹, based upon the calculations of Zelinka et al. (2016) applied to all available models. While clouds at all vertical levels of the atmosphere decrease, the majority of this net cloud feedback comes from the reduction in low clouds, which increases the absorption of solar radiation but does not appreciably affect the emission to space of LW radiation. Apart from GCMs, observations show decreases in surface relative humidity over recent decades (Willett et al., 2018), which are consistent with those predicted by the primary explanation given the observed amount of ocean warming (Byrne & O'Gorman, 2018). These relative humidity reductions may be attributed to anthropogenic forcing of the climate system (Douville & Plazzotta, 2017).

In summary, we assess this feedback to be credible and assign a maximum likelihood value of +0.08 W m⁻² K⁻¹, which matches the mean of available GCM predictions. However, we assign a higher standard deviation, 0.08 W m⁻² K⁻¹, to reflect the fact that GCMs have substantial biases in land climate, which indicates some structural uncertainty. In particular, GCMs markedly underestimate the relative humidity, cloudiness, and precipitation and overestimate surface temperature during the warm season (Ma et al., 2014; Morcrette et al., 2018). Furthermore, biases in the mean climate appear to project upon climate responses to warming at least in middle latitudes (Cheruy et al., 2014; Y. Lin et al., 2017).

3.3.5. Midlatitude Marine Low‐Cloud Amount Feedback

Middle‐latitude (30–60°) cloud coverage is strongly modulated by baroclinic disturbances in the storm track. A positive extratropical cloud feedback has long been expected to accompany global warming owing to the poleward shift of the storm track and its attendant clouds toward regions of less incoming solar radiation. In apparent support of this notion, trends in satellite and ground‐based cloud observations indicate poleward shifts of middle latitude cloud maxima and/or subtropical cloud minima (Bender et al., 2012; Eastman & Warren, 2013; Marvel et al., 2015; Norris et al., 2016), but the exact magnitude of these shifts is uncertain owing to observational data artifacts that can introduce spurious trends. Moreover, the observed sensitivity of net cloud radiative effects to interannual variations in jet latitude appears surprisingly small, owing to compensation between high‐ and low‐cloud responses. Namely, whereas upper‐level clouds tend to move poleward with the jet, low‐level clouds (which can be more tied to surface conditions) do not. Rather, enhanced subsidence, stability, and cold advection lead to increased low‐cloud coverage in regions vacated by higher clouds (Grise & Medeiros, 2016; Tselioudis et al., 2016; Zelinka et al., 2018). Thus, it is unlikely that substantial cloud feedbacks arise from storm track shifts (Ceppi & Hartmann, 2015; Grise & Polvani, 2014).

Midlatitude, low‐cloud responses could also be driven by thermodynamic processes similar to those governing the tropical low‐cloud response (Narenpitak et al., 2017; Qu et al., 2014). Indeed, Norris and Iacobellis (2005) infer a positive midlatitude cloud feedback based on observed variations in midlatitude cloud properties with temperature, while controlling for other meteorological influences. Zhai et al. (2015) and McCoy et al. (2017) also infer a positive feedback from observed variations of low clouds with temperature in the 30–40° latitude band.

GCMs consistently predict reduced cloud fraction throughout the midlatitude troposphere with warming (Figure 5a), and the reduction in low‐cloud amount induces a strong positive feedback (Figure 5e). Modeled midlatitude net cloud‐radiative effect anomalies attributable to future jet shifts are small compared to the total predicted radiative change (Ceppi & Hartmann, 2015; Kay et al., 2014; Wall & Hartmann, 2015), consistent with the observational results above. A positive midlatitude cloud feedback may be caused by SST increases and stability decreases, but further study is needed to quantify the dependence of low cloud on SST and inversion strength or other cloud‐controlling factors at midlatitudes before making confident attribution statements.

In summary, despite the apparent lack of a substantial cloud feedback from poleward shifts of the midlatitude storm track, observed variations of midlatitude low clouds (McCoy et al., 2017; Norris & Iacobellis, 2005; Zhai et al., 2015) provide qualitative support to the strong positive midlatitude low‐cloud amount feedbacks robustly predicted by GCMs. Based upon the calculations of Zelinka et al. (2016) applied to all available models, the GCM contribution to global feedback from ocean areas between 30° and 60° latitude (27% of the globe) has a mean of 0.12 W m⁻² K⁻¹ with a standard deviation of 0.08 W m⁻² K⁻¹. Extrapolating the observationally derived tropical low‐cloud feedback (Klein et al., 2017) to the midlatitude oceans after accounting for reduced insolation yields a feedback between 0.08 and 0.20 W m⁻² K⁻¹, depending upon whether the observed tropical low‐cloud sensitivities are assumed to apply to the entire 30–60° latitude band or only to the 30–40° latitude band investigated in Zhai et al. (2015) and McCoy et al. (2017). Considering both the GCM and observational estimates, we assign a maximum likelihood value of +0.12 W m⁻² K⁻¹, consistent with the GCM mean and observational estimates, but increase the standard deviation to 0.12 W m⁻² K⁻¹ to reflect uncertainty in GCM simulations of marine low cloud and the range of observational estimates.

3.3.6. High‐Latitude Low‐Cloud Optical Depth Feedback

Cloud optical depth (opacity) can increase due to either smaller cloud particles (for a given cloud water path) and/or increases in water path (Stephens, 1978). Several mechanisms that favor increased optical depth with warming have been proposed. First, a shift of cloud ice to liquid upon warming leads to brighter clouds, as a given amount of cloud water is more reflective if distributed among liquid droplets, which tend to be smaller, rather than fewer large ice crystals (Storelvmo et al., 2015). Second, increases in the liquid fraction of condensate can inhibit precipitation (Klein et al., 2009; Solomon et al., 2011), resulting in clouds with more total water content. Third, the adiabatic water content of clouds increases with temperature following fundamental thermodynamic theory (Betts & Harshvardan, 1987). Opposing these effects, liquid clouds may be thinned via increased entrainment drying with warming due to the greater saturation deficit (Blossey et al., 2013; Bretherton, 2015; Bretherton & Blossey, 2014; Bretherton et al., 2013; Brient & Bony, 2013; Rieck et al., 2012; Sherwood et al., 2014), though this mechanism has only been investigated for subtropical low clouds, and its relevance for cloud thickness as opposed to cloud fraction is uncertain.

GCMs simulate a negative feedback poleward of about 40° latitude from optical depth increases, especially for low clouds (Figures 5d and 5e). GCMs also exhibit a strong correspondence across time scale for the temperature sensitivities of high‐latitude cloud optical depth and liquid water path (i.e., an emergent constraint; Ceppi et al., 2016; Gordon & Klein, 2014), suggesting that present‐day observations can be used to assess this feedback. Terai et al. (2016) inferred a SW low‐cloud optical depth feedback of +0.24 W m⁻² K⁻¹ averaged between 40° and 70° of both hemispheres by quantifying the sensitivity of low‐cloud optical depth to surface temperature in Moderate Resolution Imaging Spectroradiometer satellite observations. In an independent analysis also using these observations, Ceppi et al. (2016) derived a SW cloud optical depth feedback of −0.35 W m⁻² per degree of 850‐ to 500‐hPa temperature change averaged over 45–60°S. Renormalizing by global surface warming and accounting for the fact that the feedback is weaker in the Northern Hemisphere (NH) yields a value of −0.20 W m⁻² K⁻¹. Assuming that these values also apply to the 40–70° latitude band (30% of the globe) yields values of −0.06 W m⁻² K⁻¹ (Ceppi et al., 2016) and +0.07 W m⁻² K⁻¹ (Terai et al., 2016). Quantitative differences in these results likely arise from differences in cloud types analyzed and in the predictors used in deriving cloud optical depth sensitivities. Guided by these two studies, we assign the maximum likelihood value for the high‐latitude low‐cloud optical depth feedback to 0.0 W m⁻² K⁻¹. The standard deviation of the likelihood function we assign to 0.10 W m⁻² K⁻¹, which allows for additional uncertainties beyond these two studies.

This assessed feedback value is consistent with observational evidence suggesting that the negative high‐latitude optical depth feedback simulated by many GCMs is too strong, likely due to an exaggerated phase change feedback. In GCM experiments in which mean‐state supercooled liquid water content more closely matches observations (Frey & Kay, 2018; Tan et al., 2016), the negative SW optical depth feedback at high latitudes is weakened considerably. This negative feedback has also weakened in some CMIP6 models, possibly related to improvements in mean‐state cloud phase distribution (Zelinka et al., 2020).

3.4. Process Assessment of λ and Implications for S

Sections 3.2 and 3.3 have assessed the process evidence and assigned a Gaussian prior for ∆F _2xCO2 and Gaussian likelihoods for individual climate feedbacks. Table 1 records the values of these terms and which lines of process evidence were used in their derivation.

According to Equation 18, the climate feedback parameter λ is equal to the linear sum of individual feedbacks. We further assumed that the total cloud feedback can be written as a linear sum of the individual cloud type feedbacks we assessed in section 3.3. Linearity of radiative feedbacks has been established (Colman & McAvaney, 1997; Mauritsen et al., 2013; M. H. Zhang et al., 1994; Wetherald & Manabe, 1980), although independence is another matter (see below). We formulate a Gaussian PDF for λ _clouds by adding the standard deviations for the individual cloud feedbacks in quadrature (assuming independent and uniform λ _i priors) and, similarly, formulate a PDF for λ by adding the standard deviations of all feedbacks in quadrature (cf. Equation 13). Note this manner of combining feedbacks is valid only for the Baseline prior (see section 2.3). The resulting PDF for the total cloud feedback is N(+0.45, 0.33) (Table 1 and Figure 7). Relative to the mean cloud radiative effect of around −20 W m⁻² in today's climate (Loeb, Doelling, et al., 2018), a cloud feedback of +0.45 W m⁻² K⁻¹ is equivalent to an ~2% decrease in the net radiative effect of clouds for every K of temperature increase. Interpreting standard deviations as uncertainty, the total cloud feedback has the largest uncertainty relative to the other feedbacks (Planck, water vapor + lapse rate, surface albedo, atmospheric composition, and stratospheric), just as it has in past assessments. In addition, quadrature summing of our assessed values shows that the uncertainty from all high cloud types combined is approximately equal to that of all low‐cloud types combined, indicating that future research is needed to improve the physical understanding of both high and low clouds.

Figure 7.

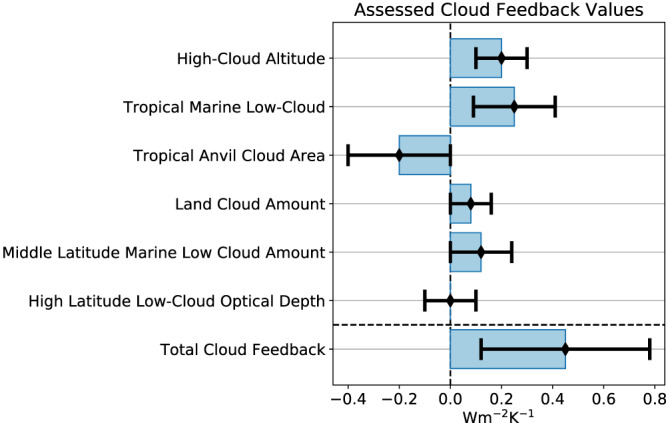
Assessed values of individual cloud feedbacks and the total cloud feedback based upon process evidence. For individual cloud feedbacks, maximum likelihood values are shown by black diamonds and the widths of blue rectangles, with 2 times the 1‐sigma likelihood values shown by the width of the black uncertainty bars. For the total cloud feedback, the mean value of the PDF is shown by a black diamond and the width of the accompanying blue rectangle, with 2 times the PDF standard deviation shown by the width of the black uncertainty bar.

Our PDF for λ is N(−1.30, 0.44) (Table 1 and Figure 8a). Also assuming the prior on ∆F _2xCO2 is independent from λ, the PDF of S using only process evidence can be derived (Figure 8c). The 50th percentile (median) of the S PDF occurs at 3.1 K, with the 17th and 83rd percentiles at 2.3 and 4.6 K. The asymmetric shape to the S PDF results from taking the inverse of the symmetric λ PDF following Equation 4 and the fact that in relative terms, λ is much more uncertain than ∆F _2xCO2 (Roe & Baker, 2007). This implies that shifting the S PDF downward would require the identification of an unknown negative feedback much larger in magnitude than the unknown positive feedback that would be required to shift the S PDF upward by an equal amount (Schlesinger, 1989). Equivalently, the process assessment constrains the lower bound of S more tightly than its upper bound.

Figure 8.

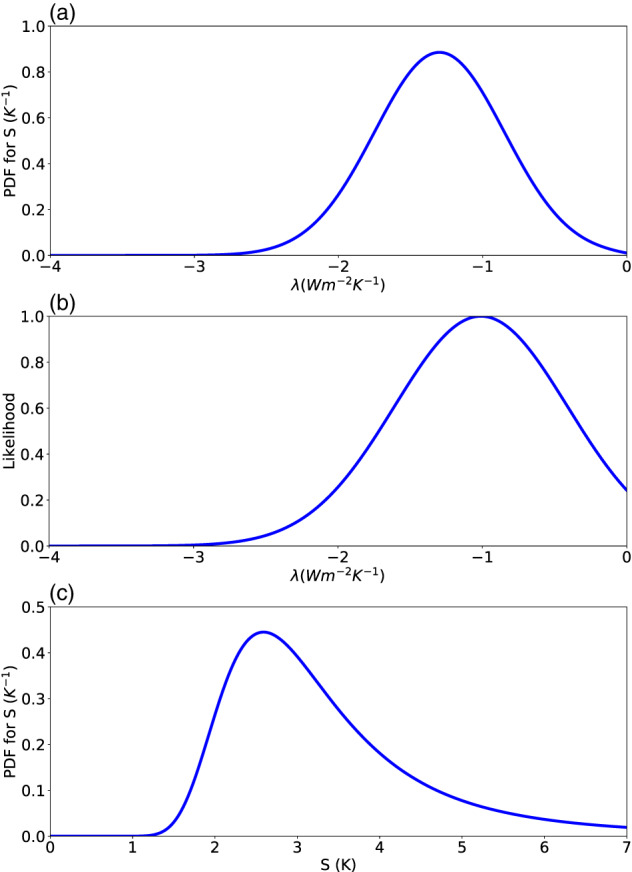
PDFs and likelihood functions based upon the assessment of individual climate feedbacks and the emergent constraint literature. (a) PDF for λ from combining evidence on individual feedbacks using the Baseline λ _i prior. (b) Emergent constraint likelihood for λ. Note that this likelihood is not a PDF. See section 3.6 for an explanation of how the parameters of this likelihood function were determined and why they differ from the parameters recorded in Table 2. (c) PDF for S from combining evidence on ∆F _2xCO2 and individual feedbacks using uniform λ _i priors.

One may question our assumption of independence between ∆F _2xCO2 and λ, as well as among likelihoods for all feedbacks except those for water vapor and lapse rate which we treat together in Table 1. Of particular importance is a significant anticorrelation between ∆F _2xCO2 and λ in GCMs (Andrews, Gregory, Webb, et al., 2012; Webb et al., 2013), which acts to reduce CMIP5 intermodel spread of S by about 0.6 K relative to what would be anticipated if these were uncorrelated (Andrews, Gregory, Webb, et al., 2012; Caldwell et al., 2016). This anticorrelation cannot be explained as an artifact of the Gregory method for calculating ∆F _2xCO2 and λ (Gregory et al., 2004) as it is seen in GCM experiments with both realistic and idealized configurations (e.g., fixed SST with globally uniform SST increases of 4 K) (Ringer et al., 2014). It is also seen in ensembles of untuned perturbed‐parameter versions of single models as well as ensembles of tuned GCMs (Webb et al., 2013). A compensation between cloud feedback and adjustment is found to be the direct cause of this ∆F _2xCO2‐λ covariance (Chung & Soden, 2017; Ringer et al., 2014), but covariance exists even between feedbacks (Caldwell et al., 2016; Huybers, 2010; McCoy et al., 2016). Unlike the case of the water vapor and lapse rate anticorrelation, the mechanisms behind feedback covariances are generally not understood although new research attempts to explain these issues (McCoy et al., 2016). In conclusion, because these GCM covariances are not understood and initial analyses suggest that they are weaker in the CMIP6 model ensemble (Zelinka et al., 2020), we conservatively overlook the anticorrelation found in some GCMs, leading to a somewhat broader overall uncertainty. But given the potential of feedback and forcing anticorrelations to reduce the overall uncertainty in S calculated from individual feedbacks and forcing, it should be a high priority for future research to determine the physical basis of these relationships and their relevance for the real world.

3.5. Constraints From Observations of Global Interannual Radiation Variability

A significant concern with our primary approach is whether we have recognized all important feedbacks, that is, whether there could be large missing feedbacks, particularly from any cloud types that we did not assess. While GCMs indicate that the cloud feedbacks we have not assessed are small in magnitude having a mean and standard deviation of −0.02 and 0.15 W m⁻² K⁻¹, respectively (not shown), a more powerful way to address this concern is by considering the studies that have attempted to constrain the total climate feedback parameter λ via analysis of observed interannual variability in globally averaged TOA net radiation. The premise is that interannual temperature fluctuations will have had the chance to activate feedbacks from any and all cloud types. This premise is plausible (a) because the warming correlated with interannual fluctuations of global mean temperature is global in nature, occurring in both the tropics and extratropics (Dessler, 2013), and (b) because the inherent time scales of all clouds are from minutes to at most a few days, and thus, there is more than enough time available for clouds to respond to the interannual changes in temperature.

After accounting for changes in forcing, linear regression of observed anomalies in global net radiation ΔN on observed anomalies in global surface temperature ΔT provides an empirical estimate of λ according to section 3.1. The reviews of Forster et al. (2016) and Loeb et al. (2016) report that the studies with the most robust methods and recent radiation data found λ values ranging from −1.13 ± 0.5 to −1.25 ± 0.5 W m⁻² K⁻¹ (1‐sigma) (Dessler, 2013; Donohoe et al., 2014; Murphy et al., 2009; Trenberth et al., 2015). Dessler et al. (2013) additionally estimated values of individual feedbacks in section 3.1 such as the water vapor, lapse rate, cloud, and surface albedo feedbacks, which we have discussed in section 3.2 and displayed in Figure 4.

Empirically estimated feedback values change somewhat depending on the regression method and the observational data sets (Forster, 2016; Loeb et al., 2016; Proistosescu et al., 2018), although differences are generally small (Dessler & Loeb, 2013; Zhou et al., 2013). Larger changes occur when the regression is calculated over different time periods; Loeb et al. (2016) report feedback values of −1.18 ± 0.58 but −0.27 ± 0.47 W m⁻² K⁻¹ (1‐sigma) for the 2001–2013 and 2001–2015 periods, respectively. Considering the range of uncertainty, these values are not inconsistent with each other, and taken together, they provide a similar mean and spread as our PDF for λ from combining feedbacks (Figure 8a). Because the latter used Dessler's (2013) observed estimates of the clear‐sky feedbacks in section 3.2, this comparison only tests the consistency of our assessment of the total cloud feedback with Dessler's estimate which is +0.49 ± 0.35 W m⁻² K⁻¹ (1‐sigma) for the 2000–2010 period. This value overlaps well with the PDF for the total cloud feedback (Table 1). However, estimates for periods including more recent years are more positive (A. E. Dessler, personal communication, 2017).

A fundamental question is whether feedbacks diagnosed from short time scales are representative of the long‐term feedbacks (Forster, 2016; Loeb et al., 2016; Proistosescu et al., 2018). Because many atmospheric processes involved in climate feedbacks evolve on short time scales (hours to weeks) and thus quickly adjust to more slowly changing boundary conditions such as surface temperature, the radiative response to warming of all climate feedback processes might be invariant from interannual to long‐term time scales. However, to the extent that unrelated radiation anomalies drive surface temperature anomalies, the climate feedback parameter diagnosed from the relationship between anomalies in radiation and temperature might be biased high (Spencer & Braswell, 2010). Calculations though suggest that this is a relatively minor concern as the dominant source of interannual variability in temperature is from ocean forcing and not radiation (Dessler, 2011; Proistosescu et al., 2018).

Another aspect of this question is whether the spatial patterns of surface temperature change seen in interannual variability provoke global mean responses similar to those of the smoother pattern anticipated from long‐term CO₂ warming (Proistosescu et al., 2018). For example, low‐cloud and lapse rate feedbacks depend strongly upon the pattern of surface temperature change (sections 3.3.2 and 4.2). The warming pattern from interannual variability is dominated by El Niño variability within the tropics but also has warming at higher latitudes (Dessler, 2013). As such, while not as uniform, the interannual warming pattern exhibits some similarity to the long‐term warming pattern projected by GCMs, which has often been called “El Niño like” (Meehl & Washington, 1996; Vecchi et al., 2008; Yu & Boer, 2002, also see section 4.2). Most notably at both long‐term and interannual time scales, there is greater warming in the central and eastern Pacific relative to that in the western Pacific and this favors positive low‐cloud and lapse rate feedbacks. Given the similarity in spatial pattern of surface temperature change, global averages of the feedbacks inferred from interannual time scales might be expected to exhibit some similarity to those associated with long‐term warming.

GCMs can be used to test the similarity between global feedbacks at different time scales. Colman and Hanson (2017) examined individual feedbacks in CMIP5 models and found that interannual values diagnosed from preindustrial control simulations were generally consistent with values in response to climate warming for the water vapor, lapse rate, surface albedo, and total cloud feedbacks (Figure 9). A general consistency also applies to decadal time scale feedbacks derived from preindustrial control simulations (Colman & Hanson, 2018). In particular, cloudiness exhibits similar spatial responses to increasing temperature at interannual and long‐term time scales (i.e., an emergent constraint is present), with interannual and long‐term feedbacks well correlated across models, albeit with a slope different than unity (Zhou et al., 2015). The consistency of GCM climate feedbacks between interannual variability and long‐term warming supports the use of the interannual observations in assessing climate feedbacks. We conclude that the chances of major errors or omissions in our assessment are reduced, particularly for our assessment that the total cloud feedback is positive, since we do not find any evidence of missing feedbacks in the interannual variability.

Figure 9.

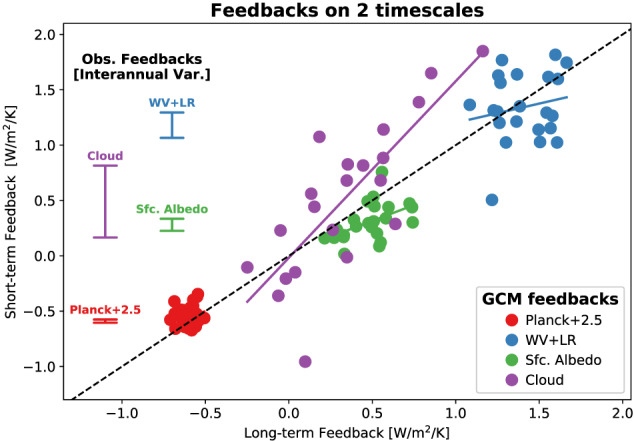
Individual feedbacks in CMIP5 climate models (circular symbols) and inferred from observations (error bars along the y axis). The y axis displays relationships derived from natural variability at the interannual time scale using 100 years of preindustrial control simulations from CMIP5 climate models (Colman & Hanson, 2017) and using ~11 years of observations between March 2000 and December 2010 (Dessler, 2013). Error bars span the 1‐sigma uncertainties of the observed feedback estimates. The x axis displays the long‐term feedbacks from climate model simulations of the response to an abrupt quadrupling of CO₂ (Colman & Hanson, 2017). The black dashed line is the 1:1 line, whereas the short solid thick lines among the climate model points display the ordinary least squares linear regression lines between simulated interannual and long‐term feedbacks.

In summary, examining global mean radiation variations provides a similar central estimate of λ and comparable spread to that obtained from combining feedbacks. On its own, there is a danger that our combining‐feedback approach could miss unassessed feedbacks—particularly from clouds—and to account for this quantitatively we should broaden the PDF given in section 3.4 (without shifting its central value). On the other hand, the global mean satellite evidence in principle includes all rapid feedbacks including those from the clouds we did not assess. Moreover, it is largely independent from the individual process evidence; bear in mind that although a similar approach was used in section 3.2 to help constrain clear‐sky feedbacks, the main concern is clouds. Therefore, updating the PDF from section 3.4 with this additional evidence would make the PDF narrower, again without shifting its central value. In light of these opposing considerations, both of which are hard to quantify precisely, we judge the result obtained in section 3.4 to be a fair representation of the overall probabilities given all evidence, and will be adopted in this assessment.

3.6. Emergent Constraints on S From Present‐Day Climate System Variables

In recent years, a wide variety of present‐day climate system variables including clouds, water vapor, precipitation, radiation, circulation, and temperature has been identified with skill at predicting S through emergent constraints (Table 2). Emergent constraints on S also exist related to the rate of warming since 1970 and tropical temperature changes during the LGM and mid‐Pliocene warm period (mPWP) and are discussed elsewhere (sections 4.1.3, 5.2.4, and 5.3.1, respectively). The common occurrence of variables related to clouds, and tropical low clouds in particular, is not surprising given the leading role of the SW cloud feedback from tropical low clouds in explaining S variance in CMIP ensembles (Caldwell et al., 2018; Qu et al., 2018). Several constraints involve the short‐term temperature sensitivity of low clouds, which is likely related to their long‐term feedback, and perhaps total λ, if the relationship between clouds and their cloud‐controlling factors were constant across time scales (section 3.3.2). Indeed, if total λ were constant, the fluctuation‐dissipation theorem suggests that the amplitude and autocorrelation of interannual temperature variability would depend on λ (among other factors), such that observations of temperature variability might constrain λ and hence S. This is the physical explanation given for the temperature variability emergent constraint of Cox et al. (2018).

Table 2.

Emergent Constraints for S Based Upon Present‐Day Climate System Variables and CMIP Models

Category	Present‐day climate system variable	Reference	Authors' statements about S	Central estimate of S (K) from ordinary linear regression	Central estimate of λ (W m−2 K−1) from ordinary linear regression
Low cloud	Boundary layer cloud amount response to SST variations in subtropical stratocumulus regions (after removing the stability contribution)	Qu et al. (2014)	No statement	3.74	−1.03
	Seasonal response of boundary layer cloud amount to SST variations in oceanic subsidence regions between 20°and 40° latitude	Zhai et al. (2015)	Models consistent with observation “have S higher than the multi‐model mean with “an ensemble mean S of 3.9 K and a standard deviation of 0.45 K.”	4.13	−0.82
	Fraction of tropical clouds with tops below 850 hPa whose tops are also below 950 hPa	Brient et al. (2016)	Models consistent with observation “have S between 2.4 and 4.6 K.”	3.06	−1.20
	Sensitivity of cloud albedo in tropical oceanic low‐cloud regions to present‐day SST variations	Brient and Schneider (2016)	“Most likely S estimate around 4.0 K; an S below 2.3 K becomes very unlikely (90% confidence).”	3.68	−0.92
General cloud	Difference between tropical and Southern Hemisphere midlatitude total cloud fraction	Volodin (2008)	An estimate of S is “3.6 ± 0.3” (1‐sigma).	3.63	−0.97
	Extent to which cloud albedo is small in warm SST regions and large in cold SST regions	Siler et al. (2017)	A likely value of S is “3.68 ± 1.30 K (90% confidence).”	3.55	−0.97
Humidity	Southern Hemisphere zonal average midtropospheric relative humidity in dry zone between 8.5°S and 20°S	Fasullo and Trenberth (2012)	“Many models, particularly those with low S, … are identifiably biased.”	4.12	−0.96
	Tropical zonal average lower tropospheric relative humidity in moist convective region	Fasullo and Trenberth (2012)	“Only a few models, generally of lower sensitivity, are identifiably biased.”	3.42	−1.06
	Tropospheric zonal average relative humidity vertically and latitudinally resolved between 40°N and 40°S	Su et al. (2014)	“Models closer to the satellite observations tend to have S higher than the multi‐model mean.”	3.85	−0.90
	Strength of resolved‐scale humidity mixing between the boundary layer and the lower troposphere in tropical East Pacific and Atlantic	Sherwood et al. (2014)	No specific statement	4.13	−0.76
	Strength of small‐scale humidity mixing between the boundary layer and the lower troposphere in tropical convective regions	Sherwood et al. (2014)	No specific statement	3.26	−1.14
	Sum of Sherwood resolved‐scale and small‐scale humidity mixing	Sherwood et al. (2014)	“Observations at face value implies a most likely S of about 4 K, with a lower limit of about 3 K.”	4.07	−0.83
Precipitation	Strength of model's precipitation bias in the “double‐ITCZ” (Intertropical Convergence Zone) region	Tian (2015)	“S might be in the higher end of its range (~4.0 K).”	4.02	−0.87
Radiation	Net top‐of‐atmosphere radiation averaged over the Southern Hemisphere	Trenberth and Fasullo (2010)	“Only the more sensitive [higher S] models are in the range of observations.”	3.53	−1.05
Temperature	Amplitude of seasonal cycle of surface temperature	Covey et al. (2000)	No specific statement	3.23	−1.16
	Strength of global average surface temperature interannual variations and their temporal autocorrelation	Cox et al. (2018)	The emergent constraint “yields a central [S] estimate of 2.8 K with 66% confidence limits … of 2.2–3.4 K.”	2.91	−1.22
Circulation	Latitude of the southern edge of the Hadley cell in austral summer	Lipat et al. (2017)	Models “closer to the observations … tend to have smaller S values.”	2.80	−1.23
Average				3.60 ± 0.42	−1.01 ± 0.14

Note. Emergent constraints are categorized by the type of present‐day climate system variable (Columns 1 and 2) with the reference for each constraint in Column 3. Column 4 reports the authors' statements about S quoted directly from the cited reference. Column 5 reports a central estimate of S from each constraint calculated from the ordinary least squares linear regression of S on the present‐day climate system variable evaluated at its observed value. The data used in these calculations are taken from that compiled by Caldwell et al. (2018). Column 6 reports a central estimate for λ calculated in the same manner as Column 5. The last row reports the averages and standard deviations of the data in Columns 5 and 6.

It is a relatively new activity to constrain future climate using the intermodel spread of a GCM ensemble and observations of a correlated present‐day climate system variable. Hall et al. (2019) give a framework to consider this activity and provide “confirmation indicators” to gauge the trustworthiness of an emergent constraint. This is helpful as spurious predictors may be present in climate model ensembles due to their small size (Caldwell et al., 2014).

One confirmation indicator is out‐of‐sample testing, which can partially be achieved by comparing results across generations of CMIP ensembles. Caldwell et al. (2018) found that four out of five emergent constraints constructed using the earlier CMIP ensembles had no skill at predicting S in the CMIP5 ensemble. It will be interesting to see how many of the constraints in Table 2 will have predictive capability in the new CMIP6 ensemble.

Another confirmation indicator is having a verified and plausible mechanism explaining the constraint. Although the proponents of each constraint have offered explanations, verifying them is difficult. One test is whether the present‐day predictor is also correlated with available measures of the specific climate feedback identified in the physical explanation (Caldwell et al., 2018). Unfortunately, the lack of specificity in the physical explanations for many constraints limits the applicability of this test. In this assessment, we take the viewpoint that all emergent constraints have some (even if limited) information about S.

The application of the same mathematical approach to all constraints facilitates comparison of their predictions. Column 5 of Table 2 reports a central estimate of S derived for 17 emergent constraints. This estimate is calculated from the ordinary least squares linear regression of S on the present‐day climate system variable evaluated at its observed value using the data for the combined CMIP3/CMIP5 ensemble compiled in Caldwell et al. (2018) and, hence, represents the maximum‐likelihood value of S assuming a linear relationship. More advanced methods of determining the predictand S from emergent constraint relationships are discussed in Bowman et al. (2018), Schneider (2018), Williamson and Sansom (2019), and Brient (2020).

All emergent constraints predict this maximum‐likelihood value of S to lie between 2.8 and 4.2 K, consistent with the statements given in the original papers (Column 4 of Table 2). A general tendency for greater agreement with observations of present‐day climate system variables for GCMs with S values in this range was also found in related model‐weighting studies using observations of multiple present‐day climate system variables (Brown & Caldeira, 2017; Huber et al., 2011; Knutti et al., 2006; Murphy et al., 2004).

Overall, these studies suggest that observations of a wide range of present‐day climate system variables are more consistent with S higher than 2.8 K. This consistency of predictions suggests that it may be possible to form a single likelihood function to represent this evidence. We proceed approximately, as there is no established literature on how to combine constraints, particularly when dependencies between constraints may exist (Hall et al., 2019). (See Bretherton and Caldwell [2020] for a first attempt to combine the predictions from multiple emergent constraints.)

First, we consider these emergent constraints using present‐day climate system variables to be constraints on the climate feedback parameter λ, rather than S, since the present‐day climate system variables are not directly a function of CO₂ variations and are more closely related to climate feedback processes than S itself. To determine their predictions for λ, we calculate central estimates for λ from the regression of λ on the present‐day climate system variables in the identical way as for S (Column 6 of Table 2). The central values of λ locate on average at −1.01 W m⁻² K⁻¹, and this average does not vary by more than 0.05 W m⁻² K⁻¹ if one excludes the emergent constraints that do not pass the ensemble robustness and physical mechanism tests of Caldwell et al. (2018). We therefore assign −1.01 W m⁻² K⁻¹ as the mean of a Gaussian likelihood function for λ based upon this emergent constraint evidence.

The second step of assigning a standard deviation to the likelihood function is more complicated. The uncertainties in λ calculated from the errors in the linear regression fit and the observational uncertainty in the present‐day climate system variable are insufficient to characterize the structural uncertainty, especially for λ values outside the range seen in the available GCMs. Several considerations favor assigning a larger width to the likelihood function. First, the authors of individual constraints may have consciously or unconsciously chosen details of their present‐day climate system variable to optimize its correlation with S over the GCMs they were examining, which results in an overconfident prediction. Furthermore, the emergent constraint approach implicitly assumes that all other GCM characteristics relevant for λ except the present‐day climate system variable are unbiased and complete, and to the extent that this is not the case, predictions could be biased (Klein & Hall, 2015). Finally, when compared with the individual feedback approach, the emergent constraint approach appears less rigorous given the general lack of verified mechanisms and relative indirectness of the relationship between the present‐day climate system variable and a highly integrated quantity like the total climate feedback parameter λ, which is dependent on multiple feedbacks (Hall et al., 2019; Klein & Hall, 2015). (This is less of a concern for emergent constraints for individual climate feedbacks.) With these considerations in mind, we assign the Gaussian width of the likelihood function from emergent constraints to be 0.6 W m⁻² K⁻¹, a value ~40% larger than the uncertainty in λ from the primary process approach assessing individual feedbacks (section 3.4). The likelihood function from emergent constraints is thus N(−1.01, 0.6) and illustrated in Figure 8b. It indicates very low likelihood on the low end of S (large negative λ) but much less constraint on the high end of S (small negative λ).

One may wonder how independent emergent constraints are from the primary approach, given that both approaches use GCMs and in some cases the same present‐day observational evidence (particularly for tropical low clouds). One could perhaps treat the latter issue by only examining those constraints using present‐day climate system variables not already considered by the primary assessment, but a common reliance on GCM simulations of present‐day climate would remain. Furthermore, while independent information is suggested by the fact that all emergent constraints have a central estimate of λ smaller than that of the process central estimate of −1.30 W m⁻² K⁻¹, the difference in predicted λ is not large compared to the overall uncertainty and could be the result of a missing process biasing the prediction of either emergent constraints or the individual feedbacks. Other arguments supporting independence are that the emergent constraint and individual feedback methodologies are very different and that some emergent constraints use present‐day climate system variables not considered by the primary approach. We conclude that the two approaches are not wholly dependent, but are also unlikely to be wholly independent.

In summary, we consider the emergent constraints from present‐day climate system variables to offer evidence favoring S above 2.8 K. However, the evidence comes with a greater number of issues than those affecting the primary approach. These issues are that (a) many of these emergent constraints for S are not confirmed with respect to either robustness to model ensemble or a known physical mechanism, making it difficult to know how much confidence to give them; (b) it is unclear whether the evidence from these emergent constraints is independent of the evidence used in the primary approach to assess individual feedbacks; and (c) we formulated a likelihood function in an ad hoc manner. While future work may address these issues, they currently warrant a cautious approach to the treatment of these emergent constraints in the Bayesian analysis of S. Accordingly, in section 7 we use the emergent constraint likelihood function only for a sensitivity study, not for our Baseline calculation. In the sensitivity study, the emergent‐constraint evidence is assumed to be independent in order to explore its maximum impact.

3.7. Summary

The climate sensitivity S is determined by the radiative forcing per CO₂ doubling ∆F _2xCO2, and the sensitivity of TOA net radiation to global mean temperature (“total climate feedback”), λ. In this section, we assessed the various lines of evidence—observations, theory, GCMs, and process‐resolving models—directly constraining these two quantities. The focus is on physical processes that control the TOA energy balance via the global albedo and the greenhouse effect. ∆F _2xCO2 is relatively well known, and its direct component can be calculated from the equations of radiative transfer using line‐by‐line models. Most uncertainty therefore comes from the climate feedback parameter λ, which is in turn the sum of contributions λ _i from a set of distinct feedbacks.

Among these distinct feedbacks, those due to clouds remain the main source of uncertainty in λ, although the uncertainty in the other feedbacks is still important. It follows from Equation 4 and the relatively small uncertainty in other feedbacks and CO₂ forcing that a negative feedback from clouds is required to push S near or below 2 K. Moreover, this negative feedback must strengthen nonlinearly to push S progressively lower, since dS/dλ ~ λ ⁻². We find that a negative total cloud feedback is very unlikely and that there is sufficient evidence to effectively rule out the values of λ required to bring S below 1.5 K, thus placing a strong constraint against very low S.

Carefully quantifying these inferences on a feedback‐by‐feedback basis and for the CO₂ forcing produces a process‐based PDF for S which has its median value at 3.1 K and the 17th and 83rd percentiles at 2.3 and 4.6 K (Figure 8c). This is based on Gaussian means and standard deviations for ∆F _2xCO2 and each λ _i (Table 1), with broad prior probabilities and a priori independence assumed for all quantities. Results are robust to sensitivity tests as discussed later in section 7.3. This PDF still stands when accounting for (a) the additional constraint from separate evidence from observations of global interannual radiation variability on λ and (b) the additional uncertainty associated with possible errors in identifying a complete set of feedbacks λ _i, the two of which we take to roughly cancel out. In this sense, the total λ evidence from observations of interannual radiation variability makes an important contribution even though it is not directly used in the likelihood.

Separately, emergent constraints on S based upon present‐day climate system variables offer an alternative, but not entirely independent approach to assess S, based upon exploiting the relationship across a GCM ensemble between S and an observed present‐day climate system variable. By combining the evidence from the available constraints, we assess a separate emergent constraint likelihood function for λ (Figure 8b). Relative to the individual feedback approach, the emergent constraint approach points toward a somewhat smaller λ and larger S, but with considerably less precision. It also comes with greater caveats necessitating a more cautious treatment.

Regardless of approach, the total cloud feedback is the key quantity driving the uncertainty, since other feedbacks are well constrained by multiple lines of evidence supported by good basic physical understanding. The cloud feedback is constrained mainly by summing up feedbacks associated with different cloud regimes (section 3.3) but also by observable indicators of the total global sensitivity (section 3.5). Over the past decade, the contribution to this feedback from tropical marine low clouds has received the greatest attention due to its dominant contribution to the spread in total cloud feedback across different GCMs (Bony & Dufresne, 2005). Recent research has produced strong new evidence that these clouds provide positive feedback (section 3.3.2 and Figure 6). The reduced uncertainty surrounding this feedback component should be viewed as a significant advance. However, uncertainty from other cloud responses remains significant and possibly underappreciated, thus worthy of greater attention in the future.

The inferred positive total cloud feedback arises from several contributions. These include (1) a lifting of high cloud tops in warmer climates, as indicated by detailed numerical cloud simulations, observed trends since the 1980s, climate models and expected from theory; (2) a dissipation of tropical and midlatitude marine low cloud, probably due to increased mixing of environmental air into clouds as the climate warms, as indicated by observed cloud variability, and detailed numerical cloud simulations; and (3) a dissipation of warm‐season low cloud over land due to decreasing boundary layer relative humidity, as expected because land warms faster than oceans, and as seen in observed humidity trends since the 1970s and in GCM simulations of warming. Meanwhile, a sizable negative feedback from clouds in tropical deep convection regions is inferred from observations of interannual variability but does not overwhelm the combined positive feedbacks from rising high cloud tops and reduced low‐cloud cover. Separately, a negative feedback due to transitions from ice to liquid in high‐latitude clouds present in many GCMs is now thought to be unrealistic. Interannual fluctuations in TOA energy balance, which reflect the net effect of all cloud types, also point to a positive total feedback, suggesting that we have not missed any major feedbacks by assessing only a finite set of individual cloud types.

To reconcile all of the above evidence with an overall negative feedback from clouds (which is what would be required for S to be below 2 K given the other feedbacks, as discussed above) would require multiple lines of evidence to have failed significantly for at least one cloud type. For example, the low‐cloud feedback could be negative only if observed sensitivities have been misinterpreted, numerical cloud models are incorrect, the overall cloud feedback is near one end of the range indicated by satellite data, and several emergent‐constraint studies are incorrect. It would be perhaps easier to imagine some unanticipated negative cloud feedback—but one that simultaneously has not appeared in climate models, detailed cloud simulations, or observed interannual variability or trends since 1979, so all lines of evidence would somehow have missed this feedback. Similar multiple failures or misinterpretations of the evidence are probably required to make the cloud feedback strongly positive enough to yield S significantly above 4.5 K, although high S values are harder to rule out than low ones because S increases nonlinearly as positive feedback increases.

Several research trends have contributed to the recent progress in constraining S with process understanding and are expected to contribute in the future:

• Increased use of high‐resolution process models such as LESs and cloud‐resolving models to understand and constrain the feedbacks from a wider variety of cloud types. Increasing computational power allows for longer simulations of models with finer‐resolution and larger domains. For example, larger domains will permit LES to simulate the impact of mesoscale circulations on the feedbacks from tropical marine low clouds (Nuijens & Siebesma, 2019). Furthermore, short simulations of global models with a horizontal grid of O(1 km) are now feasible. However, progress for cold clouds requires improved representations of ice cloud microphysics.

• Increased use of high‐quality satellite observations with longer records to better constrain climate feedbacks and the physical processes responsible for them. Continuing cloud and radiation observations from both passive and active sensors will reduce uncertainty in feedbacks inferred from interannual variability and identify whether the feedbacks exhibited through trends to the emerging warming are consistent with current understanding. However, progress requires maintaining observations that are in danger of disappearing at the end of current satellite missions. High‐quality in situ observations will also help constrain key process uncertainties not amenable to satellite observations.

• Increased analysis and understanding of climate feedbacks. New diagnostics have improved quantification and understanding of specific cloud feedbacks in both GCMs and observations. Emergent constraints aid in identifying which present‐day observations are of most value for inferring climate feedbacks. The interplay between GCM experimentation and observational analysis has yielded important insights into topics such as the relationships among climate feedbacks and their dependence on the spatial pattern of warming. An important goal is to develop a more complete understanding of how the climate feedbacks from short‐term variability we observe relate to the feedbacks from long‐term forced climate change we seek.

4. Constraints From the Historical Climate Record

What can we learn about climate sensitivity from the historical record of changes in global mean temperature and the energy budget? The world has warmed by approximately 1 K since the eighteenth century (Allen et al., 2018). This warming is primarily attributable to the net effect of anthropogenic GHGs and aerosols, but other external influences on the climate system and internal variability have also played a role (see assessment in Bindoff et al., 2013). A number of studies have estimated climate sensitivity based on observed changes in temperature and ocean heat uptake over a given period, along with the radiative forcing estimated from emissions inventories, observations, and climate models. Best estimates of climate sensitivity from such approaches range from 1–3 K and feature wide uncertainty ranges, particularly toward high values. More recent studies appear to have lowered the upper limits on sensitivity owing primarily to better constrained and stronger estimates of radiative forcing (see Knutti et al., 2017, and Forster, 2016, for reviews of recent progress), although recent wider ranges of aerosol forcing have put this narrowing into question (see below).

It is not straightforward to infer a constraint on climate sensitivity from the historical record. GHG forcing is not the only driver of historical climate change, and climate generates substantial variability. Also, as introduced in section 2.3, the climate is not in equilibrium with the forcing, and the feedbacks operating over the recent period may be different from those that determine sensitivity at equilibrium (see also Knutti et al., 2017). In section 4.1 we first diagnose climate sensitivity using the traditional approach, using Equations 2 and 4, where we ignore the role of variability in TOA radiation (V). We refer to the quantity thus estimated as S _hist. Section 4.2 then diagnoses a value of S employing the full Equation 6, taking into account differences between radiative processes over the historical period compared to those over 150 years of a hypothetical CO₂ quadrupling. Results are summarized and compared to earlier estimates in section 4.3.

4.1. Inferring S _hist From the Historical Climate Record

Most published estimates of S _hist based on the instrumental climate record directly or indirectly rely on a simple global energy balance model for the climate system (Equation 19) (see Forster, 2016; Gregory et al., 2002; Otto et al., 2013). Expressed in terms of the inferred climate sensitivity for the historical record, S _hist, combining Equation 2 with Equation 4 and neglecting internal variability V, the energy balance model becomes

$$S_{\text{hist}}=∆F_{\text{2xCO2}}∆T/\left(∆F-∆N\right)$$ (19)

where ∆T is the forced change in global mean surface temperature, ∆F is the global mean radiative forcing, and ∆N is the change in global mean downward net TOA energy imbalance. Here, ∆N can be measured directly either from the ocean heat content and/or from satellite observations constrained by ocean heat content (Forster, 2016), and ∆F _2xCO2 is the radiative forcing for CO₂ doubling. The change ∆ is taken between the present day and a base period early in the historical record, boundary conditions that will be discussed in detail in section 4.1.1.

This inferred historical sensitivity S _hist should not be confused with the TCR, which measures the transient warming of the Earth system before it reaches equilibrium. By contrast, Equation 19 attempts to use transient observations to estimate an equilibrium quantity by accounting for the radiative imbalance ∆N (Frame et al., 2005; Otto et al., 2013).

Here, we assess the observationally based constraints on each of the three quantities: ∆T, ∆F and ∆N (section 4.1.1). We combine them with the PDF of ∆F _2xCO2 from Table 1 to calculate the resulting likelihood for different values of S _hist assuming this simple energy balance model (section 4.1.2). We further investigate how such likelihoods change if the simple energy balance model (Equation 19) is modified by applying it to the changes in surface temperature and warming attributed to GHGs only and by fitting models of varying complexity to observed spatial and temporal patterns of climate change (section 4.1.3).

4.1.1. Observationally Based Estimates, Their Inputs, and Uncertainties

Observationally based changes and their uncertainties depend on which periods of the historical record are used to estimate them. We define the “base period” from which anomalies are taken to be the average over years 1861–1880 (1 January 1861 to 31 December 1880) because during this time GHG levels were relatively close to (although not at) preindustrial levels, there were no large volcanic eruptions, and temperature records have adequate global coverage (see Hawkins et al., 2017; Schurer et al., 2017). We also consider the alternative base period 1850–1900 (1 January 1850 to 31 December 1900), which spans some major volcanic eruptions but reduces the impact of internal climate variability due to its extended length. We define “present day” as the average over years 2006–2018 (1 January 2006 to 31 December 2018), a period over which the global energy imbalance was observed with relatively small uncertainty. We use differences between these two periods to estimate ∆T, ∆F, and ∆N and produce constraints on S _hist.

4.1.1.1. Forced Surface Temperature Change (∆T)

In order to estimate the global mean temperature change ∆T, we rely on gridded surface temperature data. There are two recognized uncertainties associated with this observational record. First, the surface network is sparse, particularly in the early portion of the historical record, potentially leading to biased estimates of global mean temperature changes if observations are missing over regions that are warming more (e.g., the Arctic) or less rapidly (e.g., the Southern Ocean) than the global mean. Second, gridded temperature records generally blend SST over the oceans with near‐SATs over land, potentially leading to an inconsistency, as S and S _hist are often assumed to be based on global mean SAT changes. For example, using observations that are based on a combination of SAT and SSTs to estimate global SAT changes can lead to a small underestimate of observed warming (Richardson et al., 2016). The underestimate becomes more severe when missing coverage data is neglected as well (Schurer et al., 2018). This then would lead to an underestimate of S based on SAT.

To account for coverage bias in the observations, we use the data set developed by Cowtan and Way (2014), which corrects for missing data in the observational network. To compare blended SST/SAT data in observations with SAT‐only trends in the energy budget, we add an offset term to the “blended” observations. This term is derived from the difference between CMIP5 model SAT fields and blended model SAT/SST fields (here, taken from the “xax” blended fields in Richardson et al., 2016). Uncertainties in the resulting estimated observational SAT fields were calculated by adding in quadrature the 5% to 95% uncertainties in the Cowtan and Way (2014) trends to the 5–95% range of the difference between SAT‐only fields and blended model SAT/SST fields across all CMIP5 RCP8.5 simulations, as the uncertainties were assumed to be independent and PDFs are presumed Gaussian. The results were found to be insensitive to the choice of RCP scenario and model. These estimates are detailed in Table 3.

Table 3.

Temperature Trends Used to Assess Energy Budget Constraints on S_hist

Data set	Time period	Observed blended trend (SAT/SST) (K)	Observed blended trend uncertainty (K)	SAT‐blended trend from models (K)	SAT‐blended trend uncertainty (K)	Estimated SAT trend (K)	SAT trend uncertainty (K)
Cowtan and Way	2006_2018 minus 1850–1900	0.96	±0.07	0.09	±0.04	1.02	±0.08
Cowtan and Way	2006_2018 minus 1861–1880	0.94	±0.07	0.08	±0.04	1.03	±0.08

Note. Uncertainties are 5% and 95% ranges and exclude the contribution from internal variability (section 4.1.1). The bold row marks the baseline values chosen for the main estimate of S _hist, although the full range of estimates is used in assessing uncertainties.

The relatively small uncertainties in Table 3 account for temporal error autocorrelation (e.g., Morice et al., 2012) but do not factor in internal variability. We quantify internal variability of global mean temperature by considering all possible combinations of global temperature changes between periods of the same length as used in our calculations (20 years to imitate Years 1861–1880, 51 years for Years 1850–1900, and 13 years for 2006–2018) that are separated by more than a century within unforced preindustrial control simulations of 21 CMIP5 models, giving an average standard deviation of 0.08 and 0.07 K for the shorter and longer base periods, respectively. Absent knowledge of whether this has contributed to or detracted from the observed warming, we combine (in quadrature) the uncertainty in warming arising from internal variability with that arising from instrumental uncertainties (presented in Table 3). This yields our overall estimates of uncertainty of ±0.14 and ±0.12 K (5–95% ranges) for forced warming relative to 1861–1880 and 1850–1900, respectively (expressed as ranges in Column 6 of Table 5). The main ∆T used in this analysis (e.g., Figure 11) is taken over 1861–1880 to 2006–2018 as 1.03 (0.89 to 1.17 K, 5 to 95% range) K (Table 5, Line 1, Column 6) due to the greater availability of data since 1861, compared to 1850 and a relatively reduced level of volcanic activity.

Table 5.

Comparison of Our S_hist Estimates With Previous Studies That Are Representative of the Literature Range of Sensitivity Estimates (for a Complete Collection See Knutti et al., 2017)

Study	Periods	ΔF 2xCO2 (W m−2)	ΔF (W m−2)	ΔN (W m−2)	ΔT (K)	S (K) published	S hist (K) Equation 19	S hist (K) Equation 21 with uniform S hist prior
This study (Cowtan and Way, SAT, Bellouin et al. (2020) aerosol ERF) BASELINE	1861–1880 2006–2018	4.0 (3.51,4.49)	1.83 (−0.03,2.71)	0.6 (0.3,0.9)	1.03 (0.89,1.17)	—	3.11 (1.86,14.41)	4.26 (2.04,16.13)
This study (Cowtan and Way, blended)	1861–1880 2006–2018	BASELINE	BASELINE	BASELINE	0.96 (0.82,1.1)		2.90 (1.73,13.52)	4.02 (1.90,16.01)
This study BASELINE SAT, modified start dates	1850–1900 2006–2018	BASELINE	2.09 (0.25,2.96)	BASELINE	1.02 (0.9,1.14)		2.63 (1.66,10.97)	3.52 (1.80,15.33)
This study BASELINESAT, AR5 aerosol ERF	1861–1880 2006–2018	BASELINE	2.27 (1.45,2.98)	BASELINE	BASELINE		2.49 (1.66, 5.05)	2.79 (1.76,7.48)
Lewis and Curry (2018)	1869–1882 to 2007–2016	3.8 (3.06,4.54)	2.5 (1.68, 3.36)	0.5 (0.25, 0.75)	0.8 (0.65, 0.95)	1.5 (1.05,2.45)
Skeie et al. (2014)	observations up to 2010 (from 1850 and 1945/1950 for OHC)		1.5 (0.27–2.5) in 2010		1.4 (0.79–2.2) TCR	1.8 (0.9, 3.2)
Skeie et al. (2018)	observations extended up to 2014		2.3 (1.3, 3.4)		1.4 (0.9, 2.0) TCR	2.0 (1.2, 3.1)
Johansson et al. (2015)	observations up to 2011 (from 1880, 1957 for OHC)	3.71	2.29 (ERF from IPCC AR5 Table 8. SM5)		0.37–11.1 (prior ECS range for CO2 doubling)	N/A (2.0, 3.2) 90% CI 2.50 mode

Note. Medians and 5–95% ranges are shown. The temperature estimates include the effects of internal variability (section 4.1.1). When not given, these are inferred assuming Gaussian distributions. The row appearing in boldface contains the values used in the Baseline calculation.

Figure 11.

(a) Likelihood function for S _hist derived from the planetary energy budget of the 2006–2018 period compared to the 1861–1880 period. Different analyses are shown based on the alternative estimates in Table 5. The dashed line shows the impact of reducing the uncertainty in ΔT and ΔN by 90%. The gray line shows the impact of using the original Cowtan and Way (2014) blended data set that mixes surface air temperature observations with sea surface temperature observations. The orange line shows the impact of using 1850–1900 for the earlier period, while the red line shows the impact of using the AR5 aerosol forcing. (b) PDF of S _hist based on likelihood function in (a) combined with a uniform prior on S _hist (black line) and PDF derived directly from Equation 19 (green line).

4.1.1.2. Global Energy Imbalance Change (∆N)

Since the ocean accounts for most of the energy storage in the climate system, ocean heat uptake dominates the change in global energy imbalance ∆N. This means that a tight constraint on ocean heat content changes can make the difference between a strong and very weak constraint on climate sensitivity (e.g., Johnson et al., 2016). Uncertainty in the data set arises from incomplete coverage, similar to the surface temperature discussed above, measurement techniques, and preindustrial reference period.

Here we estimate Earth's global energy imbalance for 2006–2018 as 0.8 W m⁻² (0.55 to 1.05, 5–95% range). This global imbalance is estimated from the change in ocean heat content over time, estimated using in situ ocean observations with near‐global ocean coverage (Desbruyères et al., 2016; Johnson et al., 2016; Purkey & Johnson, 2010) combined with heat content changes associated with ice sheet changes, sea ice loss, and land warming (Mouginot et al., 2019; Schweiger et al., 2011; Shepherd et al., 2018; Zemp et al., 2019). It is dominated by the uptake of heat by the ocean, which accounts for over 95% of the imbalance (Johnson et al., 2016). This range of global energy imbalance is supported by other analyses of in situ observations (Cheng et al., 2017; Ishii et al., 2017; Levitus et al., 2012). It is also supported by several independent lines of evidence suggesting that in situ observations are accurate: (i) a high correlation between interannual variations in in situ and satellite energy imbalance estimates (Johnson et al., 2016) and (ii) the closure of the global sea level budget (Chambers et al., 2017).

The global energy imbalance assumed for both 1861–1880 and 1850–1900 base periods is 0.2 W m⁻² (0 to 0.4 W m⁻², 5 to 95% range), where these values are chosen to span those derived from GCMs (Lewis & Curry, 2015), energy balance modeling (Armour, 2017), and inferred ocean warming given observed SSTs using ocean GCMs (Gebbie & Huybers, 2019; Zanna et al., 2019). As above, we quantify internal variability by considering all possible combinations of global energy imbalance changes between periods of 20 (or 51) and 13 years in length that are separated by more than a century within unforced detrended preindustrial control simulations of CMIP5 models, giving an average standard deviation of 0.07 W m⁻² for both base periods. The resulting value of the change in global energy imbalance is ∆N 0.6 W m⁻² (0.3 to 0.9, 5% to 95% ranges assumed Gaussian, errors added in quadrature) for both base periods.

4.1.1.3. Radiative Forcing Change (∆F)

The third important input is the total radiative forcing ∆F. While often referred to as an observable quantity, radiative forcing is not directly observable and must be derived from radiative transfer models supported by estimates of rapid adjustments from climate models. While GHGs have dominated the forcing over the historical record, other forcing agents such as aerosols and land use change have played important roles as well. Even relatively small forcings can matter: While volcanic forcing is short‐lived, cases where volcanic forcing is markedly different between the beginning and end of a period analyzed could lead to long term climate variations as seen in the last millennium (see PAGES‐2k; Schurer et al., 2014). These effects can contaminate constraints (Lewis & Curry, 2015), and errors in volcanic forcing could indirectly impact the magnitude of the forced response (see Johansson et al., 2015; Santer et al., 2014). We chose the reference periods at the beginning and end of the historical record to minimize this effect. However, uncertainty in radiative forcing is dominated by the contribution from anthropogenic aerosols, especially via their impact on clouds, which is relatively unconstrained by process knowledge or direct observations (Bellouin et al., 2020). Here, to avoid circular reasoning, we try not to use constraints on aerosol forcing based on idealized models fit to the historical record (see review in Bindoff et al., 2013), and instead, we rely on bottom‐up estimates of aerosol forcing from models with comprehensive atmospheric physics.

We obtain our prior PDF of ΔF based on the approach of IPCC AR5 Chapter 8 (Myhre et al., 2013), but using data extended through 2018 (Forster, 2016) and updating a number of forcing components. First, we use the SARF formula (see section 3.2.1) for CO₂, CH₄, and N₂O, from Table 1 of Etminan et al. (2016). These SARF estimates increase CH₄ forcing by 25% compared to AR5, mainly to account for previously underestimated SW absorption (Etminan et al., 2016). To this, we add tropospheric adjustments and surface albedo estimated from the radiative kernel analyses of Smith et al. (2018) to estimate a CH₄ ERF over the historical period. Section 3.2.1 details a similar approach for CO₂. To estimate the evolution of CO₂ ERF over the historical time period, the ERF‐to‐SARF ratios for CH₄ and N₂O are assumed to be constant over the period, implying that the tropospheric and land‐albedo adjustments scale with their SARF values. Compared to the original AR5 time series, ozone ERFs and their time series are updated following Myhre et al. (2017).

Aerosol ERFs are taken from Bellouin et al. (2020), using the unconstrained PDF (Figure 8 of their paper, with correction). The best estimate from Bellouin et al. (2020) utilizes top‐down energy budget constraints and attribution studies, so to avoid circular arguments, we only employ the unconstrained estimate, which does not rely on detection and attribution studies to constrain aerosol through observed warming or energy budget estimates. Compared to that of AR5, this PDF has a longer tail toward strong negative ERF, thus representing an increased uncertainty, with a peak around −0.8 W m⁻² and a 5% to 95% range of −3.15 to −0.37 W m⁻². This PDF is based on combining ranges of estimates from known physical processes involved in aerosol forcing and satellite and other observations.

To calculate the forcing time series and its uncertainty, individual ERF time series for CO₂, other GHGs, stratospheric ozone, tropospheric ozone, land use surface albedo, black carbon on snow, stratospheric water vapor, contrails, and solar and stratospheric volcanic aerosols are combined using Monte Carlo draws, assuming that each time series has constant fractional uncertainty computed from the best estimate and the 5% to 95% range of the individual ERFs. These fractional uncertainties were based on the 1750–2011 ERF uncertainties from Myhre et al. (2013). Since historical CO₂ concentrations are accurately known, the uncertainty in CO₂ ERF is assumed proportional to that in ∆F _2xCO2. For terms other than aerosol, individual half‐Gaussian PDFs are used for lower and upper bounds (Forster, 2016; Myhre et al., 2013). For the total aerosol forcing including aerosol cloud interaction, samples from the unconstrained PDF of Bellouin et al. (2020) are scaled by a factor that reproduces the ranges of their PDF when applied to their forcing period (1850/2005–2015). The resulting PDF for ΔF has a long tail toward smaller values because of the aerosol component (Figure 10), with a median of 1.83 W m⁻² and a 5–95% range of (−0.03, 2.71) W m⁻². Table 4 details the ERF best estimates used for the individual components and periods. The PDF of ∆F _2xCO2 is given in section 3.2.1 (see Table 1).

Figure 10.

Prior and posterior PDFs of total (anthropogenic plus natural) ΔF (W m⁻²), comparing the 2006–2018 period with the 1861–1880 period. The black curve shows the prior forcing used in the Baseline calculation, which uses the unconstrained aerosol forcing based on Equation (8) from Bellouin et al. (2020). The green curve shows the extended AR5 aerosol forcing. The orange curve shows the posterior PDF produced when all prior PDFs are updated by all evidence used in the full Baseline calculation (see section 7), including process, historical, and paleoclimate evidence.

Table 4.

Historic ERF Medians for the Full 1750–2018 Period and the Two Time Periods Analyzed in This Report

Periods	Carbon dioxide	Other well mixed greenhouse gases	Tropospheric ozone	Stratospheric ozone	Aerosol	Land use albedo	Stratospheric water vapor	Black Carbon on snow	Contrails	Solar	Volcanic
BASELINE ERFs with Bellouin et al. ( 2020 ) unconstrained aerosol PDF
1750 to 2018	2.147	1.110	0.425	−0.050	−1.395	−0.163	0.079	0.040	0.050	0.000	−0.171
1861–1880 to 2006–2018	1.731	0.969	0.348	−0.050	−1.179	−0.106	0.064	0.020	0.048	0.017	−0.113
1850–1900 to 2006–2018	1.705	0.961	0.344	−0.050	−1.092	−0.105	0.064	0.018	0.048	0.011	0.180
Modified aerosol ERF to extended Boucher et al. ( 2013 ) estimate, other columns as above
1750 to2018					−0.842
1861–1880 to 2006–2018					−0.667

Note. Half Gaussians are used to create the individual PDFs for sampling unless except for the aerosol ERF in the BASELINE case which employs the unconstrained PDF from Figure 8 of Bellouin et al. (2020). The row appearing in boldface contains the values used in the Baseline calculation.

Results shown for comparison in Tables 4 and 5 also employ an aerosol estimate based on AR5 data (Boucher et al., 2013), which did not explicitly include energy budget studies but did rely on expert judgment based on selected GCM results and satellite analyses. Figure 10 compares both estimates for the Baseline period used here. The increased uncertainty range in Bellouin et al. (2020) compared to AR5 comes from assessing an increased number of aerosol‐cloud‐interaction processes, less confidence in the satellite‐based estimates of aerosol forcing and different choices in expert judgment. The orange line in Figure 10 is the posterior of ΔF that has been computed from the overall assessment of S in section 7 of the manuscript. In comparison to the prior PDFs, this is much more tightly constrained to positive forcing, ruling out a strongly negative aerosol ERF. This means that, in our analysis, it is more S that is providing a constraint of forcing over the historical period than vice versa (see Bellouin et al., 2020, and section 7).

4.1.2. Computing the Likelihood

The observed warming, increase in ocean heat uptake, and overall positive radiative forcing change constitute evidence for S _hist of above 0. To inform a PDF of S _hist, we need the likelihood P (E _hist |S_hist , ∆N, ∆F, ∆F _2xCO2), which quantifies how likely it is that such evidence E _hist would be observed given a putative value of S _hist (see section 2.3). To obtain this, we rearrange the energy balance (Equation 19) so that a forward model (cf. Equation 3) arises for the predicted temperature response ΔT from each combination of inputs ∆F, ∆N, ∆F _2xCO2, and S _hist:

$$∆T=S_{\text{hist}}\left(∆F-∆N\right)/∆F_{\text{2xCO2}}$$ (20)

where ∆F, ∆N, and ∆F _2xCO2 are random variables having specified prior distributions (i.e., uncertainties), which we randomly sample, hence generating a sample of possible ∆T values, for any given S _hist. In doing this, to allow for the correlation between the CO₂‐forced part of ∆F and ∆F _2xCO2 (Lewis & Curry, 2015; Otto et al., 2013), we decompose ∆F into its CO₂ and non‐CO₂ constituent time series and sample the latter independently of ∆F _2xCO2 before recombining to obtain the sample ∆F. We assume that the (prior) PDFs of ∆F and ∆N are uncorrelated (independent). Note that ∆T is not the observed warming but the expected warming based on the other information, given S _hist. The difference between ∆T and the best‐estimate observation, ΔT _obs, equals the sum of the observational error and unforced variation of global mean surface temperature, which has a Gaussian prior distribution with standard deviation σ _e. Hence, the likelihood of the observed warming for any particular sampled combination of (∆F, ∆N, and ∆F _2xCO2) is a Gaussian of width σ _e evaluated at ΔT _obs − ∆T, and the overall or “marginal” likelihood of the evidence given S _hist is found by averaging over the sample (see section 2.4.2). This analysis assumes that observational errors plus internal variability of ∆N and ∆T are independent. While it is possible there may be some correlation in geographic sampling errors, we expect any added uncertainty due to this to be swamped by other errors discussed below. (Our calculations do not account for a small correlation between ∆N and ∆T (mean r ² of ~0.1) in the control simulations, which would have a negligible impact on the results.)

Figure 11a shows the resulting likelihood for S _hist, with the maximum likelihood S _hist = 2.5 K. If combined with a broad, uniform prior on S _hist ~ U(0,20) as common in published studies, this likelihood produces a posterior PDF for S _hist with a 5–95% range of 2.0–16.1 K and a median of 4.3 K. These values of S _hist are higher than reported in recent publications (e.g., Forster, 2016; Lewis & Curry, 2018; Table 5) for two reasons. First, we are using updated values of ∆T, ∆F, and ∆N. Second, this Bayesian PDF for S _hist is slightly different to the non‐Bayesian distribution that would be obtained by substituting those of ∆T, ∆F, ∆N, and ∆F _2xCO2 directly into Equation 19 (5–95% range of 1.9–14.4 K and a median of 3.1 K; Table 5 and the green curve in Figure 11b).

The primary contributor to uncertainty in S _hist is our limited knowledge of the historical forcing associated with anthropogenic, tropospheric aerosols (Figure 11a). Aerosol forcing is important in determining the left‐hand tail of the S _hist estimates: The lowest estimates of S _hist result when aerosol forcing is estimated to be small or positive. If aerosol forcing were around 0, S _hist could be as low as 1.2 K. The possibility of net positive aerosol forcing is also considered to be small based on process‐based (thus, independent of energy balance models) estimates of aerosol effects (Bellouin et al., 2020). On the other hand, as we cannot rule out an aerosol forcing more negative than −2 W m⁻², relatively high values of S _hist cannot be ruled out either.

Secondary contributors to uncertainty in S _hist are the global warming trend and energy imbalance. Sensitivity tests are shown in Table 5 assessing the impact of (i) using a different aerosol forcing estimate, (ii) using a different base period (1850–1900 rather than 1861–1880), and (iii) using a global temperature estimate that is a blend of SST over oceans and SAT over land rather than being adjusted to produce a global SAT product. These secondary contributors produce ~10% or smaller changes to central estimates of S _hist. Our main analysis in Table 5 uses Cowtan and Way SAT‐derived temperatures from 1861–1880. While the present‐day energy imbalance is well constrained by ocean temperature observations, the energy imbalance prior to about 2002 is uncertain, and we must rely entirely on models to estimate energy imbalance prior to about 1950. A sensitivity test of eliminating nearly all uncertainty in ∆T and ∆N (Figure 11a) demonstrates that the uncertainties in these values contribute little to the overall uncertainty in S _hist.

4.1.3. Consistency With Estimates Based on Other Forward Models

The energy budget approach used above facilitates comparison with several previous estimates. However, it does not make full use of the observational record. In particular, by using only global mean quantities diagnosed as differences between the two periods over a century apart, it does not make use of any spatial or temporal information within the historical climate record. Temporal information may be particularly useful to reliably account for the effect of volcanic forcing, which can cause long‐term change (e.g., Broennimann et al., 2019) including in the ocean (Gregory et al., 2013; note that as section 4.1.2 uses model‐based estimates of ocean ∆N to 1950 prior to observations being available, this effect is negligible here). It can also make use of the difference in time evolution of GHGs versus aerosols after the 1980s, which can help disentangle their effects (e.g., Undorf et al., 2018, and references therein). We ask in the present section: Do estimates that use both the spatial and temporal history of anthropogenic and naturally forced warming further constrain S? In other words, would we get different or stronger constraints if we made use of that additional information?

We address this question by first comparing the above results to an estimate based on the portion of the observed surface and ocean warming that has been attributed to increasing GHGs (Tokarska, Schurer, et al., 2020): ∆T _ghg, ∆F _ghg, and ∆N _ghg. Attribution makes use of the time‐space pattern of warming to disentangle the effects of other forcings, particularly aerosols, from those of GHGs and then applies the same energy budget (Equation 20) as above, but uses attributed warming and greenhouse‐gas‐only forcing changes. This sharply reduces forcing uncertainty but increases uncertainty in the warming in the ocean and atmosphere, as there is uncertainty in the amount of warming that can be attributed to GHGs (see Bindoff et al., 2013, for an assessment of attributed warming). Note that the analysis ends in 2012 due to the availability of single‐forcing simulations. Note also that it neglects changes in ∆N other than ocean warming, which are estimated to be small above. The results, shown in Figure 12, illustrate that the use of the time‐space pattern from observations in deriving attributed inputs to Equation 20 reduces uncertainty by effectively downweighting very strong aerosol forcing as less consistent with observations. Note that PDFs arising from this approach, using a flat prior in S _hist, yield S _hist of 1.3 to 3.1 K (5% to 95% interval with the most likely value at 2 K, and median 2.1 K). Some studies have chosen to double the noise variance to address uncertainty in the pattern of warming (e.g., Schurer et al., 2018), which would widen our results if done here (dotted lines in the figure). In contrast, direct sampling of the distribution (dashes) rather than using a flat prior in S has a small influence on the PDF.

Figure 12.

Illustration of probability density functions from alternative, published approaches (as labeled). Tokarska, Schurer, et al. (2020) rely on an energy budget approach using the observed warming and ocean heat uptake attributed to greenhouse warming and is most directly comparable to our main approach. The solid line relies on a flat prior in S, the dashed line is directly sampled (see text; similar to green line in Figure 11), and the dotted line is the same as the solid line, but based on doubled variance of climate variability when deriving the attributed warming estimates. Johansson et al. (2015) and Skeie et al. (2018) results are based on time‐space analysis using simple climate model fits to observations and are also depicted for a uniform prior in S. Results suggest that use of time‐space patterns (either in simple model fits or deriving attributed surface and ocean warming) reduces the upper tail of climate sensitivity yet is affected by uncertainty in methods used, particularly if using simple models.

As an alternative to the energy‐budget approach, where S _hist is diagnosed from long‐term changes in Earth's energy budget discussed in section 4.1.2 and above for a greenhouse‐gas‐only energy budget, several groups have employed a framework in which S _hist (or a feedback parameter λ, which is the inverse of S _hist) is only one of multiple parameters of a simple dynamical model simulating multiple physical processes. These dynamical models exploit differences in the spatiotemporal responses to different forcings and are particularly effective in distinguishing between the responses to abrupt forcings like volcanic eruptions and slower‐varying forcings like GHGs. Generally, approaches use Bayesian priors and multiple free parameters (variables) including climate sensitivity, aerosol forcing, and ocean effective diffusivity or a similar quantity. For a given set of these variables, the dynamical model is integrated forward, and the likelihood is computed by comparing observations to the full spatiotemporal model output. Posterior estimates of S _hist arise from updating prior information on S _hist, aerosol forcing, and rate of ocean heat uptake, using the dynamical model and observations and then integrating out the latter two variables (Forest et al., 2002; Frame et al., 2005). Many published estimates are available (e.g., Aldrin et al., 2012; Andronova & Schlesinger, 2001; Forest et al., 2002; Johansson et al., 2015; Lewis & Curry, 2015; Libardoni & Forest, 2011; Skeie et al., 2018; see Knutti et al., 2017, for references and details). Estimates will be the more powerful and reliable, the more data they use up to the present period, the more effectively they use time‐space patterns to distinguish between causes of change, and the more state‐of‐the‐art the aerosol forcing and climate models. Note that posterior ranges of S _hist are sensitive to the choices of dynamical model and observational data set, suggesting that the complex spatiotemporal likelihoods employed with these models can amplify both model structural differences (Annan, 2015; Bodman & Jones, 2016) and observational errors (Libardoni & Forest, 2011). Furthermore, the ranges are sensitive to the choice of prior distributions (see, e.g., Bodman & Jones, 2016; Frame et al., 2005; Knutti et al., 2017; Lewis, 2014; see also sections 2.4.4 and 7.2). Figure 12 shows (for illustration only) the results of two approaches when using a uniform prior in S _hist, which yields an estimate of what a likelihood function against S would look like for comparison to the result of section 4.1.1. Both estimates shown (Johansson et al., 2015; Skeie et al., 2018) use a full Bayesian treatment. These studies analyze similar observed periods (1880–2011 for Johannson and 1850–2014 for Skeie et al., 2018) but use slightly different data sets for surface temperature and ocean heat content and employ different time‐dependent dynamical models, with separate representations for land and ocean in Johansson et al. (2015) and separate representations for Northern and Southern Hemispheres in Skeie et al. (2018). They also use different priors for model parameters other than S _hist, differ in their treatment of volcanism and total forcing uncertainty, and use different estimates of natural variability (e.g., the Johannsen et al. estimate widens if not using El Niño–Southern Oscillation [ENSO] as a covariate).

These choices translate to large differences in estimates of S _hist. Skeie et al. (2018) report a 90% interval of 1.2–3.1 K, while Johansson et al. (2015) estimate a 5–95% range of 2.0 to 3.2 K (for a comparison of all available estimates to date, see Knutti et al., 2017). We attempted to encompass both results into a synthetic PDF based on an inverse Gaussian (not shown), which maintained a thicker tail on the right‐hand side from both estimates by matching the 95th percentile but encompassed the Skeie et al. lower 5% tail and widened this tail (making the 10–90% range fit the 5–95% range) to account for overall structural uncertainties. The resulting PDF was very close to the greenhouse‐gas‐attributed case (red curve) for doubled variance shown in Figure 11.

We emphasize that neither the global energy budget approach (section 4.1.2) nor fitted dynamical models provide a purely observational constraint on S _hist. The estimates of ∆T, ∆F, ∆N, and ∆F _2xCO2 used are necessarily based on a combination of observational data with multiple models. Climate model data are employed to estimate global mean, near‐SAT change, to infer missing values, or the effects of blending (Cowtan et al., 2015; Richardson et al., 2016). ERF time series depend on radiative transfer models and model‐estimated aerosol effects and climatological atmospheric structure. And though observations of ocean warming over recent decades provide increasingly precise estimates of the modern global energy imbalance (Johnson et al., 2016; Trenberth et al., 2016), climate models are necessary to evaluate the global energy imbalance during the preindustrial period against which historical warming is compared (e.g., Lewis & Curry, 2015) as well as its internal variability.

Moreover, even the energy budget equation (section 4.1) is a simplified model (Hegerl & Zwiers, 2011). There are several notable assumptions inherent in this model (see section 2.2). For instance, it assumes that the global temperature response to an equivalent magnitude of forcing associated with different radiative forcing agents or global ocean heat uptake will be the same. Equation 19 also assumes that global radiative response to warming is exactly proportional to global mean temperature change and that the radiative feedbacks governing radiative response do not vary in time or state. As the radiative response to warming varies within comprehensive global climate models (e.g., Andrews et al., 2015, 2018; Armour, 2017; Armour et al., 2013; Ceppi & Gregory, 2017; Dong et al., 2020; Marvel et al., 2015, 2018; Proistosescu et al., 2018; Rose et al., 2014; Shindell, 2014; Winton et al., 2010) energy‐balance models could be developed that account for such variation (e.g., Ceppi & Gregory, 2019). In the next section, we explore these limitations and consider the extent to which estimates of S _hist from the historical record constrain the effective climate sensitivity S targeted in this assessment.

The rate of warming since only the 1970s or 1980s can also be exploited as an emergent constraint on TCR and on climate sensitivity (when accounting for the nonlinearity in the response between the present day and equilibrium), as aerosol forcing changes are thought to be relatively small over this period in the global mean (Jiménez‐de‐la‐Cuesta & Mauritsen, 2019; Tokarska, Stolpe, et al., 2020). The more recent CMIP6 models have a wider range of climate sensitivity than CMIP5, and many exhibit a strong warming since the 1970s (Forster et al., 2020), allowing for a relatively strong emergent constraint on TCR (Nijsse et al., 2020; Tokarska, Stolpe, et al., 2020; Winton et al., 2020). These estimates are susceptible to potentially large and unaccounted for uncertainties in the pattern effect which make it challenging to constrain S from such methods (Jiménez‐de‐la‐Cuesta & Mauritsen, 2019). They also likely underestimate the role of aerosol radiative forcing and its uncertainty as they assume the models' small aerosol forcing change since 1970 is correct, whereas aerosol forcing evolution might be more complicated (Regayre et al., 2015).

Overall, using the time‐space information of past warming, either by fitting a simple model or estimating the GHG contribution only to recent observed changes, tends to reduce the upper tail of S _hist while maintaining the lower (cf. Figures 11 and 12). This suggests that some of the stronger aerosol forcing values included in the recent, wider estimate of forcing uncertainty used in section 4.2 are not readily compatible with historical observations, although uncertainty in these “top‐down” estimates of aerosol are substantial, and the time evolution of the forcing rather than its magnitude can also contribute to any poor fit seen with historical observations. Nevertheless, we carry forward the estimate of S _hist that is based on the overall energy budget (section 4.1.2 and Figure 11). We do so because it is the most up‐to‐date estimate and requires the least assumptions such as in the time‐space pattern of aerosol forcing, which is quite uncertain (Schurer et al., 2018).

4.2. Transitioning From S _hist to S

Given constraints on S _hist from the historical climate record, what can be said about the effective sensitivity S as defined in section 2.1? If radiative feedbacks near equilibrium under CO₂ forcing were identical to the responses governing historical warming—in other words if there were a unique, linear relationship between ∆N‐∆F and ∆T—then S would be equivalent to S _hist. However, there is growing evidence that this relationship has not been constant in time and that the sensitivity S _hist inferred over the historical period may underestimate S, due to complications noted at the end of section 2.2.

Recognition of this problem began with model studies, but its key components have since been identified in observations as well. Many studies spanning multiple generations of climate models have found a strong tendency for radiative feedbacks to become less negative—an increase in climate sensitivity—as equilibrium is approached (Andrews et al., 2015; Armour, 2017; Armour et al., 2013; Ceppi et al., 2017; Geoffroy et al., 2013; Gregory & Andrews, 2016; Knutti & Rugenstein, 2015; C. Li et al., 2013; Lewis & Curry, 2018; Marvel et al., 2015; Murphy, 1995; Proistosescu & Huybers, 2017; Rose et al., 2014; Rugenstein et al., 2016; Senior & Mitchell, 2000; K. D. Williams et al., 2008; Winton et al., 2010; Zhou et al., 2016). This behavior arises from the fact that the global radiative response ∆N to surface warming depends on the spatial pattern of that warming (Andrews et al., 2015, 2018; Andrews & Webb, 2018; Armour et al., 2013; Dong et al., 2019; Gregory & Andrews, 2016; Marvel et al., 2018; Paynter & Frölicher, 2015; Winton et al., 2010; Zhou et al., 2017). The spatial pattern of warming can evolve for a number of reasons including the different time scales of ocean adjustment at different geographic locations (e.g., Marshall et al., 2015; Rugenstein et al., 2016; Stouffer, 2004), an evolving importance of different radiative forcing agents (Hansen et al., 2005; Marvel et al., 2015; Shindell, 2014), and internal climate variability (note that while the estimates of S _hist discussed above include the effect of internal variability on ∆T itself, they do not include its other impacts on the radiation balance ∆N). The resulting changes in apparent feedback strength as spatial patterns of warming evolve have therefore been termed “pattern effects” (SSBW16), distinguishing them from a feedback dependence on the magnitude of global mean warming (e.g., Bloch‐Johnson et al., 2015; Caballero & Huber, 2013; Meraner et al., 2013; see section 5.2.3).

New studies have clarified how pattern effects are likely to work. Figure 13 illustrates the key components of how temperature patterns are expected to affect ∆N. Warming in the West Pacific warm pool, a region of deep ascent in the troposphere, warms the troposphere and increases tropospheric stability throughout the tropics. In turn, this gives rise to enhanced radiation to space and enhanced low‐cloud cover (e.g., Andrews & Webb, 2018; Ceppi & Gregory, 2017; Dong et al., 2019; Wood & Bretherton, 2006; Zhou et al., 2016). In contrast, warming in the East Pacific, a region of overall descent, is trapped in the lower troposphere, decreasing tropospheric stability and leading to a reduction in low‐cloud cover (see section 3.3.2). The result is that warming in the West Pacific produces negative cloud and lapse rate feedback responses, while warming in the East Pacific produces more positive ones (Figure 13c). Warming at high latitudes produces a muted radiative response associated with positive lapse rate and sea ice feedbacks (Armour et al., 2013; Dong et al., 2019; Po‐Chedley et al., 2018) as well as through an impact on cloud cover through changes in tropospheric stability (Rose & Rayborn, 2016; Rose et al., 2014; Senior & Mitchell, 2000; Trossman et al., 2016; Winton et al., 2010).

Figure 13.

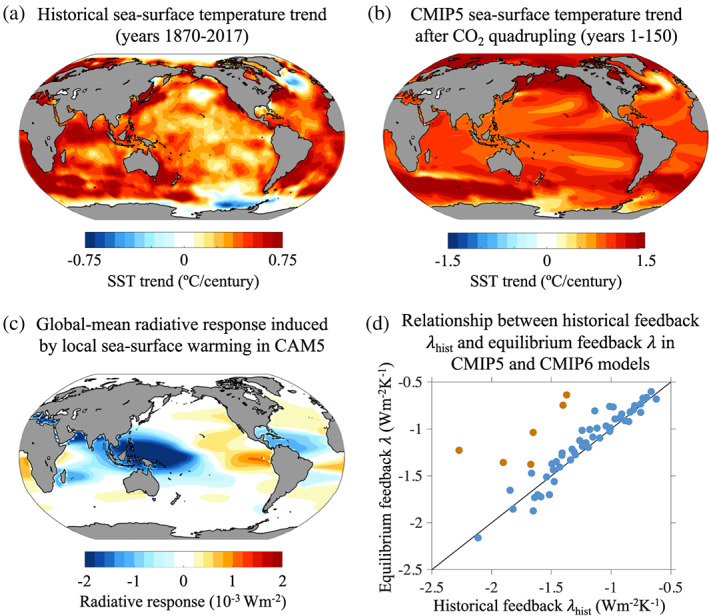
Illustration of the pattern effect. (a) Linear trend in observed sea surface temperatures (SSTs) over years 1870–2017 from the AMIP2 data set (Hurrell et al., 2008). (b) Linear trend in CMIP5 mean SSTs over 150 years following abrupt CO₂ quadrupling. (c) Global mean TOA radiative response induced by perturbing SSTs in one region at a time, calculated as anomalous TOA radiative fluxes in response to local SST perturbations in NCAR's Community Atmosphere Model Version 5 (CAM5) (Zhou et al., 2017; see also Dong et al., 2019, for comparison to CAM4). (d) Relationship between historical feedbacks λ _hist and the long‐term λ in coupled CMIP5 and CMIP6 models using values from analysis in Lewis and Curry (2018) and Dong et al. (2020) (blue points), respectively, and for atmosphere‐only simulations from Andrews et al. (2018) (orange points).

The impact of varying tropical SST patterns on cloud cover on decadal to centennial time scales, which is thought to dominate the pattern effects in models (Andrews et al., 2015; Dong et al., 2019; Zhou et al., 2017), has been seen in satellite observations as well. Specifically, the observational studies of Zhou et al. (2016), Loeb, Thorsen, et al. (2018), Ceppi and Gregory (2017), Fueglistaler (2019), and Loeb et al. (2020) find evidence for a pattern effect in the satellite records of cloud cover and TOA radiation as well as in atmospheric reanalysis fields of tropospheric stability. Importantly, GCMs appear to be able to capture the essential physical mechanisms linking SST patterns to radiative response (Loeb et al., 2020), providing confidence in the theory behind the pattern effect and the use of models to estimate how radiative feedbacks may change with evolving warming patterns (section 4.2.1).

The dependence of ∆N on warming pattern implies that S _hist will provide an accurate estimate of S only if the pattern of long‐term forced warming is similar to the observed pattern of warming over the historical record. However, the projected pattern of long‐term warming in response to CO₂ forcing (Figure 13b) is strikingly different from the pattern of observed warming over the historical period (Figure 13a). While the predicted forced pattern is smooth, the observed pattern is highly heterogeneous with little long‐term warming in the East Pacific and Southern Ocean. This indicates that if our understanding of cloud responses and the forced warming patterns is correct, the historical record includes cloud responses that have damped warming, but which will not persist in the long term. While the observed pattern is subject to uncertainties especially earlier in the record, the pattern since 1900 is robust across several station‐based data sets (Solomon & Newman, 2012), and its key features are supported by sea level pressure trends (L'Heureux et al., 2013) and are consistent with trends reported for more recent periods in Pacific trade winds (England et al., 2014) and sea level (Rhein et al., 2013; White et al., 2014).

There are likely multiple reasons for the heterogeneous historical warming. As discussed above, comprehensive GCMs predict some robust changes in the pattern of warming as the climate equilibrates to an imposed GHG forcing. In particular, warming tends to be delayed within the eastern equatorial Pacific and Southern Ocean, which are regions of ocean upwelling (e.g., Armour et al., 2016; Clement et al., 1996; Marshall et al., 2015). Yet the GCMs predict that warming in those regions will eventually become amplified relative to their surroundings (e.g., C. Li et al., 2013), resulting in more positive climate feedbacks and an increase in climate sensitivity as equilibrium is approached (Andrews et al., 2015; Armour, 2017; Geoffroy et al., 2013; Proistosescu et al., 2017; Rugenstein, Caldiera, & Knutti, 2016; Winton et al., 2010). Indeed, enhanced warming within these regions can be seen in the warming predicted by CMIP5 models over the 150 years following an abrupt CO₂ quadrupling (Figure 13b)—the period corresponding to our climate sensitivity metric S within the models. Enhanced temperature changes within these regions are also supported by proxy reconstructions of past climate states (Masson‐Delmotte et al., 2013; Tierney et al., 2019, 2020). The observed warming pattern (Figure 13a) is atypical compared to historical simulations of climate models. Some of the heterogeneity in early twentieth century SST trends may reflect unaccounted‐for offsets among groups of measurements (Chan et al., 2019), but there remain discrepancies between modeled and observed warming over this period (Hegerl et al., 2018). It is unclear if these reflect stronger internal variability than simulated in some GCMs, observational error, or a combination of both. GCMs are also not generally able to capture the far‐better observed pattern of SST trends since ~1980, particularly in the tropical Pacific Ocean (Zhou et al., 2016) and Southern Ocean (Kostov et al., 2018).

The observed pattern of SST changes since ~1980 resembles internal variability such as the negative phases of the Interdecadal Pacific Oscillation (Mauritsen, 2016; Meehl et al., 2016) and Southern Annular Mode (Kostov et al., 2018), and recently, each seems to have begun reversing (e.g., Loeb, Thorsen, et al., 2018; Stuecker et al., 2017). This suggests a likely contributing role from unforced variability. It is possible the observed warming pattern also contains a signature of external forcing, such as by stratospheric ozone changes (Marshall et al., 2014), aerosols or volcanic eruptions (Santer et al., 2014; Schmidt et al., 2014; Takahashi & Watanabe, 2016) or that it constitutes a forced response not captured by models (e.g., Kohyama et al., 2017; McGregor et al., 2018; Seager et al., 2019; see discussion in section 5).

Regardless of the cause, the relative lack of observed warming within these key geographic regions implies that radiative feedbacks will become less negative in the future if the long‐term warming pattern becomes more similar to that suggested by GCM simulations, paleo proxies and theory, suggesting that S may be larger than that implied by S _hist.

4.2.1. Quantifying the Historical Pattern Effect

The implication from current evidence outlined above is that the long‐term feedback under CO₂ forcing, λ, will be less negative than the apparent historical feedback, λ _hist. Here we use CMIP5 and CMIP6 GCMs to quantify this feedback change, denoted Δλ = λ − λ _hist. Rearranging Equation 6 following Equation 20, we write

$$\mathit{∆T}=-\left(\mathit{∆F}-∆N\right)/\left(\lambda -\mathrm{\Delta \lambda }\right)$$ (21)

allows us to evaluate the likelihood function of λ and in turn of our target climate sensitivity according to S = −∆F _2xCO2 /λ (see section 2.3).

Climate models generally suggest that feedbacks will become less negative in the future (Δλ > 0) as the spatial pattern of warming evolves, but because models do not fully reproduce observed patterns, there are uncertainties in how best to quantify this. Armour (2017) and Lewis and Curry (2018) considered changes in radiative feedbacks in CMIP5 model simulations with gradually increasing CO₂ at a rate of 1% per year (“1pctCO₂”) (Armour, 2017; Gregory et al., 2015), taking Year 100 as an analog for historical warming. Comparing λ _hist with each model's effective feedback λ (estimated as λ = −∆F _2xCO2 /S within simulations of abrupt CO₂ quadrupling abrupt4xCO₂), they find that the majority of models show a less negative global radiative feedback under abrupt4xCO₂ than under 1pctCO₂, with an average radiative feedback change of Δλ = +0.2 W m⁻² K⁻¹ (−0.1 to +0.6 W m⁻² K⁻¹ range across models) from Armour (2017) and Δλ = +0.1 W m⁻² K⁻¹ (−0.2 to +0.2 W m⁻² K⁻¹ range across models) from Lewis and Curry (2018). Note these values differ slightly from those in Armour (2017) and Lewis and Curry (2018) who estimated S based on a regression over Years 21–150 following abrupt CO₂ quadrupling rather than Years 1–150 as done here. Using the early portion of abrupt4xCO₂ simulations as an analog for historical warming and following the methods of Lewis and Curry (2018), Dong et al. (2020) find an average radiative feedback change of Δλ = +0.1 W m⁻² K⁻¹ (−0.2 to +0.3 W m⁻² K⁻¹ range across models) for CMIP5 models and Δλ = +0.1 W m⁻² K⁻¹ (−0.1 to +0.3 W m⁻² K⁻¹ range across models) for CMIP6 models.

A limitation of using 1pctCO₂ and abrupt4xCO₂ simulations to estimate feedback changes is that they do not account for the influence of non‐CO₂ forcing agents (in particular, aerosols which force the system very heterogeneously) and internal variability. Ideally, feedback changes could be quantified within historical forcing simulations, but this quantification has been made for only those few GCMs within which the historical radiative forcing has been quantified accurately enough for calculations of λ _hist to be performed. Using historical simulations of the latest Hadley Centre Global Environmental Model (HadGEM3‐GC3.1‐LL), Andrews et al. (2019) find an average radiative feedback change of Δλ = +0.2 W m⁻² K⁻¹ (−0.2 to +0.6 W m⁻² K⁻¹ range across four ensemble members). This value is on average larger than the Δλ = +0.04 W m⁻² K⁻¹ estimated using the early portion of the model's abrupt4xCO₂ simulation (Dong et al., 2020), suggesting that the value of Δλ may depend on having a realistic representation of historical forcing and of volcanic forcing in particular (Gregory et al., 2020). However, there is substantial spread in the value of Δλ across ensemble members, consistent with the results of Dessler et al. (2018) who find that internal climate variability alone results in a 0.5 W m⁻² K⁻¹ spread in λ _hist and thus also in the value of Δλ across a 100‐member, historical‐simulation ensemble of the Max Planck Institute Earth System Model (MPI‐ESM 1.1). Altogether, these coupled model results suggest mean value of around Δλ = 0.2 W m⁻² K⁻¹ ± 0.4 W m⁻² K⁻¹ (5–95% range). Assuming Gaussian uncertainties, Equation 21, along with historical estimates of ∆T, ∆F, and ∆N, results in a maximum likelihood for S = 2.9 K (green line in Figure 14; Table 6), somewhat higher than the equivalent value of 2.5 K for S_hist (black line in Figure 11a; Table 6).

Figure 14.

Likelihoods for S based on historical energy budget estimates accounting for pattern effects using different methods. The black curve shows the likelihood we use for our main analysis in section 7, which is based on feedback changes estimated using observed SST patterns (Andrews et al., 2018) but with inflated uncertainty to account for several considerations described in the text. The dotted black line shows the effect of halving the uncertainty in Δλ. The green line shows the likelihood accounting for feedback changes estimated from transient simulations of coupled climate models (Armour, 2017).

Table 6.

Statistics of the Likelihood P (E_hist|S) Combined With a Uniform Prior (From 0 to 20 K) on S, Based on the Two Different Estimates of Future Feedback Changes as Outlined Above

Scaling method	Max likelihood (K)	Median (K)	5% value (K)	95% value (K)
None	2.5	4.3	2.0	16.1
Transient simulations	2.9	6.2	2.3	17.9
Observed SST pattern	3.8	8.5	2.8	18.6

Note. The method based on prescribed observed SST patterns is chosen as the preferred estimate (in bold).

If models are to be a credible guide to the size of the pattern effect, they must accurately capture the relative patterns of historical and long‐term temperature change. However, historical and 1pctCO₂ simulations of coupled models generally produce patterns of warming that more closely resemble that of their abrupt4xCO₂ simulations rather than that of observed warming (Figure 13; Seager et al., 2019), suggesting that these simulations may underestimate the pattern effect (Andrews et al., 2018; Marvel et al., 2018).

An alternative approach is to estimate the pattern effect on the basis of differences between the observed ∆SST pattern and the anticipated long‐term one. This method does not rely on model calculations of transient change but does rely on an accurate long‐term ∆SST pattern. To implement this method, we use atmosphere‐only simulations wherein observed SSTs and sea ice concentrations are prescribed as boundary conditions (Andrews et al., 2018; Dong et al., 2019; Gregory & Andrews, 2016; Zhou et al., 2016). All other boundary conditions (GHGs, aerosols, etc.) are held fixed in time such that the SST and sea ice impact on the radiation balance (the feedback) can be estimated by linear regression. These atmosphere‐only model simulations exhibit values of S _hist that range from 1.6–2.1 K, in good agreement with that derived from global energy budget constraints (section 4.1.2) and unanimously lower than values of S found in abrupt4xCO₂ simulations using the same models (2.4 to 4.6 K) (Andrews et al., 2018). Andrews et al. (2018) collect all existing such model runs (from six different models, albeit only from four modeling centers) and find an ensemble mean value of ∆λ = +0.6 W m⁻² K⁻¹ (+0.3 to +1.0‐W m⁻² K⁻¹ range across models). Similar values are found if the equilibrium feedback is estimated as λ = −∆F _2xCO2 /S rather than from the regression over Years 1–150 following abrupt CO₂ quadrupling as in Andrews et al. (2018).

We prefer this approach for estimating the pattern effect because it is derived using observed SSTs and is thus not biased by errors in historical SSTs simulated by coupled models. However, this estimate still hinges on several key considerations. The first is that it relies on the accuracy of the observed SST and sea ice changes. Using alternative SST data sets, Andrews et al. (2018) found little change in the value of ∆λ within two models (HadGEM3 and HadAM3). The sensitivity of results to the choice of data set represents a source of uncertainty in the quantification of ∆λ using atmosphere‐only GCMs that has not been fully explored. The second consideration is that it relies on the abrupt4xCO₂ pattern of warming simulated by coupled models (Figure 13b) being an accurate representation of long‐term response to CO₂ forcing. If the long‐term warming pattern were to resemble that of observed historical warming, this would imply a value of S that is closer to our assessed value of S _hist. The inability of coupled models to capture the observed pattern of warming in the tropical Pacific (e.g., Seager et al., 2019) and Southern Ocean (e.g., Armour et al., 2016) may call into question their ability to accurately simulate the long‐term pattern of warming. However, a range of observational evidence from paleoclimate proxies and theory suggest that amplified warming in the southern high latitudes will indeed eventually emerge (Masson‐Delmotte et al., 2013) once the deep ocean waters that are upwelled to the Southern Ocean surface are warmed, likely taking hundreds of years or more (Armour et al., 2016). Moreover, proxy data since the Pliocene suggest that warming in the eastern tropical Pacific will eventually become amplified relative to the west (Tierney et al., 2019, 2020) as the upwelled water stems mostly from midlatitudes (Fedorov et al., 2015). Moreover, as noted above, much current evidence points to the observed pattern of warming being strongly influenced by internal variability and/or short‐lived climate forcers. This suggests that the observed warming pattern is transient in nature. Thus we assign a low probability that the forced pattern will strongly resemble the historically observed one.

A third consideration is whether the models used here to quantify the pattern effect faithfully represent the clouds and corresponding radiation response to these SST patterns. Comparison of National Center for Atmospheric Research (NCAR)'s CAM5 to observed low‐cloud trends in the East Pacific revealed that the model may underestimate the cloud increase (Zhou et al., 2016). Analysis of six CMIP6 models driven by observed SST and sea ice boundary conditions suggests that the models can generally replicate TOA radiation changes observed by satellite over 2000–2018 but that the models may underestimate the sensitivity of global radiation to SST changes and thus the magnitude of Δλ (Loeb et al., 2020). A final consideration is the extent to which the quantification depends on the selection of models used. The six models used here (from Andrews et al., 2018) represent an ensemble of opportunity, and it is unlikely that they capture all possible future feedback changes. A broader analysis would be needed to draw conclusions as to whether the methods employed here are biased.

In light of these considerations, we choose for our main analysis ∆λ = +0.5 W m⁻² K⁻¹ with Gaussian uncertainty ±0.5 W m⁻² K⁻¹ (5–95% range). This range is informed by the Andrews et al. (2018) estimate of the pattern effect based on observed SSTs but allows for a greater (though still small) possibility that the pattern effect may be smaller than reported in that study. Using this mean value of ∆λ and uncertainty in Equation 21, along with historical estimates of ∆T, ∆F, and ∆N, results in a maximum likelihood for S = 3.8 K, substantially higher than that of S _hist derived in section 4.1.2 or that of S derived from transient coupled models (Figure 14 and Table 6). Combining this likelihood (black line in Figure 14) with a broad uniform prior on S ~ U(0,20) yields a posterior with a 2.8 to 18.6 K 5–95% range (note that this large upper limit indicates that the data do not constrain the upper limit of climate sensitivity beyond the prior).

This estimate of the historical likelihood for S using a pattern effect based on observed SSTs follows our preferred approach, and we carry this forward into section 7 to be combined with other lines of evidence. However, we also consider the sensitivity of the results to a halving of the uncertainty on our assessed value of ∆λ (Figure 14). This reduces the 5–95% range slightly when combined with a S U(0,20) prior slightly from 2.8–18.6 to 2.9–18.5 K. These results suggest that the historical record currently provides only weak constraints on S and that improved quantification of both the pattern effect and the historical aerosol forcing is necessary to rule out high values of S in particular.

4.3. Summary

Because the climate sensitivity S would directly affect the magnitude of any radiatively forced climate change, the magnitudes of known changes can constrain S if enough is known about what drove them. The best‐observed example is the warming over the instrumental period. In this section we assessed what this warming tells us about S. Over this period the GHG forcings are known fairly accurately, while the largest uncertainties are the strength of non‐GHG forcings and the impact of nonequilibrium effects. These effects matter because the warming period is not very long compared to time scales of natural variability and system response lags.

The best‐known nonequilibrium effect is the TOA (and surface) energy imbalance, which persists for decades to centuries after an applied forcing due to the long time required for the oceans to fully equilibrate. This imbalance is reflected in changes in global ocean heat content, which, along with the surface warming, is reasonably well measured in recent decades, albeit with errors larger than sometimes appreciated.

To quantify how consistent various climate sensitivities are with the evidence, following past studies, we calculate a likelihood of the observed ocean heat content and surface temperature changes as a function of S. This calculation employs a PDF of total radiative forcing, based on direct observations and models of the various forcing agents and their radiative effects.

A second nonequilibrium effect has recently come to the fore which significantly affects the likelihood function, called here the historical “pattern effect.” Ocean surface warming in recent decades has occurred in a much more heterogeneous geographic pattern than that predicted at equilibrium under CO₂ forcing. Model simulations and satellite observations now show that this recent heterogeneity has driven net increases in low‐cloud cover and global albedo, reducing the warming relative to what it would have been with a smoother, equilibrium pattern of warming. If as expected this heterogeneous pattern is temporary (either a transient or a natural fluctuation), the implication is that S inferred from historical warming using straightforward assumptions or simple models with constant S, which we have denoted S _hist, is less than the true S. The direction of this bias is physically understood, and we are confident about that, but its magnitude is highly uncertain because we rely heavily on GCM simulations to quantify it. The development of observational constraints on the magnitude of the pattern effect is critical to be able to better constrain the likelihood of high values of S based on historical evidence.

Taking all the above factors into account, we find that given the historical evidence, the maximum‐likelihood value is S = 3.8 K, but values between 1.9 and 20 K and above can still be considered consistent with the evidence (likelihood >0.2). In particular, the historical observed climate change provides a strong constraint on the lower bound of S, effectively ruling out negative feedbacks, but only a very weak constraint on the upper bound. This latter conclusion, which differs from many previously published studies using the historical record, arises in part because the “pattern effect” could potentially allow even high values of S to be reconcilable with only moderate historical warming. The possibility of strong negative aerosol ERF also precludes setting a tight upper bound on S. Indeed our high‐likelihood range for S _hist (not accounting for the pattern effect) is consistent with most of those previous studies if we use older forcing and warming estimates, so the increase here is due to revised estimates rather than any difference in methodology. The Bellouin et al. (2020) aerosol ERF used here allows more negative tails than some recent estimates, especially those that implicitly match aerosol forcing to the observed warming. Previous studies that have not accounted particularly for the pattern effect produced energy budget constraints on S that were unjustifiably tight and too low.

The historical warming does provide strong evidence against S of ~1.5 K or less, because roughly 1 K of warming has already occurred, and this is likely all a forced signal (Allen et al., 2018; see also Bindoff et al., 2013; Schurer et al., 2018); this realized warming is less than the equilibrium warmingand from a forcing almost certainly less than ∆F _2xCO2. Even assuming a very small aerosol forcing, the lowest plausible observed warming (neglecting known negative biases), and the highest plausible radiative imbalance during the base period, it seems nearly impossible to assign nonnegligible likelihoods to values of S _hist (let alone S) less than 1.2 K. To reconcile the evidence with an S below even 2 K under reasonable PDFs of observed warming and imbalance would require either aerosol forcing to be near 0, or for aerosol forcing to be weak and the pattern effect to be weaker than expected.

Accordingly, the historical record offers potential to further narrow the S range at both ends with further research progress. If weak aerosol forcings can be ruled out, for example, the constraint at the low end could rise (this may also gradually happen with further warming, if it continues at the pace of the last few years). If the limit of strongly negative aerosol forcing were constrained, this would sharply reduce the upper tail as it would no longer allow very small net forcing which, in combination with large warming, leads to high estimates. On the other hand, if further research can limit the maximum size of the pattern effect on the historical radiative balance, this could permit the record to bound the high end of S, especially if aerosol forcing uncertainty is reduced. Future avenues of research employing decadal changes and regional patterns with emergent constraints over the historical period may eventually be able to place a tighter constraint on S _hist that avoids issues of circularity arguments with estimates of aerosol forcing, which combined with improved quantification of the pattern effect, may lead to a tight bound on S.

5. Constraints From Paleoclimate Records

Climate sensitivity estimates using paleoclimate information rely on a basic paradigm that there are times before the instrumental period for which we have a reasonable estimate of a climatic state. In particular, this concerns an estimate for global mean temperature that was sufficiently stable over centuries to millennia (i.e., in a quasi‐equilibrium state), together with estimates of how forcings differed from the “preindustrial” state. From these we can derive estimates of the overall sensitivity of the climate state to radiative forcings. This means that, in contrast to studies of historical constraints (section 4), paleoclimate studies do not consider disequilibrium in the planetary energy budget or ocean heat content and in principle we can use the energy balance Equation 3. However, we must contend with not just changes in GHGs but also changes in land surface vegetation, ice (land and sea), topography, and even potentially continental shapes and position (Farnsworth et al., 2019) for deep time periods, as well as other forcing and climate uncertainties that arise from the more limited information available. This requires Equation 3 to be modified with various additional terms (see also section 2.2). These terms will be discussed in more detail as they are introduced in the following subsections.

To make climate sensitivity estimates from paleoclimate data compatible with the parameter S targeted in this report (section 2.1), the influence of slow feedback processes needs to be explicitly resolved. Feedbacks resulting from the expansion and reduction of continental ice sheets are particularly important. The effects of vegetation and land surface changes and (partly vegetation‐related) dust aerosol influences also need to be considered. While CO₂ and CH₄ concentrations can act as feedbacks to other climate changes as well as forcings on paleo time scales, care needs to be taken to account for this in estimates of S; all that is available are total values for CO₂ and CH₄ concentrations during the last 800,000 years (from ice cores) and only CO₂ for older times. Furthermore, in reality feedback strength is not a constant parameter of the climate system; in particular, it may vary with the climate state and applied forcing, and this variation may be significant in the context of paleoclimate.

We consider colder climates than preindustrial (including glacial cycles), and warmer periods than preindustrial separately, with the LGM (~20,000 years ago) and mPWP (3.3–3.0 Ma) being the best known and most comprehensively studied examples. In accordance with section 2, we develop estimates for a likelihood function of the temperature change and priors on the forcings. Our basic approach is to generate ranges that encapsulate the range of plausible estimates presented in the literature. These are expressed in the form N(X, Y), which is a Gaussian distribution with mean X and standard deviation Y (all uncertainties are one standard deviation unless otherwise stated). We then calculate sensitivity likelihoods based on these constraints using the modified versions of Equation 3. The modifications to Equation 3 are necessarily different in form for the cold and warm periods due to the different level of evidence and the differing approaches in published research. Information from other intervals can, in principle, be included following a similar style of argument, especially as further detailed records through older intervals of the last 1 to 2 Myr emerge and as greater spatial coverage is developed. As an additional example, and as supporting evidence, we show the results obtained from analysis of the very warm period of the Paleocene‐Eocene Thermal Maximum (PETM), but this is not used in our final estimate.

As discussed in section 5.1, there is considerable uncertainty in measurements of climate variables gleaned from paleoclimate. Therefore, researchers interested in climate sensitivity have focused on intervals in the past when temperatures and GHG forcings have been very different to those of today and thus where the signal is also large. In sections 5.2 and 5.3 we present numerical values based primarily on our expert assessment of the relevant literature. We then combine the information in section 5.4 to produce a likelihood function for S based on paleoclimate information.

5.1. Estimating Climates in the Past—Methods and Sources of Uncertainty

The methods for obtaining paleoclimate changes and forcings from geologic evidence are less direct than those using the instrumental record. This results in considerable additional uncertainty, much larger than the uncertainty for direct measurements over the last few hundred years. We outline some of the methods and sources of uncertainty here. Reducing the uncertainties has the potential to lead to major improvement in future estimates of climate sensitivity using evidence from the geological past.

In practical terms, continental ice sheet variations are approximated using global sea level reconstructions and modeling (Clark & Mix, 2002; Clark & Tarasov, 2014; de Boer et al., 2010, 2012, 2014; Grant et al., 2014; Hansen et al., 2007, 2008, 2013; Lambeck et al., 2006, 2010, 2014, 2017; Rohling et al., 2012, 2017). Vegetation and land surface changes are very poorly constrained. For a few rare intervals, large‐scale biome reconstructions have been produced (typically ~125,000, ~20,000, and ~6,000 years ago; Bartlein et al., 2011; Harrison & Prentice, 2003; Harrison et al., 1995; Hopcroft & Valdes, 2015b; Kageyama et al., 2017; Otto‐Bliesner et al., 2017; Prentice et al., 1993; Wu et al., 2007). It is very difficult to obtain sufficiently dense global networks of well‐dated pollen data for such exercises; even for the well‐studied LGM a robust vegetation map has yet to be developed. High‐resolution dust‐aerosol records exist from only a few locations and mostly from the very remote polar regions (ice core records; Lambert et al., 2008; Schüpbach et al., 2018). Although dust is being incorporated in models (Kageyama et al., 2017; Otto‐Bliesner et al., 2017), and quality dust‐flux records from downwind of the dominant source regions (the world's great deserts) are being developed, a high density of such records is needed because dust is poorly homogenized in the atmosphere; it mainly influences the radiative balance close to, and downwind of, the source regions.

Past estimates of climate properties from direct measurements of atmospheric composition comprise only GHG concentrations (CO₂, CH₄, and to some extent also N₂O) in air bubbles preserved in ice cores. The oldest records, from Antarctic ice cores, cover the last 800,000 years (Siegenthaler et al., 2005), and there is some further information as far back as 1 Ma from shallow blue ice samples in Antarctica (Higgins et al., 2015; Yan et al., 2019). For other properties, including CO₂ concentrations, so‐called “proxy” measurements are used, which are empirically calibrated to climate properties on the basis of their modern spatial distributions and/or on the basis of calculations through the underpinning physical or chemical relationships (notably Boron‐isotope data; see below).

For properties that are less globally homogeneous (e.g., sea level, land ice sheets, or temperature), some level of modeling is required to transform sparse measurements into global estimates. Such models vary in complexity, from a simple metric for latitudinal variation, smoothing toward present‐day patterns, or utilizing patterns from paleoclimate simulations with state‐of‐the‐art climate models. In all cases, the community aims to develop a variety of independent proxies for each predominant climate property (for a CO₂ example, see Badger et al., 2019; Dyez et al., 2018), so that confidence in individual measures may be evaluated through comparison. This is important because certain climate proxies may, for example, be affected by changes through time in initial seawater ratios of the elements or isotopes used or respond nonlinearly to change in the controlling climate property (with one end of the relationship relatively insensitive to change, so that the proxy loses fidelity, or saturates). Cross validation is especially valuable if it can be performed between a proxy and direct measurements from ice cores; a key example concerns the validation of CO₂ reconstructions from the Boron‐isotope proxy by intercomparison with direct measurements of CO₂ changes from ice cores (e.g., Chalk et al., 2017; Foster, 2008; Honisch & Hemming, 2005; Martínez‐Botí et al., 2015; Raitzsch et al., 2018).

Another issue with proxies is that many rely on fossilizing biological signal carriers (e.g., foraminifera or concentrations of specific biomarkers), which implies a dependence over time on species‐specific behaviors, ecological niche changes, and biomineralization pathways. The impacts of these issues are commonly minimized by limiting analyses to a single, well‐defined species or biomolecule, but further back in time we are inevitably dealing with species that are no longer extant. Ecological equivalence is commonly assumed (mostly based on shape and shell‐development similarities), supported by whole‐assemblage evaluations of the entire suite of past species' ecological niche occupations relative to one another (commonly using stable oxygen and carbon isotopes). However, working with extinct species in ancient time intervals clearly introduces greater uncertainty than working with species alive today.

Finally, good chronology (dating) is essential when comparing records of different proxies or ice core data. Here, relative age equivalence is even more important than absolute age control: For evaluating paleoclimate sensitivity, past (proxy) values of climate forcing factors need to be compared to synchronous values of temperature, no matter what the absolute age of the interval is. Chronological control for such records is best in the past 40,000 years, when radiocarbon dating is available, and age uncertainties are only up to a century or two in the best cases (Hogg et al., 2013; Reimer et al., 2013). Next best control exists for the last glacial cycle (past 100,000 years), with strong constraints from ice core chronologies from Greenland and the West Antarctic, supported by U‐series dated cave deposits, allowing comparisons between records with age uncertainties of the order of at best 500 years (e.g., Shackleton et al., 2000; Grant et al., 2012; WAIS Divide Project Members, 2015; Marino et al., 2015). In older levels still, down to half a million years ago or so, combined application of U‐series dated cave deposits and astronomical time scale tuning of exceptionally rhythmic sedimentation systems (like that in the Mediterranean) provide a sound level of age control with uncertainties of the order of ±1,000 to 2,000 years (Grant et al., 2014). Targeted use of events, such as instantaneous volcanic ash deposits, can provide selected intervals of improved control relative to the uncertainties stated above. But it is evident that comparison between records is hindered to some extent by chronological control, which by itself introduces an unavoidable portion of uncertainty in calculated paleoclimate sensitivity estimates.

The types of proxies used for estimating climate variables for cold periods over the last 800 kyr are mostly different from those used for the warm periods further back in time. This means that we may expect uncertainties for these cold and warm periods, which we evaluate separately below, to be largely independent.

5.2. Evidence From Cold Periods: LGM and Glacial‐Interglacial Transitions

Glacial‐interglacial cycles of the Pleistocene (last 2.5 Myr) are best known from the last half million years. Over that time they were characterized by well‐documented CO₂ fluctuations between ~180 and ~280 ppm (Siegenthaler et al., 2005; we quote all gas concentrations by volume) and methane fluctuations between ~350 and ~700 ppb (Loulergue et al., 2008). Sea level/ice volume fluctuations took place over a total range of about −130 to +10 m (e.g., Grant et al., 2014; Rohling et al., 2009, 2014).

We focus mostly on the LGM (between 19,000 and 23,000 years before present) as it is the most recent quasi‐stable cold period and has been extensively studied. Relative to other, earlier but similarly cold, glacial maxima there is a wealth of data available for the LGM from both paleo archives and modeling studies.

In this section, the focus is on summarizing our understanding of paleoclimates using information from observations and modeling in order to derive priors on ΔF and likelihoods for ΔT for different intervals. For all temperature changes and forcings in this section, we use a Gaussian error distribution and give the uncertainty as one standard deviation, unless otherwise indicated.

5.2.1. Surface Temperature Change ∆T

Last glacial to interglacial global mean temperature change estimates have been much studied and remain debated. Across studies, the inferred range is between ~3 and ~7 K below preindustrial with little probability of lying outside this range (Annan & Hargreaves, 2013; Friedrich et al., 2016; Hansen et al., 2007; Köhler et al., 2010; MARGO, 2009; Masson‐Delmotte et al., 2010; Rohling et al., 2012; Schmittner et al., 2011; Snyder, 2016a). We therefore take N(−5, 1) as our observational likelihood of the temperature change.

5.2.2. Forcings Contributing to ∆F

Radiative forcing at the LGM consists of several components, and we describe the most significant of these here. Note that changes in global annual mean orbital forcing are negligible (~0.1 W m⁻²), although regional and seasonal changes range from −9 to −3 W m⁻² (Kageyama et al., 2017). Here we consider estimates from the literature, and estimate values for these forcings, in order to calculate an overall best estimate for the total forcing. Some of the literature also provides quantitative uncertainty estimates, which we use as an approximate guide, although finally we use a somewhat larger value to reduce the possibility of overconfidence in our estimate.

Lower GHG concentrations are well characterized for the LGM. Here we use the latest PMIP4/CMIP6 LGM estimates of [CO₂] = 190 ppm, [CH₄] = 375 ppb, and [N₂O] = 200 ppb (Kageyama et al., 2017). For the preindustrial GHGs, we use the CMIP6 estimates for 1850 (Meinshausen et al., 2017), [CO₂] = 284 ppm, [CH₄] = 808 ppb, and [N₂O] = 273 ppb. The forcing formulae from Etminan et al. (2016) translate these concentrations into CO₂: −2.16 W m⁻², CH₄: −0.37 W m⁻², and N₂O: −0.27 W m⁻². However, in line with the discussion in section 3.2.1 we increase the GHG forcings by 5% to account for the land warming effect (tropospheric and surface albedo adjustments). They therefore become −2.27, −0.39 and −0.28, respectively. Because the forcing due to a doubling of CO₂, ∆F _2xCO2, is considered uncertain in our analysis (with a central estimate of 4.0 W m⁻², see section 3.2.1), we represent the CO₂ component of the forcing as −2.27/4.0 = −0.57 ∆F _2xCO2 in our calculation. We further increase the CH₄ value by 45% to −0.57 W m⁻² to account for ozone and stratospheric water vapor effects (following Hansen et al., 2005).

Forcing from the large ice sheets, via albedo and elevation changes (lapse rate feedback) and the concomitant drop in sea level, have been estimated at around −3.2 W m⁻² by the IPCC AR4 (Hegerl et al., 2007) and −3.7 W m⁻² ± 0.7 W m⁻² in a review by Köhler et al. (2010). The single model analysis of Friedrich et al. (2016) obtains a rather lower value of −1.6 W m⁻² for the ice sheet forcing, which they ascribe to the effect of cloud cover substantially masking the ice albedo change. The climate models that participated in the second and third Paleoclimate Model Intercomparison Projects (PMIP2 and PMIP3) have values from −2.6 to −3.5 W m⁻² (PMIP2, Braconnot et al., 2012) and from −3.6 to −5.2 W m⁻² (PMIP3, Braconnot & Kageyama, 2015). The different ice sheet reconstruction used for PMIP2 and PMIP3 led to a difference in forcing of about −1 W m⁻² (Abe‐Ouchi et al., 2015). We represent this evidence with an estimate of −3.2 W m⁻² ± 0.7 W m⁻².

The radiative impact of changes in vegetation is estimated to be −1.1 ± 0.6 W m⁻² (Köhler et al., 2010; Rohling et al., 2012, and references therein). A variety of estimates have been made of the forcing due to the glacial increase in atmospheric dust loadings, with a range of best estimates of 0.1 to −2.0 W m⁻² (Albani et al., 2014; Claquin et al., 2003; Hopcroft et al., 2015; Köhler et al., 2010; Mahowald et al., 2006; Ohgaito et al., 2018; Rohling et al., 2012; Takemura et al., 2009; Yue et al., 2011). While some research suggests that models tend to overestimate the influence of dust because of an inappropriate distribution of grain size and shape (Kok et al., 2017), we use a range of −1.0 ± 1 W m⁻² at one standard deviation in order to include the full range of published results with a significant likelihood that the forcing is outside that range.

Having separated out the CO₂ forcing as −0.57 ∆F _2xCO2, the rest (∆F′) sums to −6.15 W m⁻², consisting of −3.2 W m⁻² (ice sheet), −0.57 W m⁻² (CH₄), −0.28 W m⁻² (N₂O), −1.1 W m⁻² (vegetation), and −1.0 W m⁻² (dust). Our maximum likelihood estimate for total forcing is therefore −8.43 W m⁻². Köhler et al. (2010) also suggest that additional, less commonly discussed factors, such as surface albedo change due to shelf exposure related to glacial sea level lowering, bring the total glacial‐interglacial radiative forcing closer to −10 W m⁻². Models from PMIP2 suggest that the albedo effect of exposed shelf is −0.7 to −1.3 W m⁻² (Braconnot et al., 2012). Friedrich et al. (2016) estimate a substantially weaker total forcing of −7.6 W m⁻², largely due to weaker ice sheet forcing, and Rohling et al. (2012) estimate −8 W m⁻² (with a plausible range of −6.25 to −9.75 W m⁻²). Combining in quadrature the uncertainty ranges provided by Köhler et al. (2010) for the components of the forcing generates a nominal uncertainty of ±1.4 W m⁻². However, this calculation ignores nonlinearity in the addition of different forcings (for which there is limited evidence, but it may be significant; e.g., Yoshimori et al., 2009) and also may not account fully for the range of published estimates. To account for this, we use a somewhat larger overall uncertainty estimate of ±2 W m⁻² (1‐sigma). In sum, we use N(−8.43, 2) W m⁻² as our observational estimate of the forcing change.

5.2.3. Corrections for State Dependence of Sensitivity and Slowness of Equilibration

A direct application of energy balance Equation 3 thus points to a moderate sensitivity of around 2.4 K having highest likelihood (i.e., 5 × 4.0/8.43; see dashed line in Figure 15). However, such a calculation rests on the assumption that feedbacks remain constant over a wide range of climate states and forcings. This has been the approach generally taken in paleodata‐based studies (Hansen et al., 2007; Köhler et al., 2010; Martínez‐Botí et al., 2015; Masson‐Delmotte et al., 2010; PALAEOSENS, 2012; Rohling et al., 2012). However, it is increasingly being questioned by studies concerned with potential state dependence of paleoclimate sensitivity (Friedrich et al., 2016; Köhler et al., 2015; Rohling et al., 2018; Stap et al., 2019; von der Heydt et al., 2014, 2016; Zeebe, 2013). Several of these studies suggest that the relationship between forcing and temperature response might not be linear, indicating that sensitivity depends on the background climate state and/or the efficacy of the forcings.

Figure 15.

Likelihood arising from cold‐period evidence (solid line). Dashed line shows the likelihood that would arise if state dependence of λ were omitted (α = 0).

Quantitative estimates of feedbacks through glacial cycles suggest that, for the LGM, the difference due to the nonlinearity may be of the order 0.5 W m⁻² K⁻¹, both in models (Crucifix, 2006; IPCC, 2013; Yoshimori et al., 2009, 2011) and in data from observations (Friedrich et al., 2016; Köhler et al., 2015, 2018), though there are large uncertainties in these estimates. Most analyses suggest stronger net feedback for glacial states (i.e., λ more negative, implying a lower sensitivity), but even this is not certain. We parameterize this uncertainty in feedback through an additive term, which is linear with temperature change; that is, the local feedback at temperature anomaly ∆T is given by λ + α ΔT, where α is an uncertain parameter and λ is the feedback for the modern state. The total radiative anomaly relative to equilibrium arising from a temperature anomaly of ΔT is then given by the integral of this varying feedback which amounts to λ ΔT + α/2 ΔT². Based on the above references, we choose our prior for α to be N(0.1, 0.1), which implies a mean change in feedback of −0.5 W m⁻² K⁻¹ at an estimated glacial cooling of −5 K, with a likely range of 0 to −1 W m ⁻² K⁻¹ and a significant chance of exceeding these limits.

Additional to this nonconstancy in feedback strength, we also account for uncertainty in relating the quasi‐equilibrium response to the regression‐based (see section 2.1) estimate of S. Modeling experiments (Rugenstein, Bloch‐Johnson, Abe‐Ouchi, et al., 2019; Rugenstein, Bloch‐Johnson, Gregory, et al., 2019; and see section 2.1) suggest modest differences between the long‐term equilibrium sensitivity and our target S based on regression of an abrupt 4xCO₂ simulation. We use the symbol ζ to represent this difference, with 1 + ζ therefore being the ratio of our target S to the long‐term equilibrium (Equation 8). The mean value of 1 + ζ is 1.06, arising from the eight models for which these estimates are available, suggesting that sensitivity as inferred from the quasi‐equilibrium paleoclimate states considered here is slightly larger than the target S for this assessment. Because this result is obtained from a small ensemble, we use a slightly inflated uncertainty of 0.2 relative to the ensemble spread of 0.15.

We include these effects via modifications to the basic energy balance Equation 3, writing

$$\mathrm{\Delta }T=\frac{-\left(-0.57∆F_{2\mathit{xCO}2}+\mathrm{\Delta }F\prime \right)}{\frac{\lambda }{1+\zeta }+\frac{\alpha }{2}\mathrm{\Delta }T},$$ (22)

where the term αΔT/2 represents a state dependence in the sensitivity and 1 + ζ represents the transfer between the long‐term quasi‐equilibrium and the target S. S may then be derived from λ via Equation 4.

Table 7 summarizes the distributions discussed for the various parameters in cold climate states. The resulting likelihood is shown in Figure 15, plotted in terms of S. The maximum likelihood value is at 2.5 K, dropping to about 0.1 at 1 K and 0.35 at 6 K (relative to our maximum likelihood value of 1).

Table 7.

Parameters of the Distributions That Are Used to Estimate S From the Cold Climate States, Equation 22

Term	Distribution
ΔT (K)	N(−5, 1)
∆F 2xCO2 (W m−2)	N(4.0, 0.3)
ΔF′ (W m−2)	N(−6.15, 2)
α	N(0.1, 0.1)
ζ	N(0.06, 0.2)

Note. Radiative forcing per CO₂ doubling from section 3.2.1.

5.2.4. Discussion

We now consider the consequences of low or high climate sensitivity for our understanding of the Earth system. Low present‐day sensitivity to CO₂ would require some combination of low cooling at the LGM (note, however, that there is little scope for the LGM temperature change to be less than 3 K because that is the value inferred from observations at low latitudes) and larger‐than‐estimated forcing and/or large response to non‐CO₂ forcings, of which the ice sheet albedo is dominant. A larger than expected difference between our target S and the paleo equilibrium sensitivity (i.e., large 1 + ζ) would also make low S somewhat more likely. Total CO₂ and other GHG forcing is well constrained at just under −3 W m⁻² at the LGM, and modeled responses to such forcing are close to linear when other boundary conditions are held fixed (i.e., preindustrial ice sheets) (Hansen et al., 2005). A low climate sensitivity of, say, 1 K per CO₂ doubling together with a true temperature anomaly of −3 K (at the very low end of the observed range) would require a very large additional radiative forcing effect of ice sheets (around −8 W m⁻²) to generate the additional 2 K or more of cooling. While few detailed factor analyses have been performed, estimates of the radiative effect of the continental ice sheets are typically of the order −2 to −4 W m⁻² (e.g., Köhler et al., 2010, 2015); that is, at least a factor of 2 less than would be required to support a low climate sensitivity. Furthermore, models do not tend to exhibit such a strong response to ice sheets; instead, they suggest that—if anything—the total effect of multiple forcings is generally smaller than the linear sum of responses to forcings individually (Pausata et al., 2011; Shakun, 2017; Yoshimori et al., 2009). These arguments are consistent with our inferred low relative likelihood of 0.2 at S = 1 (Figure 15).

High sensitivity to CO₂ of around 6 K per CO₂ doubling could be supported by a cooler LGM temperature anomaly of around −7 K (the higher end of the range suggested from proxy‐data evaluations; e.g., Snyder, 2016a), together with a muted response to non‐CO₂ forcings and/or substantial nonlinearity with respect to forcing magnitude (i.e., large values of α in Equation 22). Since CO₂ alone would lead to a cooling of 4 K in this case, this would imply a limited (3 K) impact of the ice sheets and other forcings (around −2 W m⁻²; less than half of what has been previously estimated). This appears to be consistent with our likelihood of 0.3 for S = 6 K (Figure 15). This picture is supported by evidence that spans the most recent five glacial cycles (Rohling et al., 2012), and we do not have conflicting evidence from other cold periods. Further back in time, uncertainties are greater as the data are substantially poorer; prior to the Pleistocene we have to go back 280 Myr to find a period when Earth's temperature was much colder than preindustrial (Montañez & Poulsen, 2013; Royer et al., 2004).

We note that the climate models included in the second and third Paleoclimate Model Intercomparison Projects (PMIP2 and PMIP3) had climate sensitivities in the range of around 2–5 K. Emergent constraint analyses have found at best a weak relationship between the cooling exhibited in each simulation and the equilibrium sensitivity of the models (Hargreaves et al., 2012; Hopcroft & Valdes, 2015a; Masson‐Delmotte et al., 2013), due to model uncertainty in processes that are important for the LGM but not related to future climate change, such as the influence of the ice sheets (Crucifix, 2006; Hopcroft & Valdes, 2015a). All of these models lie in the high likelihood region of our main result, and we therefore do not expect to be able to discriminate strongly between them.

5.3. Evidence From Warm Periods

5.3.1. Warm Periods—Mid‐Pliocene

The mPWP occurred over the interval of 3.3–3.0 Ma and is the most recent time in the past when CO₂ concentrations are thought to have been high enough to be comparable to present‐day values. During this time, there were orbital cycles with periods of 40,000 years, during which CO₂ levels inferred from high‐resolution boron isotope data varied between ~300 and ~400 ppmv (e.g., Martínez‐Botí et al., 2015) and sea level fluctuated by about 30 m (Rohling et al., 2014). Other CO₂ proxies are less conclusive, partly because they have not yet been measured in sufficient resolution to distinguish individual orbital cycles (Dyez et al., 2018). Despite progress in recent years, both the GHG forcing and the global temperature response during the mPWP warm intervals remain uncertain. Here we analyze the mPWP, in order to provide inputs to Equation 3, in a similar way to the LGM analysis above.

5.3.1.1. Surface Temperature Change ∆T

Following initial global assessments (Haywood et al., 2010), where SSTs were judged to be higher than Holocene values by about 0.8 K in the tropics, rising to 1.7 K globally, Pliocene SSTs have been considerably revised to higher values, particularly in the tropics (e.g., O'Brien et al., 2014; Y. G. Zhang et al., 2014). Compilations that focus on the more reliable geochemical proxies now place mean tropical SST during warm intervals of the Pliocene at +1.5 K, relative to the Holocene (Herbert et al., 2010). Further refinements are likely to push this estimate even higher (e.g., O'Brien et al., 2014; DiNezio et al., 2009). The compilation of Rohling et al. (2012) reveals that tropical SST change is ~50% of the global mean change over the last 0.5 Myr, a value that is also consistent with the PMIP3 ensemble at the LGM. Applying that to the mid‐Pliocene suggests a mean global SAT increase of around 3 K relative to the Holocene (although this value still has substantial uncertainty, and we therefore represent our temperature likelihood as N(3, 1) K).

5.3.1.2. Forcings Contributing to ∆F

Climate forcing during the mPWP is likely dominated by CO₂, but other forcings must also be considered, as for the LGM (i.e., Unger & Yue, 2014). There remains considerable uncertainty regarding all GHG concentrations. PlioMIP, the Pliocene Model Intercomparison Project, assumed a value of 405 ppm CO₂, which is at the high end if considering CO₂ alone, but which was chosen to implicitly include the effect of other well‐mixed GHGs.

To bracket most reported values, we set a value of N(375, 25) ppm for CO₂ and assume that N₂O and CH₄ together represent an additional 40% ± 10% of forcing (Hansen et al., 2013; Martínez‐Botí et al., 2015; Sosdian et al., 2018), which results in a best estimate for total forcing of 2.2 W m⁻² with an uncertainty of 0.6 W m⁻² at one standard deviation (not precisely Gaussian), relative to the 284‐ppm preindustrial state due to well‐mixed GHGs.

Since our aim is to estimate the short‐term response due to carbon dioxide change, we need to consider the influence of other forcings. In other words we need to consider the difference between the ESS (see section 2.1) and S. If the forcings were individually well known, then we could do this directly by including them in the energy balance equation as we did for the LGM. However, forcings such as changes in ice sheets and vegetation are difficult to quantify in detail, and tectonic and/or orographic forcings relative to the present complicate the assumption that all feedbacks were driven by CO₂ change (Lunt et al., 2010). For example, uncertainties remain with respect to the overall sizes and temporal variability of ice sheets. With Pliocene sea level at least 6 m above the present (Dutton et al., 2015), we know that ice sheets were smaller, but the upper boundary for sea level remains unclear (Dutton et al., 2015) as does the Pliocene glacial‐interglacial amplitude variability (de Boer et al., 2010; Miller et al., 2012; Naish et al., 2009; Rohling et al., 2014; Stap et al., 2016). Overall, sea level estimates (as available at the time of study) at times with ~375 ppm CO₂ reveal a median at +21 m and asymmetrical 68% and 95% probability envelopes of 9–27 and 1–33 m, respectively (Foster & Rohling, 2013). In addition, the “time slab” approach used in PlioMIP (where data from warm intervals within the longer period are amalgamated to form a single climatology) introduces further uncertainties, for example, regarding the regional influence of orbital changes. These are in the process of being quantified more carefully (Dowsett et al., 2016; Haywood et al., 2016) and time series approaches similar to those developed for the last 800 kyr are also beginning to be applied to the mPWP (e.g., Martínez‐Botí et al., 2015).

Since we do not have accurate estimates of the ice sheet and vegetation forcings, we instead use an uncertain parameter to represent the amount by which these (generally slower) responses inflate the response that would be generated by CO₂ alone. Lunt et al. (2010) argue that this ratio ESS/S is around 1.4 for the Pliocene based on simulations using HadCM3, while Haywood et al. (2013) find an ensemble mean ratio of 1.5 with considerable variation between models but with a total range of 1 to 2 across the models in the PlioMIP1 ensemble. We represent these results with an ESS inflation factor 1 + f _ESS where f _ESS is distributed as N(0.5, 0.25).

We thus represent the energy balance of the climate system for the Pliocene as

$$\mathrm{\Delta }T=\frac{-\mathrm{\Delta }{F}_{\mathrm{CO}2}\left(1+f_{\mathrm{CH}4}\right)\left(1+f_{\mathit{ESS}}\right)}{\frac{\lambda }{\left(1+\zeta \right)}}$$ (23)

where Δ F (CO₂) is the forcing due to CO₂ (i.e., ln([CO₂]/284)/ln(2) × Δ F _2xCO2), 1 + f _CH4 is the additional forcing due to methane and N₂O, which equals (1 + N(0.4, 0.1)), and 1 + ζ represents the transfer between quasi‐equilibrium and regression estimate of feedback.

Table 8 summarizes the distributions discussed for the various parameters in warm climate states. The resulting likelihood is shown in Figure 16 and has a maximum likelihood S of around 3.2 K.

Table 8.

Parameters of the Distributions That Are Used to Estimate S From the mPWP, Equation 23

Term	Distribution
ΔT (K)	N(3, 1)
CO2 (ppm)	N(375, 25)
Δ F 2xCO2 (W m−2)	N(4.0, 0.3)
f CH4	N(0.4, 0.1)
f ESS	N(0.5, 0.25)
ζ	N(0.06, 0.2)

Note. Radiative forcing per CO₂ doubling from section 3.2.1.

Figure 16.

Likelihood arising for mPWP.

5.3.1.3. Discussion

As in section 3.2.4, we now consider storylines that could explain low and high values for the sensitivity. A low climate sensitivity would require some combination of lower temperature change and/or greater response to non‐GHG/non‐CO₂ forcing. An mPWP global mean warming of 1 K would suggest a sensitivity of about 1.2 K per CO₂ doubling, but this requires that we ignore the known low‐temperature bias of some paleothermometers (e.g., O'Brien et al., 2015). This is a low‐likelihood scenario, although uncertainties in orbital forcing influences make it hard to be sure. Our calculation as presented in Figure 16 gives a likelihood of 0.3 at S = 1.2 K per CO₂ doubling.

On the other hand, if the GHG forcing were lower than recent estimates (e.g., Martínez‐Botí et al., 2015), then a high sensitivity is quite easily reconciled with the data. For example, the lowest CO₂ estimates within the mPWP reach as low as 330 to 350 ppm (Dyez et al., 2018; Martínez‐Botí et al., 2015; Pagani et al., 2010). Relative to preindustrial conditions, 350 ppm (with associated changes in CH₄ and N₂O) only represents 1.7 W m⁻². For that value, 2‐K warming would imply a sensitivity of nearly 4.5 K per CO₂ doubling, and 3 K would suggest a sensitivity of ~6.5 K per CO₂ doubling. If the CO₂ forcing were as small as 330 ppm, these values would shift to 6 and 9 K, respectively. Such a low forcing is considered unlikely and would require a minimal to nonexistent role for non‐CO₂ forcing during the mPWP. Our mPWP likelihood is around 0.4 at 6 K and drops to 0.2 at S = 8 K per CO₂ doubling.

As was the case in section 4.1, some models have been used to perform simulations of the mPWP as part of PMIP3 (PlioMIP) (Haywood et al., 2013). While all models generated plausible simulations for this period, there is little discriminatory power to distinguish between them. This is unsurprising given that their climate sensitivities range within the high likelihood range of our analysis. Emergent constraints analyses have been performed using these models (Hargreaves & Annan, 2016). While these suggest a climate sensitivity consistent with our results, we do not consider them sufficiently robust to further narrow our likelihood, due to the high uncertainty in both model boundary conditions and proxy data.

5.3.2. Warm Periods—PETM

Of the pre‐Pliocene warm intervals, the rapid global warming event known as the PETM (~56 Ma) provides perhaps the best opportunity to further constrain ECS. Here we explore this opportunity with a comprehensive analysis of the available evidence arising from this period. Due to the large uncertainties and the danger of overconstraining the likelihood should these be underestimated, however, we have chosen not to include the PETM evidence in our final likelihood estimates. We present the analysis here both because it provides supporting evidence to our overall conclusion and in the hope that it may spur future research.

Coincident with a dramatic input of biogenic carbon into the active climate system, warming occurred rapidly (in <20 kyr, likely in as little as 4 or 5 kyr; Kirtland Turner et al., 2017; Zeebe et al., 2016). Dunkley Jones et al. (2013) compiled available SST data and, comparing these with results from a single model, concluded that the global PETM temperature anomaly relative to the early Eocene was in the range 4 to 5 K. Incorporating recent SST data from the tropics, Frieling et al. (2017) estimate a tropical change of 2.7 K with 5.3 K for the global SST anomaly (<2 K very unlikely). Using a ratio for global SST to global temperature change of 0.9, based on the results from an ensemble of models run for the Eocene Climatic Optimum (EECO ~50 Ma) (Lunt et al., 2013), this gives a slightly higher global temperature estimate of 5.9 K. This suggests a central value around 5 K. Relative to the other paleointervals discussed in the previous sections, relatively few PETM studies have estimated this global value, and uncertainty in the interpretation of measurements from so deep in the paleorecord is high. Therefore, despite the closeness of the estimates in the literature, our uncertainty in this global value is greater than the equivalent for the other intervals considered in the previous sections. Here we use a range of N(5, 2) K, which includes the published values within the high likelihood range.

While rapid in geological terms, the time scale for the PETM warming is still sufficiently long for a quasi‐equilibrium temperature response to the radiative forcing. The PETM is associated with a global negative δ¹³C anomaly of around 3–4‰, which is indicative of an injection of a large amount of biogenic carbon into the Earth system driving this warmth, either in the form of CO₂, CH₄, or both. Although constraining the CO₂ change across the PETM is an area of active research, a number of first‐order constraints can be formulated for our purposes, based on Earth system modeling of the δ¹³C anomaly and accounting for the response of the deep ocean carbonate system and the carbon isotopic composition of the likely carbon sources (e.g., Cui et al., 2011). This gives a maximum CO₂ change of 5 times (from 800 to 4,000 ppm; Cui et al., 2011) and a minimum of 2 times CO₂ (1,000 to 2,000 ppm). More recent estimates, based on paleo‐observations, are consistent with this modeling approach and suggest a change from about 900 ppm to between 1,500 and 4,100 ppm (95% confidence range), with a central value of 2,200 ppm (Gutjahr et al., 2017), or a change from about 700–1,000 to about 1,400–3,300 ppm (Schubert & Jahren, 2013). Here we model the increase in CO₂ by assuming a baseline of 900 ppm increasing to a Gaussian defined as N(2,400, 700) ppm.

A large uncertainty when using the PETM in this way concerns the magnitude of the change in CH₄ concentration that is potentially associated with the event (e.g., Zeebe et al., 2009). In the absence of firm current constraints on CH₄ and N₂O concentrations at the PETM, we again use a factor applied to the CO₂ forcing to account for this additional forcing. Large and sustained inputs of CH₄ directly into the atmosphere have the potential to extend the lifetime of CH₄ in the troposphere by up to a factor of 4 (Schmidt & Shindell, 2003), so the impact of CH₄ on PETM temperatures can be larger than sometimes assumed. We therefore draw the scaling factor from N(0.4, 0.2), which is consistent with our previous assumption for the mPWP but allows twice the uncertainty.

The PETM background climate state differs substantially from the present (e.g., there are major differences in paleogeography and the basic state is much warmer), leaving open the possibility of substantial feedback differences between the PETM and the present including slow “Earth system” feedbacks such as vegetation. We have little basis for making a quantitative estimate for this and therefore include additional uncertainty in the form of an additive term β on the net feedback of magnitude N(0, 0.5) W m⁻² K⁻¹, which has a similar magnitude to the term used for the LGM, although in this case we do not suppose a direct relationship with the amount of warming. The arbitrary nature of this choice, and the possibility that this component could be much more significant, is the main reasons that we do not include the PETM result in the final summary likelihood for S obtained from paleo‐information.

The resulting equation for the PETM therefore has the form

$$\mathrm{\Delta }T=\frac{-\ln \left(\mathrm{CO}2/900\right)}{\ln \left(2\right)}\frac{\mathrm{\Delta }{F}_{2\mathrm{xCO}2}\left(1+f_{\mathit{CH}4}\right)}{\frac{\lambda }{\left(1+\zeta \right)}+\beta }$$ (24)

where Δ F _2xCO2 , λ, f _CH4, and 1 + ζ are as before and β is the additional state dependence parameter.

Table 9 summarizes the distributions discussed for the various parameters in the PETM. Our likelihood function is shown in Figure 17.

Table 9.

Parameters of the Distributions That Are Used to Estimate S From the PETM, Equation 24

Term	Distribution
ΔT (K)	N(5, 1)
CO2 (ppm)	N(2,400, 700)
Δ F 2xCO2 (W m−2)	N(4.0, 0.3)
f CH4	N(0.4, 0.2)
β	N(0, 0.5)
ζ	N(0.06, 0.2)

Note. Radiative forcing per CO₂ doubling from section 3.2.1.

Figure 17.

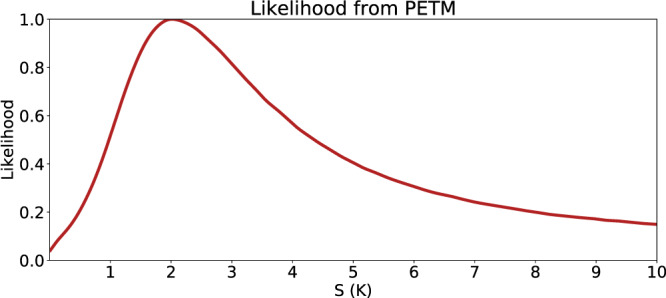
Likelihood arising for the Paleocene‐Eocene Thermal Maximum. The maximum likelihood value of around 2 K corresponds to a 5‐K warming and ~3xCO₂ change together with its accompanying CH₄ increase.

The nature of the proxies used to estimate the forcing and climate state at the PETM is very similar to that of the proxies used for the mPWP; they are likely to share some errors and biases. For this reason, we do not consider the PETM information to provide a new, fully independent line of evidence. As a sensitivity test, we consider the case that the uncertainties in CO₂ and temperature for both periods are correlated at the 80% level. We also assume the same transfer function ζ. Under these assumptions, the joint likelihood (Figure 18) is shifted slightly to lower values than the result obtained in section 5.2.1 for the mPWP alone, with the high‐value tail slightly narrower. This calculation depends on some highly uncertain parameters for which we have had to make somewhat arbitrary judgments, such as the importance of state dependence for the PETM. Differentiating between state dependence in the radiative forcing, and in the feedbacks (Caballero & Huber, 2013), could be an area of future progress. A recent modeling study found that changes in geography, ice, and vegetation may have had large impacts at the Eocene (Farnsworth et al., 2019). So, while the calculation shown here may be pessimistic, we have no firm basis for asserting a higher level of independence and choose to omit the PETM calculation from our overall result while acknowledging that it does appear to add support to the mPWP analysis.

Figure 18.

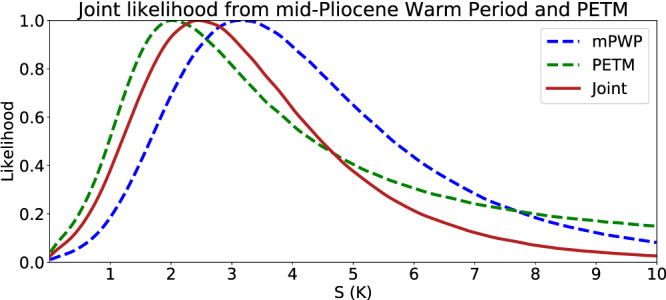
Analysis of mPWP and PETM results. Blue and green dashed lines are mPWP and PETM results as previously shown. Red line is joint likelihood obtained accounting for dependency as described in the text. As explained in section 5.3.2, the mPWP result is our proposed result.

5.4. Combining Constraints From Warm and Cold Periods

As outlined at the end of section 5, the uncertainties in the evidence that form the constraints described in sections 5.1 and 5.2 above are substantially independent, because the ways in which the GHG levels and estimated temperatures are calculated are not very related (typically different measurements and proxies are used). There are some dependencies, however, which are specifically accounted for. In particular, dependency arises through the parameters ∆F _2xCO2 and ζ. Performing the Bayesian updating across the full vector of uncertain parameters accounts for these dependencies. Tests show that these dependencies between our cold and warm period uncertainties hardly affect our results because the uncertainties constitute only a small part of the total uncertainty in our result.

The final combined likelihood function including our evidence from both cold and warm states, and including the dependencies, is shown in Figure 19.

Figure 19.

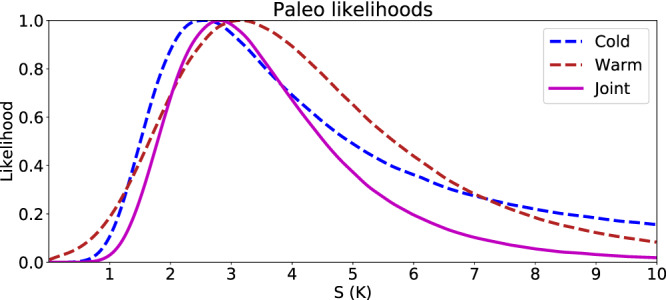
Blue‐dashed is the cold periods' likelihood. Red dashed line is the warm periods' likelihood. Magenta solid line is the final combined likelihood from paleoclimate evidence.

5.5. Summary

Like the industrial‐era warming trend (analyzed in section 4), climate changes that occurred naturally during earlier epochs also depended on S and can likewise constrain S if enough is known about what drove them. We find that the two most informative time intervals are the LGM cold period (LGM, ~20,000 years ago) and the mPWP (3.3–3 Myr ago), although we have also considered previous glacial cycles, and especially the PETM warm period (~56 Myr ago), to test for consistency. The LGM and earlier glacial maxima were 3–7 K colder than the late Holocene (recent preindustrial millennia) because the Earth's orbit favored climatic changes that included large ice sheets in the Northern Hemisphere, increasing the planetary albedo, as well as GHG drawdown (largely into the deep oceans). The mPWP was 1–5 K warmer than the Holocene due to higher ambient GHG concentrations as well as smaller ice volume, and the PETM was roughly 3–7 K warmer than the baseline Eocene climate due to a geologically rapid release of GHGs. Thus, each climate change we have examined had different aspects, which helps to provide a more reliable constraint on S. The paleoclimate data come from intervals where the climate was different to today, but fairly stable for several thousand years, meaning that slow feedback processes need to be taken into account. By treating these slow processes as forcings rather than feedbacks, we are able to make inferences about S. Both the temperature changes that are used, and the slow feedback influences that are removed, are constrained using indirect proxy records. This introduces considerable uncertainty in the climate sensitivity estimates.

Paleoclimate sensitivity estimates have been made with increasingly detailed documentation of what's included and what's uncertain. For cold periods, estimates are predominantly (but not only) from the period covered by the ice cores. The availability of ice core data means that radiative forcing estimates are well constrained (including CO₂, CH₄ and—through a scaling based on measurements in parts of the records—N₂O, and aerosol dust). We summarize that the most likely estimate for climate sensitivity for cold periods falls close to 2.5 K. Extreme estimates range from a likelihood of about 0.1 at 1 K to a high‐end likelihood of about 0.35 at 6 K. Here, the low extreme of 1 K assumes a glacial temperature anomaly of −3 K, relative to preindustrial times, which is the lowest‐magnitude end of estimates available. It also requires a very large radiative forcing effect of ice sheets that is some 2 to 4 times larger than typical reconstructions; climate models also do not exhibit such a strong response to ice sheets. So the low extreme of 1 K is highly unlikely. At the high end, 6 K assumes a glacial temperature anomaly of −7 K, relative to preindustrial times, which is at the extreme end of estimates available. It also requires a radiative forcing effect of ice sheets that is less than half of the estimates in most studies. Hence, as high as 6 K is unlikely, although it has a slightly greater likelihood than the low extreme of 1 K.

For past warm periods, we suggest a most likely S of 3.2 K, with extremes that range from about 1 to 8 K (likelihoods about 0.2 at each value). We can only give a range for the most likely estimate, because of structural uncertainties that remain in mean global SAT increase, in non‐CO₂ GHG concentrations, and in global ice volume (sea level). More, and more detailed, observational constraints are needed. Our low extreme estimate assumes that temperature changes were at the low end of the published spectrum and that there was a larger than commonly anticipated impact of non‐GHG/non‐CO₂ forcing. For our low extreme of about 1.2 K, we assumed that mid‐Pliocene global mean warming was 1 K, which equates to the present‐day climate. Though unlikely given Pliocene paleoclimate evidence, this cannot be fully excluded. High sensitivities require that mPWP CO₂ levels were at the very low end of published estimates. If we then assume that non‐CO₂ forcing was negligible, then we find an unlikely but not impossible high extreme estimate for S of up to 10 K. Information from the PETM broadly supports the estimated likelihood obtained using climate information from the Pliocene, but we consider the evidence too uncertain for it to be included in the likelihood function.

Since the dominant uncertainties for warm and cold periods are different (e.g., ice sheet forcing affects cold climates but not warm ones; GHGs are poorly known for deeper time warm climates but directly measured from ice cores for more recent cold climates), they provide a tighter constraint in combination than separately, even though they are not wholly independent. Together, they suggest that S is likely to fall within 1.5–5 K, with highest likelihood around 2.5 K. These results are fairly similar to those obtained in the PALAEOSENS assessment (PALAEOSENS, 2012). The paleoclimate evidence offers significant promise to constrain S further. In particular, if LGM ice sheet forcing and global temperature can be better constrained, the cold‐period evidence could further constrain the upper end of the current range. The PETM is an active area of research, and it may in future be possible to use evidence for this period with more confidence to further constrain sensitivity. There is also a possibility in future of using evidence from other intervals such as the Eocene and Miocene. Progress will depend equally on further development of biogeochemical paleoclimate modeling to test interpretations of existing proxy data and on collection of more such data.

6. Dependence Between Lines of Evidence

Combining evidence from multiple lines hinges on a crucial question: are they independent? Some observation, assumption, model (or model component), or unknown influence on climate could have influenced more than one line of evidence or its interpretation. Such mutual influences are inevitable at some level, since all scientists communicate regularly and share views on the climate system. What we are concerned with here is whether there are quantitatively significant codependencies across the major evidence lines, and what impact this might have on our results. A pedagogical example was given in section 2.4.1, and each of sections 3, 5 has already addressed evidence codependencies within the individual, major lines (sections 3.6, 4.1.2, and 5.3.2).

Such codependencies may either increase or decrease uncertainty. For example, some unaccounted‐for factor might cause two lines of evidence to deviate in the same direction (e.g., pushing both toward a lower apparent S) or alternatively push them in opposite directions. In the former case, the true overall uncertainty is larger than if we ignored the codependency, while in the latter case it is smaller. In this assessment we will simply ignore codependencies that appear to be of the latter, “buffered” variety (a conservative strategy, which could lead us to overestimate uncertainty). But the former, “reinforcing” codependencies require attention.

We are not revisiting here the degree of uncertainty of any one line of evidence, but instead asking whether, if one line of evidence for whatever reason points too low (or too high) in terms of S, this affects the interpretation of the other lines. For more discussion of this issue and what is meant by independence, see Annan and Hargreaves (2017).

6.1. Use of GCMs

An obvious suspect for codependent errors is our use of GCMs in various ways to interpret or support all three lines of evidence. Overreliance on these models is hence dangerous, especially since the models may differ systematically from reality in important ways.

Our use of them, however, arguably relies on different model aspects for each line of evidence. For example, they help constrain feedbacks (section 3) and play a large role in quantifying the historical “pattern effect” (section 4), but the former involves global mean temperature sensitivity of clouds and other variables, while the latter involves regional departures from the global mean. These could be seen as orthogonal and indeed appear to be uncorrelated in GCM ensembles (see below); for example, regional SST changes depend strongly on ocean processes (e.g., Kostov et al., 2018), while global feedbacks do not (Ringer et al., 2014). Moreover, both the feedbacks and pattern‐effect responses are supported by observations and process understanding. GCMs are also used to estimate adjustments to paleo forcings, but again, these involve aspects such as atmospheric responses to ice sheets and aerosol sources, which would be expected to depend on different model processes from those relevant to the other lines. GCM climate sensitivities are not directly used (although GCMs do help to constrain some of the feedbacks in section 3); in general, these models are used to quantify corrections and secondary effects (and their uncertainties), which were neglected in traditional studies.

Nonetheless some of these “secondary effects” turn out to be large, and there are some potential interdependencies between evidence lines, some of which do involve GCMs. These are now examined.

6.2. Potential Codependencies

The main potential codependencies we see are as follows.

GCM model selection bias. Modelers and process experts are aware of the historical climate record. GCM aerosol forcings might have been selected in order to match the observed warming rate over the twentieth century (e.g., Kiehl, 2007), and otherwise, plausible models or feedbacks might have been discarded because of perceived conflict with this warming rate, or aversion to a model's climate sensitivity being outside an accepted range. If so, any factor causing an error in S _hist could in principle have caused a same‐signed error in the process estimates of S, that is, a “reinforcing” codependency.

Our strategy for mitigating this is to rely on multiple lines of evidence in assessing the strength of key feedbacks (section 3). We find that there is sufficient evidence from observations of present‐day weather variations and climate variability, process models not used in climate simulations, and observational tests of GCMs unrelated to historical warming, to support the process evidence and likelihoods presented without relying on their ECS values (see section 6.1). Also, the historical evidence (section 4) relies on “bottom‐up” estimates of aerosol forcing and does not use constraints on forcing that arise from temperature trends over the historical record (see section 4.1.1). In addition, the historical record has been extensively investigated by detection and attribution methods, which allow a change in feedback or forcing strength by rescaling the time‐space pattern of response to best match the observed records. These results (see section 4.1.3) support the inferences made from the overall warming and forcing trends. Therefore, the process evidence may be considered essentially independent of the other two lines of evidence even if climate model development has indeed suffered from selection biases.

Transfer function/SST pattern error. Relating the apparent sensitivities (e.g., S _hist) from historical and paleoclimate changes to the target S requires GCMs. For the historical period this involves mainly how models capture gradients of SST from the tropical Indo‐Pacific warm ocean to other regions and their impact on cloud cover (section 4.2). There is evidence that these gradients may have been stronger during cold and weaker during warm paleoclimates. The historical SST record meanwhile shows gradients within the tropics and midlatitudes strengthening more than predicted by GCMs. Stronger gradients are expected to increase the (negative) global net cloud radiative effect (see section 3.4) for a given global mean temperature.

First, we consider the impact if this expected cloud sensitivity to warming patterns were wrong or overestimated. Since the sensitivity causes us to infer S > S _hist because of the “warm‐getting‐warmer” pattern in the historical record, an overestimated cloud sensitivity would imply an overestimate of S. However, during paleoclimate periods, where warm regions changed less than cool regions, the same error could lead to an underestimate of S. We therefore find that codependency between paleo and historical evidence is “buffered.” Codependencies are also possible whereby errors in cloud physics more generally could affect both the historical transfer function and process understanding; however, given that there are a wide range of cloud feedback behavior and transfer functions implied across GCMs, a codependency should appear as a correlation between the two, but available evidence does not suggest a correlation (Dong et al., 2020) although this merits further investigation. So we conclude that uncertainty in the cloud sensitivity to SST patterns is not an evident codependency concern.

A more serious concern is misinterpretation of observed historical surface warming patterns and/or incorrect expectations of forced patterns, which could affect historical and process evidence. The calculations of the historical pattern effect (section 4.2.1) and low‐cloud feedback (section 3.3.2) both assume that long‐term warming will be relatively uniform, as predicted by GCMs. However, the observed historical warming shows an increasing warm‐cold gradient in the tropics which is not fully predicted (section 4.2). The most likely explanations are an unforced variation, underestimated lag effect of ocean thermal inertia, and/or response to volcanic forcing. Each of these would be transient. However, there is evidence that a similar forced pattern could be missing from GCMs due to mean state biases (Kucharski et al., 2015), raising the possibility that the residual historical warming is at least partly an equilibrium response to CO₂ forcing (Luo et al., 2018; McGregor et al., 2018). If so this would imply a negative feedback mechanism missing from current GCMs and process evidence generally (section 3). It would also mean that S is closer to S _hist, that is, not as high as calculated assuming the observed historical pattern to be unforced. This is a reinforcing codependency which introduces a one‐sided uncertainty into both the process and historical evidence, addressed further below.

Aerosol forcing error. Although better recognized with respect to the historical record, aerosol forcing uncertainty also affects the paleo evidence. Given that different aerosol types are involved during each era and may have different cloud impacts, it may be expected that any aerosol forcing errors are unrelated, in which case no codependency is expected. But to consider this possibility anyway, if present‐day anthropogenic aerosol negative forcing were weak relative to expectations, S would be underestimated from historical evidence. However, since the LGM was much dustier than the Holocene, a related situation for dust forcing would cause us to overestimate S from paleo evidence. Hence, even if the errors were related they would tend to compensate if the two estimates are combined (referred to here as “buffering”). If instead preindustrial aerosol amounts are underestimated then our historical‐estimated S would be too high, yet with less vegetation‐related aerosol during the sparsely vegetated LGM our paleo‐estimated S would be too low. Thus, the errors will again tend to compensate if the two are combined.

Due to the complexity of aerosols and their effects, one cannot be sure about buffering. Therefore, we have done calculations (section 6.3 below) of the impact of codependency for extreme cases of fully codependent, versus antidependent, effects. This follows the methodology of Annan and Hargreaves (2017) but uses a more appropriate two‐layer climate model for the historical period. We find that the posterior PDF is only modestly affected even in these extreme cases. We thus conclude that it is safe to set aside major concerns about codependency of the aerosol uncertainties.

CO ₂ radiative forcing error. There is some uncertainty in the radiative forcing per doubling of CO₂, ∆F _2xCO2 (section 3.2.1). If ∆F _2xCO2 is higher than the best estimate, then the true S will be proportionately higher, since all process evidence is referenced to radiative flux variations rather than CO₂ changes, while S is defined based on CO₂ change. For other lines of evidence, an impact is also expected but it depends on the relative magnitude and direction of the CO₂ versus non‐CO₂ forcings, since the contribution of CO₂ increases with ∆F _2xCO2: For historical warming (where CO₂ and non‐CO₂ forcings oppose each other) a high ∆F _2xCO2 would push net forcing higher, thus historical‐estimated S lower, while for prehistoric changes (where other forcings reinforce CO₂) this would push paleo‐estimated S higher. Because of the buffering of effects between the historical and paleo periods, and since the uncertainty in CO₂ forcing is relatively small, we ignore this codependency.

It could be argued that the above scenarios only deal with uncertainties we know about but that some major oversight, invisible phenomenon, or structural error in how the problem is formulated could also affect multiple lines of evidence. It is, however, difficult to deal with such “unknown unknowns” without concrete proposals for particular problems whose possible impacts can be explored rationally. In trying to consider plausible candidates on the process side—very strong and unanticipated feedback from low or high clouds being the only candidates that seem physically able to deliver large feedbacks—it is difficult to see how a strong feedback would fail to have registered in either of the other lines of evidence, unless some second, unrelated surprise coincidentally canceled it out. Such multiple surprises are already catered for by considering the evidence to be independent, as long as each surprise has been allowed for properly via the tails in the respective likelihoods (see also section 7.3). Possible medium‐term Earth system responses, such as a forest dieback, could fail to register in either historical or process understanding but would not appear to deliver a large enough feedback for this dependency to significantly affect matters. Very slow responses and nonlinearities would affect only the paleo evidence and were accounted for there.

6.3. Simple Dependence Test

Since we did find a possible reinforcing codependency between the process and historical evidence associated with the pattern effect, we modeled its effect using a simplified calculation in which the historical and process likelihoods versus λ are approximated as Gaussians that each includes a distinct, unshared error component, and a shared error component from the pattern effect. We suppose here that half the variance in historical ∆λ (0.3² from section 4) arises from uncertainty in the forced SST pattern, which would also affect the evolution of cloud feedbacks; the other half is from uncertainty in the radiative response to a known pattern (accounted for separately in the process analysis). This leads to a shared error component of N(0, 0.21). The baseline process distribution, N(−1.30, 0.44) from Table 1, therefore includes this plus an unshared component N(−1.30, 0.39) and the historical likelihood, approximated as N(−1.07, 0.55), includes this plus an unshared component N(−1.07, 0.51). The two total λ likelihoods can be combined either assuming them to be independent or assuming the unshared components to be independent but the corrections to be duplicated. The PDF of S (based on the process and historical evidence only) has a 90% range of 2.2–6.9 K in the first case, widening to 2.1–7.4 K in the second case. In other words, the codependency has a fairly small effect on the final result, at least if approached in this way. The basic reason for this is that the shared error variance, 0.04 (W m⁻² K⁻¹)², is 6 times smaller than that of the unshared historical error and 3 times smaller than that of the unshared process error. Therefore, the pooled uncertainty is dominated by the unshared components. Nonetheless, this dependency may deserve further attention especially if other uncertainties (e.g., in aerosol forcing) are significantly narrowed.

6.4. Summary

We judge that for the most part, the three lines of evidence appear to be practically independent in the sense that any significant errors we can envisage would affect the lines differently. We do, however, find one important uncertainty for which this is not the case, related to “pattern effects.” If CO₂ forcing happens to produce more warm‐region warming than expected, this would potentially affect both historical and process‐based estimates of S in the same sense. Idealized calculations (section 6.3) indicate that allowing even for this relatively strong codependency does not strongly affect a combined PDF. In our subsequent analysis we will therefore proceed with a baseline approach of considering the three main lines of evidence to be independent. However, given that the possibility of major, unexpected dependencies can never be ruled out, we also explore possible impacts of this using more drastic tests where single lines of evidence are discarded altogether (section 7.3).

7. Quantitative Synthesis of Evidence for S

Here we present results from the Bayesian approach described in section 2 to produce quantitative estimates of the probability distribution for S given the evidence presented in the previous sections. This builds on many previous studies (e.g., Annan & Hargreaves, 2006; Hegerl et al., 2006; SSBW16).

First, we present the results of a “Baseline” calculation. This calculation is the synthesis of our basic assumptions as outlined in the previous sections and is not primarily intended to represent a best or consensus estimate. It is, however, based on transparent assumptions, the sensitivity to which can be tested in a relatively straightforward way. In the following sections we assess the sensitivity of the Baseline outcome to (a) the choice of prior, (b) the exclusion of each of the lines of evidence in turn, and (c) allowances for potential uncertainties not explicitly catered for elsewhere in our calculations. These tests, respectively, explore (a) the robustness of our results to alternative formulations of prior beliefs as represented in the Bayesian approach; (b) the influence of the different lines of evidence and how much of a constraint may be provided with only two independent lines; and (c) how much additional uncertainty a researcher would have to have in order for their uncertainty to significantly influence the results. These sensitivity tests inform the interpretation of our results in section 8, based in part on the “storylines” approach of SSBW16.

7.1. Baseline Calculation

Figure 20 shows our Baseline calculation of the posterior PDF for S and how the lines of evidence contribute to it. The PDF for S is calculated by sampling from a uniform prior on feedback components and performing a Bayesian update using evidence likelihoods from individual feedback components (section 3), historical evidence (section 4), and evidence from warm and cold paleoclimates (section 5). The emergent constraint evidence from section 3 is not included in the Baseline calculation. Likelihood weights for each line of evidence are multiplied, based on the assumption that the lines of evidence are independent (see section 2 for details). The 66% (17–83%) range for S, given all lines of evidence included, is 2.6–3.9 K with a median of 3.1 K. The 90% (5–95%) range is 2.3–4.7 K.

Figure 20.

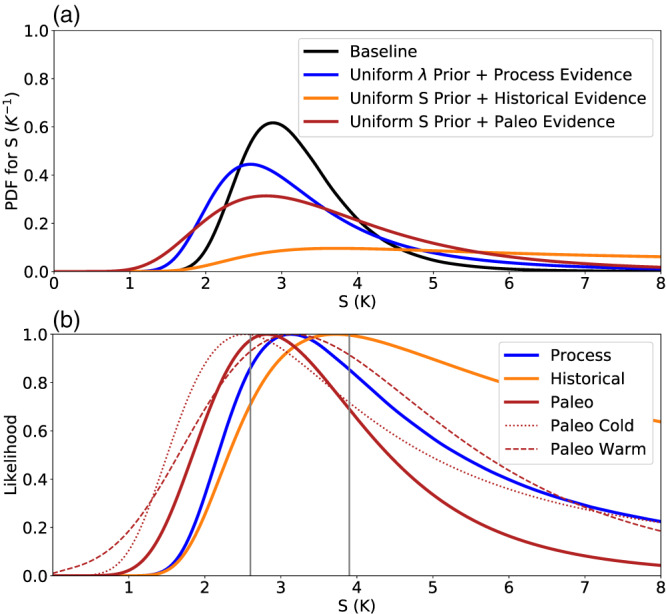
Posterior PDF for S and comparison of lines of evidence. Panel (a) shows our Baseline posterior PDF for S in black and PDFs for each main line of evidence individually, where the process evidence is combined with a uniform λ prior, while the others are combined with a uniform prior on S. Panel (b) shows marginal likelihoods for S for the various lines of evidence used in the Baseline calculation: the individual‐feedback process evidence (section 3), the likelihood from historical evidence (section 4), and the likelihoods for past warm and cold climates from paleoclimate evidence plus their combined likelihood (section 5). All likelihoods are scaled to have a maximum value of unity. Vertical gray lines show the 66% range for the Baseline posterior for S.

Figure 20b shows marginal likelihood functions for S from the various lines of evidence. The process likelihood depends on the prior (section 2) and is calculated using the default uniform λ prior used for the Baseline calculation. These likelihoods give one indication of the relative effectiveness of the various lines of evidence in constraining S. The values of these likelihoods at the vertical gray lines indicate the relative strength of the corresponding evidence in constraining the 17th and 83rd percentile values (66% range) of the posterior PDF of S, with a smaller likelihood indicating a stronger constraint. The strongest constraint at the upper end of the S range arises from the paleoclimate evidence (mainly due to that from cold climates), with a weaker constraint from the process evidence and the weakest constraint arising from the historical evidence. The strongest constraint at the lower end of the range arises from the historical evidence, with the process evidence and warm paleoclimate evidence giving weaker constraints, and the cold paleoclimate evidence providing the weakest constraint.

A limitation of comparing marginal likelihoods as above is that, unlike the historical and paleo evidence, the process evidence (based on feedback components) cannot be uniquely expressed as a function of λ and ∆F_2xCO2 (see section 2). This makes the marginal likelihood dependent on the Bayesian prior on the individual feedback variables. An alternative approach is to compare the predicted PDF of S based on the process understanding combined with a uniform λ prior with the marginal likelihoods of the historical and paleo evidence (cf. Equation 10); this is done in Figure 20a (note that for plotting consistency the historical and paleo evidence is shown as PDFs under uniform‐S priors, preserving the shape of the likelihoods).

Multiple PDFs (or likelihoods) based on different sources of information are not necessarily expected to match, only to overlap. In our case there is substantial overlap between the lines of evidence, whether regarded in terms of likelihood functions (Figure 20b) or PDFs obtained as in Figure 20a, and maximum likelihood values are all fairly close. This indicates strong consistency among the three lines of evidence. The tails of the likelihoods and PDFs are different, however, which indicates variation in the strength of the constraints.

Our Baseline calculation above is based on one particular prior, assumes independence between lines of evidence, and makes no allowances for “unknown unknowns.” We therefore perform a number of sensitivity tests to explore these limitations, to allow for the possibility that our Baseline range for S is overconfident.

7.2. Sensitivity to Priors

We now consider different prior distributions and discuss the alternative perspectives that these priors may represent.

As discussed in section 2, we place priors on all independent variables of our inference model, including the six feedbacks λ _i, and these induce a PPD on each dependent variable including S. The PPD of S indicates what its posterior PDF would be, given the inference model and priors, before any subsequent updating with evidence likelihoods. As such, the PPD for S can be a useful tool for understanding the influence of the prior on the predicted variables for a given inference model.

Our Baseline calculation places independent, uniform priors on the λ _i feedbacks, as is implicitly assumed in many past studies of these feedbacks (section 2.4.3). Although we use uniform priors on λ _i, other broad functions of λ _i yield similar results as long as the feedback priors are independent. A prior with unbounded uniformly distributed λ _i feedbacks induces a PPD for λ which is also unbounded and uniformly distributed. Hence, our Baseline prior (Figure 21a) will be called “UL”. This, given a reasonably well constrained value for ∆F _2xCO2, results in a PPD for S that decreases with increasing S (Figure 21b), because smaller and smaller changes in λ change S by a given amount as λ approaches 0 and S becomes large (Roe & Baker, 2007; Frame et al., 2005). (Note, however, that for practical reasons we place bounds on the λ _i feedback priors in our numerical calculations—see section 2.4.4.)

Figure 21.

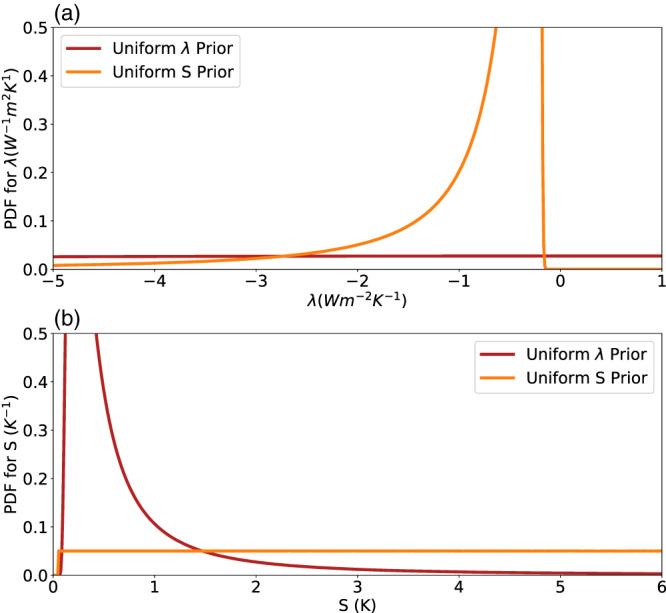
Prior predictive distributions for (a) λ and (b) S. Our Baseline (UL, red) prior is uniform in six λ _i feedbacks, each ~U(−10, 10) W m⁻² K⁻¹, compared to an alternative prior (US, orange), which reweights the Baseline prior to be uniform in S from near 0 to 20 K.

It may be argued that a uniform λ prior is undesirable since it assigns low probability density in the PPD for S at high values of S from the outset, and it has been argued in previous studies (e.g., Frame et al., 2005) that a state of ignorance about S is represented by considering a uniform prior probability density of S (see section 4). Therefore, we also consider an alternative prior that induces an approximately uniform PPD on S, which we refer to as the uniform S prior (US) for brevity (Figure 21).

Specifying a prior that is uniform in S is not straightforward in our inference model. There is no unique way to choose priors on the feedbacks λ _i to yield any given PPD for S; there are many possible joint feedback priors that yield a uniform PPD for S over some interval. Different such joint priors over λ _i can induce different posterior PDFs on S, even though their induced PPD(S) is the same. The specific case of a uniform PPD on S implies that the feedbacks have a high probability of summing to a relatively small value. Accordingly, any US prior must possess at least one of two characteristics: It must either assume the uncertainties in the feedbacks to be anticorrelated or else assume that the individual feedbacks are likely to take extremely small values. In the former case, the feedbacks are likely to have a small sum because of a natural tendency to oppose one another; in the latter case, because sufficiently small feedbacks will have a small sum. Although we experimented with both types of prior, we judged the latter, small‐feedback type to be unacceptable because it would assign an extremely small prior probability to the most likely values of some of the feedback components (e.g., Planck, see section 3). We therefore limit further consideration to US priors achieved by feedback anticorrelation.

To construct a prior with a uniform PPD for S using the full inference model, we take the sample from the Baseline UL prior and weight each sample instance according to its predictive value for S in order to give a uniform PPD for S (see section 2.3). This approach is similar to that followed by Aldrin et al. (2012) to construct a uniform prior for S when using an inference model with priors on multiple variables. Recalculation of the posterior PDF of S from all evidence using this prior gives a 66% range of 2.8–4.5 K (Table 10). This shows that our final result with all evidence is encouragingly stable to changes in prior; even with this quite drastic change in the prior and corresponding PPD for S, the posterior PDF of S only changes by 0.2 K at the lower end and 0.6 K at the upper end of the 66% range. While other priors could be considered, the UL and US priors appear to span the range of reasonable options for broad priors.

Table 10.

Mean, Mode, Median, and Percentile Values of Posterior PDFs for S

	5th percentile	17th percentile	50th percentile	83rd percentile	95th percentile	Mode	Mean
Baseline (UL, uniform λ Prior) a	2.3	2.6	3.1	3.9	4.7	3.0	3.2
US (Uniform S prior) a	2.4	2.8	3.5	4.5	5.7	3.1	3.7
UL No Process	2.0	2.4	3.1	4.1	5.2	2.7	3.3
UL No Historical a	2.0	2.3	2.9	3.7	4.6	2.6	3.1
UL No Paleo Warm a	2.2	2.5	3.1	4.0	5.1	2.9	3.3
UL No Paleo Cold a	2.3	2.6	3.2	4.1	5.1	3.0	3.4
UL No Paleo	2.2	2.6	3.3	4.6	6.4	2.9	3.8
US No Process	2.3	2.8	3.7	5.2	6.9	3.1	4.0
UL + EC (emergent constraints)	2.4	2.7	3.2	4.0	4.8	3.1	3.4
Fat tails	2.2	2.5	3.1	4.0	4.9	2.8	3.3

^aSensitivity tests considered to bound plausible structural uncertainty.

Note. Further statistics are available in the online data repository (see Data Availability Statement).

This US prior does, however, have characteristics that some may find hard to justify. It requires abandoning the presumption that feedbacks are a priori independent, instead assuming that they are anticorrelated or naturally compensate (in our prior sample, the prior correlation of any one λ _i component with the sum of the other five is −0.83). While some feedbacks do indeed negatively correlate (e.g., water vapor and lapse rate, see section 3.2.3), discovering this for some feedbacks through process knowledge and evidence is not the same as assuming it beforehand for all feedbacks. Doing so would imply that if knowledge is gained about one feedback (say, ice albedo), one's confidence in the other feedbacks (e.g., clouds) will automatically improve and best estimates possibly shift, even though nothing was directly observed about the others, and we have no evidence for such a link. It would also imply that uncertainty could become smaller when feedbacks are summed, rather than larger as would normally be the case. There is no evident a priori rationale for preferring this negative (compensating) correlation over a positive (reinforcing) one—and allowing for a broad range of possible correlations of both directions and averaging the results would produce an outcome very close to that with no correlation (our Baseline UL prior). Previous work on feedbacks or using climate models has never, to our knowledge, treated evidence in this way.

Note that our priors on λ _i feedbacks should not be considered comparable to priors used in Bayesian studies (e.g., Johansson et al., 2015; Skeie et al., 2014, and others discussed in section 4) that do not explicitly consider individual feedback processes as evidence, and which take S or λ as an independent variable, rather than λ _i which are the independent variables used here. In our inference model, the process information and prior together play the same role as would the prior in any study not treating process information about individual feedbacks as evidence (cf. Equation 10), and a good deal of this information is not new (e.g., the Planck response and lapse rate/water vapor feedbacks). Therefore, such studies would in principle be expected to include some of our process evidence in their prior, which should be considered if comparing assumptions here to those used elsewhere.

7.3. Sensitivity to Specification of Evidence

Here we test the sensitivity of our calculations to modifying the evidence as encoded in our likelihood functions for S. First, we exclude each line of evidence in turn from the Baseline calculation. These “leave‐one‐out” calculations give an indication of the relative effectiveness of the various lines of evidence in constraining S. Although we compared marginal likelihoods and PDFs from individual lines of evidence compared with priors in section 7.1, the sensitivity tests shown here may be considered more relevant to identifying the impacts of individual lines of evidence on the posterior PDF in a context where the majority of evidence is being applied. The results are summarized in Table 10 and Figure 22 (see UL No Process, UL No Historical, UL No Paleo Warm, and UL No Paleo Cold). Comparing the results of the different leave‐one‐out tests confirms the relative strengths of the constraints of the individual lines of evidence on the upper and lower bounds for S reported in section 7.1 (see Figure 20).

Figure 22.

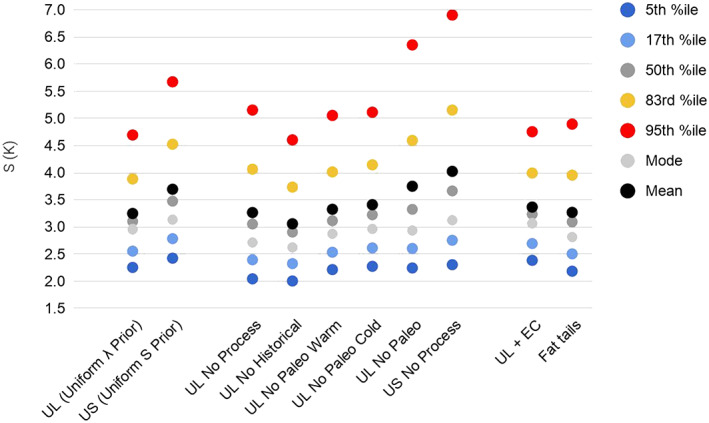
Graphical summary of statistics of posterior PDFs for S. UL is the Baseline calculation with a uniform prior on λ and US has a uniform prior on S. The middle group shows the effect of removing various lines of evidence in turn. UL + EC shows the impact of including the effect of emergent constraints. The effect of substituting fat‐tailed distributions for some lines of evidence is also shown for the Baseline case.

We also show the impact of removing the process evidence under a uniform Prior for S (US No Process). This mimics some past studies that did not use process understanding and expressed a uniform prior on S; it therefore considers the situation where one views the process understanding (including a UL prior and the structural understanding of Equation 5) as a process model replacing a uniform‐S prior (see US No Process BU, Table 10, and Figure 22; Figure 20b). This results in higher sensitivities than UL No Process BU, such that if one considers the removal of this process model and replacement with uniform‐S, the process model is found to exert a stronger constraint at the high end but less at the low end, compared to the conclusions if one discards only the process evidence but still maintains a consistent UL prior.

In addition, we explore the possibility that our Baseline range for S may be overconfident due to limitations in our treatment of the various lines of evidence. The Bayesian approach is by its very nature subjective, and our inference model (or some other analysis choice) may have limitations that potentially result in overconfident predictions. Other researchers may make different assumptions, and we would like to explore what range of results is at the edges of what we think plausible. Hence, we use sensitivity tests to explore the consequences of possible alternative assumptions. For further discussion of the limitations of our approach, see section 7.5 below.

First we revisit the “leave‐one‐out” calculations, which may also be considered as worst‐case explorations of what our results would look like if a line of evidence were for some reason substantially compromised, or not accepted by some readers, or highly codependent with another evidence line in some way unrecognized in our analysis. As such these can be used to place generous upper bounds on the impacts of uncertainties in individual lines of evidence on our posterior PDF for S.

Excluding the process evidence from the Baseline calculation increases the 66% posterior range for S from 2.6–3.9 to 2.4–4.1 K and the 5–95% range from 2.3–4.7 to 2.0–5.2 K. Excluding the process evidence from the calculation with the uniform S prior has a larger effect, increasing the 66% and 5–95% ranges to 2.8–5.2 and 2.3–6.9 K, respectively. Hence, the upper tail of the distribution is not robustly constrained by historical and paleoclimate information combined alone, as the resulting constraint depends strongly on the prior. Nevertheless, even then sensitivities beyond 5.9 K are estimated to have <10% probability, yielding a similar upper bound to the IPCC AR5 assessment, which estimated the probability of sensitivities above 6 K as “very unlikely,” that is, <10%.

These are very extreme sensitivity tests; for them to be considered reasonable, new evidence would need to come to light that would justify complete dismissal of all of the multiple elements of the process evidence (and hence much of our physical understanding of the climate system). Since this is a very extreme scenario, we do not consider the “No Process” case to plausibly represent the overall structural uncertainty. The strong sensitivity to removing the Process evidence illustrates how important this line of evidence is to constraining the upper bounds on S, under a uniform‐S prior.

The other leave‐one‐out tests may be considered less extreme in that they gauge the impact of excluding individual sets of observations (historical, warm, and cold paleoclimate) from the Baseline calculation for S. Excluding these lines of evidence from the Baseline calculation individually reduces the 5th percentile by at most 0.3 K, to 2.0 K and increases the 95th percentile value by at most 0.4 K, to 5.1 K. Although we consider it extremely unlikely that new information could ever lead a future assessment to dismiss an entire line of evidence, it is conceivable that multiple lines of evidence (including the process evidence) could weaken or be interdependent to a level which has a similar‐order effect on the range of S to the above (see Figure 24). The leave‐one‐out tests also place a generous upper bound on the effects of dependencies between any two lines of evidence, given that removing one line of evidence in a pair will remove the effect of dependencies between that pair but also removes the independent contribution of that line of evidence.

Figure 24.

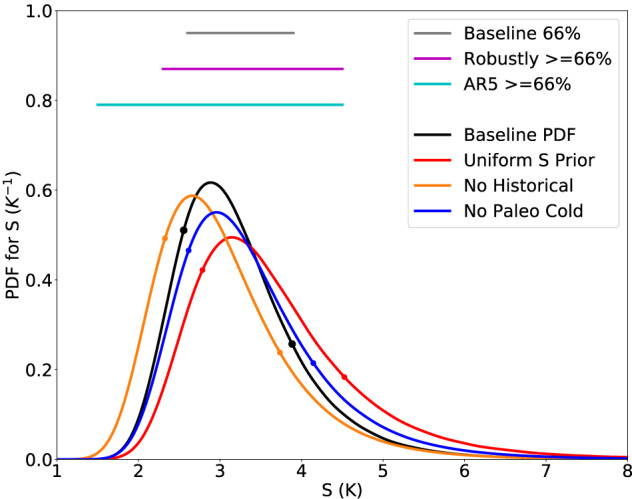
PDFs of S in comparison with AR5. The Baseline PDF is shown in black, and its 66% range (2.6–3.9 K) in gray. Colored curves show PDFs from sensitivity tests which cover a range for S, which could plausibly arise given reasonable alternative assumptions or interpretations of the evidence, summarized by the magenta line (2.3–4.5 K). These are the Baseline case but with a uniform S prior (red), the Baseline without the Historical evidence (orange), and the Baseline case without the cold paleoclimate evidence (blue). The 66%‐or‐greater (“likely”) range from the most recent IPCC assessment (AR5) (1.5–4.5 K) is shown in cyan. Circles indicate 17th and 83rd percentile values.

The Baseline calculation does not include any evidence arising from emergent constraints based upon present‐day climate observations (see discussion in section 3.6). In addition to the above sensitivity tests, we test the impact of adding this line of evidence to the Baseline calculation (see UL + Emergent Constraints in Table 10 and Figure 22). This shifts the 66% range from 2.6–3.9 to 2.7–4.0 K and the 5–95% range from 2.3–4.7 to 2.4–4.8 K. The shift upward of 0.1 K is consistent with the higher S suggested by this evidence and demonstrates the potential for future revisions to our assessment of the evidence to improve our estimate of S. However, its impact is small and is bounded by the selected leave‐one‐out tests above. This reflects the relatively low confidence placed in this line of evidence and the fact that its maximum‐likelihood S is not far from that of the other evidence.

Another potential limitation of our approach is that we assume Gaussian distributions for many prior expert PDFs on independent variables. This does not allow for uncertainty in the assigned means and standard deviations themselves. Accounting for this uncertainty by sampling from a distribution of candidate standard deviation values would lead to a distribution with more kurtosis, that is, fatter tails. Another way of looking at this is that Gaussians may express overconfidence in our ability to dismiss surprising values far from the most likely one and may therefore not well represent fully informed beliefs that are appropriately aware of structural uncertainty. To address this concern, we include an additional sensitivity test in which we replace many of the Gaussian evidence distributions with Student's t distributions with 5 degrees of freedom. (A t distribution formally results if the Gaussian parameters are being estimated empirically from a finite, unbiased sample, see Gelman et al., 2013; although our distributions are arguably better viewed as expert judgments, the t distribution is still a useful generalization for our purposes.) We perform this replacement for variables where small samples, structural uncertainty or possible unrecognized factors could be a significant concern. The choice of 5 degrees of freedom is motivated by the historical pattern effect correction term Δλ, which is informed by the sample mean and standard deviation of six GCM experiments. This is represented by the Gaussian N(−0.5, 0.3) in the Baseline calculation. In our sensitivity test we replace this with a t distribution with 5 degrees of freedom and mean and scale parameters equal to the mean and standard deviation of the Gaussian distribution, respectively. This increases the standard deviation by 30% from 0.3 to 0.39. The resulting distribution has a 66% range of [−0.82, −0.18], which is very similar to that for the Gaussian distribution ([−0.79, −0.21]) but has a 5–95% range of [−1.1, +0.1], which is 22% wider than that from the Gaussian distribution ([−0.99, −0.01]). We apply the same procedure to fatten the tails of the following other independent variables: the process evidence feedback likelihoods λ _i, the adjusted forcing ∆F and state dependence correction factor α for the paleoclimate cold periods, the CO₂ concentration and slow‐feedback scaling f _ESS for the paleoclimate warm periods, and the ratio (1 + ζ) of ECS to S. In each case the t distribution gives a very similar 66% range to that of the Gaussian distribution it replaces. We find that substituting these fat‐tailed distributions for all of the above into the Baseline calculation increases the width of the 66% range for S slightly from 2.6–3.9 to 2.5–4.0 K and increases the width of the 5–95% range a little more, from 2.3–4.7 to 2.2–4.9 K. These wider ranges are already encompassed by our other plausible sensitivity tests described above, indicating that our conclusions on the bounds of both ranges for S are reasonably robust to structural uncertainty.

7.4. Implications for Related Sensitivity Measures and Future Warming

Here we present results showing how S and its PDF map onto a few other related quantities of interest. To relate these, we must rely entirely on GCMs, which can predict S and the other quantities.

Via Equation 8 and the PDF on ζ given in section 5.2.3, our calculation provides a simultaneous calculation of the posterior PDF of ECS, which may be compared with that of S. For our Baseline case the 5–95% (2.2–4.9 K) and 66% (2.6–4.1 K) ranges of ECS (Table 11) are slightly wider and stretched higher than those for S (2.3–4.7 and 2.6–3.9 K, respectively). This is as expected from the comparison shown in Figure 1 and resulting distribution of ζ. There is only a modest increase in the widths of the ECS PDFs compared to those for S, presumably because the paleo evidence more directly constrains ECS, while other evidence more directly constrains S. Under our uniform‐S prior, however, the 66% range for ECS (2.7–4.6 K) expands slightly compared to that for S (2.8–4.5 K) but does not shift upward, while the 5–95% range for ECS (2.3–5.6 K) is shifted slightly toward lower values than for S (2.4–5.7 K). This counterintuitive result may be due to the a priori correlation structure implicitly required to reconcile the physical model (section 2.2) with a uniform prior probability of S: Because ζ is uncertain, the strong expectation for high S expressed by this prior (compared to that of the Baseline prior) combined with the evidentiary constraints against high S implies that a posteriori ζ has a strong chance to be negative even though a priori it was expected to be positive on average (remembering that, in a Bayesian analysis, the PDFs of all variables are updated when evidence is considered). Because of this, the bounds from reasonable sensitivity tests we obtain for ECS are slightly smaller than those for S.

Table 11.

Medians and 66% Probability Ranges (in Brackets), for ECS (for One Doubling of CO₂), TCR, and Warmings in Figure 23, for Our Baseline and Using a Uniform Prior on S

	Baseline	Uniform‐S PPD
ECS	3.2 [2.6,4.1]	3.5 [2.7,4.6]
TCR	1.8 [1.5, 2.2]	1.9 [1.6, 2.4]
RCP2.6 warming	1.0 [0.7, 1.4]	1.2 [0.8, 1.7]
RCP4.5 warming	1.8 [1.4, 2.3]	2.0 [1.5, 2.6]
RCP6.0 warming	2.0 [1.6, 2.6]	2.3 [1.7, 3.0]
RCP8.5 warming	3.5 [3.0, 4.2]	3.8 [3.2, 4.8]

Note. All values are in K.

For other quantities (TCR and future warming), we obtained approximate PDFs from their fits to S, broadened according to the sample spread about this fit. These fits were shown in Figure 1; the resulting PDFs of warming are shown in Figure 23 for the Baseline case, and ranges are given in Table 11 for other cases. As the relationship between the different climate sensitivity measures is not well understood (e.g., AR4; Figure 10.15, Frey et al., 2017; Grose et al., 2018), we choose linear fits. These linear fits do not extrapolate through the origin for nonequilibrium scenarios, but this is expected, as the fraction of warming that remains unrealized (at the end of century in the case of the RCPs, or time of doubling in the case of TCR) will vary with S. Within the range of substantial probability of S, the relationships do not show any robust nonlinearity, so none is accounted for.

Figure 23.

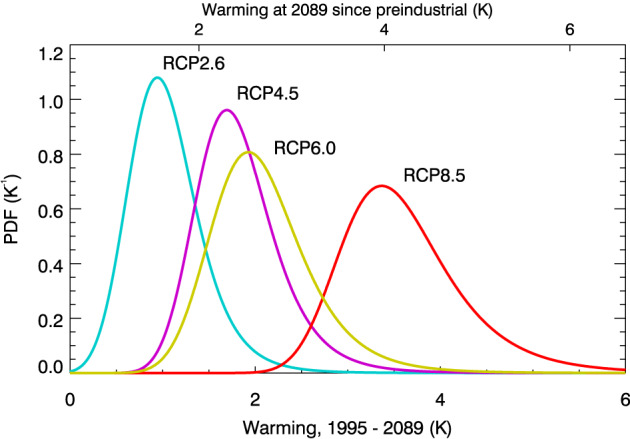
PDFs of the warming by late this century, from our Baseline PDF of S. These warming PDFs are obtained by converting S to warming using the best linear fit and then convolving the induced PDF with Gaussian uncertainty, as shown by the shading in Figure 1b. Results from RCP6.0 employ data from Forster et al. (2013). Note that the warming is calculated relative to 1985–2005; approximate warming relative to preindustrial is shown at the top, based on 0.6‐K warming having occurred by 1985–2005. Warming was estimated using the difference of 20‐year means centered on the years 1995 or 2089.

The 66% range we find for TCR (1.5–2.2 K in the Baseline calculation and up to 2.4 K otherwise) is much narrower than the IPCC AR5 likely range of 1.0–2.5 K. However, our assessment of this quantity is very limited and should be treated with considerable caution, as it comes largely from sources of information more relevant to S (paleoclimate and atmospheric process evidence), which is then converted to TCR using coupled climate models from AR5, rather than a bottom‐up assessment of TCR that properly accounts for our physical understanding, uncertainties in transient processes (in particular, ocean processes), and historical changes on shorter time horizons of greater relevance to TCR. A more thorough assessment of TCR is set aside for future projects.

For the Baseline case shown, the future‐warming PDFs indicate that the probability that warming relative to 1995 will exceed 1.4 K (roughly equivalent to 2 K above preindustrial, Hawkins et al., 2017) by late this century is 17% under RCP2.6, 83% under RCP4.5, 92% under RCP6.0, and >99% under RCP8.5. Note that while RCP8.5 has sometimes been presented as a “business as usual” scenario, it is better viewed as a worst case (e.g., Hausfather & Peters, 2020). We make no claims here on scenario probabilities, only on warming probabilities conditional on a broad range of possible scenarios.

7.5. Limitations, Caveats, and Potential Future Approaches

Our assessment has taken an ambitious approach that has for the first time attempted to model the relationships between diverse lines of evidence (including feedback components and pattern effects) with S in a consistent overarching inference model framework. This approach like any other has its potential limitations, which will only become clearer in future work which develops the approach. Here we discuss various limitations of the statistical approach outlined here that could potentially be improved in future work.

First, in each section we have made those choices that we consider the most defensible and carried a single likelihood function for each line of evidence forward into the synthesis calculations. In future work it could be possible to develop a range of plausible alternative likelihoods for each line of evidence and apply these as sensitivity tests in the synthesis. While we have tested the effect of substituting symmetric fatter‐tailed distributions for Gaussian distributions, future studies could test the sensitivity to other changes, for example, skewed distributions. The statistical models developed here are intended to codify the existing knowledge from the literature. Future research should develop these models, and it is quite likely that they may be reparameterized and may even be formulated in terms of other variables.

Our treatment of possible dependencies across evidence lines was limited to use of ∆F _2xCO2 throughout and some sensitivity tests around pattern effect dependence. Treatments for dependencies are best addressed by modeling them directly within the inference model. This could be taken further in future work, for instance, by explicitly building in additional dependencies between feedback components, forcings and feedbacks, or other quantities for which there is evidence of dependence (e.g., see Annan & Hargreaves, 2017). In particular, dependencies arising from pattern effects could be modeled more carefully once better understood, and other dependencies (including “buffered” ones) could be modeled. The dependence between forcing and feedbacks remains poorly understood (section 3.4), and better understanding might suggest a different approach to that taken here, although we do not expect this to significantly affect results.

Zelinka et al. (2020) show that the range in S increases from 2.1–4.7 K in CMIP5 to 1.8–5.6 K in CMIP6. This demonstrates the importance of combining multiple lines of evidence, as GCMs alone are not producing increasingly confident estimates. We have deliberately not used the range of S values from climate models to directly inform our likelihoods, but climate models inevitably inform our estimates, for example, in the estimation of the pattern effect term in the historical likelihood, some of the feedback subcomponents from the process evidence, and some of the paleo radiative forcing estimates (see section 6.2). We have incorporated some new results from CMIP6, but results from CMIP6 models on the strength of the pattern effect are not yet fully available. It is in principle possible that our results could change, for example, if new models predicted radically different pattern effects, which could change our interpretation of evidence from the historical period, or different feedbacks which are not strongly constrained by other evidence. However, any change in the range of S from a synthesis of all lines of evidence would be expected to be smaller than the change in the model range alone.

Finally, there are other possible choices that could be made for the synthesis methodology, or in the use of alternative lines of evidence, and sometimes our reasons for choosing one over another are based on very subjective judgments. Some of the difficult issues (arising around the specifications of the priors for example) could potentially be addressed in future using statistical simulation approaches.

7.6. Summary

Our Baseline calculation gives a 66% (17–83%) range for S of 2.6–3.9 K (gray line, Figure 24) and a 5–95% range of 2.3–4.7 K. This case includes all evidence considered in this report, except the “emergent constraint” evidence, whose independence from other evidence is uncertain (section 3.6). We consider the sensitivity tests where we individually remove the historical, cold, or warm paleoclimate evidence to bound any changes to these ranges that could plausibly occur due to reasonable alternative interpretations of the evidence (see orange and blue lines in Figure 24). These place bounds of 2.3 and 4.1 K on the 66% range and 2.0 and 5.1 K on the 5–95% range for S. If we additionally include a sensitivity test where we substitute a uniform S prior into the Baseline calculation, we obtain bounds of 2.3 and 4.5 K on the 66% range (see magenta line, Figure 24) and 2.0 and 5.7 K on the 5–95% range for S. Modifying the baseline calculation to include the emergent constraint evidence or to assume fat tailed‐distributions results in ranges which are bounded by the above.

All of our plausible alternate calculations for the PDF of S suggest a considerable narrowing of the range compared to that assessed at the time of the AR5 (cyan line, Figure 24). This remains true for the ECS. A weaker constraint would be found if we disregarded all process evidence, since in that case the resulting combined paleo and historical PDF would be highly sensitive to prior information in the upper tail. Yet even the most generous allowances for uncertainty result in a stronger constraint on S than that which was available at the time of the AR5 assessment, indicating an advance in our assessment of the evidence for S. This increased constraint comes almost entirely from bringing up the low end, rather than reducing the high end.

8. Summary and Conclusions

8.1. Considerations

The objective of this work was to analyze all important evidence relevant to climate sensitivity and use that evidence to draw conclusions about the probabilities of various values of the sensitivity. In so doing we have examined the interdependence of different lines of evidence and the possibility that structural or other flaws in our understanding might affect conclusions or lead to overconfidence. There are subjective elements to such an exercise, but there are also objective ones—in particular, enforcing mathematical rules of probability to ensure that our beliefs about climate sensitivity are internally consistent and consistent with our beliefs about the individual pieces of evidence.

All observational evidence must be interpreted using some type of model that relates underlying quantities to observables; hence, there is no such thing as a purely observational estimate of climate sensitivity. Uncertainty associated with any evidence therefore comes from three sources: observational uncertainty, potential model error, and unknown influences on the evidence such as unpredictable variability (which may or may not be accounted for in one's model). By comparing past studies that used different models for interpreting similar evidence (see, e.g., section 4.1), we find that the additional uncertainty associated with the model itself is considerable compared with the stated uncertainties typically obtained in such studies assuming one particular model. When numerical global climate models (GCMs) are used to interpret evidence, they reveal deficiencies in the much simpler models used traditionally—in particular, the failure of these models to adequately account for the effects of inhomogeneous warming. This insight is particularly important for the historical temperature record (section 4.2), which is revealed by GCMs to be compatible with higher climate sensitivities than previously inferred using simple models. In general, many published studies appear to have overestimated the ability of a particular line of evidence to constrain sensitivity, sometimes leading to contradictory conclusions (see section 4.1). When additional uncertainties are accounted for, single lines of evidence can sometimes offer only relatively weak constraints on the sensitivity.

The effective sensitivity S analyzed here is defined based on the behavior during the first 150 years after a step change in forcing, which is chosen for several practical reasons explained in section 2.1. While our study also addresses other measures of sensitivity (the TCR and long‐term equilibrium sensitivity), the calculations of these were not optimal and future studies could apply a methodology similar to that used here to quantify them, or other quantities perhaps more relevant to medium‐term warming, more rigorously.

After extensively examining the evidence qualitatively and quantitatively (sections 3, 5), we followed a number of past studies and used Bayesian methods to attempt to quantify the implications and probability distribution function (PDF) for S. It must be remembered that every step of this process (choosing priors, computing likelihoods, etc.) involves judgments or models, and results will depend on assumptions and assessments of structural uncertainties that are hard to quantify. Thus, we emphasize that a solid qualitative understanding of how the evidence stacks up is at least as important as any probabilities we assign. Nonetheless, sensitivity tests shown in section 7 suggest that our results are not very sensitive to reasonable assumptions in the statistical approach.

8.2. Key Findings

Each main line of evidence considered here—process knowledge, the historical warming record, and the paleoclimate record—accords poorly with values outside the traditional “Charney” range of 1.5–4.5 K for climate sensitivity S. When these lines of evidence are taken together, because of their mutual reinforcement, we find the “outside” possibilities for S to be substantially reduced compared to those from individual lines of evidence. Whatever the true value of S is, it must be reconcilable with all pieces of evidence; if any one piece of evidence effectively rules out a particular value of S, that value does not become likely again just because it is consistent with some other, weaker, piece of evidence as long as there are other S values consistent with all the evidence (see SSBW16). If on the other hand every value of S appeared inconsistent with at least one piece of evidence, the evidence would need reviewing to look for mistakes. But we do not find this situation. Instead, we find that the lines are broadly consistent in the sense that there is plenty of overlap between the ranges of S each supports. This strongly affects our judgment of S: if the true S were 1 K, it would be highly unlikely for each of several lines of evidence to independently point toward values around 3 K. And this statement holds even when each of the individual lines of evidence is thought to be prone to errors.

We asked the following question (following SSBW16): What would it take, in terms of errors or unaccounted‐for factors, to reconcile an outside value of S with the totality of the evidence? A very low sensitivity (S ~ 1.5 K or less) would require all of the following:

1. Negative low‐cloud feedback. This is not indicated by evidence from satellite or process‐model studies and would require emergent constraints on GCMs to be wrong. Or, a strong and unanticipated negative feedback from another cloud type such as cirrus, which is possible due to poor understanding of these clouds but is neither credibly suggested by any model, nor by physical principles, nor by observations (section 3).

2. Cooling of climate by anthropogenic aerosols over the instrumental period at the extreme weak end of the plausible range (near 0 or slight warming) based both on direct estimates and attribution results using warming patterns. Or, that forced ocean surface warming will be much more heterogeneous than expected and cooling by anthropogenic aerosols is from weak to middle of the assessed range (section 4).

3. Warming during the mPWP well below the low end of the range inferred from observations and cooling during the LGM also below the range inferred from observations. Or, that S is much more state‐dependent than expected in warmer climates and forcing during these periods was higher than estimated (section 5).

In other words, each of the three lines of evidence strongly discounts the possibility of S around 1.5 K or below: The required negative feedbacks do not appear achievable, the industrial‐era global warming of nearly 1 K could not be fully accounted for, and large global temperature changes through Earth history would also be inexplicable.

A very high sensitivity (S > 4.5 K) would require all of the following to be true:

1. Total cloud feedback stronger than suggested by process‐model and satellite studies (section 3).

2. Cooling by anthropogenic aerosols near the upper end of the plausible range. Or, that future feedbacks will be much more positive than they appear from this historical record because the mitigating effect of recent SST patterns on planetary albedo has been at the high end of expectations (section 4).

3. Much weaker‐than‐expected negative forcing from dust and ice sheets during the LGM (section 5). Or, a strong asymmetry in feedback state dependence (significantly less positive feedback in cold climates than in the present, but relatively little difference in warmer paleoclimates).

Thus, each of the three lines of evidence also argues against very high S, although not as strongly as they do against low S. This is mainly because of uncertainty in how strongly “pattern effects” may have postponed the warming from historical forcing, which makes it difficult to rule out the possibility of warming accelerating in the future based on what has happened so far. Indeed, we find that the paleoclimate record (in particular, the LGM) now provides the strongest evidence against very high S, while all lines provide more similar constraints against low S (paleo slightly less than the others).

An important question governing the probability of low or high S is whether the lines of evidence are independent, such that multiple chance coincidences would be necessary for each of them to be wrong in the same direction (section 6). For the most part, the various elements in low‐ and high‐S scenarios do appear superficially independent. For example, while possible model errors are identified that (if they occurred) could affect historical or paleo evidence, they mostly appear unrelated to each other or to global cloud feedback or model‐predicted S. Some key unknowns act in a compensating fashion (i.e., where an unexpected factor would oppositely affect two lines of evidence, effectively canceling out most of its contributed uncertainty). Even in the one identified possibility (see below) where an unknown could affect more than one line of evidence in the same direction, modeling indicates a relatively modest impact on the PDF.

IPCC AR5 concluded that climate sensitivity is likely (≥66% probability) in the range 1.5–4.5 K. The probability of S being in this range is 93% in our Baseline calculation and is no less than 82% in all other “plausible” calculations considered as indicators of reasonable structural uncertainty (see section 7.3). Although consistent with IPCC's “likely” statement, this indicates considerably more confidence than the minimum implied by the statement. We also find asymmetric probabilities outside this range, with negligible probability below 1.5 K but up to an 18% chance of being above 4.5 K (7% in the Baseline calculation). This is consistent with all three lines of evidence arguing against low sensitivity fairly confidently, which strengthens in combination. Given this consensus, we do not see how any reasonable interpretation of the evidence could assign a significant chance to S < 1.5 K. Moreover, our plausible sensitivity experiments indicate a less‐than‐5% chance that S is below 2 K: Our Baseline 5–95% range is 2.3–4.7 K and remains within 2.0 and 5.7 K under reasonable structural changes.

Since the extreme tails of the PDF of S are more uncertain and possibly sensitive to “unknown unknowns” and mathematical choices, it may be safer to focus on 66% ranges (the minimum for what the IPCC terms “likely”). This range in our Baseline case is 2.6–3.9 K, a span less than half that of AR5's likely range, and is bounded by 2.3 and 4.5 K in all plausible alternative calculations considered. Although we are more confident in the central part of the distribution, the upper tail is important for quantifying the overall risk associated with climate change and so does need to be considered (e.g., Sutton, 2019; Weitzman, 2009). We also note that allowing for “surprises” in individual lines of evidence via “fat‐tailed” likelihoods had little effect on results, as long as such surprises affect the evidence lines independently.

Our S is not the true equilibrium sensitivity ECS, which is expected to be somewhat higher than S due to slowly emerging positive feedback. Values are similar, however, because we define S for a quadrupling of CO₂, while ECS is defined for a doubling, which cancels out most of the expected effect of these feedbacks (section 2.1). We find that the 66% ECS range, at 2.6–4.1 K (Baseline) bounded by 2.4 and 4.6 K, is not very different from that of S, though slightly higher. Thus, our constraint on the upper bound of the “likely” range for ECS is close to that of the IPCC AR5 and previous assessments, which formally adopt an equilibrium definition. The constraint on the lower bound of the “likely” range is substantially stronger than that of AR5 regardless of the measure used. The uncertainties in ECS and S assessed here are similar because each is somewhat better constrained than the other by some subset of the evidence.

Among the plausible alternate calculations (see section 7.3), the one producing the weakest high‐end constraint on S uses a uniform‐S‐inducing prior, which shifts the ranges upward to 2.8–4.5 K (66%) and 2.4–5.7 K (90%). Our Baseline calculation assumes feedbacks are independent (or that dependence is unknown), which predicts a nonuniform prior PDF for S; to predict a uniform one requires instead assuming a known, prior dependence structure among the feedbacks (see section 7.2). Although lack of consensus on priors remains a leading‐order source of spread in possible results, we still find that sensitivity to this is sufficiently modest that strong constraints are possible, especially at the low end of the S range.

The main reason for the stronger constraints seen here in contrast to past assessments is that new analysis and understanding has led us to combine lines of evidence in a way the community was not ready to do previously. We also find that the three main lines of evidence are more consistent than would be expected were the true uncertainty to be as large as in previous assessments. While some individual past studies have assigned even narrower ranges, as discussed above, past studies have often been overconfident in assigning uncertainty so not too much weight should be given to any single study. We note that although we did not use GCM “emergent constraint” studies using present‐day climate system variables in our base results, our results are nonetheless similar to what those studies suggest in the aggregate (see section 3.6 for discussion of these studies and why they were excluded from our Baseline calculation).

New models run for CMIP6 are showing a broader range of S than previous iterations of CMIP (Zelinka et al., 2020). Our findings are not sensitive to GCM S distributions since we do not directly rely on them (see section 6.1). The highest and lowest CMIP6 S values are much less consistent with evidence analyzed here than those near the middle of the range. Some of the effects quantified in this paper with the help of GCMs were looked at only with pre‐CMIP6 models, and interpretations of evidence might therefore shift in the future upon further analysis of newer models, but we would not expect such shifts to be noteworthy unless they involved significant improvements in model skill against relevant observations (see below).

8.3. Looking Forward

Our approach not only yields new estimates of uncertainty but points to particular directions in which research could most productively improve constraints in the future. Here we review these; for more details see sections 3.7, 4.3, 5.5, and 6.2.

One uncertainty particularly stands out in our analysis. Recent inhomogeneities of surface warming in the Pacific (with less or no warming in the cooler regions compared to the warmer regions) are not fully captured by any CMIP5 coupled climate models with historical forcings, and we are unsure whether this is due predominantly to model errors in internal variability, ocean heat uptake, or the equilibrium forced SST warming pattern. Internal variability is strongly suspected and ocean heat uptake errors are also likely; but if unexpected model errors in the equilibrium response pattern are involved, this would affect both process and historical evidence, compromising the assumed independence. A preliminary calculation (section 6.3) suggests that this issue is unlikely to substantially change results, but the matter needs further exploration. Therefore, a high priority for further constraining climate sensitivity, especially at the high end, is to more convincingly explain this pattern of surface warming (related to the so‐called “warming hiatus”) and quantify its impact on the planetary energy balance. It might be similarly helpful to better understand the “Grand Hiatus” of the 1960s. Doing so would make historical warming a better constraint.

Process information played a significant role in our analysis (section 3) but is currently limited by our understanding of how behavior we observe in response to short‐term (i.e., interannual) variability relates to feedbacks on forced climate change. Further modeling work is needed to improve this. There has been rapid progress in recent years in the understanding of cloud feedback mechanisms, and continued progress could substantially improve constraints—but with much recent progress on tropical low clouds, more emphasis is needed on other cloud types. Satellite observations that provide information on the vertical distribution of clouds and its changes have recently proven valuable in testing model feedback predictions, and their continuation would increase the chances of further constraints.

The historical record currently provides a useful constraint only against very low S, but there is potential for improvement. Better constraints on aerosol forcing have proven elusive, but with further effort using more comprehensive models, the time and geographic evolution of climate signals may finally allow the cooling by aerosols and warming by GHGs to be teased apart, with the decrease in emissions from some regions providing potential for better constraints already. Progress on quantifying “pattern effects” (see above) is also ongoing and will benefit from improved process understanding. To fully resolve both issues may require further improvement of climate models to better reproduce decadal climate variations. Evidence from the historical record will also continue to grow in its power to constrain S with the gradual lengthening of the record (with the crucial proviso that the key variables continue to be well monitored by global observing systems). This should particularly help with disentangling aerosol cooling from greenhouse warming, due to divergent forcing patterns with aerosol influences globally close to flat while GHGs are continuing to sharply increase.

Evidence from the paleorecord will benefit from the continuing growth of modeling activities and improved observation/proxy characterization of other warm periods in the geological past, which are not yet sufficiently understood to be considered here. Additionally, research into the magnitudes, efficacies and uncertainties of forcings in the paleoclimate periods assessed is also needed. In particular, better characterization of ice sheets, dust, and potentially other aerosol effects are needed. How S depends on background state remains a critical topic where better observations and modeling are needed. We strongly suggest that more work on paleoclimate be performed with the same models that are being used for the historical and future projections.

Although any single metric of global warming has limitations, S is a bedrock parameter of the global climate system. The scientific community has had difficulty narrowing its uncertainty range far beyond the prescient initial estimate by Charney (National Research Council, 1979), which was based on very limited information. While much research since has confirmed this range, we now argue that in combination this wealth of evidence has indeed narrowed it and shifted the central value upward. Moreover, we see prospects for research to further narrow the range in the not too distant future, and believe that this is an important continuing goal for climate science.

Sherwood, S. C. , Webb, M. J. , Annan, J. D. , Armour, K. C. , Forster, P. M. , Hargreaves, J. C. , et al. (2020). An assessment of Earth's climate sensitivity using multiple lines of evidence. Reviews of Geophysics, 58, e2019RG000678 10.1029/2019RG000678

Data Availability Statement

Data and code supporting this analysis have been made publicly available via Zenodo archive site (available via http://doi.org/10.5281/zenodo.3945276).