Validity of flexicurve and motion capture for measurements of thoracic kyphosis vs standing radiographic measurements

Abstract

Thoracic kyphosis varies among healthy adults and typically increases with age. Excessive kyphosis (hyperkyphosis) is associated with negative health. Spinal alignment also affects spine loading, with implications for conditions such as vertebral fractures and back pain. Valid measurements of kyphosis are necessary for clinical and research assessment of age‐related posture changes, and to support improved biomechanical understating of spine conditions. Independent validation of non‐radiographic techniques, however, remains limited. The goal of this study was to compare standing radiographic kyphosis measurements with non‐radiographic measurements and predictions of thoracic kyphosis using flexicurve and motion analysis markers, in order to determine their validity. Thirteen non‐radiographic measures of thoracic kyphosis were obtained in each of 40 adult subjects who also underwent standing radiographs of the thoracic spine. Measures included estimates derived by fitting of polynomials or circles to the non‐radiographic data, as well as predictions calculated using previously published methods. Intra‐class correlations (ICC) and root‐mean square errors (RMSEs) were calculated between radiographic and non‐radiographic measures to determine validity. Most non‐radiographic estimates of kyphosis show similar, weak to moderate levels of validity when compared to radiographic measurements, and RMSEs ranging from 8.0° to 20.8°. Unbiased estimates of radiographic measurements with moderate to good ICCs were identified, however, based on marker measurements, and new prediction equations were created with similar validity that also account for age and body habitus. Clinical significance: These non‐radiographic measurements of thoracic kyphosis can be applied to clinical practice or to clinical studies with recognition of specific limitations.

Independent validation of non‐radiographic measurements of thoracic kyphosis remains limited. In this study, flexicurve and motion‐analysis based measurements were validated versus standing radiographic measurements of thoracic kyphosis in a sample of adults aged 19 ‐ 93. Unbiased measurements based on motion analysis with moderate to good validity were identified, and new prediction equations were created with similar validity that also account for age and body habitus.

1. INTRODUCTION

Sagittal spine curvature varies greatly among healthy adults. Thoracic kyphosis in adults without spinal disease (measured from T4‐T12) averages 44 ± 11°, suggesting a range from 19° to 63° across 95% of the normal adult population. ¹ Thoracic kyphosis typically increases over time in older adults, ² sometimes leading to hyperkyphosis or excessive forward curvature of the thoracic spine. Factors associated with larger kyphosis angles include vertebral fractures and disc degeneration, ² smaller and lower‐density trunk muscles, ³ and genetic predisposition. ⁴ Hyperkyphosis is associated with a number of negative health outcomes including physical functional limitations, ⁵ impaired respiratory function, ⁶ increased risk of injurious falls, ⁷ and greater mortality. ⁸ Moreover, spine loading is an important factor in understanding the etiology of conditions such as vertebral fractures ⁹ and low back pain. ¹⁰ , ¹¹ Musculoskeletal modeling studies have shown that loading of the spine is sensitive to spine curvature, ¹² and greater thoracic kyphosis significantly increases loading of the spine. ¹³ , ¹⁴ Thus, valid measurements of thoracic kyphosis are necessary for clinical and research assessment of age‐related changes in posture, and to support improved biomechanical understanding of spine conditions.

There are numerous radiographic and non‐radiographic techniques for measuring thoracic kyphosis. The current standard is the radiographic‐modified Cobb angle, which uses a lateral radiograph of the spine and measures the angle between two vertebral endplates, frequently T4 and T12. ¹⁵ An alternative radiographic measure is the vertebral centroid angle, which is reported to have greater consistency of measurement than the Cobb angle. ¹⁶ Radiographic measurements of kyphosis are often used clinically, and in research, but there are significant barriers to obtaining these measures, including cost and radiation exposure. ¹⁷ , ¹⁸ With this in mind, physicians and researchers have created alternative non‐radiographic techniques for measuring kyphosis that rely on skin‐surface curvature, as measured with a flexicurve ruler ¹⁹ , ²⁰ or motion analysis markers. ²¹ Several studies have created techniques that could be used to predict radiographic kyphosis angles based on non‐radiographic measures. Greendale et al ²² calibrated the flexicurve kyphosis angle to the radiographic Cobb angle, while Furlanetto et al ²³ calibrated skin‐surface curvature to the centroid angle. Nerot et al ²⁴ established methods to predict the location of intervertebral joint centers from motion‐analysis marker data. These joint centers can be used to calculate a kyphosis angle.

The validation of non‐radiographic techniques for kyphosis measurement remains limited. Previous studies have separately compared flexicurve‐based measurements to the Cobb angle and reported similar repeatability and reproducibility for both measurements ²² , ²⁵ , ²⁶ , ²⁷ ; however, the majority of these studies examined limited age ranges (either young or elderly subjects) and thus may not fully represent possible kyphosis ranges. Furthermore, only a few studies have examined marker‐based spinal curvature validity against curvature from spine imaging, ²¹ , ²⁸ and no study has previously validated the kyphosis angles produced by published prediction methods against radiographic measurements in independent datasets.

A fast, non‐invasive, and inexpensive technique to assess thoracic kyphosis would be valuable to researchers studying posture, aging, and spine conditions, as well as those seeking to create musculoskeletal models incorporating subject‐specific spine curvature. Thus, the primary aim of this study was to examine the validity of flexicurve and motion‐capture marker based measures of kyphosis angles, including those generated by previously published prediction methods, compared against radiographic measures. The secondary aim was to examine whether validity might vary between age groups (young and older) and with body habitus (normal and overweight) in order to gain better insight into the validity and applicability of these techniques. Finally, new prediction methods were created to predict radiographic measures based on marker or flexicurve measures, plus age, and body habitus.

2. MATERIALS AND METHODS

2.1. Participants

Forty‐one adult volunteers were recruited to participate in this study, in younger (ages 18‐40) and older (ages 65+) age groups. All participants were able to perform activities, such as walking, standing, sitting, bending, or lifting, without assistance and reported no injuries or conditions currently affecting their normal activities. Individuals with known history of vertebral fractures or hyperkyphosis were included, but individuals with other conditions that might alter thoracic biomechanics, such as traumatic thoracic injury, severe scoliosis, which had been treated surgically, or neuromuscular conditions, such as Parkinson disease or muscular dystrophy, were excluded. This study was approved by the Committee on Clinical Investigations of Beth Israel Deaconess Medical Center (protocol # 2015P000394). All participants provided written informed consent before participation.

2.2. Data collection

Each participant had their spine curvature measured using standardized protocols with a lateral thoracic X‐ray, a flexicurve ruler, and motion‐capture markers, in a single session.

2.2.1. Radiographs

One lateral view X‐ray was taken of the thoracic spine at the hospital radiography department. Subjects stood in a relaxed position with arms elevated in front of them for the X‐ray.

2.2.2. Flexicurve

The flexicurve ruler (Staedtler Mars Inc, Nurnberg, Germany) is an inexpensive device that when gently pressed against the back molds to and retains the shape of the spine. Before molding the flexicurve ruler to the subject's spine, the C7, T12, and S2 posterior spinous processes were located via palpation. The flexicurve ruler was molded over the spine midline from C7 to S2. The resulting curve was traced on paper and the locations of the C7, T12, and S2 processes were labeled. The measurement was performed while the participant stood in a neutral upright posture with feet shoulder‐width apart.

2.2.3. Motion‐capture

Motion‐capture markers are small reflective balls that can be attached to the body to record motion. These were attached to the subject's skin using double‐adhesive tape. Rigid clusters of four markers were attached to the skin overlying the T1, T4, T5, T8, T9, T12, L1, and S2 posterior spinous processes, as located by palpation. An additional 69 single markers were placed on the C7, head, sternum and clavicles, and extremities. Marker data was collected with a 10‐camera motion analysis system (Vicon Motion Systems, Oxford, UK) recording at 100 Hz. Marker positions were captured while the participant stood in a neutral upright posture with feet shoulder‐width apart.

2.3. Data reduction, processing, and analysis

2.3.1. Radiographic measures

Two measurement approaches were used to quantify kyphosis from lateral thoracic radiographic images: the modified Cobb angle and the centroid angle. Radiographs were evaluated based on digitized vertebral morphometry points identified by a semi‐automated quantitative algorithm (SpineAnalyzer; Optasia Medical Ltd., Cheadle, UK). This approach has been used previously to quantify the Cobb angle and has excellent inter‐ and intra‐rater reliability. ³ , ⁴ Briefly, after a user identified the approximate centers of the T4 to T12 vertebrae, the algorithm identified vertebral body margins and placed six morphometry points representing the anterior, center, and posterior of both endplates for each vertebral body. If T4 was not visible, the measurement was performed between T5 and T12.

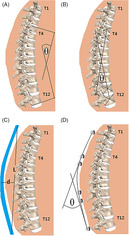
1. Cobb angle: The Cobb angle was determined as the angle between the superior endplate of T4 and the inferior endplate of T12, using the anterior and posterior morphometry points of each to define lines parallel to the endplates (Figure 1).

2. Centroid angle: Vertebral centroids were determined as the mean of the six morphometry points for each vertebral body. The centroid angle was then determined as the angle between the lines defined by the T4 to T5 and T11 to T12 centroids (Figure 1).

To confirm results obtained from the digitized morphometry points, Cobb angle was also measured manually. Specifically, the angle measurement tool of the medical imaging viewer (Conserus Enterprise Viewer, v2.1, Change Healthcare Canada Company, Richmond, BC, Canada) was used to draw straight lines parallel to the superior endplate of T4 and the inferior endplate of T12, and the resulting angle reported. The manual Cobb angle was defined as the average measurement of three raters (DG, SJM, DEA). If the SD of a manual Cobb angle among the raters was >4°, the individual measurements were adjudicated by the group and if needed measurements were discarded and/or repeated until a SD of <4° was achieved.

FIGURE 1.

Visualization of Cobb angle, A; Centroid angle, B; Flexicurve measurement, C; and Marker‐based polynomial angle, D

2.3.2. Flexicurve

Three methods were used to evaluate kyphosis from the flexicurve traces: the calculated central angle, the polynomial angle, and the circle central angle.

1. Calculated central angle (F.Calculated): The length and depth of the thoracic curve were measured from the initial flexicurve trace. Then, as described previously in Reference29, the kyphosis angle can be estimated by assuming the flexicurve trace approximates an arc of a circle, and calculated by the central angle of the arc, given the arc length, L, and depth, d. Thus, the central angle was calculated (Figure 1):

$$\theta =2{\sin }^{-1}\left(\frac{4\mathit{dL}}{4d^2+L^2}\right)$$ (1)

2. Circle central angle (F.Circle.C7; F.Circle.T4): Flexicurve traces were digitized using ImageJ, ³⁰ with 19 points evenly placed from C7 to S2, inclusive, using C7, T12, and S2 markings on the curve for guidance. The fifth point was considered the location of T4. A circle was fit to the points representing the curve between C7‐T12 using MATLAB (Version 2015a, The Mathworks, Inc., Natick, MA), The central angle theorem was then used to calculate the angles between C7 and T12 (F.Circle.C7) and T4 to T12 (F.Circle.T4). ³¹

3. Polynomial angle (F.Poly.C7; F.Poly.T4): Using the 19 digitized points, a quadratic polynomial was fit to the points between C7 and T12 using MATLAB. Angles were calculated as the intersection of the two lines normal to the curve at C7‐T12 (F.Poly.C7), and at T4‐T12 (F.Poly.T4). ³²

2.3.3. Motion‐capture markers

Marker positions were averaged over the 1 second of data selected for minimal noise and movement. The coordinates of the four markers on each cluster were averaged to provide one set of coordinates representative of a single marker at the respective posterior spinous process. Circle (M.Circle.C7; M.Circle.T4) and polynomial (M.Poly.C7; M.Poly.T4) fitting approaches (as described above for flexicurve, section 2.3.2) were applied to calculate the angles of kyphosis between C7 and T12, and between T4 and T12 (Figure 1).

2.3.4. Published prediction techniques

Three different prediction techniques were used to predict a kyphosis angle based on non‐radiographic measures.

1. Internal spine profile (P.Nerot; P.Nerot.Ext): Nerot et al ²⁴ provided two sets of prediction equations that determined spine joint centers. Both sets of equations use body weight, height, and distances between certain boney landmarks. One set uses the external profile of the spine (P.Nerot.Ext) while the other set does not (P.Nerot). We incorporated the method of Peng et al ³³ to estimate the position of the L5‐S1 joint from pelvis and lower extremity markers. Vertebral body centroids were estimated as the halfway point between neighboring intervertebral joint centers. The centroid method was applied to calculate T4 to T12 kyphosis angles from the estimated vertebral body centroids for both sets of prediction equations.

2. Internal polynomial angle (P.Furlanetto): Furlanetto et al ²³ provide a linear regression equation to estimate the internal polynomial T4 to T12 angle from a skin‐surface T4 to T12 polynomial angle. This equation was used to calibrate the marker‐based polynomial angle (M.Poly.T4) to the centroid angle.

3. Flexicurve Cobb angle (P.Greendale): Greendale et al ²² provide a linear regression equation that calibrates measurements of the flexicurve trace to the radiographic T4 to T12 Cobb angle. This was used with our flexicurve measurements to predict the Cobb angle.

2.3.5. New prediction techniques

Two new prediction techniques were created to predict Cobb angle based on marker or flexicurve measurements. Similarly, two prediction techniques to predict centroid angle were created. Multiple linear regressions were performed including a marker or flexicurve angle measurement along with age and BMI as independent variables. The predictive performance of the regression equations was evaluated using leave‐one‐out (40‐fold) cross‐validation to estimate root‐mean square error (RMSE) when applied to a new dataset. In each case, the regression resulting in the lowest estimated RMSE was selected as the prediction method.

2.4. Statistical analysis

Descriptive statistics were calculated for all outcome measures, and RMSEs were calculated for each outcome relative to radiographic Cobb and centroid angles. Agreement among the radiographic measures was examined by paired t tests and intra‐class correlation coefficients (ICCs). The validity of non‐radiographic measurements and published prediction techniques were investigated using ICCs, RMSEs, and Bland‐Altman plots. The ICCs (model two, case one, two‐way mixed effects, absolute agreement, single rater). Resulting ICCs were categorized based on the range of their 95% confidence intervals, using categories of weak (ICC < 0.5), moderate (0.5 ≤ ICC < 0.75), good (0.75 ≤ ICC < 0.9), and excellent (0.9 ≤ ICC). ³⁴ Paired t tests were used to determine whether the non‐radiographic measurements and prediction techniques were different than radiographic measurements. Bland‐Altman plots qualitatively illustrated the amount of disagreement between compared measures. The primary analysis was performed including all subjects. Secondary analyses were performed on subgroups of young and older subjects, normal weight (BMI < 25) and overweight (BMI ≥25) subjects, and low kyphosis (Cobb <42.5°) and high kyphosis (Cobb ≥42.5°) subjects separated by median Cobb angle. Statistical analyses were performed in Stata/IC 13.1 (StataCorp LP, College Station TX) with significance set at α = 0.05.

3. RESULTS

One participant was excluded from the analyses because no X‐ray was obtained. Characteristics of the 40 remaining participants (22 women, 18 men) are shown in Table 1, including for sub‐groups by age and BMI. These were an average (range) age of 55.9 ± 24.7 (19‐93) years, height of 1.67 ± 0.12 (1.41‐2.25) m, body mass of 68.6 ± 13.0 (50.8‐102.0) kg, and BMI of 24.7 ± 3.3 (18.8‐31.9) kg/m². On review of the thoracic spine in X‐rays, three participants were noted to have thoracic vertebral compression fractures, 14 had disc space narrowing, 17 had osteophytes (including three with anterior bridging osteophytes consistent with diffuse idiopathic skeletal hyperostosis), and two had scoliosis. In two participants, radiographic measures were taken between T5 and T12 as T4 was not discernable.

TABLE 1.

Mean (SD) of participant characteristic, including by age and BMI groups in sub‐analyses

	All (n = 40)	Young (n = 16)	Older (n = 24)	Normal weight (n = 26)	Overweight (n = 14)
Age (yearr)	55.9 (24.7)	27.4 (6.3)	74.8 (8.3)	53.4 (26.4)	60.4 (21.3)
Sex (M/F)	18/22	8/8	10/14	15/11	7/7
Height (m)	1.67 (0.12)	1.71 (0.13)	1.63 (0.10)	1.67 (0.11)	1.66 (0.13)
Weight (kg)	68.6 (13.0)	71.6 (14.0)	66.7 (12.3)	63.3 (9.6)	78.5 (13.1)
BMI (kg/m2)	24.7 (3.3)	24.4 (3.8)	24.9 (3.1)	22.7 (1.7)	28.3 (2.2)

3.1. Radiographic measurements

The manual Cobb method and semiautonomous Cobb method demonstrated a good to excellent ICC and a small RMSE (4.0°), suggesting that the semiautonomous Cobb measurement is a valid substitution for the manual Cobb measurement and vice versa. The centroid angle had weak to excellent ICCs compared to both Cobb angle measurements (Table 2). Bland‐Altman plots of Cobb and centroid angle vs other measurements show little evidence of proportional bias or major outliers (Supplement ).

TABLE 2.

Radiographic measures, nonradiographic measures, and predictions of thoracic kyphosis (in degrees), with differences, ICC, and RMSE relative to radiographic Cobb and Centroid angles

Measure		Mean	SD	ICC Cobb (95% CI)	RMSE Cobb	ICC Centroid (95% CI)	RMSE Centroid
Radiographic	Cobb	41.9 b	11.0	—	—	0.831 (0.162–.945)	7.2
	Centroid	36.4 a	12.3	0.831 (0.162‐.945)	7.2	—	—
	Manual Cobb	43.5 a , b	10.9	0.932 (0.857‐0.966)	4.1	0.744 (0.016‐0.914)	9.1
Marker	M.Poly.C7	50.4 a , b	11.4	0.581 (−0.002‐0.823)	11.6	0.458 (−0.097‐0.784)	16.0
	M.Poly.T4	35.1 a	9.2	0.598 (0.089‐0.818)	10.1	0.709 (0.515‐0.834)	8.3
	M.Circle.C7	55.2 a , b	12.4	0.441 (−0.102‐0.761)	15.9	0.344 (−0.082‐0.705)	20.8
	M.Circle.T4	51.7 a , b	11.9	0.533 (−0.048‐0.799)	12.9	0.410 (−0.099‐0.747)	17.6
Flexicurve	F.Calculated	51.5 a , b	9.8	0.403 (−0.042‐0.687)	13.5	0.312 (−0.103‐0.646)	18.0
	F.Poly.C7	48.2 a , b	9.2	0.481 (0.122‐0.711)	11.3	0.372 (−0.086‐0.680)	15.3
	F.Poly.T4	34.5 a	7.6	0.432 (0.022‐0.693)	11.5	0.547 (0.292‐0.731)	9.8
	F.Circle.C7	52.2 a , b	9.7	0.379 (−0.065‐0.675)	14.1	0.308 (−0.101‐0.649)	18.5
	F.Circle.T4	36.2 a	7.5	0.448 (0.118‐0.679)	10.7	0.558 (0.299‐0.740)	9.5
Prediction technique	P.Greendale	40.3 b	7.6	0.550 (0.294‐0.733)	9.0	0.526 (0.256‐0.719)	10.3
	P.Nerot.Ext	33.9 a	9.3	0.533 (0.017‐0.784)	11.2	0.589 (0.340‐0.762)	10.0
	P.Nerot	30.3 a , b	4.9	0.178 (−0.089‐0.452)	15.0	0.239 (−0.043‐0.500)	12.6
	P.Furlanetto	43.5 b	10.8	0.734 (0.552‐0.849)	8.0	0.620 (0.142‐0.825)	11.0

Abbreviations: ICC, intraclass correlations; RMSE, root‐mean square errors.

^aDifferent than Cobb angle (P < .05).

^bDifferent than Centroid angle (P < .05).

3.2. Non‐radiographic measurements

Marker‐based measurements, compared with the semiautonomous Cobb angle, reported weak to good ICCs and RMSEs between 10.1° and 15.9°. When compared with the centroid angle, M.Poly.T4 had a moderate to good ICC and RMSE of 8.3°, while other marker‐based measurements reported weak to good (M.Poly.C7) or weak to moderate (otherwise) ICCs and RMSEs between 16.0° and 20.8°. All of these measurements are different from the Cobb angle and all except M.Poly.T4 are different from the centroid angle (P < .05, Table 2).

Flexicurve‐based measurements, compared with the Cobb angle, reported weak to moderate ICCs and RMSEs between 11.3° and 14.1°. When compared with the centroid angle, flexicurve based measurements reported weak to moderate ICCs and RMSEs between 9.5° and 18.5°. All of these measurements are different from the Cobb angle and all except F.Poly.T4 and F.Circle.T4 are different from the centroid angle (P < .05, Table 2).

3.3. Published prediction techniques

When compared with the Cobb angle, P.Furlanetto had a moderate to good ICC and RMSE of 8.0, while other prediction techniques reported weak (P.Nerot), weak to moderate (P.Greendale), or weak to good (P.Nerot.Ext) ICCs and RMSEs from 9.0° to 15.0°. When compared with the centroid angles, prediction techniques reported weak (P.Nerot), weak to moderate (P.Greendale) or weak to good (otherwise) ICCs and RMSEs between 10.0° and 12.6°. P.Nerot.Ext and P.Nerot are different from the Cobb angle and all except P.Nerot.Ext are different from the centroid angle (P < .05, Table 2).

3.4. New prediction techniques

New predictions for both Cobb and Centroid angles used M.Poly.C7 and F.Poly.C7 as marker‐based and flexicurve‐based measurements, respectively (Table 3). Non‐radiographic angle was a significant factor in all predictions (P < .05), and age was significant (P < .05) except in prediction of Centroid angle with M.Poly.C7. BMI was a significant factor (P < .05) for predictions of Cobb and centroid angles using M.Poly.C7, but was not significant for predictions using F.Poly.C7. The new prediction equations showed moderate to excellent (Cobb angle from M.Poly.C7), moderate to good (Cobb angle from F.Poly.C7; centroid angle from M.Poly.C7), and weak to good (centroid angle from F.Circle.C7) ICCs. Point estimates of predictive RMSEs from cross‐validation analyses ranged between 6.5° and 9.9° for multivariate prediction equations. The inclusion of age and BMI improved performance compared to univariate equations with only the angle measures.

TABLE 3.

New prediction equations for Cobb and centroid angles, based on regressions with a marker or flexicurve‐based angle measurement

Prediction	Angle measure	Coefficients					ICC	RMSE
		Angle	Age	BMI	Intercept	R2	(95% CI)	(95% CI)
Cobb	M.Poly.C7	0.716	0.121	0.859	−22.1	0.703	0.829 (0.700‐0.906)	6.5 (4.9‐7.8)
	M.Poly.C7	0.724	—	—	5.4	0.557	0.720 (0.529‐0.842)	7.6 (5.7‐9.1)
	F.Poly.C7	0.609	0.206	0.171	−3.2	0.548	0.713 (0.518‐0.838)	8.2 (6.1‐9.9)
	F.Poly.C7	0.692	—	—	8.5	0.335	0.508 (0.233‐0.707)	9.4 (7.3‐11.1)
Centroid	M.Poly.C7	0.896	0.056	0.979	−36.0	0.684	0.816 (0.678‐0.899)	7.6 (5.2‐9.4)
	M.Poly.C7	0.842	—	—	−6.0	0.601	0.756 (0.583‐0.863)	8.0 (5.8‐9.7)
	F.Poly.C7	0.751	0.164	0.114	−11.8	0.481	0.655 (0.432‐0.802)	9.9 (7.1‐12.0)
	F.Poly.C7	0.819	—	—	−3.0	0.374	0.550 (0.288‐0.735)	10.2 (8.4‐11.8)

Note: Both multivariate (plus age and BMI) and univariate (angle measurement only) are presented. RMSE shows the estimated RMSE with 95% CI for predictive performance based on leave‐one‐out cross‐validation analyses. Coefficients in bold are significant (P < .05).

Abbreviations: BMI, body mass index; ICC, intraclass correlation; RMSE, root‐mean square error.

3.5. Secondary analysis by age

Results for the older group (Supplement 2) were similar to the primary analysis, particularly with moderate to good ICCs for P.Furlanetto vs Cobb angle (RMSE 8.2°) and M.Poly.T4 vs centroid angle (RMSE 8.3°). When examining the young group, all ICCs were weak or weak to moderate (Supplement 2). However, RMSEs remained similar to the primary analysis and the older group. For example, RMSE was 7.7° for P.Furlanetto vs Cobb angle, and 8.3° for M.Poly.T4 vs centroid angle. New marker‐based predictions were weak to good for the young group and moderate to excellent for the older group with RMSEs between 5.1° and 7.3°, while flexicurve‐based predictions were weak to moderate for the young group and weak to good for the older group with RMSEs between 6.6° ‐ 9.4° (Supplement 2).

3.6. Secondary analysis by BMI

Results for the normal weight group were similar to the primary analysis (Supplement 2), particularly with a moderate to good ICC for M.Poly.T4 vs centroid angle (RMSE 6.4°). The ICC for P.Furlanetto vs Cobb angle, however, was weak to good (RMSE 8.1°). Results for the overweight group reported weak to good ICCs for most measures, including M.Poly.T4 vs centroid angle (RMSE 11.0°), Several measures reported weak to excellent ICCs vs Cobb angle (M.Poly.C7, RMSE 8.2°; F.Poly.C7, RMSE 7.9°; P.Furlanetto, RMSE 7.7°), and P.Furlanetto reported a weak to excellent ICC vs centroid angle (RMSE 9.2°). New marker‐based predictions were moderate to excellent for the normal weight group and weak to excellent for the overweight group with RMSEs between 5.5° and 8.9°, while flexicurve‐based predictions were weak to excellent for the overweight group and weak to good otherwise with RMSEs between 6.8° and 10.6° (Supplement 2).

3.7. Secondary analysis by kyphosis angle

For the low and high kyphosis angle groups, ICCs were at best weak to moderate (Supplement 2). However, RMSEs remained similar to the primary analysis. New marker‐based predictions were weak to good for both groups (RMSEs of 5.7°‐7.1°), while new flexicurve‐based predictions were weak to moderate in the low kyphosis group (RMSEs of 8.4°‐9.7°) but weak to good in the high kyphosis group (RMSEs of 6.0°‐7.7°).

4. DISCUSSION

This is the first study to examine the validity of both flexicurve and marker‐based measurements of sagittal thoracic kyphosis vs radiographic measurements, particularly in a participant sample including a large range of ages and kyphosis angles. This study is also the first to report on the validity of kyphosis angles derived from published prediction techniques in an independent study. Determining the utility of these measurement techniques will be useful in future studies seeking to assess kyphosis, whether as a clinical outcome or for the creation of subject‐specific musculoskeletal models. The findings reported here show that for unbiased non‐radiographic measures and predictions, individual errors average between 5° and10°. However, these can still be valid substitutes for radiographic measures in study outcomes and analyses (eg, comparing group means), where they will likely fall within a few degrees of radiographic measures. Moreover, reported reliability is generally good to excellent for both radiographic ³⁵ and non‐radiographic ¹⁹ measures of kyphosis, including flexicurve and marker‐based measures. ²⁹ Thus they likely have similar utility for evaluating curvature and changes in curvature over time.

In validations of non‐radiographic measures of kyphosis, Furlanetto et al ²² prediction (P.Furlanetto) reported no difference with Cobb angle, moderate to good ICC (0.734, 95% CI 0.552‐0.849) and the smallest RMSE (8.0°). Similarly, M.Poly.T4 reported no difference with the centroid angle, moderate to good ICC (0.709, 95% CI 0.515‐0.834) and the smallest RMSE (8.3°). Thus, in predicting the T4 to T12 Cobb angle P.Furlanetto would be considered the non‐radiographic technique of choice, while for predicting the centroid angle M.Poly.T4 would be considered the non‐radiographic technique of choice. Both of these measures were marker‐based. Interestingly, P.Furlanetto was created to predict centroid angle from an external curvature and in this study was calculated from M.Poly.T4. Flexicurve‐based methods, including the P.Greendale prediction method, uniformly showed weak to moderate ICCs, suggesting limited validity for predicting radiographic measures. If using a flexicurve, Greendale et al ²² prediction (P.Greendale) may be the preferred approach for Cobb angle, while F.Circle.T4 may be the preferred approach for centroid angle, based on t‐tests and RMSE values. Flexicurve measures have been widely used to assess spine curvature, but this is the first study to assess the validity of motion analysis markers for this purpose. Overall, the marker‐based measures performed at least as well as the flexicurve, if not better. Thus, motion analysis markers offer a reasonable approach for assessing spine curvature vs other non‐radiographic measures.

Results from the secondary analyses suggest that validity of non‐radiographic measures is lower in young adults than in older adults. However, predictions of Cobb angle and centroid angle using P.Furlanetto and M.Poly.T4 have similar errors in young adults and older adults. Results separated by BMI suggest that predictions of Cobb angle using P.Furlanetto are similarly valid in normal and overweight sub‐groups as in the total sample. Predictions of centroid angle using M.Poly.T4 remained valid in the normal subgroup, but may be less so in overweight individuals. Indeed, based on RMSEs P.Furlanetto might be the preferred prediction for both Cobb angle and centroid angle in overweight individuals. Separating by kyphosis angle suggests flexicurve‐based predictions may be better in higher‐kyphosis angles, but marker‐based predictions are similar in both groups. While not conclusive, this may indicate that accuracy of flexicurve measures may be sensitive to kyphosis angle. It should be noted that sample size was lower than the primary analysis in all the secondary analysis groups, and the young group had smaller kyphosis angles and less variance in kyphosis. These limitations increase uncertainty in the ICCs and make it more difficult to show strong validity in the secondary analyses than the primary analysis.

The new predictions created in this study were comparable to the best non‐radiographic measures of kyphosis validated in this study in terms of ICCs and predictive performance (RMSEs). However, it should be recognized that the predictive RMSEs were estimated using cross‐validation methods, and these equations have yet to be evaluated in an independent dataset. Nonetheless, the proposed prediction equations offer an important advantage in that they were created using a participant sample with a large range of ages and kyphosis angles. Thus, these equations can be applied in a broad range of subjects without concerns of extrapolation. Moreover, the inclusion of age and BMI in the new predictions addresses possible effects of these factors, while comparison with the angle‐only predictions (Table 3) show age and BMI improves performance.

The discrepancy between radiographic and non‐radiographic measures may be a result of the difference in anatomy between the internal and external profile of the spine. Non‐radiographic measures of the spine examine the exterior or skin‐surface profile, which is related to the posterior spinous processes. These spinous processes have differing angles depending on the vertebrae being measured, thus creating a disparity between internally and externally measured kyphosis angles. ³⁶ Previous literature has similarly reported only moderate correlations between radiographic and non‐radiographic measures of kyphosis, ¹⁸ , ²¹ , ²² , ²⁸ , ³⁷ consistent with the findings in this study. Furthermore, the semi‐autonomous radiographic Cobb angle was systematically larger than the centroid angle by an average of 5.5°. Previous literature has similarly reported Cobb angle to be systematically larger than the centroid angle by 1° to 8°. ¹⁶ , ³⁵

A limitation of the prediction techniques P.Nerot, P.Nerot.Ext, and P.Furlanetto is that they were developed using only radiographic data, with “virtual palpation” of skin surface points. ²³ , ²⁴ We utilized motion analysis markers as the input data for these predictions, but the potential errors arising from this is unknown. Additionally, Nerot et al ²⁴ used the location of the xyphoid process as an input, but xyphoid process location was not measured in this study. This deviation from the published procedure may have degraded the accuracy of our vertebral body centroid and kyphosis angle estimates. Finally, the regression of Furlanetto et al ²³ was created with data from subjects ranging from 6 to 18 years of age, outside the age range of participants in this study. While found to be valid and the best predictor of Cobb angle in this study, it is possible that a similar regression created in an adult population would perform even better.

A limitation of our measurements is that the non‐radiographic measurements of volunteers were taken in an upright standing position with arms at their sides, while radiographic images were taken with their arms raised in front of them to better view the thoracic spine. Arm elevation in upright standing may decrease the angle of kyphosis up to 7°, ³⁸ thereby introducing a possible discrepancy between our measurements. Future studies could evaluate if arm elevation produces similar changes in non‐radiographic measurements. However, some studies comparing non‐radiographic measures to radiographic measures use supine ¹⁸ or seated ²¹ imaging, which could also affect kyphosis angles. Thus, use of a standing radiograph for comparison remains a strength of this study. An additional limitation is that spinal pathology or degenerative changes may affect the measurements in uncertain ways. One or more of the pathologies noted in this study (vertebral fractures, disc space narrowing, osteophytes, scoliosis) was present in 20 older subjects, but only one younger subject. Thus, in this study we cannot evaluate the effects of these issues separately from aging.

The strengths of this study include its diverse subject pool and inclusion of multiple measurement techniques for thoracic kyphosis. The subject pool included men and women ranging in age from 19 to 93 years and Cobb angles from 20° to 64°. This range of age and kyphosis angles suggests the findings of this study are applicable across the healthy adult population. Additionally, while palpation errors are typical for non‐invasive measurements of the spine, palpation in this study was conducted by the same trained investigator with extensive spine palpation experience (S. J. M.). Not only should this minimize variability that might arise with multiple raters, but there is evidence that rater experience minimizes palpation errors. ³⁷

In conclusion, most non‐radiographic estimates of kyphosis show similar, weak to moderate levels of validity when compared to radiographic measurements. This is also consistent with prior studies, which may be indicative of a general limit on how well non‐radiographic measurements can represent radiographic measurements. However, unbiased non‐radiographic estimates with moderate to good validity were identified using marker data for both Cobb angle and centroid angle (P.Furlanetto and M.Poly.T4, respectively). New prediction equations are provided with similar validity, with advantages of accounting for potential effects of age and BMI in the prediction. Thus while these non‐radiographic measurements and prediction equations may not directly replace radiographic techniques for individual measurements, they could be applied in future clinical research or practice with due recognition of potential differences from radiographic measures.

CONFLICT OF INTEREST

The authors declare no potential conflicts of interest.

AUTHOR CONTRIBUTIONS

Daniel M. Grindle participated in data acquisition, data analysis, and drafting and revising the manuscript. Seyed Javad Mousavi participated in data acquisition, data analysis and interpretation, and revising the manuscript. Brett T. Allaire participated in data analysis, data interpretation, and revising the manuscript. Andrew P. White participated in study design, data interpretation, and revising the manuscript. Dennis E. Anderson participated in study design, data analysis, data interpretation, and drafting and revising the manuscript. All authors have read and approved the final version to be published.

Supporting information

Supplement 1 Bland‐Altman plots for Cobb and Centroid angles vs other measures

Supplement 2 Supporting information

Grindle DM, Mousavi SJ, Allaire BT, White AP, Anderson DE. Validity of flexicurve and motion capture for measurements of thoracic kyphosis vs standing radiographic measurements. JOR Spine. 2020;3:e1120 10.1002/jsp2.1120