Industry volatility and economic uncertainty due to the COVID-19 pandemic: Evidence from wavelet coherence analysis

Highlights

• •We investigate the impact of economic uncertainty due to the coronavirus (COVID-19) pandemic on the industrial economy in the US.
• •We apply wavelet coherence analysis to economic policy uncertainty (EPU) data and monthly sector volatility of the S&P 500 index.
• •Our analysis indicates that COVID-19 has had a substantial impact on all sectors of the US stock market.
• •The influence of the pandemic on the industrial economy is larger than that of the global financial crisis (GFC) for all sectors.

Abstract

This study investigates the impact of economic uncertainty due to the coronavirus (COVID-19) pandemic on the industrial economy in the US in terms of the interdependence and causality relationship. We apply wavelet coherence analysis to economic policy uncertainty (EPU) data and monthly sector volatility of the S&P 500 index from January 2008 to May 2020. The results reveal that EPU in terms of COVID-19 has influenced the sector volatility more than the global financial crisis (GFC) for all sectors. Furthermore, EPU leads the volatility of all sectors during COVID-19 pandemic, while some sector’s volatilities lead EPU during the GFC.

1. Introduction

On March 11, 2020, the World Health Organization (WHO) officially declared the novel coronavirus (COVID-19) outbreak a global pandemic. According to WHO (2020), as of July 12, 2020, there are 12,552,765 confirmed cases and 561,614 deaths around the world, with 3,163,581 of these confirmed cases and 133,486 deaths in the US. That is, about 25% of COVID-19 victims worldwide occur in the US. The spread of COVID-19 has significantly dampened global economic activity and has also wreaked havoc on the US economy.

Recently, numerous studies have reported the effects of COVID-19. For example, the impact of the pandemic on stock markets (Zhang et al., 2020; Akhtaruzzaman et al., 2020; Shehzad et al., 2020; Leduc et al., 2020; Sharif et al., 2020). They mainly focus on investigating the negative effects of the COVID-19 pandemic on the economy. In particular, the characteristics of the pandemic are discussed in comparison to the global financial crisis (GFC) of 2008 (e.g., Shehzad et al., 2020; Laing, 2020; Yarovaya et al., 2020). Meanwhile, uncertainty plays an important role in economic fluctuations. In particular, economic policy uncertainty (EPU) has had a direct impact on stock markets (Pastor and Veronesi, 2012; Antonakakis et al., 2013; Brogaard and Detzel, 2015; Ko and Lee, 2015; Liu and Zhang, 2015; Tsai, 2017; Chen et al., 2017; Arouri et al., 2016; Yu et al., 2018; Kannadhasan and Das, 2019; Wang et al., 2020).

We investigate the impact of economic uncertainty related to the COVID-19 pandemic on the industrial economy in the US. We use the EPU measured by Baker et al. (2016) and the volatility of 11 different S&P 500 index sectors from January 2008 to May 2020. We apply wavelet coherency analysis to estimate interdependence and causality between the EPU and each sector’s volatility. Furthermore, we include the GFC in the sample period for comparison purposes. Through these experiments, we attempt to identify the features that differentiate the impact of the COVID-19 pandemic from the GFC, which have become the key implications for policy makers in terms of effective fiscal policy management. To the best of our knowledge, this is the first report on the impact of COVID-19 according to the EPU with stock market data.

The remainder of this paper is organized as follows. Section 2 describes the data and review wavelet coherence analysis. Section 3 presents the empirical results. Finally, concluding remarks are provided in Section 4.

2. Data description and methodology

2.1. Data description

The time series of EPU is obtained from (http://www.policyuncertainty.com). This website presents the data of the news-based EPU index proposed by Baker et al. (2016). The sample period runs from January 2008 to May 2020. The index measures EPU using information from keyword searches in newspapers and indicates the risk origin from changes in monetary, fiscal, and other relevant policies.

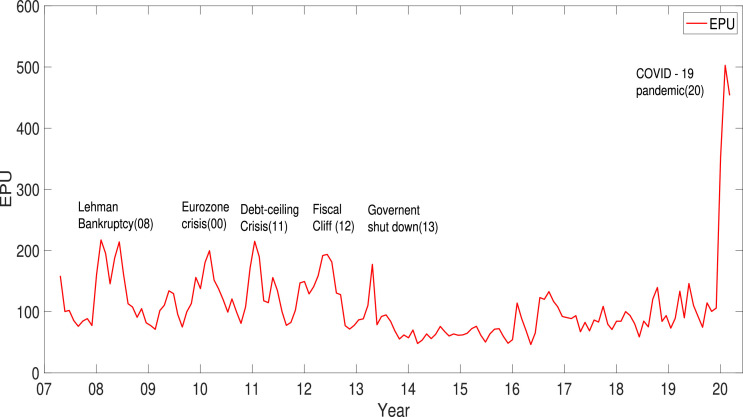
Fig. 2.1 shows the monthly time series of EPU during the sample period and several events that have shocked the market such as the GFC, the Eurozone crisis, and the COVID-19 pandemic. As can be seen, the EPU index in the period of the pandemic is significantly higher than in other periods.

Fig. 2.1.

The monthly EPU from January 2008 to May 2020. The events are based on the website.

The S&P 500 index consists of about 500 companies in the US. The market cap of the S&P 500 is 70 to 80% of the total US stock market capitalization. Thus, the industry sectors of the index naturally become a classification criterion for the total US market. The index has 11 sectors in total1 . To calculate the volatility of each sector, we first define the average log return of the i-th sector at time t as follows2 :

$$r_{i,t}=\frac{1}{N}\sum _j^N\log \frac{S_{j,t}}{S_{j,t-1}},$$

where N is the total number of stocks3 in the sector at time t and S _j,t is the close price of the j-th stock in the sector at time t. Several papers describe the relationship between EPU and the stock market using the logarithm of the returns (Brogaard and Detzel, 2015; Dakhlaoui and Aloui, 2016; Uddin et al., 2018; Fang et al., 2019; Ercolani and Natoli, 2020)4 . The summary statistics for the average log returns for all sectors and EPU are provided in Table 1 . As can be seen, the distribution of average log return data is high-peaked and left-skewed. According to the Jarque-Bera test, the null hypothesis of a normally distributed average log return is rejected for all sectors and the EPU distribution exhibits the same result.

Table 2.1.

Summary statistics for the average log return of sectors in the S&P 500 index and for EPU. The Jarque-Bera test statistic tests the null hypothesis of normality of sample returns. † indicates a rejection of the null hypothesis at the 1% significance level.

Panel A: Average daily log return
Sectors	Obs.	Mean	Max.	Min.	Std.Dev.	Skewness	Kurtosis	Jarque-Bera
Communication Services	3,123	0.0003	0.1297	−0.1204	0.0149	−0.2868	9.2732	11252†
Consumer Discretionary	3,123	0.0004	0.0909	−0.1242	0.0151	−0.4343	7.2746	6996.9†
Consumer Staples	3,123	0.0002	0.0806	−0.0953	0.0098	−0.2579	11.9576	18670†
Energy	3,123	−0.0001	0.1738	−0.2931	0.0218	−1.1414	19.126	48349†
Financials	3,123	0.00005	0.1393	−0.165	0.0199	−0.4609	13.2482	22985†
Health Care	3,123	0.0004	0.1073	−0.1073	0.0129	−0.4606	7.589	7618.2†
Industrials	3,123	0.0003	0.1198	−0.1222	0.0157	−0.4893	8.245	8986.1†
Information Technology	3,123	0.0004	0.1024	−0.1396	0.0151	−0.371	8.2062	8849.9†
Materials	3,123	0.0002	0.1093	−0.1397	0.016	−0.6225	9.0555	10891†
Real Estate	3,123	0.0001	0.1567	−0.1989	0.0203	−0.4716	15.7917	32616†
Utilities	3,123	0.0001	0.119	−0.1208	0.0126	0.0931	16.6112	35965†
Panel B: EPU
Variable	Obs.	Mean	Max.	Min.	Std.Dev.	Skewness	Kurtosis	Jarque-Bera
EPU	149	110.2554	502.7976	46.3945	61.7756	3.3993	16.3893	2014.36†

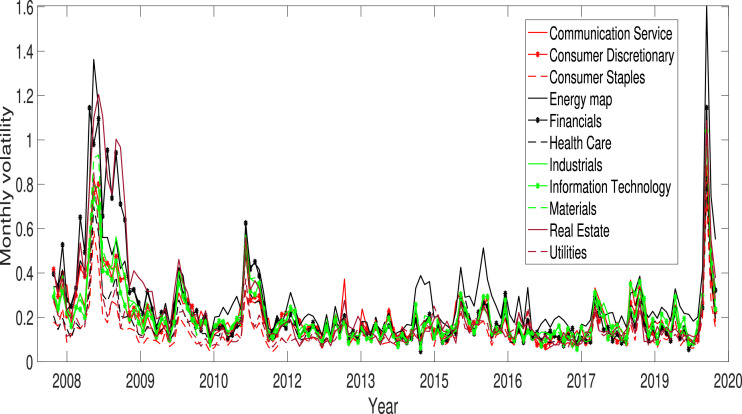
Monthly volatility is calculated based on the average daily returns in each month. Specifically, monthly volatility is the standard deviation of the average of the daily log returns in a month. We then multiply our standard deviation by the square root of 252 for annualizing. The reasons for using monthly volatility data are as follows: First, according to Baker et al. (2016), EPU is estimated based on a monthly count of articles that contain specific terms. Several studies examined the relationship between EPU and monthly data (Kido, 2016; Bilgin et al., 2018; Cheng and Yen, 2019, and Yen and Cheng, 2020). Second, the uncertainty or risk in the financial markets is usually measured as volatility. Volatility indicates the fluctuation of prices around the mean; thus, it is commonly used as a proxy for risk. In addition, historical volatility is computed as the standard deviation of the log return data. For these reasons, we use monthly volatility to measure the risk of each industry during a month, at the same frequency as the EPU. In particular, Brogaard and Detzel (2015) defined a monthly volatility index in the same way we do in the present study to investigate the forecasting performance of EPU. The monthly volatility in each sector is shown in Fig. 2.2 . Overall, each index has similar movements and some indices show different changes in certain periods. However, from the end of 2019, they all move in a similar manner.

Fig. 2.2.

The monthly volatility from January 2008 to May 2020. The volatility is annualized.

2.2. Methodology

We investigate the interdependence and causality between EPU and industry sector volatility through wavelet coherence analysis using Morlet’s specification. Through this analysis, we can draw inferences in a time–frequency frame. Based on several studies (Ko and Lee, 2015; Kristoufek, 2015; Pal and Mitra, 2019; Sharif et al., 2020), this is briefly explained below: The continuous wavelet transform of a time series x(t) is given by

$$W_x(\tau ,s)={\int }_{-\infty }^{\infty }x\left(t\right){\tilde{\psi }}_{\tau ,s}^{*}\left(t\right)dt,$$ (1)

where τ is the translation parameter controlling the wavelet location in time, and s is the scaling factor that determines the length of the wavelet. ${\tilde{\psi }}_{\tau ,s}^{*}\left(t\right)$ is the complex conjugate function of ${\psi }_{\tau ,s}^{*}\left(t\right)$ and $\tilde{\psi }$ is obtained by scaling and shifting the mother wavelet ψ:

$${\psi }_{\tau ,s}^{*}\left(t\right)=\frac{1}{\sqrt{\left|s\right|}}\psi \left(\frac{t-\tau }{s}\right),s,\tau \in \mathbb{R},s\ne 0.$$ (2)

Following Soares et al. (2011), we employ the Morlet wavelet introduced by Goupillaud et al. (1984) as the mother wavelet ψ.

Given two time series, x(t) and y(t), the cross-wavelet transform is given by

$$W_{xy}(\tau ,s)=W_x(\tau ,s)W_y^{*}(\tau ,s).$$ (3)

Based on the cross-wavelet transform, the wavelet coherence between two x(t) and y(t) is defined as follows (Torrence and Webster, 1999):

$$R^2(\tau ,s)=\frac{{\left|S\left(\frac{1}{s}{W}_{xy}(\tau ,s)\right)\right|}^2}{S\left(\frac{1}{s}{\left|W_x(\tau ,s)\right|}^2\right)S\left(\frac{1}{s}{\left|W_y(\tau ,s)\right|}^2\right)},$$ (4)

where S is the smooth operator and 0 ≤ R ²(τ, s) ≤ 1. The R ²(τ, s) is a squared correlation localized in time and frequency. Following Bloomfield et al. (2004), the phase difference from the phase angle of the cross-wavelet transform is:

$${\rho }_{xy}(\tau ,s)={\tan }^{-1}\left(\frac{\text{Im}\left[S\left(\frac{1}{s}{W}_{xy}(\tau ,s)\right)\right]}{\text{Re}\left[S\left(\frac{1}{s}{W}_{xy}(\tau ,s)\right)\right]}\right),\text{where}{\rho }_{xy}\in [-\pi ,\pi ],$$ (5)

where Im and Re are the imaginary and real parts of the smoothed cross-wavelet transform, respectively. The ρ_xy(τ, s) can demonstrate the dependence and causality relationships between two series x(t) and y(t), while the squared wavelet coherence does not include information about the direction of the relationship. According to several studies (Flor and Klarl, 2017; Cai et al., 2017; Funashima, 2017), we can determine the relationship between two x(t) and y(t) depending on the level of phase difference ρ_xy. If ρ_xy ∈ (0, π/2), x(t) and y(t) are positively related, but x(t) leads y(t). If ${\rho }_{xy}\in (-\pi /2,0),$ y(t) leads x(t). For ρ_xy ∈ (π/2, π), x(t) and y(t) are negatively correlated, but y(t) leads x(t). If ${\rho }_{xy}\in (-\pi ,-\pi /2),$ two time series are also negatively related, with x(t) leading y(t).

3. Empirical analysis

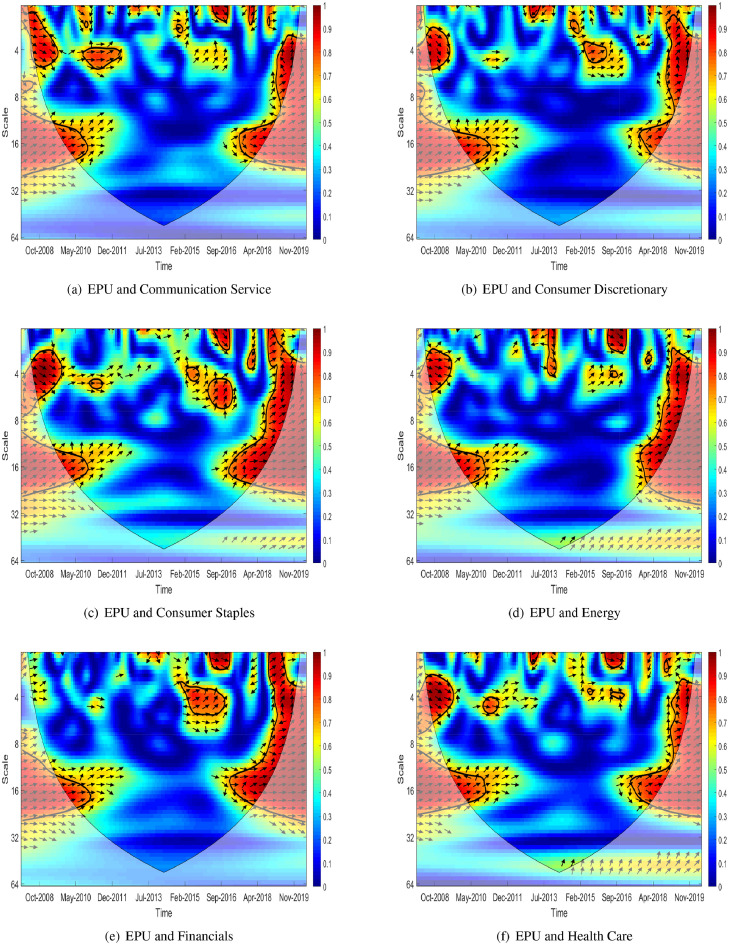
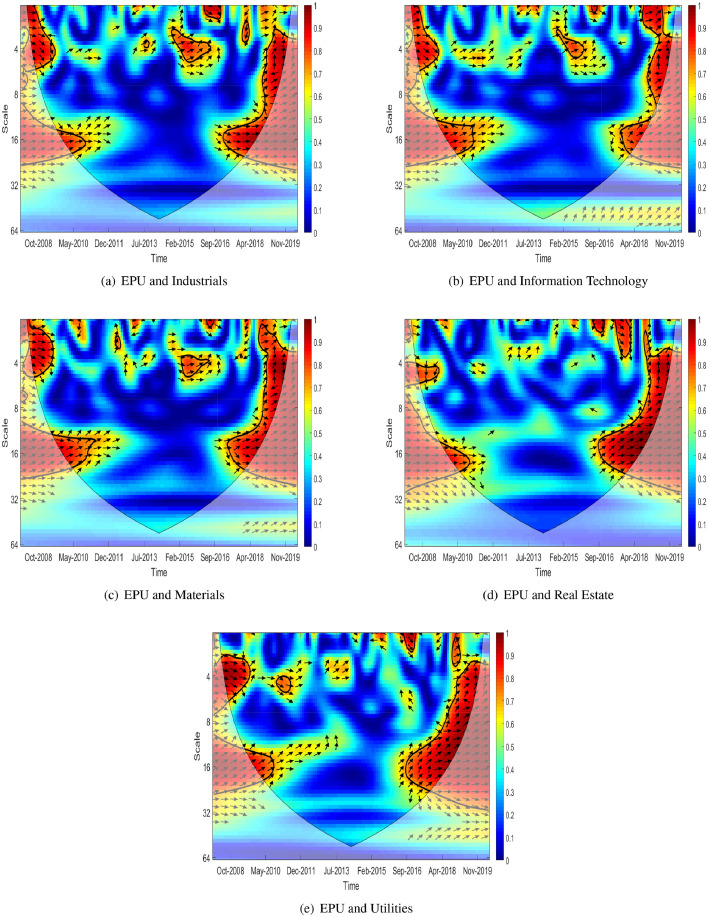
In this section, we present the wavelet coherency between EPU and monthly sector volatility for each sector to investigate the interdependence between them. We estimate the wavelet coherence of EPU and 11 sector volatility pairs and plot the results of wavelet coherence for each pair in Figs. 3.1 and 3.2 .

Fig. 3.1.

The wavelet coherence and phase plots between the EPU index and monthly volatility for six sectors(Communication Service, Consumer Discretionary, Consumer Staples, Energy, Financials, Health Care).

Fig. 3.2.

The wavelet coherence and phase plots between EPU index and monthly volatility for five sectors(Industrials, Information Technology, Materials, Real Estate, Utilities).

Figs. 3.1 and 3.2 present the estimated wavelet coherence and the relative phasing of two series represented by arrows. Time and frequency are presented on the horizontal (time period from January 2008 to May 2020) and the vertical axis, respectively. Frequency is limited to months. On the wavelet coherence plots, the black contour shows the 5% significance level, and regions with strong co-movements are represented by warmer colors (red), whereas colder colors (blue) represent regions with weak co-movements. The arrows provide the direction of interdependence and causality relationships (Torrence and Webster, 1999; Tiwari, 2013; Yang et al., 2017; Pal and Mitra, 2019; Jiang and Yoon, 2020). Arrows pointing to the right( → ) indicate that EPU and the sector volatility are positively correlated. Arrows pointing to the left( ← ) indicate that EPU and sector volatility are negatively correlated. The ↗ and ↙ arrows mean that EPU leads sector volatility, whereas the ↘ and ↖ arrows indicate that sector volatility leads EPU. The straight up(↑) and down(↓) arrows imply that the EPU is leading and lagging, respectively.

In the figures, the red area on the left and right of the wavelet coherence indicates strong interdependence, while the blue area is distributed in the central part. In other words, during the GFC and COVID-19 periods, the EPU and the sector monthly volatility have significant interconnection in all sectors. In times other than these two events, it is difficult to find a common strong interdependence between them in all sectors.

The red area during the GFC on the left is broken off in the middle, but the red area during the COVID-19 pandemic on the right is connected at the bottom (long-term) and top (short-term) for most sectors. That is, the significant interrelation between them occurs continuously from short- to long-term during the pandemic. Therefore, we can infer that the pandemic has a greater influence on all sectors than the GFC, since the former has a larger impact on sector volatility than the latter, as indicated by the fact that a significant area after November 2019 covers more timescales.

In both GFC and the COVID-19 pandemic around the 16 months scale (long-term), we observe the arrow points  →  and ↗ indicating that EPU and the sector volatility are positively correlated and EPU leads sector volatility, respectively. Noticeably, we observe that the arrow points straight up (↑) during the COVID-19 pandemic, while the arrow points  → , ↘, and ↓ are shown during the GFC for short-term scale bands(4-8 months). This implies that the economic policies generated by the spread of COVID-19 caused increased volatility in all industries, whereas some sector volatility lead the EPU during the GFC (See Fig. 3.1-(b),(f); Fig. 3.2-(b),(c)). As for the real estate industry, which has been blamed for the GFC (Forrest and Yip, 2011; Hui and Chan, 2014), the arrows point straight down, implying that ”Real Estate” sector volatility leads the EPU in the short-term during the GFC.

4. Concluding remarks

This study provides empirical evidence on the relationship between economic uncertainty due to the COVID-19 pandemic and the industrial sector with compared to the impact of GFC in the US. It covers 11 sectors of the S&P 500 index and the EPU proposed by Baker et al. (2016). Wavelet coherence analysis is used to estimate the interdependence and causality between the EPU and each sector’s volatility.

We draw the following conclusions. First, we find a high degree of interdependence between the EPU and all sector volatility for all timescales. We also find the degree is higher than that of GFC. Second, the phase patter indicates that EPU leads the sector volatility in all sectors, while the EPU lagged the sector volatility in some industries during the GFC.

The findings indicate that COVID-19 has had a substantial impact on all sectors of the US stock market. Furthermore, the influence of the pandemic on the industrial economy is larger than that of the GFC. Our study contributes a first insight on the impact of the COVID-19 pandemic on the industrial economy in the US. Nonetheless, since the pandemic is ongoing, more empirical research on its impact is needed when it finally ends.

CRediT authorship contribution statement

Sun-Yong Choi: Conceptualization, Methodology, Software, Data curation, Writing - original draft, Investigation, Writing - review & editing.

Appendix A. Supplementary materials

Supplementary Data S1

Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/