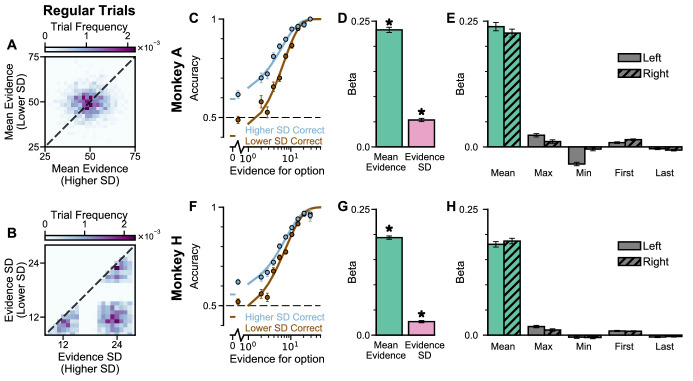
Figure 4. Subjects show a pro-variance bias in their choices on regular trials.
For these analyses, stimulus streams were divided into ‘Lower SD’ or ‘Higher SD’ options post-hoc, on a trial-wise basis. (A) On regular trials, the mean evidence of each stream was independent. (B) Each stream is sampled from either a narrow or a broad distribution, such that about 50% of the trials have one broad stream and one narrow stream, 25% of the trials have two broad streams, and 25% of the trials have two narrow streams. (C) Psychometric function when either the ‘Lower SD’ (brown) or ‘Higher SD’ (blue) stream is correct in the regular trials. (D) Regression analysis using the left-right differences of the mean and standard deviation of the stimuli evidence to predict left choice. The beta coefficients quantify the contribution of both statistics to the decision-making processes of the monkeys (Mean Evidence: t = 74.78, p<10−10; Evidence Standard Deviation: t = 19.65, p<10−10). Notably, a significantly positive evidence SD coefficient indicates the subjects preferred to choose options which were more variable across samples. Errorbars indicate the standard error.
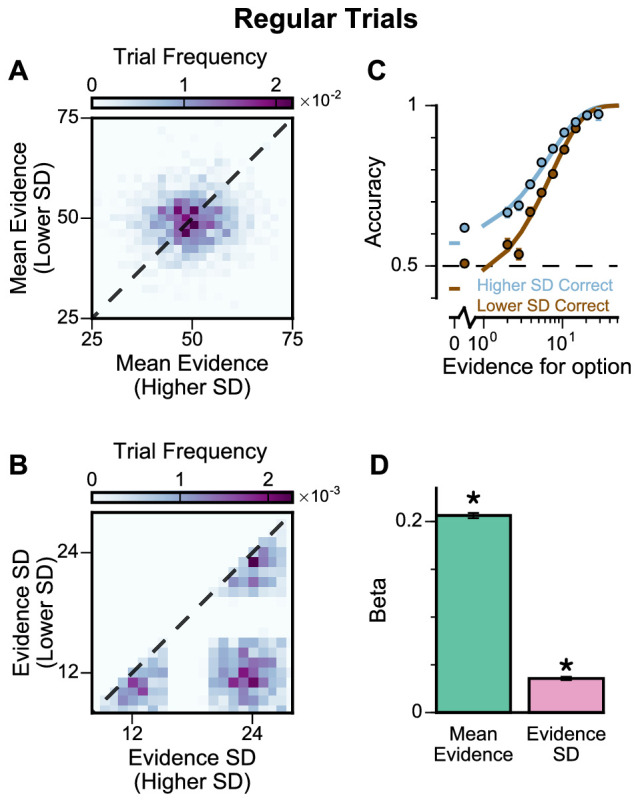
Figure 4—figure supplement 1. Extra information on Regular Trials, separated by subjects.
In the regular-trials, each of the two streams is randomly chosen to be either narrow (), or broad (), then divided into ‘Lower SD’ or ‘Higher SD’ options post-hoc, depending on the sampled standard deviation of evidence relative to the other option. (A) The distribution of the mean evidence of ‘Lower SD’ and ‘Higher SD’ streams, across all regular trials for both monkeys. (B) The distribution of the evidence variability of ‘Lower SD’ and ‘Higher SD’ streams, across all regular trials for both monkeys. (C) The psychometric function of Monkey A when either the ‘Lower SD’ (brown) or ‘Higher SD’ (blue) stream is correct. (D) A regression model using evidence mean and variability to predict the animals’ choices. Each regressor is the left-right difference of the mean and standard deviation of the evidence streams. This shows that both statistics are utilised by Monkey A to solve the task (Mean Evidence: t = 45.90, p < 10−10; Evidence Standard Deviation: t = 16.68, p < 10−10). (E) A regression model including the mean, maximum, minimum, first, and last evidence values of both the left and right streams as regressors, in order to evaluate the contribution of each quantity and the possibility that the monkey is utilising strategies alternative to evidence integration and pro-variance bias. Evidently, Monkey A mainly relies on temporal integration to solve the task, as indicated by a strong mean evidence coefficient in both regression models. See also Supplementary files 1, 2, 3 for cross-validation analysis comparing regression models including various combinations of these predictors. (F–H) Same as (C–E) but for Monkey H. The statistics of the regression model in (G) are (Mean Evidence: t = 58.88, p < 10−10; Evidence Standard Deviation: t = 12.08, p < 10−10). All errorbars indicate the standard error.
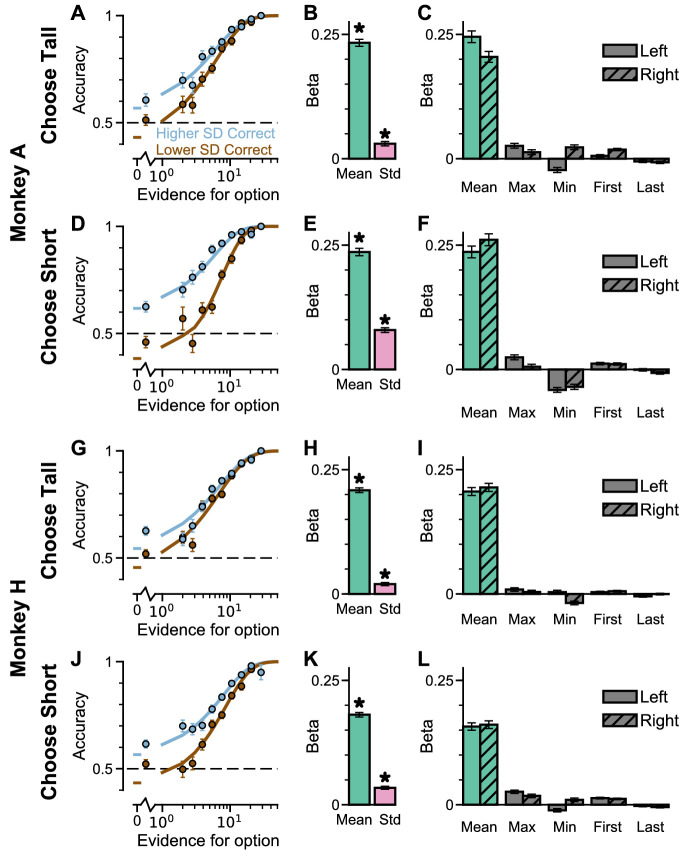
Figure 4—figure supplement 2. Extra information on Regular Trials, separated by ‘ChooseTall’ and ‘ChooseShort’ trials.
The findings are very similar on both trial types. (A) The psychometric function of Monkey A when either the ‘Lower SD’ (brown) or ‘Higher SD’ (blue) stream is correct, on ‘ChooseTall’ trials. (B) A regression model using evidence mean and variability to predict Monkey A’s choices on ‘ChooseTall’ trials. Each regressor is the left-right difference of the mean and standard deviation of the evidence streams. This shows that both statistics are utilised by Monkey A to solve the task (mean evidence: t(ChooseTall) = 32.78, p(ChooseTall)<10−10; evidence standard deviation: t(ChooseTall) = 6.81, p(ChooseTall)<10−10). (C) A regression model including the mean, maximum, minimum, first, and last evidence values of both the left and right streams as regressors, in order to evaluate the contribution of each quantity on choices on ‘ChooseTall’ trials and the possibility that Monkey A is utilising strategies alternative to evidence integration and pro-variance bias. Evidently, Monkey A mainly relies on temporal integration to solve the task, as indicated by a strong mean evidence coefficient in both regression models. (D) The psychometric function of Monkey A when either the ‘Lower SD’ (brown) or ‘Higher SD’ (blue) stream is correct, on ‘ChooseShort’ trials. (E) The same regression model as (B) applied to Monkey A’s choices on ‘ChooseShort’ trials (mean evidence: t(ChooseShort) = 32.09, p(ChooseShort)<10−10; evidence standard deviation: t(ChooseShort) = 16.47, p(ChooseShort)<10−10). (F) The same regression model as (C) applied to Monkey A’s choices on ‘ChooseShort’ trials. (G–L) Same as (A–F) but for Monkey H. The statistics of the regression model in (H) are (mean evidence: t(ChooseTall) = 42.76, p(ChooseTall)<10−10; evidence standard deviation: t(ChooseTall) = 6.19, p(ChooseTall)=5.92−10), and (K) are (mean evidence: t(ChooseShort) = 40.43, p(ChooseShort)<10−10; evidence standard deviation: t(ChooseShort) = 10.97, p(ChooseShort)<10−10). All errorbars indicate the standard error.
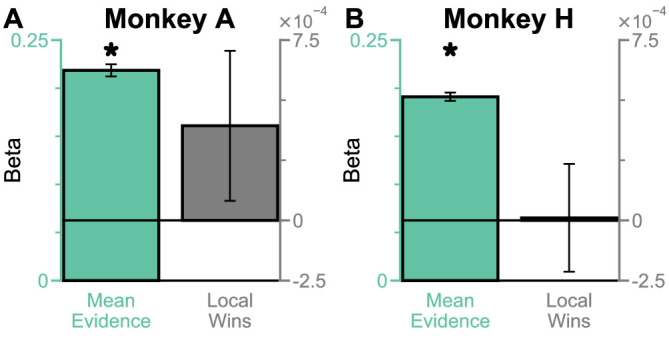
Figure 4—figure supplement 3. Extra information on Regular Trials – the subjects do not show a frequent winner bias.
(A) A regression model using evidence mean and the number of local winners to predict Monkey A’s choices. This shows that after controlling for mean evidence, Monkey A did not have a frequent winner bias (Mean Evidence: t = 34.86, p<10−10; Local Wins: t = 1.26, p=0.2068). (B) Same as (A) but for Monkey H. The statistics of the regression model in (B) are (Mean Evidence: t = 44.33, p<10−10; Local Wins: t = 0.048, p=0.9614). All errorbars indicate the standard error.