Abstract
The coronavirus disease (COVID-19) brought the world to a halt in March 2020. Various prediction and risk management approaches are being explored worldwide for decision making. This work adopts an advanced mechanistic model and utilizes tools for process safety to propose a framework for risk management for the current pandemic. A parameter tweaking and an artificial neural network-based parameter learning model have been developed for effective forecasting of the dynamic risk. Monte Carlo simulation was used to capture the randomness of the model parameters. A comparative analysis of the proposed methodologies has been carried out by using the susceptible, exposed, infected, quarantined, recovered, deceased (SEIQRD) model. A SEIQRD model was developed for four distinct locations: Italy, Germany, Ontario, and British Columbia. The learning-based approach resulted in better outcomes among the models tested in the present study. The layer of protection analysis is a useful framework to analyze the effect of different safety measures. This framework is used in this work to study the effect of non-pharmaceutical interventions on pandemic risk. The risk profiles suggest that a stage-wise releasing scenario is the most suitable approach with negligible resurgence. The case study provides valuable insights to practitioners in both the health sector and the process industries to implement advanced strategies for risk assessment and management. Both sectors can benefit from each other by using the mathematical models and the management tools used in each, and, more importantly, the lessons learned from crises.
Keywords: Risk, Process monitoring, Neural network, Pandemic, Non-pharmaceutical interventions, Layers of protection
Highlights
-
•
An advanced mechanistic model and process safety framework for risk management of the current pandemic.
-
•
An artificial neural network-based parameter learning model for effective forecasting of the dynamic risk.
-
•
Proposed susceptible, exposed, infected, quarantined, recovered, deceased (SEIQRD) model for forecasting of infections.
-
•
Insights to practitioners in health sector and the process industries for risk assessment and management.
1. Introduction
The coronavirus disease (COVID-19) has been declared a global pandemic by the World Health Organization (WHO). The high infection rate of the coronavirus and the unavailability of a vaccine have led to an unprecedented scenario. Countless numbers of people are deprived of proper medical care due to the saturation of health care facilities in many places. More than 28 million infected cases and over nine hundred thousand mortalities due to the outbreak have been reported to date (Worldometer, 2020, Sep 09).
In epidemiologic studies, mechanistic models have been widely used to forecast pandemics and their control. Kermack and McKendrick (1927) developed the SIR (susceptible, infected, recovered) model which was subsequently revised by (Anderson & May 1979; Hethcote, 1976; Hiorns and MacDonald, 1982). The SIR model assumes that the infected hosts instantaneously become infectious after being exposed to an infected carrier. However, infectious diseases typically have latency periods; incubation of the virus requires time before an infected agent truly becomes infectious. An additional exposed (E) stage was included to expand the SIR model to an improved SEIR (susceptible, exposed, infected, recovered) model. Many models with varying population size and distinct vaccination strategies towards susceptible individuals have been developed in the past (Busenberg and Driessche, 1990; Li et al., 1999; Martcheva and Castillo-Chavez, 2003; Sun and Hsieh, 2010). The basic SIR and SEIR models do not consider hospitalization and quarantine effects, which could reduce the overall number of infected people significantly. The impacts of quarantine, isolation, and other nonpharmaceutical interventions (NPIs) on the spread as well as control of infectious diseases have been studied by many authors such as Hethcote et al. (2002), Hollingsworth (2009) Lipsitch et al. (2003), and Safi and Gumel (2010). The basic and the modified SEIR models have been used to study the spread of many diseases: e.g., SARS , Influenza , Ebola , MERS , and Zika (Zhang et al., 2017).
Although process systems and epidemiology are very different fields, there are many similarities between the models used in each. Compartmental models have been in use in chemical processes for many systems; e.g., continuous stirred tank reactor, fluidized bed reactor, and bubble column for studying kinetics, velocity distribution, energy dissipation rate, crystal size distribution, and turbulence (Alvarado et al., 2012; Bermingham et al., 1998; Cui et al., 1996; Iliuta et al., 2007; Jourdan et al., 2019, Vrábel et al., 1999; Zhao et al., 2017; Word Health Organization, 2020). There is an especially strong resemblance between the epidemiological model(s) and the continuous stirred tank reactor (CSTR) kinetic model(s) used to predict the progress of the chemical reaction and product concentration. Table 1 presents similarities between the SIR epidemiological model and the reaction kinetics model in a CSTR. Nonetheless, social structure complexity, distinct individual practices, and economic disparity complicate epidemic modelling. Randomness in the parameters (e.g., incubation, infection and recovery periods) also makes epidemic modelling difficult compared to the reactor models. Demographics and chronic health conditions significantly affect the susceptibility in epidemic modelling.
Table 1.
Similarities between the epidemiological and reactor kinetics model.
| SIR epidemiological model | Reactor kinetic model | |
|---|---|---|
| System |
 Geographical Location |
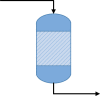 Chemical Reactor |
| Propagation/Reaction model | Series Reaction: Auto Catalytic Reaction: |
|
| Model equations |
|
Series Reaction Autocatalytic Reaction (in its simplest form) |
| Responses |  |
 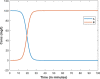
|
| Principles of conservation | Follows conservation principles; i.e., within a geographical area, the total number of people in all of the compartments remains constant. |
Follows the conservation of mass principles; i.e., the total mass of all of the species remains constant. |
| Rate of spread/transformations | The contagion rate is the determining factor for the states of the epidemic. It depends on the basic reproduction numbers of the epidemic, government regulations (e.g., limiting gathering size, closure of nonessential business and schools, emergency lockdown), and personal hygiene measures such as wearing masks in public places, frequent washing of hands, and social distancing. |
The reaction rate governs transformations in chemical reactions. Rates of chemical transformation are often affected by the rates of other processes such as heat or mass transfer, presence of a catalyst, and species concentration, dispersion, segregation, and mixing. |
Different NPIs are adopted by healthcare authorities to control the spread of a pandemic. The most notable NPIs include social distancing, frequent hand washing, use of masks, and practice of good hygiene. Numerous reports (Ferguson et al., 2020; Davies et al., 2020) show that implementation of these prevention factors significantly slows down the spread of a pandemic.
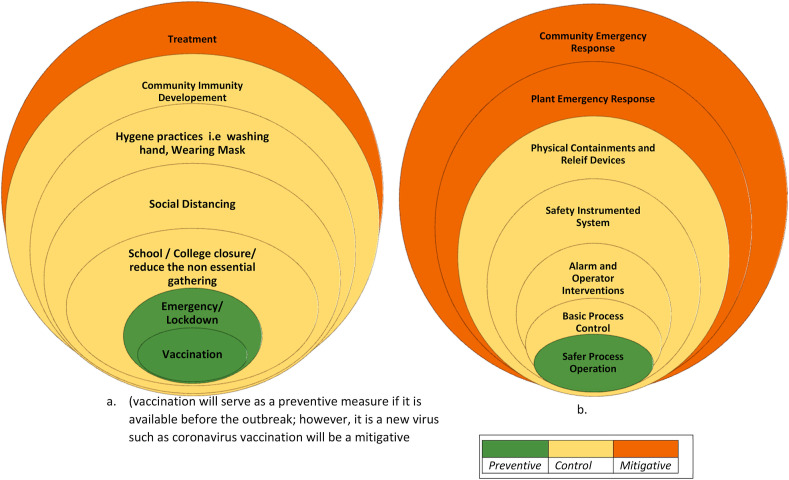
Similar to epidemiology, risk minimization is a primary goal in process industries (Khan and Abbasi, 1998). The methodology to prevent, control, and mitigate infection is analogous to the hazard control and safety frameworks used in the process industries. Over the years, different qualitative and quantitative safety management methods for the process industries have been proposed in the literature. The layer of protection analysis (LOPA) and inherently safer design (ISD) are two of the most promising risk assessment and management tools (Khan et al., 2015; Tugnoli et al., 2012). LOPA with inherent safety considerations provides better insights for decision making. Some earlier approaches to the use of LOPA for improving safety management are discussed in Dowell (1998). Gowland (2006) explained the principle of LOPA and its applicability for accidental risk assessment. An application of LOPA to estimate the risk due to reactive chemicals is presented in (Wei et al., 2008). An improved version of LOPA called ExSys-LOPA is proposed in (Markowski and Mannan, 2010). A review of inherent safety including the future scope for development is presented in (Khan and Amyotte, 2005, Marhavilas et al., 2011 Srinivasan & Natarajan, 2012). In the core of the LOPA framework, preventive measures are used to avoid a probable abnormal event. In the next layer, the control system is in place to counteract the event and slow down the escalation of the abnormalities. Following that is the emergency safety layer to restrain the impact when the control system fails to nullify the hazard. A comprehensive review of the existing literature on safety and risk is reported in (Khan et al., 2015).
One of the motivating factors for the current work is to link epidemic spread models with an engineering risk minimization framework. The other objective is to implement process safety principles in guiding pandemic risk management. We have proposed a layer of protection analysis (LOPA) for epidemic management. The performance of the safety management framework has been quantified in terms of the reduction of pandemic risk when safety layers are in effect.
We have proposed a parameter tweaking and an artificial neural network-based parameter learning method for computing the adaptive parameter of the susceptible, exposed, infected, quarantined, recovered, deceased (SEIQRD) model. The proposed hybrid SEIQRD model was employed for predicting the probability of fatalities and severity of consequences, thus enabling risk evaluation. It has also been used for calculating the risk in relaxing distinct intervention strategies. On the other hand, LOPA and inherent safety methods were used for risk management. By integrating the two approaches, a framework was developed for risk assessment and management of a pandemic, including mitigating, suppressing, and releasing factors.
The paper is organized as follows: Section 2 describes the mathematical models used to assess risk. Section 3 discusses the outcome of the risk calculations from the proposed models for different geographical locations. Section 3 also discusses the impact of the LOPA mitigation factors on risk. Finally, risk profiles for the releasing scenarios are presented. Section 4 gives the conclusion and future research directions.
2. The mathematical model
This section describes the different mathematical models to predict the spread of the epidemic risk. It begins by introducing the mechanistic model of the epidemic spread followed by the approaches of solving the model using the parameter tweaking and the ANN-based parameter learning models.
2.1. The SEIQRD epidemic model
Many studies reveal that people may be more contagious around the time of symptom onset than the diseased one (World Health Organization, 2020). Numerous reports highlighted that the pre-symptomatic (infectious before the symptom onset) and asymptomatic (does not develop symptom) are the major sources of the infections spread (Koo et al., 2020). According to an editorial published in the New England Journal of Medicine (NEJM), the asymptomatic spread of the virus is the "Achilles' heel of current strategies to control COVID-19" (Gandhi et al., 2020). The basic SIR and SIER models overpredict because they do not take into account the hospitalization and quarantine condition which severely reduces the overall spread of the infection. Thus, we have used the SEIQRD model in our simulation for capturing the transmission by the asymptomatic and pre-symptomatic cases.
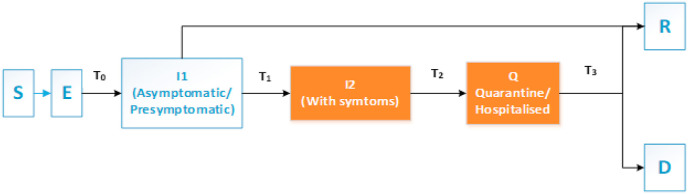
Fig. 1 presents an SEIQRD epidemic model where S, E, I, Q, R, and D represent the susceptible (S), exposed (E: infected but not yet infectious), infectious (I), quarantined or hospitalized (Q), recovered (R), and deceased (D). An additional compartment I2 (with retention period, T2 = 1 day) has been added to represent the new cases on a particular day. The host total population is N(t) = S(t)+E(t)+I1(t)+ I2(t)+Q(t)+R(t)+D(t) at time t. T0 represents the incubation period, the duration between the viral exposures, and becoming infectious. The average incubation period reported from distinct sources is 5–6 days; however, it may vary from 2 to 14 days (Aylward and Liang, 2020). In this period the virus does not have the potential to infect others. T1 denotes the infection period where a person is infectious but not symptomatic, whereas, T3 indicates the recovery period.
Fig. 1.
Schematic representation of the SEIQRD model.
The model is based on two assumptions: (i) Natural births as well as deaths due to other reasons during the study period are not considered in counting the total population, (ii) the recovered people are immune to further viral attack during the short span of analysis. The second assumption is clinically proven by many studies for various contagious viral attacks e.g., (Zhou et al., 2013); Short et al. (2018).
Eqs. (1), (2), (3), (4), (5), (6), (7)) present the mathematical formulations of the SEIQRD epidemic risk.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
is the fraction of the quarantined/hospitalized population resulting in mortality whereas, represents the fraction of the symptomatic infections. The contagion rate (a), infection rate (c), and the recovery rate (e) have been presented in Eqs. (8), (9), (10)).
| (8) |
| (9) |
| (10) |
In terms of the basic reproduction number, the rate of contagion could be presented by Eq. (11). The effective rate of contagion with the non-pharmaceutical interventions (NPI) could be given as Eq. (12),
| (11) |
| (12) |
where is the exposure factor. Its value changes with government regulations and individual practices.
The present model does not explicitly consider self-isolation of asymptomatic cases, contact tracing, and super-spreading events. These factors have been included implicitly using a lumped parameter approach. Also, the present work does not consider the distinct recovery time for mild cases and critical cases requiring ventilators and intensive care.
2.2. The approach to solving the model
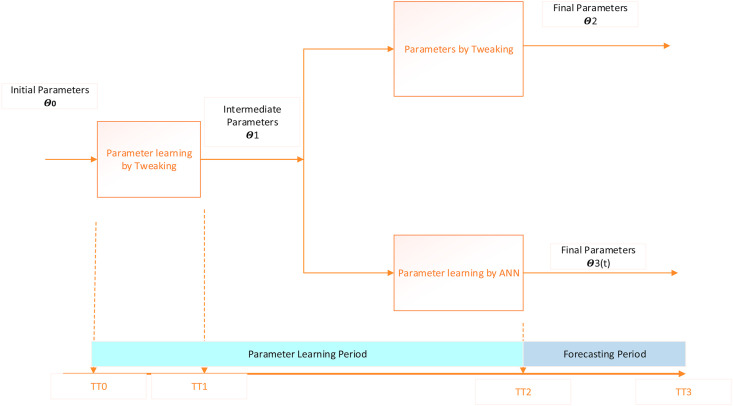
Fig. 2 presents the approaches for solving the SEIQRD epidemic model by parameter tweaking and parameter learning using the artificial neural network (ANN). TT0 is the time of the first death reported due to SARS-CoV-2. The data from TT0 to TT1 is used to determine the intermediate parameters by tweaking. We have taken 15 days between TT0 to TT1 assuming that the dynamics would be established in those 15 days. We are assuming that the incubation (b), the infection(c), and the recovery (e) parameters would almost settle during this period. The alterations in the contagion rate (a) due to the miscellaneous public safety regulations and the individual practices would be supervised between TT1 to TT2. The minor changes in other parameters would also be recorded. The manual parameter tweaking provides a better fit when done for one set of data applying a trial and error approach. This is time consuming and is not feasible for regular model updating as new data becomes available. The ANN does the calibration in a recursive manner, thus keeping the past parameter information. The ANN-based model calibration is a faster way of updating the model and can be used to calibrate the model on demand as new data becomes available.
Fig. 2.
Parameter learning of the SEIQRD model using parameter tweaking and ANN-based calibration.
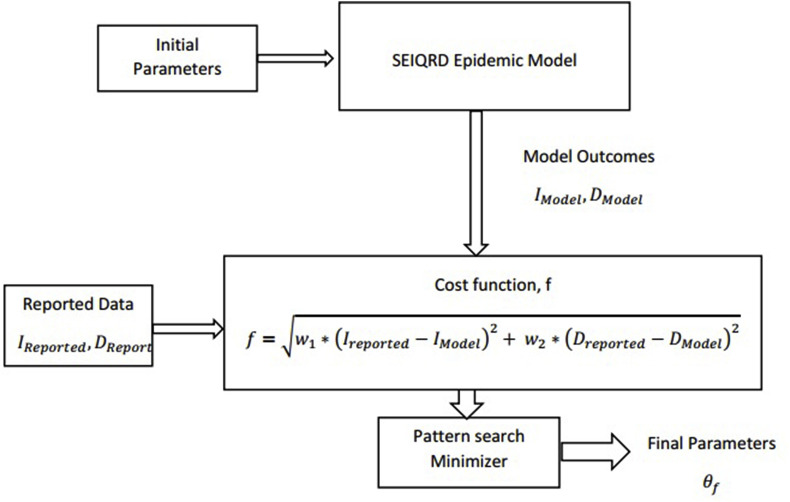
The schematic diagram of the parameter fitting has been illustrated in Fig. 3 . The parameters were initialized by the generic values given by the WHO-China joint mission report on COVID-19 (Aylward and Liang, 2020). The cost function of the minimization for determining the model parameters have been presented in Eq. (13). The mortality data is a more reliable measure for predicting the severity of an epidemic. However, the models based on the initial mortality data would not capture the surplus death caused due to the unavailability of the sophisticated treatment if the infection peak exceeds the availability of the appropriate healthcare system. The infection cases are subjected to under-reporting due to numerous reasons e.g., inferior surveillance and tracking system, poor testing policy, asymptomatic cases, and distinct immune systems. We have used both the mortality data and the new infection cases in the cost function for obtaining more robust parameters. A higher weight (w2 = 0.6–0.8) was assigned to the death data than the infection data (w1 = 0.2–0.4) assuming that the mortality data is more accurate.
| (13) |
Fig. 3.
Schematic Representation of the parameter fitting model.
3. Results and discussion
3.1. The case study
The models have been used to study the outbreak of the present pandemic caused by severe acute respiratory syndrome coronavirus (SARS-CoV-2). The virus was first identified in Wuhan, Hubei province of China in December 2019 (World Health Organization, 2020); the outbreak spread across the globe and WHO declared a global pandemic on March 11, 2020 (Kopecki et al., 2020).
The models were evaluated for forecasting the epidemic spread in four distinct places; Ontario, British Columbia, Italy, and Germany. British Columbia was one of the early affected provinces in Canada by COVID-19. Moreover, the province showed good governance in public health management which was reflected in the low number of per capita death in the province. Ontario is the most populous province in Canada with 14.66 million people representing 38.8% of the country's population (Ministry of Finance, Government of Ontario (2019)). Moreover, it is home to the country's most populous city, Toronto, and the capital city, Ottawa. Italy was the first western country to be affected by the virus and had to go through Europe's longest coronavirus lockdown. It has started returning to normal slowly by unwinding a few restrictions. Germany, one of the leading countries known for crisis management, was well prepared to restrain the risk of the coronavirus disease. Its robust response resulted in a much lower death rate compared to other western countries despite the higher number of infections.
The model has been calibrated using the pandemic data reported by John Hopkins University (Johns Hopkins University Center for Systems Science and Engineering, 2020). The distinct generic parameters used are listed in Table 2 . The average incubation period, infection period, and recovery period were 5.5, 5.1, and 11.5 days, respectively. The basic reproduction number for the COVID-19 by distinct sources has been presented in Table A1 (in the appendix). The basic reproduction number of 2.9, the median values of all the sources, has been used as the initial guess for the tweaking model.
Table 2.
Generic values of the model parameters.
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Incubation period (in days) | 5.1 | Recovery Period (in days) | 11.5 |
| Infection period (in days) | 5.5 | Basic reproduction number | 2.9 |
3.2. 2: model application in the forecasting of infections
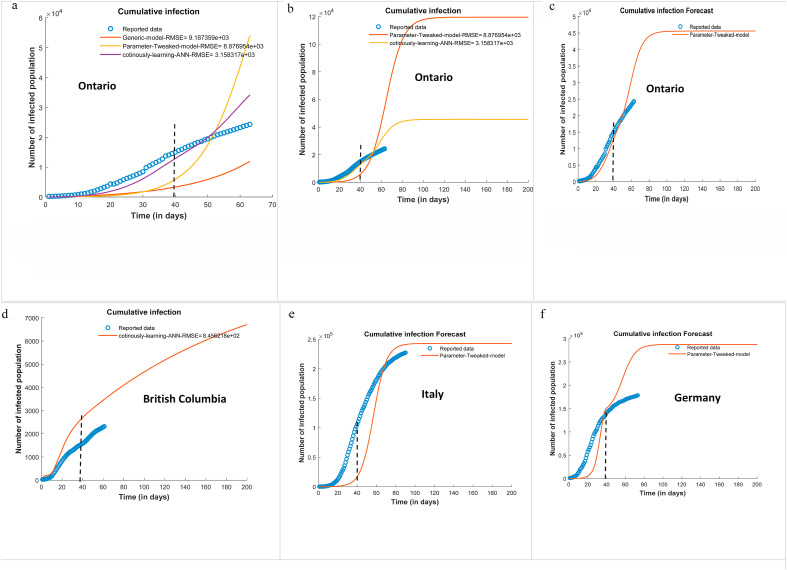
Fig. 4 presents the cumulative infections of selected regions. The models were trained up to T = 40 days and used for forecasting for the extended periods. The accuracy of distinct models is measured in terms of the root mean squared error (RMSE). The RMSE is a measure of the difference between the calculated and the observed values and is computed as . Fig. 4a depicts the forecast for Ontario by the generic model, the parameter tweak model, and the learning-based model. The RMSE values for the generic model, parameter tweek model and the continuously learning ANN- based model were found to 9.18 × 103, 8.87 × 103, and 3.15 × 103 respectively. It is observed that the generic model overpredicts the infections. A plausible reason for lower real infections could be due to social distancing and other intervention strategies already in effect during the period of study. The government enforced preventive measures such as limiting the number of people in a gathering, closure of non-essential businesses and schools, and emergency lockdown. The population is following the public advisory by maintaining social distancing, frequent hand washing, and practicing hygiene. As a result of all these, the true cases went down. This is captured by the tweaking and learning-based models. Other factors could be a lack of adequate testing, and asymptomatic infection which resulted in under-reporting of infected cases. The parameter tweaked model registers better performance compared to the generic model. However, the continuously learning ANN-based model yields the lowest RMSE among the test methods. This is due to the dynamic learning of the parameters in varying conditions.
Fig. 4.
Forecast of the infected population of COVID-19 at selected regions using the SEIQRD model (The dash line at T = 40 represent the training period of the models for the forecast of the extended period).
Fig. 4b and c present the comparative performance of the tweaking and the learning-based models. The tweaking model functions well in the training range, however, it shows poor performance in forecasting for an extended period. It may also be noticed that the learning-based methods more closely capture the dynamic variations in the parameters. Its outcomes are representing the reported data well. Similarly, the ANN based-learning model is effectively forecasting the cumulative infections of British Columbia (Fig. 4d), Italy (Fig. 4e), and Germany (Fig. 4f). It is plausible to realize a deviation of the model outcomes from the observed data if some other regulations that were not there during the training period. The performance will also be affected by the variation of individual or societal practices that were not well established during the training phase. It may be noticed that the model is slightly overpredicting for the cases of Germany. This might be due to the effect of their projects Pan-European Privacy-Preserving Proximity Tracing (PEPP-PT) and the Corona-Datenspende (Corona Data Donation) app for effective monitoring of COVID-19.
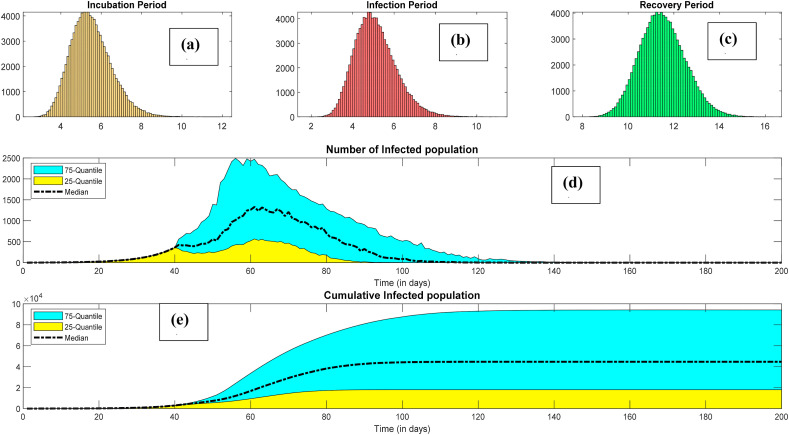
The models were also used for forecasting the infections considering random nature in the model parameters. We used the Monte Carlo simulations using the lognormal distributions of the incubation period, the infection period, and the recovery period to capture the long tail of the infection risk. Fig. 5 presents the infection forecasting considering the randomness of the model parameters. The distributions of the incubation period, the infection period, and the recovery period are presented in Fig. 5a, b, and Fig. 5c, respectively.
Fig. 5.
Predicting the infection risk considering randomness in the incubation, infection, and recovery periods (a) Incubation period, (b) infection period, (c) recovery period, (d) peak infection per day, (e) cumulative infection.
The infection per day (the new infections) grows moderately at the beginning, attain maximum, and then start descending. The peak of the infections per day is an important factor in developing treatment strategies for infected populations. It should not surpass the existing health care facility of the corresponding territory; otherwise, the fatality risk will be excessive. Prediction of the peak in advance is conducive to better preparation and effective mitigations. Distinct measures should be adopted to lower the peak, also known as flattening the epidemic curve, for restraining the pandemic. Fig. 5d presents the forecast for the peak of infection for Ontario. It can be inferred that the average value of the peak infection is around 1000 cases per day. The peaks of the infections were varying between 225 and 2500 within 25% and 75% quantiles. Similarly, the most probable value of the cumulative infection is 4.0 × 104. The maximum cumulative infection could go up to 8.0E+04 considering uncertainty in the parameters.
3.3. Model application in the management of the epidemic risk
The transmissibility of the epidemic is quantified by basic reproduction number (R0) which is defined as “the average number of secondary cases generated by a primary case in an entirely susceptible population” (Ferguson et al., 2005). The epidemic spreads for R0 > 1, and dies out if R0 < 1. The effective reproduction number can be reduced by three ways: i) reducing contact rates, ii) diminishing the infectiousness through isolation and treatment, and iii) reducing the susceptible population by vaccination (Ferguson et al., 2005).
Personal hygiene such as wearing a mask at public places, frequently washing hands and social distancing are crucial in restraining the spread of the infection risk. Government regulations and public practices play a crucial role in mitigating epidemic spread. Limiting gathering sizes, closure of nonessential business and schools, and emergency lockdown have a decisive role in controlling the epidemic spread (Davies et al., 2020; Ferguson et al., 2006). These regulations reduce the effective reproduction number by reducing the number of people exposed to an infected person. Restricting limits on gathering sizes reduces the possibility of super-spreading events (Anderson et al., 2020). The social distancing measure prevents the transmission from pre-symptomatic and asymptomatic cases. The vaccination is very effective in protecting from infectious diseases. However, several months are required to develop, produce, and distribute an effective vaccine following the outbreak of a novel pandemic strain (Germann et al., 2019). Thus, NPIs are essential for decreasing the peak demand for healthcare and reducing the overall mortality from the epidemic.
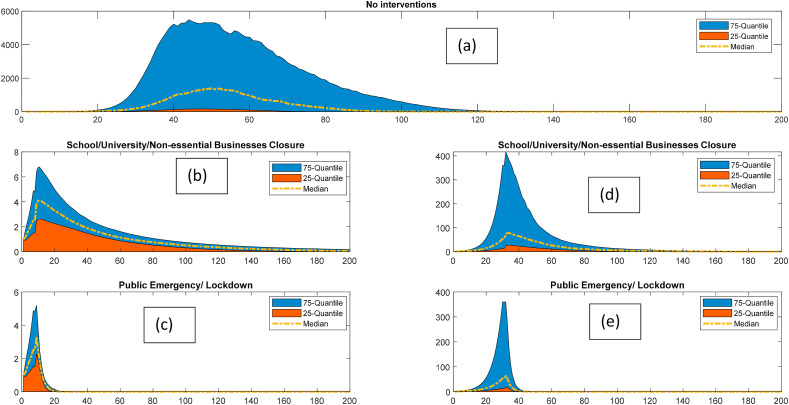
The predicted effects of interventions on the spread of the epidemic have been presented in Fig. 6 . Fig. 6a shows the impact of the pandemic if no measure is taken to restrict the outbreak. Fig. 6b and c respectively demonstrate the effect of the school and non-essential business closure and emergency lockdown after one week of the first mortality reported. Similarly, the effects of these interventions if implemented after one month of the first mortality, have been presented in Fig. 6d and e. The Monte Carlo simulation has been used for considering the uncertainties of the model parameters. We can observe that the median value of the peak infection could reach up to 3000 cases per day in case of no intervention. It could go up to 10,000 cases per day in worst-case scenario. The closure of schools and businesses and observing public emergency reduces the new cases to 6 per day as the most probable value. The lockdown results in rapid shrinkage of the epidemic compared to simply school and nonessential business closure. We can also deduce that delaying the interventions by a month leads to a several-fold increase in the peak of the infection.
Fig. 6.
Effect of interventions on controlling the epidemic risk; a: Without any intervention, b: School and non-essential business closure after one week of the first mortality), c: Enforcing public emergency/lockdown after one week of the first mortality d: School and non-essential business closure after one month of the first mortality), e: Enforcing public emergency/lockdown after one month of the first mortality.
The effect of the pandemic in terms of peak risk has been shown in Table 3 . It presents the risk estimated for different locations in terms of risk peak and the cumulative risk of infections. The risk can be defined as the product of the impact of the pandemic and the probability of the occurrence of the impact. In this SARS-CoV-2 pandemic, the impact is infections which could lead to mortality. We are studying the most probable value of infections as the potential impact of the COVID-19.
Table 3.
The risk of epidemic infections in selected regions (Risk of infection = Impact in terms of infections x probability of occurrence of the impact).
| Countries/ities | Parameters | No Measure | Interventions implemented after one week |
Intervention implemented after one month |
||
|---|---|---|---|---|---|---|
| School/Universities/non-essential business closure | With Public Emergency/Lockdown | School/Universities/non-essential business closure | With Public Emergency/Lockdown | |||
| Ontario | Peak Risk (Infections per day) | 1.39 × 103 | 3.00 × 10° | 3.00 × 10° | 4.30 × 101 | 3.90 × 101 |
| Cumulative Risk (Total Infections) | 4.26 × 104 | 1.22 × 102 | 2.00 × 101 | 2.07 × 103 | 5.64 × 102 | |
| British Columbia | Peak Risk (Infections per day) | 4.47 × 103 | 48.00 × 10° | 48.00 × 10° | 9.99 × 102 | 6.53 × 102 |
| Cumulative Risk (Total Infections) | 1.29 × 105 | 1.70 × 103 | 3.28 × 102 | 1.53 × 104 | 6.45 × 103 | |
| Italy | Peak Risk (Infections per day) | 8.62 × 105 | 9.53 × 104 | 4.00 × 10° | 4.55 × 105 | 1.20 × 101 |
| Cumulative Risk (Total Infections) | 1.18 × 107 | 3.66 × 106 | 7.60 × 101 | 8.08 × 106 | 2.70 × 102 | |
| Germany | Peak Risk (Infections per day) | 4.26 × 104 | 3.00 × 10° | 3.00 × 10° | 4.26 × 104 | 4.26 × 104 |
| Cumulative Risk (Total Infections) | 2.31 × 105 | 1.40 × 102 | 2.20 × 101 | 2.31 × 105 | 2.31 × 105 | |
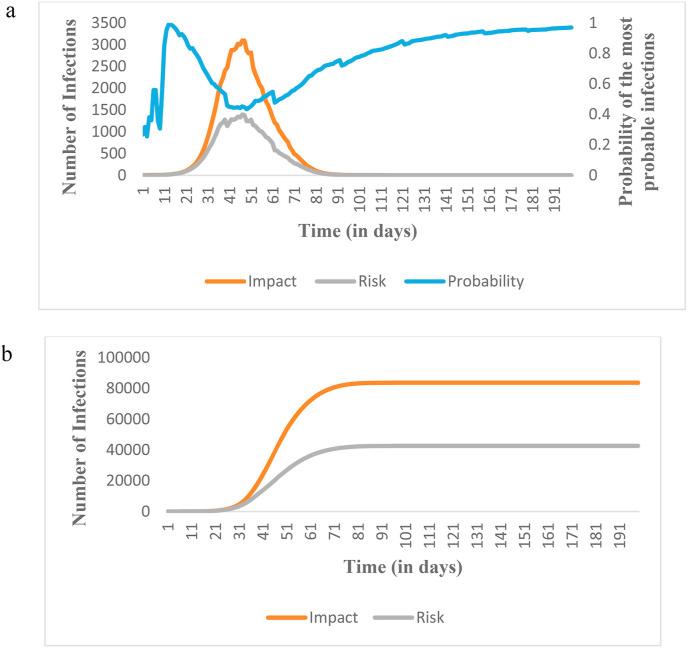
Monte Carlo simulation has been used for handling uncertainties in the number of infection cases due to the pandemic. The probability of occurrence of infection has been computed from the distribution of infections considering the randomness of the model parameters (i.e., the incubation period, infection period, and recovery period). The probability of the most probable value denotes the possibility of realization of the most probable number of infections for a given time. It has been calculated based on the distribution of impacts. For instance, the value of the most probable impact at T = 50 was found to be 2867 cases per day. The frequency of the most probable impact for T = 50 is 433 out of 1000 possible values resulting in the occurrence probability of the most probable impact of 0.433 (Thus the risk of infection at T = 50 will be 2867*0.433 = 1241 cases per day. The values of parameters of Fig. 7 a and b at other time steps have been computed in a similar way.
Fig. 7.
a: Variation of peak values of the number of infections in terms of the most probable impact and the calculated risk b: Variation of cumulative values of the number of infections in terms of the most probable impact and the calculated risk.
The peak risk (infections per day) and the cumulative risk (total infections) for Ontario when no measure is taken are 1.39 × 103 and 4.26 × 104, respectively. The risk will be reduced remarkably under non-pharmaceutical interventions. Lockdown is effective in quickly diminishing the risk of the pandemic. We can also notice that a delay in implementing intervention strategies significantly increases the risk. Table 3 shows the comparative outcomes of intervention strategies implemented after a week and a month from the first death reported. The peak risk increases from 3 to 43 (infections per day) while the cumulative risk escalates from 122 to 2.07 × 103 (total infections) in the case of a delay by a month in administering school/university and non-essential business closures. Similarly, an increase from 3 to 39 (infections per day) in peak risk and 22 to 5.64 × 102 (total infections) in cumulative risk is observed by a month-long delay in enforcing the lockdown. The marked escalation in the peak and the cumulative risk of the other locations could also be seen due to the delay in implementing the intervention strategies.
3.4. Model application in evaluating the risk in releasing scenarios
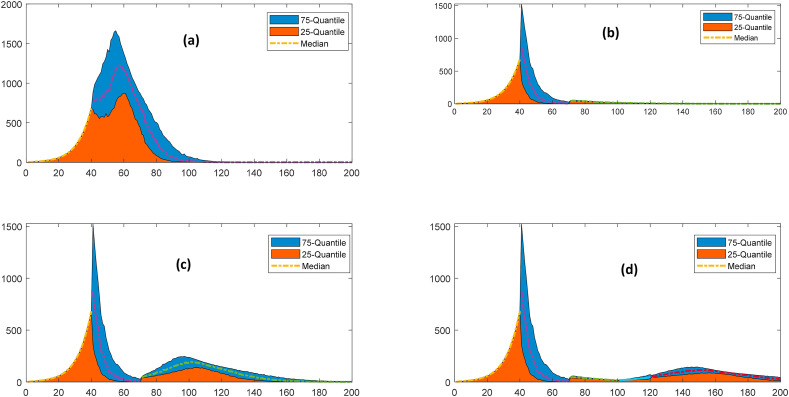
The lockdown and other government regulations have a severe economic impact. It is not viable to continue with these regulations for a prolonged duration. Thus, the enforcement and release of such regulations must be exercised judiciously to prevent the pandemic risk. The effect of relaxing the implemented interventions has been presented in Fig. 8 . The relaxing scenarios of opening school/university/non-essential business, and relaxing on social gatherings for returning to the normal state have been modeled for forecasting its impact on the overall system. The relaxing regulations on social gatherings comprise the opening of the parks, malls, bars, religious gatherings, recreation facilities, and all the sites of the interactions other than working sites. Fig. 8 depicts the comparative escalation in terms of the median values of the peak infections. It also presents the 25 and 75 quantile of the peak infections to capture the alteration due to the randomness in the model parameters. It is inferred that the release of the enforced regulations has the potential for a resurgence. The phase-wise relaxation of these regulations is most appropriate for preventing the resurgence of the pandemic risk. Relaxing regulations on social gathering at T = 70 could lead to a resurgence with the peak infection capacity of twice of that in the regulated scenario. However, the opening of schools/nonessential business and relaxing in social gatherings at T = 70 and T = 100, respectively, do not exhibit significant resurgence.
Fig. 8.
Effect of relaxing regulations on the impact of the pandemic, a: Existing scenario, b: Relaxing regulations on opening of school/university/non-essential business at T = 70, c: Relaxing regulations on social gatherings at T = 70, d: Phasewise relaxing regulations: school openings at T = 70 and social gatherings at T = 100.
3.5. Extending the concept to process safety management
The current pandemic situation and its prevention strategy can be interchangeably used for hazard identification and safety management of process facilities. Forecasting of the infection strategy stated above is applicable to identify a possible abnormal scenario. The risk-based safety management framework shown above illustrates the importance of safety management layers when an abnormal situation is triggered. The distinct strategies for handling the pandemic could be represented as the layer of protection analysis of a process system (Fig. 9 ). The processes are designed safer as a preventive strategy for reducing the risk. Different safety barriers such as basic process control, alarms, and operator interventions, safety instrumented system, relief devices, and physical containments are used as a control layer for abnormal situation management (Dowell, 1999; Willey, 2014). Finally, the plant and emergency response services are brought in operation to diminish the risk by deescalating the situation. These are analogous to the preventive, controlling, and mitigative strategies used for handling a pandemic. The hygienic practices (e.g. frequent hand washing, use of mask) and government regulations such as the closure of schools and non-essential business, limiting gathering sizes, enforcing lockdown, and vaccination are extremely effective as control and preventive strategies for limiting risk in the pandemic model. Plant and the community emergency responses are mitigative layers for industrial systems. These control measures are analogous to the treatment and medical care provided for reducing the impact of the pandemic.
Fig. 9.
Layer of protection analysis (LOPA) for epidemic and abnormal situation management in process systems; a. for epidemic management; b. for safety of a process system.
Results in Fig. 6b–e shows that effective control measures can reduce the risk of the spread of the pandemic. The results also demonstrate that early intervention of the preventive measures reduces the risk of pandemic significantly. Thus, protection layers should be put into place as soon as a hazard is identified.
We have also illustrated the impact of relaxing scenarios in Fig. 8 b-d. Releasing the different barriers causes the risk to rise. The time of the release of the barrier plays a crucial role. The risk reduces significantly when a barrier is released after the peak of the occurrence. Similarly, risk-based analysis of safety barriers could be feasible in process systems to determine how long a critical control layer should be enforced, and when it needs to be released.
The COVID-19 pandemic is a disastrous event that is affecting billions of lives and causing adverse economic impact. World Bank economic reports indicate that a severe pandemic could reduce world gross domestic product (GDP) drastically (World Bank, 2020). Nonetheless, it provided many learning opportunities to policymakers and process safety practitioners. Some of those lessons are as follows:
Early fault detection vs early case detection:
The early warning system for hazard identification is central to the abnormal situation management. A delay in detection would lead to delay in control actions which will escalate the risk resulting from abnormal situations. For instance, a delay of just a few days in releasing genetic sequences can be critical in an outbreak. Experts believe that the risk would have been reduced dramatically if the outbreak was detected earlier. This is equally applicable to a process system where early detection of a fault reduces the risk of the potential loss.
3.6. Identification of effective control mechanism
The identification of distinct control strategies is conducive to restrain abnormal situations. The restrictive measures e.g., social distancing, case detection, isolation, contact tracing, quarantine of exposed cases, and lockdown turns out to be effective strategies for restricting the spread of the COVID-19. Good hygiene practices such as frequent hand washing, wearing a mask at public places, and physical distancing are also very effective in flattening the curve and reducing the economic burden. Thus identification of an effective control mechanism plays a pivotal role in minimizing the effect of an abnormal situation.
3.7. The fast response of public health vs operator response
We can also deduce that the delay in the intervention strategies significantly increases the risk. We have analyzed the catastrophic effect of the delay in the implementation of selected intervention strategies in our model. We found a manifold increase in the peak and the cumulative risk of infection due to the delay of a month in implementing the intervention strategies. The real-world data from the COVID-19 also substantiate our findings. For instance, the immediate response by the government of Taiwan, for handling people arriving from Wuhan was instrumental to reduced risk in Taiwan. The findings uphold the importance of the operator's response to an abnormal situation. As a delay to respond to a fault can cause a detrimental consequence, prompt action from the operator is vital to ensure the safety of processing facilities.
3.8. Effective resource allocation and mobilization
Resource allocation decisions were critical segments of handling the COVID-19. The mobilization of resources in administering social distancing by school closures, limiting gathering sizes, providing efficient quarantine centers was of utmost importance in fighting the present pandemic. We had to properly allocate ventilators or intensive care beds in case of limited availability. We also experienced that many doctors, nurses, and health-workers fell victim to the pandemic. Thus, we can pledge for the exclusive treatment for healthcare workers, technicians, and security personnel who risk their lives as front liners (Khoo and Lantos, 2020). Equivalently, we can identify and provide maintenance to the pivotal elements of the process safety systems.
3.9. Use of advanced technologies
The use of advanced technology was helpful at all levels of containment. South Korea credited its use of advanced technology to uncover clusters of cases that would otherwise have gone undetected. Drones equipped with cameras hovering over parts of the Indian neighborhoods warning residents they are under surveillance turned out to be advantageous in enforcing effective lockdown. Artificial intelligence is being tested for identifying the disease by recognizing patterns in the ultrasonic images. The AI could also be useful in understanding the virus and accelerating medical research on vaccine-development and treatments. The advanced data mining tools can uncover the virus's history, transmission, diagnostics, management measures, and extracting features for combating future epidemics. Virtual assistants and chatbots have been deployed to support healthcare systems in many countries such as Canada, France, Finland, Italy, Germany, and the United States. Thus, advanced technologies can be harnessed for reducing risk and abnormal situation management in process systems.
3.10. Identification of the most vulnerable element
The COVID-19 also revealed that some people are most likely to be the hardest hit by the current pandemic. The most vulnerable and high-risk group include: an older adult, suffering from the underlying medical conditions (e.g. heart disease, hypertension, diabetes, chronic respiratory diseases, cancer), and having compromised immune system from a medical condition or treatment (e.g. chemotherapy). We provided extra care for the vulnerable population for reducing the risk. We can identify and develop effective strategies and action plans for vulnerable elements for reducing risk in process systems.
3.11. New opportunities, scale-up, and resiliency of the existing systems
The COVID-19 highlighted scaling-up requirements of health systems to expand services to accommodate rapid increases in demand. We also experienced numerous innovative initiatives during the COVID-19 pandemic. Many companies that don't regularly do the business of medical products, started producing hand sanitizer, ventilators, or personnel protection equipment (PPEs). Many businesses, schools, universities, and other organizations demonstrated resiliency by continuing their operations by quickly adopting the new normal. They widen the virtual private network (VPN) to allow all employees to work remotely; brought changes in the existing system by the necessary modification such as adding physical barriers at the help desk and cash counters; moving to online portals for meeting and instructions.
3.12. Good governance and trust building
The COVID-19 made us realize the importance of trust-building and effective governance in fighting with a catastrophe. The distinct government regulations are prone to create clashes between states and citizens, eroding state capacity, driving population displacement, and heightening social tension and discrimination. The clashes have the potential to escalate the abnormal situation to a catastrophe. The safe operation of process systems depends on the smooth functioning of equipment, operators, and managerial systems. An effective management system improves health and safety at work by optimizing the interaction of humans with their technical and social environment through proper policies, procedures, training, and supervision.
3.13. Application of expertise from similar outbreaks in past vs use of historical process data
Operators use their experience to detect, diagnose, and take mitigating action for controlling abnormal situations in process systems. In addition to this, the data based fault detection and diagnosis methods are trained based on historical fault data and expert opinion. Despite the different outcomes of epidemic disease, the expertise from past outbreaks could be conducive in credible estimation of the trajectory and slowing down the spread by implementing effective measures (Goudarzi, 2020, March 23). The social distancing measures, communication, and international cooperation, the most effective methods to slow COVID-19, were adopted by experience from the 1918 influenza pandemic and 2002–2003 SARS outbreak. The expertise from the past outbreaks e.g., the 2003 severe acute respiratory syndrome (SARS) outbreak in Singapore, and experience with 2015 Middle East respiratory syndrome (MERS) outbreak of South Korea led to an immediate fruitful response to the COVID-19. Their approach in combating COVID-19 was praised as a “the gold standard” response (Firth, 2020, March 05).
Pandemics do not remain geographically confined in contrast to other natural disasters (Jamison et al., 2017). A holistic approach with strong ethical and sensible measures is required for combating the epidemic spread (Institute of Medicine, 2007). We have to be prompt in all facets of the transmission; adequate testing facilities, active surveillance, enforcing intervention strategies, and community screening around the cluster areas. The extensive support and public endorsement can be asserted by effectively communicating the preparedness and response strategies. Research findings should be disseminated in the form of actionable points such as checklists (Khalid, 2020, March 03). The migration and other cross-border entries pose the risk of further spreading an outbreak; it must be handled effectively. All the aforementioned ideas could potentially be employed for upgrading the safety of process systems.
4. Conclusions
In the current work, a data-driven semi-mechanistic SEIQRD model was used to develop a risk management framework to forecast the spread of COVID-19 pandemic. ANN-based learning was used to evaluate the adaptive parameters of the model. The model was used to predict the number of infected and deaths for different safety barrier implementation and releasing scenario. Pandemic data from four different geographical locations were used to demonstrate the efficacy of the presented framework. The proposed models were able to forecast the propagation of the pandemic at an early stage. The risk was evaluated after implementing and relaxing different safety barriers. The results show that the implementation of nonpharmaceutical interventions has a profound impact on reducing the risk. The time of the enforcement and relaxing of NPIs also play a crucial role in restraining the epidemic risk. The NPIs will not be fruitful if the implementation delayed. It also will not be effective if relaxing it too early. The risk of pandemic increases significantly if the protection layer is released before or at the peak of spreading.
The proposed risk-based method has many similarities with process facilities for hazard identification and safety management. Hazard is analogous to the spread of a pandemic. In the current work, the implementation of the LOPA framework for managing public health safety and risk was also studied. A risk-based analysis was performed for three different scenarios: (i) no protection layer added (ii) early enforcement of protection layer (iii) delayed enforcement of protection layer. Early enforcement of a protection layer is crucial to keep the risk significantly lower. The proposed study suggests that the enforcement and relaxing of the protection layer should precisely be executed based on reliable forecasting of the model.
The model performs well when calibrated for specific regions using local data and information such as population, demographics, interaction patterns, enforced regulations, and other dynamics. The proposed SEIQRD model can be further improved. The present model does not explicitly consider contact tracing and super-spreading events. These factors have been included implicitly using a lumped parameter approach. Also, the present work does not consider the distinct recovery time for mild cases and critical cases requiring ventilators and intensive care. The model could also be improved by dividing populations based on demographics, special dispersion, and interaction patterns. The effects of a distinct degree of social distancing and the use of masks could be analyzed. Finally, the model could be used in trade-off studies for balancing economic aspects and acceptable risk when enforcing and relaxing regulations.
Authorship statement
Md Alauddin: Formal Analysis, Methodology, Software; Investigation, Validation; Writing - Original Draft; Writing - Review & Editing. Md Aminul Islam Khan: Formal Analysis, Software; Investigation; Validation; Writing - Original Draft; Writing - Review & Editing. Faisal Khan: Conceptualization, Methodology, Writing - Review & Editing; Supervision; Project administration; Funding acquisition. Salim Ahmed: Methodology, Validation; Formal Analysis; Writing - Review & Editing; Supervision; Funding acquisition. Syed Imtiaz: Methodology, Validation; Formal Analysis; Writing - Review & Editing; Supervision; Funding acquisition. Paul Amyotte: Methodology, Validation; Formal Analysis; Writing - Review & Editing; Funding acquisition.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgement
The authors thankfully acknowledge the financial support provided by the Natural Science and Engineering Council of Canada (NSERC) through Alliance Grant and the Canada Research Chair (Tier I) Program in Offshore Safety and Risk Engineering.
Appendix.
Table A1.
Basic reproduction numbers from distinct studies (adapted from (Liu et al., 2020))
| Study | Location Study | Study date Methods | Methods Approaches | Approaches | R0 estimates (average) | 95% CI |
|---|---|---|---|---|---|---|
| Joseph et al.1 | Wuhan | 31 December 2019–28 January 2020 | Stochastic Markov Chain Monte Carlo methods (MCMC) | MCMC methods with Gibbs sampling and non-informative flat prior, using posterior distribution | 2.68 | 2.47–2.86 |
| Shen et al.2 | Hubei province | 12–22 January 2020 | Mathematical model, dynamic compartmental model with population divided into five compartments: susceptible individuals, asymptomatic individuals during the incubation period, infectious individuals with symptoms, isolated individuals with treatment and recovered individuals | R0 = β/α β = mean person-to-person transmission rate/day in the absence of control interventions, using nonlinear least squares method to get its point estimate α = isolation rate = 6 | 6.49 | 6.31–6.66 |
| Liu et al. | China and overseas | January 23, 2020 Statistical | Statistical exponential Growth, using SARS generation time = 8.4 days, SD = 3.8 days | Applies Poisson regression to fit the exponential growth rate R0 = 1/M(−r) M = moment generating function of the generation time distribution r = fitted exponential growth rate | 2.90 | 2.32–3.63 |
| Liu et al. | China and overseas | January 23, 2020 Statistical | Statistical maximum likelihood estimation, using SARS generation time = 8.4 days, SD = 3.8 days | Maximize log-likelihood to estimate R0 by using surveillance data during a disease epidemic, and assuming the secondary case is Poisson distribution with expected value R0 | 2.92 | 2.28–3.67 |
| Read et al. | China | 1–22 January 2020 | Mathematical transmission model assuming latent period = 4 days and near to the incubation period | Assumes daily time increments with Poisson-distribution and apply a deterministic SEIR metapopulation transmission model, transmission rate = 1.94, infectious period = 1.61 days | 3.11 | 2.39–4.13 |
| Majumder et al. | Wuhan | December 8, 2019 and January 26, 2020 | Mathematical Incidence Decay and Exponential Adjustment (IDEA) model | Adopted mean serial interval lengths from SARS and MERS ranging from 6 to 10 days to fit the IDEA model, | 2.55 | 2.0–3.1 |
| WHO | China | January 18, 2020 | 1.95 | 1.4–2.5 | ||
| Cao et al. | China | January 23, 2020 | Mathematical model including compartments Susceptible-Exposed-Infectious- Recovered-Death-Cumulative (SEIRDC) |
R = K 2 (L × D) + K (L + D)+1 L = average latent period = 7, D = average latent infectious period = 9, K = logarithmic growth rate of the case count | 4.08 | |
| Zao et al. | China | 10–24 January 2020 | Statistical exponential growth model method adopting serial interval from SARS (mean = 8.4 days, SD = 3.8 days) and MERS (mean = 7.6 days, SD = 3.4 days) | Corresponding to 8-fold increase in the reporting rate R0 = 1/M(−r) r = intrinsic growth rate M = moment generating function | 2.24 | 1.96–2.55 |
| Zhao et al. | China | 10–24 January 2020 | Statistical exponential growth model method adopting serial interval from SARS (mean = 8.4 days, SD = 3.8 days) and MERS (mean = 7.6 days, SD = 3.4 days) | Corresponding to 2-fold increase in the reporting rate R0 = 1/M(−r) r = intrinsic growth rate M = moment generating function | 3.58 | 2.89–4.39 |
| Imai (2020) | Wuhan | January 18, 2020 | Mathematical model, computational modelling of potential epidemic trajectories | Assume SARS-like levels of case-to-case variability in the numbers of secondary cases and a SARS-like generation time with 8.4 days, and set number of cases caused by zoonotic exposure and assumed total number of cases to estimate R0 values for best-case, median and worst-case | 2.5 | 1.5–3.5 |
| Julien and Althaus | China and overseas | January 18, 2020 | Stochastic simulations of early outbreak trajectories Tang |
Stochastic simulations of early outbreak trajectories were performed that are consistent with the epidemiological findings to date | 2.2 | |
| Tang et al. | China | January 22, 2020 | Mathematical SEIR-type epidemiological model incorporates appropriate compartments corresponding to interventions | Method-based method and Likelihood-based method | 6.47 | 5.71–7.23 |
| Qun Li et al.11 | China | January 22, 2020 | Statistical exponential growth model | Mean incubation period = 5.2 days, mean serial interval = 7.5 days | 2.2 | 1.4–3.9 |
| Steven et al. | China (CDC) | Realistic distributions for the latent and infectious period to calculate R0 | 5.7 | 3.8–8.9 |
Average R0 = 3.4 Median R0 = 2.9.
References
- Alvarado A., Vedantam S., Goethals P., Nopens I. A compartmental model to describe hydraulics in a full-scale waste stabilization pond. Water Res. 2012;46(2):521–530. doi: 10.1016/j.watres.2011.11.038. [DOI] [PubMed] [Google Scholar]
- Anderson R.M., May R.M. Population biology of infectious diseases: Part I. Nature. 1979;280:361–367. doi: 10.1038/280361a0. [DOI] [PubMed] [Google Scholar]
- Anderson R.M., Heesterbeek H., Klinkenberg D., Hollingsworth T.D. How will country-based mitigation measures influence the course of the COVID-19 epidemic? Lancet. 2020;395(10228):931–934. doi: 10.1016/S0140-6736(20)30567-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aylward Bruce, (WHO) Liang W., (PRC) 2020. Report of the WHO-China Joint Mission on Coronavirus Disease 2019 (COVID-19). The WHO-China Joint Mission on Coronavirus Disease 2019, 2019(February), 16–24. Retrieved from.https://www.who.int/docs/default-source/coronaviruse/who-china-joint-mission-on-covid-19-final-report.pdf [Google Scholar]
- Bermingham S.K., Kramer H.J.M., van Rosmalen G.M. Towards on-scale crystalliser design using compartmental models. Comput. Chem. Eng. 1998;22(Suppl. 1):S355–S362. doi: 10.1016/S0098-1354(98)00075-1. [DOI] [Google Scholar]
- Busenberg S., Driessche P. Analysis of a disease transmission model in a population with varying size. J. Math. Biol. 1990 doi: 10.1007/BF00178776. [DOI] [PubMed] [Google Scholar]
- Cui Y.Q., Van Der Lans R.G.J.M., Noorman H.J., Luyben K.C.A.M. Compartment mixing model for stirred reactors with multiple impellers. Chem. Eng. Res. Des. 1996;74(2):261–271. [Google Scholar]
- Davies N.G., Kucharski A.J., Eggo R.M., Gimma A., Nightingale E.S., Quilty B.J. The effect of non-pharmaceutical interventions on COVID-19 cases , deaths and demand for hospital services in the UK : a modelling study. Cmmid. 2020:1–25. doi: 10.1016/S2468-2667(20)30133-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dowell A.M. Layer of protection analysis for determining safety integrity level. 1998;37:155–165. [Google Scholar]
- Dowell A.M. Layer of protection analysis and inherently safer processes. Process Saf. Prog. 1999;18(4):214–220. doi: 10.1002/prs.680180409. [DOI] [Google Scholar]
- Ferguson N.M., Cummings D.A.T., Cauchemez S., Fraser C., Riley S., Meeyai A. vol. 437. 2005. pp. 209–214. (Strategies for Containing an Emerging Influenza Pandemic in Southeast Asia). September. [DOI] [PubMed] [Google Scholar]
- Ferguson N.M., Cummings D.A.T., Fraser C., Cajka J.C., Cooley P.C., Burke D.S. vol. 442. 2006. (Strategies for Mitigating an Influenza Pandemic). July. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferguson N.M., Laydon D., Nedjati-gilani G., Imai N., Ainslie K., Baguelin M. 2020. Impact of Non-pharmaceutical Interventions ( NPIs ) to Reduce COVID- 19 Mortality and Healthcare Demand. (March) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Firth S. March 05). Singapore: the model for COVID-19 response? MedPage Today. 2020 https://www.medpagetoday.com/infectiousdisease/covid19/85254 [Google Scholar]
- Gandhi M., Yokoe D.S., Havlir D.V. Asymptomatic transmission, the achilles' heel of current strategies to control covid-19. N. Engl. J. Med. 2020 doi: 10.1056/nejme2009758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Germann T.C., Gao H., Gambhir M., Plummer A., Biggerstaff M., Reed C., Uzicanin A. School dismissal as a pandemic influenza response : when , where and for how long ? Epidemics. 2019;28(June):100348. doi: 10.1016/j.epidem.2019.100348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goudarzi S. Scientific American; 2020. March 23). Lessons from Past Outbreaks Could Help Fight the Coronavirus Pandemic.https://www.scientificamerican.com/article/lessons-from-past-outbreaks-could-help-fight-the-coronavirus-pandemic1/ [Google Scholar]
- Gowland R. The accidental risk assessment methodology for industries ( ARAMIS )/layer of protection analysis ( LOPA ) methodology : a step forward towards convergent practices in risk assessment ? 2006. 130, 307, 310. [DOI] [PubMed]
- Hethcote H.W. Qualitative analyses of communicable disease models. Math. Biosci. 1976 doi: 10.1016/0025-5564(76)90132-2. [DOI] [Google Scholar]
- Hethcote H., Zhien M., Shengbing L. Effects of quarantine in six endemic models for infectious diseases. Math. Biosci. 2002 doi: 10.1016/S0025-5564(02)00111-6. [DOI] [PubMed] [Google Scholar]
- Hiorns R.W., MacDonald N. Time lags in biological models. J. Roy. Stat. Soc. 1982 doi: 10.2307/2981435. [DOI] [Google Scholar]
- Hollingsworth T.D. Controlling infectious disease outbreaks: lessons from mathematical modelling. J. Publ. Health Pol. 2009 doi: 10.1057/jphp.2009.13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johns Hopkins University Center for Systems Science and Engineering 2020. https://github.com/CSSEGISandData/COVID-19/blob/master/README.md [DOI] [PMC free article] [PubMed]
- Iliuta I., Larachi F., Anfray J., Dromard N., Schweich D. Multicomponent multicompartment model for Fischer-Tropsch SCBR. AIChE J. 2007;53(8):2062–2083. doi: 10.1002/aic.11242. [DOI] [Google Scholar]
- Institute of Medicine . National Academies Press; Washington, D.C.: 2007. Ethical and Legal Considerations in Mitigating Pandemic Disease. [DOI] [PubMed] [Google Scholar]
- Jamison D.T., Gelband H., Horton S., Jha P., Laxminarayan R., Mock C.N., Nugent R., editors. third ed. Volume 9. Improving Health and Reducing Poverty. The World Bank; 2017. (Improving Health and Reducing Poverty. Disease Control Priorities). Disease Control Priorities. [DOI] [PubMed] [Google Scholar]
- Jourdan N., Neveux T., Potier O., Kanniche M., Wicks J., Nopens I. Compartmental Modelling in chemical engineering: a critical review. Chem. Eng. Sci. 2019;210:115196. doi: 10.1016/j.ces.2019.115196. [DOI] [Google Scholar]
- Kermack W.O., McKendrick A. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. - Ser. A Contain. Pap. a Math. Phys. Character. 1927;115(772):700–721. doi: 10.1098/rspa.1927.0118. [DOI] [Google Scholar]
- Khalid A.F. March 03). Coronavirus: 5 ways to put evidence into action during outbreaks like COVID-19. The Conversation. 2020 https://theconversation.com/coronavirus-5-ways-to-put-evidence-into-action-during-outbreaks-like-covid-19-131746 [Google Scholar]
- Khan F.I., Abbasi S.A. Techniques and methodologies for risk analysis in chemical process industries. 1998;11:261–277. [Google Scholar]
- Khan F.I., Amyotte P.R. vol. 18. 2005. pp. 310–326. (I2SI : A Comprehensive Quantitative Tool for Inherent Safety and Cost Evaluation). [DOI] [Google Scholar]
- Khan F., Rathnayaka S., Ahmed S. Methods and models in process safety and risk management: past, present and future. Process Saf. Environ. Protect. 2015;98:116–147. doi: 10.1016/j.psep.2015.07.005. [DOI] [Google Scholar]
- Khoo E.J., Lantos J.D. Lessons learned from the COVID‐19 pandemic. Acta Paediatr. 2020;109(7):1323–1325. doi: 10.1111/apa.15307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koo J.R., Cook A.R., Park M., Sun Y., Sun H., Lim J.T. The Lancet Infectious Diseases. 2020. Interventions to mitigate early spread of SARS-CoV-2 in Singapore: a modelling study. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lovelace J.B., Kopecki D., Feuer W., Higgins-Dunn N., H. CNBC; 2020. March 11). World Health Organization Declares the Coronavirus Outbreak a Global Pandemic.https://www.cnbc.com/2020/03/11/who-declares-the-coronavirus-outbreak-a-global-pandemic.html [Google Scholar]
- Li M.Y., Graef J.R., Wang L., Karsai J. Global dynamics of a SEIR model with varying total population size. Math. Biosci. 1999 doi: 10.1016/S0025-5564(99)00030-9. [DOI] [PubMed] [Google Scholar]
- Lipsitch M., Cohen T., Cooper B., Robins J.M., Ma S., James L. Transmission dynamics and control of severe acute respiratory syndrome. Science. 2003 doi: 10.1126/science.1086616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y., Gayle A.A., Wilder-Smith A., Rocklöv J. The reproductive number of COVID-19 is higher compared to SARS coronavirus. J. Trav. Med. 2020;27(2):1–4. doi: 10.1093/jtm/taaa021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marhavilas P.K., Koulouriotis D., Gemeni V. Journal of Loss Prevention in the Process Industries Risk analysis and assessment methodologies in the work sites : on a review , classi fi cation and comparative study of the scienti fi c literature of the period 2000 e 2009. J. Loss Prev. Process. Ind. 2011;24(5):477–523. doi: 10.1016/j.jlp.2011.03.004. [DOI] [Google Scholar]
- Markowski A.S., Mannan M.S. Journal of loss prevention in the process industries ExSys-LOPA for the chemical process industry. J. Loss Prev. Process. Ind. 2010;23(6):688–696. doi: 10.1016/j.jlp.2010.05.011. [DOI] [Google Scholar]
- Martcheva M., Castillo-Chavez C. Diseases with chronic stage in a population with varying size. Math. Biosci. 2003 doi: 10.1016/S0025-5564(02)00184-0. [DOI] [PubMed] [Google Scholar]
- Safi M.A., Gumel A.B. 2010. Global Asymptotic Dynamics of a Model for Quarantine and Isolation. Discrete and Continuous Dynamical Systems - Series B. [DOI] [Google Scholar]
- Short K.R., Kedzierska K., van de Sandt C.E. Frontiers in Cellular and Infection Microbiology. 2018. Back to the future: lessons learned from the 1918 influenza pandemic. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Srinivasan R., Natarajan S. Developments in inherent safety : a review of the progress during 2001 – 2011 and opportunities ahead. Process Saf. Environ. Protect. 2012;90(5):389–403. doi: 10.1016/j.psep.2012.06.001. [DOI] [Google Scholar]
- Sun C., Hsieh Y.H. Global analysis of an SEIR model with varying population size and vaccination. Appl. Math. Model. 2010 doi: 10.1016/j.apm.2009.12.005. [DOI] [Google Scholar]
- Tugnoli A., Landucci G., Salzano E., Cozzani V. Journal of loss prevention in the process industries supporting the selection of process and plant design options by inherent safety KPIs. J. Loss Prev. Process. Ind. 2012;25(5):830–842. doi: 10.1016/j.jlp.2012.03.008. [DOI] [Google Scholar]
- Vrábel P., Van Der Lans R.G.J.M., Cui Y.Q., Luyben K.C.A.M. Compartment model approach: mixing in large scale aerated reactors with multiple impellers. Chem. Eng. Res. Des. 1999;77(4):291–302. doi: 10.1205/026387699526223. [DOI] [Google Scholar]
- Wei C., Rogers W.J., Mannan M.S. Layer of protection analysis for reactive chemical risk assessment. 2008. 159, 19, 24. [DOI] [PubMed]
- Willey R.J. Layer of protection analysis. Procedia Engineering. 2014;84:12–22. doi: 10.1016/j.proeng.2014.10.405. [DOI] [Google Scholar]
- Word Health Organization . WHO Bulletin; 2020. Coronavirus disease 2019 (COVID-19) situation report – 73. [Google Scholar]
- World Bank . World Bank. © World Bank; Washington, DC: 2020. Global Economic Prospects, June 2020.https://openknowledge.worldbank.org/handle/10986/33748 License: CC BY 3.0 IGO [Google Scholar]
- World Health Organization Novel coronavirus (2019-nCoV) situation report - 1. WHO Bulletin. 2020 [Google Scholar]
- Worldometer 2020. https://www.worldometers.info/coronavirus/ June 21.
- Zhang X.S., Pebody R., Charlett A., de Angelis D., Birrell P., Kang H. Estimating and modelling the transmissibility of Middle East respiratory syndrome coronavirus during the 2015 outbreak in the Republic of Korea. Influenza Other Respir. Viruses. 2017;11(5):434–444. doi: 10.1111/irv.12467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao W., Buffo A., Alopaeus V., Han B., Louhi-Kultanen M. Application of the compartmental model to the gas-liquid precipitation of CO 2 -Ca(OH) 2 aqueous system in a stirred tank. AIChE J. 2017;63(1):378–386. doi: 10.1002/aic.15567. [DOI] [Google Scholar]
- Zhou L., Miranda-Saksena M., Saksena N.K. Viruses and neurodegeneration. Virol. J. 2013 doi: 10.1186/1743-422X-10-172. [DOI] [PMC free article] [PubMed] [Google Scholar]