Multimodel precipitation responses to removal of U.S. sulfur dioxide emissions

Abstract

Emissions of aerosols and their precursors are declining due to policies enacted to protect human health, yet we currently lack a full understanding of the magnitude, spatiotemporal pattern, statistical significance, and physical mechanisms of precipitation responses to aerosol reductions. We quantify the global and regional precipitation responses to U.S. SO₂ emission reductions using three fully coupled chemistry-climate models: Community Earth System Model version 1, Geophysical Fluid Dynamics Laboratory Coupled Model 3, and Goddard Institute for Space Studies ModelE2. We contrast 200 year (or longer) simulations in which anthropogenic U.S. sulfur dioxide (SO₂) emissions are set to zero with present-day control simulations to assess the aerosol, cloud, and precipitation response to U.S. SO₂ reductions. In all three models, reductions in aerosol optical depth up to 70% and cloud droplet number column concentration up to 60% occur over the eastern U.S. and extend over the Atlantic Ocean. Precipitation responses occur both locally and remotely, with the models consistently showing an increase in most regions considered. We find a northward shift of the tropical rain belt location of up to 0.35° latitude especially near the Sahel, where the rainy season length and intensity are significantly enhanced in two of the three models. This enhancement is the result of greater warming in the Northern versus Southern Hemispheres, which acts to shift the Intertropical Convergence Zone northward, delivering additional wet season rainfall to the Sahel. Two of our three models thus imply a previously unconsidered benefit of continued U.S. SO₂ reductions for Sahel precipitation.

1. Introduction

Sulfate aerosols exert a preindustrial to present-day direct global mean radiative forcing of −0.41 W m⁻² (uncertainty range of −0.62 to −0.21 W m⁻²) along with an additional negative indirect forcing of similar magnitude and sign (with larger uncertainty) from interactions with clouds [Myhre et al., 2013]. However, global anthropogenic emissions of sulfur dioxide (SO₂, precursor to sulfate aerosol) peaked around 1970 and have been declining for the last several decades [Smith et al., 2011; Klimont et al., 2013]. While SO₂ emissions in the developing world have increased or held steady, emissions in the United States decreased 73% between 1990 and 2011 due to air pollution and acid rain control policies [Environmental Protection Agency, 2011]. In the Representative Concentration Pathways, by the end of the 21st century, global SO₂ emissions are projected to decline by as much as 80% from their present-day value [van Vuuren et al., 2011]. As sulfur dioxide emissions and thus sulfate aerosols are phased out, their removal is expected to affect global and regional climate, yet we still lack a quantitative understanding of the temperature and precipitation responses to changes in regional SO₂ emissions. Here we apply three fully coupled chemistry-climate models to address this gap.

Aerosols impact precipitation through direct effects of altering the surface solar radiation balance and through indirect, microphysical effects on clouds [Myhre et al., 2013]. Historical and future projected aerosol changes are linked to a number of regional precipitation responses. For example, aerosols have been found to influence the location of the Intertropical Convergence Zone (ITCZ) [Hwang et al., 2013; Allen, 2015; Ridley et al., 2015], South Asian monsoon circulation [Bollasina et al., 2011], and late 20th century rainfall in the Sahel. An anomalous drying trend in the 1970s and 1980s over the Sahel region has been partly attributed to Northern Hemisphere aerosol forcing [Rotstayn et al., 2002; Held et al., 2005; Biasutti and Giannini, 2006; Ackerley et al., 2011; Chang et al., 2011], which peaked roughly over the same time period. The increase of anthropogenic aerosol pollution in the U.S. and Europe through the 1970s in 1980s resulted in an anomalous cooling of the Northern Hemisphere compared to the Southern Hemisphere [Shindell et al., 2013b]. This hemispheric temperature gradient likely resulted in an annual southward shift in the ITCZ location, thereby delivering less wet season rainfall to the Sahel [Hwang et al., 2013, Allen et al., 2015]. Though evidence points to aerosol influence on historical Sahel rainfall, changes in greenhouse gas forcing, changes in sea surface temperatures, and internal variability have also been shown to partly contribute to the historical drying trend [Giannini et al., 2003, 2013; Held et al., 2005].

The net effect of decreasing aerosols on precipitation is generally an enhancement because reduced aerosol extinction results in more radiation reaching the surface, thereby resulting in more available heat for evaporation and convection [Ramanathan et al., 2001; Rosenfeld et al., 2008]. Since the presence of aerosols can also slow the autoconversion rate, it follows that their removal may enhance autoconversion and thus further increase rainfall locally. However, in an opposing effect, increases in aerosols may invigorate deep convection [Fan et al., 2012; Lee, 2012; Koren et al., 2014; Storer et al., 2014; Wall et al., 2014], implying a reduction in deep convection and therefore rainfall intensity as aerosols decline and highlighting the complexity and uncertainty in the net effect of aerosol-cloud-precipitation interactions [Stevens and Feingold, 2009]. Aerosol invigoration of deep convection, however, is not represented in most coupled climate models, including those used here [Altaratz et al., 2014].

Although there is some initial evidence that regional aerosol forcing can affect local and remote precipitation [Leibensperger et al., 2012; Shindell et al., 2012; Westervelt et al., 2015; Kasoar et al., 2016], additional work is needed particularly to establish statistical significance, determine robustness across multiple models, and understand physical mechanisms. This work aims to address this knowledge gap by estimating the impact of U.S. SO₂ emissions on regional and global precipitation using three fully coupled chemistry-climate models. To determine the regional precipitation responses, multicentury perpetual year 2000 or 2005 control simulations are conducted and contrasted against identical simulations except for U.S. SO₂ emissions, which are set to zero. We show that this approach detects statistically significant Sahel precipitation responses to U.S. SO₂ emissions that are robust across multiple models.

2. Models and Simulations

We use three coupled atmosphere-ocean-land-sea-ice climate models with fully interactive chemistry of aerosols and trace gases: (1) Geophysical Fluid Dynamics Laboratory Coupled Climate Model version 3 (GFDL-CM3), (2) Goddard Institute for Space Studies ModelE2-Russell ocean (GISS-E2-R), and (3) Community Earth System Model version 1 (CESM1). The CESM1 simulations were performed by the National Center for Atmospheric Research (NCAR); we will therefore refer to these as NCAR-CESM1. Each of these models links aerosol and precursor emissions changes to climate forcing in a fully interactive manner, in which these aspects are simulated “online” in contrast to some climate models that represent aerosols as monthly mean climatology. Each model was included in the Coupled Model Intercomparison Project version 5 (CMIP5), which contributed to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change [Intergovernmental Panel on Climate Change, 2013]. The versions of each of the models used here are essentially the CMIP5 versions. We give only a brief description of key model features followed by a description of experimental setup for each model (see also Table 1). Simulation length and details for all three models are shown in Table 2.

Table 1.

Model Configuration for Each of the Three Models Used in This Study^a

Model	Horiz. Resolution	Vert. Resolution	Present-Day Emission Yearb	Aerosol Size Distribution	Anth. Aerosol Species	Aerosol Indirect Effects	Reference
GFDL-CM3	C48 cubed sphere	48 levels, 0.01 hPa top	2000	Prescribed	SO4, BC, and OM	Cloud albedo and lifetime	Donner et al. [2011]
NCAR-CESM1	1.9° by 2.5°	30 levels, 2 hPa top	2005	Prognostic (MAM-3)	SO4, BC, and OM	Cloud albedo and lifetime	Neale et al. [2012]
GISS-E2-R	2° by 2.5°	40 levels, 0.1 hPa top	2000	Prescribed	SO4, NO3, BC, and OM	Cloud albedo only	Schmidt et al. [2014]

^aAnthropogenic aerosol species refers to the anthropogenic species that are interactive with the radiation schemes.

^bYear 2000 emissions are from Lamarque et al. [2010]; year 2005 emissions (CESM) are from RCP6.0.

Table 2.

Model Simulations and U.S. Anthropogenic SO₂ Emission Perturbations

Model	CTRL Length (Years)	zUS_SO2 Length (Years)	zUS_SO2 Initial Conditions	Emission Decrease
GFDL-CM3	400	240	CTRL year 109	14.8 Tg SO2 yr−1
NCAR-CESM1	374	274	CTRL year 107	14.0 Tg SO2 yr−1
GISS-E2-R	200	200	Initialized from spin-up run (same as control)	14.4 Tg SO2 yr−1, plus 0.4 Tg SO4 yr−1 direct emissions of SO4

For each model, we first conduct a long “present-day” control simulation denoted “CTRL” of at least 200 years (see Table 2 and sections below for details), which is contrasted against a perturbation simulation, denoted “zUS_SO₂” in which anthropogenic SO₂ emissions over the United States are permanently set to zero. The control simulation is forced with perpetual year 2000 (2005 for NCAR-CESM1) inputs, including all emissions of aerosols and their precursors and greenhouse gas concentrations. Other than the anthropogenic SO₂ emissions over the U.S., all other model settings in zUS_SO₂ remain identical to CTRL. Long simulations in both CTRL and zUS_SO₂ allow us to establish statistical significance and isolate forced responses from climate variability.

2.1. GFDL-CM3

We employ the C48 horizontal resolution of the GFDL-CM3 model, which uses a finite-volume cubed-sphere horizontal grid consisting of six faces of 48 grid cells along each edge (C48), resulting in roughly a 200 km by 200 km spatial resolution. The vertical grid consists of 48 levels extending from the surface up to about 0.01 hPa (80 km). Transport of tracers uses the finite volume algorithm of Lin and Rood [1996] with updates as described by Putman and Lin [2007] and Donner et al. [2011]. Anthropogenic and biomass burning emissions of sulfur dioxide (SO₂), black carbon (BC), and primary organic matter (OM) for 2000 are taken from Lamarque et al. [2010]. Natural emissions of isoprene, soil NO_x, lightning NO_x, dust, and marine aerosol (organic, dimethyl sulfide, and sea salt) are described by Naik et al. [2013], with dust and marine aerosol responsive to meteorology (wind speed) but climatological seasonal cycles applied to the others. Concentrations of long-lived greenhouse gases are based on Meinshausen et al. [2011]. Tropospheric chemistry for aerosols and gas-phase species follows the work of Horowitz et al. [2003] and Horowitz [2006], which solves differential equations of reaction rates using an implicit Euler backward method solver with Newton-Raphson iteration. Sulfate aerosols are formed via oxidation of SO₂ by the hydroxyl radical (OH) in the gas-phase, and ozone (O₃) and hydrogen peroxide (H₂O₂) in clouds. Dimethyl sulfide (DMS) is oxidized to SO₂ by reaction with OH and nitrate radical (NO₃). Unique lognormal size distributions are assumed for each of OM, BC, and sulfate. Aerosol optical properties are based on Mie theory, and the shortwave radiation algorithm follows Freidenreich and Ramaswamy [1999], with updates as described in Anderson et al. [2004]. Aerosol activation into cloud droplets is parameterized according to Ming et al. [2006], which relates the aerosol size distribution, chemical composition, and updraft velocity to cloud droplet number concentrations (N_d) using almost entirely first principles. Aerosols in GFDL-CM3 do not exert a microphysical effect on deep convective clouds; however, they can alter deep convection and associated precipitation through the direct effect. Stratiform cloud macrophysical properties including cloud fraction, liquid, and ice content are parameterized according to Tiedtke [1993], while microphysics (other than aerosol activation) follow Rotstayn [1997]. Aerosols may activate in shallow cumulus clouds, which are parameterized according to Bretherton et al. [2004]. Vertical velocities in GFDL-CM3 are assumed to be normally distributed within a gridbox to account for subgrid variability. Additional details on the model configuration and performance can be found in Donner et al. [2011], Naik et al. [2013], and references therein.

Simulation details and lengths for GFDL-CM3 are shown in Table 2. The control simulation is 400 years long, with zUS_SO₂ initialized from year 109 of the control and run for 240 years. The control simulation is initialized using year 2000 emissions, which corresponds to a total emission decrease of 14.8 Tg SO₂ yr⁻¹ in the perturbation simulation.

2.2. NCAR-CESM1

NCAR-CESM version 1 includes the Community Atmosphere Model version 5 (CAM5) (atmospheric component of CESM), a finite-volume dynamical core on a Cartesian grid at 1.875° by 2.5° latitude by longitude and 30 vertical layers extending up to 2 hPa. As in GFDL-CM3, tracer transport is also based on the flux-form semi-Lagrangian method described in Lin and Rood [1996] and Lin and Rood [1997]. Emissions of SO₂, BC, and OM are based on Representative Concentration Pathway (RCP) 6.0 for 2005 [Thomson et al., 2011]. Greenhouse gas surface concentrations are specified following Meinshausen et al. [2011]. Natural emissions of volcanic SO₂ and DMS are prescribed from the AEROCOM project [Dentener et al., 2006]. Like GFDL-CM3, SO₂ is oxidized by OH, H₂O₂, and O₃ to form sulfate aerosol, and DMS can be oxidized by both OH and the nitrate radical (NO₃) to form SO₂. Unique to NCAR-CESM1 among our three models is an interactive, explicit treatment of the aerosol size distribution using the Modal Aerosol Model approach version 3 (MAM-3). The MAM-3 model includes three prognostic lognormal modes: Aitken, accumulation, and coarse [Liu et al., 2012]. These modes include particle number and speciated mass concentrations, which are each predicted based not only on aerosol sources and sinks but also on microphysical processes such as new particle formation, coagulation, and condensation. Radiative transfer calculations are parameterized by the Rapid Radiative Transfer Model for general circulation model algorithm [Iacono et al., 2008]. Activation of aerosols into cloud droplets is based on the scheme of Abdul-Razzak and Ghan [2000]. Like GFDL-CM3, aerosols affect deep convection only through direct effects on radiation and not through cloud microphysics. Stratiform cloud macrophysics are updated in this version of the model and detailed in Neale et al. [2012]. The stratiform cloud microphysics are parameterized using a two-moment method described in Morrison and Gettelman [2008]. Shallow convection follows Park et al. [2009]. Additional details on aspects of CESM1 and CAM5 can be found in Neale et al. [2012] and in Tilmes et al. [2015] for details on interactive chemistry.

Table 2 lists details of the simulation length for NCAR-CESM1 and perturbation branching point. Year 2005 anthropogenic SO₂ emissions are used in our NCAR-CESM1 simulations, different than the year 2000 used in GFDL-CM3 and GISS-E2. This results in a 0.8 Tg yr⁻¹ decrease in the U.S. SO₂ emissions baseline compared to GFDL-CM3 (0.4 Tg yr⁻¹ compared to GISS-E2), which is much smaller than the change due to setting sulfur dioxide emissions to zero.

2.3. GISS-E2

The version employed here, GISS-E2-R (“Russell ocean”), uses a Cartesian grid at 2° by 2.5° latitude by longitude. The dynamical core uses the linear upstream, modified “C grid” scheme based on Russell et al. [1995]. The vertical grid consists of 40 layers extending up to 0.1 hPa. Emissions of SO₂, BC, and OM are based on Lamarque et al. [2010] for the year 2000, as in GFDL-CM3. Well-mixed greenhouse gases are prescribed as in Miller et al. [2014]. Both OH and H₂O₂ oxidize sulfur dioxide and DMS in the model. The chemical mechanism is described in Shindell et al., [2013a], and references therein. In GISS-E2-R, nitrate aerosols, in addition to sulfate, BC, and OM, are interactive with the radiation and cloud activation schemes. The aerosol size distribution is prescribed as a lognormal distribution for each of the species, similar to GFDL-CM3. Scattering and absorption of aerosols and clouds are computed from Mie theory [Schmidt et al., 2006]. The radiative transfer algorithm follows the Hansen et al. [1983] radiation model. Prognostic treatment of aerosol number and mass size distributions is available in GISS-E2-R but were not used for the present study. The prognostic cloud droplet number concentration calculation follows the scheme presented in Morrison and Gettelman [2008], with aerosol activation discussed in detail in Menon et al. [2010]. As in the other two models, aerosols affect deep convection only through the direct effect and not through cloud microphysics. Cloud processes are as described in Schmidt et al. [2006] and Schmidt et al. [2014]. Unlike both NCAR-CESM1 and GFDL-CM3, GISS-E2 does not contain a parameterization for the aerosol-cloud lifetime effect. The model version used here includes an improved treatment of nitrate aerosol that appears to correct a high bias in the previous version [Shindell et al., 2013b].

The general experimental setup for GISS-E2-R follows the setup in the other two models. A long control simulation (200 years) is initialized from a 100 year spin up simulation. The perturbation simulation in which SO₂ emissions are set to zero over the United States is also initialized from this spin-up simulation and also spans 200 years. For GISS-E2-R, the SO₂ emission reduction is 14.4 Tg yr⁻¹ in SO₂ emissions and 0.4 Tg yr⁻¹ in direct emissions of SO₄, which are assumed to represent 2.5% of total sulfur emissions in this model. Like GFDL-CM3, 2000 conditions are run in perpetuity for the control and for the perturbation (with the exception of the zeroed-out U.S. SO₂ emissions).

2.4. Calculating Climate Response and Significance Testing

We define the equilibrium climate response in a particular response variable (e.g., aerosol optical depth (AOD), clouds, temperature, and precipitation) by subtracting the mean response in the control simulation from the perturbation simulation (SO₂ emissions set to zero). We difference each monthly mean response quantity over the entire simulation length, exactly matching years in both the perturbation and the control. For instance, in GFDL-CM3 the zUS_SO₂ perturbation simulation is initialized from year 109 of the control simulation and run for 240 years. Thus, for every grid location, we difference year 1 of zUS_SO₂ with year 109 of the control, continuing in chronological order until year 240 of zUS_SO₂ is differenced with year 348 of the control. A similar process is followed for NCAR-CESM1 and GISS-E2. This differencing methodology results in a time series data set that removes any model drift in the control run that may be present. We test for statistical significance using a Student’s t test on the monthly mean responses with the null hypothesis being that the difference between zUS_SO₂ and CTRL is zero. Equation (1) shows our methodology (assuming only two spatial dimensions for simplicity), with R representing the response, Z is the perturbation experiment (zUS_SO₂), C is the control (CTRL), χ represents any particular response variable (AOD, clouds, temperature, precipitation, etc.), and t, i, and j represent time and spatial dimensions, respectively.

$$R_{t,i,j}^{\chi }=Z_{t,i,j}^{\chi }-C_{t,i,j}^{\chi }$$ (1)

3. Global and Regional Aerosol and Cloud Responses to U.S. SO₂ Emission Reductions

We first analyze the equilibrium response of all-sky aerosol optical depth (AOD) at 550 nm to shutting off anthropogenic SO₂ emissions over the United States. Our definition of AOD here includes the following aerosol species: sulfate, OM, BC, and natural species such as dust and sea salt. However, since only SO₂ emissions have changed while all else is held equal between CTRL and zUS_SO₂, the changes in AOD are mostly due to sulfate reductions. We do not explicitly calculate the potential feedback of changing climate on natural emissions, though climate feedback on natural emissions (e.g., dust, sea salt, and DMS) are included in each model and may contribute to the total AOD changes here. Figure 1 shows the total AOD change (decrease) as calculated by the description in section 2.4 and equation (1). In each of the three models, there is a widespread, statistically significant decrease at the 95% confidence level (hatched areas) in AOD over North America and into the Atlantic Ocean due to shutting off U.S. SO₂ emissions, ranging from as large as −0.1 in NCAR-CESM1 to −0.25 in GFDL-CM3. Changes are largest in magnitude in GFDL-CM3 and GISS-E2 for two reasons: (1) the emission reductions of SO₂ were larger by 0.8 and 0.4 Tg SO₂ yr⁻¹ in GFDL-CM3 and GISS-E2, respectively, than in NCAR-CESM1 (due to 2000 versus 2005 control emissions) and (2) there is weaker convective scavenging of aerosols in GFDL-CM3 control simulation compared to the other models [Paulot et al., 2015; Westervelt et al., 2016]. Because the AODs in GFDL-CM3 are biased high due to a weak convective scavenging sink that leads to an excessively long sulfate lifetime (7.9 days), we also report the maximum percent differences in AOD in the three models: 70% in GFDL-CM3, 60% in NCAR-CESM1, and 65% in GISS-E2. We thus find similar relative responses to reductions in U.S. SO₂ emissions in all three models despite the high bias in GFDL-CM3 and GISS-E2 AOD. Each model also shows small yet statistically significant decreases in AOD in locations remote from the source region (U.S.), with AOD changes extending across the Atlantic Ocean. This remote effect is most pronounced in GFDL-CM3, reflecting the long sulfate lifetime. Similarly, GISS-E2 has the least impact in remote or downwind areas, owing to its relatively short sulfate lifetime of 3.3 days. NCAR-CESM1 has a sulfate lifetime of 6.4 days and thus falls intermediate between GISS-E2 and GFDL-CM3 for remote influence. Overall, the models robustly show the strongest AOD responses over the source region, with smaller downwind and remote responses.

Figure 1.

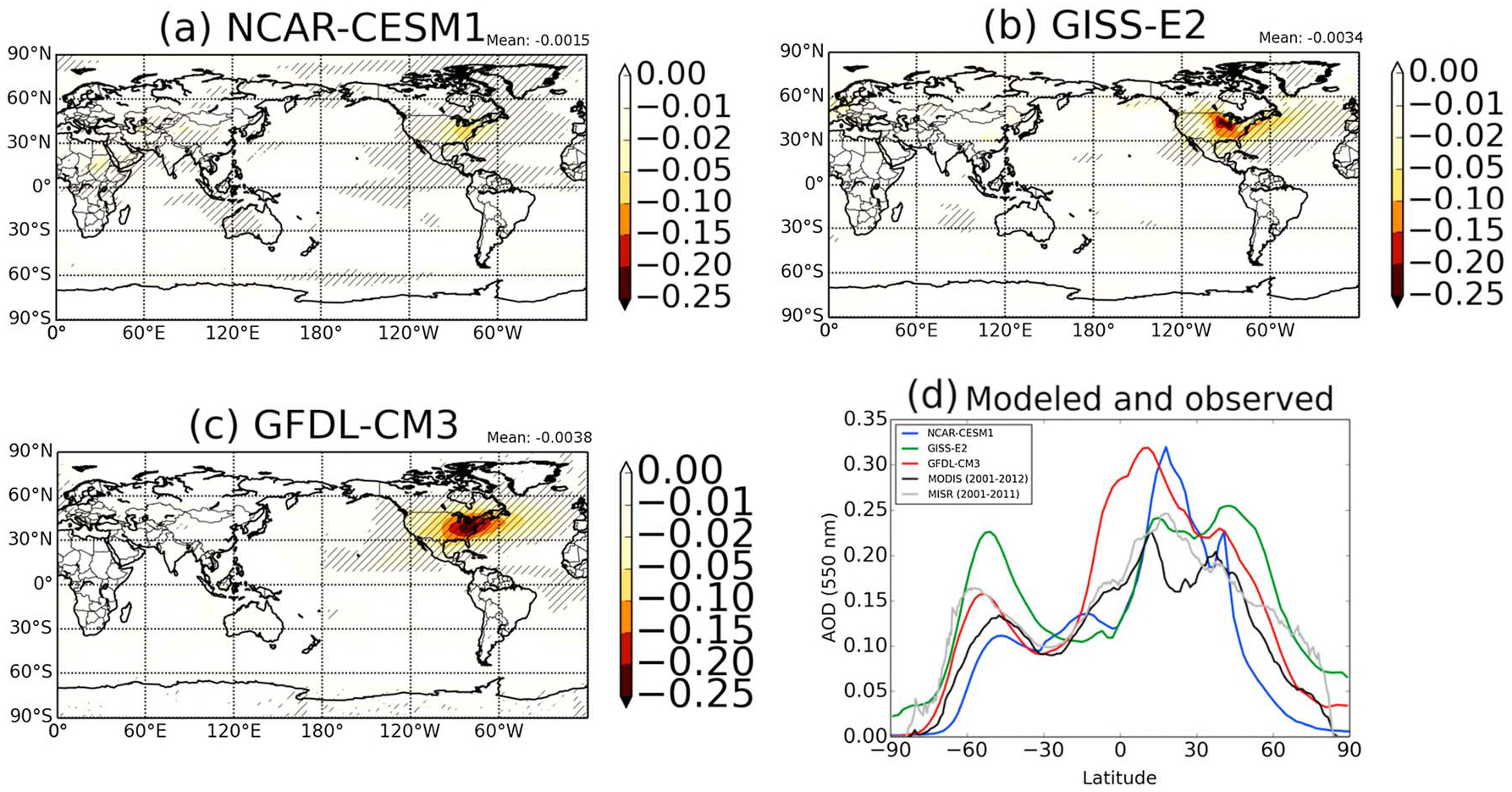
Response of annual mean global aerosol optical depth (AOD) when U.S. SO2 emissions are set to zero for (a) NCAR-CESM1, (b) GISS-E2, and (c) GFDL-CM3. Hatching represents statistical significance at the 95% confidence level. (d) Comparison of control simulation zonal mean AOD to observations from MISR and MODIS.

In Figure 1d we evaluate the control simulation AOD in each of the three models with two satellite observational data sets (the Moderate Resolution Imaging Spectroradiometer, or MODIS, and the Multiangle Imaging Spectroradiometer, or MISR). MODIS AODs at 550 nm are 2001 to 2012 mean values using the Dark Target retrieval algorithm [Wu et al., 2016]. MISR AODs at 550 nm are averaged over 2001 to 2011 and utilize the MISR Research Algorithm retrieval method [Limbacher and Kahn, 2014]. The models generally capture the zonal mean observed AOD patterns, although GFDL-CM3 and GISS-E2 overestimate AOD over the northern midlatitudes. GISS-E2 also underestimates tropical AOD and significantly overestimates over the Southern Ocean where AOD is dominated by sea salt. The observational data sets also differ, with MISR indicating higher AOD over the northern midlatitudes. Some of the discrepancies between MODIS and MISR over the Sahara reflect the inability of the MODIS Dark Target retrieval algorithm used here to retrieve AOD over the bright surface of the desert. In addition to Figure 1d, we also show a detailed comparison of MISR AOD over North America alone in Figure S1 in the supporting information. Modeled AOD is biased low in NCAR-CESM1 over the western U.S, while GFDL-CM3 and GISS-E2 are less biased over the western U.S. but biased high over the eastern U.S. The considerably large differences between modeled and satellite AOD, especially in GFDL-CM3, as well as the variation between different models, suggest deficiencies in our ability to realistically simulate some of the key aerosol processes that determine aerosol abundances in the atmosphere.

Since highly hygroscopic sulfate aerosol are efficient cloud condensation nuclei (CCN) [Petters and Kreidenweis, 2007], a zeroing out of SO₂ emissions over the U.S. should alter cloud droplet number concentrations. Here we present time-averaged in-cloud column-integrated cloud droplet number concentration (CDNC), which decreases in all three models when U.S. SO₂ emissions are set to zero (Figure 2). CDNC responses manifest mainly as decreases, since less aerosol results in less cloud droplet nucleation. The models robustly show that CDNC will decline significantly (hatched areas), mostly over the source region but also extending across the Atlantic Ocean. GFDL-CM3 (Figure 2c) estimates the largest decrease in CDNC among the three models (60% decrease). The relatively long lifetime of sulfate in GFDL-CM3 also results in a widespread impact on CDNC, extending to western Europe. Both GISS-E2 and CESM1 predict similar global mean and spatial patterns of CDNC (Figures 2a and 2b). Despite having a larger-magnitude AOD decrease, GISS-E2 has a similar CDNC response as CESM1, owing to differences in treatments of aerosol hygroscopicity and subsequent CCN activation. These CDNC results imply an impact of regional aerosols on regional climate via the cloud albedo affect.

Figure 2.

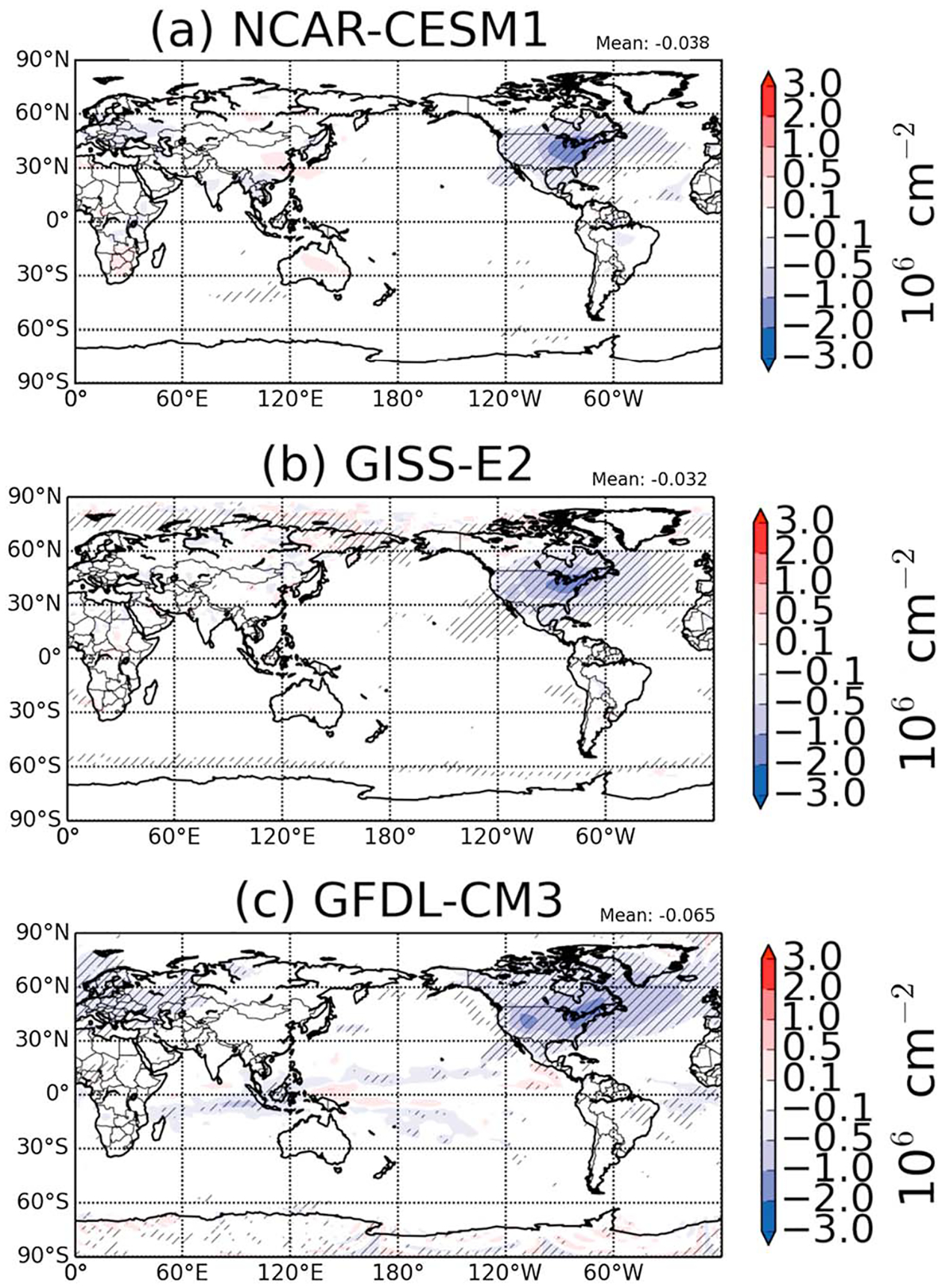
Response of annual mean global cloud droplet number concentration (CDNC) to zero U.S. SO₂ emissions for (a) NCAR-CESM1, (b) GISS-E2, and (c) GFDL-CM3. Hatching represents statistical significance at the 95% confidence level.

In addition to affecting droplet concentrations and sizes, aerosols impact cloud lifetime. An increase in aerosols and thus CDNC is typically associated with a delay in autoconversion, an increase in cloud lifetime, and an increase in cloud liquid water. Decreasing cloud droplet concentrations due to reductions of U.S. sulfate therefore may lower cloud liquid water via the cloud lifetime effect. Figure S2 shows that cloud liquid water indeed is significantly reduced over the source region in GFDL-CM3 and CESM1. The magnitudes of the LWP decrease over the source region in GFDL-CM3 and NCAR-CESM1 are similar (up to about a decrease of 10 g m⁻² in each). However, AOD decreases are much larger in GFDL-CM3 than in CESM1 (see Figure 1). Therefore, for equivalent decreases in AOD, cloud LWP is likely more susceptible to changes in aerosols in CESM1 compared to GFDL-CM3. There is no response of liquid water path (LWP) to aerosol reductions in GISS-E2, reflecting the lack of an aerosol influence on autoconversion rates in GISS-E2 (and hence no estimates of the cloud lifetime indirect effect) [Schmidt et al., 2014]. The response in LWP in the three models highlights that differences in representation across models can account for some of the model differences in the aerosol influence on climate.

Global, annual mean changes in aerosol effective radiative forcing (ERF) between the zUS_SO2 and CTRL simulation are 0.17 ± 0.04 W m⁻², 0.16 ± 0.04 W m⁻², and 0.053 ± 0.017 W m⁻² for GFDL-CM3, NCAR-CESM1, and GISS-E2, respectively. Over the eastern U.S., regional ERF values are as large as 3 to 4 W m⁻², reflecting the strong reductions in sulfate aerosol due to the removal of U.S. SO₂ emissions. The lower ERF in GISS-E2 reflects the lack of treatment of the cloud lifetime effect in that model; however, cloud lifetime effects may be overestimated in GFDL-CM3 [Westervelt et al., 2015].

4. Global and Regional Precipitation Responses

Precipitation rates change both locally over the U.S. and remotely in response to zero U.S. SO₂ emissions in the three models, generally increasing over the U.S. and over most regions, with varying amounts of consistency among models on the regional scale. Since many of the aerosol impacts on precipitation occur away from the emissions region (U.S) where the changes in AOD and CDNC are the largest (Figures 1 and 2), we conclude that remote effects of aerosols on precipitation are caused by the overall change in the radiation balance at the surface to which the large-scale atmospheric circulation responds. The impact of U.S. sulfate on precipitation (zUS_SO₂ minus CTRL) is somewhat heterogeneous regionally, although on a global mean basis, precipitation does increase slightly in each of the three models (Figures 3 and 4). Global mean increases are 0.019 (0.7%), 0.005 (0.2%), and 0.015 mm d⁻¹ (0.6%) for NCAR-CESM1, GISS-E2, and GFDL-CM3, respectively.

Figure 3.

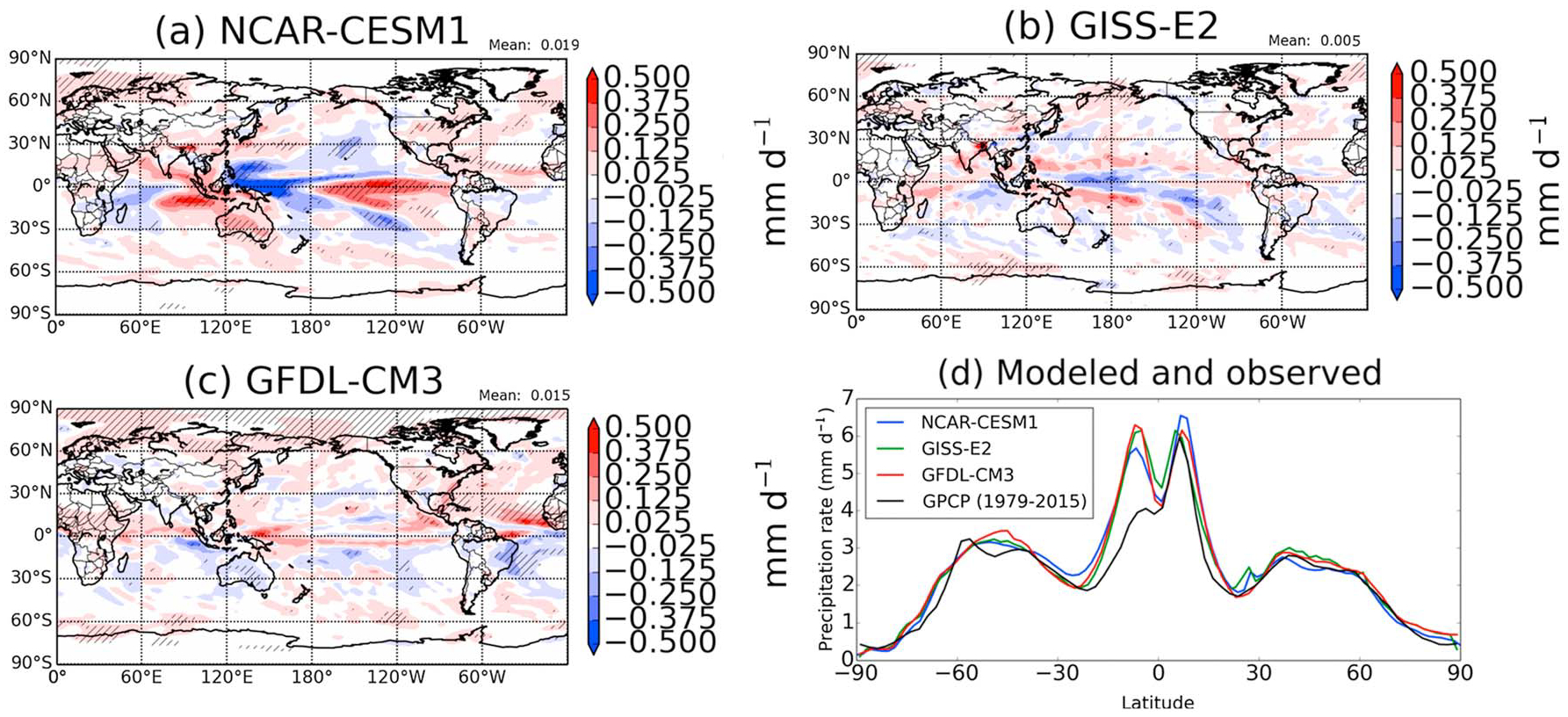
Response of annual mean global precipitation to zeroing out U.S. SO₂ emissions for (a) NCAR-CESM1, (b) GISS-E2, and (c) GFDL-CM3. Hatching represents statistical significance at the 95% confidence level. (d) Comparison of zonal mean precipitation in the control simulations to observations from GPCP (1979–2015 average).

Figure 4.

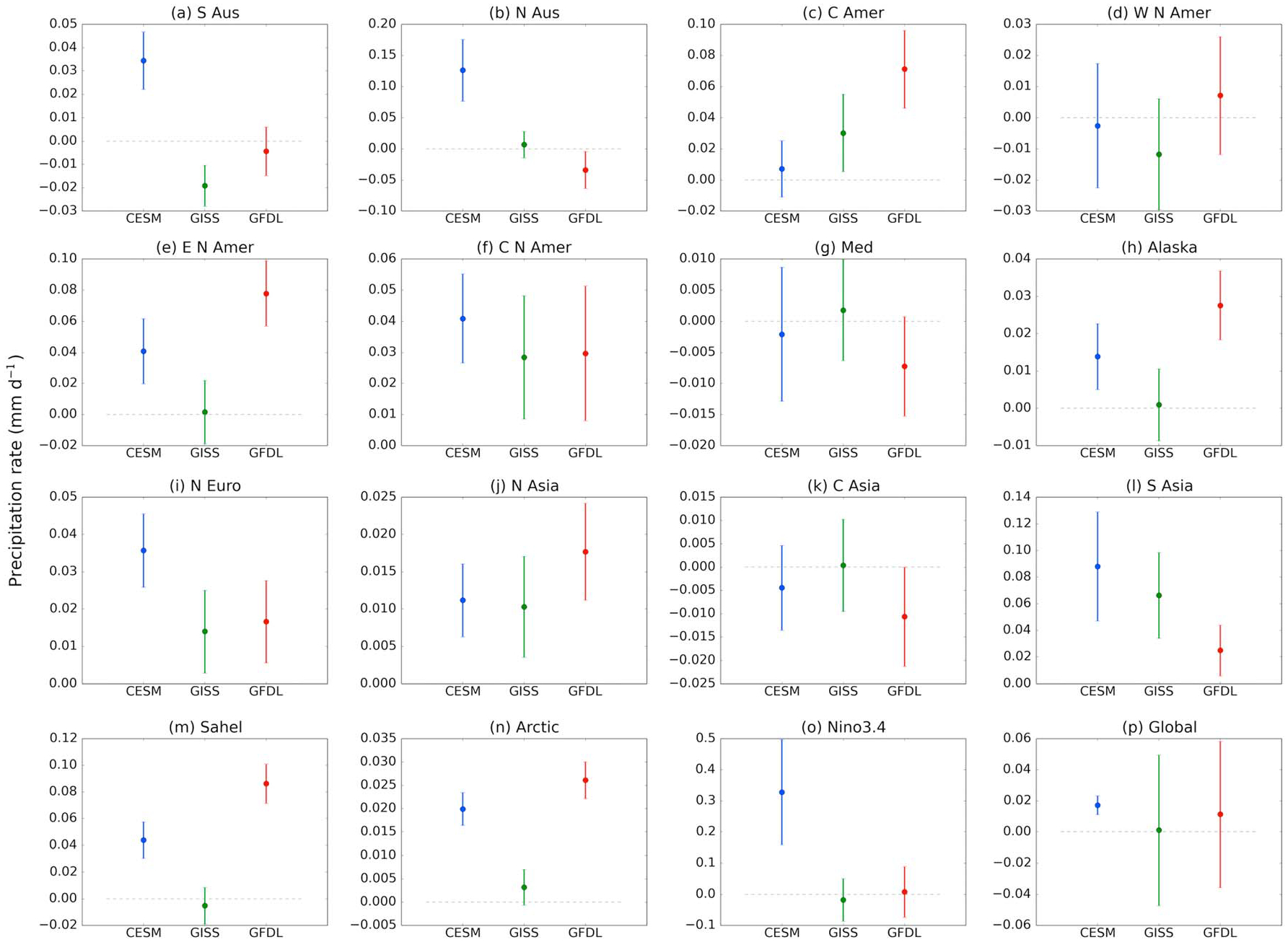
Mean (dots) and standard error (bars) of precipitation response to zero U.S. sulfate in each of the three models in 15 regions and globally. See Table S1 for region definitions.

The precipitation response in GFDL-CM3 exhibits the most statistical significance (hatching in Figure 3). In NCAR-CESM1 (Figure 3a) and GFDL-CM3 (Figure 3c), statistically significant increases occur over the U.S., the tropical North Atlantic, the Arctic, and the Sahel region. The rainfall increases in the Sahel are further examined in section 5. Increases in precipitation of similar magnitude occur in some of the same locations in GISS-E2, although most lack statistical significance (e.g., the Arctic and the central and eastern U.S.). We also find consistent responses in the tropical Atlantic Ocean between NCAR-CESM1 and GFDL-CM3, but not GISS-E2. The precipitation increases in the tropical north Atlantic are mirrored by decreases immediately south of the equator, suggesting a northward shift of the Intertropical Convergence Zone (ITCZ). With decreasing aerosols in zUS_SO₂ localized to the U.S. and immediately downwind, the Northern Hemisphere anomalously warms compared to the Southern Hemisphere relative to the control simulation. This results in an anomalous Hadley circulation and a shift northward (toward the “warmer hemisphere”) in the tropical rain belt [Hwang et al., 2013; Allen, 2015], which we show in more detail in Figures 6 and 7 and section 5. There is some evidence of similar changes in the Pacific Ocean, at least in GFDL-CM3, although this is generally weaker in magnitude and not statistically significant. Whereas decreases in global aerosols have been shown to impact both the Atlantic and Pacific ITCZ, we show here that aerosol emission changes in a specific region may impact only certain parts of the tropical rain belt within a given longitude band. In NCAR-CESM1, there is a strong east-west dipole response of precipitation in the tropical Pacific that resembles the El-Niño–Southern Oscillation (ENSO). This is confirmed in Figure S3, which shows an El Niño-like annual mean surface temperature response with cooling in the western tropical Pacific Ocean coupled with warming in the central and eastern Pacific. We can therefore conclude that either the sulfate perturbation has shifted the ENSO phase or has enhanced the drying and wettening trend normally induced by ENSO in NCAR-CESM1.

Figure 6.

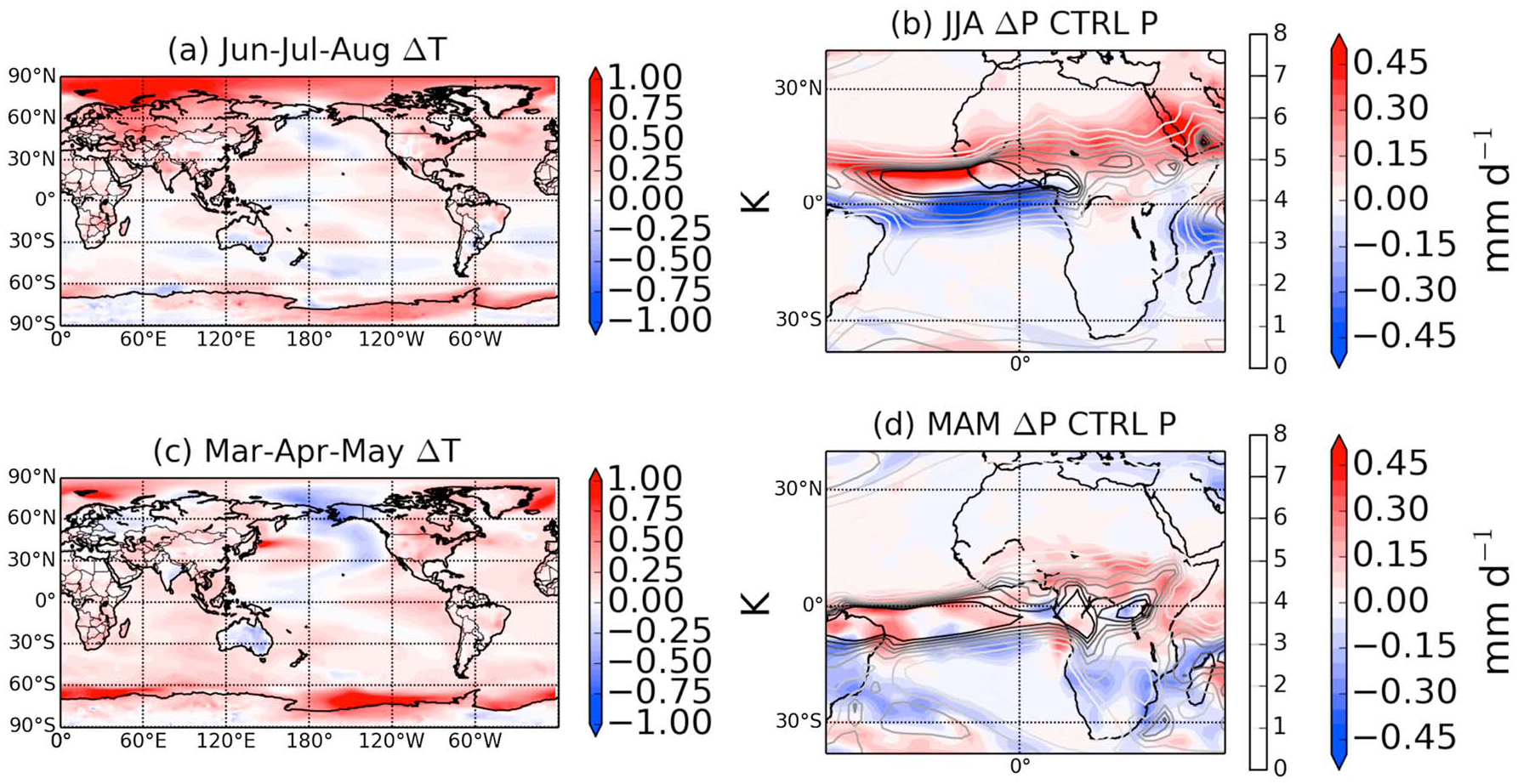
(a) NCAR-CESM1 JJA surface air temperature response between perturbation minus control. (b) NCAR-CESM1 JJA precipitation response (zUS_SO₂ minus CTRL) and CTRL precipitation (gray scale contours). (c) Same as Figure 6a but for MAM. (d) Same as Figure 6b but for MAM.

Figure 7.

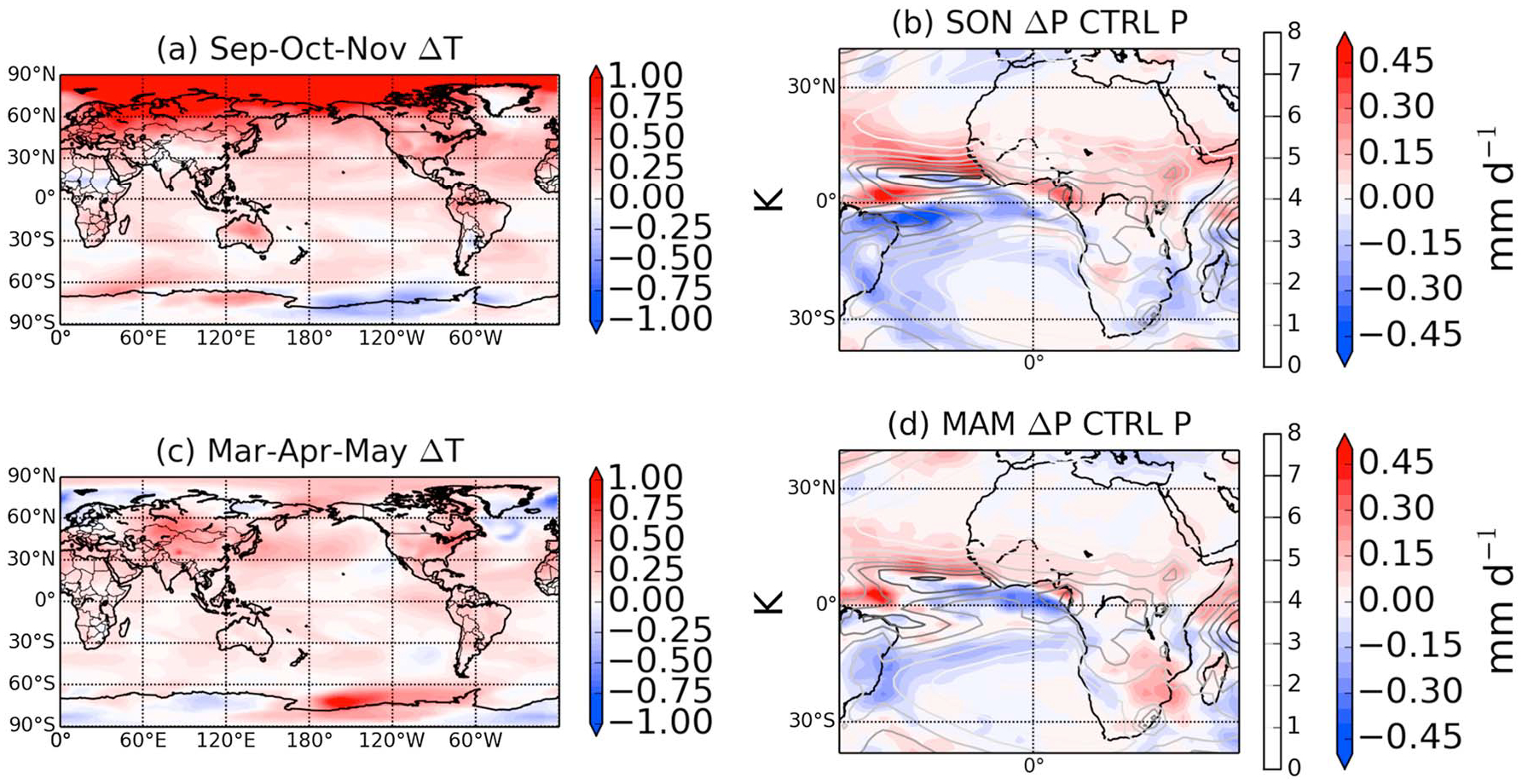
(a) GFDL-CM3 SON temperature difference between perturbation and control. (b) GFDL-CM3 SON JJA precipitation response (zUS_SO₂ minus CTRL) and CTRL precipitation (gray scale contours). (c) Same as Figure 7a but for MAM. (d) Same as Figure 7b but for MAM.

Figure 3d shows zonally averaged precipitation rate in each of the three models and in the Global Precipitation Climatology Project (GPCP). GPCP values have been aggregated and averaged over the 1979–2015 time period, whereas 200 year control run means are presented for each of the climate models. The models generally match GPCP with the exception of the well-known “double-ITCZ” problem evidenced by overestimation in precipitation rates in the 0° to 20°S latitude region. The models also overestimate precipitation rates in the southern midlatitudes and subtropics (south of 30°S).

To further analyze the robustness of precipitation responses, we plot the simulated mean (dots) and one standard error (bars), calculated from the temporal distribution of monthly mean responses (equation (1)) of regionally averaged precipitation changes for 15 regions (Table S1 in the supporting information) in Figure 4. We use all 200+ years in our standard error calculation, though the detection threshold for 95% significance level is typically lower than that (e.g., 100 years over the Sahel for NCAR-CESM1). Though global, annual mean increases in the three models are less than 1% (0.019 mm d⁻¹ in NCAR-CESM1) of the global mean control precipitation rate, regional precipitation responses to zeroing out U.S. SO₂ emissions, however, can reach up to an order of magnitude higher (annual mean increase of up to 10% or 0.2 mm d⁻¹ in NCAR-CESM1), in regions such as the Sahel, for example. This finding suggests that regional aerosol emissions exert strong effects in remote regions that are not co-located with the emissions source region [Westervelt et al., 2015]. In 8 of the 15 regions, mean values (dots) agree in sign (an increase in precipitation) across the models. The model responses are in closest agreement, and most significant, in the source region, particularly Central North America where modeled mean values are within one standard error of one another. For remote regions, the models match best over most of Asia, particularly in northern and central Asia where the mean model values again overlap within one standard error. Each of the three models agree in sign over northern latitudes such as northern Europe, Alaska, and the Arctic regions, while typically only two of the models agree in both sign and magnitude in these regions. Generally, NCAR-CESM1 and GFDL-CM3 are more consistent with each other as compared to GISS-E2. We conclude that precipitation increases in near-source regions are robust across all three models.

5. Influence of U.S. SO₂ Emissions on Sahel Rainfall

Given the evidence of ties of Sahel rainfall to remote aerosol forcing (Figures 3 and 4m and discussion in section 1), in this section we apply our equilibrium climate response analysis in further detail over the Sahel region. Figure 5a shows daily modeled Sahel precipitation in the control runs (CTRL; solid colored lines) and the zUS_SO₂ perturbation runs (dashed lines) averaged over the entire ~200 year data set, as compared to observed daily rainfall from GPCP (1979–2015 average; black). All daily data sets are smoothed using a 31 day running mean, averaging 15 days before and 15 days after each individual day. GFDL-CM3 and NCAR-CESM1 (red and blue) agree within 5% of GPCP observations in the peak rainy month of August; however, the models simulate an excessively long rainy season, with modeled precipitation rates higher than observed in April through June and October through November. We find statistically significant higher precipitation in the zUS_SO₂ runs in GFDL-CM3 and NCAR-CESM1 (dashed red and blue lines) throughout the rainy season. Figure 5b, which shows the differences in each model between the zUS_SO₂ perturbation runs and CTRL, further demonstrates this point as increases in rainfall in NCAR-CESM1 peak as high as 0.4 mm d⁻¹. We also find a large increase in GFDL-CM3 precipitation in the zUS_SO₂ run, reaching a maximum of roughly 0.2 mm d⁻¹. There is no statistically significant change in GISS-E2 (see also Figure 5c). The largest enhancements in precipitation in NCAR-CESM1 occur at the height of the Sahel rainy season (July–August), while in GFDL-CM3, increases do occur over these months but the largest increases are toward the end of the rainy season into September, October, and even November. These results suggest an extension of the rainy season in GFDL-CM3. Indeed, Figure S4 shows a statistically significant increase (P value less than 0.003) in the number of rainy days (defined as daily mean precipitation of greater than 1 mm d⁻¹) in the zUS_SO₂ simulation, with a 240 year mean increase in frequency of 0.7% or 2.5 days. Creating distributions from the control and perturbation simulations for each day of the year, we perform a Student’s t test for every individual day, to test whether the precipitation response on a particular day is statistically different from zero. The resulting P values for these tests are plotted in Figure 5c. The P values drop well below 0.05 (95% significance) for the summer and fall period for GFDL-CM3 (red) and the summer period for NCAR-CESM1 (blue). Monthly P values from GISS-E2 do not ever fall below the upper limit of the plot, indicating no statistical significance of the monthly mean GISS-E2 results. We conclude, based on the highly significant changes simulated in two of our models, that reductions in U.S. sulfate aerosol forcing may act to increase Sahel rainfall by as much as 10% in the wet season. Two of the models indicate a significant connection of Sahel precipitation to U.S. SO₂ emissions. This result also suggests that aerosol reduction as a result of air pollution regulation in northern midlatitude regions may help reduce the likelihood and/or severity of future droughts in the Sahel, such as the one that devastated the region in recent decades.

Figure 5.

(a) 31 day running mean daily Sahel precipitation in the control run (solid lines) and perturbation run (dashed lines) in each model. GPCP observations are shown in solid black. The dashed line represents GPCP annual mean. (b) Difference between perturbation and control runs in daily Sahel rainfall. (c) Daily P values from a Student’s t test on Sahel rainfall. Daily data were not available for GISS-E2, so monthly means are plotted in Figure 5. Sahel region defined as 20°W to 40°E, 10°N to 20°N.

In Figures 6 and 7, we explore the physical underpinnings behind the precipitation enhancement in the Sahel shown in Figure 5. During the period of the largest precipitation enhancements in NCAR-CESM1 (boreal summer months June-July-August (JJA); Figure 6) and GFDL-CM3 (boreal autumn months September-October-November (SON); Figure 7), we plot the seasonal mean surface air temperature change globally alongside the both the precipitation response (red/blue scale) and the control simulation precipitation (gray scale). Figure 6a shows a clear difference in the average temperature change (zUS_SO₂ minus CTRL) between the Northern and Southern Hemispheres for the JJA months. The Northern Hemisphere warms anomalously compared to the Southern Hemisphere due to the reduction of U.S. SO₂ emissions, with a difference in the hemisphere average temperature response (difference between the Northern Hemisphere “zUS_SO2 minus CTRL” and the Southern Hemisphere “zUS_SO2 minus CTRL”) of 0.172 K for the entire range of longitudes and 0.158 K for the Atlantic sector (defined as 60°W to 0°E). This hemispheric temperature change produces a northward shift in the ITCZ location (compare CTRL precipitation to precipitation response) consistent with previous studies [Ackerley et al., 2011; Allen, 2015], thus delivering more wet season rainfall to the Sahel. Using the precipitation centroid definition of Frierson and Hwang [2012], we find a northern shift of the precipitation center of 0.35° latitude. Indeed, Figure 6b shows a strong enhancement of precipitation over the Sahel region in the summer months. In the boreal spring months (March-April-May (MAM); Figure 6c and 6d), there is very little hemispheric temperature difference (mean of −0.05 K). Consistent with the physical mechanism described here, this lack of hemispheric temperature difference results in little to no ITCZ shift and an insignificant change in precipitation over the Sahel.

The same argument follows for GFDL-CM3 (Figure 7), though we use SON here, when the Sahel precipitation response peaks (Figure 5) in this model. In Figure 7a, the hemispheric average temperature response difference is even more striking (mean of 0.417 K, 0.239 K for the Atlantic sector) than for NCAR-CESM1 in JJA. As in NCAR-CESM1, this anomalous Northern Hemisphere warming in GFDL-CM3 produces a significant increase in Sahel rainfall, as the ITCZ pushes north into the Sahel deeper into the wet season. The northward shift of the ITCZ in GFDL-CM3 is smaller than in NCAR-CESM1, as the precipitation center moves northward by 0.2° latitude (see also gray scale in Figure 7b). Similar to NCAR-CESM1, the boreal spring months of MAM in GFDL-CM3 show less of a response than in SON, consistent with the absence of a strong hemispheric temperature difference (mean of only 0.062 K greater warming in the Northern Hemisphere). In addition to interhemispheric temperature differences, interhemispheric differences in albedo can also drive a northward shift of the ITCZ. We find that in GFDL-CM3, total cloud fraction decreases over the Northern Hemisphere but increases over the Southern Hemisphere (in particular over the Southern Ocean) in response to removal of U.S. SO₂ emissions, resulting in an anomalous albedo difference between the two hemispheres [Haywood et al., 2016]. The resulting equilibration of albedos between hemispheres results in enhanced cross-equatorial net energy transport into the Southern Hemisphere and thus a northward shift of the ITCZ.

In Figure 5 we showed that precipitation rate responses to reduced U.S. sulfate aerosols are not statistically significant in GISS-E2. It therefore follows that there should be little difference between hemispheric average temperatures. We find (shown in Figure S5) that there is indeed no strong temperature difference for both summer months of July-August-September and spring months of MAM. In summer, the global mean hemispheric temperature difference is only 0.067, while is it 0.006 in spring. Thus, this proposed physical explanation regarding cross-equatorial temperature differences consistently explains the responses in all three models. Additionally, GISS-E2 lacks treatment of the cloud lifetime effect, resulting in a smaller aerosol effective radiative forcing change and therefore could partially explain the lack of a precipitation response in the tropical Atlantic and the Sahel region [Allen et al., 2015].

6. Conclusions

As emissions of aerosols and their precursors continue to decrease in the U.S. and other regions, we lack a full understanding of the corresponding climate consequences, particularly local and remote changes to the hydrological cycle. To address this knowledge gap, we examine the impact of U.S. anthropogenic SO₂ emissions on aerosols, cloud droplets, and precipitation using three coupled chemistry climate models: NCAR-CESM1, GFDL-CM3, and GISS-E2-R. In each model, we contrast a control simulation with a perturbation simulation in which anthropogenic SO₂ emissions over the United States have been set to zero, with all other features identical in the two simulations. The control and perturbation experiments are simulated for hundreds of years in order to isolate the equilibrium climate response, reduce the impact of internal variability, and establish statistical significance. We investigate both local and remote changes in precipitation in each of the three models and identify robust increases across multiple models. Finally, we identify significant precipitation changes in two models over the Sahel region, motivating us to investigate reasons why U.S. sulfate aerosol might influence precipitation in the vulnerable Sahel environment.

The response of aerosols and cloud droplets to zero SO₂ emissions over the U.S. closely mirrors the emissions decreases over the source region. Total AOD decreases by as much as 70% over the U.S. in GFDL-CM3, 65% in GISS-E2, and 60% in NCAR-CESM1. Model diversity in AOD responses reflects model differences in baseline emissions (year 2000 versus 2005) and wet scavenging schemes in the models. Discrepancies with AOD retrieved from satellite and our simulations highlight flaws in our model treatment of processes that affect aerosol abundances, which limit our confidence in model skill at representing AOD responses to emission changes. Nevertheless, the percent decreases in AOD in the three models are similar, each peaking around 60–70%, implying that some of the biases with observed AOD are systematic. Cloud droplet number concentration (CDNC) responses, like AOD, are qualitatively robust across the three models, though the magnitude of the CDNC decreases varies across the models due to diversity among parameterizations.

Global precipitation rates increase slightly in each of the three models. We find the most robust and statistically significant precipitation increase in the source region (e.g., Central North America) but also find significant responses in remote regions such as Asia, northern latitudes (Arctic, northern Europe, and Alaska), and the Sahel (two out of three models). Overall, the models agree in the sign of the precipitation rate change (increase) in 8 of the 15 regions considered, and in the global mean. In four of those eight regions, the entire confidence interval for the simulated precipitation change (±1 standard error of the mean) is above zero, indicating statistical significance. We find significant increases as large as 0.4 mm d⁻¹ (10%) and 0.25 mm d⁻¹ (5%) in Sahel precipitation in NCAR-CESM1 and GFDL-CM3, respectively, and a 2.5 day mean extension of the Sahel rainy season in GFDL-CM3. We attribute this precipitation enhancement to a difference in the hemispherically averaged temperature change between the Northern and Southern Hemispheres, which influences the Hadley circulation and therefore the location and intensity of the tropical rain belt. We show that this temperature change (or lack thereof) is consistent with the precipitation changes in each of the three models.

The GISS-E2 model does not exhibit a strong interhemispheric temperature difference, likely caused by the smaller aerosol effective radiative forcing due to a lack of treatment of the cloud lifetime effect. This key difference between GISS-E2 and the other two models may at least partially explain the different precipitation responses in the Sahel in GISS-E2 [Allen et al. 2015] and also highlights the uncertainty in estimates of the aerosol indirect effect, particularly for the cloud lifetime effect [Westervelt et al., 2015; Wang et al., 2012]. Nevertheless, our estimated Sahel precipitation response in NCAR-CESM1 and GFDL-CM3 is statistically significant and is attributed to cross-equatorial net energy transport.

While most previous studies have focused on climate response to global aerosol changes [e.g., Westervelt et al., 2015], we examine here aerosol, cloud, and precipitation response on the regional scale to a regional forcing. Our novel, multimodel approach to understanding the effects of regional aerosol forcing on regional climate changes, both local to the source region and remote, allows us to draw more robust conclusions than is possible with single model studies. With SO₂ emissions already declining in the U.S. with the expectation of a continuing decline, this study sheds light upon possible ongoing and future climate responses. In particular, the finding that rainfall in the Sahel will increase due to reductions in aerosols from one region alone, if substantiated by additional studies, may be relevant to regional planning in western Africa, a region that has experienced considerable recent climate extremes. Our approach and findings for U.S. SO₂ emission reductions are a first piece of our general methodology to identify robust regional climate responses to local and remote emissions of aerosols and their precursors and to assemble them into reduced-form climate impact and integrated assessment models.

Key Points:

• Models show that U.S. SO₂ reductions increase precipitation globally and regionally

• Decreasing U.S. sulfate shifts the ITCZ northward in two of three models

• Wet season Sahel precipitation may increase up to 10% from 2000 levels