Abstract
Background:
Differential treatment between trial arms has been suggested to bias prostate cancer (PC) mortality in the European Randomized Study of Screening for Prostate Cancer (ERSPC).
Objective:
To quantify the contribution of treatment differences to the observed PC mortality reduction between the screening arm (SA) and the control arm (CA).
Design, setting, and participants:
A total of 14 136 men with PC (SA: 7310; CA: 6826) in the core age group (55–69 yr) at 16 yr of follow-up.
Outcome measurements and statistical analysis:
Observed and estimated numbers of PC deaths by treatment allocation in the SA and CA, respectively. Primary treatment allocation was modeled using multinomial logistic regression adjusting for center, age, year, prostate-specific antigen, grade group, and tumor-node-metastasis stage. For each treatment, logistic regression models were fitted for risk of PC death, separately for the SA and CA, and using the same covariates as for the treatment allocation model. Treatment probabilities were multiplied by estimated PC death risks for each treatment based on one arm, and then summed and compared with the observed number of deaths.
Results and limitations:
The difference between the observed and estimated treatment distributions (hormonal therapy, radical prostatectomy, radiotherapy, and active surveillance/watchful waiting) in the two arms ranged from –3.3% to 3.3%. These figures, which represent the part of the treatment differences between arms that cannot be explained by clinicopathological differences, are small compared with the observed differences between arms that ranged between 7.2% and 10.1%. The difference between the observed and estimated numbers of deaths among men with PC was 0.05% (95% confidence interval [CI] –0.1%, 0.2%) when applying the CA model to the SA, had the two groups received identical primary treatment, given their clinical characteristics. When instead applying the SA model to the CA, the difference was, as expected, very similar—0.01% (95% CI –0.3%, 0.2%). Consistency of the results of the models demonstrates the robustness of the modeling approach. As the observed difference between trial arms was 4.2%, our findings suggest that differential treatment explains only a trivial proportion of the main findings of ERSPC. Only data on primary treatment were available.
Conclusions:
Use of prostate-specific antigen remains the predominant explanation for the reduction in PC mortality seen in the ERSPC trial and is not attributable to differential treatment between trial arms.
Patient summary:
This study shows that prostate cancer deaths in the European screening trial (European Randomized Study of Screening for Prostate Cancer) were prevented because men were diagnosed and treated earlier through prostate-specific antigen screening, and not because of different, or better, treatment in the screening arm compared with the control arm.
Keywords: Prostate cancer, Screening, Early detection, Treatment
The reduction in prostate cancer mortality in the European Randomized Study of Screening for Prostate Cancer (ERSPC) is a result of early detection and not differential treatment between trial arms.
1. Introduction
The European Randomized Study of Screening for Prostate Cancer (ERSPC) has shown that prostate-specific antigen (PSA) can reduce prostate cancer (PC) mortality by 20% at 16 yr [1]. It has been questioned whether this reduction is an effect of screening and early detection, or whether differential treatments between trial arms could have resulted in superior outcomes in the screening arm (SA) versus the control arm (CA) of the trial [2,3]. Others have hypothesized that the net reduction in PC deaths in ERSPC was not a result of earlier detection of more curable cancers in the SA through PSA screening, but rather a result of more PC deaths in the CA where “androgen deprivation therapy treatment contributed differentially to an increase in prostate cancer deaths in control patients” [4–6].
A difference in treatment distribution between the cases in the SA and CA of a screening trial overall is entirely expected and desirable, since the purpose of screening is to find cancer at a stage where curative treatment is still possible [1]. Conversely, because of later detection at an advanced stage, hormonal therapy is more commonly used in the CA with a larger fraction of advanced cancers [1,7].
Such treatment differences cause only bias if men with similar tumors are treated differently between arms. For instance, if a man with a low-risk PC would be equally likely to receive active surveillance or undergo surgery or radiotherapy, regardless of whether the cancer was detected through screening in the SA or through clinical detection in the CA, then a treatment selection bias is an unlikely explanation for the mortality differences between groups.
An earlier study from the ERSPC, comparing the treatment distribution between trial arms by patient and tumor characteristics, showed that a man with nonmetastasized high-risk PC in the CA was more likely to receive radiotherapy, hormonal treatment, or surveillance, than a similar man in the SA. However, the trial arm had only a minor role in the choice of treatment as compared with clinicopathological variables [8]. Nevertheless, the potential impact of any differential treatment on the PC mortality results of the ERSPC trial has not been investigated previously.
Although much of the criticism has waned, this study seeks to quantify the effect on the PC mortality reduction by differences in treatments attributable to the trial arm. We undertook the present study to estimate the PC mortality that would have been observed in the SA, if similar primary treatment had been applied with identical outcomes to that in the CA, by clinical risk.
2. Patients and methods
The design of the ERSPC has been described previously [9]. The study population of the present analysis encompassed all 14 136 men diagnosed with PC (7310 in the SA; 6826 in the CA), in the core age group of 55–69 yr at randomization (analysis to core age group predefined at the outset [9] and age band that is shared by all centers), in four centers: Finland (n = 8046), The Netherlands (n = 3700), Sweden (n = 1406), and Switzerland (n = 984). These four centers were chosen as they are the largest centers that contribute the most data to the ERSPC trial (87% of PC cases and 88% of PC deaths), and all had clinical prognostic variables and updated data on treatment available for comparability. Cases included those diagnosed from randomization date to December 31, 2013, truncated at 16 yr of follow-up.
Surveillance (deferred treatment) was defined as either active surveillance or watchful waiting. Only primary treatment was available for analysis and was categorized as radical prostatectomy, radiotherapy, surveillance, or hormonal therapy alone. If hormonal treatment was recorded as primary treatment, followed by radical prostatectomy or radiotherapy, then the treatment with curative intent was used. A total of 193 cases (108 in the SA; 85 in the CA) with other or unknown primary treatment were excluded from the main analysis. Deaths were ascertained by linkage with national registries, and causes of death were evaluated in a blinded manner by an independent cause of death committee following a standard algorithm [10], except in Finland where a very high concordance (97%, kappa 0.95) between the committee assignments and official causes of death has been established, and hence the official causes of death were used [11].
2.1. Statistical analysis
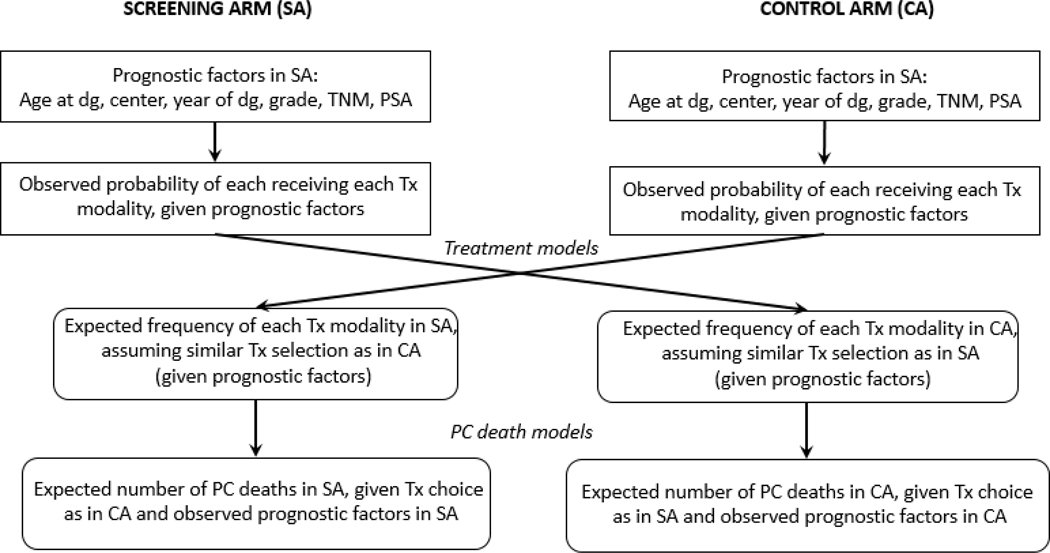
We used a potential outcome approach applying a counterfactual method, estimating what the outcome would have been if the (counterfactual) treatment allocation in one trial arm had been identical to that in the other arm, while the risk of dying from PC remained the same once the choice of treatment had been fixed [12,13]. In short, this was done in the following steps (see Fig. 1):
Fig. 1 –
Description of study methodology. CA = control arm; dg = diagnosis; PC = prostate cancer; PSA = prostate-specific antigen; SA = screening arm; TNM = tumor, node, metastasis stage; Tx = treatment.
One model for treatment allocation was fitted for each arm separately.
For each arm and treatment, a model for PC death was fitted.
The expected number of men in the SA dying from PC had they been allocated a treatment as in the CA was calculated by combining steps 1 and 2. The same procedure was carried out for the men in the CA.
The potential outcome in the SA (ie, the expected number of men in the SA dying from PC, had they been allocated a treatment as in the CA) was compared with the observed outcome, and correspondingly in the CA.
Details of the different steps are given below.
2.1.1. Treatment allocation models
Treatment allocation was modeled by means of multinomial logistic regression, for the SA and CA separately. The following variables were used as covariates: center (categorical), age at diagnosis (yr), year at diagnosis (≥year 2000 vs <year 2000; this year was chosen to mark the start of the PSA era and noticeable uptick in the incidence of PC detected at a curable stage in Europe [14,15]; a sensitivity analysis was performed, split at year 2005, when combined treatment for localized disease became available), PSA level (to reflect clinical risk grouping: ≤10 ng/ml, >10 ng/ml and ≤20 ng/ml, >20 ng/ml, missing or 0), grade group (1, 2–3, 4–5, missing), clinical T stage (T1abc/Tx/missing, T2, T3–4), N and M stages (both N0 and M0, at least one N1 or M1, otherwise missing).
2.1.2. PC death models
For each treatment, logistic regression models were fitted for risk of PC death. This was done separately for the SA and CA. Log of follow-up time from randomization was used as an offset [16,17]. The same variables were used as covariates as for the treatment allocation models.
2.1.3. Potential outcomes in the SA and CA, had the men been given treatments as in the opposite arm
For the men in the SA:
The treatment allocation model based on the CA was used to estimate potential treatments based on the men’s individual values of the covariates.
For each treatment, the risk of PC death was estimated for each man based on his values of the covariates using the PC death models based on the SA (the true arm).
The estimates in (1) and (2) were combined to achieve the risk of PC death for each man. The risk can be seen as a weighted average of the risk of PC deaths for the different treatments (using the total probability theorem).
Summing these numbers for all men in the SA gives the expected number of PC deaths.
The same procedure was carried out for the men in the CA.
2.1.4. Comparison of observed and potential numbers of PC deaths
The potential outcome in the SA (ie, the expected number of men in the SA dying from PC, had they been allocated a treatment as in the CA) was compared with the observed outcome, and correspondingly in the CA.
In order to estimate the uncertainty in the estimates, nonparametric bootstrapping was used; 2000 bootstrap samples were drawn, and the whole procedure was applied to each bootstrap sample. Confidence intervals (CIs) for the difference in the number and proportion of the different treatments, and in PC deaths were then derived by means of the so-called basic method [18]. Categories for missing data were used in the main analysis. As a sensitivity analysis, modeling was performed on complete cases only. Furthermore, three more sensitivity analyses were carried out: cutoff for the year of diagnosis at 2005 instead of 2000, excluding one center at a time, and men with “other/unknown” treatments being treated in an extreme fashion (all men with missing data in one arm got the same treatment, with a similar approach being followed in the other arm, for all combinations of treatments; Supplementary Appendix A).
Simulations of different scenarios were performed in order to show that the modeling strategy gave reliable results (Supplementary Appendix B). The actual trial data were used, but treatments and PC deaths were altered in a random fashion in two different scenarios. In the first scenario, treatment distributions and risks of death were chosen so that there was a theoretical difference between “observed” PC deaths in the CA and PC deaths predicted by the treatment model based on the SA, and vice versa. In the second scenario, random reordering of PC deaths and treatments was done, which should lead to the conclusion that “observed” and predicted PC deaths were the same. Statistical analyses were performed using R version 3.3.1.
A step-by-step example of the methodology is illustrated in Supplementary Appendix C.
3. Results
The analysis comprised 14 136 men with a follow-up of 16 yr. Supplementary Table 1 shows the number of PC cases by center and trial arm, with Finland contributing the largest number of participants, followed by The Netherlands, Sweden, and Switzerland.
Screening introduced a stage and grade shift, with a higher proportion of tumors of lower stage and grade in the SA than in the CA, and conversely, fewer men with metastasized disease in the SA (Table 1).
Table 1 –
Patient characteristics
| Screening arm | Control arm | Total | |
|---|---|---|---|
| Number of men | 7310 | 6826 | 14 136 |
| Age at diagnosis (yr), median (IQR) | 67 (64, 71) | 69 (66, 73) | 68 (65, 72) |
| PSA at diagnosis (ng/ml), median (IQR) | 6.0 (4.1, 10.5) | 9.8 (6.3, 18.4) | 7.7 (4.7, 14.0) |
| Missinga, n (%) | 159 (2) | 316 (5) | 475 (3) |
| Time from diagnosis to treatment (d), median (IQR) | 54 (33, 89) | 47 (26, 80) | 50 (29, 84) |
| Missing, n (%) | 330 (5) | 357 (5) | 687 (5) |
| Follow-up from diagnosis (yr), median (IQR) | 7.6 (4.2, 11.6) | 5.5 (2.4, 8.8) | 6.8 (3.2, 10.6) |
| Biopsy grade group, n (%) | |||
| 1 | 4680 (64) | 3137 (46) | 7817 (55) |
| 2–3 | 1671 (23) | 2185 (32) | 3856 (27) |
| 4 | 395 (5) | 574 (8) | 969 (7) |
| 5 | 339 (5) | 662 (10) | 1001 (7) |
| Missing | 225 (3) | 268 (4) | 493 (4) |
| Clinical T stage, n (%) | |||
| T1a, b, c | 4585 (63) | 3632 (53) | 8217 (58) |
| T2 | 1818 (25) | 1609 (24) | 3427 (24) |
| T3 | 708 (10) | 1169 (17) | 1877 (13) |
| T4 | 128 (2) | 293 (4) | 421 (3) |
| Missing | 71 (1) | 120 (2) | 191 (1) |
| Clinical M stage, n (%) | |||
| M0 | 5164 (71) | 4371 (65) | 9535 (68) |
| Ml | 259 (4) | 559 (8) | 818 (6) |
| Missing | 1848 (25) | 1846 (27) | 3694 (26) |
| Clinical N stage, n (%) | |||
| N0 | 2942 (40) | 1614 (24) | 4556 (32) |
| N1 | 85 (1) | 166 (2) | 251 (2) |
| Missing | 4283 (59) | 5046 (74) | 9329 (66) |
IQR = interquartile range; M = metastasis; N = node; PSA = prostate-specific antigen; T = tumor.
Missing includes men with unknown or other treatment.
Supplementary Table 2 shows the distributions of treatment by trial center and trial arm. Surveillance and radical prostatectomy were used more frequently in the SA, and conversely, radiation therapy and hormonal therapy were more common in the CA. Surveillance was frequently utilized in both trial arms in Sweden (45% in the SA and 34% in the CA), whereas radiotherapy was frequently used in both trial arms in Finland and The Netherlands. Radical prostatectomy was common in Switzerland.
Figure 2 (data included in Table 2) shows the observed and estimated treatment distributions by trial arms for the four centers together. Adjusting for center, age at diagnosis, year at diagnosis, PSA level, grade group, and tumor-node-metastasis stage, the difference between the estimated (adjusted) and observed treatment distributions in the respective arms was marginal. The difference between the observed and estimated treatment distributions (hormonal therapy, radical prostatectomy, radiotherapy, and surveillance/watchful waiting) in the two arms ranged from –3.3% to 3.3%. These figures, which represent the part of the treatment differences between arms that cannot be explained by clinicopathological differences, are small compared with the observed differences between arms that ranged between 7.2% and 10.1%.
Fig. 2 –

Observed and estimated treatments by trial arm (data included in Table 2). CA = control arm; CI = confidence interval; est = estimated; HT = hormone therapy; N = number; obs = observed; RP = radical prostatectomy; RT = radiotherapy; S = surveillance; SA = screening arm.
Table 2 –
Observed and estimated treatments by trial arm among men with prostate cancer (data illustrated in Fig. 2)
| Treatment | Screening arm (SA) | Control arm (CA) | Difference(SA – CA) | ||||
|---|---|---|---|---|---|---|---|
| Observed, N (%) | Estimated CA model, N (%) | Difference: estimated CA model – observed in SA, % (95% CI) |
Observed, N (%) | Estimated SA model, N (%) | Difference: estimated SA model – observed in CA, % (95% CI) | Observed (%) | |
| Hormonal therapy | 692 (9.6) | 709 (9.8) | 0.2 (–0.5, 0.9) | 1274 (19.0) | 1271 (18.9) | –0.1 (–1.3, 1.2) | 9.4 |
| Radical prostatectomy | 2315 (32.0) | 2298 (31.8) | –0.2 (–2.0, 1.5) | 1472 (21.9) | 1523 (22.7) | 0.8 (–0.5, 2.1) | 10.1 |
| Radiotherapy | 2202 (30.5) | 2441 (33.8) | 3.3 (1.6, 5.0) | 2575 (38.4) | 2351 (35.0) | –3.3 (–5.0, –1.6) | 7.9 |
| Surveillance | 2016 (27.9) | 1777 (24.6) | –3.3 (–4.9, –1.7) | 1387 (20.7) | 1563 (23.3) | 2.6 (1.4, 3.8) | 7.2 |
CI = confidence interval.
Similarly, as seen in Table 3, the difference in the estimated and observed numbers of PC deaths was very small. The difference between the observed and estimated numbers of PC deaths among men with PC was 0.05% (95% CI –0.1%, 0.2%) when applying the CA model to the SA and 0.01% (95% CI – 0.3%, 0.2%) when applying the SA model to the CA, had the two groups received identical primary treatment, given their clinical characteristics. As the observed difference between trial arms was 4.2%, our findings suggest that differential treatment explains only a trivial proportion of the main findings of ERSPC. Similar findings were seen in a complete case-only analysis (Fig. 3, data included in Table 2). In our simulation studies of our method, the estimates produced by our approach were similar to those entered as parameters in the simulations, hence supporting the reliability of the results presented here (Supplementary Appendix B). In the sensitivity analyses, the absolute difference between observed and estimated PC deaths was <0.2%, except for the case where Finland was excluded. Then the SA model led to a somewhat lower number of estimated PC deaths than in the CA, and the difference was 0.5% (Supplementary Appendix A).
Table 3 –
Observed and estimated numbers of prostate cancer deaths among men with prostate cancer (data illustrated in Fig. 3)a
| Screening arm (SA) | Control arm (CA) | Difference(SA – CA) | |||||
|---|---|---|---|---|---|---|---|
| Observed, N (%) | Estimated CA model, N (%) | Difference: estimated CA model – observed in SA, % (95% CI) |
Observed, N (%) | Estimated SA model, N (%) | Difference: estimated SA model – observed in CA, % (95% CI) | Observed (%) | |
| Main analysis: all data | 442 (6.1) | 446.6 (6.2) | 0.05 (–0.1%, 0.2%) | 691 (10.3) | 691.8 (10.3) | 0.01 (–0.3%, 0.2%) | 4.2 |
| Sensitivity analysis: complete cases | 388 (5.7) | 390.4 (5.7) | 0.03 (–0.2%, 0.2%) | 580 (9.5) | 580.8 (9.5) | 0.01 (–0.3%, 0.3%) | 3.8 |
CI = confidence interval.
Tumor nodal (N) and metastasis (M) stages are not used for death models in the sensitivity analysis.
Fig. 3 –

Observed and estimated numbers of prostate cancer deaths (data included in Table 3). CA = control arm; CI = confidence interval; est = estimated; HT = hormone therapy; N = number; obs = observed; PC = prostate cancer; RP = radical prostatectomy; RT = radiotherapy; S = surveillance; SA = screening arm.
4. Discussion
We undertook the present study to assess the contribution of treatment differences to the observed PC mortality reduction between trial arms in ERSPC.
Despite adjusting slight differences in treatment distributions between trial arms for prognostic variables, these differences in treatment had little effect on PC mortality. The difference in the number of PC deaths between the estimated and observed models was small (0.01–0.05%). The consistency of the results of the models supports the robustness of the modeling approach. Therefore, it is unlikely that the reduction in PC mortality in the ERSPC trial is attributable to differential treatment between trial arms; rather, the PC mortality reduction mainly reflects the effect of PSA screening leading to early detection, allowing for effective management.
This study has several strengths. Rather than using strata of tumor risk groups, prognostic variables were included in multivariable models predicting treatment and PC death. This approach minimizes subtle differences in tumor characteristics, which would have been missed if data had been categorized into risk groups. In particular, the high-risk group, as generally defined, is very heterogeneous. For instance, a man with a screen-detected, small-volume, grade group 4, clinically nonpalpable tumor (clinical stage T1c) with a low PSA value would be classified as having a “high risk,” as would a man with grade group 5, T3 tumor, and a high PSA value of up to 100 ng/ml. Owing to this heterogeneity in risk grouping, patients in the CA may still have more advanced tumor features than men in the SA, within similar risk groups. Using multivariable models rather than risk grouping thus aims to account for any slight difference in treatment distribution that can occur within risk groups, even if men with similar disease are treated similarly irrespective of the trial arm.
Furthermore, men in the SA were slightly younger at diagnosis (median 67 yr) than the men in the CA (median 69 yr), which might affect treatment choice. Even if the age difference is small, it may result in more aggressive treatment for men in the SA. We addressed this issue by adjusting for age.
As men in the CA were treated later in time, because they were diagnosed more recently than men in the SA (due to lead time gained by screening), new, effective treatments could have become available for men in the CA. For instance, during the study period, multimodal treatment of locally advanced PC has been shown to yield more favorable outcomes than surgery or radiation alone [19] In The Netherlands center, a prior study from ERSPC reported that treatment patterns differed slightly between trial arms; for instance, radiotherapy was more often combined with hormonal therapy and radiation dosages were often higher than 69 Gy in the CA, relative to the SA, likely reflecting later detection in the CA, and development and adoption of novel treatment modalities over time [20]. Despite these differences favoring the CA, differences in disease-free survival between the arms were reported to be minimal [20] We attempted to control for the effect of treatment development over the study period by adjusting for the year of treatment; however, a lack of granular information regarding treatment received remains a limitation of this study.
Others strengths are that the study is based on a very large patient cohort, and the setting of a randomized screening trial, which is a major advantage, increased comparability between the arms. Data from each center were sent to an independent central database every 6 mo from the beginning of this study. A quality control committee ensured standardized tumor classification within each center. A pathology committee co-ordinated biopsy grading. A PSA committee conducted intercomparisons of all laboratories involved in the trial. The endpoint, that is, death from PC, was evaluated by COD committees that analyzed deaths in men with PC in a blinded fashion, that is, unaware of trial allocation [9,10].
This study is not devoid of limitations. One of its limitations is that it was able to include only four centers of the ERSPC in the analysis with available clinicopathological variables and treatment data, and still had some missing data on prognostic factors (slightly more missing data in the CA) and lack of detailed treatment information, because only primary treatment data were collected in the trial. Any effect of secondary treatment upon disease recurrence on PC mortality would be smaller than that of primary treatment with curative intent, and we have no reason to believe that men in the SA received more frequent or higher-quality secondary treatments than those in the CA. The current study did not aim to address whether treatment quality differed between trial arms, or whether men received treatment at academic high-volume centers in one arm more frequently than in the other. It has been hypothesized that “men in the screening group received treatment at a few centers that specialized in treatment of prostate cancer [whereas] the men in the control group received standard care in their community [and] that is likely to account for some and possibly all of the survival benefit” [3]. In The Netherlands’ center, men diagnosed with PC were referred back to their primary care physicians for further management and referral. In the Swedish, Finnish, and Swiss centers, because the studies were concentrated in defined geographical areas, the same referral hospitals were largely responsible for treatments of men in both arms [21,22].
5. Conclusions
In conclusion, based on multivariable modeling data from the ERSPC trial, differences in the receipt of primary treatment between the SA and CA were minimal, and the potential effect of these differences on PC mortality was extremely small. These findings suggest that the effectiveness of PSA screening in reducing PC mortality in the ERSPC trial was largely due to early detection, allowing for effective management, and was not attributable to differential treatment between trial arms.
Supplementary Material
Acknowledgments:
We thank Dr. Andrew Vickers at Memorial Sloan Kettering Cancer Center for advice on the statistical methods. Gathering detailed information on treatment within ERSPC Rotterdam was made feasible through unconditional support of the Rotterdam Prostate Cancer Foundation (SWOP).
Funding/Support and role of the sponsor: The funding of the ERSPC trial was obtained from national cancer research funding agencies, European funding in the form of framework programs, private sponsors, and a grant from the former Beckman/Hybritech company. Sigrid V. Carlsson’s work on this study was supported by grants from AFA Insurance, the Swedish Cancer Society, the Sweden America Foundation, the Swedish Council for Working Life and Social Research, the Swedish Society for Medical Research, and the Swedish Prostate Cancer Foundation. Sigrid V. Carlsson is further supported in part by a Cancer Center Support Grant from the National Cancer Institute made to Memorial Sloan Kettering Cancer Center (P30-CA008748), a SPORE grant from the National Cancer Institute to Dr. H. Scher (P50-CA092629) and the David H. Koch prostate cancer research fund. This work was further supported by a Movember grant from the Cancer Society of Finland, Academy of Finland. The funding sources had no role in the study design, data collection, data analysis, data interpretation, or manuscript writing.
Footnotes
Financial disclosures: Sigrid V. Carlsson certifies that all conflicts of interest, including specific financial interests and relationships and affiliations relevant to the subject matter or materials discussed in the manuscript (eg, employment/affiliation, grants or funding, consultancies, honoraria, stock ownership or options, expert testimony, royalties, or patents filed, received, or pending), are the following: Sigrid V. Carlsson has received a lecture honorarium and travel support from Astellas Pharma (unrelated to current study). Maciej Kwiatkowski reports travel support from Janssen and Astellas. No other author has any conflict of interest to disclose.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Hugosson J, Roobol MJ, et al. A 16-yr Follow-up of the European Randomized study of Screening for Prostate Cancer. Eur Urol. 2019;76(1):43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Barry MJ. Screening for prostate cancer—the controversy that refuses to die. N Engl J Med 2009;360:1351–4. [DOI] [PubMed] [Google Scholar]
- [3].Brawley O. American Cancer Society press room. https://acspressroom.wordpress.com/2010/07/01/digging-deeper-into-prostate-screening-study/ [Google Scholar]
- [4].Haines IE, Gabor Miklos GL. Prostate-specific antigen screening trials and prostate cancer deaths: the androgen deprivation connection. J Natl Cancer Inst 2013;105:1534–9. [DOI] [PubMed] [Google Scholar]
- [5].Carlsson S, Roobol MJ, Schroder FH, Hugosson J, Auvinen A. RE: Prostate-specific antigen screening trials and prostate cancer deaths: the androgen deprivation connection. J Natl Cancer Inst 2014;106:dju079. [DOI] [PubMed] [Google Scholar]
- [6].Carter HB. Reducing prostate cancer deaths: unsupported speculation about the androgen deprivation hypothesis. Eur Urol 2014;66:973–4. [DOI] [PubMed] [Google Scholar]
- [7].Schroder FH, Hugosson J, Carlsson S, et al. Screening for prostate cancer decreases the risk of developing metastatic disease: findings from the European Randomized Study of Screening for Prostate Cancer (ERSPC). Eur Urol 2012;62:745–52. [DOI] [PubMed] [Google Scholar]
- [8].Wolters T, Roobol MJ, Steyerberg EW, et al. The effect of study arm on prostate cancer treatment in the large screening trial ERSPC. Int J Cancer 2010;126:2387–93. [DOI] [PubMed] [Google Scholar]
- [9].Schroder FH, Hugosson J, Roobol MJ, et al. Screening and prostate-cancer mortality in a randomized European study. N Engl J Med 2009;360:1320–8. [DOI] [PubMed] [Google Scholar]
- [10].De Koning HJ, Blom J, Merkelbach JW, et al. Determining the cause of death in randomized screening trial(s) for prostate cancer. BJU Int 2003;92(Suppl 2):71–8. [DOI] [PubMed] [Google Scholar]
- [11].Makinen T, Karhunen P, Aro J, Lahtela J, Maattanen L, Auvinen A. Assessment of causes of death in a prostate cancer screening trial. Int J Cancer 2008;122:413–7. [DOI] [PubMed] [Google Scholar]
- [12].Cuzick J, Edwards R, Segnan N. Adjusting for non-compliance and contamination in randomized clinical trials. Stat Med 1997;16:1017–29. [DOI] [PubMed] [Google Scholar]
- [13].Kilpelainen TP, Tammela TL, Malila N, et al. The Finnish prostate cancer screening trial: analyses on the screening failures. Int J Cancer. 2015;136:2437–43. [DOI] [PubMed] [Google Scholar]
- [14].Jonsson H, Holmstrom B, Duffy SW, Stattin P. Uptake of prostate-specific antigen testing for early prostate cancer detection in Sweden. Int J Cancer 2011;129:1881–8. [DOI] [PubMed] [Google Scholar]
- [15].Bray F, Lortet-Tieulent J, Ferlay J, Forman D, Auvinen A. Prostate cancer incidence and mortality trends in 37 European countries: an overview. Eur J Cancer 2010;46:3040–52. [DOI] [PubMed] [Google Scholar]
- [16].Anderson D, Feldblum C, Modlin D, Schirmacher D, Schirmacher E, Thandi N. A practitioner’s guide to generalized linear models. Casualty Actuarial Society Discussion Paper Program; 2004. p. 1–116. [Google Scholar]
- [17].Hilbe J. Generalized linear models and extensions. College Station, TX: Stata Press; 2001. [Google Scholar]
- [18].Davison AC, Hinkley DV. Bootstrap methods and their application. Chapter 5.2. Cambridge University Press; 1997. [Google Scholar]
- [19].Widmark A, Klepp O, Solberg A, et al. Endocrine treatment, with or without radiotherapy, in locally advanced prostate cancer (SPCG-7/SFUO-3): an open randomised phase III trial. Lancet 2009;373:301–8. [DOI] [PubMed] [Google Scholar]
- [20].Bokhorst LP, Kranse R, Venderbos LD, et al. Differences in treatment and outcome after treatment with curative intent in the screening and control arms of the ERSPC Rotterdam. Eur Urol 2015;68:179–82. [DOI] [PubMed] [Google Scholar]
- [21].Hugosson J, Carlsson S, Aus G, et al. Mortality results from the Goteborg randomised population-based prostate-cancer screening trial. Lancet Oncol 2010;11:725–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Kilpelainen TP, Tammela TL, Malila N, et al. Prostate cancer mortality in the Finnish randomized screening trial. J Natl Cancer Inst 2013;105:719–25. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.