Bayesian Utility-Based Designs for Subgroup-Specific Treatment Comparison and Early-Phase Dose Optimization in Oncology Clinical Trials

Abstract

PURPOSE

Despite the fact that almost any sample of patients with a particular disease is heterogeneous, most clinical trial designs ignore the possibility that treatment or dose effects may differ between prognostic or biologically defined subgroups. This article reviews two clinical trial designs that make subgroup-specific decisions and compares each to a simpler design that ignores patient heterogeneity. The purpose is to illustrate the benefits of accounting prospectively for treatment-subgroup interactions and how utilities may be used to quantify risk-benefit trade-offs.

METHODS

Two Bayesian clinical trial designs that perform subgroup-specific decision making and inference based on elicited utilities of patient outcomes are reviewed. The first is a randomized comparative trial of nutritional prehabilitation for patients undergoing esophageal resection that has two prognostic subgroups and is based on postoperative morbidity score. The second is a sequentially adaptive trial of natural killer cells for treating hematologic malignancies that is based on five time-to-event outcomes and that performs safety monitoring and optimizes cell dose within six disease subgroups. Computer simulations under a range of different scenarios are presented for each design to establish its operating characteristics and compare it to a more conventional design that ignores patient heterogeneity.

RESULTS

Each design has attractive operating characteristics, is greatly superior to a simplified design that ignores patient subgroups, is robust to deviations from its assumed statistical model, and is feasible to use for conducting trials.

CONCLUSION

Bayesian designs that make subgroup-specific decisions in randomized comparative trials or sequentially adaptive early-phase dose-finding trials are superior to designs that ignore patient heterogeneity. Using elicited utilities of complex patient outcomes to quantify risk-benefit trade-offs provides a practical and ethical basis for decision making and treatment evaluation in clinical trials.

INTRODUCTION

By definition, good- and poor-prognosis patients have different response rates and mean survival times. Most clinical trial designs ignore this fact. Similarly, qualitatively different disease subtypes or biologically defined subgroups typically are ignored by the decision rules and hypotheses of conventional trial designs, aside from possibly stratifying on subgroups when randomly assigning patients. Ignoring the possibility of treatment-subgroup interactions by making one-size-fits-all decisions and inferences runs the risk of making incorrect conclusions within important patient subgroups. This problem persists in all phases of conventional trial designs, from early-phase dose-finding to randomized comparative trials.

To illustrate the problem, consider a prospective randomized trial in patients with relapsed or refractory leukemia, with the aim of evaluating the effect on overall survival (OS) of adding a new targeted agent, X, to standard chemotherapy. Suppose that the historical mean OS with chemotherapy is μ_old = 15 months in older patients (age 60 years or older) and μ_young = 24 months in younger patients (age younger than 60 years), with two thirds of patients being older than age 60 years and one third being younger. A group sequential design comparing chemotherapy + X with chemotherapy constructed on the basis of the average mean OS, μ_avg = (2/3) μ_old + (1/3) μ_young, would have null mean OS μ_avg⁰ = (2/3)15 + (1/3)24 = 18 months. Suppose a design is constructed to target an improvement of 33% from μ_avg⁰ = 18 to μ_avg* = 24 months, equivalently, a targeted hazard ratio of .75 in favor of chemotherapy + X. To see what could go wrong, notice that the average target μ_avg* = 24 months for chemotherapy + X equals the null historical mean with chemotherapy alone in younger patients. Suppose that, in fact, adding X to chemotherapy decreases mean OS in older patients by 10% to 13.5 months but increases mean OS in younger patients by 30% to 31.2 months, that is, there is a treatment-age subgroup interaction. The overall mean OS with chemotherapy + X then would be (2/3)13.5 + (1/3)31.2 = 19.4 months, well below the target μ_avg* = 24 months and close to the null value μ_avg⁰ = 18 months. Thus, a group sequential test based on average mean OS would be likely to conclude that adding X to chemotherapy fails to improve OS, thus making a false-negative conclusion in younger patients. Although post-trial data analyses accounting for age may show that chemotherapy + X is superior in younger patients, such an inference may be dismissed as post hoc data dredging, that is, searching the data set for subgroups in which the X effect is nominally significant. Arguing for the future use of chemotherapy + X in younger patients thus would be problematic, and it probably would be necessary to repeat the trial, if possible.

CONTEXT

• Key Objective

• An important question in designing and conducting clinical trials is whether and how a trial design should account explicitly and prospectively for patient heterogeneity when making treatment assignment decisions and reaching final conclusions. The two designs reviewed in this article illustrate how a Bayesian utility-based framework can be used to construct practical designs that account for patient heterogeneity.

• Knowledge Generated

• Each of the two designs—one is a randomized comparative trial and the other is a complex dose-finding trial—is a novel methodology that has been published in the statistical literature. An aim of this review is to make members of the medical community aware that such designs exist so that they may consider taking this sort of approach in their own trials.

• Relevance

• The Bayesian utility-based approach may be used to construct designs for a wide variety of clinical trials that account for patient heterogeneity by making subgroup-specific, personalized treatment decisions. In the presence of patient heterogeneity, this approach refines treatment development and evaluation and thus is more likely to protect safety and provide benefit for both the patients enrolled in the trial and future patients.

Similar problems arise in early-phase trials in which the goal is to identify an optimal dose, dose pair, or (dose, schedule) combination for a new agent or treatment combination at the start of clinical evaluation. It has been well established that choosing a dose in a phase I trial on the basis of toxicity alone is a highly flawed convention that can easily lead to choosing an unsafe or ineffective dose.^1,2 As a first example of this problem, consider a trial to optimize the dose d among five levels (1, 2, 3, 4, 5). Suppose the respective toxicity probabilities are (.10, .15, .30, .40, .55) and the response probabilities are (.00, .01, .01, .02, .02). If the continual reassessment method (CRM)³ is used to choose a dose with Pr(toxicity) closest to .30, then d = 3 is most likely to be chosen, whereas a 3+3 algorithm is most likely to choose either d = 2 or d = 3. But because no dose has any substantive anti-disease effect, choosing a maximum tolerated dose (MTD) with either method is a severe error, simply because both phase I methods are based only on toxicity. As a second example, if the toxicity probabilities are (.10, .18, .30, .38, .45) and the response probabilities are (.10, .15, .30, .60, .65), then the CRM with target Pr(toxicity) = .30 will be most likely to choose d = 3, but d = 4 has toxicity probability only .08 larger than that of d = 3, whereas it doubles the response rate from .30 to .60. These examples show that the convention of choosing the dose of a new agent on the basis of toxicity while ignoring response is dysfunctional.

In contrast, phase I/II designs^1,2,4 determine an optimal dose based on both R = response and T = toxicity. For example, if both outcomes are binary, then one may assign the numerical utilities U(R, No T) = 100, U(R, T) = 70, U(No R, No T) = 40, U(No R, T) = 0 to the four possible elementary outcomes. In practice, the best and worst outcomes are assigned respective utilities of 100 and 0, and numerical utilities between these two values for intermediate outcomes are elicited from the investigators planning the trial. Suppose that the probabilities of these four events at a dose d in G = good-prognosis patients are Pr(R, No T|d, G) = .30; Pr(R, T|d, G) = .20; Pr(No R, No T|d, G) = .40; Pr(No R, T|d, G) = .10. Then the marginal probabilities of R and T at dose d in subgroup G are Pr(R|d, G) = .50 and Pr(T|d, G) = .30, and the mean utility of d in G is the average U_avg(d, G) = .30 × 100 + .20 × 70 + .40 × 40 + .10 × 0 = 60. During trial conduct, the posterior mean of U_avg(d, G) is computed for each d, and the dose giving the largest value is selected for the next good-prognosis patient enrolled. Similarly, if the corresponding elementary outcome probabilities for subgroup P are .10, .30, .30, .30, then Pr(R|d, P) = .40 and Pr(T|d, P) = .60, and the mean utility of dose d in subgroup P is U_avg(d, P) = .10 × 100 + .30 × 70 + .30 × 40 + .30 × 0 = 43. But if the prognostic subgroups are ignored, assuming that Pr(Good) = Pr(Poor) = .50, then the average mean utility of dose d would be 51.5, which understates its benefit in good-prognosis patients and overstates its benefit in poor-prognosis patients.

EVALUATING PRESURGERY NUTRITIONAL PREHABILITATION

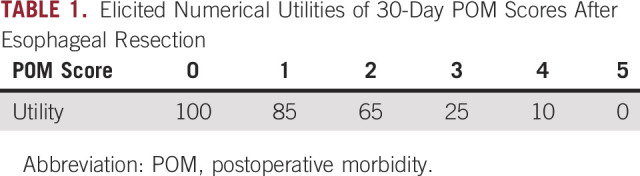
This section reviews a Bayesian design for a randomized comparative group sequential trial to compare nutritional prehabilitation (N) with standard of care (C) for patients with esophageal cancer undergoing chemoradiation and surgery.^5,6 The trial enrolls both primary (P) patients who have not been treated previously and salvage (S) patients whose disease has recurred after previous therapy. The outcome is Y = Clavien-Dindo postoperative morbidity (POM),^7-10 scored within 30 days of surgery, a six-level ordinal variable with possible integer values from 0 (normal recovery) to 5 (death). The design is based on elicited numerical utilities of these outcomes (Table 1), which show that lower POM values are much more desirable. Notice that dichotomizing POM score as high = [Y ≤ 3] versus low = [Y ≤ 2] for convenience would discard valuable information. Moreover, because differences in utilities between successive POM levels are far from being equal, using the raw scores 0, 1, 2, 3, 4, 5 would also be a misleading way to quantify POM.

TABLE 1.

Elicited Numerical Utilities of 30-Day POM Scores After Esophageal Resection

The design accounts for patient heterogeneity by allowing possibly different conclusions within the subgroups P and S when comparing treatment N to C. A group sequential testing procedure is based on the posterior utilities for the POM score computed under an assumed Bayesian probability model for Y. A key property of the model is that all treatment and subgroup effect parameters vary with the level of POM score, so it is a robust generalization of the conventional proportional odds model.¹¹ The model allows the magnitudes of the N-versus-C effects on Y to differ between subgroups and is formulated to borrow strength between subgroups, with prior location parameters determined from elicited information on POM score. Details are provided in Murray et al.⁶

The trial will enroll a maximum of 200 patients, with an interim comparative test of the N-versus-S effect on POM score after n = 100 patients have been treated and evaluated and possibly a final test at n = 200 within each subgroup P and S. The design allows different conclusions to be made within the prognostic subgroups. Denoting the utility of POM score y in Table 1 by U(y), the mean utility of treatment Z = N or S in subgroup g = P or S is the probability-weighted average

$${\text{U}}_{\text{avg}}\left(\text{Z},\text{g}\right)=100\text{Pr}\left(\text{Y}=0|\text{ Z},\text{g}\right)+85\text{Pr}\left(\text{Y}=1|\text{Z},\text{g}\right)+\dots +10\text{Pr}\left(\text{Y}=4|\text{Z},\text{g}\right).$$

The subgroup-specific comparative tests, computed under the Bayesian model, conclude that N is superior to C in subgroup g = P or S if

$$\text{Pr}\left\{{\text{U}}_{\text{avg}}\left(\text{N},\text{g}\right)>{\text{U}}_{\text{avg}}\left(\text{C},\text{g}\right)|{\text{data}}_{\text{n}}\right\}>{\text{p}}_{\text{cut}}\left(\text{n}\right),$$

and conclude that C is superior to N in subgroup g if

$$\text{Pr}\left\{{\text{U}}_{\text{avg}}\left(\text{C},\text{g}\right)>{\text{U}}_{\text{avg}}\left(\text{N},\text{g}\right)|{\text{data}}_{\text{n}}\right\}>{\text{p}}_{\text{cut}}\left(\text{n}\right),$$

for n = 100 or n = 200. The numerical cutoffs p_cut(100) = .997 and p_cut(200) = .976 were chosen by conducting preliminary computer simulations to control the overall within-subgroup type I error probability of the group sequential test procedure to be ≤ .025. The design targets mean utility differences of 89 – 75.5 = 13.5 in primary patients and 81.3 – 60 = 21.3 in salvage patients. These differences correspond to a reduction in Pr(Y ≥ 3) from 0.20 to 0.08 for primary patients and from 0.35 to 0.14 for salvage patients. As a comparator, a conventional model-based design that ignores subgroups and makes one-size-fits-all treatment comparisons was also considered. To ensure balance and comparability with either design, patients were randomly assigned in blocks of four, so for each block of four patients within each prognostic subgroup, two receive nuprehab and two receive the control.

The operating characteristics of the two designs are summarized in Table 2. For example, under treatment-subgroup interaction scenario 3, nuprehab achieves an improvement of 13.5 in POM score mean utility in the primary patients, but there is no difference between the two treatments in the salvage patients.

TABLE 2.

Operating Characteristics of the Design With Subgroup-Specific Decision Rules and of a Simpler Design That Ignores Subgroups in Each of Four Cases

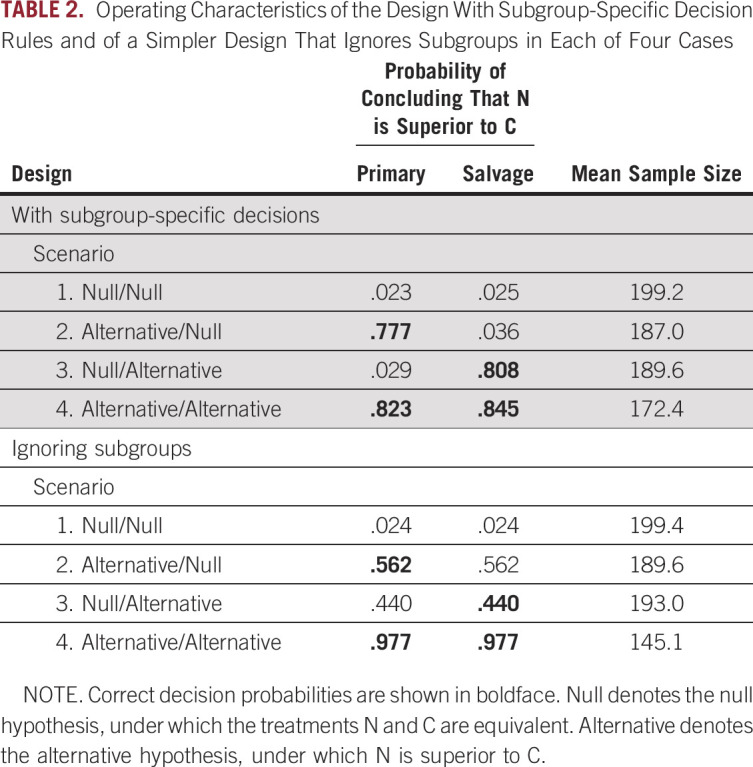
Both designs control the type I error in scenario 1 Null/Null. In scenario 2, where N is truly superior to C in salvage patients but the two treatments are equivalent in primary patients, the subgroup-specific design has power .808 in salvage patients and type I error probability .029 in primary patients. In sharp contrast, the conventional design has power .440; equivalently, type II error probability = 1 – .440 = .560 in salvage patients, and type I error probability = .440 in primary patients. The same sort of thing is seen in scenario 3. Given these huge false-positive and false-negative rates in the mixed scenarios with treatment-subgroup interactions, one could do as well by not running a trial and instead deciding which treatment is better by flipping a coin. The conventional design has much larger power than the subgroup-specific design in scenario 4, however, in which N provides an improvement over C in both subgroups. This loss of power in scenario 4 seems to be the price that must be paid for using a comparative design that allows different decisions to be made within subgroups to accommodate treatment-subgroup interactions.

Given these computer simulation results, the choice of the conventional methodology, which may have extremely large within-subgroup type I and type II error probabilities in the range of .44 to .56, should reflect a strong belief that any N-versus-C effect will be the same in the two prognostic subgroups. A computer program to implement the design, biom12842-sup-0002-SuppSimulation.R, is available from the Wiley Biometrics Web site at https://onlinelibrary.wiley.com/doi/full/10.1111/biom.12842.

OPTIMIZING NATURAL KILLER CELL DOSE

This section reviews a Bayesian design for an early-phase trial of natural killer (NK) cells for treatment of patients with advanced hematologic malignancies,^12,13 including chronic lymphocytic leukemia (CLL), acute lymphocytic leukemia (ALL), and non-Hodgkin lymphoma (NHL).¹⁴ Each patient is also classified as having low-bulk disease (LBD) or high-bulk disease (HBD), for a total of 3 × 2 = 6 (disease type, disease bulk) prognostic subgroups. The trial is designed to enroll a maximum of 60 patients. The goals are to perform safety monitoring and to identify an optimal NK cell dose from the set {10⁵, 10⁶, 10⁷} cells per kg of body weight (hereafter dose levels 1, 2, 3) within each of the subgroups, while borrowing strength between subgroups. This is an example of a sequentially adaptive “precision” or “personalized” clinical trial.

The trial has five coprimary outcomes: the times from NK cell infusion to D = death, and the four nonfatal events P = disease progression, R = response, T = severe toxicity, and C = severe cytokine release syndrome. Each patient’s events are monitored for a 365-day follow-up period. Denoting the time to event j by Y_j for j = D, P, R, T, C for each patient, each Y_j is a potential outcome because it may or may not be observed; Y_P and Y_R are competing risks because, at most, one of these two events can occur; the five potential event times are highly associated with each other; D censors any events that have not occurred, but such censoring is not independent; and the distribution of Y = (Y_D, Y_P, Y_R, Y_T, Y_C) varies substantially with disease subgroup.

Three challenges in designing an NK cell dose-finding trial are (1) if one ignores the subgroups, then there are high probabilities of making incorrect decisions within subgroups; (2) on the basis of current knowledge about NK cell biology, the rates of the five outcomes are neither monotone increasing nor decreasing in NK cell dose; and (3) small to moderate sample sizes in early-phase trials limit the reliability of subgroup-specific decisions. Given the 60-patient maximum overall sample size and assuming that Pr(CLL) = Pr(ALL) = Pr(NHL) = 1/3 and that Pr(LBD) = 1/3 and Pr(HBD) = 2/3, the expected disease subsample sizes are 7 patients for each of the subgroups (LBD, CLL), (LBD, ALL), (LBD, NHL) and 13 patients for each of the subgroups (HBD, CLL), (HBD, ALL), (HBD, NHL). Consequently, to make reasonably reliable decisions, it is essential to assume a dose-subgroup-outcome probability model that borrows strength between subgroups. Thus the design is based on a Bayesian parametric multivariable Weibull regression model with the marginal distribution of each Y_j a function of NK cell dose and disease subgroup. The model includes a hierarchical structure with latent (unobserved) patient frailties to induce association among the five outcomes and account for variability not explained by dose and subgroup. To establish a prior probability distribution, hyper parameters characterizing location were computed from elicited probabilities of particular combinations of events occurring during the first 100 days of follow-up, and prior hyper parameters characterizing dispersion were calibrated to reflect vague prior knowledge about dose effects. Details are given in Lee et al.¹⁴

First assigning utility 0 to any outcome for which the patient dies before day 100, utilities of the 12 possible combinations of nonfatal outcomes during the first 100 days following NK cell infusion were elicited from the principal investigator for the trial (Table 3).

TABLE 3.

Elicited Utilities of the 12 Possible 100-Day Outcomes for Patients in the NK Cell Dose-Finding Trial Who Survive Beyond 100 Days Given That U(Death within 100 days) = 0

Denote the vector of binary indicators of the 12 possible nonfatal outcomes within 100 days by Δ = (Δ_P, Δ_R, Δ_T, Δ_C). For example, the vector (0,1,1,0) indicates that a patient alive at day 100 experienced R and T, but not P or C. The mean utility of assigning a dose d to a patient with disease subgroup g, denoted by U_ave(d, g), is the average of the 12 values of the utility U(Δ) from Table 3, weighted by the probability distribution of [Δ|d, g]. This may be denoted by

$$\begin{array}{l}{\text{U}}_{\text{avg}}\left(\text{d},\text{g}\right)=20\times \text{Pr}\left\{\left(1,0,0,0\right)|\text{d},\text{g}\right\}+ 50\times \text{Pr}\left\{\left(0,0,0,0\right)|\text{d},\text{g}\right\}+\hfill \\ \dots +20\times \text{Pr}\left\{\left(0,0,1,1\right)|\text{d},\text{g}\right\}+ 30\times \text{Pr}\left\{\left(0,1,1,1\right)|\text{d},\text{g}\right\}. \hfill \end{array}$$

The final decision criterion for choosing an optimal dose within each of the six disease (type, bulk) subgroups is the posterior mean of U_avg(d, g) given the observed data, denoted by u(d,g|data), computed under the assumed Bayesian model.

To ensure that the trial is ethical, the design includes subgroup-specific safety monitoring rules that terminate assignment to a disease subgroup g of a dose found to have an unacceptably high probability p_D100(g) of death within 100 days for that subgroup. Elicited subgroup-specific limits on p_D100(g) were used to formulate these rules. During the trial, for each disease type, patients are randomly assigned among the three doses in order of entry to the trial by randomly permuting the integers (1, 2, 3), subject to being in accordance with the safety rule. At the end of the trial, for each disease subgroup g, the NK cell dose d that is safe and that maximizes u(d, g|data) is chosen, with no dose chosen if all three are unsafe within subgroup g.

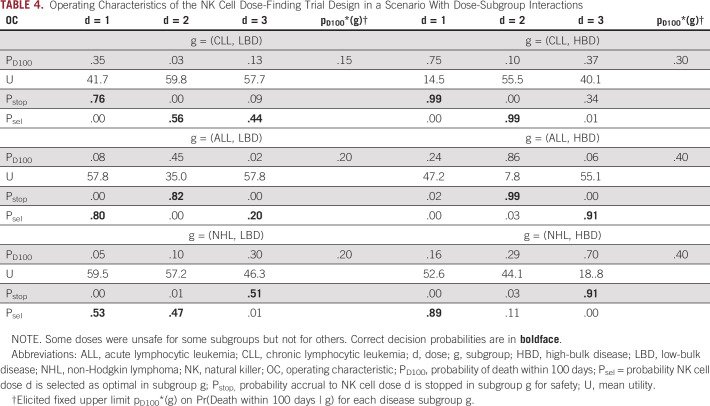
To establish its operating characteristics, the design was simulated under each of six different possible dose-subgroup-outcome scenarios. Table 4 summarizes the operating characteristics of the design in one particular scenario that includes dose-subgroup interactions, with some doses unsafe for some subgroups but not for others. The results in Table 4 show that the design is likely to stop accrual to doses in subgroups in which they are unsafe and otherwise is likely to select the truly optimal dose in each subgroup.

TABLE 4.

Operating Characteristics of the NK Cell Dose-Finding Trial Design in a Scenario With Dose-Subgroup Interactions

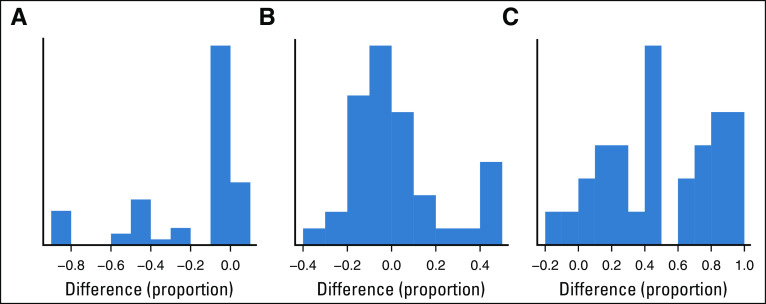
Figure 1 compares the dose-finding design that makes subgroup-specific decisions with a similar design that ignores the six disease subgroups when performing safety monitoring and dose selection. Histograms are given for the differences between the empirical proportions of Pr(stop|subgroup, dose) and Pr(stop|dose), for truly safe doses (Fig 1A) and for truly unsafe doses (Fig 1B) on the basis of computer simulations under the six dose-subgroup-outcome scenarios. Because the figure shows that it is likely that Pr(stop|subgroup, dose) < Pr(stop|dose) for truly safe doses, the design that ignores subgroups has a much larger probability of incorrectly stopping treatment in subgroups in which doses are safe. For truly unsafe doses, the two designs have similar stopping probabilities, with the important exception that the design with subgroup-specific safety monitoring is about .40 more likely to stop accrual to truly unsafe doses within subgroups. Figure 1C shows that the subgroup-specific design is much more likely to select truly optimal doses within disease subgroups.

FIG 1.

Comparison of the design with subgroup-specific safety monitoring and optimal dose selection with a design that ignores subgroups. Histograms of differences between empirical proportions of Pr(stop|subgroup, dose) – Pr(stop|dose) are given for (A) truly safe doses, (B) truly unsafe doses, and (C) Pr(select|subgroup, dose) – Pr(select|dose) differences showing the probabilities of correctly selecting truly optimal doses.

Additional computer simulations (not shown) evaluated the behavior of the NK cell dose-finding design in cases in which the true underlying time-to-event distributions were log-logistic and thus differed substantially from the assumed Weibull dose-subgroup-outcome probability model. The results show that the model and design are extremely robust to the true underlying event time distribution model and that the superior properties of the design persist. Details are provided in Lee et al.¹⁴ The NKcelldosefinding computer program for implementing this design is available at https://users.soe.ucsc.edu/∼juheelee/.

Utility-based clinical trial designs for a wide variety of other settings, assuming that patients are homogeneous, are given in Houede et al,¹⁵ Thall et al,^4,16-18 Lee et al,¹⁹ Hobbs et al,²⁰ Murray et al,²¹ and Xu et al.²² An explanation of how utility-based clinical trial design can be formulated as a decision-making problem is provided by Mueller et al.²³

The simulation results show that the designs that make subgroup-specific decisions are greatly superior to competing conventional methodologies that ignore patient heterogeneity and treatment-subgroup or dose-subgroup interactions when such subgroup effects are present. In the randomized comparative trial, this is seen in terms of extremely large within-subgroup type I and type II error probabilities of the conventional design in cases of treatment-subgroup interactions. However, when significant treatment effects are homogeneous across subgroups, the conventional design has larger power. In the dose-finding trial, there are reduced safety and also smaller probabilities of selecting truly optimal doses within disease subgroups for the design that ignores subgroups. These results strongly suggest that if patient heterogeneity is known, conventional clinical trial designs should be replaced by designs that account explicitly and prospectively for patient subgroups and treatment-subgroup or dose-subgroup effects in trial design, conduct, and decision making. An important caveat is that, if enrollment to a trial is limited to a homogeneous patient population, then a design with subgroup-specific rules would be an inappropriate elaboration.

AUTHOR’S DISCLOSURES OF POTENTIAL CONFLICTS OF INTEREST

The following represents disclosure information provided by authors of this manuscript. All relationships are considered compensated. Relationships are self-held unless noted. I = Immediate Family Member, Inst = My Institution. Relationships may not relate to the subject matter of this manuscript. For more information about ASCO's conflict of interest policy, please refer to www.asco.org/rwc or ascopubs.org/po/author-center

No potential conflicts of interest were reported.