A New Paradigm for DNA Polymerase Specificity

Abstract

We show that T7 DNA polymerase exists in three distinct structural states, as reported by a conformationally sensitive fluorophore attached to the recognition (fingers) domain. The conformational change induced by a correct nucleotide commits the substrate to the forward reaction, and the slow reversal of the conformational change eliminates the rate of the chemistry step from any contribution toward enzyme specificity. Discrimination against mismatches is enhanced by the rapid release of mismatched nucleotides from the ternary E•DNA•deoxynucleoside triphosphate complex and by the use of substrate-binding energy to actively misalign catalytic residues to reduce the rate of misincorporation. Our refined model for enzyme selectivity extends traditional thermodynamic formalism by including substrate-induced structural alignment or misalignment of catalytic residues as a third dimension on the free-energy profile and by including the rate of substrate dissociation as a key kinetic parameter.

Investigations in enzymology have long sought to define the molecular, kinetic, and thermodynamic basis for the extraordinary specificity and efficiency of catalysis. Unliganded enzymes often exist in an open configuration to allow for rapid substrate binding, and a portion of the potential substrate-binding energy is used to reorganize the enzyme structure to form an active, closed complex with the precise alignment of catalytic residues needed to accelerate the reaction. It is generally believed that enzymes discriminate against alternate substrates because the poorer substrate does not fit precisely into the active site and does not bring about the optimal configuration of catalytic residues (1), and the combined effects reduce the rate of catalysis. Although structures of open and closed forms have been solved for many enzymes, the kinetic and thermodynamic contributions to catalysis provided by the substrate-induced changes in the enzyme structure remain to be resolved. It has been argued upon theoretical grounds that a two-step binding mechanism cannot enhance substrate selectivity any more than a simple one-step binding mechanism (2, 3), but this conclusion is based on simplifying assumptions that are not valid if alternate substrates reach a different ground state (4) or if the conformational change step is rate-limiting (5).

DNA polymerases represent an ideal model system for understanding enzyme specificity because the alternate substrates are well-defined. These processive enzymes alter their substrate specificity in successive rounds of templatedependent replication and discriminate against very similar substrates with high accuracy (5, 6). Specificity for each incoming nucleotide is defined structurally by base-pairing rules, but the small differences in free energy between correct and incorrect base pairs are not sufficient to account for the observed fidelity (5, 7, 8). A two-step nucleotide binding and recognition model was originally proposed based on kinetic data that was obtained in studies using T7 DNA polymerase (9, 10), Pol I Klenow fragment (11), and HIV-1-RT (12, 13). Structural studies subsequently revealed a large change in the enzyme–DNA complex following the binding of the nucleotide to an enzyme–DNA complex formed with a dideoxy-terminated primer to prevent polymerization (14-18). Binding of the correct nucleotide leads to a rotation in the “fingers” domain as the enzyme closes to bring key catalytic residues into contact with the incoming base pair. Although structural data indicate that an induced-fit mechanism appears to be universally adopted by high-fidelity DNA polymerases, the extent to which the nucleotide-induced conformational change contributes directly to selectivity has been questioned (19-21).

Evidence for a rate-limiting conformational change was initially based on the observation of a small α-phosphothioate elemental effect (10, 11), suggesting that the rate-limiting conformational change preceded a faster chemistry step. However, rigorous interpretation of the magnitude of the elemental effect has been questioned (22). Studies on the lower fidelity repair enzyme Pol β showed two detectable fluorescence transitions reporting changes in the structure of the template strand using 2-aminopurine, one preceding and one following nucleotide incorporation (19, 23). In contrast, similar studies carried out with the Pol-I Klenow fragment drew the conclusion that the conformational change is rate-limiting (6, 24). Fluorescence resonance energy transfer (FRET) measurements using Taq polymerase showed that the large domain closure was faster than catalysis (21). However, rates of incorporation measured for Pol μ, Klenow, and Taq polymerase are much slower than the rate of incorporation catalyzed by T7 DNA polymerase, and their fidelities of incorporation are lower than that of T7 polymerase. Moreover, slow, low-fidelity enzymes involved in translesion bypass or gap filling catalyze polymerization without such conformational transitions (25) and readily bind mismatches (26), suggesting that the conformational changes may be inextricably linked to steps required to achieve high speed and fidelity in replication. Questions remain regarding the role of conformational changes in selectivity by a fast, high-fidelity, replicative DNA polymerase.

Here, we report data leading to a new paradigm for enzyme selectivity in which substrate-binding energy is utilized not only to promote catalysis of a preferred substrate but also to slow the rate of catalysis of an undesirable substrate by actively misaligning catalytic residues and promoting its rapid release.

MATERIALS AND METHODS

Mutagenesis and Purification of the T7 DNA Polymerase.

The plasmid encoding an exonuclease-deficient (exo⁻) mutant of T7 DNA polymerase, pG5X (9), was used for constructing a cys-light enzyme. A total of 8 of the 10 cysteines (C20S–C88A–C275A–C313A–C451S–C660A–C688A–C703A) were mutated using polymerase chain reaction (PCR) with synthesized DNA primers. The amplified DNA product was cloned back into BamHI–HindIII-digested pG5X plasmid and confirmed with sequencing analysis. The polymerase was expressed, purified, and then recombined with thioredoxin (27) as described previously (9) with minor modifications (28).

7-Diethylamino-3-((((2-maleimidyl)ethyl)amino)carbonyl)-coumarin (MDCC)¹ Labeling of the T7 DNA Polymerase.

A stock solution (10 mM) of MDCC (Molecular Probes) was prepared by dissolving solid MDCC with dimethyl sulfoxide (DMSO) and stored at −80 °C prior to use. Protein labeling was carried out in the labeling buffer [40 mM N-2-hydroxyethylpiperazine-N′-2-ethanesulfonic acid (HEPES) at pH 8, 0.1 mM ethylenediaminetetraacetic acid (EDTA), 10% glycerol, 50 mM NaCl, and 1 mM Tris(2-carboxyethyl)-phosphine hydrochloride]. The labeling reaction was initiated by adding 20-fold excess of MDCC over protein at 4 °C and incubated with constant mixing overnight. The reaction was quenched by adding an excess amount of dithiothreitol (DTT) solution. Labeled mutant protein (MDCC-E514C-8C) was purified through a ssDNA–cellulose column to remove excess MDCC. Eluted T7 DNA polymerase was dialyzed against the T7 storage buffer and stored at −80 °C.

DNA Substrates for Kinetic Studies.

Sequences of the 27/45-mer duplex DNA substrates for the T7 DNA polymerase assays were adopted and modified from a previous study conducted on the HIV reverse transcriptase (27-mer, GCC TCG CAG CCG TCC AAC CAA CTC AAC; 45-mer, GGA CGG CAT TGG ATC GAG GTT GAG TTG GTT GGA CGG CTG CGA GGC) (12). Duplex DNA was formed by mixing 27-mer primer and 45-mer template at a 1:1 molar ratio, heated to 95 °C, and cooled slowly to room temperature for annealing. All DNA oligomers used in the study were custom-synthesized by Integrated DNA Technologies and purified by 15% polyacrylamide/7 M urea denaturing gel electrophoresis.

Equilibrium Titration Experiments.

A 200 nM solution of MDCC-E514C-8C T7 DNA polymerase in the T7 reaction buffer (40 mM Tris-HCl at pH 7.5, 1 mM EDTA, and 1 mM DDT) and 12.5 mM MgCl₂ was preincubated in the presence of 300 nM 27-ddC/45-mer DNA duplex. Solutions containing either correctly base-paired or mismatched nucleotides and an equal amount of MgCl₂ were used to titrate the enzyme–DNA complex using a KinTek TMX titration module (www.kintek-corp.com). Fluorescent intensities at equilibrium were monitored continuously, while a solution of nucleotide was added slowly, and were corrected for the small dilution. The wavelength of excitation was set at 425 and 460 nm for emission detection. The overall dissociation constant at the equilibrium state for nucleotide binding was determined by nonlinear regression.

Stopped-Flow Experiments.

Fluorescent transients following the nucleotide binding to the MDCC-E514C-8C T7 DNA polymerase were recorded with a stopped-flow apparatus (KinTek Model SF-2003, www.kintek-corp.com). A DNA duplex with dideoxy-CMP (ddC)-terminated primer was used in stopped-flow experiments to prevent the polymerization reaction, following the nucleotide binding steps. The fluorescent signal following enzyme isomerization was recorded, beginning immediately after mixing the enzyme-DNA solution (400 nM enzyme, 8 μM thioredoxin, 600 nM 27-ddC/45-mer, and 12.5 mM MgCl₂ in T7 reaction buffer) and deoxynucleoside triphosphate (dNTP) solutions (varying nucleotide concentrations and 12.5 mM MgCl₂ in T7 reaction buffer). The MDCC-E514C-8C enzyme was excited at 425 nm, and fluorescent emission was monitored with a photomultiplier tube equipped with a 450 nm high-pass optical filter (Corion).

Rapid Chemical Quench Experiments.

The rapid quench-flow method was used to study the time dependence of nucleotide incorporation under pre-steady-state kinetic conditions. A KinTek RQF-3 Rapid Quench Flow apparatus was used. One syringe was loaded with 200 nM T7 DNA polymerase preincubated with 4 μM thioredoxin and 600 nM 5′-end ³²P-labeled 27-mer/45-mer duplex DNA in T7 reaction buffer. Another syringe was loaded with deoxyribonucleoside triphosphate solution at the desired concentration in the same reaction buffer with 25 mM MgCl₂. The reaction was started by the rapid mixing of the reactants from both syringes. The DNA polymerization reaction was then quenched after a preset reaction time with a second mixing of 500 mM EDTA to remove Mg²⁺ ions from the solution. DNA products from the nucleotide incorporation experiments were analyzed by denaturing polyacrylamide gel electrophoresis. The amounts of product formed were quantified with phosphorimager and ImageQuant software (Molecular Dynamics).

Data Analysis.

Data collected in the kinetic experiments were fitted by nonlinear regression using GraFit 5 (Erithacus Software Limited) or KinTek stopped-flow software. Data were fitted to either a single-exponential function, Y = A• exp(−λt) + C, or a double-exponential function, Y = A₁• exp(−λ₁t) + A₂•exp(−λ₂t) + C, where A is the amplitude, λ is the observed rate, and C is the endpoint. Equilibrium binding data were fitted either to a hyperbola, F = F₀ + ΔF•S₀/(K_d + S₀), or a quadratic equation, $F=F_0+\Delta F\cdot ((E_0+S_0+K_{\mathrm{d}})-\sqrt{(E_0+S_0+K_{\mathrm{d}}{)}^2-4E_0{S}_0)}∕2E_0$, where F₀ is the starting fluorescence, ΔF is the change, E₀ is the starting enzyme concentration, S₀ is the variable substrate concentration, and K_d is the dissociation constant. KinTekSim software (www.kintek-corp.com) was used to global fit the data series to obtain a set of kinetic parameters that describe a multiple conformational change pathway observed in mismatched nucleotide binding and release.

RESULTS

In this paper, we examine the kinetics and equilibria for the nucleotide-induced changes in structure using the signal provided by a fluorophore attached to the recognition domain of T7 DNA polymerase, also known as the fingers domain based on the analogy of the structure to a right hand. For reasons that will become apparent, we adopt the term “recognition domain” to describe more accurately the function of the “fingers” domain. We constructed a cys-light T7 DNA polymerase and added an E514C mutation for site-specific labeling with MDCC as illustrated in Figure 1. To evaluate the effects of the mutagenesis and labeling, single-turnover rapid quench-flow methods employing radiolabeled DNA were used to examine the rates and amplitudes of polymerization catalyzed by the labeled cys-light protein as shown in Figure 2. Active-site titration showed that the enzyme retained approximately 90% activity after mutagenesis and labeling (Figure 2A), although the K_d for DNA binding (36 ± 6 nM) was increased slightly compared to the value of 18 ± 2 nM reported previously (9). The nucleotide concentration dependence of the rate of polymerization (Figure 2B) defined a maximum rate, k_pol = 234 ± 9.4 s⁻¹ and a K_d = 24 ± 3.1 μM for nucleotide binding. These parameters are comparable to previously reported values of k_pol = 287 ± 20 s⁻¹ and K_d = 18 ± 4 μM for dTTP incorporation (9) and to our current results using wild-type (exo⁻) T7 DNA polymerase with dCTP incorporation (data not shown).

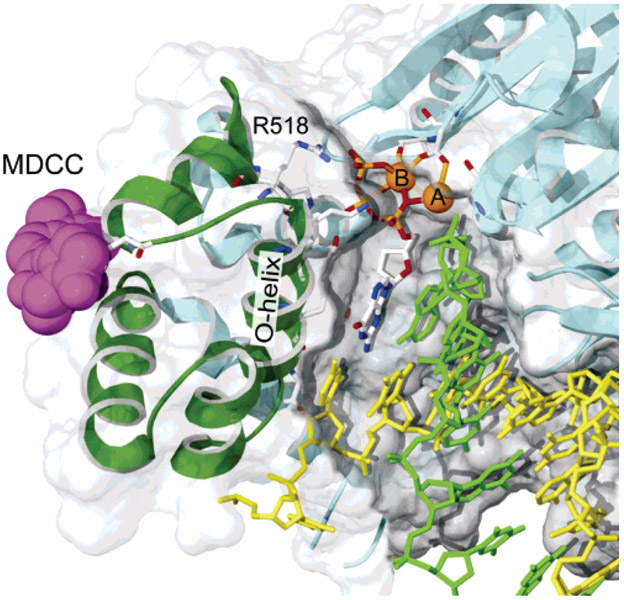
Figure 1:

CSF probe labeling. The structure of T7 DNA polymerase is shown with MDCC docked at the position expected for the labeling of C514. The thumb and thioredoxin-binding domain (residues 233–411) and primer binding loop (residues 436–454) have been removed to reveal the active site. From PDB 1T7P (14), a cys-light mutant was constructed by removing 8 of the 10 cysteines (C20S–C88A–C275A–C313A–C451S–C660A–C688A–C703A) and introducing a single-surface-exposed cysteine (E514C) and was labeled overnight at 4 °C with a 20-fold molar excess of MDCC. Only residue 514 was labeled, and 90% efficiency was achieved.

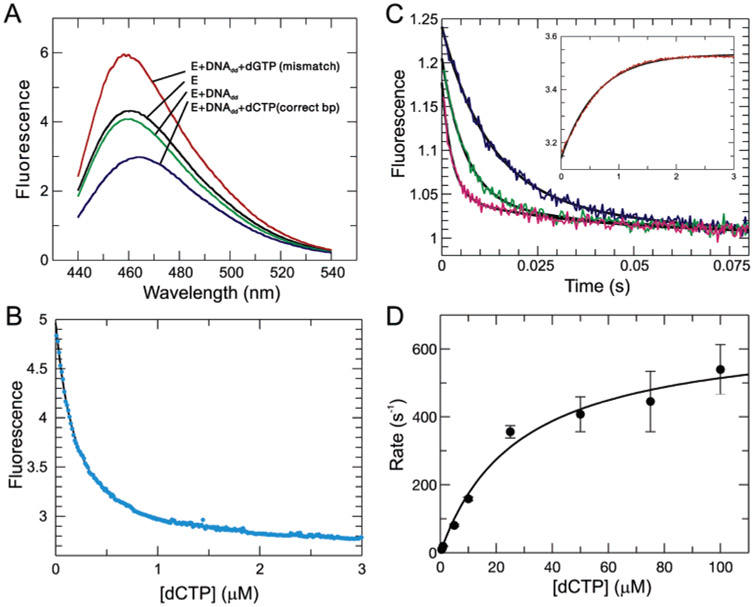
Figure 2:

Burst kinetics of the MDCC-labeled mutant T7 DNA polymerase. The time dependence of nucleotide incorporation was examined using quench-flow methods to evaluate the effects of the mutations and MDCC-labeling on the polymerase activity. (A) Amount of active enzyme after MDCC labeling was determined by an active-site titration experiment. The enzyme (200 nM, determined by a Bio-Rad protein assay with BSA standards) was preincubated with different amounts of DNA substrate. The reactions were then started by mixing the complex with 200 μM dCTP and were quenched after 18 ms. The amount of product formed as a function of the DNA concentration was fitted to a quadratic equation, ((E₀ + K_d + DNA) − ((E₀ + K_d + DNA)² − (4E₀DNA))^0.5)/2, to obtain the active enzyme concentration, E₀ = 92 ± 2.0 nM (92% active) and the dissociation constant for DNA binding, K_d = 36 ± 5.7 nM. (B) Nucleotide concentration dependence of the rate of polymerization was obtained by mixing a preformed enzyme–DNA complex (100 nM enzyme and 300 nM DNA after mixing) with various concentrations of dCTP. At each concentration, the time dependence of product formation was fit to a burst equation ([product] = A(1 – exp(−k₁t)) + k₂t) by nonlinear regression to derive the rate and amplitude of product formation. The concentration dependence of the rate of product formation (shown) was fit to a hyperbolic equation ([rate] = (k_polK_d)/(K_d + S)) to yield the smooth line defining a maximal burst rate of k_pol = 234 ± 9.4 s⁻¹ for dCTP incorporation and an apparent K_d = 24 ± 3.1 μM.

Retention of nearly full active-site concentration and the modest changes in kinetic parameters verified that the mutagenesis and labeling did not significantly alter the kinetics of nucleotide binding and incorporation. Analysis by high-performance liquid chromatography (HPLC) and mass spectrometry of tryptic peptides showed that only residue 514 was labeled, and we observed >90% efficiency of labeling based on absorbance measurements (28).

Fluorescence emission spectra were recorded for different enzyme—substrate binding states as shown in Figure 3A. Starting with free enzyme (E) and adding duplex DNA containing a dideoxy-terminated primer (E•DNA_dd) resulted in a small decrease in fluorescence (5% at the emission maximum of 460 nm). After the addition of the nucleotide that correctly pairs with the templating base, dCTP, the fluorescence intensity decreased by approximately 30%. in contrast, when a mismatched nucleotide was added (dGTP), a 40% increase in the fluorescence intensity was observed. Binding of any mismatched nucleotide produced ternary complexes with higher fluorescence states, while binding of any correct base pair (dNTP/template combination) gave a decrease in fluorescence. This surprising result implies that there are three conformational states of the enzyme distinguishable by the conformationally sensitive fluorophore (CSF) probe: one state formed in the absence of substrate, a second state formed by the binding of the correct substrate, and a third state formed after binding an incorrect substrate.

Figure 3:

Equilibrium and kinetics of the fluorescence changes resulting from nucleotide binding. (A) Fluorescence emission spectrum of the MDCC-labeled enzyme at different substrate-bound states is shown. The excitation wavelength was 425 nm. (B) Equilibrium titration experiment for dCTP binding was performed using a KinTek TMX titration module (www.kintek-corp.com) with a 200 nM enzyme–DNA complex. A dissociation constant of 140 ± 0.1 nM was determined by fitting the data to a quadratic equation by nonlinear regression (smooth line). (C) Stopped-flow fluorescence transients induced by dCTP binding: blue, 5 μM dCTP; green, 10 μM dCTP; and magenta, 25 μM dCTP. Each trace was fitted to a double-exponential function by nonlinear regression (smooth line); the fast phase defined the rate of the reaction, while the slow phase corrected for a small drop in intensity. (inset) Rate of release of dCTP follows a single-exponential transition with a rate of 1.6 ± 0.01 s⁻¹. (D) Rates of dCTP-induced conformational change were determined at various dCTP concentrations. Fitting the rates as a function of dCTP concentrations to a hyperbolic equation yielded a maximum rate of 660 ± 52 s⁻¹ and a ground-state K_d of 28 ± 6.2 μM.

Guanine nucleotides can interact with and quench the fluorescence of fluorophores through nonspecific interactions (29). Therefore, we were concerned that the observed effect of dGTP could be due to a direct, nonspecific interaction with MDCC. Several lines of evidence argue against this possibility. First, the addition of a dGTP mismatch as shown in Figure 3A leads to enhancement and not quenching of fluorescence. Second, any correct base pair causes fluorescence quenching, while any mismatch induces an increase in fluorescence, and neither effect is strictly dependent upon the addition of dGTP (data not shown). Finally, the addition of a correct base (dCTP/G) competes with the enhancement in fluorescence induced by the binding of a mismatch (dGTP/ G) (see Figure 4C), arguing that they both bind to the same site. Accordingly, the effect of dGTP in producing a conformational state with a unique fluorescence enhancement is due to the interaction of the nucleotide at the polymerase active site.

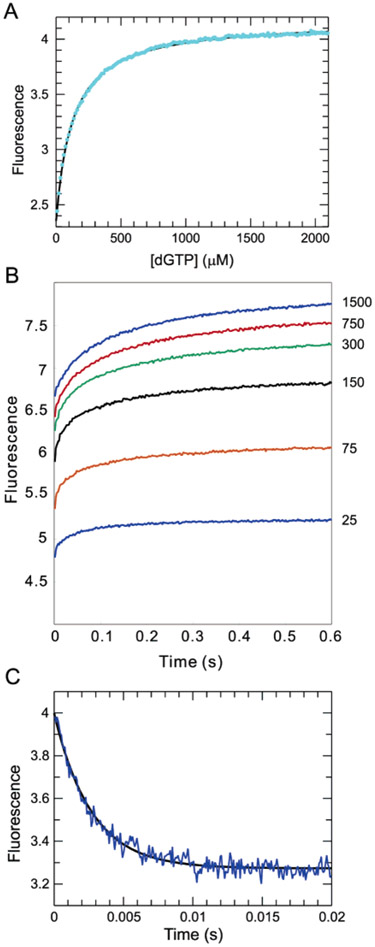
Figure 4:

Equilibrium and kinetics of the fluorescence changes following incorrect nucleotide binding. (A) Equilibrium titration data follow a hyperbolic curve with a K_d of 130 ± 0.8 μM. (B) Stopped-flow fluorescence traces corresponding to the binding of dGTP at concentrations ranging from 25 to 1500 μM. The data could be fitted globally with three isomerization steps with forward/ reverse rates of 220/420, 30/100, and 12/7, respectively, but this fit is not unique and is not shown. Rather, the minimal model with a single isomerization is shown in Scheme 1. (C) Rate of nucleotide release from a mismatched ternary complex was measured by chasing the release of the mismatch with the correct nucleotide. The E•DNA_dd•dGTP complex (200 nM) was formed with 250 μM dGTP and then mixed with 2 mM dCTP. The fluorescence transition shows a single-exponential decay with a rate of 372 ± 5.4 s⁻¹.

Correct Nucleotide Binding and Incorporation.

To quantify the dissociation constant for correct nucleotide binding, we performed an equilibrium titration as shown in Figure 3B in which an enzyme—DNA_dd complex was continuously mixed with increasing concentrations of dCTP while recording fluorescence. Data were fit by nonlinear regression to a quadratic equation (see the Materials and Methods) to define a net dissociation constant (defined by the product of equilibrium constants up to the catalytic step) of 140 ± 0.1 nM.

The kinetics of the conformational change were measured by stopped-flow methods by recording changes in fluorescence following the mixing of the enzyme—DNA complex with nucleotide. Figure 3C shows three representative traces. Each was fitted to an exponential function by nonlinear regression to obtain the rate, which was then plotted in Figure 3D as a function of the dCTP concentration. Fitting the concentration dependence of the rate of the fluorescence change to a hyperbola defines an apparent ground-state dissociation constant, K_d,1 = 28 ± 6.2 μM, and a maximum rate of k₂ = 660 ± 52 s⁻¹ according to the following pathway, where the conversion of E•D to F•D signifies the change in structure leading to a fluorescence change. Saturation of the rate as a function of the nucleotide concentration demonstrates that the reaction occurs in at least two steps, where the maximum rate is equal to the sum k₂ + k₋₂ according to the following model:

$$\mathrm{E}\cdot {\mathrm{D}}_{\text{dd}}+\text{dCTP}\stackrel{K_1}{\rightleftarrows }\mathrm{E}\cdot {\mathrm{D}}_{\text{dd}}\cdot \text{dCTP}\underset{k_{-2}}{\overset{k_2}{\rightleftarrows }}\mathrm{F}\cdot {\mathrm{D}}_{\text{dd}}\cdot \text{dCTP}$$

Evidence that the initial ground-state binding (K₁) is a rapid equilibrium reaction relies upon the observation that the kinetic traces followed a single-exponential function at all dCTP concentrations. To be valid, the rapid-equilibrium model requires k₋₁ > k₂, and simulations using KinTekSim revealed that a value of k₋₁ = 2800 s⁻¹ (corresponding to k₁ = 100 μM⁻¹ s⁻¹) was sufficient to remove any noticeable lag from the kinetics. Although k₋₁ is not well-defined, we can safely assume a rapid-equilibrium binding in forming the initial collision complex in the absence of evidence to the contrary.

We next measured the rate of release of the nucleotide from the tight ternary complex in a competition experiment to get the results shown in the inset of Figure 3C. We mixed an E•DNA_dd•dCTP complex with a 10-fold excess of unlabeled E•DNA complex, which rapidly sequesters free dCTP. The fluorescence trace follows a single-exponential function that defines an off rate of k₋₂ = 1.6 ± 0.01 s⁻¹, affording computation of the equilibrium constant for the isomerization step, K₂ = 660/1.6 = 410. We compare these results with the equilibrium titration by computing the net equilibrium dissociation constant K_d,net = K_d,1/(1 + K₂) = 68 ± 20 nM. This value is only slightly less than the value of 140 nM obtained by equilibrium titration (Figure 3B).

Rapid chemical quench studies showed that the MDCC-labeled enzyme catalyzed the incorporation of dCTP at a maximum rate of 234 ± 9.4 s⁻¹ (Figure 2B). The kinetics define the following sequence, where D_n represents duplex DNA with a primer n bases in length:

$$\begin{gathered} \mathrm{E}\cdot {\mathrm{D}}_n+\text{dCTP}\stackrel{K_1}{\rightleftarrows }\mathrm{E}\cdot {\mathrm{D}}_n\cdot \text{dCTP}\underset{k_{-2}}{\overset{k_2}{\rightleftarrows }} \\ \mathrm{F}\cdot {\mathrm{D}}_n\cdot \text{dCTP}\underset{k_{-3}}{\overset{k_3}{\rightleftarrows }}\mathrm{F}\cdot {\mathrm{D}}_{n+1}\cdot {\text{PP}}_i \end{gathered}$$

A rate of k₃ = 360 s⁻¹ is needed to get an observed rate of k_pol = 234 s⁻¹, following isomerization at k₂ = 660 s⁻¹, estimated from the relationship k₃ ≈ k₂k_pol/(k₂ – k_pol), where k_pol ~ k₂k₃/(k₂ + k₃) is the observed rate of the burst. Although one might expect the kinetics of the incorporation to show a lag at a rate of 660 s⁻¹ followed by an exponential defining k₃, the rate of the chemistry step, the rates are too close to be resolved and the lag effectively slows the rate of the observed reaction from the estimated 360 s⁻¹ to the observed 234 s⁻¹. Note that the reverse rate, k₋₃, is thought not to contribute to the observed rate of the burst because pyrophosphate release is believed to be fast. Rate constants Scheme 1 for correct and incorrect incorporation are summarized in Scheme 1 and Table 1.

Scheme 1.

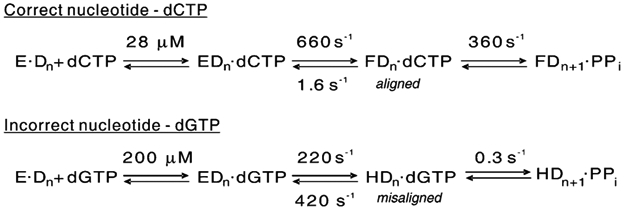
Table 1:

Kinetic Constants for Correct and Incorrect Nucleotide Incorporation^a

dNTP	Kd,1 (μM)	k2 (s−1)	k−2 (s−1)	k3 (s−1)	kcat/Km (μM−1 s−1)	kcat (s−1)	Km (μM)
dCTP	28	660	1.6	360	22	230	10
dGTP	200	220	420	0.3	0.0008	0.1	130
	$\mathrm{E}\cdot {\mathrm{D}}_n+\mathrm{N}\underset{k_{-1}}{\overset{k_1}{\rightleftarrows }}\mathrm{E}\cdot {\mathrm{D}}_n\cdot \mathrm{N}\underset{k_{-2}}{\overset{k_2}{\rightleftarrows }}\mathrm{F}\cdot {\mathrm{D}}_n\cdot \mathrm{N}\stackrel{k_3}{\to }\mathrm{E}\cdot {\mathrm{D}}_{n+1}+{\text{PP}}_i$

^aKinetic constants for correct (dCTP) and incorrect (dGTP) nucleotide binding and incorporation are listed and defined according to the model shown in the table. Kinetic parameters k_cat, k_cat/K_m, and K_m were calculated from the individual rate constants listed.

Incorrect Nucleotide Binding and Incorporation.

The binding of a mismatched nucleotide leads to an increase in fluorescence (Figure 3A), suggesting that the enzyme recognizes a mismatch by adopting an alternative conformation. An equilibrium titration using dideoxy-terminated DNA (Figure 4A) defined a net dissociation constant for mismatched nucleotide, K_d = 130 ± 0.8 μM. This value indicates that the binding of the mismatched nucleotide is about 1000-fold weaker than the binding of the correct nucleotide.

The time dependence of the conformational change induced by the binding of a mismatched nucleotide is shown at several concentrations in Figure 4B. Several aspects of the kinetics are unusual. The observed curves best fit a sum of two or three exponential terms; there is a rapid jump in fluorescence, which is not resolved on this time scale; and the magnitude of the jump increases with an increasing nucleotide concentration. The observable, slower change in fluorescence also increases in amplitude, but the rate appears to decrease with an increasing nucleotide concentration. This pattern is the kinetic signature of a series of thermodynamically unfavorable isomerization steps following the formation of a collision complex. We can fit the data globally by computer simulation using KinTekSim to a model with three isomerization steps, but the fit is not unique. The essential conclusion is that ground-state binding of a mismatch is followed by unfavorable isomerization steps, where the reverse rate is greater than the forward rate and which ultimately leads to a slow rate of incorporation, measured to be 0.12 s⁻¹ (ref 10 and data not shown). Unlike the case for correct nucleotide binding, the net equilibrium constant for the isomerization steps cannot be established accurately because the isomerization is unfavorable, K_d,net = K_d,1/(1 + K₂) and K₂ < 1. By curve fitting, we estimate the equilibrium constant for the isomerization step (K₂) to be approximately 0.5, and accordingly, we can compute the dissociation constant for the collision complex to be K_d,1 = 1.5 × 130 = 200 μM (Scheme 1). If the chemistry occurs only from the state following the isomerization to form the H•D_n•dGTP complex, then we predict that k₃ = 0.36 s⁻¹ to account for the observed rate, k_cat = K₂k₃/(1 + K₂) = 0.12 s⁻¹ and K₂ = 0.5. This computation is approximate because the value of K₂ is not known with certainty. Note that we use H•D_n•dGTP to describe the altered enzyme structure formed after mismatch binding to distinguish it from the state formed after binding a correct base (F•D_n•dCTP).

We measured the rate of dissociation of the mismatched nucleotide (dGTP) by following the fluorescence decrease after mixing an enzyme •DNA_dd•dGTP complex with a high concentration of the correct nucleotide (dCTP). The results are shown in Figure 4C and define a rate of 372 s⁻¹. We looked for but could not find a slower reaction. The rate of dissociation was measured at various dCTP concentrations and extrapolated to obtain the maximum rate of 420 s⁻¹. One might expect that the observed rate could be partially ratelimited by the rate of dCTP binding and isomerization at 660 s⁻¹. However, in this case, the observe fluorescence change is expected to be a weighed sum of species reflecting both the release of dGTP (H•DNA•dGTP → E•DNA•dGTP → E•DNA + dGTP) and the binding of dCTP (E•DNA + dCTP → E•DNA•dCTP → F•DNA•dCTP). A computer simulation using KinTekSim (www.kintek-corp.com) confirms that a rate of dGTP release is accurately measured by our method. We fit our data to a minimal model with a forward rate of isomerization, k₂ ~ 220 s⁻¹, a reverse rate of k₋₂ = 420 s⁻¹, and K₂ ~ 0.5 as summarized in Scheme 1. Fast dissociation of the mismatched nucleotide from the F•DNA_dd•dGTP ternary complex represents an important means by which the polymerase increases fidelity.

Pathway and Free-Energy Profile.

The kinetic data collected from our fluorescence experiments provide important new information to resolve the controversies surrounding DNA polymerase fidelity. Thermodynamic measurements show that the structural change preceding correct incorporation is favorable, leading to tight nucleotide binding and fast incorporation. After the binding of a mismatch, the isomerization is unfavorable and rapidly reversible to allow for the dissociation of the mismatched nucleotide. More importantly, the binding of a mismatched nucleotide leads to a different conformational state for the E•DNA•nucleotide complex, and the rate for the chemical step is reduced by 2000-fold, suggesting suboptimal alignment of the catalytic residues. For correct nucleotide incorporation, the initial, weak ground-state binding (K_d = 28 μM) induces a conformational change leading to tighter substrate binding (K₂ = 410), which is slowly reversible (1.6 s⁻¹) and, in turn, leads to a closed active site, aligning the catalytic residues properly for fast catalysis (Scheme 1). In contrast, a mismatched nucleotide binds to the enzyme with a lower ground-state binding affinity (K_d = 200 μM). Once a mismatched nucleotide is in the active site, the rate of the conformational change is only slightly reduced but is unfavorable. The rapid reversal of the isomerization step shifts the equilibrium toward the open state and facilitates the rapid dissociation of the mismatched nucleotide from the active site. Moreover, the rearrangement of the recognition domain differs from that induced by correct nucleotide binding. This altered pathway for isomerization results in a misalignment of the catalytic residues, thereby slowing the rate of the chemical step.

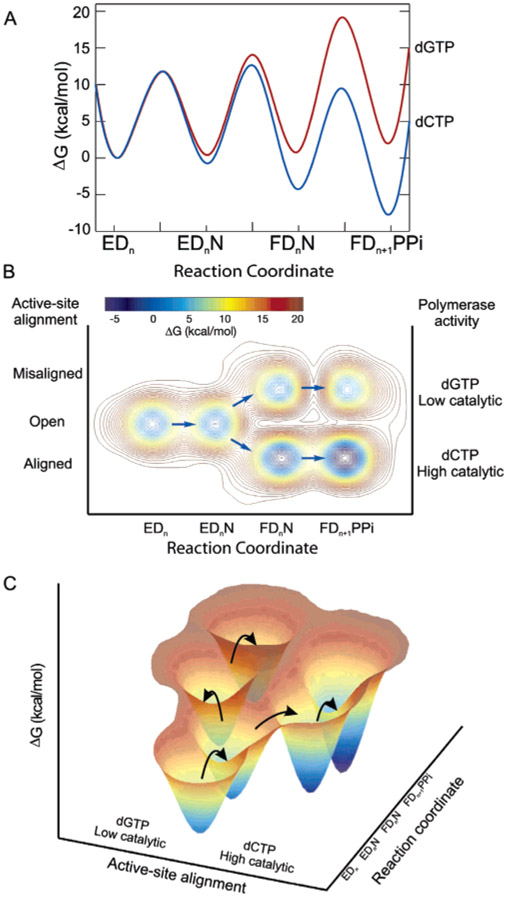
The free-energy profiles for binding and incorporation of correct and incorrect nucleotides are compared in Figure 5A. There is a small difference in the ground-state binding energy for the collision complex, but the rate and equilibrium constants for the isomerization step are much less favorable for the mismatched nucleotide. After correct nucleotide binding, isomerization of the ternary complex proceeds with a favorable free-energy change of −3.6 kcal/mol, while isomerization following incorrect nucleotide binding is unfavorable with a free-energy change estimated to be 0.4 kcal/mol.

Figure 5:

Free-energy profiles for the T7 DNA polymerase. (A) Conventional free-energy diagram for correct (dCTP) and mismatched (dGTP) nucleotide incorporation reactions. The free energy was calculated as ΔG^‡ = RT[ln(kT/h) − ln(k_obs)] kcal/mol using rate constants from Scheme 1. The constant k is the Boltzmann constant, T is 293 K, h is Planck’s constant, and k_obs is the firstorder rate constant. The nucleotide concentration was set equal to 100 μM. (B) Proposed three-dimensional free-energy diagram taking conclusions from our fluorescence studies into account. The diagram includes the alignment of active-site residues as a third axis. (C) Three-dimensional presentation of our proposed reaction free-energy profile for correct and incorrect nucleotide incorporations.

The isomerization of the E•DNA•dCTP complex to form the tight ternary complex (F•DNA•dCTP) is partially rate-limiting for incorporation, being only 2-fold faster than the chemistry step. With other nucleotides tested, the conformational change was fully rate-limiting (data not shown). In contrast, the chemistry step is fully rate-limiting for misincorporation. Most importantly, our data demonstrate that models for selectivity must account for a change in the rate-limiting step in comparing correct and incorrect nucleotides and simplified algebraic expressions for fidelity are invalid.

Although this thermodynamic formalism quantifies the changes in rates and free energy of steps leading up to the chemical reaction, it does not tell the whole story. Our data showing that the binding of a mismatch leads to an altered configuration of the enzyme adds an important piece of information. The rate of misincorporation is slow because the binding of a mismatch leads to an altered state of the E•DNA•dNTP complex. Our data suggest that perhaps enzymes have evolved to use binding energy not only to align active-site residues and stabilize the transition state for incorporation of a correct base but also to misalign the reactive groups when a mismatch is recognized. This somewhat speculative model adds a third dimension to the free-energy profile as shown in parts B and C of Figure 5. After the formation of a collision complex, the enzyme begins to discriminate between correct and incorrect nucleotides not only by binding the mismatch more weakly but also by altering the enzyme structure to bring reactive groups away from the alignment required for fast catalysis. The binding of a correct nucleotide organizes the active site to align catalytic residues and reactants, while the binding of a mismatch misaligns the catalytic residues and/or the reactants.

Although the three-dimensional structure of this misaligned state is not yet known, our CSF probe distinguishes a unique state following the binding of a mismatch. We now define three important states: open, aligned, and misaligned. In this terminology, one might consider the open state to be unaligned to distinguish it from the misaligned state formed in the presence of a mismatch. It is noteworthy that our CSF probe is only four residues from the catalytically important R518, and it is plausible that our probe senses changes in the position of this and nearby residues.

DISCUSSION

Our new data suggest a need to change the way in which we think about enzyme specificity. Alternate substrates do not react more slowly simply because they fail to bind tightly and reorganize the active-site residues for optimal catalysis. Rather, our results suggest that some of the intrinsic binding energy available from the interaction of the wrong substrate with the enzyme can be utilized in doing work to actively misalign the reactive groups. The nearly universal observation of pliant, two-state enzymes, open in the absence of substrate and closed in its presence, can be explained, in part, by the need for speed and specificity. An open state is needed to allow for rapid diffusion of the substrate into the active site, while a closed state, in which the substrate is surrounded by catalytic residues, is needed to achieve the optimal constellation of amino acids to hold the substrate and stabilize the transition state to bring about rapid catalysis. The active misalignment of catalytic residues following the binding of an alternate substrate provides a third important function for the malleable nature of enzyme active sites. We propose that the binding of the wrong substrate can perturb the constellation of amino acids to reduce the rate of the reaction. Indeed, this may be one of the factors that has constrained the evolution of enzyme activity to be able to organize residues around the desired substrate and disorganize reactive groups upon the binding of a similar but undesired substrate. In addition and equally important, the conformational transition with a correct substrate leads to a tightly bound substrate committed to catalysis, while the conformational changes following mismatch binding produce a state in which the nucleotide is weakly bound and rapidly released.

The concept of a three-dimensional free-energy surface is not new, but previous proposals were based on a more limited data set and modeled on the basis of only two conformational states leading to the suggestion that nucleotide misinsertion may occur from a “partially open” conformation (30). Our new observation of a third enzyme state and our quantification of the kinetic parameters governing its formation allow for more detailed computational modeling.

We have summarized the kinetic constant for correct and incorrect base incorporation in Table 1. Mutagenesis and labeling of the enzyme was accomplished without significantly altering the kinetics of nucleotide incorporation (Figure 2). In particular, kinetic constants for correct nucleotide binding (K_d) and incorporation (k_cat) are comparable to the values reported previously for the wild-type enzyme (9), and the active-site titration revealed that greater than 90% of the enzyme was active. Similarly, the rate of misincorporation observed with the labeled enzyme was comparable to values reported previously (10). However, there was approximately a 10-fold decrease in the ground-state dissociation constants for incorrect nucleotides seen with the labeled enzymes. This factor reduced the discrimination exhibited by the labeled polymerase in the ground-state binding step, but the contributions of the remaining steps to the overall fidelity were retained. Thus, it appears as though any adverse effect of the labeling and mutagenesis was restricted to this single ground-state binding step.

Our CSF probe clearly distinguishes three conformational states and allows for measurement of the kinetic and thermodynamic parameters governing their interconversion, but we do not know the precise structures of these states. It could be argued that there are only two-states, “open” and “closed”, and that all observable states are on a continuum. According to this interpretation, the resting state of the enzyme must be partially open, while the mismatch induces a fully open state and a correct base pair induces a fully closed state. However, this distinction is more semantic than real in that it still requires three states: resting, fully open, and fully closed. Moreover, previous proposals have suggested that the mismatch binding may induce a state between the open (resting) and closed (ternary) states, while our fluorescence data suggest, to the contrary, that the mismatch recognition state does not lie on a path between “open” and “closed” states because that would imply a fluorescent state intermediate between the open and closed states. Although our data argue for three states, a more rigorous interpretation of the CSF signal awaits a structure determination of each state.

It is tempting to suggest that our CSF probe senses the large domain movement seen in crystal structures comparing binary E•DNA and ternary F•DNA_dd•dNTP states. Alternatively, our CSF probe may be sensing a more subtle alignment of catalytic residues after domain closure but preceding the catalytic step. Analysis of Taq polymerase conformational changes by FRET (21) have shown that the large domain movement is faster than incorporation by this polymerase; however, no change in FRET was observed upon the addition of a mismatched nucleotide. It is possible that changes in CSF fluorescence reflect changes in the secondary structure and helix packing occurring within the recognition domain and that those changes are coincident with the larger domain movements seen crystallographically in comparing the EvDNA and FvDNA-dNTP states. It is also apparent that the CSF probe can sense more subtle changes in thew important to note that the MDCC label is linked to the catalytically important R518 by a three amino acid loop, and therefore, changes in fluorescence may reflect the positioning of this active-site residue, as well as others on or near the O helix. Independent of the structural interpretation, this signal has provided a means to quantify both correct and incorrect base pair binding and incorporation to yield new mechanistic insights. Our results support the conclusion that nucleotide-induced conformational changes are an important means to achieve optimal fidelity.

Role of the Conformational Change.

Arguments against the utility of a conformational change step in contributing to enzyme selectivity have been based on a simplified thermodynamic formalism that overlooks critical details of known enzymes. In the classic description of enzyme catalysis, the substrate binds in a rapidly equilibrating ground state, which is followed by a single rate-limiting catalytic step. On the basis of this simplified model, it has been argued that a two-step model could not provide more selectivity than afforded by a one-step model (2, 3). This conclusion is predicated on the assumption that the binding and conformational change steps are both in rapid equilibrium, and under that condition, of course, it is true that the pathway of achieving the final state leading to catalysis is irrelevant. A subsequent derivation modified this analysis by proposing altered ground states to achieve additional selectivity (4) but did not consider the impact of a rate-limiting conformational change.

There has been considerable debate about the relative rates of the conformational change and chemistry steps and their contributions to fidelity (5, 6, 20, 21). The data on Pol β do clearly show that the structural transition in the template strand as measured by the 2-aminopurine signal is faster than chemistry (19). From these data, it has been argued that the only parameter that matters to define specificity is the energy difference at the transition state in comparing correct and mismatched nucleotide incorporation (20, 31), and inspection of free-energy profiles has been used to justify the conclusion that a rate-limiting conformational change step only reduces specificity (20). These conclusions are a mathematical restatement of the definition of k_cat/K_m for a simplified, rapid equilibrium binding kinetic model with a single rate-limiting step but do not apply, in general. Moreover, they do not apply in the present case. The simplification fails when there are multiple binding steps because K_m is not equal to the dissociation constant for ground-state binding and a more rigorous interpretation of k_cat/K_m must be applied. Specificity cannot be accurately assessed by inspection of free-energy profiles, and asking whether the chemistry step or the conformational change is rate-limiting for incorporation is the wrong question. Rather, the important question rests on the relative magnitudes of chemistry and the reverse of the conformational change as we show by mathematical analysis of the specificity constant, k_cat/K_m.

The minimal reaction sequence for nucleotide binding, isomerization, and incorporation can be described by the following pathway:

$$\mathrm{E}\cdot {\mathrm{D}}_n+\mathrm{N}\underset{k_{-1}}{\overset{k_1}{\rightleftarrows }}\mathrm{E}\cdot {\mathrm{D}}_n\cdot \mathrm{N}\underset{k_{-2}}{\overset{k_2}{\rightleftarrows }}\mathrm{F}\cdot {\mathrm{D}}_n\cdot \mathrm{N}\stackrel{k_3}{\to }\mathrm{E}\cdot {\mathrm{D}}_{n+1}\cdot {\text{PP}}_i$$

where D_n represents duplex DNA with a primer n bases in length and N represents a deoxynucleotide. Because we believe pyrophosphate release and translocation to be rapid following chemistry (k₃), this minimal model can be used to derive k_cat/K_m

$$k_{\text{cat}}∕K_{\mathrm{m}}=\frac{k_1{k}_2{k}_3}{k_2{k}_3+k_{-1}(k_{-2}+k_3)}$$

The magnitude of k_cat/K_m is a complex ratio of individual rate constants, and discrimination, as the ratio of k_cat/K_m for correct versus incorrect nucleotides, is an even more complex ratio of ratios; therefore, generalized simplifications, prevalent in the literature, are not likely to be valid in all cases. However, given the knowledge of the magnitude of each constant, important conclusions can be derived regarding the mechanistic basis for fidelity by T7 polymerase.

In the present case, the specificity constant for correct incorporation reduces to k_cat/K_m ≈ (k₁k₂k₃)/(k₂k₃ + k₋₁k₃) = (k₁k₂)/(k₂ + k₋₁) because k₋₂, the reverse of the conformational change step, is small relative to the rate of the chemistry step (k₋₂ ≪ k₃, 1.6 versus 360 s⁻¹). This is an important conclusion, surprising to investigators in the polymerase field who have spent decades concerned with the issue of whether chemistry or the forward rate of the conformational change is rate-limiting. The specificity constant does not depend upon the rate of chemistry (k₃) if the reverse of the conformational change step (k₋₂) is slow relative to k₃, irrespective of the relative magnitudes of k₂ and k₃. The math is unequivocal and intuitively logical based on the more rigorous view of k_cat/K_m as representing the apparent second-order rate constant for substrate binding multiplied by the probability that, once bound, the substrate goes on to form the product. The high ratio of k₃/k₋₂ implies that after the isomerization step nearly all bound substrate (99.6%) goes forward to form the product and the rate of binding through the two-step process is defined by k_cat/K_m ≈ (k₁k₂)/(k₂ + k₋₁). This can be reduced further because of the rapid equilibrium binding of the nucleotide in the ground state, if k₋₁ ≫ k₂, to give k_cat/K_m ≈ K₁k₂. In either case, the magnitude of the chemistry step, k₃, does not contribute to the specificity constant for correct incorporation because it is much faster than the reverse of the isomerization step (k₃ ≫ k₋₂). This algebra and equations for k_cat and K_m are summarized in Table 2.

Table 2:

Rate Constants Governing Kinetic Parameters for Correct Incorporation^a

parameter	no simplification	k3 ≫ k−2	k−1 ≫ k2
kcat/Km	$\frac{k_1{k}_2{k}_3}{k_2{k}_3+k_{-1}(k_{-2}+k_3)}$	$\frac{k_1{k}_2}{k_2+k_{-1}}$	K1k2
kcat	$\frac{k_2{k}_3}{k_2+k_{-2}+k_3}$	$\frac{k_2{k}_3}{k_2+k_3}$	$\frac{k_2{k}_3}{k_2+k_3}$
Km	$\frac{k_2{k}_3+k_{-1}(k_{-2}+k_3)}{k_1(k_2+k_{-2}+k_3)}$	$\frac{(k_2+k_{-1})k_3}{k_1(k_2+k_3)}$	$\frac{k_3}{K_1(k_2+k_3)}$

^aMathematical simplifications are shown for steady-state parameters when the reverse of isomerization is much slower than the chemistry step (k₃ ≫ k₋₂) and the additional simplification that ground-state binding is a rapid equilibrium step (k₋₁ ≫ k₂).

Although k_cat/K_m ≈ K₁k₂, it does not follow that k_cat = k₂ and K_m = 1/K₁. Rather, k_cat = (k₂k₁)/(k₂ + k₋₂ + k₃) and K_m = (k₂k₃ + k₋₁(k₋₂ + k₃))/(k₁(k₂ + k₋₂ + k₃)). The term (k₂ + k₋₂ + k₃) appearing in both k_cat and K_m cancels in the ratio, k_cat/K_m, leading to the mathematical simplification. For this reason, one cannot simply inspect a free-energy diagram to estimate k_cat and then equate K_m to the ground-state binding K_d to come to a judgment about enzyme specificity.

This analysis corrects the misconception that chemistry must be much faster than the forward conformational change step to eliminate it from contributing to the specificity constant (5, 20, 21). Although the relative magnitudes of k₂ and k₃ define k_cat [k_cat = (k₂k₁)/(k2 + k₋₂ + k₃) for this model], the question of whether chemistry is faster or slower than the conformational change does not dictate their relative contributions to fidelity as measured by k_cat/K_m. It is the relative magnitudes of k₋₂ and k₃ that matter most. In the present case, two-step binding gives an apparent second-order rate constant for binding defined by K₁k₂ and the probability that the bound correct substrate (after isomerization) goes forward to form the product is near unity. The locking down of the correct nucleotide following the conformational change step commits it to be incorporated, and it does not matter how fast chemistry is relative to the rate of the conformational change step so long as it is faster than the reverse of the conformational change limiting the release of the nucleotide.

In the case of mismatch incorporation, the specificity constant reduces to k_cat/K_m ≈ (k₁k₂k₃)/(k₂k₃ + k₋₁k₋₂), because chemistry is much slower than the reverse of the conformational change step, that is, k₃ ≪ k₋₂. Further simplification based on rapid equilibrium ground-state substrate binding gives k_cat/K_m ≈ K₁K₂k₃ (summarized in Table 3). The important conclusion to be made is that fidelity is increased because the conformational change step no longer leads to tight nucleotide binding but rather affords rapid release of the nucleotide and binds it in a conformation that slows the rate of catalysis. The combined effect leads to the release, rather than incorporation, of 99.9% of bound mismatches.

Table 3:

Rate Constants Governing Kinetic Parameters for Mismatch Incorporation^a

parameter	no simplification	k−2 ≫ k3	k−1k−2k2k3
kcat/Km	$\frac{k_1{k}_2{k}_3}{k_2{k}_3+k_{-1}(k_{-2}+k_3)}$	$\frac{k_1{k}_2{k}_3}{k_2{k}_3+k_{-1}{k}_{-2}}$	K1K2k3
kcat	$\frac{k_2{k}_3}{k_2+k_{-2}+k_3}$	$\frac{K_2{k}_3}{K_2+1}$	$\frac{K_2{k}_3}{K_2+1}$
Km	$\frac{k_2{k}_3+k_{-1}(k_{-2}+k_3)}{k_1(k_2+k_{-2}+k_3)}$	$\frac{k_2{k}_3+k_{-1}{k}_{-2}}{k_1(k_2+k_{-2})}$	$\frac{1}{K_1(K_2+1)}$

^aMathematical simplifications are shown for steady-state parameters under the conditions where the reverse of isomerization is much faster than the chemistry step (k₋₂ ≫ k₃) and the additional simplification that ground-state binding is a rapid equilibrium step, such that k₋₁k₋₂ ≫ k₂k₃.

Most important to our current discussion is the observation that there is a change in the identity of the rate-limiting step in comparing correct and incorrect nucleotide incorporation in our system. The conformational change step is the only rate-limiting step governing correct incorporation, while the chemistry step is fully rate-limiting for the incorporation of a mismatch and further attenuated by the unfavorable equilibrium for the isomerization. The change in the identity of the specificity-determining rate step in comparing correct and incorrect nucleotides precludes a simplified analysis of fidelity by traditional means attempting to assess contributions to fidelity in ground-state binding and chemistry steps as separate check points. According to our analysis and the set of rate constants governing fidelity for T7 DNA polymerase, the discrimination reduces to the following:

$$\mathrm{D}=\frac{(k_{\text{cat}}∕K_{\mathrm{m}}{)}_{\text{correct}}}{(k_{\text{cat}}∕K_{\mathrm{m}}{)}_{\text{incorrect}}}\approx \frac{(K_1{k}_2{)}_{\text{correct}}}{(K_1{K}_2{k}_3{)}_{\text{incorrect}}}$$

This analysis reinforces the notion of ground-state discrimination as the ratio of K₁ values but removes from consideration other simplifications and arguments regarding checkpoints involving the chemistry step. The specificity for correct incorporation is dictated by the rate of the conformational change step (k₂) but is determined by the product of the equilibrium constant for the unfavorable isomerization step (K₂) and the rate of chemistry (k₃) for mismatch incorporation. Moreover, the conformational change step is used by the enzyme to improve selectivity by committing a correct substrate to forward polymerization while favoring dissociation of a mismatch.

Arguments that an enzyme could be made faster if a rate-limiting conformational change step did not precede an inherently faster chemistry step (20) ignore the fact that the speed of the chemistry step is limited by how fast the nucleotide can bind and how fast the catalytic residues can be aligned during the conformational change step but, more importantly, ignore the fact that the rate of the chemistry step does not contribute to k_cat/K_m if the conformational change step is not readily reversible relative to the chemical reaction. Under conditions where the alignment of catalytic residues in the conformational change step is critically dependent upon recognition of the correct substrate, the importance of isomerization in contributing to selectivity cannot be denied. The chemistry step for incorporation of a correct nucleotide is fast because the conformational change step brings catalytic residues into alignment, while the rate of the reaction of a mismatch is slow because they induce a distinctly different conformational change leading to misalignment of catalytic residues and rapid release of the nucleotide. In addition, binding to an “open” state through a weak, rapidly reversible, ground state affords fast sampling of nucleotides from solution, while subsequent isomerization of the ternary complex determines the fate of the bound nucleotide.

The Meaning of k_cat, K_m, k_pol, and K_d.

It has long been established that steady-state kinetic measurements of DNA polymerase single-nucleotide incorporations are dominated by the slow release of the DNA product from the enzyme and that application of such steady-state analysis to DNA polymerases fails to provide accurate parameters (5, 11, 32). To circumvent these difficulties, one of us (K.A.J.) has long been a proponent of the single-turnover rapid kinetic approach in which the concentration dependence of the nucleotide incorporation rate defines an apparent K_d thought to represent ground-state nucleotide binding and k_pol, the maximum rate of incorporation (5, 33, 34). Reference to parameters k_pol and apparent K_d have been used to distinguish these values from the inaccurate k_cat and Km measurements made by steady-state methods as applied to DNA polymerases. Evaluation of the apparent K_d and k_pol governing incorporation by single-turnover rapid quench methods has become the standard for estimating DNA polymerase fidelity as the ratio of k_pol/K_d (5). One confusing point here is that we are mired in the terminology that has been previously applied. In this context, we will refer to K_m and k_cat values assuming that they would be measured accurately for processive synthesis without the complications as a result of slow DNA release or the use of homopolymeric templates.

The approximate equality of k_pol/K_d and the steady-state specificity constant, k_cat/K_m, was based on data suggesting that nucleotide binding was a rapid equilibrium process and that incorporation was governed by a single rate-limiting isomerization step (5, 9). Our new data demand re-evaluation of this interpretation. For both correct and incorrect nucleotide incorporation, k_pol measures the rate of polymerization more accurately than can be achieved by steady-state measurements on a processive enzyme and provides an accurate quantity to define k_cat. Measurement of the apparent K_d provides a value approximating the K_m in defining the substrate concentration dependence of the rate of each incorporation event. However, the mechanistic meaning of k_pol and apparent K_d requires a deeper understanding and differs for correct and incorrect base pairs. Because of the three-step sequence (ground-state binding, isomerization, and chemistry), one can no longer apply the simplified, model-dependent conclusion that the apparent K_d, measured in the quench-flow experiment, is the true ground-state K_d. Rather, the apparent K_d is a function of the substrate concentration dependence of the approach to the maximum rate and, as such, is an approximate measure of K_m, including terms for isomerization and chemistry and relying upon fast pyrophosphate product release as described above. The maximum rate of polymerization, k_pol, measured in the rapid quench experiment is a composite of isomerization and chemistry steps and approximates k_cat. Theoretically, measurements of k_pol in single-turnover experiments should be biphasic when k₂ and k₃ are comparable, but in practice, the resolution of a lag phase is difficult and the phases blend together to yield k_pol ~ k₂k₃(k₂ + k₃). In the final analysis, the conclusion that k_pol/K_d = k_cat/K_m defining specificity appears to be valid, but interpretation of the individual parameters k_pol and K_d is model-dependent and, in particularly, the apparent K_d can no longer be equated to the ground-state dissociation constant.

According to our model and the kinetic constants for correct incorporation, K_m is approximately 10 μM, while K_d = 28 μM. This difference is certainly within the range of errors that one could expect in comparing binding using dideoxy-terminated DNA with measurements of incorporation using normal DNA in our experiments. It should be noted that the concentration dependence of the rate of the fluorescence transient defines the true K_d for ground-state nucleotide binding (as in Figure 3), while concentration dependence of the rate of incorporation defines what was previously referred to as the apparent K_d but is closer to the K_m.

For T7 DNA polymerase, the apparent K_d is comparable to (within a factor of 3) the true equilibrium dissociation constant for ground-state binding (1/K₁) for both incorrect and correct base pairs but for different reasons, as summarized in Tables 2 and 3. In the case of a correct base pair, the equality K_m ≈ K_d is approximately true because the conformational change and chemistry steps are comparable and combine to define the maximum observed rate of incorporation that is within a factor of 3 of the rate constant for isomerization, k₂. As shown in Table 2, K_m = K_dk₃/(k₂ + k₃) and the term k₃/(k₂ + k₃) is only 0.35 with our constants. In the case of a mismatch, the observed K_d approximates the ground-state dissociation constant because the conformational change is unfavorable, and therefore, the collision complex dominates the equilibrium; that is, K_m = K_d/(K₂ + 1), and K₂ is less than unity (Tables 1 and 3).

The rate of catalysis after binding a mismatch (0.12 s⁻¹, observed; 0.3 s⁻¹, inferred for k₃) is reduced by a factor of at least 1000-fold from the rate of the reaction with the correct base. This reduction in rate is consistent with what might be expected if one or more key catalytic residues were removed from contact with the substrate. Thus, it is reasonable to suppose that key catalytic residues are pulled out of contact with the substrate by the active recognition of a mismatch. There are several likely candidates for important catalytic residues whose position in the recognition domain is altered to attenuate the rate of the reaction, including R518, H506, K522, Y526, and Y530. The CSF signal may sense subtle changes in positions of these residues because of the positional proximity between the MDCC probe and these residues, each of which make contacts with the incoming dNTP. Catalysis by the two metal ions at the active site is thought to occur by activation of the 3′-OH and by stabilizing the developing charge on the α-phosphate in the transition state (35, 36). Residual catalysis by the two metal ions may provide a basal rate of misincorporation when the recognition domain is disordered. According to our model, residues contributed by the recognition domain move in to contact the substrate to enhance catalysis 1000-fold by anchoring the β,γ-phosphates and further stabilizing the developing negative charge. Accordingly, the recognition domain functions as a molecular switch, triggering the reaction of a correct substrate but slowing the reaction of a mismatch.

Not all polymerases achieve the rates and fidelity exhibited by T7 DNA polymerase, which is the only replicative polymerase that has been fully characterized. Other polymerases that have been examined closely, Pol β, Taq polymerase, and the Pol-I Klenow fragment, are all DNA repair enzymes. Each enzyme is an order of magnitude slower than T7 DNA polymerase and an order of magnitude less accurate. These enzymes may not have fine-tuned the nucleotide-induced alignment of active-site residues to the same degree as seen by T7 polymerase. The fidelity of a particular enzyme appears to be directly correlated with the role of the nucleotide-induced conformational changes in achieving high enzyme specificity.

Induced-Fit Enhances Specificity.

Previous analysis based on equilibrium thermodynamic binding cycles has led to the conclusion that an induced fit will reduce enzyme specificity toward a good substrate as compared to an enzyme with a rigid, preformed active site (4, 37). The argument was based on the realization that a portion of that intrinsic substrate-binding energy must be consumed to reorganize the active site and is therefore not available to stabilize the transition state. However, our analysis shows that specificity is determined by the rate of the conformational change if isomerization is not readily reversible and the actual rate of the chemistry step is immaterial in defining specificity under these conditions. Therefore, energy sacrificed to organize the active-site residues is not lost by being unavailable for transition-state stabilization. Although k_cat may be reduced by the energy consumed in the conformational change step, specificity will not. An enzyme can increase specificity by using a fast conformational change step to commit a desired substrate to catalysis at a rate that exceeds the catalytic step.

Structures have been obtained for polymerases with mismatches in the primer/template (38) and with mismatches bound to lower fidelity repair enzymes. Although low-fidelity enzymes accommodate mismatches in a large, rather open active site (26), higher fidelity polymerases appear to sterically restrict the binding of mismatches (39). The structure of T7 DNA polymerase with 8-oxo-7,8-dihydroguanosine (8-oxo-G) in the active site suggests that the enzyme uses the side chain of K536 to sterically or electrostatically block 8-oxo-G (in the syn conformation) from mispairing with dATP, by blocking the formation of a closed conformation. The wild-type enzyme with 8-oxo-G in the template shows an open configuration with the incoming dATP disordered (40). Mutation of K536A allows for the formation of a closed conformation of a misinsertion complex with dATP, which mimics the closed complex formed with a correct base pair (41). These data support our contention that T7 polymerase may have evolved to actively recognize mismatches, because it apparently actively blocks the formation of a closed complex with 8-oxo-G(syn)/dATP, a common oxidative metabolite of guanosine. No one has succeeded in obtaining a crystal structure of a mismatch bound to a high-fidelity enzyme. This may be due to the weak binding of mismatches to high-fidelity enzymes or the multiple, open conformations induced by a mismatch as reported here.

Is This a “New Paradigm” for Enzyme Specificity? In the long history of attempts to understand enzyme specificity, many papers have been written including one that purports to outline all possible mechanisms of achieving specificity (37). In many ways, elements of our model have been discussed before; for example, we proposed more than a decade ago that there may be different rate-limiting steps for correct and incorrect base incorporation (5). It could be argued that it has long been known that mismatches bind more weakly and incorporate more slowly; therefore, it is not such a great surprise that they dissociate rapidly and, when bound, may lead to a disorganized active site. Although many of the concepts presented here have been described in general terms, this is the first instance in which a comprehensive comparison of binding, isomerization, and chemistry steps of favored and disfavored substrates have been compared. Moreover, we are the first to recognize that the conformational change step committing the substrate to forward catalysis eliminates the chemistry step from the specificity constant. This is an important conclusion because it eliminates from consideration overly simplified models based on estimations of ground-state free energy and transition-state stabilization as the sole basis for selectivity. Our data refute the conclusion that only the free-energy difference between the free enzyme and the enzyme-bound transition state determines the specificity constant (20, 42).

Evidence for a third enzyme state involved in mismatch recognition expands our understanding of the mode by which enzymes enhance their differential discrimination between favored and disfavored substrates. In this sense, we argue that our model represents a new paradigm, in which specificity can only be understood by measuring the forward and backward rates of all steps defining k_cat/K_m, that fast conformational changes can be used to select a favored substrate and at the same time restrict the binding and incorporation of a disfavored substrate. Moreover, our model is somewhat speculative in that it proposes that enzymes may have evolved to specifically recognize known alternate substrates and use binding energy to misalign catalytic residues.

It remains to be seen whether enzymes other than DNA polymerases are able to discriminate against undesirable substrates by an active misalignment of catalytic residues. Moreover, the open-closed enzyme structural transition may be used to commit the desired substrate to catalysis while facilitating rapid release of an undesired alternate substrate. It is also interesting to speculate that enzymes may have evolved to use similar means to slow the reverse reaction by altering the dynamics of binding and isomerization induced by the products of their reactions.

Abbreviations:

CSF

conformationally sensitive fluorophore

MDCC

7-diethylamino-3-((((2-maleimidyl)ethyl)amino)carbonyl)coumarin

dNTP

deoxynucleoside triphosphate