Sequential Time-Kill, a Simple Experimental Trick To Discriminate between Pharmacokinetics/Pharmacodynamics Models with Distinct Heterogeneous Subpopulations versus Homogenous Population with Adaptive Resistance

Experiments were conducted with polymyxin B and two Klebsiella pneumonia isogenic strains (the wild type, KP_WT, and its transconjugant carrying the mobile colistin resistance gene, KP_MCR-1) to demonstrate that conducting two consecutive time-kill experiments (sequential TK) represents a simple approach to discriminate between pharmacokinetics/pharmacodynamics models with two heterogeneous subpopulations or adaptive resistance.

ABSTRACT

Experiments were conducted with polymyxin B and two Klebsiella pneumonia isogenic strains (the wild type, KP_WT, and its transconjugant carrying the mobile colistin resistance gene, KP_MCR-1) to demonstrate that conducting two consecutive time-kill experiments (sequential TK) represents a simple approach to discriminate between pharmacokinetics/pharmacodynamics models with two heterogeneous subpopulations or adaptive resistance.

TEXT

Semimechanistic pharmacokinetics/pharmacodynamics (PK/PD) modeling is a modern approach that offers unique opportunities to simulate CFU versus time after antibiotic exposures corresponding to various multiple-dosing strategies (1). Time-kill (TK) experiments constitute a simple and inexpensive approach to generate in vitro data in static conditions for antibiotics PK/PD modeling. After an initial decay of CFU with time, regrowth is frequently observed that can be described by a number of models. However, in the absence of precise mechanistic information, PD models with two stable, heterogeneous subpopulations, i.e., sensitive (S) and resistant (R) (referred to as S/R), would most often demonstrate superiority over models relying on adaptation phenomena (2). Although these models should then be challenged in dynamic (hollow-fiber) conditions, these experimental settings are much more expensive and complex to handle than TK experiments. However, conducting two consecutive TK experiments (sequential TK) may offer a pragmatic alternative. Indeed, the S/R model assumes that initial decay is due to the (S) disappearance and regrowth to (R) selection. However, the (S) and (R) subpopulations are supposed to be stable with time, so no regrowth would be expected after conducting a second TK experiment with the resistant subpopulation bacteria that regrew after the first TK experiment. Such a second regrowth would rather suggest progressive adaptation. Our objective was to confirm experimentally that sequential TK would offer a simple approach to discriminate between regrowth due to heterogeneous subpopulations and adaptive resistance (AR).

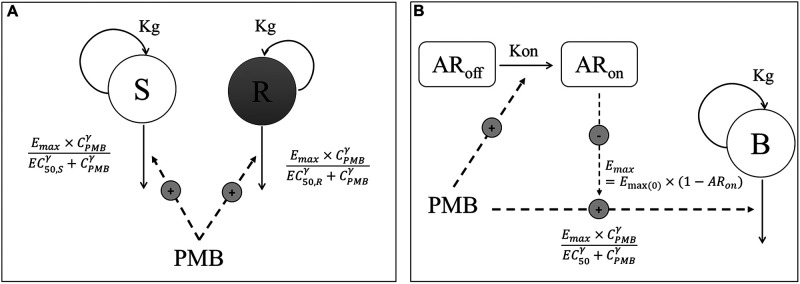
Two isogenic isolates were used in this study: a wild-type Klebsiella pneumonia R2292 (KP_WT) and its transconjugant carrying the mobile colistin resistance gene MCR-1 (KP_MCR-1), kindly provided by P. Nordmann (University of Fribourg, Switzerland). This strain was built by transferring the MCR-1 plasmid from MCR-1-positive Escherichia coli isolates as donors (3). TK experiments were conducted in duplicate in cation-adjusted Mueller-Hinton broth over 30 h at an initial inoculum close to 10⁶ CFU/ml in the presence of polymyxin B (PMB) ranging from 0.0625 to 1 mg/liter for KP_WT and 0.5 to 8 mg/liter for KP_MCR-1. At 30 h, bacteria that regrew up to 10⁸ CFU/ml were harvested by centrifugation and resuspended to immediately begin the second TK experiment at an initial inoculum close to 10⁶ CFU/ml again, with PMB concentrations ranging from 0.0625 to 1 mg/liter for KP_WT and 1 to 32 mg/liter for KP_MCR-1. Modeling was conducted after the first TK and then simultaneously after the two sequential TK experiments for both strains, using NONMEM 7.4 with Laplacian numerical algorithm and the M3 method for handling observations below the limit of quantification (4). Each model incorporated a logistic growth expression to describe bacterial population dynamics. PMB bactericidal effect was modeled according to an E_max function for both strains. Two different model structures were investigated to characterize the emergence of resistance. The first model, S/R, includes two independent subpopulations of bacteria with different susceptibilities and regrowth explained by a higher EC₅₀ (concentration that produces 50% of E_max) value for the (R) than the (S) subpopulation (Fig. 1A) (5–7). The fraction of (S) and (R) bacteria in the initial inoculum was estimated as a parameter, and fitness cost resulting in a lower growth rate for the (R) subpopulation was investigated. The second model, AR, includes a single homogenous bacterial population with adaptive resistance (Fig. 1B). At the beginning of the experiment, all bacteria were assumed to be nonadapted, but an adaptation developed over time in the presence of PMB, affecting E_max (8). The fraction of (S) and (R) or adapted bacteria, depending on the model, at the end of the first TK experiment was used as the initial condition for the second TK experiment. Model selection was based on objective function value and goodness-of-fit plots. For nonnested models, the Bayesian information criterion (BIC) was calculated and compared between models.

FIG 1.

Schematic illustrations of the S/R model (A) and AR model (B). C_PMB, PMB concentration; S, compartment with PMB-sensitive bacteria; R, compartment with resistant bacteria; B, compartment with homogenous bacterial population; K_g, rate constant for multiplication of bacteria; E_max, maximum kill rate constant; E_max(0), maximum kill rate constant when no adaptive resistance has developed; EC₅₀, PMB concentration producing 50% of E_max(0); EC_50,S and EC_50,R, PMB concentration producing 50% of E_max for (S) and (R) bacteria, respectively; γ, sigmoidicity factor; AR_off and AR_on, compartments describing adaptive resistance being off and on, respectively; K_on, rate constant for development of adaptive resistance.

Genes assumed to be involved in polymyxin resistance, i.e., pmrA, pmrB, phoP, phoQ, pmrC, pmrE, lpxM, arnT, cptA, lpxT, eptB, and mcr-1, were sequenced. Expression was analyzed by real-time quantitative PCR (RT-qPCR) and analyzed with the 2^−ΔΔCT method, by normalizing the relative expression of selected genes to the expression of rpsL used as an internal control (9), to determine their expression levels before and after the first and second TK experiments for both strains.

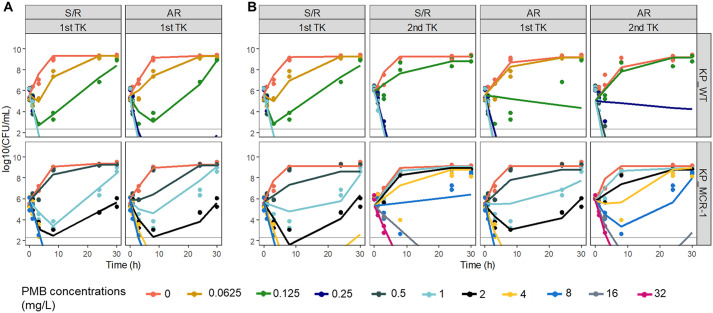
An initial CFU decay followed by regrowth was observed in both strains after the first single TK experiment, at PMB concentrations of 0.125 mg/liter for KP_WT and 1.0 and 2.0 mg/liter for KP_MCR-1 (Fig. 2). The S/R and AR models provided relatively good data fitting, although, as expected, statistical comparisons favored the S/R model (see BIC values in Table 1) (2). However, differences were observed between strains during the second TK experiment. In the presence of KP_WT, PMB apparent activity was slightly reduced, no initial CFU decay was observed at a concentration of 0.125 mg/liter anymore, but no regrowth was observed after the rapid decay observed at 0.25 mg/liter, consistent with (S) and (R) stable heterogeneous subpopulations (Fig. 2B, top). Accordingly, the S/R model was still able to describe the experimental data after simultaneous analysis of the two sequential TK experiments and to quantify the phenotypic difference between the two subpopulations with precision, with the reduced apparent activity for the (R) population reflected by an EC₅₀ value (EC_50,R) that was slightly higher than that for the (S) population (EC_50,S) (0.132 versus 0.065 mg/liter). In contrast, with KP_MCR-1, regrowth was observed at concentrations of 1 and 2 mg/liter after the first TK experiment and again after the second TK experiment, but at slightly higher concentrations of 4 and 8 mg/liter (Fig. 2B, bottom), indicating that PMB continued to lose efficacy during the second TK experiment. This sustained changing activity with time is not consistent with a stable (R) subpopulation but rather suggests continuous adaptation with time. Only the AR model was able to provide a relatively good fit of these sequential TK data for KP_MCR-1.

FIG 2.

Comparison of predictions from the S/R and AR models after analysis of a single TK experiment (A) or after simultaneous analysis of the sequential TK data (B) for 2 isogenic isolates. (Top) K. pneumonia R2292 (KP_WT); (bottom) its MCR-1 transconjugant (KP_MCR-1). For KP_WT, PMB concentrations ranging from 0.0625 to 1 mg/liter were used for the 2 sequential TK experiments. For KP_MCR-1, PMB concentrations ranging from 0.5 to 8 and 1 to 32 mg/liter were used for the first and second TK experiments, respectively. Symbols, experimental data (n = 2); color-matched lines, model predictions; gray solid lines, limit of quantification.

TABLE 1.

Statistical comparison of various parameters for S/R and AR models

Parametera	Model results [estimate and relative standard errorb (%)] for strain:
	KP_WT				KP_MCR-1
	1 TK		Sequential TK		1 TK		Sequential TK
	S/R	AR	S/R	AR	S/R	AR	S/R	AR
BIC	23.4	39.5	35.1	208.8	14.1	47.1	163.7	86.5
INOC (log10 CFU/ml)	5.60 (2.1)	5.52 (2.5)	5.63 (2.0)	5.55 (4.1)	5.78 (1.8)	5.9 (2.5)	5.64 (2.9)	5.56 (2.2)
INOC2 (log10 CFU/ml)			5.93 (0.9)	5.03 (3.2)			5.3 (2.6)	5.85 (1.9)
Bmax (log10 CFU/ml)	9.29 (1.2)	9.32 (1.1)	9.24 (1.3)	9.19 (2.0)	9.34 (1.6)	9.24 (1.4)	9.1 (1.6)	9.13 (1.0)
mutf (log10 CFU/ml)	−3.69 (9.0)		−3.49 (10.4)		−4.46 (8.9)		−10.5 (7.8)
Kg (h−1)	1.54 (8.1)	1.15 (15.2)	1.42 (10.4)	0.935 (20.1)	(S), 1.03 (12.8); (R), 0.568 (8.0)c	0.959 (15.9)	(S), 1.64 (20.0); (R), 1.19 (8.4)c	1.58 (7.9)
Emax (h−1)	4.40 (5.9)		4.36 (4.8)		3.24 (6.4)		5.41 (10.3)
Emax(0) (h−1)		5.18 (8.2)		4.92 (13.7)		5.28 (10.8)		7.43 (7.0)
EC50 (mg/liter)		0.121 (5.7)		0.371 (14.3)		1.85 (23.3)		6.98 (14.6)
EC50,S (mg/liter)	0.0631 (2.2)		0.065 (15.6)		0.932 (7.2)		1.87 (31.0)
EC50,R (mg/liter)	0.141 (1.3)		0.162 (4.5)		3.9 (13.8)		31.1 (18.1)
γ	10 (fixed)d	2.39 (15.1)	5.01 (15.3)	3.33 (33.4)	3.8 (18.7)	1 (fixed)e	1 (fixed)e	1 (fixed)e
Kon (h−1)		0.0956 (17.5)f		0.001 (1.2)f		0.0856 (17.2)f		0.0547 (7.5)g
Kon50 (mg/liter)								2.89 (7.4)
δ								3.63 (9.8)
σ (log10 CFU/ml)	0.255 (19.3)	0.382 (20.4)	0.29 (10.7)	1.97 (14.9)	0.226 (17.0)	0.498 (18.1)	0.825 (13.3)	0.469 (8.4)

^aINOC, bacterial count at time 0 (before the start of the 1st TK); INOC₂, bacterial count at 30 h (before the start of the 2nd TK); B_max, maximum bacterial population size supported by the system; mutf, fraction of resistant bacteria (R) at time 0; K_g, apparent growth rate constant; E_max, maximum kill rate constant; E_max(0), maximum kill rate constant when no adaptive resistance has developed; EC₅₀, PMB concentration that produces 50% of E_max(0); EC_50,S and EC_50,R, PMB concentrations that produce 50% of E_max for the (S) and (R) subpopulations, respectively; γ, Hill coefficient in PMB effect relationship; K_on, rate constant for development of adaptive resistance to PMB; K_on50, PMB concentration yielding 50% of K_on; δ, Hill coefficient for rate constant for development of AR; σ, additive residual error on log₁₀ scale for total bacteria count.

^bRelative standard error obtained by sampling importance resampling.

^cThe sensitive (S) and resistant (R) subpopulations were assumed to grow at different rates, with the estimation of 2 different K_g for (S) and (R) resulting in a significant decrease in the objective function value given by NONMEM.

^dThe Hill coefficient for this relationship, initially estimated to fall between 10 and 20, was fixed to 10 to improve model stability (13).

^ePMB bactericidal effect was modeled using an ordinary E_max model, with the estimation of Hill coefficient resulting in a nonsignificant decrease in the objective function value given by NONMEM.

^fK_on was estimated in the presence of PMB but was not dependent on its concentration.

^gThe resistance onset rate was determined by the PMB concentration through a sigmoid E_max model. K_on corresponds to the maximal rate constant for development of AR in this case.

However, these models were not really supported by RT-qPCR investigations. No mutation was observed with KP_WT to support the two heterogeneous subpopulations for the S/R model. With KP_MCR-1, an overexpression was observed for the mcr-1 gene but with the same magnitude (5.5-fold) at the end of the first and second TK experiments compared with time zero, which is not consistent with continuous progressive adaptation during the first and second TK experiments. In this study, only two simple models, representative of the two basic situations, i.e., stable heterogeneous subpopulations (S/R) versus unstable homogenous population (AR), were tested. Although they provided relatively good fit, these models were not supported by the mechanistic experiments, suggesting that real life is likely to be more complex, with combined heterogeneity and instability issues requiring more complex models (1). Furthermore, mutant selection or adaptation phenomena may occur slowly and only be observable after several days of hollow-fiber experiments, which remain the most demanding but best approach for in vitro semimechanistic PK/PD modeling of antibiotics (10–12). Yet, although this study suffers from limitations, it shows that sequential TK experiments constitute a simple approach to disqualify S/R models selected after traditional TK experiments and that these S/R models should not be used without further validation to predict treatment outcomes after multiple dosing.