A framework for developing a spatial high-resolution daily precipitation dataset over a data-sparse region

Abstract

This paper outlines a framework in order to provide a reliable and up-to date local precipitation dataset over Sistan and Baluchestan province, one of the poorly rain gauged areas in Iran. Initially, the accuracy of GPCC data, as the reference dataset, was evaluated. Next, the performance of eight gridded precipitation products (namely, CHIRPS, CMORPH-RAW, ERA5, ERA-Interim, GPM-IMERG, GSMaP-MVK, PERSIANN and TRMM3B42) were compared based on the GPCC observations during 1982–2016 over the study area. The evaluation was done by using eight commonly used statistical and categorical metrics. Then, among the products, the most suitable ones on the basis of their better performance and least time delay in providing data, were utilized as the constituent members of the proposed hybrid dataset. Using several statistical/machine learning approaches (namely, NSGA II, ETROPY and TOPSIS), daily weights of the chosen datasets were estimated, while the correlation coefficient and the estimation error of the data were maximized and minimized, respectively. Finally, the efficiency of the proposed hybrid precipitation dataset was investigated. Results indicate that the developed hybrid dataset (2014-present), using the estimates of the chosen ensemble members (GPM-IMERG, GSMaP-MVK and PERSIANN) and their respective weighting coefficients, provides accurate local daily precipitation data with a spatial resolution of 0.25°, representing the minimum time delay, compared to the other available datasets.

Atmospheric science, Environmental science, Geophysics, Earth sciences, Hydrology, Precipitation evaluation, Optimally weighted data, Merged dataset, Sistan and Baluchestan.

1. Introduction

Access to climate data (i.e., rainfall, temperature, etc) is one of the fundamental prerequisites for hydro-climatological applications (Kucera et al., 2013; Lettenmaier et al., 2015; Abdulrazzaq et al., 2019). Typically, station-based observation data is considered as the most reliable source of this data. The quality required to exploit this data depends on the essential features including: existence of a long-term statistical period of overlapping data between the stations, appropriate spatial-temporal coverage across the region, sufficiently accurate precipitation estimates, data recording in accordance with the international standards, timely data presentation with minimum delay, etc. Not all of these features are easy to obtain. However, remote sensing data provides the opportunity to use the precipitation estimates as a data source. Today, a wide range of data centres provide gridded precipitation products, which can be generally classified into four categories (Duan et al., 2016): 1) precipitation products from gauge-based data e.g., CPC (the Climate Precipitation Center), CRU (the Climatic Research Unit), GPCC (the Global Precipitation Climatology Centre) (Xie et al., 2007; Harris et al., 2013; Schneider et al., 2014); 2) satellite-only products such as CMORPH-RAW (CPC MORPHing technique-RAW), GSMaP-MVK (Global Satellite Mapping of Precipitation Moving Vector with Kalman) (Joyce et al., 2004; Iguchi et al., 2009); 3) reanalysis data created from combining observation and simulation/measurement data, for example: NCEP-CFSR (National Centers for Environmental Prediction- Climate Forecast System Reanalysis) (Saha et al., 2010); and 4) satellite-gauge products, for instance PERSIANN (Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks), TRMM (Tropical Rainfall Measuring Mission) (Sorooshian et al., 2000; Huffman et al., 2007). Therefore, the precipitation datasets do not necessarily use the same basic data and data preparation methods. As a result, performance evaluation of different datasets is always considered as a necessity for the climatic research. Evaluation results from several studies demonstrate that satellite-only products are reasonably accurate and can be used for various applications such as hydrologic applications; however, the results have always been interpreted differently. For example, the datasets may overestimate or underestimate the amount of precipitation in hot and cold seasons (e.g. Behrangi et al., 2011; Basheer and Ahmed Elagib, 2019). Some other studies showed that the accuracy of the estimated values, not only depends on temporal distribution, but also on the spatial distribution and topography of the area (e.g. Duan et al., 2016; Henn et al., 2018; Yang et al., 2019). In addition, using raw precipitation products may provide more accurate estimates, compared to the interpolated gridded precipitation, derived from inadequate spatial coverage of land stations (e.g. Ghulami et al., 2017). Results also show that satellite-based datasets provide better outcomes in hot and dry regions, reanalysis datasets are ideally suited for the areas with dense network of ground-based stations, and finally, multi-source datasets are especially appropriate for estimating the rainfall at regional or local levels (Bosilovich et al., 2008; Xue et al., 2013; Wang et al., 2019).

The common theme among all the studies is that the performance assessment process is mainly carried out either directly (calculating statistical and categorical metrics e.g. Sun et al., 2018; Ahmed et al., 2019; Thanh, 2019) or indirectly (evaluation of hydrologic-hydraulic models e.g. Voisin et al., 2008; Getirana et al., 2011; Wu et al., 2018). More information, about the performance assessment of precipitation datasets can be found in several studies (e.g. Yong et al., 2010; Gao and Liu, 2013; Tan et al., 2015).

Although the results of the evaluations indicate the effectiveness of different datasets, sometimes their precipitation estimates contain systematic and random errors and even different datasets present different amounts of rainfall in the same spatial location and temporal position. This leads to uncertainties in the accurate estimation of precipitation. Recent studies show that multi-source datasets, providing maximum similarity with the observed values, have several gains (Grimes et al., 1999; Todini, 2001; Heidinger et al., 2012): 1) they take advantage of the selected data sources; 2) they can reduce the impact of systematic errors and biases; 3) they consider the interactions of different datasets with others at different times and locations; and 4) they may reduce, as much as possible, the sensitivity to the factors decreasing the accuracy of precipitation estimates.

Among currently available designed hybrid datasets, PFD (Precipitation Frequency Data Server) and WFDEI (Watch Forcing Data ERA-Interim) may be referred to (Sheffield et al., 2006; Weedon et al., 2014), which are based on rescaling reanalysis data to force agreement with gauge-interpolated data as well as TMPA3B43 (TRMM Multi-satellite Precipitation Analysis) and CHIRPS (Climate Hazards group Infrared Precipitation with Stations), through combining gauge-based data with satellite-only products, using inverse-error weighted averaging (Huffman et al., 2007; Funk et al., 2015b). In a more recent approach, Beck et al. (2017) put forward the idea of a novel merging technique and developed MSWEP (Multi-Source Weighted-Ensemble Precipitation). The estimated precipitations are calculated by weighting the seven datasets where the basis of weighting was the three-day correlation coefficients. However, use of MSWEP can provide better performance for water storage and discharge studies but it has no obvious advantages compare to some rainfall products on other aspect (Awange et al., 2019).

As these merged datasets generate data globally/quasi-globally, their use may be challenging as (a) all of them may not provide up-to-date data (e.g. Joyce et al., 2004; Huffman et al., 2007; Awange et al., 2019); (b) the performance assessment process in some of them has been carried out indirectly by the evaluation of hydrologic-hydraulic models (e.g. Beck et al., 2017; Awange et al., 2019), which may not necessarily be a definitive confirmation of the accuracy of the precipitation data; (c) they do not provide reliable precipitation estimates in different time periods (e.g. Behrangi et al., 2011; Awange et al., 2019; Basheer and Ahmed Elagib, 2019); and (d) the spatial distribution of the accuracy of precipitation estimates are not the same in different areas (e.g. Ghulami et al., 2017; Henn et al., 2018; Awange et al., 2019).

Therefore, the main motivation for the present study was to develop a local hybrid dataset, thereby taking advantage of the individual used datasets, minimizing their limitations and presenting precipitation data in a timely manner, believed to be crucially important for gauge-based data-sparse regions. The Sistan and Baluchestan province, located in the southeast of Iran with varying challenging issues including floods and droughts, has been selected as the study area, in this research, for developing a local precipitation dataset.

This paper is organized as follow. Section 2, in three subsections, presents the study area, the used datasets as the materials of this study and the methodology describing the notion of the hybrid technique for the proposed dataset. Section 3 presents the obtained results and consequently the relative discussions and conclusion are described in Sections 4 and 5.

2. Material and methods

2.1. Study area

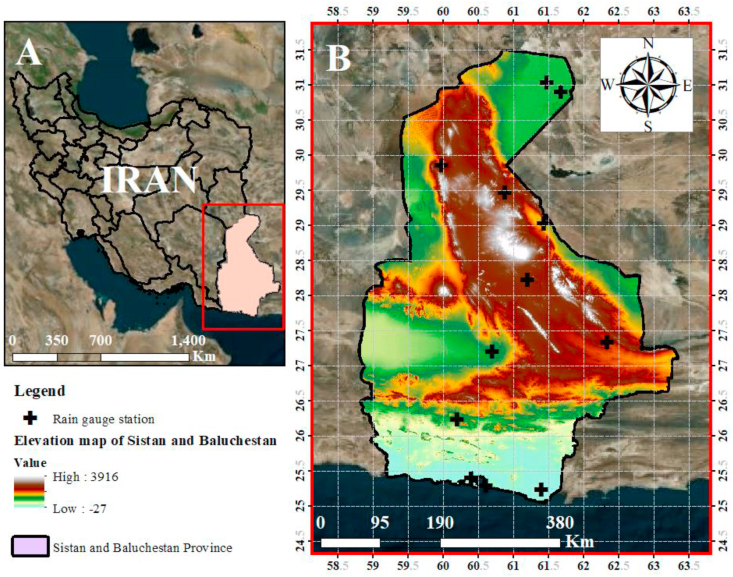
Lack of adequate coverage (existence) of rain gauge stations, especially in arid and semi-arid areas of Iran is a major management and research predicament. In this term, the province of Sistan and Baluchestan is one of the remarked poorly rain gauged areas of the country. This province with a population of approximately 2,800,000 people (according to the latest census of the country in 2015), situated in the southeast of Iran, is enclosed between a longitude of 58°50′-63°02′ E and a latitude of 25°03′-31°27′ N. It covers an area of about 181,000 km² and as such it is the second largest province in the country. The prevailing climate of this vast province is hot desert climate and meteorological parameters suggest that the average annual precipitation and the average annual temperature varies from 22 to 37 °C (Barthold, 1984; Abbasnia et al., 2018). Most of this information is captured and stored by the weather station in the analyzed area (Figure 1). Based on official reports, this province is one of the most deprived areas of Iran in terms of water resources availability. In addition, the region is facing serious challenges, including severe floods and droughts, scarce land-based data, water conflicts with riparian neighboring countries, etc. Thus, development of a reliable precipitation dataset, which can be used in various aspects of research and management, is imperative.

Figure 1.

(A) Location of Sistan and Baluchestan Province and (B) the rain gauge stations, used in the present study.

2.2. Data

2.2.1. Observational data

Usage of rain gauge records, as the primary source of rainfall measurements, are exposed to several challenges: 1) discontinuous data on the stations; 2) insufficient periods of records; 3) point specific measurements and small sampling areas resulting in uncertainties in the spatial variability of precipitation (Cánovas-García et al., 2018). The location of the 12 rain gauge stations, situated in the study area, provided by the Iranian Meteorological Organization (IRIMO), are shown in Figure 1 and Table 1. Inadequate spatial and temporal coverage of the stations led to utilize GPCC as the reference precipitation dataset, using high-density gauge data (Rudolf and Schneider, 2005). GPCC, which was established by the Germany's National Meteorological Service at the Deutscher Wetterdienst (DWD) on invitation of the World Meteorological Organization (WMO) in 1989, uses rain gauge stations to analyze precipitation for the global land areas and it aims to provide users with their needs, especially in determining the accuracy of gridded precipitation data (Schneider et al., 2011, 2014). This product provides gridded precipitation data, comprising several different sources such as WMO, GTS (Global Telecommunication System), SYNOP (SYNoptic Ocean Prediction), CLIMAT (ground surface targets), CRU (Climate Research Unit), FAO (Food and Agriculture Organization), and GHCN (Global Historical Climatology Network). The GPCC data is produced through a systematic process including: data collection, quality control, spatial analysis, and error quantification (Sun et al., 2018). This procedure for producing gridded precipitation data, has led to the introduction of GPCC as a reliable reference observation dataset in Iran, by different studies (Raziei et al., 2011; Azizi et al., 2015; Darand and Zand Karimi, 2016).

Table 1.

Summary of the rain gauge stations, utilized in the present study.

Station	longitude	Latitude	Altitude (m)	Period of record
Chabahar	60 37 E	25 17 N	8	1963–2019
Iranshahr	60 42 E	27 12 N	591	1964–2019
Khash	61 12 E	28 13 N	1394	1986–2019
Konarak	60 24 E	25 24 N	12	1984–2019
Mirjaveh	61 26 E	29 01 N	836	2006–2019
Nik Shahr	60 12 E	26 14 N	510	2006–2019
Nosrat Abad	59 59 E	29 51 N	1127	2011–2019
Rask	61 24 E	25 14 N	406	2009–2019
Saravan	62 20 E	27 20 N	1195	1986–2019
Zabol	61 29 E	31 02 N	489	1962–2019
Zahedan	60 53 E	29 28 N	1370	1951–2019
Zehak	61 41 E	30 54 N	895	1992–2019

2.2.2. Precipitation products

In this study, eight gridded precipitation products were employed in accordance with Table 2. The following gives a brief description of each.

Table 2.

Characteristics of the used precipitation products in the present study.

Dataset	Spatial resolution	Temporal resolution	Zonal coverage	Availability	Reference
CHIRPS	0.05°	Daily	50° N-50° S	1981-present	Funk et al. (2015a)
CMORPH_RAW	0.25°	30 min	60° N-60° S	1998-present	Joyce et al. (2004)
ERA5	0.25°	1 Hourly	Global	2008–2018	Hersbach and Dee (2016)
ERA-Interim	0.25°	3 Hourly	Global	1979–2018	Dee et al. (2011)
GPM-IMERG	0.10°	30 min	60° N-60° S	2014-present	Huffman et al. (2014)
GSMaP-MVK	0.10°	1 Hourly	60° N-60° S	2000-present	Iguchi et al. (2009)
PERSIANN	0.25°	Daily	60° N-60° S	2000- present	Sorooshian et al. (2000)
TRMM (3B42-RT)	0.25°	3 Hourly	50° N-50° S	2000–2016	Huffman et al. (2007)

CHIRPS is a quasi-global dataset with a statistical length of almost 40 years. Combining satellite-based rainfall products with gauge-based data provides a gridded precipitation dataset in time series (Funk et al., 2015a). This study uses the CHIRPS2.0 version of the dataset.

CMORPH stands for the precipitation products, estimated by NOAA Climate prediction center MORPHing technique, combining existing passive microwave-based precipitation estimates from multiple low orbit satellites and infrared data from multiple geostationary satellites (Joyce et al., 2004). In the present study, the CMORPH-RAW, one of the latest CMORPH products, was utilized.

Reanalysis is a procedure for generating climate data for climate monitoring and prediction. An unchanging data assimilation scheme and the relative models are utilized for manufacturing data; available observations are ingested every 6–12 h over the period being analyzed, since the observational network is altering. This framework provides a dynamically consistent estimate of the climate state at each time step. During each reanalysis product, the changing observation mix can produce artificial variability and spurious trends. ECMWF (European Centre for Medium-Range Weather Forecasts) is one of the centres that produces and presents reanalysis data, including ERA5, ERA-Interim, etc, in different spatial and temporal resolutions (Hersbach and Dee, 2016; Dee et al., 2011).

GSMaP-MVK is a satellite-based dataset, aiming to develop high resolution precipitation data from passive microwave and infrared satellites. The GSMaP-MVK product stands for the GSMaP Moving Vector with Kalman-filter product (Iguchi et al., 2009). The GSMaP-MVK provides data in different versions and the version 6.0 (second edition) was utilized in the present study.

Among other satellite-based precipitation datasets, PERSIANN is a system that uses an artificial neural network algorithm to estimate the amount of rainfall per pixel by using satellite longwave infrared images (Sorooshian et al., 2000). It offers data in three versions and this study used the PERSIANN version.

One of the first attempts to estimate precipitation by satellites, was the TRMM project in 1997, which was a joint project between NASA (National Aeronautics and Space Administration) and JAXA (Japan Aerospace Exploration Agency). The satellite was dedicated to estimate tropical precipitation by different microwave and visible infrared sensors, using a set of algorithms. Although passive microwave sensors benefit from more accurate estimates of precipitation, satellite infrared algorithms can produce high temporal sampling. The data collection started by TRMM and is currently continued by GPM-IMERG, launched in 2014 (Huffman et al., 2007, 2014).

All daily datasets used in the study have a spatial resolution of 0.25°. In cases where pixel size was less than 0.25° (i.e. CHIRPS, GPM-IMERG, GSMaP-MVK with higher spatial resolution than GPCC), data were resampled using the pixel averaging aggregation method.

2.3. Methodology

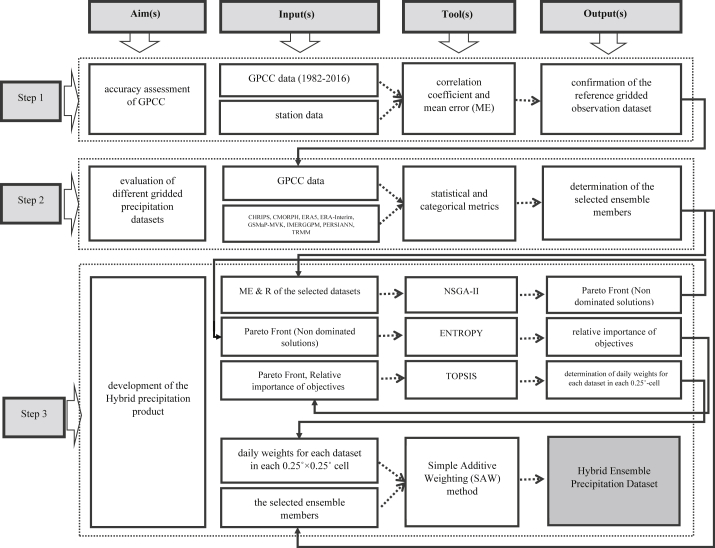
With the aim of providing a local precipitation dataset with high spatial-temporal resolution, the dominant perspective on the present study is summarized in Figure 2. Each of these steps is discussed in details below.

Figure 2.

The dominant perspective on the present study.

2.3.1. Evaluation of GPCC dataset accuracy

To ensure GPCC's ability in estimating precipitation and confirm it as the reference database, its agreement with the station data in the target region was monitored between 1982 and 2016. In this respect, daily precipitation data of GPCC with the spatial resolution of 0.25 ° × 0.25 ° was applied. Subsequently, the correlation coefficient and mean precipitation values, derived from GPCC data, were compared with the observed values in cells containing stations.

2.3.2. Evaluation of different gridded precipitation datasets

After the ratification of GPCC as the reference database, in order to select the best datasets in the study area, these datasets were evaluated. For this purpose, different statistical and categorical metrics were computed based on daily GPCC data with spatial resolution of 0.25° during the period from 1982 to 2016 (Table 3). The categorical metrics, used in the assessments, are based on four combinations of forecasts and observations: 1) Hit (H): the number of observed precipitations, correctly detected by the products; 2) Miss (M): the number of observed precipitations, not detected by the products; 3) False alarm (F): the number of the precipitation detected by the products but not observed by rain gauge stations; And 4) Correct negative (C): the number of precipitations, not detected by the products and not observed by rain gauge stations. Note that as the categorical metrics depend on a thresholds value, the value used in the study was precipitation>0 (mm).

Table 3.

List of the statistical and categorical metrics, used in the present study for the evaluation of precipitation products.

Evaluation Indexes	Describing	Type	Equation	Unit	Range	Optimal value
Mean Absolute Error (MAE)	the average magnitude of the forecast errors	statistical	$\text{MAE}=\frac{\sum _{\text{i}=1}^{\text{N}}\left|{\text{P}}_{\text{i}}-{\text{O}}_{\text{i}}\right|}{\text{N}}$	mm	[0~∞)	0
correlation coefficient (R)	the degree of collinearity between observed precipitation data and the gridded products	statistical	$\text{R}=\frac{\sum _{\text{i}=1}^{\text{N}}\left(\left|{\text{P}}_{\text{i}}-{\overline{\text{P}}}_{\text{i}}\right|\right)\left(\left|{\text{O}}_{\text{i}}-{\overline{\text{O}}}_{\text{i}}\right|\right)}{\sqrt{{\sum _{\text{i}=1}^{\text{N}}\left(\left|{\text{P}}_{\text{i}}-{\overline{\text{P}}}_{\text{i}}\right|\right)}^2}\times \sqrt{\sum _{\text{i}=1}^{\text{N}}{\left(\left|{\text{O}}_{\text{i}}-{\overline{\text{O}}}_{\text{i}}\right|\right)}^2}}$	NA	[-1~1]	1
BIAS score (BIAS)	the ratio of the frequency of forecast events to the frequency of observed events	categorical	$\text{BIAS}=\frac{\text{H}+\text{F}}{\text{H}+\text{M}}$	NA	[0~∞)	1
False Alarm Ratio (FAR)	the fraction of events, detected by the product but not observed	categorical	$\text{FAR}=\frac{\text{F}}{\text{H}+\text{F}}$	NA	[0~1]	0
Probability Of Detection (POD)	the fraction of the observed precipitation events, which were detected by the assessed product	categorical	$\text{POD}=\frac{\text{H}}{\text{H}+\text{M}}$	NA	[0~1]	1
Probability Of False Detection (POFD)	the fraction of the number of the precipitation events detected by the products but not observed by rain gauge stations	categorical	$\text{POFD}=\frac{\text{F}}{\text{F}+\text{C}}$	NA	[0~1]	0
Critical Success Index (CSI)	the proportion of events that were predicted correctly	categorical	$\text{CSI}=\frac{1}{\left(\frac{1}{1-\text{FAR}}\right)+\left(\frac{1}{\text{POD}}\right)-1}$	NA	[0~1]	1
Heidke Skill Score (HSS)	the fractional improvement of the forecast over the standard forecast	categorical	$\text{HSS}=\frac{2\left(\text{HC}-\text{FM}\right)}{\left(\text{H}+\text{M}\right)\left(\text{M}+\text{C}\right)+\left(\text{H}+\text{F}\right)\left(\text{F}+\text{C}\right)}$	NA	[-1~1]	1

Note: N is the number of samples; O_i is the observed precipitation, P_i is the estimated precipitation from the evaluated products, Ō_i and P_i are the average of corresponding data during N events.

At the end of this step, the datasets, which performed better and had the least time delay in providing data, were introduced as the constituent members of the proposed local hybrid dataset.

2.3.3. Hybrid precipitation product

In order to achieve the best combination of the chosen rainfall datasets, three preconditions are obligatory: (a) finding different combination of alternatives (the best feasible solution space of the datasets) satisfying the objectives; (b) distinguishing between the possible solutions based on the achievement of the objectives; and (c) choosing the best final alternative based on the results of the previous steps. Here, the framework presented by Yazdandoost and Izadi (2016) was utilized to address these prerequisites in finding the best combination of ensemble members. The proposed framework applies (1) NSGA-II (Non dominated Sorting Genetic Algorithm II) with the aim of finding the best solution space of the datasets with assessing the trade-offs between the objectives, (2) ENTROPY theory to find the relative importance of the objectives and (3) TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution) to choose the best alternative from the available options. The following part elaborates a brief outline of the steps of this framework and complete information can be found in Yazdandoost and Izadi (2016) and Yazdandoost et al. (2020).

Initially, the NSGA-II optimization algorithm (as a robust Pareto optimal solution approach proposed by Deb et al., 2002) was used to find suitable weights for each precipitation dataset. This weighting was performed separately for each 0.25° cell at daily spatial-temporal resolution. Not surprisingly, the more precise precipitation estimates were available for any dataset during the past years, the more weight was assigned to that dataset. In order to do that, the objective functions (R and ME) and constraints were set as the following equation. In fact, in the process of solving this optimization algorithm, the daily weights of each dataset (as the decision variables) were determined in such a way that in each cell the ME and R were minimized and maximized, respectively (Eq. (1)).

$$\text{Objective:}\left\{\begin{array}{l}\text{Minimize:}\text{ME}=\sum _{\text{i}=1}^{\text{L}}\left|{\left({\left({\text{P}}_{\left(\text{ij}\right)}^{\text{d}}\right)}_{\text{obs}}\right)}_{\text{i}}-{\left(\sum _{\text{z}=1}^{\text{k}}{\left({\text{W}}_{\text{ij}}^{\text{d}}\right)}_{\text{z}}\times {\left({\text{P}}_{\left(\text{ij}\right)}^{\text{d}}\right)}_{\text{z}}\right)}_{\text{i}}\right|\hfill \\ \text{Minimize:}\text{R}=\frac{\sum _{\text{i}=1}^{\text{L}}\left({\left(\sum _{\text{Z}=1}^{\text{K}}{\left({\text{W}}_{\text{ij}}^{\text{d}}\right)}_{\text{z}}\times {\left({\text{P}}_{\left(\text{ij}\right)}^{\text{d}}\right)}_{\text{z}}\right)}_{\text{i}}-\overline{{\left(\sum _{\text{z}=1}^{\text{k}}{\left({\text{W}}_{\text{ij}}^{\text{d}}\right)}_{\text{z}}\times {\left({\text{P}}_{\left(\text{ij}\right)}^{\text{d}}\right)}_{\text{z}}\right)}_{\text{i}}}\right)\left({\left({\left({\text{P}}_{\left(\text{ij}\right)}^{\text{d}}\right)}_{\text{obs}}\right)}_{\text{i}}-\overline{{\left({\left({\text{P}}_{\left(\text{ij}\right)}^{\text{d}}\right)}_{\text{obs}}\right)}_{\text{i}}}\right)}{\sqrt{\sum _{\text{i}=1}^{\text{L}}{\left({\left(\sum _{\text{Z}=1}^{\text{K}}{\left({\text{W}}_{\text{ij}}^{\text{d}}\right)}_{\text{z}}\times {\left({\text{P}}_{\left(\text{ij}\right)}^{\text{d}}\right)}_{\text{z}}\right)}_{\text{i}}-\overline{{\left(\sum _{\text{z}=1}^{\text{k}}{\left({\text{W}}_{\text{ij}}^{\text{d}}\right)}_{\text{z}}\times {\left({\text{P}}_{\left(\text{ij}\right)}^{\text{d}}\right)}_{\text{z}}\right)}_{\text{i}}}\right)}^2\times }\sqrt{\sum _{\text{i}=1}^{\text{L}}{\left({\left({\left({\text{P}}_{\left(\text{ij}\right)}^{\text{d}}\right)}_{\text{obs}}\right)}_{\text{i}}-\overline{{\left({\left({\text{P}}_{\left(\text{ij}\right)}^{\text{d}}\right)}_{\text{obs}}\right)}_{\text{i}}}\right)}^2}}\hfill \end{array}\right\}$$

$$\text{Subject to:}\left\{\begin{array}{c}{\left({\text{W}}_{\text{ij}}^{\text{d}}\right)}_{\text{z}}=0\\ \sum _{\text{z}=1}^{\text{k}}{\left({\text{W}}_{\text{ij}}^{\text{d}}\right)}_{\text{z}}=0\end{array}\right\}$$ (1)

Where ${\left({\text{P}}_{\left(\text{ij}\right)}^{\text{d}}\right)}_{\text{z}}$ is the amount of rainfall, given by the selected z^th dataset, by the coordinates of (i, j) on the d^th day of the year and ${\left({\text{W}}_{\left(\text{ij}\right)}^{\text{d}}\right)}_{\text{z}}$ is the amount of the assigned weight to the dataset, corresponding to the same cell and same day. And l is the length of the overlapping period between the dataset and GPCC in years.

The output of this optimization is a set of optimal compromise solutions that one solution can be better in one objective and worse in other. This set of all solutions is called Pareto front or Pareto frontier. Therefore, the Pareto front can show the changes in the values of the objective functions relative to each other. With this knowledge, more flexibility in the selection of final alternative can be offered to the decision maker.

In order to distinguish between alternatives, next, the ENTROPY method (introduced by Shannon and Weaver, 1947) by emphasizing the objectives with higher differences in their values, specifies the relative weight of objectives. In other words, the ENTROPY idea is mainly useful to express which set of data is less variable and consequently may have lower priority in decision making (Hwang and Yoon, 1981). Therefore, the result of this part would determine which of the objectives (ME or R) is more important in the selection of the final combination of datasets.

Then, by using the Entropy weights (as the input weight of ME and R) and Pareto optimal solutions (different alternatives of dataset combinations) as the input variables, the TOPSIS method was selected, among the multi-criteria decision making methods, for various reasons such as: simplicity, rationality, comprehensibility and good computational efficiency (Roszkowska, 2011). The base of this method is established on this rule that the preferred alternative must have the highest similarity to the ideal solutions. Further information about this method is provided in Hwang and Yoon (1981) and García-Cascales and Lamata (2012).

Finally, in order to develop the desired precipitation dataset, the SAW method (Eq. (2)) is used to estimate merged daily precipitation for each 0.25°-pixel:

$${\text{P}}_{\left(\text{ij}\right)}^{\text{d}}=\underset{\text{i}=1}{\overset{\text{m}}{\Sigma }}\underset{\text{j}=1}{\overset{\text{n}}{\Sigma }}\underset{\text{z}=1}{\overset{\text{k}}{\Sigma }}{\left({\text{W}}_{\left(\text{ij}\right)}^{\text{d}}\right)}_{\text{z}}\times {\left({\text{P}}_{\left(\text{ij}\right)}^{\text{d}}\right)}_{\text{z}}$$ (2)

Where: ${\left({\text{P}}_{\left(\text{ij}\right)}^{\text{d}}\right)}_{\text{z}}$ is the amount of produced rainfall by the coordinates of (i, j) on the d^th day of the year. Also, ${\left({\text{P}}_{\left(\text{ij}\right)}^{\text{d}}\right)}_{\text{z}}$ is the amount of the assigned weight to the selected z^th dataset and ${\left({\text{P}}_{\left(\text{ij}\right)}^{\text{d}}\right)}_{\text{z}}$ is the amount of precipitation, corresponding to that dataset in the same cell and same day. And m and n are matrix dimensions, consisting of pixels and k is the number of selected datasets. The output of this step is the proposed hybrid dataset, providing daily precipitation values with a delay in accordance with the maximum delay of the selected datasets.

3. Results and discussion

3.1. Evaluation of GPCC dataset accuracy

To ensure full compliance of GPCC data with the station data in the study area and ratify it as the reference database, the mean values of rainfall, provided by GPCC, and the correlation coefficients of the stations were calculated (Table 4). Results confirm the GPCC's ability to estimate rainfall in the area. Based on the results, the average error and the average of correlation coefficients at all stations were 0.02 (mm/day) and 0.84, respectively. So, the reliability of using GPCC, as the reference gridded dataset, was accepted without any modification.

Table 4.

Evaluation of GPCC data based on the station data.

Station	Period of record	R	Observed mean (mm/day)	Estimated mean (mm/day)
Chabahar	1963–2016	0.60	0.31	0.34
Iranshahr	1964–2016	0.95	0.29	0.36
Khash	1986–2016	0.94	0.32	0.39
Konarak	1984–2016	0.88	0.30	0.34
Mirjaveh	2006–2016	0.78	0.11	0.20
Nik Shahr	2006–2016	0.66	0.48	0.46
Nosrat Abad	2011–2016	0.83	0.21	0.14
Rask	2009–2016	0.68	0.35	0.40
Saravan	1986–2016	0.95	0.29	0.27
Zabol	1962–2016	0.95	0.15	0.17
Zahedan	1951–2016	0.94	0.24	0.23
Zehak	1992–2016	0.89	0.13	0.13

3.2. Evaluation of different gridded precipitation datasets

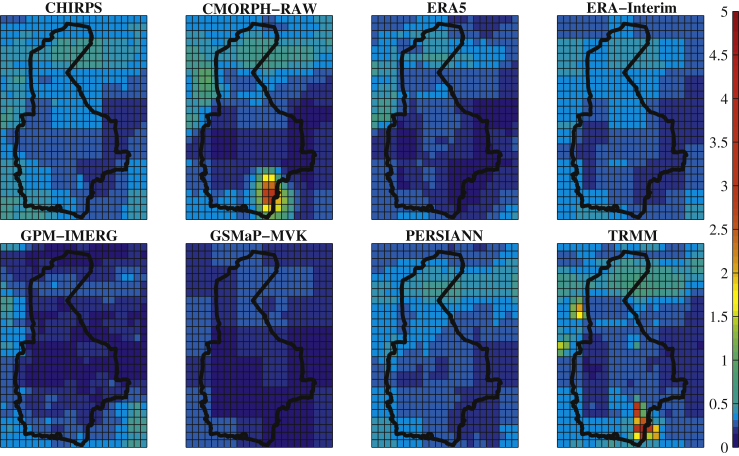
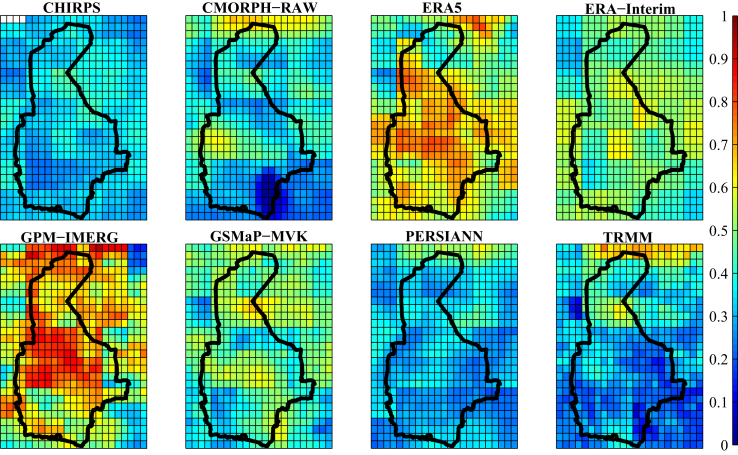
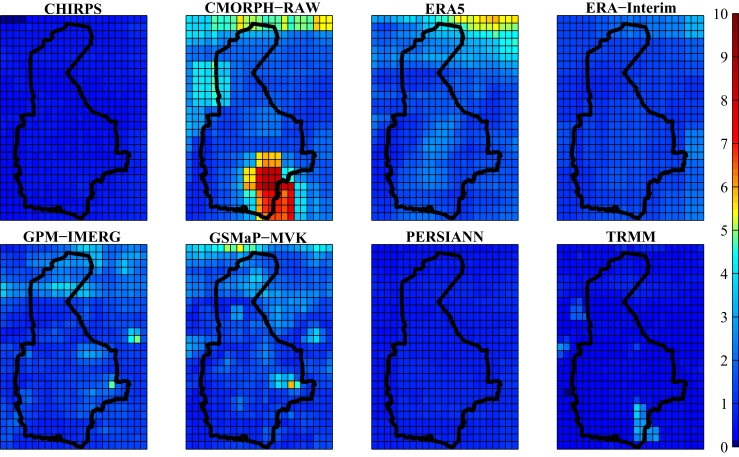
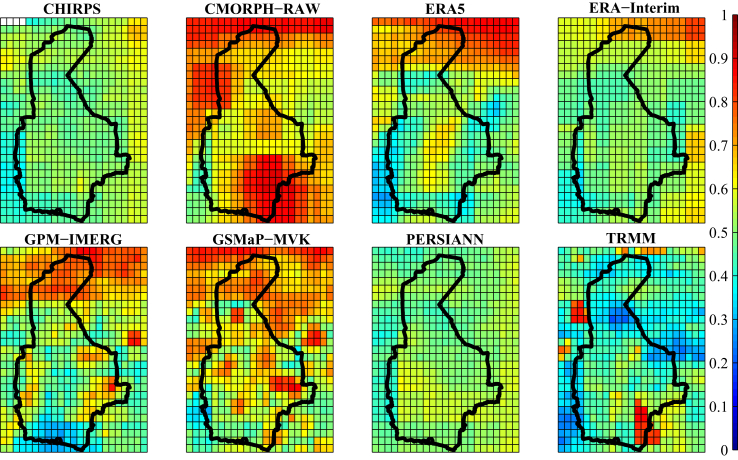
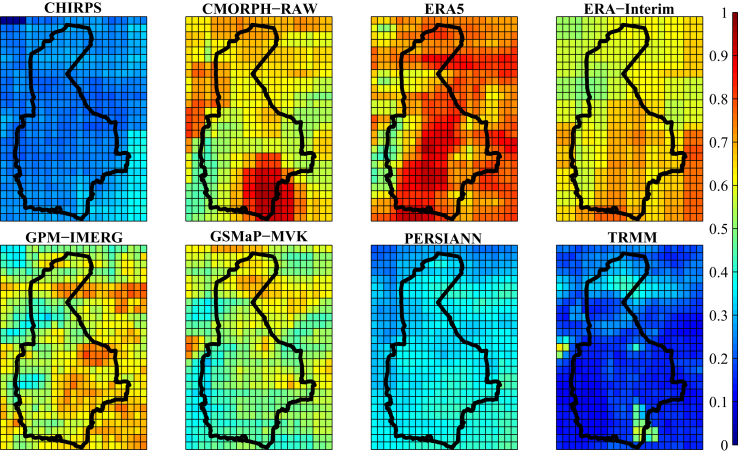
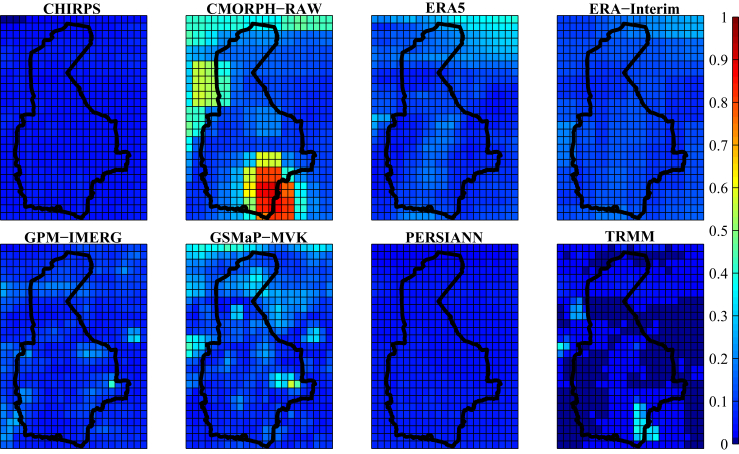
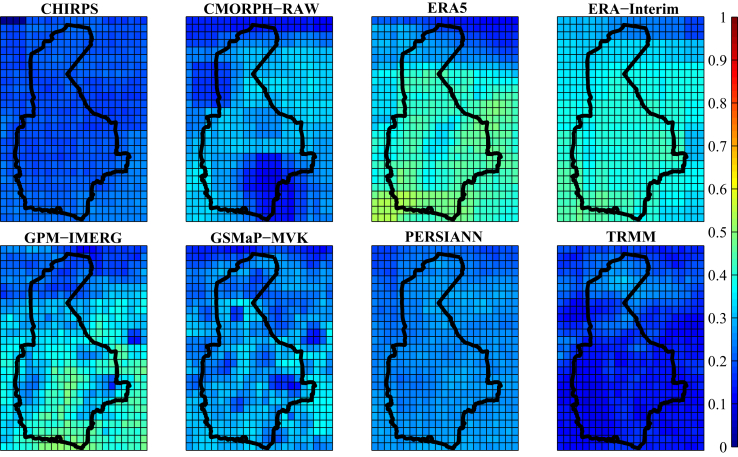
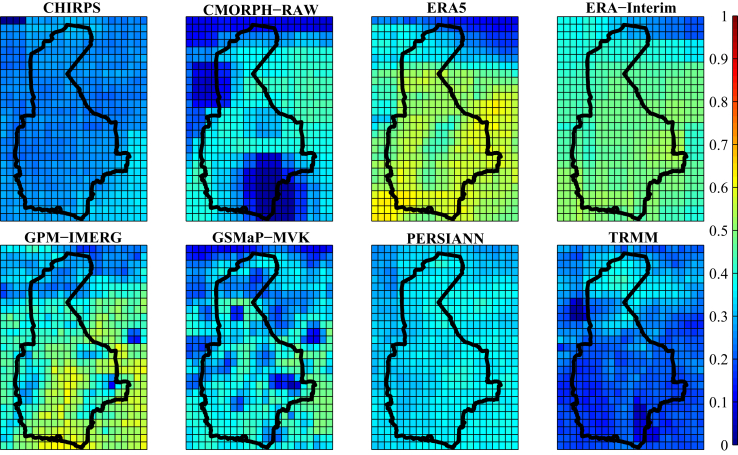
The performance of the eight precipitation datasets was evaluated by calculating the metrics, listed in Table 3. In the process of calculation, the overlapping periods of GPCC with the other datasets were used. Table 5 indicates the average values of these metrics in the whole region and the rank of each dataset (the number in parentheses), compared to the others. Based on the results, it can be claimed that GPM-IMERG and GSMaP-MVK had the best performances in terms of estimating the precipitation values; and in terms of detecting the occurrence or absence of precipitation, ERA5 and ERA-Interim made the best judgments. In addition, as shown in the table, TRMM, CMORPH and CHIRPS did not perform well compared to the other datasets. In contrast, ERA5, ERA-Interim, and GPM-IMERG provided the best results, respectively; and the next rankings included GSMaP-MVK and PERSIANN. This is while, as of August 2019, ERA-Interim has been suspended from production. On the other hand, as ERA5 is published with an offset of about three months from the dataset's reference date, it is impossible to provide early estimates of rainfall by this dataset. Given the results and the limitations of development of an up-to-date precipitation dataset, finally, GPM-IMERG, GSMaP-MVK and PERSIANN were selected. Elucidating their contributions, as an inter-model comparison, GPM-IMERG was observed to present highly accurate datasets in terms of MAE, R, CSI and HSS. In the case of PERSIANN this was true for BIAS, FAR and POFD, while the GSMaP-MVK datasets measured the amount of precipitation data more accurately than the others based on MAE (see Table 5). Details of the spatial distribution of the applied metrics throughout the analyzed area are shown in Figures 3, 4, 5, 6, 7, 8, 9, and 10.

Table 5.

Comparison of different precipitation datasets based on statistical and categorical metrics.

	CHIRPS	CMORPH	ERA5	ERA-Interim	GPM-IMERG	GSMaP-MVK	PERSIANN	TRMM
MAE	0.339	0.358	0.255	0.305	0.226	0.194	0.308	0.378
	(6)	(7)	(3)	(4)	(2)	(1)	(5)	(8)
R	0.333	0.363	0.576	0.479	0.614	0.454	0.326	0.334
	(7)	(5)	(2)	(3)	(1)	(4)	(8)	(6)
BIAS	0.527	2.53	2.085	1.45	1.534	1.698	0.716	0.421
	(3)	(8)	(7)	(2)	(5)	(6)	(1)	(4)
FAR	0.509	0.69	0.567	0.537	0.57	0.632	0.509	0.449
	(3)	(8)	(5)	(4)	(6)	(7)	(2)	(1)
POD	0.253	0.62	0.742	0.632	0.582	0.524	0.346	0.197
	(7)	(3)	(1)	(2)	(4)	(5)	(6)	(8)
POFD	0.043	0.241	0.135	0.125	0.086	0.137	0.045	0.029
	(2)	(8)	(6)	(5)	(4)	(7)	(3)	(1)
CSI	0.197	0.241	0.364	0.36	0.321	0.261	0.252	0.161
	(7)	(6)	(1)	(2)	(3)	(4)	(5)	(8)
HSS	0.257	0.271	0.454	0.435	0.417	0.321	0.342	0.229
	(7)	(6)	(1)	(2)	(3)	(5)	(4)	(8)

Note: The numbers in parentheses represents the rank of each dataset for the corresponding metrics.

Figure 3.

Comparing the performance of the applied precipitation datasets indicated by MAE.

Figure 4.

Comparing the performance of the applied precipitation datasets indicated by R.

Figure 5.

Comparing the performance of the applied precipitation datasets indicated by BIAS.

Figure 6.

Comparing the performance of the applied precipitation datasets indicated by FAR.

Figure 7.

Comparing the performance of the applied precipitation datasets indicated by POD.

Figure 8.

Comparing the performance of the applied precipitation datasets indicated by POFD.

Figure 9.

Comparing the performance of the applied precipitation datasets indicated by CSI.

Figure 10.

Comparing the performance of the applied precipitation datasets indicated by HSS.

3.3. Hybrid precipitation product

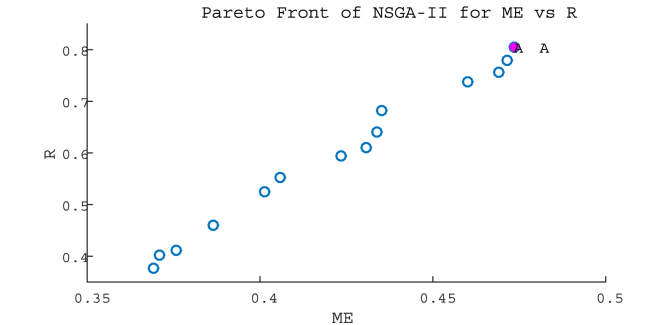
At this stage, NSGA-II was utilized to find the best weight combination of the ensemble members. Figure 11 illustrates the result of the genetic algorithm for one cell of the region (Lon = 60.375, Lat = 29.375) on March 7^th. Given the trend of the Pareto front, the inference that ‘as the error in the estimation of the merged precipitation increases, the correlation coefficient increases too’, can be correctly drawn.

Figure 11.

Pareto front of NSGA-II in one cell (lon = 60.375, lat = 29.375) on March 7^th.

As can be seen in Figure 11, the proposed genetic algorithm is capable of discovering different points in the solution domain over a wide range. This range varies from 0.36 to 0.48 mm and 0.35 to 0.85 for ME and the R, respectively. Although the points are able to exhibit different weight combinations of the ensemble members, they have led to the challenge of distinguishing between these options and subsequently selecting the most optimal combination. Next, in response to this challenge, the ENTROPY method was used to reveal the relative importance of ME and R as the decision criteria. Whenever the amplitude variation of ME for the optimal solutions (Pareto front) has a lower value compared to the amplitude variation of R, ENTROPY assigns less weight to ME and more to R, and vice versa. Since the amplitude variation of R over ME, for optimal solutions, is more than 4 times (Figure 11), ENTROPY has estimated the relative importance (ENTROPY weights) of the parameters R and ME: 0.888 and 0.112, respectively. The final step is to determine the best combination of the chosen datasets by TOPSIS, using the decision matrix (optimal solutions of Pareto front) and the relative importance of the decision criteria. Point A in Figure 11, was introduced as the final option for the merged dataset in the proposed cell on March 7^th by the TOPSIS method. Here, results of the best weight combination of GPM-IMERG, GSMaP-MVK and PERSIANN were 0.764, 0.039 and 0.183, respectively. This three-step process was performed separately and repeatedly in each cell for each day of the year using Eq. (2). By this way, the daily precipitation of each 0.25°-cell of the network was obtained from the summation of multiplying each dataset precipitation value by its corresponding weight.

At this stage, to evaluate the effectiveness of the proposed dataset, it is absolutely necessary to answer three basic questions: 1) can the hybrid dataset provide accurate estimates of rainfall? 2) does it provide better estimates, compared to the other existing precipitation datasets? and 3) can it be trusted as a timely and a generally valid dataset?

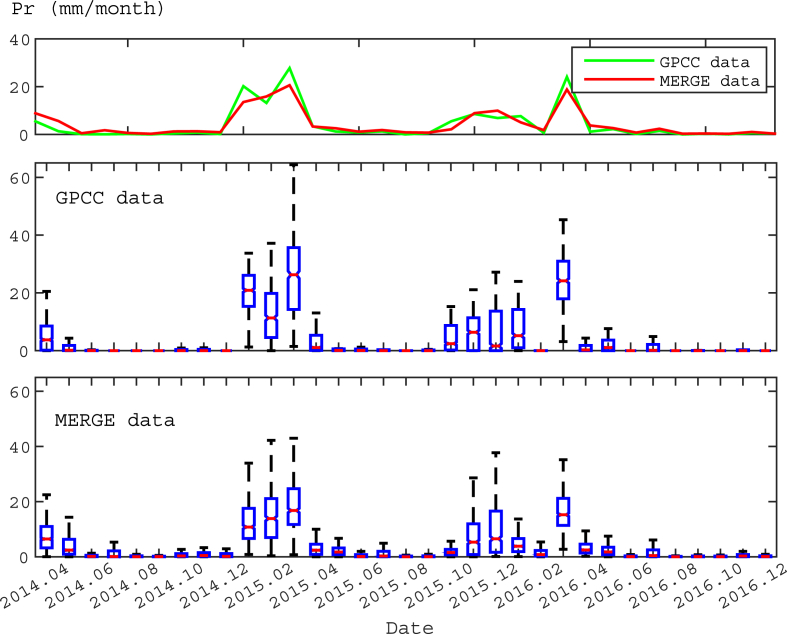
In response to the first challenge, the results of monthly cumulative precipitation from the merged dataset, were compared with monthly cumulative precipitation from the GPCC throughout the area. The comparison results are shown in Figure 12 in the mean of the whole region (graphs) and their range of changes in different cells (box plots). As the figure demonstrates, the maximum difference between the two graphs is 7.17 mm and the correlation coefficient is 0.95, indicating the high accuracy of synchronization between the hybrid dataset and the observed rainfall values during the entire study period.

Figure 12.

Mean of monthly cumulative precipitation results, obtained from the hybrid dataset and GPCC.

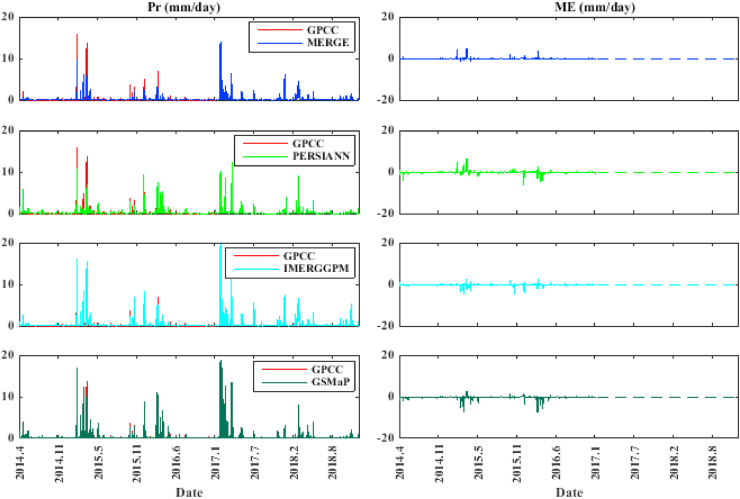
In response to the second question, the precipitation values from the proposed dataset and the other three selected datasets, were compared with observational data from GPCC. Figure 13 shows the time series of daily precipitation and its difference values from GPCC data for the entire area, for the proposed dataset and the other three datasets. As can be seen from this figure, there are several reasons why the hybrid dataset performs better than the other three datasets: 1) the mean of ME at the region was much lower for the hybrid dataset. 2) the number of days, when the rainfall estimation error was significant (number of peaks), was much lower in the hybrid dataset. and 3) the estimation error of PERSIANN did not follow a specific pattern, while GPM and GSMaP-MVK overestimated the amounts of precipitation. Therefore, it can be claimed that the developed hybrid dataset, utilizing the other datasets in the target region, has achieved better results.

Figure 13.

Time series of mean daily precipitation and its difference values from GPCC data for the hybrid proposed dataset and the three selected datasets.

In answer to the third question, since the observational database (GPCC) does not provide daily precipitation during the period from 2017 to present, the preference for using the hybrid dataset as an appropriate alternative, needs to be investigated. In response to this need, data from regional weather stations (2017–2018) were used to evaluate the accuracy of the proposed dataset and compared with the others. The results are shown in Table 6. In this evaluation, Konarak station was not used due to lack of data in 2018. As expected, the merged dataset never performed the worst in the region and has always been among the top three datasets.

Table 6.

Evaluation of merged data and the selected datasets based on in-situ data in 2017–2018.

Station	R				ME (mm/day)
	Merge	GPM-IMERG	GSMaP-MVK	PERSIANN	Merge	GPM-IMERG	GSMaP-MVK	PERSIANN
Chabahar	0.95 (2)	0.95 (2)	0.95 (2)	0.97 (1)	0.45 (3)	0.73 (4)	0.12 (2)	0.02 (1)
Iranshahr	0.79 (2)	0.81 (1)	0.72 (4)	0.76 (3)	0.10 (2)	0.15 (3)	0.24 (4)	0.00 (1)
Khash	0.88 (1)	0.79 (2)	0.72 (3)	0.67 (4)	0.07 (2)	0.02 (1)	0.28 (4)	0.11 (3)
Mirjaveh	0.67 (3)	0.68 (2)	0.90 (1)	0.51 (4)	0.06 (1)	0.12 (3)	0.07 (2)	0.12 (3)
Nik Shahr	0.98 (1)	0.94 (2)	0.87 (3)	0.84 (4)	0.28 (3)	0.55 (4)	0.26 (2)	0.02 (1)
Nosrat Abad	0.86 (3)	0.73 (4)	0.96 (1)	0.88 (2)	0.02 (1)	0.03 (2)	0.11 (4)	0.10 (3)
Rask	0.58 (1)	0.57 (2)	0.55 (3)	0.55 (3)	0.25 (3)	0.46 (4)	0.19 (2)	0.11 (1)
Saravan	0.50 (3)	0.55 (2)	0.83 (1)	0.48 (4)	0.19 (3)	0.34 (4)	0.12 (1)	0.15 (2)
Zabol	0.95 (1)	0.89 (2)	0.95 (1)	0.82 (3)	0.16 (2)	0.19 (3)	0.03 (1)	0.23 (4)
Zahedan	0.79 (2)	0.69 (3)	0.91 (1)	0.60 (4)	0.04 (1)	0.07 (2)	0.09 (3)	0.10 (4)
Zehak	0.75 (2)	0.72 (4)	0.74 (3)	0.77 (1)	0.14 (2)	0.18 (4)	0.06 (1)	0.16 (3)

Note: The numbers in parentheses represents the rank of each dataset for the corresponding metrics.

Based on the results, it can be claimed that the hybrid dataset, not only provides a higher accuracy in precipitation estimates, but these estimates are quite timely and represent the least environmental sensitivities, making it the top choice for estimating rainfall in the region.

As seen from the results presented in Section 3, along with previous studies (e.g., Moazami et al., 2016; Henn et al., 2018; Wang et al., 2020), the performance of precipitation datasets varies in time and space. As a result, earlier studies (e.g., Beck et al., 2017; Shen et al., 2018; Beck et al., 2019) tend to design hybrid precipitation datasets, which optimally merge the most reliable precipitation datasets available as a function of time and location. In addition, localized merged datasets are needed to correct the drawbacks and enhance the advantages of individual sources (Shrestha et al., 2011; Beck et al., 2017; Shen et al., 2018). As inferred from these documented studies, merging algorithms for multi-source datasets should be developed at regional scale before any further analysis. Consistent with this suggestion, using the NSGA-II multi-objective optimization method, daily weights of three selected datasets were calculated for each 0.25° cell in Sistan and Baluchestan.

A review of previous studies on the assessment of precipitation datasets in Iran and especially those covering the study area, revealed that most of the studies have focused on evaluating the performance of TRMM and PERSIANN (e.g. Javanmard et al., 2010; Alijanian et al., 2017; Darand et al., 2017). The results of these studies indicated that TRMM has been able to provide better estimation of the amount of precipitation while PERSIANN has been presented better results in terms of POD in the study area (Moazami et al., 2013, 2016; Katiraie-Boroujerdy et al., 2013). The present study showed that GPMIMERG and GSMaP-MVK were far more accurate in estimating the amount and detection of the precipitation events (see Table 5). These findings were consistent with the results from studies by Sharifi et al. (2016), Khodadoust Siuki et al. (2016), Beck et al. (2017). In addition, GPMIMERG and GSMaP-MVK have better spatial resolution and provide timely data with less delay.

Comparing the proposed hybrid dataset with the merged precipitation dataset, MSWEP, it should be acknowledged that although it has also used observational data (e.g., GPCC as an ensemble member of its development), it has only been able to provide a maximum R of 0.72 in Iran. However, the maximum and minimum R of this study were 0.98 and 0.60, respectively. Therefore, the algorithm proves effective. In addition, MSWEP has provided data until 2017 and cannot be an up-to-date dataset. In addition, MSWEP used ERA-Interim data (suspended providing precipitation data since 2019), putting the application of the dataset in serious jeopardy. Furthermore, it has not utilized the GPMIMERG dataset (the most accurate dataset in the study area) as one of its ensemble members (Beck et al., 2017). Hence it is safe to ascertain that the presented merged dataset can be nominated as the best localized precipitation dataset in the study area.

As the developed dataset was constructed from an analysis of satellite-derived precipitation estimates, and satellite-derived data are still not as reliable as desired (Shrestha et al., 2011; Tesfagiorgis et al., 2011; Golian et al., 2015), further investigations will be necessary with focus on combining different types of datasets: gauge observations, satellite remote sensing and atmospheric model reanalysis data, taking full advantage of the complementary nature of the data recognized in previous studies (e.g., Peña Arancibia et al., 2013; Xu et al., 2019; Tarek et al., 2019).

4. Conclusions

In the present study, a framework was proposed to develop a merged precipitation dataset over a poorly gauged area, Sistan and Baluchestan province, Iran. In the proposed framework, at first, performance of different datasets was compared to GPCC dataset (as the observational reference dataset) over the period of 1982–2016 in order to identify the best ensemble members. Then, using a combination of NSGA-II, ENTROPY, and TOPSIS methods, a decision-making framework was presented in which daily weights of the chosen datasets were estimated for each 0.25° cell, while the correlation of coefficient and also the estimation error were maximized and minimized, respectively. Finally, the hybrid precipitation dataset was evaluated.

The results showed that since the performance of different datasets is not the same over time and space, the hybrid dataset, taking advantages of the three selected datasets of GPM-IMERG, GSMaP-MVK and PERSIANN, is a reliable local daily precipitation product. In fact, it can provide acceptable performance for the study area with the spatial resolution of 0.25° $\times$ 0.25° with less time delay compared to the other datasets.

Declarations

Author contribution statement

F. Yazdandoost: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

S. Moradian: Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

A. Izadi: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

A. Massah Bavani: Conceived and designed the experiments.

Funding statement

This work was supported by the Regional Water Company of Sistan and Baluchestan of Iran.

Competing interest statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.