Distribution of the environmental and socioeconomic risk factors on COVID-19 death rate across continental USA: a spatial nonlinear analysis

Abstract

The COVID-19 outbreak has become a global pandemic. The spatial variation in the environmental, health, socioeconomic, and demographic risk factors of COVID-19 death rate is not well understood. Global models and local linear models were used to estimate the impact of risk factors of the COVID-19, but these do not account for the nonlinear relationships between the risk factors and the COVID-19 death rate at various geographical locations. We proposed a local nonlinear nonparametric regression model named geographically weighted random forest (GW-RF) to estimate the nonlinear relationship between COVID-19 death rate and 47 risk factors derived from the US Environmental Protection Agency, National Center for Environmental Information, Centers for Disease Control and the US census. The COVID-19 data were employed to a global regression model random forest (RF) and a local model GW-RF. The adjusted R² of the RF is 0.69. The adjusted R² of the proposed GW-RF is 0.78. The result of GW-RF showed that the risk factors (i.e. going to work by walking, airborne benzene concentration, householder with a mortgage, unemployment, airborne PM_2.5 concentration and per cent of the black or African American) have a high correlation with the spatial distribution of the COVID-19 death rate, and these key factors driven from the GW-RF were mapped, which could provide useful implications for controlling the spread of the COVID-19 pandemic.

Instruction

The 2019 novel coronavirus disease (COVID-19) caused by SARS-CoV-2 is a rapidly spreading infectious disease that mainly affects the respiratory system (Landi 2020). Because the disease is highly contagious with rapid transmission between humans (Huang et al. 2020), the World Health Origination (WHO) declared on March 11, 2020 that the COVID-19 outbreak is a global pandemic (World Health Organization 2020). As of July 6, 2020, a total of 11,520,953 COVID-19 confirmed cases and 532,633 deaths have been recorded worldwide. The current epicentre of the COVID-19 is the USA with 2,982,928 confirmed cases and 132,569 deaths as of July 6, 2020. The economic impact of the COVID-19 crisis is unprecedented in USA with a substantial stock market shifting and unemployment rate reaching the peak (O’Connor et al. 2020). The health care system is also overwhelmed across the world, which are already operating at full capacity struggling to meet the demand for ventilators, intensive care beds and personal protective equipment.

Some researches about the COVID-19 have found that various factors including environment (Xu et al. 2020; Ahmadi et al. 2020; Bashir et al. 2020), socioeconomic (de León-Martínez et al. 2020; Zheng et al. 2020), demographic (Serge et al. 2020) and underlying disease (Marhl et al. 2020; Ruthberg et al. 2020; Dariya and Nagaraju 2020; Malik et al. 2020) may influence the transmission of COVID-19. Bashir et al. (2020) found that air pollution including PM₁₀, PM_2.5, SO₂, NO₂ and CO is a significant risk factor to the COVID-19 epidemic. Tosepu et al. (2020) analysed the correlation between weather and the COVID-19 and found that the average temperature was highly correlated with the COVID-19. Virus carried via public transportation played an important role in the transmission of COVID-19 (Zheng et al. 2020). Serge et al. (2020) found that males are about 60% more likely than females to suffer severe illness or death from the COVID-19 complications. Targher et al. (2020) found that patients with diabetes were at an approximately 4 times risk of having severe COVID-19. Chronic diseases such as diabetes, hypertension and cholesterol levels are apparently related to the severity of COVID-19 (Zaki et al. 2020). The risk of COVID-19 is related to blood type, in which people with blood type A have a higher risk of COVID-19, while people with blood type O have a lower risk (Pourali et al. 2020). Low-income older people are at higher risk of COVID-19 because they are more likely to suffer from chronic diseases, loneliness, uneven diet and lack of exercise etc. (Calderón-Larrañaga et al. 2020). The epidemic had a greater psychological impact on people with female gender, student status and specific diseases (e.g. hypertension and chronic lung diseases) (Wang et al. 2020).

With the increased availability of health care data online and the development of spatial analysis techniques, multiple analyses by the GIS tool (Guliyev 2020; Rosenkrantz et al. 2020) found that the distribution of COVID-19 cases (Desjardins et al. 2020; Shim et al. 2020; Lau et al. 2020) and its risk factors (Mollalo et al. 2020) exhibits patterns of spatial heterogeneity. A study by Lau et al. (2020) showed that the number of flight routes was a highly relevant factor of the COVID-19 spread. Their study showed that regions in Asia, North America and Europe were at a serious risk of constant exposure to highly infected countries, while the exposure risk to COVID-19 was relatively low in South America and Africa. Liu et al. (2020) employed a contact model to reconstruct the contact and air spread to simulate the outbreak of COVID-19 on the “diamond princess.” They suggested rigorous prevention measure should be followed by high-risk susceptible people. Mollalo et al. (2020) mapped the spatial variability of the relationships between COVID-19 incidence rate and income inequality, median household, the proportion of black females and proportion of nurse practitioners using multiscale geographically weighted regression (MGWR). Sun et al. (2020) used several spatial models including spatial lag, spatial error and spatial autoregressive model to examine geographic differences in COVID-19 in US counties and found that the spatial model was able to better estimate COVID-19 prevalence in counties compared with aspatial models. Sannigrahi et al. (2020) found that the uneven distribution of the COVID-19 confirmed cases and deaths across Europe, and this can be attributed to the discrepant sociodemographic factors such as the old population and income between European counties.

Many mathematical models have been employed to explore the risk factors of COVID-19. Typical global models such as partial correlation coefficient (PCC) (Ahmadi et al. 2020), ordinary least squares (OLS), Poisson regression model (Xu et al. 2020) and Bayesian hierarchical model (Millett et al. 2020) and geographical local model such as geographically weighted regression model (GWR) (Mollalo et al. 2020; Imran et al. 2015) were used to model the correlations between COVID-19 data and other impacting factors. However, the global model assumes the relationship between risk factors does not vary over space and is inconsistent with the imbalanced distribution of COVID-19. Although spatial error model (SEM) and spatial lag model (SLM) do consider spatial factors, they focus more on the analysis of spatial correlation and do not analyse the spatial variation of the relationships between variables in different regions from the perspective of spatial heterogeneity (Ahmadi et al. 2020). The GWR (Brunsdon 2010; Fotheringham et al. 2002; Lu et al. 2017) as a local regression model can obtain the linear relationship between variables in different locations. However, the GWR is constructed based on multiple linear regression models; thus, it is not suitable to estimate the nonlinear relationships between independent and dependent variables, and local multicollinearity exists when dealing with correlated variables (Wheeler and Tiefelsdorf 2005). The real relationship between risk factors and COVID-19 is complex and is not always linear. In order to explore the spatial variation of the nonlinear relationship between multiple risk factors and COVID-19, it is necessary to deal with the nonlinear situation in a local regression model.

The uneven spatial distribution of COVID-19 is related to environmental and socioeconomic and demographic differences among counties. Analysis of the relationship between these possible risk factors (e.g. air pollution, old age, diabetes) and COVID-19 in different counties will be helpful in developing policies to prevent and control the spread of COVID-19. The relationship between risk factors and mortality is not completely linear in the real world. In this study, we proposed a local nonlinear nonparametric regression method, geographically weighted random forest (GW-RF), to evaluate the geographical difference in the relationship between COVID-19 death rate and multiple risk factors including air pollution, climate, land cover, disaster, health status, commuting to work and socioeconomic and demographic indicators at county level across the continental USA. This paper tries to explore the variation in the nonlinear relationships between multiple risk factors and COVID-19 death rate in different locations by using the GW-RF for the first time. We expect that this study can provide scientific evidence for implementing control and prevention measure in COVID-19.

Materials and methods

Data and preparation

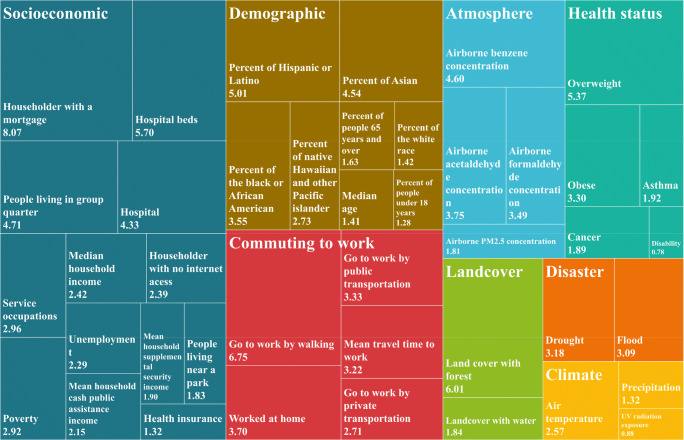
The county-level daily COVID-19 death cases data and population data of 3108 counties of continental USA from Jan 22, 2020 to June 26, 2020 were downloaded from the website of USA FACTS (https://usafacts.org/). The death rate at county level was calculated based on the daily COVID-19 death cases and population data. We selected 47 indicators including atmosphere, climate, land cover, disaster, health status, commuting to work and socioeconomic and demographic factors as independent variables to evaluate their correlation with the COVID-19 death rate. The indicators we selected and their meanings and sources are presented in Table 1. The shapefile of the selected 3108 counties was downloaded from geographical program of US Census Bureau (https://www.census.gov/programs-surveys/geography.html).

Table 1.

Definitions of indicators and sources

Theme	Indicators	Indicator meaning	Source
Atmosphere	Airborne PM2.5 concentration	Annual average ambient concentrations of PM2.5 in micrograms per cubic metre	US Environmental Protection Agency (https://www.epa.gov/) and Centers for Diseases Control and Prevention (https://www.cdc.gov/)
	Airborne benzene concentration	Annual average concentration of benzene estimates in microgram per cubic metre
	Airborne formaldehyde concentration	Annual average air concentration of formaldehyde estimates in microgram per cubic metre
	Airborne acetaldehyde concentration	Annual average air concentration of acetaldehyde estimates in microgram per cubic metre
	Airborne carbon tetrachloride concentration	Annual average air concentration of carbon tetrachloride estimates in microgram per cubic metre
Climate	Air temperature	Average daily max air temperature (°F)	National Center for Environmental Information (https://www.ncei.noaa.gov/)
	Precipitation	Average daily precipitation (mm)
	Sunlight exposure	Annual average sunlight exposure measured by solar irradiance (kJ/m2)	Centers for Diseases Control and Prevention (https://www.cdc.gov/)
	UV radiation exposure	Annual average daily dose of UV irradiance (J/m2)
Land cover	Land cover with water	Per cent of land covered by water
	Land cover with forest	Per cent of land covered by forest
Disaster	Drought	Number of weeks of moderate drought or worse per year
	Flood	Percentage of people within FEMA-designated flood hazard area
Health status	Disability	Percentage of population aged 5 years and over with a disability
	Asthma	Per cent of adults diagnosed with asthma
	Obese	Percentage of adults aged 18 years and over who were obese
	Overweight	Percentage of adults aged 18 years and over who were overweight
	Cancer	Number of people with lung and bronchus cancer per 1,000,000 population
Commuting to work	Go to work by private transportation	Percentage of workers 16 years and over who drove alone (car, truck or van)	US Census Bureau (https://www.census.gov/en.html)
	Go to work by public transportation	Percentage of workers 16 years and over who go to work by public transportation (excluding taxicab)
	Go to work by walking	Percentage of workers 16 years and over who go to work by walking
	Work at home	Percentage of workers 16 years and over who worked at home
	Mean travel time to work	Mean travel time to work (min) of the workers 16 years and over
Socioeconomic	Health insurance	Percentage of population without health insurance
	Householder with a mortgage	Percentage of household with a mortgage
	Poverty	Percentage of population whose income is below the poverty level
	Service occupations	Percentage of employed population 16 years and over with service occupations
	Unemployment	Percentage of population 16 years and over unemployed
	Hospital	Number of hospitals	Centers for Diseases Control and Prevention (https://www.cdc.gov/)
	Hospital beds	Number of hospital beds per 10,000 population
	People living in group quarter	Percentage of population living in group quarter	US Census Bureau (https://www.census.gov/en.html)
	People living near a park	Percentage of population living within a half mile of a park
	Householder with no internet access	Percentage of households with no internet access
	Median household income
	Mean household retirement income
	Mean household cash public assistance income
	Mean household supplemental security income
Demographic	Per cent of males
	Median age
	Per cent of people under 18 years
	Per cent of people 65 years and over
	Per cent of the white race
	Per cent of the black or African American
	Per cent of American Indian and Alaska Native
	Per cent of Asian
	Per cent of native Hawaiian and other Pacific islander
	Per cent of Hispanic or Latino

Due to the units of these 47 indicators are different, the indicators should be normalized before regression. The method is as follows:

$$X_{\mathit{ki}}=\frac{X_{\mathit{ki}}-{\overline{X}}_k}{{\sigma }_k}\left(i\in 1,2,\cdots 2056;k\in 1,2,\cdots ,28\right)$$ 1

where X_ki represents the normalized value of the kth indicator in the ith county, X_ki represents the original value of the kth indicator in the ith county;${\overline{X}}_k$ represents the average value of the kth indicator; σ_k represents the standard deviation of kth index. The COVID-19 death rate and 47 indicators were joined to the county-level shapefile for further processing.

Nonlinear nonparametric model

RF

We selected the random forest (RF) machine learning method (Breiman 2001) because it is nonparametric; it can easily learn nonlinear relationships and interactions from data without explicitly modelling them. RF is an ensemble of multiple decision trees. The decision tree is a nonparametric model that does not have a fixed structure. The decision tree grows according to the complexity of the input data in the learning process. The RF works well for high-dimensional variables with a relatively small number of samples and can access variable importance (Grömping 2009). The algorithm flow of the RF is as follows:

1. The n data sets D₁, D₂, ⋯, D_n are extracted by repeatedly using the bootstrap method to randomly extract the whole dataset D, and the corresponding n decision trees H₁, H₂, ⋯, H_n are generated.

2. At each node of the decision tree, randomly select m (m < k) variables from all the k variables of the decision tree, and each node is split using the selected m variables by the optimal segmentation method determined by a segmentation criterion.

3. The value of m remains unchanged while the forest grows. Each tree grows to its largest extent without pruning until it cannot be split.

Thus, the correlation between the decision trees in the forest decreases through a random selection of variables at each node of the tree and the optimal split of each node is determined by the selected variables only, instead of all variables. Each tree can grow to its largest extent without pruning. Therefore, the algorithm can deal with excessive redundant features and avoid over fitting.

In the first step in constructing the RF, whether with or without replacement, approximately 36.8% of the data samples are not used to grow the tree; these samples are the out-of-bag (OOB) for the tree. The accuracy of the RF model can be estimated from the OOB data as presented by Eq. (2):

$$\mathrm{MSE}=\frac{1}{N}{\sum }_{i=1}^N{\left(y_i-{\overline{\widehat{y}}}_i\right)}^2$$ 2

where N is the number of samples from the OBB data, y_i is the actual value of the ith sample, and ${\overline{\widehat{y}}}_i$ is the average prediction for the ith sample from all trees.

The overall sum of squares (SST) and coefficient of determination (R²) are respectively defined in Eqs. (3) and (4):

$$\mathrm{SST}={\sum }_{i=1}^N{\left(y_i-\overline{y}\right)}^2$$ 3

$$R^2=1-N\frac{\mathit{MSE}}{\mathit{SST}}$$ 4

where R² ∈ (0, 1). The closer the value of R² to 1, the better the regression performance of the GW-RF will be.

Variable importance can sort the independent (predictor) variables according to their degree of correlation to the dependent (response) variable. There are two popular methods to measure the variable importance in the RF, which are average impurity reduction (Gini importance) and mean square error (MSE) reduction. Because the result of variable importance by impurity reduction is biased (Strobl et al. 2007), many researchers have verified and suggested choosing the MSE reduction method when permuting the variables (Strobl et al. 2008; Ishwaran 2007). The MSE reduction method uses the MSE value of the out-of-bag (OOB) data to evaluate the variable importance (Cai et al. 2018). It is determined as follows:

1. Calculate the MSE of the OBB data for each tree. For tree t, the MSE of OOB data is calculated by Eq. (5):

$${\mathit{MSE}}_t=\frac{1}{N_t}{\sum }_{i=1}^{N_t}{\left(y_i-{\widehat{y}}_{i,t}\right)}^2$$ 5

where N_t is the number of samples from the OBB data in the tree t; ${\widehat{y}}_{i,t}$ is the prediction for the ith sample of the tree t.

• 2.Randomly replace the target variable j, and then the new value of the MSE of tree t is calculated by Eq. (6):

$${\mathit{MSE}}_t\left(j\right)=\frac{1}{N_t}{\sum }_{i=1}^{N_t}{\left(y_i-{\widehat{y}}_{i,t}\left(j\right)\right)}^2$$ 6

where ${\widehat{y}}_{i,t}\left(j\right)$ is the prediction for the ith sample of the new tree t when randomly replacing the target variable j.

• 3.Calculate the difference between MSE_t and MSE_t(j), and the MSE reduction is the variable importance for variable j of tree t. The MSE reduction of variable j of the whole forest is obtained as the average over MSE reduction of all n trees. The variable importance of variable j is expressed as in Eq. (7):

$$\mathrm{VI}\left(j\right)=\mathrm{MSE}\left(j\right)=\frac{1}{n}{\sum }_{t=1}^n\left({\mathit{MSE}}_t-{\mathit{MSE}}_t\left(j\right)\right)$$ 7

GW-RF

In this section, a local nonlinear machine learning method, denoted as GW-RF, is proposed. The GW-RF is designed by integrating spatial weight matrix (SWM) and RF into a local regression analysis framework. The GW-RF inherits the merits of the RF, making the RF from being applicable from a global system to a local system. Thus, it can handle high-dimensional variables with nonlinear relationships and multicollinearity. The variable importance for each spatial unit can be obtained from the GW-RF. The process of constructing the GW-RF model is designed as follows:

1. The SWM for each spatial unit of the study area should first be made according to the specified spatial weight rule. The SWM for the whole study area with p spatial units can be expressed as in Eq. (8):

$$W=\left[\begin{array}{c}W\left(1\right)\\ W\left(2\right)\\ ⋮\\ W\left(i\right)\\ ⋮\\ W\left(p\right)\end{array}\right]=\left[\begin{array}{c}{w}_{11}{w}_{12}\cdots w_{1p}\\ w_{21}{w}_{22}\cdots w_{2p}\\ ⋮⋮⋮⋮\\ w_{i1}{w}_{i2}\cdots w_{\mathit{ip}}\\ ⋮⋮⋮⋮\\ w_{p1}{w}_{p2}\cdots w_{\mathit{pp}}\end{array}\right],i\in \left(1,2,\cdots ,p\right)$$ 8

As the local random forest of an individual unit needs to consider the unit itself, the value of w_ii is set to 1 (w_ii = 1). According to the spatial weight rule, for spatial unit i, if sample j (j ∈ (1, 2, ⋯, p) ∧ i ≠ j) is a “neighbour” of unit i, the value of spatial weight between them is set to 1, that is, w_ij = 1. While spatial unit j is far away from spatial unit i, not a neighbour of spatial unit i, w_ij = 0.

• 2.Select all the neighbours of each spatial unit according to the spatial weight matrix. For unit i, the neighbours of it can be selected from the special weight matrix W where w_ij ≠ 0, (j ∈ (1, 2, ⋯, p) ∧ i ≠ j).
• 3.The spatial unit i and its neighbours are as the inputs to construct a local RF for unit i (RF (i)). By executing RF (i), the variable importance for spatial unit i can be computed.
• 4.Repeat steps (2) and (3) to construct a local RF for each spatial unit in the study area and estimate the local variable importance for each spatial unit.

The nonlinear nonparametric models (RF, GW-RF) do not need to consider multicollinearity and can analyse all independent variables without screening. R software (version 3.5.3, http://cran.r-project.org) was used to perform the regression analysis.

Results

All 47 indicators were employed to the nonlinear nonparametric models (RF, GW-RF). The adjusted fitting coefficient (R²) of the RF was 0.69, while the adjusted R² of the GW-RF was 0.78, indicating that the regression result of the GW-RF was more accurate than that of the RF. The variable importance of an independent variable represents the correlation between the independent variable and the dependent variable, and the higher the value of the variable importance is, the stronger the correlation will be. The variable importance of 47 independent variables in modelling COVID-19 death rate using the RF is shown in Fig. 1. The risk factors referring to socioeconomic are most correlated with COVID-19 death rate, followed by risk factors referring to demographic, commuting to work, atmosphere, health status, land cover, disaster and climate. The variables including householder with a mortgage, going to work by walking, land cover with forest, hospital beds, overweight, per cent of Hispanic or Latino, people living in group quarter and airborne benzene concentration have a high correlation with the COVID-19 death rate.

Fig. 1.

The variable importance of the independent variables of the RF model in modelling COVID-19 death rate

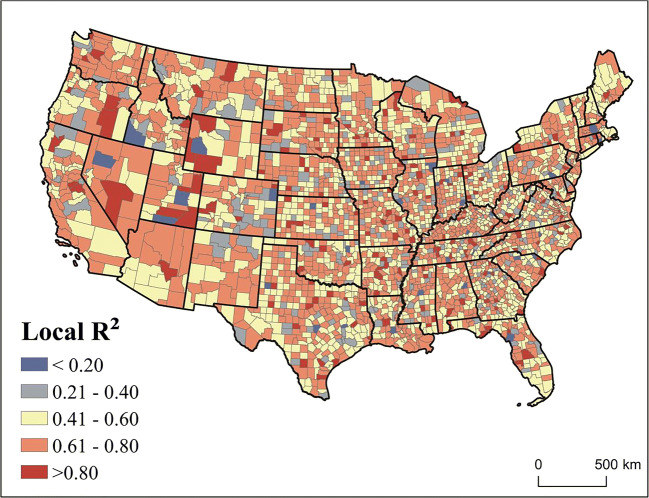
We used the local R² to estimate the performance of the GW-RF. Table 2 describes the statistic of local R² of the GW-RF. The average value of local R² was 0.59. The value of local R² was higher than 0.4 in 89.4% of the counties and higher than 0.6 in 50.5% of the counties. This shows that the GW-RF can accurately evaluate the correlation between the risk factors and the COVID-19 death rate in most of the study areas.

Table 2.

The statistic of local R² of the GW-RF in modelling COVID-19 death rate; we calculated the average value of local R² and the percentage of counties in five local R² range (≤ 0.2, (0.2, 04], (0.4, 06], (0.6, 08], > 0.8)

The value of local R2	GW-RF
Average value	0.59
≤ 0.2	1.1%
(0.2, 04]	9.5%
(0.4, 06]	38.9%
(0.6, 08]	44.8%
> 0.8	5.7%

Figure 2 shows the distribution of the local R² of the GW-RF across the study area. As can be seen from Fig. 2, the distribution of local R² was imbalanced in the whole study area. The local R² value of the GW-RF was high in most of the counties across the whole continental USA, indicating that the GW-RF worked well in the prediction of the local COVID-19 death rate in most regions across the study area, especially in Nevada, Arizona, Washington and some counties in the East-central region.

Fig. 2.

The distribution of local R² of the GW-RF

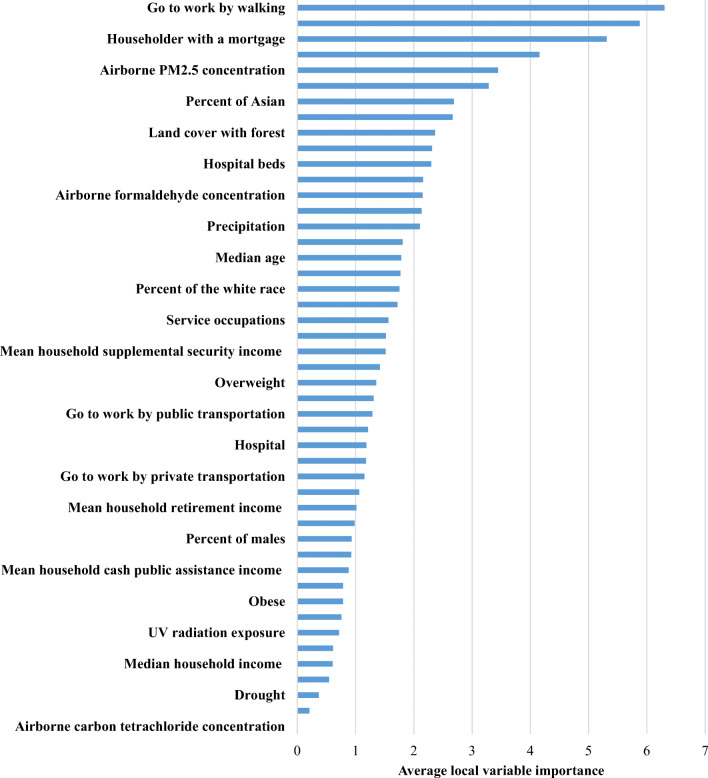
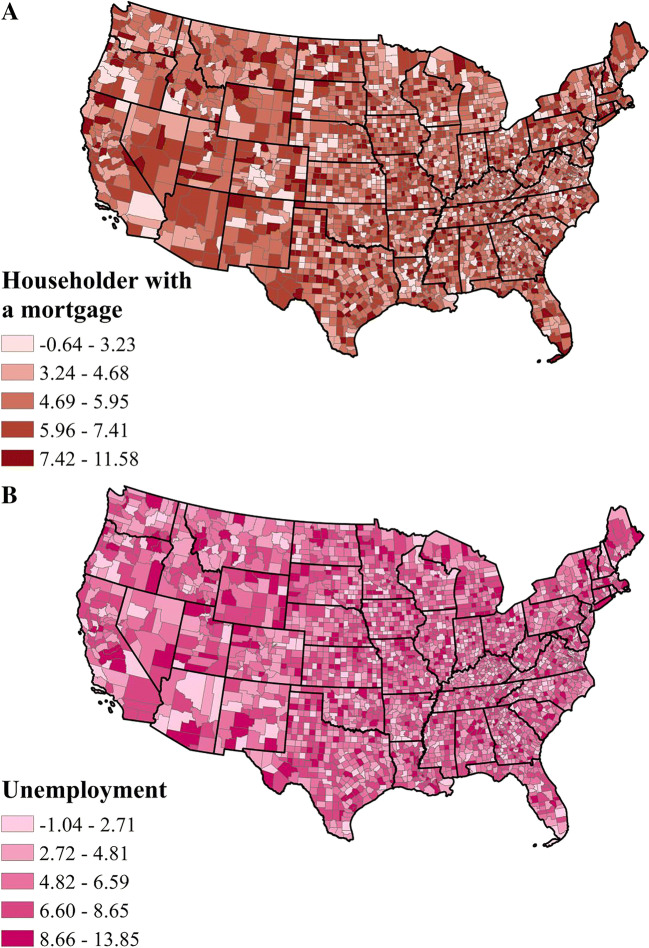
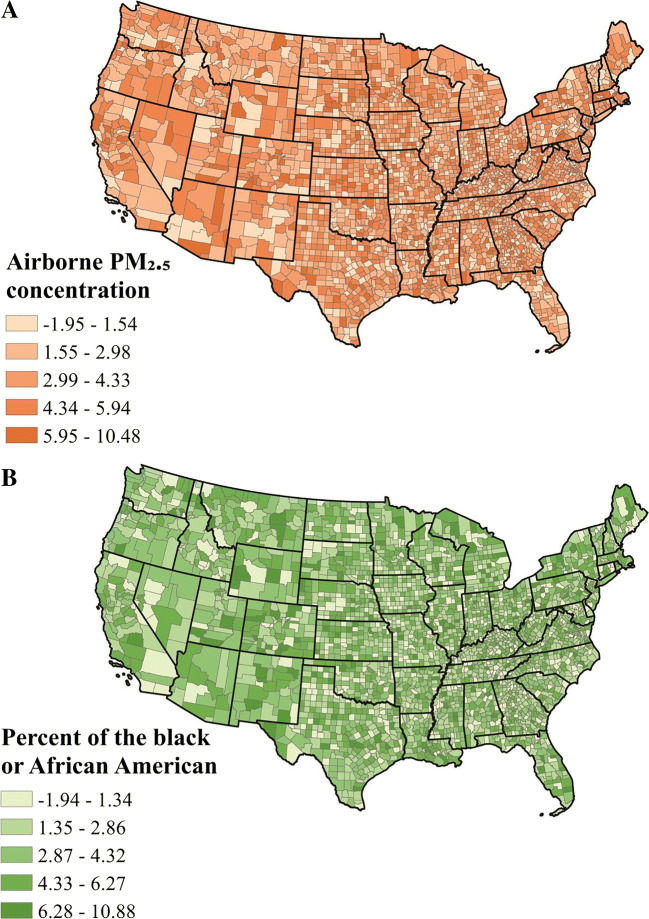
We computed the average local effect of each independent variable on COVID-19 death rate in the GW-RF model (see Fig. 3). The effect of going to work by walking had the highest correlation with the COVID-19 death rate, followed by airborne benzene concentration, householder with a mortgage, unemployment, airborne PM_2.5 concentration and per cent of the black or African American.

Fig. 3.

The average local variable importance of 47 potential risk factors on COVID-19 death rate in the GW-RF model

The proportion of counties with local primary risk factor (the risk factor with the highest value of local variable importance) at county level in the GW-RF was calculated (see Table 3). Going to work by walking was the most influential risk factor in 35% of the counties. As SARS-CoV-2 can spread through the air, going to work by walking will shorten the social distance between people, thereby increasing the likelihood of person-to-person contact, which increases the risk of COVID-19 infection. The airborne benzene concentration was the leading risk factor in 24% of the counties. It is because that the virus always attaches to suspended particles to spread in the air, so the higher the concentration of pollution particles, the more conducive to the spread of the virus. The COVID-19 outbreak has also changed people’s emotions dramatically, especially for those who are already in danger, such as people who suffer from depression. Thirteen per cent of counties were most affected by householder with a mortgage. The outbreak of COVID-19 placed great financial and emotional pressure on householders with a mortgage, which has led to them suffering from psychological illness and do not have enough money for treatment for COVID-19, thus leading to an increased risk of COVID-19. Twelve per cent of counties were most affected by unemployment. During the period of COVID-19, the unemployment rate increased greatly, and some unemployed people are more inclined to have negative emotions, which in turn are more likely to suffer from depression. Moreover, depression is not conducive to the treatment of COVID-19 patients, thus leading to an increased COVID-19 death rate. Figures 4, 5 and 6 provide a detailed spatial distribution of the local variable importance of the first six factors with the highest value of average variable importance on the COVID-19 death rate using the GW-RF.

Table 3.

The proportion of counties with local primary risk factor (the risk factor with the highest value of local variable importance) on COVID-19 death rate at county level in the GW-RF

Local primary risk factor	Proportion of counties
Go to work by walking	35%
Airborne benzene concentration	25%
Householder with a mortgage	13%
Unemployment	12%
Other risk factors	16%

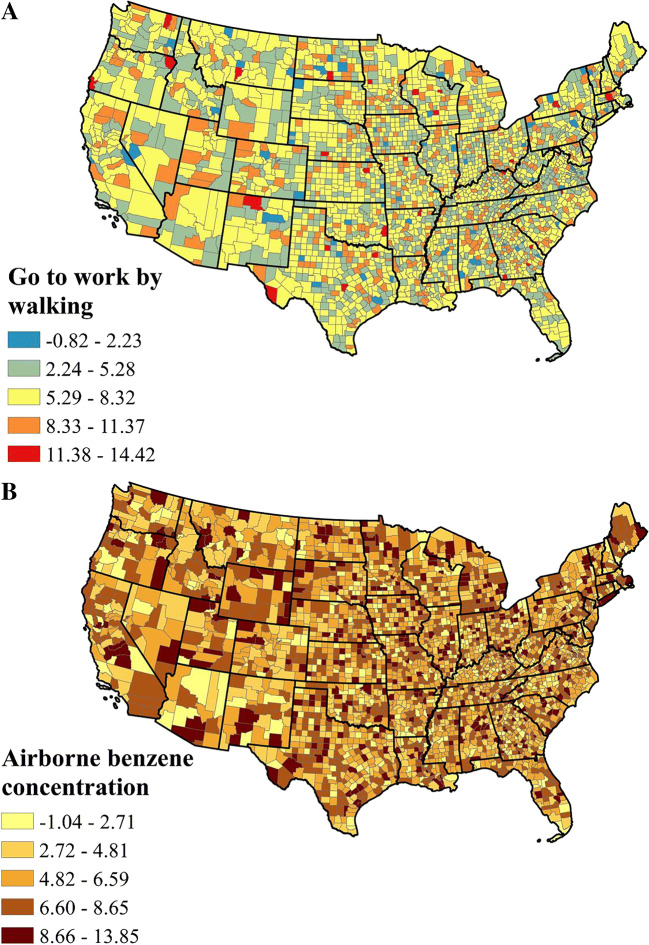
Fig. 4.

The spatial distribution of the local variable importance of a going to work by walking and b airborne benzene concentration on COVID-19 death rate in GW-RF model

Fig. 5.

The spatial distribution of the local variable importance of a householder with a mortgage and b unemployment on COVID-19 death rate in GW-RF model

Fig. 6.

The spatial distribution of the local variable importance of a airborne PM_2.5 concentration and b per cent of the black or African American on COVID-19 death rate in GW-RF model

From Figs. 4, 5 and 6, the distribution of the variable importance of each variable on COVID-19 death rate in GW-RF model was imbalanced in different counties even the counties in the same state. For example, in the southern part of Arizona, the COVID-19 death rate was mainly affected by the airborne benzene concentration and unemployment, and the northern part was mainly affected by going to work by walking and airborne PM_2.5 concentration. The regions obviously affected by going to work by walking were distributed in California, Arizona, the west of Utah, South Carolina and Massachusetts. The areas influenced by airborne benzene concentration were scattered throughout the study area. New Mexico, Florida, Texas, Missouri, the south of Nevada, the north of Arizona, Massachusetts and Connecticut were sensitive to householder with a mortgage. The regions obviously affected by airborne PM_2.5 concentration and per cent of the black or African American are similar, mainly located in the north of Nevada, the north of Arizona, the southeast of Oregon, the east of Wyoming and the central part of the continental USA. In addition, the same area was affected by several risk factors. For example, airborne benzene concentration, householder with a mortgage, unemployment and the per cent of black of African American were influential factors in the southeast of Arizona.

Discussion and conclusion

Identifying the risk factors that highly correlated with the transmission will provide guidance in containing the spread of the COVID-19 disease. In this study, we selected 47 potential risk factors from atmosphere, climate, land cover, disaster, health status, commuting to work and socioeconomic and demographic categories as independent variables to estimate their impact on the distribution of the COVID-19 death rate at county level across continental USA. Due to the imbalanced distribution of COVID-19 death rate and the complex relationship between the COVID-19 death rate and its risk factors, the linear models could not accurately identify the key risk factors in different locations. To solve this problem, we applied GW-RF, a local regression model capable of identifying nonlinear relationships between variables at various geographical locations and suitable for dealing with high-dimensional variables even for correlated variables.

In this study, we used two nonlinear regression models (RF, GW-RF) to identify the key risk factors to the COVID-19 death rate. The result showed that the nonlinear models effectively modelled the relationship between the risk factors and the COVID-19 death rate both in global and local regressions. The adjusted R² of the GW-RF was 0.78, higher than that of the RF, indicating the GW-RF is more suitable to estimate the local risk factors of the COVID-19 death rate compared with the global model RF. The average value of local R² of the GW-RF is 0.59. In GW-RF, the value of local R² is higher than 0.4 in 89.4% of the counties and higher than 0.6 in 50.5% of the counties, indicating that the GW-RF performed well in most of the study area. This shows that that the local nonlinear nonparametric model GW-RF can accurately estimate the relationship between the risk factors and COVID-19 death rate at various geographical locations.

Our result shows that several risk factors from environment, socioeconomic, demographic and commuting to work are associated with the COVID-19 death rate. Finding of the global model RF showed that householders with a mortgage had the highest correlation with the number of COVID-19 death rate, followed by going to work by walking, land cover with forest, hospital beds and overweight. Findings of the geographical local model GW-RF is similar to that of the RF, but a little different. The GW-RF results show that going to work by walking, airborne benzene concentration, householder with a mortgage, unemployment, airborne PM_2.5 concentration and per cent of the black or African American played an important role in the distribution of the COVID-19 death rate. Most of our findings are consistent with previous research on COVID-19. Zheng et al. (2020) found that the frequency of public transportation including flights, trains and buses from the epicentre is an important determinant of transmission risks of COVID-19. They suggested preventive measures should be taken in public transportation in order to contain the COVID-19 epidemic. Several studies found that air pollution has a significant correlation with the COVID-19 confirmed cases (Xu et al. 2020; Bashir et al. 2020). Viruses are usually not spread as independent individuals in air; they are more likely to attach to other suspended particles (Yang et al. 2011). Therefore, the concentration of air pollutants may affect the aerosol transmission of SARS-CoV-2. These studies encouraged the formulation of environmental policies to control pollution sources, which can reduce the harmful effects of air pollutants. Studies from Li et al. (2020) and DiMaggio et al. (2020) showed that compared with the general population of the USA, black Americans were at apparently higher risk of COVID-19 infection and mortality nationwide. It is probably because black Americans suffer more from poverty, environmental pollution, overcrowded housing and less access to health care than do the general population of the USA. The prevalence of smoking and chronic diseases such as cardiovascular disease, diabetes, hypertension, obesity and chronic respiratory diseases has increased among black Americans, all of which increase the risk of COVID-19 (Fang et al. 2020; Zhou et al. 2020; Fouad et al. 2020). Mollalo et al. (2020) found that the proportion of black females and median household income had significant influence on the spatial distribution of the COVID-19 incidence rate.

By exploring the spatial distribution of risk factors of the COVID-19 death rate, we found that COVID-19 death rate in each region was affected by various factors, and the association between each risk factor and the COVID-19 death rate was not consistent in different spatial locations. The result showed that going to work by walking, airborne benzene concentration, householder with a mortgage, unemployment, airborne PM_2.5 concentration and per cent of the black or African American had significant relation with the distribution of the COVID-19 death rate. Other risk factors such as mean travel time to work, hospital distribution and air temperature may require more data to estimate their relationship with the distribution of the COVID-19 death rate. About 35% of the counties are most affected by going to work by walking, so it is necessary to call on people to pay attention to social distancing and to wear medical masks. The western and central east regions were affected by the airborne benzene concentration; toxic particles in the air affect the spread of viruses. Therefore, these regions should pay attention to the impact of air pollution on human health and take measures to protect the environment. The southern part of the continental USA was heavily affected by the proportion of the black or African American and householder with a mortgage, so some assistance probably can be taken in these regions to provide people with financial help such as food and medical supplies.

The current research, despite showing the spatial variability of the correlation between multiple risk factors and the COVID-19 death rate at a county level, has the following limitations. First, the current study only focused on the spatial dimension of the data based on a period, but the data about the COVID-19 death rate is constantly changing over time. Future study can study its spatiotemporal distribution. Secondly, we do not account for policy factors at local area. Policy factors would be an interesting research contribution to the transmission of COVID-19. Thirdly, the GW-RF model only assesses the goodness-of-fit test of the regression but does not assess the significance of the single variable. The test method of this model needs to be improved in the future study.

At present, few geographic local models study the nonlinear relationship between variables. The proposed GW-RF model could accurately estimate the spatial variability of nonlinear relationship between the risk factors and COVID-19 death rate; thus, this method is applicable in many use instances where this is an issue about selecting significantly correlated variables at various geographical locations. Our results confirmed the findings of existing work on COVID-19 but extend it by using a nonlinear approach to quantify the impact of risk factors relevant in local areas. We expect this study could provide a reference for the geographical local nonlinear modelling in the future epidemiological studies.

Author contribution

Yaowen Luo: conceptualization, writing—original draft, formal analysis, methodology, software, formal analysis, investigation, visualization. Jianguo Yan: conceptualization, validation, writing—review and editing, supervision, funding acquisition. Stephen McClure: validation, writing—review and editing.

Funding

This research is supported by a grant provided by National Scientific Foundation of China (Grant No. U1831132 and 41374024), Innovation Group of Natural Fund of Hubei province (Grant No. 2018CFA087) and the fundamental research funds for the central universities (2042018KF0231).

Data availability

The datasets used during the current study are available from the corresponding author on reasonable request.

Compliance with ethical standards

Competing interests

The authors declare that they have no competing interests.

Ethical approval

Not applicable.

Consent for publication

All the co-authors consent the publication of this work.

Consent to participate

Not applicable.