Emission of single photons in the weak coupling regime of the Jaynes Cummings model

Abstract

A recently proposed variant of an unconventional photon blockade scheme is studied for a single emitter weakly coupled to a resonator mode. By controlling two weak coherent fields driving the emitter and the resonator mode, a strongly nonclassical output field is obtained, which is not only antibunched, but has vanishing higher photon number coincidences. For a given set of system parameters, the frequencies and strengths of the driving fields that yield such an output are given.

Introduction

Producing nonclassical light, especially single photons, is an important goal in quantum optics with applications in quantum technologies^1–4. In cavity QED systems single photons can be produced through the so-called photon blockade effect⁵, in which a strong coupling between an emitter and a cavity mode yields an effective photon-photon interaction that prevents occupation of multiple photons in the cavity mode^6,7. Photon blockade is characterized by vanishing second-order correlation functions at zero delay, and have been observed in many physical systems^8–11. It is generally associated with the so-called strong coupling regime, but actually can be observed in weak coupling regimes¹² just like other nonclassical features^13,14.

More recently, it has been found that photon blockade can be observed for arbitrarily small coupling strengths by carefully tuning parameters in a two-cavity system¹⁵. The system under investigation was a coupled weakly Kerr-nonlinear oscillators where individually the nonlinearity was not large enough to induce photon blockade. Soon after, the cause of the phenomenon was identified to be quantum interference, and it was further shown that only one of the oscillators needs to be nonlinear and that the effect persists if the nonlinearity is provided by coupling a two-level atom to the oscillator¹⁶. This inspired interference-based phenomena in similar setups involving two cavity modes and a quantum dot^17,18 and led to experimental demonstrations^19,20. Generalizations such as asymmetric losses²¹, cavities with second order susceptibility²², with two driving fields^23–25, under pulsed excitation²⁶ have also been investigated. Effects of mixing the output channels have also been investigated²⁷ and the antibunching obtained by interfering a nonclassical and a classical states of light has been shown to be related to UPB²⁸.

In Ref.²⁹, it was discovered that the fine-tuning can be relegated to an additional driving field. The experimentally difficult task of fine-tuning the required system parameters can therefore be bypassed, making it much easier to produce antibunched photons with weakly nonlinear cavities. The purpose of this work is to investigate the scheme in detail for an emitter–resonator system described by the Jaynes–Cummings model. The emitted photons are found to be not only antibunched, but have suppressed higher-order photon coincidences to all order. This feature therefore goes beyond UPB, which was shown to be equivalent to optimizing a Gaussian state to suppress the two-photon coincidences³⁰, with enhanced probabilities for higher photon numbers²⁹. This means that photons are emitted one-by-one. The cause of this behaviour can be attributed to the strong nonlinearity in the two-level emitter, as will be explained throughout this work.

Model

The Jaynes–Cummings Hamiltonian reads

$$\begin{array}{c}\hfill H_{\mathrm{JC}}={\omega }_r{a}^{†}a+{\omega }_0{\sigma }_{+}{\sigma }_{-}+g\left(a,{\sigma }_{+},+,a^{†},{\sigma }_{-}\right),\end{array}$$ 1

which describes a resonator with a natural frequency ${\omega }_r$ coupled to a two-level emitter with a transition frequency ${\omega }_0$. If both the resonator mode and emitter are driven with monochromatic fields of frequencies ${\omega }_p$ and ${\omega }_d$ respectively, it becomes

$$\begin{array}{c}\hfill H=H_{\mathrm{JC}}+{\mathrm{\Omega }}_p^{\ast }{e}^{i{\omega }_{p}t}a+{\mathrm{\Omega }}_p{e}^{-i{\omega }_{p}t}{a}^{†}+{\mathrm{\Omega }}_d^{\ast }{e}^{i{\omega }_{d}t}{\sigma }_{-}+{\mathrm{\Omega }}_d{e}^{-i{\omega }_{d}t}{\sigma }_{+}.\end{array}$$ 2

Going into the frame rotating at the probe frequency ${\omega }_p$, the Hamiltonian changes to

$$\begin{array}{cc}\hfill H=& {\mathrm{\Delta }}_r{a}^{†}a+{\mathrm{\Delta }}_0{\sigma }_{+}{\sigma }_{-}+g\left(a,{\sigma }_{+},+,a^{†},{\sigma }_{-}\right)\hfill \\ \hfill & +{\mathrm{\Omega }}_p(a+a^{†})+{\mathrm{\Omega }}_d^{\ast }{e}^{i{\mathrm{\Delta }}_{d}t}{\sigma }_{-}+{\mathrm{\Omega }}_d{e}^{-i{\mathrm{\Delta }}_{d}t}{\sigma }_{+},\hfill \end{array}$$ 3

in which ${\mathrm{\Delta }}_r={\omega }_r-{\omega }_p$, ${\mathrm{\Delta }}_0={\omega }_0-{\omega }_p$ and ${\mathrm{\Delta }}_d={\omega }_d-{\omega }_p$. For ${\omega }_p={\omega }_d$, the Hamiltonian becomes time independent:

$$\begin{array}{c}\hfill H={\mathrm{\Delta }}_r{a}^{†}a+{\mathrm{\Delta }}_0{\sigma }_{+}{\sigma }_{-}+g\left(a,{\sigma }_{+},+,a^{†},{\sigma }_{-}\right)+{\mathrm{\Omega }}_p(a+a^{†})+{\mathrm{\Omega }}_d^{\ast }{\sigma }_{-}+{\mathrm{\Omega }}_d{\sigma }_{+}.\end{array}$$ 4

This case was briefly studied in²⁹ showing that, surprisingly, ${\mathrm{\Omega }}_d$ can always be tuned to obtain UPB given an arbitrary ${\mathrm{\Omega }}_p$.

To see this, consider the quantum master equation, which includes dissipations in the emitter and resonator modes:

$$\begin{array}{c}\hfill \dot{\rho }=-i[H,\rho ]+\mathcal{D}[\sqrt{\kappa }a]\rho +\mathcal{D}[\sqrt{\gamma }{\sigma }_{-}]\rho ,\end{array}$$ 5

in which

$$\begin{array}{c}\hfill \mathcal{D}[c]\rho =c\rho c^{†}-\frac{1}{2}{c}^{†}c\rho -\frac{1}{2}\rho c^{†}c.\end{array}$$ 6

$\kappa$ and $\gamma$ denote dissipation rates for the resonator and atom, respectively. Next, approximating the dissipative part by ignoring the $c\rho c^{†}$ parts of the dissipators, the above master equation reduces to the Schrödinger equation with a non-Hermitian Hamiltonian,

$$\begin{array}{c}\hfill H_{\mathrm{nH}}=H-i\frac{\kappa }{2}{a}^{†}a-i\frac{\gamma }{2}{\sigma }_{+}{\sigma }_{-},\end{array}$$ 7

which amounts to making changes ${\mathrm{\Delta }}_r\to {\mathrm{\Delta }}_r-i\kappa /2\equiv {\tilde{\mathrm{\Delta }}}_r$ and ${\mathrm{\Delta }}_0\to {\mathrm{\Delta }}_0-i\gamma /2\equiv {\tilde{\mathrm{\Delta }}}_0$ in Eq. (4)

Now let us label the state as $|n,\alpha ⟩$, in which n indicates the number of excitations in the resonator mode and $\alpha =\{g,e\}$ denotes the ground and excited state of the atom, respectively. Then to a low number of excitations, a general state is given by

$$\begin{array}{cc}\hfill |\psi (t)⟩& =c_{0g}|0,g⟩+c_{1g}|1,g⟩+c_{0e}|0,e⟩+c_{2g}|2,g⟩+c_{1e}|1,e⟩+\cdots .\hfill \end{array}$$ 8

In this basis, ignoring the contributions from the states with a higher number of excitations, the equations of motion are

$$\begin{array}{cc}\hfill i{\dot{c}}_{0g}& ={\mathrm{\Omega }}_p^{\ast }{c}_{1g}+{\mathrm{\Omega }}_d^{\ast }{c}_{0e},\hfill \\ \hfill i{\dot{c}}_{1g}& ={\mathrm{\Omega }}_p{c}_{0g}+g{c}_{0e}+{\tilde{\mathrm{\Delta }}}_r{c}_{1g}+\sqrt{2}{\mathrm{\Omega }}_r^{\ast }{c}_{2g}+{\mathrm{\Omega }}_d^{\ast }{c}_{1e},\hfill \\ \hfill i{\dot{c}}_{0e}& ={\mathrm{\Omega }}_d{c}_{0g}+g{c}_{1g}+{\tilde{\mathrm{\Delta }}}_0{c}_{0e}+{\mathrm{\Omega }}_p^{\ast }{c}_{1e},\hfill \\ \hfill i{\dot{c}}_{2g}& =\sqrt{2}{\mathrm{\Omega }}_p{c}_{1g}+\sqrt{2}g{c}_{1e}+2{\tilde{\mathrm{\Delta }}}_r{c}_{2g},\hfill \\ \hfill i{\dot{c}}_{1e}& ={\mathrm{\Omega }}_p{c}_{0e}+\sqrt{2}g{c}_{2g}+{\mathrm{\Omega }}_d{c}_{1g}+\tilde{\mathrm{\Delta }}{c}_{1,e},\hfill \end{array}$$ 9

in which $\tilde{\mathrm{\Delta }}\equiv {\tilde{\mathrm{\Delta }}}_r+{\tilde{\mathrm{\Delta }}}_0$.

To solve for the steady state, one assumes $c_{0g}\approx 1$ and solves for $c_{1g}$ and $c_{0e}$ ignoring the contributions from higher number of excitations¹³. This yields

$$\begin{array}{c}\hfill c_{1g}\approx \frac{g{\mathrm{\Omega }}_d-{\tilde{\mathrm{\Delta }}}_0{\mathrm{\Omega }}_p}{{\tilde{\mathrm{\Delta }}}_0{\tilde{\mathrm{\Delta }}}_r-g^2},c_{0e}\approx \frac{g{\mathrm{\Omega }}_p-{\tilde{\mathrm{\Delta }}}_r{\mathrm{\Omega }}_d}{{\tilde{\mathrm{\Delta }}}_0{\tilde{\mathrm{\Delta }}}_r-g^2},\end{array}$$ 10

which can be substituted into the last two equations of motion to give

$$\begin{array}{cc}\hfill c_{1e}& \approx \frac{{\mathrm{\Omega }}_d{\mathrm{\Omega }}_p(g^2+{\tilde{\mathrm{\Delta }}}_r^2+{\tilde{\mathrm{\Delta }}}_r{\tilde{\mathrm{\Delta }}}_0)-g({\mathrm{\Omega }}_p^2\tilde{\mathrm{\Delta }}+{\mathrm{\Omega }}_d^2{\tilde{\mathrm{\Delta }}}_r)}{({\tilde{\mathrm{\Delta }}}_0{\tilde{\mathrm{\Delta }}}_r-g^2)(\tilde{\mathrm{\Delta }}{\tilde{\mathrm{\Delta }}}_r-g^2)},\hfill \\ \hfill c_{2g}& \approx \frac{\tilde{\mathrm{\Delta }}{\mathrm{\Omega }}_p({\tilde{\mathrm{\Delta }}}_0{\mathrm{\Omega }}_r-2g{\mathrm{\Omega }}_d)+g^2({\mathrm{\Omega }}_p^2+{\mathrm{\Omega }}_d^2)}{\sqrt{2}({\tilde{\mathrm{\Delta }}}_0{\tilde{\mathrm{\Delta }}}_r-g^2)(\tilde{\mathrm{\Delta }}{\tilde{\mathrm{\Delta }}}_r-g^2)}.\hfill \end{array}$$ 11

The condition for vanishing two-photon excitation, $c_{2g}=0$, is then approximated by

$$\begin{array}{c}\hfill g^2{\mathrm{\Omega }}_d^2-2g\tilde{\mathrm{\Delta }}{\mathrm{\Omega }}_p{\mathrm{\Omega }}_d+{\mathrm{\Omega }}_p^2(\tilde{\mathrm{\Delta }}{\tilde{\mathrm{\Delta }}}_0+g^2)\approx 0.\end{array}$$ 12

The solutions

$$\begin{array}{c}\hfill {\mathrm{\Omega }}_d^{\pm }=\frac{{\mathrm{\Omega }}_p}{g}\left(\tilde{\mathrm{\Delta }}\pm \text{sgn}({\mathrm{\Omega }}_p)\sqrt{\tilde{\mathrm{\Delta }}{\tilde{\mathrm{\Delta }}}_r-g^2}\right)\end{array}$$ 13

thus give two values of ${\mathrm{\Omega }}_d$ for which the two photon correlation function $g^{(2)}(0)$ vanishes. This condition, first derived in²⁹, shows that a low value of $g^{(2)}(0)$ can be achieved in the weakly-driven regime if one carefully tunes the amplitude and phase of the field driving the atom.

Single driving field

Let us first consider the case in which ${\mathrm{\Omega }}_d=0$. In this case, antibunching can only be observed if both the coupling strength and one of the detunings are chosen carefully. From (12), one readily sees that these are

$$\begin{array}{c}\hfill {\mathrm{\Delta }}_0^{\mathrm{opt}}=-\frac{\gamma {\mathrm{\Delta }}_r}{\kappa +2\gamma },g^{\mathrm{opt}}=\pm \sqrt{\frac{\gamma {\mathrm{\Delta }}_r^2(\kappa +\gamma )}{{(\kappa +2\gamma )}^2}+\frac{(\kappa +\gamma )\gamma }{4}}.\end{array}$$ 14

With these parameters, destructive interference occurs between the pathways to reach $|2,g⟩$, resulting in an almost-vanishing second order correlation function

$$\begin{array}{c}\hfill g^{(2)}(0)=\frac{⟨a^{†}{a}^{†}aa⟩}{{⟨a^{†}a⟩}^2}.\end{array}$$ 15

For example, with ${\mathrm{\Delta }}_r=0$, ${\mathrm{\Omega }}_p=0.01$, and $\kappa =\gamma =1$, we have ${\mathrm{\Delta }}_0^{\mathrm{opt}}=0$ and $g^{\mathrm{opt}}=1/\sqrt{2}$, giving $g^{(2)}(0)\approx 0.003$ in the steady state with the average photon number $\overline{n}\approx 4\times {10}^{-5}$. These and all numerical results in this work are obtained by numerically solving Eq. (5) using QuTiP³¹. For a larger value of detuning ${\mathrm{\Delta }}_r$, the required value of $g^{\mathrm{opt}}$ becomes larger as can be clearly seen from Eq. (14).

In³⁰, UPB was shown to be related to Gaussian states: the fine tuning of the parameters correspond to choosing optimal values of squeezing in a generic Gaussian state. Because of this Gaussianity, the suppression from the Poisson photon number distribution is limited to the two-photon manifold for UPB and comes at the cost of enhanced probabilities for higher photon numbers²⁹. This means that the output field in the UPB scheme is n-photon bunched for $n\ge 3$, i.e. $g^{(n)}(0)=⟨a^{†n}{a}^n⟩/{⟨a^{†}a⟩}^n>1$. Similar behaviour is observed for the current weakly coupled case with a single driving field. For the above parameters, $g^{(n)}(0)=13,158,903$ for $n=3,4,5$ respectively. Introducing the atom-driving field changes this—the higher photon number manifolds are also suppressed.

Two driving fields

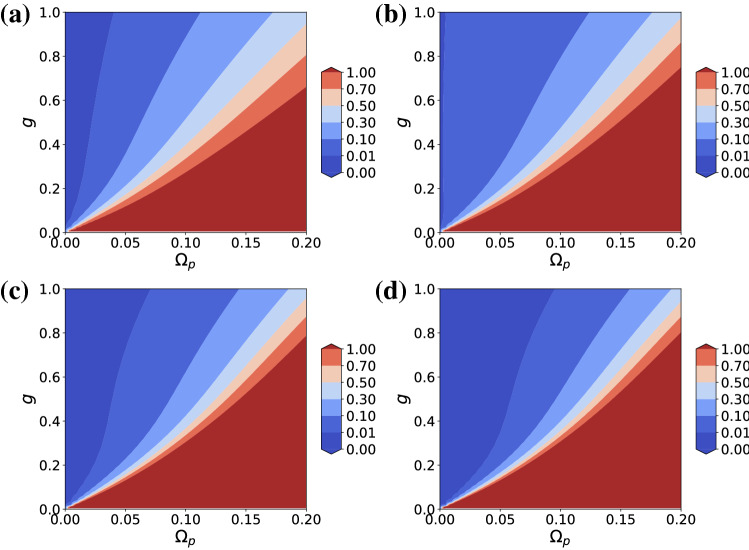
With two driving fields, it is no longer necessary to tune the ‘internal’ values g and ${\mathrm{\Delta }}_0$. The addition of 2 more control parameters is enough to guarantee vanishing second order correlation function even in the weak coupling regime $g\lesssim \kappa ,\gamma$. Figure 1a shows the contour plot of $g^{(2)}(0)$ in the steady state as a function of g and ${\mathrm{\Omega }}_p$. The driving frequency is fixed to the first excited state (assuming ${\omega }_r\ge {\omega }_0$) of the JC model, ${\omega }_{-}=({\omega }_r+{\omega }_0-\sqrt{{\mathrm{\Delta }}^2+4g^2})/2$, with $\mathrm{\Delta }={\omega }_r-{\omega }_0$ and will remain so unless otherwise stated. ${\mathrm{\Omega }}_d={\mathrm{\Omega }}_d^{+}$ is chosen for reasons that will be explained below. The result makes sense intuitively. The larger the value of g the larger the nonlinearity, which in turn allows for a stronger drive strength until nonclassicality is lost. In other words, the strength of the driving field is limited by the value of the coupling strength, which sets the nonlinearity of the system. Unlike in the UPB scheme, higher order correlations are also suppressed as shown in Fig. 1b–d. Three photon coincidence as given by $g^{(3)}(0)$ has a smaller region of suppression compared to $g^{(2)}(0)$, but higher order correlations are suppressed in wider regions. Higher order $g^{(n)}(0)$’s not shown are also suppressed. For weak driving strengths as considered here, average photon number $\overline{n}\ll 1$ and the chance of observing n-photons decreases exponentially with n, but in view of possible generalization to single photon applications it is nice to have suppressed coincidence counting too all orders.

Figure 1.

Contour plots of (a) $g^{(2)}(0)$, (b) $g^{(3)}(0)$, (c) $g^{(4)}(0)$, and (d) $g^{(5)}(0)$ as functions of g and ${\mathrm{\Omega }}_p$ for $\mathrm{\Delta }=0$ and ${\omega }_p={\omega }_{-}$. All units are in terms of $\kappa =\gamma =1$.

The fact that merely adding another driving field can make such a big change to all orders of correlation functions may seem surprising, but one should note that the additional driving field addresses the highly non-linear two-level emitter as emphasized in¹¹. In fact, in the bad cavity regime characterized by $\kappa \gg g^2/\kappa \gg \gamma$, the emitter-driven system is commonly used as a single-photon source². One can therefore understand the suppressed occurrences of two or more photons as resulting from a combination of non-classical light produced by driving the emitter and UPB which further suppresses the two-photon coincidence. To see this, let us consider the case in which only the atom is driven, i.e. ${\mathrm{\Omega }}_p=0$ and ${\mathrm{\Omega }}_d=0.01$. This simplification allows one to obtain an analytic solution for higher-order correlation functions in a manageable form. For a given n the equations of motion (9) generalizes to (still ignoring the contributions from the higher number excitations)

$$\begin{array}{cc}\hfill i{\dot{c}}_{\mathit{ng}}& \approx \sqrt{n}g{c}_{n-1e}+n{\tilde{\mathrm{\Delta }}}_r{c}_{\mathit{ng}},\hfill \\ \hfill i{\dot{c}}_{n-1e}& \approx \sqrt{n}g{c}_{\mathit{ng}}+\left((n-1),{\tilde{\mathrm{\Delta }}}_r,+,{\tilde{\mathrm{\Delta }}}_0\right)c_{n-1e}+{\mathrm{\Omega }}_d{c}_{n-1g}.\hfill \end{array}$$ 16

In the steady state the solutions are

$$\begin{array}{c}\hfill c_{n-1e}\approx -\frac{\sqrt{n}{\tilde{\mathrm{\Delta }}}_r}{g}{c}_{\mathit{ng}},c_{\mathit{ng}}\approx \frac{g{\mathrm{\Omega }}_d}{\sqrt{n}\left[{\tilde{\mathrm{\Delta }}}_r,\left((n-1),{\tilde{\mathrm{\Delta }}}_r,+,{\tilde{\mathrm{\Delta }}}_0\right),-,g^2\right]}{c}_{n-1g}.\end{array}$$ 17

Repeatedly applying the second equation to itself, one obtains

$$\begin{array}{cc}\hfill c_{\mathit{ng}}& \approx \prod _{j=1}^n\frac{g{\mathrm{\Omega }}_d}{\sqrt{n+1-j}\left[{\tilde{\mathrm{\Delta }}}_r,\left((n-j),{\tilde{\mathrm{\Delta }}}_r,+,{\tilde{\mathrm{\Delta }}}_0\right),-,g^2\right]}\hfill \\ \hfill & =\prod _{j=0}^{n-1}\frac{g{\mathrm{\Omega }}_d}{\sqrt{j+1}\left[{\tilde{\mathrm{\Delta }}}_r,\left(j,{\tilde{\mathrm{\Delta }}}_r,+,{\tilde{\mathrm{\Delta }}}_0\right),-,g^2\right]}\hfill \\ \hfill & =\frac{g^n{\mathrm{\Omega }}_d^n}{\sqrt{n!}}\prod _{j=0}^{n-1}\frac{1}{\left[{\tilde{\mathrm{\Delta }}}_r,\left(j,{\tilde{\mathrm{\Delta }}}_r,+,{\tilde{\mathrm{\Delta }}}_0\right),-,g^2\right]}.\hfill \end{array}$$ 18

Using Eq. (10), nth order correlation function at zero delay can thus be approximated by

$$\begin{array}{c}\hfill g^{(n)}(0)\approx \frac{n!|c_{\mathit{ng}}{|}^2}{|c_{1g}{|}^{2n}}\approx \prod _{j=0}^{n-1}\frac{{\left|{\tilde{\mathrm{\Delta }}}_0,{\tilde{\mathrm{\Delta }}}_r,-,g^2\right|}^2}{{\left|{\tilde{\mathrm{\Delta }}}_r,\left(j,{\tilde{\mathrm{\Delta }}}_r,+,{\tilde{\mathrm{\Delta }}}_0\right),-,g^2\right|}^2}.\end{array}$$ 19

We get ${\mathrm{\Delta }}_r={\mathrm{\Delta }}_0=-g$ for $\mathrm{\Delta }=0$ and assuming $g\ll \gamma ,\kappa$, the above equation can be further simplified to

$$\begin{array}{c}\hfill g^{(n)}(0)\approx \prod _{j=0}^{n-1}\frac{{\left(-,\frac{\gamma \kappa }{4}\right)}^2}{{\left|-,j,\frac{{\kappa }^2}{4},-,\frac{\gamma \kappa }{4}\right|}^2}=\prod _{j=0}^{n-1}\frac{{\gamma }^2{\kappa }^2}{{\kappa }^2{\left(\gamma ,+,j,\kappa \right)}^2}=\prod _{j=0}^{n-1}\frac{{\gamma }^2}{{\left(\gamma ,+,j,\kappa \right)}^2}.\end{array}$$ 20

For $\gamma =\kappa$, $g^{(n)}(0)\approx {\prod }_{j=0}^{n-1}1/{(1+j)}^2$. This formula yields $g^{(2)}(0)\approx 1/4$, $g^{(3)}(0)\approx 1/36\approx 0.027$, and $g^{(4)}(0)\approx 1/576\approx 0.0017$ for the set of parameters used in Fig. 1, except for ${\mathrm{\Omega }}_d=0.01$ and ${\mathrm{\Omega }}_p=0$. These agree reasonably well with the numerically obtained results $g^{(2)}(0)=0.26$, $g^{(3)}(0)=0.03$, and $g^{(4)}(0)=0.002$, for g = 0.1, where the differences are due to the terms ignored in going from Eqs. (19) to (20). The above formula shows that higher-order correlations are well-suppressed for $n>2$ when the atom is driven and the atom-field coupling is weak, but that antibunching is not strong.

Upon increasing ${\mathrm{\Omega }}_p^{\mathrm{opt}}$, which is to be obtained from Eq. (12) after allowing ${\mathrm{\Omega }}_p$ to be complex, a numerical calculation shows that $g^{(2)}(0)$ varies rapidly while higher-order correlations do not, as illustrated in Fig. 2. This shows that one can obtain good suppression of all nth order correlation functions for n ≥ 2, by controlling the magnitude of ${\mathrm{\Omega }}_p$. We can therefore understand the single-photon behaviour of the emitted photons as resulting from a combination of non-classical light produced by driving the emitter, and UPB which suppresses the two-photon coincidence.

Figure 2.

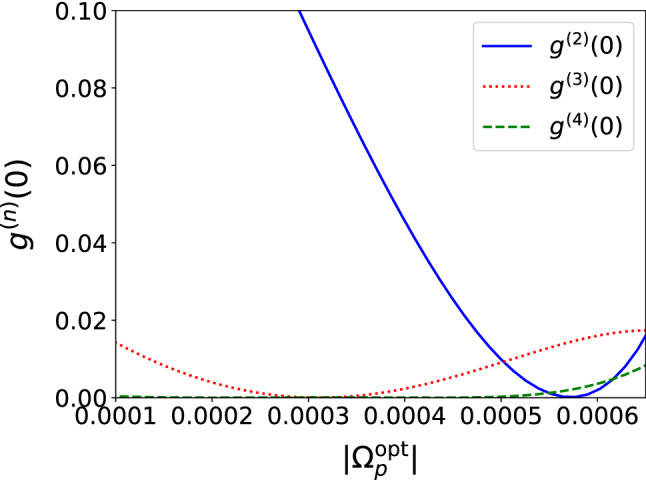
$g^{(n)}(0)$ for $n=2,3,4$ as functions of $|{\mathrm{\Omega }}_p^{\mathrm{opt}}|$. g = 0.1, $\mathrm{\Delta }=0$, ${\omega }_p={\omega }_{-}$ and ${\mathrm{\Omega }}_d=0.01$. The phase of ${\mathrm{\Omega }}_p$ has been set to its optimal value and only the overall magnitude is varied. All units are in terms of $\kappa =\gamma =1$.

Strength of the atom-driving field

In Eq. (13), there were two choices for ${\mathrm{\Omega }}_d$. So far, ${\mathrm{\Omega }}_d^{+}$ has been chosen, but what if ${\mathrm{\Omega }}_d^{-}$ were used instead? It turns out that all correlation functions become larger in the parameter regimes considered above. For example, for $g=0.1$, ${\mathrm{\Omega }}_p=0.01$, $g^{(n)}(0)=(0.145,14.2,200,1580)$ is obtained instead of $(0.022,0.026,0.005,3.50\times {10}^{-4})$ for $n=2,3,4,5$. The difference is in the magnitude of ${\mathrm{\Omega }}_d$. For our choice of the resonator-driving frequency ${\omega }_p={\omega }_{-}$, $|{\mathrm{\Omega }}_d^{+}|>|{\mathrm{\Omega }}_d^{-}|$ and it is evidently advantageous to drive the emitter more strongly. If ${\omega }_p$ were chosen to be ${\omega }_{+}=({\omega }_r+{\omega }_0+\sqrt{{\mathrm{\Delta }}^2+4g^2})/2$, such that the second excited state is driven, the situation is reversed. The magnitudes of ${\mathrm{\Omega }}_d^{\pm }$ are merely reversed although their phases are changed. The values $g^{(n)}(0)=(0.145,14.2,200,1580)$ are obtained for ${\mathrm{\Omega }}_d={\mathrm{\Omega }}_d^{+}$, and the lower values are obtained for ${\mathrm{\Omega }}_d={\mathrm{\Omega }}_d^{-}$. Therefore, ${\omega }_p$ can be chosen to be either ${\omega }_{+}$ or ${\omega }_{-}$ as long as the correct ${\mathrm{\Omega }}_d$ is used.

This freedom only holds as long as the atomic transition is resonant to the cavity mode, i.e. ${\omega }_r={\omega }_0$. If this were not the case, as in many experimental implementations, merely choosing the larger of ${\mathrm{\Omega }}_d^{\pm }$ turns out to be insufficient. In addition, the correct resonator-driving frequency must be chosen, which in this case (Δ > 0) is ${\omega }_{-}$. For example, with ${\omega }_p={\omega }_{+}$, ${\omega }_r=12$ and the rest of the parameters remaining the same, neither ${\mathrm{\Omega }}_d^{+}$ nor ${\mathrm{\Omega }}_d^{-}$ yields single-photon correlations. For ${\mathrm{\Omega }}_d={\mathrm{\Omega }}_d^{-}$, $g^{(n)}(0)=(0.068,0.90,2.06,10.0)$ for $n=2,3,4,5$ while for ${\mathrm{\Omega }}_d={\mathrm{\Omega }}_d^{+}$, $g^{(n)}(0)=(0.107,11.9,160,1470)$. This asymmetry between ${\omega }_{-}$ and ${\omega }_{+}$ can be understood by noting that for $\mathrm{\Delta }={\omega }_r-{\omega }_0\ge 0$ the first excited state is predominantly in $|0,e⟩$, which is the preferred state to be driven (because we want to drive the atom, not the cavity). On the other hand, if $\mathrm{\Delta }<0$, then the situation is reversed and the privileged role is taken by the second excited state.

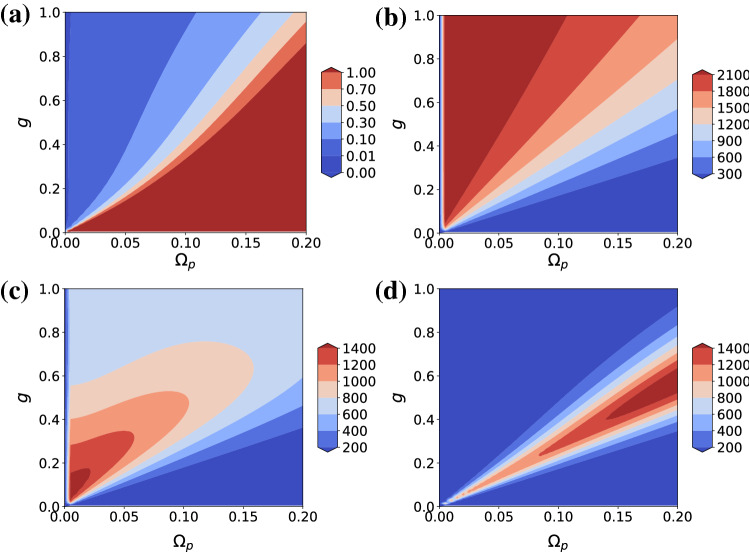
To quantify the suppression of higher-order photon coincidences let us adopt a measure called $n-norm$, defined as $||(g^{(k)}){||}_n=\sqrt[n]{{\sum }_{k=2}^{n+1}[g^{(k)}]}$³². It measures the distance in the correlation space between the given source and an ideal single-photon source. $4-norm$s are adopted in this work, but higher-order norms are also suppressed. Figure 3a–d show that out of the four different combinations with ${\omega }_p={\omega }_{\pm }$ and ${\mathrm{\Omega }}_d={\mathrm{\Omega }}_d^{\pm }$, the combination $({\omega }_{-},{\mathrm{\Omega }}_d^{+})$ gives the best result as explained above. It is not shown but $g^{(2)}(0)$ is always suppressed and the corresponding figures are qualitatively similar to Fig. 1a.

Figure 3.

Contour plots of $||(g^{(k)}){||}_4$ for (a) $({\omega }_{-},{\mathrm{\Omega }}_d^{+})$, (b) $({\omega }_{-},{\mathrm{\Omega }}_d^{-})$, (c) $({\omega }_{+},{\mathrm{\Omega }}_d^{+})$, and (d) $({\omega }_{+},{\mathrm{\Omega }}_d^{-})$ as functions of g and ${\mathrm{\Omega }}_p$ for $\mathrm{\Delta }=2$. All units are in terms of $\kappa =\gamma =1$.

Figure 4a gives a close-up view of Fig. 3d, which shows that $({\omega }_{+},{\mathrm{\Omega }}_d^{-})$can in fact yield good single-photon characteristics in a limited region of the parameter space. Note the changes in the range of ${\mathrm{\Omega }}_p$ and the color coding. However, the figure shows that it is very difficult to obtain good single-photon characteristics for $g\ll \gamma ,\kappa$. Figure 4b is the corresponding figure for ${\omega }_r={\omega }_0$, showing a much wider region of suppressed $||(g^{(k)}){||}_4$. It is exactly the same as the one obtained using $({\omega }_{-},{\mathrm{\Omega }}_d^{+})$. From these facts we see that non-zero detuning breaks the symmetry between $({\omega }_{+},{\mathrm{\Omega }}_d^{-})$ and $({\omega }_{-},{\mathrm{\Omega }}_d^{+})$, which can again be explained by the relative fraction of $|0,e⟩$ in the addressed state.

Figure 4.

Contour plots of $||(g^{(k)}){||}_4$ for (a) $\mathrm{\Delta }=2$ and (b) $\mathrm{\Delta }=0$ as functions of g and ${\mathrm{\Omega }}_p$. ${\omega }_p={\omega }_{+}$ and ${\mathrm{\Omega }}_d={\mathrm{\Omega }}_d^{-}$. All units are in terms of $\kappa =\gamma =1$. Note the differences in the contour values.

To sum up, to obtain good single-photon characteristics one must: (1) choose the driving frequency such that the state $|0,e⟩$ is predominantly driven and (2) choose the driving strength such that the emitter-driving field is the stronger of ${\mathrm{\Omega }}_{\pm }$ in Eq. (13). Then the strong nonlinearity of the atom guarantees that the photons are emitted one by one in a large region of parameter space. If a ‘wrong’ choice is made, two-photon coincidences are still suppressed but higher-order ones are not, as in UPB.

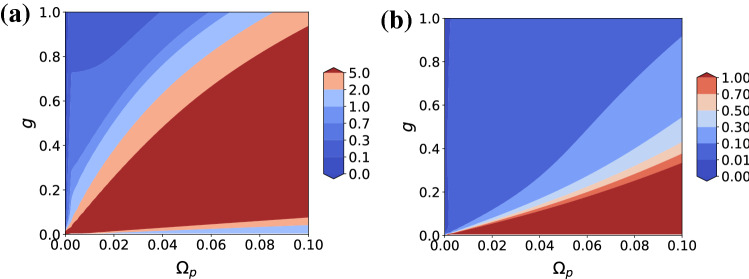
Lastly, let us briefly consider asymmetries in $\kappa$ and $\gamma$. The bad-cavity regime characterized by $\kappa \gg g^2/\kappa \gg \gamma$ is often invoked for the purpose of creating single photons. The emitter is driven, which mainly emits into the leaky cavity mode. Even in this regime, additional cavity-driving field improves the quality of output single photons. For example, for $\kappa =1,g=0.1,\gamma =0.01,{\omega }_r={\omega }_0=10$, ${\omega }_p={\omega }_{-}$, and $|{\mathrm{\Omega }}_d|\approx 0.11$, the first three values of $g^{(n)}(0)$ are (0.10, 0.0032, 0.000046) for ${\mathrm{\Omega }}_p=0$ and (0.0079, 0.0012, 0.000062) for ${\mathrm{\Omega }}_p=0.01$ (obtained from ${\mathrm{\Omega }}_d^{+}$ in Eq. (13)). On the other hand, if the atom decays much faster, i.e., $\gamma \gg g,\kappa$ the driving field strengths need to be reduced and the suppression for higher order photon coincidences are not so good. For $\gamma =1,\kappa =g=0.1$ and ${\mathrm{\Omega }}_p=0.01$, the first three values of $g^{(n)}(0)$ are (0.19,0.82,1.2), which reduces to (0.0019,0.54,0.25) for ${\mathrm{\Omega }}_p=0.001$. Figure 5 shows how $||g^{(n)}{||}_4$ changes as a function of g for ${\mathrm{\Omega }}_p=0.01$ (solid blue curve) and ${\mathrm{\Omega }}_p=0.001$ (dashed red curve). The values differ significantly for $g<0.5$. For ${\mathrm{\Omega }}_p=0.01$ it is interesting that $||g^{(k)}{||}_4$ gets bigger first before it decreases, indicating strong multi-photon bunching.

Figure 5.

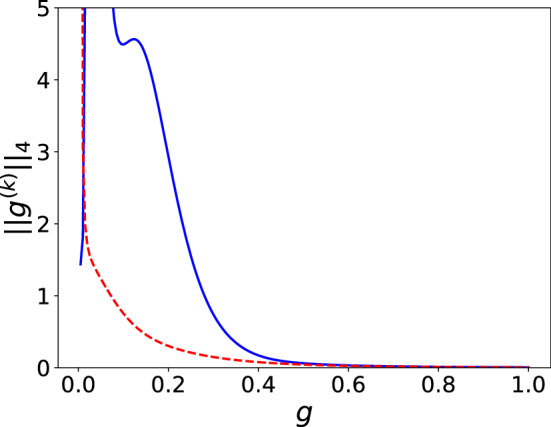
$4-norm$s as functions of g for ${\mathrm{\Omega }}_p=0.01$ (solid blue curve) and ${\mathrm{\Omega }}_p=0.001$ (dashed red curve). $\mathrm{\Delta }=0$, $\kappa =0.1$, and $\gamma =1$.

In summary, a generalization of a scheme based on UPB proposed recently in²⁹ has been investigated in detail. It is shown that unlike in UPB, the output field has suppressed probabilities for all n-photon coincidences for $n\ge 2$. The main reason for the suppression can be attributed to the strong nonlinearity of the 2-lv system, upon which the interference effects of UPB are added to reduce the two-photon coincidences further. One aspect not discussed in this work is the time-variation of the correlation functions. In the conventional UPB scenario, the coupling strength J between the resonators need to be large for weak nonlinearities. This causes the second order correlation function to oscillate rapidly on the time scale of order 1/J. Such rapid oscillations are absent in the system investigated in this work, because there is no large parameter involved. That the correlation functions change on the time scale of $1/\gamma$ and $1/\kappa$ has been checked by numerical calculations.

As a future work it would be interesting to investigate whether the proposed scheme can be generalized to produce an on-demand single photon source which typically requires a multi-level emitter. Due to the small coupling strength required and the ease of parameter tuning, such a scheme would prove to be very useful.

Author contributions

C.N. carried out all calculations and wrote the manuscript.

Competing interests

The author declares no competing interests.