Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2020 Sep 18;5(38):24311–24317. doi: 10.1021/acsomega.0c02506

Exploring the Origin of the Axial-Conformation Preferences in the 3-Halopiperidinium Cations: the Importance of the Coulombic Potential Energies

Farnousha Khani 1, Hooshang Atabaki 1,*
PMCID: PMC7528170  PMID: 33015447

Abstract

graphic file with name ao0c02506_0006.jpg

Although there are some published conclusions in the literature concerning the origin of the axial-conformation preference in 3-fluoropiperidinium cations (charge–dipole orientation effect), the origin of the axial-conformation preferences in the 3-halopiperidinium cations [halogen = F (1), Cl (2), Br (3)] has remained an open question. To explore the origin of the axial-conformation preferences in compounds 1–3, we assessed the roles and contributions of the hyperconjugative interactions, the Coulombic electrostatic interactions, the electrostatic model associated with dipole–dipole interactions, and the steric effects associated with the Pauli exchange-type repulsions on the conformational properties of compounds 1–3 utilizing the G3MP2, LC-ωPBE, and B3LYP methods and natural bond orbital (NBO) interpretations. Natural Coulombic potential energies are in favor of the axial conformations of compounds 1–3, and justify their corresponding total energy differences. The through-space hyperconjugative interactions between the donor lone pairs of halogen atoms (LP3X) and the acceptor antibonding orbitals of H–N bonds [σ*(H–N)⊕], LP3X → σ*(H–N)⊕, increase from compound 1 to compound 3. The inspection of the dipole moments of the parallel C–X and H–N bonds in the axial conformations of compounds 1–3 revealed that the variations of their corresponding four-center dipole–dipole interactions correlate well with their corresponding conformational behaviors. The steric effects associated with the Pauli exchange-type repulsions are strongly in favor of the equatorial conformations of compounds 1–3. Accordingly, the charge–dipole orienting effect associated with the four-center dipole–dipole interactions is a dominant factor in the conformational behaviors of compounds 1–3.

Introduction

It has been well established that due to steric hindrance in the axial conformations of the monohalocyclohexane derivatives, halogen atoms prefer the equatorial conformations in the six-membered ring chains. On the contrary, the substitution of their C-2 atoms with O, N, S, etc. leads to the preference of their corresponding axial conformations. The origin of this fact is related to the anomeric effect.1−19 The anomeric effect is known as the most dominant conformation-controlling factor in the structures of the chemical compounds including carbohydrates, which is defined as the preference of the axial conformation compared to its equatorial conformation. Besides the anomeric effect, the published information in the literature shows that the charge–dipole orienting effects lead to the axial-conformation preferences in some chemical species. In this context, Lankin, Sydney, and co-workers have pointed out that the C–F···H–N charge–dipole orienting effect leads to the axial-conformation preference in N-protonated 3-fluoropiperidine salts.20−23

In 2014, Freitas and co-workers examined the contributions of the hyperconjugative and electrostatic interactions on the conformational behaviors of compound 1.24 They pointed out that according to the quantum theory of atoms in molecules (QTAIM), in the bond path between the F atom of the axial C–F bond and the axial H–N+ bond, the strong preference for the axial conformation of compound 1 results from the electrostatic attraction between F and N+ and electrostatic H-bond (F···HN+), and hyperconjugation was not found to play a relevant role for the axial conformation preference. The results of this work revealed the presence of the through-space LP3F → σ*(H–N)⊕ hyperconjugative interaction, which describes the presence of a quantum H-bond in the axial conformation of compound 1.

The main goal of the current work is the examination of the roles and contributions of the hyperconjugative interactions, the steric effects, the Coulombic electrostatic interactions associated with the attractive or repulsive interactions between adjacent or nonadjacent atoms, and the electrostatic model associated with the dipole–dipole interactions on the conformational behaviors of N-protonated 3-fluoropiperidine (1), 3-chloropiperidine (2), and 3-bromopiperidine (3) by means of G3MP2-,25 the long-range-corrected version of the Perdew–Burke–Ernzerhof (PBE) exchange functional (LC-ωPBE)-,26 and hybrid-density functional (B3LYP)-27 based methods with the 6-311++G** basis set28−31 on all atoms, and natural bond orbital (NBO) analysis.32−37 (Scheme 1).

Scheme 1. Schematic Representation of the Axial and Equatorial Conformations of Compounds 1–3.

Scheme 1

Open in a new tab

Computational Details

The conformational behaviors of the axial and equatorial conformations of compounds 1–3 were examined using G3MP2, B3LYP, and LC-ωPBE methods with the 6-311++G** basis set on all atoms and their corresponding electronic energies and thermodynamic functions were obtained with the GAMESS US package of programs.38,39

G3MP2 is a variation of the Gaussian-3 (G3) theory in which the basis set extensions are obtained at the second-order Møller–Plesset (MP2) level.25 This method gives more accurate energy and its corresponding average absolute deviations for the full G3 theory are negligible. Importantly, G3MP2 saves significant computational time compared to the G3 theory.

One of the most commonly used versions of hybrid functional is B3LYP that includes exact exchange and generalized-gradient-approximation (GGA) corrections in addition to local-density approximation (LDA) electron–electron and electron–nuclei energy.27 Overall, the B3LYP hybrid functional yields relatively accurate results for the geometry optimization, zero-point energies, and atomization energies of molecules.

Since there are smallest many-electron self-interaction errors in the kernel of the LC-ωPBE functional among the wide exchange-correlation functionals, the degree of electron localization and delocalization could be correctly predicted by this functional.26,40−42

Natural bond orbital analysis was performed with the well-tested B3LYP/6-311++G** level of the hybrid-density functional theory43 to estimate the contributions of the plausible hyperconjugative interactions (specifically the through-space LP3X → σ*(H–N)⊕ negative hyperconjugative interactions), Pauli exchange-type repulsions, natural Coulombic energies (NCE),44 and electrostatic model associated with dipole–dipole interactions on the conformational and structural properties of compounds 1–3. Also, the natural bond orbital dipole moments of the axial conformations of compounds 1–3 and their corresponding bonding and antibonding orbital occupancies and energies were investigated by means of NBO-B3LYP/6-311++G** interpretation with the NBO 5.G program.45

The stabilization energies (second-order perturbational energies) associated with the hyperconjutative interactions (donor (i) → acceptor (j) electron delocalization) are directly proportional to the magnitudes of the orbital overlap integrals46,47 and inversely proportional to the energy differences between the donor and acceptor orbitals.

Stabilization or Resonance Energy α (Sij2/Δεij)

Accordingly, the stabilization or second-order perturbative energy (E2) associated with i → j electron delocalization is explicitly estimated by the following equation

graphic file with name ao0c02506_m001.jpg 1

where qi is the ith donor orbital occupancy, εi and εj are diagonal elements (orbital energies), and F(i,j) is the off-diagonal natural bond orbital Fock matrix element.

Results and Discussion

Conformational Preferences

Enthalpy, entropy, and Gibbs free energy differences between the axial and equatorial conformations of compounds 1–3, as calculated at the G3MP2, LC-ωPBE/6-311++G**, and B3LYP/6-311++G** levels of theory, are summarized in Tables 12–3.

Table 1. G3MP2-Calculated Thermodynamic Functions and Parameters [H, G (in hartree), and S (in cal mol–1K–1)] for the Axial and Equatorial Conformations of Compounds 1–3.

  G3MP2
  H S G ΔHa ΔSa ΔGa
1-ax –350.947309 79.608 –350.985012 0.00 0.000 0.00
1-eq –350.939285 80.296 –350.977289 0.008024(5.04)a 0.688 0.007723(4.85)a
2-ax –710.948226 81.755 –710.987051 0.00 0.000 0.00
2-eq –710.941226 82.492 –710.980401 0.007000(4.39)a 0.737 0.00665(4.17)a
3-ax –2824.023404 84.501 –2824.063533 0.00 0.000 0.00
3-eq –2824.016863 85.278 –2824.057361 0.006541(4.10)a 0.777 0.006172(3.87)a
Open in a new tab

Table 2. LC-ωPBE/6-311++G**-Calculated Thermodynamic Functions and Parameters [H, G (in hartree), and S (in cal mol–1K–1)] for the Axial and Equatorial Conformations of Compounds 1–3.

  LC-ωPBE/6-311++G**
  H S G ΔHa ΔSa ΔGa
1-ax –351.237685 78.331 –351.274903 0.00 0.000 0.00
1-eq –351.228892 78.942 –351.266399 0.008793(5.52)a 0.611 0.008504(5.34)a
2-ax –711.506266 80.353 –711.544444 0.00 0.000 0.00
2-eq –711.499679 81.195 –711.538258 0.006587(4.13)a 0.842 0.006186(3.88)a
3-ax –2825.185238 82.978 –2825.224663 0.00 0.000 0.00
3-eq –2825.178974 83.892 –2825.218834 0.006264(3.93)a 0.914 0.005829(3.66)a
Open in a new tab

Table 3. B3LYP/6-311++G**-Calculated Thermodynamic Functions and Parameters [H, G (in hartree), and S (in cal mol–1K–1)] for the Axial and Equatorial Conformations of Compounds 1–3.

  B3LYP/6-311++G**
  H S G ΔHa ΔSa ΔGa
1-ax –351.447593 78.843 –351.485054 0.00 0.000 0.00
1-eq –351.439751 79.346 –351.477451 0.007842(4.92)a 0.503 0.007603(4.77)a
2-ax –711.803039 81.072 –711.841559 0.00 0.000 0.00
2-eq –711.797387 81.853 –711.836278 0.005652(3.55)a 0.781 0.005281(3.31)a
3-ax –2825.724623 83.830 –2825.764454 0.00 0.000 0.00
3-eq –2825.719303 84.680 –2825.759537 0.00532(3.34)a 0.850 0.004917(3.09)a
Open in a new tab

It is well known that the axial conformations of fluoro, chloro, and bromocyclohexanes are less stable than their corresponding equatorial conformations (due to the presence of 1,3-diaxial repulsions in their axial conformations), while the axial conformations of compounds 1–3 are the most stable than their corresponding equatorial conformations. We examined total steric exchange energies (TSEE) of the axial and equatorial conformations of compounds 1–3. Based on the results obtained, total steric exchange energies (TSEE) are in favor of the equatorial conformations of compounds 1–3, and Δ(TSEEax – TSEEeq) parameters decrease from compound 1 to compound 3. Since the strong axial-conformation preferences decrease from compound 1 to compound 3, there are no correlations between their conformational behaviors and their corresponding Δ(TSEEax – TSEEeq) parameters (Tables 1–4). The calculated entropies of the equatorial conformations of compounds 1–3 are greater than those of their corresponding axial conformations, and the entropy differences between the equatorial and axial conformations increase slightly from compound 1 to compound 3.

Table 4. NBO-B3LYP/6-311++G**-Calculated Total Steric Exchange Energies (TSEE, in kcal mol–1) for the Equatorial and Axial Conformations of Compounds 1–3.

  NBO-B3LYP/6-311++G**
  1 2 3
  ax eq ax eq ax eq
TSEE 310.48 294.32 330.71 323.46 337.61 329.87
ΔTSEE 16.16 0.00 7.25 0.00 7.74 0.00
Open in a new tab

Assessing the Correlations between the Natural Coulombic Energies (NCE) and the Axial-Conformation Preferences in Compounds 1–3

The attractive and repulsive electrostatic interactions between adjacent and nonadjacent atoms in a molecule can be associated to the Coulombic electrostatic interactions. Therefore, a simple electrostatic descriptor can be formulated in terms of the effective net atomic charges (qA) and the associated Coulombic potential energy function (VNCE)

graphic file with name ao0c02506_m002.jpg 2

Equation 2 expresses natural Coulombic energy (NCE) as a qualitative measure of overall atom–atom attractive or repulsive electrostatic interactions. Given two distinct isomeric geometries and associated natural atomic charges, we may evaluate the natural Coulombic potential energy differences (ΔVNCE) that might be reasonably attributed to their corresponding electrostatic-type forces. We examined the impacts of the attractive or repulsive electrostatic interactions between the natural atomic charges of the adjacent and nonadjacent atoms on the conformational preferences of compounds 1–3 (Table 4). On the basis of the results obtained, the natural Coulombic potential energy differences between the axial and equatorial conformations of compounds 1–3 [ΔE(es)(L + NL) = VNCE(ax)- VNCE(eq)] are in favor of the axial conformations, and ΔE(es) parameter (without considering their negative signs) decreases significantly from compound 1 to compound 3 (Table 5).

Table 5. B3LYP/6-311++G**-Calculated Natural Coulombic Potential Energy (VNCE) and its Lewis [E(L)] and Non-Lewis [E(NL)] Components (in au) and also Their Corresponding Differences for the Axial and Equatorial Conformations of Compounds 1–3b.

  NBO-B3LYP/6-311++G**
  1 2 3
  ax eq ax eq ax eq
E(es)(L) –0.40435 –0.39341 –0.36185 –0.34828 –0.36954 –0.35619
ΔE(es)(L) –0.01094(−6.86)a 0.00000 –0.01357(−8.52)a 0.00000 –0.01335(−8.38)a 0.00000
E(es)(NL) 0.01801 0.02026 0.00303 0.00069 0.00250 –0.00092
ΔE(es)(NL) –0.00225(−1.41)a 0.00000 0.00234(1.47)a 0.00000 0.00342(2.15)a 0.00000
VNCE –0.38634 –0.37315 –0.35882 –0.34759 –0.36704 –0.35712
ΔE(es) –0.01319(−8.28)a 0.00000 –0.01123(−7.05)a 0.00000 –0.00992(−6.22)a 0.00000
Open in a new tab
a

Values are in kcal mol–1.

b

ΔE(es) = VNCE(C2h) – VNCE(D2h).

This fact shows that Coulombic electrostatic interactions fairly explain the decrease of the axial-conformation preferences from compound 1 to compound 3. Interestingly, the resonance-enhanced electrostatic effect (non-Lewis component of Coulombic potential energy, [Ees(NL)]) is in favor of the axial conformation of compound 1 while it is oppositely in favor of the equatorial conformations of compounds 2 and 3. In contrast, the Lewis components [E(es)(L)] have significant contributions in the magnitudes of the natural Coulombic potential energies. Although Δ[Ees(L)(ax) – Ees(L)(eq)] parameter is in favor of the axial conformations of compounds 1–3, the natural Coulombic potential energy differences [ΔE(es)] between the axial and equatorial conformations of compounds 1–3 result from the combinations of their Lewis and non-Lewis components [ΔE(es)(L + NL) = VNCE(ax) – VNCE(eq)]. Accordingly, the variations of the axial-conformation preferences in compounds 1–3 could be controlled by their corresponding ΔE(es) parameters.

The electrostatic interactions between the axial halogen atoms and the axial hydrogen atoms of the H–N bonds in the axial conformations of compounds 1–3 have a significant impact on their corresponding ΔE(es) parameters. NBO-B3LYP/6-311++G** results showed that the axial fluorine atom of the axial conformation of compound 1 possesses (as it is expectable) negative natural charges, while the chlorine atom consists of smaller negative natural atomic charge (≈0) and the bromine atom of the axial conformation of compound 3 possesses a positive natural atomic charge. Since the hydrogen atoms of the axial H–-N bonds of compounds 1–3 possess positive natural atomic charges (≈0.50), accordingly, the strength of the attractive electrostatic interaction decreases significantly from compound 1 to compound 2, but there is a repulsive electrostatic interaction between the axial bromine atom and the hydrogen atom of the axial H–N bond in compound 3.

Assessing the Impacts of the Hyperconjugative Interactions on the Axial-Conformation Preferences in Compounds 1–3

There are through-space hyperconjugative interactions between the lone pairs of the axial halogen atoms [LP3X, X = F(1), Cl(2), Br(3)] and the antibonding orbitals of the axial H–N bonds [LP3X → σ(H–N*)⊕]. NBO-B3LYP/6-311++G** results revealed that the stabilization energies associated with the through-space LP3X → σ(H–N*)⊕ negative hyperconjugative interactions increase slightly from the axial conformations of compound 1 to compound 3, which may lead to the increase of the axial-conformation stability compared to their corresponding equatorial conformations (Figure 1).

Figure 1.

Figure 1

Open in a new tab

Through-space negative hyperconjugative interactions between the halogen nonbonding (LP3X, X = F, Cl, Br) and nitrogen–hydrogen antibonding (σ*N–H⊕) orbitals in compound 1 (left), compound 2 (center), and compound 3 (right).

Although the resonance energy associated with the through-space LP3X → σ*(H–N)⊕ negative hyperconjugative interactions increases slightly from the axial conformations of compound 1 to compound 3, their corresponding axial-conformation preferences decrease. Accordingly, the through-space LP3X → σ(H–N*)⊕ negative hyperconjugative interactions play an important (but not determining) role in the axial-conformation preferences in compounds 1–3.

Examination of the Role and Contribution of the N–H...X–C Dipole Orientation Effect in the Conformational Behaviors of Compounds 1–3

The electrostatic model associated with dipole–dipole interactions fails to account quantitatively for the rationalization of the variation of the axial-conformation preferences in compounds 1–3. To explore the impact of the N–H···X–C dipole orientation effect on the conformational properties of compounds 1–3, we investigated the dipole moments of the natural bond orbitals of the axial conformations of compounds 1–3 (Table 6).

Table 6. NBO-B3LYP/6-311++G**Z-Calculated Molecular Dipole Moment Contributions in Terms of Natural Bond Orbital Contributions (μ, in Debye) for the Equatorial and Axial Conformations of Compounds 1–3.

  NBO-B3LYP/6-311++G**
  1 2 3
  ax eq ax eq ax eq
μ(total) 5.10 6.91 6.07 8.05 7.77 10.31
  0.00 1.81 0.00 1.98 0.00 2.54
μ(N–Hax) 0.50   0.50   0.49  
μ(C–X) 2.08   0.87   0.60  
μ(LP1X) 2.27   2.91   2.86  
μ(LP2X) 0.27   0.58   0.63  
μ(LP3X) 0.19   0.28   0.18  
Open in a new tab

On the basis of the results obtained, total dipole moments of the C–X [X = F(1), Cl(2), Br(3)] bonds result from the combinations of the natural bond orbital dipole moments of C–X bonds and the s-type nonbonding orbitals of the halogen (X) atoms, μ(C–X) + μ(LP1X) (Figure 2). Effectively, μ(C–X) + μ(LP1X) parameters and the natural bond order dipole moment of the H–N bonds [μ(H–N⊕)] are in the opposite directions and their instructive interactions lead to the N–H···X–C dipole orientation effects (Figure 2).

Figure 2.

Figure 2

Open in a new tab

NBO-B3LYP/6-311++G**-calculated dipole moments of the C–F, C–Cl, C–Br, and N–H⊕ bonds and the lone pairs of fluorine, chlorine, and bromine atoms in the axial conformations of compounds 1–3.

μ(C–X) + μ(LP1X) parameter decreases from the axial conformations of compound 1 to compound 3, while no significant change is observed for μ(H–N⊕). Accordingly, the variations of the N–H···X–C dipole orientation effects correlate well with the variations of the axial-conformation preferences in compounds 1–3.

Structural Properties of Compounds 1–3

Selected structural parameters of the axial conformations of compounds 1–3, as calculated at the B3LYP/6-311++G** level of the theory are shown in Figure 3.

Figure 3.

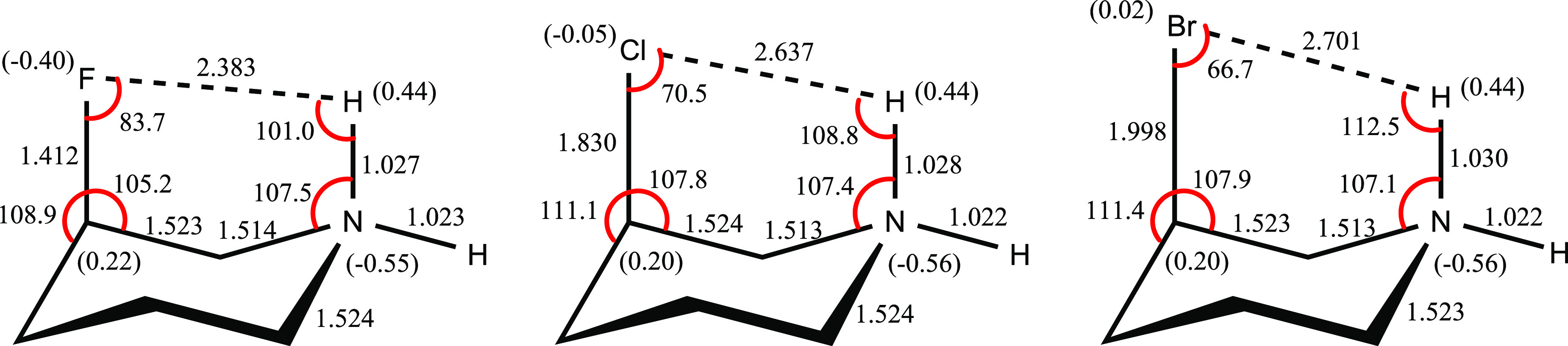
Figure 3

Open in a new tab

B3LYP/6-311++G**-calculated structural parameters [bond lengths (in angstrom) and bond angles (in degree)] and natural atomic charges (NAC, in parenthesis) for the axial conformations of compounds 1–3.

Interestingly, the N1–C2 bonds of the axial conformations of compounds 1–3 are significantly contracted than their corresponding N1–C6 bonds. The inspection of the roles and contributions of the attractive electrostatic interactions between two adjacent atoms and hyperconjugative interactions in the contractions of the N1–C2 bonds of the axial conformations of compounds 1–3 revealed that these two factors have no significant impact on the contractions of N1–C2 bonds compared to the N1–C6 bonds. Accordingly, we may conclude that the attractive interactions between two oppositely oriented dipole moments of the C–F and H–N bonds lead to the contractions of the N1–C2 bonds. Interestingly, the contractions of the N1–C2 bonds compared to the N1–C6 bonds are also observed in the equatorial conformations of compounds 1–3. The N1–C2 bond lengths in the axial conformations of compounds 1–3 are smaller than those in their corresponding equatorial conformations. This fact could be explained with the greater attractive interactions between two oppositely (in-plane) oriented dipole moments of the C–F and H–N bonds in the axial conformations of compounds 1–3 compared to their corresponding nonplanar dipole in the equatorial conformations. Seemingly, this phenomenon is an interesting example, which shows the greater contribution of the attractive dipole interactions in the structural parameters of chemical compounds.

Conclusions

The G3MP2 composite method, long-range-corrected hybrid-density functional theory (LC-ωPBE), B3LYP, and natural bond orbital interpretation provided a clear and reasonable picture from structural, bonding, stereoelectronic, natural electrostatic energies, dipole–dipole interaction, and energetic points of views to explore the origin of the axial-conformation preferences in compounds 1–3. Effectively, natural Coulombic potential energies associated with attractive or repulsive interactions between adjacent or nonadjacent atoms are in favor of the axial conformations of compounds 1–3, and the natural Coulombic potential energy differences [ΔE(es)] between the axial and equatorial conformations justify their corresponding total energy differences. The NBO–dipole moment analysis revealed that the C–X···H–N charge–dipole orienting effect decreases from the axial conformations of compound 1 to compound 3, which is in line with the variations of their corresponding axial-conformation preferences. Importantly, the attractive electrostatic interaction between the halogen atoms and the hydrogen atoms of the axial H–N bonds decrease drastically from compound 1 to compound 3, justifying the conformational preferences of compounds 1–3.

Acknowledgments

The authors are grateful to the research council of the Islamic Azad University of Arak. They further extend their gratitude to Professor Davood Nori-Shargh for his helpful discussions.

The authors declare no competing financial interest.

References

  1. Juaristi E.; Cuevas G.. The Anomeric Effect; CRC Press: Boca Raton, FL, 1995. [Google Scholar]
  2. Deslongchamps P.Stereoelectronic Effects in Organic Chemistry; Pergamon Press: Maxwell House, Fairview Park, Elmsford, NY, 1983. [Google Scholar]
  3. Kirby J.The Anomeric Effect and Related Stereoelectronic Effects at Oxygen; Springer Verlag: New York, 1983. [Google Scholar]
  4. Cramer C. J. Anomeric and Reverse Anomeric Effects in the Gas Phase and Aqueous Solution. J. Org. Chem. 1992, 57, 7034–7043. 10.1021/jo00052a012. [DOI] [Google Scholar]
  5. Cramer C. J.; Truhlar D. G.; French A. D. Exo-anomeric effects on energies and geometries of different conformations of glucose and related systems in the gas phase and aqueous solution. Carbohydr. Res. 1997, 298, 1–14. 10.1016/S0008-6215(96)00297-2. [DOI] [Google Scholar]
  6. Perrin C. L.; Armstrong K. B.; Fabian M. A. The Origin of the Anomeric Effect: Conformational Analysis of 2-Methoxy- 1,3-dimethylhexahydropyrirnidine. J. Am. Chem. Soc. 1994, 116, 715–722. 10.1021/ja00081a037. [DOI] [Google Scholar]
  7. Juaristi E.; Cuevas G. Recent studies of the anomeric effect. Tetrahedron 1992, 48, 5019–5087. 10.1016/S0040-4020(01)90118-8. [DOI] [Google Scholar]
  8. Lesarri A.; Vega-Toribio A.; Suenram R. D.; Brugh D. J.; Nori-Shargh D.; Boggs J. E.; Grabow J.-U. Structural Evidence of Anomeric Effects in the Anesthetic Isoflurane. Phys. Chem. Chem. Phys. 2011, 13, 6610–6618. 10.1039/c0cp02465a. [DOI] [PubMed] [Google Scholar]
  9. Vila A.; Mosquera R. A. Atoms in Molecules Interpretation of the Anomeric Effect in the O-C-O Unit. J. Comput. Chem. 2007, 28, 1516–1530. 10.1002/jcc.20585. [DOI] [PubMed] [Google Scholar]
  10. The Anomeric Effect and Associated Steroelectronic Effects;Thacher G. R. J.; Thacher G. R. J., Eds., ACS Symposium Series No. 539; American Chemical Society: Washington, DC, 1993. [Google Scholar]
  11. Hasanzadeh N.; Nori-Shargh D.; Yahyaei H.; Mousavi S. N.; Kamrava S. J. Phys. Chem. A 2017, 121, 5548–5560. 10.1021/acs.jpca.7b04447. [DOI] [PubMed] [Google Scholar]
  12. Praly J.-P.; Lemieux R. U. Influence of Solvent on the Magnitude of the Anomeric Effect. Can. J. Chem. 1987, 65, 213–223. 10.1139/v87-034. [DOI] [Google Scholar]
  13. Nori-Shargh D.; Boggs J. E. Complete basis set, hybrid-DFT study and NBO interpretations of conformational behaviors of trans-2,3- and trans-2,5-dihalo-1,4-dithianes. J. Phys. Org. Chem. 2011, 24, 212–221. 10.1002/poc.1728. [DOI] [Google Scholar]
  14. Nori-Shargh D.; Mousavi S. N.; Kayi H. Conformational Behaviors of trans-2,3- and trans-2,5-Dihalo-1,4-Diselenanes. A Complete Basis Set, Hybrid-Density Functional Theory Study and Natural Bond Orbital Interpretations. J. Mol. Model. 2014, 20, 2249 10.1007/s00894-014-2249-x. [DOI] [PubMed] [Google Scholar]
  15. Juaristi E.; Cuevas G.; Vela A. Stereoelectronic Interpretation for the Anomalous 1H NMR Chemical Shifts and One-Bond C-H Coupling Constants (Perlin Effects) in 1,3-Dioxanes, 1,3-Oxathianes, and 1,3-Dithianes. Spectroscopic and Theoretical Observations. J. Am. Chem. Soc. 1994, 116, 5796–5804. 10.1021/ja00092a034. [DOI] [Google Scholar]
  16. Ghanbarpour P.; Nori-Shargh D. Exploring the Origin of the Anomeric Relationships in 2-Cyanooxane, 2-Cyanothiane, 2-Cyanoselenane and their Corresponding Isocyano Isomers. Correlations between Hyper-Conjugative Anomeric Effect, Hardness and Electrostatic Interactions. RSC Adv. 2016, 6, 46406–46420. 10.1039/C6RA06080C. [DOI] [Google Scholar]
  17. Nori-Shargh D.; Mousavi S. N.; Tale R.; Yahyaei H. Hyperconjugative Interactions are the Main Responsible for the Anomeric Effect: A Direct Relationship between the Hyperconjugative Anomeric Effect, Global Hardness and Zero-Point Energy. Struct. Chem. 2016, 27, 1753–1768. 10.1007/s11224-016-0791-0. [DOI] [Google Scholar]
  18. Kleinpeter E.Conformational Behavior of Six-Membered Rings; Juaristi E., Ed.; VCH Publishers Inc: New York, 1995; pp 201–243. [Google Scholar]
  19. Hasanzadeh N.; Nori-Shargh D.; Farzipour M.; Ahmadi B. The Origin of the Anomeric Effect: Probing the Impacts of Stereoelectronic Interactions. Org. Biomol. Chem. 2015, 13, 6965–6976. 10.1039/C5OB00585J. [DOI] [PubMed] [Google Scholar]
  20. Lankin D. C.; Chandrakumar N. S.; Rao S. N.; Spangler D. P.; Synder J. P. Protonated 3-fluoropiperidines: an unusual fluoro directing effect and a test for quantitative theories of solvation. J. Am. Chem. Soc. 1993, 115, 3356–3357. 10.1021/ja00061a055. [DOI] [Google Scholar]
  21. Synder J. P.; Chandrakumar N. S.; Sato H.; Lankin D. C. The Unexpected Diaxial Orientation of cis-3,5-Difluoropiperidine in Water: A Potent CF- - -NH Charge-Dipole Effect. J. Am. Chem. Soc. 2000, 122, 544–545. 10.1021/ja9934504. [DOI] [Google Scholar]
  22. Lankin D. C.; Grunewald G. L.; Romero F. A.; Oren I. Y.; Synder J. P. The NH---FC Dipole Orientation Effect for Pendant Exocyclic CH2F. Org. Lett. 2002, 4, 3557–3560. 10.1021/ol026358c. [DOI] [PubMed] [Google Scholar]
  23. Sun A.; Lankin D. C.; Hardcastle K.; Synder J. P. 3-Fluoropiperidines and N-Methyl-3-fluoropiperidinium Salts: The Persistence of Axial Fluorine. Chem. - Eur. J. 2005, 11, 1579–1591. 10.1002/chem.200400835. [DOI] [PubMed] [Google Scholar]
  24. Silla J. M.; Silva W. G. D. P.; Cormanich R. A.; Rittner R.; Tormena C. F.; Freitas M. P. Gauche Preference of β-Fluoroalkyl Ammonium Salts. J. Phys. Chem. A 2014, 118, 503–507. 10.1021/jp410458w. [DOI] [PubMed] [Google Scholar]
  25. Curtiss L. A.; Redfern P. C.; Raghavachari K.; Rassolov V.; Pople J. A. Gaussian-3 Theory Using Reduced Møller-Plesset Order. J. Chem. Phys. 1999, 110, 4703–4709. 10.1063/1.478385. [DOI] [Google Scholar]
  26. Vydrov O. A.; Scuseria G. E. Assessment of a Long-Range Corrected Hybrid Functional. J. Chem. Phys. 2006, 125, 234109 10.1063/1.2409292. [DOI] [PubMed] [Google Scholar]
  27. Becke A. D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. 10.1063/1.464913. [DOI] [Google Scholar]
  28. Krishnan R.; Binkley J. S.; Seeger R.; Pople J. A. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys. 1980, 72, 650–654. 10.1063/1.438955. [DOI] [Google Scholar]
  29. McLean A. D.; Chandler G. S. Contracted Gaussian basis sets for molecular calculations. I. Second row atoms Z=11–18. J. Chem. Phys. 1980, 72, 5639–5648. 10.1063/1.438980. [DOI] [Google Scholar]
  30. Blaudeau J.-P.; McGrath M. P.; Curtiss L. A.; Radom L. Extension of Gaussian-2 (G2) Theory to Molecules Containing Third-Row Atoms K and Ca. J. Chem. Phys. 1997, 107, 5016–5021. 10.1063/1.474865. [DOI] [Google Scholar]
  31. Curtiss L. A.; McGrath M. P.; Blandeau J. -P.; Davis N. E.; Binning R. C. Jr.; Radom L. Extension of Gaussian-2 Theory to Molecules Containing Third-Row Atoms Ga–Kr. J. Chem. Phys. 1995, 103, 6104–6113. 10.1063/1.470438. [DOI] [Google Scholar]
  32. Reed A. E.; Curtiss L. A.; Weinhold F. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. 10.1021/cr00088a005. [DOI] [Google Scholar]
  33. Reed A. E.; Weinhold F.; Curtiss L. A.; Pochatko D. J. Natural bond orbital analysis of molecular interactions: Theoretical studies of binary complexes of HF, H2O, NH3, N2, O2, F2, CO, and CO2 with HF, H2O, and NH3. J. Chem. Phys. 1986, 84, 5687–5705. 10.1063/1.449928. [DOI] [Google Scholar]
  34. Carpenter J. E.; Weinhold F. Transferability of Natural Bond Orbitals. J. Am. Chem. Soc. 1988, 110, 368–372. 10.1021/ja00210a008. [DOI] [Google Scholar]
  35. Glendening E. D.; Weinhold F. Natural resonance theory: I. General formalism. J. Comput. Chem. 1998, 19, 593–609. . [DOI] [Google Scholar]
  36. Glendening E. D.; Weinhold F. Natural resonance theory: II. Natural bond order and valency. J. Comput. Chem. 1998, 19, 610–627. . [DOI] [PubMed] [Google Scholar]
  37. Glendening E. D.; Badenhoop J. K.; Weinhold F. Natural resonance theory: III. Chemical applications. J. Comput. Chem. 1998, 19, 628–646. . [DOI] [Google Scholar]
  38. Schmidt M. W.; Baldridge K. K.; Boatz J. A.; Elbert S. T.; Gordon M. S.; Jensen J. H.; Koseki S.; Matsunaga N.; Su K. A.; Nguyen S. J.; Windus T. L.; Dupuis M.; Montgomery J. A. Jr. General Atomic and Molecular Electronic Structure System. J. Comput. Chem. 1993, 14, 1347–1363. 10.1002/jcc.540141112. [DOI] [Google Scholar]
  39. Gordon M. S.; Schmidt M. W.. Advances in Electronic Structure Theory: GAMESS a Decade Later In Theory and Applications of Computational Chemistry, the First 40 Years; Dykstra C. E.; Frenking G.; Lim K. S.; Scusaria G. E., Eds.; Elsevier: Amsterdam, 2005. [Google Scholar]
  40. Izmaylov A. F.; Scuseria G. E. Why Are Time-Dependent Density Functional Theory Excitations in Solids Wqual to Band Structure Energy Gaps for Semilocal Functionals, and How Does Nonlocal Hartree-Fock Type Exchange Introduce Excitonic effects?. J. Chem. Phys. 2008, 129, 034101 10.1063/1.2953701. [DOI] [PubMed] [Google Scholar]
  41. Foster M. E.; Wong B. M. Nonempirically Tuned Range-Separated DFT Accurately Predicts Both Fundamental and Excitation Gaps in DNA and RNA Nucleobases. J. Chem. Theory Comput. 2012, 8, 2682–2687. 10.1021/ct300420f. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Körzdörfer T.; Sears J. S.; Sutton C.; Brédas J. -L. Long-Range Corrected Hybrid Functionals for π-Conjugated Systems: Dependence of the Range-Separation Parameter on Conjugation Length. J. Chem. Phys. 2011, 135, 204107 10.1063/1.3663856. [DOI] [PubMed] [Google Scholar]
  43. Foresman J. B.; Frisch A. E.. Exploring Chemistry with Electronic Structure Methods: A Guide to Using Gaussian; 3rd ed.;Gaussian, Inc: Pitsburg, PA, 2015. [Google Scholar]
  44. Glendening E. D.; Badenhoop J. K.; Reed A. E.; Carpenter J. E.; Bohmann J. A.; Morales C. M.; Weinhold F.. NBO Version 5.G; Theoretical Chemistry Institute: University of Wisconsin: Madison, WI, 2004. [Google Scholar]
  45. Weinhold F.; Landis C. R.; Glendening E. D. Int. Rev. Phys. Chem. 2016, 35, 399–440. 10.1080/0144235X.2016.1192262. [DOI] [Google Scholar]
  46. Weinhold F.; Landis C. R.. Discovering Chemistry with Natural Bond Orbitals; Wiley-VCH: Hoboken NJ, 2012. [Google Scholar]
  47. Petillo P. A.; Lerner L. E.. The Anomeric Effect and Associated Steroelectronic Effects; Thacher G. R. J.; Thacher G. R. J. Eds.; ACS Symposium Series No. 539; American Chemical Society: Washington, DC, 1993. [Google Scholar]

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES