Neurostatistical approach to toxicological testing in honeybees

Graphical abstract

Abstract

We present method that detects changes in mortality as a consequence of application of a chemical/pharmacological agent. Often is the evaluation of consequential mortality impaired by natural mortality, especially in organisms with high turn of generations, like honeybees. Investigators in the field of olfactory neurophysiology are faced with similar situation in which olfactory receptor neuron is spontaneously active. This activity makes it difficult to evaluate the onset or the offset of the response to a stimulus. The investigators have bridged this issue by developing the detection of response via change of slope in cumulative firing rate of the olfactory receptor neuron. We have adjusted this method to the requirements of toxicological test and used in the analysis lithium toxicity. The method has several steps in which the absolute mortality counts are converted in cumulative sum of dead bees, followed with a normalization of cumulative sum to the last sampling point before the application of the lithium. The changes of the normalized curve from time point to time point are calculated as slope, which is then statistically compared between groups. The method was validated on unrelated dataset, giving an estimation of the duration of agents’ effect.

• • Contain between 1 and 3 bullet points highlighting the customization rather than the steps of the procedure.

  • ○ The method enables to evaluate the toxicological effect of the tested substance by overcoming the issues related to natural mortality and difference between tested biological systems, here specifically demonstrating its utility and effectiveness in evaluating the impact of lithium on honeybee colonies mortality rate.
  • ○ Simple set up of conditions for toxicological testing in honeybee colonies is described.
  • ○ Shorten the window to exclude the history since there is no refractory period is known within normal mortality rate.

Specifications table

Subject area	Pharmacology, Toxicology and Pharmaceutical Science
More specific subject area	Toxicological tests
Method name	Toxicity assesment with change in cumulative mortality
Name and reference of original method	[1]. Statistical method for detection of firing rate changes in spontaneously active neurons. Neurocomputing, 65 – 66: 557 – 563.
Resource availability	If applicable, include links to resources necessary to reproduce the method (e.g. data, software, hardware, reagent)

Method details

Toxicological tests are often impaired by natural mortality due to the turn of generations. In honeybee colonies, deceased worker bees, daily removed from the hive, represent background noise within which it is difficult to identify the impact of toxin or pharmacological agent, especially when its effects are less acute. Furthermore, despite all the attempts in keeping colonies balanced, there is persistent difference in behavior, cycles, food preferences and consequently natural mortality. To overcome these differences and to evaluate the impact of tested substance it is necessary to be able to determine this background noise and to extract the effects caused by the tested substance. This situation is analogous in the olfactory receptor neurons (ORN) which often fire spontaneously thus making it difficult to pinpoint the beginning, the duration or the peak of the response produced by unknown or weak stimuli. To overcome this situation, a simple method was developed, using the change in cumulative firing rate to determine the onset of the excitatory or inhibitory response [1]. Calculating slope within moving window allows taking into the account both excitation and suppression of normal activity, as demonstrated on fish data or insect olfaction [4], with length of the window adjustable to the rate of firing. We have adopted the method for the purpose of evaluating the impact of bioactive substance – in our case lithium [3] – on the honeybee colony. With the proposed method the investigator avoids absolute numbers in natural mortality and thus makes colonies comparable among themselves. In analogy with analysis ORN response to the odorant, periodical sampling is required. In our case, the acquisition frequency was set 1/day, when the dead bees were counted in traps in front of the hives.

The adjusted approach was used in the investigation of lithium toxicity on the honeybee colony. We have established an experimental apiary in which the natural mortality of the worker bees was observed eighteen pre-treatment days (from $d=i$ till day $d=18$). The lithium treatment was delivered for three treatment days ($d=19$ till day $d=21)$. Days following the treatment were termed post-treatment days $(d=22$ till day $d=30$). Our method of detection of increased mortality due to applied bioactive substance has following steps:

• (1)Organization of the apiary: the colonies are placed at the same location to ensure comparable environmental conditions and arranged in interleaved fashion, several parallels p each. Each of the colonies is equipped with box trap under the entrance to the colony to enable to count deceased honeybees each day.
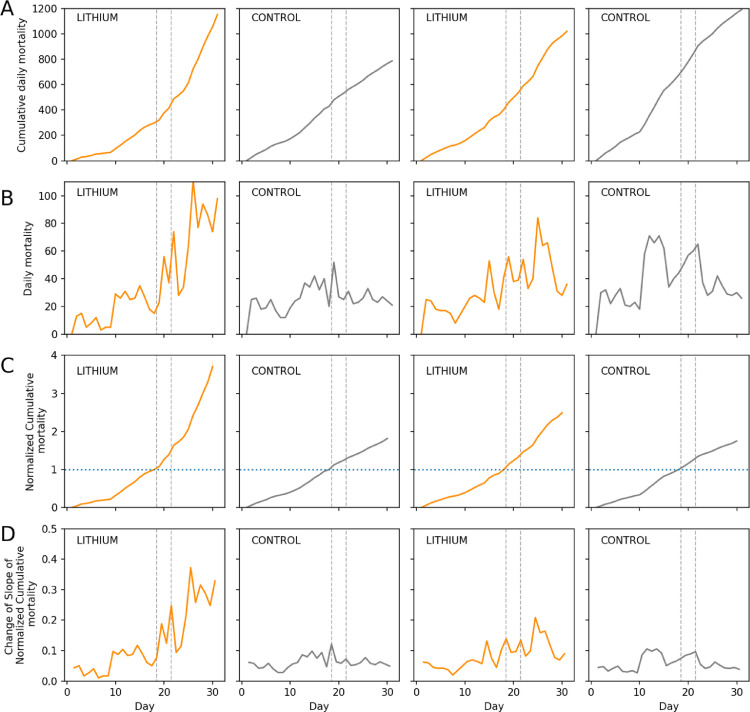
• (2)The dead workers removed by undertakers are counted in regular time units – in our case daily – and removed from the boxes to prevent double counting. Each trap constitutes its own count, using absolute numbers of dead individuals Fig. 1A represents absolute number of counted dead honeybees per time unit.
• (3)
  Daily cumulative sum ($cs{d}_{d=i}$) of counted dead workers m_d for day$d=i$ from day $d=1$ is calculated as shown in Eq. (1). Fig. 1B shows the daily increase of cumulative sum of dead worker bees, hive-by-hive.

  $$cs{d}_{d=i}=\sum _{d=1}^{d=i}{m}_d$$ (1)
• (4)
  The daily cumulative sum calculated for each colony normalized to the last pre-treatment day, in this case $d=18$, thus obtaining normalized daily cumulative sum of dead worker bees ($ncs{d}_{d=i}$, Fig. 1C, Eq. (2)).

  $$ncs{d}_{d=i}=\frac{cs{d}_{d=i}}{cs{d}_{d=lastpretreatmentday}}$$ (2)
• (5)
  The slope of normalized cumulative sum is evaluated between two consecutive time points by dividing the difference between the elevations of two points with the distance between them and thus decreasing the number of observations for one time point (Eq. (3)).

  $$K_{cs{d}_{d=i}}=\frac{cs{d}_{d=i}+cs{d}_{d=i-1}}{2}$$ (3)
• (6)
  The calculated slope changes are averaged over parallels p for each time point (Eq. (4)) and time of maximum slope change read out (Fig. 2).

  $${\overline{K}}_{cs{d}_{d=i}}=\frac{1}{n}\sum _{p=1}^n{K}_{cs{d}_{d=i,p}}$$ (4)
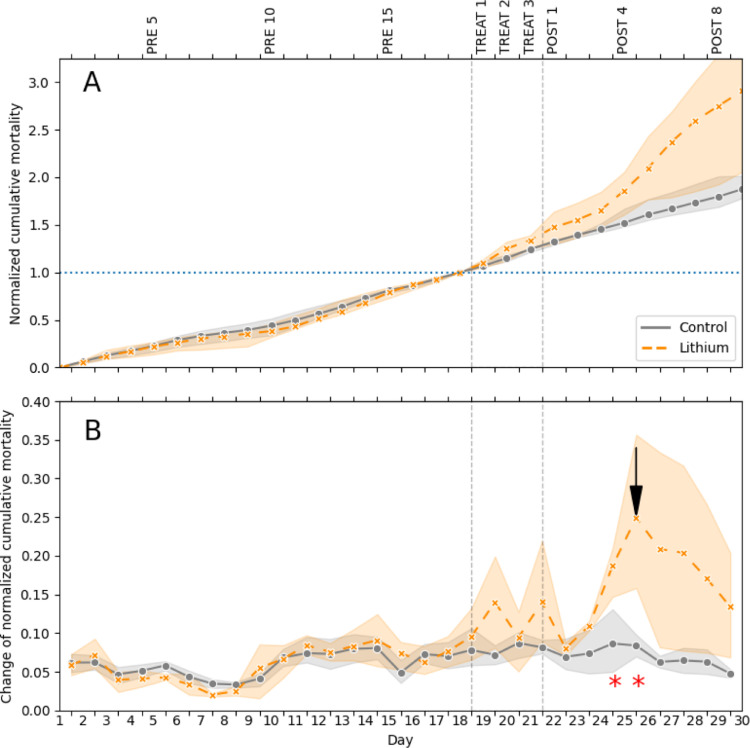
• (7)Duration of the effect is estimated using the statistical comparison between the control and treatment group: a simple independent t-test calculated pointwise from beginning of treatment till the end. The increased mortality in the lithium-treated colonies was observed with the start of the treatment (Fig. 2), but statistically significant difference between the groups in the slope change was detected between post-treatment days 3 and 4 and between post-treatment days 4 and 5.
• (8)In the experiment presented in Fig. 2, the changes were expected on day-to-day basis, matching the working rhythm of the investigator. In situation in which the changes are not expected from time point-to-time point – that is, when the events are “oversampled” - it is possible to calculate slope in broader time window using the ordinary linear least square fit lsfit between the points in selected time window, minimizing the residual sum of squares.

Fig. 1.

(A): The absolute number of counted dead per time unit. (B): Cumulative sum of dead worker bees per time unit (day). Grey dashed lines show treatment period. (C): Cumulative sum of dead worker bees per time unit, normalized to last pre-treatment day (18). Blue dotted line shows time point of normalization. (D): Change of slope in normalized cumulative sum of dead worker bees per time unit, normalized to last pre-treatment day (18). Grey dashed lines show treatment period.

Fig. 2.

(A): averaged normalized cumulative sum of dead bees for control and lithium treatment. (B): Change of normalized cumulative sum of dead bees due to the different treatments. Arrow points maximum efficiency. Grey dashed lines show treatment period. Opaque areas shows standard deviation. Red asterisks mark statistically significant difference between control and test group (p < 0.05, *), thus marking duration of the effect.

Validation

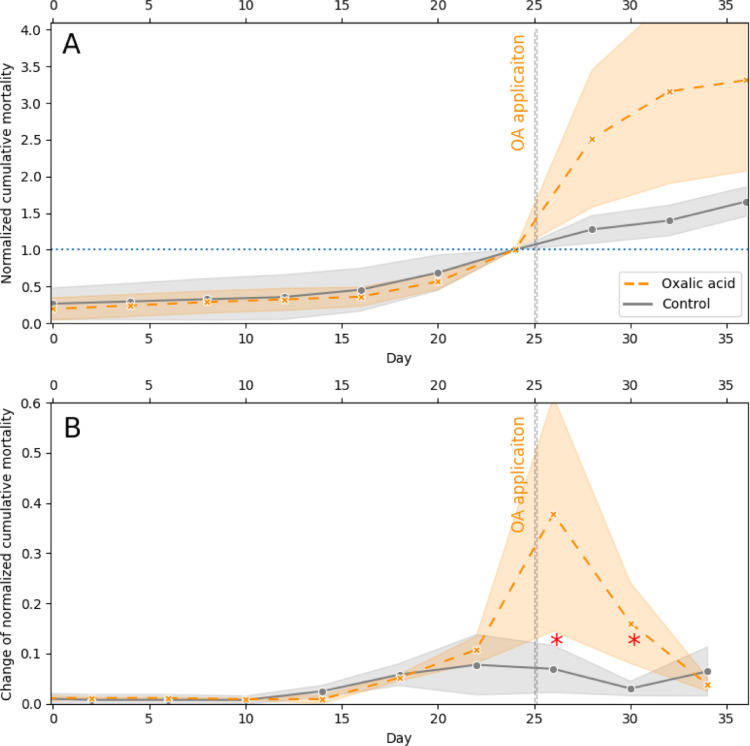
We have performed validation of the method using partial dataset from unrelated experiment, during which the oxalic acid (OA) spraying was applied in the colony on day 25 of the experiment as treatment against ectoparasitic mite Varroa destructor, attached to the adult bees (for review see [2]). The presented data are from two treatment groups, “control” and “oxalic acid”, five colonies each. The varroa mortality was followed by counting dead mites on bottom board of each hive every four days – these counts represent time points - and cumulative sum calculated and normalized to last counting before treatment (day 24, Fig. 3A). During pre-treatment period of 24 days, the shape of the normalized cumulative mortality curve was similar between the groups. The OA application was performed by spraying 4.2% OA solution on both side of combs of each hive on 25th day, treatment lasting ~15 min per hive. In Fig. 3B, the changes in varroa mortality rate – as changes in the normalized cumulative mortality slope - are shown. The calculated mortality rate peaked on 26^th day of observation, with statistically significant difference between treatment and control group, denoted with red asterisk in the Fig. 3B (independent t-test: p = 0.045, t = 2.66). The effect lasted at least for another time point at which the normalized mortality rate of varroas from the treated colonies was still significantly different from the control (independent t-test: p = 0.022, t  = 3.28). Please note that method calculates slope between two counts of dead varroas: the statistically significant change in mortality occurred between 24^th day and 28^th day of the experiment and between 28^th and 32^nd day of experiment. Given the sampling rate (once every four days) we can conclude that oxalic acid effect lasted minimum of four days, though it can be more.

Fig. 3.

Validation of the method on the data collected during the study of oxalic acid treatment of honeybee ectoparasite Varroa destructor. (A): Normalized cumulative mortality, normalized to last observation before treatment (24th day). (B): Change of normalized cumulative mortality. The red asterisks denote time points in which the change of varroa mortality in treated group is significantly different compared to control.

Supplementary material and/or Additional information: [OPTIONAL. We also give you the option to submit both supplementary material and additional information. Supplementary material relates directly to the work that you have submitted and can include extensive excel tables, raw data etc. We would also encourage you to include failed methods or describe adjustments to your methods that did not work. Additional information can include anything else that is not directly related to your method, e.g. more general background information, useful links etc. Introduction is not a section included in the MethodsX format. This information could be moved to the end under Additional Information.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.