Abstract
The growing bacterial resistance to available antibiotics makes it necessary to look for new drug candidates. An example is the lanthionine-containing nisin, which has a broad spectrum of antimicrobial activity. While nisin is widely utilized as a food preservative, its poor solubility and low stability at physiological pH hinder its use as an antibiotic. As the solubility of nisin is controlled by the residues of the hinge region, we have performed molecular dynamics simulations of various mutants and studied their effects on nisin’s solubility. These simulations are complicated by the presence of two uncommon residues (dehydroalanine and dehydrobutyrine) in the peptide. The primary goal of the present study is to derive rules for designing new mutants that will be more soluble at physiological pH and, therefore, may serve as a basis for the future antibiotic design. Another aim of our study is to evaluate whether existing force fields can model the solubility of these amino acids accurately in order to motivate further developments of force fields to account for solubility information.
Introduction
The growing resistance to antibiotics, caused by injudicious use and overutilization in humans and animals, has become a threat to the global health care system and the safety of food supply. New drugs are desperately needed to control the increasing spread of infectious diseases in humans and farm animals. Promising candidates are antimicrobial peptides (AMPs) produced by bacteria that target peptidoglycans in bacterial cell walls as they show little cross-resistance.1,2 Such bacteriocins are, in general, only effective against closely related strains. An exception is nisin, produced by the Gram-positive bacterium Lactococcus lactis, which exhibits a broad-spectrum of antibacterial activity because of its stability at higher temperatures, tolerance to low pH, and dual mode of action. When combined with high temperature and chelating agents, it is effective even against Gram-negative bacteria, making nisin one of the most utilized food preservatives in the world.3
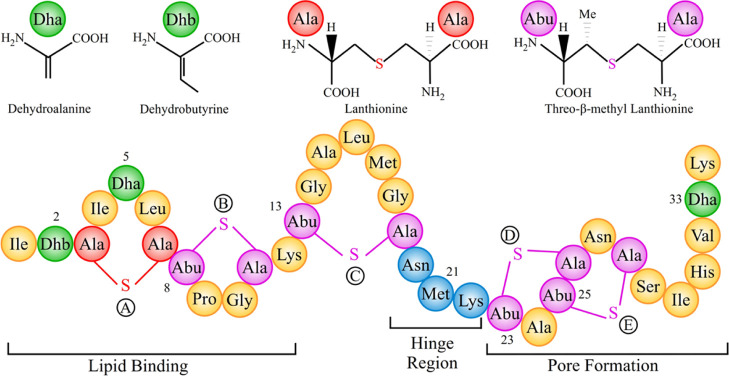
Nisin belongs to the class of lantibiotics, characterized by uncommon residues such as dehydrated and lanthionine residues. The amphipathic 34-residue long peptide carries an overall positive charge, and its sequence of amino acids contains two unusual amino-acids, dehydroalanine (Dha) and dehydrobutyrine (Dhb), and five thio-ether rings (one lanthionine and four threo-β-methyl lanthionine), see Figure 1. The antimicrobial activity of nisin relies on two modes: “lipid II trapping” and “pore formation”. The first mode is due to the N-terminal residues (1–12) binding to the pyrophosphate moiety of lipid II,4 which carries the peptidoglycan unit, thus competing with the biosynthesis of the cell wall. At the same time, the C-terminus of nisin enables the formation of pores in the cell membrane, thus causing cell leakage resulting in cell death.5
Figure 1.
Bottom: primary structure of nisin, highlighting the regions involved in distinct aspects of nisin’s antimicrobial activity. Top: chemical formula of Dha, Dhb, and lanthionine rings.
Despite its antimicrobial activity and nontoxicity, the use of nisin as a food preservative is restricted by its poor solubility and low stability at physiological pH and high temperature.6,7 These factors restrict even more its possible employment as an antibiotic. The solution structure of the nisin–3LII complex (nisin in complex with lipid II) and homology modeling of several related lantibiotics indicates that the main chain interaction between nisin and lipid II dominates. The lesser importance of side chain interactions, therefore, provides an opportunity to design mutants with improved solubility that do not interfere with the lipid II binding of the peptide. For instance, Rollema et al.(8) have reported two mutants, N27K and H31K, that have similar activity as wild-type nisin but higher solubility at physiological pH (pH: 7). In a similar vein, Yuan et al.(9) altered various residues in the hinge region of nisin by site-directed mutagenesis and showed that the hinge region is essential for the conformational flexibility necessary for disrupting the bacterial membranes as well as controls the solubility of the peptide. Two mutants, N20K and M21K, have threefold and fivefold higher solubility than the wild type at a pH of 8; however, the double mutant N20K–M21K has lower solubility. They also reported other mutants such as N20Q and M21G that are considerably more stable than the wild-type at higher temperatures and neutral or alkaline pH. Nevertheless, despite these reports of mutants with improved solubility and higher stability at neutral pH, there exists no procedure for a rational design of mutants bearing all these properties and, specifically, the cause for the unexpected solubility of the reported mutants remains unclear.
A computational investigation of these questions is not only less costly and faster than the mutagenesis experiments but also gives insight into the energetics responsible for the observed solubilities. One problem that hampers the computational investigation of nisin is the presence of dehydroamino acids, and the thio-ether bridges are not parameterized in standard force fields such as CHARMM used in this study. Two sets of CHARMM-compatible parameters have been proposed for the dehydroamino acids and the thio-ether bridges by Turpin et al.(10) and de Miguel et al.;11 however, solubility predictions based on these models were never checked and validated. We note that computational prediction of solubility has many challenges both from force field and simulation perspectives. Solubility depends exponentially on the solvation free energy, which in turn is affected by peptide conformation and the hydration environment of each residue. Hence, not only an extensive sampling of peptide conformations is required, but also an adequate force field is needed for proper modeling of conformation distributions and local hydration environments. The protonation states, which vary as a function of pH, also play an important role. Absolute solubility predictions depend on the free energy of the solid phase; thus, this work only focuses on relative solubilities. Utilizing long trajectories that sample adequately the conformation distributions, we investigate in the present work first the effect of force field on the solubility of nisin, using all-atom molecular dynamics (MD) simulations and solvation free energy calculations that rely on Poisson–Boltzmann and surface area (PBSA) continuum solvation and generalized Born and surface area (GBSA) continuum solvation methods. In a second step, we propose three new mutants of nisin with improved solubility [N20K+–M21K+ (KK-PP), N20R–K22R, and N20R] and introduce rules for predicting the solubility of nisin mutants as needed for future antibiotic design.
Results and Discussion
Effect of Force Field on Structural Properties and Solubility of Nisin
The activity of AMPs is determined by their secondary structure, charge, hydrophobicity, and solubility. While most have random disordered configurations in an aqueous environment, they fold into an α-helix or β-sheet when interacting with membranes. Given the importance of secondary structure and solubility for the functions of AMPs, it is important for the computational studies to employ force fields that do not introduce a bias into either structural properties or solubility of the peptides. This is especially a concern for nisin as it has dehydroamino acids and thio-ether bridges, which are not parameterized in standard implementations of most force fields such as CHARMM36 used by us. Hence, we have to rely on modifications such as the ones proposed by Turpin et al.(10) and de Miguel et al.(11) For this reason, we first evaluate the suitability and limitations of these two parameterizations by probing their effect on structural properties and solubility of nisin.
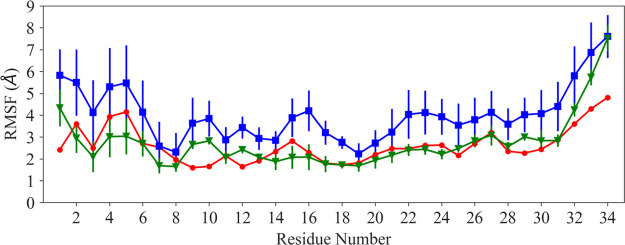
The NMR model of nisin (with 20 downloaded solution structures in the PDB under identifier 1WCO) has a stable N-terminus and a flexible C-terminal tail.4 The N-terminus was stabilized into the cage-like structure by binding to the lipid II model. As lipid II was deleted in our simulation, we anticipate nisin to exhibit little canonical secondary structure. This can be seen in Figure 2, where we compare the root-mean-square fluctuations (RMSFs) of each residue using both the parameter sets. Although both parameter sets lead to similar trends, the fluctuations of the residues are larger in the simulations relying on the parameters of de Miguel et al. than in the ones that used the set proposed by Turpin et al. Similarly, Figure S1 shows that the distribution of the phi–psi (ϕ/ψ) backbone dihedral angles is broader when using the de Miguel et al. parameters for the dehydroamino acids, while when using the Turpin et al. parameters, the distribution of dihedral angles is more narrow, indicating sampling of a more restricted set of backbone conformations. This is consistent with the observation that the structural ensembles obtained using Turpin et al. parameters resemble more closely the ensemble of NMR structures than the ensembles obtained from simulations relying on the parameters of de Miguel et al. This is not surprising considering that the de Miguel parameters had not been validated specifically for nisin simulations, but it does not necessarily indicate the de Miguel parameters to be of lower accuracy as increased flexibility is anticipated upon removal of the lipid II. While the NMR results suggest a stable small 310 helix conformation at the N-terminus that might be essential for binding of nisin to lipid II, we did not observe such a 310 helix in our simulations with either parameter set. Instead, we find at the N-terminus for both parameters set only flexible turns and random coil conformations. This result is consistent with circular dichroism measurements, which indicate that nisin typically assumes a random coil configuration in aqueous environment.12 This suggests that nisin adopts a 310 helix only when bound to lipid II or that this secondary structure results from the combined effect of lipid II binding and the use of dimethyl sulfoxide during structure determination. Hence, we believe that the absence of the 310 helix in our simulation does not point to shortcomings of the two parameter sets.
Figure 2.
RMSF of Cα-atoms of nisin, comparing experimental values (drawn in red) with such derived from simulations relying on the parameter sets of de Miguel et al.(11) (blue) and Turpin et al.(10) (green).
Comparing solubility measurements with the calculated solvation free energy of nisin and its mutants allows one to probe the performance of these force fields in reproducing experimental trends. As described in the Materials and Methods section, we estimate the solvation free energies by PBSA and GBSA approximations. Using Welch’s t-test for comparing the numerical results obtained from simulations with the two parameter sets, we find significant differences (p-value < 0.001) between the two parameter sets for the solvation free energies (ΔGsol) of the wild-type and mutants. The only exceptions are the KK-PP mutant (where the GBSA values agree) and the N20R mutant (where both GBSA and PBSA values agree), see also Tables 1 and S1. Note also that although the differences between the two parameter sets are small in the averages, there are substantial differences in the standard deviations, which, with only a few exceptions, are always larger with de Miguel et al. parameters. Table 1 also shows that solvation free energy estimates obtained by GBSA and PBSA agree with each other, once one accounts for the choice of the solute dielectric constant. With an εin of 4 in PBSA, ΔGsol values (and the corresponding standard deviations) computed with PBSA are four times smaller than the corresponding values obtained using GBSA. While the GBSA and PBSA in general lead to similar results, the case of the KK-PP mutant, where the GBSA values, but not the PBSA values, agree for both force fields, may point to the possibility that GBSA overestimates the polar component of the solvation energy, a problem that can be easily addressed in PBSA by using a more realistic internal dielectric constant (εin). Hence, despite GBSA being the less costly approach, we focus in the following analysis on our PBSA data.
Table 1. Calculated p-values of a Statistical Test (Welch’s t-test) for Solvation Free Energy (GBSA and PBSA) of Nisin and Its Mutant Forms Using Parameters of de Miguel et al.(11) and Turpin et al.(10).
| ΔGsol (GBSA) |
ΔGsol (PBSA) (εin = 4) |
||||||
|---|---|---|---|---|---|---|---|
| se. no. | de Miguel parameter set | Turpin parameter set | significantly different? (p-value) | de Miguel parameter set | Turpin parameter set | significantly different? (p-value) | |
| 1. | Wt | –594.3 ± 31.5 | –584.0 ± 26.8 | yes (<0.001) | –136.0 ± 7.4 | –134.1 ± 6.1 | yes (<0.001) |
| 2. | N20K | –732.2 ± 34.4 | –743.6 ± 29.7 | yes (<0.001) | –170.0 ± 8.5 | –171.8 ± 7.0 | yes (<0.001) |
| 3. | M21K | –752.3 ± 36.8 | –739.9 ± 34.6 | yes (<0.001) | –173.9 ± 8.7 | –171.6 ± 8.0 | yes (<0.001) |
| 4. | KK-NP | –592.9 ± 36.6 | –610.0 ± 25.7 | yes (<0.001) | –136.0 ± 8.3 | –139.4 ± 6.4 | yes (<0.001) |
| 5. | KK-PP | –917.1 ± 29.3 | –914.2 ± 31.9 | no (0.101) | –214.5 ± 7.0 | –212.9 ± 7.2 | yes (<0.001) |
| 6. | N20Q | –595.6 ± 31.3 | –603.0 ± 24.4 | yes (<0.001) | –136.5 ± 7.2 | –137.9 ± 5.7 | yes (<0.001) |
| 7. | N20R | –731.4 ± 36.3 | –729.8 ± 31.1 | no (0.412) | –168.4 ± 8.6 | –168.7 ± 7.1 | no (0.51) |
| 8. | K22R | –581.6 ± 29.2 | –589.9 ± 26.6 | yes (<0.001) | –131.6 ± 6.8 | –134.0 ± 6.0 | yes (<0.001) |
| 9. | RR | –731.3 ± 33.7 | –710.1 ± 36.7 | yes (<0.001) | –168.0 ± 7.9 | –164.2 ± 8.3 | yes (<0.001) |
| 10. | K22H | –470.0 ± 31.7 | –490.7 ± 28.3 | yes (<0.001) | –105.9 ± 7.2 | –111.3 ± 6.5 | yes (<0.001) |
| 11. | K22E | –486.9 ± 36.9 | –495.7 ± 32.6 | yes (<0.001) | –108.8 ± 8.6 | –111.4 ± 7.9 | yes (<0.001) |
| 12. | K22G | –454.6 ± 34.4 | –484.5 ± 23.5 | yes (<0.001) | –102.3 ± 7.8 | –108.8 ± 5.5 | yes (<0.001) |
| 13. | FLQ | –481.4 ± 23.4 | –476.2 ± 22.4 | yes (<0.001) | –108.2 ± 5.4 | –106.6 ± 5.1 | yes (<0.001) |
In order to understand why simulations with the two parameter sets lead to the above observed differences, we compare the polar component of solvation free energy (ΔGsol,pol). Again, we find only small differences in the mean values of ΔGsol,pol but much larger ones in the standard deviations (Tables 2 and S2). Similar behavior is seen for the nonpolar component of solvation free energy (Tables 2 and S2) and, in general, arises the disparity in the ΔGsol values from the additive effect of the smaller differences in the two components of ΔGsol. Only in a few cases, the differences arise from either the polar component (K22H, N20E, K22E, etc.) or the nonpolar component (N20F) of solvation free energy.
Table 2. Calculated Components of Solvation Free Energy (ΔGsol) for Nisin and Mutants Using Parameters of de Miguel et al.(11) and Turpin et al.(10) Using PBSA.
| de Miguel
parameter set |
Turpin parameter set |
||||||
|---|---|---|---|---|---|---|---|
| se. no. | ΔGsol,pol | ΔGsol,np | ΔGsol | ΔGsol,pol | ΔGsol,np | ΔGsol | |
| 1. | Wt | –152.9 ± 7.5 | 16.8 ± 1.5 | –136.0 ± 7.4 | –150.6 ± 6.6 | 16.5 ± 1.1 | –134.1 ± 6.1 |
| 2. | N20K | –186.0 ± 8.0 | 15.9 ± 1.5 | –170.0 ± 8.5 | –189.5 ± 7.1 | 17.7 ± 1.4 | –171.8 ± 7.0 |
| 3. | M21K | –191.3 ± 8.9 | 17.4 ± 1.0 | –173.9 ± 8.7 | –189.1 ± 8.3 | 17.4 ± 1.5 | –171.6 ± 8.0 |
| 4. | KK-NP | –152.8 ± 9.0 | 16.8 ± 1.4 | –136.0 ± 8.3 | –157.6 ± 6.0 | 18.2 ± 1.3 | –139.4 ± 6.4 |
| 5. | KK-PP | –231.6 ± 6.9 | 17.1 ± 1.5 | –214.5 ± 7.0 | –230.9 ± 7.6 | 18.0 ± 1.0 | –212.9 ± 7.2 |
| 6. | N20Q | –153.1 ± 7.4 | 16.6 ± 0.8 | –136.5 ± 7.2 | –154.6 ± 5.8 | 16.7 ± 0.7 | –137.9 ± 5.7 |
| 7. | N20R | –185.7 ± 8.2 | 17.3 ± 1.1 | –168.4 ± 8.6 | –186.2 ± 7.5 | 17.5 ± 1.0 | –168.7 ± 7.1 |
| 8. | K22R | –149.7 ± 7.2 | 18.1 ± 1.2 | –131.6 ± 6.8 | –151.5 ± 6.4 | 17.6 ± 1.1 | –134.0 ± 6.0 |
| 9. | RR | –186.3 ± 7.9 | 18.2 ± 1.4 | –168.0 ± 7.9 | –181.0 ± 8.7 | 16.8 ± 1.2 | –164.2 ± 8.3 |
| 10. | K22H | –122.8 ± 7.7 | 17.0 ± 1.2 | –105.9 ± 7.2 | –128.3 ± 6.9 | 17.0 ± 0.8 | –111.3 ± 6.5 |
| 11. | K22E | –125.8 ± 9.5 | 17.0 ± 1.4 | –108.8 ± 8.6 | –128.0 ± 7.9 | 16.6 ± 1.0 | –111.4 ± 7.9 |
| 12. | K22G | –118.1 ± 9.1 | 15.8 ± 1.9 | –102.3 ± 7.8 | –126.3 ± 6.0 | 17.4 ± 1.4 | –108.8 ± 5.5 |
| 13. | FLQ | –125.2 ± 5.9 | 17.0 ± 1.7 | –108.2 ± 5.4 | –124.1 ± 5.3 | 17.6 ± 0.9 | –106.6 ± 5.1 |
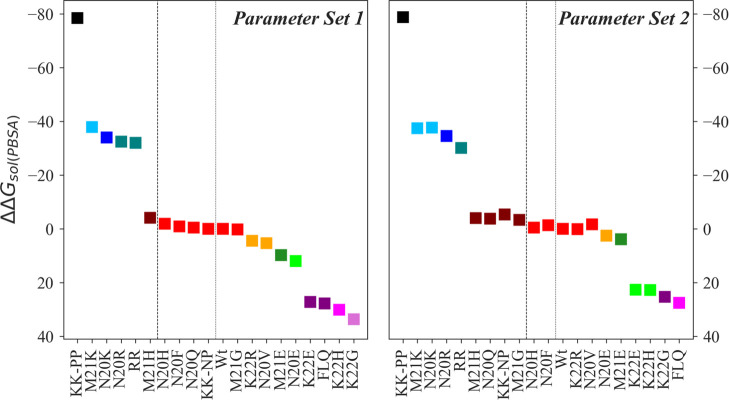
As the significant differences in the calculated solubilities arise from a complex interplay between electrostatic and nonelectrostatic interactions between peptide and solvent, it is not possible to decide a priori which of the two parameter sets is more appropriate. Experimentally, M21K and N20K have been shown to be fivefold and threefold more soluble than the wild-type, respectively. Hence, we have used Tukey’s test to compare the relative order of solvation free energies (as calculated from simulations with the two parameter sets) with the experimental results. While with both parameters set, the mutants led to different solvation free energies than for the wild type, the Turpin et al. parameters could not differentiate between the two mutant forms. Only the de Miguel et al. parameters correctly predicted the order of the solubility of the two mutants (Figures 3 and S2). At the same time, the double mutant N20K–M21K (deprotonated form) is experimentally known to be less soluble than the wild type, but the Miguel et al. parameters could not distinguish mutant and wild type, and the Turpin et al. parameters even predicted higher solubility for the mutant. On the other hand, the solubility of the M21G and N20Q mutants could only be differentiated using Turpin et al. parameters, while in case of the K22H mutant (slightly lower soluble than wild type), both parameter sets appear to be equally reliable in predicting the order of solvation free energy (Figures 3 and S2).
Figure 3.
Effect of mutation on the solubility of nisin estimated using PBSA. The figure shows the difference between the solvation free energies of mutant and wild-type nisin (ΔΔGsol = ΔGmutant – ΔGWt). Nisin and mutants are ranked in decreasing order of solubility. A different color is used for each rank, and a matching color is assigned to the mutants with the same rank. Statistical significance is determined by using multiple comparison Tukey’s test at α = 0.05. The left figure shows data derived in simulations relying on the parameter set of de Miguel et al.(11) (parameter set 1, left sub-figure), and the right one such derived from simulations using Turpin et al.(10) parameters (parameter set 2, right subfigure).
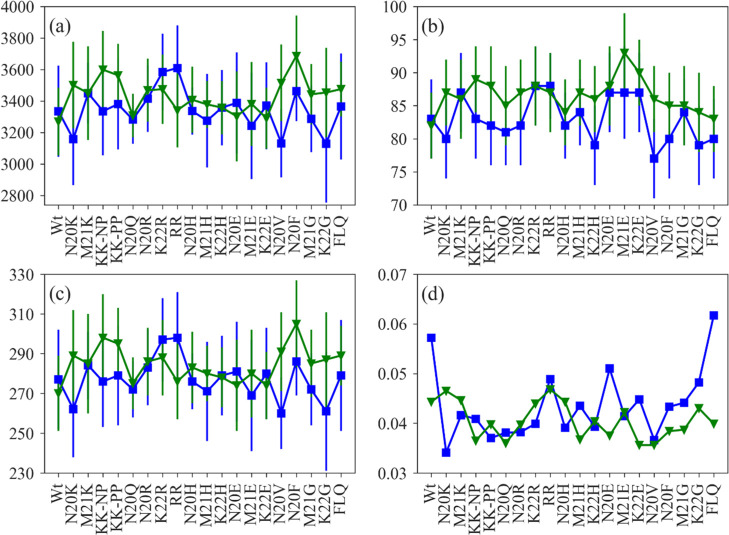
Hence, while the two force fields allow one in most cases to predict qualitatively the relative solubility of mutants, they do differ significantly in the predicted solvation free energies, and the Turpin et al. parameters seem to favor more extended configurations than the de Miguel et al. parameters. We believe that the discrepancies in the calculated solvation free energy are a synergetic effect of the collapse of the polypeptide chain and dissimilarities in the first solvation shell resulting likely from the different partial atomic charges in the two parameter sets for the amide group and the carbonyl group of the dehydroamino acids (also the Cα atom). We have analyzed the collapse of the polypeptide chain and the behavior of water molecules by measuring the solvent-accessible surface area (SASA), number of peptide-water hydrogen bonds, number of water molecules in the first solvation shell (defined by a cut-off distance of 3.5 Å from the peptide surface), and the mean deviation of the water number fluctuation function (Nw(t)), shown in Figure 4. The Nw(t) is defined as
where nw(t) represents the number of water molecules in the first hydration shell at time “t” and nw is the average number of hydration water.
Figure 4.
Collapse of the polypeptide chain and behavior of water molecules in the first hydration shell of nisin and mutants as a function of SASA (a), peptide-water hydrogen bond (b), number of water molecules in the first solvation shell (c) and mean deviation of water number fluctuation function (d). Color scheme: data relying on the parameter set of de Miguel et al.(11) are drawn in blue and such relying on the parameter set of Turpin et al.(10) are drawn in green.
Figure 4a shows that with the exception of K22R, RR, and N20E, the SASA is larger for both wild type and mutants when using Turpin et al. parameters. The measured numbers of peptide-water hydrogen bonds in Figure 4b also indicate that for this parameter set, nisin remains in an extended conformation. With the exception of K22R, RR, and again N20E, the number of water molecules in the first hydration shell is higher when using the parameters of Turpin et al. (Figure 4c), although the mean deviation of the water number fluctuation function is lower (Figure 4d). If nisin, when using Turpin et al. parameters, mostly remains in an extended conformation, it is expected to have more water molecules in the first solvation shell. As in the Turpin et al. parameter set, the partial charges for the amide group of both dehydroamino acids take values of −0.67 (N) and 0.36 (H) and have a larger magnitude than in the de Miguel et al. parameter set [−0.47 (N), 0.31 (H)], it is expected that the nisin variants form stronger hydrogen bonds to the hydrating water molecules. These results also corroborate the mean deviation of water number fluctuation function, which is always low using Turpin et al. parameters (Figure 4d).
We conclude that the differences in both components of the solvation free energy likely arise from the differing behavior of the water molecules in the hydration layer of the peptide. As the hydration layers of the peptide using Turpin et al. parameter sets are more ordered and also the peptide-water association is stronger, it restricts the motion of the polypeptide chain, and therefore, we see less structural fluctuations using Turpin et al. parameters than de Miguel et al. parameters. However, while the two parameter sets sample different structural ensembles, they reproduce with a few exceptions qualitatively the experimentally measured solubility differences between wild-type and mutants, with no clear trend of which of the two sets is more accurate.
We note that as for the amino group, the partial charges for the carbonyl group also differ in both parameters sets [de Miguel et al.: 0.51 (C) and −0.51 (O); Turpin et al.: 0.635 (C) and −0.635 (O)]. Varying these parameters and comparing calculated solvation free energies with the measured solubilities of the mutants may allow to optimize the parameter sets. However, our present investigation shows that the current two parameter sets agree with few exceptions in most cases with experimental solubility ranking. Further development of parameters either for the whole lantibiotics peptide or for the Dha and Dhb residues would be of significant value.13−16 While such a re-parameterization of the dehydroamino amino acids is beyond the scope of this paper, our evaluation and comparison of the two parameter sets allows us already to list the issues that need to be addressed:
-
1.
During force field parameterization, all isomeric forms need to be considered. For the parameterization of Dhb, de Miguel et al. considered only the Z-isomer, while Turpin et al. considered the E-isomer. Both forms are synthetized from the same precursor, threonine,17−19 and while in general the Z-isomer is more stable than the E isomer,20 the latter is observed in several cases, alone or together with the Z-isomer.21
-
2.
Both parameter sets do not use CMAP corrections. As the torsion parameters strongly influence the molecular structures, it is necessary to provide the correct degree of rigidity as well as the flexibility to ensure and reproduce the significant conformational changes due to rotations about bonds. Hence, the torsion parameters used in these two parameter sets need to be refined.
-
3.
There seems to be a disparity between the partial charges of the amide group and the carbonyl group of the dehydroamino acids (also the Cα atom) in both parameter sets, which affects the anchoring of the water molecules and therefore needs to be optimized.
Effect of Mutations on the Solubility of Nisin
While our above analysis has demonstrated significant shortcomings in the two parameter sets used to simulate nisin, it has shown at the same time that simulations with these sets allow one to reproduce qualitatively the experimentally observed differences in solubility between wild type and a few previously studied mutants. Hence, we conjecture that such simulations may already be sufficient to design new mutants that will be more soluble at physiological pH and, therefore, can serve as a basis for the future antibiotic design. Taking wild-type nisin as our reference point, we want to understand the effect of various sidechain replacements on the solubility limit of the peptide in solution and use this knowledge to design new mutants with improved solubility. We estimate solubility again by the solvation free energy as approximated with the PBSA approach. We use both parameter sets (de Miguel and Turpin) in our analysis; however, the presented solvation free energy differences ΔΔGsol, between wild type and mutant, rely on the parameter set by Turpin et al., as only this parameter set allowed to differentiate the N20Q and M21G mutants from the wild type. Furthermore, where the Turpin et al. parameter led to discrepancies with experimental solubility measurements, the computational results did not improve when using data from the simulations that relied on the de Miguel et al. parameters. We remark, however, that the ΔΔGsol values are usually larger for positively charged mutations using Turpin et al. parameters, while the reverse is the case with the negatively charged mutations and mutation to histidine, that is, ΔΔGsol values are higher when using de Miguel et al. parameters, and there is no clear trend in case of replacements to hydrophobic residues. The distribution of the solvation free energy for wild-type nisin and mutants using parameters of Turpin et al. is shown in Figure S3a,b.
Effect of Mutations to Positively Charged Residues
Introduction of a positively charged lysine at the positions 20, 21, and 20–21 results in a significant increase in the solubility of nisin (by a factor of 1.25–1.5 over the solubility of the wild-type, Figure 3). Especially the mutation to protonated lysine at position 20–21 (KK-PP) leads to a 1.5-fold increase in solubility (ΔΔGsol = −78.8 kcal/mol), while replacement by the deprotonated lysine (KK-NP) resulted in little change (ΔΔGsol = −5.3 kcal/mol, Figure 3). These results are consistent with earlier work in refs (8) and (9). Replacements with positively charged arginine at positions 20 and 20–22 only moderately increased the solubility (∼1.23 times, ΔΔGsol N20R = −34.6 kcal/mol and ΔΔGsol RR = −30.1 kcal/mol), and at position 22 they did not enhance the solubility of nisin (ΔΔGsol = 0.1 kcal/mol). Less effective are mutations to histidine (ΔΔGsol ∼ −4.0–22.8 kcal/mol, Figure 3), and the K22H mutant even decreases the solubility below that of the wild-type (ΔΔGsol = 22.8 kcal/mol, Figure 3). Hence, mutations to a positively charged residue in the hinge region maximize the solubility of nisin, with lysine and arginine mutations to be the most effective ones. Of special importance here is our observation of the role of arginine mutations. As the pKa of titratable arginine group is high (∼12.1), the mutants bearing arginine in the hinge region are less likely to be affected by the change in pH. We report three mutants (N20K+–M21K+, N20R–K22R, and N20R) with improved solubility compared to wild-type nisin.
Effect of Mutations to Negatively Charged Residues
A mutation to glutamic acid in the hinge region has been investigated experimentally, showing a significant decrease or even loss in the production of nisin.9 It has been speculated that this loss is associated with an increase in steric hindrance in the hinge region. The assumption is that side chain replacement to negatively charged amino acids will interfere with the thioether bridge formation (ring D), but further investigation is needed to determine the stages of biosynthesis that are blocked by such mutations. Nevertheless, even if such mutants with negatively charged side chains in the hinge region could be synthesized, a mutation to glutamic acid in the hinge region will likely not expand the solubility limit of nisin (K22E (ΔΔGsol = 22.7 kcal/mol) < M21E (ΔΔGsol = 3.9 kcal/mol) < N20E (ΔΔGsol = 2.5 kcal/mol) < Wt), presumably because of the decrease in the net charge of the peptide. In particular, the solvation free energy difference shown in Figure 3 indicates that a mutation to glutamic acid at position 22 will decrease the solubility of nisin by about 20%. Further, mutation to a negatively charged residue may also prevent the association of nisin and phospholipid bilayer as bacterial membranes carry a net negative surface charge, thereby decreasing the affinity of nisin. Hence, it appears that a positively charged residue such as arginine at position 22 is a better approach for expanding the solubility spectrum of nisin.
Effect of Mutations to Uncharged Polar and Hydrophobic Residues
While a mutation to an uncharged polar residue (N20Q) yields a slightly more soluble form of the peptide (ΔΔGsol = −3.8 kcal/mol), mutations to a hydrophobic residue have little or no effect on nisin solubility (ΔΔGsol ranges from −3.4 to −1.4 kcal/mol, Figure 3). An exception is a K22G mutant, which diminishes the solubility of nisin (ΔΔGsol = 25.3 kcal/mol). A triple mutation (FLQ) designed to retain polarity at position 22, while increasing the hydrophobicity at two other positions, also only decreases the solubility of the peptide (ΔΔGsol = 27.5 kcal/mol).
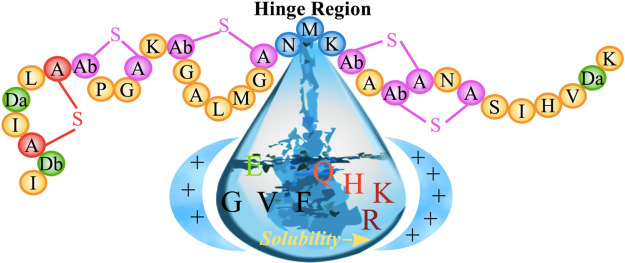
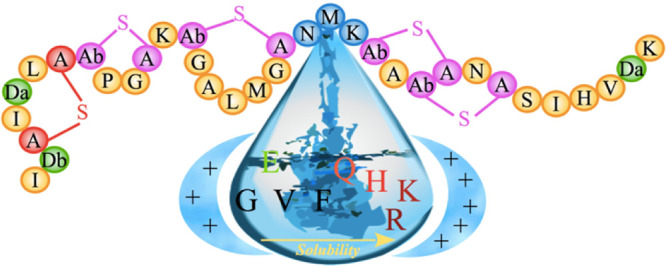
Hence, the hinge region (Asn-Met-Lys) in nisin controls not only the conformational flexibility needed for the antimicrobial activity but also modulates the solubility of the peptide as summarized in the sketch of Figure 5. Especially effective are mutants introducing a positively charged residue into the hinge region. While introducing either a lysine or an arginine in the hinge region will increase the solubility, we believe that mutation to arginine will, in addition, increase nisin–membrane interaction, enhancing the antimicrobial activity of nisin. This is because the guanidium group of arginine binds more strongly to the phosphate groups of lipids than the amino group of lysine,22 and while bound to the lipid, the polarity on the guanidium group is reduced, thereby increasing the capability to internalize membrane.23,24
Figure 5.
Schematic of effect of mutations in the hinge region on the solubility of nisin.
Conclusions
Although nisin possesses excellent antimicrobial activity, its poor solubility and stability at physiological pH and temperature limit its use as a food preservative and even more as an antibiotic.6,7 Several efforts have been made in the past decades to achieve a more soluble and antimicrobial active form of the peptide. While such a mutant would increase the range of conditions where nisin can be used as a food preservative, it would also open the door for possible uses of nisin as an antibiotic, as previous efforts have remained unsatisfactory. In this work, we use all-atom molecular dynamics simulations to understand the underlying mechanism for designing new mutants with improved solubility.
One of the challenges was the lack of standard CHARMM force field parameters for the two dehydroamino acids (Dha and Dhb) and the thio-ether rings. Two sets of CHARMM-compatible parameters have been proposed earlier that differ in the choice of the isomeric form of Dhb, partial charges, and dihedral parameters. As in neither of the two studies were solubility calculations reported, we have first evaluated the relative merits of the two parameter sets for reproducing experimental solubility measurements for nisin. Estimating solubility by solvation free energies as approximated with the computationally cheaper PBSA continuum solvation, we find that not only do absolute values differ between the two parameter sets, but also, in general, the corresponding standard deviations are larger when using de Miguel et al. parameters. The choice of parameter set affects both components of the solvation free energy. We conjecture that the differences in the solvation free energy likely arise because the hydration layer of the peptide is more ordered and with a stronger peptide–water association when using the Turpin et al. parameter set. While both parameter sets reproduce qualitatively the experimentally measured solubility differences between wild-type and mutants, our results do not allow us to select one parameter set over the other as being more accurate. Instead, they demonstrate the need for further improvements of the two parameter sets and pinpoint some of the shortcomings. Especially, we show the need to consider correct isomeric forms of Dhb, dihedral parameters, and partial atomic charges for optimization of the force field parameters.
As the existing parameter sets allow already for a qualitative assessment of solvation free energies, we used both sets in tandem to evaluate the change of solvation free energy and ranking of mutants. We observe that mutations to a positively charged amino acid typically increases the solubility of the peptide, while the reverse is the case with the mutation to a negatively charged amino acid. Mutation to hydrophobic amino acids does not change systematically the solvation free energy, and mutations such as K22H, K22E, K22G, and N20F–M21L–K22Q that decrease the net charge also decrease the solubility. The effect of the various mutations is summarized in the sketch of Figure 5. Of special interest for possible applications are the new mutants N20R–K22R and N20R, as the high pKa (∼12.1) ensures that arginine remains protonated under acidic, physiological, and alkaline pH without sacrificing the binding affinity of nisin toward the membrane. Hence, these mutants promise to extend the solubility of nisin over a broad range of pH values and therefore broaden its use as a food preservative or potential antibiotic.
In conclusion, our study demonstrates that minor differences in force field parameters of even a few amino acids (Dha and Dhb, in case of nisin) can change dramatically the solubility of a peptide. This points to the need for a careful calibration of the force field parameters of the two dehydroamino acids not found in the standard CHARMM parameter set but common in AMPs. Nevertheless, existing parameters allow already a qualitative assessment of solvation free energy differences, allowing us to propose new mutants, such as N20R–K22R and N20R, with potential applications as food preservative or antibiotics. In that, our study provides a basis for future antibiotic design.
Materials and Methods
Design of Mutants and Simulation Set
To understand the factors that alter the solubility of nisin and to study the extent by which the force field parameterization of the uncommon dehydroamino acids determines structural properties and solubility of nisin, we have carried out multiple MD simulations of both wild-type and suitable mutants. The mutations that we have studied are located in the hinge region of the peptide (residues 20–22) and are listed in Table 3. Note that lysine, arginine, and histidine in the mutants are protonated (i.e., positively charged), while glutamic acid is deprotonated (i.e., negatively charged). For clarity, the protonation states of Lysines are marked explicitly.
Table 3. List of Mutants of Nisin Considered in This Study.
| mutants | |
|---|---|
| positively charged | N20K+ (denoted as N20K), M21K+ (denoted as M21K), N20K–M21K (denoted as KK-NP), N20K+–M21K+ (denoted as KK-PP), N20R, K22R, N20R–K22R, N20H, M21H, K22H |
| negatively charged | N20E, M21E, and K22E |
| uncharged polar | N20Q |
| hydrophobic | N20V, N20F, M21G, K22G |
| other | N20F–M21L–K22Q (denoted as FLQ) |
The initial coordinates of wild-type nisin required for the molecular dynamics simulations were obtained from the nisin–lipid II complex as resolved by NMR and are deposited in the Protein Data Bank (PDB) (PDB ID: 1WCO).4 The three models with the lowest energy were selected from the deposited 20 solution NMR structures. After deletion of the model lipid II, mutants were derived for each of the three nisin models by altering the corresponding residue. In this way, we minimize the possibility that our results depend on the specifics of the selected NMR model and take into account the inherent flexibility of the peptide. Containing five thio-ether bridged rings and two uncommon amino acids, Dha and Dhb, nisin does not attain regular secondary structural elements such as α-helices and β-sheets. Computationally, this adds the difficulty that carefully designed parameters for the uncommon amino acids have to be added to the existing protein force fields in order to ensure reliable simulations. In the case of the CHARMM force field, two sets of parameters have been proposed for these unusual amino acids (Dha and Dhb) and the thio-ether bridges, one by Turpin et al.(10) and one by de Miguel et al.(11)
The Turpin parameters were fitted for the E-isomer of Dhb by using scaled Hartree–Fock for partial charges and MP2/6-31G*//MP2/cc-pVTZ for torsional and other intramolecular parameters and validated on hydrated nisin to reproduce adequately experimental NMR data and hydrogen bonds information for nisin. The de Miguel parameters were fitted using the Z-isomer commonly observed in AMPs, following the same procedure as done by Turpin to be compatible with the remaining CHARMM parameters. The de Miguel parameters were validated by simulating lantibiotics, such as Lchα and Lchβ, but they were not tested specifically for nisin. Especially, the suitability of the parameters for estimating solubility was not tested during the development of either of the parameter sets. In order to compare the suitability of the two sets, we, therefore, carried out two sets of MD simulations, both using the CHARMM3625 force field for standard amino acids but differing in the parameters for dehydroamino acids and the thio-ether bridges.
We use for our MD simulations the software package GROMACS-2018.1.26,27 Each peptide was put into the center of a cubic box with a minimum peptide-box distance of 15 Å; then the box was subsequently filled with TIP3P water28 and 0.15 M NaCl, including neutralizing counter-ions. Because of periodic boundary conditions, electrostatic interactions are evaluated by particle-Ewald summation,29,30 and a cut-off of 12 Å was used to calculate vdW-interactions. The resulting systems were energy-minimized by steepest descent, followed by equilibration of 500 ps at constant volume and subsequent 500 ps at constant pressure. Temperature and pressure were regulated by a Parrinello–Danadio–Bussi thermostat31 and Parrinello–Rahman barostat32 and set to 300 K and 1 bar, respectively. The integration step was 2 fs. Production runs were performed for 200 ns, and the coordinates were saved every 1 ps for subsequent analysis. For each system, three independent simulations were carried out starting from different velocity distributions. This resulted in a 600 ns data for each peptide, 12 μs for each of the two force fields for dehydroamino acids and therefore, a total of 24 μs data.
Solvation Free Energy Estimation
The solubility of the nisin and mutants is described by the solvation free energy of the peptides. Two popular and computationally efficient continuum solvation models, PBSA and GBSA calculations,33,34 were employed by us for estimating the solvation free energy of the peptides. Both methods work by taking snapshots from an MD trajectory and replacing the explicit water by a dielectric continuum. In PBSA, the polar part of the solvation energy, that is, the electrostatic component is evaluated by solving the Poisson equation (if there is no salt) or Poisson–Boltzmann equation (if salt is present in the system). Here, the Poisson equation models the variation of the electrostatic potential in a medium with a uniform dielectric constant ε, and the Boltzmann distribution governs the ion distribution in the system. GBSA differs from PBSA in that the electrostatic contribution is estimated using the generalized Born approximation. In both methods, the nonpolar component of the solvation free energy is approximated by a surface-area based approach. For details of the two methods, see, for instance, ref (35). Both approaches are implemented in the MMPBSA.py36 script as available in AmberTools18.37 We used this script for our analysis, extracting evenly spaced snapshots from the last 50 ns of the production runs. A salt concentration of 0.15 M is used in all calculations, and the solute dielectric constant, εin, is set to 4 in PBSA calculations.
Statistical Tests
Both assessing the suitability of the two force fields variants by comparing computational and experimental results and comparing the solubility of the nisin and its mutant forms require careful choice of an appropriate statistical test. While the t-test is good for comparing the difference between means of two groups, it can result in type-I error (occurs when H0 is statistically rejected even though it is true), also known as “family-wise error”, when performing multiple pairwise comparisons.38 Hence, a t-test was used only for comparison of the two force field variants, while in contrast, the multiple comparison Tukey’s test is used to differentiate the solubility of the nisin and its mutant forms. This is because Tukey’s test is more robust and precise as the variance is estimated from the whole data set as a pooled estimate. In addition, Tukey’s test adjusts the p-values for multiple comparisons, and, therefore, controls the family-wise error rate. Tukey’s test was performed by calculating the q-statistic for each pair, which is defined as the difference between the means of two groups (X̅A – X̅B) divided by the standard error (SE).
The q-statistic is given by
where X̅A and X̅B are the larger and smaller means of the two groups being compared and SE is the standard error defined as
where s2 is the error mean square by analysis of variance (ANOVA) computation and n is the number of observations in each group.
The null hypothesis H0: X̅A = X̅B, indicating that the two means are equal is rejected if q is equal to or greater than the critical value qα,ν,k. Here, α is the level of significance, ν is the error degrees of freedom, and k is the number of groups in the multiple comparison. The critical value can be obtained from a table of the studentized range distribution.
In other words, the difference between the two means is significant, if it is greater than or equal to the HSD (honestly significant difference).
where MSE is the mean square error from the ANOVA table.
Acknowledgments
The simulations in this work were done using the SCHOONER cluster of the University of Oklahoma, and XSEDE resources allocated under grant MCB160005 (National Science Foundation). We acknowledge financial support from the National Institutes of Health under research grant GM120578.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c03594.
Calculated p-values of a statistical test (Welch’s t-test) for solvation free energy (GBSA and PBSA) of nisin and its mutant forms; calculated components of solvation free energy (ΔGsol) for nisin and mutants; phi–psi (ϕ/ψ) backbone dihedral angle distribution of Dha and Dhb; effect of mutation on the solubility of nisin estimated using GBSA; and distribution of solvation free energy of wild-type nisin and mutants estimated using PBSA using parameters of Turpin et al.(10) (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Lei J.; Sun L.; Huang S.; Zhu C.; Li P.; He J.; Mackey V.; Coy D. H.; He Q. The Antimicrobial Peptides and Their Potential Clinical Applications. Am. J. Transl. Res. 2019, 11, 3919–3931. [PMC free article] [PubMed] [Google Scholar]
- Shin J. M.; Gwak J. W.; Kamarajan P.; Fenno J. C.; Rickard A. H.; Kapila Y. L. Biomedical Applications of Nisin. J. Appl. Microbiol. 2016, 120, 1449–1465. 10.1111/jam.13033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Field D.; Cotter P. D.; Hill C.; Ross R. P. Bioengineering Lantibiotics for Therapeutic Success. Front. Microbiol. 2015, 6, 1363. 10.3389/fmicb.2015.01363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsu S.-T. D.; Breukink E.; Tischenko E.; Lutters M. A. G.; de Kruijff B.; Kaptein R.; Bonvin A. M. J. J.; van Nuland N. A. J. The Nisin–Lipid II Complex Reveals a Pyrophosphate Cage That Provides a Blueprint for Novel Antibiotics. Nat. Struct. Mol. Biol. 2004, 11, 963–967. 10.1038/nsmb830. [DOI] [PubMed] [Google Scholar]
- Breukink E.; Wiedemann I.; van Kraaij C.; Kuipers O. P.; Sahl H. G.; de Kruijff B. Use of the Cell Wall Precursor Lipid II by a Pore-Forming Peptide Antibiotic. Science 1999, 286, 2361–2364. 10.1126/science.286.5448.2361. [DOI] [PubMed] [Google Scholar]
- Lehrer R. I.; Ganz T. Antimicrobial Peptides in Mammalian and Insect Host Defence. Curr. Opin. Immunol. 1999, 11, 23–27. 10.1016/s0952-7915(99)80005-3. [DOI] [PubMed] [Google Scholar]
- Bhatti M.; Veeramachaneni A.; Shelef L. A. Factors Affecting the Antilisterial Effects of Nisin in Milk. Int. J. Food Microbiol. 2004, 97, 215–219. 10.1016/j.ijfoodmicro.2004.06.010. [DOI] [PubMed] [Google Scholar]
- Rollema H. S.; Kuipers O. P.; Both P.; de Vos W. M.; Siezen R. J. Improvement of Solubility and Stability of the Antimicrobial Peptide Nisin by Protein Engineering. Appl. Environ. Microbiol. 1995, 61, 2873–2878. 10.1128/aem.61.8.2873-2878.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan J.; Zhang Z.-Z.; Chen X.-Z.; Yang W.; Huan L.-D. Site-Directed Mutagenesis of the Hinge Region of NisinZ and Properties of NisinZ Mutants. Appl. Microbiol. Biotechnol. 2004, 64, 806–815. 10.1007/s00253-004-1599-1. [DOI] [PubMed] [Google Scholar]
- Turpin E. R.; Mulholland S.; Teale A. M.; Bonev B. B.; Hirst J. D. New CHARMM Force Field Parameters for Dehydrated Amino Acid Residues, the Key to Lantibiotic Molecular Dynamics Simulations. RSC Adv. 2014, 4, 48621–48631. 10.1039/c4ra09897h. [DOI] [Google Scholar]
- de Miguel A.; Tapia-Rojo R.; Utesch T.; Mroginski M. A. Structure, Dynamics and Kinetics of Two-Component Lantibiotic Lichenicidin. PLoS One 2017, 12, e0179962 10.1371/journal.pone.0179962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dykes G. A.; Hancock R. E. W.; Hastings J. W. Structural Variations in Nisin Associated with Different Membrane Mimicking and PH Environments. Biochem. Biophys. Res. Commun. 1998, 247, 723–727. 10.1006/bbrc.1998.8849. [DOI] [PubMed] [Google Scholar]
- Ercolessi F.; Adams J. B. Interatomic Potentials from First-Principles Calculations: The Force-Matching Method. Europhys. Lett. 1994, 26, 583–588. 10.1209/0295-5075/26/8/005. [DOI] [Google Scholar]
- Izvekov S.; Parrinello M.; Burnham C. J.; Voth G. A. Effective Force Fields for Condensed Phase Systems from Ab Initio Molecular Dynamics Simulation: A New Method for Force-Matching. J. Chem. Phys. 2004, 120, 10896–10913. 10.1063/1.1739396. [DOI] [PubMed] [Google Scholar]
- Akin-Ojo O.; Wang F. The Quest for the Best Nonpolarizable Water Model from the Adaptive Force Matching Method. J. Comput. Chem. 2011, 32, 453–462. 10.1002/jcc.21634. [DOI] [PubMed] [Google Scholar]
- Li J.; Wang F. Accurate Prediction of the Hydration Free Energies of 20 Salts through Adaptive Force Matching and the Proper Comparison with Experimental References. J. Phys. Chem. B 2017, 121, 6637–6645. 10.1021/acs.jpcb.7b04618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferreira P. M. T.; Maia H. L. S.; Monteiro L. S.; Sacramento J. High Yielding Synthesis of Dehydroamino Acid and Dehydropeptide Derivatives. J. Chem. Soc., Perkin Trans. 1 1999, 3697–3703. 10.1039/a904730a. [DOI] [Google Scholar]
- Ferreira P. M. T.; Monteiro L. S.; Pereira G.; Ribeiro L.; Sacramento J.; Silva L. Reactivity of Dehydroamino Acids and Dehydrodipeptides TowardsN-Bromosuccinimide: Synthesis of β-Bromo- and β,β-Dibromodehydroamino Acid Derivatives and of Substituted 4-Imidazolidinones. Eur. J. Org Chem. 2007, 5934–5949. 10.1002/ejoc.200700669. [DOI] [Google Scholar]
- Tian X.; Li L.; Han J.; Zhen X.; Liu S. Stereoselectively Synthesis and Structural Confirmation of Dehydrodipeptides with Dehydrobutyrine. SpringerPlus 2016, 5, 400. 10.1186/s40064-016-2005-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dugave C.; Demange L. Cis–Trans Isomerization of Organic Molecules and Biomolecules: Implications and Applications. Chem. Rev. 2003, 103, 2475–2532. 10.1021/cr0104375. [DOI] [PubMed] [Google Scholar]
- Siodłak D. α,β-Dehydroamino Acids in Naturally Occurring Peptides. Amino Acids 2015, 47, 1–17. 10.1007/s00726-014-1846-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robison A. D.; Sun S.; Poyton M. F.; Johnson G. A.; Pellois J.-P.; Jungwirth P.; Vazdar M.; Cremer P. S. Polyarginine Interacts More Strongly and Cooperatively than Polylysine with Phospholipid Bilayers. J. Phys. Chem. B 2016, 120, 9287–9296. 10.1021/acs.jpcb.6b05604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vazdar M.; Uhlig F.; Jungwirth P. Like-Charge Ion Pairing in Water: An Ab Initio Molecular Dynamics Study of Aqueous Guanidinium Cations. J. Phys. Chem. Lett. 2012, 3, 2021–2024. 10.1021/jz3007657. [DOI] [Google Scholar]
- Schwieger C.; Blume A. Interaction of Poly(l-Arginine) with Negatively Charged DPPG Membranes: Calorimetric and Monolayer Studies. Biomacromolecules 2009, 10, 2152–2161. 10.1021/bm9003207. [DOI] [PubMed] [Google Scholar]
- Huang J.; MacKerell A. D. CHARMM36 All-Atom Additive Protein Force Field: Validation Based on Comparison to NMR Data. J. Comput. Chem. 2013, 34, 2135–2145. 10.1002/jcc.23354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abraham M. J.; Murtola T.; Schulz R.; Páll S.; Smith J. C.; Hess B.; Lindahl E. Gromacs: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1-2, 19–25. 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
- Páll S.; Abraham M. J.; Kutzner C.; Hess B.; Lindahl E.. Tackling Exascale Software Challenges in Molecular Dynamics Simulations with GROMACS. In Solving Software Challenges for Exascale; Markidis S., Laure E., Eds.; Springer International Publishing: Cham, 2015; pp 3–27. [Google Scholar]
- Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
- Darden T.; York D.; Pedersen L. Particle Mesh Ewald: An N ·log(N) Method for Ewald Sums in Large Systems. J. Chem. Phys. 1993, 98, 10089–10092. 10.1063/1.464397. [DOI] [Google Scholar]
- Essmann U.; Perera L.; Berkowitz M. L.; Darden T.; Lee H.; Pedersen L. G. A Smooth Particle Mesh Ewald Method. J. Chem. Phys. 1995, 103, 8577–8593. 10.1063/1.470117. [DOI] [Google Scholar]
- Bussi G.; Donadio D.; Parrinello M. Canonical Sampling through Velocity Rescaling. J. Chem. Phys. 2007, 126, 014101. 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
- Parrinello M.; Rahman A. Polymorphic Transitions in Single Crystals: A New Molecular Dynamics Method. J. Appl. Phys. 1981, 52, 7182–7190. 10.1063/1.328693. [DOI] [Google Scholar]
- Genheden S.; Ryde U. The MM/PBSA and MM/GBSA Methods to Estimate Ligand-Binding Affinities. Expet Opin. Drug Discov. 2015, 10, 449–461. 10.1517/17460441.2015.1032936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang C.; Nguyen P. H.; Pham K.; Huynh D.; Le T.-B. N.; Wang H.; Ren P.; Luo R. Calculating Protein-Ligand Binding Affinities with MMPBSA: Method and Error Analysis. J. Comput. Chem. 2016, 37, 2436–2446. 10.1002/jcc.24467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kollman P. A.; Massova I.; Reyes C.; Kuhn B.; Huo S.; Chong L.; Lee M.; Lee T.; Duan Y.; Wang W.; Donini O.; Cieplak P.; Srinivasan J.; Case D. A.; Cheatham T. E. Calculating Structures and Free Energies of Complex Molecules: Combining Molecular Mechanics and Continuum Models. Acc. Chem. Res. 2000, 33, 889–897. 10.1021/ar000033j. [DOI] [PubMed] [Google Scholar]
- Miller B. R.; McGee T. D.; Swails J. M.; Homeyer N.; Gohlke H.; Roitberg A. E. MMPBSA.Py: An Efficient Program for End-State Free Energy Calculations. J. Chem. Theory Comput. 2012, 8, 3314–3321. 10.1021/ct300418h. [DOI] [PubMed] [Google Scholar]
- Case D.; Ben-Shalom I.; Brozell S.; Cerutti D.; Cheatham T. III; Cruzeiro V.; Darden T.; Duke R.; Ghoreishi D.; Gilson M.; others. AMBER 18; University of California: San Francisco, 2018.
- Zar J. H.Biostatical Analysis, 5th ed.; Pearson College Division, 2011. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.