Theoretical Study on Neutral Molecules with Square Planar Tetracoordinate Oxygen O(B)4 Arrangements

Abstract

As we know, oxygen usually forms two single bonds with other atoms, whereas in this work, we reported the neutral molecules with square planar O(B)4-type tetracoordinate oxygen substructures. The difficulty to achieve a square planar O(B)4-type arrangement is not only to overcome the strain from the planar to tetrahedral configuration but also to constrain it in a right system with the proper symmetry. Several neutral molecules with square planar O(B)4-type arrangements have been studied using the DFT method at the B3LYP/6-311++G(3df,3pd) level of theory. The computational results show that they are all real minima on potential energy hypersurfaces. Thus, it has been shown theoretically that the square planar O(B)4-type arrangement is achieved. The molecular orbitals among the square planar O(B)4-type substructure at D_2d symmetry have been suggested. Using the molecular orbitals, it has been explained that the oxygen 2p_z-π electrons in the square planar O(B)4-type arrangement are no longer the lone-pair electrons.

Introduction

Oxygen occupies a central position in inorganic chemistry. It has four valence orbitals and six valence electrons; therefore, it usually forms two single bonds with other atoms. When an oxygen atom bonds to four or more atoms in the same plane, the oxygen is called a planar hypercoordinate oxygen (phO).¹ Species with planar tetracoordinate oxygen (ptO) arrangements are the most studies among phOs. In the past three decades, species with planar hypercoordinate oxygen atoms have been made notable progress. In 1991, the species Al₄O with planar tetracoordinate oxygen and D_4h symmetry was found by Schleyer and Boldyrev.² The hydrometal complexes Cu₄H₄O²⁺ with ptO(Cu)₄ and Ni₄H₄O²⁺ with ptO(Ni)₄ substructures were studied by Li and co-workers in 2004.³ A planar pentacoordinate oxygen, the hydrometal complexes Cu₅H₅O²⁺ with a ptO(Cu)₅ substructure, also has been reported in 2005.⁴ A perfectly square-planar tetracoordinate oxygen atom in a tetracopper cluster-based coordination polymer was experimentally detected by Zhang and co-workers in 2011.⁵

Most of the successful examples of ptOs are used metal-based groups as ligands previously. The achievement of ptO-used nonmetal-based groups as ligands, where the central oxygen is surrounded by four nonmetal-based groups, is more challenging. Until now, to our knowledge, no structure with a ptO(X)₄ (X = nonmetal atom) substructure has been reported. Among all ptO(X)₄ (X = nonmetal atom) substructures, the configuration of the highest symmetry is the square arrangement. It is intriguing to ask whether a square ptO(X)₄ (X = nonmetal atom) arrangement could exist or not? In order to answer the question, we will study neutral molecules with square ptO(B)₄ arrangements here.

As to design species with square ptO(B)₄ arrangement, we used three strategies in this work. The first is that using electron-deficient boron as donor atoms to compensate electron-rich oxygen. Because oxygen has six valence electrons and four valence orbitals, when it bonds with four atoms, the better approach is bonding with an electron-deficient element, such as boron. Thus, we used four boron-based groups as ligands to achieve the square ptO(B)₄ substructure.

The second is that constricting a ptO(B)₄ arrangement in a more buttress cage-like molecule to overcome the strain of the planar-tetracoordinate oxygen to transfer to a tetrahedral substructure, such as oxygen in the tetrahedral substructure of Zn₄O in MOF-5^5a and Be₄O in “basic beryllium acetate”.^5b Radom and co-workers^6,7 used the “mechanical” strategy to design a family of buttress alkaplane molecules, which constricted the planar tetracoordinate carbon (ptC) arrangements in hydrocarbon cages. In 2002, Wang and Schleyer⁸ stated that “although approaching a planar C(C)₄-type ptC more closely than ever before, such “mechanical” designs without “electronic” assistance must struggle hard to overcome the enormous strain of a ptC with a p-π lone pair HOMO.” Therefore, the candidates of cage-like molecules with more buttress than those of the alkaplane molecules designed by Radom and co-workers are required.

The third is selecting a more buttress cage-like molecule with the proper symmetry. To achieve a square ptO(B)₄ arrangement, except to overcome the enormous strain from the planar to tetrahedral, another problem is that the more buttress cage-like molecule should have a proper symmetry to make the ptO(B)₄ arrangement squarely.

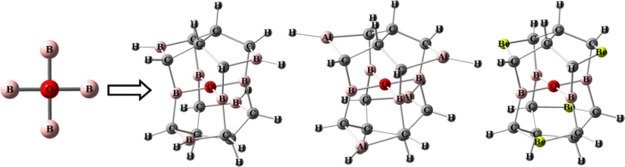
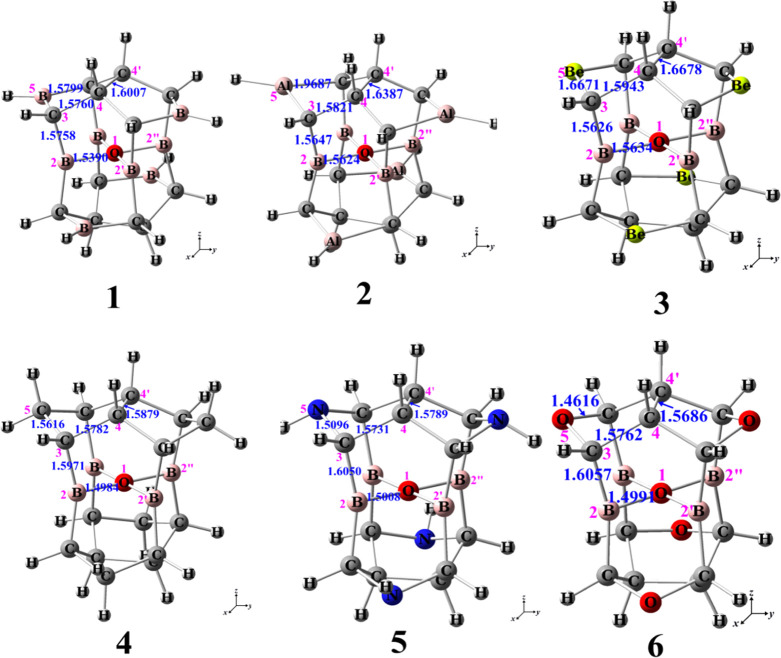
Because the buttresses of the cage-like molecules are not enough, the singlet neutral molecule containing the square ptO(B)₄ substructure could not be achieved with the structures of the alkaplane designed by Radom and co-workers,^6,7 and the boraplane designed by Wang and Schleyer.⁸ We considered another cage-like molecule, isopagodane C₂₀H₂₀.⁹ Because there are two C4–C4′ bonds in isopagodane (Figure 1), the structure of isopagodane is different from that of the alkaplane designed by Radom and co-workers^6,7 but more rigid than the structures described above. Based on the isopagodane-like structure, we designed the singlet neutral molecules 1–6 containing the square ptO(B)₄ substructures (Figure 1). Using four boron atoms and four BH groups to replace the four carbon atoms at the center and the four CH₂ groups in isopagodane, 1 was obtained. Based on the structure of 1, using four AlH, Be, CH₂, NH, and O groups to replace the four BH groups in 1, 2–6 have been obtained.

Figure 1.

Structures of 1–6 with key parameters at the B3LYP/6-311++g(3df,3pd) level of theory.

In order to verify whether 1–6 are candidates with successfully square ptO(B)₄ substructures or not, they have been studied using the DFT method.

Results and Discussion

Geometries and Stability

The optimized geometries of 1–6 are all converged with D_2d point groups at the B3LYP/6-311++G(3df,3pd) level of theory. Based on D_2d point groups, all bond angles of ∠BOB are equal to 90°. Therefore, all ptO(B)₄ arrangements in 1–6 are all perfectly square planar tetracoordinate oxygen arrangements. The smallest vibrational frequencies of 1, 2, and 3 are 170.6, 127.7, and 180.8 cm^–1, respectively, without any imaginary vibrational frequency, which confirms that 1–3 correspond to true minima on the potential energy hypersurfaces (PES). In contrast, each of 4–6 has two imaginary vibrational frequencies, verifying that 4–6 could not be stable molecules.

There are two ranges of vibrational frequencies of 1, 170–1316 cm^–1, the vibrations of the atoms on the skeleton of cage, and 2632–3127 cm^–1, the vibrations of the B–H and C–H bonds. As for 2, the vibrational frequencies of the atoms on the skeleton of cage are among 127–1312 cm^–1 and the vibrational frequencies of the Al–H and C–H bonds are in the 1922–3115 cm^–1 range. The vibrational frequencies of the atoms on the skeleton of cage and the C–H bonds of 3 are in the 180–1303 and 3062–3147 cm^–1 ranges, respectively.

The optimized structures of 1–6 with key parameters are shown in Figure 1. It can be seen that the lengths of O–B bonds in square ptO(B)₄ arrangements for 1, 2, 3, 4, 5, and 6 are 1.5390, 1.5624, 1.5634, 1.4984, 1.5008, and 1.4991 Å, respectively, which are all longer than those of single O–B in boric acid B(OH)₃ (1.376 Å).¹⁰ From the bond lengths, it could be seen that the O–B bonds in 4–6 are stronger than those in 1–3. Because the stronger the O–B bonds, the greater the energy difference between the tetrahedral and planar O(B)₄ arrangements as the ptC,¹¹ the planar geometries of 1–3 may be more stabilized or the tetrahedral more destabilized than those of 4–6.

In the structures of 1–3, the lengths of B2–C3 (see the labels in Figure 1, similarly hereinafter) bonds, 1.5758, 1.5647, and 1.5626 Å for 1, 2, and 3, respectively, are all shorter than those of the B–C bond in trimethylborane (CH₃)₃B (1.578 Å),¹⁰ which makes the structures of 1–3 more buttress, achieving the square ptO(B)₄ arrangements successfully; while the lengths of B2–C3 bonds, 1.5971, 1.6050, and 1.6057 Å for 4, 5, and 6, respectively, are all longer than that of the B–C bond in (CH₃)₃B (1.578 Å).¹⁰ Thus, the “mechanical” strength or rigidity around the square ptO(B)₄ arrangements of 4–6 is all lower than that of 1–3. Therefore, the square planar substructures of O(B)₄ in 4–6 are not the stable, 4–6 are the saddle points on the PES, not the stable molecules. According to the computational results, the differences of energies between the saddle points and the stable structures of 4–6 are 13.0, 60.3, and 67.9 kJ·mol^–1, respectively.

As we know, a small HOMO–LUMO gap has long been recognized as being correlated with reactivity and structural instability, while a large gap is associated with kinetic and structural stability.¹² The HOMO–LUMO gaps of 1–3 are 3.91, 3.16, and 2.67 eV at the B3LYP/6-311++G(3df,3pd) level of theory, respectively, and they are all larger than that of the boraplane C₁₇B₄H₂₄ designed to achieve perfectly planar carbon tetracoordination by Wang and Schleyer, 2.64 eV at the B3LYP/6-311++G(3df,3pd) level of theory.^8b Hence, 1–3 are all stable than the boraplane C₁₇B₄H₂₄.^8b Therefore, our work could be used to achieve the planar-tetracoordinate oxygen.

From the results described above, the greater “mechanical” strength or rigidity and the lower destabilized planar geometries of the square ptO(B)₄ arrangements are the key reasons to achieve the square ptO(B)₄ arrangements.

Bonding Interactions of the Square ptO(B)₄ Arrangement

The molecular orbitals of planar methane have been proposed using the molecular symmetry and group theory by Hoffmann, Alder, and Wilcox in 1970.¹¹ We could use the method to discuss the nature of the bonding interactions in the square ptO(B)₄ arrangement. It could be roughly considered that every B2 atom uses two sp hybrids, formed by 2s and 2p_z, and two electrons to bond with two C3 atoms and leave 2p_x and 2p_y orbitals and one electron to bond with the central O1 atom.

The representations of the basis sets formed by the eight orbitals, 2p_x and 2p_y of four B2 atoms, could be reduced to Γ_4B2 = a₁ + a₂ + b₁ + b₂ + 2e at the D_2d symmetry of the whole molecule. The a₁, a₂, b₁, and b₂ are all one-dimensional, and the e is two-dimensional irreps. According to the a₁, a₂, b₁, b₂, and 2e irreps, the ligand group orbitals formed by the 2p_x and 2p_y of four B2 atoms could be derived out as the symmetry-adapted linear combinations to interact with central O1 atomic valence orbitals of the same symmetry, and form the molecular orbitals (MOs). The central O1 atomic valence orbitals belong to a₁(2s), b₂(2p_z), and e(2p_x and 2p_y) symmetries. Thus, the diagram of various orbitals in the ptO(B)₄ substructure have been shown in Figure 2. Because every B2 atom uses two electrons to form two B2–C3 bonds and leaves only one electron to bond with the central O1 atom and there are no formal charges on four B2 and O1 atoms, a total of ten electrons occupy the five MOs according to the Aufbau principle. According to the electronegativities of boron and oxygen, the MOs of 1a₁, 1e, and 1b₂ possesses predominantly oxygen 2s, 2p_x and 2p_y, and 2p_z characters, respectively, and 2b₂ MO possesses predominantly boron 2p_x and 2p_y characters (see HOMO(b₂) in Figure 3). Thus, the six electrons of oxygen occupy 1a₁, 1e, and 1b₂ MOs predominantly, and the four electrons of the four perimeter boron atoms occupy 1e and 2b₂ MOs, respectively.

Figure 2.

Various orbitals with symmetries in the square ptO(B)₄ arrangement in D_2d symmetry.

Figure 3.

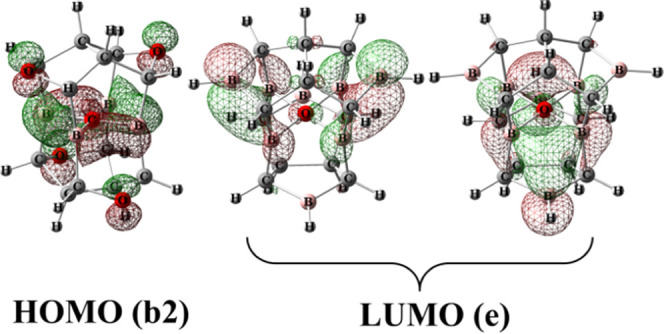
HOMO and LUMO of 1 [MO contour values are 0.05(e/ų)^1/2].

Because the central O1 atomic 2p_z orbital has the b₂ irrep, it could interact with the ligand group orbitals of the b₂ symmetry to form the bonding 1b₂ and 2b₂ MOs; thus, the 2p_z-π electrons of oxygen in the square ptO(B)₄ arrangement are no longer the lone-pair electrons (see the 1b₂ and 2b₂ MOs in Figure 2). However, oxygen is an electron-rich atom, and using the electron-deficient element, such as boron, as donor atom may delocalize the electron density of the central O1 atom, which could decrease the energy of the bonding MOs containing the 2p_z-π electrons of the central O1 atom and stabilize the ptO(B)₄ substructure. Thus, the “electronic” approach, stabilized by π acceptor substituents or by aromatic delocalization and benefited from σ donation by electropositive groups, for designing the ptC compounds^7,8,11 is also suitable for the ptO substructure.

Figure 3 shows the frontier orbitals of 1 at the B3LYP/6-311+G(3df,3pd) level of theory for the view of comparing. It could be seen that the HOMO and LUMO of 1 are in accordance with those in Figure 2.

Because the oxygen atom form four O–B bonds at the same plane, the Wiberg bond indexes of O–B bonds in ptO(B)₄ are low. According to the ρ(r_c)s, 0.1084–0.1240 a.u., in Table 2, the strength of the O–B bonds are similar to BrF and IF.

Table 2. Electron Density ρ(r_c)/(e·Bohr^–3), Laplacian of Electron Density ∇²ρ(r_c)/(e·Bohr^–5), the Densities of Kinetic Energy G(r_c)/(Hartree·Bohr^–3), Potential Energy V(r_c)/(Hartree·Bohr^–3), Total Electronic Energy Density E_b^e(r_c)/(Hartree·Bohr^–3), and the Ellipticity ε of BCPs of Some Bonds in 1–6 at the B3LYP/6-311++G(3df,3pd) Level of Theory^a.

molecule	bond	ρ(rc)	∇2ρ(rc)	Ebe(rc)	Gb(rc)	Vb(rc)	ε
1	O1–B2	0.1154	0.5690	–0.0756	0.2178	–0.2934	0.4017
	B2–C3	0.1872	–0.4379	–0.1979	0.0884	–0.2864	0.1783
	C3–C4	0.2207	–0.4298	–0.1620	0.0546	–0.2166	0.0250
	C3–B5	0.1795	–0.3164	–0.1940	0.1149	–0.3090	0.0967
	C4–C4′	0.2186	–0.4273	–0.1554	0.0486	–0.2040	0.0307
	O1···C4	0.0305	0.1606	0.0033	0.0369	–0.0336	4.0782
2	O1–B2	0.1090	0.5182	–0.0701	0.1996	–0.2697	0.3955
	B2–C3	0.1901	–0.4050	–0.2048	0.1035	–0.3083	0.2193
	C3–C4	0.2158	–0.3994	–0.1554	0.0555	–0.2109	0.0446
	C3–Al5	0.0821	0.2396	–0.0283	0.0881	–0.1164	0.1580
	C4–C4′	0.2028	–0.3640	–0.1343	0.0432	–0.1775	0.0199
	O1···C4	0.0312	0.1548	0.0029	0.0359	–0.0330	2.6694
3	O1–B2	0.1084	0.5233	–0.0692	0.2000	–0.2691	0.3607
	B2–C3	0.1902	–0.3952	–0.2059	0.1071	–0.3131	0.2221
	C3–C4	0.2089	–0.3623	–0.1466	0.0560	–0.2027	0.0711
	C3–Be5	0.1010	0.2312	–0.0544	0.1122	–0.1667	0.0924
	C4–C4′	0.1922	–0.3221	–0.1213	0.0408	–0.1621	0.0153
	O1···C4	0.0307	0.1509	0.0027	0.0350	–0.0323	2.4556
4	O1–B2	0.1240	0.7094	–0.0797	0.2571	–0.3368	0.0803
	B2–C3	0.1869	–0.4412	–0.1988	0.0885	–0.2873	0.1093
	C3–C4	0.2227	–0.4398	–0.1636	0.0537	–0.2173	0.0108
	C3–C5	0.2278	–0.4662	–0.1731	0.0565	–0.2296	0.0161
	C4–C4′	0.2226	–0.4378	–0.1616	0.0521	–0.2138	0.0119
5	O1–B2	0.1232	0.7050	–0.0790	0.2552	–0.3342	0.1292
	B2–C3	0.1874	–0.4640	–0.1980	0.0820	–0.2801	0.0855
	C3–C4	0.2271	–0.4646	–0.1692	0.0531	–0.2223	0.0243
	C3–N5	0.2445	–0.5412	–0.2291	0.0938	–0.3230	0.0589
	C4–C4′	0.2253	–0.4494	–0.1662	0.0538	–0.2201	0.0091
6	O1–B2	0.1238	0.7103	–0.0795	0.2571	–0.3366	0.1545
	B2–C3	0.1886	–0.4691	–0.2008	0.0835	–0.2843	0.0680
	C3–C4	0.2271	–0.4630	–0.1686	0.0528	–0.2214	0.0357
	C3–O5	0.2432	–0.5416	–0.2910	0.1556	–0.4466	0.0536
	C4–C4′	0.2283	–0.4604	–0.1713	0.0562	–0.2276	0.0036
B(OH)3	B–O	0.2163	0.6511	–0.2224	0.3851	–0.6075	0.0547

^aLabels of atoms of 1–6 given in Figure 1.

Although the distances between B2 and B2′, 2.11–2.21 Å for 1-6, are much longer than the length of the B–B bond (1.590 Å for B₂),¹⁰ some bonding interactions among perimeter four boron atoms in the square ptO(B)₄ still remain according to the MOs given in Figure 2. This can be seen from the Wiberg bond indexes of B2···B2′ and B2···B2″ in Table 1, and the bonding interactions among perimeter four boron atoms are much stronger than expected. The unexpected strong bonding interactions among perimeter four boron atoms bring the square ptO(B)₄ substructure more rigidity than expected, which is another reason to achieve the square ptO(B)₄ arrangement.

Table 1. Electronic States (ES); Point Groups (PG); Smallest Frequencies Freq (in cm^–1); Wiberg Bond Indexes (WBI); Total Wiberg Bond Indexes (tWBI), and NBO Charges by Atoms Q_NBO,^a Occupations Valence Orbitals of Central Oxygen Atoms in 1–6.

properties	1	2	3	4	5	6
ES	1A1	1A1	1A1	1A1	1A1	1A1
PG	D2d	D2d	D2d	D2d	D2d	D2d
freq	170.6	127.7	180.8	121.2i	215.6i	219.2i
WBIO1–B2	0.3321	0.3414	0.3510	0.3589	0.3641	0.3697
WBIB2–C3	0.8473	0.9652	0.9705	0.8392	0.8602	0.8689
WBIC3–C4	0.9652	0.9821	0.9681	0.9736	0.9739	0.9704
WBIC3–X5	0.8654	0.5146	0.5195	0.9976	0.9540	0.8818
WBIC4–C4′	0.9775	0.9967	0.9518	0.9739	0.9730	0.9762
WBIB2···B2′	0.1803	0.1849	0.1791	0.2582	0.2559	0.2513
WBIB2···B2″	0.0704	0.0635	0.0580	0.1545	0.1519	0.1544
tWBIO1	1.5880	1.6404	1.6659	1.6748	1.6949	1.7094
tWBIB2	2.9703	3.1151	3.1134	2.9739	3.0230	3.0256
tWBIC3	3.7330	3.5705	3.5489	3.8342	3.8300	3.7673
tWBIC4	3.9979	4.0103	3.9984	3.9925	3.9901	3.9844
tWBIX5	3.1483	2.1932	1.4516	3.9421	2.9703	1.9890
QNBO,O1	–1.1421	–1.1052	–1.0767	–1.1489	–1.1267	–1.1166
QNBO,B2	0.9731	0.7933	0.7905	0.9584	0.8896	0.8799
QNBO,C3	–0.8974	–1.0911	–1.0905	–0.6015	–0.3935	–0.2227
QNBO,C4	–0.1633	–0.2007	–0.1994	–0.1758	–0.1852	–0.2238
QNBO,X5	0.5949	1.5207	1.1491	–0.3279	–0.6352	–0.5828
QptO-2s	1.5730	1.5694	1.5677	1.5671	1.5691	1.5701
QptO-2pz	1.9551	1.9508	1.9529	1.9563	1.9570	1.9571
QptO-2px	1.7872	1.7739	1.7619	1.7781	1.7682	1.7627
QptO-2py	1.7872	1.7739	1.7619	1.7781	1.7682	1.7627

^aLabels of atoms of 1–6 given in Figure 1.

Characterization of Bonding Interactions

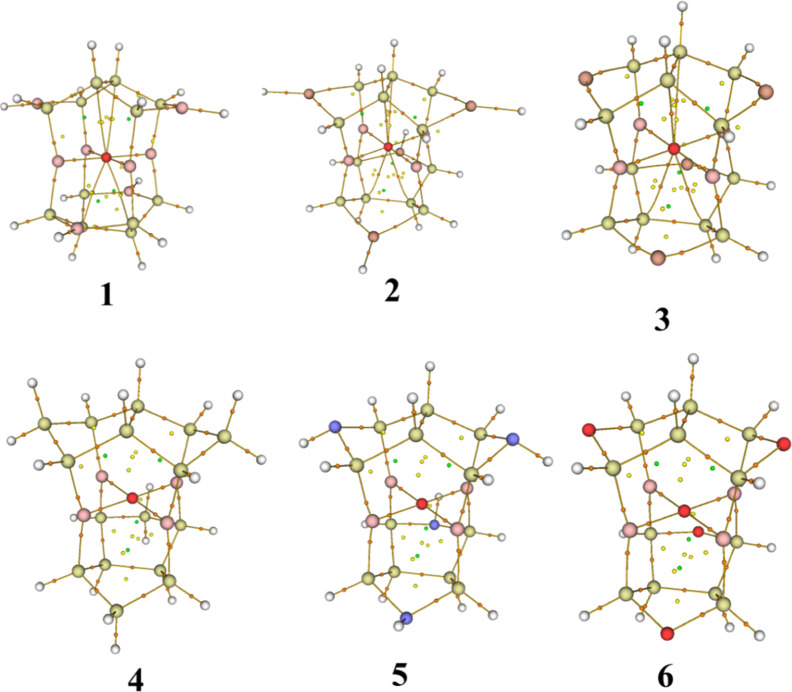
In order to understand the bonding interactions, we used the critical points (CPs) and their properties of the quantum theory of atoms in molecules (QTAM)^13,14 to quantify the bonding interactions of atoms in 1–6, which were performed using the program Multiwfn.¹⁵ In QTAM, the critical points (CPs) are the points with a vanishing gradient of the electron density ρ(r), that is, ∇ρ(r) = 0 and could be divided into nuclear, bond, ring, and cage CPs, depending on the nature of the extremum of ρ(r). When n, b, r, and c used to represent numbers of nuclear, bond, ring, and cage CPs, they are governed by the Poincaré–Hopf relationship¹⁴ as n – b + r – c = 1. All CPs in 1–6 have been searched out using the Multiwfn program.¹⁵ They are all satisfied the Poincaré–Hopf relationship. All CPs and the bond paths of 1–6 have been shown in Figure 4.

Figure 4.

All CPs and bond paths of 1–6. Big balls are atoms. Orange, yellow, and green small spheres correspond to bond, ring, and cage CPs. Brown lines denote bond paths.

The properties of CPs, electron densities ρ(r_c), Laplacian of electron densities ∇²ρ(r_c), the densities of kinetic energy G(r_c), potential energy V(r_c), total electronic energy densities E_b^e(r_c) = G(r_c) + V(r_c), and the ellipticities of all bonds in the cage skeletons of 1–6 at the B3LYP/6-311++G(3df,3pd) level of theory are listed in Table 2.

It can be seen that all B2–C3, C3–C4, C4–C4′, and C3–X5 (X5 = B5, C5, N5, O5) bonds in 1–6 are typical covalent bonds, according to the classifications,^16,17 but C3–Al5 in 2 and C3–Be5 bonds in 3 could be regarded as charge-shift bonds. As for O1–B2 bonds in the square ptO(B)₄ substructures of 1–6, although the ρ(r_c)s, 0.1084–0.1240 a.u., are all relatively large, the V(r_c)s are all slightly greater than the corresponding G(r_c)s, so the values of E_b^e(r_c)s are all negative and low, and the ∇²ρ(r_c)s all with positive values. Like BrF and IF,¹⁷ these bonds have features of intermediate interaction and could be considered as partially covalent and partially electrostatic, or strongly polar bonds. The ellipticities in Table 2 also reveal that O1–B2 bonds have large π bonding interactions.

Figure 4 shows that there are some weak interactions between O1 and C4 in 1–3, but 4–6 do not have these weak interactions (see 4–6 in Figure 4). Table 2 gives the CPs’ properties of these weak interactions. The ρ(r_c)s (0.0305–0.0312 a.u.), the E_b^e(r_c)s (0.0027–0.0033 a.u.), and the ∇²ρ(r_c)s (0.1509–0.1606 a.u.) are all in accordance with the typical weak interactions.¹⁹ These weak interactions are the one of reasons to achieve the square ptO(B)₄ arrangement.

Conclusions

The singlet neutral molecules 1–6 with the square planar-tetracoordinate oxygen surrounded by four boron-based groups have been designed and studied at the B3LYP/6-311++G(3df,3pd) level of theory. The results show that 1–3 are all real minima on PES, but 4–6 are not. The reasons have been discussed in this work. The main conclusions of this work could be summarized as follows:

• (1)To design the square ptO(B)₄ arrangement, the strategy of “mechanical” approach is very important. Short B2–C3 bonds make the structures of 1–3 more rigid than those of 4–6, which is the key reason to achieve the square ptO(B)₄ arrangement successfully. The unexpected strong bonding interactions among perimeter four boron atoms and the weak interactions between O1 and C4 in 1–3 are the other reasons to achieve the square ptO(B)₄ successfully.
• (2)The bonding interactions of the square ptO(B)₄ arrangement have been proposed according to the D_2d symmetry. The shapes and symmetries of frontier orbitals, HOMO and LUMO of 1 with b₂ and e symmetries, respectively, have been discussed and are in accordance with the results at the B3LYP/6-311+G(3df,3pd) level of theory.

Although the 2p_z-π electrons of electron-rich oxygen in the square ptO(B)₄ arrangement are no longer the lone-pair electrons and interact with perimeter four boron atoms to form bonding MOs. The “electronic” approach, stabilized by π acceptor substituents or by aromatic delocalization and benefited from σ donation by electropositive groups, is also suitable for the ptO substructure.

• (3)The nature of the bonding interactions in the square ptO(B)₄ arrangement has been studied using the quantum theory of atoms in molecules. The O1–B2 bonds with large π bonding interactions could be considered as strongly polar bonds.

The conclusions of our work could be used to achieve the planar polycoordinate oxygen or other elements.

Computational Details

The B3LYP hybrid density functional is used in this study based on the statement that “the B3LYP hybrid density functional is still the preferred method for studying species with ptC atoms.”¹⁸ Geometries of all molecules studied here were optimized at the B3LYP/6-311G(d,p) level of theory first and reoptimized at the B3LYP/6-311++G(3df,3pd) level of theory. Based on the B3LYP/6-311++G(3df,3pd) geometries, properties were also calculated at the same level of theory.

The quantum theory of atoms in molecules^13,14 is used here to understand the bonding interactions of all molecules studied in this work. All computations here were performed using the GAUSSIAN 09 program¹⁹ apart from the critical bond points and their properties of atoms in molecules, which were performed using the program Multiwfn.¹⁵

Glossary

Abbreviation

ptO(X)₄

planar tetracoordinate oxygen surrounded by four X-based groups

Author Contributions

All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.