Fully Integrated Time-Gated 3D Fluorescence Imager for Deep Neural Imaging

Abstract

This paper presents a device for time-gated fluorescence imaging in the deep brain, consisting of two on-chip laser diodes and 512 single-photon avalanche diodes (SPADs). The edge-emitting laser diodes deliver fluorescence excitation above the SPAD array, parallel to the imager. In the time domain, laser diode illumination is pulsed and the SPAD is time-gated, allowing a fluorescence excitation rejection up to O.D. 3 at 1 ns of time-gate delay. Each SPAD pixel is masked with Talbot gratings to enable the mapping of 2D array photon counts into a 3D image. The 3D image achieves a resolution of 40, 35, and 73 in the x, y, z directions, respectively, in a noiseless environment, with a maximum frame rate of 50 kilo-frames-per-second. We present measurement results of the spatial and temporal profiles of the dual-pulsed laser diode illumination and of the photon detection characteristics of the SPAD array. Finally, we show the imager’s ability to resolve a glass micropipette filled with red fluorescent microspheres. The system’s 420 μm-wide cross section allows it to be inserted at arbitrary depths of the brain while achieving a field of view four times larger than fiber endoscopes of equal diameter.

1. Introduction

While the superficial brain has been extensively studied with the development of modem neural imaging techniques, the deep brain largely remains an elusive area of investigation. Deep-brain imaging with conventional free-space optics is challenged by the scattering and absorption of photons in tissue, which appears opaque in the visible spectrum. Scattering events, which occur with mean free paths of ~50 μm for visible light in grey matter [1], cause photons to quickly lose directionality with depth in tissue. Ongoing developments in multiphoton microscopy [2, 3] and super-resolution microscopy [4] have enabled near single-cell resolution at depths of up to two millimeters in the mouse brain, but imaging depths are not expected to improve significantly beyond this.

One way to acquire an image at greater depths is to guide photons through a non-scattering medium. In particular, imagers with graded index rod lenses (1.8 mm diameter) [5] and multimode fiber endoscopes (50 μm core diameter) [6, 7] have successfully imaged neural structures several millimeters deep. Nonetheless, their fields of view (FoVs) are inherently limited by the diameter of the lens or waveguide, which can only be increased with a more invasive insertion cross section. This tradeoff between FoV and invasiveness makes waveguides an unscalable solution for scanning large volumes in the deep brain.

Another approach to deep brain imaging is to insert an integrated imaging system into the brain itself, with photons converted into electrical signals before they scatter. The difficulty here lies in miniaturizing or replacing the function of optical components of an imaging system—illumination source, spectral filter, detector array, and interconnects—to minimize invasiveness while maximizing the FoV and resolution of the imager. Several forms of such a fully-integrated implantable CMOS surface imager have been demonstrated using two different types of illumination sources: micro-light-emitting diodes (μLEDs) [8, 9] and fiberoptic cables [10], Although these imagers achieve single-μm resolution with tightly-pitched CMOS pixels and on-chip spectral filters, they cannot focus at depth, effectively limiting the total number of simultaneously imaged neurons to those at the very surface. As a solution, pixel masking methods have proven useful in turning two-dimensional detector arrays into depth-perceiving light-field-sensitive arrays, allowing volumetric discemability [11–13].

In this work, we further develop our previous work on a deep-implantable fluorescence imager with pulsed μLEDs [14] into a system using two edge-emitting laser diode (LD) illumination sources and 512 single-photon-avalanche-diode (SPAD) detectors, measuring only 420 μm by 150 μm in cross section and 4 mm in length. Light generation and collection by digitally addressable devices with in-pixel memory allow the compression of an image into a time-series data set delivered through a few metal interconnects, whereas an optical fiber or rod lens delivers an image size strictly in proportion to its diameter. The result is the potential for a significant advantage in functional scalability for implantable electrical imagers over passive implanted optics.

With a cross-sectional width of only 420 μm, the imager can be combined with a standard 1.8mm-diameter cannula and delivered into deep brain regions that lie beyond the reach of conventional optics (Fig. 1). Each SPAD pixel is masked with a set of semi-unique Talbot gratings used for spatial sampling, the collective image of which allows the computational localization of a light source in three dimensions (3D) [13]. In the subsequent discussion, the positive X-axis denotes the long axis of the imager in the direction of insertion, the Y-axis denotes the short axis of the imager, and the Z-axis denotes the vertical distance away from the imager. (Fig. 1) The origin of this spatial reference is denoted as the location of the left-and-bottom-most SPAD pixel in the array.

Fig. 1.

3D model of the deep brain fluorescence imager, comprised of 512 SPAD pixels and two laser diodes, packaged onto a 20 μm-thick polyimide flexible substrate; red arrows indicate the direction of excitation light. The imager is delivered through a 1.8 mm diameter cannula.

2. Design of Imaging System

Time-Gated Fluorescence Imaging

Fluorescent biomarkers serve as highly effective contrasting agents for highlighting a targeted biological structure or activity over a nonspecific background. Fluorescence imaging has proven to be a powerful tool for studying the brain, especially with the growing variety of genetically encoded fluorescent proteins [15, 16]. Fluorescence imagers require a minimum of three components: an excitation light source, a filter, and a detector.

The excitation light source illuminates a volume of tissue with a wavelength that is best absorbed by the fluorophore. A filter, placed before the detector, rejects the scattered excitation background and passes only the fluorescence emission. The detector finally converts incoming photons into electrons, carrying information of intensity and time of arrival.

The construction of a filter that efficiently passes fluorescence emission and rejects excitation is key in achieving images with a high signal-to-background ratio (SBR). The ability to reject excitation on a base-10 log scale is known as optical density (O.D.), a figure of merit for fluorescence filters. A common epifluorescence microscope requires the addition of absorption or interference filters providing at least three, and typically six, O.D. [17]. Absorption filters show a gradual ramp of transmission from stop band to pass band, while interference filters have a much sharper wavelength selectivity. This makes interference filters a highly desirable choice of filter, but their passing wavelengths alter with incident angle, meaning that they have limited use for a light-field imager that collects light equally from all incident angles. Composite on-chip filters combining absorption and interference filters have been demonstrated on surface imagers with an O.D. as high as 8 [18] with thicknesses as small as 16 μm [10], but their angular dependency makes them unsuitable for light-field imagers.

Another method of fluorescence filtering is performing it in the time domain, which relies on the time-lag between the moment of fluorescence excitation and emission. Fluorescence emission is a stochastic process where an excited fluorophore may emit a Stokes-shifted photon with an exponentially decreasing probability over time, typically with time constants of single nanoseconds for widely used fluorophores. This exponential decay of fluorescence intensity can be used as an identifier of the fluorophore, as well as for time-domain fluorescence filtering [19–21].

In order to minimize the implantation cross section of the deep brain fluorescence imager and, in turn, maximize the volume of simultaneously imaged tissue above the detector array, we implemented a time-domain fluorescence filter. Time-resolved fluorescence imagers have typically used discrete laser sources [22–24] or μLEDs [25] as pulsed excitation sources, which are often tabletop or printed circuit-board systems. Rarely are the excitation source and detector integrated onto a single IC [26]. The deep brain fluorescence imager developed here, due to its tight size constraints, uses on-chip integrated gain-switched solid-state LDs as its pulsed excitation source.

Time-gated fluorescence filtering requires two time-critical edges to have sub-nanosecond rise/fall times: the falling edge of the excitation pulse and the rising edge of the detector enable signal. Shortening the fall-time of the pulsed LD illumination and rise-time of the SPAD enable signal have been the two critical design points of the system.

System Design

The deep brain fluorescence imager consists of two laser diode excitation sources, a time-gated fluorescence filter, and an 8-by-64 SPAD detector array. The laser drivers and SPAD array are fabricated on the same custom integrated circuit (IC) using a 0.13 μm bipolar-CMOS-DMOS (BCD) process. Fig. 2a shows the full system including a PC interface, a field-programmable gate array (FPGA) board implementing a finite state machine (FSM) and phase-locked loop (PLL), and the IC connected through a 26-wire flat flexible cable. The two LDs are silver-epoxied on chip by machine-assisted placement.

Fig. 2.

(a) Time-gated imaging system comprising PC, FPGA-implemented PLL and FSM, and IC with two integrated laser diodes and an 8-by-64 SPAD array, (b) Laser Diode driver and (c) single-pixel SPAD quenching and reset circuit, (d) Timing diagram of time-gated fluorescence photometry achieved with two phase-locked clocks, LDON and SPADON.

The LD drivers are designed with the goal of minimizing the turn-off time. Each on-chip LD driver is a three-stage buffer chain with increasing output drive resulting in a peak current drive of 70 mA at the final stage (Fig. 2b). The three consecutive drivers are skewed to favor the pull-down, pull-up, and pull-down transistors across the three stages, respectively, to achieve a fast turn-off of the LDs. Two commercial edge-emitting LDs (Roithner Lasertechnik, CHIP-635-P5), each with a center wavelength of 635 nm and dimensions of 250 μm × 300 μm × 100 μm, are mounted on the surface of the chip facing each other. Denoted as LD1 and LD2, both LDs are switched by a shared clock LDON delivered at 1.5 V logic levels. A level shifter converts this to a 5 V peak-to-peak drive signal, which drives a 100pF load with a fall-time of 700 ps and rise-time of 2.2 ns. On-chip decoupling capacitors (Decaps) between the anodes (LDAN) and cathodes (LDCATH) of LD1 and LD2, 35 and 75 pF in size, respectively, act as charge reservoirs for fast switching. An additional decoupling capacitance of 100 nF is implemented off chip between LDAN and LDCATH.

An FPGA-implemented PLL realizes the time-domain fluorescence filter by phase-locking the two clock signals LDON and SPADON as demonstrated in the timing diagram of Fig. 2d. A 900 MHz clock internal to the FPGA board, further divided into eight phases, allows the rising and falling edges of both signals to be positioned at a resolution of 140 ps. At this resolution, determination of the fluorescence lifetime of the fluorophore is also possible [24]. Once an optimal time-gate position is found for SPADON that yields the most excitation rejection and fluorescent emission collection for a particular fluorophore, it remains static while the FSM cycles through record and readout states.

The 8-by-64 SPAD array, designed with a pixel pitch of 25.3 and 51.2 μm in the X and Y directions, respectively, is driven by a global shutter SPADON, the tum-on edge of which is timed to occur a programmable length of time after the turn-off edge of LDON. All SPADs share a common cathode voltage (SPCATH) set 1.5 V higher than the SPAD’s breakdown voltage (V_BD) of 15.5V (Fig. 2c). Each SPAD pixel’s individual anode toggles between ground and the reset voltage (VRST) to put the SPAD in and out of Geiger mode. At the rising edge of every SPADON cycle, the active reset circuitry (RST in Fig. 2) turns on M1, which sufficiently pulls down the SPAD anode to ground, and leaves it in a high-impedance state such that the SPAD is ready to create an avalanche in response to an incoming photon. M2 provides a high-resistance path at the SPAD anode, which turns off when an avalanche is detected. The event-detection inverter, labeled ‘hv,’ is designed with thick oxide devices to allow for up to 5V range at VRST, and the following logic, including the inverter labeled ‘lv,’ are designed with thin oxide devices to reduce pixel area. The pixel is able to detect up to a single photon per SPADON clock cycle, incrementing a 6-bit ripple counter to achieve a dynamic range of 63. In the read-out state, the FSM cycles through the 9-bit addresses and transfers the 6-bit count of each SPAD pixel to an on-FPGA RAM, and clears the counter in preparation for the next record state. The cycle time, or frame rate, can reach a maximum of 50 kfps, limited by the setup and hold times of the FPGA I/O interface.

The IC consumes 14.1 mW in the 1.5 V digital core and 3.3 V pad frame combined under count-saturating illumination conditions when operating at a 20 MHz repetition rate. The LD drivers consume 9.8 mW when biased at 4.9 V and pulsed at 4% duty cycle, emitting a total irradiance of 1.4 μW. Modeling the imager as a rectangular heat source of 420 μm by 150 μm by 4 mm dimension, the maximum emitted heat flux is 510mW/cm². A study on the effect of heating in cortical implants suggests that a heat flux limit of approximately 24.2mW/cm² keeps tissue temperature increases below 1 ° C [27]. This implies two options for operating the deep brain fluorescence imager: duty-cycling system-level operation to 4.7% or operating in continuous time with a repetition rate of ~1 MHz.

A total of 26 power and signal wires on the IC connect through a flat flexible cable, with careful grounding to prevent crosstalk between LDON and SPADON. The number of wires can be reduced in future versions of the IC with the addition of serializers, on-chip voltage regulators and timing control circuitry. A flip-chip bump bonding approach is used to mount the IC onto a flexible cable with twenty-six 50 μm-wide metal traces with 50 μm spacing, resulting in a total lateral width of 2.9 mm for the cable (Fig. 1). When printed on a 20 μm-thick polyimide substrate, the cable may be rolled up to the width of the IC and inserted through al.8 mm-diameter cannula.

3. Pulsed Laser Diode Illumination

Spatial Illumination Profile

In contrast with free space imaging systems which typically have uniform excitation illumination in the detector’s FoV, this system places two edge-emitting laser diodes on each end of the SPAD array, creating a conical volumetric illumination profile, which must be corrected in the resulting fluorescence image.

Each LD radiates in the shape of a narrow cone along the LD’s waveguide positioned 100 μm above the surface of the SPADs. Due to our inability to measure LD irradiance over all voxels in the imager’s FoV, we measured instead the irradiance of a single LD across azimuthal and elevation angles, and mapped the illumination intensity in 3D space. The irradiance had a full width at half-maximum (FWHM) of 17° and 24° in the azimuthal and elevation angles, resulting in a vertically elongated elliptical beam.

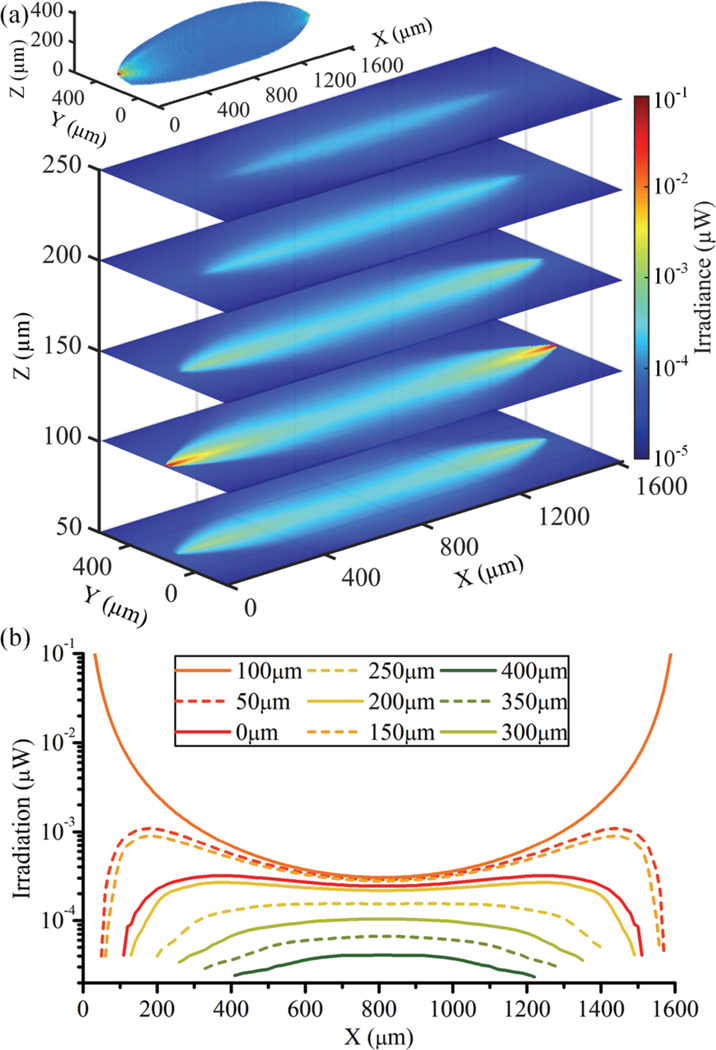
Fig. 3a shows a log-scale colormap of the illumination created by two LDs emitting 1μW each, placed 1600 μm apart. The irradiance received per 10 μm-cubic voxel is shown in the form of five 2D cross sections at different heights above the SPAD array, where the voxel size was chosen to approximate a typical neuronal soma 10 μm in diameter. The inset of Fig. 3a shows a semi-transparent view of irradiance per voxel in the imager’s full FoV. Scattering was not taken into account. The LDs produced a concentrated irradiance along the center of the SPAD array, which is where target neurons will be able to absorb the highest intensity of fluorescence excitation.

Fig. 3.

(a) Illumination profile of two laser diodes facing each other from a 1600 μm distance, emitting 1 μW each, constructed from irradiance measurements of a single laser diode; inset shows a 3D view of the same, (b) Line-scans of irradiance at various Z-heights along the axis of emission (Y=200 μm, Z=100 μm).

Fig. 3b shows line-scans of the illumination parallel to the insertion axis (X-axis) for incremental 50 μm cross-sections of the illumination volume (Z-axis, 0 to 400 μm from the imager). As expected, irradiance per voxel reached its peak at the two cleaved LD waveguides and varied widely with X and Z coordinates. Near the center of the SPAD array (X range 3001300 μm) where the radiation profile becomes relatively uniform, however, the received irradiance ranged between 0.25 to 1 nW for Z distances between 0 and 200 μm. Here, the irradiance varies by a factor of four, allowing for wide-volume single-shot imaging in this region.

Temporal Illumination Profile

In order to characterize the time-domain waveform of the LD pulse, the imager was placed in a dark environment and the SPAD array was allowed to collect direct illumination from the LDs. With an equal repetition rate of 20 MHz, LDON and SPADON clocks were given duty cycles of 4% and 9%, respectively. Due to internal circuit delays, LDON drives the LDs with a near-zero effective duty cycle, creating pulsed illumination. While keeping LDON fixed in phase, SPADON was shifted by steps of 140 ps in a sliding window fashion, essentially performing a convolution between the LD pulse and the instrument response function (IRF) of the SPAD detector. Fig. 4a shows the pulsed LD irradiances for different values of LDAN voltages between 4.3 and 4.9 V, while LDCATH was fixed at a global ground of 0 V. LD Irradiances in this range of bias voltages experience a drop-off of larger than three decades within 1.5 ns after its peak, demonstrating that it is possible to use the imager in conjunction with fluorophores with longer fluorescence lifetimes. Past a 1.5 ns time delay, at which point the LD irradiation has nearly extinguished, the SPAD IRF dominates with a decay rate of one decade every 7 ns, characteristic of a ~3 ns time constant. The IRF is believed to be the result of trapped carriers generated near the multiplication region which subsequently diffuse and are captured in the multiplication region [24]. The measured average irradiance at these forward bias voltages is plotted in Fig. 4b.

Fig. 4.

(a) Time-gated photon count of on-chip laser diode for different values of LDAN, normalized; (b) corresponding peak irradiance of single laser diode, (c) Pulse shape of on-chip laser diode (LDON 20 MHz, 4% duty cycle) and external laser measured with a third-party time-of-flight imager, (d) Time-gated photon counts collected with external pulsed 488 nm laser, using different fluorophore solutions placed over chip: FL-Fluorescein, YG-Fluoresbrite YG, L-latex.

Compared to μLEDs, which achieve fast extinction only at the cost of lower irradiance, and thus require longer integration times to perform time-gating [14], the LDs offer a combination of faster extinction and higher irradiance, enabling the option of high frame-rate imaging.

A third-party time-of-flight SPAD imager (LinoSPAD) was used to confirm the LD pulse shape [28], Plotted in Fig. 4c is an LD pulse biased at LDAN=4.7 V and LDON operating at 4% duty cycle, compared with a supercontinuum laser pulse also at 635 nm (NKT Photonics, SuperK Fianium). A rejection rate of 2 O.D. at 2 ns time delay was measured for the LD, compared to 2 O.D. at 1.5 ns for a 50 ps laser pulse.

Finally, in Fig. 4d, we demonstrate time-gated fluorescence lifetime photometry using the SPAD array while providing illumination with a femtosecond Ti:Sapphire laser (Coherent, Chameleon Vision II), frequency doubled to 488 nm. Three different aqueous solutions were aliquoted into vials: 30 μM fluorescein (FL; fluorescence lifetime of 4.1 ns [29]), green fluorescent microspheres in water (YG; Polysciences, Fluoresbrite YG 10.0 μm; fluorescence lifetime unknown), and 3 μm latex beads in water (L). The vials were placed on top of the detector array and illuminated with a collimated laser beam parallel to the array. The opaque latex bead solution served to diffuse the laser light into the SPADs as a measure of SPAD IRF in the absence of fluorescence. SPAD counts were integrated with an 80 MHz repetition rate and a rolling window of 32% duty cycle. A single-exponential decay fit for photon counts in the time interval of 6–12 ns suggest decay lifetimes of FL—5.5 ns, YG—3.6 ns, and L—2.1 ns, where the lifetime of L suggests the decay rate of the SPAD IRF.

4. 3D Image Reconstruction

SPAD Device Characterization

The signal-to-noise ratio (SNR) and SBR of the deep brain fluorescence imager are dependent on SPAD performance, tissue properties, and LD illumination profiles. It is useful to identify the key contributors of signal, noise, and background. Signal is comprised of fluorescently emitted photons in non-scattering media. Noise can be decomposed into shot noise in signal, shot noise in the dark count, and deflections of signal photons caused by scattering in tissue. Background is the sum of the median dark count and photon counts from insufficiently rejected excitation light, where the latter dominates in our case. To maximize SNR, an optimal value of overdrive voltage V_OV (=SPCATH - V_BD) must be chosen where V_BD for these SPADs is fixed at 15.5 V.

The median photon detection probability (PDP, Fig. 5a) and dark count rate (DCR, Fig. 5b) were measured in an integrating sphere for different values of V_OV in the range of 0.5 to 2.0 V. The integrating sphere provides an isotropic illumination environment for the imager to be tested in. Median PDP reached its maximum between 550 and 600 nm wavelengths, with a peak value still under 1%, which is low relative to other SPAD imagers. The same device without Talbot gratings measured a PDP approximately thirty times higher, showing that the PDP reduction was due to the light obstruction of the gratings [22], Fig. 5b shows the DCR distribution of all pixels in the 512-pixel array. Hot pixels, defined as those with counts larger than five times the median DCR, occupied 2% of the array and their data were removed during 3D reconstruction. Unlike PDP, DCR increases nonlinearly with V_OV (Fig. 5). Hence an optimal value of V_OV exists where the chance of detecting a photon is highest while that of detecting a noise event is lowest. Following a figure-of-merit analysis, we found that the V_OV is optimized at voltages below 1.5 V for a wide range of photon flux [22], We chose to bias SPCATH at 17 V and VRST at 1.5 V, resulting in a V_OV of 1.5 V for the remaining discussions, where the median PDP for detecting 640 nm is 0.48%, and median DCR is 37.9 counts per second (cps) over 512 pixels, corresponding to 0.81 cps/μm² for the 7.7 μm-diameter SPAD aperture.

Fig. 5.

(a) Median photon detection probability versus wavelength and (b) dark count rate for all pixels in the array, for different SPAD overdrive voltages.

Angular Modulation Using Talbot Gratings

The lack of refractive focusing optics results in a resolution that declines rapidly with distance from the array surface. Many have, therefore, used 2D imagers as surface imagers [18, 30], A light-field 3D imager has been implemented using a 2D imaging array with a far-field spatial sampling mask [31], but requires a 200 μm spacer between the imager and mask, which constitutes an excessive displaced volume for implantable imagers. Instead, in this work, we rely on near-field spatial modulation masks in the form of Talbot gratings which are built directly into the CMOS back-end metal layers [32].

Talbot gratings are implemented in Ml, M3, and M5 layers of the six-metal stack to yield sixteen unique angular modulation patterns, with the goal of achieving maximally uncorrelated spatial sampling of voxels in the imager’s FoV. A combination of two directions (X, Y), two angular frequencies (β=low, high), and four grating offsets (0, π/2, π, 3π/2) creates a variety of sixteen unique sets of gratings, two examples of which are shown in Fig. 6a [22]. The ensemble of sixteen gratings repeats periodically for every 8-by-2 pixel group, the periodicity of which is also reflected in the 3D reconstructed image.

Fig. 6.

(a) Top- and side-view layouts of two example Talbot gratings implemented in three back-end metal layers, drawn to scale, (b) Measured angular modulation responses of four chosen pixels with given modulation direction / angular frequency(β) / grating offset.

The angular amplitude modulation for each set of gratings was measured by placing the imager on two orthogonal rotating stages and illuminating it with a collimated light source. The resulting modulation is shown versus elevation and azimuthal angles θ and φ, pivoting around the Z and Y axes, respectively, for four selected pixels (Fig. 6b). The imager uses this per-pixel spatial sampling approach to convert a 2D SPAD count into a 3D back-projected volumetric image.

Reconstruction Resolution

To reconstruct a 3D image from 2D data, the mapping function y=Ax is solved for x, where y is the 512-pixel SPAD count, x is the N-voxel image, and A is the 512-by-N sensing matrix constructed from the 16-pixel angular modulation measurements and coordinates of all pixels in the array. Defining the imaging volume to be the 1600 × 800 × 400 μm³ volume above the SPAD array with a 10 μm voxel grid size, we get a total of 512,000 voxels, resulting in a 512-by-512,000 sensing matrix. The nth column of A is the 512-pixel 2D image that would result from an ideal point source placed at the nth voxel. Given a 2D SPAD image y, the back-projection x = A⁺y yields the least-mean-squares error solution of the 3D scene, where A⁺ is the left pseudoinverse matrix of A.

The point-spread function (PSF) is an imager’s perceived image of an infinitesimally small point source. For an optical microscope, this is a 3D Gaussian blur around the point of interest, and its FWHM is commonly referred to as the system’s resolution. The PSF of this imaging system can be computed by placing an imaginary point source at a voxel, and measuring the computational 3D ‘blur’ around its back-projection. Under ideal conditions of zero noise and background, the pseudoinverse back-projection of a single voxel is formulated as x_PSF = [A⁺A]x_source. Here, x_source is an N-by-1 array which has a value of unity at the chosen voxel and a value of zero everywhere else.

The resulting PSF of an example point source located at Cartesian coordinates [830 μm, 220 μm, 150 μm] is shown in Fig. 7. Fig. 7a shows a 3D model of the point source location, and Figs. 7b-d show YZ, XZ, and XY slices of the PSF, respectively. The Gaussian-fit FWHM along the X, Y, and Z axes are found to be 63 μm, 26 μm, and 51 μm, respectively, depicting the theoretical maximum achievable resolution of the Talbot grating ensemble for this voxel. The nonzero intensity in the voxels surrounding the point source is an artifact created by the overlap in the pixels’ FoVs, with a noticeable periodicity in the X and Y directions matching that of the Talbot grating ensemble (Fig. 7d).

Fig. 7.

Point spread function of an imaginary point source placed at X=830 μm, Y=220 μm, Z=150 μm reconstructed with a 10 μm voxel resolution, (a) 3D drawing of the point source location; cross sections of PSF in (b) YZ-, (c) XZ-, and (d) XY-planes. (e) Box chart of Gaussian-fitted PSF FWHM values, for all voxels located at given Z height; boxes indicate median and 25 and 75 percentiles, and rod terminations indicate 5 and 95 percentiles.

Since the PSF is unique to each voxel, we extend the analysis to all voxels in the imager’s imaging volume and compute the Gaussian-fit FWHM of the PSF across three Cartesian axes. The box chart in Fig. 7e shows the distribution of FWHMs at each Z-height above the imager, revealing that the perceived shape of a fluorescent target will vary with its location. The best, or smallest, of three-axis FWHMs for each voxel is plotted in Fig. 8. Voxels very close to the imager (Z<25 μm) are seen by few SPADs, leading to a decline in Z resolution. Voxels far away from the imager (Z>200 μm) see a linear decline in resolution with increasing Z because angular modulation blurs out with increasing distance. The maximum resolution is, therefore, found in voxels between the Z range of 25 to 150 μm, with median FWHM values under 40, 35, and 73 μm in the X, Y, and Z directions, respectively.

Fig. 8.

Gaussian-fitted PSF FWHM for all voxels in the imaging volume, represented in Z-slices and 3D volumetric view (inset). Resolution at a given voxel is defined as the smallest of PSF FWHM values in the X, Y, Z directions.

We find that the FWHM of the PSF is roughly at the same order of magnitude as the 25.3 and 51.2 μm X- and Y-direction pixel pitch of the SPAD array. The resolution of the imager is expected to improve alongside with tighter pixel pitch. Well-sharing [33] or guard ring-sharing [34] techniques for SPADs have been reported with 8.25 μm and 2.2 μm pitch, respectively.

5. Fluorescent Target Imaging

We demonstrate the imager’s ability to reconstruct a glass micropipette tip filled with red fluorescent microspheres (Polysciences, Fluoresbrite 641 Carboxylate Microspheres 1.75 μm). The tip was placed at Z=100 μm and moved along the X-axis to three different locations: loci, loc2, and loc3. The fluorescent microspheres used are reported to have peak absorption and emission wavelengths of 641 nm and 662 nm, respectively. Fig. 9a shows a brightfield image of the pipette tip located at loc3 (X=990 μm), and Fig. 9b shows an epifluorescence image of the same scene filtered with a 660 nm cut-on dichroic mirror.

Fig. 9.

Glass pipette filled with red fluorescent microspheres placed at Z=100 μm above the imager. Microscope images in (a) brightfield and (b) epifluorescence modes, (c) 2D slices of the pseudoinverse back-projection at indicated Z-heights (20, 100, 200, and 300 μm) with the pipette tip placed at three different X positions: loci, loc2, and loc3.

The time-gated fluorescence image was acquired at a 20 MHz repetition rate while pulsed LDs illuminated the scene with 160 nW of average irradiance each. The 9% duty cycled SPADON signal was positioned with a time delay of 540 ps after the irradiance peak, achieving an excitation rejection of ~1.5 O.D. The SPAD image was acquired over a total integration time of 22.5 ms, which translates to a 44.4 fps frame rate. The photon count rate for a pixel directly under the pipette tip was 2.8×10⁵ counts, converting to an average of 12.8×10⁶ cps, which is far higher than the median dark count rate of37.9 cps.

In order to counterbalance insufficient excitation rejection, a calibration image was taken in the absence of the pipette tip, and subtracted from subsequent pipette tip images. The difference between the images was then back-projected into a 3Dvolume with a 10 μm voxel resolution. Fig. 9c shows Z-slices of the reconstruction at different heights above the SPAD array, with the image resolving the pipette tip most sharply at Z=100 μm, as expected.

Conclusion

An implantable 3D deep brain fluorescence imager was fabricated in a 0.13 μm BCD technology and tested. Fluorescence excitation was provided by pulsed laser diodes on each side of the detector array, and time-gated fluorescence emission was collected by a 512-pixel SPAD array. The timedomain rejection of pulsed excitation light reached 3 O.D. 1 ns after the irradiance peak, reaching O.D. levels of low-end chromatic filters. A future addition of an absorption filter may further enhance the rejection rate, which will improve the system’s SBR, and in turn, allow the imaging of smaller fluorescent targets with higher resolution.

The excitation illumination profile in this work is tied to the properties of the edge-emitting LD. It may be shaped differently with the integration of different light-emitting devices such as vertical cavity surface emitting lasers (VCSELs), or additional optics such as or diffusers or waveguides at the output of the LD cavity. LDs with different excitation wavelengths may also be explored for imaging the wide variety of fluorophores.

The side-viewing, digitally accessible SPAD array leaves room for scalability, as increasing the array size by a factor of two in the long axis only requires an additional address bit, while the cross-section of the system and packaging remains virtually unchanged. This is an advantage over fiber endoscopes which must expand in fiber diameter to deliver larger FoVs. Uniform light delivery over the larger detector array would be a problem, however, and will need to be accounted for during image reconstruction.

The imager, only measuring 420 μm in width, can be used together with a cannula to be inserted several centimeters deep in the brain. The limit of insertion depth is set by the RC parasitics of the flexible cable interconnect, which will hinder clean clock and data delivery past a certain length.

Biography

Jaebin Choi (S’14) received the B.S. degree in engineering physics from Cornell University, Ithaca, NY, in 2011 and the M.S. degree in electrical engineering from Columbia University, New York, NY, in 2012. He worked as a research scientist in the Korea Institute of Science and Technology, Seoul, Korea from 2014 to 2017, and is currently pursuing a Ph.D. degree in electrical engineering at Columbia University, New York, NY. His current research interest is in optoelectronic neural interfaces.

Adriaan J. Taal received the B.S. and M.S. degrees in electrical engineering from Delft University of Technology, Delft, the Netherlands, in 2014 and in 2017, respectively. He is currently pursuing the Ph.D. degree in electrical engineering at Columbia University, New York, NY. His research interests are in optoelectronic circuit design, computer vision, and developing imaging applications for neuroscience.

William Meng (S’20) received the B.S. degree in electrical engineering from Columbia University, New York, NY, USA, in 2020, where he performed research in low-cost ultrasound imaging and SPAD sensors for neural imaging. He is currently pursuing the Ph.D. degree in electrical engineering at Stanford University, Stanford, CA, USA. He spent summer 2018 with the software engineering team at Altair, Sunnyvale, CA, USA, and summer 2020 with the SDR Hardware team at Astranis, San Francisco, CA, USA. His current research interests include CMOS bioelectronics, neural interfaces, and computational imaging. Mr. Meng was a recipient of the NSF GRFP and Stanford Graduate Fellowship (SGF) in 2020.

Eric H. Pollmann (S’ 19) received the B.S. degree in electrical engineering from the Georgia Institute of Technology, Atlanta, GA, in 2017 and the M.S. degree in electrical engineering from Columbia _M University, New York, NY, in 2018. He is currently pursuing the Ph.D. degree in electrical engineering at Columbia University, New York, NY. His research interests are in implantable CMOS fluorescence imagers for applications in biology and neuroscience.

John W. Stanton (S’09) received the B.S. degree (magna cum laude) and the M.S. degree from Case Western Reserve University, Cleveland, in 2008 and 2010 respectively, both in electrical engineering. He is currently pursuing the Ph.D. degree in the Bioelectronic Systems Group at Columbia University in the field of low-power wireless electronics for biomedical applications.

Changhyuk Lee (S’08-M’14) is currently a Senior Research Scientist at Brain Science Institute of Korea Institute of Science and Technology (KIST). He received the B.S. degree in electrical and computer engineering from Korea University, Seoul, Korea, in 2005, and the M.S. and Ph.D. degrees from Cornell University, Ithaca, NY, USA. Before starting his research at Cornell, he worked at Samsung, Chang-won from 2004 to 2006, and he also worked for Com2us, Seoul, Korea, from 2007 to 2008. His Ph.D. work focuses on the light field (Angle Sensitive) photon counting CMOS image sensors, neural interface, and RFIC. He is a recipient of the Qualcomm Innovation Fellowship 2013–2014. His current research interests include optoelectronic neural interfaces, implantable biomedical devices, computational neuroscience and behavioral studies.

Sajjad Moazeni (M’14) received the B.S. degree from Sharif University of Technology, Tehran, Iran, in 2013, and the M.S. and Ph.D. degrees from UC Berkeley in Electrical Engineering and Computer Sciences in 2016 and 2018, respectively. He is currently a postdoctoral research scientist at Columbia University. He spent Oracle America, Inc. in the mixed-signal design group. His research interests are system integration for emerging technologies, integrated photonics, bio and neurophotonics, and analog/mixed-signal integrated circuits.

Laurent C. Moreaux is a permanent Research Scientist for the French National Center for Scientific Research (CNRS), and also a Senior Research Scientist at the California Institute of Technology. He earned an optoelectronics degree from Polytech Paris-Sud in Orsay in 1997, an M.S. degree in optics and photonics from the Institut d’Optique in Orsay in 1998, and his Ph.D. degree in physics at the ESPCI Paris with Drs. Jerome Mertz and Serge Charpak focusing on the development of novel, non-linear optical microscopy tools and methods for biological imaging. He continued as a postdoctoral scholar in the lab of Dr. Gilles Laurent in the Caltech Division of Biology in 2002, and was awarded a permanent Research Scientist position with the CNRS in 2004, where he continued working on the development of optical techniques to probe neuronal activity in several model systems. He returned to Caltech in 2009, where he has since held positions in both the Division of Biology and Bioengineering as well as in the Division of Physics, Mathematics and Astronomy. He has contributed his technical expertise to many projects in neuroscience at Caltech, including developing methods for whole-cell recordings combined with extracellular arrays and two-photon microscopy in the hippocampus of awake and behaving mice. With the current depth limitation of free space optical microscopy, he believes that the use of integrated photonics will allow us to directly bring the microscope “into” the brain to probe the activities of an unprecedented number of neurons. With this vision in mind, his most recent efforts have focused upon fundamental conceptualization, device design, and initial characterization of novel integrated neurophotonic probes.

Michael L. Roukes received B.A. degrees in both physics and chemistry in 1978 from the University of California, Santa Cruz, CA; and the M.S. and Ph.D. degrees in physics in 1985 from Cornell University, Ithaca, NY. Thereafter, he was a Member of Technical Staff/Principal Investigator at Bell Communications Research, Red Bank, NJ. He is currently Frank J. Roshek Professor of Physics, Applied Physics, and Bioengineering at the California Institute of Technology (Caltech), Pasadena, CA, where he has been since Fall 1992. His research has spanned mesoscopic electron and phonon transport at ultralow temperatures, physics of nanoelectromechanical systems (NEMS), biomolecular detection and imaging, ultrasensitive NEMS-based mass spectrometry, and ultrasensitive calorimetry. Dr. Roukes is a Fellow of the American Physical Society, was an NIH Director’s Pioneer Awardee, and was named Chevalier (Knight) of the Ordre des Palmes Académiques by the Republic of France.

Kenneth L. Shepard (M 91–SM 03–F’08) received the B.S.E. degree from Princeton University, Princeton, NJ, in 1987, and the M.S. and Ph.D. degrees in electrical engineering from Stanford University, Stanford, CA, in 1988 and 1992, respectively. From 1992 to 1997, he was a Research Staff Member and the Manager with the VLSI Design Department, IBM Thomas J. Watson Research Center, Yorktown Heights, NY, where he was responsible for the design methodology for IBM’s G4S/390 microprocessors. He was the Chief Technology Officer with CadMOS Design Technology, San Jose, CA, until its acquisition by Cadence Design Systems in 2001. Since 1997, he has been with Columbia University, New York, NY, where he is currently the Lau Family Professor of Electrical Engineering and Biomedical Engineering and the Co-Founder and the Chairman of the Board of Ferric, Inc., New York, NY, which is commercializing technology for integrated voltage regulators. His current research interests include power electronics, carbon-based devices and circuits, and CMOS bioelectronics. He has been an Associate Editor of the IEEE TRANSACTIONS ON VERY LARGE-SCALE INTEGRATION SYSTEMS, the IEEE JOURNAL OF SOLID-STATE CIRCUITS, and the IEEE TRANSACTIONS ON BIOMEDICAL CIRCUITS AND SYSTEMS.