Planning of school teaching during Covid-19

Abstract

Learning and education are two of the biggest world issues of the current pandemic. Unfortunately, it is seen in this work that, due to the length of the incubation period of Covid-19, full opening of schools in the Fall of 2020 seems to be impractical unless the spread of the virus is completely under control in the surrounding region (e.g. with fewer than 5 active cases every million people).

In order to support the possibility of some in-person learning, we model the diffusion of the epidemic within each single school by an SEAIR model with an external source of infection and a suitable loss function, and then evaluate sustainable opening plans. It turns out that blended models, with almost periodic alternations of in-class and remote teaching days or weeks, are generally (close to) optimal. In a prototypical example, the optimal strategy prescribes a school opening of 90 days out of 200 with the number of Covid-19 cases among the individuals related to the school increasing by about 67% with respect to no opening, instead of the about 200% increase that would have been a consequence of full opening. As clinical fraction is low in children, these solutions could lead to very few or no symptomatic cases within the school during the whole school year.

Using the prevalence of active cases as a proxy for the number of pre- and asymptomatic, we get a preliminary indication for each country of whether either full opening, or blended opening with frequent testing, or no school opening at all, is advisable.

Highlights

• •An SEAIR model for Covid and schools, with external source, loss function and control.
• •Optimal opening strategies determined by simulated annealing are blended solutions.
• •An indication for each country of feasibility of school reopening in 2020.
• •Needed for reopening: low prevalence of active cases in the region, frequent testing, and distancing.

1. Introduction

More than one billion students are out of school because of Covid-19 [1]; most of them are now using remote learning practices that present several drawbacks [2] and, in most cases, have been hurriedly arranged.

In addition, in most schools, school districts, and countries there is uncertainty on how to plan school activities for the 2020–2021 school year [3]. As a result, learning and education are two of the biggest world issues of the current pandemic [4], [5]. As we see below, the characteristics of Covid-19, and in particular the length of its incubation period of about $5$ days [6], [7], are such that cases within each single school tend to undergo a multifold increase should the school be completely open in the upcoming school year. This makes full opening of schools impractical unless the epidemic in completely under control in a region, or till a vaccine is available: difficulties have been already experienced by the first reopening attempts [8], [9].

On the other hand, remote teaching has been put together in an emergency situation, and it appears to have badly affected most students [10], [11], [12], especially those from less advantaged contexts [13]. At the same time, it has imposed, and it is likely to impose again, an additional burden on many families. Therefore, the hypothesis of a fully remote 2020–2021 school year is also impractical for different reasons.

To help reconcile such conflicting circumstances, there is thus a need for studies and methods that suggest sustainable opening strategies; they should be aimed at supporting the possibility of some in-person learning while simultaneously containing extra infection transmissions, both at the level of each single school, and in a broader context. In this first work, we focus on a single school. What each school needs is a flexible instrument that incorporates some of the specific details of the school, the students, the personnel, and the surrounding area, and provides indications of the outcome of in-person school activities in terms of the potential spread of Covid-19 within the school. Some of the difficulties in this process are that it is hard to estimate the transmission rate within schools; that the individuals involved in the school are subject to potential external infectious transmissions; that asymptomatics are hard to detect; and that policy makers have to establish a relative importance of the two targets (in-person teaching and Covid-19 containment).

In this paper, we provide a model whose set-up and parameters incorporate several features of Covid-19 dynamics related to a single school, and then outline the optimization process. We then study optimal solutions for a wide variety of plausible values of the parameters of the model, obtaining both an adaptable procedure that can be conformed to specific situations, and general policy indications. Blended solutions appear to be extremely efficient in reducing the potential spread, and together with some detection of asymptomatic cases could offer the possibility of a sustainable planning for the whole year.

Besides containing the Covid-19 diffusion, these solutions could be pedagogically acceptable, and could also become a driving model for the society at large.

2. Methods

2.1. Epidemic model

In this work we focus on a single school. To model the diffusion of Covid-19 among the personnel and the students of the school, we set up a suitable system of ordinary differential equations. In particular, we consider an SEAIR, a version of the SIR model [14], with an external source of infection [15], [16] and a control.

The population is divided into: susceptible (S), pre-symptomatic or, equivalently, exposed (E), asymptomatic (A), infected (I) and recovered (R). Variables are normalized so that $S+E+A+I+R=1$.

We assume that susceptible individuals might become pre-symptomatic or exposed (E) at transmission, entering a latency period in which they have contracted the virus and are contagious, without showing symptoms. The contagion can be caused by contact with other individuals with viral load, at a rate $\beta c\left(t\right)$ ($c\left(t\right)$ is the control, as described below); or, alternatively, it is caused by an infectious contact outside the school taking place at rate $\alpha$. The asymptomatic members of the school community present a challenge, as they cannot be easily detected while still being infectious for a relatively long time: we assume accessibility to some type of fast screening with sufficient sensitivity [17]: the contacts with asymptomatics within the school are then reduced by a parameter $\eta$, the false negative rate of the screening procedure. Exposed individuals either develop symptoms at a constant rate $\delta$, becoming infected, or progress into being asymptomatic with rate $\gamma$. The viral load is carried by exposed (E), asymptomatic (A) or infectious (I) individuals; however, infectious individuals are assumed to be isolated, while a large fraction of asymptomatic (A) is supposed to be detected by the screening procedure. Both asymptomatic and infected individuals recover at rate $\rho$. As COVID-19 mortality is particularly low in a mostly young population [18], we disregard mortality.

The key differences with the usual SEIR model [14] are: an external source of infection [15], [19], the possibility of transmission limited to $7$ hours per working day; a control indicating from the start whether, for each day, schools are open or closed; and the presence of asymptomatic individuals.

With these assumptions, the system of OdE modeling infectious transmissions of concern for the school is:

$$\text{Susceptible:}\frac{dS}{dt}=-\alpha (1-c\left(t\right))S-\beta Sc\left(t\right)(E+\eta A)$$ (1)

$$\text{Exposed:}\frac{dE}{dt}=\beta Sc\left(t\right)(E+\eta A)+\alpha (1-c\left(t\right))S-(\gamma +\delta )E$$ (2)

$$\text{Asymptomatic:}\frac{dA}{dt}=\gamma E-\rho A$$ (3)

$$\text{Infected:}\frac{dI}{dt}=\delta E-\rho I$$ (4)

$$\text{Recovered:}\frac{dR}{dt}=\rho (A+I)$$ (5)

for a certain time interval $[0,T]$. We consider $40$ weeks, and count time in hours, so that $T=6720$. The initial population at the beginning of the school year might be partly immune due to previous infections, but to avoid issues about efficacy and duration of the immunity, we assume that the initial population consists primarily of susceptible, $S\left(0\right)\approx 1$, and a small fraction of exposed, so that $S\left(0\right)+E\left(0\right)=1$.

The function $c\left(t\right)$ describes the control variable, and $c\left(t\right)=0$ for all times when the school is closed; these include all hours except from $8$ am to $3$ pm of those working days in which it has been decided that the classes are in person. For each of the $200$ working days, $c\left(t\right)$ can be $0$ again if remote activities have been decided for that day, or $1$ if teaching is in person. Formally, with $t$ measured in hours, let $\mathcal{M}$ indicate the class of controls $c\left(t\right)$ such that

$$c\left(t\right)=\left\{\begin{array}{c}{c}_{i,j}\text{ if }i=\lfloor t∕168\rfloor ,j=\lfloor (t-168\lfloor t∕168\rfloor )∕24\rfloor \le 5\text{ and }\hfill \\ 8\le t-168\lfloor t∕168\rfloor -24\lfloor (t-168\lfloor t∕168\rfloor )∕24\rfloor \le 15\hfill \\ 0\text{ otherwise }\hfill \end{array}\right)$$ (6)

for some $c_{i,j}\in \{0,1\},i=1,\dots ,40,j=1,\dots ,7$, and $0\le t\le 6720$.

2.2. Mathematical analysis

Lemma 2.1

For each solution of (1) – (5) , the total population $S+E+A+I+R$ is preserved. In addition, $0\le S,E,A,I,R\le 1$

Proof

Let $\varphi \left(t\right)=S\left(t\right)+E\left(t\right)+A\left(t\right)+I\left(t\right)+R\left(t\right)$; we have that $\varphi \left(0\right)=1$ and $\frac{d\varphi }{dt}=0$ for all $t$ from (1)–(5); it follows that $\varphi \equiv 1$ by uniqueness of solutions of linear differential equations.

In addition, $R\left(0\right)\ge 0$ and $R^{\prime }\ge 0$, so that $R\left(t\right)\ge 0$ for all $t$. The other functions have to take the value $0$ before becoming negative by continuity. If $I\left(t\right)=0$ for some $t$, then $I^{\prime }\left(t\right)>0$ unless $E\left(t\right)=0$, and the same applies to $A\left(t\right)$, therefore let us consider the case that $E\left(t\right)=0$. But then $E^{\prime }\left(t\right)>0$ unless $S\left(t\right)=0$. In this last case, (1) implies that all derivatives $\frac{d^{n}S\left(t\right)}{d{t}^n}=0$, in which case $S\left(t\right)\equiv 0$; on the other hand, the system (2)–(5) with $S=0$ and nonnegative initial condition has an explicit, unique solution, which is seen to be non negative.  □

Lemma 2.2

For all initial conditions $\overrightarrow{X}\left(0\right)=(S\left(0\right),E\left(0\right),A\left(0\right),I\left(0\right),R\left(0\right))$ such that $0\le S\left(0\right),E\left(0\right),A\left(0\right),I\left(0\right),R\left(0\right)\le 1$ there exists a unique solution of the system (1) – (5) for all times.

Proof

Let $\overrightarrow{X}\left(t\right)=(S\left(t\right),E\left(t\right),A\left(t\right),I\left(t\right),R\left(t\right))$ and express (1)–(5) as ${\overrightarrow{X}}^{\prime }\left(t\right)=\overrightarrow{F}(c,\overrightarrow{X})$, where $c=c\left(t\right)$ is the control. Notice that the function $F(c,\overrightarrow{X})$ is $C^1$ in the whole of ${\mathbb{R}}^6$, so that $F(c\left(t\right),\overrightarrow{X})$ is $C^1$ in each domain ${\mathcal{R}}_k=\{(t,\overrightarrow{x}):168k<x<168(k+1),\overrightarrow{x}\in {\mathbb{R}}^5\}$, $k\in \mathbb{N}$, where $168$ is the number of hours in a week.

Take $k=0$. Extending $c\left(t\right)=c_0$ for $t\le 0$, the conditions of Peano’s Theorem are satisfied ([20], Ch. 6, Th. 9), so that there is a solution to the initial boundary value problem (1)–(5) for some positive $t$’s. By considering ${\mathcal{R}}_0$ as above, one can see that the solution can be continued to the boundary of ${\mathcal{R}}_0$ ([20], Ch. 6, Th. 11), which is $t=168$. In addition, as each component of $\overrightarrow{X}\left(t\right)$ satisfies $0\le X_i\le 1$ by Lemma 2.1, $\overrightarrow{F}(c,\overrightarrow{X})$ is seen to be Lipschitz in $[0,1]\times \{\overrightarrow{x}:0\le x_i\le 1\text{ for }i=1,\dots ,5\}$. Hence, the solution is unique (see [20], Ch. 6, Th. 1). The same reasoning can now be repeated from $t=168$ and with initial conditions given by the limit $t\to 168$ of the unique solution determined in the previous time interval. As $c\left(t\right)$ has only jump discontinuities, the same procedure can be repeated in each interval, (see [21]), to show that there always exists a unique solution for all times $t$ of the system (1)–(5).  □

Lemma 2.3

If $(S\left(0\right)+E\left(0\right)+A\left(0\right)+I\left(0\right)+R\left(0\right))=1$ then there is a unique stationary solution, namely $S=E=A=I=0,R=1$ , which then attracts the solution for all initial conditions.

Proof

For a stationary solution, ${\overrightarrow{X}}^{\prime }=0$ implies $S=0$ by (1). Then, (2) implies $E=0$, and (3)–(4) imply $A=I=0$. By Lemma 2.1, it must then be $R=1$.  □

We are, however, interested in a finite time interval $[0,T]$, and hence in the transient solution up to time $T$.

2.3. Parameter selection

In the first part of the analysis, we will explore the effect of the opening policies on the number of remote teaching days and infection spreading. For this, we need an appropriate parameter selection. We make a first choice based on current observations, and present results in Section 3, and then evaluate the modifications for a wide range of possible values in the Sensitivity Analysis Section.

As time is counted in hours, we need to scale all available parameter estimates, usually expressed for time counted in days, by a factor of $24$.

Estimates of the daily infection rate $\beta$ are typically around 0.1–0.4 [22]; however, as the school is likely to elicit more frequent contacts, we adopt the somewhat higher value of $\beta =0.9∕24\approx 3.75\times 10^{-2}$ hourly. The value of $\beta$ can also be computed from contact matrices and susceptibility. [23] has contact matrices in school for most countries: averaging the contacts for class ages $0$–$19$ with a factor $16$ for the number of classes, one gets an average number of daily contacts varying between $6$ (Germany) and $20$ (Italy); the contacts need to be revised by the recent containment measures, and related awareness of the population; a reasonable figure would be a factor of $1∕2$. Covid susceptibility (probability of infection upon contact) in school is estimated around 0.01–0.02, see [18] Figure $1\left(b\right)$. As our equations are written for the school population only, which is about $1∕6$ of the total population, one needs to use a scale factor $6$; in addition, one needs to divide by $7$ to have the hourly contact number during school hours. In the end, estimates of hourly $\beta$ range from ${\beta }_m\approx 0.01\times 1∕2\times 6\times 6∕7\approx 2.5\times 10^{-2}$ to ${\beta }_M\approx 0.02\times 1∕2\times 20\times 6∕7\approx 1.7\times 10^{-1}$ (this is a range of 0.175–1.2 for the daily $\beta$), slightly below with our choice above. In the stability analysis we consider the other values in this range.

The duration of the latency period after infection and before symptoms are developed has been estimated at about $5$ days (see for example [6] and [7]), so that $\gamma +\delta \approx 1∕5\times 1∕24=0.2∕24$; the clinical fraction, which is the fraction of symptomatic cases, depends on many factors [24], and it is substantially lower for younger individuals [18]. We take a ratio of about $100$, which is $\gamma =0.198∕24\approx 8.25\times 10^{-3}$, and $\delta =0.002∕24\approx 8.33\times 10^{-5}$ Similarly, the average recovery period is about $7$ days, for mild cases [25], suggesting $\rho =0.14∕24\approx 5.8\times 10^{-3}$; more severe cases (I) are excluded from contacts, so their recovery rate is irrelevant: we use the same value of $\rho$.

The parameter $\eta$ describes how asymptomatic individuals are excluded from contacts with the other individuals; such a separation depends on the availability of detecting tests: we assume that a sufficiently reliable test is available, with a 90% test sensitivity, so that $\eta =0.1$. This assumption is subject to parameter sensitivity analysis in Section 4, where we see that a test sensitivity of at least 45% is needed for our calculations to make sense.

We finally consider the external rate of infection. This is due to encounters of infectious individuals from the schools with others outside of the school; it is primarily based on the prevalence of presymptomatic and asymptomatic individuals in the region around the school. This number is clearly unavailable, but an approximation can be obtained from the prevalence of active cases, which is a well established figure [26]: since about half of the infected shows symptoms, and the symptomatic period lasts longer than (perhaps $3$ times as long as) the asymptomatic, which itself lasts as the presymptomatic period of everyone infected, the prevalence of presymptomatic and asymptomatic together is about the same as the prevalence of active cases; the asymptomatics are not assumed to be detected outside of the school, so we take the prevalence of active cases as a proxy for the prevalence of infectious individuals that can be met outside of the school. A survey of the current situation in about $200$ countries shows that the prevalence of active cases to the population ranges between $1.7\times 10^{-7}$ and $1.2\times 10^{-2}$ (see [26]). This number must then be multiplied by the average number of contacts, similar to what done above to select $\beta$. As external contacts are, for the most part, between students and other individuals outside schools, we use the corresponding matrices in [23], with entries averaged over the various age classes: the averages vary between 6.02 for Germany and 10.5 for Italy; we then add a factor $1∕2$ for reduced mobility and awareness, and $1∕17$ for the $17$ hours in which schools are not open nor remote teaching takes place. Susceptibility is taken again at 0.01–0.02, and the scale factor is $6$. Plausible values of $\alpha$ are then in the range from $0.01\times 6.02\times 6\times 1∕2\times 1∕17\times 1.7\times 10^{-7}\approx 1.80\times 10^{-9}$ to $0.02\times 10.50\times 6\times 1∕2\times 1∕17\times 1.2\times 10^{-2}\approx 4.44\times 10^{-4}$

We take an intermediate external infection rate $\alpha \approx 2\times 10^{-5}$. With this value, in the observation period of $40$ weeks there is a moderate, but non negligible number of cases even if the school is totally closed; with our selection of parameters the individuals infected outside of the school will be about 12.2% of the total. The parameter $\alpha$ will be carefully monitored in the sensitivity analysis, where it is seen that our optimality results are insensitive to the specific value of $\alpha$ provided that this lies in a specific range.

To aid readability, one can consider an approximate conversion factor of 0.02 (to be adapted to local characteristics) between $\alpha$ and the prevalence of active cases: $\alpha \approx 2\times 10^{-5}$ corresponds to an overall prevalence of active cases of approximately $1.8\times 10^{-5}∕0.02\approx 1\times 10^{-3}$ active cases, or $1$ active case in $1000$ people. This conversion factor and the above range of $\alpha$ will also be used to give a tentative indication of which countries can reopen schools and which cannot.

As initial condition, we consider two possibilities. In the first one, we assume that there are a few (about 1%) exposed individuals already present at the start of the school year: we start from $E\left(0\right)=0.01$. All others are susceptible, so $S\left(0\right)=0.99$. In the second, we assume that a careful screening is carried out at the beginning of the school, so we take $S\left(0\right)=1$.

2.4. Planner’s objectives

In the second part of the analysis, we introduce a loss function which incorporates the aim of the planner to maximize the number of days with in-class vs. remote teaching, and simultaneously minimize the number of extra infectious transmissions due the opening of the school. For this, it is essential that the planner determines the relative weight $\tau$ of these two objectives. Once a value of $\tau$ is fixed, the aim of the planner becomes that of minimizing a functional that combines these two objectives by the relative weight. To achieve her/his targets, the planner can fix a school calendar, deciding ahead of time which days are in-class and which are restricted to remote teaching; for simplicity, we consider here a plan for the whole year, but monitoring and en route adjustments can also be incorporated. We remain agnostic as to the value of the relative weight $\tau$, and develop tools to analyze all possible scenarios.

Let $S_0\left(t\right)$ be the fraction of susceptibles at time $t$ in the hypothesis that teaching is completely remote, that is with $c\equiv 0$; $S_0\left(0\right)-S_0\left(T\right)$ is then the fraction of individuals who receive an infectious transmission even if the school never opens; then, let $S\left(t\right)=S_c\left(t\right)$ be the fraction of susceptibles with opening plan $c\left(t\right)$; we have that $S_0\left(T\right)-S\left(T\right)=S_0\left(T\right)-S_c\left(T\right)=(S_c\left(0\right)-S_c\left(T\right))-(S_0\left(0\right)-S_0\left(T\right))$ is the fraction of extra infectious transmissions due to the opening of the school according to plan $c\left(t\right)$. In addition, let $N\left(c\right)=200-{\int }_0^{T}c\left(t\right)dt∕7$ be the number of remote teaching days (the factor $1∕7$ is due to the number of hours that the school is open in a regular day). The loss function combining the two effects is then

$$\mathcal{L}=(S_0\left(T\right)-S\left(T\right))+(N\left(c\right)∕\tau )$$ (7)

where $\tau$ is the relative weight of a day of in-class teaching to infectious transmissions: $\tau ∕100$ can be interpreted as the number of days of in-class teaching that the planner considers equivalent to a 1% increase in the infectious transmissions in the school.

The planner’s objective becomes then

$$\underset{c\in \mathcal{M}}{min}\mathcal{L}$$ (8)

with $\mathcal{M}$ as in (6). It is easy to see that using the system (1)–(5) the optimization problem can be cast in a more standard form [27], [28], in which

$$\mathcal{L}=E_c\left(T\right)-E_0\left(T\right)+{\int }_0^T\left((\gamma +\delta )(E_c\left(t\right)-E_0\left(t\right)+\frac{1}{7\tau }{c}^2\left(t\right))\right)dt$$

where $E_0\left(t\right)$ is the exposed component of the solution of the system (1)–(5) for the case $c\equiv 0$; however, as we optimize over the very restricted class of functions (6), which are piecewise constant and depend on the finite number of parameters $c_{i,j}$’s, the general theory of control optimization is not needed here: (8) becomes a discrete optimization problem.

2.5. Minimization by simulated annealing

Once the parameters have been selected, for instance with the values given in Table 1, we have optimized for each fixed value of $\tau \in [0.5,2000]$ by Simulated Annealing [29]. For simplicity, we assume here that the decision about remote or in-class teaching is taken for each week, so the control $c_i=c_{i,j}$ depends only on $i=1,\dots ,40$. This still includes $2^{40}$ possible policies.

Table 1.

Recap of the model parameters and their selected values.

Parameter	Selected value
$\alpha$	$2\times 10^{-5}$  [h${}^{-1}$]
$\beta$	$3.75\times 10^{-2}$  [h${}^{-1}$]
$\gamma$	$8.25\times 10^{-3}$  [h${}^{-1}$]
$\delta$	$8.33\times 10^{-5}$  [h${}^{-1}$]
$\rho$	$5.83\times 10^{-3}$  [h${}^{-1}$]
$\eta$	0.1

For a fixed value of $\tau$, we take vanishing “temperatures” ${ϵ}_k={ϵ}_0{e}^{-k}$ with ${ϵ}_0\in (0,1]$, and a random initial configuration ${\mathbf{c}}^{\left(0\right)}\left(\tau \right)=\{c_1,\dots ,c_{40}\}\in {\{0,1\}}^{40}$. At iteration $k=1,\dots ,50$, a random position $m$ between $1$ and $40$ is selected and $c_m$ is changed into ${\tilde{c}}_m=1-c_m$, while ${\tilde{c}}_{m^{\prime }}=c_{m^{\prime }}$ for all other $m^{\prime }$’s. The system is solved using the opening rule $\tilde{\mathbf{c}}$, and the loss function is computed in the solution. If the loss decreases, then ${\mathbf{c}}^{(k+1)}\left(\tau \right)=\tilde{\mathbf{c}}$; else, we set ${\mathbf{c}}^{(k+1)}\left(\tau \right)=\tilde{\mathbf{c}}$ with probability ${ϵ}_k$ and ${\mathbf{c}}^{(k+1)}\left(\tau \right)={\overrightarrow{c}}^{\left(k\right)}\left(\tau \right)$ with probability $1-{ϵ}_k$. We then repeat by drawing a new random integer $m$. This is repeated $50$ times for each initial configuration.

The sequence ${\tilde{\mathbf{c}}}^{\left(k\right)}\left(\tau \right)$ tends to a (local) minimum of the loss functional; the output $\tilde{\mathbf{c}}\left(\tau \right)={\tilde{\mathbf{c}}}^{\left(50\right)}\left(\tau \right)$ of $50$ iterations is retained as a candidate (close to) optimal strategies for the given value of $\tau$.

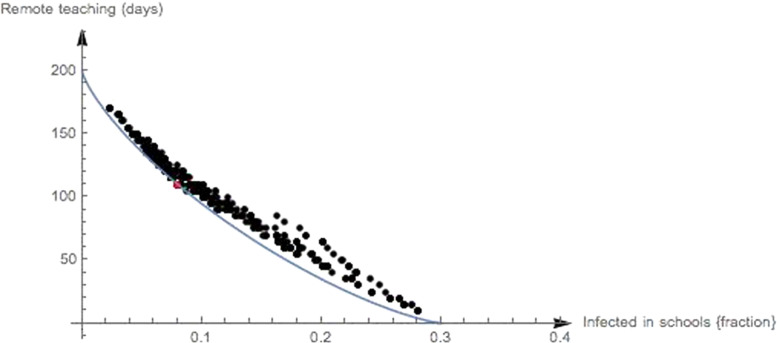
In addition to the above, all the configurations ${\mathbf{c}}^{\left(k\right)}\left(\tau \right),k=1,\dots ,50$, not only the (close to) optimal ones, are recorded for several values of $\tau$, to get an idea of the possible scenarios. Fig. 1 reports remote teaching days vs. fraction of infected in school at the end of the school year for each ${\mathbf{c}}^{\left(k\right)}\left(\tau \right),k=1,\dots ,50$ and for various values of $\tau$.

Fig. 1.

Fraction of extra infected, next to the 12.2%, vs. days of remote teaching, for several opening strategies. The potentially perfect, and hence optimal ones for some values of $\tau$, are close to the continuous curve. One special possibly perfect and hence optimal solution corresponds to the red dot.

3. Results

3.1. Full closure vs. complete opening

As benchmark cases we consider the full closure and the complete opening of the school, which is to say, the two most extreme choices of a fully remote teaching or regular $7$ hours a day in-class activities for the whole year.

As we have assumed that there is a constant source of external infection in the region surrounding the school, even if the school is completely closed, which is $c\equiv 0$, the simulations based on (1)–(5) determine a number of cases. We have simulated the fraction of cases at school year end, and the number of cases in a school of $1000$ individuals in the first two months. The parameters are those selected in Section 2.3, except that we consider a variety of possible rates for the external source of infection.

For example, for $\alpha =2\times 10^{-5}$, we have that with the school completely closed there would be about 12.57% cases (A+I). In a school with $1000$ individuals this means that about $125$ individuals of the school would be infected (with or without symptoms) in the course of the year from contacts outside of the school. At Day $60$ the number of infected individuals showing symptoms is about $28$, and we assume that this is in line with the rate of infection in the overall community.

If the school is completely open, on the other hand, simulations with $c\equiv 1$ show a fraction of infected of about 37.8% at the end of the school year, with already 11.5% of new cases, infected or asymptomatic, in the first $60$ days. In a school of $1000$, one would observe about $115$ cases, with perhaps several symptomatic, in the first $60$ days, vs. the expected $28$ and very likely no symptomatic; a deviation which would not pass unnoticed.

Table 2 compares the percentage of cases at the end of the school year, and the number of likely cases in the first two months, in the two cases of completely remote and fully in-class teaching. The values of $\alpha$ can be either determined from active cases in the area, contact matrix and susceptibility, as done in Section 2.3, or from the fraction of infected (A+I) that it causes at the end of the observation period. This last fraction is called seropositivity, and it is discussed in [30] and [31]). Seropositivity at the end of the school year, assuming the school is closed. is in Table 2, Column $2$. The range of $\alpha$ covers all cases of interest.

Table 2.

Comparison of complete opening vs. full closure for various values of the external rate of infection $\alpha$. Cases include asymptomatic. An initial screening is assumed so that there are no active cases at school start. Column 2 indicates cases per million in the surrounding area; the correspondence with $\alpha$ is based on an average contact rate (see Section 2.3).

$\alpha$$\left[h^{-1}\right]$	Cases per million	$\text{\%}$ cases at school end		Number of cases by 60 days in a school of 1000
		Remote	In-class	Remote	In-class
$10^{-8}$	0.5	0.006	0.1	0	0
$10^{-7}$	5	0.06	1	0	1
$10^{-6}$	50	0.67	7.1	1	7
$10^{-5}$	500	6.5	27.33	14	64
$2\times 10^{-5}$	1110	12.57	37.80	28	115
$10^{-4}$	5000	48.93	70.51	134	353
$10^{-3}$	50000	99.87	99.81	753	859

In Table 2 we assume that there are no active cases in the school at the start of the school year due to a sufficiently accurate initial testing. There is not much difference if we assume a 1% active cases for the largest values of $\alpha$, but this last assumption would not be appropriate for small values of $\alpha$ and hide the possibility of opening the schools with almost no restrictions should the virus be completely under control.

One can see that complete opening of the school determines about a four fold increase in the number of cases, except for the extreme values of $\alpha$. If the virus is completely under control, which is less than $50$ active cases per million, or $\alpha <10^{-6}$, then the number of cases is so limited that schools can be safely reopen completely (with an initial screening and maintaining the physical distancing measures that are controlling the spread of the virus). If, on the other hand, there are more than about $5000$ active cases per million in the surrounding region, or $\alpha >10^{-4}$ then opening of the specific school would not particularly aggravate the situation; but the number of cases is already so high that drastic measures need to be taken, such as keeping all schools closed.

The conclusion is that, except in the extreme situations of almost complete elimination of Covid-19, or uncontrollable outbreak, the number of cases registered in a fully open school is likely to raise concerns from authorities before the end of the second month of school opening in any reasonable scenario; this is very likely to lead to the application of containment measures to the school, such as a forced, unplanned remote teaching. For these reasons, since this situation is likely to occur in most schools and in almost every external evolution of the epidemic, simulations indicate that it is advisable to attempt a sustainable, partial opening. This is the question faced here below.

3.2. In-person teaching vs. epidemic containment

With the reference parameters identified in Section 2.3, we have explored various opening strategies; for each policy $c$ we have recorded the total fraction of infected, measured by the marginal decrease in susceptible $S_c\left(0\right)-S_c\left(T\right)$, and the total number of remote teaching days $N\left(c\right)$. Recall that we consider policies with opening or closure applied for entire weeks.

One can notice that, due to the form of the loss functional, some policies $c$ are uniformly better than others regardless of the value of $\tau$: define $c_1$ as strictly preferable to $c_2$ if $S_{c_1}\left(0\right)-S_{c_1}\left(T\right)\le S_{c_2}\left(0\right)-S_{c_2}\left(T\right)$ and $N\left(c_1\right)\le N\left(c_2\right)$ with at least one inequality strict; if a policy admits another one which is strictly preferable, the first policy can clearly be disregarded. We say that a policy is perfect with respect to the loss functional if there does not exist a strictly preferable one.

On the other hand, once a value of $\tau$ is fixed, an optimal policy for $\tau$ is a policy minimizing the functional in (8). Clearly, an optimal policy for some $\tau$ is perfect with respect to the loss functional, and, vice versa, a perfect policy with respect to the loss functional can be optimal for an interval of values of $\tau$.

In Fig. 1 we plot remote teaching days vs. fraction of infected in school at the end of the school year for each ${\overrightarrow{c}}^{\left(k\right)}\left(\tau \right),k=1,\dots ,50$ and for various values of $\tau \in [0.5,2000]$. Such range corresponds to between 0.5 and $20$ days of in-class teaching rated equivalent to a 1% increase in the number of infected. Notice, though, that Fig. 1 does not allow one to retrieve the value of $\tau$. One of the (likely) perfect opening strategies is represented by the red dot: it is very likely optimal for $\tau$ around $800$. Notice, finally, that the figure reports some, but very few of the strategies that are far from perfect or optimal. There are many others that our runs of the simulated annealing algorithm never visited.

Before turning to the exploration of specific optimal strategies, let us discuss the solid line in Fig. 1. Experimentally, we have noticed that the outcomes of the perfect policies seem to lie close to a specific curve $\mathcal{C}$, which corresponds approximately to

$${\left(\frac{x}{0.3}\right)}^{0.76}+{\left(\frac{y}{200}\right)}^{0.76}=1,$$ (9)

where $x$ is the percentage of Covid-19 cases in the school population, and $y$ is the number of remote teaching days. The curve $\mathcal{C}$ can be thought of as parametrized by $\tau$, the relative importance of in-class teaching and Covid-19 cases; in an abstract sense, each point on the curve $\mathcal{C}$ corresponds to one value of $\tau$, although, as mentioned above, by the discrete nature of the opening strategies, more values of $\tau$ give the same perfect strategy. As indicated before, the red dot corresponds to a perfect strategy which is optimal for $\tau \approx 800$ (see below).

The curve $\mathcal{C}$ is of both theoretical and practical importance. In fact, 0.76 turns out to be a characteristic exponent of the comparison of opening days vs. extra infected; theoretically, it is quite interesting to explore the analytical reasons behind the appearance of such a curve; its role in the analysis of the solutions of the differential system (1)–(5); and the functional dependence of the value of the exponent on the values of the parameters in the system. In practice, if one was able to have some information about the dependency of the exponents from the parameters of the model different from $\tau$, this would give an explicit benchmark for perfect strategies: for instance, if one fixes the number of opening days, then the curve indicates the best result that can be ideally achieved in the containment of the infection, or vice versa, without the need of an explicit numerical minimization.

3.3. Optimal policies

In this section we show one example of (nearly) optimal policy. As mentioned, a choice has been required by the policy maker: such a choice could have consisted of the minimal number of opening weeks, or of the maximal fraction of cases which is allowed by the circumstances. However, we adopted the less intuitive, but more intelligible possibility of using the relative weight of remote teaching vs. percentage of cases, as incorporated by the parameter $\tau$ (see Section 2.4).

We consider the parameters identified in Section 2.3 and $\tau =800$, which means that $8$ days of remote teaching are considered equivalent to a 1% increase in the number of cases. The aim of the planner becomes then to solve the optimization problem (8), with the functional $\mathcal{L}$ defined in (7). This can be achieved by a discrete optimization in ${\{0,1\}}^{40}$. We use here simulated annealing with $50$ iterations from a random seed, repeated for $100$ random initial conditions. The (possibly) perfect opening strategy indicated by the algorithm is

$$(0,0,1,0,1,0,1,0,1,0,0,0,1,0,1,0,1,0,1,0,1,0,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1)$$ (10)

where $0$ indicates a week of remote, and $1$ a week of in-class activities; notice that there is an initial period of closure, before progressing to a regular alternation of openings and closures. This is due to the assumed presence of 10% of cases at the start of the school year, and could be avoided with a very efficient screening before the start of the school year.

The solution in (10) has $90$ days of in-class teaching, with the additional infectious transmissions contained to 8.4%, which is an increase of 67% of the cases with respect to remote only activity. In a school of $1000$ individuals this corresponds to creating an extra $84$ cases of COVID-19 in the school year, in addition to the $125$ who would have been infected in any case. The administrators can decide to realize a stricter or more relaxed containment of the extra cases by assigning more or less weight to infectious transmissions.

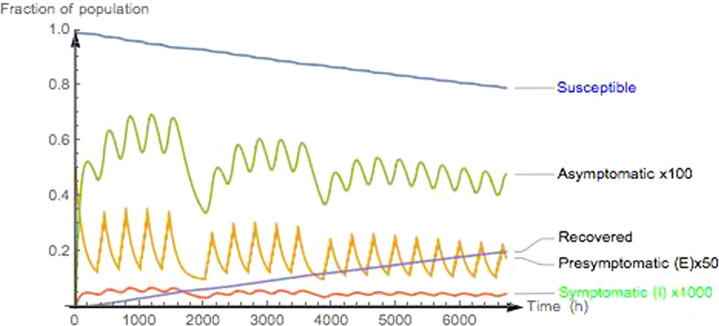
Notice that the solution in (10) is quite periodic, with alternated weeks of in-class and remote activities; Fig. 2 shows the evolution of the epidemic trajectories under the policy in (10). Table 3 summarizes the change in infectious transmissions with the solution in (10); notice that there is an increase of 67% in the number of the positive cases due to the $90$ days of school opening vs. an increase of 200% if the school was open all the $200$ days. This realizes an effective containment of the extra diffusion of the virus, while still having the possibility of offering a substantial portion of the teaching in person.

Fig. 2.

Epidemic functions under the, presumably optimal, policy in (10). For visualization purposes, variables are multiplied as indicated. Time is in hours.

Table 3.

Performance of optimal and random solutions with 90 days of in-class teaching. First 4 columns: total number of infectious transmissions; last 3 columns: percentage increase with respect to remote only solution. “Optimal” refers to the policy in (10) identified by simulated annealing.

	Cases by school year end				Increase w.r.t. full closure
	Remote	Optimal	Random	In-class	Optimal	Random	In-class
$\text{\%}$	12.57	20.99	$23.96\pm 1.25$	37.80	67	$90.61\pm 9.94$	200

We have also explored the possibility of selecting at random which weeks to open or close, with the constraint of having $90$ days of in-class activities, which is to say $18$ open out of the $40$ weeks. A simulation of the distribution gives that the increment in the number of cases is 90.61% on average, with a Standard Deviation of 9.94%, hence the solution in (10) is more than $2$ SD’s below what the average random selection would provide; in addition, it is also not subject to possible adverse fluctuations, so it is definitely preferable to a random, unjustified selection. It is, however, the case, that adopting a blended model with alternated open and closed weeks does provide in any case, even without optimization, a sizeable containment of the infection within the school.

In Section 4 we carry out a sensitivity analysis, which shows that the optimal planning is pretty stable in case of some extra opening or remote days, and is only moderately affected by errors in parameter selection, within certain ranges.

3.4. Pedagogical considerations about blended models

The optimal solutions turn out to be blended models, with approximately one week of in person teaching, and one week of remote learning. The pedagogical aspects of such models have been examined in various researches, for instance [32], [33].

It turns out that there are several advantages in blended learning:

• •in the current context, it seems to allow a sustainable programming of school operations;
• •it permits to take advantage of both in person and remote teaching, limiting drawbacks of both; one can, for instance, shift in person tests and labs to the in-class weeks, and reserve less participative moments for remote teaching;
• •in general, it allows the use of a variety of learning modes and methods;
• •it can provide a pedagogical experience that can be replicated and expanded in the future in order to exploit new technologies while keeping regular personal contacts;
• •it can be flexibly adatpted in some ways, should a sudden change in conditions occur.

Of course, there are challenges, in particular concerning the ability of teachers and students to master the needed technologies and the alternating formats [32], [33].

In addition, as schools could attempt planning in advance, especially if this is coordinated for most schools in some location, the regular economic and social activities could be somewhat adapted to the school calendar; for instance, more working hours could be planned during the weeks in which schools are open.

Clearly, there are several difficulties in implementing blended strategies, but the alternative, which is already unfolding in many situations, seems to be chaotic schedules, with schools attempting full openings, and then suddenly going back to closure as the first COVID cases surface.

3.5. Sensitivity analysis

We provide a sensitivity analysis in four parts.

The first part concerns errors in the determination of the optimal solution. If one of the weeks for which remote teaching is planned by the optimal solution is instead changed to an in-class week, then the increment in the number of cases due to school opening ranges from an extra 72% to an extra 78%, compared to the extra 67% of the optimal solution. If one week is moved remote from in-class, then the increment in the number of cases is reduced to about 64%. This suggests that altering the number of weeks of opening is not optimal, but does not substantially change the final outcome: therefore, once an optimal policy has been determined, extra openings or closures can be adopted if needed without major changes in the final outcome. In addition, once the flexible blended model has been adopted, one can quickly and easily adapt to major changes in the external conditions, such as a sudden outbreak or a vaccine.

The second part of the sensitivity analysis concerns each of the parameters of the model used to determine the optimal solution in (10). We assume that the optimal policy has been determined, and observe deviations from the expected performance due to possible errors in the parameter determination.

For each possible value of the parameters, we compute the fraction of cases if complete closure $f_{cc}$, full opening $f_{fo}$, or the optimal solution $f_{opt}$ are adopted. Then compare the percentage increase of optimal solution with respect to complete closure $(f_{opt}-f_{cc})∕f_{cc}$ with the analogous increment for the full opening $(f_{fo}-f_{cc})∕f_{cc}$. Such comparison is reported in Table 4 for the largest and the smallest value of $(f_{opt}-f_{cc})∕f_{cc}$ in the given range of the parameter.

Table 4.

Sensitivity analysis. For each parameter, the second column gives the tested range; the third column indicates the change in number of cases compared to the change in case of full opening for that value of the parameter in the indicated range which gives the minimal increase in infection rate, i.e. $(f_{opt}-f_{cc})∕f_{cc}$ vs. $(f_{fo}-f_{cc})∕f_{cc}$ where $(f_{opt}-f_{cc})∕f_{cc}$ is minimal; the fourth column reports the case in which the increase $(f_{opt}-f_{cc})∕f_{cc}$ is maximal. The last column reports the range in which the optimization is effective, but the number of cases doubles at the most, i.e. $(f_{opt}-f_{cc})∕f_{cc}\le min(1∕3(f_{fo}-f_{cc})∕f_{cc},1)$ .

Parameter	Test range	Minimal effect	Maximal effect	Range
$\alpha$ (h${}^{-1}$)	$10^{-7}\text{–}10^{-4}$	$19\text{\%}\text{ vs. }44\text{\%}$	$307\text{\%}\text{ vs. }18925\text{\%}$	$10^{-6}\text{–}10^{-4}$
$\beta$ (h${}^{-1}$)	$1.25\text{–}9.75\times 10^{-2}$	$5\text{\%}\text{ vs. }15\text{\%}$	$329\text{\%}\text{ vs. }626\text{\%}$	$1.25\text{–}5\times 10^{-2}$
$\gamma$ (h${}^{-1}$)	$5.25\text{–}23.25\times 10^{-3}$	$12\text{\%}\text{ vs. }37\text{\%}$	$97\text{\%}\text{ vs. }400\text{\%}$	Whole range
$\delta$ (h${}^{-1}$)	$3.33\text{–}233\times 10^{-5}$	$40\text{\%}\text{ vs. }150\text{\%}$	$61\text{\%}\text{ vs. }256\text{\%}$	Whole range
$\rho$ (h${}^{-1}$)	$8\text{–}200\times 10^{-4}$	$44\text{\%}\text{ vs. }171\text{\%}$	$133\text{\%}\text{ vs. }487\text{\%}$	Whole range
$\eta$	$2\text{–}20\times 10^{-2}$	$43\text{\%}\text{ vs. }167\text{\%}$	$179\text{\%}\text{ vs. }555\text{\%}$	$0.02\text{–}0.45$

In addition, we indicate of each parameter the range of values for which the optimal solution achieves a substantial reduction with respect to complete opening, but limited to determining at most an 100% increase in the number of cases with respect to school closure.

We see that the most critical parameters are $\alpha$, $\beta$ and $\eta$.

The range of $\alpha$ in which the optimization process has a chance of being effective is $10^{-6}\text{-}10^{-4}$, which corresponds to about $50$ to $5000$ active cases per million in the area around the school.

For the infection rate $\beta$, the range in which optimization is effective is $1.25\text{-}5\times 10^{-2}$; this is a very critical parameter, as observations in different countries lead to a range of $2.5\times 10^{-2}\text{-}17\times 10^{-2}$. So, each region or country should monitor this rate and introduce strict measures to keep $\beta$ within the above limits.

Finally, the fraction of undetected asymptomatic $\eta$ must not exceed 45%: we assume availability of an easy, rapid and cheap test with a sensitivity of at least 55%, such as CRISPR [34].

The third part is about the selection of $\tau$. In fact, the sensitivity to $\tau$ has already been discussed in Section 3.2: Fig. 2 shows that the optimal strategies lie approximately on the curve $\mathcal{C}$ described by Eq. (9); even if the equation is not exact and the dependency on $\tau$ is not known analytically, it nonetheless gives an idea of the variability of the optimal solutions as function of $\tau$. The data plotted in Fig. 2 has been obtained with $\tau$ ranging from $200$ to $1400$, which corresponds to a range between $2$ and $14$ days of in-class teaching equivalent to a 1% of extra cases. There is at most doubling of the cases for $\tau \ge 700$, and, correspondingly, for at least $85$ of remote teaching. This seems to indicate that next school year will allow no more than $115$ days of in-class teaching without pharmaceutical progress; recall that possibly one of two extra weeks can be gained with an efficient initial screening.

The last part of the sensitivity analysis is about the weekly schedule. A possible alternative is to schedule opening or closure of the schools for each single day (still with a calendar fixed in advance). The optimization is now over $2^{200}$ possible policies. Optimization by simulated annealing in this case determines a plot similar to that of Fig. 1. For instance, the optimal policy for $\tau =800$ gives an increase of 65.24% in the number of cases, vs. the 67% increase of the weekly schedule; the daily schedule consists of $89$ of in-class teaching, instead of the $90$ which are considered by the weekly schedule. In summary, the daily schedule turns out to offer little advantage with respect to the weekly option, but a more complicated implementation process.

4. Summary and discussion

4.1. Summary

We have considered the issue of planning in-class activities for the school year ’20–’21. Education is, in fact, one of the areas in which the measures to contain the current Covid-19 pandemic have had a negative impact, with many countries and local authorities struggling to find acceptable plans for the next academic year. In this work we have focused on a single school.

To aid the planning of teaching for the school, we have modeled the evolution of the Covid-19 epidemic in the school by an extension of the SIR model, with asymptomatic; an external, constant, source of infection; interactions within the school happening only during the $7$ hours of opening during week days; a reduced rate of encounter with asymptomatic due to a somewhat efficient screening system applied weekly. We have then determined realistic values for the remaining parameters of the model.

Next, we have set up an optimization problem, based on a preliminary assessment by the planner of the relative importance of ensuring in-class teaching vs. containing the epidemic spread. For each value of such relative importance and of the other parameters, we have carried out a discrete optimization by simulated annealing to obtain a (close to) optimal strategy within the space of all possible weekly opening policies.

4.2. Related studies

Modeling of epidemic outbreaks by differential equations dates back to the original paper by Kermack and McKendrick [35], with an enormous number of recent works on the current Covid-19 outbreak. Among these, [36] discusses the impact of reopening various combinations of schools in England vs. keeping schools closed; results in [36] are expressed in terms of the reproduction number $R_0$, and show that, in many cases, opening of all schools would bring the reproduction number above the critical value of $1$. Our model has many fewer categories and variables, and it is focused on one single school. In any case, our results also confirm that opening all schools is not advisable in UK, even with extra testing and blended models (see Supplementary Material).

As far as optimization is concerned, methods similar to those used in this paper have appeared in many other contexts. In particular, several recent studies have considered optimal planning strategies in response to general epidemics [14], [37] or, more specifically, to the COVID-19 pandemic [28], [38]; to our knowledge, however, none has considered the current optimization problem for school planning.

4.3. Limitations

There are several limitations to our study. We use a variation of the SIR model, in which we have averaged encounter rates and susceptibilities over several age classes and different countries to obtain reasonable parameters. It could be that local deviations from the values we have used might lead to sensibly different outcomes.

The model includes no randomness, which, however, is an essential feature of both human interactions and virus spreading; randomness would also allow us to assess the variability of the predictions. As a result, there are no error bars in our predictions, except for the case of a random selection of the weeks of in-person teaching.

The external infection rate is taken to be constant, as focusing on a single school does not allow us to model the evolution of the epidemic in the overall area. This rate, however, is not likely to be constant over a long period of time, but is subject to many variations due to expansion or containment of the outbreak.

In addition, our results are only a first indication of a modeling methodology for the search of an optimal trade off between in-class teaching and containment of infectious transmissions. Even if parameters are carefully and realistically selected, the values are based on information known at the time of this study; when a parameter has a wide range of variability we settle for one representative value; in addition, the worked out examples refer to an ideal school: for each particular concrete situation, one needs to adapt the model to the specific case.

We also did not consider other alternatives, such as reducing the number of in-class students for each lesson. Many possible alternatives could be conveniently incorporated in a more elaborate model.

4.4. Conclusions

First, we have seen in Section 3.1 that the regular opening of a typical school would cause a multifold increase in the number of cases among the individuals involved with the school itself, both at $60$ days and at school year end. The only exception would be if the virus is under tight control in the region around the school, which is to say with less than $50$ active cases per million, in which case one can safely plan a complete reopening. If there are more than about $5000$ active cases per million in the surrounding region, then the opening of the school would not particularly aggravate the situation; in that case it would, however, not be advisable to carry out any in person activity as the number of cases would be out of control (at least 35% of the school population in the first $60$ days of opening).

The second conclusion, discussed in Section 3.2, is that careful planning of the opening weeks is capable of making a drastic reduction on the number of extra cases induced by opening the school. Optimal or close to optimal solutions consist of blended models, with an alternation of weeks of remote and in-class activities; with about half of the weeks in class, for instance, one can reduce the increase in the number of cases by a factor of $3$; we have also seen that schedules with a choice between in-class and remote on a daily basis would not improve the reduction much. The likely cause of the need for the weekly alternation is the duration of Covid-19 incubation period.

The third result, in Section 3.3, is that to identify an optimal opening strategy suitable for a specific situation, planners are first required to explicitly incorporate into their objective the relative value of in-person teaching vs. reduction of Covid-19 spread; once this is done, optimal or close to optimal solutions can be numerically estimated to produce one of the optimal or close to optimal strategies mentioned above. A random choice of the weeks of in-class activities would not reduce the number of new cases as effectively as an optimal choice, but would nonetheless achieve a substantial reduction with respect to full opening. In Section 4 we have also seen that the achieved reduction is preserved by small changes in the weeks of in-person activities. As such, one school could identify the number of in-class days or weeks, and slightly adjust the calendar to other needs.

Finally, in Section 4, we have carried out a sensitivity analysis of the results. These have turned out to be rather stable for small errors in the selection of the model parameters. The more critical parameters are

• •the contact rate during school opening, a parameter which should be very carefully monitored and controlled via physical distancing and other measures;
• •the fraction of detected asymptomatic, for which schools should adopt some frequent and possibly not very expensive testing procedure; there is no need to have an exceptionally high reliability of the test itself, and we have shown viable opening policies based on sensitivity above 55%;
• •the external risk rate: as mentioned, one can achieve some control on the spread of the virus in the school only if there are no more than about $5000$ active cases per million in surrounding area.

Based on the above broad indications, and pending adaptation to specific situations, we have determined for each country whether full opening is feasible, or whether a blended opening of schools for about half of the weeks, with systematic quick testing of all students and personnel, and physical distancing within the schools, would be sustainable. Or whether, finally, school opening is not advisable in the current situation (see Supplementary Material).

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Communicated by V.M. Perez-Garcia

Appendix A. Supplementary data

The following is the Supplementary material related to this article.

MMC S1

Worldwide School Opening Opportunities.