Is there a social cost of randomization?

Abstract

Randomized controlled trials, which randomly allocate benefits to a treatment group and not a control group, ascribe differences in post-treatment welfare to the benefits being allocated. However, it is possible that potential recipients’ welfare is not only affected by the receipt of the program, but also by the allocation mechanism (procedural utility). In this paper, we ask whether potential recipients support or oppose random allocation of financial benefits, by allowing them to reward or punish an allocator conditional on her choice of allocation mechanism: direct allocation to one recipient vs. randomization among potential recipients. We find that when potential recipients have equal endowments, they on average reward the allocator for randomizing. When instead there is inequality in the potential recipients’ endowments, the relatively poorer recipients punish allocators who randomize, while the relatively richer potential recipients neither reward nor punish the allocator for randomizing. Our results suggest that an allocator who chooses to randomize between potential recipients with unequal endowments imposes a social cost on the relatively poorer potential recipients.

1. Introduction

In 1662, the Belgian physician van Helmont proposed one of the first randomized controlled trials in medicine. He suggested randomly assigning patients to a bloodletting treatment and a control treatment without bloodletting, and then ask “how many funerals both of us shall have” (van Helmont 1662). The 19th century saw the advent of systematic randomized trials in medicine (Silverman and Chalmers 2001). More recently, randomized controlled trials are widely used in the evaluation of social programs in both developed and developing countries (Fisher 1925; Newman et al. 1994; Harrison and List 2004; Duflo and Kremer 2005; Thomas 2010). In these trials, participants usually know that they are randomly assigned to experimental conditions. If participants only care about final allocations, the choice of allocation mechanism should not affect outcomes. However, if participants care about procedural fairness in addition to final outcomes, they may experience changes in welfare and/or behavior as a result of the allocation mechanism, potentially leading to bias in observed means and treatment effect estimates. In this paper, we present a simple laboratory demonstration which suggests that individuals do respond to randomization as an allocation mechanism: in our laboratory experiment, potential recipients of a benefit punish an allocator for choosing randomization rather than direct allocation as the allocation mechanism. This finding suggests that there is a social cost, or procedural disutility, of randomization (Frey et al. 2004): potential recipients regard randomization as unfair and are willing to signal their opposition to it through costly punishment.

Random allocation of benefits and burdens has often been thought to be acceptable or preferred on a priori theoretical grounds, especially when resources are scarce (Lockwood and Anscombe 1983; Lilford and Jackson 1995; Toroyan et al. 2000). Furthermore, random allocation of interventions has scientific advantages: randomization ensures that the treatment and control groups are statistically identical, and thus allows attributing any differences in behavior or welfare outcomes to an intervention. It is due to this feature that RCTs are so widely used in clinical trials (Sacks et al. 1982) and, more recently, the evaluation of social programs (Duflo and Kremer 2005).

Whether potential recipients regard randomization as fair has only been tested in a handful of studies, all of which are survey-based. Hillis and Wortman (1976) provide survey evidence showing that randomization for scientific purposes is perceived to be permissible when the study is scientifically necessary; however, these authors also find that scarce resources are not regarded as a sufficient justification for randomization. Innes (1979) found that college students reported high perceived moral justifiability of randomization of juvenile offenders into institutionalization vs. family therapy. In contrast, Erez (1985) surveyed prison inmates about their opinions regarding four different selection criteria for special beneficial programs: need; merit; first come, first served; and random assignment. Need was perceived as the fairest allocation criterion, and randomization as the least fair. Similarly, Johnson et al. (1991) found that people generally deem randomization to be unacceptable in clinical trials when one treatment is better than the other; even when expert opinion about which treatment is better is split 80% vs. 20%, only 3% of respondents find randomization acceptable. However, randomization is deemed more acceptable when the treatment is not a life-saving intervention. These findings echo Gary Burtless’ (1995) claim that “except among philosophers and research scientists, random assignment is often thought to be an unethical way to ration public resources.”

Thus, previous research on the perceived fairness of randomization has yielded mixed results. In addition, it is based on survey responses, which can differ from behavior in incentivized settings (Konow 2000; Falk and Szech 2013). Surprisingly, we know of no study that has gone beyond using surveys and tested whether potential recipients support or oppose randomization in an incentive compatible fashion. The purpose of the present study is to fill this gap. We set up experimental groups of three participants, in which one allocator decides how to allocate an indivisible prize of CHF 5 (equivalent to approximately USD 5) to one of two potential recipients. The allocator can choose between allocating the prize directly to one of the two potential recipients, or to let the computer randomize between the potential recipients with equal probabilities. We then ask whether the potential recipients support or oppose the different allocation mechanisms by allowing them to either reward or punish the allocator conditional on her allocation choice. Importantly, we elicit this information in an incentive-compatible way, as rewards and punishments of the allocator are costly to the potential recipients. In addition, we ask whether differences in endowments between potential recipients affect their reward/punishment behavior; for instance, when one potential recipient is relatively poorer than the other, we might expect that random allocation is perceived as less acceptable by the relatively poorer recipient. Finally, we test whether uncertainty about the distribution of endowments between the potential recipients affects their behavior; for instance, we might expect that uncertainty about initial endowments makes randomization more acceptable.

We hypothesized that there would be a social cost of randomization, in the sense that recipients would reward randomization when endowments are equal, but that the poorer recipients would punish randomization when endowments are unequal. Indeed, we find that when recipients have equal endowments, they support randomization on average, in the sense that they reward the allocator for randomizing. In contrast, when recipients have unequal endowments, recipients on average punish the allocator for randomizing. This finding is driven by the relatively poorer recipients, of which 21% punish the allocator for randomizing, while 69% award exactly CHF 0, and 10% reward the allocator for randomizing. The relatively richer recipients on average neither reward nor punish randomization. The magnitude of the effect is small, with the average punishment amounting to 1 % of the relatively poorer recipients’ endowment; however, this response is a lower bound on the social cost of randomization borne by this group. In addition, this study is a laboratory proof of principle; future work should quantify the magnitude of the effect in field settings.

The main goal of our study is to illustrate that randomization is potentially associated with a social cost among potential recipients, especially those who are poorer. However, our study also contributes to several literatures in behavioral economics: second-party punishment, willful ignorance, responsibility aversion, and procedural vs. outcome fairness. To see the connection to second-party punishment, note that our design is a modified dictator game, in which the second mover has a punishment option.¹ Because the allocator’s endowment remains constant across conditions, any differences in reward or punishment must stem from differences in recipient endowment. Our findings therefore complement and extend previous work on second-party punishment by (1) including a randomization option for the first mover, and (2) showing that reward and punishment can depend on the recipient’s endowment relative to a third player. In this context, our findings also shed light on existing theories of second-party punishment, summarized in Leibbrandt and López-Pérez (2012). Our findings are inconsistent with both selfishness motives and inequity aversion (Fehr and Schmidt 1999), since reward or punishment of the allocator does nothing to offset the payoff distance between the recipients.² They are also inconsistent with an efficiency rule (López-Pérez 2008) because allocations in our setup are always efficient; with spiteful punishment (Kirchsteiger 1994; Levine 1998), which predicts no differences across conditions; with an anti-greed rule (Levine 1998) because the allocator in our setup cannot be greedy; and with competitiveness, because allocator reward/punishment does not alter the other recipients’ payoff. In contrast, our results are consistent with an equity rule (Elster 1989; López-Pérez 2008), which implies punishment of allocators who generate the largest payoff distance among recipients; with a maximin rule, which predicts that punishment occurs when allocators do not maximize the minimum payoff across the two recipients; and with reciprocity (Rabin 1993; Dufwenberg and Kirchsteiger 2004), in that poor recipients appear to wish to harm allocators who do not allocate directly to them. We do not attempt to further distinguish between these theories, as our primary motivation is to ask how recipients respond to randomization.

In addition, our paper also contributes to the literature on willful ignorance, in two ways. First, Bartling et al. (2014) find that ignorance reduces third-party punishment for unfavorable final allocations, but that third parties punish dictators for remaining willfully ignorant instead of informing themselves about the consequences of their actions. We show that this finding also holds in a second-party punishment setting, but only when endowments are unequal: recipients punish allocators who randomize when recipients have unequal endowments, but reward randomization when endowments are equal.

Second, the original finding in the willful ignorance literature is that dictators have a preference for leaving outcomes uncertain when it allows them to shroud their own self-interested behavior (Danaet al. 2006). In our analysis of allocator behavior, we find that allocators randomize between recipients more frequently than is optimal to maximize their own payoff. This finding holds regardless of whether actual recipient responses or allocator beliefs about these responses are used as the metric for payoff maximization suggesting that allocators have a preference for randomization. Thus, we find that allocators prefer ignorance even at a cost to themselves, which is consistent with willful ignorance. It should be noted, however, that this finding is also consistent with responsibility aversion (see e.g. Alan et al. 2016), and we are not able to distinguish between these two motivations for allocator behavior with our design.

Finally, our findings also contribute to the literature on procedural vs. outcome fairness (Frey et al. 2004; Bolton et al. 2005; Trautmann 2009; Krawczyk 2009). The fact that recipients punish allocators for randomizing suggests that they care about procedural fairness at least to some extent. In addition, the finding that allocators show a preference for randomization that differs from that of recipients suggests that allocators and recipients prioritize different types of fairness: allocators focus more on procedural fairness, while recipients care more about outcome fairness.

The remainder of the paper is organized as follows: Sect. 2 outlines the experimental setup; Sect. 3 reports the econometric approach and results; Sect. 4 concludes.

2. Design and procedures

2.1. Participants

We recruited 105 participants from the subject pool at the University of Zurich. Their mean age was 22.08 ± 3.31 (mean ± S.D.). We excluded students of economics and psychology to avoid “professional” participants who are highly familiar with tasks such as the one studied here. All participants gave written informed consent. There was no show-up fee; remunerated was based on the outcome of the tasks, described in detail below. An experimental session lasted 2 h.

2.2. Session structure

The experiment was conducted in three sessions with 36, 36, and 33 participants, respectively. Participants were seated at networked computers in the behavioral laboratory of the Department of Economics at the University of Zürich. Each participant was randomly assigned the role of Allocator or Recipient at the beginning of the session and kept this role for the entire session. The sessions were divided into two parts: the main experiment and the belief elicitation. The main experiment consisted of two blocks and each block consisted of six trials. In each trial participants completed a task in groups of three, with two potential recipients and one allocator. All participants knew their own role and those of the other players, but did not know the personal identities of the other players. Allocators received a starting endowment of CHF 32;³ recipients received varying endowments depending on the condition (see details below). In the belief elicitation part of the experiment, participants were incentivized to estimate the behavior of the other participants during the main experiment (details about the incentive scheme are described in Sect. 2.5. At the end of the experiment, all participants filled out a socioeconomic questionnaire.

2.3. Trial structure

After being given detailed instructions and correctly answering test questions that probed understanding of the task, participants performed 12 trials of the allocation task. Each block consisted of six trials; each trial was structured as follows. At the beginning of the trial, all three members of a group were informed about the endowments of the two recipients, and every participant was made aware that all participants were given the same information about recipients’ endowments. Recipients never received information about the endowment of the allocator.

The allocators were then asked to decide how to allocate an indivisible prize of CHF 5 between the two recipients. They had three options: allocate the prize directly to Recipient A; allocate the prize directly to Recipient B; or let the computer randomize to whom to allocate the prize. If the allocator chose randomization, the ex ante probability distribution was 50/50, and all participants were informed about this probability distribution.⁴

Simultaneously, Recipients A and B were given the option to punish or reward the allocators based on their allocation choices. We elicited recipient reward/punishment behavior using the strategy method, i.e. in each trial recipients made a reward/ punishment decision for each possible choice of the allocator {Give to me, Give to other, or Randomize} before knowing the decision of the allocator.⁵ Each recipient had a reward/punishment budget of CHF 8 on top of their endowment. From this budget they could spend CHF x ∈ [0, 8] on rewarding or punishing the allocator conditional on her allocation choice, and keep the remainder, CHF 8 — x. The reward/punishment technology was 1 : 2, i.e. for each CHF a recipient spent rewarding or punishing the allocator, CHF 2 were added to or subtracted from the allocator’s income.⁶ Allocators knew that recipients had this reward/punishment opportunity and were informed about the reward/punishment technology.⁷

2.4. Block structure and conditions

Each trial of the allocation task corresponded to a different condition, and the trials were organized into two blocks consisting of six similar conditions. The conditions differed in terms of the distribution of endowments between the two potential recipients, and in the information revealed to the three participants about this distribution. Figure 1 gives an overview over the six conditions and the two blocks. The six conditions within each block were: Equal Certain, Richer Certain, Poorer Certain, Equal Uncertain, Richer Uncertain, and Poorer Uncertain. The order of conditions was randomized to avoid order effects. In all “Certain” conditions, the exact endowments of the two potential recipients were revealed to all three participants. In all “Uncertain” conditions, the participants were informed only about an interval from which the endowment of Recipient A would be drawn, and an interval from which the endowment of Recipient B would be drawn. Within these intervals, initial endowments were drawn at random using a uniform probability distribution. Neither recipients nor allocators were informed about the probability distribution of the incomes within the intervals, but the midpoints of the intervals were always equal to the endowments in the corresponding “Certain” condition.⁸ The two blocks differed in terms of the absolute levels of endowments given to the two potential recipients; in the second block the six conditions were repeated with the modification that all endowments and interval midpoints were increased by CHF 10, while the length of the intervals remained the same in the “Uncertain” conditions. We refer to the first block as the Low Endowment block and to the second block as the High Endowment block.⁹

Fig. 1.

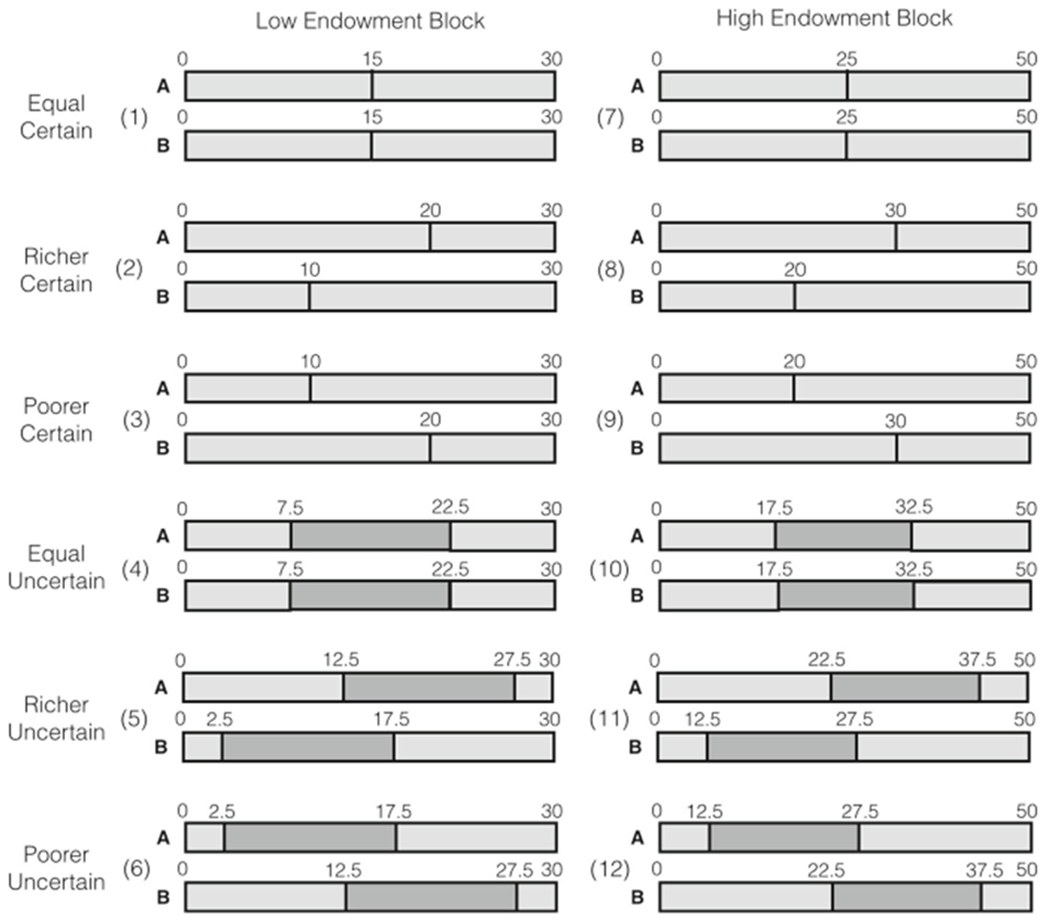
Overview over the six experimental conditions and the two blocks. Each participant completed two blocks of six trials of the task. The two blocks differed by the magnitude of the initial endowments, which were increased by CHF 10 in Block 2 (high endowment block) relative to Block 1 (low endowment block). Within each block, the two recipients were either given equal endowments (Conditions 1, 4, 7, 10) or unequal endowments (Conditions 2, 3, 5, 6, 8, 9, 11, 12) in expectation; in the latter case, this resulted in a relatively poorer and a relatively richer potential recipient. In addition, initial endowments were either known with certainty (Conditions 1–3, 7–10), or with some degree of uncertainty (Conditions 4–6, 10–12). Under uncertainty, initial endowments were randomly and uniformly distributed in an interval of ± CHF 7.50 around the endowments in the Certain conditions. All members of each group (i.e. both recipients and the allocator) knew about the relative endowments of the two potential recipients in each group. The figure shows the information given to the participants about the endowments of Recipients A and B in each experimental condition. For each condition the top bar indicates the endowment of Recipient A, while the bottom bar indicates the endowment of Recipient B. In conditions 1–3 and 7–9 the exact endowments are indicated by black vertical lines inthe interior of the bar. In conditions 4–6 and 10–12 the startand endpoints of the endowment intervals are indicated by black vertical lines and the interval itself is filled with a darker grey shade

Within each block, each participant played one trial in each of the six conditions presented in Fig. 1. Thus, each recipient assumed the “Equal Certain”, “Richer Certain”, “Poorer Certain”, “Equal Uncertain”, “Richer Uncertain”, and “Poorer Uncertain” roles exactly once within each block. The order in which recipients experienced the different conditions was counterbalanced between recipients A and B, such that for each sequence experienced by a Recipient A, there was a Recipient B who experienced the same sequence, and vice versa.¹⁰

After each group of three participants had played six trials, groups were randomly re-assigned, and the second, high endowment block began. No participants who had played together in the first block met each other again in the second block.

Across the six conditions and two blocks, the allocator made a total of twelve allocation decisions (6 conditions × 2 blocks), while the recipients made a total of 36 contingent reward/punishment decisions (6 conditions × 2 blocks × 3 choices). Importantly, neither the allocator nor the recipients were informed of the decisions of the other group members within each trial; this information was not revealed until the very end of the experiment. The lack of information about the behavior of others and the reassignment without replacement between blocks rules out reputation effects and strategic behavior.

2.5. Estimates of others’ preferences

In the belief elicitation part of the experiment, all participants repeated the same tasks as above, except they were now asked to estimate the average choices of all participants in the first part of the experiment. Specifically, the allocators were asked to estimate the average reward or punishment from each recipient type for each possible allocation. The recipients were asked to estimate the average reward or punishment of all other recipients for each possible allocation.

Each participant estimated the reward/punishment response of both Recipient A and Recipient B for all possible allocation choices in each condition in the low endowment block. Each participant thus made 36 estimates in total (6 conditions × 2 blocks × 3 choices). To incentivize the participants to give their best estimate of the others’ choices, they were initially rewarded with CHF 1 for each estimate they made; for every CHF the estimate deviated from the actual reward/punishment mean realized within each condition in the first part of the experiment, CHF 0.10 were subtracted from this amount.

2.6. Payment

At the end of the experiment, one trial from each block was chosen at random and paid out to all participants; thus, the allocator received their initial endowment of CHF 32 plus or minus the aggregate reward or punishment from the recipients for the specific allocation choice in that trial. Conversely, the recipients received their initial endowment plus the CHF 8 reward/punishment budget, minus the money spent out of this budget on rewarding or punishing the allocator in the randomly chosen trial. In addition, one of the potential recipients received the CHF 5 prize based on the allocator’s choice in the randomly chosen trial. Finally, all participants received the payment from the belief elicitation part of the experiment, as described above.

3. Results

Our main question is whether recipients support or oppose randomization as an allocation mechanism; we therefore focus on the behavior of the recipients. We also discuss briefly how allocators decide to allocate a scarce resource, and how their decisions are informed by their beliefs about recipient behavior. For ease of exposition we focus on the main dimensions of interest in each analysis, but we present a fully saturated model in Table 9 in Appendix.

3.1. Recipient behavior

Recipients could reward or punish the allocator conditional on her allocation choices. We interpret a recipient’s reward for a specific allocation choice as support for that choice, and punishment as opposition. This interpretation allows us to avoid making assumptions about the functional form of recipients’ utility function. Since purely selfish recipients can experience positive or negative utility without being willing to incur a cost to signal this, reward and punishment are conservative measures of positive and negative utility, respectively.

We generate a linear reward/punishment variable (Reward) where rewards are coded as positive, punishments are coded as negative, and the unit of measurement is Swiss Francs (CHF). Subsequently we will refer to this linear variable as “Reward”, with an upper case R, while we will refer to only the positive domain of this variable as “reward”, with a lower case r. We interpret a positive average Reward for a specific allocation choice as average support for that choice, and a negative average Reward as average opposition. We pool recipients A and B, since these are identical in expectation, and study instead the behavior of different recipient “types” defined by the recipients’ relative position in the endowment distribution: whether they were equal in expectation (Equal), relatively poor (Poor), or relatively rich (Rich).

From each recipient’s point of view, the possible choices of the allocators were (1) to allocate directly to that recipient (Give to Me), (2) to allocate directly to the other recipient (Give to Other), or (3) to randomize between the two potential recipients (Randomize). As described in Sect. 2.3, the experiment was designed to rule out strategic behavior by maintaining anonymity throughout the experiment and by not revealing any information about behavior of the other participants before the very end of the experiment. Furthermore, rewarding and punishing allocators was costly to the recipients, and thus a recipient who wanted to maximize her own payoff should neither reward nor punish the allocators regardless of their allocation choice.

Across recipients, we find that the median response to each allocation choice was to neither reward nor punish the allocator (see Table 5 in Appendix). However, only 22 recipients (31.4%) never rewarded nor punished the allocator across all 36 choices. The remaining 48 recipients (68.6%) changed their reward/punishment behavior at least once during the experiment. Thus, the majority of recipients were at some point during the experiment willing to incur a cost to signal their support/opposition toward the choices of the allocator.

Figure 2 presents simple summary statistics of recipients’ Reward for the different allocator choices across the low endowment/high endowment and certainty/uncertainty conditions. The dark gray bars show recipients’ average response to direct allocation to themselves, the medium grey bars show recipients’ average response to direct allocation to the other recipient, and the light grey bars show recipients’ average response to randomization.

Fig. 2.

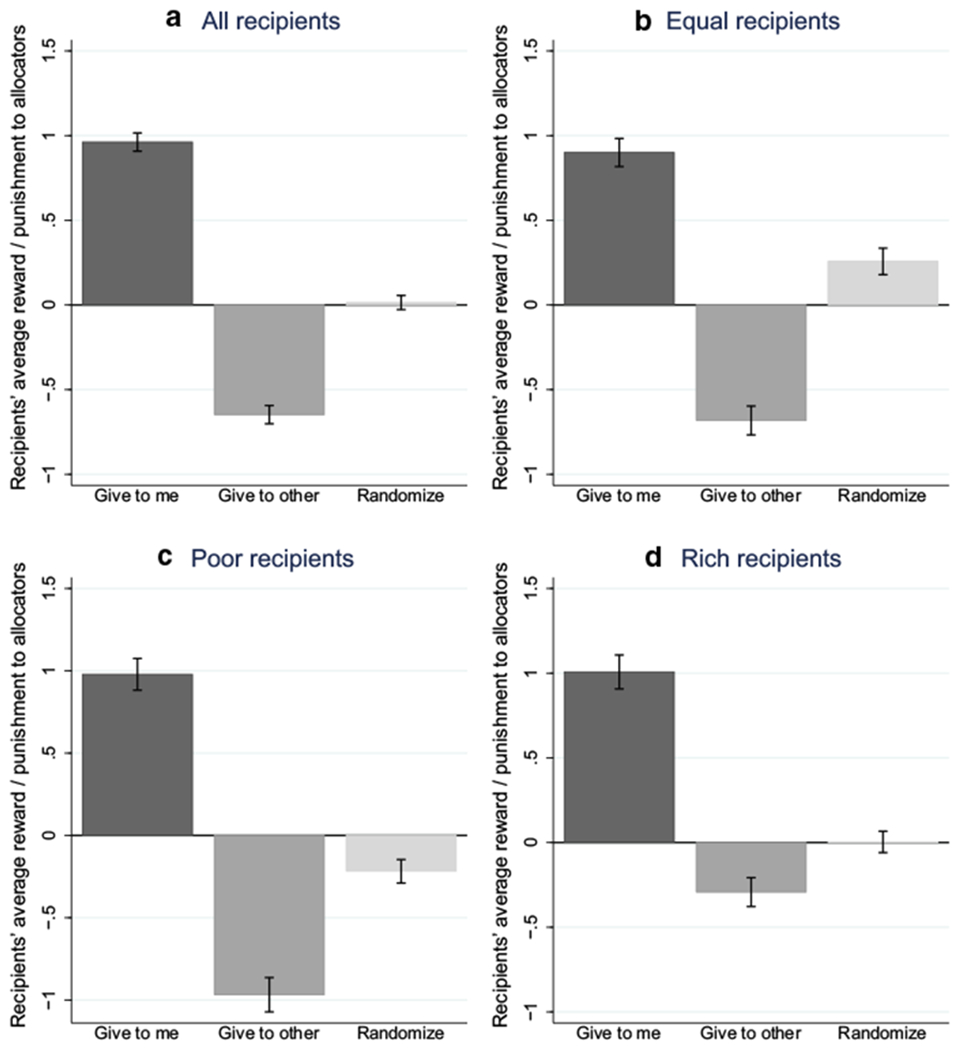
Recipients’ average reward/punishment to the allocators conditional on the allocators’ choices. Dark gray bars show recipients’ average Reward to the allocators for direct allocation to themselves, medium gray bars show recipients’ average Reward to the allocators for direct allocation to the other recipient, and light gray bars show recipients’ average Reward to the allocators for randomization. The top left panel shows the average Reward of all recipients across all conditions. The top right panel shows the average Reward of all recipients across the equal endowment conditions. The bottom panel shows the average Reward of all the relatively poorer recipients (left panel) and of all the relatively richer recipients (right panel) across the unequal endowment conditions. Error bars are naive standard errors, calcualted as $\frac{S.D.}{\sqrt{N}}$

The first two bars in each panel reveal that all recipient types, on average, rewarded the allocator for direct allocation to themselves, and punished the allocator for direct allocation to the other recipient. As pointed out above, this behavior is inconsistent with payoff maximization, inequity aversion, and efficiency, but is consistent with reciprocity and an equity rule (under the assumption that lottery outcomes are evaluated as their expectation). When the prize was allocated directly to themselves, recipients rewarded the allocator with similar amounts regardless of initial endowment (equal: CHF 0.90; poor: CHF 0.98; rich: CHF 1.01). When the prize was allocated directly to the other recipient, recipients with equal endowments punished the allocator with CHF − 0.68, poorer recipients with CHF − 0.97, and richer recipients with CHF − 0.29. The relatively poorer recipients thus punished direct allocation to the other recipient more than three times as much as the relatively richer recipients, again consistent with a combination of reciprocity and and equity rule (Elster 1989; López-Pérez 2008; Rabin 1993; Dufwenberg and Kirchsteiger 2004).

The third bar in Fig. 2a shows that, on average across all conditions, potential recipients neither rewarded nor punished the allocator for randomizing. However, the next three diagrams reveal heterogeneity by recipient type: recipients with equal endowments rewarded the allocator for randomizing (CHF 0.26), poor recipients punished (CHF − 0.22), and rich recipients neither rewarded nor punished (CHF 0.00). The average punishment from the relatively poorer recipients constituted 2.75% of their reward/punishment budget, or approximately 1% of their average total endowments. It is driven by 21% of the relatively poorer potential recipients, while 69% of these recipients awarded CHF 0 for randomization, and 10% rewarded randomization (see Tables 5 and 6 in Appendix). Thus, we observe a social cost of randomization, but it is relatively small.

Table 1 assesses whether the differences presented in Fig. 2 are statistically significant. We estimate the following equation separately for each possible allocation choice (Give to Me, Give to Other, and Randomize):

$$\mathrm{Re}war{d}_{ic}={\beta }_0+{\beta }_{1}Poo{r}_{ic}+{\beta }_{2}Ric{h}_{ic}+{\alpha }_i+{\epsilon }_{ic}.$$ (1)

Table 1.

Effect of the recipient’s relative endowment on her reward/punishment to the allocator

	Dependent variable: Reward
	(1) Give to me	(2) Give to other	(3) Randomize
Poor	0.08	− 0.29**	− 0.47***
	(0.09)	(0.11)	(0.12)
Rich	0.11	0.39**	− 0.25**
	(0.10)	(0.15)	(0.11)
Constant	0.90***	− 0.68***	0.26***
	(0.05)	(0.06)	(0.07)
Mean of dep. variable	0.96	− 0.65	0.01
Poor + constant	0.98***	− 0.97***	− 0.22***
(s.e.)	(0.06)	(0.10)	(0.05)
Rich + constant	1.01***	− 0.29**	0.00
(s.e.)	(0.07)	(0.12)	(0.05)
F stat: poor = rich	0.06	10.16	9.87
p value	0.80	0.00***	0.00***
Observations	840	840	840

Effect of the recipient’s relative endowment on her reward/punishment to the allocator. The constant term captures recipients’ average Reward when endowments are equal. Regressions control for individual level fixed effects; standard errors are heteroskedasticity-robust and clustered at the participant level. A linear combination of β₁ and β₀, capturing the average Reward from the relatively poorer recipients, and a linear combination of β₂ and β₀, capturing the average Reward from the relatively richer recipients’, as well as F statistics and corresponding p values from Wald tests for coefficient equality between β₁ and β₂, are reported in the lower panel of the regression table.

^*Significant at the 10% confidence level,

^**significant at the 5% confidence level,

^***significant at the 1% confidence level

Reward_ic is the linear reward/punishment variable described above; Poor_ic and Rich_ic are indicators that the recipient assumed the role of the relatively poorer or richer recipient, respectively. The omitted category is recipients with equal endowments. Coefficient β₀ thus denotes the average Reward for recipients with equal endowments, while coefficients β₁ and β₂ capture the difference in average Reward between the recipients with equal endowments and the relatively poorer and the relatively richer recipients, respectively. α_i captures individual level fixed effects, ε_ic is an error term clustered at the participant level, i is a participant index and c is a condition index, i ∈ [1, 70] and $c\in \left\{(\text{Certain, Uncertain})\times \left(\begin{array}{c}\text{High endowment}\\ \text{Low endowment}\end{array}\right)\right\}.$Linear combinations of coefficients are reported in the lower panel of the table, along with corresponding standard errors. The interpretation of the linear combination of β₀ and β₁ is the average Reward awarded by the relatively poorer recipients, and the linear combination of β₀ and β₂ is the average Reward awarded by the relatively richer recipients. The F-statistic and the corresponding p value from a Wald test of equality between β₁ and β₂ is reported in the lower panel of the table.

Column (1) confirms that all three recipient types, on average, significantly rewarded the allocator for direct allocation to themselves, and that the differences between the average rewards of CHF 0.90 (Equal), CHF 0.98 (Poor) and CHF 1.01 (Rich) are not statistically different from each other. Column (2) confirms that all three recipient types, on average, significantly punished the allocator for direct allocation to the other recipient, and that average punishment from the relatively poorer recipient (CHF – 0.97) is statistically different from the average punishment from relatively richer recipient (CHF – 0.29). The average punishment for recipients with equal endowments (CHF – 0.68) is statistically different from both averages. Column (3) reveals that the average responses to randomization both from the recipients with equal endowments (CHF 0.26) and the relatively poorer recipients (CHF – 0.22) were statistically different from zero and each other. The average response to randomization from the relatively richer recipients (CHF 0.00) was not statistically different from zero, but differed significantly from that of the equal and poor recipients.

In sum, we find that, on average, recipients rewarded randomization when there was equality in endowments; punished randomization when they were relatively poor; and neither rewarded nor punished randomization when they were relatively rich.

Recipient behavior from the perspective of the allocator

We have seen that randomization is acceptable under certain conditions, and is punished under others. What are the implications of these findings for a social planner who chooses between randomization and other allocation mechanisms? The crucial factor is the overall welfare impact of her choice; however, a full welfare analysis is beyond the scope of this paper. Instead, we here approximate the overall support vs. opposition to randomization by analyzing a proxy variable, i.e. the sum of rewards and punishments for a given choice. Figure 3 shows the allocators’ expected net Reward (the sum of rewards/punishments from the two recipients, not taking into account the 1:2 reward/punishment technology) for each allocation choice across the equal endowment conditions and across the unequal endowment conditions, respectively.

Fig. 3.

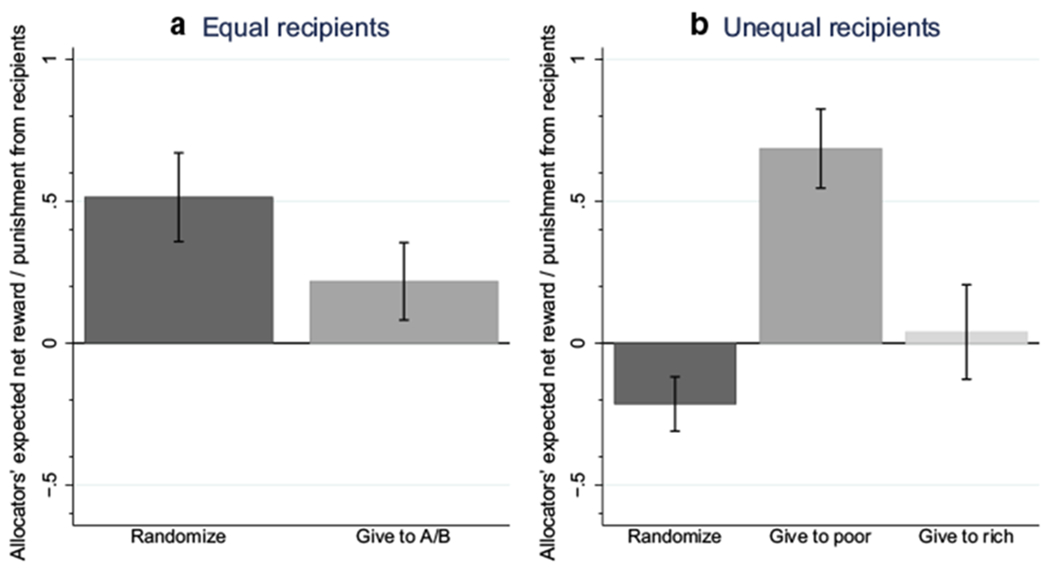
Allocators’ expected net Reward for each possible allocation choice. Dark gray bars show allocators’ expected net Reward, defined as the sum of rewards and punishments from both recipients within a given trial, when they chose to randomize between the two recipients in the equal endowment conditions (left panel) and in the unequal endowments conditions (right panel). Medium gray bars show allocators’ expected net Reward when they chose to allocate directly to either Recipient A or Recipient B in the equal endowments conditions (left panel) or to the relatively poorer recipient in the unequal endowment conditions (right panel). The light grey bar (right panel) shows allocators’ expected net Reward when they chose to allocate directly to the relatively richer recipient in the unequal endowment conditions. Error bars are naive standard errors, calculated as $\frac{S.D.}{\sqrt{N}}$

In the equal endowment conditions, allocators maximized their expected net Reward by choosing to randomize, but they also received a positive expected net Reward when allocating directly to either Recipient A or Recipient B. In the unequal wealth condition, allocators maximized their expected net Reward by allocating directly to the relatively poorer recipient, received a negative expected net Reward when they chose to randomize, and a small but positive expected net Reward when they chose to allocate directly to the relatively richer recipient.

Table 2 assesses whether these differences are statistically significant. In column (1) we estimate the following equation for the equal endowment conditions:

$$\mathrm{Re}war{d}_{ic}={\beta }_0+{\beta }_{1}Give\mathit{ to A/}{B}_{ic}+{\alpha }_i+{\epsilon }_{ic},$$ (2)

where Reward is the same variable as used in the previous regressions and Give to A/B is an indicator that the allocator chose to allocate directly to either Recipient A or Recipient B. i is a subject index, and c is a condition index. α captures group level fixed effects, and ε is an error term clustered at the individual level.

Table 2.

Allocators’ expected net Reward for each possible allocation choice

	Dependent variable: net Reward
	(1) Equal conditions	(2) Unequal conditions
Give to A/B	− 0.30
	(0.24)
Give to poor		0.90***
		(0.22)
Give to rich		0.25
		(0.27)
Constant	0.51***	−0.21
	(0.16)	(0.14)
Mean of dep. variable	0.32	0.17
Give to A/B + constant	0.22***
(s.e.)	(0.08)
Give to poor + constant		0.69***
(s.e.)		(0.14)
Give to rich + constant		0.04
(s.e.)		(0.17)
F stat: give to poor = give to rich		5.67
p value		0.02**
Observations	840	1680

Allocators’ expected net Reward or each possible allocation choice. The constant term captures allocators’ net Reward for randomization. Regressions control for individual level fixed effects; standard errors are heteroskedasticity-robust and clustered at the group level. In column (1) the linear combination of β₁ and β₀ captures allocators’ expected net Reward for direct allocation to either Recipient A or Recipient B in the equal endowment conditions. In column (2) the linear combination of β₁ and β₀ captures allocators’ expected net Reward for direct allocation to the relatively poorer recipient in the unequal endowment conditions, and the linear combination of β₂ and β₀ captures allocators’ expected net Reward for direct allocation to the relatively richer recipient in the unequal endowment conditions. The F statistics and corresponding p values for a Wald test of coefficient equality between β₁ and β₂ in the unequal endowment conditions are also reported in the lower panel of the table.

^*Significant at the 10% confidence level,

^**significant at the 5% confidence level,

^***significant at the 1% confidence level

In column (2) we estimate a similar equation for the unequal endowment conditions:

$$\mathrm{Re}war{d}_{ic}={\beta }_0+{\beta }_{1}Give\text{ to }poo{r}_{ic}+{\beta }_{2}GivetoRic{h}_{ic}+{\alpha }_i+{\epsilon }_{ic},$$ (3)

where Give to Poor and Give to Rich are indicators for allocating directly to the relatively poorer or richer recipient, respectively. Everything else is as in Eq. 2. In both columns (1) and (2), the interpretation of the coefficient β₀ is allocators’ expected net Reward for randomization. In column (1), coefficient β₁ denotes the change in net Reward for allocating directly to Recipient A or B under equal endowments. In column (2), coefficients β₁ and β₂ measure the change in net Reward for direct allocation to the poor and rich recipients, respectively, under unequal endowments. Linear combinations of coefficients β₀ and β₁ are reported in the lower panel of the table. In column (1) this linear combination captures allocators’ net Reward for direct allocation to either recipient under equal endowments, and in column (2) for direct allocation to the relatively poorer or richer recipient under unequal endowments. In column (2) a linear combination of β₁ and β₂ captures allocators’ expected Reward for direct allocation to the relatively richer recipient. F-statistic and corresponding p value from a Wald test of equality between β₁ and β₂ are also reported in the lower panel.

Table 2 shows that randomization under equal endowments yielded a significantly positive net Reward of CHF 0.51, or more than 10% of the prize being allocated. Direct allocation to either Recipient A or Recipient B received a net Reward of CHF 0.22, but the difference to the reward for randomization was not significant.

Table 2 also shows that randomization under unequal endowments yielded a net punishment of CHF − 0.21, or 4.2% of the prize being allocated. However, when controlling for individual level fixed effects, this average punishment is not statistically different from zero, and is not significantly different from what allocators could expect if they chose to allocate directly to the relatively richer recipient, CHF 0.04. However, it is significantly lower than their expected net Reward for allocating directly to the relatively poorer recipient, CHF 0.69. Thus, an allocator who chose to randomize between unequal recipients was awarded CHF 0.90 less in expectation (CHF 0.69 − (−0.21)) than an allocator who chose to allocate directly to the relatively poorer recipient.

Robustness

Effects of uncertainty on recipient behavior

In practice, allocators often do not have reliable information about recipient wealth. We therefore ask whether uncertainty about the distribution of endowments affect recipients’ reactions to different allocations. The results reported above average over the Certain/Uncertain conditions; however, we might expect recipients to reward the allocators more/punish the allocators less when there is uncertainty about the exact distribution of endowments. To test this hypothesis, we estimated Eq. 1 with an indicator that participants (both allocators and recipients) had uncertainty about the distribution of recipients’ endowments, and interactions between this variable and whether the recipient was relatively poorer or relatively richer, respectively. Estimation results are reported in Table 7 in Appendix. We find that no recipient type behaved significantly differently when there was uncertainty about the distribution of the recipients’ endowments. Most importantly, we find no increase in recipients’ Reward for randomization when there was uncertainty about the distribution of endowments.

Effects of absolute endowments on recipient behavior

A potential concern with the findings reported above is that there could be income effects. In expectation, relatively poorer recipients were endowed with CHF 10/20 (low endowment/high endowment block), relatively richer recipients were endowed with CHF 20/30, and recipients with equal wealth were endowed with CHF 15/25. Thus, if a decreasing marginal utility of endowments affected recipients’ willingness to incur costs to signal their support/opposition toward different allocator choices, we would not be able to directly compare average behavior across the three recipient types.

To test for this confound, we estimate Eq. 1 with an indicator for the high endowment conditions and interaction terms between the high endowment conditions and whether the recipient assumed the role of the relatively poorer or the relatively richer recipient, respectively. Estimation results are presented in Table 8 in Appendix. We find that neither the indicator for the high endowment conditions, nor any of the interaction terms, are statistically significant. This result suggests that none of the recipient types significantly changed their reward/punishment behavior when we introduced the uniform increase in recipients’ endowments. Specifically, the relatively poorer recipients did not change their behavior in the high endowment conditions to match that of the relatively richer recipients in the low endowment conditions, even though those two recipient types were given the same absolute endowment of CHF 20. This lack of differential response indicates that recipients’ reward/punishment behavior was driven by whether they were relatively poorer or richer than the other recipient, and not whether they were poor or rich in absolute terms. We therefore conclude that differences in absolute endowments cannot account for the differences in reward/punishment behavior between the three recipient types. Table 10 in Appendix shows that allocators are somewhat less likely to randomize under high wealth, but otherwise show no differences in behavior.

3.2. Allocator behavior

As described above, our main interest is in the response of recipients to randomization. For completeness, we now turn to the behavior of the allocators and ask: do they allocate so as to maximize their expected net Reward given recipients’ reward/punishment behavior? This question is particularly interesting because all participants were randomized into being either allocators or potential recipients. Thus, support and opposition to randomization was identical in expectation among allocators and potential recipients at the outset, and any differences in support/opposition between the allocators and the potential recipients can thus be attributed to the participants’ assigned roles.

We begin by presenting simple summary statistics for allocator behavior in Fig. 4 and Table 3. The left panel in Fig. 4 and the first column in Table 3 show the proportion of trials in which allocators chose to randomize, allocate directly to Recipient A, or allocate directly to Recipient B, respectively, in the equal endowment conditions (direct allocation to recipients A and B is pooled in Table 3). The right panel in Fig. 4 and the second column in Table 3 show the proportion of trials in which allocators chose to randomize, allocate directly to the relatively poorer recipient, or allocate directly to the relatively richer recipient, respectively, in the unequal endowment conditions. The lower panel of Table 3 shows the t statistics and corresponding p values of t tests comparing the different proportions to each other within the equal endowment conditions and the unequal endowment conditions, respectively. All proportions average over the high endowment/low endowment and certain/uncertain conditions.

Fig. 4.

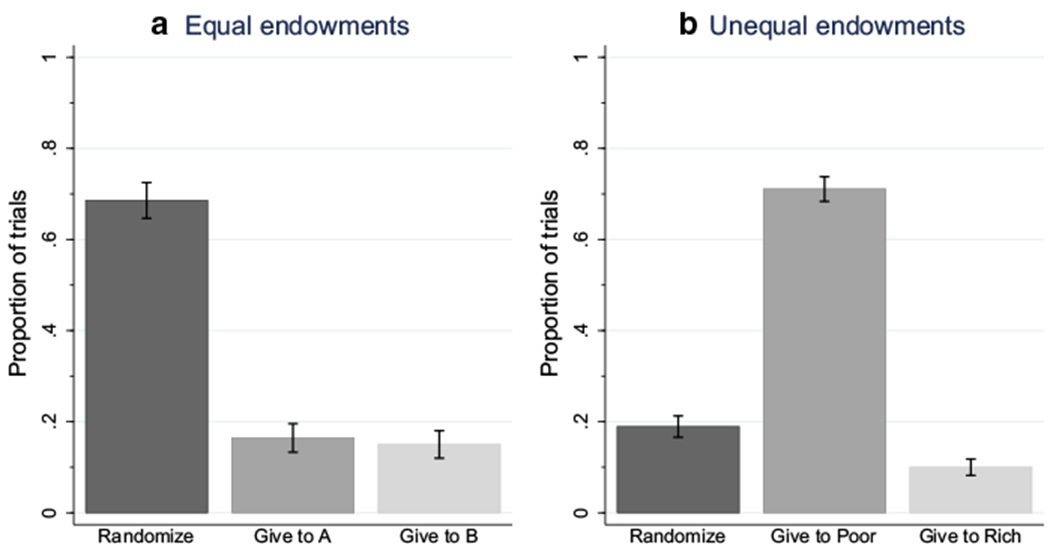
Proportions of trials in which allocators chose to randomize or to allocate directly to one of the two potential recipients. Dark gray bars show the proportion of trials in which allocators chose to randomize in the equal endowment conditionss (left panel) and in the unequal endowmenet conditions (right panel). Medium gray bars show the proportion of trials in which allocators chose to allocate directly to Recipient A in the equal endowment conditions (left panel), or to the relatively poorer recipient in the unequal endowment conditions (right panel). Light gray bars show the proportion of trials in which allocators chose to allocate directly to Recipient B in the equal endowment conditions (left panel), or to the relatively richer recipient in the unequal endowment conditions (right panel). Error bars are naïve standard errors, calculated as $\sqrt{\frac{p(1-p)}{N}}$

Table 3.

Proportions of trials in which allocators chose to randomize or to allocate directly to one of the two potential recipients

	(1) Equal endowments	(2) Unequal endowments
Randomize	0.69	0.19
	(0.05)	(0.05)
Give to A/B	0.31
	(0.00)
Give to poor		0.71
		(0.00)
Give to rich		0.10
		(0.00)
t stat: randomize = give to A/B	4.72
p value	0.00***
t stat: randomize = give to poor		− 10.99
p value		0.00***
t stat: randomize = give to rich		2.81
p value		0.01***
t stat: give to poor = give to rich		15.42
p value		0.00***
Observations	140	280

Proportions of trials in which allocators chose to randomize, or allocate directly to one of the two potential recipients in the equal endowment conditions; or randomize, allocate directly to the relatively poorer recipient, or allocate directly to the relatively richer recipient in the unequal endowment conditions. Naïve standard errors, calculated as $\sqrt{\frac{p(1-p)}{N}}$, are reported in parentheses. t statistics from t tests comparing the different proportions to each other are reported in the lower panel of the tabel together with corresponding p values.

^***significant at the 1% confidence level

When recipients had equal endowments in expectation, the modal allocator choice, chosen in 69% of trials, was to randomize between the two potential recipients. In fact, 19 out of 35 allocators (54.3%) randomized in all trials in which recipients had equal endowments, and every single allocator randomized in at least one trial in which recipients had equal endowments. Even allocators who chose to allocate directly to either Recipient A or Recipient B seem to have “randomized” between the two potential recipients, as they allocated directly to Recipient A in 16% of trials and directly to Recipient B in 15% of trials. Thus, there seems to be no label effect in allocator behavior.

Since the potential recipients on average rewarded randomization when they had equal endowments, the allocators’ choices were a relatively good match of recipients’ behavior in the equal endowment conditions. This leads to a high allocator “efficiency” of 82.4%, calculated as the average net Reward obtained by the allocators as a fraction of the average net Reward the allocators could have obtained, if they had all chosen the net Reward maximizing strategy $\left(\frac{\mathrm{0.69.0.51}+\mathrm{0.31.0.22}}{0.51}⠂\text{100\% = 82.4\%}\right)$.

When recipients had unequal endowments in expectation, the modal allocator choice, chosen in 71% of trials, was to allocate directly to the relatively poorer recipient. In fact, 15 out of 35 allocators (42.9%) allocated to the relatively poorer recipient in all trials in which recipients had unequal endowments. Allocators also randomized in a substantial proportion of trials, 19%. Since the potential recipients on average punished the allocator for randomizing when they had unequal endowments, this proportion is surprisingly large. The same holds for the proportion of trials in which the allocators chose to allocate directly to the relatively richer recipient, 10%. When there was inequality between the potential recipients, the allocators’ choices therefore did not match the behavior of the recipients very well; in this case the allocator “efficiency” only amounts to 65.8% $\left(\frac{0.19⠂(-0.21)+0.71⠂0.69+\mathrm{0.10.0.04}}{0.69}⠂\text{100\%}\right)$.

Thus, a question emerges: given that allocators’ expected net Reward for randomization is significantly negative when the potential recipients were unequal in expectation, why did 19% of the allocators choose to randomize between them? Why do allocators randomize between potential recipients with unequal endowments? If the allocators tried to match the preferences of the reward/punishment behavior of the potential recipients, we would expect that all the allocators chose the net Reward maximizing allocation strategy. Equivalently, we would expect that no allocator expected to “leave money on the table” with their allocation choice. Since we elicited allocators’ beliefs about the behavior of the potential recipients in the end of the experiment, we can directly test whether this is the case.

Table 4 assesses whether the allocators expected to leave money on the table with their allocation choices. We estimate the following equation for both the equal endowment conditions (column 1) and the unequal endowment conditions (column 2):

$$D{(\text{Allcator Expected to Leave Money on the Table})}_{ic}={\beta }^{\prime }Allocatio{n}_{ic}+{\epsilon }_{ic}.$$

D (Allocator Expected to Leave Money on the Table) is an indicator that the allocator believed that she was leaving money on the table in a given trial. Allocation is a vector of indicators for the different allocator choices, i.e. Allocation = (Randomize, Give to A/B) in the equal endowment conditions and Allocation = (Randomize, Give to Poor, Give to Rich) in the unequal endowment conditions. The regressions are run without a constant term, which means that all coefficients can be interpreted directly as proportions.¹¹ In columns (1) and (2) β₁ captures the proportion of trials in which the allocators chose to randomize despite believing that they were leaving money on the table. In column (1) β₂ captures the proportion of trials in which allocators chose to allocate directly to recipients A or B in the equal wealth condition despite believing that they were leaving money on the table. In column (2) β₂ and β₃ capture the proportions of trials in which allocators chose to allocate directly to the relatively poorer recipient or the relatively richer recipient, respectively, despite believing that they were leaving money on the table. Standard errors are clustered at the participant level.

Table 4.

Proportions of trials in which allocators believed that they were leaving money on the table with their allocation choices

	Dependent variable: dummy for whether the allocator expected to leave money on table
	(1) Equal endowments	(2) Unequal endowments
Randomize	0.40***	0.60***
	(0.08)	(0.09)
Give to A/B	0.24**
	(0.09)
Give to poor		0.30***
		(0.06)
Give to rich		0.70***
		(0.13)
Mean of dep. variable	0.36	0.39
F stat: randomize = give to A/B	1.49
p value	0.23
F stat: randomize = give to poor		8.91
p value		0.01***
F stat: randomize = give to rich		0.42
p value		0.52
F stat: give to poor = give to rich		8.32
p value		0.01***
Observations	70	140

Proportions of trials in which allocators believed that they were leaving money on the table with their allocation choices. Regressions are run without a constant term. Standard errors are heteroskedasticity-robust and clustered at the participant level. F statistics and corresponding p values from Wald tests for coefficient equality between β₁ and β₂ in column (1) and between β₁ and β₂, β₁ and β₃ as well as β₂ and β₃ in column (2) are reported in the lower panel of the table.

^*Significant at the 10% confidence level,

^**significant at the 5% confidence level,

^***significant at the 1% confidence level

The first column in Table 4 reveals that the allocators believed that they were leaving money on the table in 40% of trials in which they chose to randomize and in 24% of trials in which they chose to allocate directly to either Recipient A or Recipient B when the recipients had equal endowments in expectation. More interestingly, the second column reveals that the allocators expected to leave money on the table in 60% of the trials in which they chose to randomize when recipients had unequal endowments in expectation. On the other hand, allocators expected to leave money on the table in only 30% of trials in which they chose to allocate directly to the relatively poorer recipient.

The fact that allocators believed that they were maximizing their net Reward in the majority of trials in which they chose to allocate directly to the relatively poorer recipient does not imply that they were motivated by trying to maximize their net Reward. However, the fact that allocators believed that they were leaving money on the table in the majority of trials in which they chose to randomize implies that their choice of randomization cannot have been motivated by an attempt to maximize their expected net Reward. We thus conclude that allocators must have had preferences for randomization over and above what can be explained by their expectations for recipients’ reward/punishment behavior.

In sum, we identify a disconnect between allocators choices and what recipients rewarded the allocator for choosing: allocators randomized to a greater extent than was optimal in terms of maximizing their net Reward. This disconnect cannot be explained by allocators having systematically wrong beliefs aboutrecipients’ reward/punishment behavior, since they choose to randomize despite expecting that this was not their net Reward maximizing strategy. Thus, we conclude that allocators had preferences for randomization over and above what can be explained by a motivation to maximize their net Reward from the recipients.¹²

4. Conclusion

Randomized controlled trials typically assume that the choice of allocation mechanism—i.e., randomization—does not affect recipient welfare and behavior. In this paper we tested whether potential recipients of a financial benefit support or oppose randomization as an allocation method (Frey et al. 2004). We set up experimental groups of three participants, in which one allocator decides how to allocate an indivisible prize of CHF 5 (equivalent to approximately USD 5) to one of two potential recipients. The allocator could choose between allocating the prize directly to one of the two potential recipients, or to let the computer randomize between the potential recipients with equal probabilities. We then asked whether the potential recipients supported or opposed the different allocation mechanisms by allowing them to either reward or punish the allocator conditional on her allocation choice.

We find evidence of a social cost of randomization. When recipients had equal endowments, they on average supported randomization, i.e. rewarded the allocator for randomizing. When instead recipients had unequal endowments, the relatively poorer potential recipients on average opposed randomization, i.e. punished the allocator for randomizing. Since the average punishment is a conservative measure of average disutility, we therefore identify a social cost of randomization when there is inequality between the potential recipients, and this cost is disproportionally borne by the relatively poorer potential recipients. The average punishment is small in magnitude (it constitutes 1% of poor recipients’ endowment and is carried by 21% of these recipients), and we see no average punishment among the relatively richer potential recipients. We interpret this result as showing that recipients support randomization as an allocation mechanism when randomization leads to ex ante equality (or expected equality) between potential recipients, but that they oppose randomization when this leads to ex post inequality in a predictable direction.

Given that a desire for equality is a well-documented phenomenon (Dawes et al. 2007; Cruces et al. 2012; Rutstrom and Williams 2000), and given that allocating directly to the relatively poorer potential recipient maximized allocators net Reward, it is not surprising that the majority of allocators chose to direct the prize to the relatively poorer potential recipient when such a recipient existed. What is perhaps more surprising is that a significant proportion of allocators (19%) chose to allocate the prize by randomizing between the two potential recipients when these were unequal in expectation, despite facing an expected net punishment from the potential recipients for doing so. This finding suggests that the allocators had an intrinsic preference for randomization as an allocation method.

This study was intended as a proof of principle. It is conducted in a simplified lab setting where both recipients and allocators are provided endowments by the experimenters. The fact that we find effects in the hypothesized direction suggests that the direction of the effects will replicate in a field setting. However, the extent to which this is true depends on a number of factors that were beyond the scope of the present study. First, it is unclear whether recipients’ willingness to incur a small cost in the laboratory extends to more consequential behaviors in the field, and how large these effects are. Second, the present study presented randomization as an alternative to direct allocation, but not other possible methods that might be used in “real-world” settings, such as allocation based on recipient merit or competition. Future research should therefore test whether recipients respond differently to randomization in the presence of different alternative allocation schemes. Third, in our study, the allocator’s funds were simply endowed by the experimenter; it remains to be elucidated how recipients respond to random allocation of privately of collectively earned income or goods. Fourth, in our study, randomization was presented a context-free allocation mechanism; in contrast, in randomized experiments in the field, it would typically be presented to potential recipients as a mechanism that is important for methodological integrity, and researchers would appeal to respondents’ desire to support science in responding to it. It is possible that under such circumstances, randomization would be considered acceptable by respondents, even when initial endowments are unequal. Fifth, it is possible that recipients’ reactions to randomization differ when the behavior of interest is measured after randomization, as in most field settings, compared to when it is measured before, as in our study. And finally, in our study, the benefits being allocated were certain. In contrast, in field settings, respondents may perceive the benefits of the program being allocated as uncertain, e.g. in the case of training programs. Again it is possible that such uncertainty would mitigate their responses to randomization as an allocation mechanism. Thus, a number of factors may lead to differences in reactions to randomization in field settings compared to our lab setting; future studies could systematically vary these factors to assess their relative importance. In addition, once the magnitude of the social cost of randomization has been established in the field, it also remains to be discussed whether the ex ante fairness and scientific benefits of randomizing treatment outweigh the cost to the recipients.

In sum, we identify no social cost of randomization when endowments are equal, but we do identify a (small) social cost of randomization when endowments are unequal. This social cost is borne solely by the relatively poorer potential recipients. It remains to be studied how large these effects are in field settings; if they are economically important, they increase the value of targeting goods directly to the most disadvantaged potential recipients.

Appendix

See Figs. 5, 6 and Tables 5, 6, 7, 8, 9, 10, 11 here.

Fig. 5.

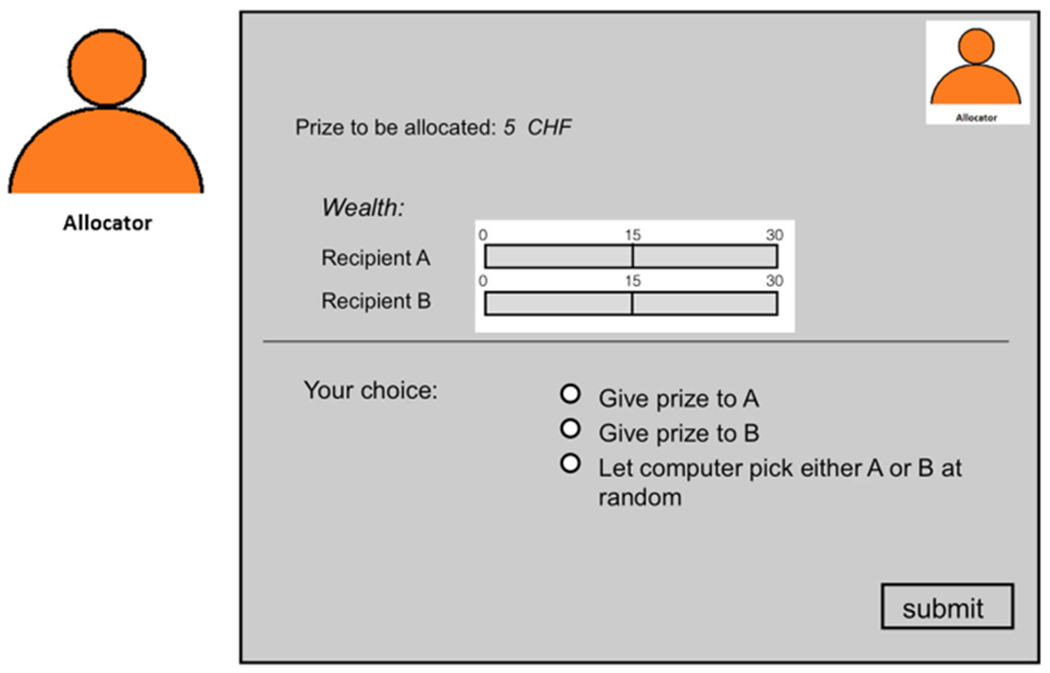
Example screen for the decisions of allocators. Example of what the allocators saw in the experiment before they made their allocation decision. This screen has been translated from German

Fig. 6.

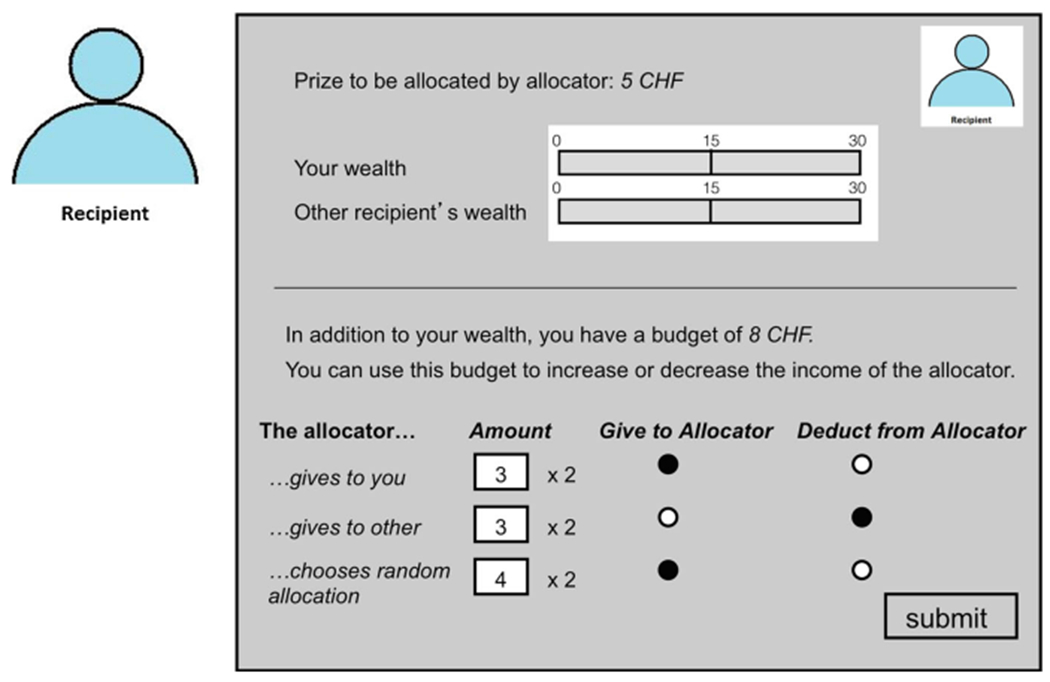
Example screen for the decisions of the potential recipients. Example of what the potential recipients saw in the experiment before they made their reward/punishment decision. This screen has been translated from German

Table 5.

Proportions of trials in which recipients awarded CHF 0 to the allocator

	Dependent variable: dummy for whether the recipient awarded CHF 0 to the allocator
	(1) Give to me	(2) Give to other	(3) Randomize
Equal	0.53***	0.62***	0.66***
	(0.05)	(0.05)	(0.05)
Poor	0.53***	0.57***	0.69***
	(0.05)	(0.05)	(0.05)
Rich	0.53***	0.66***	0.71***
	(0.05)	(0.05)	(0.05)
Mean of dep. variable	0.53	0.62	0.69
F stat: equal = poor	0.01	3.42	0.47
p value	0.91	0.07*	0.50
F stat: equal = rich	0.00	1.30	1.88
p value	1.00	0.26	0.18
F stat: poor = rich	0.01	4.89	0.31
p value	0.93	0.03**	0.58
Observations	840	840	840

Proportions of trials in which recipients awarded CHF 0 to the allocator. “Equal” is an indicator that the recipients had equal wealth, “Poor” and “Rich” are indicators that the recipient was relatively poor or relatively rich, respectively. Regressions are run without a constant term such that all coefficients directly capture proportions of trials. Standard errors are clustered at the participant level. F statistics and corresponding p values from Wald tests of coefficient equality between β₁ and β₂, β₁ and β₃, as well as β₂ and β₃ are reported in the lower panel of the table.

^*Significant at the 10% confidence level,

^**significant at the 5% confidence level,

^***significant at the 1% confidence level

Table 6.

Proportions of trials in which recipients rewarded or punished the allocator, respectively, conditional on the choice of the allocator

	Dependent variable: dummy for whether the recipient rewarded the allocator			Dependent variable: dummy for whether the recipient punished the allocator
	(1) Give to me	(2) Give to other	(3) Randomize	(4) Give to me	(5) Give to other	(6) Randomize
Equal	0.44***	0.05**	0.22***	0.04**	0.33***	0 11***
	(0.05)	(0.02)	(0.04)	(0.02)	(0.05)	(0.03)
Poor	0.43***	0.04**	0.10***	0.04**	0.38***	0.21***
	(0.05)	(0.02)	(0.03)	(0.02)	(0.05)	(0.04)
Rich	0.43***	011***	0.16***	0.05**	0.23***	0.13***
	(0.05)	(0.03)	(0.04)	(0.02)	(0.04)	(0.03)
Mean of dep. variable	0.43	0.07	0.16	0.04	0.31	0.15
F stat: equal = poor	0.01	0.52	12.43	0.00	4.47	7.36
p value: equal = poor	0.91	0.47	0.00***	1.00	0.04**	0.01***
F stat: equal = rich	0.05	4.27	3.27	0.33	5.92	0.40
p value: equal = rich	0.83	0.04**	0.07*	0.57	0.02**	0.53
F stat: poor = rich	0.01	5.37	4.83	0.40	11.21	8.34
p value: poor = rich	0.93	0.02**	0.03**	0.53	0.00***	0.01***
Observations	840	840	840	840	840	840

Proportions of trials in which recipients rewarded or punished the allocator, respectively, conditional on the choice of the allocator. Regressions are run without a constant term such that all coefficients directly capture proportions of trials. Standard errors are heteroskedasticity-robust and clustered at the participant level. F statistics and corresponding p values from Wald tests of coefficient equality between β₁ and β₂, β₁ and β₃, as well as β₂ and β₃ are reported below the table.

^*Significant at the 10% confidence level,

^**significant at the 5% confidence level,

^***significant at the 1% confidence level

Table7.

Effects of uncertainty on recipients’ reward/punishment behavior

	Dependent variable: Reward
	(1) Give to me	(2) Give to other	(3) Randomize
Poor	0.10	− 0.24*	− 0.42***
	(0.10)	(0.13)	(0.13)
Rich	0.08	0.44**	− 0.18*
	(0.16)	(0.20)	(0.10)
Uncertain	0.04	0.01	0.04
	(0.08)	(0.08)	(0.12)
Poor × uncertain	− 0.04	− 0.10	− 0.11
	(0.13)	(0.12)	(0.20)
Rich × uncertain	0.06	− 0.09	− 0.15
	(0.17)	(0.14)	(0.15)
Constant	0.88***	− 0.69***	0.24***
	(0.07)	(0.08)	(0.07)
Mean of dep. variable	0.96	− 0.65	0.01
F stat: uncertain	0.45	0.53	1.39
p value	0.72	0.66	0.25
Observations	840	840	840

Effects of uncertainty on recipients reward/punishment behavior. The constant term captures recipients average reward/punishment behavior in the equal wealth condition when participants have certainty about the distribution of recipients’ endowments. Regressions control for individual level fixed effects; standard errors are heteroskedasticity-robust and clustered at the participant level. F statistics and corresponding p values from a Wald test of joint significance of β₃, β₄ and β₅ for each regression are reported below the table.

^*Significant at the 10% confidence level,

^**significant at the 5% confidence level,

^***significant at the 1 % confidence level

Table 8.

Effects of recipients’ absolute endowments on their reward/punishment behavior

	Dependent variable: Reward
	(1) Give to me	(2) Give to other	(3) Randomize
Poor	0.01	− 0.36***	− 0.49***
	(0.11)	(0.13)	(0.16)
Rich	− 0.03	0.34**	− 0.25**
	(0.13)	(0.16)	(0.12)
High endowment	− 0.21**	0.02	− 0.03
	(0.08)	(0.08)	(0.08)
Poor × high endowment	0.13	0.14	0.04
	(0.12)	(0.12)	(0.15)
Rich × high endowment	0.27	0.09	−0.01
	(0.17)	(0.10)	(0.16)
Constant	1.01***	− 0.69***	0.27***
	(0.07)	(0.08)	(0.08)
Mean of dep. variable	0.96	− 0.65	0.01
F stat: high endowment	2.64	1.85	0.12
p value	0.06*	0.15	0.95
Observations	840	840	840

Effects of recipients’ absolute endowments on their reward/punishment behavior. The constant term captures recipients’ average reward/punishment behavior in the equal wealth condition with low endowments. Regressions control for individual level fixed effects; standard errors are heteroskedasticity-robust and clustered at the participant level. F statistics and corresponding p values from a Wald test of joint significance of β₃, β₄ and β₅ for each regression are reported below the table.

^*Significant at the 10% confidence level,

^**significant at the 5% confidence level,

^***significant at the 1% confidence level

Table 9.

Effects of all conditions on recipients’ reward/punishment behavior

	Dependent variable: Reward
	(1) Give to me	(2) Give to other	(3) Randomize
Poor	0.13	− 0.41***	− 0.50***
	(0.13)	(0.15)	(0.15)
Rich	0.00	0.46*	− 0.14
	(0.19)	(0.25)	(0.12)
Uncertain	0.07	− 0.04	0.09
	(0.12)	(0.13)	(0.17)
High endowment	− 0.19**	− 0.03	0.01
	(0.09)	(0.14)	(0.12)
Poor × uncertain	− 0.23	0.11	0.01
	(0.18)	(0.21)	(0.21)
Rich × uncertain	− 0.06	− 0.23	− 0.21
	(0.23)	(0.23)	(0.16)
Poor × high endowment	− 0.06	0.36*	0.16
	(0.17)	(0.21)	(0.20)
Rich × high endowment	0.16	− 0.04	− 0.07
	(0.21)	(0.20)	(0.22)
Uncertain × highwealth	− 0.06	0.10	− 0.09
	(0.12)	(0.21)	(0.15)
Poor × uncertain × high endowment	0.37	− 0.43	− 0.24
	(0.22)	(0.31)	(0.21)
Rich × uncertain × high endowment	0.23	0.27	0.13
	(0.22)	(0.35)	(0.21)
Constant	0.97***	− 0.67***	0.23**
	(0.09)	(0.11)	(0.10)
Mean of dep. variable	0.96	− 0.65	0.01
Observations	840	840	840

Effects of all conditions on recipients’ reward/punishment behavior. The constant term captures recipients’ average reward/punishment behavior in the equal wealth condition with low endowments and no uncertainty. Regressions control for individual level fixed effects; standard errors are heteroskedasticity-robust and clustered at the participant level.

^*Significant at the 10% confidence level,

^**significant at the 5% confidence level,

^***significant at the 1% confidence level

Table 10.

Effect of recipients’ absolute endowments on allocators’ probability of randomizing or allocating directly to one of the two potential recipients

	Equal endowments		Unequal endowments
	(1) Randomize	(2) Give to A/B	(3) Randomize	(4) Give to poor	(5) Give to rich
High endowment	− 0.14***	0.14***	− 0.05	− 0.01	0.06
	(0.05)	(0.05)	(0.04)	(0.05)	(0.04)
Constant	0.76***	0.24***	0.21***	0.71***	0.07***
	(0.02)	(0.02)	(0.02)	(0.03)	(0.02)
Mean of dep. variable	0.69	0.31	0.19	0.71	0.10
Observations	140	140	280	280	280

Effect of recipients’ absolute endowments on allocators’ probability of randomizing or allocating directly to one of the two potential recipients. The constant term captures allocators’ probability of allocating as indicated in the column head in the low endowment condition. Regressions control for individual level fixed effects; standard errors are heteroskedasticity-robust and clustered at the group level.

^*Significant at the 10% confidence level,

^**significant at the 5% confidence level,

^***significant at the 1% confidence level

Table 11.

Proportions of trials in which allocators believed that they were leaving money on the table

	Dependent variable: dummy for whether the allocator expected to leave money on the table
	(1) Equal endowments	(2) Unequal endowments
Give to A/B	− 0.60
	(0.37)
Give to poor		0.38**
		(0.15)
Give to rich		0.13
		(0.26)
Constant	0.50***	0.32***
	(0.09)	(0.12)
Mean of dep. variable	0.36	0.61
F stat: give to poor = give to rich		1.36
p value		0.25
Observations	70	140

Proportions of trials in which allocators believed that they were leaving money on the table. Regressions control for individual level fixed effects; standard errors are heteroskedasticity-robust and clustered at the participant level. F statistics and corresponding p values from a Wald test of coefficient equality between β₁ and β₂ in the unequal wealth condition is reported below the table in column (2).

^*Significant at the 10% confidence level,

^**significant at the 5% confidence level,

^***significant at the 1% confidence level