RETRACTED ARTICLE: A new emergency response of spherical intelligent fuzzy decision process to diagnose of COVID19

Abstract

The control of spreading of COVID-19 in emergency situation the entire world is a challenge, and therefore, the aim of this study was to propose a spherical intelligent fuzzy decision model for control and diagnosis of COVID-19. The emergency event is known to have aspects of short time and data, harmfulness, and ambiguity, and policy makers are often rationally bounded under uncertainty and threat. There are some classic approaches for representing and explaining the complexity and vagueness of the information. The effective tool to describe and reduce the uncertainty in data information is fuzzy set and their extension. Therefore, we used fuzzy logic to develop fuzzy mathematical model for control of transmission and spreading of COVID19. The fuzzy control of early transmission and spreading of coronavirus by fuzzy mathematical model will be very effective. The proposed research work is on fuzzy mathematical model of intelligent decision systems under the spherical fuzzy information. In the proposed work, we will develop a newly and generalized technique for COVID19 based on the technique for order of preference by similarity to ideal solution (TOPSIS) and complex proportional assessment (COPRAS) methods under spherical fuzzy environment. Finally, an illustrative the emergency situation of COVID-19 is given for demonstrating the effectiveness of the suggested method, along with a sensitivity analysis and comparative analysis, showing the feasibility and reliability of its results.

Introduction

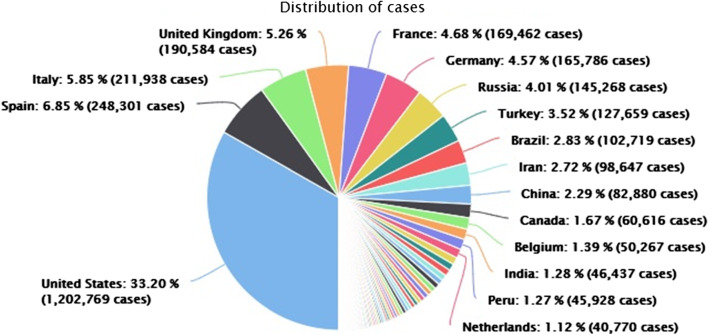
The situation of the world for the people is very risky to spend the peaceful life due to the spreading of the COVID-19. The COVID-19 is viral disease, a pandemic and the world health organization (WHO) declared an emergency situation due the spreading of COVID-19. In the end of 2019, some cases reported as same symptoms in the Wuhan city, province Hubei, China, after the diagnosing of these cases reported as novel coronavirus (COVID-19). This deadly virus has infected the entire world and many people have died as a result of this insuperable virus. The name “coronavirus” comes from the Latin word “corona” which means a “crown, circle of light or nimbus”. This virus influences immediately to your lungs. It has comparable symptoms as influenza and pneumonia. In the beginning, various of those infected worked or shopped at a wholesale seafood market in Wuhan, China. After that it radiates universally through import, export, travelling and social contacting of infected people. The Fig. 1 represents the world wide confirmed cases till May 4, 2020.

Fig. 1.

COVID-19 confirmed cases distribution

Several researchers investigated and developed different methods for addressing obstacles to medical and decision-making. In practical decision making, there are a great quantity of uncertainties, imprecise and vague information, whose representations and managements are always the central issues. Health professionals and healthcare administrators are working to reduce clinical and maintenance costs for the prevention and management of corona disease. Expenditure and need for health care are both growing fast. Health care practitioners, administrators and other sectors collectively perform a range of healthcare management techniques with the goal of facilitating effective disease prevention approaches using scarce resources. Such principles are used to build a decision-making model using a number of parameters and alternatives (Cromwell et al. 2015). The purpose of the multiple criteria decision making (MCDM) frameworks is to prepared an appropriate decisions at different levels of health care, such as operational, methodical, and functional. There may be an ideal solution to any difficult decision-making problem, but it is a difficult task to find such a method. In particular, management decisions are taken by managers or senior management to grow and maintain the organization. In fact, there are contradictions in strategic decisions, possible synergies between different options, and uncertainty in the final result. When strategic decisions are taken, the company shall agree on tactical and operational planning decisions. Strategic, tactical, and operational planning are grouped together as a taxonomy of health planning (Kumar et al. 2017). Disease prevention and control approaches include multiple management roles like as facility preparation, organization and decision making.

MCDM problems with spherical fuzzy environment took much attention to the real-life problems where the goal is associated for selecting the best alternative in contrast to the nite values under the different criteria where the evaluation terms are SFNs given by decision experts (DEs). However, in order to process the ambiguity /imprecision in the data, theories like as fuzzy set (FS) (Zadeh 1965), intuitionistic FS (IFS) (Attanassov 1986), picture FS (Cuong and Kreinovich 2013), spherical FS (Ashraf and Abdullah 2019), are applied widely. Presently, decision-making is a hot topic in the field of research which includes the following three main steps:

1. To describe the information, collect the data on an appropriate scale.

2. Obtain the totally preference value of the object by assigning the various attribute values.

3. Rank the objects in a transparent process to get the suitable alternative(s).

Therefore, the intention of the present research is to describe a group decision making method to resolve the multicriteria group decision making (MCGDM) problems for SFSs with robust generalized TOPSIS-COPRAS approach based on the spherical fuzzy information. The novelty of fuzzy set firstly defined by Zadeh (1965) to use non-statistical and vague phenomena. Since the inception, the theory of FS became a more interesting research area, e.g., image processing, data mining, engineering, medical sciences, clustering, statistical information theory and information technology. Since FSs assign only a crisp membership function of an element to show the double conflicting states, one is support and other is disagree. Thus, fuzzy set theory faces the limitation to show the negative state. To avoid this limitation, Atanassov (Attanassov 1986) developed the idea of intuitionistic fuzzy sets (IFSs) theory based on the notion of fuzzy set (FS) by Zadeh. The application of IFSs have investigated by many authors (Mendel et al. 2019a, b; Mendel 2019b). Atanassov Atanassov (2018a, 2018b, 2015) presented the dfferent decision making techniques to tackle the uncertainty in real life decision making problems. Sotirov et al. (2018) introduced the hybrid approach for modular neural network design using intercriteria analysis and intuitionistic fuzzy logic. Sotirov et al. (2016); Castillo et al. (2015) proposed the novel modular neural network preprocessing procedure with intuitionistic fuzzy intercriteria analysis method to tackle the uncertainty in real life DMPs. Although, IFS based models have been successfully implemented in different areas since its appearance, but there are practical situations in real-world which cannot be represented by the traditional IFSs. Recently, (Cuong and Kreinovich 2013) filled these gaps by introducing the neutral membership in Atanassov’s IFS theory. Picture fuzzy set (PFS) in a finite fixed set $\mathfrak{R}$ is written as $\left\{〈{\partial }_{\gamma },,,P_{♭},\left({\partial }_{\gamma }\right),,,I_{♭},\left({\partial }_{\gamma }\right),,,N_{♭},\left({\partial }_{\gamma }\right)〉,|,{\partial }_{\gamma },\in ,\mathfrak{R}\right\}$ where $P_{♭},I_{♭},N_{♭}\in \left[0,,,1\right]$ with condition that $0\le P_{♭}+I_{♭}+N_{♭}\le 1$. Basically, PFSs can precisely describe a human views, including more responses, such as: “yes”, “abstain”, “no” and “refusal”. Many researcher (Ashraf et al. 2019e, f; Khan et al. 2019a, b, c; Wei 2017; Zeng et al. 2019) contributed to the picture FS. Since the introduction of IFS, the theories and applications of IFS have been studied comprehensively, including its’ applications in DMPs. These researches are very appropriate to tackle DMPs under PFS environment only owing to the condition $0\le P_{♭}+I_{♭}+N_{♭}\le 1$. However, in practical DMPs, the decision makers provides evaluation value in the form of $\left(P_{♭},,,I_{♭},,,N_{♭}\right)$, but it may be not satisfy the condition $0\le P_{♭}+I_{♭}+N_{♭}\le 1$ and beyond the upper bound 1. Aiming at this limitation which PFN can not handle, (Ashraf and Abdullah 2019) established a new concept of spherical fuzzy (SF) set to handle with this situation. SFS is an extension of PFS by slackening the condition $0\le P_{♭}^2+I_{♭}^2+N_{♭}^2\le 1$. We must also note that the acceptable spherical fuzzy space increases, thus providing more freedom for observers to express their belief in supporting membership. Therefore, SFSs express more extensive fuzzy information; Whilst, SFSs are more maneuverable and more appropriate for dealing with uncertainties information. Several researchers have done quite valuable contributions in the expansion of SF set and its approach to different fields, their results shows the great success of SF set in theoretical and technical aspects. As aggregation operators have a strong role to play in decision-making problems (DMPs), several researchers have done quite valuable contributions to introduce aggregation operators for SF set. Spherical aggregation operators based on algebraic norms (Ashraf et al. 2019a) dealing with uncertainty and inaccurate information in DMPs. SF set the representation of SF norms (Ashraf et al. 2019b) and TOPSIS methodology introduced for SF information. SF Dombi aggregation operators based on Dombi norm are introduced in Ashraf et al. (2019c). SF Logarithmic aggregation operators based on entropy are proposed in Jin et al. (2019a). Linguistic SF aggregation operators are presented in Jin et al. (2019b) for SF information to tackle the uncertainty in DMPs. Cao (2019) proposed the spherical linguistic Muirhead mean operators and discussed their application in group DMP. GRA methodology based on spherical linguistic fuzzy Choquet integral is proposed (Ashraf et al. 2018) for SF information. Cosine similarity measures are presented in Rafiq et al. (2019) to discussed the application in DMPs. Application of SF distance measures are discussed in Ashraf et al. (2019d) to determined the child development influence environmental factors using SF information. In Zeng et al. (2019) proposed the TOPSIS approach based on SF rough Set and discussed their application in DMPs. Gündoğdu et al. (2020b) presented the TOPSIS methodology using SF information and discussed their real life application in DMPs. Gündoğdu and Kahraman (2020c) introduced the QFD method and also presented its application to the linear delta robot technology development problem. Gündoğdu (2020a); Gündoğdu and Kahraman (2019) exted the concept of spherical fuzzy set to interval-valued fuzzy set and presented the decision making methodology to tackle in uncertainty in DMPs. Khan et al. (2020a) introduced the distance and similarity measures for spherical fuzzy sets and discussed their applications in selecting mega projects. Ashraf et al. (2020g) proposed the symmetric sum based aggregation operators for spherical fuzzy information and discussed their application in multi-attribute group decision-making problem. Ashraf et al. (2020h) presented the decision making technique using sine function and Barukab (Barukab et al. 2019) introduced new approach to fuzzy TOPSIS method based on entropy measure under spherical fuzzy information.

Just like these DM methods, we have the most fruitful method called TOPSIS method, which was introduced in 1981, by Hwang and Yoon (1981). The abbreviation, TOPSIS stands for “technique for order preference by similarity to the ideal solution. This method was developed later by many authors. The high flexibility of the TOPSIS concept allows us to add additional extensions to make the best choices in different situations. Practically, TOPSIS and its modifications are used to solve many theoretical and real-world problems (Boran et al. 2009; Chen 2000; Nag and Helal 2016; Wang and Elhag 2006; Wang et al. 2018). In complex decision making, where the results can be easily evaluated by using TOPSIS method, contains a lot of qualitative information. The decision makers have limited attention and information processing skills. The TOPSIS method is a practical and useful technique for ranking and selection of alternatives.

Complex Proportional Assessment (COPRAS) (Zavadskas and Kaklauskas 1996) methodology proposed by Zavadskas and Kaklauskas in 1996, which is most effectively and commonly used technique to deal with the uncertainty in DMPs. It is used to evaluate alternatives dependent on several criteria by applying the corresponding weights of parameters and the degree of usefulness of alternatives. Choosing the appropriate alternative is achieved by focusing at the ideal and anti-ideal solutions. COPRAS claims that the importance and usefulness features under investigation are directly and proportionately dependent on a set of criteria that describes alternatives efficiently and on the criteria’s values and weights. COPRAS has many benefits, such as less processing time, a very easy and straightforward method of computing etc, over other MCDM methods such as EVAMIX, VIKOR and AHP.

With respect to the advantages of SF set in describing uncertain information, also, regardless of the motivation and inspiration of all the above debate, we enlist the main objectives of the article:

1. Article main objective to provides a new strategy to SF set through emergency group decision making problem (GDMP) for control and prevent the COVID-19 effectively.

2. In this paper, a new methodology based on TOPSIS approach hybrid with the COPRAS, which can deal much more uncertainties in the form of spherical fuzzy sets. Note that, in comparisons with the classic fuzzy sets, spherical fuzzy set has more capability to deal the different situations more successfully. In fact, these sets consider opinions of DMs better than classic fuzzy sets. That is why, to use advantages and flexibility of the SF sets, the introduced technique is established under these sets to discourse the uncertainty of real-life in better way.

3. We design an algorithm to tackle emergency decision-making problem of COVID-19.

4. We shall collect the exact data disaster during the COVD-19 and then construct the mathematical model of emergency decision support systems for COVD-19 under generalized structure of spherical fuzzy sets and compare our propose technique with existing techniques to shows the validity and effectiveness of the proposed methodology.

To achieve the list of goals the structure of the paper is arranged as follows: In Sect. 2, some basic concepts are introduced. In Sect. 3, proposed the different types of distance between SF numbers. Section 4, gave the main contribution of the paper, introduced the TOPSIS-COPRAS technique to deal with the uncertainty in DMP using SF information. Section 5, propose the numerical case study of outbreak of coronavirus as an emergency decision support problem to demonstrate the applicability and reliability of the proposed technique. Section 6 presents the comparison analysis to shows the applicability of the proposed methodology and concluded remarks are discussed in Sect. 7.

Preliminaries

In this section, for better understanding of the spherical fuzzy sets, some related basic concepts will be briefly reviewed.

Definition 1

Zadeh (1965) A fuzzy set $\epsilon$ in fixed set $\mathfrak{R}$ is described as

$$\begin{array}{c}\hfill \epsilon =\left\{〈{\partial }_{\gamma },,,P_{♭},\left({\partial }_{\gamma }\right)〉,|,{\partial }_{\gamma },\in ,\mathfrak{R}\right\},\end{array}$$

where $P_{♭}\left({\partial }_{\gamma }\right)\in \left[0,,,1\right]$ called positive membership grade.

By ${\epsilon }_1\subseteq {\epsilon }_2$ we mean that $P_{{♭}_1}\left({\partial }_{\gamma }\right)\le P_{{♭}_2}\left({\partial }_{\gamma }\right)$ for each ${\partial }_{⋎}\in \mathfrak{R}.$ Clearly ${\epsilon }_1={\epsilon }_2$ if ${\epsilon }_1\subseteq {\epsilon }_2$ and ${\epsilon }_2\subseteq {\epsilon }_1.$

Utilizing (Zadeh 1965), proposed min–max system to define basic operational laws as follows:

1. ${\epsilon }_1\cap {\epsilon }_2=\left\{min,\left(P_{{♭}_1},\left({\partial }_{\gamma }\right),,,P_{{♭}_2},\left({\partial }_{\gamma }\right)\right),|,{\partial }_{\gamma },\in ,\mathfrak{R}\right\},$

2. ${\epsilon }_1\cup {\epsilon }_2=\left\{max,\left(P_{{♭}_1},\left({\partial }_{\gamma }\right),,,P_{{♭}_2},\left({\partial }_{\gamma }\right)\right),|,{\partial }_{\gamma },\in ,\mathfrak{R}\right\},$

3. ${\epsilon }_1^c=\left\{1,-,P_{{♭}_1},\left({\partial }_{\gamma }\right),|,{\partial }_{\gamma },\in ,\mathfrak{R}\right\},$where ${\epsilon }_1,{\epsilon }_2\in ϝ\widehat{S}\left(\mathfrak{R}\right)$ and ${\partial }_{⋎}\in \mathfrak{R}.$

Definition 2

(Ashraf and Abdullah 2019)A spherical fuzzy set $\epsilon$ in fixed set $\mathfrak{R}$ is described as

$$\begin{array}{c}\hfill \epsilon =\left\{〈{\partial }_{\gamma },,,P_{♭},\left({\partial }_{\gamma }\right),,,I_{♭},\left({\partial }_{\gamma }\right),,,N_{♭},\left({\partial }_{\gamma }\right)〉,|,{\partial }_{\gamma },\in ,\mathfrak{R}\right\},\end{array}$$

where $P_{♭}\left({\partial }_{\gamma }\right)\in \left[0,,,1\right]$ positive membership, $I_{♭}\left({\partial }_{\gamma }\right)$ $\in \left[0,,,1\right]$ neutral membership and $N_{♭}\left({\partial }_{\gamma }\right)\in \left[0,,,1\right]$ negative membership grades, respectively. In addition, it is necessary to $0\le P_{♭}^2\left({\partial }_{\gamma }\right)+I_{♭}^2\left({\partial }_{\gamma }\right)+N_{♭}^2\left({\partial }_{\gamma }\right)\le 1,$ for each ${\partial }_{⋎}\in \mathfrak{R}$.

To what follows, we symbolize the collection of all spherical fuzzy sets in $\mathfrak{R}$ by $\widehat{S}ϝ\widehat{S}\left(\mathfrak{R}\right)$. For convenience, the spherical fuzzy number (SFN) is symbolized by the triplet $\epsilon =\left(P_{♭},,,I_{♭},,,N_{♭}\right).$

Let ${\epsilon }_1,{\epsilon }_2\in \widehat{S}ϝ\widehat{S}\left(\mathfrak{R}\right).$ Ashraf and Abdullah (2019) defined the following notions:

1. ${\epsilon }_1⊑{\epsilon }_2$ $⟺$ if $P_{{♭}_1}\left({\partial }_{\gamma }\right)\le P_{{♭}_2}\left({\partial }_{\gamma }\right),I_{{♭}_1}\left({\partial }_{\gamma }\right)\le I_{{♭}_2}\left({\partial }_{\gamma }\right)$ and $N_{{♭}_1}\left({\partial }_{\gamma }\right)\ge N_{{♭}_2}\left({\partial }_{\gamma }\right)$ for each ${\partial }_{⋎}\in \mathfrak{R}.$ Clearly ${\epsilon }_1={\epsilon }_2$ if ${\epsilon }_1⊑{\epsilon }_2$ and ${\epsilon }_2⊑{\epsilon }_1.$

2. ${\epsilon }_1\sqcap {\epsilon }_2=\left\{\begin{array}{c}min\left(P_{{♭}_1},\left({\partial }_{\gamma }\right),,,P_{{♭}_2},\left({\partial }_{\gamma }\right)\right),min\left(I_{{♭}_1},\left({\partial }_{\gamma }\right),,,I_{{♭}_2},\left({\partial }_{\gamma }\right)\right),\\ max\left(N_{{♭}_1},\left({\partial }_{\gamma }\right),,,N_{{♭}_2},\left({\partial }_{\gamma }\right)\right)|{\partial }_{\gamma }\in \mathfrak{R}\end{array}\right\},$

3. ${\epsilon }_1\bigsqcup {\epsilon }_2=\left\{\begin{array}{c}max\left(P_{{♭}_1},\left({\partial }_{\gamma }\right),,,P_{{♭}_2},\left({\partial }_{\gamma }\right)\right),min\left(I_{{♭}_1},\left({\partial }_{\gamma }\right),,,I_{{♭}_2},\left({\partial }_{\gamma }\right)\right),\\ min\left(N_{{♭}_1},\left({\partial }_{\gamma }\right),,,N_{{♭}_2},\left({\partial }_{\gamma }\right)\right)|{\partial }_{\gamma }\in \mathfrak{R}\end{array}\right\},$

4. ${\epsilon }_1^c=\left\{N_{{♭}_1},\left({\partial }_{\gamma }\right),,,I_{{♭}_1},\left({\partial }_{\gamma }\right),,,P_{{♭}_1},\left({\partial }_{\gamma }\right),|,{\partial }_{\gamma },\in ,\mathfrak{R}\right\},$

   where ${\epsilon }_1,{\epsilon }_2\in \widehat{S}ϝ\widehat{S}\left(\mathfrak{R}\right)$ and ${\partial }_{⋎}\in \mathfrak{R}.$

Definition 3

(Ashraf and Abdullah 2019)Let ${\epsilon }_1=\left\{P_{{♭}_1},\left({\partial }_{\gamma }\right),,\right)\left(I_{{♭}_1},\left({\partial }_{\gamma }\right),,,N_{{♭}_1},\left({\partial }_{\gamma }\right)\right\}$ and ${\epsilon }_2=\left\{P_{{♭}_2},\left({\partial }_{\gamma }\right),,,I_{{♭}_2},\left({\partial }_{\gamma }\right),,,N_{{♭}_2},\left({\partial }_{\gamma }\right)\right\}\in \widehat{S}ϝN\left(\mathfrak{R}\right)$ with $\varpi >0.$ Then, the operational rules are as follows:

1. ${\epsilon }_1\otimes {\epsilon }_2=\left\{P_{{♭}_1},P_{{♭}_2},,,I_{{♭}_1},I_{{♭}_2},,,\sqrt{N_{{♭}_1}^2+N_{{♭}_2}^2-N_{{♭}_1}^2{N}_{{♭}_2}^2}\right\};$

2. ${\epsilon }_1\oplus {\epsilon }_2=\left\{\sqrt{P_{{♭}_1}^2+P_{{♭}_2}^2-P_{{♭}_1}^2{P}_{{♭}_2}^2},,,I_{{♭}_1},I_{{♭}_2},,,N_{{♭}_1},N_{{♭}_2}\right\};$

3. ${\epsilon }_1^{\varpi }=\left\{{\left(P_{{♭}_1}\right)}^{\varpi },,,{\left(I_{{♭}_1}\right)}^{\varpi },,,\sqrt{1-{\left(1,-,N_{{♭}_1}^2\right)}^{\varpi }}\right\};$

4. $\varpi ·{\epsilon }_1=\left\{\sqrt{1-{\left(1,-,P_{{♭}_1}^2\right)}^{\varpi }},,,{\left(I_{{♭}_1}\right)}^{\varpi },,,{\left(N_{{♭}_1}\right)}^{\varpi }\right\}.$

Definition 4

Ashraf et al. (2019a)Let ${\epsilon }_k=\left\{P_{{♭}_k},\left({\partial }_{\gamma }\right),,\right)\left(I_{{♭}_k},\left({\partial }_{\gamma }\right),,,N_{{♭}_k},\left({\partial }_{\gamma }\right)\right\}\in \widehat{S}ϝN\left(\mathfrak{R}\right)$ and $SFWA:SF{N}^n\to SFN$ be a mapping defined as

$$\begin{array}{c}\hfill SFWA\left({\epsilon }_1,,,{\epsilon }_2,,,\dots ,,,{\epsilon }_n\right)=\sum _{k=1}^n{\tau }_k{\epsilon }_k.\end{array}$$

Then, by operational laws of SFNs, we obtained spherical fuzzy weighted averaging operator as

$$\begin{array}{cc}& SFWA\left({\epsilon }_1,,,{\epsilon }_2,,,\dots ,,,{\epsilon }_n\right)\hfill \\ \hfill & =\left\{\begin{array}{c}\sqrt{1-{\mathrm{\Pi }}_{k=1}^n{(1-P_{{♭}_k}^2)}^{{\tau }_k}},{\mathrm{\Pi }}_{k=1}^n{(I_{{♭}_k})}^{{\tau }_k},\\ {\mathrm{\Pi }}_{k=1}^n{(N_{{♭}_k})}^{{\tau }_k}\end{array}\right\}.\hfill \end{array}$$

where the weight vector of ${\epsilon }_k(k\in N)$ with ${\tau }_k\ge 0$ and ${\sum }_{k=1}^n{\tau }_k=1$ is $\tau =\left\{{\tau }_1,,,{\tau }_2,,,\dots ,,,{\tau }_n\right\}.$

Definition 5

Ashraf et al. (2019a) Let ${\epsilon }_k=\left\{P_{{♭}_k},\left({\partial }_{\gamma }\right),,\right)\left(I_{{♭}_k},\left({\partial }_{\gamma }\right),,,N_{{♭}_k},\left({\partial }_{\gamma }\right)\right\}\in \widehat{S}ϝN\left(\mathfrak{R}\right)$ and $SFWG:SF{N}^n\to SFN$ be a mapping defined as

$$\begin{array}{c}\hfill SFWG\left({\epsilon }_1,,,{\epsilon }_2,,,\dots ,,,{\epsilon }_n\right)=\prod _{k=1}^n{\epsilon }_k^{{\tau }_k}.\end{array}$$

Then, by operational laws of SFNs, we obtained spherical fuzzy weighted geometric operator as

$$\begin{array}{c}\hfill SFWG\left({\epsilon }_1,,,{\epsilon }_2,,,\dots ,,,{\epsilon }_n\right)=\left\{\begin{array}{c}{\mathrm{\Pi }}_{k=1}^n{(P_{{♭}_k})}^{{\tau }_k},{\mathrm{\Pi }}_{k=1}^n{(I_{{♭}_k})}^{{\tau }_k},\\ \sqrt{1-{\mathrm{\Pi }}_{k=1}^n{(1-N_{{♭}_k}^2)}^{{\tau }_k}}\end{array}\right\}.\end{array}$$

Where the weight vector of ${\epsilon }_k(k\in N)$ with ${\tau }_k\ge 0$ and ${\sum }_{k=1}^n{\tau }_k=1$ is $\tau =\left\{{\tau }_1,,,{\tau }_2,,,\dots ,,,{\tau }_n\right\}.$

Distance of spherical fuzzy sets

Definition 6

Let ${\epsilon }_1=\left\{P_{{♭}_1},\left({\partial }_{\gamma }\right),,,I_{{♭}_1},\left({\partial }_{\gamma }\right),,,N_{{♭}_1},\left({\partial }_{\gamma }\right)\right\}$ and ${\epsilon }_2=\left\{P_{{♭}_2},\left({\partial }_{\gamma }\right),,,I_{{♭}_2},\left({\partial }_{\gamma }\right),,,N_{{♭}_2},\left({\partial }_{\gamma }\right)\right\}\in \widehat{S}ϝN\left(\mathfrak{R}\right).$ Then maximum distance $d_{\mathrm{Max}}({\epsilon }_1,{\epsilon }_2)$ is defined as

$$\begin{array}{c}\hfill d_{\mathrm{Max}}({\epsilon }_1,{\epsilon }_2)=\frac{1}{n}\sum _{p=1}^{n}max\left(\left\{\begin{array}{c}\left|P_{{♭}_1},\left({\partial }_{{\gamma }_p}\right),-,P_{{♭}_2},\left({\partial }_{{\gamma }_p}\right)\right|+\\ \left|I_{{♭}_1},\left({\partial }_{{\gamma }_p}\right),-,I_{{♭}_2},\left({\partial }_{{\gamma }_p}\right)\right|+\\ \left|N_{{♭}_1},\left({\partial }_{{\gamma }_p}\right),-,N_{{♭}_2},\left({\partial }_{{\gamma }_p}\right)\right|\end{array}\right\}\right)\text{.}\end{array}$$

Definition 7

Let ${\epsilon }_1=\left\{P_{{♭}_1},\left({\partial }_{\gamma }\right),,,I_{{♭}_1},\left({\partial }_{\gamma }\right),,,N_{{♭}_1},\left({\partial }_{\gamma }\right)\right\}$ and ${\epsilon }_2=\left\{P_{{♭}_2},\left({\partial }_{\gamma }\right),,,I_{{♭}_2},\left({\partial }_{\gamma }\right),,,N_{{♭}_2},\left({\partial }_{\gamma }\right)\right\}\in \widehat{S}ϝN\left(\mathfrak{R}\right).$ Then minimum distance $d_{\mathrm{Min}}({\epsilon }_1,{\epsilon }_2)$ is defined as

$$\begin{array}{c}\hfill d_{\mathrm{Min}}({\epsilon }_1,{\epsilon }_2)=\frac{1}{n}\sum _{p=1}^{n}min\left(\left\{\begin{array}{c}\left|P_{{♭}_1},\left({\partial }_{{\gamma }_p}\right),-,P_{{♭}_2},\left({\partial }_{{\gamma }_p}\right)\right|+\\ \left|I_{{♭}_1},\left({\partial }_{{\gamma }_p}\right),-,I_{{♭}_2},\left({\partial }_{{\gamma }_p}\right)\right|+\\ \left|N_{{♭}_1},\left({\partial }_{{\gamma }_p}\right),-,N_{{♭}_2},\left({\partial }_{{\gamma }_p}\right)\right|\end{array}\right\}\right)\text{.}\end{array}$$

Definition 8

Let ${\epsilon }_1=\left\{P_{{♭}_1},\left({\partial }_{\gamma }\right),,,I_{{♭}_1},\left({\partial }_{\gamma }\right),,,N_{{♭}_1},\left({\partial }_{\gamma }\right)\right\}$ and ${\epsilon }_2=\left\{P_{{♭}_2},\left({\partial }_{\gamma }\right),,,I_{{♭}_2},\left({\partial }_{\gamma }\right),,,N_{{♭}_2},\left({\partial }_{\gamma }\right)\right\}\in \widehat{S}ϝN\left(\mathfrak{R}\right)$. Then Hamming distance $d_{\mathit{HD}}({\epsilon }_1,{\epsilon }_2)$ is defined as

$$\begin{array}{c}\hfill d_{\mathit{HD}}({\epsilon }_1,{\epsilon }_2)=\frac{1}{n}\sum _{p=1}^n\left(\left\{\begin{array}{c}\left|P_{{♭}_1},\left({\partial }_{{\gamma }_p}\right),-,P_{{♭}_2},\left({\partial }_{{\gamma }_p}\right)\right|+\\ \left|I_{{♭}_1},\left({\partial }_{{\gamma }_p}\right),-,I_{{♭}_2},\left({\partial }_{{\gamma }_p}\right)\right|+\\ \left|N_{{♭}_1},\left({\partial }_{{\gamma }_p}\right),-,N_{{♭}_2},\left({\partial }_{{\gamma }_p}\right)\right|\end{array}\right\}\right)\text{.}\end{array}$$

Definition 9

Let ${\epsilon }_1=\left\{P_{{♭}_1},\left({\partial }_{\gamma }\right),,,I_{{♭}_1},\left({\partial }_{\gamma }\right),,,N_{{♭}_1},\left({\partial }_{\gamma }\right)\right\}$ and ${\epsilon }_2=\left\{P_{{♭}_2},\left({\partial }_{\gamma }\right),,,I_{{♭}_2},\left({\partial }_{\gamma }\right),,,N_{{♭}_2},\left({\partial }_{\gamma }\right)\right\}\in \widehat{S}ϝN\left(\mathfrak{R}\right)$. Then Euclidean distance $d_{\mathit{ED}}({\epsilon }_1,{\epsilon }_2)$ is defined as

$$\begin{array}{c}\hfill d_{\mathit{ED}}({\epsilon }_1,{\epsilon }_2)=\sqrt{\frac{1}{n}\sum _{p=1}^n\left(\begin{array}{c}{(P_{{♭}_1}\left({\partial }_{{\gamma }_p}\right)-P_{{♭}_2}\left({\partial }_{{\gamma }_p}\right))}^2+\\ {(I_{{♭}_1}\left({\partial }_{{\gamma }_p}\right)-I_{{♭}_2}\left({\partial }_{{\gamma }_p}\right))}^2+\\ {(N_{{♭}_1}\left({\partial }_{{\gamma }_p}\right)-N_{{♭}_2}\left({\partial }_{{\gamma }_p}\right))}^2\end{array}\right)}\text{.}\end{array}$$

Definition 10

Let ${\epsilon }_1=\left\{P_{{♭}_1},\left({\partial }_{\gamma }\right),,,I_{{♭}_1},\left({\partial }_{\gamma }\right),,,N_{{♭}_1},\left({\partial }_{\gamma }\right)\right\}$ and ${\epsilon }_2=\left\{P_{{♭}_2},\left({\partial }_{\gamma }\right),,,I_{{♭}_2},\left({\partial }_{\gamma }\right),,,N_{{♭}_2},\left({\partial }_{\gamma }\right)\right\}\in \widehat{S}ϝN\left(\mathfrak{R}\right)$. Then normalized Hamming distance $d_{\mathit{NHD}}({\epsilon }_1,{\epsilon }_2)$ is defined as

$$\begin{array}{c}\hfill d_{\mathit{NHD}}({\epsilon }_1,{\epsilon }_2)=\frac{1}{2n}\sum _{p=1}^n\left(\left\{\begin{array}{c}\left|P_{{♭}_1},\left({\partial }_{{\gamma }_p}\right),-,P_{{♭}_2},\left({\partial }_{{\gamma }_p}\right)\right|+\\ \left|I_{{♭}_1},\left({\partial }_{{\gamma }_p}\right),-,I_{{♭}_2},\left({\partial }_{{\gamma }_p}\right)\right|+\\ \left|N_{{♭}_1},\left({\partial }_{{\gamma }_p}\right),-,N_{{♭}_2},\left({\partial }_{{\gamma }_p}\right)\right|\end{array}\right\}\right)\text{.}\end{array}$$

Definition 11

Let ${\epsilon }_1=\left\{P_{{♭}_1},\left({\partial }_{\gamma }\right),,,I_{{♭}_1},\left({\partial }_{\gamma }\right),,,N_{{♭}_1},\left({\partial }_{\gamma }\right)\right\}$ and ${\epsilon }_2=\left\{P_{{♭}_2},\left({\partial }_{\gamma }\right),,,I_{{♭}_2},\left({\partial }_{\gamma }\right),,,N_{{♭}_2},\left({\partial }_{\gamma }\right)\right\}\in \widehat{S}ϝN\left(\mathfrak{R}\right)$. Then normalized Euclidean distance $d_{\mathit{NED}}({\epsilon }_1,{\epsilon }_2)$ is defined as

$$\begin{array}{c}\hfill d_{\mathit{NED}}({\epsilon }_1,{\epsilon }_2)=\sqrt{\frac{1}{2n}\sum _{p=1}^n\left(\begin{array}{c}{(P_{{♭}_1}\left({\partial }_{{\gamma }_p}\right)-P_{{♭}_2}\left({\partial }_{{\gamma }_p}\right))}^2+\\ {(I_{{♭}_1}\left({\partial }_{{\gamma }_p}\right)-I_{{♭}_2}\left({\partial }_{{\gamma }_p}\right))}^2+\\ {(N_{{♭}_1}\left({\partial }_{{\gamma }_p}\right)-N_{{♭}_2}\left({\partial }_{{\gamma }_p}\right))}^2\end{array}\right)}\text{.}\end{array}$$

Proposed methodology

In this segment, we proposed the methodology to deal with uncertainty and inaccurate information in the form of SFSs in DMPs. The proposed methodology has following steps:

Step-1

Data Collection

Judgements of specialists’ decision maker (DM) experts on assessments criteria for every activity and each criterion weights are assembled in the shape of initial decision matrixes. At primary, the $D_k$ matrix constructed on ideas of kth DM is computed as below:

$$\begin{array}{c}\hfill {\left[D_k\right]}_{\alpha \gamma }=\begin{array}{cc}\begin{array}{c}\text{activity}1\\ ⋮\\ \text{activity}p\end{array}& \left[\begin{array}{ccc}{\epsilon }_{11}^k& \cdots & {\epsilon }_{1j}^k\\ ⋮& \ddots & ⋮\\ {\epsilon }_{p1}^k& \cdots & {\epsilon }_{\mathit{pj}}^k\end{array}\right]\end{array}\end{array}$$ 4.1

where, $1\le \alpha \le p$ denotes the activities, $1\le \gamma \le j$ denotes the criteria, respectively, and $1\le k\le m$ represents the specialists’ decision makers. Then, the $D_k$ spherical fuzzy matrix constructed on ideas of kth DM is computed as follows:

$$\begin{array}{c}\hfill {\left[D_k\right]}_{\beta \gamma }=\begin{array}{cc}\begin{array}{c}\text{activity}1\\ ⋮\\ \text{activity}q\end{array}& \left[\begin{array}{ccc}{\epsilon }_{11}^k& \cdots & {\epsilon }_{1j}^k\\ ⋮& \ddots & ⋮\\ {\epsilon }_{q1}^k& \cdots & {\epsilon }_{\mathit{qj}}^k\end{array}\right]\end{array}\end{array}$$ 4.2

where, $1\le \beta \le q$ denotes the numbers of paths (alternatives).

Step-2

Calculation Of DMs Weights

Each specialists’ decision maker give specified weight to decision matrix. In this step, we calculate the weights of the decision matrices by utilizing the closeness to average ideal solution and maximum distance from positive and negative ideal solutions.

Step-2(a)

In this step, utilizing (Yue 2011) methodology to find the average $D^{\ast }$, left negative $L{D}^{-}$ and right negative $R{D}^{-}$ ideal solutions as follows

$$\begin{array}{c}\hfill D^{\ast }={\epsilon }_{\beta \gamma }^{\ast }=\left[\begin{array}{ccc}{\epsilon }_{11}^{\ast }& \cdots & {\epsilon }_{1j}^{\ast }\\ ⋮& \ddots & ⋮\\ {\epsilon }_{q1}^{\ast }& \cdots & {\epsilon }_{\mathit{qj}}^{\ast }\end{array}\right]\end{array}$$ 4.3

where ${\epsilon }_{\beta \gamma }^{\ast }=\left(\frac{1}{m},\sum _{k=1}^m,P_{\beta \gamma }^{(k)},,,\frac{1}{m},\sum _{k=1}^m,I_{\beta \gamma }^{(k)},,,\frac{1}{m},\sum _{k=1}^m,N_{\beta \gamma }^{(k)}\right)$ with $1\le \beta \le q$ and $1\le \gamma \le j.$

$$\begin{array}{c}\hfill L{D}^{-}={\epsilon }_{\beta \gamma }^{l-}=\left[\begin{array}{ccc}{\epsilon }_{11}^{l-}& \cdots & {\epsilon }_{1j}^{l-}\\ ⋮& \ddots & ⋮\\ {\epsilon }_{q1}^{l-}& \cdots & {\epsilon }_{\mathit{qj}}^{l-}\end{array}\right]\end{array}$$ 4.4

where ${\epsilon }_{\beta \gamma }^{l-}={min}_{1\le k\le t}\left({\epsilon }_{\beta \gamma }^k\right)$$=\left({min}_{1\le k\le t},P_{\beta \gamma }^{(k)},,,{min}_{1\le k\le t},I_{\beta \gamma }^{(k)},,,{min}_{1\le k\le t},N_{\beta \gamma }^{(k)}\right)$ with $1\le \beta \le q$ and $1\le \gamma \le j.$

$$\begin{array}{c}\hfill R{D}^{-}={\epsilon }_{\beta \gamma }^{R-}=\left[\begin{array}{ccc}{\epsilon }_{11}^{R-}& \cdots & {\epsilon }_{1j}^{R-}\\ ⋮& \ddots & ⋮\\ {\epsilon }_{q1}^{R-}& \cdots & {\epsilon }_{\mathit{qj}}^{R-}\end{array}\right]\end{array}$$ 4.5

where ${\epsilon }_{\beta \gamma }^{R-}={max}_{1\le k\le t}\left({\epsilon }_{\beta \gamma }^k\right)$$=\left({max}_{1\le k\le t},P_{\beta \gamma }^{(k)},,,{max}_{1\le k\le t},I_{\beta \gamma }^{(k)},,,{max}_{1\le k\le t},N_{\beta \gamma }^{(k)}\right)$ with $1\le \beta \le q$ and $1\le \gamma \le j.$

Step-2(b)

To measure decision level of each DM, we find the distance between each individual decision matrix $D_k$ $\left(1,\le ,k,\le ,m\right)$ with average ideal matrix $D^{\ast },$ left negative ideal solution $L{D}^{-}$ and right negative ideal solution $R{D}^{-}$. Consider that the Euclidean distance is the most widely used tool to measure the separation of two objects in practical applications, we utilize it to measure the separation between $D_k$ with $D^{\ast },L{D}^{-}$ and $R{D}^{-}$ as follows.

$$\begin{array}{cc}& S{M}_k=∥D_k,-,D^{\ast }∥\hfill \\ \hfill & =\sqrt{\frac{1}{n}\left[\begin{array}{c}{\sum }_{\beta =1}^q{\sum }_{\gamma =1}^j{\left(P_{\beta \gamma }^{(k)},-,\left(\frac{1}{m},\sum _{k=1}^m,P_{\beta \gamma }^{(k)}\right)\right)}^2+\\ {\sum }_{\beta =1}^q{\sum }_{\gamma =1}^j{\left(I_{\beta \gamma }^{(k)},-,\left(\frac{1}{m},\sum _{k=1}^m,I_{\beta \gamma }^{(k)}\right)\right)}^2+\\ {\sum }_{\beta =1}^q{\sum }_{\gamma =1}^j{\left(N_{\beta \gamma }^{(k)},-,\left(\frac{1}{m},\sum _{k=1}^m,N_{\beta \gamma }^{(k)}\right)\right)}^2\end{array}\right]}\hfill \\ \hfill & S{M}_k^{l-}=∥D_k,-,L,D^{-}∥\hfill \\ \hfill & =\sqrt{\frac{1}{n}\left[\begin{array}{c}{\sum }_{\beta =1}^q{\sum }_{\gamma =1}^j{\left(P_{\beta \gamma }^{(k)},-,\left({min}_{1\le k\le t},P_{\beta \gamma }^{(k)}\right)\right)}^2+\\ {\sum }_{\beta =1}^q{\sum }_{\gamma =1}^j{\left(I_{\beta \gamma }^{(k)},-,\left({min}_{1\le k\le t},I_{\beta \gamma }^{(k)}\right)\right)}^2+\\ {\sum }_{\beta =1}^q{\sum }_{\gamma =1}^j{\left(N_{\beta \gamma }^{(k)},-,\left({min}_{1\le k\le t},N_{\beta \gamma }^{(k)}\right)\right)}^2\end{array}\right]}\hfill \\ \hfill & S{M}_k^{R-}=∥D_k,-,R,D^{-}∥\hfill \\ \hfill & =\sqrt{\frac{1}{n}\left[\begin{array}{c}{\sum }_{\beta =1}^q{\sum }_{\gamma =1}^j{\left(P_{\beta \gamma }^{(k)},-,\left({max}_{1\le k\le t},P_{\beta \gamma }^{(k)}\right)\right)}^2+\\ {\sum }_{\beta =1}^q{\sum }_{\gamma =1}^j{\left(I_{\beta \gamma }^{(k)},-,\left({max}_{1\le k\le t},I_{\beta \gamma }^{(k)}\right)\right)}^2+\\ {\sum }_{\beta =1}^q{\sum }_{\gamma =1}^j{\left(N_{\beta \gamma }^{(k)},-,\left({max}_{1\le k\le t},N_{\beta \gamma }^{(k)}\right)\right)}^2\end{array}\right]}\hfill \end{array}$$

Step-2(c)

Proposed the final closedness coefficient value of each DM is calculated as

$$\begin{array}{c}\hfill FC{V}^{(k)}=S{M}_k^{-}+\frac{{\sum }_{k=1}^{m}S{M}_k}{S{M}_k{\sum }_{k=1}^m\frac{1}{S{M}_k}}\end{array}$$ 4.8

where $S{M}_k^{-}=max\left\{S,M_k^{l-},,,S,M_k^{R-}\right\}$

Step-2(d)

Final weights ${♭}_k$ of each DM is obtained as

$$\begin{array}{c}\hfill {♭}_k=\frac{FC{V}^{(k)}}{\sum _{k=1}^{m}FC{V}^{(k)}}\end{array}$$ 4.9

Step-3

Aggregated matrix is obtained by using spherical fuzzy weighted averaging operator

$$\begin{array}{cc}& SFWA\left({\epsilon }_1,,,{\epsilon }_2,,,\dots ,,,{\epsilon }_n\right)\hfill \\ & =\left\{\begin{array}{c}\sqrt{1-{\mathrm{\Pi }}_{k=1}^n{(1-P_{{♭}_k}^2)}^{{\tau }_k}},{\mathrm{\Pi }}_{k=1}^n{(I_{{♭}_k})}^{{\tau }_k},\\ {\mathrm{\Pi }}_{k=1}^n{(N_{{♭}_k})}^{{\tau }_k}\end{array}\right\}\hfill \end{array}$$ 4.10

Step-4

Aggregated spherical matrix for all the possible paths is constructed by using the addition rules of spherical fuzzy set as follows

$$\begin{array}{c}\hfill \left({\epsilon }_1,\oplus ,{\epsilon }_2,\oplus ,\cdots ,\oplus ,{\epsilon }_n\right)=\left\{\begin{array}{c}{\left(\begin{array}{c}{P}_{{♭}_1}^2+P_{{♭}_2}^2+\cdots +P_{{♭}_n}^2-\\ \left(P_{{♭}_1}^2,P_{{♭}_2}^2,\dots ,P_{{♭}_n}^2\right)\end{array}\right)}^{\frac{1}{n}},\\ I_{{♭}_1}{I}_{{♭}_2}\dots I_{{♭}_n},N_{{♭}_1}{N}_{{♭}_2}\dots N_{♭n}\end{array}\right\}\end{array}$$

Step-5

Positive ideal $\left({\rho }_{\beta \gamma }^{+}\right)$ and negative ideal $\left({\rho }_{\beta \gamma }^{-}\right)$ solutions are calculated as

$$\begin{array}{c}\hfill {\rho }_{\beta \gamma }^{+}=\left\{v_{\gamma }^{+},|,\left({max}_{\gamma },\left(P_{\beta \gamma }\right),,,{min}_{\gamma },\left(I_{\beta \gamma }\right),,,{min}_{\gamma },\left(N_{\beta \gamma }\right)\right)\right\}\\ \hfill \end{array}$$ 4.11

and

$$\begin{array}{c}\hfill {\rho }_{\beta \gamma }^{-}=\left\{v_{\gamma }^{-},|,\left({min}_{\gamma },\left(P_{\beta \gamma }\right),,,{min}_{\gamma },\left(I_{\beta \gamma }\right),,,{max}_{\gamma },\left(N_{\beta \gamma }\right)\right)\right\}\\ \hfill \end{array}$$ 4.12

Step-6

Calculate the Euclidean distance of aggregated spherical fuzzy information from the positive and negative ideal solutions as follows

$$\begin{array}{c}\hfill E{D}_{\beta \gamma }^{+}=\sqrt{\frac{1}{n}\left[\begin{array}{c}{\sum }_{\beta =1}^q{\sum }_{\gamma =1}^j{\left(P_{\beta \gamma },-,\left({max}_{\gamma },\left(P_{\beta \gamma }\right)\right)\right)}^2+\\ {\sum }_{\beta =1}^q{\sum }_{\gamma =1}^j{\left(I_{\beta \gamma },-,\left({min}_{\gamma },\left(I_{\beta \gamma }\right)\right)\right)}^2+\\ {\sum }_{\beta =1}^q{\sum }_{\gamma =1}^j{\left(N_{\beta \gamma },-,\left({min}_{\gamma },\left(N_{\beta \gamma }\right)\right)\right)}^2\end{array}\right]}\\ \hfill \end{array}$$ 4.13

and

$$\begin{array}{c}\hfill E{D}_{\beta \gamma }^{-}=\sqrt{\frac{1}{n}\left[\begin{array}{c}{\sum }_{\beta =1}^q{\sum }_{\gamma =1}^j{\left(P_{\beta \gamma },-,\left({min}_{\gamma },\left(P_{\beta \gamma }\right)\right)\right)}^2+\\ {\sum }_{\beta =1}^q{\sum }_{\gamma =1}^j{\left(I_{\beta \gamma },-,\left({min}_{\gamma },\left(I_{\beta \gamma }\right)\right)\right)}^2+\\ {\sum }_{\beta =1}^q{\sum }_{\gamma =1}^j{\left(N_{\beta \gamma },-,\left({max}_{\gamma },\left(N_{\beta \gamma }\right)\right)\right)}^2\end{array}\right]}\\ \hfill \end{array}$$ 4.14

Step-7

Closeness relation to ideal solutions are calculated as follows

$$\begin{array}{c}\hfill {\mu }_{\beta }=\frac{E{D}_{\beta \gamma }^{-}}{E{D}_{\beta \gamma }^{+}+E{D}_{\beta \gamma }^{-}}\end{array}$$ 4.15

To ranked the set of paths (alternatives) by preference according to the descending order of ${\mu }_{\beta }.$ Means highest ${\mu }_{\beta }$ will be our finest path (alternative).

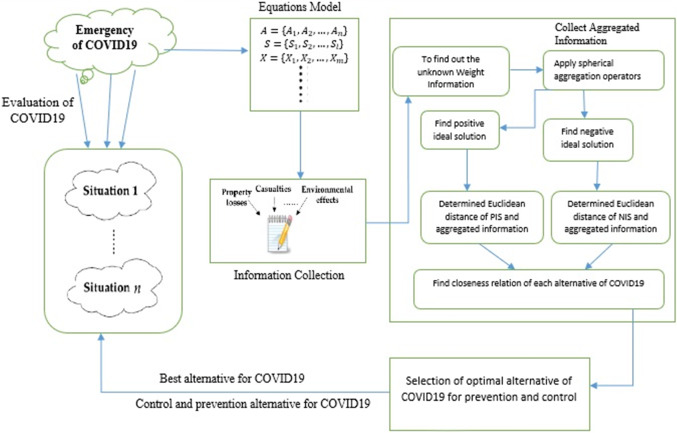
Flow chart of the proposed technique is given in Fig. 2:

Fig. 2.

Flow chart of the TOPSIS-COPRAS technique

Application

To study the prevention and control of COVID-19, we have developed a novel hybrid methodology for selecting the best alternatives using a critical path strategy that will help to choose the best path to overcome this deadly disease.

Case Study: To demonstrate the applicability and validity of the proposed methods, we extant a real case study about an emergency caused by an outbreak of novel Coronavirus disease (COVID-19) pandemic that occurred in China.

Since 19 December 2020, in Wuhan, China, there have been several unidentified cases of pneumonia with cough, dyspnea, exhaustion and fever as the major symptoms reported in a short time. The Chinese health officials and CDC immediately identified the pathogen of these cases as a new form of coronavirus which was called COVID-19 by the World Health Organization (WHO) on 10 Janvary-20 (World 2020). The Chinese government’s information department held a press conference on pneumonia prevention and control of new coronavirus infections on January 22, 2020. The same day, a strategy for the prevention and control of pneumonitis of new coronavirus infection was announced by the People’s Republic of China, along with COVID-19 epidemic research, sample collection and testing, monitoring and management of close contacts, and public propaganda, education and risk communication (Shen et al. 2020).

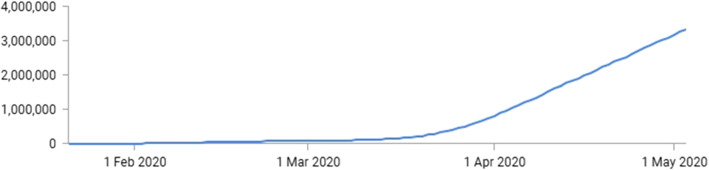
As of May 4, 2020, more than 3 442 234 confirmed cases and 239 740 confirmed deaths are reported in 215 Countries, areas or territories. The infected cases graph are as follows in Fig. 3:

Fig. 3.

Infected cases

In such emergency situation, it is essential to provide an efficient way in emergency response for avoiding additional losses and to save the lives of the people. Preventive and mitigation measures are key in both health care and community settings. Due to such an emergency decision, the health experts have to make an immediate response, urgently rescue to control the situation efficiently and stop it from more deaths.

The panel of three experts ratings on the set of criteria are collected and illustrated for each activity shown in Tables 1, 2.

Step-1

Decision makers activities information computed in spherical fuzzy sets using Table 2:

Step-2(a)

Utilizing (Yue 2011) methodology to find the average $D^{\ast }$, left negative $L{D}^{-}$ and right negative $R{D}^{-}$ ideal solutions are given as follows

$$\begin{array}{cc}& D^{\ast }=\left[\begin{array}{ccccccccccccccc}0.20& 0.17& 0.86& 0.20& 0.17& 0.86& 0.20& 0.17& 0.87& 0.37& 0.20& 0.66& 0.60& 0.10& 0.37\\ 0.40& 0.23& 0.76& 0.63& 0.23& 0.53& 0.40& 0.26& 0.77& 0.60& 0.20& 0.63& 0.53& 0.23& 0.67\\ 0.60& 0.20& 0.63& 0.86& 0.17& 0.23& 0.73& 0.17& 0.34& 0.20& 0.17& 0.86& 0.50& 0.07& 0.50\\ 0.76& 0.23& 0.43& 0.50& 0.26& 0.63& 0.37& 0.20& 0.67& 0.60& 0.20& 0.63& 0.53& 0.23& 0.67\\ 0.76& 0.23& 0.43& 0.63& 0.23& 0.53& 0.40& 0.23& 0.77& 0.76& 0.13& 0.37& 0.57& 0.07& 0.47\\ 0.46& 0.23& 0.70& 0.40& 0.23& 0.76& 0.70& 0.23& 0.50& 0.70& 0.23& 0.46& 0.53& 0.23& 0.67\\ 0.46& 0.23& 0.73& 0.56& 0.26& 0.56& 0.50& 0.17& 0.57& 0.76& 0.23& 0.43& 0.40& 0.23& 0.77\\ 0.20& 0.17& 0.86& 0.46& 0.20& 0.73& 0.40& 0.23& 0.77& 0.46& 0.23& 0.73& 0.57& 0.07& 0.47\\ 0.27& 0.13& 0.83& 0.53& 0.23& 0.66& 0.60& 0.20& 0.60& 0.56& 0.26& 0.56& 0.56& 0.26& 0.57\\ 0.27& 0.17& 0.80& 0.86& 0.26& 0.30& 0.33& 0.13& 0.77& 0.57& 0.17& 0.53& 0.70& 0.13& 0.44\\ 0.73& 0.20& 0.53& 0.73& 0.26& 0.40& 0.63& 0.26& 0.53& 0.33& 0.13& 0.76& 0.20& 0.17& 0.87\\ 0.50& 0.26& 0.63& 0.56& 0.26& 0.56& 0.56& 0.23& 0.60& 0.47& 0.13& 0.66& 0.47& 0.13& 0.67\\ 0.33& 0.13& 0.76& 0.56& 0.26& 0.56& 0.70& 0.23& 0.47& 0.63& 0.17& 0.47& 0.63& 0.26& 0.53\\ 0.53& 0.23& 0.66& 0.56& 0.26& 0.56& 0.76& 0.23& 0.43& 0.57& 0.17& 0.53& 0.63& 0.17& 0.47\\ 0.56& 0.26& 0.56& 0.83& 0.13& 0.33& 0.43& 0.17& 0.63& 0.53& 0.23& 0.66& 0.40& 0.23& 0.77\\ 0.83& 0.23& 0.40& 0.40& 0.20& 0.80& 0.43& 0.20& 0.60& 0.50& 0.17& 0.56& 0.50& 0.17& 0.57\end{array}\right]\hfill \\ \hfill & L{D}^{-}=\left[\begin{array}{ccccccccccccccc}0.01& 0.01& 0.8& 0.01& 0.01& 0.8& 0.01& 0.01& 0.8& 0.01& 0.01& 0.2& 0.01& 0.01& 0.01\\ 0.2& 0.2& 0.6& 0.4& 0.2& 0.2& 0.2& 0.2& 0.5& 0.4& 0.2& 0.5& 0.2& 0.2& 0.5\\ 0.4& 0.2& 0.5& 0.8& 0.01& 0.01& 0.4& 0.01& 0.01& 0.01& 0.01& 0.8& 0.01& 0.01& 0.01\\ 0.6& 0.2& 0.2& 0.2& 0.2& 0.2& 0.01& 0.01& 0.2& 0.4& 0.2& 0.5& 0.2& 0.2& 0.5\\ 0.6& 0.2& 0.2& 0.4& 0.2& 0.2& 0.2& 0.2& 0.6& 0.6& 0.01& 0.01& 0.01& 0.01& 0.01\\ 0.2& 0.2& 0.6& 0.2& 0.2& 0.6& 0.4& 0.2& 0.2& 0.6& 0.2& 0.2& 0.2& 0.2& 0.5\\ 0.2& 0.2& 0.5& 0.2& 0.2& 0.2& 0.01& 0.01& 0.2& 0.6& 0.2& 0.2& 0.2& 0.2& 0.6\\ 0.01& 0.01& 0.8& 0.4& 0.2& 0.6& 0.2& 0.2& 0.6& 0.2& 0.2& 0.5& 0.01& 0.01& 0.01\\ 0.01& 0.01& 0.8& 0.2& 0.2& 0.5& 0.6& 0.2& 0.6& 0.2& 0.2& 0.2& 0.2& 0.2& 0.2\\ 0.01& 0.01& 0.6& 0.8& 0.2& 0.2& 0.01& 0.01& 0.6& 0.01& 0.01& 0.2& 0.4& 0.01& 0.01\\ 0.6& 0.2& 0.5& 0.4& 0.2& 0.2& 0.2& 0.2& 0.2& 0.01& 0.01& 0.6& 0.01& 0.01& 0.8\\ 0.2& 0.2& 0.2& 0.2& 0.2& 0.2& 0.4& 0.2& 0.2& 0.01& 0.01& 0.5& 0.01& 0.01& 0.5\\ 0.01& 0.01& 0.6& 0.2& 0.2& 0.2& 0.6& 0.2& 0.2& 0.2& 0.01& 0.01& 0.2& 0.2& 0.2\\ 0.2& 0.2& 0.5& 0.2& 0.2& 0.2& 0.6& 0.2& 0.2& 0.01& 0.01& 0.2& 0.2& 0.01& 0.01\\ 0.2& 0.2& 0.2& 0.8& 0.01& 0.01& 0.01& 0.01& 0.2& 0.2& 0.2& 0.5& 0.2& 0.2& 0.6\\ 0.8& 0.2& 0.2& 0.4& 0.2& 0.8& 0.2& 0.01& 0.01& 0.01& 0.01& 0.2& 0.01& 0.01& 0.2\end{array}\right]\hfill \\ \hfill & R{D}^{-}=\left[\begin{array}{ccccccccccccccc}0.4& 0.3& 0.9& 0.4& 0.3& 0.9& 0.4& 0.3& 0.9& 0.9& 0.3& 0.9& 0.9& 0.3& 0.9\\ 0.6& 0.3& 0.9& 0.9& 0.3& 0.8& 0.8& 0.3& 0.9& 0.8& 0.2& 0.8& 0.8& 0.3& 0.9\\ 0.8& 0.2& 0.8& 0.9& 0.3& 0.5& 0.9& 0.3& 0.8& 0.4& 0.3& 0.9& 0.9& 0.2& 0.9\\ 0.9& 0.3& 0.6& 0.9& 0.3& 0.9& 0.9& 0.3& 0.9& 0.8& 0.2& 0.8& 0.8& 0.3& 0.9\\ 0.9& 0.3& 0.6& 0.9& 0.3& 0.8& 0.6& 0.3& 0.9& 0.9& 0.2& 0.6& 0.9& 0.2& 0.9\\ 0.6& 0.3& 0.9& 0.6& 0.3& 0.9& 0.9& 0.3& 0.8& 0.9& 0.3& 0.6& 0.8& 0.3& 0.9\\ 0.8& 0.3& 0.9& 0.9& 0.3& 0.9& 0.9& 0.3& 0.9& 0.9& 0.3& 0.6& 0.6& 0.3& 0.9\\ 0.4& 0.3& 0.9& 0.6& 0.2& 0.8& 0.6& 0.3& 0.9& 0.8& 0.3& 0.9& 0.9& 0.2& 0.9\\ 0.4& 0.2& 0.9& 0.8& 0.3& 0.9& 0.6& 0.2& 0.6& 0.9& 0.3& 0.9& 0.9& 0.3& 0.9\\ 0.6& 0.3& 0.9& 0.9& 0.3& 0.5& 0.6& 0.2& 0.9& 0.9& 0.3& 0.9& 0.9& 0.2& 0.8\\ 0.8& 0.2& 0.6& 0.9& 0.3& 0.8& 0.9& 0.3& 0.9& 0.6& 0.2& 0.9& 0.4& 0.3& 0.9\\ 0.9& 0.3& 0.9& 0.9& 0.3& 0.9& 0.9& 0.3& 0.8& 0.8& 0.2& 0.9& 0.8& 0.2& 0.9\\ 0.6& 0.2& 0.9& 0.9& 0.3& 0.9& 0.9& 0.3& 0.6& 0.9& 0.3& 0.9& 0.9& 0.3& 0.9\\ 0.8& 0.3& 0.9& 0.9& 0.3& 0.9& 0.9& 0.3& 0.6& 0.9& 0.3& 0.9& 0.9& 0.3& 0.9\\ 0.9& 0.3& 0.9& 0.9& 0.2& 0.5& 0.9& 0.3& 0.9& 0.8& 0.3& 0.9& 0.6& 0.3& 0.9\\ 0.9& 0.3& 0.5& 0.4& 0.2& 0.8& 0.9& 0.3& 0.9& 0.9& 0.3& 0.9& 0.9& 0.3& 0.9\end{array}\right]\hfill \end{array}$$

Table 1.

Information of each activities on criteria

$\text{Activity}$	Experts
	Amount			Period			Reputation
	DMs			DMs			DMs
	1	2	3	1	2	3	1	2	3
(a)
0-1	H	MH	VH	H	MH	VH	H	MH	VH
1-3	MH	M	H	MH	M	L	H	ML	H
3-4	M	ML	MH	VL	ML	L	MH	VL	L
4-5	ML	L	M	H	VH	MH	VH	L	H
5-6	ML	L	M	MH	M	VH	H	M	MH
6-14	M	M	H	M	H	MH	L	MH	ML
0-2	H	ML	MH	H	VH	M	L	VH	M
2-3	H	MH	VH	MH	MH	M	M	H	MH
3-7	MH	MH	VH	M	ML	H	M	M	M
7-8	M	VH	H	ML	VH	L	VH	M	MH
8-9	ML	M	ML	MH	L	L	ML	L	H
9-14	MH	H	L	M	H	L	MH	L	MH
10-14	MH	VH	M	H	L	M	M	M	L
11-14	ML	H	M	L	H	M	L	ML	M
12-14	M	M	L	VL	ML	ML	VH	MH	L
13-14	L	ML	ML	MH	MH	MH	H	VL	H

Activity	Experts
	Specialty			Safety
	DMs			DMs
	1	2	3	1	2	3
(b)
0-1	VH	H	L	L	VL	VH
1-3	M	MH	ML	M	ML	H
3-4	MH	VH	H	VH	VL	M
4-5	ML	M	MH	M	ML	H
5-6	VL	ML	M	VL	VH	ML
6-14	M	M	L	M	ML	H
0-2	L	ML	M	MH	H	M
2-3	MH	H	ML	ML	VL	VH
3-7	M	L	H	M	L	H
7-8	VH	ML	L	ML	MH	VL
8-9	MH	VH	M	VH	H	MH
9-14	VH	ML	M	M	ML	VH
10-14	ML	VL	H	L	ML	H
11-14	L	ML	VH	VL	H	ML
12-14	ML	M	H	H	M	MH
13-14	VH	M	L	M	L	VH

Table 2.

Linguistic variables and their corresponding SFNs

Very low (VL)	$\left(0.9,,,0.01,,,0.01\right)$
Low (L)	$\left(0.9,,,0.3,,,0.2\right)$
Medium low (ML)	$\left(0.8,,,0.2,,,0.5\right)$
Medium (M)	$\left(0.6,,,0.2,,,0.6\right)$
Medium high (MH)	$\left(0.4,,,0.2,,,0.8\right)$
High (H)	$\left(0.2,,,0.3,,,0.9\right)$
Very high (VH)	$\left(0.01,,,0.01,,,0.9\right)$

Step-2(b)

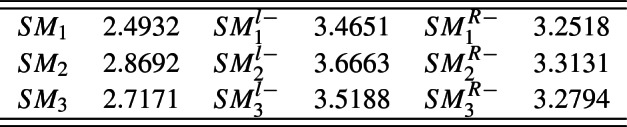
We find the $S{M}_k,$ $S{M}_k^{l-}$ and $S{M}_k^{R-}$ by using formulas of Step-2(b).

Step-2(c)

The final closedness coefficient values are obtained using Eq.4.8 and

Step-2(d)

Weights using Eq.4.9 are follows as

Step-3

Calculate the aggregated matrix by using spherical fuzzy weighted averaging operator defined in Eq. 4.10 in Table 3(a), (b).

Notation	Criteria	Description
${\mathbb{C}}_1$	High temperature and high humidity	High temperature and humidity positively correlate with the number of COVID-19 cases
${\mathbb{C}}_2$	Resources and facilities	Infrastructure: Hospitals, Lab, and in-patient beds
		Transport: Ambulance and other vehicles
		Skilled personnel: Doctors and nurses
		Working cost: Cost for the building, medical equipment,
		drugs, costs for staff commitment and
		other various purposes
${\mathbb{C}}_3$	Resources and facilities	Considering daily travel plan, persons travelling
		more are more likely to get COVID-19 infection
${\mathbb{C}}_4$	Socio demographic variable	People who work in urban areas, where
		the hygienic levels are lower more
		likely to get COVID-19 infection
${\mathbb{C}}_5$	Quarantine	People may spent most of their time in at home
		Due to this period no more spreading
		of COVID-19 deduction

Table 3.

Aggregated information

$\text{Activity}$	Amount	Period	Reputation
(a)
0-1	$\left(0.26,,,0.08,,,0.87\right)$	$\left(0.26,,,0.08,,,0.87\right)$	$\left(0.26,,,0.08,,,0.87\right)$
1-3	$\left(0.44,,,0.23,,,0.76\right)$	$\left(0.73,,,0.23,,,0.46\right)$	$\left(0.54,,,0.26,,,0.75\right)$
3-4	$\left(0.64,,,0.2,,,0.62\right)$	$\left(0.88,,,0.08,,,0.09\right)$	$\left(0.82,,,0.09,,,0.13\right)$
4-5	$\left(0.8,,,0.23,,,0.4\right)$	$\left(0.67,,,0.26,,,0.54\right)$	$\left(0.64,,,0.09,,,0.57\right)$
5-6	$\left(0.8,,,0.23,,,0.4\right)$	$\left(0.73,,,0.23,,,0.46\right)$	$\left(0.44,,,0.23,,,0.76\right)$
6-14	$\left(0.52,,,0.23,,,0.69\right)$	$\left(0.45,,,0.23,,,0.75\right)$	$\left(0.79,,,0.23,,,0.42\right)$
0-2	$\left(0.57,,,0.23,,,0.72\right)$	$\left(0.7,,,0.26,,,0.49\right)$	$\left(0.72,,,0.09,,,0.46\right)$
2-3	$\left(0.26,,,0.08,,,0.87\right)$	$\left(0.48,,,0.2,,,0.73\right)$	$\left(0.45,,,0.23,,,0.75\right)$
3-7	$\left(0.33,,,0.07,,,0.83\right)$	$\left(0.62,,,0.23,,,0.65\right)$	$\left(0.6,,,0.2,,,0.6\right)$
7-8	$\left(0.4,,,0.09,,,0.78\right)$	$\left(0.87,,,0.26,,,0.28\right)$	$\left(0.42,,,0.07,,,0.76\right)$
8-9	$\left(0.76,,,0.2,,,0.53\right)$	$\left(0.82,,,0.26,,,0.33\right)$	$\left(0.77,,,0.26,,,0.46\right)$
9-14	$\left(0.68,,,0.26,,,0.52\right)$	$\left(0.72,,,0.26,,,0.47\right)$	$\left(0.68,,,0.23,,,0.41\right)$
10-14	$\left(0.44,,,0.08,,,0.75\right)$	$\left(0.7,,,0.26,,,0.49\right)$	$\left(0.76,,,0.23,,,0.41\right)$
11-14	$\left(0.64,,,0.23,,,0.64\right)$	$\left(0.73,,,0.26,,,0.46\right)$	$\left(0.81,,,0.23,,,0.38\right)$
12-14	$\left(0.72,,,0.26,,,0.47\right)$	$\left(0.84,,,0.07,,,0.12\right)$	$\left(0.68,,,0.08,,,0.52\right)$
13-14	$\left(0.84,,,0.23,,,0.36\right)$	$\left(0.4,,,0.2,,,0.8\right)$	$\left(0.65,,,0.11,,,0.23\right)$

$\text{Activity}$	Specialty	Safety
(b)
0-1	$\left(0.66,,,0.09,,,0.54\right)$	$\left(0.82,,,0.2,,,0.13\right)$
1-3	$\left(0.65,,,0.2,,,0.62\right)$	$\left(0.62,,,0.45,,,0.65\right)$
3-4	$\left(0.27,,,0.09,,,0.86\right)$	$\left(0.7,,,0.16,,,0.2\right)$
4-5	$\left(0.65,,,0.2,,,0.62\right)$	$\left(0.62,,,0.45,,,0.65\right)$
5-6	$\left(0.81,,,0.07,,,0.13\right)$	$\left(0.78,,,0.22,,,0.15\right)$
6-14	$\left(0.76,,,0.23,,,0.41\right)$	$\left(0.62,,,0.45,,,0.65\right)$
0-2	$\left(0.81,,,0.23,,,0.38\right)$	$\left(0.45,,,0.37,,,0.75\right)$
2-3	$\left(0.58,,,0.23,,,0.71\right)$	$\left(0.76,,,0.19,,,0.18\right)$
3-7	$\left(0.7,,,0.26,,,0.49\right)$	$\left(0.7,,,0.47,,,0.49\right)$
7-8	$\left(0.76,,,0.08,,,0.45\right)$	$\left(0.79,,,0.67,,,0.16\right)$
8-9	$\left(0.44,,,0.08,,,0.75\right)$	$\left(0.26,,,0.09,,,0.87\right)$
9-14	$\left(0.61,,,0.07,,,0.66\right)$	$\left(0.61,,,0.17,,,0.65\right)$
10-14	$\left(0.77,,,0.09,,,0.18\right)$	$\left(0.78,,,0.52,,,0.44\right)$
11-14	$\left(0.77,,,0.08,,,0.44\right)$	$\left(0.78,,,0.54,,,0.15\right)$
12-14	$\left(0.63,,,0.23,,,0.64\right)$	$\left(0.44,,,0.35,,,0.76\right)$
13-14	$\left(0.71,,,0.08,,,0.48\right)$	$\left(0.7,,,0.17,,,0.49\right)$

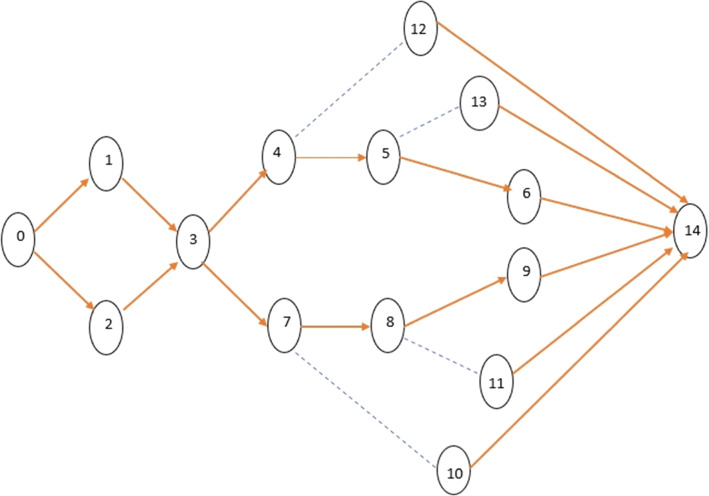
There is a panel of experts to determined the critical path (given in (Fig. 4)) for prevent and control of COVID-19 with respect to the following criteria’s:

Fig. 4.

Critical Path Strategy

Step-4

Calculated aggregated spherical matrix for paths by using addition rule of spherical fuzzy set are evaluated in Table 4(a), (b).

Step-5

Calculate the Positive ideal $\left({\rho }_{\beta \gamma }^{+}\right)$ and negative ideal $\left({\rho }_{\beta \gamma }^{-}\right)$ solution by using Eq.4.11 and Eq.4.12.

$$\begin{array}{c}\hfill {\rho }_{\beta \gamma }^{+}=\left\{\begin{array}{c}\left(0.430,,,0.00,,,0.043\right),\left(0.536,,,0.00,,,0.004\right),\\ \left(0.458,,,0.00,,,0.006\right),\left(0.526,,,0.00,,,0.008\right),\\ \left(0.547,,,0.00,,,0.003\right)\end{array}\right\}\end{array}$$

and

$$\begin{array}{c}\hfill {\rho }_{\beta \gamma }^{-}=\left\{\begin{array}{c}\left(0.140,,,0.00,,,0.414\right),\left(0.367,,,0.00,,,0.128\right),\\ \left(0.309,,,0.00,,,0.162\right),\left(0.333,,,0.00,,,0.186\right),\\ \left(0.362,,,0.00,,,0.030\right)\end{array}\right\}\end{array}$$

Step-6

Calculate the Euclidean distance of aggregated spherical fuzzy information from the positive and negative ideal solutions by using Eqs. 4.13 and 4.14 as follows in Table 5(a):

Step-7

Calculate the closeness relation value by using Eq. 4.15. and Final ranking are as follows in Table 5(b):

Table 4.

Aggregated information in paths

Paths	Amount	Period	Reputation
(a)
$0-1-3-4-12-14$	$\left(0.296,,,0.001,,,0.194\right)$	$\left(0.515,,,0.0001,,,0.371\right)$	$\left(0.371,,,0.0002,,,0.045\right)$
$0-1-3-4-5-13-14$	$\left(0.404,,,0.0002,,,0.06\right)$	$\left(0.393,,,0.00,,,0.016\right)$	$\left(0.371,,,0.00,,,0.011\right)$
$0-1-3-4-5-6-14$	$\left(0.37,,,0.00,,,0.046\right)$	$\left(0.424,,,0.00,,,0.007\right)$	$\left(0.376,,,0.00,,,0.015\right)$
$0-1-3-7-10-14$	$\left(0.14,,,0.0001,,,0.414\right)$	$\left(0.367,,,0.0012,,,0.128\right)$	$\left(0.322,,,0.001,,,0.162\right)$
$0-1-3-7-8-11-14$	$\left(0.187,,,0.00,,,0.273\right)$	$\left(0.454,,,0.0003,,,0.033\right)$	$\left(0.309,,,0.00,,,0115\right)$
$0-1-3-7-8-9-14$	$\left(0.261,,,0.00,,,0.118\right)$	$\left(0.489,,,0.00,,,0.011\right)$	$\left(0.325,,,0.00,,,0.072\right)$
$0-2-3-4-12-14$	$\left(0.328,,,0.001,,,0.184\right)$	$\left(0.536,,,0.0003,,,0.004\right)$	$\left(0.458,,,0.0001,,,0.023\right)$
$0-2-3-4-5-13-14$	$\left(0.43,,,0.0002,,,0.057\right)$	$\left(0.418,,,0.0002,,,0.014\right)$	$\left(0.444,,,0.00,,,0.006\right)$
$0-2-3-4-5-6-14$	$\left(0.391,,,0.00,,,0.43\right)$	$\left(0.445,,,0.00,,,0.006\right)$	$\left(0.438,,,0.00,,,0.008\right)$
$0-2-3-7-10-14$	$\left(0.172,,,0.00011,,,0.393\right)$	$\left(0.395,,,0.0031,,,0.115\right)$	$\left(0.410,,,0.001,,,0.086\right)$
$0-2-3-78-11-14$	$\left(0.213,,,0.00,,,0.259\right)$	$\left(0.477,,,0.0008,,,0.03\right)$	$\left(0.383,,,0.00,,,0.060\right)$
$0-2-3-7-8-9-14$	$\left(0.282,,,0.00,,,0.112\right)$	$\left(0.509,,,0.0002,,,0.010\right)$	$\left(0.387,,,0.00,,,0.038\right)$

Paths	Specialty	Safety
(b)
$0-1-3-4-12-14$	$\left(0.333,,,0.0004,,,0.186\right)$	$\left(0.426,,,0.00,,,0.013\right)$
$0-1-3-4-5-13-14$	$\left(0.372,,,0.00,,,0.086\right)$	$\left(0.477,,,0.00,,,0.005\right)$
$0-1-3-4-5-6-14$	$\left(0.431,,,0.00,.,0.010\right)$	$\left(0.484,,,0.00,,,0.001\right)$
$0-1-3-7-10-14$	$\left(0.473,,,0.0004,,,0.03\right)$	$\left(0.518,,,0.0005,,,0.018\right)$
$0-1-3-7-8-11-14$	$\left(0.501,,,0.00,,,0.033\right)$	$\left(0.547,,,0.00,,,0.0001\right)$
$0-1-3-7-8-9-14$	$\left(0.416,,,0.00,,,0.037\right)$	$\left(0.436,,,0.00,,,0.004\right)$
$0-2-3-4-12-14$	$\left(0.366,,,0.0011,,,0.151\right)$	$\left(0.362,,,0.00,.,0.021\right)$
$0-2-3-4-5-13-14$	$\left(0.399,,,0.00,,,0.070\right)$	$\left(0.426,,,0.00,,,0.009\right)$
$0-2-3-4-5-6-14$	$\left(0.453,,,0.00,,,0.008\right)$	$\left(0.440,,,0.00,,,0.002\right)$
$0-2-3-7-10-14$	$\left(0.503,,,0.0012,,,0.024\right)$	$\left(0.461,,,0.00045,,,0.03\right)$
$0-2-3-78-11-14$	$\left(0.526,,,0.00,,,0.027\right)$	$\left(0.499,,,0.00,,,0.002\right)$
$0-2-3-7-8-9-14$	$\left(0.438,,,0.00,,,0.030\right)$	$\left(0.391,,,0.00,,,0.006\right)$

Table 5.

(a): Aggregated distance. (b): Closeness relation value and final ranks of each alternative

Paths	Distance from ${\rho }_{\beta \gamma }^{+}$	Distance from ${\rho }_{\beta \gamma }^{-}$
(a)
$0-1-3-4-12-14$	0.1636	0.1628
$0-1-3-4-5-13-14$	0.1126	0.2288
$0-1-3-4-5-6-14$	0.0846	0.2407
$0-1-3-7-10-14$	0.2504	0.1173
$0-1-3-7-8-11-14$	0.1759	0.1600
$0-1-3-7-8-9-14$	0.1293	0.1872
$0-2-3-4-12-14$	0.1492	0.1879
$0-2-3-4-5-13-14$	0.0990	0.2421
$0-2-3-4-5-6-14$	0.0733	0.2513
$0-2-3-7-10-14$	0.2185	0.1294
$0-2-3-78-11-14$	0.1477	0.1728
$0-2-3-7-8-9-14$	0.1146	0.2024

Paths	Closeness relation value	Final ranking
(b)
$0-1-3-4-12-14$	0.4988	9
$0-1-3-4-5-13-14$	0.6702	4
$0-1-3-4-5-6-14$	0.7400	2
$0-1-3-7-10-14$	0.3189	12
$0-1-3-7-8-11-14$	0.4763	10
$0-1-3-7-8-9-14$	0.5916	6
$0-2-3-4-12-14$	0.5574	7
$0-2-3-4-5-13-14$	0.7097	3
$\mathbf{0}-\mathbf{2}-\mathbf{3}-\mathbf{4}-\mathbf{5}-\mathbf{6}-\mathbf{14}$	$\mathbf{0.7741}$	$\mathbf{1}$
$0-2-3-7-10-14$	0.3720	11
$0-2-3-78-11-14$	0.5392	8
$0-2-3-7-8-9-14$	0.6383	5

Bold value indicates the best alternative in critical path strategy

Comparison analysis

In the following, we will demonstrate the effectiveness and advantages of proposed operators by comparing with the existing methods. The final ranks of alternatives (paths) are similar. In view of this the approach proposed is valid. Table 6 displays the final results of the proposed approach and TOPSIS process.

Table 6.

Comparison analysis

Paths	Proposed technique	Ranking	Conventional TOPSIS method	Ranking
$0-1-3-4-12-14$	0.4988	9	0.41	10
$0-1-3-4-5-13-14$	0.6702	4	0.539	5
$0-1-3-4-5-6-14$	0.7400	2	0.661	2
$0-1-3-7-10-14$	0.3189	12	0.401	11
$0-1-3-7-8-11-14$	0.4763	10	0.49	8
$0-1-3-7-8-9-14$	0.5916	6	0.53	6
$0-2-3-4-12-14$	0.5574	7	0.5077	7
$0-2-3-4-5-13-14$	0.7097	3	0.555	4
$\mathbf{0}-\mathbf{2}-\mathbf{3}-\mathbf{4}-\mathbf{5}-\mathbf{6}-\mathbf{14}$	$\mathbf{0.7741}$	$\mathbf{1}$	$\mathbf{0.697}$	$\mathbf{1}$
$0-2-3-7-10-14$	0.3720	11	0.395	12
$0-2-3-78-11-14$	0.5392	8	0.447	9
$0-2-3-7-8-9-14$	0.6383	5	0.557	3

Bold value indicates the best alternative in critical path strategy

In addition, comparisons of the current approach with the preceding studies to clearly clarify the implications of the proposed approach are displayed in Table 7.

Table 7.

Comparison analysis

Scholars	Uncertainty model			Modeling Approach			Specify weights of DMs
	Fuzzy Set	PyF Set	SF Set	Group decision making	TOPSIS-COPRAS Approach	TOPSIS	Linguistic variables	COPRAS approach
Amiri et al.	Yes	No	No	No	No	Yes	Yes	No
Zammori et al.	Yes	No	No	No	No	Yes	Yes	No
Gupta et al.	Yes	No	No	Yes	No	No	Yes	No
Mousavi et al.	Yes	Yes	No	Yes	Yes	Yes	Yes	Yes
Proposed method	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes

Additionally, the comparisons between two forms of fuzzy sets are shown in Table 8. As can be shown, under IFSs and PFSs environments, the essential path of the project network remains the same; however, other ranks (project paths) have been modified. With all of this in view, the SF sets may understand uncertainty better than the existing fuzzy set structure. The critical path of the network is identified correctly by using the proposed methodology. As a result, project scheduling and planning may be closely related to reality. In fact, in an uncertain environment, the critical path of the projects and the degree of criticality of each path are specified.

Table 8.

Comparison with PyF sets

Paths	Spherical fuzzy sets	Ranking	Pythagorean fuzzy sets	Ranking
$0-1-3-4-12-14$	0.4988	9	0.41	10
$0-1-3-4-5-13-14$	0.6702	4	0.539	5
$0-1-3-4-5-6-14$	0.7400	2	0.661	2
$0-1-3-7-10-14$	0.3189	12	0.401	11
$0-1-3-7-8-11-14$	0.4763	10	0.49	8
$0-1-3-7-8-9-14$	0.5916	6	0.53	6
$0-2-3-4-12-14$	0.5574	7	0.5077	7
$0-2-3-4-5-13-14$	0.7097	3	0.555	4
$\mathbf{0}-\mathbf{2}-\mathbf{3}-\mathbf{4}-\mathbf{5}-\mathbf{6}-\mathbf{14}$	$\mathbf{0.7741}$	$\mathbf{1}$	$\mathbf{0.697}$	$\mathbf{1}$
$0-2-3-7-10-14$	0.3720	11	0.395	12
$0-2-3-78-11-14$	0.5392	8	0.447	9
$0-2-3-7-8-9-14$	0.6383	5	0.557	3

Bold value indicates the best alternative in critical path strategy

Method flexibility with various input and outputs

The proposed methodology are flexible, and can be efficiently used for various input and output circumstances. Because of the different score functions and its generalization, the ranking of the proposed technique seems to differ little. This model is more efficient than most because, in decision-making methods, spherical fuzzy set increases grade space and can variate according to the emergency situations.

Superiority of suggested methodology and comparison with other frameworks

Fuzzy set, intuitionistic FS, picture FS have some space limitation on their grades. Spherical FS fills this gap in the literature and offers significant space than FS, intuitionistic FS, picture FS. The suggested framework enhances existing approaches and the decision-maker can choose the grades freely by using the condition $0\le P_{♭}^2+I_{♭}^2+N_{♭}^2\le 1.$

Limitations

The limitation of this analysis is that the developed model determines the best alternative in a single setting based on the input of considered experts.

Conclusion

The novel 2019 Coronavirus, SARS-CoV-2 (COVID-19), originated in the city of Wuhan in the People’s Republic of China’s Hubei province towards the end of 2019 and has spread very quickly in a very short time to the world. This article aimed to analyze the pandemic trajectory using mathematical modeling based on the information used by fuzzy decision making methodology to select the best alternative using critical path strategy.

Spherical fuzzy set plays a vital role in solving emergency decision making in the emergency situation of COVID-19, as they can optimal describe a preference when there is vague or uncertain information. In this study, a new integrated TOPSIS-COPRAS approach is established to handle emergency MCGDM problems with unknown weight information. The presented approach simultaneously considers a DMs’ limiting rationality and interdependence among criteria. The objective weight vectors are obtained by using the distance measure and were combined with subjective weights in the spherical fuzzy MCGDM model. Moreover, the operating of the proposed method is thoroughly explained with the assistance of a numerical example on the basis of the TOPSIS-COPRAS method. We testified the effectiveness and rationality of the proposed MCGDM approach, its output is compared with other MCGDM problems to make a comparison. The proposed MCGDM approach can also be used to other complicated problems like risk evaluation, emerging technology, uncertain decision-making, project installation, site selection etc.

The approach proposed in this paper will be extended in future research to other ambiguous fields, such as linguistic term sets, probabilistic linguistic term sets, hesitant fuzzy sets etc. The suggested approach can also be extended to other fields, such as medical diagnosis of nutrition, sustainable choice of suppliers, pattern recognition and so on. We will also try to extend this work for interval valued spherical fuzzy environments.

Compliance with Ethical Standards

Conflict of interest

The authors declare that they have no conflict of interest.

Ethical approval:

This article does not contain any studies with human participants or animals performed by any of the authors.