Summary
Tracing the lineage history of cells is key to answering diverse and fundamental questions in biology. Coupling of cell ancestry information with other molecular readouts represents an important goal in the field. Here, we describe the CARLIN (for CRISPR Array Repair LINeage tracing) mouse line and corresponding analysis tools that can be used to simultaneously interrogate the lineage and transcriptomic information of single cells in vivo. This model exploits CRISPR technology to generate up to 44,000 transcribed barcodes in an inducible fashion at any point during development or adulthood, is compatible with sequential barcoding, and is fully genetically defined. We have used CARLIN to identify intrinsic biases in the activity of fetal liver hematopoietic stem cell (HSC) clones and to uncover a previously unappreciated clonal bottleneck in the response of HSCs to injury. CARLIN also allows the unbiased identification of transcriptional signatures associated with HSC activity without cell sorting.
Graphical Abstract
Introduction
Generating animal models that enable cell lineage tracing in vivo has been a long-standing aim in biological research. Historically, lineage tracing in mammals has been limited to labelling and tracking small populations of cells through the use of dyes or fluorescent markers (Kretzschmar and Watt, 2012). Although these techniques helped resolve major questions in biology, from lineage commitment during early development (Balakier and Pedersen, 1982) to adult stem cell behavior (Snippert et al., 2010), the low number of clones analyzed at any one timepoint limit comprehensive understanding of global stem cell dynamics within tissues. These approaches are also intrinsically limited in their ability to trace individual cells and therefore provide limited insight into heterogeneity in cell populations. Retrovirally-delivered DNA barcodes have been used as clonal markers particularly in the context of blood generation (Gerrits et al., 2010; Lu et al., 2011; Schepers et al., 2008). However, introduction of such barcodes requires stem cells to be extracted from the tissue and manipulated. Recently, two mouse models have been developed that enable barcoding of cells in their native environment using randomly integrated transposons (Sun et al., 2014) or recombinases that create genetic diversity in a distinct locus (Pei et al., 2017). The use of these models has revealed dramatic differences between hematopoietic stem cell (HSC) behavior in unperturbed conditions versus transplantation, and has highlighted important functional heterogeneity within the HSC compartment (Pei et al., 2017; Rodriguez-Fraticelli et al., 2018). However, these models are limited in that they only provide lineage information and do not provide molecular insight into the genetic program driving heterogeneous behavior.
The advent of CRISPR/Cas9 has led to the development of additional lineage tracing tools that use errors from non-homologous end-joining DNA repair to generate a high diversity of unique and heritable DNA barcodes. A first proof-of-principle study demonstrated the feasibility of lineage tracing via this method in the zebrafish embryo (McKenna et al., 2016). Modified variants of this system that use expressed barcodes have allowed for the simultaneous measurements of single-cell gene expression levels and lineage tracing (Alemany et al., 2018; Raj et al., 2018; Spanjaard et al., 2018). More recently, systems combining delivery of expressed barcodes with transposons in the mouse embryo have been described (Chan et al., 2019; Kalhor et al., 2018). Both of these approaches use constitutively expressed Cas9 and use multiple target arrays (barcodes) to generate diversity. However, new embryonic manipulations are required to generate mice every time, and the resulting mice are impractical for breeding given the high number of randomly inserted transgenes. Therefore, these models are unsuitable for lineage analysis of adult tissues.
Here we present a versatile mouse model that allows inducible CRISPR-based lineage tracing that is genetically defined, incorporates inducible, transcribed barcodes, and works across adult mouse tissues. Furthermore, we have developed the analysis tools and reference data sets required to interpret the detected barcodes and quantify their statistical significance. Due to our ability to simultaneously interrogate lineage and transcriptional profiles of single-cells, the CARLIN system presents unique advantages to study stem cell clonal dynamics compared with previously generated cell lineage tracing tools. We exploit these advantages here to unveil unknown aspects of hematopoiesis during development and in adulthood following stress.
Results
Inducible and dose-dependent molecular barcoding in mouse embryonic stem cells
We set out to generate a genetically-defined mouse model in which we could (i) record the lineage histories of individual cells within their own DNA and (ii) read out lineage histories alongside gene expression profiles at the single-cell level. Based on the GESTALT model that has been successfully used for molecular recording in zebrafish (McKenna et al., 2016), we designed 10 sgRNAs that enable efficient cutting of target sites in the presence of Cas9 (Supplementary Figure 1A) with minimal off-target activity within the mouse genome (Methods). We designed the gRNA cassette in two iterations, one where individual U6 promoters drove sgRNA expression (Figure 1A), and a second cassette carrying tetO-operons upstream of each sgRNA (iCARLIN; Supplementary Figure 1B). Unless otherwise stated, all data presented here correspond to the first system. We also designed a 276 bp array containing target sites perfectly matching each of the expressed gRNAs (Figure 1A,B; Supplementary Table 1). Constitutive expression of the molecular recorder array is achieved through its placement in the 3’ UTR of a fluorescent protein driven by the constitutive CAG promoter. All of these elements were inserted together in the widely-used Col1a1 locus via recombinase-mediated integration into mouse embryonic stem (ES) cells that also express an enhanced reverse tetracycline transactivator (M2-rtTA) from the ubiquitous Rosa26 promoter (Beard et al., 2006). We then generated mouse lines from these ES cells. To have temporal control of Cas9 expression, we separately created a mouse line that expresses both doxycycline-dependent Cas9 (tetO-Cas9; integrated in the Col1a1 locus) and M2-rtTA (integrated in the Rosa26 locus). Finally, we crossed these two mice lines to generate CARLIN ES cells and CARLIN mice that carry all the transgenic elements.
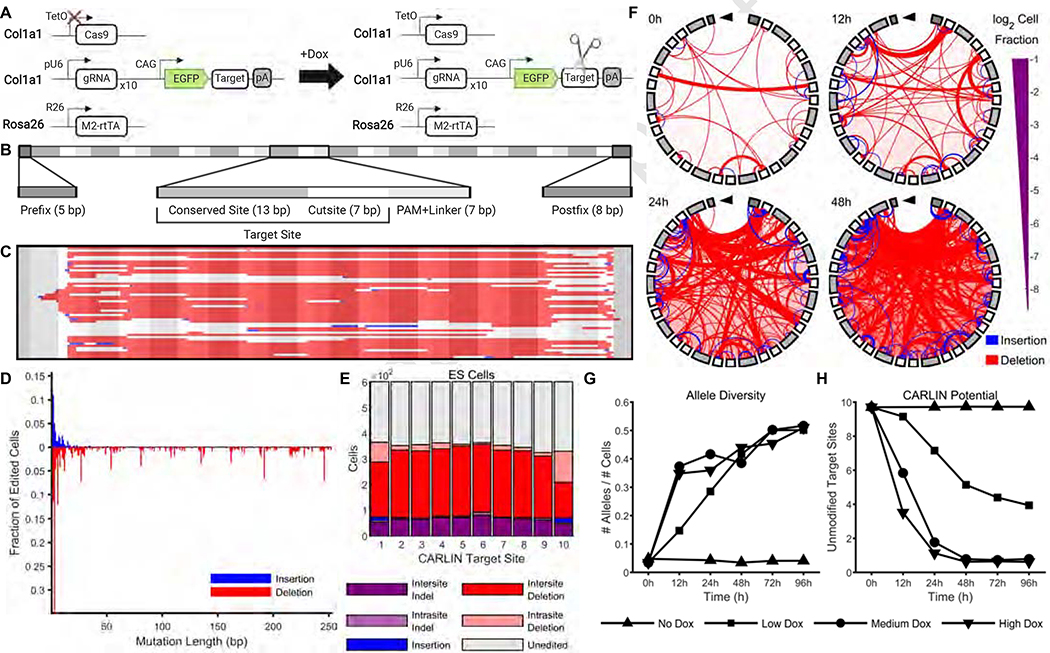
Figure 1: A high diversity of edits are generated by CARLIN in embryonic stem cells.
A. Schematic of CARLIN system. Guides RNAs, target sites and inducible Cas9 components are contained within the Col1a1 locus. The expression of each of the 10 gRNAs is driven by a separate U6 promoter (pU6). The CARLIN array sits in the 3’UTR of GFP and consists of 10 sites that perfectly match the gRNAs. The doxycycline (Dox) reverse tetracycline-controlled transactivator (rtTA) is contained within the Rosa26 locus. Schematic created with BioRender.
B. For computational purposes, we consider the CARLIN array as a series of motifs. We divide each target site into a 13bp conserved site (that lies outside the expected range of Cas9 editing) and 7bp cutsite. Consecutive target sites are interleaved by a 3bp protospacer adjacent motif (PAM) and 4bp linker sequence. There is a 5bp prefix motif upstream of the first target site and an 8bp postfix motif downstream of the last target site.
C. The 50 most common edited CARLIN alleles generated in CARLIN mouse embryonic stem (ES) cells following 96h induction with 0.04 μg/mL Dox. Each row represents a different allele. Deletions are marked in red. Insertions are shown in blue with the left endpoint indicating the start of the insertion; the length of the strip matches the length of the insertion (except when occluded by a subsequent deletion). A grayscale mask as in (B) is overlaid to demarcate the CARLIN motifs.
D. The fraction of edited ES cells, following 96h induction with 0.04 μg/mL of Dox, in which insertions and deletions of various lengths are observed.
E. Distribution of mutation types across different target sites in ES cells following 96h induction with 0.04 μg/mL of Dox.
F. Chord plots of CARLIN alleles before induction and at 12h, 24h, and 48h after induction with 0.04 μg/mL of Dox. The shading of the iris (ccw. from top) corresponds to the shading of the motifs in Figure 1B (from left to right). The thickness of an interior line is proportional to the number of cells with that mutation. The endpoints of a red line indicate the starting and ending bps of a deletion. The upstream endpoint of a blue line indicates the insertion site, and the downstream endpoint is offset by an amount equal to the insertion length.
G. Time-course of the total number of distinct alleles detected normalized by the total number of cells, and (H) average CARLIN potential (Methods) across cells in the absence of Dox and after induction with 0.04 μg/mL (low), 0.2 μg/mL (medium) and 1 μg/mL (high) of Dox.
Taken together, doxycycline (Dox) induction drives Cas9 expression, which leads to double-strand DNA breaks in the target array. These breaks are repaired to result in a diverse range of altered DNA sequences (referred to as CARLIN alleles) that are expressed and stably inherited (Figure 1A). To analyze the CARLIN alleles from sequencing of the target array, we developed a novel bioinformatic pipeline that accounts for the location at which the Cas9-dependent alterations are expected (Methods; Figure 1B; Supplementary Figure 2A–C; Supplementary Tables 2–3). This code is available at https://gitlab.com/hormozlab/carlin.
To test the ability of our system to generate inducible and detectable CARLIN alleles at the DNA level, we characterized the CARLIN edits present in CARLIN ES cells following Dox treatment (Methods). While we observed little background editing in the absence of Dox (Supplementary Figure 1C,F), a diverse set of repair outcomes was generated following Dox exposure (Figure 1C,D) as determined by high-throughput sequencing. These edits included deletions spanning 1–252 bps, the most common of which spanned multiples of 27 bps (the length of a target site and adjoining PAM+linker sequence), and insertions of up to 51 base pairs in length (Figure 1D). The edits occurred throughout the array, with different target sites displaying slightly different indel preferences (Figure 1E). In initial experiments, we observed 301 distinct alleles in 453 cells with edited alleles, 219 of which were only observed in one cell, indicating that CARLIN can generate highly diverse repair outcomes following Cas9 activity. Since CARLIN alleles are generated by different indel events, the distribution of CARLIN alleles detected may be distorted due to length-dependent amplification of transcripts during library preparation and sequencing. We verified that the distribution of allele lengths produced by the bioinformatics pipeline was consistent with the distribution produced by fragment analysis as a partial validation that the experimental protocol and bioinformatics pipeline preserve the distribution of CARLIN alleles observed in the biological sample (Supplementary Figure 2D).
We also investigated how CARLIN editing is influenced by the duration and magnitude of Cas9 expression. We exposed ES cells to low, medium and high dosages of Dox (0.04, 0.20 and 1.00 μg/mL respectively), and performed bulk DNA sequencing prior to induction and at a series of timepoints up to 96h. As expected, both the fraction of cells with edited CARLIN sequences and the diversity of CARLIN alleles increases with both length and dose of induction (Figure 1F,G; Supplementary Figure 1C–F). This analysis also reveals that the nature of CARLIN edits can act as a readout of induction duration and strength. Specifically, we observe a decrease in the number of unmodified target sites (calculated as CARLIN potential; Methods; Figure 1H) and an increase in the average length of deletions with increasing time and concentration of doxycycline (Supplementary Figure 1F). Together, these data demonstrate that CARLIN is edited in an inducible way with the extent of editing dependent both on the duration and magnitude of the induction, indicating that the system can be used as a heritable molecular recorder.
Sequential CARLIN induction permits lineage reconstruction
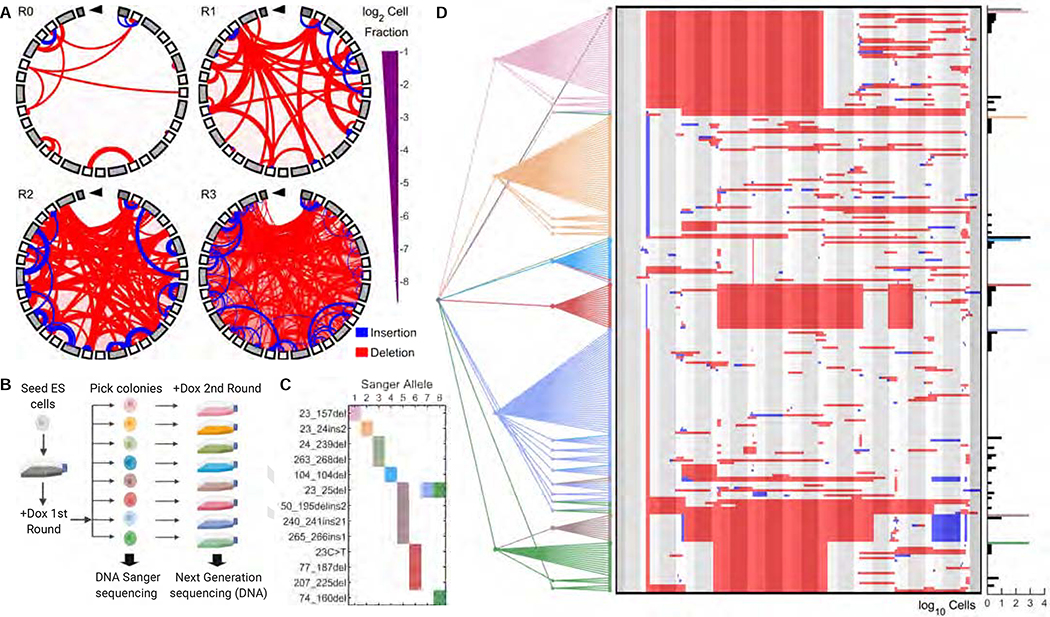
Having shown that we could regulate the extent and nature of editing, we next tested whether we could accrue sequential edits on the same CARLIN array. CARLIN ES cells were exposed to one, two or three 6h pulses of Dox (0.04 μg/mL) interspersed by 24h in fresh media. Indeed, we observed an increase in the fraction of cells with edited CARLIN alleles, the number of mutations accrued in each allele, and the diversity of CARLIN alleles over the three pulses (Figure 2A; Supplementary Figure 1G). This finding indicates that sequential pulses of Dox can incorporate additional information and can potentially be used to build multi-level, hierarchical histories for lineage reconstruction. To test this last hypothesis, we exposed ES cells to one pulse of Dox, picked 8 ES cell clones for outgrowth, and exposed them to a second pulse of Dox (Figure 2B). Sanger sequencing of the 8 ES cell clones after the first timepoint allowed us to establish a ‘ground truth’ of edits generated after the initial pulse (Figure 2C). We devised a basic lineage tree reconstruction algorithm that accounts for the expected CARLIN mutation patterns and assumes that the internal nodes are restricted to the observed alleles (Figure 2D; Methods). Applied to these data, we achieved a false positive rate of 0.6% (the fraction of cells in which the most recent ancestor of an allele is a clone other than where the allele came from) and a false negative rate of 18% (the fraction of cells in which none of the 8 selected clones is found as an ancestor of an allele). False negatives arise when alleles from a specific Next Generation Sequencing (NGS) library cannot be matched to a parent clone because of large subsuming deletions that erase the mutations that uniquely identify the parent allele. In these cases, we always link the child allele back to the unedited reference, to avoid false positives. Taken together, sequential Dox pulses allow multiple stages of lineage reconstruction.
Figure 2: Multiple pulses of doxycycline can consecutively label lineages and enable phylogenetic tree reconstruction in embryonic stem cells.
A. Chord plots of CARLIN alleles in the absence of doxycycline (Dox) and after one, two or three 6h pulses of Dox (R0–3, respectively). Color scheme as in Figure 1F.
B. Following one 6h round of Dox induction, cells were seeded at single-cell density and 8 colonies were picked for further outgrowth and Sanger sequencing. Following a second round of Dox, DNA from cells was collected and sequenced by Next Generation Sequencing (NGS). Schematic created with BioRender.
C. Mutations called in each of the 8 colonies from the CARLIN pipeline applied to the Sanger sequences. Colonies are colored according to the schematic in (B). Colonies 5, 7 and 8 share a common mutation.
D. (Left panel) The consensus tree, accounting for 95% of cells, obtained from 10,000 lineage reconstruction simulations applied to alleles pooled from all libraries (Methods; Supplementary Figure 4C). The color of a node and its branch to a parent corresponds to the NGS library in which the allele was observed. Leaves that connect to internal nodes of a different color correspond to false positives. (Centre panel) Sequence of each CARLIN allele visualized as in Figure 1C. (Right panel) Histogram of the number of cells in which each allele was detected. Colored bars correspond to NGS sequences which match a Sanger sequence.
CARLIN generates a high diversity of barcodes in vivo
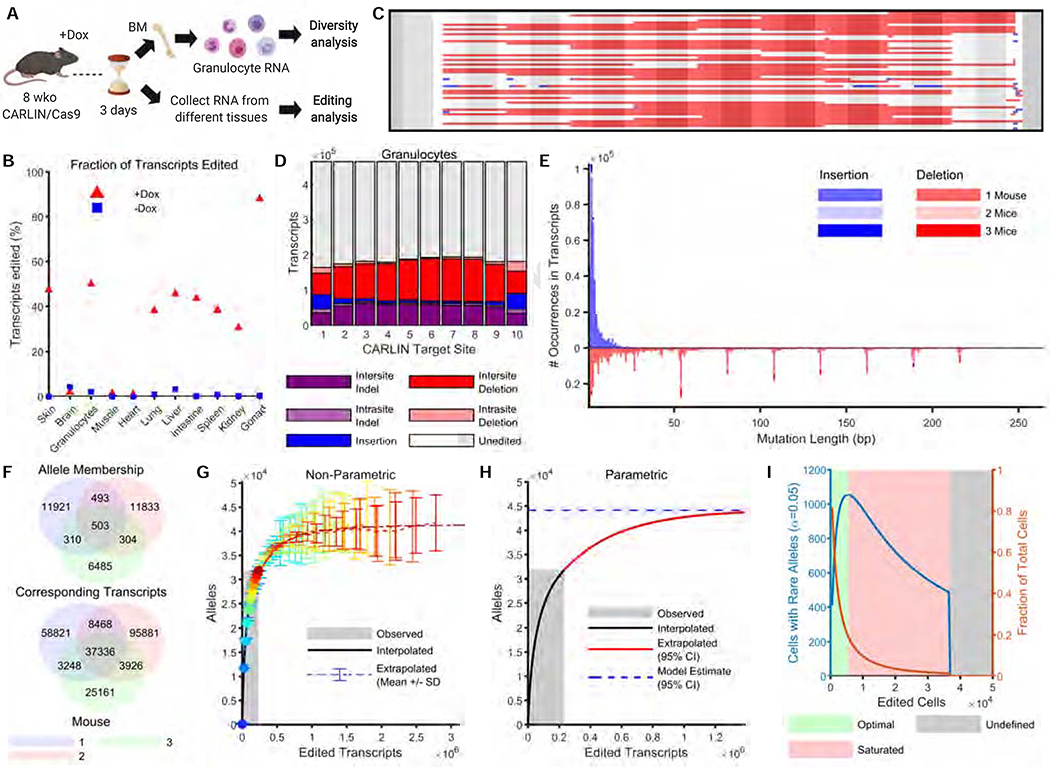
We next generated mice carrying the CARLIN transgenes and assessed allele generation following Dox induction in adults. Because dose and timing of Dox concentration is critical to induce editing in a large fraction of cells, we tested multiple dosing regimes of Dox (not shown) and selected a protocol in which CARLIN mice were exposed to Dox for 7 days (Methods). Following this protocol, we harvested RNA from multiple tissues from CARLIN mice for bulk sequencing of the CARLIN array (Figure 3A). We observed that the fraction of CARLIN transcripts that were edited ranged from 31% to 88% across all tissues analyzed, with the exception of the brain, that is inaccessible to Dox, and the heart and skeletal muscle, in which expression from the Col1a1/Rosa26 loci has been previously shown to be low (Beard et al., 2006; Figure 3B, Supplementary Figure 3A). To investigate editing in different cell types, we sorted blood, mesenchymal, and epithelial cells from a variety of tissues of two induced mice and assessed the fraction of edited transcripts by RNA sequencing. Similar to our bulk tissue data, we observed robust editing in the presence of Dox across multiple cell types and tissues (Supplementary Figure 3B). Importantly, background editing in the absence of Dox is negligible (averaging 1%) across all tissues of an uninduced 8-week old mouse (Figure 3B). Therefore, CARLIN represents a useful model to barcode adult tissues systematically.
Figure 3: Inducible CARLIN editing in vivo.
A. 8-week old mice were induced with doxycycline (Dox) for one week. RNA from granulocytes and other tissues were collected following 3 days chase. Schematic created with BioRender.
B. Fraction of transcripts edited across tissues in the presence and absence of Dox.
C. The 50 most common edited CARLIN alleles observed in granulocytes, visualized as in Figure 1C.
D. Distribution of mutation types across different target sites in granulocytes comprising the allele bank (Methods).
E. Histogram of insertion and deletion lengths found in the allele bank shaded according to presence across mice.
F. Venn diagram showing number of edited alleles (and the corresponding number of edited transcripts) in the bank shared across the three induced mice.
G. Non-parametric and (H) parametric extrapolation of the total allele diversity achievable by the CARLIN system as a function of the number of edited transcripts observed (Methods). The system is estimated to saturate at an allele diversity of 44,000 ± 400. The area shaded in grey indicates the number of observed transcripts used to construct the bank.
I. Number of cells expected to harbor rare alleles (that are unlikely to occur independently in multiple cells) as a function of the number of cells edited. When the number of cells is small with respect to the CARLIN diversity (shaded in green), many cells harbor rare alleles. As the number of edited cells increases (shaded in red), the probability that a given allele marks only one cell decreases (orange curve), so that the number of cells that are uniquely marked with a CARLIN allele decreases (blue curve). In the regime shaded in grey, no cell can confidently be said to be uniquely marked by an allele (Methods).
We next assessed the full extent of the barcode diversity that could be generated in vivo. For this we compared CARLIN edits observed in large numbers of bone marrow granulocytes across three induced CARLIN mice following 1 week of Dox induction and two uninduced controls. Similar to our in vitro analysis, we detected a high diversity of edits in the induced mice generated through deletions and insertions across the length of the array (Figure 3C,D,E). Across the induced mice we observed the fraction of edited CARLIN transcripts ranging 29%−63%, compared to an average of 2.1% editing in the two uninduced mice (Supplementary Figure 3C,D). The editing in the uninduced mice is largely attributable to a low level of background Cas9 activity rather than resulting from errors introduced during library preparation, since editing in the absence of Cas9 was 0.3% (Supplementary Figure 3E). On average, 88% of the edited alleles (6485–11921) found in each mouse were not observed in the other mice (Figure 3F), indicating that the majority of edits represent unique repair outcomes. However, it also indicated that a small percentage (~12%) of alleles were generated at a higher frequency due to common indel mutation events (such as deletions spanning multiples of 27bps noted earlier) that independently generate the same allele sequence in different cells (Figure 3E). We pooled the edited alleles from across all induced mice together to form an allele bank, consisting of a total of ~32,000 distinct edited alleles over ~233,000 edited transcripts.
We used the allele bank to computationally estimate the total number of distinct alleles that CARLIN could generate (i.e. the maximum barcode diversity) and the expected occurrence frequency of these alleles. High diversity corresponds to many alleles that occur at equal frequencies. Conversely, low diversity corresponds to few dominant alleles that occur at high frequencies. By extrapolating the frequency distribution of alleles in the bank, we estimate that CARLIN is able to generate up to 44,000 ± 400 distinct alleles (Figure 3G,H; Methods), consistent with a high diversity system. Additionally, we used the bank to discriminate between rare alleles that occur at low frequencies and commonly-occurring alleles. To do so, we used the allele bank to estimate the probability that a CARLIN allele is unique for a given number of observed cells, obtaining a p-value of significance (Figure 3I; Methods). The curves in Figure 3I can be used by an experimentalist to determine how many cells will be uniquely marked for a given number of edited cells. This discrimination is critical for any experiment to ensure that an allele detected in many cells is due to the shared lineage history of those cells, as opposed to independent CARLIN editing events that coincidentally produced the same allele. We also verified that alleles deemed rare by our statistical procedure are less likely to occur simultaneously across biological replicates (Supplementary Figure 4A). Critically, these statistical measures can be adjusted to account for other experimental parameters (such as number of cells in the system, number of detected CARLIN alleles, etc.) and may be applied to other CARLIN experiments.
Finally, we also investigated edited alleles generated in granulocytes of iCARLIN mice, in which the expression of the sgRNAs, as well as Cas9, is driven by a tetO promoter (Supplementary Figure 1B). Similar to the constitutive guide CARLIN system, we observed a high diversity of edits (Supplementary Figure 3F), indicating that this system may be used as well to label cells with even tighter inducibility and potentially shorter labelling windows.
Lineage reconstruction in vivo
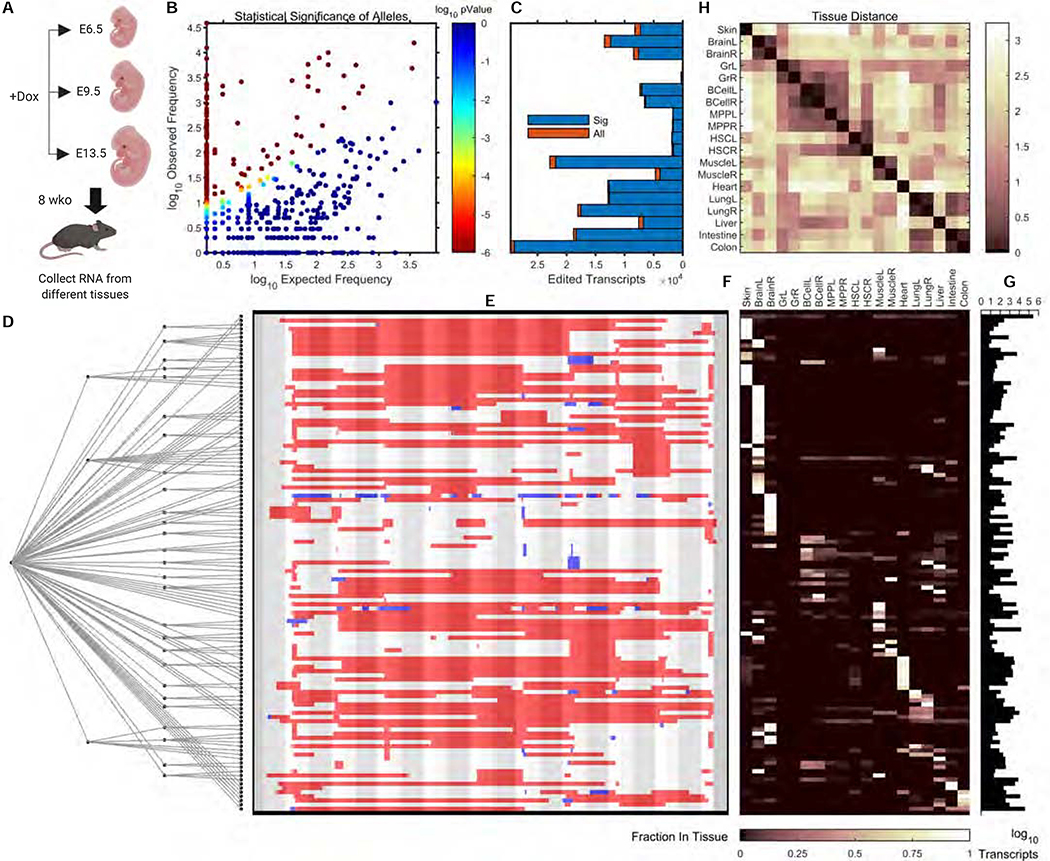
To investigate whether multiple rounds of CARLIN labelling could be used to gain insight into cellular phylogeny in vivo as done in vitro (Figure 2D), we set up timed pregnancies and delivered three pulses of Dox to pregnant dams at E6.5, E9.5 and E13.5 (Figure 4A). When the 3x labelled CARLIN embryos reached 8 weeks of age, we collected RNA from the skin, heart, liver, intestine and colon, and also separately sampled the left and right brain, muscle, lung and bone marrow HSCs, MPPs, granulocytes, and B-cells. We employed the same tree reconstruction algorithm developed for analyzing the in vitro experiment with ES cells (Figure 2D). However, as a pre-processing step we only retained alleles whose observed frequency was significantly higher than their frequency in the bank (using a FDR=0.05 on their frequency p-values – see Methods; Figure 4B). Only a small fraction of CARLIN transcripts were discarded based on this filtering step across all tissues (Figure 4C). We computed a consensus lineage tree, by simulating 10,000 stochastic reconstructions (Methods), which allowed us to visualize a hierarchy of clades across multiple tissues (Figure 4D–G; Methods). Based on this lineage tree, we computed a pairwise similarity matrix of the tissues and observed that contra-lateral tissues were closely related, as were multiple cell types of hematopoietic origin, and tissues of endodermal origin (Figure 4H), which is consistent with known lineage relationships. We also observed a low level of allele sharing across other tissues, some of which were derived from the same embryonic germ layer (Figure 4F,H). This indicates limited lineage mixing between these tissues and suggests that they began to develop independently prior to the stages of induction used in our analysis. Taken together, CARLIN can be useful for multi-level tissue reconstruction in vivo.
Figure 4: Lineage reconstruction in vivo through multiple pulses of doxycycline.
A. Pregnant dams were induced with doxycycline at E6.5, E9.5 and E13.5. At 8 weeks, RNA from different tissues was collected and sequenced by Next Generation Sequencing (NGS). Schematic created with BioRender.
B. Scatter plot of observed allele frequencies vs. expected frequencies obtained by querying the bank. Alleles whose statistical significance did not survive a FDR of 0.05 were discarded (Methods).
C. Number of edited transcripts found in different tissues after running the CARLIN pipeline (All), and after screening for significant alleles (Sig) as described in (B).
D. The consensus tree which accounts for 95% of edited transcripts, obtained from 10,000 simulations, using the same algorithm as in Figure 2D (Supplementary Figure 4D; Methods).
E. Allele sequences called from NGS corresponding to the leaf nodes, visualized as in Figure 1C.
F. Distribution of number of transcripts corresponding to each allele across tissues (row normalized to 1).
G. Histogram of total transcript counts across all tissues for each allele.
H. Pairwise similarity matrix of tissues computed across alleles of the consensus tree (Methods).
Simultaneous detection of CARLIN barcodes and whole-transcriptomes from single cells
We next set out to develop a platform to detect CARLIN alleles using single-cell sequencing technologies. Our pipeline for this analysis involves: (i) exposure of mice to Dox, (ii) encapsulation of single cells from the cellular population of interest into droplets containing barcoded polyT-coated beads, (iii) amplification of whole cellular transcriptome, (iv) targeted amplification of the CARLIN array, and (v) sequencing using NGS (Figure 5A). After optimization, we were able to detect CARLIN in 32–63% of cells in which we could also measure a full transcriptional profile (for the criteria used to select single cells, see Supplementary Table 4 and Methods). To check for reproducibility of our protocol, we prepared two CARLIN amplicon libraries independently starting from the same single-cell transcriptome library. We observed that 89% of the cell barcodes were shared across the two libraries. We also verified that the same CARLIN alleles occurred across the two samples with consistent frequencies (Supplementary Figure 6A; Methods).
Figure 5: Clonal tracing of blood progenitors to adulthood.
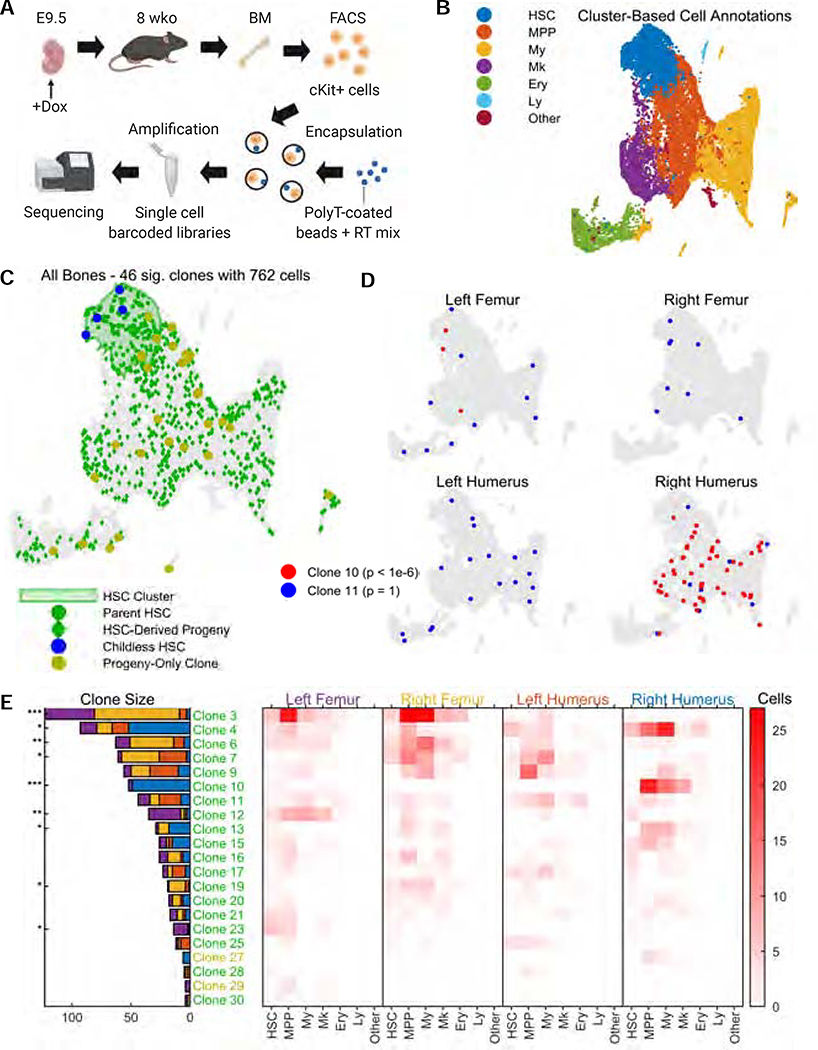
A. CARLIN mice were labelled at E9.5. At 8 weeks, bone marrow cells were collected, sorted, and encapsulated for single-cell RNA sequencing. Schematic created with BioRender.
B. UMAP representation of pooled transcriptome data from the bone marrow of 4 separate bones. See Supplementary Figure 5D,E for the breakdown of clusters and markers used for annotation. HSC, hematopoietic stem cell; MPP, multipotent progenitor cell; My, myeloid progenitor cells; Ery, erythrocyte; Ly, lymphoid cell.
C. Statistically significant CARLIN alleles (FDR = 0.05; Methods) across all bones combined, overlaid onto the UMAP plot from (B). The green shaded area corresponds to the HSC cluster in the transcriptome, shown in (B). We are able to directly map the ancestry between differentiated cells (green diamonds) and HSCs (green circles) which share the same set of alleles. HSCs without children are shown in blue, and differentiated cells that do not share their allele with HSCs are shown in yellow.
D. CARLIN clones overlaid onto the transcriptome of individual bones; a non-biased clone (blue) and a biased clone (red) are shown with the Bonferroni-corrected p-values for bone bias (Methods).
E. (Left) Bar graph indicating the prevalence of each statistically significant allele across the 4 bones, with the Bonferroni-corrected p-value for bone bias marked as *p<0.05; **p<10−3; ***p<10−6. (Right) Heatmap indicating occurrence frequency of alleles across bones and cell types. Alleles found in fewer than 4 cells are not displayed. The clone labels follow the color scheme in (C).
As a proof-of-principle experiment, we used CARLIN to characterize clonal properties of hematopoietic development. Here, we barcoded HSC precursors during embryogenesis and characterized their clonal lineages in adulthood. In the mouse, definitive blood progenitors arise at embryonic day (E) 10.5 with the formation of Runx1-expressing clusters within the main arteries of the embryo (Dzierzak and Bigas, 2018). From E11 onwards, these progenitors migrate to the fetal liver where they undergo extensive expansion before colonizing the bone marrow at around the time of birth. Although several studies have investigated the process through which the progenitors are formed, the dynamics of HSC expansion and migration to the bone marrow are still poorly resolved. In particular, it is unclear whether HSCs derived from the same developmental precursor clone already exhibit intrinsic functional biases.
We applied a single pulse of Dox at E9.5 to label the earliest emerging definitive blood progenitors (Figure 5A). Accounting for delays in Dox response and Cas9-protein stability (Alemany et al., 2018; Traykova-Brauch et al., 2008), this represents actual labelling times of approximately E10-E12.5. Once the labelled animals reached 8 weeks of age, we sorted a combination of cKit+ progenitors, including HSCs, multipotent progenitors (MPPs) and lineage-restricted progenitor cells (Supplementary Figure 5A) from four separate bones (right and left humerus and femur) and encapsulated the cells from each bone into separate single-cell libraries. We combined the 3755–5261 cells per bone that passed quality control cutoffs (Supplementary Table 4; Methods) into one dataset encompassing 19,056 cells (Supplementary Figure 5C). Unsupervised hierarchical clustering resulted in 36 distinct clusters that we annotated as HSC, MPP, myeloid, megakaryocyte, erythroid and lymphoid using previously described markers (Figure 5B; Supplementary Figure 5D,E). We considered cells belonging to the HSC-like clusters to be HSCs, and cells belonging to other clusters to be non-HSCs for all subsequent analysis. Finally, we visualized the single-cell gene expression profiles using uniform manifold approximation and projection (UMAP) plots, overlaid with the detected CARLIN alleles (Figure 5C).
From a total of 60 clones, each marked with a different CARLIN allele, our high-stringency analysis determined 46 (20–29 in each bone) to be significant (assessed using their clonal p-value at a FDR=0.05 – see Methods; Supplementary Table 4). We restricted all further analysis to these significant clones. The sizes of these clones ranged from 1 to 123 cells comprising numerous cell types across the hematopoietic hierarchy. We initially assessed the extent to which clones that contained HSCs (HSC-rooted clones) also contained hematopoietic progeny (non-HSCs). Previous studies suggest that hematopoiesis is driven by HSCs that are progeny of definitive embryonic precursors (Dzierzak and Bigas, 2018). Indeed, we find that 23 out of 27 clones containing an HSC have detectable hematopoietic progeny (we refer to these HSCs as parent HSCs). Such HSC-rooted hematopoietic progeny make up most of the cellular composition in the analyzed bone marrow samples, i.e. 95% of non-HSCs displaying a significant CARLIN allele (p < 10−6; Figure 5C; Methods). Interestingly, we observed that the distribution of HSC-rooted clone sizes was significantly non-uniform (p<10−6; Figure 5E; Methods). This finding points towards significant heterogeneity across embryonic-derived HSCs.
We next separated out the transcriptional and lineage profiles of cells across the four bones (Figure 5D). With this analysis we could assess both the presence and behavior of HSCs across multiple bone marrow compartments. We observed 13 of the 46 significant clones in all bones, accounting for 46% of cells displaying an edited CARLIN allele (Figure 5E). Notably, across all clones we observed that many of the largest clones were not uniformly distributed across bones, but were more likely to be found in a subset of the bones analyzed (Methods). For example, clone #10 appeared in 49 cells of the right humerus but appeared in only 3 cells of the left femur and was completely absent in the other analyzed bones (p < 10−6; Figure 5D,E). Similarly, clone #3 appeared in 42 and 72 cells of the left and right femur, respectively, but appeared in only 6 and 3 cells of the left and right humerus (p < 10−6; Figure 5E). No clone had a statistically significant fate bias, as judged by its occurrence among cell types as defined in Figure 5B, either within bones or pooled across all bones (Methods). Assuming equal expansion in the fetal liver, our data suggest that the expansion potential of fetal liver-derived HSCs might not be pre-determined but that it might be conferred by the niche into which they home. It is also possible that fetal liver-derived HSCs exhibit biases in colonization of different bones.
Clonal bottlenecks during hematopoietic regeneration
Next, we applied CARLIN to investigate the clonal dynamics of adult hematopoiesis following perturbation. Decades of work have established that following acute myeloablation, most HSCs exit their quiescent state and undergo cell division (Harrison and Lerner, 1991; Wilson et al., 2008). It has been assumed that these divisions are asymmetric cell divisions and correspond to HSC activation, implying that most HSCs participate in regeneration. However, this process has never been studied at a clonal level and the extent to which each individual HSC participates in regeneration is unclear.
To measure how much individual HSCs contribute to regeneration, we studied the HSC response to 5-fluorouracil (5-FU), a widely used model of myeloablation in the mouse. 5-FU induces proliferation of most HSCs within 4 days (Harrison and Lerner, 1991; Wilson et al., 2008) and by 10 days post 5-FU, most cellularity is recovered in the bone marrow (Harrison and Lerner, 1991). We induced CARLIN labelling in 8-week old mice before administering one dose of 5-FU via intraperitoneal injection (Figure 6A). Following 10 days recovery, we sorted the cKit+ population from the marrow of single bones (Supplementary Figure 5A,B) and generated single-cell RNA libraries. Across five independent experiments in control and 5-FU treated groups, we detected between 4073–6025 cells with high resolution whole transcriptome information (Supplementary Table 4) that we compiled into one dataset following batch correction (Supplementary Figure 6B). Unsupervised hierarchical clustering resulted in 34 distinct clusters to which we assigned coarse-grain annotations as before (Figure 6B; Supplementary Figure 6C,D).
Figure 6: Clonal dynamics of adult hematopoiesis following perturbation.
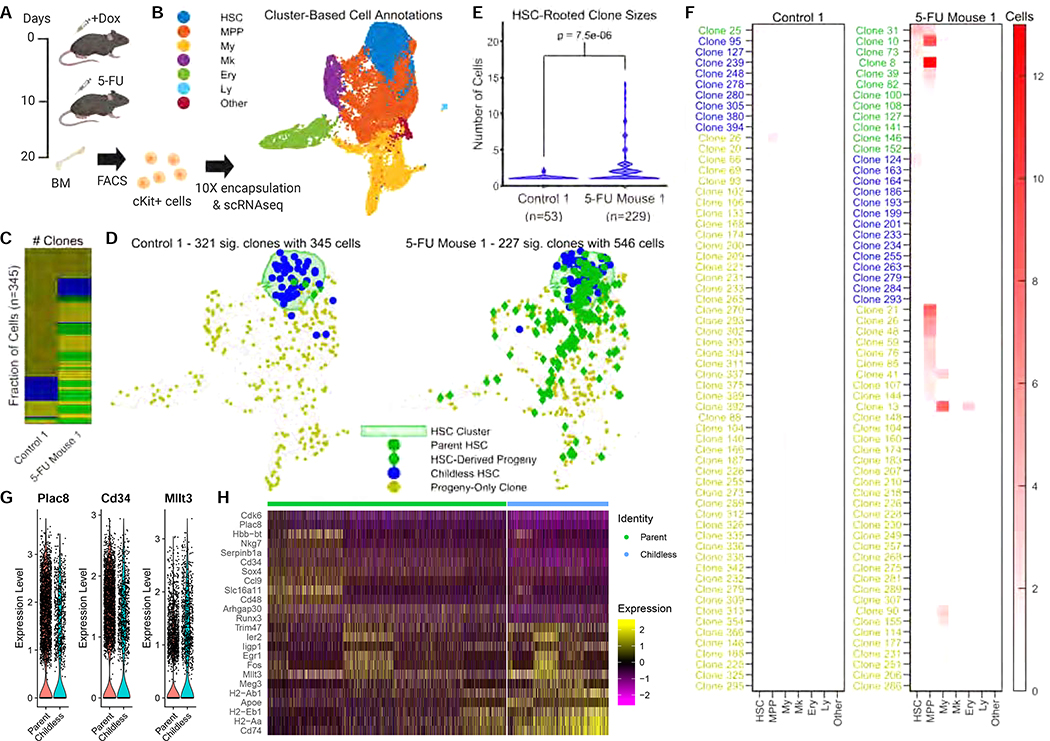
A. 8-week old CARLIN mice were labelled with doxycycline and injected with 5-FU after 10 days. After another 10 days, bone marrow cells were sorted and encapsulated for single-cell RNA sequencing. Schematic created with BioRender.
B. UMAP representation of pooled transcriptome data from control and 5-FU treated mice. See Supplementary Figure 6C,D for the breakdown of clusters and markers used for annotation. Cluster labels as in Figure 5B.
C. Number of statistically significant clones in the first control and 5-FU treated mouse (FDR=0.05; Methods) after downsampling the 5-FU treated mouse to have the same number of cells marked by statistically significant alleles as the control mouse. The control mouse has many small clones. The colors correspond to the legend for (D) below with blue clones containing only HSCs, yellow clones containing only non-HSCs, and green clones containing both.
D. Statistically significant CARLIN alleles (as defined in C) overlaid onto the transcriptome indicating childless HSCs (blue), parent HSCs (green circles), non-HSC cells in an HSC-rooted clone (green diamonds) and non-HSC cells not in an HSC-rooted clone (yellow). The green shaded area corresponds to the HSC cluster in the transcriptome shown in (B).
E. Violin plot showing the distribution of the number of cells in statistically significant HSC-rooted clones (as defined in C) in the first control and 5-FU treated mouse (the green and blue markers in D). The total number of cells in statistically significant HSC-rooted clones is shown in brackets under the sample label.
F. Heatmap indicating occurrence frequency of statistically significant alleles (as defined in C) across different cell types in the first control and 5-FU animals. The clone labels are colored according to the scheme in (D). The number of clones has been downsampled for both animals.
G. Violin plots of log-normalized expression levels of selected genes differentially expressed between the parent and childless HSC cluster group (as defined in Supplementary Figure 6C).
H. Heatmap of the z-score of log-normalized expression levels of genes most differentially expressed between the parent and childless HSC cluster group (as defined in Supplementary Figure 6C).
As with the previous experiment, we restrict our attention to clones corresponding to significant CARLIN alleles (assessed using their clonal p-value at a FDR=0.05; Methods). Of the 1619 statistically significant alleles detected across samples, 1580 were unique and found only in one sample, corroborating that our filtering procedure for rare alleles was effective. We detected important differences in the clonal composition of control versus 5-FU treated bone marrow. First, we observed a significant reduction in the number of clones detected in the 5-FU treated marrow (p<10−6; Figure 6C; Supplementary Figure 6E; Methods), which likely reflects the massive cellular and clonal loss after injury. Additionally, we used CARLIN to analyze the clonal contribution of HSCs to hematopoietic production. In the absence of 5-FU, only 24 of 1330 clones across all samples, representing 65 of 1522 (4%) edited CARLIN cells, contained both hematopoietic progeny and HSCs (Figure 6C,D,F; Supplementary Figure 6E,F,H). This suggests minimal contribution of HSCs at steady state, at least over 20 days, consistent with other studies (Busch et al., 2015; Sun et al., 2014). In the presence of 5-FU, this landscape was significantly altered with 48 of 289 clones containing both hematopoietic progeny and HSCs (p<10−6; Methods), representing 217 of 695 (31%) of cells carrying an edited CARLIN allele (p<10−6; Figure 6D,F; Supplementary Figure 6F,H; Methods). Additionally, there was a significant increase in the average size of HSC-rooted clones (p=7.5×10−6; Figure 6E; Supplementary Figure 6G; Supplementary Table 5; Methods). Surprisingly however, the distribution of the sizes of the HSC-rooted clones was significantly non-uniform (Methods), with 12 of 92 HSC clones making up 45% of all cells in HSC-rooted clones in the first 5-FU treated mouse (p<10−6; Figure 6E) and 4 of 19 HSC clones making up 67% of all cells in the HSC-rooted clones in the second 5-FU treated mouse (p=5.2×10−3; Supplementary Figure 6G). These findings indicate that a small number of highly-active HSCs are responsible for the replenishment of the blood system following cytotoxic injury. Therefore, our results indicate a clonal bottleneck during regeneration where only a handful of HSC clones can generate productive flow into the MPP and downstream compartments.
CARLIN allows the identification of gene signatures underlying functional heterogeneity
As highlighted above, current clonal tracing models (Sun et al, 2014; Pei et al, 2017) in the hematopoietic system are able to identify heterogeneity in function. However, these studies cannot provide any molecular insight into potential drivers of function in HSCs. We explored whether CARLIN could allow us to identify gene signatures specific to the ‘active’ HSC state. Initially, we performed differential gene expression analysis comparing the parent HSCs (n=93) to childless HSCs (n=265) across the control and 5-FU single-cell datasets (Supplementary Table 6). After applying a Bonferroni correction, 27 genes showed a statistically significant change at a log-fold change cutoff of 0.2 including CD48 and Plac8. To increase the number of cells used for the differential analysis, we took advantage of our observation that, as visualized using UMAP, the parent HSCs were not uniformly spread across the HSC clusters (Figure 6B,D; Supplementary Figure 6F). To delineate the parent HSC region, we grouped the HSC clusters into a parent HSC cluster group and a childless HSC cluster group, such that the former contained a significantly larger fraction of parent HSCs (p=4.2×10−4; Supplementary Figure 6C; Methods). Differential gene expression analysis across these two cluster groups revealed 45 significantly different genes, in addition to CD48 and Plac8 (Figure 6G,H; Supplementary Figure 6I,J; Supplementary Table 6). Some of these genes have known involvement in HSC quiescence/activity (Mllt3, Cd34, Pdzk1ip1; Forsberg et al., 2010; Pina et al., 2008; Wilson et al., 2008), hematopoietic differentiation (Mpo and CD48) and cell proliferation (Cdk6, Plac8; Rogulski et al., 2005), as well as a number of genes with described but poorly-defined links to hematopoiesis (e.g. Nkg7; Wilson et al., 2015). The grouping of HSC clusters into parent and childless HSC cluster groups could not have been achieved without taking into account the relative prevalence of parent HSCs in each cluster as determined by CARLIN, since HSCs overexpressing proliferation markers did not localize in the parent HSC cluster group (Methods). Additionally, HSCs overexpressing proliferation markers were also not significantly over-represented among parent HSCs as determined by CARLIN. Lastly, partitioning HSCs according to expression of these proliferation markers alone, and performing a differential gene expression analysis between the subsets that most highly and lowly expressed these markers, also failed to identify any of the aforementioned genes, with the exception of Cdk6 (Methods; Supplementary Table 6). Taken together, these data demonstrate that the combined analysis of lineage and gene expression profiles can in principle identify molecular profiles underlying heterogeneous HSC behavior in vivo, without a need for a priori known markers or cell sorting.
Discussion
Here, we present CARLIN, a new resource for lineage tracing research that can be used to simultaneously interrogate lineage histories and gene expression information of single cells in the mouse in an unbiased, global manner. We have demonstrated that CARLIN mice can be used to generate up to 44,000 distinct CARLIN alleles (barcodes) in vivo, and that these alleles can be detected and read out using single-cell droplet sequencing alongside the transcriptome of individual cells. We also demonstrated that multiple pulses of labelling can be used to enhance our understanding of tissue phylogeny.
CARLIN has a number of unique advantages over existing mouse lines for in vivo lineage tracing. Unlike models that use Polylox (Pei et al, 2017) or Sleeping Beauty transposons (Sun et al, 2014), the barcodes generated by CARLIN are transcribed, enabling (i) high-throughput readout of lineage histories in single cells and (ii) simultaneous measurement of gene expression profiles in the same cells. Because of this, we can characterize the identity of the cells that have been traced using their gene expression profiles in a precise and unbiased fashion. In contrast, existing techniques sort cells into subpopulations based on known cell types before readout of lineage histories. This requires prior knowledge of the markers associated with each cell type of interest and existence of antibodies that can enrich for these subpopulations. Strategies that rely on cell type specific expression of fluorescent reporters require costly and time consuming genetic engineering. Even with available established cell sorting strategies, resulting cell purity is limited and cells can be lost during sorting. Critically, CARLIN can be used to read out the lineage histories of any cell type, in any tissue and organ, even in the absence of known cell surface markers for sorting. Therefore, CARLIN enables precise annotation of cell types whose lineage has been traced beyond what can be gleaned from cell surface markers alone. Complete gene expression profiles also provide information about mechanisms that drive cell behaviour. Finally, CARLIN can directly quantify clone sizes by counting the occurrence frequency of barcodes across individual cells. Existing methods rely on bulk sequencing and are therefore less accurate because of PCR amplification biases.
Innovations that have increased our ability to both modify and detect DNA sequences in single cells has led to sophisticated lineage tracing systems based on CRISPR-Cas9 gene editing, with recent implementations in mice (Chan et al., 2019; Kalhor et al., 2018). In these previously described models, constitutive Cas9 expression generates evolvable barcodes in hundreds of random genomic target sites. Our system offers a number of advantages over these previously described models. First, our system is inducible, allowing cells to be barcoded at precise timepoints. Second, all transgenic elements in CARLIN mice are contained in defined genomic loci, enabling straightforward crossing into alternative genetic backgrounds, and minimizing damage caused by continuous double-strand DNA breaks. Third, CARLIN mice represent a stable and practical mouse line that can be utilized by others in the scientific community, avoiding the use of zygote microinjection or complex mouse crosses. Finally, we have created a bank of alleles and statistical methods to create a confidence score for each allele, allowing us to quantify the statistical significance of alleles that are shared across multiple cells.
We have used CARLIN to shed light on two aspects of hematopoiesis. First, we applied our tool to track early blood progenitor clones to adulthood. A surprising observation was that the majority of the largest clones detected exhibited significant bias in their representation across the four bones analyzed. One possible explanation for this is heterogeneity in the niche environments resulting in different seeding success and subsequent expansion (Gao et al., 2018). Alternatively, our data could indicate that only a subset of HSCs in the fetal liver expand or seed the bone marrow (Ganuza et al., 2017). Finally, we also cannot rule out that migration of HSC clones during adulthood occurs between bones, contributing to a skewed distribution of clones (Wright et al., 2001).
Second, we used CARLIN to analyze the clonal dynamics of blood replenishment following chemotherapeutic lympho/myeloablation. Analysis of CARLIN alleles uncovered a reduced clonal diversity of the blood following 5-FU treatment. Furthermore, we observed that a small number of HSCs were responsible for replenishment of the blood. This finding is surprising given that previous reports indicated homogenous cycling within the HSC compartment following 5-FU treatment (Harrison and Lerner, 1991; Wilson et al., 2008). Taken together, it is possible that 5-FU treatment could initiate widespread cycling within the HSC niche with only a small number of clones continuing to cycle and contributing to downstream blood populations. Interestingly, similar dynamics were observed following transplantation into irradiated or cKit-depleted mice (Lu et al., 2019) where only a subset of HSCs replenished the blood, suggesting that skewed blood production from HSCs could be a generalized response to hematopoietic stress. Differential gene expression analysis comparing these ‘active’ HSCs with their ‘inactive’ counterparts revealed increased expression of cell proliferation and cell differentiation genes among others; of particular interest is Plac8 that has been previously implicated in proliferation (Rogulski et al., 2005), host defence (Ledford et al., 2007) and has reduced expression in aged HSCs (Mann et al., 2018). Our identification of a potential new candidate gene involved in the regulation of HSC quiescence/activation highlights the value of using CARLIN to interrogate the molecular drivers underlying the heterogeneous clonal output of HSCs.
Our method can potentially be improved in several ways. First, while our diversity estimates have established the maximum diversity of the CARLIN system to be ~44,000 alleles, which is sufficient for many applications, higher diversity may be desired when analyzing whole adult tissues. Diversity of the system could be increased through simple modifications such as use of homing guide RNAs (Kalhor et al., 2018) or combining the system with Cre-based tracing lines. Second, the current iteration of CARLIN can result in a limited fraction of cells edited (16–74% of cells have edited CARLIN alleles across our single-cell datasets). Editing efficiency could potentially be increased by optimizing the timing and/or dose of doxycycline. Third, a CARLIN capture rate of 32–63% (fraction of cells in which CARLIN was detected across our single-cell datasets) may be limited by low expression/stability of CARLIN RNA, transcriptional bursting from the promoter used, or errors in PCR/sequencing resulting in loss of reads in silico. Incorporating CARLIN into loci that are more highly expressed, using additional CARLIN arrays, or further optimizing the promoter or RNA stabilization sequences could potentially circumvent these deficiencies and increase the fraction of cells from which lineage histories can be extracted.
Finally, this work among others (Alemany et al., 2018; Chan et al., 2019; Frieda et al., 2017; Kalhor et al., 2018; Raj et al., 2018; Spanjaard et al., 2018) represents a proof-of-principle study for the robust recording of cellular information using genome editing. In principle, CARLIN can be extended so that Cas9 expression is controlled by environmentally-sensitive promoters rather than doxycycline. Such a system could record histories of specific stimuli such as pathogen exposure, nutrient intake and signaling activity, in addition to lineage.
STAR Methods
RESOURCE AVAILABILITY
Lead Contact
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Fernando Camargo (fernando.camargo@childrens.harvard.edu).
Materials Availability
Plasmids generated by this study are available upon request. Mouse lines generated by this study are available upon request and will be deposited to The Jackson Laboratory.
Data and Code Availability
All sequencing data used in this paper is available on the NCBI GEO database (Accession Number GSE146972). The CARLIN software package, together with the allele bank, is available at https://gitlab.com/hormozlab/carlin. Instructions and code to reproduce all results, numerics and figures in the paper can be found at https://gitlab.com/hormozlab/cell_2020_carlin.
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Mice
8–12-week-old mice (Mus musculus) were used in all the experiments unless noted in the text or figure legends. Both male and female mice were used indistinctly as we have not observed any difference associated with sex in the biological processes studied; mice were randomly assigned to the different experimental groups in the experiments shown. CARLIN and Cas9 mice were derived from the KH2 mouse embryonic stem cell (ESC) line, with a mixed C57BL/6 × 129 genetic background. Experimental mice used in this study were from F2/F3 generations resulting from the breeding of F1-C57BL/6 × 129 with the tetO-Cas9 mice (also mixed C57BL/6 × 129 genetic background). All mice were maintained in standard conditions of housing and husbandry at Boston Children’s Hospital, and all the procedures involving animals were approved by the Boston Children’s Hospital Institutional Animal Care and Use Committee.
Cell Lines
The CARLIN mouse embryonic stem cell (ESC) line used in some experiments was derived from a male embryo from the F3 generation. Karyotype analysis was performed on the cells to ensure proper genome stability. ESCs were maintained in KO-DMEM, supplemented with 15% ES-FBS, 10 ng/mL LIF and non-essential amino-acids, and grown over a mono-layer of mitomycin C-inactivated mouse embryonic fibroblasts (MEFs), for the time points indicated in the results and figure legend sections. All cultures were maintained in standard tissue culture conditions of 37°C and 5% CO2.
METHOD DETAILS
Design and Assembly of CARLIN Array
The CARLIN reference sequence was designed as an array of ten sense-oriented CRISPR/Cas9 target sites, each with a length of 20 bp and separated from each other by a 3 bp protospacer adjacent motif (PAM) sequence and 4 bp linker. In order to design a mouse-optimized array containing 10 CRISPR/SpCas9 target sites, we started from the set of guides previously tested for the zebrafish GESTALT system development (McKenna et al., 2016; v6 and v7 arrays). From that set, we first excluded all target sites showing any homology with the mouse genome. Secondly, we used the CRISPR design tool (crispr.mit.edu) to select guides with the strongest score factor (highest efficiency and lowest off-target) possible. Based on these criteria we preserved 6 guides from the GESTALT system and designed from scratch the other 4 using the same criteria described. To test each guide, we cloned each one of the 10 sgRNAs individually under the control of the U6 promoter and transduced along with a plasmid containing the CARLIN array into 293T cells. 48 hours after transduction we lysed cells and PCR amplified the array for fragment analysis. All guides selected for the final design showed a similar activity in this assay.
For array synthesis, the final sequence was synthesized as a gBlock (IDT) and is provided in Supplementary Table 1. The CARLIN reference sequence was cloned into the 3’-UTR region of a GFP open reading frame in an intermediate cloning vector, upstream of the bGH-polyA sequence, and under the control of the CAG promoter to ensure robust expression.
Design and Cloning of the CARLIN sgRNA Multiplexes
10 sgRNAs perfectly matching the target sites of the CARLIN reference sequence were expressed as a multiplex, in which each sgRNA is driven by its own promoter. We assembled two different multiplexes, one with Dox-inducible sgRNAs (iCARLIN; see Supplementary Figure 1B), and one with constitutive sgRNAs (constitutive CARLIN, used for all data in the paper with the exception of Supplementary Figure 3F), using the same Golden Gate assembly strategy. In the inducible multiplex, we used the FgH1tUTG donor plasmid (Addgene plasmid #70183; Aubrey et al., 2015) to clone each one of the sgRNAs using the BsmBI restriction sites, whereas in the constitutive multiplex, we used the pU6-(BbsI)_CBh-Cas9-T2A-mCherry plasmid (Addgene plasmid #64324; Chu et al., 2015). Then, the 10 blocks containing the promoter and the sgRNA were PCR-amplified using specific primers with overhangs for the Golden Gate assembly method. The Golden Gate assembly protocol was adapted from the Addgene protocol (https://media.addgene.org/cms/files/GoldenGateTALAssembly2011.pdf; Cermak et al., 2011). All primer sequences are provided in Supplementary Table 1.
Targeting ESCs with the CARLIN Transgene
Both the CARLIN reference sequence and the sgRNA multiplex were cloned adjacently into the pBS31 targeting vector (Beard et al., 2006) to target the ESCs in the Col1a1 locus. For an efficient targeting of the transgene in this locus we used the KH2 ESC line, containing a donor FRT site in the Col1a1 locus, as well as the M2-rtTA transgene introduced in the Rosa26 locus to allow expression of Dox-inducible systems. Approximately 1.5×107 KH2 ESCs were electroporated using 50 μg of the pBS31-CARLIN vector and 25 μg of pCAGGS-FLPe-puro (Buchholz et al., 1998) at 240 V and 500 μF using a Gene PulserII (Bio- Rad, Hercules, CA). Hygromycin selection (140 μg/mL) was started 24h after electroporation. The genomic DNAs from the selected clones were screened by PCR using the Col1a1 genotyping primers (listed in Supplementary Table 1). The same protocol was independently performed for the inducible and constitutive CARLIN systems.
Mice Generation
Two targeted ESC clones were selected from each of the inducible and constitutive CARLIN systems and injected into BL/6 embryos to form mouse chimeras. At least two chimeras with >90% of chimerism from each ESC clone were used as founders of our experimental mouse cohort. The ESCs were injected at the Mouse Gene Manipulation Core at Boston Children’s Hospital. To generate experimental mice, descendants from the F1 of the injected ESCs were bred with Col1a1-TetO-SpCas9, generated at Stuart H. Orkin’s laboratory. Primers for genotyping the Col1a1 and Rosa26 loci are listed in Supplementary Table 1.
Animal Procedures
Unless noted elsewhere, Dox was administered to 8–12-week-old mice via drinking water for one week (2 mg/mL supplemented with 10 mg/mL sucrose) and three intraperitoneal injections (50μg/g) every other day. For the embryonic labeling, Dox was administered to pregnant females via retro-orbital (RO) injection with 25 μg/g of a 10mg/mL solution of Dox at E9.5. 5-fluorouracil (5-FU) was intraperitoneally injected (150 mg/kg) into 8-week-old mice. To prepare 10 mL of the 15 mg/mL 5-FU injectable solution, the chemical was first suspended in 500 μL NaOH 1N and then dissolved in 9.5 mL of phosphate-buffered saline (PBS). For peripheral blood extraction (used to assess fraction of CARLIN sequences edited before performing the single-cell experiments), mice were anesthetized using isoflurane and 2–3 capillaries were collected from the RO sinus. Following erythrocyte removal by osmotic lysis, cells were pelleted and DNA extracted for fragment analysis.
Tissue Processing
For assessment of CARLIN barcode editing and expression in unsorted tissue samples (as in Figure 3B), samples of freshly dissected tissue were snap frozen in liquid nitrogen before RNA purification by Trizol.
To sort epithelial and mesenchymal cells from the lung, mice were euthanized by CO2 and lungs were injected with 2U/mL dispase. Following this, lungs were minced and incubated in 6mL 2U/mL dispase supplemented with 15μL DNase I at 37°C for 30min with rotation. Cells were then filtered through 40μm strainers and centrifuged at 800 rpm, 6 min at 4°C. Staining was performed in 10% FBS/PBS with conjugated Pdgfra, EPCAM, CD45, Ter119, Mac1, and Ly6G antibodies.
To sort epithelial cells from the intestine, approximately 1-inch of intestine was flushed with PBS and incubated in 10mL 4mM EDTA in PBS for 40min at 4°C. After shaking, the smooth muscle layer was removed and the remaining supernatant centrifuged and resuspended in 10mL collagenase/dispase (Roche, 60μL of 50mg/mL stock into 10mL PBS) and incubated at 37°C for 6 minutes. After pipetting to dissociate single cells, the sample was centrifuged, filtered through 70μm strainers and stained in 2% FBS/PBS with conjugated EPCAM, CD45, Ter119, Mac1, and Ly6G antibodies.
To sort epithelial cells from the skin, hair was removed by shaving, and whole back skin removed and washed in PBS. Following fat removal by scraping, skin was incubated in 0.25% trypsin for 1hr at 37°C. The epidermis was then removed from the dermis by razor, minced and filtered using a 100μm strainer to remove residual hair. The suspension was then washed twice in PBS by centrifugation at 300g for 15 min and stained in 2% FBS/PBS with conjugated integrin a6, CD45, Ter119, Mac1, and Ly6G antibodies.
To sort mesenchymal cells from the liver, mice were euthanized and immediately perfused through the suprahepatic vena cava with pre-warmed perfusion buffer (50 mM EDTA, 10 mM HEPES in 1X HBSS) followed by Liver Digest Medium (Gibco). The isolated livers were then subjected to subsequent serial digestions with Accutase (EMD Millipore, Billerica, MA) and 0.25% trypsin (Gibco) for 30 min at room temperature and 37°C, respectively. Cells were collected at each step and filtered through a 100 μm cell strainer, washed and re-suspended in resuspension buffer (1.25 mM CaCl2, 4 mM MgCl2, 10mM HEPES and 5 mM Glucose in 1X HBSS). Staining was performed in 10% FBS/resuspension buffer with conjugated Pdgfra, CD45, Ter119, Mac1, and Ly6G antibodies.
To sort blood cells from bone marrow, bones were immediately dissected from euthanized mice and crushed in 2% fetal bovine serum in PBS. Erythrocytes were removed by osmotic lysis before antibody staining and fluorescence-activated cell sorting. Unless noted, lineage depletion was performed in the whole bone marrow samples using magnetic-assisted cell sorting (Miltenyi Biotec) using the biotin-conjugated lineage markers CD3e, CD19, Gr1, Mac1, and Ter119. To sort mesenchymal cells from bone marrow, bones were prepared as previously described (Houlihan et al., 2012). In short, bones were dissected, cleaned of muscle, lightly crushed and chopped with scissors. The bone fragments were then washed and incubated in 0.25% collagenase for 1h at 37°C whilst shaking. The bones were further lightly crushed and the supernatant passed through a 70μm strainer. Erythrocytes were removed by osmotic lysis and staining was performed in 2% FBS/PBS using conjugated Pdgfra, CD45, Ter119, Mac1, and Ly6G antibodies.
Fluorescence-Activated Cell Sorting
Cell populations were sorted using FACSAria (Becton Dickinson) and the flow cytometry data was analyzed using FlowJo (Tree Star). The following combinations of cell surface markers were used to define the analyzed populations: LT-HSC: Lin−Kit+Sca1+CD150−CD48−; MPP3/4: Lin−Kit+Sca1+CD150−CD48+; ST-HSC: Lin−Kit+Sca1+CD150−CD48−; MPP2: LinKit+Sca1+CD150+CD48+; MyP: Lin−Kit+Sca1−CD150−CD41−; MkP: Lin−Kit+Sca1−CD150+CD41+; granulocytes: Ly6G+Mac1+B220−Ter119−; monocytes: Ly6G−Mac1+B220−Ter119−; pro-pre-B cells: Ly6G−Mac1−B220+Ter119−; erythroblasts: Ly6G+Mac1+B220−Ter119+CD71+. Sorting of epithelial and mesenchymal cells from lung, liver, bone marrow was performed using the following cell surface markers: lung epithelial, CD45− Pdgfra-EPCAM+; skin epithelial, CD45-integrin-a6+; lung/ BM mesenchymal, CD45-EPCAM-Pdgfra+; liver mesenchymal, CD45-EPCAM-Pdgfra+Gr1−; all tissue monocytes, CD45+Ter119-Mac1+Ly6G−. For all sorts, 4’, 6-diamidino-2-phenylindole (DAPI) was used to eliminate dead cells. Representative examples of sorted populations can be found in Supplementary Figure 5A,B. The antibodies were used at a 1:100 dilution.
CARLIN Amplification and Bulk Sequencing Protocols
The sequences of all primers listed here are shown in Supplementary Table 1. For all applications, the PCR amplification of the CARLIN array was performed using primers flanking the 5’ and 3’ external regions of the array (primers CARLIN_fwd1, CARLIN_fwd2 and CARLIN_rev). Illumina adaptor regions, unique motif identifiers (UMI), biotin and fluorescent tags are added to these primers according to the experiment needs. For fragment analysis, the CARLIN_fwd2 was conjugated with 6-carboxyfluorescein (6-FAM) in the 5’ position (FAM_CARLIN_fwd), and PCR products were separated by capillary electrophoresis.
For sequencing the CARLIN array from the genomic DNA (gDNA) of pooled cellular populations, up to 250 ng of input gDNA were used per library. We first performed a UMI-tagging reaction using the CARLIN_fwd2 primer attached to the Illumina sequencing adapter and a 10 bp region of fully degenerate DNA sequence (primer NGS_UIM_D_F). This reaction was performed as a single extension step, in which temperature ramped between annealing and extension for five cycles without a denaturalization step to prevent re-sampling of gDNA CARLIN sequences (McKenna et al., 2016). The DNA product was then purified using AMPure XP beads (Beckman Coulter) and the whole volume was loaded into a PCR reaction to amplify UMI-tagged CARLIN sequences (primers NGS2_F, NGS1_R; 35 cycles). Finally, an indexing PCR was performed (primers P5, NGS2R_I#; 10 cycles) before sequencing.
For preparing libraries from RNA of pooled cellular populations, up to 1μg of total RNA was retro-transcribed using a gene specific primer that contains a 10 bp region of fully degenerated sequence (RT_Bulk_CARLIN) and SuperScript III (Invitrogen). For all in vitro applications, this cDNA product was then purified using AMPure XP beads (1X; Beckman Coulter) and loaded into a PCR reaction for CARLIN amplification (primers NGS2_F, NGS1_Bulk_R; 35 cycles; Platinum Taq enzyme (Invitrogen)). Following AMPure XP bead purification (0.8X), the indexing PCR was performed (primers P5, NGS2R_I#; 10 cycles). For all in vivo applications, the protocol was optimized for a nested PCR approach. The purified cDNA product was loaded into a first PCR reaction (primer NGS1_F, NGS1_Bulk_R; 15 cycles; Q5 High Fidelity Polymerase (M0491, New England Biosciences)). Following AMPure XP beads purification (0.8X), half the product was loaded into a second PCR reaction (primer NGS2_F, NGS1_Bulk_R; 15 cycles; Q5 High Fidelity Polymerase). Finally, after AMPure XP bead purification (0.8X) the indexing PCR was performed (primers P5, NGS2R_I#; 9 cycles). The final indexed libraries were purified with AMPure XP bead purification (0.8X). Libraries were sequenced on Illumina MiSeq using paired-end 500 cycles v2 kits (Read 1: 250 cycles; Index Read: 6 cycles; Read 2: 250 cycles) with 10% PhiX sequencing control v3 (Illumina).
Single-Cell RNA Sequencing Protocols
10X Chromium single cell 3’ (10X) protocols were performed following the manufacturer’s instructions and step-by-step protocols can be found at the companies’ websites. For the 10X Chromium Single Cell 3’ libraries, whole-transcriptome libraries were prepared following the 10X v2 (Figure 5; https://bit.ly/2OUeaUj) and v3 protocol (Figure 6; https://bit.ly/2YP9Lol). Whole-transcriptome libraries were sequenced on Illumina NextSeq500 using paired-end 150 cycles v3 kits (Read 1: 28 cycles; Index Read 1 (i7): 8 cycles; Read 2: 91 cycles).
For targeted CARLIN amplification, 3–5 ng of the amplified cDNA (Step 2.3) was loaded into an initial PCR reaction (10X-CARLIN_1-bio, P5-PR1; 15 cycles). Following cleanup with 0.8X SPRIselect (Beckman Coulter), biotin-tagged products were purified using Dynabeads kilobaseBINDER Kit (Invitrogen) following the manufacturer’s instructions. In short, Dynabeads were incubated with the PCR product on a roller for 3h at room temperature before supernatant removal using magnet separation and washing. Half of the CARLIN-tagged Dynabeads were then loaded into a second PCR reaction (10X-CARLIN_2, P5-PR1; 15 cycles). Following Dynabead removal by magnet, libraries were purified with 0.8X SPRIselect and the indexing step was performed using one tenth of the PCR product (SI primer, Chromium i7 sample primer; 8 cycles). For all 10X PCR reactions, the polymerase supplied with the 10X v3 kit was used. 10X CARLIN single-cell libraries were sequenced on Illumina MiSeq using paired-end 500 cycles v2 kits (Read 1: 28 cycles; Index Read (i7): 8 cycles; Read 2: 350 cycles) with 10% PhiX sequencing control v3 (Illumina).
QUANTIFICATION AND STATISTICAL ANALYSIS
Preprocessing
For bulk experiments, raw Illumina paired-end reads of the CARLIN amplicon were merged using PEAR v0.9.11 (Zhang 2014) with parameters --min-overlap=1, --min-assembly-length=1, --min-trim-length=1, and --quality-threshold=30. Amplicon and transcriptome libraries prepared with 10X were preprocessed using CellRanger v2.2.0 (for 10X V2 libraries) and v3.0.2 (for 10X V3 libraries) according to the standardized workflow with default parameters. Transcriptome libraries were aligned against the mm10 reference genome provided by CellRanger.
Although no data presented in the paper was generated with InDrops (Zilionis 2017), it is a supported platform, though a modified version of the InDrops pipeline should be used (available at https://gitlab.com/hormozlab/indrops). The InDrops pipeline should be run with the parameters (LEADING=10, SLIDINGWINDOW=4:5, MINLEN=16) for Trimmomatic and (m=200, n=1, l=15, e=500) for Bowtie. Additionally, amplicon libraries prepared with InDrops should be processed with the ‘--no_clean_barcodes’ flag, which preserves the uncleaned version of the Cell Barcode (CB) and logs QC information for the CB and UMI in the header (see Filtering Reads and CB and UMI Error Correction below).
Cells were additionally filtered by removing CBs in which the number of detected UMIs was below a threshold that was determined programmatically using MATLAB’s findpeaks function based on the distribution of UMI counts (thresholds are listed in Supplementary Table 4). CBs where the percentage of UMIs corresponding to mitochondrial genes exceeded 15% were also discarded. The remaining CBs constitute a reference list against which CBs found in CARLIN amplicon sequencing can be collapsed (see CB and UMI Error Correction).
CARLIN Pipeline
Custom software was developed in MATLAB to perform alignment and allele calling, which can handle both bulk and single-cell amplicon sequencing of the CARLIN array. The software is trivial to install, simple to run, and produces data diagnostics useful for an experimentalist. The CARLIN software package is available at https://gitlab.com/hormozlab/carlin. Supplementary Table 3 presents the number of reads retained at each step of the CARLIN pipeline described below, for the 3 mice used in the allele bank.
Filtering Reads
For bulk sequencing runs of genomic DNA, reads were filtered on possessing an exact match to the 20 bp CARLIN_fwd2 primer starting at the 11th bp of the read, since the UMI-tagging reaction adds a 10 bp randomer upstream of the CARLIN_fwd2 primer (Supplementary Table 1; Methods). To ensure that the entire CARLIN sequence was read, we retained reads that had good alignment to the 31 bp pre-polyA UTR sequence (hereafter referred to as the secondary sequence; Supplementary Table 1) located downstream of the 10th CARLIN target site – specifically, we require MATLAB’s nwalign function with glocal=true (hereafter referred to as just nwalign) to return a score ≥30.
For bulk sequencing runs of RNA, reads were reverse-complemented as the read is anti-sense. Because the UMI tagging protocol results in a 10 bp randomer being appended to the 20 bp CARLIN_rev primer (Supplementary Table 1; Methods), we retained reads that had an exact match to the primer, starting at 30 bp upstream of the end of the read. Additionally, to ensure that the whole CARLIN sequence was read and to simplify subsequent alignment, we only retained reads that had good alignment to the CARLIN_fwd2 primer and secondary sequence (nwalign scores ≥15 and 30 respectively).
For all bulk reads, there is additional filtering to only retain reads with UMIs that have a QC of at least 30 at all 10 bps.
For sequencing runs of 10X CARLIN amplicon libraries, to ensure the whole CARLIN construct is sequenced, reads were filtered on possessing an exact match to the CARLIN_fwd2 primer starting at the 1st base pair, and a good alignment (nwalign scores ≥ 30) to the secondary sequence. Additionally, reads in which the CB or UMI are of the incorrect length, have uncalled base pairs, or in which the QC of any base pair is < 20, were discarded.
For all reads which pass the above filters, the CARLIN sequence was extracted by trimming the flanking primers and secondary sequence. If the resulting sequence has any uncalled base pair or was shorter than 26 bps (the combined length of the prefix, first conserved site and postfix – see Figure 1B), it was discarded.
Alignment
Here, we will describe the procedure used to determine how a CARLIN read has been altered with respect to the unmodified CARLIN sequence (referred to hereafter as the reference; see CARLIN reference sequence in Supplementary Table 1). As Cas9 modifications are expected to predominantly be indels, to identify alterations, we first aligned the CARLIN sequences against the reference. We found that existing alignment algorithms do not account for where Cas9 alterations are expected to appear along the reference (3 bp upstream of the PAM sequence, in a region referred to here as the cutsite). For example, NeedleAll (Rice 2000), a software package that implements the standard Needleman-Wunsch (NW) algorithm, was used in GESTALT (McKenna 2016), but yielded mixed results when aligning 75 modified CARLIN sequences read out using bulk Sanger sequencing. First, the NW algorithm did not preferentially select indel locations to coincide with the expected activity of Cas9 when multiple indel locations were equally plausible. Second, the default parameters used in the NW algorithm (NUC44 scoring matrix, gap opening penalty of 10, gap extension penalty of 0.5), precludes insertions and deletions from occurring consecutively, which is unrealistic given that the activity of Cas9 can result in such alterations. Third, the default value of the gap extension penalty parameter penalizes insertions and deletions according to length. Finally, customizing these parameters cannot cluster the alterations into expected regions of Cas9 activity.
To overcome these limitations, we developed our own alignment algorithm. Our algorithm is a modified version of the NW algorithm that performs alignment while accounting for where along the sequence alterations are expected with respect to the reference. We introduced a site-dependent cost function that penalizes alterations outside the expected regions of Cas9 activity. The cost function was minimized using a dynamic programming approach. Although the parameters used are specific to CARLIN, they can be modified to accommodate other systems that rely on Cas9 editing. Next, we describe our algorithm in full detail.
Let be the set of nucleotides, B denote a gap, and . Let , J ≥ 1, be the nucleotide string of length J. to align and denote the reference of length K by , K ≥ 1. Let , 0 ≤ j ≤ J, and , 0 ≤ k ≤ K, be prefix strings of and ending with sj and rk respectively (or empty strings if j = 0 or k = 0). Denote by , the operator which removes gaps from the input string.
Define , with max(j, k) ≤ L ≤ j + k, as an alignment of against with and , and let be a scoring function, that yields higher values for better alignments. We do not enumerate all alignments and rank them according to any explicit evaluation of this scoring function. Instead, we use a recursive formulation where we determine the maximum possible score for . This requires us to distinguish between three kinds of alignment: neither of the terminal characters are gaps, or the two cases where one terminal character is a gap but not the other. Using our notation, the three cases are (i) in which and , (ii) in which d1,L = B and , and (iii) in which and i2,L = B. Denote by , , the set of all such alignments.
We can then note the following recursive relationships, which simply state that an alignment of two strings can be decomposed into an alignment of two substrings, comprised of the first characters through to the penultimate characters, and an alignment of the terminal characters. We write down this recursive relationship for the three kinds of alignments defined above, using ⊎ to denote string concatenation.
The base cases are the empty sets , and the singleton sets for 1 ≤ k ≤ K and for 1 ≤ j ≤ J.
We now elucidate the score to rank the alignments in these sets. Briefly, we penalize deletions that do not begin and finish near the expected cutsites, and insertions that do not occur near the expected cutsites. We do not favor insertions over deletions, discriminate based on the length of the alteration, or penalize consecutive deletions or insertions.
Let , be a scoring function for aligning different nucleotides (we use the same NUC44 scoring matrix used in the default NW algorithm). Define PD,B(k) ≥ 0 and PD,E(k) ≥ 0, 1 ≤ k ≤ K to be site-dependent penalties for beginning and ending a deletion at rk from alignments which end or begin in paired nucleotides respectively. Similarly, define PI,B(k) ≥ 0, and PI,E(k) ≥ 0 for 1 ≤ k ≤ K to be the site-dependent penalty for beginning an insertion after rk and ending an insertion before rk respectively. Let Mj,k, Dj,k, Ij,k be the highest scores of the alignments in , and respectively.
Using the set recurrences above and the introduced scoring scheme, we arrive at a new set of scalar recurrences for the highest scores, so that we don’t have to compute these quantities explicitly by exhaustively searching over a full enumeration of alignments.
As evident in the last two equations, there is no incremental cost in extending an insertion or deletion along either one of the two strings. Since insertions and deletions are penalized equally, we make the following simplifying assumption, which in turn also reduces the number of parameters: PD,B(k) = PI,B(k) ≡ PB(k) and PD,E(k) = PI,B(k) ≡ PE(k). We abuse notation to let PB(0) be the penalty for starting insertions prior to the first character of the reference. Consistent with the previously defined base cases, the initialization is Mj>0,0 = M0,k>0 = Dj≥0,0 = I0,k≥0 = −∞, D0,k>0 = PB(1), Ij>0,0 = PB(0), M0,0 = 0
There is no guarantee that a single alignment achieves the highest score . Multiple alignments can achieve the maximum score within each of , and , and also across the three. To select the optimal alignment amongst the alignments that share the maximum score, we need to retain which argument in the recurrence relationships for , and (see above) realize the maximum score. Let , L > 0, be the operator which strips the terminal character from the aligned sequence and reference. Given , let , 0 ≤ j ≤ J, 0 ≤ k ≤ K, be an indicator function such that
For example, if both the first and third terms realize the maximum in the recurrence for Dj,k, then we set and . We will use this indicator function to select the optimal alignment as described below. In accordance with the previous base cases, the initialization is .
The alignment algorithm is implemented in two stages, a forward stage in which we tabulate the maximum score, and a reverse stage in which we construct the optimal alignment. In the forward stage, the maximum scores are first initialized as outlined above. Next, we solve the recurrences using a dynamic programming approach in time by sweeping across all nucleotides in the sequence from j = 1 to J, and for each value of j, iterating over all the nucleotides in the reference, k = 1 to K. At each (j, k) ordered pair, we compute and store Mj,k, Dj,k and Ij,k in three two-dimensional arrays of size (J + 1) × (K + 1), and update a 3 × 3 × (J + 1) × (K + 1) Boolean array for , which retains the alignment type (gap in the reference, gap in the sequence, or no gap) that achieves the maximum scores.
In the reverse stage, we incrementally build the optimal alignment by backtracking from the last aligned pair of nucleotides (J, K) using the following rules, picking the first lettered rule that applies within each numbered rule. These rules were formulated to ensure continuity among mutation types, which allows us to group distinct mutations more easily (see Mutation Calling) and attribute them to a single Cas9 cutting event.
- Let .
- If , let .
- If , let .
- If , let .
Repeat rules 3–5 until j = 0 and k = 0.
- If :
- If , let .
- If , let .
-
If , let .Let .
- If :
- If , let .
- If , let .
-
If , let .Let .
- If :
- If , let .
- If , let .
-
If , let .Let .
The result is a unique alignment such that .The algorithm above can be used to generate improved alignments for any CRISPR-Cas9 system for suitably chosen penalties PB(k) and PB(k). We provide a standalone C++ implementation of the described algorithm for groups interested in performing alignment on custom CRISPR-Cas9 templates, outside the context of CARLIN.
Lastly, we turn our attention to the values chosen for the penalty functions, for CARLIN specifically. Because we expect the alterations to be localized to the cutsites, the minimum value of the penalty was set to occur within 3 bp upstream of the PAM sequences with the penalty increasing linearly moving away from this location. We used the same penalty function for all the target sites. We manually selected the parameters of the penalty function, i.e. the minimum value and the slopes, to promote alignments comprised of insertions and deletions in the cutsites for the 75 CARLIN sequences characterized using bulk Sanger sequencing. The same parameters also resulted in desired alignment properties when applied to the bulk RNA sequencing data used to make the allele bank (Supplementary Figure 2A–C). For the numerical values of the penalty functions, refer to Supplementary Table 2.
Motif Classification
We partitioned the reference into 31 consecutive regions (called motifs), according to the locations of the reference prefix sequence, conserved sites, cutsites, PAM+linkers, and postfix sequence (Figure 1B). After aligning a sequence to the reference, we identified the same motifs in the aligned sequence according to the nucleotide boundaries of the motif in the reference. Each aligned motif was then assigned a classification: (1) ‘N’: all the nucleotides of the sequence match that of the reference exactly and there are no gaps in the sequence or reference. (2) ‘E’: motif is completely absent in the aligned sequence. (3) ‘D’: any (but not all) bps of the motif are deleted in the sequence, and there are no gaps in the reference. (4) ‘M’: there are no insertions or deletions relative to the reference, only substitutions. (5) ‘I’ otherwise. These motifs were used to correct potential sequencing errors and establish a consensus sequence across multiple reads (as described below).
Sequence Error Correction
Sequencing and amplification (technical) errors can, in addition to Cas9 activity, also introduce alterations in the CARLIN sequence. We assumed that any individual SNP that occurs outside of a 3 bp window around the cutsite is a technical error. To remove these technical errors, we took the aligned CARLIN sequences and reverted the SNPs in these regions (classified as ‘M’ in non-cutsite motifs) to the corresponding base pair in the reference. We also trimmed nucleotides in the aligned sequence that extended beyond the reference in either direction.
CB and UMI Error Correction
CBs and UMIs are also subject to the same technical errors as the CARLIN sequence. Denoising of CBs and UMIs is performed according to the directional adjacency method developed in UMI-tools (Smith 2017). In short, the method starts by making a list of tags (either CBs or UMIs) sorted in descending order by the number of reads corresponding to each tag. Next, a directed graph is constructed with nodes representing tags. The objective is to connect the nodes whose tags are different only due to technical errors.
To do so, first, the top-ranked node is selected as the current node. An edge is drawn from the current node to all candidate nodes that satisfy the following criteria: the candidate node does not already have an incident edge, the tag of the candidate node is different by only one base pair from the tag of the current node, and the number of reads of the candidate node’s tag is less than half of the current node’s tag. The current node is then updated to be the next most common node. The process is repeated until the entire sorted list has been traversed, resulting in disjoint sets of connected nodes (connected components). In each connected component, the reads of all the tags are merged under the tag of the top-ranked node in that connected component.
For bulk samples where no CB exists, we do not apply this algorithm directly to all of the detected UMIs. Instead, we first group the UMIs by their consensus CARLIN sequence with no read threshold (see Consensus Calling and Read Thresholds for Denoised CBs and UMIs below for definition of consensus sequence and use of read thresholds respectively). Next, the directional adjacency method (describe in the previous paragraph) is applied across all UMIs with the same consensus sequence. This extra step prevents accidental merging of UMIs that differ by only 1 bp when the number of detected UMIs is large with respect to the possible UMI diversity.
For single-cell data, directional adjacency denoising is also used but with CBs for tags. If there is a reference CB list (for e.g. obtained after preprocessing of the transcriptome library, see Preprocessing), then we include two additional requirements: (i) top-ranked nodes in each connected component need to belong to the reference CB list (or else the whole connected component is discarded), and (ii) candidate nodes cannot belong to the reference CB list. Next, for each denoised CB (which is now guaranteed to be in the reference list, if supplied), directional adjacency denoising is performed on its constituent UMIs. The result of this procedure is a denoised list of CBs and/or UMIs.
Read Thresholds for Denoised CBs and UMIs
Since we do not necessarily have a ground truth list of tags which we expect to detect in the data, tags with few reads may be spurious, even if they have been denoised. Additionally, to call a consensus sequence for each tag, we need to be able to find a common sequence among a sufficiently large number of reads; repeat occurrences of a CARLIN sequence over many reads gives us confidence that the sequence is the correct one. Averaging over many reads also allows us a secondary mechanism of correcting for technical errors (especially at cutsites, which we left untouched in the Sequence Error Correction section). Here we describe how we determine a threshold on what is a sufficient number of reads.
Let Ri be a sorted list of the number of reads associated with each of N denoised tags (UMIs/CBs) with R1 ≥ … ≥RN. We only attempt to call a consensus sequence for tag i if Ri meets a minimum threshold, T, for the number of reads, and discard tags which fail to achieve this threshold.
Nexpected is the expected number of tags in the experiment (or ∞ if unknown or Nexpected > N, so that {R∞ = 0), p is the 95th percentile value of the transformed QC scores (error probability) across all tag bps for all filtered reads, and L is the number of base pairs in the tag.
Our threshold function is a heuristic and was empirically optimized by comparing the length distribution of the consensus alignments called from the consensus sequence (see Consensus Calling) to fragment length analysis of the same libraries (Supplementary Figure 2D). We observed that the log-log plot of the rank-ordered number of reads across the tags, Ri, exhibited a plateau (roughly constant number of reads) after the first percentile with a sharp fall off (a knee) when the number of reads decreased to one tenth of that of the plateau. Similar empirical criteria are used to select single-cell barcodes by other single-cell analysis tools such as CellRanger. The next two terms of the threshold function ensure that the number of tags does not exceed the expected number of molecules. The fourth term sets a conservative estimate on the number of reads expected from a single sequencing error across a tag of length L. Finally, we also required that any tag is observed in at least 10 reads. This last condition reflects the minimum number of sequences we would like to have for consensus calling (see below). The choices for the threshold function were made conservatively to minimize false-positives.
For SC data for which a reference CB list is not available, first Ri is tabulated as the number of reads for a given CB. A CB read threshold, TCB, is computed using Ri as described above. Next, the number of reads is also tabulated for each CB-UMI pair, to compute TUMI. Only cell barcodes which have at least TCB reads, and within each CB, UMIs which have at least TUMI reads are retained.
For SC data for which a reference CB list is available, only CBs found in the reference CB list survive the denoising procedure. Since the reference CB list is separately subject to quality control in the software generating the list (for e.g. CellRanger), we trust all denoised CBs, so that the threshold is only required to ensure there are sufficient reads for consensus calling. To that end, we only use the last term in our heuristic function, effectively setting TCB = TUMI = 10. The mean number of reads, Ri, among CBs that pass this threshold criterion is typically one or two orders of magnitude larger than T (see Supplementary Table 4).
Consensus Calling
Next, we describe the procedure used to call the consensus sequence for tags that pass the threshold criterion. First, we selected the tags for which greater than 50% of the reads are of the same length and possess the same 31-character motif classification string (see Motif Classification above). Next, for the selected tags, we retained the reads that comprised this majority. The consensus sequence was constructed bp-by-bp by selecting the most commonly occurring nucleotide across all the retained reads (i.e. taking a per bp mode of the retained reads).
For single-cell data, this procedure is performed on each UMI of a CB separately. Next, we collected the consensus sequence across different UMIs that passed the threshold and selection criteria. If more than 50% of the consensus sequences are of the same length and possess the same 31-character motif classification string, we proceeded as follows. We retained the consensus sequences that comprised this majority. The CB consensus sequence was constructed bp-by-bp, selecting the most commonly occurring nucleotide across the retained UMI consensus sequences.
To construct the consensus alignment, we removed the gaps from the consensus sequence and realigned to the reference. To define CARLIN alleles, we pooled all consensus alignments, and removed all repeated instances, so that each consensus alignment is represented only once. We define an allele to be an element of the resulting set, so that alleles are unique by definition. An allele is defined to be edited if its consensus alignment does not match the reference exactly. In the text, edited transcript/cell refers to a UMI/CB which has a corresponding CARLIN allele that is edited. The frequency of an allele in a sample is the number of tags whose consensus alignment matches that allele.
Mutation Calling
To explicitly associate mutations with the alterations harbored by an allele, we first tabulated the starting and ending locations of the deletions, insertions, and substitutions in the consensus alignment. Next, to account for a single Cas9 cutting event that could result in multiple alterations, we combined two mutations if they were adjacent – the ending location of one mutation was one bp upstream of the starting location of the other— or if the ending location of one was co-localized to the same cutsite as the starting location of the other. We iterated the process of combining mutations until no further combinations were possible. The combined mutations were always designated as indels. For example, a typical allele can harbor a single bp deletion, and a 5 bp insertion at the cutsite of target site 3, two mutations which are merged into a single indel event using this procedure.
For the purpose of preparing figures, we considered all substitutions as indels (1 bp deletion of the reference nucleotide, and 1 bp insertion of the mismatched sequence nucleotide). In figures where only insertions and deletions are shown (e.g. Figure 1C,D,F), indels are represented twice, once as an insertion corresponding to the length of the new sequence, and once as a deletion for the length of the deleted portion of the reference.
CARLIN Potential
To quantify the extent to which a CARLIN allele is altered with respect to the reference, we define the CARLIN potential of an allele as the number of target sites whose sequence and the sequence of the adjacent PAM+linker domain exactly matches that of the reference. Alterations in the prefix and postfix are considered to be alterations of the first and last target site respectively. The CARLIN potential is a whole number between 0 and 10.
Quantifying Diversity
Effective Alleles
Since independent Cas9 activity across different cells may lead to the same altered sequences, the number of alleles detected will generally be less than the number of cells, even if all cells are edited. Furthermore, not all alleles are equally likely. Some occur more frequently than others.
Ideally, we want detection of a particular allele to restrict the cell in which the allele is observed to the smallest possible subset of the original population. For a given number of alleles, this occurs if all alleles are equally likely (i.e. the observation carries maximal information in the language of information theory). For the case where the allele frequencies are not equal, the observation of a particular allele is, on average, not as informative for constraining the subpopulation of cells from which the allele came. How many equally likely alleles are required to carry the same amount of information in this case?
To answer this question, we devised a metric, the effective number of alleles, calculated as 2H where H is the Shannon entropy of the normalized allele frequency distribution across the edited cells. In the limit that each edited allele appears in an equal number of cells, the effective number of alleles is simply the number of edited alleles. Conversely, in the limit where a single allele appears in all edited cells, the number of effective alleles is 1. The effective allele measure seeks to discount the effect of over-represented alleles, which are less informative. The effective number of alleles in the bank of 44000 alleles is 14700.
Diversity Index
The diversity index is computed by dividing the effective number of alleles (see above) by the number of cells in the population. (Alternatively, dividing by the number of edited cells can be used to compute diversity index across only the edited cells, independent of the fraction of cells edited). The diversity index is 0 when only the reference is present in the sample, and 1 when the reference is entirely absent and each cell has its own allele. The diversity index is α when the cutting efficiency is α, and each edited cell has a distinct allele, and is less than α if some cells share the same allele. The reciprocal of the diversity index is the average number of cells labeled by each effective allele.
Allele Bank
To estimate the total number of alleles which can be generated by the CARLIN system, we pooled the edited transcripts collected from granulocytes harvested from 3 mice, to create a bank of ~233K transcripts resulting in ~32K alleles. As granulocytes are not expected to proliferate appreciably in the 3 days between induction and collection, shared alleles across multiple cells are coincidental and not due to shared ancestry of the cells.
Estimating Number of Unseen Alleles
The total number of alleles that CARLIN can generate is the sum of the number of alleles observed in the bank and the number of alleles that have gone undetected because only a finite number of cells were measured. To extrapolate the total number of alleles, we need to estimate the number of unobserved alleles. To intuitively understand the extrapolation, we consider two extreme cases. If most alleles are only observed once, then we expect many new alleles would turn up under more exhaustive sampling. (In the limit that all alleles are observed only once, the total number of alleles is indeterminate). Conversely, if most alleles are observed many times, the system has been sufficiently sampled and few unobserved alleles are expected. To estimate the number of unobserved alleles, we use tools developed in the field of ecology, where the problem is referred to as the unseen species problem. See (J. A. Bunge 2014) for example, for a review of techniques in the field.
Non-Parametric Diversity Estimation
We use the Smoothed Goodman-Toulmin estimator (SGT) proposed by (Orlitsky 2016) to estimate the expected number of alleles, N, in M observations given that n alleles were detected in m observations (m < M). This estimator is near-optimal in the sense of mean-squared error and works for M of the order of , the theoretical extrapolation limit (Orlitsky 2016). To check the consistency of the estimator, we subsample the data to have observations (colored dots in Figure 3G), and compute the expected number of alleles for an extrapolated number of observations in the interval (dotted lines in Figure 3G colored to correspond to the subsample size).
Parametric Diversity Estimation
To validate the non-parametric method, and obtain an analytic expression for occurrence frequency of the alleles for subsequent calculations, we tabulate the frequency of allele i as Xi and generate a histogram of frequency counts, , representing the number of alleles that are detected Z times. Note that , the number of edited alleles observed, and , the number of observations of edited alleles.
Conceptually, sampling of an allele can be approximated as a Poisson process. The number of observations of a particular allele, Xi, given a total number of observations, M, is drawn from a Poisson distribution with a rate parameter, λi, that is proportional to the prevalence of that allele in the bank. The Poisson approximation allows for an elegant analytical solution for estimating the occurrence frequency of an allele:
To model the variability in the prevalence of different alleles, we need to associate a Poisson rate parameter with each allele. Although in general, each allele can have a unique Poisson rate parameter, for simplicity, we assume that the rate parameters are drawn from a distribution that can be succinctly described using a few parameters.
We use CatchAll (v4.0), a software package described in (J. L. Bunge 2012), to fit a distribution of intensive Poisson rate parameters for alleles, fθ(λ), to our observed data. If all alleles are equally prevalent with , , and ℎ(Z), when normalized, would converge to a Poisson distribution. CatchAll determined that for our data, ℎ(Z) mostly closely resembles a mixture geometric distribution so that fθ(λ) is a 4-component exponential mixture model.
The probability that an allele remains unobserved after m observations is then given by
The number of unseen alleles is therefore nP0/(1 − P0) and the total number of alleles is given by N = n/(1 − P0). For our bank, m ≈ 233000, n ≈ 32000 and P0 ≈ 0.28 so that the number of unseen alleles is estimated to be ≈ 12000 and consequently, the total number of alleles is estimated to be N ≈ 44000. The curves in Figure 3H are obtained by using this estimate for N, and the endpoints of the 95% CI of N, in the estimators for interpolation and extrapolation provided in equations (6) and (12) respectively of (Colwell 2012).
Prevalence of Unseen Alleles
Given our analytical model, we can now determine the distribution of the Poisson rate parameters for the unobserved alleles. It is a conditional distribution given by Bayes’ rule:
For simplicity, we assign all alleles unobserved in the bank the mean Poisson rate under this conditional distribution.
Usage of Allele Rates
For subsequent experiments, we query the alleles observed in the experiment against the alleles in the bank. If an observed allele matches an allele in the bank, that allele is assigned the rate parameter based on its empirical prevalence in the bank, where Xi is the frequency of the allele in the bank and m is the total number of observations constituting the bank. Otherwise, we assign it the rate λ0.
Statistical Analysis
Limitations of a Finite Number of Alleles for Uniquely Marking Clones
Here, we consider the implications of having a finite set of alleles with which we can mark a (possibly infinite) number of cells. How useful are the alleles in uniquely marking clones if multiple cells can be marked with the same allele? To answer this question, the following factors need to be considered: the frequency of the allele in the bank, the number of cells marked initially, potential proliferation of the cells after they are marked, and the number of cells sampled at the final timepoint.
Suppose that at induction, C ≥ 1 cells are randomly assigned one of N alleles, according to a distribution ρ of allele probabilities. Let Lj ∈ {1 …. N} be the allele label of the jth induced cell and let , be the number of cells marked with allele i. Then and the conditional probability given that allele i is present in at least one cell is
We define the singleton probability and duplication probabilities as
See Supplementary Figure 4B for an illustration of how psingleton, the probability that an allele uniquely marks a cell, depends on C and N in the case that ρ is uniform.
In practice, we do not know how the cells are labeled initially but instead observe alleles from an unbiased sampling of M ≥ 1 cells at some later time. Subsequent to induction, assume that cell j expands such that at the sampling time, the probability that cell j is a progenitor of a sampled cell is given by pprogenitor(j; b), where b is a parameter, which will be defined later.
Our goal is to label each progenitor uniquely but it could be that some progenitors were coincidentally marked with the same allele. At the time of sampling, if we observe the same allele across multiple cells, we would like to know the probability that all the cells came from a single progenitor.
If we assume that the proliferation rates are not dependent on the allele label, we will be able to develop a useful bound on the above probability. Let Xi be the number of cells in the observed sample marked with allele i. If progenitor proliferation rates are uncorrelated with progenitor allele labels, it follows that the distribution of allele frequencies in the sample is equal to that of the induced pool
Let Yi be the number of progenitors of the sampled cells marked with allele i (note the distinction from Ci, the number of progenitors marked with allele i). We know that generally P(Yi = m; M) depends on the induction itself (since P(Yi > Ci; M) = 0, for example, when the realization of Ci corresponds to the same experiment as Yi). But what can we say about P(Yi = m; M) when we don’t know Ci for the same experiment, only P(Ci = c; C)?
First note that the conditional probability of the number of progenitors Yi given that allele i is observed at least once is
The specific form of P(Yi = m|Xi = k) depends on the proliferation model. For an observed allele i, let us consider the ratio of the probability that more than one progenitor gave rise to the cells labeled with allele i at the sampling timepoint, to the probability that more than one cell was labeled with allele i at the initial timepoint:
We note that we calculate these probabilities independently because in general we might not know the number of cells that were initially labeled with allele i. We show that γ(1) ≤ 1, so that the probability of more than one progenitor giving rise to cells labeled with allele i is smaller than the probability of labeling more than one cell with allele i at the initial timepoint, given that the number of cells sampled is less than or equal to the initial number of cells:
This result can be generalized to bound any number of progenitor cells:
How close is γ(1) to 1 for a given choice of parameters? Intuitively, the more heterogeneous the proliferation rates, the less likely we are to observe cells that share the same allele but not the same progenitor, since the clone that proliferates faster will tend to dominate the sample.
To show this mathematically we note γ(1) is maximized when P(Yi = 1|Xi = k) is minimized for each 1 < k ≤ M. To determine when P(Yi = 1|Xi = k) is minimized, we turn our attention to the b parameter of pprogenitor(j; b). Let b be any parameterization of pprogenitor such that as b → ∞, and . Note that
This is minimized for ∀ k (for example, by Lagrange multipliers) when each of its constituent terms is , so that i.e. b = 0.
To consider the effect of sampling, we resort to numerical simulations and consider a specific proliferation model given by , which results in without loss of generality. is a normalizing constant. We simulate induction of an initial pool with N = 2000 alleles (the results are insensitive to N) drawn from a uniform ρ, subsequent expansion using this proliferation model, followed by sampling of a different number of cells at the final timepoint (resulting in different instances of f). Supplementary Figure 4B shows γ(f) ≤ 1 for different values of f and b where each data point is the mean of a 1000 simulations. The more uneven the proliferation rates (larger values of b), the less likely it is to observe the same allele shared across multiple cells that arise from different progenitors. However, as the number of observed cells increases (larger values of f), even progeny from slowly-proliferating progenitors that were redundantly marked are more likely to be observed.
In summary, if we assume that proliferation rates are not dependent on allele marking then:
The probability that cells that share a given allele at the final timepoint came from more than one progenitor is less than the probability that more than one cell would have been labeled with the same allele in the initial population, if the number of cells sampled is less than the initial population size. This means that underestimates the probability that observed cells share a unique progenitor and conversely overestimates the probability that the observed cells arise from multiple progenitors. Therefore, in practice, if the initial population size C is not known, computing using the number of sampled cells (in place of the unknown initial population size) is a conservative bound on the probability that allele i is marking a unique clone, as long as M < C. In the case where M > C, the estimate is by definition more conservative because it assumes more cells were initially labeled than was actually the case.
The more non-uniform the proliferation rates of progenitor cells, the more conservative we are in using and as bounds.
The fewer cells sampled at the final timepoint, the more conservative we are in using and as bounds, achieving equality only in the limit of perfect sampling, where M ≫ C.
Statistical Significance of Alleles
Previous barcoding systems fail to account for the natural ubiquity of alleles, mistakenly attributing kinship to cells coincidentally marked by the same allele. Since common alleles by definition occur in many cells, the number of cells implicated in these false-positive conclusions can be high. We circumvent this issue by assigning a p-value to each allele, which quantifies statistical significance of the allele according to the biological application, so that standard statistical best practices can be used.
Case 1: p-value for marking clones when C is known or C < M
Consider the case where C, the number of cells initially labeled, is known (or there is an estimate on the upper bound ≤ M, the number of cells observed at the sampling timepoint). If at the sampling timepoint, we observe at least one cell harboring allele i, Xi > 0, we would like to quantify the probability that the Xi cells arose from more than one progenitor (Ci > 1) coincidentally marked with the same allele at the initial induction. If this probability is < α, we can be confident at significance level α, that all Xi cells marked with allele i, originated from a single progenitor. This probability is just pduplicate introduced above, where we now use the approximation that the occurrence frequency of a given allele follows a Poisson distribution.
Note that conditional on allele i being observed, pduplicate does not depend on the number of cells observed (Xi). Given the number of alleles and the distribution of their Poisson rates in the CARLIN system, for sufficiently large C, pduplicate will always be larger than a preset significance level for some of the alleles. For example, at C = 5000, 72% of alleles are significant at α = 0.05, representing a cumulative allele frequency probability of 20% so that a fifth of cells will be marked uniquely at this significance level (Figure 3I).
Case 2: p-value for marking clones when M < C or C is unknown
In this case, we still seek to quantify the probability that Xi cells arose from multiple progenitors, but without knowing the size of the initial pool. We assume that the Xis form an unbiased sampling. The probability of observing more than one cell independently labeled with allele i conditioned on having observed the allele is given by,
Note that pclonal is just pduplicate evaluated at C = M, according to our earlier justification (see Limitations of a Finite Number of Alleles for Uniquely Marking Clones) and constitutes an upper bound on the probability (a conservative p-value). We separately annotate this as pclonal instead of pduplicate to make clear that in this case, we have no knowledge C of or Ci.
As M grows, we are more likely to sample redundantly marked cells. Once M ≥ 35,000, even the most rare allele is expected to mark multiple progenitors at significance level α = 0.05. The upper limit on M is determined by the smallest Poisson rate in our bank, the mean rate assigned to the unobserved alleles. Although there is actually a distribution of rates for unobserved alleles, we still cannot theoretically go beyond the limit imposed by the mean (as we cannot actually associate an unobserved allele to a particular rate in this distribution). This regime is indicated in grey in Figure 3I. We use this p-value for all our SC analysis where M < 1500.
Case 3: p-value for allele frequency
Lastly, we define a p-value that quantifies the probability of observing allele i expressed in Xi cells or more, under the null model that the allele has Poisson rate parameter λi.
If pfrequency(i; M) < α, this means that cells marked with allele i are significantly over-represented in a library of M cells (at significance level α). This does not necessarily indicate that all cells expressing the allele are related. However, it does indicate that at least one progenitor marked with the allele expanded more compared to progenitors marked with other alleles. The more skewed the proliferation rates (b → ∞ according to notation introduced in Limitations of a Finite Number of Alleles for Uniquely Marking Clones), the more likely the over-representation is due to a single progenitor.
Statistically Significant Clones for SC Analysis
An allele was determined to be statistically significant if it had a pclonal that survived multiple hypothesis testing using the Benjamini-Hochberg procedure at a false discovery rate (FDR) of 0.05. A clone (a group of cells marked with the same allele) was said to be statistically significant, if its allele was statistically significant. For the 5-FU experiments, the number of observed cells (M) was set separately for each sample to equal the number of cells with an edited CARLIN allele in that sample (Supplementary Table 4). For the embryonic induction experiment, the number of observed cells (M) was the total number of cells with an edited CARLIN allele across the four bones (Supplementary Table 4).
Comparing Progeny Origin in Development and Adult Hematopoiesis
To quantify what fraction of statistically significant clones included both HSCs and non-HSCs, we computed the proportion of statistically significant alleles that marked cells belonging to both the HSC and non-HSC clusters for each sample. For the controls, we aggregated this proportion over the three controls as an average of the three proportions, weighted by the number of statistically significant alleles in each control. We similarly computed an aggregated proportion over the two 5-FU mice. We performed a two-proportion z-test for the alternative hypothesis that the proportion is larger in the developmental/adult hematopoiesis than in the control, rejecting at significance level α = 0.05.
To quantify what fraction of the observed non-HSCs share an allele with an observed HSC (i.e. belong to an HSC-rooted clone) in the embryonic induction and 5-FU experiments, we computed the proportion of cells in non-HSC clusters that had a statistically significant allele which also appeared in a cell found in the HSC cluster for each sample. For the controls, we aggregated this proportion over the three controls as an average of the three proportions, weighted by the number of non-HSCs marked with statistically significant alleles in each control. We similarly computed an aggregated proportion over the two 5-FU mice. We performed a two-proportion z-test for the alternative hypothesis that the proportion is larger in development/adult hematopoiesis than in the control, rejecting at significance level α = 0.05.
Comparing Number of Clones in Development and Adult Hematopoiesis
To determine if there were significantly fewer statistically significant clones in a 5-FU treated mouse, relative to a negative control, we first selected cells belonging to statistically significant clones. Let M′ be the minimum of the number of selected cells across the two treatments. We sampled M′ cells with replacement from each pool of selected cells, and counted the number of observed alleles. We repeated this procedure 10,000 times to get a distribution of the number of observed alleles in the two treatments. We performed a t-test for the alternative hypothesis that the mean of the number of observed alleles is less in the 5-FU treated sample at a significance level of α = 0.05. We conducted this test pairwise between each 5-FU treated and control mouse (see Supplementary Table 5).
Comparing Clone Size Distributions in Development and Adult Hematopoiesis
To determine if the average HSC-rooted clone size is significantly larger in a 5-FU treated mouse, relative to a negative control mouse, we selected cells marked by statistically significant alleles that also appear in at least one cell belonging to the HSC cluster. Let M′ be the number of selected cells in a given treatment. We sample M′ cells with replacement, and divide M′ by the number of alleles encountered in the sample, to compute the average HSC-rooted clone size. We repeat this procedure 10,000 times for each treatment, and perform a t-test for the alternative hypothesis that the average HSC-rooted clone size in the 5-FU treated mouse is larger at a significance level of α = 0.05. We conducted this test pairwise between each 5-FU treated and control mouse (see Supplementary Table 5).
To determine if the distribution of HSC-rooted clone sizes was significantly non-uniform, we selected cells marked by statistically significant alleles that also appear in at least one cell belonging to the HSC cluster. Suppose M′ cells are selected in a particular sample in this fashion, yielding N ≤ M′ alleles. Let Lj ∈ {1 … N}, 1 ≤ j ≤ M′, be the allele label of cell j. We sample M′ cells with replacement from this selected set of cells, and construct a CDF over the occurrence frequency of sampled allele labels . We also sample allele labels M′ times from a discrete uniform distribution with bins, and again construct a CDF over the occurrence frequency of allele labels. We compute the p-value associated with the KS-statistic derived from comparing these two CDFs. We repeat this procedure 10,000 times, and report the 99th percentile for the p-value distribution (see Supplementary Table 5).
Statistical Significance of Bone/Fate Bias
To quantify whether an allele i displays significant fate bias, we consider the deviation of the observed number of cells marked with allele i, , across B possible bins (representing bones or phenotypes), against a multinomial null distribution given by . For the embryonic induction dataset, we tested fate bias over different bones (B = 4). We also tested for bias over phenotypes, annotated from the Louvain clusters as defined in Figure 5B (B = 5; the lymphoid cluster which only had a few dozen cells was omitted), for each bone separately and pooling across bones.
The bin probabilities are the maximum likelihood estimators found by normalizing frequency counts after pooling all edited alleles, so that . The fate bias p-value that is reported is the probability under the null model of the range (the difference between the largest and smallest frequency across the bins for each allele) being greater or equal to the range observed. We compute this probability exactly according to the method described in (Corrado 2011). We note that while this method does not require that all bins have equal probability, using this measure to test bias is prone to false negatives when there is a large skew in bin probabilities, since the range does not take into account whether the maximum frequency occurred at a bin with low probability; in our data, all the bins (whether they are bones or coarse-grained phenotypes), have roughly the same probability. We only report fate bias p-values for statistically significant alleles (as defined in Statistically Significant Clones for SC Analysis) and reject at significance level α = 0.05 (Bonferroni-corrected on the number of statistically significant alleles).
Equivalence Testing for SC Amplicon Protocol Reproducibility
To quantify the reproducibility of our single-cell CARLIN amplicon protocol, we prepared libraries in duplicate starting from the same single-cell transcriptome library for the samples in the 5-FU experiment. We performed equivalence testing on the frequency distribution of alleles (edited and unedited) called by the CARLIN pipeline, when applied independently on these replicates (Supplementary Figure 6A). We used the KS-statistic at a test value of 0.05 to determine whether two replicates are equivalent. We performed 10,000 bootstrapping trials, and computed the KS-statistic for each trial, to obtain a distribution over all trials. For all samples, the one-sided (1-α) confidence interval excluded the test value of 0.05, so replicates are said to be equivalent at significance level α = 0.05. The results presented in the main text and Figure 6, were generated by pooling the sequencing data from the replicates, and running the CARLIN pipeline on the combined data.
Lineage Reconstruction
We pool together all cells/transcripts across all libraries/tissues, so that the reconstruction is agnostic to the origin of the alleles in the data. We use the specific details of mutations called in the alleles (see Mutation Calling) to establish a hierarchy across the alleles and thereby obtain a simplified phylogeny tree.
Filtering Alleles
For the in vivo data, we discarded alleles whose pfrequency did not satisfy an FDR threshold of 0.05 under the Benjamini-Hochberg procedure. The number of observations, M, used in computing pfrequency, was the total number of edited transcripts after pooling the data. We used pfrequency as opposed to pclonal because even if we are not confident that all cells that share a given allele came from the same progenitor, the relative expansion of one allele compared with another contains important information about clonal expansion across different tissues.
Tree Reconstruction Algorithm
Here, we describe a simple tree reconstruction algorithm used as a proof of concept for lineage tracing in the CARLIN system. Since a primary contribution of this paper is not in the domain of tree reconstruction, we defer investigation of how more sophisticated schemes like those newly developed in (Feng 2019) may improve the analysis.
For this algorithm, we make two assumptions, both of which are justified empirically by the data (see Figure 2D):
Both leaf and internal nodes of the tree can only be occupied by alleles observed in the sample. Since the efficiency of Cas9 is not 100%, we expect that every allele found after editing round T will also be present after editing round T + 1, because not every cell marked with a particular allele is further modified. The task of tree reconstruction is therefore simplified from inference of a novel set of mutations harbored by internal nodes, to identification of alleles which could likely be the internal nodes. In this scheme, we note that an allele must appear as a leaf node exactly once. Some leaf nodes may additionally appear once as an internal node with the same allele. In such cases, the internal node will always appear as a parent to the leaf node.
A child allele may only differ from its parent allele by either having additional mutations to those harbored by its parent, and/or possessing a subsuming deletion, whose endpoints are located at pristine target sites in the parent. The subsuming deletion would remove any history of parental mutations between deletion endpoints. This assumption therefore requires that there are no repair mechanisms, precluding the possibility of mutations that are observed in the parent at sites that are unmodified in the child.
Assumption (2) allows us to determine whether any pair of alleles fall along the same lineage, in which one allele could be an ancestor of the other. Given a list of n alleles (including the unmodified reference), we construct an n x n Boolean matrix A where Ai,j = 1 if allele j can be a descendent of allele i. We subsequently set to zero some of the non-zero entries using the following rules:
Frequency Criteria: We set Ai,j = 0 if the number of cells with allele j is larger than the number of cells with allele i. We impose this criteria, consistent with Assumption (1), because we expect the number of cells with the parent allele to exceed the number of cells with the child allele for two reasons: (i) the cutting efficiency is typically <<100% so that the parent allele remains substantially represented among cells and (ii) multiple distinct outcomes can result from additional modifications to a starting allele, so that a single child allele is unlikely to become more prevalent than the parent, its prevalence being diluted by its siblings.
Maximum Mutation Preservation: For each child allele that can potentially be descended from multiple parent alleles, only the candidate parent alleles that share the maximum number of mutations with the child allele are retained as the potential parents, and the other entries are set to zero. This entails that the number of mutations required to transform from parent to child allele is the minimum among possible parents, based on the reasoning that multiple editing events leading to a child allele are more unlikely than a single editing event. This criterion ensures that a given allele is most likely to be connected to its nearest ancestor so that matrix A can be interpreted as the set of parent-child relationships.
Alleles that have no parent allele after this pruning procedure are linked to the reference allele at the root of the tree.
A limitation of CARLIN is that alleles exhibiting large deletions could potentially be descended from almost any parent allele. In these cases, we have no choice but to connect the allele to the root of the tree as the lineage information in the allele is lost. However, such alleles are generally common in the bank and are therefore likely to be filtered out using our statistical significance tests (Figure 4B; Filtering Alleles).
Even after the pruning procedure, a given allele can still have multiple parent alleles. To construct a consensus tree from these potentially contradictory lineage relationships, we generate an ensemble of trees, by running simulations in which we probabilistically sample the parent edges of children with multiple candidate parents.
The tree is reconstructed recursively as follows: given a partially reconstructed tree and the current node, we randomly select one of the remaining unplaced alleles that is a child of the current node according to the A matrix. We attach the selected allele to the current node as its child. The added node then becomes the current node. When none of the remaining unplaced alleles is a valid child of the current node, we backtrack by setting the current node to be the parent node. We initialize the algorithm by starting with the reference allele as the current node (defined as the root of the tree). Lastly, we include a leaf node for each internal node.
Consensus Tree
To determine lineage relationships that are conserved across our simulated trees, we focused on nodes that occur closer to the root, reasoning that they are less variable across different reconstructions and carry more information because they have more cells associated with their alleles (due to the frequency criteria).
The depth of a given node is one less than the number of nodes on the path from the root to the node. Define a depth-X rooted path for a given internal node at depth-X, to be a sequence of alleles occurring on the path from the root of the tree (depth-0) to the internal node. We tabulate the number of times we observe a particular depth-X rooted path over the ensemble of trees. In addition, for each simulation in which the depth-X rooted path occurs, we tabulate the sum of the frequency of the alleles (referred to as the clade population) of all the leaves that descend from the terminating node of the path. Over the ensemble of trees, we obtain a distribution of clade populations for each depth-X rooted path.
We consider a depth-X rooted path to be stable if it appears in fraction f of the simulated trees. For the reconstructions presented in the paper, we used f = 1, and constructed a consensus tree by aggregating all stable depth-X rooted paths, for X ≤ 3. We chose f = 1 by rank-ordering the occurrence frequency of the rooted paths of a given depth across all simulated trees (Supplementary Figure 4C,D) and observing that (i) the top-ranked paths occurred across all simulations, (ii) the occurrence frequency decayed rapidly for paths that don’t appear in all simulations, and (iii) the clade populations associated with the paths that did not occur in all simulations were not substantial.
Given our choice of f = 1, the same consensus tree could have been reconstructed by simply removing child alleles that had multiple potential parents in the A matrix. In general, other choices of f permit reconstruction of trees with contradictory lineage information.
Since there is no contradictory lineage information for f = 1, the consensus tree can be visualized unambiguously. For aesthetic reasons, in Figure 2D and 4D we omitted display of depth-1 rooted paths whose terminal nodes are leaves with a minimum clade population across simulations less than 100.
Tissue Distance
We use the same tissue distance metric outlined in (Feng 2019). In short, for the consensus tree, we compute the distance between tissues i and j by first identifying all leaves corresponding to alleles found in tissue i. For each allele, we compute the distance to its closet ancestor which has a progeny allele that was found in tissue j (one less than the number of nodes along the path connecting the leaf to the internal node). Next, we average this distance over all alleles for tissue i. We weight each term in the average by the product of the number of cells found in tissue i marked by the leaf allele and the number of cells found in tissue j marked by progeny alleles of the closest ancestor. In Figure 4H we show the matrix obtained from this procedure after symmetrization.
Transcriptomic Analysis and Visualization
After discarding cells with few UMIs and high expression of mitochondrial genes (see Preprocessing), the resulting gene expression matrices were processed using Seurat (v3.1.2 with default parameters except where indicated) as follows (Stuart 2019). First, cell cycle scores were assigned to each cell using the CellCycleScoring function. Next, UMI counts were normalized according to a regularized negative binomial regression model while regressing out the effect of cell cycle and mitochondrial genes (using the SCTransform function with vars.to.regress = c(“percent.mt”, “S.Score”, “G2M.Score”)).
The 4 bones of the embryonic induction dataset were aligned (and similarly the 5-FU and control samples), by finding 2000 common features using the FindIntegrationAnchors function, and specifying these, together with marker genes (Supplementary Figure 5E,6D), as landmarks to the IntegrateData function (Supplementary Figure 5C,6B). Joint dimensionality reduction was performed on the aligned datasets using RunPCA. Points in this embedding were used to construct UMAP plots (RunUMAP), and find neighbors for clustering (FindNeighbors). For all relevant functions, 30 principal components were used.
FindClusters (algorithm=2, resolution=1.5) was used to run the Louvain clustering algorithm with multilevel refinement (Supplementary Figure 5D,6C). The dot plots in Supplementary Figures 5E and 6D were generated using data from Seurat’s DotPlot function. Differential gene expression was performed using the FindMarkers function, whose output when applied to our data is shown in Supplementary Table 6.
To test whether proliferation markers alone could be used to predict parent and childless HSCs, we assigned all cells in the HSC clusters a proliferation score (using AddModuleScore on the following gene list: Mki67, Pbk, Birc5, Ube2c, Top2a, Tk1, Aurkb, Cdkn3, Cenpf, Cdk1, Zwint). We designated HSCs in the upper (lower) quartile as highly (lowly) proliferating HSCs. We performed a two-proportion z-test for the alternative hypothesis that the proportion of highly proliferating HSCs is larger in the parent HSCs than in the childless HSCs, rejecting at significance level α = 0.05. We also performed a two-proportion z-test for the alternative hypothesis that the proportion of highly proliferating HSCs is larger among cells belonging to the parent HSC cluster group than among cells belonging to the childless HSC cluster group, rejecting at significance level α = 0.05.
Visualization of differentially expressed genes was handled using Seurat’s VlnPlot function for Figure 6G and Supplementary Figure 6I,J, and DoHeatmap function for Figure 6H.
Supplementary Material
Supplementary Figure 1: Additional quantification of editing in ES cells (related to Figures 1 and 2)
A. Fragment analysis results indicating cutting efficiency of individual sgRNAs.
B. Schematic of inducible CARLIN system, created with BioRender.
C. Chord plots of CARLIN alleles at 24h, 48h, and 72h (left to right) in the absence of doxycycline (Dox), as in Figure 1F.
D. Chord plots of CARLIN alleles at 12h, 24h, and 48h (left to right) after induction with 0.20 μg/mL (medium) of Dox, as in Figure 1F.
E. Chord plots of CARLIN alleles at 12h, 24h, and 48h (left to right) after induction with 1.00 μg/mL (high) of Dox, as in Figure 1F.
F. From left to right, fraction of cells edited, diversity index (see Methods), and average base pairs deleted in CARLIN alleles across edited cells, for chronic induction experiments shown in Figure 1G–H. Legend as in Figure 1G–H
G. Fraction of cells edited (top left), CARLIN potential (top right; see Methods), diversity metrics (middle row), average base pairs deleted in CARLIN alleles across edited cells (bottom left), and frequency distribution of mutation counts (bottom right) for the pulsed induction experiment shown in Figure 2A.
Supplementary Figure 2: Comparison of CARLIN analysis pipeline with NW alignment and fragment analysis (related to STAR Methods)
A. Frequency of indels, deletions and insertions called using the standard Needleman-Wunsch (NW) and the CARLIN algorithm, when applied to the CARLIN sequences of alleles in the bank. For the series labelled ‘Unmerged’ we refrained from merging mutations (Methods).
B. Frequency of indels, deletions and insertions called as a function of their location along different motifs on the CARLIN array. Repetitions of the same motif in target sites are overlaid. Relative to the NW algorithm, the CARLIN algorithm tends to cluster mutations more frequently at the expected cutsites. Shading as in Figure 1B.
C. CDF of the difference between the NW score of the optimal alignment produced by the NW algorithm and the optimal alignment produced by the CARLIN algorithm. About half the alleles in the bank have alignments that match the NW algorithm. The remainder would have been discarded as suboptimal by the NW algorithm.
D. Comparison of fragment lengths as measured by fragment analysis (Methods), and the frequency-weighted distribution of allele lengths called by the CARLIN pipeline applied to Next Generation Sequencing data. The data correspond to four timepoints from the three doxycycline concentrations used in the chronic induction experiment shown in Figure 1G–H.
Supplementary Figure 3: Mutations in different tissues, and additional details of the allele bank (related to Figure 3)
A. Site decomposition plot for the tissues shown in Figure 3B, under doxycycline (Dox) induction, as in Figure 3D, which shows results for granulocytes comprising the bank.
B. Blood, mesenchymal and epithelial cells were sorted from different tissues of two induced 8–12-week old CARLIN/Cas9 mice and the proportion of edited RNA transcripts was assessed by bulk RNA sequencing.
C. Distribution of observed allele frequencies for the bank. The top-ranked allele is the unedited reference.
D. (Top) Distribution of allele frequencies as in (C) and (bottom) the 50 most common edited alleles as in Figure 3C for a –Dox control obtained by harvesting ∼310K granulocytes from each of two uninduced mice.
E. (Top) Distribution of allele frequencies as in (C) and (bottom) all edited alleles as in Figure 3C for a –Cas9 control obtained by harvesting ∼125K granulocytes from a single mouse.
F. (Top) Distribution of allele frequencies as in (C), (middle) the 50 most common edited alleles as in Figure 3C, (bottom left) site decomposition plot as in Figure 3D, and (bottom right) histogram of mutation frequencies as in Figure 3E, obtained from harvesting granulocytes from two Dox-induced iCARLIN mice (Methods).
Supplementary Figure 4: Additional details of allele diversity and lineage tree reconstruction simulations (related to Figures 2, 3, 4)
A. 120K granulocytes were harvested from each of two doxycycline-induced mice as done for the preparation of the allele bank (see Figure 3A). To corroborate that the false positive rate predicted by our statistical framework bears out in an in vivo experiment, we compare how frequently CARLIN alleles appear across the biological replicates. We sample with replacement the number of edited cells indicated along the x-axis, with half the cells drawn from each mouse. (Top) The membership of the detected alleles across the mice. (Middle) pclonal (see Methods) for alleles shared between mice (red markers) is generally larger than for those found in a single mouse (blue markers). (Bottom) The fraction of alleles found in both mice satisfying pclonal < α, for a significance level α = 0.05. Errorbars are the standard deviation of this fraction derived from repeating the sampling procedure for 1000 trials.
B. (Top) Lower bound on the probability of observing an allele marking cells belonging to a unique progenitor (psingleton, see Methods) for different numbers of observed cells, in the case of equally likely alleles. As the number of cells observed increases, the chance of observing cells that coincidentally share the same allele increases. This effect is counteracted by increasing the number of alleles available (different colored traces). (Bottom) When multiple progenitors are marked with the same allele, the more uneven the proliferation rates (larger values of the parameter in the b proliferation model, see Methods), the less likely it is to observe the same allele shared across multiple cells that arise from different progenitors (see Methods for definition of γ(f)). However, as the number of observed cells increases (increasing f, see Methods), even progeny from slowly-proliferating progenitors that were redundantly marked are more likely to be observed, so that the fraction of alleles that ambiguously mark the ancestry of observed cells increases.
C. Number of instances (blue) of rooted paths (Methods) of depth 1–3 (left to right), found across 10,000 simulations for the in vitro tree reconstruction shown in Figure 2D. We deem a rooted path stable if it is found in all 10,000 simulations. In orange, we show the median clade population (across all simulations in which it appears) for each rooted path (Methods). Error bars (shaded) are min/max across the simulations.
D. Same as in (C) but for the in vivo tree reconstruction shown in Figure 4D.
Supplementary Figure 5: FACS plots and extended data for embryonic induction experiment (related to Figures 5 and 6)
A. FACS strategy used for sorting cells for encapsulation from bone marrow (BM) in the embryonic induction experiment (Figure 5) and control 5-FU experiment (Figure 6).
B. FACS strategy used for sorting cells for encapsulation from BM in the 5-FU experiment (Figure 6).
C. Overlay of transcriptome data from the 4 separate bones following batch correction.
D. Unsupervised Louvain clustering on the aligned transcriptomes from the 4 bones used in the embryonic induction experiment, generated 36 distinct clusters.
E. Dot plots of canonical blood cell-type specific markers used for fine-grain cell annotations of each Louvain cluster (HSC, hematopoietic stem cell; MPP, multipotent progenitor cell; MyP, myeloid progenitor; Neu, neutrophil; Mono, monocyte; DC, dendritic cell; Ba, basophil; Eos, eosinophil; Mk, megakaryocyte; Ery, erythrocyte; Ly, lymphoid cell). MyP, Neu, Mono, DC, Ba and Eos were further grouped to form the coarse-grained clusters shown in Figure 5B. Colors correspond to the average z-score of log-normalized expression values across cells in a cluster.
Supplementary Figure 6: Extended data for 5-FU experiment (related to Figure 6)
A. The libraries for the 5-FU experiment (Figure 6) were prepared in replicate to analyze reproducibility. Each point corresponds to the proportion of cells in each replicate in which a given allele is found. Points shown in blue correspond to alleles found in both replicates, while points shown in red correspond to alleles found in a single replicate. For visualization purposes, the point corresponding to the unedited reference allele has been omitted and jitter has been added to distinguish stacked points.
B. Overlay of transcriptome data from three control and two 5-FU treated animals following batch correction (Methods).
C. Unsupervised Louvain clustering after aligning the transcriptomes of the 5-FU and control samples generated 34 distinct clusters. The parent HSC cluster group was formed from clusters 0 and 2. The childless HSC cluster group was formed from clusters 17 and 19.
D. Dot plots of canonical blood cell-type specific markers used for cluster annotation in 5-FU and control mice, using the same two-tier scheme described in Supplementary Figure 5E.
E. Number of statistically significant clones in the second control and second 5-FU treated mouse after downsampling the control mouse to have the same number of cells marked by statistically significant alleles as the 5-FU treated mouse. Color scheme as in Figure 6C.
F. Statistically significant CARLIN alleles overlaid onto the transcriptome for the second control and 5-FU treated mouse, as in Figure 6D.
G. Violin plot showing the distribution of the number of cells in statistically significant HSC-rooted clones in the second control and second 5-FU treated mouse, as in Figure 6E.
H. Heatmap indicating occurrence frequency of statistically significant alleles across different cell types in the second control and 5-FU animals, where the number of clones has been downsampled in the control mouse to match the number of clones in the 5-FU animal.
I. Violin plots of selected genes differentially overexpressed in the HSC parent cluster group relative to the HSC childless cluster group, as in Figure 6G.
J. Violin plots of selected genes differentially underexpressed in the HSC parent cluster group relative to the HSC childless cluster group, as in Figure 6G.
Table S1: Primers and sequences for CARLIN construct design and detection (5’-3’; related to Methods)
Table S6: Differential gene expression (Related to Figure 6)
Highlights.
CARLIN is a stable, genetically-defined mouse line for CRISPR-based lineage tracing
Can be activated at any point to generate 44000 transcribed barcodes across tissues
Sequential, pulsed induction can be used to determine cellular phylogeny in vivo
Heterogeneity in HSC proliferation following myeloablation revealed
CARLIN is an approach that allows for simultaneous analysis of lineage and transcriptomic information of single cells in vivo
Acknowledgements
We thank members of the Camargo lab and Dr. Donna Neuberg for helpful discussions. We also thank Ronald Mathieu for help with FACS and flow cytometry. Schematics were created with BioRender. SB and FGO were funded by EMBO (ALTF 798-2018 and ALTF 655-2016, respectively). DS was funded in part by the Natural Sciences and Engineering Research Council of Canada (NSERC PGSD2-517131-2018). SHO acknowledges support from the NIDDK-supported Cooperative Centers of Excellence in Hematology (CCEH) at BCH (U54 DK110805). SH acknowledges support from NIH R00GM118910 and the Harvard University William F. Milton Fund. This study was supported by awards from the National Institute of Health (HL128850-01A1 and P01HL13147 to FDC). FDC is a Leukemia and Lymphoma Society and a Howard Hughes Medical Institute Scholar.
Footnotes
Declaration of Interests
The authors declare no competing interests.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alemany A, Florescu M, Baron CS, Peterson-Maduro J and Van Oudenaarden A (2018). Whole-organism clone tracing using single-cell sequencing. Nature 556, 108–112. [DOI] [PubMed] [Google Scholar]
- Aubrey BJ, Kelly GL, Kueh AJ, Brennan MS, O’Connor L, Milla L, Wilcox S, Tai L, Strasser A, and Herold MJ (2015). An inducible lentiviral guide RNA platform enables the identification of tumor-essential genes and tumor-promoting mutations in vivo. Cell Rep 10, 1422–1432 [DOI] [PubMed] [Google Scholar]
- Balakier H and Pedersen RA (1982). Allocation of cells to inner cell mass and trophectoderm lineages in preimplantation mouse embryos. Dev. Biol. 90, 352–362. [DOI] [PubMed] [Google Scholar]
- Beard C, Hochedlinger K, Plath K, Wutz A and Jaenisch R (2006). Efficient method to generate single-copy transgenic mice by site-specific integration in embryonic stem cells. Genesis 44, 23–28. [DOI] [PubMed] [Google Scholar]
- Buchholz F, Angrand PO, and Stewart AF (1998). Improved properties of FLP recombinase evolved by cycling mutagenesis. Nat Biotechnol 16, 657–662. [DOI] [PubMed] [Google Scholar]
- Bunge John, Willis Amy, and Walsh Fiona. (2014). Estimating the number of species in microbial diversity studies. Annual Review of Statistics and Its Application 1: 427–445 [Google Scholar]
- Bunge John, Woodard Linda, Böhning Dankmar, Foster James A., Connolly Sean, and Allen Heather K. (2012). Estimating population diversity with CatchAll. Bioinformatics 28 (7): 1045–1047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Busch K, Klapproth K, Barile M, Flossdorf M, Holland-Letz T, Schlenner SM, Reth M, Höfer T and Rodewald HR (2015). Fundamental properties of unperturbed haematopoiesis from stem cells in vivo. Nature 518, 542–546. [DOI] [PubMed] [Google Scholar]
- Cermak T, Doyle EL, Christian M, Wang L, Zhang Y, Schmidt C, Baller JA, Somia NV, Bogdanove AJ, and Voytas DF (2011). Efficient design and assembly of custom TALEN and other TAL effector-based constructs for DNA targeting. Nucleic Acids Res 39, e82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan MM, Smith ZD, Grosswendt S, Kretzmer H, Norman TM, Adamson B, Jost M, Quinn JJ, Yang D, Jones MG, et al. (2019). Molecular recording of mammalian embryogenesis. Nature 570, 77–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chu VT, Weber T, Wefers B, Wurst W, Sander S, Rajewsky K, and Kuhn R (2015). Increasing the efficiency of homology-directed repair for CRISPR-Cas9-induced precise gene editing in mammalian cells. Nat Biotechnol 33, 543–548. [DOI] [PubMed] [Google Scholar]
- Colwell RK, Chao A, Gotelli NJ, Lin SY, Mao CX, Chazdon RL and Longino JT (2012). Models and estimators linking individual-based and sample-based rarefaction, extrapolation and comparison of assemblages. Journal of plant ecology 5 (1): 3–21. [Google Scholar]
- Corrado CJ (2011). The exact distribution of the maximum, minimum and the range of Multinomial/Dirichlet and Multivariate Hypergeometric frequencies. Statistics and computing 21 (3): 349–359. [Google Scholar]
- Dzierzak E and Bigas A (2018). Blood Development: Hematopoietic Stem Cell Dependence and Independence. Cell Stem Cell 22, 639–651. [DOI] [PubMed] [Google Scholar]
- Feng J, DeWitt WS III, McKenna A, Simon N, Willis A, Matsen IV and Frederick A, (2019). Estimation of cell lineage trees by maximum-likelihood phylogenetics. arXiv. doi:arXiV:1904.00117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forsberg EC, Passegué E, Prohaska SS, Wagers AJ, Koeva M, Stuart JM and Weissman IL (2010). Molecular signatures of quiescent, mobilized and leukemia-initiating hematopoietic stem cells. PLoS One 5, e8785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frieda KL, Linton JM, Hormoz S, Choi J, Chow KHK, Singer ZS, Budde MW, Elowitz MB and Cai L (2017). Synthetic recording and in situ readout of lineage information in single cells. Nature 541, 107–111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ganuza M, Hall T, Finkelstein D, Chabot A, Kang G and McKinney-Freeman S (2017). Lifelong haematopoiesis is established by hundreds of precursors throughout mammalian ontogeny. Nat. Cell Biol. 19, 1153–1163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao X, Xu C, Asada N and Frenette PS (2018). The hematopoietic stem cell niche: From embryo to adult. Development 145, dev139691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerrits A, Dykstra B, Kalmykowa OJ, Klauke K, Verovskaya E, Broekhuis MJC, de Haan G and Bystrykh LV (2010). Cellular barcoding tool for clonal analysis in the hematopoietic system. Blood 115, 2610–2618. [DOI] [PubMed] [Google Scholar]
- Harrison DE and Lerner CP (1991). Most primitive hematopoietic stem cells are stimulated to cycle rapidly after treatment with 5-fluorouracil. Blood 78, 1237–1240. [PubMed] [Google Scholar]
- Houlihan DD, Mabuchi Y, Morikawa S, Niibe K, Araki D, Suzuki S, Okano H, Matsuzaki Y (2012). Isolation of mouse mesenchymal stem cells on the basis of expression of Sca-1 and PDGFR-α. Nat Protoc 7, 2103–11 [DOI] [PubMed] [Google Scholar]
- Kalhor R, Kalhor K, Mejia L, Leeper K, Graveline A, Mali P and Church GM (2018). Developmental barcoding of whole mouse via homing CRISPR. Science (80-. ). 361, eaat9804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kretzschmar K and Watt FM (2012). Lineage tracing. Cell 148, 33–45. [DOI] [PubMed] [Google Scholar]
- Ledford JG, Kovarova M and Koller BH (2007). Impaired Host Defense in Mice Lacking ONZIN. J. Immunol. 178, 5132–5143. [DOI] [PubMed] [Google Scholar]
- Lu R, Neff NF, Quake SR and Weissman IL (2011). Tracking single hematopoietic stem cells in vivo using high-throughput sequencing in conjunction with viral genetic barcoding. Nat. Biotechnol. 29, 928–933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu R, Czechowicz A, Seita J, Jiang D and Weissman IL (2019). Clonal-level lineage commitment pathways of hematopoietic stem cells in vivo. Proc. Natl. Acad. Sci. 116, 1447–1456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mann M, Mehta A, de Boer CG, Kowalczyk MS, Lee K, Haldeman P, Rogel N, Knecht AR, Farouq D, Regev A, et al. (2018). Heterogeneous Responses of Hematopoietic Stem Cells to Inflammatory Stimuli Are Altered with Age. Cell Rep. 25, 2992–3005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKenna A, Findlay GM, Gagnon JA, Horwitz MS, Schier AF and Shendure J (2016). Whole-organism lineage tracing by combinatorial and cumulative genome editing. Science (80-. ). 353, aaf7907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orlitsky Alon, Suresh Ananda Theertha, and Yihong Wu. (2016). Optimal prediction of the number of unseen species. Proceedings of the National Academy of Sciences 113 (47): 13283–13288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pei W, Feyerabend TB, Rössler J, Wang X, Postrach D, Busch K, Rode I, Klapproth K, Dietlein N, Quedenau C, et al. (2017). Polylox barcoding reveals haematopoietic stem cell fates realized in vivo. Nature 548, 456–460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pina C, May G, Soneji S, Hong D and Enver T (2008). MLLT3 Regulates Early Human Erythroid and Megakaryocytic Cell Fate. Cell Stem Cell 2, 264–273. [DOI] [PubMed] [Google Scholar]
- Raj B, Wagner DE, McKenna A, Pandey S, Klein AM, Shendure J, Gagnon JA and Schier AF (2018). Simultaneous single-cell profiling of lineages and cell types in the vertebrate brain. Nat. Biotechnol. 36, 442–450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rice Peter, Longden Ian, and Bleasby Alan. (2000). EMBOSS: The European Molecular Biology Open Software Suite. Trends Genet. 16: 276–277. [DOI] [PubMed] [Google Scholar]
- Rodriguez-Fraticelli AE, Wolock SL, Weinreb CS, Panero R, Patel SH, Jankovic M, Sun J, Calogero RA, Klein AM and Camargo FD (2018). Clonal analysis of lineage fate in native haematopoiesis. Nature 553, 212–216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rogulski K, Li Y, Rothermund K, Pu L, Watkins S, Yi F and Prochownik EV (2005). Onzin, a c-Myc-repressed target, promotes survival and transformation by modulating the Akt-Mdm2-p53 pathway. Oncogene 24, 7524–7541. [DOI] [PubMed] [Google Scholar]
- Schepers K, Swart E, van Heijst JWJ, Gerlach C, Castrucci M, Sie D, Heimerikx M, Velds A, Kerkhoven RM, Arens R, et al. (2008). Dissecting T cell lineage relationships by cellular barcoding. J. Exp. Med. 205, 2309–2318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith Tom Sean, Heger Andreas, and Sudbery Ian. (2017). UMI-tools: Modelling sequencing errors in Unique Molecular Identifiers to improve quantification accuracy. Genome research gr-209601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snippert HJ, van der Flier LG, Sato T, van Es JH, van den Born M, Kroon-Veenboer C, Barker N, Klein AM, van Rheenen J, Simons BD, et al. (2010). Intestinal crypt homeostasis results from neutral competition between symmetrically dividing Lgr5 stem cells. Cell 143, 134–144. [DOI] [PubMed] [Google Scholar]
- Spanjaard B, Hu B, Mitic N, Olivares-Chauvet P, Janjuha S, Ninov N and Junker JP (2018). Simultaneous lineage tracing and cell-type identification using CrIsPr-Cas9-induced genetic scars. Nat. Biotechnol. 36, 469–473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stuart T, Butler A, Hoffman P, Hafemeister C, Papalexi E, Mauck III WM, Hao Y, Stoeckius M, Smibert P and Satija R (2019). Comprehensive integration of single-cell data. Cell 177 (7): 1888–1902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun J, Ramos A, Chapman B, Johnnidis JB, Le L, Ho YJ, Klein A, Hofmann O and Camargo FD (2014). Clonal dynamics of native haematopoiesis. Nature 514, 322–327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Traykova-Brauch M, Schönig K, Greiner O, Miloud T, Jauch A, Bode M, Felsher DW, Glick AB, Kwiatkowski DJ, Bujard H, et al. (2008). An efficient and versatile system for acute and chronic modulation of renal tubular function in transgenic mice. Nat. Med. 14, 979–984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson A, Laurenti E, Oser G, van der Wath RC, Blanco-Bose W, Jaworski M, Offner S, Dunant CF, Eshkind L, Bockamp E, et al. (2008). Hematopoietic Stem Cells Reversibly Switch from Dormancy to Self-Renewal during Homeostasis and Repair. Cell 135, 1118–1129. [DOI] [PubMed] [Google Scholar]
- Wilson NK, Kent DG, Buettner F, Shehata M, Macaulay IC, Calero-Nieto FJ, Sánchez Castillo M, Oedekoven CA, Diamanti E, Schulte R, et al. (2015). Combined Single-Cell Functional and Gene Expression Analysis Resolves Heterogeneity within Stem Cell Populations. Cell Stem Cell 16, 712–724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright DE, Wagers AJ, Pathak Gulati A, Johnson FL and Weissman IL (2001). Physiological migration of hematopoietic stem and progenitor cells. Science (80-. ). 294, 1933–1936. [DOI] [PubMed] [Google Scholar]
- Zhang Jiajie, Kobert Kassian, Flouri Tomáš, and Stamatakis Alexandros. (2014). PEAR: a fast and accurate Illumina Paired-End reAd mergeR. Bioinformatics 30 (5): 614–620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zilionis R, Nainys J, Veres A, Savova V, Zemmour D, Klein AM, and Mazutis L (2017). Single-cell barcoding and sequencing using droplet microfluidics. Nat Protoc 12: 44–73. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Figure 1: Additional quantification of editing in ES cells (related to Figures 1 and 2)
A. Fragment analysis results indicating cutting efficiency of individual sgRNAs.
B. Schematic of inducible CARLIN system, created with BioRender.
C. Chord plots of CARLIN alleles at 24h, 48h, and 72h (left to right) in the absence of doxycycline (Dox), as in Figure 1F.
D. Chord plots of CARLIN alleles at 12h, 24h, and 48h (left to right) after induction with 0.20 μg/mL (medium) of Dox, as in Figure 1F.
E. Chord plots of CARLIN alleles at 12h, 24h, and 48h (left to right) after induction with 1.00 μg/mL (high) of Dox, as in Figure 1F.
F. From left to right, fraction of cells edited, diversity index (see Methods), and average base pairs deleted in CARLIN alleles across edited cells, for chronic induction experiments shown in Figure 1G–H. Legend as in Figure 1G–H
G. Fraction of cells edited (top left), CARLIN potential (top right; see Methods), diversity metrics (middle row), average base pairs deleted in CARLIN alleles across edited cells (bottom left), and frequency distribution of mutation counts (bottom right) for the pulsed induction experiment shown in Figure 2A.
Supplementary Figure 2: Comparison of CARLIN analysis pipeline with NW alignment and fragment analysis (related to STAR Methods)
A. Frequency of indels, deletions and insertions called using the standard Needleman-Wunsch (NW) and the CARLIN algorithm, when applied to the CARLIN sequences of alleles in the bank. For the series labelled ‘Unmerged’ we refrained from merging mutations (Methods).
B. Frequency of indels, deletions and insertions called as a function of their location along different motifs on the CARLIN array. Repetitions of the same motif in target sites are overlaid. Relative to the NW algorithm, the CARLIN algorithm tends to cluster mutations more frequently at the expected cutsites. Shading as in Figure 1B.
C. CDF of the difference between the NW score of the optimal alignment produced by the NW algorithm and the optimal alignment produced by the CARLIN algorithm. About half the alleles in the bank have alignments that match the NW algorithm. The remainder would have been discarded as suboptimal by the NW algorithm.
D. Comparison of fragment lengths as measured by fragment analysis (Methods), and the frequency-weighted distribution of allele lengths called by the CARLIN pipeline applied to Next Generation Sequencing data. The data correspond to four timepoints from the three doxycycline concentrations used in the chronic induction experiment shown in Figure 1G–H.
Supplementary Figure 3: Mutations in different tissues, and additional details of the allele bank (related to Figure 3)
A. Site decomposition plot for the tissues shown in Figure 3B, under doxycycline (Dox) induction, as in Figure 3D, which shows results for granulocytes comprising the bank.
B. Blood, mesenchymal and epithelial cells were sorted from different tissues of two induced 8–12-week old CARLIN/Cas9 mice and the proportion of edited RNA transcripts was assessed by bulk RNA sequencing.
C. Distribution of observed allele frequencies for the bank. The top-ranked allele is the unedited reference.
D. (Top) Distribution of allele frequencies as in (C) and (bottom) the 50 most common edited alleles as in Figure 3C for a –Dox control obtained by harvesting ∼310K granulocytes from each of two uninduced mice.
E. (Top) Distribution of allele frequencies as in (C) and (bottom) all edited alleles as in Figure 3C for a –Cas9 control obtained by harvesting ∼125K granulocytes from a single mouse.
F. (Top) Distribution of allele frequencies as in (C), (middle) the 50 most common edited alleles as in Figure 3C, (bottom left) site decomposition plot as in Figure 3D, and (bottom right) histogram of mutation frequencies as in Figure 3E, obtained from harvesting granulocytes from two Dox-induced iCARLIN mice (Methods).
Supplementary Figure 4: Additional details of allele diversity and lineage tree reconstruction simulations (related to Figures 2, 3, 4)
A. 120K granulocytes were harvested from each of two doxycycline-induced mice as done for the preparation of the allele bank (see Figure 3A). To corroborate that the false positive rate predicted by our statistical framework bears out in an in vivo experiment, we compare how frequently CARLIN alleles appear across the biological replicates. We sample with replacement the number of edited cells indicated along the x-axis, with half the cells drawn from each mouse. (Top) The membership of the detected alleles across the mice. (Middle) pclonal (see Methods) for alleles shared between mice (red markers) is generally larger than for those found in a single mouse (blue markers). (Bottom) The fraction of alleles found in both mice satisfying pclonal < α, for a significance level α = 0.05. Errorbars are the standard deviation of this fraction derived from repeating the sampling procedure for 1000 trials.
B. (Top) Lower bound on the probability of observing an allele marking cells belonging to a unique progenitor (psingleton, see Methods) for different numbers of observed cells, in the case of equally likely alleles. As the number of cells observed increases, the chance of observing cells that coincidentally share the same allele increases. This effect is counteracted by increasing the number of alleles available (different colored traces). (Bottom) When multiple progenitors are marked with the same allele, the more uneven the proliferation rates (larger values of the parameter in the b proliferation model, see Methods), the less likely it is to observe the same allele shared across multiple cells that arise from different progenitors (see Methods for definition of γ(f)). However, as the number of observed cells increases (increasing f, see Methods), even progeny from slowly-proliferating progenitors that were redundantly marked are more likely to be observed, so that the fraction of alleles that ambiguously mark the ancestry of observed cells increases.
C. Number of instances (blue) of rooted paths (Methods) of depth 1–3 (left to right), found across 10,000 simulations for the in vitro tree reconstruction shown in Figure 2D. We deem a rooted path stable if it is found in all 10,000 simulations. In orange, we show the median clade population (across all simulations in which it appears) for each rooted path (Methods). Error bars (shaded) are min/max across the simulations.
D. Same as in (C) but for the in vivo tree reconstruction shown in Figure 4D.
Supplementary Figure 5: FACS plots and extended data for embryonic induction experiment (related to Figures 5 and 6)
A. FACS strategy used for sorting cells for encapsulation from bone marrow (BM) in the embryonic induction experiment (Figure 5) and control 5-FU experiment (Figure 6).
B. FACS strategy used for sorting cells for encapsulation from BM in the 5-FU experiment (Figure 6).
C. Overlay of transcriptome data from the 4 separate bones following batch correction.
D. Unsupervised Louvain clustering on the aligned transcriptomes from the 4 bones used in the embryonic induction experiment, generated 36 distinct clusters.
E. Dot plots of canonical blood cell-type specific markers used for fine-grain cell annotations of each Louvain cluster (HSC, hematopoietic stem cell; MPP, multipotent progenitor cell; MyP, myeloid progenitor; Neu, neutrophil; Mono, monocyte; DC, dendritic cell; Ba, basophil; Eos, eosinophil; Mk, megakaryocyte; Ery, erythrocyte; Ly, lymphoid cell). MyP, Neu, Mono, DC, Ba and Eos were further grouped to form the coarse-grained clusters shown in Figure 5B. Colors correspond to the average z-score of log-normalized expression values across cells in a cluster.
Supplementary Figure 6: Extended data for 5-FU experiment (related to Figure 6)
A. The libraries for the 5-FU experiment (Figure 6) were prepared in replicate to analyze reproducibility. Each point corresponds to the proportion of cells in each replicate in which a given allele is found. Points shown in blue correspond to alleles found in both replicates, while points shown in red correspond to alleles found in a single replicate. For visualization purposes, the point corresponding to the unedited reference allele has been omitted and jitter has been added to distinguish stacked points.
B. Overlay of transcriptome data from three control and two 5-FU treated animals following batch correction (Methods).
C. Unsupervised Louvain clustering after aligning the transcriptomes of the 5-FU and control samples generated 34 distinct clusters. The parent HSC cluster group was formed from clusters 0 and 2. The childless HSC cluster group was formed from clusters 17 and 19.
D. Dot plots of canonical blood cell-type specific markers used for cluster annotation in 5-FU and control mice, using the same two-tier scheme described in Supplementary Figure 5E.
E. Number of statistically significant clones in the second control and second 5-FU treated mouse after downsampling the control mouse to have the same number of cells marked by statistically significant alleles as the 5-FU treated mouse. Color scheme as in Figure 6C.
F. Statistically significant CARLIN alleles overlaid onto the transcriptome for the second control and 5-FU treated mouse, as in Figure 6D.
G. Violin plot showing the distribution of the number of cells in statistically significant HSC-rooted clones in the second control and second 5-FU treated mouse, as in Figure 6E.
H. Heatmap indicating occurrence frequency of statistically significant alleles across different cell types in the second control and 5-FU animals, where the number of clones has been downsampled in the control mouse to match the number of clones in the 5-FU animal.
I. Violin plots of selected genes differentially overexpressed in the HSC parent cluster group relative to the HSC childless cluster group, as in Figure 6G.
J. Violin plots of selected genes differentially underexpressed in the HSC parent cluster group relative to the HSC childless cluster group, as in Figure 6G.
Table S1: Primers and sequences for CARLIN construct design and detection (5’-3’; related to Methods)
Table S6: Differential gene expression (Related to Figure 6)
Data Availability Statement
All sequencing data used in this paper is available on the NCBI GEO database (Accession Number GSE146972). The CARLIN software package, together with the allele bank, is available at https://gitlab.com/hormozlab/carlin. Instructions and code to reproduce all results, numerics and figures in the paper can be found at https://gitlab.com/hormozlab/cell_2020_carlin.