How Subgroup Analyses Can Miss the Trees for the Forest Plots: A Simulation Study

Abstract

Objective:

Subgroup analyses of clinical trial data can be an important tool for understanding when treatment effects differ across populations. That said, even effect estimates from pre-specified subgroups in well-conducted trials may not apply to corresponding subgroups in the source population. While this divergence may simply reflect statistical imprecision, there has been less discussion of systematic or structural sources of misleading subgroup estimates.

Study Design/Setting:

We use directed acyclic graphs to show how selection bias caused by associations between effect measure modifiers and trial selection, whether explicit (e.g. eligibility criteria) or implicit (e.g. self-selection based on race), can result in subgroup estimates that do not correspond to subgroup effects in the source population. To demonstrate this point, we provide a hypothetical example illustrating the sorts of erroneous conclusions that can result, as well as their potential consequences. We also provide a tool for readers to explore additional cases.

Conclusion:

Treating subgroups within a trial essentially as random samples of the corresponding subgroups in the wider population can be misleading, even when analyses are conducted rigorously and all findings are internally valid. Researchers should carefully examine associations between (and consider adjusting for) variables when attempting to identify heterogeneous treatment effects.

Background/Aims

A common sight in the published results of a randomized controlled trial is a forest plot showing the treatment effect in trial participants separately for two or more groups: for example, for men and women, or for those over and under the median age of participants, or for smokers and non-smokers. The expectation is that the treatment effect within each subgroup shows the effect in that type of participant, because randomization is maintained within subgroups.^{1, 2}

Unfortunately, these simple analyses can lead to inaccurate conclusions about the benefits to patients in the corresponding subgroups in the source population.^3–6 One subtle fact is that subgroup estimates can become misleading when trial participation depends on multiple factors, even when not all of these factors are associated with the outcome in the source population. This occurs whether factors are explicitly associated with participation (e.g. through eligibility criteria) or implicitly by virtue of self-selection (e.g. through lower participation of older patients or people of color).

Here, we use causal graphs to help explain this problem, and walk through an example of a potentially misleading subgroup analysis. We also provide a tool for researchers to construct and examine additional scenarios that may be relevant to their specific area of study and show that appropriately adjusted subgroup analyses can yield more informative results.

Methods

Theoretical Framework

Suppose we are planning a randomized controlled trial of a treatment X on an outcome Y (say, mortality). We are interested in examining whether the effect of X differs depending on the level of another categorical variable, V₁, in the source population: that is, not just in the sample in which our study is conducted, but in the population which gave rise to our study sample (sometimes known as the target population).⁷ For example, if V₁ is self-reported race, then our question is whether the effect of treatment is the same in each racial group. In this example, we assume that there is no effect of V₁ on Y, no common causes of V₁ and Y, and no effect measure modification of the treatment effect by V₁ in our target population; i.e., that the effect of X on Y on the scale of interest is the same at both levels of V₁. If the probability of participation for those with V₁ is equal to the probability of participation for those without V₁, each subgroup defined by V₁ will yield an unbiased estimate of the treatment effect in the corresponding portion of the source population in expectation.

However, when V₁ and another variable V₂ (say, severity of illness) are both associated with study participation a problem can arise. Consider the directed acyclic graphs in Figure 1.⁸ The arrows from V₁ and V₂ into participation on the left represent the fact that altering either of the variables changes the chances of trial participation. This might be the case if Black adults and adults with more severe illness were less likely to participate in the trial.⁹ Variable V₁ and V₂ also share no common causes-meaning that there are no other variables, measured or unmeasured, that cause both V₁ and V₂. Because of this, there is only one causal path from V₁ to Y in the source population in Figure 1A: the path from V₁ -> Participation <- V₂ -> Y. This path is blocked, however, because participation is a collider (so-called because the arrows from V₁ and V₂ “collide” at participation).¹⁰ As a result, we expect to see no association between V₁ and Y in the full population and V₁ should not modify the effect of X on Y.¹¹

Figure 1.

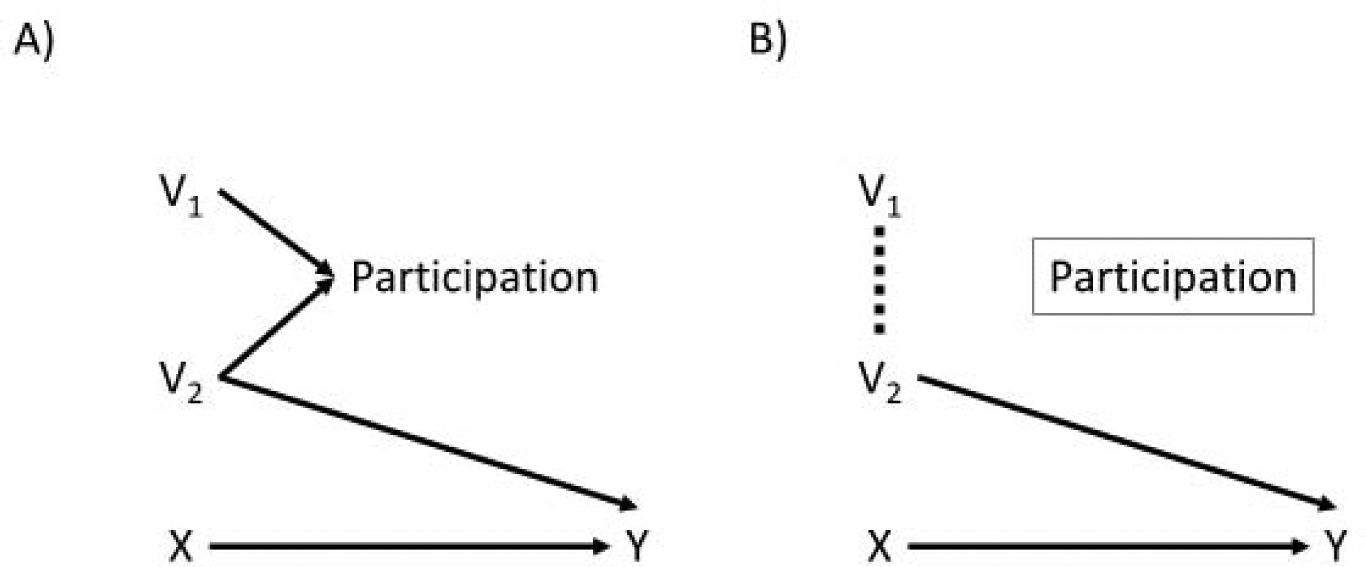
Two directed acyclic graphs. Panel A shows the causal relationships between V1, V2, X, participation, and Y in the source population; since there is no open path from V1 to Y in panel A, V1 will not modify the treatment effect of X on Y. Panel B shows the causal relationships between the same variables in the study population. Because we are conditioning on study participation, which depends on V1 and V2, there is now an open path from V1 to Y that can make V1 act as an effect modifier in the study population.

Of course, when we conduct a trial, the trial population naturally restricts to those who were recruited into the study - we cannot study people who were not recruited or did not participate. This leads to the situation shown in Figure 1B. Conditioning on the participation collider opens up an association between its parents, V₁ and V₂, in at least one stratum of participation. This means that we can expect V₁ to be associated (via V₂) with the outcome in the trial; if we look for variation of the effect of X on Y by levels of V₁ within the trial participants we might well find it and, indeed, will find it on at least one of the relative (i.e. risk ratio) and absolute (i.e. risk difference) scales.^{11, 12} We put numbers to an example scenario.

Hypothetical Example

Suppose researchers are conducting a placebo-controlled trial of a novel therapeutic agent, Fakeium (X), that may reduce the 5-year risk of all-cause mortality (Y) after myocardial infarction when added to standard treatment. To achieve power to address a safety concern that has been seen in other drugs in the class, they had to recruit 89,375 patients from a source population of 1,000,000. Knowing that minority populations and people of color are often underrepresented in clinical trials and unsure about whether they may benefit more or less from treatment,^{13, 14} they pre-specified subgroup analyses of those who identified as Black and those who did not (they anticipated being underpowered for any analyses in smaller ethnic groups).

One-quarter of patients in the source population are Black (V₁), half of the myocardial infarctions (MIs) in the source population are less severe and half were more severe (V₂), and race and MI severity are independent. Severity modifies treatment effect in that Fakeium is effective only in those with less severe MIs: these patients had a 30% chance of death in the placebo arm and a 25% chance of death in the Fakeium arm, while higher severity patients have a 40% chance of death regardless of treatment status. Race, however, does not modify treatment effect, and is not associated with the outcome. In the study, patients with severe myocardial infarctions had a 2% chance of being recruited if Black and a 10% chance of being recruited if non-Black. If the infarction was less severe, patients were more likely to participate regardless of race, with participation rates of 11% in non-Black and 8% in Black participants.

Table 1 shows the expected distributions of race and myocardial infarction severity in the source population and the trial population. While the odds for mild infarction are identical in Black and non-Black participants in the source population, they differ substantially in the trial because both race and MI severity have an effect on study sampling. This has direct consequences for the trial subgroup analyses. Table 2 presents the expected results of 1) an imaginary study and subgroup analyses conducted on the source population and 2) a study conducted in the trial population.

Table 1:

Expected distributions of race and myocardial infarction severity in the 1,000,000 patients in the source population and the 89,375 patients in the trial.

Population	Severe infarctions	Mild infarctions	Odds of mild infarction	Odds ratio of severe vs mild infarction
Source population
Non-Black race	375,000	375,000	1:1	Ref.
Black race	125,000	125,000	1:1	1.00
Trial population
Non-Black race	37,500	41,250	1:1.1	Ref.
Black race	2,500	10,000	1:4	3.63

Table 2:

Expected results of two randomized studies, one conducted in the source population if we did not have to recruit participants and one conducted in the trial population under our participation criteria above.

Analysis and treatment arm	Participants	Deaths	Risk of five-year mortality	Risk difference for five-year mortality (95% CI)
Source population
Placebo	500,000	175,000	35.00%	Ref.
Fakeium	500,000	160,000	32.00%	−3.00% (−3.18%, −2.82%)
Source population Black subgroup
Placebo	125,000	43,750	35.00%	Ref.
Fakeium	125,000	40,000	32.00%	−3.00% (−3.37%, −2.63%)
Source population non-Black subgroup
Placebo	375,000	131,250	35.00%	Ref.
Fakeium	375,000	120,000	32.00%	−3.00% (−3.21%, −2.79%)
Trial population
Placebo	45,625	15,687	34.38%	Ref.
Fakeium	45,625	14,150	31.01%	−3.37% (−3.98%, −2.76%)
Trial Black subgroup
Placebo	6,250	2000	32.00%	Ref.
Fakeium	6,250	1700	27.20%	−4.80% (−6.40%, −3.20%)
Trial non-Black subgroup
Placebo	39,375	13,687	34.76%	Ref.
Fakeium	39,375	12,450	31.62%	−3.14% (−3.80%, −2.48%)

Two conclusions might be drawn from the trial results. First, that Fakeium protects against mortality in the overall trial population (number needed to treat, NNT, of 30). Second, that Fakeium has a substantially more potent protective effect in those that identify as Black than those that do not (NNT of 21 in those patients versus NNT of 32 in the remaining patients). The p-value for heterogeneity between the two groups is 0.06. With these results Fakeium might be used more often in Black patients than non-Black patients, especially if it is expensive or has a burdensome side effect profile.

Of course, as discussed above and shown in the full population data, Fakeium is equally effective in Blacks and non-Blacks in the source population (the p value for interaction there is 1.00); when we do not condition on trial participation, only myocardial infarction severity modifies the effect of Fakeium.

This finding is not the result of statistical noise or hunting for significant p values but instead the result of conditioning on a collider inflating the prevalence of lower severity myocardial infarctions among black trial participants. Even if we repeated the trial an infinite number of times, or tripled the trial enrollment, estimated benefits in Blacks would still be exaggerated in this analysis in the trial population; the problem arises from the causal structure of selection from the source population into the trial, not from random chance.

Generally, this type of non-random selection requires external data from the source population to recover unbiased effects in said source population.^{15, 16} Here, however, we can account for this non-random selection by performing a subgroup analysis that adjusts for both race (V₁) and MI severity (V₂) by fitting a multivariable identity-link linear regression with a term for treatment, a term for race, a term for MI severity, and an interaction term between race and treatment.

Because MI severity is now being held constant, the interaction between race and treatment will appear to be null (even though the lack of an interaction term between MI severity and treatment means the model is technically misspecified). If we instead fit a regression that includes a term for treatment, a term for MI severity, an interaction term between the two, and a term for race, we can see that the treatment effect varies across MI severity even if race is held constant. Including these predictors of the outcome in the model also has the advantage of helping reduce the impact of chance imbalances between study arms and between subgroups.¹⁷ By looking at the full constellation of variables that might impact treatment effect at once (the trees, collectively) instead of just looking at them one by one (the forest), it can become much clearer which variables are associated directly with better or worse treatment effects in the trial.

Discussion

In our sample case, taking marginal subgroup analyses at face value was dangerous even when the analysis was pre-specified. Considering this finding through the lens of collider bias-a problem much discussed as a threat to internal validity^{10, 18}-helped clarify both why it occurred and how it might be resolved. This potential bias extends to many other scenarios where multiple variables are associated with trial participation, which we explored with the help of an Excel spreadsheet (eSupplement 1) that readers can use themselves as well. These associations can be implicit (via cultural or institutional norms related to trial participation) or explicit (via inclusion and exclusion criteria).

This work is not meant to discourage researchers from conducting subgroup analyses or attempting to identify heterogeneity of treatment effect across different groups; identifying and understanding interaction, particularly additive-scale interaction, is vital for public health.^{7, 19} Rather, it seeks to encourage researchers to move beyond simple stratification and to think deeply about the relationships between various subgroups, trial participation, and the outcome. They can then conduct adjusted subgroup analyses that inform later research using statistical methods (like outcome modeling or weighting) to generalize or transport treatment effects to other target populations.^{20, 21}

From experimentation with the spreadsheet, the magnitude of the V₁-V₂ association that is created by conditioning on participation varies heavily depending on the strength of the individual V₁ and V₂ causal effects on participation, as well as whether they interact with one another with respect to participation. In fact, if their effects on participation are perfectly multiplicative and V₁ and V₂ are independent, no V₁-V₂ association is present within the trial sample (though one is created in the unsampled individuals). For the most part, this type of exact mathematical cancellation (called unfaithfulness in the world of causal diagrams) is not likely to occur naturally.^{22, 23}

If there are multiple explicit inclusion criteria that can overlap, such as requiring at least one of hypertension and diabetes after myocardial infarction in cardiovascular trials, the bias is present in the subgroups that do not possess one of the inclusion criteria (e.g. those without hypertension and those without diabetes). This occurs because hypertension only has a causal effect on participation in those without diabetes and diabetes only has a causal effect on participation in those without hypertension; the result is that the collider-generated association is only present in those strata. When the associations are due to implicit factors, as in our example, subgroups across levels of V₁ are all potentially misleading.

Notably, even if V₁ does modify the treatment effect (Figure 2), the subgroup effects in the trial can still become a biased estimate of the effects in the source population. Additionally, any subgroup analyses for V₂ will now differ as well. The collider-induced association could push the difference between groups either further from or closer to the null, depending on the direction of the modification and the specific relationships between the variables and participation. Changes in subgroup composition and participation across attempts to replicate the subgroup results could result in failure to reject null hypotheses of homogeneity, even when real effect measure modification does exist.

Figure 2.

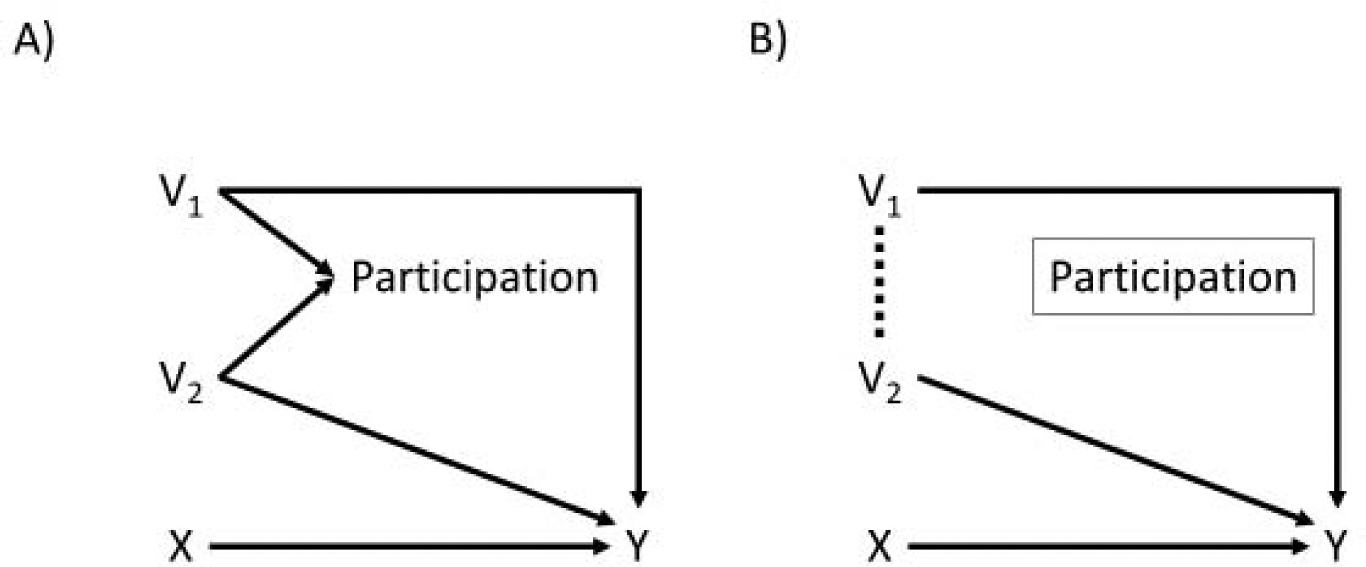
Directed acyclic graphs for when both V1 and V2 directly modify the treatment effect of X on Y. Panel A is the directed acyclic graph for the full population, while Panel B is the directed acyclic graph for the trial population. Both variables now have arrows indicating a causal effect on Y, and as a result both V1 and V2 are expected to have a different association with Y before and after conditioning on study participation.

We used a hypothetical example because that was the only way to know and tweak the input parameters; that said, we think this problem may occur frequently. With respect to explicit associations with participation, trials (especially cardiovascular trials like AFCAPS¹ or the trials of direct-acting oral anticoagulants in atrial fibrillation^24–26) often only enroll patients with a high enough risk based on some risk score, and then stratify by the components of the risk score in subsequent subgroup analyses. While it is more difficult to assess the prevalence of the implicit associations with participation, demographic factors such as sex, race, and age (which have historically been associated with trial participation)²⁷ may impact participation differently in those with and without various chronic conditions. In either case, these risk factors or variables associated with the outcome will act as effect measure modifiers on the additive (i.e. risk difference) or relative (i.e. risk ratio) scale, if not both.¹² The final result is misleading subgroup effects across the demographic factors, the chronic conditions, or (most likely) both.

There are several important limitations to this work. The extent of this problem can vary substantially depending on the underlying causal relationships between variables. The degree to which the results are misleading largely depends on whether and by how much V₂ modifies the treatment effect of interest-if it only modifies the risk difference, the subgroup risk ratios can be unbiased, and vice versa (and unfortunately, whether a variable modifies the risk difference, risk ratio, or both cannot be derived from a directed acyclic graph).²⁸ Another limitation is that we only explored binary variables; while these findings likely generalize to multilevel categorical or continuous variables, their magnitude and severity may differ. Our spreadsheet worked with relatively few potential effect modifiers, examining at most three modifiers simultaneously (V₁, V₂, V₃). That said, with a larger covariate space, this phenomenon becomes more and more likely to occur.

Additionally, chance imbalances between treatment arms or between subgroups are not captured in these types of diagrams and can also result in biased estimates, particularly in smaller studies.¹⁷ Finally and perhaps most importantly, we merely demonstrated the existence of this potential problem; further work to understand its plausibility and impact in different types of trials using real data and more complex simulations is necessary to understand its impact.

Two final notes: first, this is not an internal validity problem. The estimates within each subgroup are valid estimates of treatment effect for that subgroup of trial participants. There is no graphical basis for adjustment for V₁ and V₂ when estimating these internal effects. But if subgroup analyses are being performed to help understand differences in treatment effects in larger (target) populations, they can easily mislead investigators, potentially with significant clinical consequences.⁷ Second, while we presented this through the lens of randomized trials because of their analytic simplicity, the same types of causal relationships can cause problems for observational data that undergoes an analogous selection process (e.g. prospective enrollment or restricting to those with specific insurance plans) if researchers simply split the study population after adjusting for confounding.

Conclusion

It is critical to identify heterogeneity in the effects of treatments in the source population of a study and not just in the study population. Subgroup analyses appear to be a simple method of doing so, but associations between subgroup strata and trial participation can lead to biased and potentially dangerous conclusions about treatment effects in subgroups in the source population. Moving beyond crude subgroup analyses is a crucial step towards the end goal of estimating treatment effects in routine clinical care; glances at forest plots are poor substitutes for in-depth and considered examinations of the trees.

What is new?

Subgroup results can be misleading for reasons based on the factors underlying trial participation.

These results can result in incorrect beliefs about the efficacy of treatments in clinical populations.

Examining multiple potential modifiers of treatment effect at once, rather than conducting multiple crude subgroup analyses, can yield useful information about how and why variables are associated with subgroup differences in treatment effects.