Map making: Constructing, combining, and inferring on abstract cognitive maps

SUMMARY

Cognitive maps enable model-based inferences from limited experience that can guide novel decisions. We tested whether the hippocampus (HC), entorhinal cortex (EC), and ventromedial prefrontal cortex (vmPFC)/medial orbitofrontal cortex (mOFC) organize abstract and discrete relational information into a cognitive map to guide novel inferences. Subjects learned the status of people in two unseen 2-D social hierarchies, with each dimension learned on a separate day. Although one dimension was behaviorally relevant, multivariate activity patterns in HC, EC and vmPFC/mOFC were linearly related to the Euclidean distance between people in the mentally reconstructed 2-D space. Hubs created unique comparisons between the hierarchies, enabling inferences between novel pairs. We found that both behavior and neural activity in EC and vmPFC/mOFC reflected the Euclidean distance to the retrieved hub, which was reinstated in HC. These findings reveal how abstract and discrete relational structures are represented, combined, and enable novel inferences in the human brain.

eTOC Blurb

Park et al. show that the human brain constructs a multidimensional cognitive map from piecemeal observations of the outcomes of individual decisions. The cognitive map constructed in the hippocampal-entorhinal system and orbitofrontal cortex represents abstract relationships between discrete entities, enabling efficient inferences to guide new decisions.

INTRODUCTION

To form rich world models, sparse observations often sampled from separate experiences need to be integrated into a coherent representation. There has been a recent surge of interest in the long-standing theory that the hippocampus (HC) and entorhinal cortex (EC) may organize spatial and non-spatial relational information into such a ‘cognitive map’ for goal-directed behavior (Behrens et al., 2018; Bellmund et al., 2018; Cohen, 2015; Constantinescu et al., 2016; Eichenbaum and Cohen, 2014; Ekstrom and Ranganath, 2018; Hafting et al., 2005; Moser et al., 2008; O’Keefe and Nadel, 1978; Schiller et al., 2015; Schuck et al., 2016; Tolman, 1948; Wikenheiser and Schoenbaum, 2016). While past studies have identified neural signals in the HC and EC indicative of a cognitive map primarily using continuous task dimensions with online sensory feedback during task performance (e.g. visual, auditory, vestibular) (Aronov et al., 2017; Bao et al., 2019; Constantinescu et al., 2016; Doeller et al., 2010; Eichenbaum and Cohen, 2014; Hafting et al., 2005; Nau et al., 2018; O’Keefe and Nadel, 1978; Theves et al., 2019), many important everyday decisions involve discrete entities that vary along multiple abstract dimensions that are sampled piecemeal, one experience at a time, in the absence of continuous sensory feedback, such as with whom to collaborate or where to eat. Whether, and if so, how the brain constructs a cognitive map of abstract relationships between discrete entities from piecemeal experiences is unclear.

A powerful advantage of a cognitive map of an environment or task is the ability to make inferences from sparse observations that can dramatically accelerate learning and even guide novel decisions never faced before (Banino et al., 2018; Behrens et al., 2018; Jones et al., 2012; Stachenfeld et al., 2017; Tolman, 1948; Vikbladh et al., 2019), a hallmark of behavioral flexibility and a key challenge in artificial intelligence (Behrens et al., 2018; Kriete et al., 2013; Wang et al., 2018). This is in part because a cognitive map of a task space would in theory allows “shortcuts” and “novel routes” to be inferred, as in physical space. To provide a concrete example, understanding the structure of family trees allows one to infer new relationships, such as the following: because Sally is John’s sister and Sue is John’s daughter, Sue must be Sally’s niece without ever directly learning this relationship (Fig. 1A). Biologically inspired computational models show the map-like coding schemes found in the HC and EC can in principle enable agents to perform vector navigation, including planning new routes and finding shortcuts to a goal in physical space (Banino et al., 2018; Bush et al., 2015; Dordek et al., 2016; Whittington et al., 2019). In particular, so-called place cells in HC and grid cells in medial EC contain neural codes that permit calculation of predicted position (Moser et al., 2008; O’Keefe and Nadel, 1978; Stachenfeld et al., 2017), direction (Banino et al., 2018; Chadwick et al., 2015), and Euclidean distance (Behrens et al., 2018; Bellmund et al., 2018; Howard et al., 2014) in physical space. Yet despite recent theoretical proposals (Whittington et al., 2019), empirical evidence concerning how neural representations of abstract cognitive maps relate to such direct novel inferences outside of physical space has been lacking.

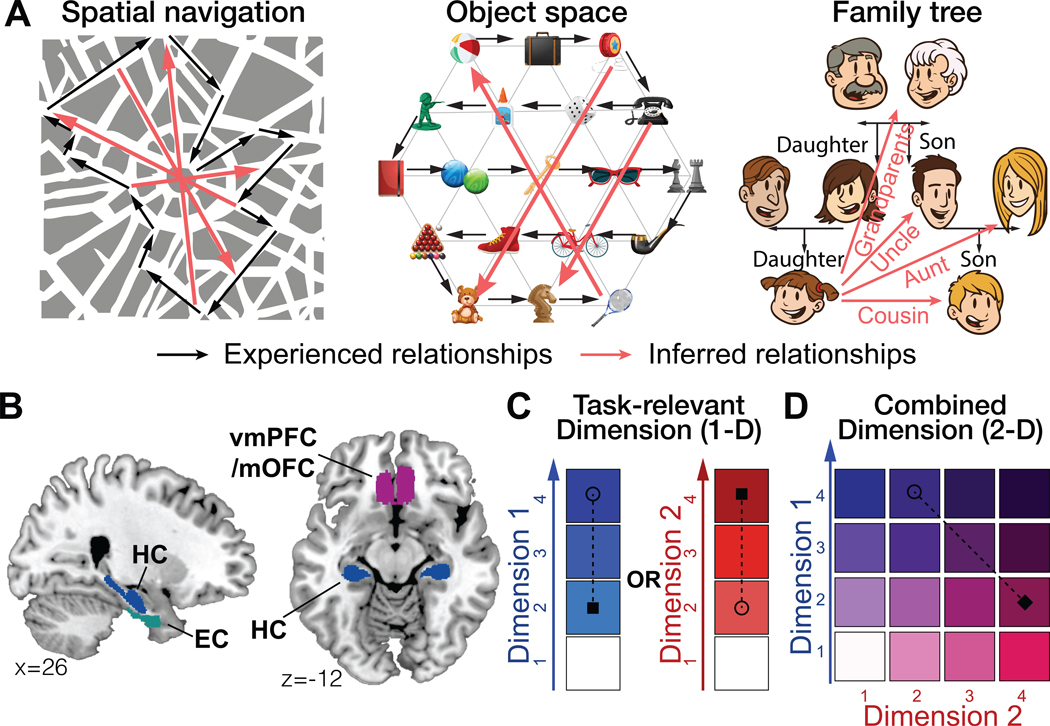
Figure 1.

A. Examples of “zero-shot inferences” in physical space, transitions between objects, and family trees. Representing abstract relationships as a cognitive map allows making novel direct inferences that do not only rely on previously experienced associations. Black: experienced relationships; Red: inferred relationships. B. Bilateral ROIs generated independently from probabilistic maps. C and D. Two hypotheses concerning how the brain could represent and flexibly switch between different dimensions that characterize the same entities to guide inferences. C. The brain could construct two separate maps for representing each 1-D hierarchy learned on a separate day and distinct regions could encode the one-dimensional (1-D) rank difference in the task-relevant dimension (D) and the task-irrelevant dimension (I). D. Alternatively, the brain could construct a unified map consisting of two dimensions and encode the inferred Euclidean distance (E) over the 2-D representation.

A parallel literature based on recent studies focusing on the orbitofrontal cortex (OFC) has motivated a related theory that the OFC represents one’s current position in a cognitive map, not of physical space, but of task space (Schuck et al., 2016; Takahashi et al., 2017; Walton et al., 2010; Wikenheiser and Schoenbaum, 2016; Wilson et al., 2014). Recent findings further suggest a specialized role for mOFC in representing the latent (or perceptually unsignaled) components of the task space that define one’s current state in the task (Muller et al., 2019; Schuck et al., 2016; Wilson et al., 2014). Recent studies have indeed discovered that the OFC represents latent task states during learning and choice in support of this theory (Chan et al., 2016; Schuck et al., 2016; Wikenheiser et al., 2017), yet to our knowledge there has been little direct evidence of map-like representations (e.g. position, direction, or distance) of the task space in OFC. Moreover, whether this proposed OFC function would extend to representing a cognitive map of an abstract social space, or whether it would instead transfer to areas implicated in social cognition is unclear.

In addition to representing cognitive maps, both the HC and OFC have been implicated in model-based inference, such that distinct stimuli, or stimuli and rewards, that were not directly associated can be associated or integrated through an overlapping, shared associate (Jones et al., 2012; Koster et al., 2018; Kurth-Nelson et al., 2016; Schlichting and Preston, 2014; Tompary and Davachi, 2017; Wimmer and Shohamy, 2012). Computational models have proposed how a related mechanism in the HC-EC system may additionally underlie transitive inferences about ordinal rank (Koster et al., 2018; Kumaran and McClelland, 2012) (though see (Frank et al., 2005)). In addition to demonstrations that the HC-EC system is necessary for transitive inferences (Dusek and Eichenbaum, 1997), studies in animal models have demonstrated that the OFC is necessary for model-based inferences based on previously learned associations, but not for decisions based on directly learned cached values (Jones et al., 2012). While these HC-EC and OFC roles for associating or integrating individual items have been documented, how the brain constructs broader cognitive maps and makes direct inferences beyond chaining or integrating previously experienced elementary associations has been elusive. In particular, it is possible that similar mechanisms of integration, and/or distinct mechanisms that leverage an explicit representation of the relational structure of the space or task (Whittington et al., 2019), would allow for the integration of distinct relational structures into a single larger cognitive map from sparse observations (e.g. the integration of family trees through marriage) that even respects metric relationships (e.g. vector directions and distances) and enables direct inferences that have never been experienced before (e.g. Sue is Sally’s niece; Fig. 1A).

Here, we asked participants to learn two 2-D social hierarchies from the outcomes of binary decisions about individuals’ rank on either of the two dimensions, with each dimension learned on a different day. During fMRI participants were asked to make novel inferences about the relative status of a novel pair across hierarchies in only one dimension at a time. This manipulation meant subjects were required to flexibly switch between currently relevant and irrelevant social dimensions that described the same entities for decisions. We tested two non-mutually exclusive hypotheses concerning how the human brain could represent and flexibly switch between different dimensions that characterize the same entities to guide direct inferences. Based on previous decision-making studies showing behaviorally-relevant decision value signals in vmPFC/mOFC, and pending or currently irrelevant value signals in separate prefrontal areas (Boorman et al., 2009, 2011; Nicolle et al., 2012; Park et al., 2017), one hypothesis predicts that neural activity in vmPFC/mOFC, and the HC-EC system (Fig. 1B), would depend on the current behaviorally relevant dimension alone, while other prefrontal areas may simultaneously reflect the currently irrelevant dimension (Fig. 1C). On the other hand, if relationships between people are projected into a unitary space defined by their respective values on two independent dimensions, then we would predict a single neural representation in vmPFC/mOFC and the HC-EC system such that behavioral and neural activity reflect the Euclidean distance over a 2-D space between entities, rather than the behaviorally relevant 1-D rank alone (Fig. 1D).

RESULTS

Participants learned relational maps of two 2-D social hierarchies and used hubs between them to make inferences between novel pairs of individuals

We asked participants to learn the status of unfamiliar people in two separate groups organized hierarchically on two orthogonal dimensions: competence and popularity (Fig. 2A). Importantly, participants never saw the 1- or 2-D hierarchies. Instead, they were able to learn the relative ranks of neighboring people who differed by only one level on one dimension at a time through a series of feedback-based dyadic comparisons and use transitive inferences to infer the remaining ranks (see (Kumaran et al., 2012)).

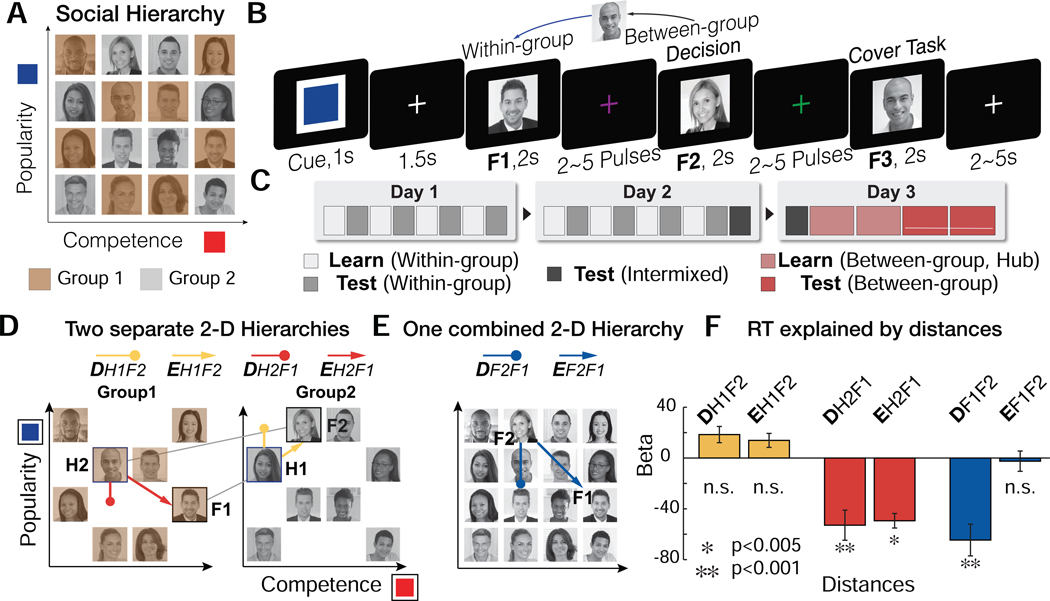
Figure 2.

A. Participants learned the rank of members of each of two groups (brown and gray) separately in two dimensions: competence and popularity. Subjects were never shown the 1- or 2-D structures. B. Illustration of a trial of the fMRI experiment. Participants made inferences about the relative status of a novel pair (F1 and F2) in a given dimension (signaled by the Cue color). A cover task (to indicate the gender of the face stimulus, F3) followed at the end of every trial. C. On day 1 and day 2, participants learned within-group ranks of the two groups in each of two dimensions through binary decisions about the status of members who differed by only one rank level in a given dimension. On day3, subjects learned from between-group comparisons limited to ‘hub’ individuals, which created a unique path between groups per person in each dimension. Subsequently, on day3, participants were asked to infer the unlearned between-group status while undergoing fMRI. D. Participants could use hubs to infer the relationship between novel pairs. Possible trajectories for example inferences can be shown for each trajectory: the behaviorally-relevant 1-D distance (D, Fig.1C) and the 2-D Euclidean distance (E, Fig.1D). Subjects could use either of two trajectories: a forward inference from F1 to its hub (H1) that has a unique connection to F2 (D_H1F2, E_H1F2; yellow); or a backward inference from F2 to its hub (H2) that has a unique connection to F1 (D_H2F1, E_H2F1; red). E. As alternative paths, subjects may not use the hubs, but instead compute the distance in the relevant dimension between F1 and F2 directly (D_F1F2), or their Euclidean distance (E_F1F2) in the combined cognitive map of two groups (blue). F. Multiple linear regression results show that both the rank distance (D_H2F1) and the Euclidean distance from H2 (E_H2F1), but not from H1, significantly explain variance in RTs, in addition to the direct distance between F1 and F2 (D_F1F2), while competing with other distance terms.

During the first two days of training (Fig. 2C), participants learned the relative status of two groups of 8 “entrepreneurs” separately, on only one dimension per day (Fig. S1A for Day 1 and Fig. S1B for Day 2 training). For the third day of training, fMRI participants learned from select hubs enabling between-group comparisons between people in each group for the first time (Fig. S1C). By limiting between-group comparisons only to hubs (Fig. S1D and S1E), we were able to create comparative paths connecting each of the individuals in different groups, which could be leveraged to perform inferences between novel pairs between groups.

We analyzed fMRI data acquired from 27 subjects who successfully learned the relative ranks of the two social hierarchies (> 85% performance criterion in both dimensions, tested on Day 2 training). In each fMRI trial, participants were asked to make a binary decision about who was higher rank in one or the other dimension between a first face (F1) and second face (F2) presented sequentially (Fig. 1F). These faces were selected from different groups and were not hubs in the relevant dimension (non-hubs; Fig. S1F), meaning they had not been previously compared. Successful inferences, therefore, could rely on building an internal representation of the social hierarchies and a relational memory of the relative positions of F1, F2, and the hub. We predicted that the inference is made along a trajectory connecting the two individuals via the (unseen) hub (Fig. 2D).

Participants were able to successfully infer the relative position of these novel pairs of individuals (mean accuracy ±s.e.m.=93.6±0.77%). Nonetheless, the shorter the distance between individuals, the more difficult the decision about relative positions in the hierarchy. To examine the effects of distance of potential trajectories on decision making, we regressed choice reaction times (RT) on different distance measures using a multiple linear regression model, thereby allowing them to compete to explain RT variance. We included the Euclidean distance from the hub (H2) to F1 (E_H2F1), the Euclidean distance from the other hub (H1) to F2 (E_H1F2), the relative rank in the task-relevant dimension, which is the 1-D distance between H2 and F1 (D_H2F1), the 1-D distance between H1 and F2 (D_H1F2), (Fig. 2D), as well as both 1-D and 2-D distances between F1 and F2 (D_F1F2 and E_F1F2, respectively), (Fig. 2E) to control for their possible covariation with hub-related distances. We found that the greater the 1-D and 2-D Euclidean distance between F1 and H2 (D_H2F1 and E_H2F1, respectively), the faster the RT ( D_H2F1±sem=−52.9±11.9, t₂₆=−4.5, p=4.5e-05; E_H2F1±sem=−49.4±5.7, t₂₆=−8.8; p=0.003), in addition to an effect of the 1-D distance between F1 and F2 (D_F1F2) ( D_F1F2±sem=−64.6±12.5, t₂₆=−5.3, p=0.0002), (Fig. 2F; see Fig S2C and S2D for confirmatory and control analyses). Our behavioral results show that participants preferentially recall H2 as the task-relevant hub to aid in the comparison between novel pairs of faces, with the Euclidean distance to H2 explaining variance over and above the 1-D distance alone.

Neural activity reflects the Euclidean distance to the retrieved hub during inferences

To examine whether neural activity during choices was likewise modulated by the distance of inference trajectories via the hub over in a 2-D space, first, we regressed BOLD activity at the time of the inference (F2) against the parametric regressors of Euclidean distance between the hub and the target face (E_H2F1 and E_H1F2) and their (cosine) vector angles (A_H2F1 and A_H1F2). We first tested for effects in a priori regions of interest (ROI) that combined multiple anatomically defined ROIs, including the bilateral HC, EC, and vmPFC/mOFC (Fig. 1B). We found neural correlates of the Euclidean distance of the decision trajectory via hub H2 (E_H2F1) in the vmPFC/mOFC (peak voxel [x,y,z]=[2,44,−10], t₂₆=4.71 for right vmPFC/mOFC; [x,y,z]=[−2,28,−4], t₂₆=4.28 for left vmPFC/mOFC), and bilateral EC (at the peak level, [x,y,z]=[24,−20,−26], t₂₆=3.81 for right EC; [x,y,z]=[−18,−10,−26], t₂₆=3.49 for left EC) corrected for multiple comparisons over the combined anatomical ROI using permutation-based Threshold-Free Cluster Enhancement (TFCE) (Smith and Nichols, 2009) (p_TFCE<0.05). We did not find significant effects in HC (p>0.005, uncorrected).

To examine effects outside of our a priori ROIs, we performed an exploratory whole-brain analysis. These analyses showed the right lateral OFC (lOFC, [x,y,z]=[30,34,−18], t₂₆=4.12,) also reflected the Euclidean distance to the context-relevant latent hub H2 (Fig. 3A). For exploratory analyses we apply whole-brain TFCE corrections at the threshold p_TFCE<0.05 (see Table S1 for a full list of brain areas surviving correction). No significant effects were found for the alternative metric terms including the vector angle A_H2F1, or for metrics associated with the alternative hub, H1 (E_H1F2 and A_H1F2) at these thresholds (Fig. 3A; Fig. S3). These analyses show that activity in vmPFC/mOFC, lOFC, and the EC, but not HC, reflects the Euclidean distance of the trajectory via Hub 2 (E_H2F1), but not Hub 1 (E_H1F2), consistent with choice behavior.

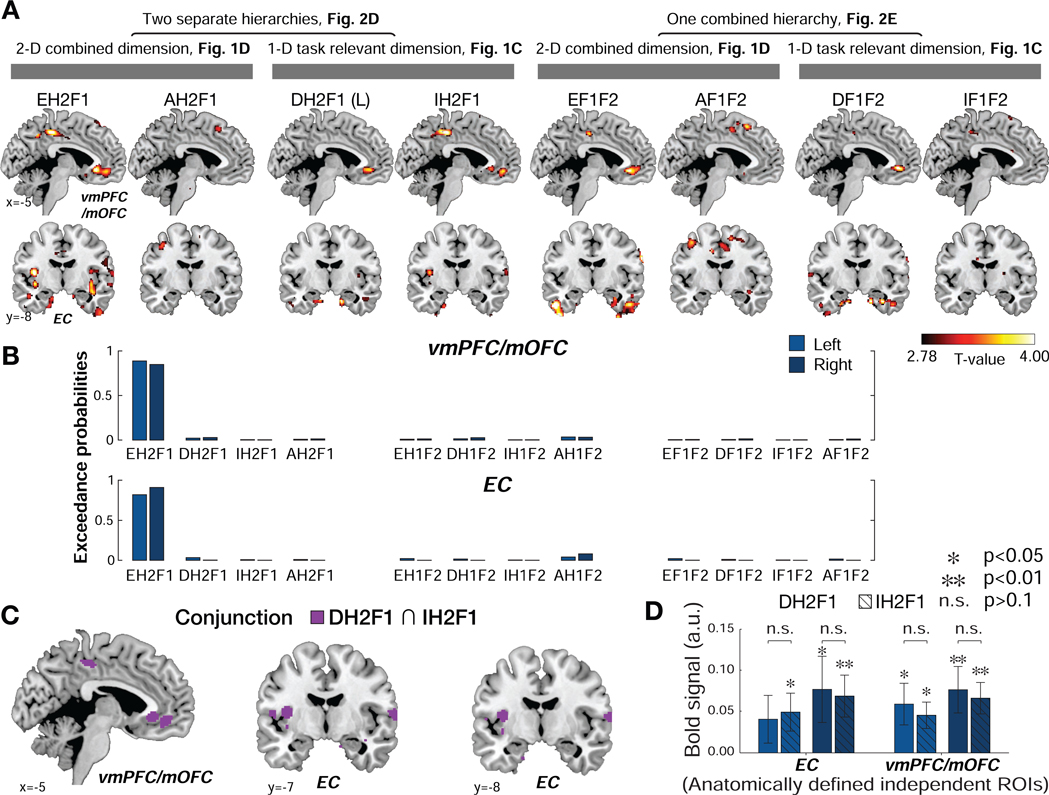
Figure 3.

A. The bilateral entorhinal cortex (EC) and ventromedial prefrontal cortex (vmPFC/mOFC), p_TFCE<0.05 corrected within a small volume ROI encode the Euclidean distance from the hub (H2) to F1 in the 2-D social space (E_H2F1). Whole-brain parametric analyses showing neural correlates of each of the distance metrics that could theoretically drive inferences between pairs at the time of decisions (F2 presentation). D: 1-D rank distance in the task-relevant dimension (D_H2F1 and D_F1F2); L: the shortest link distance between F1 and F2 (L equals to D_H2F1+1); I: the 1-D rank distance in the task-irrelevant dimension (I_H2F1 and I_F1F2); A: the cosine vector angle (A_H2F1 and A_F1F2). For visualization purposes, the whole-brain maps are thresholded at p<0.005 uncorrected. B. The results of Bayesian model selection (BMS). The exceedance probabilities revealed that the Euclidean distance from the hub (E_H2F1) best accounted for variance in both EC and vmPFC/mOFC activity compared to the other distance measures, providing evidence that these regions compute or reflect a Euclidean distance metric to a retrieved hub (H2) in abstract space in order to infer the relationship between F1 and F2. C. Conjunction analysis shown in purple revealed that both D_H2F1 and I_H2F1 are reflected in the vmPFC/mOFC and the EC bilaterally. D. The effect of D_H2F1 does not differ from I_H2F1 in the EC or vmPFC/mOFC, even at a lenient threshold (p>0.1), suggesting that these areas assign equal or similar weights to D_H2F1 and I_H2F1, consistent with activity reflecting E_H2F1, during decision-making.

Next, we investigated our competing hypothesis that the brain flexibly switches between behaviorally relevant and irrelevant dimensions with simultaneous coding of both dimensions, but in different brain regions. Specifically, we tested whether the current behaviorally relevant rank distance (D_H2F1) and the behaviorally irrelevant rank distance (I_H2F1) better explain neural activity in the same ROIs, or elsewhere in the brain (GLM2). This analysis revealed positive effects of both D_H2F1 and I_H2F1 in vmPFC/mOFC (Fig. 3A; Table S1) (D_H2F1: [x,y,z]=[−2,32,−6], t₂₆=5.25, and [x,y,z]=[4,30,−6], t₂₆=4.96, and I_H2F1: [x,y,z]=[6,36,−6], t₂₆=3.73, [x,y,z]=[−4,30,−4], t₂₆=3.48) (p_TFCE<0.05). We found similar effects in the EC (D_H2F1: [x,y,z]=[24,−20,−32], t₂₆=3.84 and I_H2F1: [x,y,z]=[22,−14,−42], t₂₆=3.46) at the uncorrected threshold of p<0.001, but they did not survive TFCE correction. Consistent with our analysis of E_H2F1, we did not find any effects of D_H2F1 and I_H2F1 in the HC even at a reduced threshold (p>0.005, uncorrected). To test whether any areas preferentially encoded task-relevant (D_H2F1) or irrelevant (I_H2F1) distances, we also directly contrasted these distance terms. Effects in the vmPFC/mOFC and EC were not significant when contrasting D_H2F1 over I_H2F1 and I_H2F1 over D_H2F1 (Fig. S2E). Importantly, we did not find evidence to support the hypothesis that the task-relevant distance (D_H2F1) was encoded in one set of brain regions and the task-irrelevant distance (I_H2F1) was simultaneously encoded in a different set of brain regions, even at a liberal threshold (p<0.01, uncorrected) (Fig. S2E).

To examine whether the brain preferentially encodes the Euclidean distance of the decision trajectory (E_H2F1) over and above the rank difference in the 1-D social hierarchy (D_H2F1), we conducted several additional analyses (see methods for details). First, we confirmed the effect of E_H2F1 in vmPFC/mOFC ([x,y,z]=[6,42,−14], t₂₆=3.75, and [x,y,z]=[−12,24,−20], t₂₆=3.72) and EC ([x,y,z]=[30,- 14,−30], t₂₆=3.35), even after partialling out the 1-D task-relevant distance, D_H2F1 (p_TFCE<0.05) (Fig. S2F). Second, if the vmPFC/mOFC and EC reflect E_H2F1, we would expect to find the effects of D_H2F1 and I_H2F1 in the same voxels (though the effects of D_H2F1 and I_H2F1 would be expected to be weaker compared to E_H2F1 because E_H2F1 is factorized into vectors D_H2F1 and I_H2F1 and each of these only partially explain the variance in E_H2F1; Fig. S2E). Note, the objective of this analysis is to examine what combination of D and I are reflected in vmPFC/mOFC and EC activity, rather than test the hypothesis that these areas independently code for both D and I. If a brain area encoding E_H2F1 assigns equal or similar weights to D_H2F1 and I_H2F1 during decision-making, we would expect that a conjunction null analysis (Nichols et al., 2005) would reveal overlapping effects of D_H2F1 and I_H2F1. We found inclusive masking between D_H2F1 and I_H2F1 (at t₂₆>2.78, p<0.005) in the vmPFC/mOFC and EC (Fig. 3C). Collectively, the results of these analyses support the interpretation that vmPFC/mOFC and EC activity encodes or reflects E_H2F1, which is composed of similar weighting of D_H2F1 and I_H2F1 (Fig. 3D), during novel inferences, consistent with a direct inference over the 2-D space (see Fig. 1A and 1D).

Finally, to formally arbitrate between different possible decision trajectories, we used Bayesian model selection (BMS) to compare 2-D and 1-D metrics for different possible trajectories. This formal comparison revealed clear evidence in favor of the Euclidean distance through hub H2 (E_H2F1) in the EC and vmPFC/mOFC, supporting the hypothesis that the relevant latent hub H2 is used for model-based inference using a 2-D cognitive map (exceedance probability=0.82 in left EC; 0.91 in right EC; 0.89 in left vmPFC/mOFC;0.85 in right vmPFC/mOFC; Fig. 3B; Table S2). Taken together, our findings show that EC and vmPFC/mOFC compute or utilize Euclidean distances over the 2-D social space to guide inference decisions.

HC reinstates the hub to guide inferences

The behavioral and neural analyses presented so far provide independent and convergent evidence that the context-relevant hub is retrieved from memory to guide inferences. We therefore searched for neural evidence of a reinstatement of the latent hub along this trajectory to guide decisions. Given the well-established role of the HC in episodic memory retrieval (Diana et al., 2007; O’Reilly et al., 2014), we predicted that the HC specifically would reinstate the context-relevant hub to guide inferences between two faces that had never been compared before. To address this question, we adopted a variant of repetition suppression (RS) (Barron et al., 2016; Boorman et al., 2016), but for a retrieved rather than explicitly presented item. During F3 presentation, participants were exposed to one of eight hub individuals matched for presentation frequency and win/loss history (Fig. S1G). We hypothesized that if the relevant hub that bridges F1 and F2 in the given dimension is presented during F3 presentation, directly after participants retrieve the relevant hub, then the BOLD signal in areas reinstating that hub should be suppressed compared to other trials presenting matched but non-relevant hubs.

We found that the right HC (peak voxel [x,y,z]=[38,−22,−12], t₂₆=3.41, p_TFCE<0.05 corrected in our bilateral HC ROI showed greater suppression, specifically for the relevant H2 presentations ( =−0.46±0.13) compared to all non-relevant hub presentations ( =−0.19±0.11) (t₂₆=4.54, p<0.001, paired t-test in the independent, anatomically defined ROI) (Fig. 4; Fig. S4). Furthermore, in an exploratory whole-brain analysis, we confirmed that the right HC was the only brain area showing this suppression effect at this threshold. Control analyses indicated this effect was specific to H2 and ruled out distance confounds (Fig. S4) Taken together, these findings show that HC reinstates the behaviorally relevant hub H2 to guide model-based inferences between distinct relational structures.

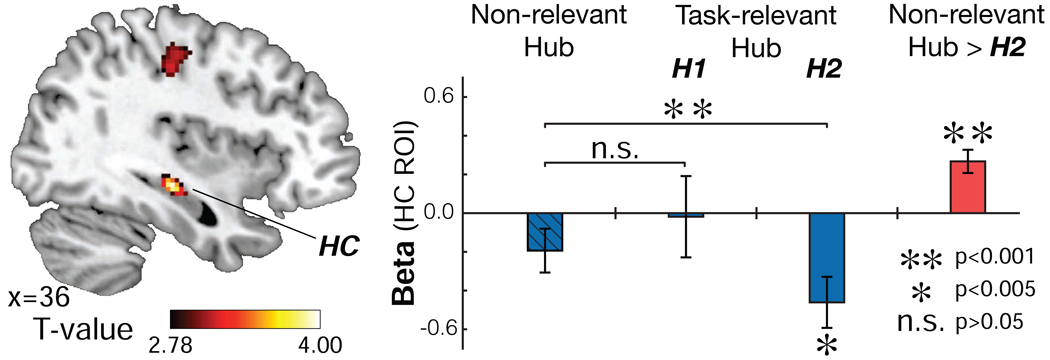
Figure 4.

Repetition suppression analyses. Left: When one of the eight hubs was presented randomly following F2 presentation, as subjects performed a cover task (F3 presentation), BOLD contrast of task-irrelevant hub (Non-relevant hub) > H2, displayed at p<0.005 uncorrected (no masking is applied to the image). The HC effect is significant at p_TFCE<0.05 corrected in an independent anatomically defined bilateral HC ROI. Right: beta estimates from an independently defined right HC ROI (see Fig. 1B). The activity in the right HC differed significantly according to which type of hub was shown at F3 presentation (Wilks’ =.553, F_2,25=10.11, p=0.001, repeated-measures ANOVA). Activity in the right HC was suppressed when the relevant hub (H2) was presented, compared to matched Non-relevant hubs (p<0.001). No suppression was found when the hub inferred from F1 (H1) was presented (p>0.05; See Fig. S4 for additional confirmatory analyses).

HC, EC, and vmPFC/mOFC represent social hierarchies in a 2-D space

To directly examine the cognitive map’s representational architecture, we measured the pattern similarity between different face presentations during F1 and F2. Under the hypothesis that more proximal positions in the cognitive map will be represented by increasingly similar patterns of neuronal activity, we used representational similarity analysis (RSA) to test the extent to which patterns of activity across voxels in the HC, EC and vmPFC/mOFC are linearly related to the Euclidean distance between faces in the true 4-by-4 social network. We reasoned that if the cognitive map of the social network is characterized by two independent dimensions represented in a 2-D space, the level of dissimilarity between neural representations evoked by each face (Fig. 5A) should be explained by pairwise Euclidean distances (E) (Fig. 1D), in addition to the pairwise rank differences in the task-relevant dimension (D) (Fig. 1C).

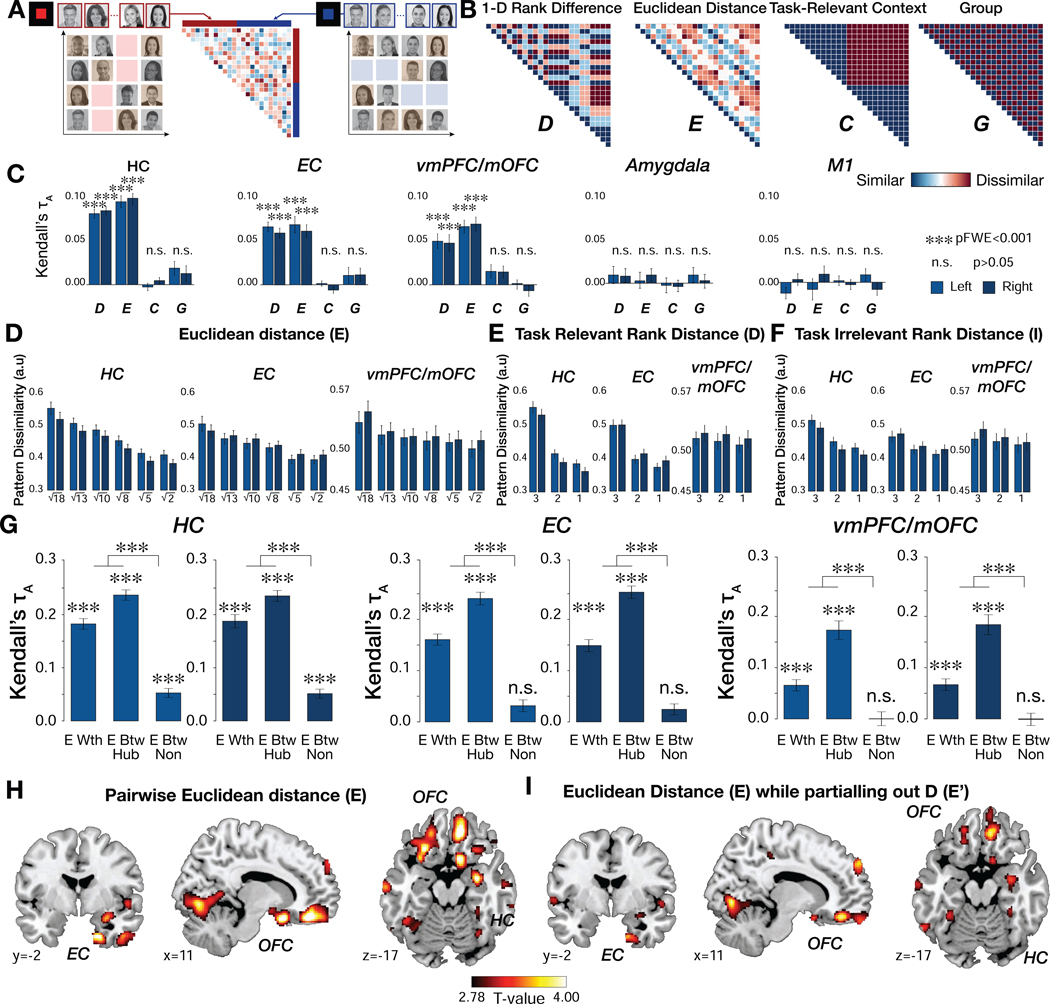
Figure 5.

Representational similarity analysis (RSA). A. The representational dissimilarity matrix (RDM) was computed in a priori ROIs from the pairwise Mahalanobis distance in the multi-voxel activity patterns evoked when face stimuli were presented at the time of F1 and F2. People were modeled separately when they were shown in the competence (left panel) and popularity contexts (right panel). B. The neural RDM was tested against model predictions of four separate dissimilarity matrices, including pairwise differences in the rank in the task-relevant dimension (D), pairwise Euclidean distances on the 2-D social space (E), the behavioral context indicating for which social hierarchy dimension the face was presented (C), and in which group (group 1 or 2) the face belonged during training (G). C. Kendall’s τ indicates to what extent a predictor RDM explains the pattern dissimilarity between voxels in each of the ROIs. The model RDMs of D and E, but not C or G, show robust effects on the pattern dissimilarity estimated in the HC, EC, and vmPFC/mOFC but not in amygdala and primary motor cortex (M1) (***, p_FWE<0.001 corrected for the number of ROIs as well as the number of comparisons with the Bonferroni-Holm method). D. The patterns dissimilarity in bilateral HC, EC, and vmPFC/mOFC increases in proportion to the true pairwise Euclidean distance between individuals in the 2-D abstract space. E and F. The pattern dissimilarity increases not only with the task-relevant distance (D) but also the task-irrelevant distance (I), suggesting that the HC-EC system utilizes 2-D space (E). G. The effects of pairwise Euclidean distance (E) between faces and the pattern dissimilarity in the HC, EC, and vmPFC/mOFC were separately analyzed for within-group (E Wth) and between-group relationships (G). Moreover, the interaction effect between E and G were separately analyzed also based on whether the faces had been directly compared during training (E Btw Hub) or not (E Btw Non). Effects are strongest for those individuals who had been previously compared during training. That is, activity patterns are better explained by E Wth and E Btw Hub than E Btw Non (two-sided Wilcoxon signed-rank test). The between-group E for novel pairs is only significant in HC. Multiple comparisons are corrected with the Holm-Bonferroni method (***, p_FWE<0.001). H. Whole-brain searchlight RSA indicates effects of E in the HC, EC, mOFC (a part of vmPFC), central OFC, and lateral OFC, among other regions (p_TFCE<0.05). I. The activity patterns in the HC, EC, and central and medial OFC are still explained by the model RDM for pairwise Euclidean distance (E) after partialling out its correlation with the model RDM for D (p_TFCE<0.05; Fig. S5B). For visualization purposes, the whole-brain searchlight maps are thresholded at p<0.005 uncorrected.

In hypothesis-driven analyses, we first analyzed data from our a priori selected anatomical ROIs (Fig. 1B), including the bilateral HC, EC, and vmPFC/mOFC. The representational dissimilarities estimated in the ROIs were explained both by the model representational dissimilarity matrix (RDM) of pairwise Euclidean distance in 2-D space (E; Fig. 5B) and, in a separate RDM, by the pairwise rank difference in the task-relevant distance (D; Fig. 5B) between individuals (one-sided Wilcoxon signed rank test, df=26, p_FWE<0.05 HolmBonferroni correction for multiple comparisons across numbers of model RDMs (n=4) and bilateral ROIs (n=6)). Based on demonstrations that amygdala activity (Kumaran et al., 2012) and gray matter density (Bickart et al., 2011; Noonan et al., 2014; Sallet et al., 2011), correlate with social dominance status, we also tested anatomically defined amygdala ROIs (Tzourio-Mazoyer et al., 2002). The amygdala pattern similarity was neither explained by E nor by D, even at a reduced threshold (p>0.05, uncorrected) (Fig. 5C). As a control region, we also tested the pattern similarity in primary motor cortex (M1) (Glasser et al., 2016), which was not explained by either predictor (p>0.05, uncorrected), (Fig. 5C).

Notably, the pattern similarity in HC, EC, and vmPFC/mOFC was not explained by the behavioral “context” of the task-relevant dimension (C, defined as popularity or competence trials; Fig. 5B), nor whether individuals belonged to the same group or not during training (G; Fig. 5B), (p>0.05, uncorrected), (Fig. 5C; Table S3). Importantly, the predictor of pairwise Euclidean distance (E) still significantly accounted for the pattern similarity in HC, EC, and vmPFC/mOFC (Rank correlation τ_A =0.045±0.005 for HC; τ_A =0.027±0.007 for EC; τ_A=0.048±0.006 for vmPFC/mOFC; p_FWE<0.001) after partialing out its shared correlation with rank distance (D) to ensure that D alone was not driving the pattern similarity effects (Fig. S5B). To confirm that the pattern similarity truly reflected E, we tested for separate effects of D and I. Decomposing E into the terms D (Fig. 5E) and I (Fig. 5F) revealed a linear relationship between pattern similarity and both distance components (See Table S3 for mean rank correlations τ_A; all p_FWE<0.05 with Holm-Bonferroni correction). These analyses show that, in addition to D, I contributed significantly to representations in these regions, supporting the interpretation that the social hierarchy was represented in 2-D, even though only one dimension was behaviorally relevant.

A natural question arises from this finding: Why do participants need to retrieve the hub for inferences if they have already integrated the two hierarchies into a single cognitive map? We reasoned that if the two 2-D maps, one for each group, had not yet been fully integrated into a single map, then the effect of E should be weakest for different members who had never been compared during training. We found that the effect of E was strongest for within-group pairs (i.e. individuals who were part of the same group during training; Fig. 5G; Fig. S5D) and for between-group pairs involving hubs (i.e. individuals and their hubs who were compared during between-group learning in day 3 training; Fig. 5G; Fig. S5E), and weakest for never-compared between-group pairs of non-hubs (Fig. 5G; Fig. S5F) in the bilateral HC, EC and vmPFC/mOFC (p_FWE<0.001, two-sided Wilcoxon signed-rank test; Fig. 5G; mean rank correlations τ_A are shown in Table S3). Notably, however, the effect of E was still significant, though weaker, for never-compared between-group pairs of non-hubs in HC alone, suggesting that HC integration may lead EC and vmPFC/mOFC, since there was no significant effect for these novel pairs in these latter regions. As an alternative, we tested for individual differences in the level of hub reinstatement and found that it could not account for the strength of neural representations (Fig. S5G). These findings suggest that the previously experienced pairs may have been fully integrated into a single map in each region, but that the novel unlearned pairs were not as accurately integrated, and only present in the HC (Fig. S5D-G).

In addition to these hypothesis-driven analyses, we also performed whole-brain exploratory analyses to test whether the neural representation of the social network extends to a broader set of regions. Specifically, we measured the extent to which each predictor (the model RDM of E and D) explains the pattern similarity measured from searchlight-based pattern analyses across the whole brain. This analysis revealed that the pairwise Euclidean distance (E) significantly explained the representational similarity between faces in HC and EC, as shown by the ROI analyses, and also in medial, central, and lateral OFC, among other areas (p_TFCE<0.05; Fig. 5H; Table S4). A separate RDM based on the pairwise 1-D rank distance (D) significantly explained representational similarity between activity patterns in the lateral OFC, medial prefrontal cortex (mPFC), and posterior cingulate cortex (PCC) (p_TFCE<0.05; Fig. S5A; Table S4). Furthermore, partialing out D from the RDM for E revealed significant effects in these same areas of HC, EC, and central/medial OFC, confirming that these representations were not simply driven by D alone (Fig. 5I; Table S4). Our findings suggest that the HC, EC and vmPFC/mOFC do not treat dimensions separately when representing individuals in a social network space. Instead, representations vary along a multidimensional cognitive map even when only one dimension is relevant to current behavioral goals.

DISCUSSION

The HC formation is thought to contain relational codes of our experiences that integrate spatial and temporal dimensions into a multidimensional representation (Buzsáki, 2013; Eichenbaum, 2017a; Eichenbaum and Cohen, 2014; Konkel and Cohen, 2009). Memories of place and their spatial relationship are key elements to constructing a cognitive map of physical space (Butler et al., 2019; Kropff et al., 2015; Moser et al., 2008). In humans, the ability to construct an accurate cognitive map of relationships between abstract and discrete information is proposed to be critical for high-level model-based decision making and generalization (Behrens et al., 2018; Bellmund et al., 2018; Vikbladh et al., 2019). We show that the HC and EC, which are well known for their proposed roles in the ability to navigate physical space (Moser et al., 2008; O’Keefe and Nadel, 1978) and simultaneously their roles in episodic memory (Eichenbaum et al., 2007; Ekstrom and Ranganath, 2018), contribute in a more general way to the organization and ‘navigation’ of social knowledge in humans (Cohen, 2015; Rubin et al., 2014; Tavares et al., 2015). Although participants were never asked to combine the two social dimensions, we found that the brain spontaneously represents individuals’ status in social hierarchies in a map-like manner in 2-D space. Such a cognitive map can be used to compute routes through the 2-D space and corresponding distances (Behrens et al., 2018), which we found were computed or used to guide inferences in EC and interconnected vmPFC/mOFC, a region known to be important for value-based decision making (Boorman et al., 2009; FitzGerald et al., 2009; Hunt et al., 2012; Lim et al., 2011; Nicolle et al., 2012; Noonan et al., 2011, 2017; Papageorgiou et al., 2017; Rushworth et al., 2011; Strait et al., 2014). Moreover, our results show that the HC-EC system did not selectively represent the task-relevant information in our task, but the relative positions in the multidimensional space. More broadly, these findings support the HC-EC system’s role in representing a cognitive map of abstract and discrete spaces to guide novel inference decisions that relied on that cognitive map.

We found that during novel inferences, RTs and neural activity in EC, vmPFC/mOFC, and lOFC reflected the Euclidean distance of navigational trajectories on 2-D space via relevant hubs, over and above the behaviorally-relevant 1-D ranks. We interpret these findings as reflecting a decision process that uses a vector over the 2-D cognitive map. We note that, depending on how certainty is defined, this univariate effect may also be interpreted as reflecting the certainty of the decision. This interpretation is consistent with an attractor decisionmaking network whose speed of accumulation to an attractor state will reflect the decision certainty, as has been proposed previously for vmPFC/mOFC in the context of value-based decision making (Hunt and Hayden, 2017; Hunt et al., 2012). That EC also reflects the same term suggests that, unlike in most value-based decision-making studies, it also contributes to the decision computation when based on a relational cognitive map. Notably, previous findings using human fMRI have reported that EC activity increases with longer Euclidean distances of planned and taken routes and reflects the planned direction of future routes during spatial navigation tasks (Chadwick et al., 2015; Doeller et al., 2010; Howard et al., 2014). Moreover, the global relational codes provided by grid cells can be used for straightforward computation of Euclidean distance from grid fields (Behrens et al., 2018; Bush et al., 2015), and has been interpreted as a mechanism, in combination with other neural codes in EC and HC, for vector navigation to goals during planning (Banino et al., 2018; Behrens et al., 2018). This view suggests that greater EC activation for greater Euclidean distances may reflect this computation for the inferred vectors that guide inferences for non-spatial decision making, in concert with choice selection processes in vmPFC/mOFC.

We found that the pattern similarity between faces in HC, EC, and in vmPFC/OFC was robustly and linearly related to the true Euclidean distance between faces in the 4-by-4 social network, such that closer faces in the abstract space were represented increasingly more similarly. This finding is striking for two reasons: first, the two dimensions never had to be combined to perform the task accurately; and second, the true structure was never shown to participants, but had to be reconstructed piecemeal from the outcomes of binary comparisons between neighbors in each dimension separately learned on separate days. There are several strategies that could, in principle, be used to solve this task that do not rely on a 2-D representational space. For example, the task-relevant and irrelevant dimensions could be represented in separate brain areas, a hypothesis for which we did not find support. Alternatively, each person’s rank could have been represented by a linear (or logarithmic) number line, such as that found in the bilateral intraparietal area (Piazza et al., 2004), or as a scalar value that is updated using model-free mechanisms. That the neural representation in the HC, EC, and vmPFC/OFC areas automatically constructed the 2-D relational structure in our tasks instead suggests that the brain may project people, or perhaps any entities, into a multidimensional cognitive or relational space such that the entity’s position is defined by the relative feature values on each dimension (Bellmund et al., 2018; Buzsáki and Tingley, 2018; Eichenbaum, 2017a). It is unclear from our study whether this finding is specialized to representing people, who are likely to be ecologically perceived as coherent entities over time, and characterized by multiple attributes, or more general to representing any entity. Precisely how this construction takes place and its generality will be an important topic for future studies to investigate.

Our findings suggest that the brain may utilize the same neural system for representing and navigating continuous space to code the relationships between discrete entities in an abstract space. Following recent theoretical proposals (Eichenbaum and Cohen, 2014; Whittington et al., 2019), we hypothesize that subjects abstract structural representations from the ordinal comparisons about rank in the social hierarchy, which, by virtue of the inferred structure, allows efficient direct inferences to be made from limited observations. Further, our findings suggest that accurate inferences about relative ranks of novel pairs of individuals may depend on the ability to find a direct “route” in this multidimensional space. This vector-based navigation over the cognitive map may be critical for efficient decision making and knowledge generalization. Moreover, accurate knowledge about the position of others in a social space should provide a solid foundation for sound inferences, thereby supporting effective model-based decision making. We found that the same cognitive map constructed by the HC-EC system is present in other brain areas, including the interconnected vmPFC/mOFC (Barbas and Blatt, 1995; Eichenbaum, 2017b; Insausti and Muñoz, 2001; Preston and Eichenbaum, 2013; Wikenheiser and Schoenbaum, 2016) and neighboring central/lateral OFC, generally supporting the theory that OFC represents a cognitive map of task space (Baram et al., 2019; Schuck et al., 2016; Wikenheiser et al., 2017; Wilson et al., 2014), though in our study not only of the behaviorally relevant task space, but also the broader task space. Moreover, we show here that the OFC’s representation of the task space respects map-like Euclidean distances of vectors through that space and that OFC activity reflects these distances to latent hubs retrieved from memory to guide inference. These findings thus cast light on why the OFC plays a critical role in model-based inference on the one hand (Jones et al., 2012), and damage to the HC-EC system also impairs model-based decision making on the other (Dusek and Eichenbaum, 1997; Gupta et al., 2009; Miller et al., 2017; Vikbladh et al., 2019).

Finally, we suggest that the HC-EC system may play a key role in constructing a global map from local experiences, which may guide model-based decisions in vmPFC/mOFC, a region previously implicated in value-guided choice (Boorman et al., 2009; Chib et al., 2009; Grabenhorst and Rolls, 2011; Hunt et al., 2012; Lim et al., 2011; Papageorgiou et al., 2017; Strait et al., 2014). This same cognitive map appears to further guide how humans integrate knowledge in the social domain, a critical ability for navigating our social worlds (Kaplan and Friston, 2019; Kumaran et al., 2012, 2016; Tavares et al., 2015).

STAR★METHODS

Lead Contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Seongmin A. Park (seongmin.a.park@gmail.com).

Participants

A total of 33 participants (16 female, age range: 19–23, normal or corrected to normal vision) were recruited for this study via the University of California, Davis online recruitment system. Six participants were excluded due to strong head movements larger than the voxel size of 3 mm. In total, 27 participants entered the analysis (mean age: 19.37±0.26, standard error mean (SEM)). The study was approved by the local ethics committee, all relevant ethical regulations were followed, and participants gave written consent before the experiment.

Stimulus

The stimuli consisted of 16 grayscale photographic images of faces (Strohminger et al., 2016) and two colored cues (red and blue squares). Each of the colored cues indicated the taskrelevant dimension of the social hierarchy for the current trial. The red square indicated the competence hierarchy for one-half of participants and the popularity hierarchy for the other half. All images were adjusted to the same mean grayscale value. The inter-trial fixation target was a white cross in the middle of a black screen. For hub learning and the fMRI experiment, the interstimulus fixation target was a purple cross (between F1 and F2) and a green cross (between F2 and F3) in the middle of a black screen, which indicates the progress of each trial to participants. The stimuli were presented to participants through a mirror mounted on the head coil. Note that face stimuli presented in this paper are license-free images for display purposes. Prior to the experiment on the first day of training, participants performed a 1-back task where they viewed each individual face three times to minimize stimulus novelty effects.

Social hierarchies

Participants were asked to learn the relative ranks of 16 individuals (face stimuli) in two dimensional social hierarchies defined by popularity and competence. The 16 face stimuli were introduced as entrepreneurs; participants were asked to learn about which individuals were more capable to attract crowd funds (labelled popularity) and which individuals had higher technical proficiency (labelled competence) and used this information to guide investment decisions.

Each hierarchy has four levels of ranks. Four individuals were allocated at the same rank at each level of the hierarchy. Therefore, the structure of multidimensional social hierarchies is 4×4 (Fig. 2A). The rank of an individual in one dimension was not related to his/her rank in the other dimension. For instance, the rank of four individuals who are at the 1^st rank in the popularity dimension are the 1^st, the 2^nd, the 3^rd, and the 4^th, respectively in the competence dimension. During first two days of training, the relative status of one individual is only compared to one-half of the other face stimuli, which implicitly creates two groups in which each group comprised eight individuals (Fig. S1). In each group, two individuals were allocated into the same rank of each of the dimensions (2 × 4 ranks = 8 individuals). The sub-group structure is shown in Fig. 2A. The allocation of each face to the position in the social hierarchies was pseudo-randomized, in order to make sure that any visual features of the face (gender, race, and age) were not associated with the rank of the individuals. To do this, we prepared eight stimuli sets. Each of the stimuli sets comprise 16 different faces. A stimuli set was randomly assigned across participants.

Task instruction and experiment procedures.

Participants were instructed to imagine that they were a venture capitalist and decide where to invest after learning the relative ranks of 16 entrepreneurs in two independent dimensions − competence and popularity. Participants were asked to learn which individual was better in technical proficiency – competence hierarchy, and which individual was better in attracting crowd funding – popularity hierarchy. During the learning block, participants were presented with two face stimuli of entrepreneurs with a contextual cue indicating the task-relevant dimension, chose the higher rank individual in the given dimension, and received feedback at the end of every trial. Participants were told that they would need to use the knowledge acquired during the learning block to decide in which entrepreneur they would want to invest when the ability in only one social hierarchy dimension is important. During the test block, participants chose one of two face stimuli who they believed was higher in the given dimension. They did not receive any feedback during test block trials.

Before training, the following instructions were clearly given to participants: (1) two entrepreneurs presented in the learning block have one rank difference whereas two entrepreneurs presented in the test block can have one or more rank differences. (2) Multiple individuals could be allocated to the same rank. Importantly, participants were never given any information implying the structure of social hierarchies, such as the total number of ranks in each dimension, or the number of individuals allocated into the same rank and were never asked to solve the task spatially. Each subject participated in behavioral training across three separate days, at least 48 hours apart. After the behavioral training on the third day, subjects participated in the fMRI experiment.

Behavioral training

During the first two days of training, participants learned the relative status of two groups of 8 “entrepreneurs” separately, on only one dimension per day (Fig. S1A for Day 1 and Fig. S1B for Day 2 training), such that people in a group were only compared against others belonging to the same group (two groups of 8 entrepreneurs, Fig. 2A). At the end of Day 2, test trials without feedback ensured subjects could make transitive inferences to determine the status of remaining members within a group, on each dimension separately (test2 in Fig. S1B), indicating they had learned the two 1-D hierarchies for both groups. Importantly, participants were never asked to combine the two dimensions in either group. We included four rank levels per dimension to ensure that differences between rank levels 2 and 3 could not simply be explained by differences in win frequency, since these people each “won” and “lost” on ½ of trials. For the third day of training, fMRI participants learned from select between-group comparisons for the first time (Fig. S1C). That is, participants only learned the relative rank of selected entrepreneurs in each group referred to as ‘hubs’, who were paired against both group members (Fig. S1D and S1E). By limiting between-group comparisons only to hubs, we were able to create comparative paths connecting each of the individuals in different groups, which could be leveraged to perform model-based inferences between novel pairs of entrepreneurs between groups.

The behavioral training comprised ‘learning’ blocks and the ‘test’ blocks (Fig. 2C). Training began with learning block mini-blocks. In the beginning of each of the mini-blocks, participants were presented which block they were in (competence or popularity). The purpose of the learning blocks was to provide an experimental setting in which participants would gradually acquire knowledge of two social hierarchies (one per group) through piecemeal experiences of comparisons for pairs with only one rank-level difference.

For the test blocks during training, participants were asked to infer the relative rank between any two individuals. To perform correctly, therefore, participants need to make successful transitive inferences. If they adopted an alternative learning strategy, such as model-free learning – i.e. comparing the values assigned to each of the face stimuli according to their number of wins/loses − participants should not be able to distinguish the second and third rank individuals, since their number of wins/loses were equal (though see (Frank et al., 2005)). Participants who successfully distinguished the second and third rank individuals above chance while also reaching above 85% accuracy overall in each test block were invited to continue participating in the fMRI experiment.

It is important to note that, during three days of training, each of the 16 individuals was presented the same number of times to participants. For trials in which participants responded too slowly (>2s), feedback was not given and the missing trial was tested again after a random number of trials to ensure all participants could in principle acquire the same level of knowledge. Importantly, participants were never asked to combine individuals’ ranks in both dimensions to make decisions, and they were never shown either the one-dimensional (1-D) or two-dimensional (2-D) social hierarchies.

Learning blocks of day 1 and day 2 training: Learning relative ranks of within-group members

During learning blocks, participants were presented two face stimuli having one rank difference on a black screen with a colored contextual cue indicating which was the task-relevant dimension in the current trial (learning block in Fig. S1A). They were asked to indicate who was superior in the given social dimension. Participants learned the relative status of all possible one rank difference pairs with feedback in random order. Feedback (correct/ incorrect) followed at the end of all responded trials. For the learning block of day 1 training, participants learned the relative status of an eight-individual group in one of two social hierarchies for the first mini-block (e.g. the hierarchy in the competence dimension for group 1 individuals). For the second mini-block, they learned the relative status of the other eight-individual group in the other social hierarchy (e.g. the hierarchy in the popularity dimension for group 2 individuals). For the learning block of day 2 training (the learning block in Fig. S1B), they learned the relative status of each group individuals in the unlearned hierarchy dimension (e.g. the hierarchy in the popularity dimension for group1 individuals and the competence dimension for group2 individuals). After two days of training, in principle participants could have learned the two different 2-D social hierarchies (one per group). The right panel in Fig. S1A and B shows the hypothesized structure of the cognitive map that participants could have built at the end of each training day. For both day 1 and day 2 training, participants completed eight mini-blocks in the learning blocks (Fig 2C). One-half of participants learned the relative ranks of group 1 in the competence dimension for the first day and the other half of participants learned the relative ranks of the group 1 in the popularity dimension for the first day.

Test blocks of day 1 and day 2: Transitive Inferences

After the learning block, we tested whether participants could generalize their knowledge to infer the relative status between individuals having one or more rank-level differences. This test block followed each learning mini-block (the test blocks in Fig. S1A and B). During the test block, all possible pairs of within-group individuals were presented to participants except for the pair of individuals who are at the same rank in the given dimension (meaning there was always a correct answer). In each trial, participants were choosing the superior face in the given dimension. Participants were instructed that their choices would count towards their final payout (the greater the payout when overall accuracy >90%). No feedback was given during test blocks to prevent further learning.

Test 2 blocks of day 2: Flexible inferences in intermixed behavioral contexts

At the end of the second day of training, an additional test block was presented. During this test 2 block, trials asking the relative rank of group 1 individuals and group 2 individuals were intermixed, as was the task-relevant dimension (the test 2 block in Fig S1B). Otherwise, these trials were identical to the other test blocks.

Hub learning block of day 3: Learning ‘hubs’ between-groups

On the third day of training, participants learned the relative ranks of pairs of between-group individuals for the first time. Importantly, the purpose of the hub learning was to provide limited experience about relative ranks of certain between-group individuals. That is, participants did not learn the relative rank of all pairs of between-group individuals but only the relative rank of selected pairs of between-group individuals.

During the hub learning block, participants learned the relative status between one individual in one group (hub) and another individual in the other group (non-hub) with one rank level difference in the given dimension (Fig. S1C). In each group, four individuals (two per group) were selected as hubs in one dimension. In the other dimension, a different four individuals played a role as hubs (eight hubs in total; Fig. S1G). For those two hubs in each group, one was at the second rank, and the other was at the third rank in the given dimension. Each of the hubs was paired with four different individuals in the other group (See the possible pairs in S1D and S1E). With this procedure, all eight individuals in one group (non-hub; Fig S1F) were paired with two selected individuals in the other group in one dimension (they were never paired with the other six individuals who were not selected as hubs). In particular, a hub in group 1 who was at the third-rank in the dimension was paired with four non-hub individuals in group 2 including two second-rank individuals and two fourth-rank individuals (the top panel in Fig. S1D). The other hub in group 1 who was at the second-rank in the given dimension was paired with the other four individuals in group 2 including two first-rank individuals and two third-rank individuals (the bottom panel in Fig. S1D). This is also true for hubs in group 2 (Fig. S1E). During hub learning, participants have therefore learned the relative rank of some pairs of between-group individuals who have one rank difference, as they learned for the pairs of within-group individuals during the previous learning blocks. The hub learning block allowed us to create a unique “path” between members of different groups. That is, each of 12 non-hubs individuals (six per each group; Fig. S1F) has a unique connection to a specific hub in the other group (one among eight hubs in Fig. S1G) in one of two hierarchy dimensions. Note that the hubs in competence dimension differed from the hubs in popularity dimension (e.g. Fig S1H).

For each trial in the hub learning block, three face stimuli (F1, F2, and F3) were presented for 2 s sequentially after the presentation of a conditional cue (1 s) indicating the task-relevant dimension of the current trial (Fig. S1C). Participants were asked to indicate one who is superior rank between F1 and F2 in the given dimension while F2 was presented. Feedback (correct/ incorrect) followed after each decision (2 s). Between F1 and F2, one was the hub in the given dimension and the other was a non-hub in the different group who has one rank difference from the hub. A third face (F3) was presented (2 s) at the end of every trial, and participants were asked to press a button indicating the gender of the F3 face stimuli. F3 was selected from 12 non-hubs in the given dimension (Fig. S1F). By presenting non-hub faces at the F3, we controlled the number of presentations of each of the face stimuli to be equivalent. No feedback was given for the gender discrimination task. The inter-stimulus interval (ISI) was 2 s and the inter-trial interval (ITI) was 4 s. While learning between-group relationships via hubs, participants simultaneously became familiar with the task procedure that we used for the fMRI experiment (Fig. 2B).

Sample size calculation and participant retention

The sample size was determined on the basis of a power calculation using G*Power assuming a medium to large effect (d = 0.6), and resulting in a sample size of 24 to achieve a statistical power of 80% (α = 0.05, two-tailed test).

For the behavioral training, we recruited 282 participants. They received course credit as compensation. Among participants who completed the two days of training, 82 participants achieved a higher accuracy than our threshold during the ‘flexible inferences’ block in day 2 (participants who successfully distinguished the second and third rank individuals above chance while also reaching >85% accuracy overall). We included a high-performance threshold because we needed to ensure accurate representations of cognitive maps, should they exist, to be able to measure them reliably. Moreover, the relatively high drop-out rate in part reflects difficulties retaining subjects for three-day studies, variable performance due in part to using course credit as incentives (e.g. many students had achieved full credits for their courses before the end of Day 2 training), and true variability of task performance.

Among 65 participants who agreed to continue on Day 3 training with monetary compensation, 51 participants made correct inferences during the hub learning more than at chance level during the last training session of the day 3 training. Of these 51 participants, 33 further participated in the fMRI experiment and 18 participated in a behavioral version of the inferences task (see Fig. S3A and S3B).

Behavioral version of the inferences task

To ensure that this procedure of 3 days of behavioral training was sufficient to construct the hierarchies for both groups, a separate behavioral experiment after Day 3 training, conducted on different participants, showed that they had successfully learned the four levels for each dimension in the social hierarchy, and importantly, could accurately differentiate between rank levels 2 and 3 for both dimensions (Fig. S3A and S3B).

fMRI experiment

The purpose of the fMRI experiment paradigm was to test whether and how participants represent their knowledge of social hierarchies of the two groups of individuals and make inferences about relative ranks of novel pairs of individuals. Fig. 2B illustrates an example trial of the fMRI experiment. In each trial, three face stimuli (F1, F2, and F3) were shown sequentially following a conditional cue (1 s) with an inter-stimuli fixation cross (1.5 s). The color of a square shown as the conditional cue indicated the relevant dimension of the current trial. These conditions were equated and randomly interleaved. Each face stimulus was shown for 2 s. Between face stimuli, we presented a fixation cross for inter-stimuli-intervals (ISI) which were jittered between 2 ~ 5 pulses (TR=1200ms). The first decision was made during the F2 presentation. Participants were asked to press a button to indicate who is superior rank between F1 and F2 in the given social hierarchy dimension. They were asked to respond as quickly as possible but also as accurately as possible. No feedback was given. The second decision was made during the F3 presentation. Participants were asked to press a button to indicate the gender of F3 as quickly as possible. The F3 was included to test for hypothesized fMRI suppression of the relevant latent hub, relative to other matched but non-relevant hubs, that may have been retrieved from memory to guide model-based inferences. The buttons allocated to indicate the gender of presenting face stimuli were counterbalanced across participants. If the response was missed in the inference decision due to a slow response, we showed a ‘missed’ sign and proceeded to the next trial. The missed trial was then tested again after a random number of trials, which allowed us to collect responses to all trials from all participants.

The following was not told to participants: (1) during the fMRI experiment, F1 and F2 were selected from different groups among 12 non-hubs individuals in the given dimension (Fig. S1F) – F1 was selected from group 1 for one-half of trials and F2 was selected from group 1 for the other half; (2) F3 was selected from among eight individuals who played a role as hubs regardless of the social hierarchy dimension (Fig. S1G).

All eight hubs were shown the same number of trials at the time of the F3 presentation. Participants were asked to make the same type of decisions as they did for the third-day behavioral training (i.e. choosing a higher rank individual between the first two faces in the given context dimension and indicating the gender of the third face). However, unbeknownst to participants, all pairs were novel (i.e. they had never been compared before). This manipulation meant we were able to test whether and how participants make inferences about the relative rank of unlearned pairs of individuals. The fMRI experiment comprised two blocks. Each block included 104 trials which included all possible between-group pairs of non-hubs who have different ranks in the given dimension. Note that, during the fMRI experiment, all F1-F2 pairs were also presented in reverse order in both context dimensions. The order of the trials was randomized across participants.

Inferences of relative status of unexperienced pairs via hubs

During training, participants never directly learned the relative status between two face stimuli (F1 and F2) presented during the fMRI paradigm. Instead, participants could make transitive inferences about relative status of unlearned pairs via one of two hub individuals (H1 and H2), (Fig. 2D). The hubs were two individuals (H1 and H2) who had been paired with both individuals (F1 and F2) in a task-relevant dimension. The H1 (H2) was uniquely paired with F1 (F2) in between-group comparisons and belongs to the same group with F2 (F1). These taskrelevant hubs in one dimension differ from those in the other dimension, which means that to make an accurate inference of the relative status of the same pair of individuals in the two different dimensions, participants needed to retrieve different hubs, which would alter the inference trajectories (e.g. Fig. S1H). Note that, for every F1-F2 pair, there were only two individuals (H1 and H2) that have been paired with either F1 or F2 during training in the given dimension. That is, H1 belonged to the same group with F2 (within-group) and had been uniquely paired with F1 during the hub learning block (between-group). Likewise, H2 belonged to the same group with F1 (within-group) and had been uniquely paired with F2 during the hub learning block (between-group). The direction and the distance of inference trajectories on the social cognitive map were, therefore, determined by which of the hubs (H1 or H2) was preferentially recalled by participants for making inferences. The between-group relationship to the hub (F1→H1 and F2 H2) had one rank difference in the given dimension. If participants recalled H1, the transitive inference depended on the within-group distance (H1→F2), and the inference was made in the forward direction (F1→F2). If participants recalled H2, the inference depended on the within-group distance (H2→F1), and the inference was made in the backward direction (F2→F1). We examined which trajectory participants used for making transitive inferences by examining which unseen hub was selectively retrieved during inferences. This was possible because the inference trajectory is anchored by the position of the hub. We tracked the putative trajectory used by participants by examining which hub between H1 and H2 was selectively retrieved during inferences. Furthermore, we examined whether participants utilize only the task-relevant rank distance (D) or also the Euclidean distance (E) between individuals’ positions and the hubs in the cognitive map.

Behavioral data analysis

We analyzed the reaction times (RT) and accuracy in inferences of the relative status between a novel pair of individuals (F1 and F2). The choice RT was measured from the F2 onset to the response. To make successful inferences, participants could use the cognitive map of social space to make inferences via an unseen hub. The inference trajectories, therefore, were grounded by the location of the hub. To examine whether either or both hubs were selected for inferences, we regressed choice RT on different distance measures of putative inference trajectories in the same multiple linear regression model (Fig. S2A). We focused our regression analysis on choice RT only because choice accuracy showed a ceiling effect (Fig. S2B). As regressors, we included both distances which were measured from each of two potential hubs: the distance between H1 and F2 and the distance between H2 and F1 in addition to the distance between F1 and F2 by allowing them to compete to explain RT variance. Moreover, the distance was measured in both of the rank difference in the task-relevant dimension (D) and Euclidean distance (E). We regressed RT of inference decisions on four different distance measures of trajectories via hubs, D_H1F2, D_H2F1,E_H1F2, and E_H2F1 (Fig. 2D) and two direct distance measures between F1 and F2, D_F1F2 and E_F1F2 (Fig. 2E), (Eq. 1).

$$RT=C+{\beta }_1{E}_{H1F2}+{\beta }_2{E}_{H2F1}+{\beta }_3{E}_{F1F2}+{\beta }_4{D}_{H1F2}+{\beta }_5{D}_{H2F1}+{\beta }_6{D}_{F1F2}$$ Eq. 1

We performed an additional multiple linear regression as a confirmatory analysis in which the 1-D distances in task-irrelevant dimension (I) were entered as an alternative regressor instead of E (Fig. S2C). The correlation between different distance measures is shown in Fig. S3D. Group level effects of each of the distance measures were tested with a one-sample t-test to account subjects as a random variable.

Functional imaging acquisition

We acquired T2-weighted functional images on a Siemens Skyra 3 Tesla scanner. We used gradient-echo-planar imaging (EPI) pulse sequence that sets the slice angle of 30° relative to the anterior-posterior commissure line, minimizing the signal loss in the orbitofrontal cortex region (Weiskopf et al., 2006). We acquired 38 slices, 3mm thick with the following parameters: repetition time (TR) = 1200 ms, echo time (TE) = 24 ms, flip angle = 67°, field of view (FoV) = 192mm, voxel size = 3 × 3 × 3 mm³. Contiguous slices were acquired in interleaved order. We also acquired a field map to correct for potential deformations with dual echo-time images covering the whole brain, with the following parameters: TR = 630 ms, TE1 = 10 ms, TE2 = 12.46 ms, flip angle = 40°, FoV = 192mm, voxel size = 3 × 3 × 3 mm³. For accurate registration of the EPIs to the standard space, we acquired a T1-weighted structural image using a magnetization-prepared rapid gradient echo sequence (MPRAGE) with the following parameters: TR = 1800 ms, TE = 2.96 ms, flip angle = 7°, FoV = 256mm, voxel size = 1 × 1 × 1 mm³.

Pre-processing

The preprocessing of functional imaging data was performed using SPM12 (Wellcome Trust Centre for Neuroimaging). Images were corrected for slice timing, realigned to the first volume, and realigned to correct for motion using a six-parameter rigid body transformation. Inhomogeneities created using the phase of nonEPI gradient echo images at 2 echo times were coregistered with structural maps. Images were then spatially normalized by warping subject-specific images to the reference brain in MNI (Montreal Neurological Institute) coordinates (2mm isotropic voxels). For the univariate analysis images were smoothed using an 8-mm full-width at half maximum Gaussian kernel (Mikl et al., 2008).

Univariate analysis

We implemented several general linear models (GLMs) to analyze the fMRI data. All GLMs contained separate onset regressors for the contextual cue which indicates the task-relevant dimension, F1, F2, and F3 stimuli presentations for each of the trials. Specifically, the F3 onsets were separately modeled when F3 was (1) the task-relevant hub, H1, (2) the task-relevant hub, H2, and (3) neither H1 nor H2, but the hub for other pairs of individuals (non-relevant hub). A stick function modeled the contextual cue and the F3 presentation and a 2 s boxcar function modeled the presentation of F1 and F2. The F1 onset regressors were modulated with parametric regressors of the rank of the individual in the task-relevant hierarchy (F1_R) and the rank in the task-irrelevant hierarchy (F1_I). The F2 onset regressors were modulated by the rank in the task-relevant hierarchy (F2_R), the rank in the task-irrelevant hierarchy (F2_I), and additional regressors of interest representing the putative inference trajectories which varied according to which structure of cognitive map was tested (1-D or 2-D) (Fig. S3C). The onset of button presses (stick function) and the 6 motion parameters obtained during realignment were entered into the GLM as regressors of no interest. The orthogonalization function was turned off. All these regressors, except for the motion parameters, were convolved with the canonical hemodynamic response function in SPM12.

To test whether the brain encodes the trajectories via hubs over Euclidean space, for GLM1, we included parametric regressors of Euclidean distance and cosine angle of the vector between F1 and H2 and those of the vector between F2 and H1 (E_H2F1, A_H2F1, E_H1F2, and A_H1F2). The Euclidean distance between face stimuli was defined over the two-dimensional (2-D) space characterized by their relative rank in each of two social hierarchies. The cosine angle represents the normalized function of competence modulated by popularity. The value of these regressors was invariant to the relevant dimension for the current trial.

From the first-level analysis, contrast images of parameter estimates from regressors of inference trajectories (E_H2F1, A_H2F1, E_H1F2, and A_H1F2) at the time of F2 presentation were estimated from each of the participants. In addition, during the cover task (at the time of F3 presentation), the following contrasts images were estimated for the cross stimuli suppression analysis: trials when F3 was the task-relevant hub, H1, compared to when F3 was a nonrelevant hub (H1 < Non-relevant hub); and when F3 was the task-relevant hub (H2) compared to when F3 was a non-relevant hub (H2 < Non-relevant hub).

For GLM2, we tested whether the brain uses different cognitive maps for each dimension learned on a different day (popularity and competence), for which we would predict task-modulated distance terms for current behaviorally-relevant and irrelevant task dimensions. We therefore inputted the rank difference in the task-relevant dimension (D) and that of the task-irrelevant dimension (I) as the parametric regressors, which includes the 1-D distances between H2 and F1 and those of H1 and F2 (D_H2F1, I_H2F1, D_H1F2 and I_H1F2), in addition to the other regressors not associated with the distance measures that we inputted in GLM1. The value of these regressors was dependent on the task-relevant dimension on the current trial.

For GLM3, we tested whether the brain has already integrated the cognitive map for group 1 and that for group 2 into a combined cognitive map and encodes the inference trajectories between F1 and F2. We included the regressors of Euclidean distance and cosine angle of the vector between F1 and F2 (E_F1F2 and A_F1F2), in addition to the other regressors that we inputted in GLM1.

For GLM4, we tested whether the brain uses different combined cognitive maps for making inferences in different contextual dimensions. We inputted the rank difference in the task-relevant dimension and that of the task-irrelevant dimension as 1-D distances between F1 and F2 (D_F1F2 and I_F1F2) in addition to the other regressors that we inputted in GLM1. Fig. S3C illustrates the regressors of different models to examine how the brain constructs and use a cognitive map of abstract social hierarchies.

Group-Level Statistical Inference

We perform group-level inference both on hypothesis-driven a priori ROIs in the HC, EC, and vmPFC/mOFC bilaterally and exploratory whole-brain analyses. For our a priori ROIs, we reported our results in these areas at the threshold p_TFCE<0.05 using threshold-free cluster enhancement (TFCE) (Smith and Nichols, 2009) for correction of multiple comparisons within a combined ROI which integrated anatomically defined HC, EC, and vmPFC/mOFC in bilateral hemispheres into a single mask. For the whole brain analyses, we enter the individual contrast images into the second-level analysis. For the whole-brain analysis, we reported the whole-brain permutation-based threshold-free cluster enhancement (TFCE)-corrected images at the threshold p_TFCE<0.05 (1000 iterations of simulation).

Model comparisons using Bayesian model selection

To formally arbitrate between different possible decision trajectories, we used Bayesian model selection (BMS) to compare 2-D and 1-D metrics for different possible trajectories (or comparisons) through the hub H1 (E_H1F2, D_H1F2, and I_H1F2), those through the hub H2 (E_H2F1, D_H2F1, and I_H2F1), and also direct distances between F1 and F2, rather than trajectories via the hub (E_F1F2, D_F1F2, and I_F1F2). In addition, different hypothetical cognitive spaces may have different underlying metrics. That is, if participants do not construct a cognitive map in a 2-D space, but rather a different architecture for representing social hierarchies, alternative distance metrics may better account for the neural data than the Euclidean distance. For example, if inferences were made through the sequential retrieval of individuals linking F1 to F2, the brain activity engaged in novel inferences should be better explained by the shortest number of links (L; note this is equivalent to 1+D_H2F1). Alternatively, if a cognitive map encodes only the vector angle between individuals in a polar coordinate system, neural activity should encode the angle between individuals (A_F1F2, A_F1H1 and A_F2H1), while it should be invariant to the length. We formally compared GLMs including these four terms (E, D, I, and A) for three different possible trajectories (H1F2, H2F1, F1F2) in left and right EC and vmPFC/mOFC (Fig. S3C).

Repetition suppression analysis

Recent findings have shown that blood-oxygen-level-dependent (BOLD) suppression can be measured not only to repetition of a stimulus, but also to pairs of stimuli that have been well-learned though association and to a predicted or imagined outcome (Barron et al., 2016; Boorman et al., 2016). This cross-stimulus suppression (CSS) approach allows us to examine the underlying neural representations of retrieved memories. In the current study, if the relevant hub is presented during the suppression phase, at the time of F3 presentation, directly after participants recall the relevant hub for making inferences of relative ranks between faces, then the BOLD signal in the areas reinstating the relevant hub should be suppressed compared to the non-relevant hubs. Considering that effects of CSS did not depend on the responses of participants during the cover task, we included the BOLD responses in every F3 presentation into the analysis. Moreover, the BOLD signal should be suppressed specifically for the relevant and preferentially selected hub compared to the relevant but unselected hubs. Considering that the hippocampus (HC) was our a priori ROI, we reported our results at a threshold p_TFCE<0.05 using TFCE within an anatomically defined independent ROI that includes bilateral HC for correction of multiple comparisons.

It is important to note that the hub face in each trial was not determined by F3 stimuli but by the combination of task-relevant dimensions, F1 and F2. That is, the same face stimuli presented at F3 could be the relevant hub (e.g. H2) in one trial but it could be an alternative hub (e.g. H1) or non-relevant hub (the faces that have not been paired with both F1 and F2 in the given dimension) in other trials. Therefore, the effects of RS were not driven by the comparison of specific stimuli set but the comparison between conditions.

Neural model comparison

The different hypothetical structure of the cognitive map and putative inference trajectories cannot be accurately tested in a single GLM while there is potential multicollinearity between different distance measures. By definition, this was the case for some of our distance terms because, for example, E is correlated with D and I. The cross-correlation between different distance measures is shown in Fig. S3D. To formally compare the predictability of each distance measure in different models, we therefore used Bayesian model selection (BMS), (Stephan et al., 2009).

We tested whether neural activity in the vmPFC/mOFC and EC, which showed effects of the Euclidean distance of the inference trajectory from the hub ( ), is better explained with alternative distance measures of inference trajectories. To test this, we ran several GLMs in which the brain activity at the time of inferences (F2 presentation) was modeled with only one of candidate distance measures as a parametric regressor. Specifically, we compared the models having one of the following distance measures as parametric regressors: E_H2F1, E_H1F2, E_F1F2, D_H2F1, D_HF1F2, A_H2F1, A_H1F2, and A_F1F2. The inference process can alternatively be modeled with the link distance ( ), which indicates the minimum number of links between F1 and F2 in the social network. The shortest link distance, equals the sum of the number of links from F2 to H2 (between-group) and the number of links from H2 to F1 (within-group). Since we controlled the between-group distances as one, the brain areas encoding can be estimated by the GLM which includes as a parametric regressor. In addition to the parametric regressors of distance, all GLMs also included the rank of the task-relevant dimension and the rank of the task-irrelevant dimension of presenting faces as additional regressors at the time of F1 and F2 presentation (F1_R, F1_I, F2_R, and F2_I). As before, the onsets of the contextual dimension cue, F3 presentation, and button presses were also entered as additional regressors in all GLMs.

For the univariate neural model comparisons, we first estimated the log-likelihood of each of GLMs. Following previous work (Kumaran et al., 2016; Wilson and Niv, 2015), the loglikelihood (LL) of each of the models was calculated (Eq.2) separately for the a priori anatomically defined ROIs: the EC and vmPFC/mOFC.

$$LL=-n\left(\ln \sqrt{2\pi {\sigma }^2}+0.5\right)$$ Eq. 2

where n is the total number of scans, and ² is the variance of the residuals after subtracting the best-fit linear model. Considering that the linear model provides the maximum likelihood solution to each model with Gaussian-distributed noise, the likelihood was computed from residuals in the ROIs after subtracting the best-fit linear model. Since all models had the same number of parameters, their likelihoods could be directly compared to ask which model accounted best for the neural activation patterns. We further entered the LL to Bayesian model selection (BMS) to compare the goodness of fit of the model with the exceedance probability (XP).

Regions of Interest (ROI) analyses

The ROIs were defined in the bilateral HC (Yushkevich et al., 2015), bilateral EC (Amunts et al., 2005; Zilles and Amunts, 2010), bilateral amygdala (AM) (Tzourio-Mazoyer et al., 2002), and bilateral vmPFC/mOFC (Neubert et al., 2015) using probabilistic map of anatomical ROIs. We also included additional ROIs in the bilateral primary motor cortex (M1) (Glasser et al., 2016) as control regions. The ROIs in the HC, AM, and M1 have been already binarized by the authors of each study ((Yushkevich et al., 2015) for HC; (Tzourio-Mazoyer et al., 2002) for AM; (Glasser et al., 2016) for M1). Neubert et al. also provided the binarized ROIs in vmPFC/mOFC (Neubert et al., 2015) and noted that they set the maximum threshold to 25 meaning it includes voxels that belong to any given mask in 25–100% of participants. The EC defined by Juelich atlas (Amunts et al., 2005; Zilles and Amunts, 2010) allowed us to choose the threshold of images based on probability. To define ROIs in the EC, we binarized the probabilistic map in which the minimum threshold was 0 and the maximum threshold was 10. Note that ROIs were independently defined from the current task. For display purposes, all statistical parametric maps presented in the manuscript are unmasked.

ROI-based representational similarity analysis (RSA)

Neural representation of social hierarchies

In hypothesis-driven analyses, we performed a representational similarity analysis (RSA) (Kriegeskorte, 2008; Nili et al., 2014) to test whether the a priori ROIs contain hypothesized cognitive map structures with respect to the social hierarchies. To test our hypotheses, we first estimated Beta coefficients when each of the individual faces was shown at the time of F1 or F2 in each of our same anatomical ROIs in HC, EC, and vmPFC/mOFC. We then averaged the unsmoothed Beta maps across F1 and F2 presentations, allowing us to estimate the patterns of neural activity in each ROI. These patterns were separately estimated according to which social hierarchy dimension (competence or popularity) was relevant to the current decision. Reliability of data was improved by applying multivariate noise normalization (Walther et al., 2016). We quantified the representational similarity for the two independent fMRI blocks (i.e. runs) using the Mahalanobis distance between the activity patterns, which generated a 24×24 representational dissimilarity matrix (RDM; 12 non-hub individuals were presented in each of two dimensions; Fig. 5A). These analysis steps were repeated per ROI.

Next, we confirmed that the RDM estimated from the brain activity patterns in each of the ROIs discriminated different face stimuli with good sensitivity using the exemplar discriminability index (EDI) (Nili et al., 2016), which is defined as the average of the pattern dissimilarity estimates between different stimuli compared to the average of the pattern dissimilarity estimates between the same stimuli. We confirm that the EDI in all ROIs was positive (one-sample t-test, p<0.01) suggesting that the different sets of stimuli were discriminable based on their multivariate activity patterns.

We predicted the RDM estimated from the patterns of neural activity in a priori ROIs using several candidate model-based predictor RDMs (Model RDM; Fig. 5B). The model RDMs included (1) pairwise Euclidean distances between individuals in 2-D social space (E); (2) pairwise rank difference between individuals in the task-relevant hierarchy (D); (3) the context of which social hierarchy dimension (competence or popularity) the face stimulus was presented in (C, task-relevant dimension); (4) which group the face stimulus belonged to during training (G).

The extent to which the brain RDM of each ROI was explained by the model RDM was estimated with the rank correlation (Kendall’s _A). For group-level inference, this effect was then compared to the permuted baseline at the group-level with the non-parametric Wilcoxon signed-rank test across participants (Nili et al., 2014). The ROI-based analysis uses the pattern of beta coefficients across voxels in the entire ROI. Therefore, correction for multiple comparisons was made over the number of ROIs (n=6), as well as by the number of model RDM comparisons (n=4). We report results corrected for family-wise error (FWE) with the Holm-Bonferroni method at p<0.05, but also note stronger effects with asterisks.

Partial correlation analyses

In addition to the model RDMs, using partial correlation, we also tested for an effect of E while controlling for the shared covariance between E and D. Specifically, we estimated the extent to which the RDM estimated in each ROI was explained by E’. E’ denotes the pairwise Euclidean distances between individuals (E) while regressing out its partial correlation with the pairwise rank difference in the task-relevant distance (D):E’ = E ‒ DD⁺E where D⁺ is the Moore-Penrose generalized matrix inverse (D⁺ = pinv(D), Fig. S5B). This partial correlation method gives an advantage over the other methods such as orthogonalization which often lose the original correlation structure (Fig. S5B). Note that, as Fig. S5B shows, E’ differs from E^Orth which denotes E orthogonalized by D using the Gram-Schmidt method, or the pairwise rank difference in the task-irrelevant dimension (I). After regressing out the partial correlation, the predictors are independent from each other while preserving high correlation with its original correlation structure. That is, E’ does not correlate with D while it still highly correlates with E (Fig. S5B).

Last, we examined the relationship between pattern dissimilarities in each of the ROIs and pairwise Euclidean distances (E), the pairwise task-relevant rank differences (D), and the pairwise task-irrelevant rank differences (I) between all individual faces in the social cognitive map. The brain RDM of each participant was normalized into a range between 0 and 1. The upper triangular part of the normalized 24×24 RDM was arranged according to the distance measure in each model RDM, providing model predictions of representational dissimilarity. We estimated the mean pattern dissimilarity per bin across participants. This analysis was only performed for visualization purposes (Fig. 5D for E, Fig. 5E for D, and Fig. 5F for I) Using the same methods, we also showed the effects of pairwise Euclidean distance (E) between faces and the pattern dissimilarity which were separately analyzed for within-group (E Wth; Fig. S5D) and between-group relationships considering the group effects (G). The between-group relationships were separately analyzed also based on whether the faces had been directly compared during training (E Btw Hub; Fig. S5E) or not (E Btw Non; Fig. S5F). We did not make any statistical interpretation based on this analysis.

Searchlight-based RSA

Whole-brain searchlight RSA was performed to examine brain areas in which the activity patterns reflect the hypothesized relational structure of the social hierarchies both within and outside of HP, EC, and vmPFC/OFC. Moreover, the searchlight analysis allows us to examine to what extent the model RDM explains the neural representation dissimilarity with a fixed number of voxels examined across regions. We defined a sphere containing 100 voxels around each searchlight center voxel. Consistent with the ROI analysis, we estimated the neural activity patterns elicited while each of the individuals was presented at the time of F1 or F2 from each of the searchlights. These neural representations were separately estimated according to which social dimension was relevant to the current task. The dissimilarity matrices were quantified with the Euclidean distance between neural patterns estimated from different blocks. For each searchlight, therefore, a 24×24 dissimilarity matrix was generated based on neural activity patterns elicited by each of face stimuli in two different task-relevant dimensions (Fig. 5A). We used the same predictors (i.e. model RDMs) that we used for ROI-based RSA analysis to estimate the neural representational dissimilarity across searchlights with Kendall’s τ_A rank correlation. To assess neural dissimilarity specific to E, we also tested the RDM E’ while partialling out its covariance with D. The computed Kendall’s _A values were then mapped back on the central voxel, allowing continuous mapping of information in the whole-brain per subject. These images were further smoothed using an 8-mm full-width at half maximum (FWHM) Gaussian kernel and Fisher’s Z transformed. We further performed one-sample t tests compared to the permuted baseline for a group-level analysis. We corrected for multiple comparisons using TFCE (Smith and Nichols, 2009) with 1000 iterations of simulation. We reported the results corrected for family-wise error (FWE) for multiple comparisons across searchlights (p_TFCE<0.05).

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and Algorithms
MATLAB ver.2018a	Mathworks	https://www.mathworks.com
Presentation Ver. 21.0	Neurobehavioral Systems	http://www.neurobs.com/
Psychopy 3	Peirce et al., 2019	https://www.psychopy.org/
SPM12	Penny et al., 2007	https://www.fil.ion.ucl.ac.uk/spm/software/
MarsBaR Ver. 0.44	Brett et al., 2002	http://marsbar.sourceforge.net/
RSA toolbox	Nili et al., 2014	https://git.fmrib.ox.ac.uk/hnili/rsa
Other
The MR2 (Facial stimuli)	Strohminger et al., 2016	http://ninastrohminger.com/the-mr2

Highlights.

• Human brains map abstract relationships between entities from piecemeal learning

• Separately learnt dimensions are combined and represented in a 2-D social hierarchy

• To make novel inferences, HC reinstates a hub which connects two social hierarchies

• EC and vmPFC encode Euclidean distances of inferred vectors for novel inferences