Cell Mechanics at the Rear Act to Steer the Direction of Cell Migration

Summary:

Motile cells navigate complex environments by changing their direction of travel, generating left-right asymmetries in their mechanical subsystems to physically turn. Currently little is known about how external directional cues are propagated along the length scale of the whole cell and integrated with its force-generating apparatus to steer migration mechanically. We examine the mechanics of spontaneous cell turning in fish epidermal keratocytes and find that the mechanical asymmetries responsible for turning behavior predominate at the rear of the cell, where there is asymmetric centripetal actin flow. Using experimental perturbations, we identify two linked feedback loops connecting myosin II contractility, adhesion strength and actin network flow in turning cells that are sufficient to explain the observed cell shapes and trajectories. Notably, asymmetries in actin polymerization at the cell leading edge play only a minor role in the mechanics of cell turning – that is, cells steer from the rear.

Graphical Abstract

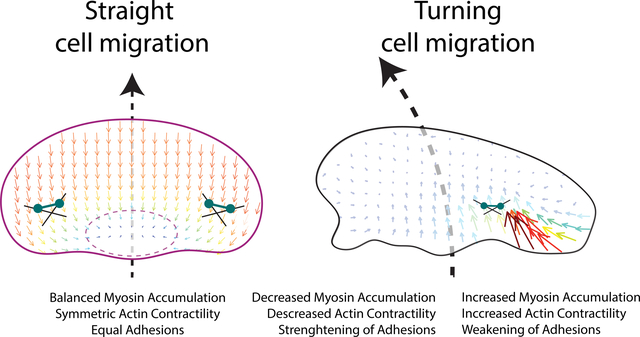
Motile cells must be able to turn to navigate complex environments. Currently, little is known about mechanical actions that allow a cell to turn. We examine the mechanics of spontaneous cell turning in fish epidermal keratocytes and find that asymmetries responsible for turning behavior predominate at the rear of the cell. We find that as a cell turns myosin, bound to the actin cytoskeleton, is swept to the outer side of the cell where it acts to locally increase contraction of the actin cytoskeleton and weaken cellular adhesion to the surface that the cell crawls along. These mechanical forces lead to the outer cell wing to move faster and drive turning. On the opposing inner side of the turning cell, myosin is relatively sparse leading to a reduction in the contraction of actin and to strong cellular adhesion to the surface. Essentially, the cell sticks on one side and slips on the other, pivoting into a turn. These interlinked feedback loops connecting myosin contractility, adhesion strength and actin network flow in turning cells are sufficient to explain the observed cell turning. Notably, asymmetries in actin polymerization at the cell leading edge play only a minor role in the mechanics of cell turning – that is, cells steer from the rear.

Introduction

Directed cell migration is required for many fundamental processes in multicellular animals, including wound healing, immune cell trafficking and embryonic development. In order to achieve these complex behaviors, cells must have both an ability to translocate in space and a mechanism to determine and alter the direction of this migration. Previous work has established a good understanding of the physical mechanisms that drive steady state migration (Blanchoin et al., 2014; Lauffenburger and Horwitz, 1996; Mogilner and Rubinstein, 2010; Pollard and Borisy, 2003) while also mapping out the signaling pathways that dictate the choice of direction of motion in response to environmental cues (Jin, 2013; Parent and Devreotes, 1999; Ridley et al., 2003; Schneider and Haugh, 2006; Xiong et al., 2010). However, the physical mechanisms that cells use to transduce asymmetries in signaling pathways into the coordinated large-scale reorientation of the entire motile cell remain obscure. In this work we seek to map out how an individual cell physically adapts the machinery of cell motility to change its direction of travel while maintaining persistent polarization.

All migrating cells are structurally polarized along the direction they migrate. Actin-based locomotion typically involves preferential localization of the assembly of actin filaments to the front of the cell (Theriot and Mitchison, 1991; Wang, 1985) while the cell body and the contractile activity of non-muscle myosin-II typically localize to the rear (Vicente-Manzanares et al., 2007; Wilson et al., 2010; Yumura et al., 1984). This polarization is sufficient to weakly determine the direction that a cell will travel at a given instant in time (Jiang et al., 2005); yet, over a distance of even a few cell lengths (~100 μm) no cell follows a completely persistent path in space (Arrieumerlou and Meyer, 2005; Dunn, 1983; Li et al., 2008). In principle, transient left-right asymmetries in any of the mechanical components contributing to directed migration including protrusion at the leading edge, retrograde flow of the polymerizing actin network, adhesive coupling to the substrate, retraction at the rear, or contraction of the cell body could cause slight changes in the overall orientation of a migrating cell and alter its direction of movement. If these variations are random and uncorrelated, as might be expected for a cell moving spontaneously in a uniform environment, the resultant path of motion would be a persistent (or correlated) random walk (Dunn, 1983). Indeed, persistent random walk statistics are approximately able to fit the long-distance trajectories observed for many types of cells moving spontaneously in two dimensions, although detailed analysis often reveals that there must also be non-random components (Hartman et al., 1994; Selmeczi et al., 2005; Stokes et al., 1991)

Migrating cells can also actively change direction in response to spatial cues from their environments, including signals from soluble or matrix-attached chemical gradients, or even electric fields (Cortese et al., 2014; Ridley et al., 2003). For rapidly moving cells that tend to maintain strong front-rear polarization, such as human neutrophils and fish epidermal keratocytes, motile cells exposed to a rapid change in their primary directional cue tend to reorient their migration in a gradual U-turn rather than depolarizing and then repolarizing along a new front-rear axis (Cooper and Schliwa, 1986; Xu et al., 2003; Zigmond et al., 1981). This observation indicates that rapidly motile, persistently polarized cells are capable of generating persistent mechanical left-right asymmetries that result in cell turning.

Most studies of the mechanics of cell turning during persistent migration have focused on characterization of asymmetries at the cell leading edge (Insall, 2010). For example, the direction of travel in fibroblasts and endothelial cells is thought to be altered by the summation of competing weakly stable PI3K dependent protrusive branching events (Weiger et al., 2010; Welf et al., 2012), with a relationship between asymmetric calcium flickers and the direction of travel (Tsai and Meyer, 2012; Wei et al., 2009). Work in axonal growth cones of neurons has also implicated local variation in microtubule dynamics (Buck and Zheng, 2002) and adhesion turnover (Myers and Gomez, 2011) in turning behavior. This prior work examining the leading edge, though, has not taken into account the complete set of physical interactions inherent to turning in cell migration, as significant mechanochemical systems that orchestrate cell motility exist outside of this region. For instance it has been established that the initial process of polarization can originate at the cell rear (Cramer, 2010; Mseka et al., 2007; Yam et al., 2007), and that positive feedback between myosin contraction and actin flow and negative feedback between actin flow and adhesion are responsible for this polarization (Barnhart et al., 2015). Furthermore, it has not been possible to use the mechanics of cell migration to recreate the detailed trajectories that cells have been observed to take when only the behavior of the leading edge is taken into account (Selmeczi et al., 2005; Stokes et al., 1991).

In order to develop an understanding of the cell-scale mechanics necessary to change the direction of travel, we have used the model system of the fish epidermal keratocyte. These rapidly moving cells are mechanically and geometrically simpler than fibroblasts or neutrophils, allowing construction of quantitative mechanistic models that can replicate even complex aspects of their observed behavior (Barnhart et al., 2011; Keren et al., 2008). Motile keratocytes also normally maintain only a single protrusion with an extremely long persistence time, making them an ideal system to study the methods for mechanical determination of left-right turning behavior at steady state.

Migration in keratocytes is governed by a set of fundamental forces and mechanical actors that have been integrated into a general mechanical model (Barnhart et al., 2011). Driving protrusion is a densely branched polymerizing dendritic actin network at the leading edge (Svitkina et al., 1997). Opposing the force of actin polymerization is the tension in the plasma membrane of the cell, which spatially integrates force across the cell (Keren et al., 2008; Mueller et al., 2017). Nascent adhesions are laid down at the leading edge (Lee and Jacobson, 1997) and coordinate the protrusive force of the actin network into mechanical work with only a minimal rate of slip relative to the substrate, otherwise known as retrograde flow (Wilson et al., 2010). Adhesions chemically mature and become mechanically weaker as the cell translocates over them (Barnhart et al., 2011). A large set of binding proteins interact with the actin network to bundle filaments, cap barbed ends, create new branch points, and sever filaments. This set includes the force-generating protein myosin II, which binds the actin network and acts to contract and disassemble it at the rear of the cell (Wilson et al., 2010). This contraction of the actin network creates retrograde flow of filamentous actin at the cell rear oriented towards the cell body and perpendicular to the direction of motion.

Prior examination of keratocyte turning has shown a correlation between asymmetric traction stresses and sharp turns (Oliver et al., 1999) as well as an asymmetry in the coupling of actin filament motion and traction forces (Fournier et al., 2010). However, these prior analyses were limited in scope to only the forces applied to the substrate. In this work we seek to determine how all known mechanical actors of cell motility (actin network assembly, network disassembly, network contraction, adhesion to the substrate and membrane tension) produce lateral asymmetry and consequently turning behavior in motile keratocytes. We find that left-right asymmetries determining turning behavior are controlled by the interwoven actions of myosin II contraction and substrate adhesion at the rear of the cell, and not by actin polymerization at the front of the cell, producing a form of “rear-wheel steering”. These mechanical systems are organized in a combination of feedback loops, such that these cells can enter into and exit from states of stable persistent turning.

Results

Keratocytes enter into persistent turning states

To begin to explore the physical mechanisms that underlie cell turning, we first measured the trajectories of 38 spontaneously migrating individual cells over time periods of four to eighteen hours (Figure 1A). While a minority of cells (9 of 38 examined) seemed to follow a meandering trajectory approximating a persistent random walk, the majority (29 of 38) exhibited trajectories that included at least some persistent segments, where the cell typically turned in a small circle several times, intermixed with periods of nearly straight movement, reminiscent of “knots on a string” (Figure 1B). These two qualitatively distinct types of motion could be distinguished quantitatively by comparing their angular speed (w) over time and the autocorrelation of the angular speed A(w) (Figure 1C–E). Persistent cells (e.g. cell-7; magenta) typically moved with a fairly constant angular speed for many minutes before switching (Figure 1C), generating strong positive autocorrelation signals (Figure 1D) and bimodal distributions of angular speeds (Figure 1E), while non-persistent cells (e.g. cell-8; gold) showed a much faster decay in autocorrelation and a unimodal distribution of angular speeds centered around 0. Persistently turning cells were equally likely to travel in clockwise or counterclockwise circles, and individual cells could switch between CW and CCW turns without apparent bias or memory (Figure S1A). The dwell time between switching events was broadly distributed (Figure S1B).

Figure 1. Long-term trajectories of single cells exhibit persistent turning states.

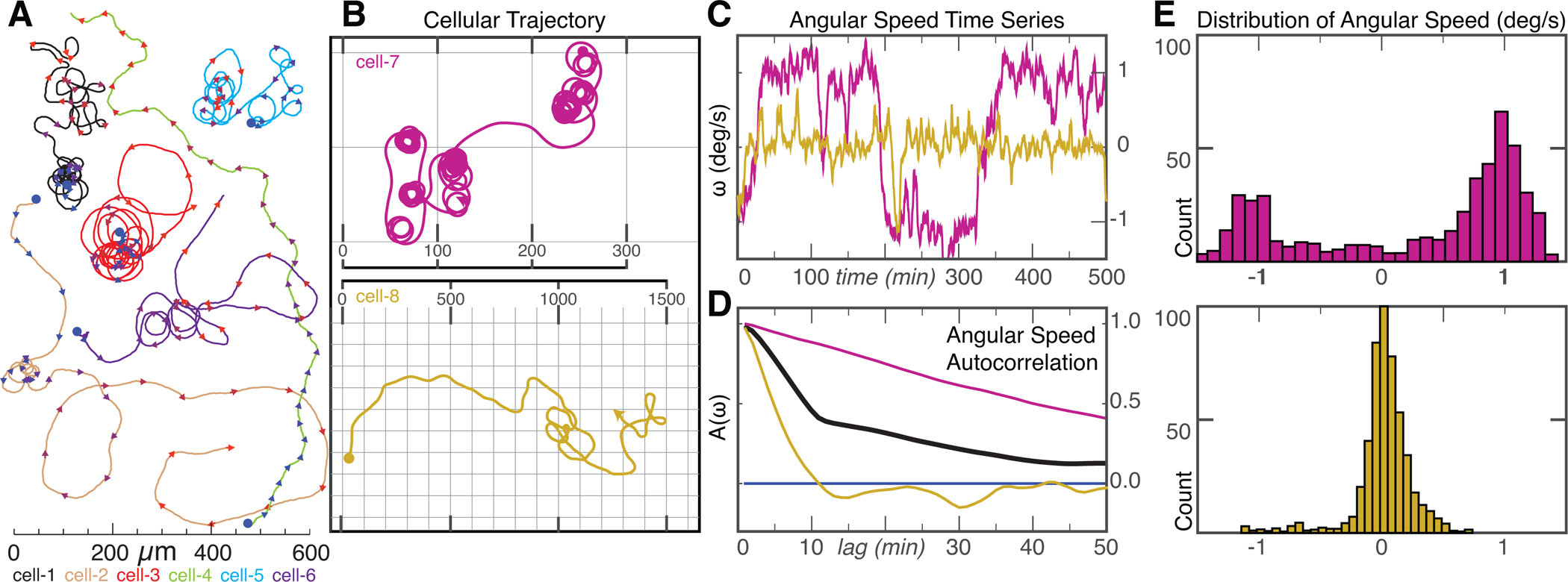
(A) Example trajectories of 6 keratocytes cells over a time scale of ~10 hours. Trajectories start at blue dots, and each color represents a different cell. Arrowheads indicate the current direction of motion every 20 minutes and are colored from blue/start to red/finish. Scale bar indicates distance traveled. Note cells can exhibit two phases of migration with long periods of persistent turning intermixed with periods of straighter paths.

(B) Example trajectory of a cell exhibiting prolonged periods of persistent turning (cell-7, magenta, top) and a cell following a wandering path (cell-8, gold, bottom). Scale in micrometers.

(C) Time series of angular velocity, (ω), for cell-7 (magenta) and cell-8 (gold).

(D) Auto-correlation of angular velocity (A(ω)) as a function of lag time in minutes for cell-7 (magenta), cell-8 (gold) and average of all 38 cells (black).

(E) Distribution of angular velocities for the persistently turning cell-7 (magenta, top) and the wandering cell-8 (gold, bottom).

Using simulations of randomly generated trajectories, we explored whether any kind of simple stochastic fluctuations could account for these observed behaviors (Figure S1C). A simple random walk model where the direction of motion is randomized at each time step (Figure S1C, Model A) gives a uniform distribution of angular speeds, and no persistent directional autocorrelation. A more realistic model of a persistent random walk in which a cell tends to continue moving in the same direction but with slight random turns at each step, such as has been used to describe the motility of Dictyostelium discoideum (Van Haastert, 2010), fibroblasts (Gail and Boone, 1970), endothelial cells (Stokes et al., 1991) and granulocytes (Hall and Peterson, 1979) (Figure S1C, Model B) could produce trajectories that resembled those of the subset of less persistent keratocytes with an appropriate distribution of angular speeds, but with less angular autocorrelation than was experimentally observed. In an attempt to appropriately simulate the trajectories of the majority of keratocytes with persistent turning and high A(ω), we next attempted simulating stochastic variations in the time derivative of ω rather than in ω itself (Figure S1C, Model C). This model, in essence a correlated random walk in angular velocity space, has been used previously to describe the paths of humans who have been blindfolded to their external environment, who frequently generate trajectories qualitatively similar to “knots on a string” (Souman et al., 2009), an interesting parallel to the non-chemotactic keratocytes. The blindfolded human model produced trajectories that were somewhat reminiscent of the keratocytes and did exhibit slow autocorrelation decay of angular speed but could not reproduce the frequently observed bimodal distribution of instantaneous angular speeds (Figure S1C, Model C). The nature of the quantitative mismatch between this model and the experimental observations can also be seen by examining the mean squared displacement of angular speed over time; the model shows a diffusive (approximately linear) relationship while the experimental data for keratocytes quickly rises and then plateaus (Figure S1D). Thus, the observed keratocyte behavior cannot be adequately explained by any simple fluctuation-based model.

Mechanically, the existence of persistently turning keratoctyes with bimodally distributed angular speeds informs us that there must exist persistent asymmetries in mechanical behavior that are perhaps maintained by feedback of the act of turning on the mechanical asymmetries that produce turning. Individual cells with particularly strong autocorrelations in angular speed were also typically fast-moving and typically turned in tight circles (Figure S1E,F), although in the population as a whole there was no strong correlation between net speed and angular velocity (Figure S1G).

Turning cells exhibit an asymmetric shape and F-actin distribution

The observation that many keratocytes can enter a persistently turning state afforded us the opportunity to examine cytoskeletal variations associated with cell turning. For cells to enter persistent turns, there must be a persistent imbalance in at least one of the mechanical elements that produce motility. Images of a typical persistently turning cell (Figure 2A,B and Movie S1) showed that the cell body at the rear is biased toward the inner side of a turn, in contrast to the typical symmetric fan shape of a keratocyte that is moving in a straight line (Csucs et al., 2007; Goodrich, 1924). The flat, actin filament rich-lamellipodium at the front of the turning cell is also not symmetric, but instead is elongated in the “wing” on the outer side. Whole cells with an overall increased aspect ratio (elongated lamellipodia) tend to also exhibit increased cellular speed (Keren et al., 2008) suggesting that there may be asymmetric protrusion along the leading edge for turning cells, such that the part of the lamellipodium on the outside of the turn is effectively moving faster than the part on the inside.

Figure 2. Turning cells have asymmetric shapes and F-actin distributions.

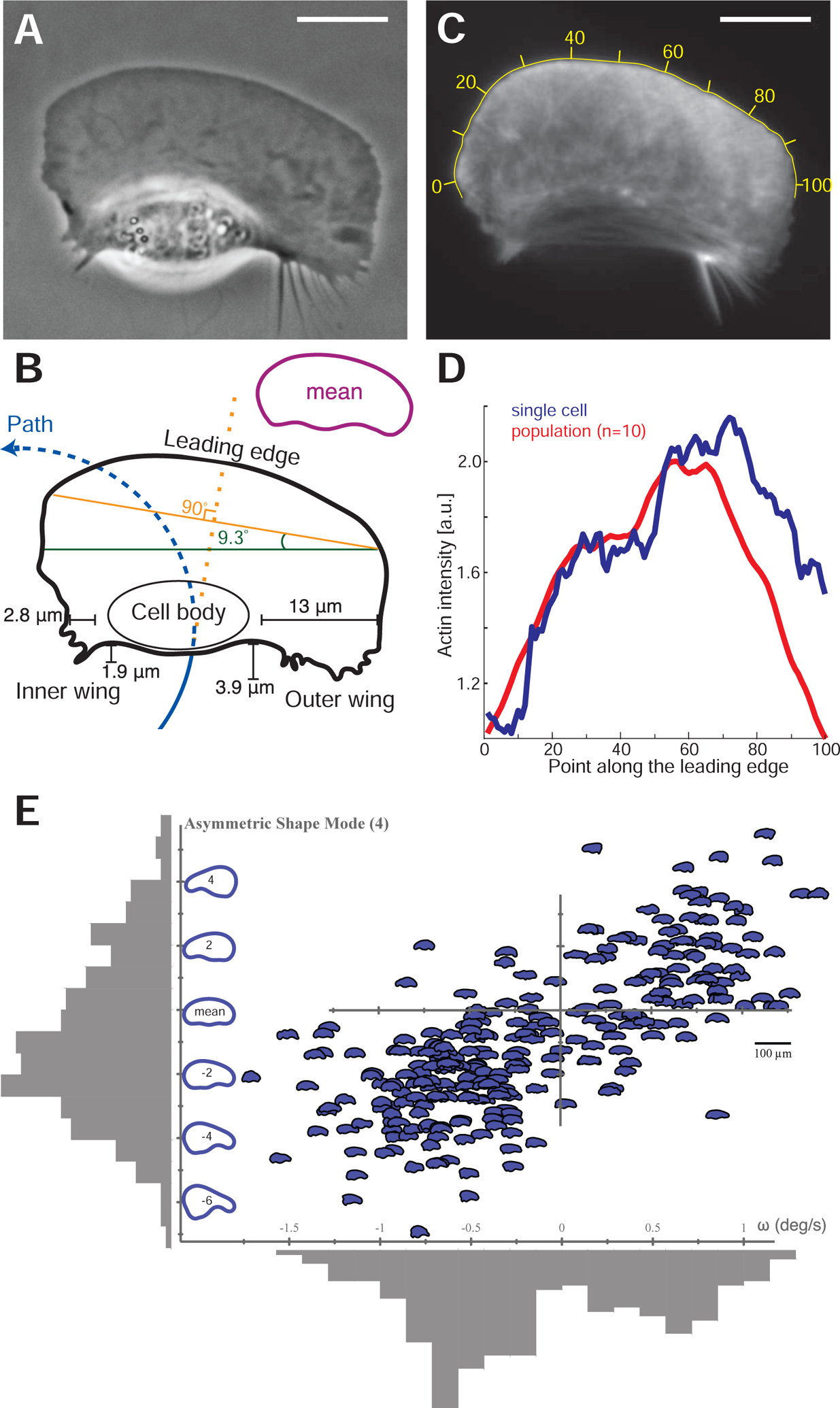
(A) Example phase-contrast image of a cell in an asymmetric circular path turning counter-clockwise. Scale bars in all panels are 10 μm.

(B) The contour of this cell illustrating the cell path (blue line) as well as the elongated aspect ratio on the outer side of the turning cell. The cell body is displaced towards the inside of the turn, and the outer wing lags behind the cell. The leading edge orientation (orange line) is orthogonal to the direction that the cell was previously traveling previously (dashed orange line) and the rear edge orientation (green line) is orthogonal to the direction the cell is currently traveling. The inset contour shows the average shape of 22 mutually aligned turning cells.

(C) F-actin distribution from this turning cell as visualized by AF-488 phalloidin labeling, with yellow numbers indicating position along the leading edge.

(D) Measured density of F-actin along the points of the leading edge of the cell in panel C (blue line) and in the average of a population of 10 turning cells (red line). Note the asymmetric accumulation of actin filaments at the leading edge on the outer side.

(E) For a single cell that is being forced to turn at a high rate by exposure to multiple external electric fields over 272 time points over approximately 20 minutes, the angular velocity at each time point, ω, is plotted against the left-right asymmetric PCA shape mode (Keren et al., 2008) as depicted on the vertical axis. The distribution of values for both asymmetric shape and angular velocity are plotted in grey adjacent to each axis. Calculated correlation coefficient is 0.73, calibration bar for cell outline images is 100 μm.

The shape of the turning cells suggests that there are two relevant axes that describe the shape of the cell relative to its trajectory. One is the orientation of the leading edge, as defined by the front two corners of the approximately rectangular lamellipodium (Figure 2B, orange line), which appears to lie on an axis approximately perpendicular to direction that the cell was traveling recently (dashed orange line). The other axis is defined by the rear of the cell through the cell body (green line) and is observed to be oriented perpendicular to the direction that the cell is currently traveling (dashed blue line). The characteristic asymmetric shape of turning cells was confirmed by creating an average shape from 22 cells selected for their persistent turning behavior, which shares the major features noted in the example shown (Figure 2B, inset). Although a previous statistical analysis of shape had shown that only ~1% of total shape variation arises from left-right asymmetry (Keren et al., 2008), within the population of turning cells we found that this particular mode of shape variation was strongly correlated with angular speed (Figure 2E, Figure S2A).

Imaging the filamentous actin cytoskeleton driving cell motility in a persistently turning cell (Figure 2C) revealed consistent asymmetries in the cytoskeleton that correlated with the observed asymmetries in shape. Our initial expectation was that protrusion would be fastest in the direction the cell was traveling towards, that is on the inside of the turn (Mogilner and Rubinstein, 2010). In this situation actin filament density, D, would be expected to be highest on the inner part of the turn as the cell lays down an asymmetrically protruding network. However, we observed instead that the distribution of filamentous actin at the leading edge showed higher F-actin density on the outer wing of the lamellipodium of turning cells (Figure 2D), matching the higher aspect ratio on the outer side of the cell. Furthermore, turning cells exhibited significantly faster rates of actin network disassembly in the outer wing of the lamellipodium (Figure S2B–D). Thus, instead of protruding into turning behavior, cells are actually pivoting around turns with faster lamellipodial protrusion on the outer side of the turn. Quantitatively we note that there is an ~20% increase in F-actin density on the outer side of the turning cell (Figure 2D), which can at most account for a few tens of percent increase in the protrusion rate (Keren et al., 2008). Yet, given that the typical radius of curvature of the centroid motion for a persistently turning cell is ~25 μm with a typical cell width of ~ 40 μm, there must be a ~9-fold gradient in effective net speed from the inside of the cell to the outside. Therefore, protrusion asymmetry alone can only be a minor factor in cell turning.

Turning cells have a stereotyped asymmetric myosin II organization that is necessary to maintain persistent turning

An alternative hypothesis is that whole-cell turning is not primarily driven by asymmetry in actin filament polymerization at the cell leading edge, but rather by asymmetry in the myosin-II driven centripetal flow of actin filaments toward the cell body at the cell rear. We found that the distribution of non-muscle myosin II regulatory light chain at the cell rear, normally found in two similar spots on either side of the cell body in a straight-moving cell (Wilson et al., 2010), is strongly asymmetric in a persistently turning cell, with greater myosin II density on the outer wing of the cell (Figure 3A, B, Movie S2). In addition, the degree of left-right asymmetry in myosin II heavy chain as determined by immunofluorescence among a population of individual cells correlated with a smaller radius of path curvature (tighter turning) for each cell (Figure 3C). We also generated a spatial map of myosin activity by comparison of extracted actin networks of turning cells before and after addition of ATP to trigger myosin II network disassembly activity (Wilson et al., 2010), which revealed a pattern of activity that extended more prominently into the outer wing for turning cells (Figure S2E), consistent with the faster rate of actin network disassembly observed in this region (Figure S2D).

Figure 3. Asymmetric myosin activity drives persistent cell turning.

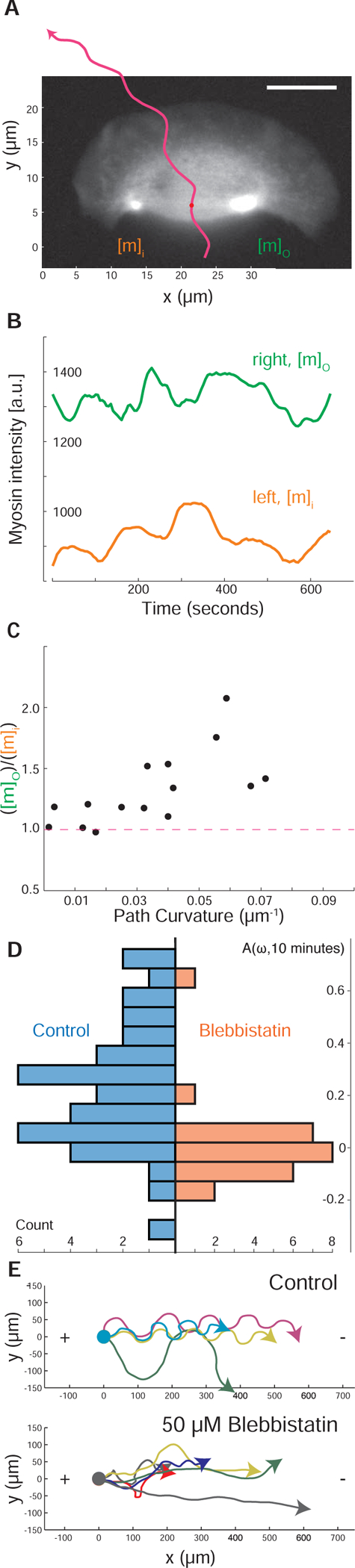
(A) A sample image of myosin regulatory light chain-YFP distribution in a turning cell with a counter-clockwise path (magenta line). Note that the myosin II density is higher on the outer side of the turning cell.

(B) Time series of the myosin density in the outer wing, m_o (green), and inner wing, m_i (orange), of the cell from panel A, showing consistently higher myosin on the outer side of this turning cell over time. Note that the vertical axis does not start at 0.

(C) The relative concentration of myosin II heavy chain as determined by immunofluorescence on the outer and inner sides of cells that were imaged live prior to fixation (vertical axis), plotted against the cell’s path curvature prior to fixation (horizontal axis). Note that cells with a greater degree of turning had an increase in the asymmetry of myosin II localization, correlation coefficient is 0.67 for 15 cells.

(D) The distribution of calculated auto-correlation of angular velocity with a lag of 10 minutes was calculated for control cells (left/blue) and cells treated with the myosin-II inhibitor blebbistatin (right/orange). Inhibition of myosin-II drastically reduced the number of cells exhibiting persistent turns.

(E) The trajectories of cells exposed to an electric field of 5 V/cm under control conditions (top) and with inhibition of myosin II (bottom). All cells migrate towards the cathode on the right, but only cells under control conditions have a periodic overshoot of a straight trajectory suggestive of persistence of a previous angular velocity.

Global pharmacological inhibition of myosin II activity in keratocytes using the small molecule blebbistatin (Straight et al., 2003) decreased the amount of time cells exhibited persistent turning, producing cellular trajectories that were noticeably straighter over long (10 minute) time scales than those of untreated cells (Figure 3D). This selective loss of persistent turning in response to myosin II inhibition was also observed in the directed migration of keratocytes toward the cathode in a DC electric field (Allen et al., 2013). Typical cells will turn toward the cathode and then continue to turn persistently, overshooting the straight path predicted by the directional cue of the electric field and therefore producing characteristic strongly periodic oscillations (Figure 3E, top). Addition of the myosin II inhibitor blebbistatin inhibits this persistent turning, and therefore cells follow relatively straight trajectories toward the cathode (Figure 3E, bottom). Direct observation of cells turning in an electric field following inhibition of myosin II contractility showed that turning under these conditions was driven morphologically by asymmetric actin polymerization (Figure S2F), distinct from the persistent turning behavior described above for unperturbed cells. Thus, pharmacological inhibition of myosin II activity does not prevent the detection of electric fields by keratocytes but does prevent them from entering a persistent turning state either spontaneously or following exposure to an electric field. These observations hint at positive feedback between the kinematics of turning and the left-right asymmetry of myosin distribution in moving cells: such feedback ‘locks’ the cell into a turning state, until a sufficiently large disruption breaks the feedback loop.

Asymmetric myosin II activity drives asymmetric inward actin flow at the cell rear, producing cell turning

Myosin II acts at the rear of the motile cell in part to contract the filamentous actin cytoskeleton, generating net flow of the actin network. Asymmetric actin flow due to the asymmetric myosin II localization described above might lead to cell turning by at least two distinct mechanisms. First, enhanced myosin II activity at the rear at the outside edge of the cell might generate faster retrograde flow relative to the substrate on that side, resulting in actin network slippage relative to the substrate and therefore slower net forward protrusion. Alternatively, enhanced myosin II activity at the outside edge might cause faster inward (centripetal) flow at the rear of the cell only, without affecting retrograde actin flow at the leading edge, such that cells are able to turn by pivoting the orientation of their lamellipodia around their cell bodies.

To determine feedbacks between the actin network motion and the persistent asymmetry in myosin II distribution associated with persistent cell turning, we directly measured F-actin network flow using fluorescent speckle microscopy (Danuser and Waterman-Storer, 2006). Speckle microscopy visualizes motion, and it is helpful to describe this motion using two frames of reference. In one frame of reference, that of the cell, the cell looks static, but everything around it moves (this is depicted in the inset of Figure 4A and Movie S3). This frame is useful to understand how the cell turning generates the asymmetric myosin distribution: myosin is transported inside the moving cell by the F-actin network flow in this frame, and we can predict where myosin accumulates by simply following where the F-actin network flows in the moving cell frame. In the other frame of reference, that of an observer in the lab, the cell looks like it’s moving, but everything around it looks static (this is depicted in the inset of Figure 4B and Movie S3). This frame is useful for answering the question about where the F-actin network flow is asymmetric – at the front or rear of the cell.

Figure 4. Asymmetric centripetal actin network flow in turning cells produces an asymmetric myosin distribution.

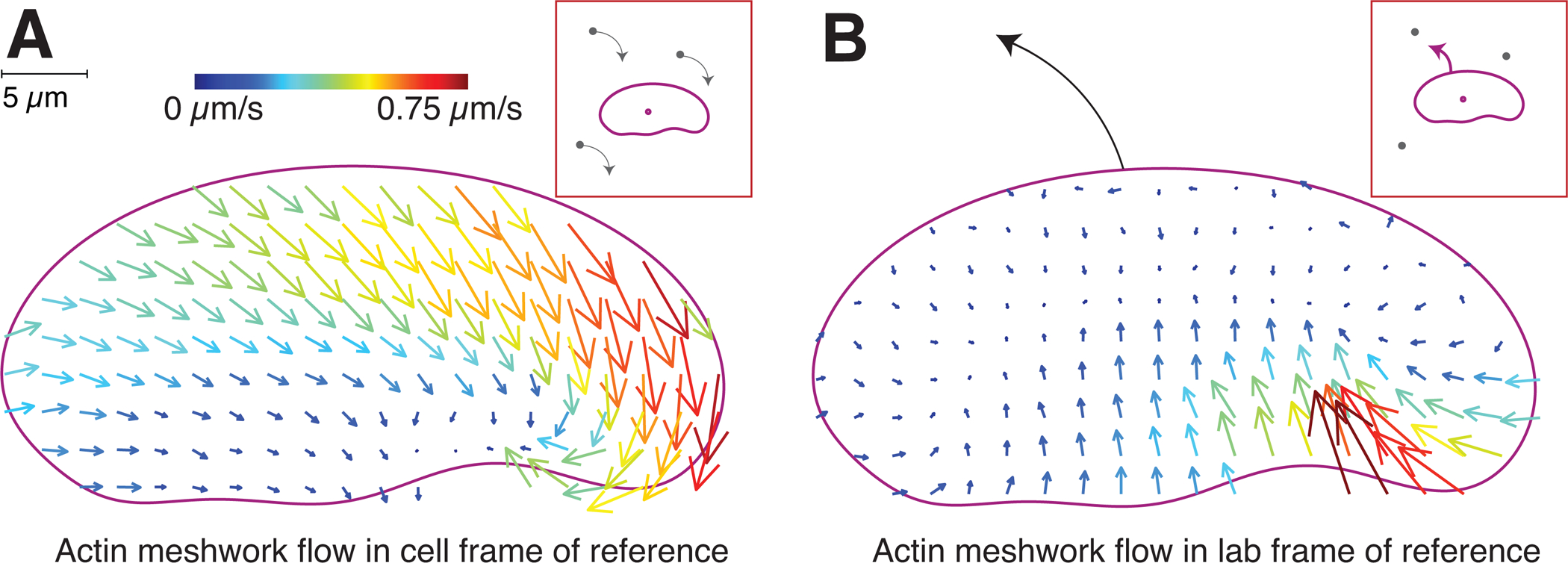
Experimentally determined vector maps representing fluorescence speckle microscopy measurements of the flow of the F-actin network in the cell frame of reference (A) and in the lab or substrate frame of reference (B) for a cell turning counter-clockwise. Results are representative of measurements made in 12 separate cells. Graphical depictions of each frame of reference are presented in insets. Scale bar indicates 5 μm, and vector arrow size and color scales with magnitude of flow speed.

In the laboratory frame of reference, the F-actin network remained essentially static relative to the substrate at the leading edge, with measurable flow only at the rear of the cell, about 5-fold faster inward on the outside of the turning cell relative to the inside (Figure 4B, Movie S3). This observation is consistent with previous observations for keratocyte motility suggesting that newly polymerized actin is tightly coupled to the substrate by integrin-mediated adhesions, resulting in very little retrograde flow at the leading edge (Theriot and Mitchison, 1991; Wilson et al., 2010). Furthermore, this observation rules out the possibility that a hidden asymmetry in relative protrusion is occurring at the leading edge secondary to asymmetric retrograde flow at the leading edge. Instead this result indicates that the lamellipodium of a turning cell can best be thought of as a filamentous actin network that is laid down roughly symmetrically at the front but acted on asymmetrically at the rear by inward myosin II-dependent contractility to produce large-scale cellular turning.

In the moving cell frame of reference, we found that actin network flow relative to the leading edge was strongly tilted toward the outside rear corner of the cell (Figure 4A, Figure S3A, Movie S3), in contrast to the typical flow pattern for the cell frame of reference in cells moving straight, where the network flows straight backward from the leading edge to the cell rear (Wilson et al., 2010). Conceptually, in the framework of the cell moving forward and turning to the left, the actin network slides diagonally inward from the front left to the rear right (Figure 4A, Movie S3). Myosin largely sticks to and moves with the actin network (Barnhart et al., 2011; Barnhart et al., 2015; Tsai et al., 2019), and so the actin flow ‘sweeps’ myosin to the rear right of the cell turning to the left (Figure 3A,B). The resulting myosin concentration at the rear right of the cell causes elevated level of contraction of the actin network, weakened by disassembly (Wilson et al., 2010; Ofer et al., 2011), and this contraction translates into the accelerated centripetal flow of the lamellipodial network at the rear right (Figure 4B, Movie S3). This accelerated flow brings the rear right end of the cell forward and to the left, effectively reorienting the cell’s rear edge pivoting it to the counterclockwise. Thus, the asymmetric myosin II localization, dynamic geometry of the turning cell and asymmetric actin network flow combine into a positive feedback loop enabling the cell to enter a persistent turning state.

Traction force asymmetry implicates asymmetric cell adhesion during turning

Given that cell-substrate adhesion in migrating cells is coupled to both actin network flow and to myosin II contractility (Gardel et al., 2010) we explored whether asymmetries in adhesion might also contribute to the persistent turning state.

Measuring adhesion strength directly is not possible, however, the ratio between the local traction force and the local actin flow rate is the accepted harbinger for the local adhesion strength (Gardel et al., 2008; Fournier et al., 2010; Barnhart et al., 2011; Barnhart et al., 2015). Indeed, when the actin network flows relative to the substrate, the molecular adhesion complexes dynamically connect the actin network and substrate and switch between gripping the surface and slipping along it, effectively creating friction between the substrate and flowing actin network (Vicente-Manzanares et al., 2007; Gardel et al., 2008; Fournier et al., 2010; Barnhart et al 2011; Barnhart et al., 2015). Due to this friction, the cell applies force to the substrate, called the traction force (Sabass et al., 2008; Gardel et al., 2008; Fournier et al., 2010) that is locally proportional to the actin flow rate, according to the widely assumed viscous character of the friction between the cell and substrate (Fournier et al., 2010; Barnhart et al., 2011). The proportionality coefficient between the actin flow rate and traction force is the local adhesion strength (Fournier et al., 2010). (We explain the motile cell mechanics further in Figure 7 and Box 1.)

Figure 7. Schematic of mechanical actions underpinning cell turning.

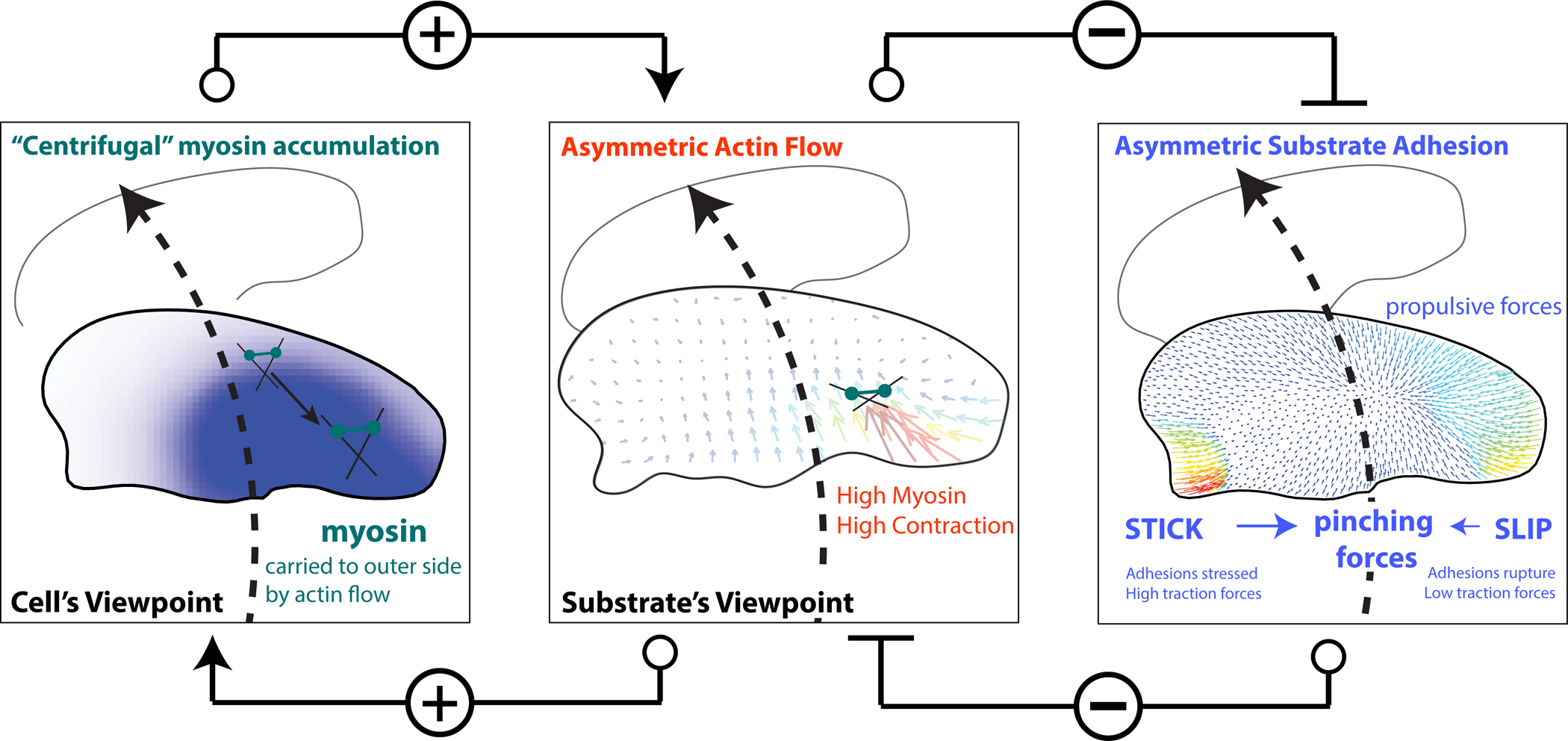
A mechanical model of cell turning in keratocytes. (left panel) The act of turning creates the “centrifugal” accumulation of myosin bound to the actin filaments to the outer side of the cell. (center panel) Myosin accumulation on the outer side of a turning cell, increases local myosin contractility and the centripetal flow of actin slipping over the substrate on the outer side of the cell driving turning. Typical actin meshwork flow from the substrate’s frame of reference is shown. Positive connectors indicate positive feedback between asymmetric actin flow and myosin accumulation.

(right panel) Increased myosin contractility and actin flow on the outer side of the turning cell breaks adhesions on the outer edge of the cell (SLIP), weak traction forces (colored vectors) and further promoting the centripetal sliding of the outer actin network over the substrate and consequently turning. Conversely, STICK conditions on the inner side of a turning cell, create strong adhesion and large traction forces. Pinching traction forces perpendicular to the direction of movement are asymmetric. Traction forces at the leading edge are propulsive, and at the rear – resistive. Thus, the elevated contractility and flow on the outer edge inhibit the formation of strong adhesion on the outer edge, which would otherwise inhibit turning (Negative connectors indicate double negative feedback between asymmetric actin flow and adhesion strength). The traction forces and asymmetric adhesions are explained further in Box 1.

Box 1. A turning cell’s mechanics: a primer.

Inside the cell the mechanics of the turning keratocyte cell is, roughly speaking, dominated by myosin clusters contracting the depolymerization-weakened actin network at the rear centripetally inward towards the center. This contraction generates the centripetal actin flow, which is faster at the outer cell edge of a turning cell (to which myosin is swept “centrifugally” in the framework of the turning cell). These internal forces are coupled to the substrate outside the cell by adhesions.

Complex molecular chains of adhesive proteins can be simplistically thought of as springs attached to the substrate, with sticky ends that randomly and dynamically associate and dissociate with the lamellipodial actin network. When the actin network begins to flow, the attached adhesive springs get stretched, and when the stretched springs are detached, the elastic energy of the stretch is dissipated, generating an effective viscous drag. When the actin flow is slow, a significant fraction of the adhesive springs is associated with the actin network and stretched, and the drag is significant – this is the STICK (or GRIP) state. On the other hand, when the flow is fast, many sticky ends of the springs are ripped off the rapidly moving actin network, and the springs do not have time to stretch causing a drop in the effective drag – this is the SLIP state.

On the outside of the cell we can measure the adhesive force of the cell on the substrate, also called the ‘traction’ force, which is equal to the product of the adhesion strength and actin flow velocity. Due to the greater contractility and faster flow, the adhesions at the outer edge are slipping, in fact, they get weakened so much that the resulting ‘traction’ force, is smaller at the outer edge, despite the faster flow there.

Geometrically, the traction force can be decomposed into the pinching, side-to-side contracting, force, and the propulsive-resistive, front-to-rear, force. The easiest way to visualize these forces is to imagine a person training a horse; she stands at the center of a circle and holds a rope, while the horse, harnessed to the rope, runs along the circle’s perimeter. The person is the cell’s inner wing; the horse is the cell’s outer wing. The person’s and horse’s muscles are myosin; their feet are adhesions; the rope is the lamellipodial actin network. The person’s feet grip the surface, and there is a significant pinching (radial) traction force that her feet exert on the surface. Each of the horse’s hoofs is not exactly slipping (this is where the analogy does not quite hold) but exert a smaller pinching traction force (only the sum of all hooves’ pinching traction is equal to the person’s pinching traction). Now, imagine that the horse also pulls a sled. The feet of the horse generate propulsive traction force applied to the surface from the front to the rear (along the circumference) – these are the forces propelling the running animal forward. The sled behind creates a resistive drag applied to the surface in the rear-to-front (again, along the circumference) direction. This analogy, with all its imperfections (after all, the inner wing of the cell is not stuck but is moving slowly), illustrates all crucial left-right asymmetries of the forces and adhesion in the turning cell. Amusingly, even asymmetric contractile strength (the horse is stronger than the person) is the same in this analogy and turning cell.

We measured the traction forces that a turning cell applied to the substrate through its actin network using traction force microscopy (Sabass et al., 2008) in order to experimentally distinguish between these two possibilities (Figure 5A). We found that motile keratocytes primarily generated traction forces orthogonal to the direction of motion, confirming prior results (Oliver et al., 1999). Cells that moved straight showed midline symmetry in the inward forces exerted on the substrate (T⊥(in/out) =1.1±0.3, n = 4) whereas turning cells had an increase in inward-directed traction forces on the inner side (T⊥(in/out) =1.7±0.7, n = 5). Thus, on the side of the cell where actin flow was slower the generated traction forces were actually higher indicating strong adhesion of the cell on the inside of the cell. Conversely on the faster side of the cell where actin flow is faster, traction forces were smaller indicating weaker adhesion on the outside of the cell. Mechanistically, the observed large inward traction force on the inner side of the turning cell must result from the gripping traction from high local adhesion at the pivoting point, which is balanced by opposing traction throughout the rest of the cell.

Figure 5. Turning cells apply asymmetric traction forces.

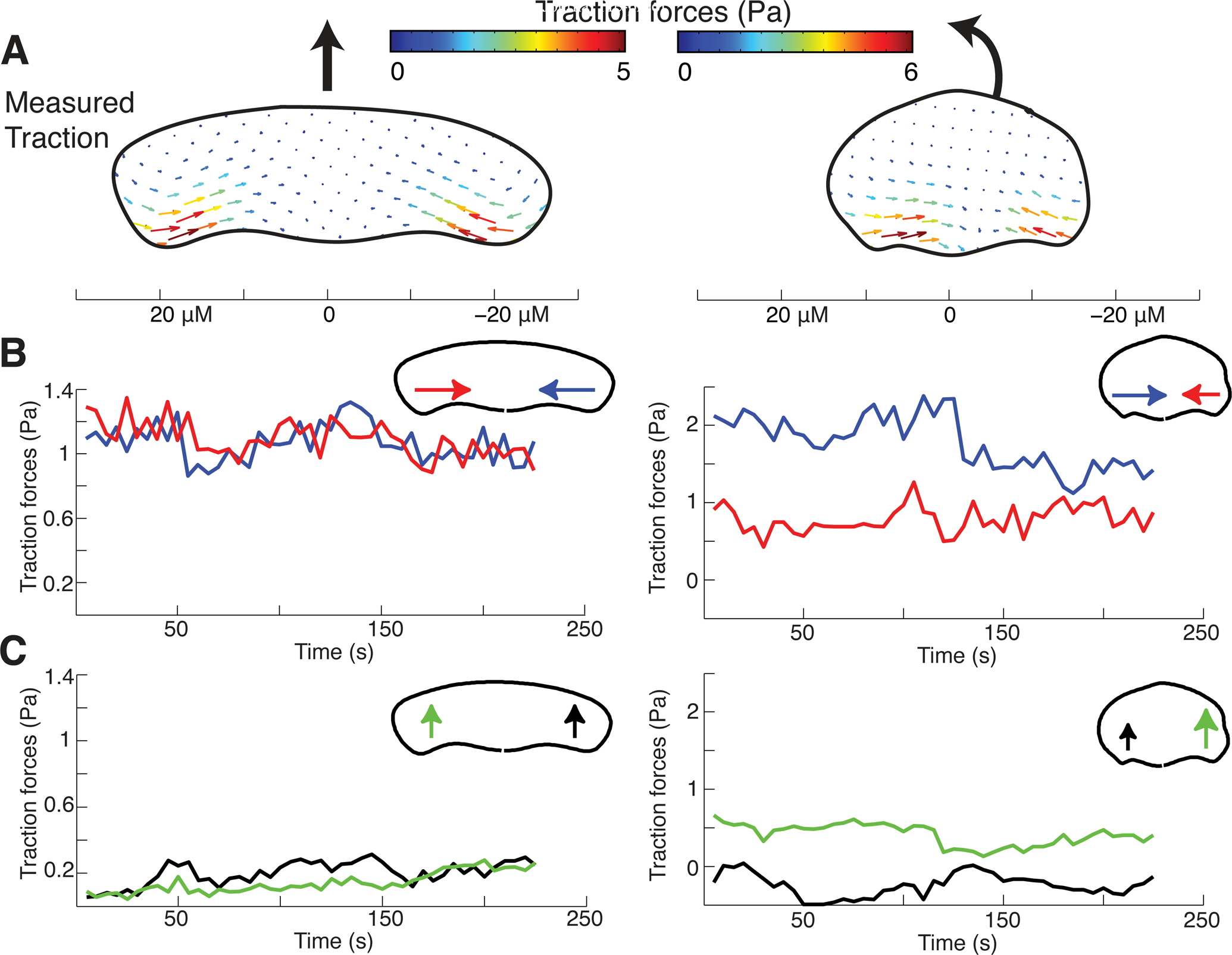
(A) Vector maps of average experimentally measured traction forces created by a cell migrating along a straight path (left) and a cell turning counterclockwise (right). Scale bar presented below is in microns.

(B) Time series of the spatial average of the inward component of traction forces on the left (red) and right (blue) sides of the same cells as in panel C. Note that turning cells have persistently higher inward traction forces on the inside of the turn when compared to the outside, which matches simulations performed with higher adhesion strength on the inside of a turning cell.

(C) Time series of the spatial average of the forward component of traction forces on the left (green) and right (black) sides of the same cells. Note that turning cells have persistently higher forward traction forces on the outer side of the turning cell when compared to the inner side, again matching simulations with left-right adhesion asymmetry.

In addition, forces were found to have a more forward orientation at the outside rear for turning cells, as compared to either the inside rear of a turning cell or the rear of a cell moving straight (Figure 5C). The forward component of the traction force at the rear of the outer side of the cell is a “slipping” resistive adhesion force due to forward locomotion and is balanced by the “gripping” retrograde traction force spread over the wide leading edge.

Together, our observations of faster inward actin network flow on the outside of a turning cell (Figure 4B) coupled with stronger traction force on the inside of the turning cell (Figure 5A–B) are consistent with a non-linear “stick-slip” mechanism for traction force generation (Sabass and Schwarz, 2010), where traction stresses are proportional to F-actin flow at low F-actin flow speeds and inversely proportional to flow at high speeds, as has been experimentally observed in mammalian epithelial cells (Gardel et al., 2008) as well as in keratocytes undergoing spontaneous symmetry-breaking during movement initiation (Barnhart et al., 2015). As the inward flow of the actin network at the keratocyte rear is driven by myosin II contractility (Wilson et al., 2010), this sets up a second feedback loop, where increasing the myosin contraction of the actin network accelerates the F-actin flow until it is too fast to be sustained, at which point increasing contractility weakens adhesions, further facilitating rapid flow of the actin network on the outer side of the cell.

Local modification of adhesion or myosin contractility is sufficient to induce cell turning.

From these observations, we predicted that experimental perturbation of either local myosin contractility or local adhesion on one side of the rear of a moving keratocyte should be sufficient to induce cell turning. Indeed, we found that direct local application of the myosin II activating serine-threonine phosphatase inhibitor calyculin A using a micro-needle to one side of individual cells was sufficient to induce cells to turn away from the site of drug application (dθ = 46±24 degrees, Figure 6A), unlike control dye administration (dθ = −10±50 degrees). Similarly, when we examined the migration of individual cells crossing boundaries between substrates of normal to low adhesivity (Barnhart et al., 2011) we found that asymmetry in adhesion could cause cell turning towards the higher adhesion substrate (Figure 6B,C, Movie S4). The average induced turn was ~90 degrees and as expected had an apparent dependence on the angle of incidence, which dictates the degree of adhesion asymmetry. Cells crossing the boundary in the opposite direction (from low to normal adhesivity) also turned toward the substrate of higher adhesivity (Figure 6C). Importantly, we found that directionality changes predominantly (>70%) occurred as the rear of the cell crossed the adhesion boundary. This confirms that asymmetric myosin II contraction of the actin network at the cell rear alone or asymmetric coupling of the myosin II mediated centripetal actin flow to the substrate are both sufficient to trigger a cell to transiently turn away from the side of faster inward actin network flow. However, neither treatment could routinely induce a persistent turning state where cells generated circular trajectories as described above; instead most cells returned to a fairly straight path after transient perturbation (Figure 6A,C).

Figure 6. Myosin or adhesion asymmetry is sufficient to induce turning.

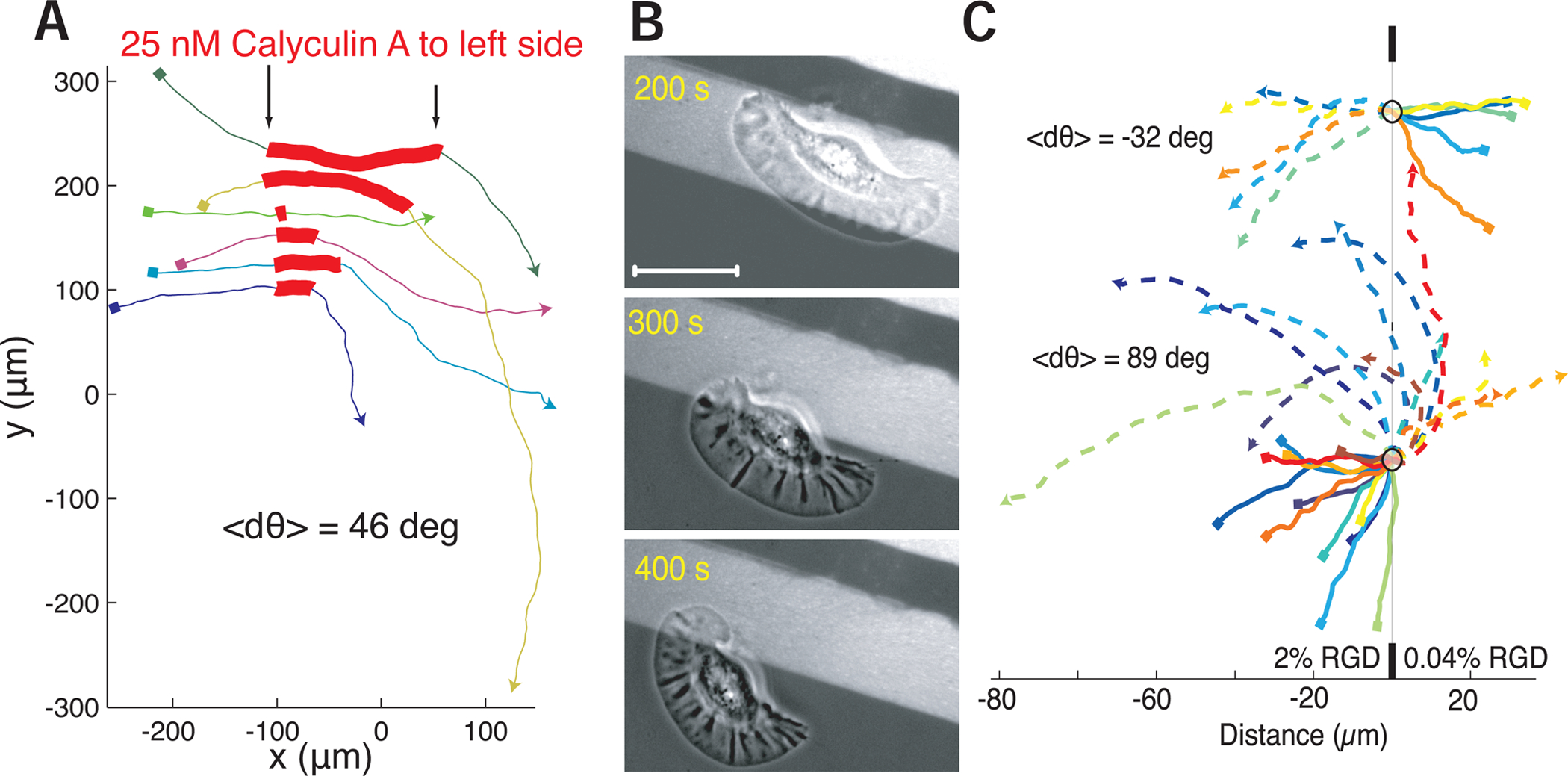
(A) The trajectories of a set of cells that were asymmetrically exposed to calyculin locally on the left side of the cell during the portion of the trajectory marked in red. Local calyculin exposure induced cells to turn away from the side of upregulated myosin II activity. Trajectories start at squares and proceed from left to right. Each color indicates a different cell.

(B) Images of a single cell crossing a boundary between a 2% RGD normal adhesion substrate (light) on to a 0.04% RGD low adhesion substrate (dark), causing the cell to turn toward the high adhesion side of the cell when adhesion at the rear becomes unbalanced. Scale bar indicates 10 μm.

(C) Trajectories of a set of cells crossing a boundary of normal adhesion density (2% RGD) to low adhesion density (0.04% RGD) on the bottom and from low adhesion density to normal adhesion density on the top. Start positions are marked with small squares, dashed lines indicate trajectories after hitting boundary. All trajectories are centered on the boundary collision point marked with circle. Cells either reflect off the adhesion boundary or refract towards the side of higher adhesion, where the change in direction is dependent on the incident angle with the boundary. Scale bar on bottom indicates distance in microns.

Thus, our results are consistent with a complete mechanical model of cell turning involving two feedback loops: asymmetric actin/myosin II contraction driving asymmetric inward actin flow that is perpetuated both by asymmetric delivery of myosin II and asymmetric engagement of adhesions (Figure 7).

Discussion

Our results detail a mechanical model for cells with a stable lamellipodia turn. Turning starts with asymmetric actin flow created by asymmetry in adhesion and/or asymmetry in myosin II contractile activity at the cell rear. This rotates the “corners” that define the lamellipodial leading edge, which effectively rotates the protruding actin network relative to the cell body and changes the direction of movement of the front of the cell as a result of mechanical changes at the rear. The resulting turning causes the filamentous actin network and the attached myosin II to sweep preferentially into the outer wing, which maintains the flow asymmetry, enhancing further myosin II accumulation in the outer wing, and producing positive feedback (Figure 7 and Box 1). This type of kinematic feedback loop of an inhibitory molecule from the front to the rear of the turning cell has previously been predicted in amoeboid cells such as Dictyostelium discoideum to produce random turns that become uncorrelated over long time scales (Nishimura et al., 2012).

We also experimentally observed a peaked F-actin distribution on the outer side of the turning cell leading edge, which typically signifies a faster protrusion rate. This is a likely result of the mechanics of cell turning, as any given molecule limiting actin polymerization that diffuses along the leading edge will be biased to outer side of the turning cell by rotational drift (Lacayo et al., 2007). Increased myosin II activity and concomitant F-actin disassembly (Wilson et al., 2010) will also produce a local increase in monomeric G actin on the outer side of the turning cell, further promoting faster protrusion on the outer side. Quantitatively, however, these changes in protrusion are not sufficient to explain the degree of turning seen experimentally. Thus, these asymmetries in protrusion at the leading edge appear to play only a minor role in cell turning, becoming dominant only when the role of myosin II contractility is inhibited. It is interesting to note that local photoactivation of G-actin sequestering thymosin β−4 was reported to induce keratocytes to turn towards the side of less protrusion, though without directional persistence and with a reported decrease in contractility on the thymosin β−4 exposed side of the cell (Roy et al., 2001).

We suggest that the positive feedback between the kinematics of turning, myosin II redistribution and actin flow asymmetry are not strong enough by themselves to be self-sustaining, unless the increased myosin II contractility is sufficient to weaken or break adhesions on the outer side of the cell, creating a more locked-in asymmetry in both myosin contractility and adhesion strength (Figure 7). Interestingly, a simplified computational free-boundary model lacking the dynamic feedback between adhesion strength and myosin contractility (Nickaeen et al., 2017) also showed that the kinematics of myosin II redistribution and actin flow are sufficient to break left-right symmetry, but did not produce realistic turning behavior: in the simplified model, cells pivoted around a fixed point instead of circling with the observed range of turning radii.

To determine if two mechanical feedbacks are sufficient to reproduce turning behavior in keratocytes, and to explicitly examine the evolution of asymmetric cell shape over time (Nickaeen et al., 2017), we employed a simulation of a mechanical model of the keratocyte lamellipodium as previously tested and calibrated for non-turning steady-state motility (Barnhart et al., 2011) and for the process of polarization and motility initiation (Barnhart et al., 2015). In brief, this model uses the balance of forces of myosin contraction, adhesive drag and actin network viscosity to determine the cell’s mechanical behavior (Lee et al., 2020). In this simplified model, myosin contractile stress is proportional to the myosin density and myosin density is determined by the actin flow transporting myosin. Actin flow is generated by the gradient of the contractile stress mediated by the adhesion drag and actin viscous resistance. The local adhesion strength is set as a nonlinear function of the local actin flow rate. Cell shape is determined by deformations of the cell free boundary due to the balance between the actin polymerization-driven protrusion and myosin-driven retraction. Starting from a stable symmetrical shape, the simulated free boundary cell incorporating only the feedback loop between actin flow and myosin contractility (but not the second feedback loop connecting contractility to adhesion) evolves into a polarized, motile configuration with a relatively straight, slightly meandering path (Lee et al., 2020). However, in simulations with the addition of a strong negative feedback between actin flow and adhesion that we have identified, turning becomes persistent (Lee et al., 2020). The full free boundary model including both feedback loops was also able to reproduce the behaviors we observed for cells crossing boundaries from high to low or low to high substrate adhesivity (Lee et al., 2020). In addition, the model reproduces the experimental observation that the degree of left-right myosin II asymmetry correlates with a smaller radius of curvature (Figure 3C), that asymmetric protrusion alone cannot drive cell turning and the observed effect of periodic oscillations of the cell trajectory in the applied electric field.

Previous attempts to understand the mechanics of keratocyte turning behavior (Oliver et al., 1999) focused on the asymmetry of traction forces, insightfully decomposing the forces into propulsive, pinching and resistive parts. However, this previous study interpreted the traction asymmetry from the point of view of an effective torque rotating a rigid cell body and did not address the cytoskeletal asymmetries underlying the turning mechanism. Our analysis suggests that the traction forces are coupled to the asymmetric viscous contractile actin-myosin network within the free boundary of the cell, and the key to cell turning is the combination of the force asymmetries with the kinematics of actin flow and cell shape deformations. It is not the case that the turning cell rotates as a rigid body; instead the asymmetrically dynamic lamellipodium slides laterally relative to the cell body to produce a change in the net direction of whole-cell movement.

Our work identifies how the mechanical actors of cell migration work together to follow a cell’s internal compass in generating left-right asymmetry while still maintaining constant front-rear polarization. In vivo, these cells will be under the constant influence of external tactic cues. In neutrophils and Dictyostelium discoideum, these tactic cues have been thought to act to promote migration by co-opting the internal compass at the front of the cell to promote protrusion through secondary chemical messengers (local excitation) and to suppress migration at the cell rear by activation of myosin II based contraction (global inhibition) (Gutierrez et al., 2011; Xiong et al., 2010). However, we have found that contractility at the rear of the cell may also act asymmetrically to direct the motion of the front, due to the internal reorientation of the lamellipodium, i.e. rear-wheel steering. Because our analysis has focused primarily on cells turning persistently at steady state, we are not able to determine which events are most likely to initiate the cascade of positive feedback loops we have described here, though it is clear that it is possible to trigger at least some part of the rear-wheel steering process by altering either contractility or adhesion asymmetrically at the cell rear. In a recent project involving human neutrophils (Tsai et al., 2019), we have found that asymmetrical delivery via actin network flow of myosin II to the outside rear of turning neutrophils follows patterns very similar to those described here in keratocytes, with the distinction that the left-right myosin II asymmetry at the cell rear is not persistently maintained, so neutrophils do not enter into persistent turning states. For neutrophils, the first step in both spontaneous and induced cell turning appears to be reorientation of the actin network flow at the leading edge, leading to asymmetric myosin II delivery and the same sequelae as described here for keratocytes.

Equally important is the question how the cell stops turning and resumes relatively straight locomotion. Based on our experiments with electric field, we suggest that one potential mechanism is for the cell front to stop being passively turned by the rear when an outside signal biases the actin network growth at the front in a certain direction. Then, because of the mechanical coupling between the front and rear, the continuing turning of the rear is slowed down, breaking the feedback between the turning and actin flow, which in turn weakens the myosin and then adhesion asymmetry, and the rear returns into the stable symmetric state. The model in (Lee et al., 2020) suggests that another way to stop turning is by global downregulating of myosin contractility: according to the model, in the presence of sufficiently strong positive feedback between turning and myosin asymmetry, and sufficiently strong negative feedback between contraction and adhesion strengths, the asymmetric cytoskeletal distributions accompanied by cell turning are mechanically stable. In contrast, the model predicts that if the combination of these feedbacks is too weak, the cell stably goes straight, meandering only due to the stochastic noise. The latter model prediction also agrees with our observation that cells with weaker overall myosin contractility have meandering trajectories without entering persistent turning states (Figure 3D).

Several recent lines of experiment have implicated large-scale actin network flow from the front to the rear as a conserved property of many migrating cell types that can serve to integrate cell-scale behavior (Callan-Jones and Voituriez, 2016). In particular, actin cortical flow driven by myosin II contractility in amoeboid cells in the developing zebrafish embryo is sufficient to generate robust self-reinforcing front-rear polarity (Ruprecht et al., 2015). Across a wide variety of motile cell types, there is a strong correlation between the speed of cell movement and directional persistence, which can be simply modeled with the proposition that the net rearward movement of the flowing actin network transports molecules responsible for the reinforcement of front-rear polarity to the back of the moving cell (Maiuri et al., 2015). Our present findings on persistent turning in keratocytes reveal similar mechanisms at play in motility driven by lamellipodia, where the primary factor transported by the actin network to determine front-rear polarity is simply myosin II itself (Ofer et al., 2011; Svitkina et al., 1997; Wilson et al., 2010; Yam et al., 2007). The implication that left-right asymmetries in network flow and therefore in delivery or activation of myosin II might also contribute to cell turning in other motile cell types beyond keratocytes and neutrophils remains to be explored.

METHODS

RESOURCE AVAILABILITY

Lead Contact:

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, (mogilner@cims.nyu.edu).

Materials Availability:

This study did not generate new unique reagents.

Data and Code Availability:

All code used in this paper was generated previously and is available through cited manuscripts (Wilson and Theriot 2006, Sabass and Schwarz 2010, Pincus and Theriot 2007).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Source of Primary Epithelial Keratocytes

Scales from the Central American cichlid Hypsophrys nicaraguensis were isolated and cultured between two 18 mm coverslips with 23 μL of Leibowitz-15 media (Invitrogen) supplemented with 10% fetal bovine serum (Gemini Bio-Products) and 1% ABAM (Invitrogen) for one to three. Cells were isolated with .25% trypsin and replated typically on to #1 thickness coverslips. Coverslips were pre-treated with acetone for ten minutes and then rinsed with isopropanol and dried prior to replating. Animal use was subject to approval by institutional animal care and use committee (IACUC), protocol #6588.

METHOD DETAILS:

Microscopy:

Cells were imaged at room temperature exposed to ambient atmosphere on either a Nikon Diaphot 300, a Nikon Eclipse TiE, or a Zeiss TIRF Axiovert. Fluorescence images were acquired with high numerical aperture oil immersion objectives, using either wide field illumination or total internal reflection excitation. Transmitted light images were obtained using phase-contrast optics with both oil and air immersion objectives. Images were collected on 1k back-thinned cooled EM-CCD cameras, Andor DU888 (Andor) or Hamamatsu ImageEM (Hamamatsu). Long tracks of cells were obtained from cells replated into an Ibidi μ-Dish 35 mm I high (Ibidi) sealed with Parafilm and imaged across a 4×4 grid of images with each position sampled every minute. A red filter was applied to the transmitted light illuminating cells to be imaged over a long period of time in blebbistatin.

Staining:

Subcellular distribution of proteins was determined by observation of cellular shapes and trajectories using phase-contrast microscopy followed by immediate fixation with 4% formaldehyde in 0.32 M sucrose in PBS for 15 minutes, permeabilization with 0.5% triton-X 100 for 10 minutes, blocking with PBS-BT (3% bovine serum albumin, 0.1% triton X-100, and 0.02% sodium azide in PBS) and staining in PBS-BT. Filamentous actin was stained with a 1:1000 dilution of 6.6 μM AF-488 Phalloidin (Invitrogen). Myosin distribution was stained with 1:200 polyclonal rabbit anti-myosin antibodies (ab2480, Abcam, Cambridge MA) in cells that were initially permeabilized and stabilized with a salt solution (50 mM imidazole, 50 mM KCl, 0.5 mM MgCl2, 1 mM EDTA, 1 mM EGTA) containing 1% Triton-X 100, 4% PEG and 0.5 μM TMR-Phalloidin (Invitrogen); cells were then fixed in 4% formaldehyde in PBS, blocked with PBS-BT and stained with 1:1000 goat-anti-rabbit AF-488 (Abcam). Myosin was additionally visualized in living cells, 24 hours after transfection by electroporation with a plasmid containing a Xenopus myosin regulatory light chain-EYFP fusion transgene (gift of Aaron Straight).

Fluorescent Speckle Microscopy:

Actin meshwork flow was measured using low-doses of fluorescently-conjugated phalloidin. Briefly dilute mixtures of AF-546 phalloidin (Invitrogen) were electroporated into cells in a Warner slotted bath with electric field stimulation chamber (Warner Instruments). Phase and epifluorescent measurements were collected every 3 seconds for 90 seconds for 7 cells. Cells were transformed to the cell frame of reference as described previously (Wilson and Theriot, 2006). A bandpass spatial filter was applied to the fluorescent images, and an adaptive multi-frame correlation algorithm was used to determine F-actin movement (Yam et al., 2007). The correlation template size was adaptively adjusted between 11 × 11 pixels and 21 × 21 pixels, over a 5 frame (15 second) temporal window. Speckle tracks were then converted back to the lab or substrate frame of reference.

Traction Force Microscopy:

Cells were imaged on prepared silicone gels (Gutierrez et al., 2011) with a Poisson ratio of 0.5 and a Young’s Modulus of 0.4 kPa. Substrates were incubated with 0.02 nM 40 nm dark red COOH beads (Invitrogen) and 0.1 mg/mL 1-Ethyl-3-(3-dimethylaminopropyl) carbodiimide (Sigma) for 10 minutes, washed with PBS, and then incubated in media overnight. Cells were replated onto the substrate, and phase and fluorescent images were captured at a rate of 5 seconds per frame. Displacements of fluorescent beads on the substrate by a cell at a given time point was assessed by cross-correlating the micrograph of the beads at this time point with a micrograph of the same beads without the cell (under no stress) using small, uniform interrogation windows. The initial ~75 seconds of cell motion were excluded to allow differentiation of pre-stressed and stressed substrate. Traction forces were calculated from the displacement field using Fourier-transform traction cytometry (Sabass et al., 2008). Calculated traction force maps were then aligned to the frame of reference of the cell, using the affine transforms that maximally align the set of polygonal representation of cell shape over time. Traction forces in the cell frame of reference were then averaged over time to produce average maps.

Patterned Substrates:

Substrates were patterned with 50 μm stripes by micro-contact printing of an Arg-Gly-Asp (RGD) functionalized poly-L-lysine-graft-(polyethylene glycol) copolymer (PLL-PEG-RGD). Stamps were incubated with 0.5 mg/mL 1:50 PLL-PEG/PLL-PEG-RGD plus 1% PLL-PEG-FITC and backfilled with 0.5 mg/mL 1:2500 PLL-PEG/PLL-PEG-RGD.

Galvanotaxis:

Keratocytes were provided directional cues using DC electric fields. Cells were replated into flow cells of minimal thickness and width to minimize Joule heating. Tygon tubing was filled with 2% agarose in Steinberg’s Salt Solution, and used to connect the media on each side of the flow cell to a pair of salt water baths. Platinum electrodes ran out of the salt water baths and into a DNA gel power supply. Potential drop was measured across the flow cell, and current was measured in series with the constructed circuit. Applied voltage was typically at 5 V/cm with a current density of 0.75 × 10⁻⁷ mA/m².

Local Drug Application:

Drugs were applied locally to different regions of cells using micropipets created by a Sutter micropipet puller (Sutter). Pipets were filled at their rear with 2 μL of a mixture of drug and 0.025 mg/mL rhodamine B for visualization in serum free media. Micropipets were held in place with a Sutter micromanipulator (Sutter). Laminar flow was applied across the cell culture anti-parallel to the direction of the needle, creating an approximately ~50 μm size bolus of drug locally. Cells were imaged both before and after drug application.

Myosin Activity Assay:

Myosin activity on ex-vivo cytoskeletons was measured by imaging cells undergoing a turning event and then rapidly permeabilized with 1.0% Triton X-100, 4% polyethylene glycol and 0.2 uM TMR-phalloidin for 30 seconds. The cytoskeleton was stabilized with cytoskeleton buffer (50 mM imidazole, pH 7.4, 50 mM KCl, 0.5mM MgCl2, 0.1 mM EDTA, 1 mM EGTA) and 0.2 uM TMR-phalloidin for 5 minutes. Meshwork disassembly was assessed ~ 5 minutes after activation of myosin activity by perfusion with an ATP-regenerating system (1 mM ATP, 5 mM creatine phosphate (Sigma), 10 μgml⁻¹ creatine phosphokinase (Sigma). Meshwork disassembly was calculated by subtracting the post-ATP phalloidin image from the pre-ATP phalloidin image.

Image Analysis:

Cell shapes were determined by manually masking using the magnetic-lasso tool in Adobe Photoshop. Using the freely available Celltool software suite, http://zplab.wustl.edu/celltool/ (Pincus and Theriot, 2007), polygonal outlines were extracted from these masks, aligned, and used to generate relevant modes of shape variation using principal component analysis. Phalloidin intensity was determined along the leading edge by averaging the intensity of background-corrected fluorescence images between the cell edge (as determined by the polygon) and 1 μm inward from there. Image swaths for phalloidin intensity from front to rear were calculated by averaging phalloidin intensity between a 9 pixel width region connecting evenly spaced points from the front of cell to back on the left, center and right side of the polygonal representation of the cell. Myosin intensity in the left and right side of the cell was measured by the average intensity of myosin in the thresholded region of the hotspot of myosin concentration at the left and right rears of cells.

Mathematical simulations of cell trajectories

For simplicity, in our simulations to describe the large-scale effects of angular variation on cell trajectories, we decompose each cell’s trajectory in two-dimensional space to a set of vectors of fixed magnitude, v, but variable angle, θ. Of note, the assumption of fixed magnitude is not crucial, as long as there is not a significant relationship between δθ and v. We can consider three simple sources of variation in θ: (A) a randomly chosen value of θ at each time point where θ ϵ [0, 2π), (B) a randomly chosen angular velocity, ω, at each time point from a normal distribution where $\omega ~\omega ~\mathcal{N}\left({\mu }_{\omega },{\sigma }_{\omega }^2\right)$, (C) a randomly chosen change in angular velocity, dω/dt, at each time point where $d\omega /dt~\mathcal{N}\left({\mu }_{\left(\frac{d\omega }{dt}\right)},{\sigma }_{\left(\frac{d\omega }{dt}\right)}^2\right)$. Simulated trajectories for each of these models are presented in Figure S1C.

Model A represents a uniform distribution of possible angles, creating trajectories that resemble a classic random walk. Variation of this model have been used successfully to describe the motion of Paramecium (Selmeczi et al., 2008) and the running and tumbling motion of Escherichia coli (Berg and Brown, 1972). However, as expected, such models do a poor job of qualitatively replicating the persistence over time of keratocyte trajectories or quantitatively reproducing the observed distribution in angular speeds, and auto-correlations in angular speed.

To take into account path persistence, established by the persistence of the polarized lamellipodia (Keren et al., 2008), Model B incorporates a simple correlated random walk in the direction of travel over time, with

$${\theta }_i={\theta }_{i-1}+\omega *\mathit{\text{dt,\hspace{0.17em}where\hspace{0.17em}}}\omega ~\mathcal{N}\left({\mu }_{\omega },{\sigma }_{\omega }^2\right).$$

We have defined μ_ω as 0 and ${\sigma }_{\omega }^2$ as 1 deg/s² for these simulations. This simple simulation produces trajectories that are wandering in nature. Models of this type have been highly effective in describing the motion of Dictyostelium discoideum where the angle of motion from one time point to the next is correlated due to coupling of future protrusion to sites of previous protrusion (Li et al., 2011; Van Haastert, 2010), as well as the movement of other tissue culture cell lines (Selmeczi et al., 2005).

Qualitatively, these wandering trajectories are similar to a subset of the observed keratocyte trajectories. These models also are able to replicate the appropriate distribution of angular speeds; however, they fail to recreate the persistent turning behavior that is intermittently exhibited by keratocytes as quantitatively observed by the elevated auto-correlations in angular speed for some cells.

Model C explicitly introduces this correlation between angular speeds, such that the change in direction traveled at one time point is related to the change in direction traveled at the next time point,

$${\omega }_i={\omega }_{i-1}+\left(\frac{d\omega }{dt}\right)*\mathit{\text{dt,\hspace{0.17em}where\hspace{0.17em}}}\left(\frac{d\omega }{dt}\right)~\mathcal{N}\left({\mu }_{\left(\frac{d\omega }{dt}\right)},{\sigma }_{\left(\frac{d\omega }{dt}\right)}^2\right).$$

This produces trajectories that qualitatively resemble actual keratocyte migration as well as a realistic distribution of angular speed and observed high angular speed autocorrelation functions seen in some cells (Souman et al., 2009).

Supplementary Material

2

Supplementary Video 1, related to Figure 1: Phase contrast time lapse acquisition of a sample keratocyte undergoing a persistent turn. Scale bar in bottom left indicates 10 μm. Time elapse in minutes is indicated on top right.

3

Supplementary Video 2, related to Figure 3: Time lapse acquisition of a sample keratocyte showing both phase contrast images (left) and wide-field fluorescence of myosin-II regulatory light chain (right) in a turning cell. As the cell turns myosin accumulates on the outer wing of the turning cell. Scale bar in bottom right indicates 20 μm. Time elapsed in minutes is indicated on bottom right.

4

Supplementary Video 3, related to Figure 4: Phase contrast time lapse acquisition of a turning cell (left) with wide-field fluorescence of actin-binding phalloidin speckles shown in the frame of reference of the cell (center) and substrate (right). Calculated flow field of the actin meshwork from the phalloidin speckles are overlaid on the fluorescent images. In the cell frame of view, actin flows asymmetrically towards the outer side. In the lab frame of view, there is increased centripetal flow on the outer-side of the cell. Scale bar in bottom right indicates 20 μm. Time elapse in minutes is indicated on top right.

5

Supplementary Video 4, related to Figure 6: Phase contrast time lapse acquisition of a sample keratocyte crossing boundaries between high adhesion (light regions) and low adhesion (dark regions). When a differential in adhesion across the rear of the cell developed the cell would turn towards the side with higher adhesion to the substrate. Scale bar in bottom left indicates 10 μm. Time elapsed in minutes is indicated on top right.

Key Resources Table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Polyclonal rabbit anti-myosin antibody	Abeam	Cat# ab75590
AlexaFlour488 goat anti-rabbit antibody	Abeam	Cat#ab1500777
Chemicals, Peptides, and Recombinant Proteins
4% Formaldehyde	Thermo Fisher	Cat#28908
Sodium Azide	Sigma	Cat#S2002
Bovine Serum Albumin	Thermo Fisher	Cat#15561020
Triton-X	Thermo Fisher	Cat#HFH10
AF-488 Phalloidin	Thermo Fisher	Cat#A12379
Imidazole	Sigma	Cat#I5513
EDTA	Thermo Fisher	Cat#AM9260G
EGTA	Thermo Fisher	Cat#N6802
TMR-Phalloidin	Invitrogen	Cat#R415
Rhodamine B	Invitrogen	Cat#O246
ATP	Sigma	Cat#34369-07-8
Creatine phosphate	Sigma	Cat#71519-72-7
Creatine phosphokinase	Sigma	Cat#C3755
Cell Culture Reagents
PBS	Gibco	Cat#10010023
Fetal Bovine Serum	Gemini Bio products	Cat#900–108
ABAM	Gibco	Cat#1540112
Leibovitz’s L-15 Medium	Gibco	Cat#11415064
Recombinant DNA
Myosin regulatory light chain-EYFP fusion expression plasmid	Straight et al. 2003	Myosin light chain uniprot: Q2F834
Software and algorithms
Cell Shape Analysis	Pincus and Theriot, 2007	Code available through cited manuscript

Highlights.

• Fish keratocytes can migrate with persistent angular velocity, straight or in circles

• The leading edge’s protrusion asymmetry isn’t sufficient to generate persistent turning

• Asymmetric myosin II contraction, actin flow and adhesion at the cell rear cause turns

• These symmetries are connected within feedback loops to generate persistent turning