Summary
A common approach to benchmarking of single-cell transcriptomics tools is to generate synthetic data sets that statistically resemble experimental data. However, most existing single-cell simulators do not incorporate transcription factor-gene regulatory interactions that underlie expression dynamics. Here we present SERGIO, a simulator of single-cell gene expression data that models the stochastic nature of transcription as well as regulation of genes by multiple transcription factors according to a user-provided gene regulatory network. SERGIO can simulate any number of cell types in steady-state or cells differentiating to multiple fates. We show that data sets generated by SERGIO are statistically comparable to experimental data generated by Illumina HiSeq2000, Drop-seq, Illumina 10X chromium and Smart-seq. We use SERGIO to benchmark several single-cell analysis tools, including GRN inference methods, and identify Tcf7, Gata3, and Bcl11b as key drivers of T-cell differentiation by performing in silico knockout experiments. SERGIO is freely available for download here: https://github.com/PayamDiba/SERGIO.
Graphical Abstract
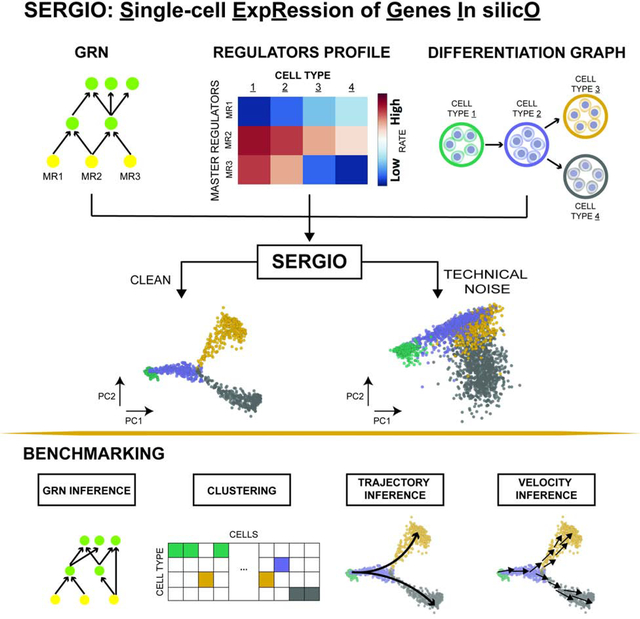
We present SERGIO, a software tool that can simulate realistic single-cell transcriptomics data sets based on a user-specified gene regulatory network (GRN). Data sets simulated using SERGIO can be used to benchmark a variety of single-cell analysis tools, especially GRN inference methods.
Introduction
Single-cell transcriptomics technologies are revolutionizing biology today (Hedlund and Deng, 2018; Kelsey et al., 2017; Papalexi and Satija, 2018; Park et al., 2018), and have led to the rapid development of computational tools for analyzing the resulting data sets (Buettner et al., 2015; Butler et al., 2018; Stegle et al., 2015; Wolf et al., 2018). These tools, developed for a wide array of tasks such as clustering (Aibar et al., 2017; Kiselev et al., 2017; Satija et al., 2015), trajectory inference (Herring et al., 2018; Street et al., 2018) and gene regulatory network (GRN) reconstruction (Aibar et al., 2017; Chan et al., 2017; Mohammadi et al., 2018), as well as pre-processing operations such as imputation (van Dijk et al., 2018; Eraslan et al., 2019; Li and Li, 2018), adopt complementary strategies whose relative merits and weaknesses are not clear a priori. In some cases, single-cell data sets annotated using domain knowledge (Hou et al., 2019; Schaum et al., 2018a) allow objective evaluations of different strategies, but this is not a scalable approach to systematic benchmarking. A promising alternative approach is to synthesize single-cell expression data sets that mimic real data in their statistical properties and for which underlying biological relationships, e.g., cell type labels, regulatory influences, etc., are known by construction. One advantage of such synthetic data sets is the ability to systematically modify the biological and technical parameters underlying the data in order to understand their effects on a tool’s performance, as well as the ability to obtain replicates of data sets for robust statistical estimates of performance.
Simulation tools (“simulators”) for single-cell expression data have been reported in various forms. Several studies offering novel analysis tools use in-house simulators to benchmark those tools (Van den Berge et al., 2018; Campbell and Yau, 2018; Chen et al., 2020; Gong et al., 2019; Korthauer et al., 2016; Risso et al., 2018; Wolf et al., 2018), while other studies specifically develop simulators for use by the community (Holm, 2019; Marouf et al., 2020; Papadopoulos et al., 2019; Vieth et al., 2017; Zappia et al., 2017; Zhang et al., 2019). Most of these simulators are geared towards capturing the noise characteristics of technologies such as single-cell RNA-seq (scRNA-seq), by first estimating statistical quantities describing real data sets and then sampling single-cell expression profiles from probability distributions that mirror those quantities. A crucial aspect of biology missing in current simulators is the gene regulatory network (GRN): the set of transcription factor (TF)-gene relationships that underlies the dynamics and steady states of gene expression in each cell. In other words, when sampling an expression value for a gene in a cell, these simulators do not account for the fact that the gene is expressed under the control of one or more TFs, whose concentrations in the cell have a major role in determining the target gene’s expression. We thus sought to develop a single-cell expression simulator that is guided by an underlying GRN, not only because of the biological realism that it represents, but also because this is the only direct way to benchmark tools specifically designed for GRN reconstruction. Some existing tools do attempt to induce gene-gene relationships in synthetic data using multi-gene statistical models for sampling purposes (Intosalmi et al., 2018; Marouf et al., 2020), but these attempts do not explicitly incorporate the special properties of gene regulatory networks that have been reported in the literature (Karlebach and Shamir, 2008; Kepler and Elston, 2001; El Samad et al., 2005; Wilkinson, 2009), including non-linear response to TFs, intrinsic fluctuations in expression and propagation of such “biological noise” along the GRN.
In the realm of “bulk” transcriptomics, GRN-driven simulations are already the norm, as exemplified by the simulation tool called GeneNetWeaver (GNW) (Schaffter et al., 2011), which was used in a community-wide effort to benchmark numerous GRN reconstruction tools (Bellot et al., 2015; Marbach et al., 2010; Saelens et al., 2018; Siegenthaler and Gunawan, 2014). GNW is not meant to simulate scRNA-seq data, and though some studies have employed workarounds to use it for this purpose (Chan et al., 2017; Chen and Mar, 2018), it is believed that such synthetic data do not exhibit the statistical characteristics of contemporary single-cell data sets (Chen and Mar, 2018). Furthermore, such workarounds do not offer key features necessary for a single cell expression simulator, such as simulation of multiple cell types and cells differentiating from one cell type to another.
In this work, we develop a simulator tool that (1) uses a principled mathematical description of transcriptional regulatory processes to synthesize single-cell expression data associated with a specified GRN, (2) includes stochasticity of gene expression as an integral part of the process, thus capturing biological noise expected to manifest in cell-to-cell variability, and (3) incorporates various types of measurement errors (“technical noise”) that are typical of single-cell technologies. The new tool, called SERGIO (Single-cell ExpRession of Genes In silicO), is freely available as a stand-alone software package. It borrows some of its modeling assumptions from the widely used GNW simulator, but relinquishes the more complex features of GNW, such as a thermodynamics-based model of regulation and explicit modeling of translation processes, which would have necessitated use of poorly-understood parameters during simulation and slowed down simulations of large GRNs.
SERGIO uses a stochastic differential equation (SDE) called the chemical Langevin equation (Gillespie, 2000) to simulate a gene’s expression dynamics as a function of the changing (or fluctuating) levels of its regulators (TFs), as prescribed by a fixed GRN. It performs such simulations for any pre-specified number of genes in parallel and generates single-cell expression “profiles” (expression values of all genes) by sampling from these temporal simulations in steady-state, thus mimicking established cell types. It allows users to specify the number of cell types to be simulated, via steady-state levels of a few “master” regulators in the GRN. SERGIO also allows users to simulate single-cell expression data from a specified differentiation program, for which it samples cells from transient portions of temporal simulations. In this simulation mode, SERGIO explicitly models the splicing step with an additional SDE, resulting in simulations of unspliced and spliced transcript levels. SERGIO subjects the synthesized expression data to a multi-step transformation where technical noise is incorporated in a manner reflecting noise in real scRNA-seq data.
SERGIO is a stand-alone simulator tool for single-cell transcriptomics that offers all of the above-mentioned features while basing its simulations on a given GRN. Here, we outline key aspects of its model and implementation and show that it may be used to generate realistic data sets that resemble experimental data obtained from popular scRNA-seq technologies, by several statistical measures. We then showcase its use to benchmark a number of popular single-cell analysis tools. We find that while modern tools are able to accurately identify cell types and differentiation trajectories from suitable data sets, their ability to reconstruct gene regulatory relationships remains severely limited. To demonstrate the use of SERGIO beyond benchmarking studies, we apply it to simulate expression T-cell differentiation data at single-cell resolution, using two different draft GRNs, show that the simulated data matches a recently published data set for this differentiation process, and also examine the effects of specific perturbations on the process.
Results
We developed SERGIO to simulate how expression values of a specified number of genes vary from cell to cell under the control of a given GRN, and how such information is captured in modern single-cell RNA-seq data sets. We first simulate “clean” gene expression data based on the GRN and mathematical models of transcriptional processes, including stochasticity of such processes (“biological noise”). We then add “technical noise” to the clean data, mimicking the nature of measurement errors attributed to scRNA-seq technology (Kolodziejczyk et al., 2015) (Figure 1).
Figure 1: Overview of steady-state simulation pipeline.
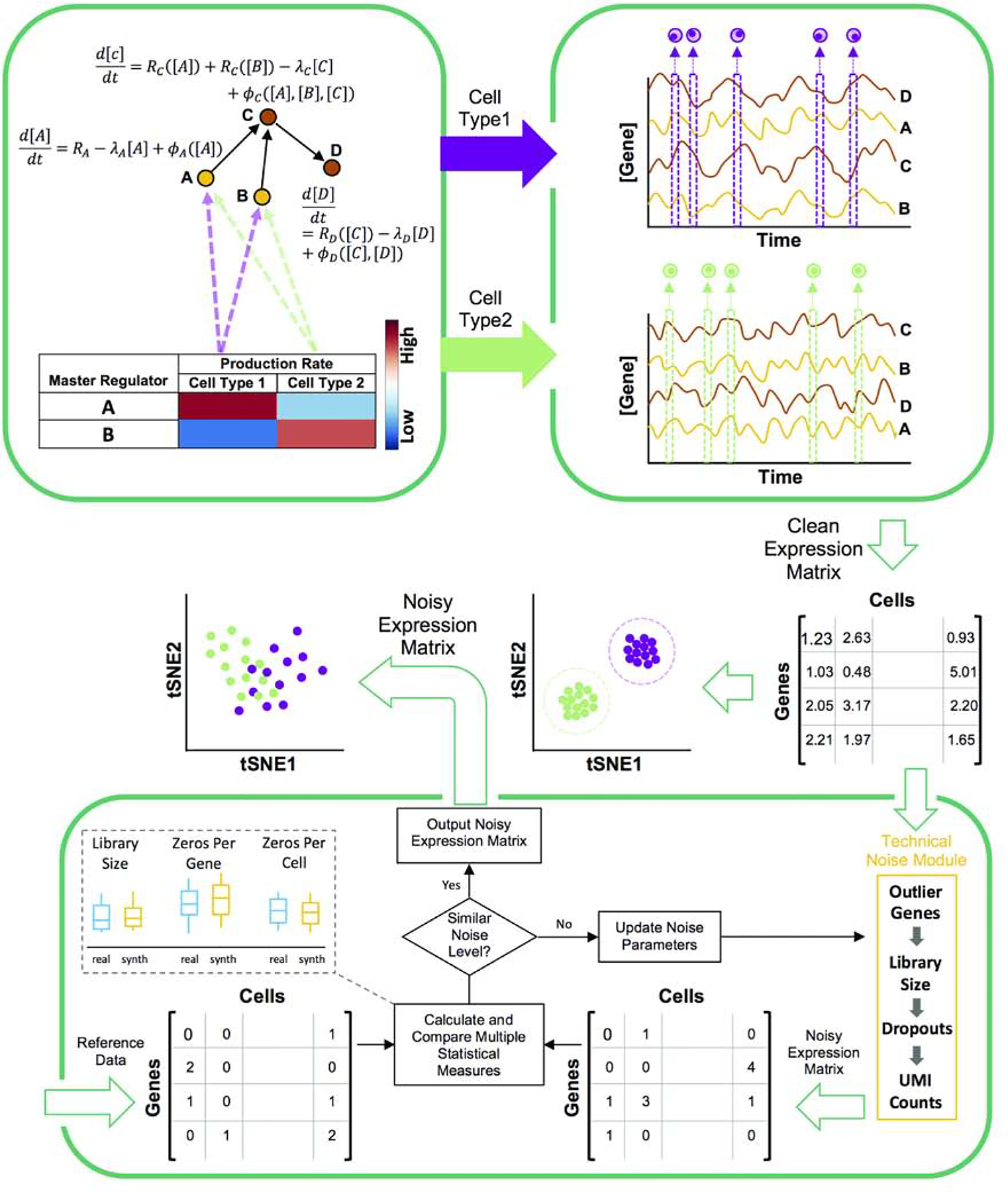
SERGIO uses stochastic differential equations (SDE) to describe the dynamics of mRNA transcripts of each gene (A,B,C,D) in a specified GRN (top left). Each gene’s SDE consists of a production rate which is modeled as the sum of contributions the gene receives from its regulators (e.g., from A and B for gene C). Such a contribution is modeled as a regulatory function (Rgene) of the concentration of the TF except for “master regulators” (genes without regulators) for which the production rate is a constant (e.g., RA). Also, each SDE contains a term representing the decay of mRNA transcripts (e.g. λc[C]) and a term representing biological noise (e.g., ϕc([A], [B], [C])). A cell type is specified by the production rates of MRs, and SERGIO performs separate simulations for each cell type using these MR production rates. It initializes the concentration of genes to their estimated averaged steady-state concentrations and continues simulations in steady-state region for all genes simultaneously to generate time-course expression data (top right). Finally, it samples single-cells from the time-course uniformly at random over the steady-state region and outputs the “clean” expression matrix. A cartoon illustration of the clean data generated by SERGIO (after dimensionality reduction) shows single-cells tightly clustered by cell type. Bottom panel: Clean expression matrix is fed into the technical noise module. Parameters of this module are manually tuned so that the noise level in simulated data is similar to that in a user-selected reference (“reference”) data set. Multiple statistical measures are used to compare the noise level between reference and simulated data sets. Upon adding technical noise, cells of different types become less well-separated but are still distinguishable by clustering algorithms.
Simulation of “clean” data
We generate expression profiles of single cells by sampling them from the steady state of a dynamical process that involves genes expressing at rates influenced by other genes (transcription factors) (Figure 1, top). A select few of the genes are pre-designated as master regulators (MRs); these have no regulatory inputs in the GRN and their expression evolves over time under constant production and decay rates (see STAR METHODS). Expression of every other gene (non-MR) evolves under a production rate determined by adding contributions from its GRN-specified regulators (equation 5 in STAR METHODS) and a constant decay rate. Each regulator’s contribution to a gene depends on the former’s current concentration and an interaction parameter (strength of activation or repression) specific to the regulator and regulated gene. This dependence is described by a Hill function (Chu et al., 2009), thus allowing for non-linear effects.
Each gene’s time course is simulated while incorporating biological noise, using the chemical Langevin equation (Gillespie, 2000), as adopted in the GeneNetWeaver (GNW) simulator (Schaffter et al., 2011). Once the system of evolving expression profiles reaches steady state, we sample profiles from randomly selected time points. Variation in expression profiles across cells of the same type is assumed to mimic variation across time points in the steady state (the “ergodic assumption” (Prill et al., 2015)), hence the temporally sampled cells are used as the collection of cells in the synthetic data.
Specifying the fixed production rates of MRs determines the average steady state expression profile of the sampled cells and is used to generate data for a single cell type. In order to synthesize a data set with multiple cell types, the above simulation is performed as many times, with each simulation using a different setting of MR production rates. The aggregate of expression profiles sampled (from steady state) across all simulations forms the “clean” synthetic data set. Due to the underlying simulation model being stochastic, distinct runs of the entire process provide distinct “replicates” of the data set.
The clean expression data resulting from the above-mentioned step form a matrix of continuous values that represent mRNA concentrations of each gene in each cell. Unlike data obtained from RNA-seq technologies, the clean data do not comprise discrete mRNA “count” values; simulating such counts to mimic experimental data involves a further sampling step described below.
Incorporation of technical noise
In the second phase (Figure 1, bottom), we use the clean data to simulate integer-valued “count” data, as are produced in current scRNA-seq technologies, by sampling from a Poisson distribution whose mean is the real-valued expression level. However, prior to this conversion, the real-valued expression data matrix (genes × cells) is operated upon by modules that incorporate three different types of technical noise - outlier genes, library size effects, and dropouts (see STAR METHODS). The statistical details of these modules are borrowed from the Splatter simulation tool (Zappia et al., 2017) and re-implemented in SERGIO. A user-provided real single-cell data set is used as a reference for adding technical noise. In particular, parameters of the technical noise modules are iteratively tuned until a level of noise comparable to that in the real data is achieved (Figure 1). Comparison of noise levels between the simulated noisy data and the provided real data is performed using multiple statistical summaries of the two data sets, as explained in the next section.
It is worth noting here that several existing single-cell expression simulators employ a probabilistic model whose parameters are directly estimated from a real data set, and then sample synthetic data from the model. This approach is not feasible in SERGIO since the true GRN underlying the real data set is unknown and notoriously hard to reconstruct, and the explicit use of a GRN is a crucial distinguishing feature of SERGIO. As such, SERGIO uses a randomly generated GRN to first synthesize clean expression data, and uses the real data set only in the second phase, to determine the extent of technical noise to add to the clean data.
SERGIO simulates realistic data sets
We used SERGIO to generate eight synthetic data sets under three different settings of the underlying GRN (Table1, Network IDs 2–4). These three settings use GRNs with 100, 400 and 1200 genes, that were sampled from real regulatory networks in E. coli or S. cerevisae (Table 1, also see Supplemental Figure S1 for graphical representation of the extracted networks). The motivation for this sampling is not to mimic expression data from these species, but to use a realistic regulatory network for simulations. All of the eight simulations included 300 cells for each of 9 cell types, for a total of 2700 single cells. Each data set was synthesized in 15 “replicates” by re-executing SERGIO with identical parameters multiple times.
Table 1:
Description of the synthetic data sets used in this study
| Data Set ID | Network ID | Species | #Genes | #Cells | #Regulators | #Edges | #Cell types | Differentiation | Matched Against |
|---|---|---|---|---|---|---|---|---|---|
| DS1 | 2 | Ecoli | 100 | 2700 | 10 | 258 | 9 | No | Mouse cerbal cortex (Illumina HiSeq 2000) |
| DS2 | 3 | Yeast | 400 | 2700 | 37 | 1155 | 9 | No | Mouse cerbal cortex (Illumina HiSeq 2000) |
| DS3 | 4 | Ecoli | 1200 | 2700 | 127 | 2713 | 9 | No | Mouse cerbal cortex (Illumina HiSeq 2000) |
| DS4 | 4 | Ecoli | 1200 | 2700 | 127 | 2713 | 9 | No | Mouse MGE, and … (10X Chromium) |
| DS5 | 4 | Ecoli | 1200 | 2700 | 127 | 2713 | 9 | No | Human kidney (10X chromium) |
| DS6 | 4 | Ecoli | 1200 | 2700 | 127 | 2713 | 9 | No | Human PBMC (10X chromium) |
| DS7 | 4 | Ecoli | 1200 | 2700 | 127 | 2713 | 9 | No | Human lung (Drop-seq) |
| DS8 | 4 | Ecoli | 1200 | 2700 | 127 | 2713 | 9 | No | Mouse heart (Smart-seq2) |
| DS9 | 1 | Ecoli | 100 | 900 | 10 | 137 | 3 | Yes | - |
| DS10 | 1 | Ecoli | 100 | 1200 | 10 | 137 | 4 | Yes | - |
| DS11 | 1 | Ecoli | 100 | 1800 | 10 | 137 | 6 | Yes | - |
| DS12 | 1 | Ecoli | 100 | 2100 | 10 | 137 | 7 | Yes | - |
| DS13 | 1 | Ecoli | 100 | 24000 | 10 | 137 | 4 | Yes | Mouse dentate gyrus (10X chromium) |
| DS14 | 1 | Ecoli | 100 | 36000 | 10 | 137 | 6 | Yes | Mouse cerbal cortex (Illumina HiSeq 2000) |
| DS15 | 1 | Ecoli | 100 | 900 | 10 | 137 | 3 | Yes | - |
For each of simulated data sets, we configured SERGIO to introduce technical noise to an extent that matches published real scRNA-seq data sets. Our goal was to compare data generated by SERGIO against various scRNA-seq technologies including Illumina HiSeq2000, Drop-seq, Illumina 10X chromium and Smart-seq. We matched data sets DS1–3 against a published data from mouse brain sequenced by Illumina HiSeq2000 comprising expression profiles of cells that are categorized into nine cell types with high confidence (Zeisel et al., 2015). DS4 was compared against a published single-cell RNA-seq data from Medial Ganglionic Eminences (MGE), Caudal Ganglionic Eminences (CGE), and cortical regions of mouse sequenced by 10X chromium (Mayer et al., 2018), while DS5 and DS6 were respectively compared against data from human kidney (Lindström et al., 2018) and human Peripheral Blood Mononuclear Cells (PBMC) (Paulson et al., 2018), both sequenced by 10X chromium. DS7 was matched against a single-cell RNA-seq data from human Lung (Vieira Braga et al., 2019) sequenced by Drop-seq, and DS8 was matched against single-cell expression from mouse heart obtained from the Tabula Muris Consortium (Schaum et al., 2018b), sequenced by Smart-seq2. These comparisons were done through manual iteration of the technical noise parameters (see STAR METHODS), and comparison of statistical properties between the synthetic and real data sets, as described next. First, we sampled from each of the real data sets the same number of genes as in the corresponding synthetic data, repeating this 50 times to obtain 50 “replicates” for each of the (sampled) real data sets, each of which was compared to the 15 replicates of the corresponding synthetic data set. All comparisons were performed using synthetic data with or without technical noise, referred to as the “noisy” and “clean” forms of the data set respectively. Note that DS3–8 share the same settings of GRN topology and parameters (Network ID 4), and therefore they all correspond to the same “clean” simulated data.
We used several commonly used summary statistics, reflecting coverage and noise levels in scRNA-seq, to compare each synthetic data set with a matching real data set (Figure 2). These include two cell-level statistics - “library size” and “zero count per cell” (number of genes with zero recorded expression in a cell) - and three gene-level statistics - “zero count per gene” (number of cells in which a gene has zero recorded expression), “mean count” and “variance count” (mean and variance of expression of genes). As shown in Figure 2A–J, there is strong qualitative agreement between real and synthetic (noisy) data sets in terms of each of these five statistics. (The noise level used in generating the synthetic data sets shown were obtained after tuning the noise parameters.) This qualitative agreement is consistently observed across different scRNA-seq technologies. As expected, the clean form of each synthetic data set has substantially different statistical properties from real data. (For a more intuitive interpretation of the “total variation” metric used to compare distributions, see Supplemental Figure S2).
Figure 2: Comparisons between synthetic data generated by SERGIO and real scRNA-seq data sets.
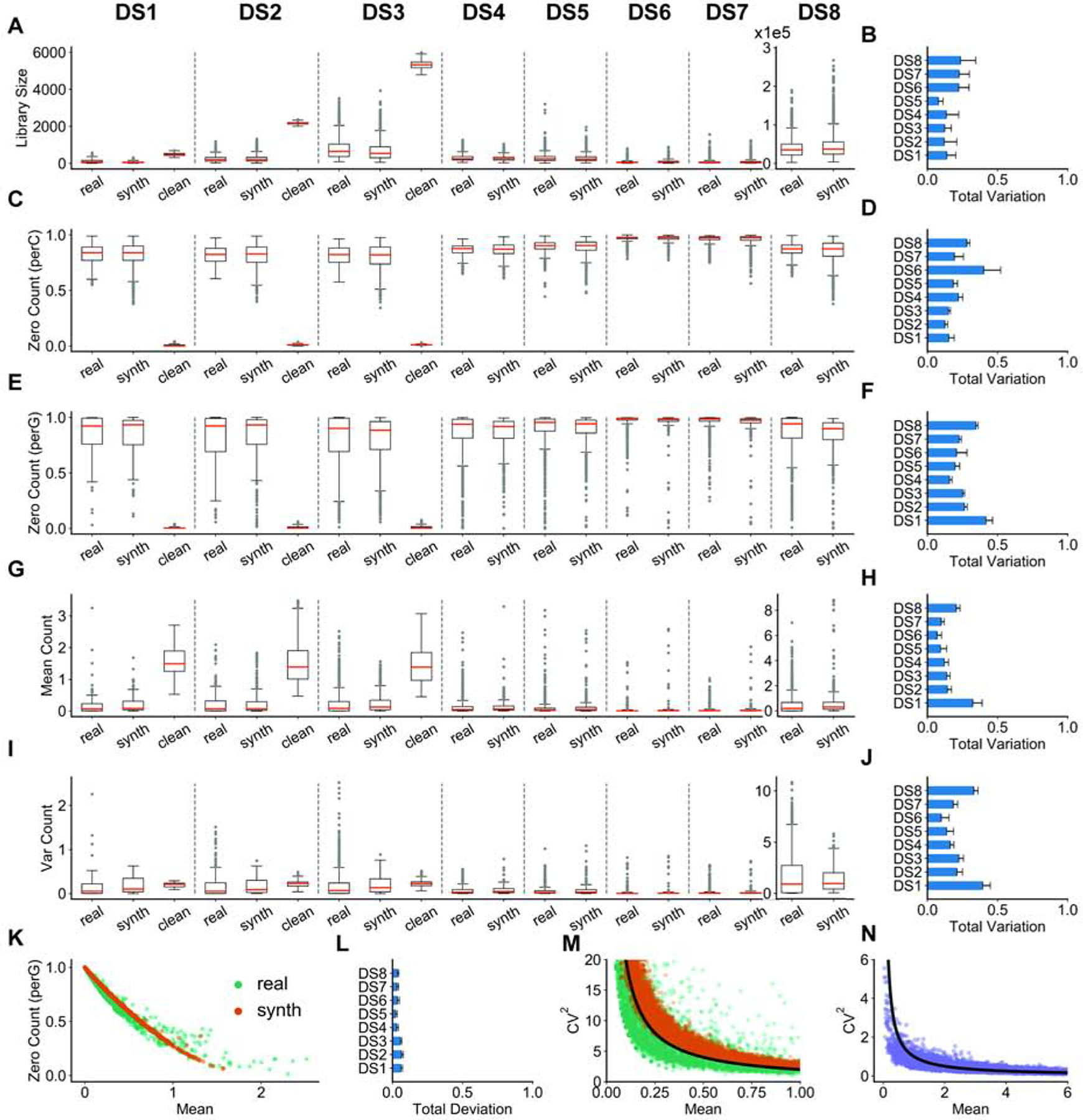
We show the distributions of per-cell quantities in (A,C), and per-gene quantities in (E, G, I), for DS1–8 separated by dashed lines. These comparisons are shown between one sample from the real data set (“real”), one replicate of clean simulated data (“clean”), and its technical noise-added version (“synth”). DS4–8 have the same underlying “clean” data as DS3 (only shown for DS3). More comprehensive comparisons - between every pair of a noisy simulated replicate and a real sample - are shown in panels to the right: the total variation (see STAR METHODS) is calculated to compare the real and synthetic distributions and the average total variation across all such pairs is shown in panels (B, D, F, H, J). (A,B) Distributions and total variation of library sizes. (C,D) Distributions and total variation of zero counts per cell (normalized by number of genes). (E,F) Distributions and total variations of zero counts per gene (normalized by total number of cells). (G,H) Distributions and total variations of genes’ mean expression. (I,J) Distributions and total variations of genes’ expression variances. (K) Inverse relation between normalized zero count of each gene and its mean expression. Data are shown for one of the simulated replicates of DS3 and one sample from the real data containing 2500 single cells and 1200 genes selected at random. (L) Total deviation (see STAR METHODS) is calculated between two curves derived from real and synthetic points shown in (K) repeated for every pair of a noisy simulated replicate and a real sample, and the average total deviation is shown. (M) Inverse relation between squared coefficient of variation (see STAR METHODS) and mean expression of genes over all single-cells. Data are shown for one of the simulated replicates of DS3 and one sample from the real data containing 2500 single cells and 1200 genes selected at random. The black line shows an arbitrary function of form y ~1/x which completely matches with the observed behavior in both real and synthetic data. (N) The inverse relation of form y ~1/x is not a result of technical noise and is also observed in clean simulated data.
An empirical observation about scRNA-seq data reported in the literature is that there is an inverse relationship between the number of zeros in the recorded expression of a gene and its mean expression level across cells (Andrews and Hemberg, 2019; Pierson and Yau, 2015). This inverse relationship is clearly seen in our (noisy) synthetic data sets and their corresponding real data sets (Figure 2K,L), and arises not only because genes with lower expression levels are more likely to result in sampled zero counts, but also because the simulator creates “dropouts” (a form of technical noise) with higher probability for such genes. Similarly, an inverse relationship between the coefficient of variation (CV) - a common measure of expression noise - and mean expression of a gene has been extensively discussed in the literature (Dar et al., 2016; Franz et al., 2011; McCarthy et al., 2012). Figure 2M shows the existence of this relationship in a representative synthetic data set as well as in a corresponding real data set. This inverse relationship is not the result of adding technical noise and is present in the clean synthetic data sets as well (Figure 2N). It arises naturally from the gene regulatory model implemented in SERGIO, in contrast to other single cell simulators that explicitly add such a relationship to their statistical sampling procedures (Zappia et al., 2017). In other words, the synthetic data sets generated by SERGIO not only exhibit realistic distributions of key summary statistics (Figure 2A–J), they also exhibit second-order relationships between pairs of variables that are characteristic of real data sets (Figure 2K–N).
The simulation capability of SERGIO is not limited to small GRNs sampled from E. coli or S. cerevisiae and it can be used to simulate large mammalian networks also. To illustrate this, we obtained a curated regulatory network for mouse from RegNetwork database (Liu et al., 2015), which included 15,272 genes (43 are master regulators) and 76,483 gene-gene interactions after preprocessing. This GRN was used in SERGIO to simulate a single-cell data set containing 3600 single-cells, resulting in a simulated data comparable in size with a real scRNA-seq data of mouse brain (Zeisel et al., 2015). By adding technical noise, we were able to match key summary statistics, CV-vs-mean and zero-vs-mean relationships between the simulated data and mouse brain HiSeq2000 data (Zeisel et al., 2015) (Supplemental Figure S3), with a similar quality of match as that seen in DS1–8.
Simulated data exhibit cell heterogeneity similar to real data
Motivated by the growing use of single cell RNA-seq data to characterize cellular heterogeneity in biological samples, we next asked if the synthetic data sets from SERGIO exhibit heterogeneity similar to real ones. We first used Principal Components Analysis (PCA) to reduce each cell’s representation (without any pre-processing on data) to ten dimensions (by using the first 10 PCs). Then the popular tSNE (Van Der Maaten and Hinton, 2008) algorithm was used to reduce the 10 dimensional representation of cells into 2 dimensions for visualization. Figures 3A,B show such tSNE plots for a representative synthetic data set (in the DS3 setting) in their clean and noisy forms respectively. It is clear that in the absence of technical noise the nine cell types (as specified during simulation) are highly distinguishable, and that the noisy data sets smear this visual separability significantly. In addition to tSNE, we tested an alternative non-linear dimensionality reduction algorithm called Uniform Manifold Approximation and Projection (UMAP) (McInnes et al., 2018) that has been recently shown to outperform tSNE in capturing local and global structures in single-cell data (Becht et al., 2019). As above, we applied UMAP on the 10-dimensional PC space of data to obtain a two dimensional representation of cells. Figure 3C,D show these representations in clean and noisy versions respectively of the representative data set. A comparison between Figure 3B,D reveals the better ability of UMAP to resolve cellular heterogeneity.
Figure 3: Cell heterogeneity in synthetic data generated by SERGIO.
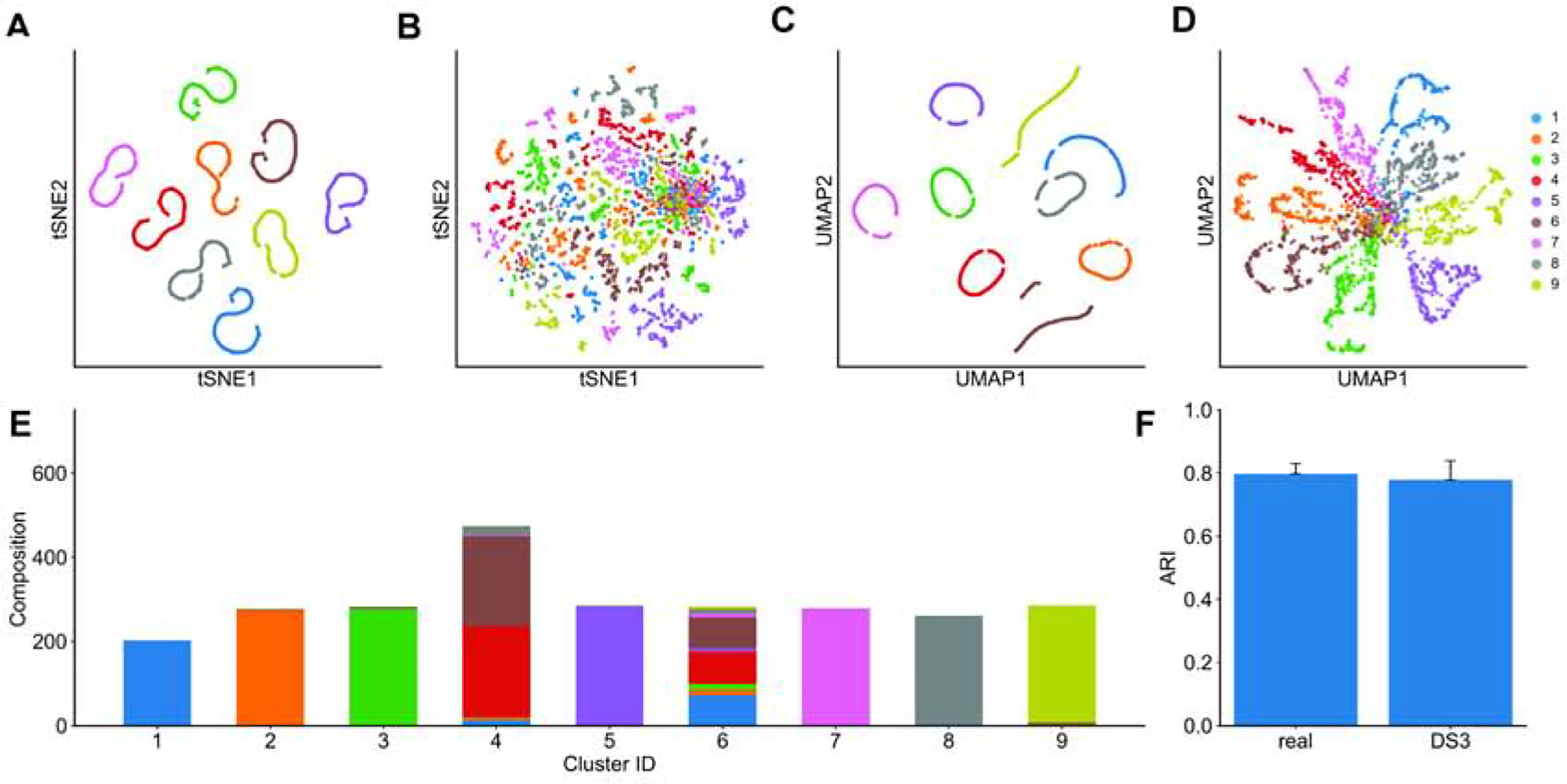
(A) tSNE plot of the single-cells in one clean simulated replicate of DS3. All cells of the same cell type are correctly clustered together. (B) tSNE plot of the same data set after adding technical noise. Cells are scattered such that two dimensions of tSNE representation are not sufficient for the human eye to distinguish different cell types. (C) UMAP plot of the clean simulated replicated of DS3 shown in (a). (D) UMAP plot of the noisy data set shown in (B). In contrast to tSNE, cell types are visually distinguishable in the UMAP representation of single-cells. (Data sets were not normalized for library sizes or filtered for rare genes prior to applying tSNE and UMAP.) (E) The noisy data set shown in (B and D) was clustered into nine groups using SC3 clustering method. Cell type compositions of all nine groups are shown, revealing that SC3 can correctly separate 7 of 9 cell types. Clusters 4 and 6 are less homogeneous and comprise a mixture of multiple cell types. (F) SC3 was applied to all 50 real samples (random subsets of the real data set), each containing 2500 cells and 1200 genes, as well as to all 15 simulated replicates of DS3. The adjusted rand index (ARI) was calculated for each clustering task, comparing the SC3 clusters to (known) true clusters defined by cell types and the average ARI is shown for each type of data (real or synthetic). ARI values obtained from simulated data are very close to those observed in real data sets.
However, cell type detection in practice does not rely only on visual separation, and specialized high-dimensional clustering algorithms are being developed for the purpose. One such algorithm is SC3 (Kiselev et al., 2017), which has been shown to have high accuracy for the task. It was used by Aibar et al. (Aibar et al., 2017) to cluster mouse cortex cells in the “real data set” of our study (Zeisel et al., 2015) and the clusters were found to closely correspond to the true cell types present in the sample (Adjusted Rand Index, ARI, of ~0.8). If our synthetic data sets exhibit similar levels of cellular heterogeneity as the real set, then we expect SC3-reported clusters to have similar levels of concordance with “true” cell types as known to the simulator. Figure 3E shows the composition of nine clusters found by SC3 on the (noisy) synthetic data set visualized in Figures 3B,D, in terms of the true cell types present in each cluster. We note that seven of the nine reported clusters predominantly comprise cells of one (distinct) type, and only two of the clusters are of mixed composition, thus suggesting a high accuracy of clustering. To make this observation more formal, we computed the Adjusted Rand Index (ARI) between SC3-reported clusters and true cell types for each of the 15 replicates of the DS3 data set, noting an average ARI of 0.78. We repeated this for each of the 50 sampled subsets of the real data set corresponding to DS3 settings (using prior knowledge of true cell types in these data), and found the average ARI to be 0.80, very close to that seen in synthetic data. This exercise demonstrates that synthetic data sets generated by SERGIO exhibit realistic levels of cellular heterogeneity, and also illustrates the use of SERGIO to benchmark clustering methods.
Benchmarking GRN reconstruction methods
A unique aspect of the simulator is that the generated gene expression values, prior to adding technical noise, are the result of direct regulatory influence of transcription factors, and a comprehensive GRN comprising these TF-gene relationships is at the core of its simulations. We next illustrate how this unique feature makes SERGIO-simulated data sets ideal for benchmarking GRN reconstruction tools. In our first tests we worked with clean data sets generated by SERGIO, reasoning that these should provide an upper bound for performance on noisy realistic data sets. We evaluated the popular GRN inference algorithm called GENIE3 (Huynh-Thu et al., 2010), which was originally developed for analyzing bulk RNA-seq data but has since been used successfully on single cell data as well. We applied GENIE3 on the (clean) data sets DS1 (100 genes) and DS3 (1200 genes) and evaluated the predicted TF-gene pairs based on the underlying GRNs in these data sets, using the common metrics Area Under Receiver Operating Characteristics (AUROC) and Area Under Precision-Recall Curve (AUPRC). Recall that these data sets were synthesized to include 300 cells for each of nine cell types. To assess the impact of data set size, we created smaller sets by sampling 200, 100 or 10 cells per cell type from the original simulated data (for each replicate of DS1 and DS3), and repeated the GRN reconstruction assessments for these. We also sought to assess the advantage of having single cell resolution in the data, and thus synthesized “bulk” expression data sets by averaging the expression of each gene in all cells of the same type, mimicking a situation where each cell type has been sorted separately and subjected to traditional expression profiling. (The resulting synthetic data sets included nine conditions with “bulk” expression values of each of 100 or 1200 genes, depending on the original data set.)
Figures 4A,B show the ROC and PRC respectively for a representative replicate of the DS3 data set, in its original setting (300 cells per type) as well as its sampled smaller versions and their respective “bulk” data set versions. A more comprehensive view, spanning all replicates of DS1 and DS3, is shown in Figure 4C–F. Several points are apparent from these figures. First, in nearly all versions of the data sets, GENIE3 performs significantly better than random, as is evident from AUROC values well above the 0.5 value expected from a random predictor. Second, we note that while performance is significantly better on larger data sets than on the smallest data set (10 cells per type), there is not a clear difference among the data sets with 100 cells per type or more. This suggests that, at least in the absence of technical noise, the benefits of greater cell count for GRN reconstruction accuracy saturate at commonly seen data set sizes. Third, the “bulk” data sets consistently yielded lower accuracy than the single-cell data sets, regardless of the numbers of cells, confirming the potential value of single-cell data for regulatory inference. Finally, we noted that although the DS1 and DS3 data sets had similar AUROC values, the AUPRC values revealed significantly worse predictions in the larger (DS3, 1200 genes) data sets. This is expected, in part because the random baseline is lower for DS3 (random AUPRC of 0.002) than for DS1 (random AUPRC of 0.026), but also suggests that high levels of gene co-expression may confound methods such as GENIE3 more for larger data sets.
Figure 4: GRN inference from synthetic data generated by SERGIO.
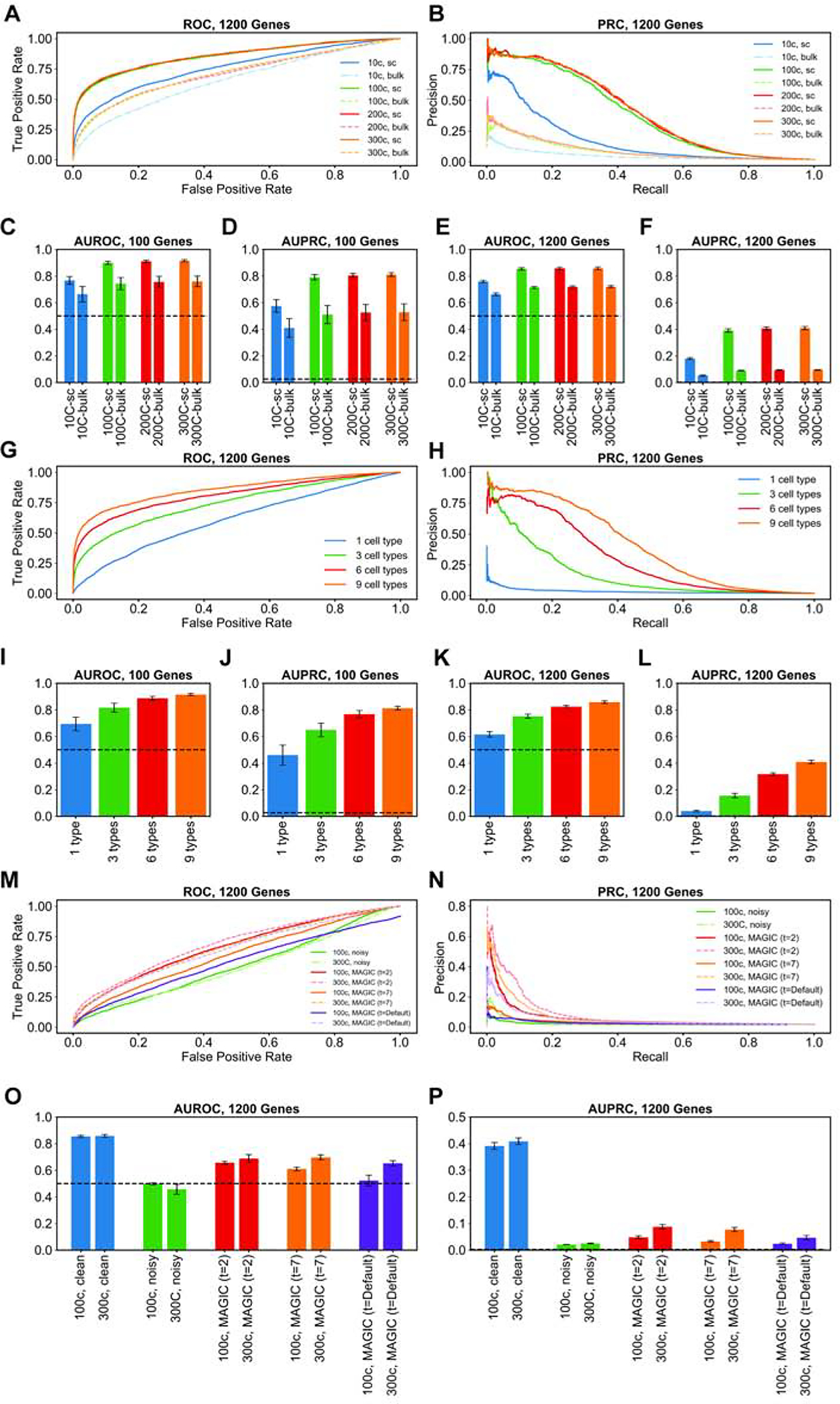
(A,B) Receiver Operating Characteristic (ROC) curves and Precision-Recall Curves (PRC) respectively of GRN inferred by GENIE3 on one replicate of clean synthetic data (DS3) and various subsets thereof consisting of varying number of cells per cell type. “300c” setting refers to the entire DS3 replicate, including 300 cells per cell type. The other settings (“200c”, “100c”, “10c”) refer to data sets where we sampled 200, 100, or 10 cells respectively from each cell type in DS3. For each data set, we evaluated GENIE3 on single-cell data (“sc” setting), and bulk data (“bulk” setting) which are obtained by averaging expression profiles of all cells of the same type in the corresponding single-cell data set. (C-F) Area under ROC curve (AUROC) and area under PR curve (AUPRC) of the GRN inferred by GENIE3, averaged over al clean replicates of DS1 (C,D) or DS3 (E,F) and their subsets comprising varying number of cells per cell type in both single-cell and bulk settings. (G,H) Similar to (A,B), except that subsets of the clean synthetic data set DS3 were created to have varying numbers of cell types; every cell type retains all of its 300 simulated single-cells in the original DS3 replicate. (I-L) AUROC and AUPRC of GRN inference by GENIE3, averaged overall all replicates of DS1 (I,J) or DS3 (K,L), as well as their subsets comprising varying numbers of cell types; as in (C-F), evaluations were done for the single-cell data set as well as bulk data sets derived from them. (M,N) ROC and PRC of the GRN inferred by GENIE3 on one noisy replicate of DS3 (“300c”) with 300 cells per type and a sub-sample of it (“100c”) containing 100 cells per type. Also shown are results of GRN inference by the same method on the same data sets, but using data imputation by MAGIC in three different settings (t=2, t=7, t=default). (O,P) AUROC and AUPRC of the inferred GRN by GENIE3 on all replicates of the data sets used in (M,N) as well as all the clean replicates of DS3 (“300c, clean” and “100c, clean”).
We next examined the impact of cellular heterogeneity on GRN reconstruction accuracy, using our clean synthetic data sets. For this, we sampled from each replicate of DS1 and DS3 (at their original setting of 300 cells per type) smaller data sets comprising 6, 3 or 1 cell type rather than the 9 cell types simulated. As shown via AUROC and AUPRC measures in Figures 4I–L (with representative ROC and PRC curves in Figures 4G,H), we found data sets with greater heterogeneity to consistently improve GENIE3 performance, which remained clearly above the random baseline (AUROC of 0.5 and AUPRC of 0.026 and 0.002 for DS1 and DS3 respectively) for all but the “1 cell type” setting. This is expected, since the latter setting includes gene expression variation resulting only from biological noise, and even though extrinsic noise (fluctuations in TF levels reflected in target gene levels (Swain et al., 2002)) may be exploited to infer TF-gene relationships, such correlations are diluted by the presence of intrinsic gene expression noise in the simulations (see STAR METHODS). On the other hand, in settings with 3 – 9 different cell types, the dominant form of expression variation arises from differences in the steady state profiles of the cell types, making regulatory inferences more effective.
We next examined the effect of technical noise on GRN reconstruction. For this, we compared GENIE3 performance on clean and noisy versions of each replicate of DS3 (1200 genes), in the original setting of 300 cells per type as well as a sampled version thereof with 100 cells per type. The complete results are shown in Figures 4O,P, with representative ROC and PRC curves shown in Figures 4M,N. Both performance metrics (AUROC and AUPRC) deteriorate to levels expected from random prediction when analyzing noisy synthetic data, in contrast to the very high levels seen prior to introducing technical noise. Notably, increasing the number of cells (from 100 per type to 300) does not change our conclusion. Such nearly-random performance of GENIE3 on noisy single-cell expression data has been reported in previous studies conducted based on real as well as synthetic single-cell expression data sets (Chen and Mar, 2018; Matsumoto et al., 2017). It also provides support for the need to combine expression-based inference with cis-regulatory data such as TF-ChIP during GRN reconstruction (Aibar et al., 2017; Siahpirani and Roy, 2017).
In light of the above finding, we considered the possibility of using imputation tools specialized for single cell RNA-seq data as a means to improve the signal necessary for GRN reconstruction. We thus utilized the popular imputation tool called MAGIC (van Dijk et al., 2018) to pre-process the noisy synthetic data sets prior to analyzing them with GENIE3, and compared the performance metrics to those obtained above. Results were only modestly improved from those without imputation, with AUROC values ~ 0.65 in the 300 cell/type setting and ~ 0.52 in the 100 cell/type setting (Figures 4M–P). Closer examination revealed that the default settings of MAGIC made the data overly structured, resulting in unrealistically large gene-gene correlations (Supplemental Figures S4,5), similar to previous reports (Huynh-Thu et al., 2010; Peng et al., 2019; Zhang and Zhang, 2018). In order to address this issue, we employed two smaller values of the ‘t’ parameter in MAGIC (t = 2 or 7), in separate runs, prior to GRN reconstruction. Both of these settings resulted in improved performance over the default setting of MAGIC, and substantially better than that seen in noisy data sets without imputation (Figures 4M–P). For instance, AUROC values for the 300 cell/type setting were at ~0.70 (t = 7), squarely in the middle of those without imputation (~0.46) and those on clean data sets (~0.86). AUPRC values (~0.08) were also significantly above random expectation (~0.002), though far from the high values ~0.4 observed on clean data sets. Although we noted above that GRN reconstruction accuracy on clean data sets did not improve when increasing the cell counts (300 versus 100 cells per type), we do notice a significant and consistent effect of cell counts in performance on imputed data (Figures 4O,P). Presumably, greater cell counts are beneficial for the imputation step, which in turn results in higher performance of GENIE3. Our overall conclusion from the above tests (Figure 4) is that a state-of-the-art GRN reconstruction method such as GENIE3 (Huynh-Thu et al., 2010) can perform accurately on single cell expression data in the hypothetical scenario where technical noise is absent, but falls to near-random performance in the face of realistic levels of technical noise. The accuracy does improve above random baseline if the data are imputed with specialized tools but remains far short from the upper bar observed in clean data, making technical noise a major factor for future GRN reconstruction methods to address.
SERGIO’s simulation model relies on the assumption that the combined effect of multiple regulators is simply the sum of their individual effects. Cooperative regulation by multiple regulators is not considered, so as to reduce the number of parameters that need to be specified and to facilitate the simulation of large regulatory networks where first-order regulatory effects may be known but second-order effects (dependent on pairs of regulators) are mostly unknown. However, to investigate the impact of this simplifying assumption on benchmarks of GRN inference, we conducted a set of simulations using an in-house version of SERGIO that includes cooperative regulation by pairs of activators. Upon addition of technical noise, the resulting synthetic data sets were comparable to a real mouse brain scRNA-seq data set (Zeisel et al., 2015) in terms of overall statistical characteristics, with the quality of match being similar to that seen in DS1–8 (Supplemental Figure S6). Moreover, we confirmed that the performance of GRN inference by GENIE3 is not different between synthetic data sets that do or do not include cooperative regulation. This was observed in our evaluations on clean and noisy (with technical noise) simulated data sets as well as noisy simulated data imputed by MAGIC (Supplemental Figure S7).
Simulating single-cell expression dynamics of early T-cell development
T-cell development and the gene regulatory processes that underlie the T lineage dynamics have been extensively studied, most recently through a comprehensive analysis involving bulk and single-cell RNA-seq profiling (Zhou et al., 2019). Zhou et al. used highly sensitive, sequential single molecule fluorescent in situ hybridization (seqFISH) to profile the expression of 65 marker genes, including important regulators of T-cell development, in 4551 cells belonging to different stages ranging from “early T-cell precursor” (ETP) to committed T-cells. Clustering analysis of these data revealed nine cell clusters, eight of which were associated with one of the developmental stages according to expression of the marker genes. These seqFISH data have far less technical noise than that observed with scRNA-seq technologies, providing us with a unique opportunity to simulate them through the “clean” simulation mode of SERGIO.
To simulate T-cell development expression dynamics as captured by Zhou et al., we first used GENIE3 on the seqFISH data from that study to obtain a GRN containing 108 interactions among the 65 genes (see STAR METHODS). We then used this network to fit a regression model for each gene as a function of its regulators prescribed by the GRN, such that its average predicted expression in each cluster matches seqFISH data (see STAR METHODS). Regression parameters thus obtained, along with the GRN (henceforth called “parameterized GRN”), were used in SERGIO to simulate nine cell types, each of which was represented by a similar number of cells as in the seqFISH data. Figure 5A shows the PC plots of real and synthetic data sets. Note that we used the same cluster IDs and developmental stage labels as in (Zhou et al., 2019). This plot reveals a qualitative agreement between the simulated and real data in terms of ordering of cell types (stages) in development.
Figure 5: Simulations of T-cell differentiation.
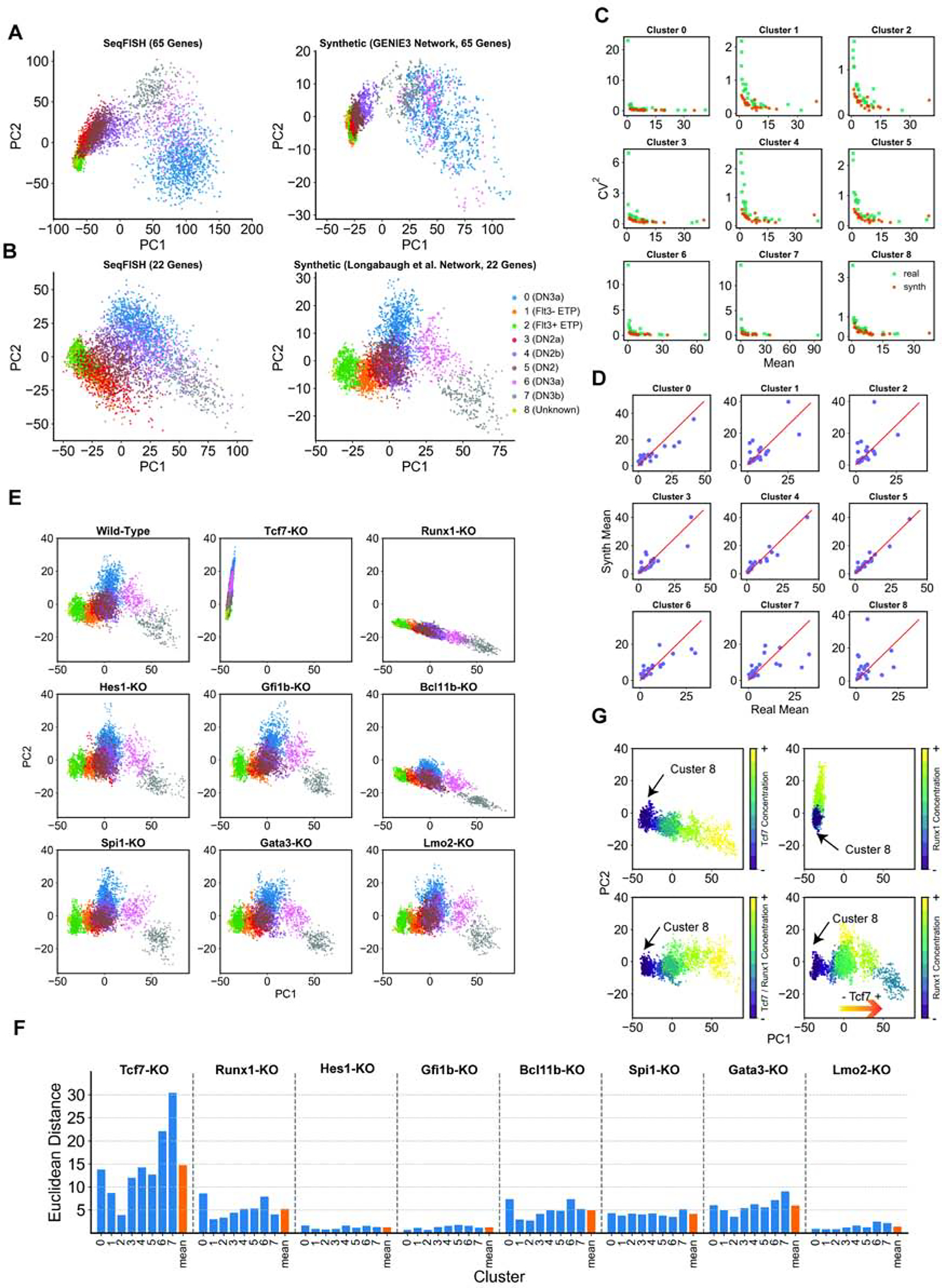
(A) Left: Principal Components (PC) representation of seqFISH data based on expression of all 65 genes in the data set. Right: PC representation of simulated data using the GRN inferred by GENIE3 on seqFISH data. Clusters are labeled by the IDs (stages) used in the original study by Zhou et al., and cells are colored by their cluster IDs. (B) Left: PC representation of seqFISH data based on expression of 22 genes present in the Longabaugh et al. GRN model. Right: PC representation of simulated data using the GRN obtained from Longabaugh et al. Cells are colored by the same scheme as in (A). (C) Coefficient of variation and mean expression of genes, across cells in a cluster, shown for each of the 9 clusters, for real and synthetic data (corresponding to (B)). (D) Mean expression of genes, across all cells in a cluster, from real and synthetic data (corresponding to (B)), shown for each of the 9 clusters. (E) PC representation of the simulated data generated as in (B) (Wild-type; WT), and upon in silico knockout (KO) of each TF. (The two-dimensional projection is identical in all nine plots.) (F) For each TF, Euclidean distance is computed between a cluster’s center in the simulations under that TF’s in silico knockout and those under wild-type conditions, in a 10-dimensional projection. This Euclidean distance is shown for each cluster, representing the impact of the TF’s KO on the average profile of that cluster. The mean across all nine clusters is also shown. (G) Movement of cluster 8 upon in silico overexpression of Tcf7 (upper-left), or Runx1 (upper-right), both, in fully correlated manner (bottom-left), and with expression of both factors set to their cluster-specific levels in wild-type conditions (bottom-right).
See also Figure S8.
We speculated on the possibility of erroneous inferences in the GENIE3 network due to the small number of genes in the training data set. We therefore repeated the simulations with a literature-based GRN for early T-cell differentiation, reported by Longabaugh et al. (Longabaugh et al., 2017). This GRN model contains 22 of the 65 genes present in the seqFISH data, including Tcf7, Bcl11b, and Gata3 that are known to be important regulators of T-cell differentiation. The GRN contains 32 interactions involving a total of 10 regulators, of which four are master regulators (as defined above). We used the same regression-based approach as used for GENIE3 network (above) to parameterize this GRN model. Figure 5B shows the PC plot of the expression of the 22 genes in seqFISH and simulated data generated by SERGIO using this literature-based GRN model. Again, a good qualitative match between real and synthetic data is observed in terms of the ordering of developmental stages, although the three cell types belonging to DN2 stages (cluster 3–5) are less well separated in the simulated data. Interestingly, we noted that the two-dimensional representation of the data set with 22 genes (Figure 5B) shows a correct ordering of stages at the right end of the lineage (DN3a (cluster 0) - DN3a (cluster 6) - DN3b (cluster 7)), while PC representation of the data with all 65 genes (Figure 5A) shows an opposite ordering of these stages at the end of the lineage. In the rest of this section, we discuss findings using the simulated data generated using the literature-based 22 gene GRN model.
Figure 5C shows the relationship between coefficient of variation and mean of gene expression values across cells of each cluster, in real (teal) and synthetic (orange) data. Also, Figure 5D directly compares the mean expression values of genes in each cluster, between real and synthetic data. Both comparisons revealed a reasonable level of agreement between real and synthetic data. Note that our only objective during the simulation was to match a gene’s mean expression value between the two data sets using a very simple model of regulation. Future studies may employ more complex optimization strategies to improve the quality of match.
Next, we sought to use SERGIO simulations to evaluate the significance of different regulators in T-cell development. We performed “in silico knockout” of eight regulators including the four master-regulators, i.e. Tcf7, Runx1, Hes1, Gfi1b (Figure 5E). In order to visualize the effect of knockouts, we projected the single-cell trajectory of each knockout (KO) simulation onto the two-dimensional PC space of the simulated wild-type expression (Figure 5E, top left). The most pronounced effect on the trajectory is observed in the knockouts of Tcf7, Bcl11b, and Runx1. Tcf7 and Bcl11b are known to be major regulators of T-cell differentiation (Longabaugh et al., 2017; Zhou et al., 2019), and Runx1 is also known to play a role via up-regulation of Bcl11b (Longabaugh et al., 2017). In order to accurately quantify the contribution of each regulator in T-cell differentiation, we projected the single-cell trajectory of its KO simulation onto the 10-dimensional PC space of the simulated wild-type data and measured, for each cluster (excluding cluster 8), the Euclidian distance between the cluster centers of the wild-type and KO trajectories. As shown in Figure 5F, Tcf7 has the most prominent effect on the differentiation trajectory, on average, followed by Gata3, Runx1, Bcl11b and Spi1. Four of these TFs (Tcf7, Gata3, Bcl11b and Spi1) are known to have important roles in T-cell differentiation (Longabaugh et al., 2017; Zhou et al., 2019). Interestingly, KO of Tcf7, Gata3, and Spi1 in the network obtained by GENIE3 show smaller effects on the differentiation trajectory compared to the network obtained from Longabaugh et al. (Supplemental Figure S8).
In addition to seqFISH profiling, Zhou et al. carried whole-transcript single-cell RNA sequencing using Smart-seq2 as well as 10X Chromium v2 (Zhou et al., 2019). In all three profiling methods, their clustering analysis consistently revealed an outlier cluster (e.g., cluster 8 in the seqFISH analysis) that was not identified as any of the established differentiation stages (Zhou et al., 2019). We sought to utilize SERGIO simulations to better understand this phenomenon, in particular the outlier status of cluster 8 in seqFISH data. This cluster lacks expression of Tcf7 - the key regulator of T-cell development. For our simulations, we defined nine artificial stages (cell types), each matching cluster 8 of real data in its master regulator profile except that Tcf7 that is gradually overexpressed across different stages. We simulated 300 cells per artificial stage and visualized the simulated single-cell trajectory (Figure 5G, upper-left) in the same two-dimensional space as that used for wild-type simulated data (Figure 5B, right). Although the overexpression of Tcf7 causes cluster 8 to migrate toward committed T-cells, the overall trajectory does not resemble the differentiation trajectory of T-cells. We noticed that cluster 8 also lacks expression of Runx1 - the other important regulator according to our KO analysis above. We performed a similar simulation of artificial stages as above, but now driven by overexpression of Runx1, and found (Figure 5G, upper-right) that expression of this TF alone is not sufficient for triggering cluster 8 to follow the wild-type differentiation trajectory. A similar result was observed when Tcf7 and Runx1 were both overexpressed in a completely correlated manner (Figure 5G, bottom left). However, when we induced an overexpression pattern for Tcf7 and Runx1 similar to their expressions in the eight established stages (clusters) in the seqFISH data, we observed a developmental trajectory (Figure 5G, bottom-right) similar to wild-type T-cell differentiation. This suggests that the down-regulation of Tcf7 and Runx1 contribute to the divergence of cluster 8 from the T-cell differentiation program, a hypothesis that merits future experimental investigation.
Benchmarking differentiation trajectory inference tools
Our analysis so far involved using SERGIO to synthesize steady-state expression profiles representing different established cell types. We were able to use steady-state simulations even for reproducing the dynamics of T-cell differentiation, by utilizing data and knowledge of established cell types located on the differentiation trajectory and simulating those cell types in steady-state. However, this approach is infeasible in the absence of real data and a well-characterized GRN tied to those data. We next sought to demonstrate how to use SERGIO for simulating a differentiation program using any given GRN. SERGIO offers the capability of synthesizing dynamic expression data on a set of genes controlled by a given regulatory network in single cells differentiating along a given trajectory. In this mode the simulator is provided with a differentiation graph whose nodes represent established cell types in a differentiation program and whose edges represent differentiation from the parent cell type to child cell type (Figure 6A). The simulator samples expression profiles from the steady state represented by the parent cell type, and then simulates a dynamical process (identical to that described above) that begins with one of these expression profiles and evolves into the steady state represented by the child cell type. It then samples expression profiles from the temporal duration when the cells are transitioning from the initial to final cell type (Figure 6B). The entire “clean” data set is synthesized by repeating this simulation process for each edge in the differentiation graph. Technical noise is then added in a manner identical to the steady state simulation mode.
Figure 6: Overview of differentiation simulation pipeline.
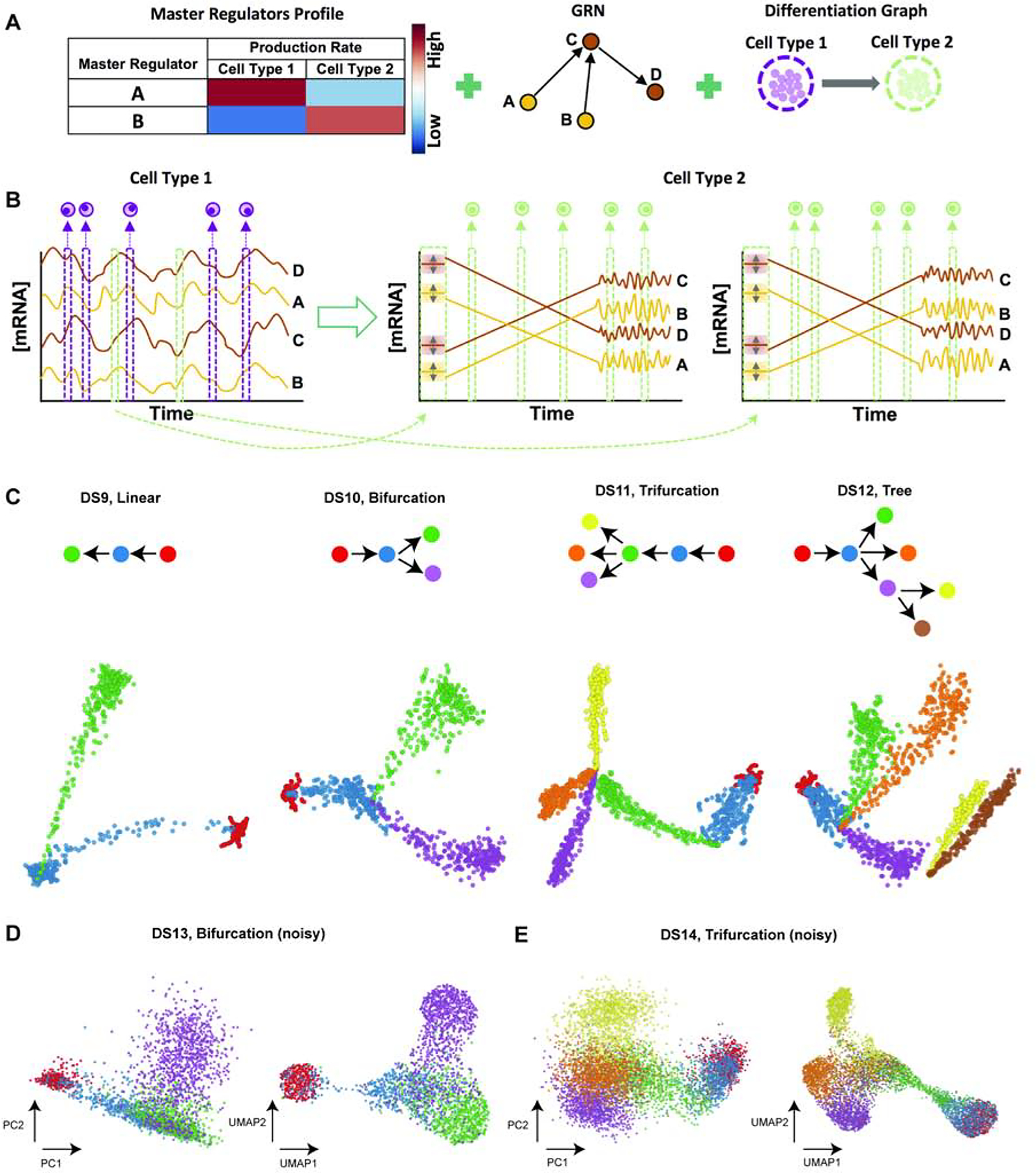
(A) Inputs required for simulation of differentiation programs: in addition to master regulators’ profiles defining cell types and the GRN, this simulation mode requires a differentiation graph as an input (right). (B) Differentiation simulation is started from the origin of differentiation trajectory (cell type 1 here). Since the origin cell type is not differentiated from any other cell type, its samples (cells) are drawn from steady-state simulations (left). For each child cell type (cell type 2 in this case), SERGIO initializes transcript levels to values close to their steady-state concentrations in the parent cell type (cell type 1 here). Simulations are then performed so that transcript levels reach their steady-state concentrations in the child cell type, after which simulations continue for a user-defined number of additional steps so as to collect sufficient time-course data in steady-state. SERGIO repeats simulation of the child cell type (from initialization until steady-state) for a user-defined number of times to sample enough paths between the parent and the child cell type. (Two such repeats are shown here.) Finally, single-cells belonging to the child cell type are sampled from the aggregated pool of all time-course data from the initial to the last simulation time point. Temporal fluctuations of expression in the transient region are often negligible in amplitude compared to the overall change in expression from initial to new steady state, hence the transient region is shown with a straight line in this cartoon illustration. (C) PCA plots of single-cell data sets synthesized for differentiation graphs shown at top: DS9 (linear), DS10 (bifurcation), DS11 (trifurcation), and DS12 (tree). Cells of or differentiating into each cell type are shown by a distinct color. (D,E) PCA and UMAP representation of noisy data set DS13 synthesized for bifurcation differentiation graph (D) and noisy data set DS14 synthesized for trifurcation differentiation graph (E).
An emerging approach to describe the dynamics of differentiation programs through single-cell expression profiling involves examination of spliced as well as unspliced transcript levels in the data and inferring “RNA velocity” of each cell (La Manno et al., 2018). To allow synthesizing data sets amenable to such analysis, the differentiation simulation mode uses a variation on the underlying model described above. In particular, it invokes two chemical Langevin equations (CLE) similar to equation 1 to generate unspliced and spliced transcript levels (see Equation 11 and 12 in STAR METHODS). It reports the simulated expression values as levels of unspliced as well as spliced transcripts, whose sum may be considered the total expression of a gene.
To illustrate these features of the simulator, we generated four synthetic differentiation data sets (DS9 - DS12), each containing 100 genes controlled by the same GRN, but obeying different differentiation graphs - linear (DS9), bifurcation (DS10), trifurcation (DS11) and tree (DS12) (Figure 6C). Figure 6C also shows the two dimensional PCA plot of the clean total transcriptome (without technical noise added) for the four types of differentiation graphs. It is visually evident that these two-dimensional representations of cells based on their gene expression profiles match their corresponding graphs used in the simulations. We note that the dispersion of cells of each type (end points of each branch of a graph) as well as the width of the differentiation path from one type to another in the clean simulated data can be controlled by user-specified parameters in SERGIO (Supplemental Figure S9).
In order to obtain synthetic data comparable in sizes with data sets obtained from single-cell RNAseq technologies, we simulated larger versions of DS10 (bifurcation) and DS11 (trifurcation), containing 6000 cells per cell type. This gives us a clean bifurcation data set containing 100 genes and 24000 single cells (DS13) and a clean trifurcation data set containing 100 genes and 36000 single cells (DS14). Supplemental Figure S10 shows the PCA plots of these two data sets, which closely resemble their respective smaller versions (DS10 and DS11) since the same simulation parameters were used for the small and large versions. Next, DS13 and DS14 were used to synthesize noisy expression data for the bifurcation and trifurcation trajectories. We used a recently published 10X genomics single-cell data set representing dentate gyrus of mouse hippocampus (Hochgerner et al., 2018) as a reference for calibrating technical noise in DS13 (bifurcation). Separately, we employed the mouse cortex data set (Zeisel et al., 2015) that we used in steady-state simulations above as the reference for adding technical noise to DS14 (trifurcation). In both cases, similar to our approach in steady-state simulations, we sampled 50 comparison data sets from the real data each having 100 genes randomly selected out the pool of all genes. These sampled data sets were then compared against the noisy data generated by SERGIO to calibrate the level of technical noise (Supplemental Figure S11). We confirmed once again that with the appropriate parameter settings noisy data sets synthesized can match real data sets in their statistical properties.
In order to visualize the above data sets, we used the preprocessing functions of Velocyto (La Manno et al., 2018) to normalize expression matrices and filter low quality cells from noisy versions of DS13 and DS14, preserving only the top 2999 and 6560 high quality cells in bifurcation and trifurcation trajectories, respectively. We used PCA to reduce the dimensionality of these data to the first 10 PCs, and then applied UMAP to obtain a two dimensional representation of single cells. Figures 6D,E show these data in their PCA-based (top two PCs) and UMAP-based representations. Although significant amount of technical noise has been added to the simulated data, the underlying bifurcation and trifurcation trajectories of cells are clearly evident in the noisy versions of DS13 and DS14.
Differentiation data sets synthesized by SERGIO can be used to benchmark trajectory inference algorithms since the underlying differentiation trajectory (graph) is known for these data. To illustrate this, we applied the Slingshot (Street et al., 2018) tool on the clean as well as noisy data sets synthesized based on bifurcation and trifurcation trajectories. Slingshot is a tool specifically developed for trajectory inference, with published reports of high accuracy. For the clean data sets DS10 (bifurcation) and DS11 (trifurcation), Slingshot infers the correct lineages (Figures 7A,B); however, it did not fully reconstruct the underlying trajectories for the noisy data sets DS13 and DS14, failing to separate one of the lineages in either case (data not shown). On the other hand, once we provide prior information about the undetected terminal cell types to Slingshot, it correctly infers the trajectories for the noisy data sets DS13 and DS14 (Figures 7A,B).
Figure 7: Evaluation of differentiation data sets generated by SERGIO.
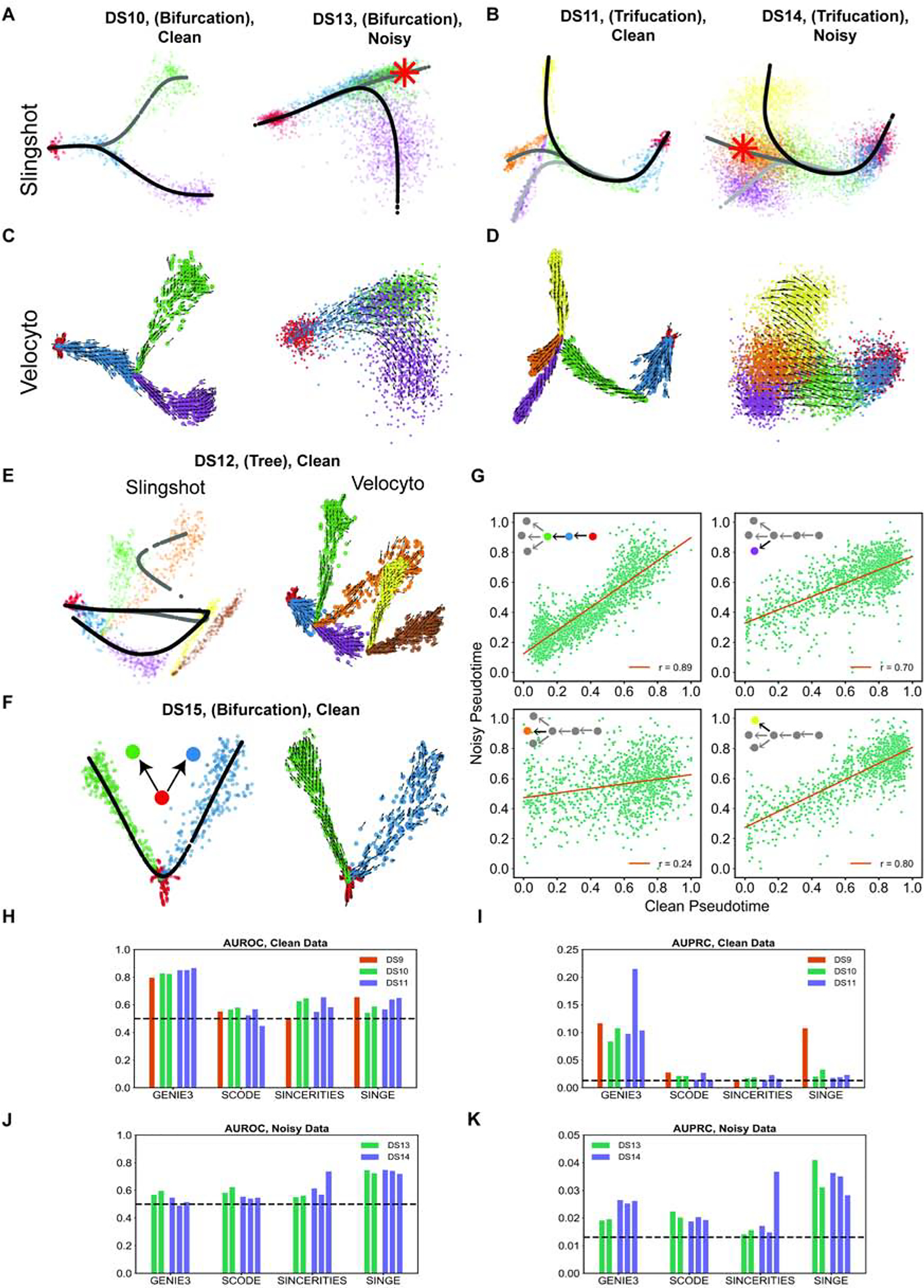
(A,B) Differentiation trajectories inferred by Slingshot on clean and noisy simulated data for bifurcation (A) and trifurcation (B) trajectories of differentiation programs. Each line with a slightly different grayscale color denotes a distinct inferred path. Slingshot infers correct trajectory without any prior knowledge for clean data, and with knowledge of one of the terminal cell types (green cell type in DS13, and orange cell type in DS14 marked by asterisks) for noisy data. (C,D) Velocity fields inferred by Velocyto on clean and noisy simulated data for bifurcation (C) and trifurcation (D) differentiation trajectories. In all four cases, the inferred velocity field is consistent with the underlying differentiation trajectory. (E) Differentiation trajectory inferred by Slingshot (left) and the velocity field inferred by Velocyto (right) on clean simulated expression data set DS12. (F) Differentiation trajectory inferred by Slingshot (left) and the velocity field inferred by Velocyto (right) on a simple bifurcation data set (DS15) synthesize by SERGIO. (G) Pseudotime inferred by Slingshot from noisy versus clean simulated data of DS14 (see Supplemental Figure S10 for clean version of DS14) on four separate segments of the underlying differentiation trajectory. See also Figure S12. (H,I) AUROC and AUPRC respectively of the GRN inferred by various methods on the pseudotime-ordered single cells in clean data sets DS9, DS10, and DS11. GRN inference was performed on each differentiation branch separately and AUROC and AUPRC is calculated and shown for each branch of DS10 and DS11. (J,K) AUROC and AUPRC respectively of the GRN inferred by various methods on the pseudotime-ordered single cells in noisy data sets DS13 and DS14. GRN inference was performed on each differentiation branch separately and AUROC and AUPRC is calculated and shown for each branch.
We also analyzed the above synthetic data sets with the Velocyto (La Manno et al., 2018) tool, which infers an “RNA velocity” field in a low dimensional representation of single cells that indicates the direction in which each cell’s expression profile appears to be changing. The velocity field also provides an intuitive visualization of differentiation trajectories. Figures 7C,D depict the inferred velocity fields for clean as well as noisy data sets with bifurcation or trifurcation trajectories, demonstrating how Velocyto correctly captures these differentiation trajectories. We found that for the more complex differentiation trajectory of DS12 (tree) Slingshot is unable to recover correct lineages, while Veloycto infers a velocity filed that is indicative of the correct underlying trajectory (Figure 7E). Thus, we find that use of an additional layer of information - separation of spliced and unspliced mRNA counts - can improve trajectory inference from single cell transcriptomic data. This is not limited to data sets with complex underlying trajectories - Figure 7F shows an example data set (“DS15”) generated using a simple bifurcation graph for which Slingshot infers a linear trajectory while Velocyto reports a velocity field clearly indicative of the true bifurcation trajectory. It is worth noting that here we did not provide any prior information regarding terminal cell types to Slingshot, which may resolve the errors noted above. To summarize, synthetic data sets generated by SERGIO show that, at least in the absence of prior information on established cell types, RNA velocity-based approaches may have an advantage in terms of trajectory inference on single cell data.
Trajectory inference in differentiation data sets allows researchers to assign a (partial) ordering among single cells along the differentiation trajectories, resulting in assignment of a so-called “pseudotime” value to the cell (Trapnell et al., 2014). We noted above (Figures 7A,B) that differentiation trajectories can be inferred with reasonable accuracy using Slingshot, but also observed that the reduced dimension representation places individual cells more diffusely along the trajectory when analyzing noisy data sets than for clean data sets. This suggests that the technical noise present in single cell data may affect the inferred temporal ordering (pseudotime) of cells. To quantify this effect, we simulated clean and noisy data for a trifurcation trajectory similar to DS9 and used Slingshot to assign pseudotime labels to cells in the two data sets (These two versions have synthetic expression data for the same cells, differing only in the presence of technical noise.) Figure 7G depicts the correlation between these two pseudotime labels, separately for four segments of the underlying differentiation trajectory. We noted that for three of the four segments the pseudotime inference is relatively robust to presence of technical noise (correlation coefficient r being 0.89, 0.70 and 0.80), but for one of the segments - the lineage leading specifically to the cell type shown in orange in Figure 7D - the pseudotime inferences on clean and noisy data sets were poorly correlated (r = 0.24). We noted that the dropout rate was higher for cells in this lineage (Supplemental Figure S12) compared to the three other lineages, providing a plausible explanation for the above observation and suggesting that the pseudotime inference on cells with high dropout rate may need to be interpreted with greater caution.
Benchmarking GRN reconstruction on differentiation data
Single-cell transcriptomic profiles of differentiation processes offer unique opportunities for GRN reconstruction, since pseudotime labels can be exploited to infer causal relationships between TFs and target genes. Several methods have been recently proposed that specifically channel this opportunity, including SCODE (Matsumoto et al., 2017), SINCERITIES (Papili Gao et al., 2018) and SINGE (Deshpande et al., 2019). We used the differentiation data simulated by SERGIO to benchmark these specialized GRN-reconstruction algorithms, using Slingshot for pseudotime inference. In particular, we used one simulated replicate of clean data sets DS9 (linear), DS10 (bifurcation) and DS11 (trifurcation) and two noisy data sets DS13 (bifurcation) and DS14 (trifurcation) for which we verified above that Slingshot infers correct trajectories. For each data set, we evaluated and compared the three above-mentioned GRN reconstruction methods on single cells associated with a single branch of the inferred differentiation trajectory (see STAR METHODS). We also used GENIE3 as a baseline method to infer TF-gene relationships without utilizing pseudotime information. Interestingly, in the absence of technical noise, GENIE3 clearly outperforms the three specialized algorithms in five out of six evaluations (Figure 7H, I). However, for DS9 (linear) SINGE outperforms SCODE and SINCERITIES, and performs as well as GENIE3 in terms of AUPRC. In general, the use of temporal ordering of single cells does not seem to help GRN reconstruction in the absence of technical noise. This result is consistent with findings of Pratapa et al. (Pratapa et al., 2020), where GENIE3 was placed among the top three GRN inference methods evaluated, above SCODE, SINCERITIES, and SINGE, when applied on synthetic data sets based on curated Boolean networks and without technical noise. Interestingly, the authors found that GENIE3 is among the best performing GRN inference methods even when evaluated on real scRNA-seq expression data sets.
On the other hand, for noisy data sets DS13 and DS14, performance of GENIE3 (in terms of AUROC) falls down to random levels (Figure 7J, K) similar to what we observed for steady-state data sets. Here, SINGE clearly outperforms the other methods, including GENIE3, in four out of five evaluations, and in the fifth evaluation both SINCERTIES and SINGE show equally strong performance. Interestingly, the performance of SINGE here is significantly above random and is even better than its performance on the clean data sets DS9–11, at least in terms of AUROC. This suggests that SINGE is robust to technical noise present in the single-cell RNA-seq technologies. Next to SINGE, GENIE3 has the best overall performance in terms of AUPRC, followed by SCODE and SINCERITIES. The same overall performance order among the last three methods was reported by Pratapa et al. (Pratapa et al., 2020) in evaluations on real scRNA-seq data sets (SINGE was excluded from these evaluations in (Pratapa et al., 2020)). In four out of our five evaluations, performance of SINCERITIES in terms of AUPRC is worse than the other methods and is close to random. This is also consistent with evaluations of this tool on real scRNA-seq data sets by Pratapa et al. (Pratapa et al., 2020).
Discussion
The main distinguishing quality of SERGIO is its ability to simulate single-cell expression data based on a specified GRN. Its implementation strikes a balance between a biologically realistic model of transcriptional processes and simplifying assumptions that facilitate fast simulation, capable of scaling to thousands of genes and regulatory interactions. To mimic cellular heterogeneity commonly seen in single-cell data, SERGIO employs an intuitive definition of cell types as steady states of GRN dynamics (Huang et al., 2005). The steady-state assumption is admittedly a simplification, and in reality, some genes in a cell type might have out-of-equilibrium expression states. However, this simplification allows for a more robust benchmarking of single-cell tools that do not examine cell state transitions and differentiation information. On the other hand, SERGIO can also simulate collections of cells differentiating from one cell type to another, an important feature not available in GNW (Schaffter et al., 2011) even after modifications to simulate single-cell data.
We showed that with a reliable and properly parameterized GRN, SERGIO can reproduce the expression dynamics of early T-cell development, capturing the significant regulatory effects of key regulators of T-cells, such as Tcf7, Gata3, and Bcl11b, and suggesting an important role for Runx1. These observations were made using a well-studied GRN model we attained from the literature (Longabaugh et al., 2017), but could not be fully reproduced when using a GRN reconstructed with GENIE3 (Supplemental Figure S8). This suggests that SERGIO can be utilized to examine alternative networks of transcription regulation in light of single-cell expression data and prior knowledge, and to rank or exclude possible interactions. In addition, we showed how SERGIO can be used to predict the broader effects of a perturbation in the GRN model.
Furthermore, we demonstrated that SERGIO is a powerful tool for benchmarking a wide variety of single-cell analysis tools. For instance, our assessment of a leading GRN inference tool found that it is rendered largely inaccurate (close to random performance) due to technical noise typical of contemporary data sets, even though it is capable of far greater accuracy in the absence of measurement errors. We also evaluated GRN inference methods designed specifically for time-ordered single-cell expression data (Deshpande et al., 2019; Matsumoto et al., 2017; Papili Gao et al., 2018), and found that in the absence of technical noise, a more general-purpose method - GENIE3 (Huynh-Thu et al., 2010) - outperforms these specialized methods; however, SINGE (Deshpande et al., 2019) shows the best performance when technical noise is present. Future studies can use SERGIO to study the effect of technical noise on GRN inference. Moreover, the performance of these specialized tools depends on the type of differentiation trajectories, number of single-cells and other factors. For example, SCODE has a hyper-parameter named D, whose appropriate value is not known a priori and might vary from one data set to another. Similarly, SINGE uses a hyper-parameter named lambda to control the sparsity of the inferred network. It is common for GRN inference tools to resort to user-defined hyper-parameters, and future studies on GRN inference can utilize SERGIO to examine such hyper-parameters as a function of data set properties.
An important work related to ours is the BoolODE simulator developed by Pratapa et al. (Pratapa et al., 2020), which adapts the model of GeneNetWeaver (GNW), but allows the user to provide a Boolean function to describe combinatorial influence of multiple regulators on each gene, thereby making the GNW model more configurable. SERGIO, on the other hand, simplifies the GNW model in its treatment of combinatorial regulation, modeling the influence of multiple regulators as the sum of their independent contributions. This difference has the following practical consequences: (1) The time complexity of simulating a target gene in SERGIO is linear in the number of regulators while that in BoolODE is exponential in this number. We found SERGIO to run significantly faster than BoolODE for the same networks (see STAR Methods and Supplemental Table S4); (2) When simulating data sets from a random network, the rules of combinatorial regulation are much simpler to specify in SERGIO than in BoolODE (influence of multiple TFs is additive in SERGIO, while BoolODE requires combination rules to be explicitly specified for each target gene). The SERGIO model also ignores protein translation and degradation, which are featured in BoolODE, thus marking another difference between the simulators in their tradeoffs between model simplicity and realism. We believe the simplifications made in SERGIO to be a practical advantage since large GRNs are rarely characterized in the necessary detail. Secondly, stochastic expression in BoolODE arises only from the biological noise term in the GNW model, and a dropout rate. SERGIO on the other hand incorporates multiple sources/types of noise beyond the biological noise, viz., outlier expressions, library size effects and dropout through appropriate statistical distributions discussed in the literature (Zappia et al., 2017). Thirdly, the dynamic mode of SERGIO enables simulations of spliced and unspliced mRNA counts for user-defined differentiation trajectories (a feature not included in BoolODE currently), which allows the benchmarking of RNA velocity and trajectory inference algorithms.
Recent work has also examined the related but distinct task of learning a generative model from a given scRNA-seq data set, to be then used for simulations. Marouf et al. (Marouf et al., 2020) employed a neural network to automatically learn the underlying distributions of gene expression from a real single-cell data set and used the learnt model to generate synthetic expression profiles (cells) that are indistinguishable from real profiles. Interestingly, they showed that this machine learning approach captures gene-gene dependencies in its latent space, therefore implicitly including regulatory relationships in the model. Our work differs fundamentally from (Marouf et al., 2020) in that we seek to simulate data with an explicit GRN as input (a forward simulation goal), rather than attempt to estimate it from data (a reverse engineering goal). This key difference allows SERGIO to be useful for benchmarking of GRN inference tools.
It should be noted that the GRN benchmarking in this study considered methods based on expression only, while better accuracy can result from existing tools that use additional information such as TF-DNA binding data (Aibar et al., 2017). Future work can combine SERGIO simulations of single-cell expression with existing ideas on benchmarking GRN inference from bulk data and prior information (Siahpirani and Roy, 2017). Expression data from TF knockout experiments can also be exploited by GRN inference algorithms (Bonneau et al., 2006), and knockout of regulators can be easily simulated in SERGIO to assess such algorithms.
In conclusion, we believe that SERGIO will prove useful to a number of researchers developing tools for the rapidly developing field of single-cell transcriptomics. It will be especially useful for testing GRN reconstruction methods, which according to our assessments is the analytical task most in need of future improvements. But its usefulness will extend to future tools for other popular tasks as well, since synthetic data sets that capture real data more closely naturally provide more reliable assessments of those tools. Moreover, the “clean” simulated data sets (without technical noise) generated by SERGIO should be useful in their own right, since they also capture realistic expression variation due to biological noise and can provide upper bounds on accuracy in the idealized scenario where measurement noise has been eliminated.
STAR METHODS
RESOURCE AVAILABILITY
Lead Contact
Further information and request for resources should be directed to the Lead Contact, Saurabh Sinha (sinhas@illinois.edu).
Materials Availability
This study did not generate new reagents.
Data and Software Availability
This study used several published and publicly available data sets. We obtained the raw mouse cortex data set (Zeisel et al., 2015) from Gene Expression Omnibus (GEO) with accession GSE60361. The raw 10X genomics expression for mouse MGE, CGE, and cortical regions (Mayer et al., 2018) obtained from GEO with accession GSE104156. The raw 10X genomics expressions for human kidney (Lindström et al., 2018) and human PBMC cells (Paulson et al., 2018) obtained from GEO with accession GSE102596 and GSE117988, respectively. The raw Drop-seq expression for human lung (Vieira Braga et al., 2019) obtained from GEO with accession GSE130148. The raw Smart-seq2 expression for mouse heart (Schaum et al., 2018a) obtained from GEO with accession GSE109774. Also, we obtained raw 10X genomics expression data for dentate gyrus of mouse hippocampus from GEO with accession GSE104323 (Hochgerner et al., 2018).
SERGIO v1.0.0 used to generate synthetic data sets in this study is available as a python package on GitHub: (https://github.com/PayamDiba/SERGIO).
METHOD DETAILS
Steady-State Simulations
The Chemical Master Equation (CME) offers a paradigm for modelling stochastic transcription of genes (Gillespie, 1992; Khanin and Higham, 2008). Gillespie’s stochastic simulation algorithm (Gillespie, 1976, 1977) enables the computation of trajectories according to CME. However, simulating trajectories of CME for large biomolecular systems is computationally expensive (Khanin and Higham, 2008). Chemical Langevin equation (CLE) (Gillespie, 2000) that is derived from CME under two additional assumptions provides a more tractable system of differential equations compared to CME; therefore, CLE can be integrated with numerical methods in a computationally efficient manner and allows for practical simulations. It has been shown that Gillespie’s stochastic simulations of CME and numerical simulations of CLE generate trajectories that have comparable mean, variance and correlations (Khanin and Higham, 2008). Hence, we model the dynamics of the concentration of genes using systems of stochastic differential equations (SDE) that have been previously employed in GeneNetWeaver (GNW) (Marbach et al., 2010; Schaffter et al., 2011) and which are derived from the chemical Langevin equation (CLE) (Gillespie, 2000). The time-course of mRNA concentration of gene i is modeled by:
| (1) |
where xi is the expression of gene i, Pi is its production rate, which reflects the influence of its regulators as identified by the given GRN (details below), λi is the decay rate, and qi is the noise amplitude in the transcription of gene i. α and β are two independent Gaussian white noise processes. This model relies on the assumption that there is no delay between TF-mediated regulation and mRNA production. In order to obtain the mRNA concentrations as a function of time, we integrate the above stochastic differential equation for all genes:
| (2) |
where Wα and Wβ are two independent stochastic Wiener processes. We integrate this equation in pre-defined time steps of duration Δt, according to Euler-Maruyama method (Schaffter, 2010) using the Itô scheme:
| (3) |
| (4) |
Each iteration yields the mRNA concentrations of all genes at time step t + Δt using each gene’s own concentration and all of its regulators’ concentrations at time step t.
We model each gene’s production rate, Pi, as the sum of contributions from each of its regulators (as prescribed by the GRN):
| (5) |
where Ri is the set of all regulators of gene i, bi is the basal production rate of gene i, and pij is the regulatory effect of gene (TF) j on gene i. The latter is modeled as a non-linear saturating Hill function of the mRNA concentration of the TF (Chu et al., 2009):
| (6) |
| (7) |
where Kij denotes the maximum contribution of regulator j to target gene i, nij is the Hill coefficient that introduces non-linearity to the model and hij is the regulator concentration that produces half-maximal regulatory effect (half-response). If gene i is a user-designated “master regulator” (MR), i.e., no gene regulates it, then its production rate Pi is entirely determined by basal production rate bi which is a user-defined parameter. For simplicity, we set bi = 0 for genes other than master regulators. Kij and nij are user-defined parameters, and the type of each interaction (activation or repression) is also user-specified. The hij parameter is set to be the average of the regulators’ expression among the cell types to be simulated. The parameters α and β in equation 1 characterize the intrinsic noise associated with the production and decay processes of the mRNA transcript of gene i, Moreover, the intrinsic noise in the transcription of regulators propagates along the GRN and thus influences the production rate Pi to become an extrinsic noise source in the transcription of gene i. We support three forms of noise:
Dual Production Decay (“dpd”): the form of stochastic noise that is shown in equation 1.
Single Production (“sp”): including only the noise term associated with the production process (equivalently, set β = 0).
Single Decay (“sd”): including only the noise term associated with the decay process (equivalently, set α = 0)
We note that the current version of SERGIO is not capable of simulating GRNs containing auto-regulatory edges or cycles. This is because of a topological sorting algorithm in SERGIO that enables the automatic selection of half-response parameters (see STAR Methods) and fails in the presence of cycles in GRN. It is a shortcoming as cycles are often present in real GRNs, but it can be resolved by eliminating the dependency of SERGIO on the topological sorting algorithm. Future releases of the software will address this issue.
Sampling Single-Cells
We use the above system of equations to simulate the time-course of each gene’s expression in a cell, starting with a given initial value, and record expression values of all genes at randomly selected time points after the simulation has reached steady state. Invoking the ergodic assumption (Prill et al., 2015), we treat the expression profiles at these time points to represent single-cell profiles. In order to speed up the simulation, we estimate the steady-state concentrations of all genes given the input parameters (see STAR Methods) and initialize the time-course simulation with those values. Also, we ensure that a sufficient number of time steps, which is controlled by a user-defined parameter, are simulated in the steady state prior to sampling cells.
Cell Types
The above simulation is performed for each “cell type” separately. We define a cell type (or cell state) by the average concentration of master regulators. A cell type differs from another cell type by the average concentration of one or more of the master regulators among the population of cells belong to each cell type. This can be controlled by the basal production rate b for master regulators (see STAR Methods). SERGIO takes as input the basal production rate of all master regulators in each of the cell types to be simulated.
Estimating Steady-State Concentrations
In steady state-simulations, Sergio approximates the steady-state concentrations of all genes in all cell types prior to starting the simulations. Then, Sergio initializes all the concentrations with their corresponding estimated stead-states values. This is particularly useful for speeding up the simulations since initial concentrations are so close to the values to which the numerical integration is supposed to converge. To do so, Sergio applies a topological sort algorithm on the gene regulatory network in order to layer the graph. After layering the GRN graph using topological sorting, all the regulators of the genes of any layer reside in the preceding layers. Sergio starts estimation of steady-state concentrations (as well as half-response parameters of the hill functions) from the top most layer and continues layer-by-layer until the very last layer of genes. Therefore, all information required for estimating the steady-state concentrations (and half-responses) of genes in the current layer is already available from the user-defined parameters and the estimated concentrations of the genes in the previous layers. Below we demonstrate how Sergio estimates steady-state concentrations.
We start with equation 1 that describes the rate of changes in mRNA concentration xi of gene i. In order to reach the steady-state regime, we need to have , where E[.] denotes the expectation operator. Since is well defined and is bounded, we have . So, we get:
Also recall that α and β are two Gaussian white noise processes which have a zero mean, so we get:
If gene i is a master regulator, according to equation 5 its production rate is solely determined by its user-defined production rate bi and therefore we can accurately estimate the expected steady-state concertation xi:
| (8) |
However, if gene i is not a master regulator, according to equation 5 we get:
| (9) |
where Ri is the set of all regulators of gene i, and pij is a hill function. We use the following approximation for calculating E[pij(xj)]:
Note that this a loose approximation as it clearly over-estimates or under-estimates the true value of E[pij(xj)], yet it is good enough for our ultimate goal which is initializing mRNA concentrations. Substituting this back into the equation 9 we obtain an estimate of the steady-state concertation of gene i:
| (10) |
At the time we calculate the concentration of gene i we have already calculated the steady-state concertation of all of its regulators (which reside in the preceding layers of the sorted GRN), hence we have all the information required for this calculation. Note also that the goal of the above estimation is not to find steady-state concentrations per se, but to find values close to these concentrations so as to reduce simulation time by starting the simulations at these concentrations.
Estimating Half-Response Parameter
We model each interaction with a Hill function that has a half-response parameter h that needs to be pre-specified for the simulations. If we use a small value of half-response (h ≪ [TF]), then the Hill function becomes a constant function independent of TF concentration:
On the other hand, if we use a very large value for half-response (h ≫ [TF]), then the Hill function does not have its non-linear saturating form anymore (especially for n=1, where it becomes linear):
So, we considered it important to set the half-response parameter to a value that yields the saturating non-linear behavior of Hill functions, across different cell types. While it is difficult for user to define this parameter (because, for an arbitrary TF->target interaction, user may not know the expected concentration of TF a priori), SERGIO can determine reasonable values of the half-response parameter using the concentration of all regulators of the current target (that reside in the previous layers obtained by topological sorting algorithm). In the current implementation of SERGIO, for each interaction, we set half-response to the mean expression of the regulator in all cells (belonging to multiple cell types). This guarantees that we see a large range of response over different cells and cell types. As explained in “Estimating Steady-State Concentrations” section above, at the time we get to a new gene, the expression of all of its regulators (which live in upper levels of sorted GRN) have been already simulated because of the topological sorting algorithm. This enables the calculation of half response parameter based on the expression of regulators. This design choice was made so as to take the burden of setting the half-response parameter away from the user, that also necessitates the topological sorting of the GRN graph and thus demands an acyclic graph.
Simulation of Differentiation Trajectories
In addition to simulating one or more “cell types” in steady state, SERGIO may be used to simulate cells on the differentiation trajectory from one cell type to another, i.e., between two steady states. More generally, given a “differentiation graph” where nodes represent cell types and directed edges indicate differentiation from one cell type to the other, SERGIO can simulate expression profiles of cells spanning different stages of differentiation specified by the graph. Such cells are either in one of the steady states represented by nodes or have departed away from the steady-state of their “parent” cell type of an edge and are migrating toward the steady-state of the corresponding “child” cell type. The differentiation is presumed to commence when one or more master regulators change their expression from that in the steady state of the parent cell type, e.g., due to a signaling event (Albert Basson, 2012) or due to a noise-driven switch (Balázsi et al., 2011). Thus, given a differentiation graph and average expression levels of master regulators for each cell type (nodes), we simulate each differentiation trajectory (edge) as follows: 1) Cells representing the parent cell type are sampled from the corresponding steady state. 2) Production rates (Pi) of master regulators are changed from those specified for the parent cell type to those of the child cell type, and time-course simulations are performed following equations 3–4 as explained above. As these simulations proceed, all genes ultimately converge to their steady-state concentrations in the child cell type. 3) Cells (expression profiles) are sampled at random from the entire simulation, including cells in the parent and child cell types (steady states) as well as cells on the differentiation trajectory (transient states). Multiple such time-course simulations are performed and the sampled cells are randomly chosen from the entire collection of such simulations. Also, after each simulation reaches the steady-state of the child cell type, it may be continued for a user-defined number of additional steps. This controls the ratio of the cells in the steady states of the differentiation graph to the number of cells in differentiating (transient) states.
Simulations of differentiation trajectories in SERGIO generate not only the total mRNA concentration of each gene (in a time-course), but the changing levels of spliced and unspliced mRNA transcripts separately. To this end, we express the rate of change in the concentration of unspliced and spliced RNA using ordinary differential equations (ODEs), following prior work (La Manno et al., 2018; Svensson and Pachter, 2018). Furthermore, we introduce noise terms to these ODEs in a manner similar to steady-state simulations (equation 1). Thus, the time-course of the spliced (s) and unspliced (u) transcript level of gene i is modeled as:
| (11) |
| (12) |
where Pi(t) is the production rate of pre-mRNA (unspliced transcript) that includes regulatory interactions, λi and μi are the degradation and splicing rate respectively of pre-mRNA and is the noise amplitude associated with the transcription of pre-mRNA. For simplicity, we assume the degradation rate λ of pre-mRNA is zero and all of its decay is due to splicing (user-defined parameter μi). Also, γi is the degradation rate of spliced mRNA and is the noise amplitude associated with the transcription of spliced mRNA. α, β,ϕ and ω are independent Gaussian white noise processes. All the three form of stochastic noise (“dpd”, “sp”, “sd”) described for steady-state simulations are also supported in dynamics simulation. Moreover, production-rate Pi is modeled as in steady-state simulations (equations 5–7 above). Both of the SDEs in equations 11–12 are integrated according to Euler-Maruyama scheme to obtain time-courses of unspliced and spliced mRNA concentrations.
Technical Noise
SERGIO adopts methods similar to Splatter (Zappia et al., 2017) for adding technical noise to the simulated single-cell expression data. One module introduces the phenomenon of “outlier genes”, which refers to the empirical observation that a small set of genes appear to have unusually high expression measurements across cells in typical scRNA-seq data sets. A second module incorporates the noted phenomenon of different cells having different total counts (library size), that follows a log-normal distribution. A third module introduces “dropouts”, which refers to the observation that a high percentage of genes are recorded at zero expression in any given cell, indicating an experimental failure to record their expression rather than true non-expression. These three modules may be invoked optionally, and in any combination and order specified by the user. Each of the modules outlined below adds a single type of technical noise to the data set provided to it.
Outlier genes:
Each gene is designated as an outlier with a user-defined probability. If so, its expression (in every cell) is multiplied by a factor sampled from a log-normal distribution, otherwise the expression is left unchanged. In the steady-state mode, outlier genes are introduced as following:
where G and C denote the total number of simulated genes and cells respectively, and denotes the simulated expression of gene i in cell c. is a binary variable indicating if gene i is an outlier, and is sampled from a Bernoulli distribution with parameter π0. Also, μ0 and σ0 are user-defined mean and standard deviation of the lognormal distribution from which the outlier scaling factor is sampled.
We follow a similar scheme in differentiation mode by changing both unspliced and spliced transcripts:
where and denote the simulated unspliced and spliced concentrations respectively of gene i in cell c.
Library size:
For every cell (library) a library size parameter is sampled from a lognormal distribution, and expression values of all genes in the cell are scaled by a constant factor such that the resulting total cell depth matches the sampled library size. In steady-state mode we have:
where μL and σL are the user-defined mean and standard deviation of the lognormal distribution from which the desired library size Lc of cell c is sampled.
Following the same approach, we scale both unspliced and spliced transcripts in the differentiation mode:
Dropout:
To introduce dropouts to the simulated data, we first assign a probability to the expression of each gene in each of the simulated cells not being a dropout. This probability is modeled as a logistic function of the expression of the gene in that cell, so that a high expression value is less likely to be zeroed out. This probability is then used as the parameter of a Bernoulli distribution from which a binary variable is sampled to indicate whether the gene is not a dropout in the cell. Dropout is introduced to the steady-state simulations as following:
where Y is the expression matrix in logarithmic scale:
Also, k and q are two user-defined parameters that determine the logistic probability πD.
In real single-cell data, dropout impacts unspliced and spliced transcripts independently. To model this in the differentiation mode, we employ a similar approach as we use for steady-state simulations but add dropout to spliced and unspliced expressions independently:
where Y denotes the total mRNA expression matrix in logarithmic scale:
Also, we define:
Conversion to UMI counts:
In steady-state simulations, we generate UMI counts (UC) by sampling from a Poisson distribution whose mean is the simulated expression level of the gene in the cell:
In differentiation simulations, spliced (UCS) and unspliced (UCU) mRNA counts are independently sampled from a Poisson distribution whose mean is the simulated expression level of the gene in the cell:
Controlling Spliced to Unspliced Count Ratio
We can estimate and control the ratio of the expected spliced to unspliced expression in the stationary region of the stochastic transcription process. Using equation 12, under steady-state condition we get:
Sergio, as an input, takes the decay rate μ of the unspliced mRNA as well as the splicing ratio ; these two together determine the degradation rate of spliced RNA γ according to the last equation. This enables the user to simulate gene expressions with any desired spliced to unspliced ratios in order to reproduce different experimental settings.
Synthetic Data Set Generation
We now describe how we set simulation parameters to generate the data sets analyzed in this study.
We sampled four gene regulatory networks (GRNs) from the known regulatory networks in S. cerevisiae and E. coli using GNW (Schaffter et al., 2011) using the “random seed” argument to select genes and the “random among top 20%” setting for neighbor selection. Two of the networks consist of 100 genes and were separately sampled from Ecoli, a third network containing 1200 genes was sampled from E. coli, and the fourth network comprising 400 genes was sampled from S. cerevisiae. We also used GNW to designate each TF-gene edge as either an activating or a repressive interaction. Auto-regulatory edges were removed from the sampled networks and cycles were broken at a randomly selected edge, since SERGIO does not support these two graph properties. These four networks were used to simulate 15 data sets described in Table 1. Except for DS13 and DS14 that were simulated in only one “replicate”, fifteen replicates of each data set were created that had identical simulation parameters and differed due to the stochastic noise and random sampling. For all data sets, interaction strengths Kij (equations 6–7) were uniformly sampled from the range 1 to 5. Each cell type to be simulated was specified by the expression state (high or low) of each master regulator (MR); the basal production rate (bi in equation 5) of each MR was sampled from a pre-defined range that depends on the expression state and varies among different data sets (see Supplemental Table S3). We used a hill coefficient of 2 for all interactions in all data sets. We used the same noise amplitude parameter q = 1 and the same decay parameter λ = 8 for all genes in all steady-state data sets. In dynamics simulations, we used an unspliced noise parameter qu = 0.3 and a spliced noise parameter qs = 0.07 for all genes. Also, we used an unspliced transcript decay rate of μ = 0.8 and a spliced transcript decay rate of γ = 0.2 that maintains a ratio of spliced to unspliced expression of a gene at ~4. We used “dpd” setting of intrinsic noise and an integration time step of 0.01 for both steady-state and dynamics simulations.
We compared the simulated expression matrices (genes × cells) of DS1, DS2, DS3, and DS9 to a single-cell RNA-seq data set from the mouse cerebral cortex (Zeisel et al., 2015), which includes 3005 cells from nine cell types, as a reference for adding technical noise. We sampled the mouse cortex data set by drawing cells of each type at random: for cell types with less than 300 cells, we retained all the cells, while for the other cell types we randomly sampled 300 cells such that a total of 2500 single cells were sampled. Our simulations generated expression values for 100, 400 or 1200 genes depending on the data set, hence we randomly sampled from the real data set the same number of genes as present in the synthetic data. Moreover, we used five other published single-cell RNA-seq data sets as a reference for adding technical noise to data sets, which respectively contain 16383 cells of mouse MGE, CGE, cortical and subcortical regions (Mayer et al., 2018), 3745 cells of human kidney (Lindström et al., 2018), 12874 of Human Peripheral blood mononuclear cells (PBMC) (Paulson et al., 2018), 10360 cells of human lung (Vieira Braga et al., 2019), and 6002 cells of mouse heart (Schaum et al., 2018b). These resulted in the data sets DS4–8 respectively, and for each of these we repeated the same sampling strategy described above to create comparison data sets, sampling 1200 genes at random while preserving all the cells in each sample. We also we used a published single-cell RNA-seq data set containing 24185 cells from developing mouse dentate gyrus (Hochgerner et al., 2018) as a reference for adding technical noise to the data set DS13. We generated comparison data sets by sampling 100 genes at random, while all single-cells were preserved.
To add technical noise, we used the above-mentioned modules for outlier genes, library size effect and dropouts in that order, and finally converted the expression levels to UMI counts. For each data set, we manually tuned the input parameters (see Supplemental Table S1) to each of the technical noise modules to obtain a comparable noise level between the synthetic and real data.
Simulations of T-Cell Differentiation
Simulations of T-cell development involved two important steps: first obtaining a GRN model and second parameterizing the GRN and tuning other parameters of SERGIO. Here we describe these two steps in detail.
GRN model:
We considered two GRN models for regulation of T-cell development. One model was obtained from (Longabaugh et al., 2017), which provides a GRN model for pre (stages ETP to DN2a) and post commitment (DN2b to later stages) in BioTapestry format. We assembled the part of this GRN that involves genes present in the seqFISH data. GRN edges (regulatory interactions) in the pre and post commitment stages were combined to obtain a single GRN that includes 32 interactions among 22 genes, four of which are master regulators, i.e., do not have regulators in the GRN. Another GRN model was obtained from the sorted list of possible interactions inferred by GENIE3 on the seqFISH data. We considered the top 126 interactions, and since SERGIO requires GRNs to be acyclic, we opened up the cycles by removing an interaction in each cycle, making sure that the removed interaction is not present in the literature-based GRN of Longabaugh et al. This resulted in a GRN containing 108 interactions among the 65 genes in the seqFISH data, of which 23 are modeled as master regulators.
Parameterizing GRN model
Our goal was to parameterize either GRN discussed above such that the simulated data resembles the real seqFISH data. For this, we tuned the interaction parameters such that the mean gene expression values in each cluster match between the real and simulated data. Based on the structure of a GRN, we first separated the master regulators (MR) - genes without any incoming regulatory edge - from “non-MR” genes. For each MR gene i, the production rate is determined only by a basal production rate bi which is defined per each cluster separately. According to equation 8, for each gene i, we computed the basal production rate bi in each of the clusters (stage) from the real mean expression of gene i in the same cluster, which is known from seqFISH data, and an assumed decay rate of λi = 0.8.
where E[.] denotes the expectation operator.
However, for non-MR genes, the production rate is a function of its regulators’ concentrations as shown in equations 5–7. By using a relatively large value for half-response parameters in all interactions, for a non-MR gene i, equations 5–7 are simplified to the following equation:
where Ai and Ri are the set of all activators and repressors of gene i, respectively. Similar to equation 9, we can express mean expression values as a function of production and decay rates:
Note that this equation holds for each cluster, where expectation is calculated over the cells of that cluster only. So, the expectation appearing on the left-hand side of the above equation can be calculated for every target gene i in each cluster from the seqFISH data. Also, for any fixed value of the Hill coefficient parameter n, the expectations appearing on the right-hand side can be similarly computed for each of the regulators of gene i known from the GRN model. Therefore, with an assumed decay rate (e.g., we used λi = 0.8 for all genes), large enough half-response parameters h, and fixed Hill coefficients n we can solve this regression problem for each target non-MR gene i over the 9 clusters to determine interaction strengths K, and the basal production rate bi. In contrast to the other simulations in this study, we allowed non-MR genes to have a non-zero basal production rate, shared among all clusters, in order to improve the fitting accuracies. For both GRN models, we solved these regression problems by minimizing the least square errors. For each target gene i we used the sign of the regression coefficient to determine the role (activator or repressor) of its regulators (i.e., whether the regulator belongs to set Ai or Ri). Also, various values of Hill coefficient n were tested, while requiring the same value to be used for all interactions. The smallest fitting error was obtained with n = 2 for the GENIE3 network and with n = 1 for Longabaugh et al. network. The obtained interaction parameters and basal production rates for non-MR and MR genes, together with the optimal Hill coefficients and half-response parameters and decay rates used for fitting the model, formed a “parameterized GRN model” that was used by SERGIO to perform simulations. Moreover, a noise amplitude parameter q = 0.5 and q = 1 was used for all genes in simulations of GENIE3 and Longabaugh et al. GRNs respectively. For each cluster, we simulated the same number of single-cells as in the seqFISH data. Although our simplified optimization strategy produced fitting errors sufficiently small for our down-stream analysis, future studies with SERGIO may employ more sophisticated optimization strategies. This might involve the optimization of all hyper-parameters including n, h, K and q, especially when enough data are available.
Simulations with Cooperative Regulation
We developed an in-house version of SERGIO that includes cooperative regulation. In this mode of simulation, production rate of a target gene i is calculated as:
where Ri is the set of all regulators of gene i, and pij is calculated using equations 6–7. Also, Ci denotes the set of all activator pairs (x, y), x ∈ Ri, y ∈ Ri, x ≠ y that cooperatively regulate gene i, and si,(mn) denotes contributions from cooperative regulation of gene i by two of its activators, m and n, which is calculated as following:
where Ki,(mn) denotes the maximum contribution of m-n cooperative interaction to regulation of target gene i, xm and xn respectively represent the concentration of regulator m and n, hi,(mn) is the product of concentration values that produces the half maximal response and ni,(mn) is Hill coefficient that introduces non-linearity to the model. This cooperative regulation term uses a similar Hill function form as was used to model individual regulatory effects, pij; however, it depends on both regulators’ concentration, and thus approximates an AND operation.
We used a GRN containing 1200 genes and 2713 regulatory interactions (the same GRN as in DS3–8) to simulate synthetic data sets via the cooperative regulation mode of SERGIO. To this end, for each target gene i that at least has two activators we selected one or more pairs at random from its regulators set Ri to construct Ci. As a result of this step, we incorporated 268 cooperative regulation in the GRN. For calculating pij and master regulators’ concentration we used the exact same parametrization as that we used for DS3. For calculating si,(mn) terms we set hi,(mn) to the E[xm]E[xn], where E[.] denotes average over all cells and cell types, also we set ni,(mn) = 2 for all cooperative interactions. Moreover, we sampled the maximum cooperative effect parameter Ki,(mn) in one set of simulations from range 1 to 5 (moderate cooperative regulation; referred to as “w/ Coop”) and from range 50 to 100 in another set of simulations (large cooperative regulation; “w/ large Coop”) with 15 replicates for each set (see Supplemental Figure S6 and S7).
A Comparison Between Running Time of SERGIO and BoolODE
We compared the running time of SERGIO with that of BoolODE (Pratapa et al., 2020) on the same networks with varying numbers of genes. To this end, we converted the gene regulatory networks prepared for SERGIO to a format suitable for running BoolODE. Since BoolODE requires the explicit regulatory rules for each target gene, we combined all of the activators of each target gene with “AND” operands and we did the same for all repressors of each target gene. For a fair comparison, in each experiment we set the “number of cell type” parameter in SERGIO and “number of simulation time” parameter in BoolODE to the same number. We conducted four comparisons, and results are summarized in Supplemental Table S4. SERGIO runs significantly faster than BoolODE on the same networks. Since BoolODE cannot handle more than ~10 regulators for a target gene, in the third experiment (400 genes) we removed 63 interactions from BoolODE’s network to satisfy this constraint. These interactions were not removed from SERGIO’s network (see Supplemental Table S4).
QUANTIFICATION AND ANALYSIS
Settings of Single-Cell Analysis Tools
In this study we applied several tools to the real or synthetic data sets to mimic real-world analysis of such data and to benchmark these tools. We did not normalize the data sets prior to using these tools unless otherwise specified. We note below the specific settings used for each of the tools we tested:
SC3 (Kiselev et al., 2017):
We did not run SC3 to infer the number of cell types, instead we treated the number of cell types as a known quantity and required SC3 to cluster data sets into 9 cell types.
GENIE3 (Huynh-Thu et al., 2010) v1.4.3:
We provided the identities of true regulators to the GENIE3 tool except when analyzing the differentiation data sets where we used all the genes as potential regulators. Also, for differentiation analysis GENIE3 was run on the exact same expression matrices as used for the other GRN inference tools in this study.
MAGIC (van Dijk et al., 2018) v1.10.1:
Prior to running MAGIC, we filtered the synthetic data for rare genes (those expressed in less than 5 cells), and performed library size normalization as well as a square root transformation. We used MAGIC with the parameter t = 2, t = 7, and default setting where t is inferred from data.
SLINGSHOT (Street et al., 2018) v1.0.0:
We used the first two PCs as a low-dimensional representation of single-cells, and provided these as input to SLINGSHOT, along with the cell type labels. We did not provide any further prior information about origin and end cell types of trajectories.
VELOCYTO (La Manno et al., 2018) v0.17.17:
In addition to velocity inference from clean and noisy expression matrices, we used Velocyto to pre-process and normalize data sets. In particular, we used Velocyto to filter low-quality cells and normalize the two noisy differentiation data sets, i.e. DS13 and DS14, prior to using Slingshot and GRN reconstruction tools. We performed all of the filtering and normalization steps for spliced and unspliced counts that are recommended by developers of the software. We removed all cells whose total unspliced count is smaller than the 70th percentiles of unspliced counts for noisy differentiation data sets. We also performed K-nearest neighbor imputation on 20-dimensional PCA representations of single cells with K = 5 for clean and K = 400 for noisy differentiation data sets. The “constant velocity” model was employed for inferring velocity fields, and square root transformation was used for estimating transition probabilities from PCA representation of clean data sets, while log-transformation was used for noisy data sets.
SCODE (Matsumoto et al., 2017):
For each differentiation trajectory, we used SCODE with D = 2, 4, 6, 8, and 10 to infer regulatory relationships and report the results that produce the highest AUROC. Also, for each differentiation trajectory and setting of D parameter, we ran SCODE for 100 iterations and averaged results over 5 trials as recommended by the tool’s developers. All genes were considered as potential regulators. The inferred sign of interactions (activating or repressing) was ignored in evaluation of the tool’s performance: we sorted all gene-gene interactions by the absolute value of their inferred scores and assessed this ranked list for accuracy. Thus, the reported performance values are an overestimate of GRN inference accuracy in our setting.
SINCERITIES (Papili Gao et al., 2018) v2.0:
For each differentiation trajectory, we used the tool with parameters specifying Kolmogorov-Smirnov distance, Ridge regularization, and no auto-regulatory edge setting for unsigned GRN inference. As for SCODE, performance evaluation ignored signs in the true GRN.
SINGE (Deshpande et al., 2019) v0.4.1:
For each differentiation trajectory, we executed the tool with λ = 0, 0.01, 0.1. For each setting of λ, we evaluated the tool on an ensemble of 200 hyper-parameter settings (see Supplemental Table S2). For each λ, we aggregated the results over its ensemble of 200 parameter settings and reported the result that produced the best AUROC (in clean data sets, all three settings of λ showed equal AUROC, in noisy data sets λ = 0, 0.01 showed an equal but better AUROC than λ = 0.1).
Data sets for evaluating GRN inference on differentiation data:
For each differentiation simulation data set, we generated sub-matrices that represent cells belonging to a single lineage. Therefore, we obtained 1, 2, and 3 sub-matrices for clean data sets DS9, DS10, and DS11 respectively, and 2 and 3 sub-matrices for noisy data sets DS13 and DS14 respectively. Assignment of cells to different lineages was performed according to the pseudotime inferred by Slingshot, and the assigned sets of cells need not be mutually exclusive (i.e., some single cells might be assigned to more than one lineage). GRN inference was performed for each of the lineages separately.
Technical Definitions
Total Variation (TV):
It is a measure for the distance between two probability distributions. For two probability distributions P and Q over a finite countable set X, total variation is defined as:
where.∥. ∥1 denotes the L1 norm. Note that total variation varies in range [0 1].
Total Deviation (TD):
It is a measure for evaluating the difference between two functions of the same variable. For two bounded continuous function F and G, the normalized total deviation in range [a b] is defined as:
Note that if F and G are lower-bounded by zero and upper-bounded by h, the normalized total deviation TD(F, G) is also bounded similarly.
Coefficient of Variation (CV):
Characterizes the dispersion of data around its mean and is defined as the ratio of the standard deviation to the mean:
Supplementary Material
Highlights.
SERGIO simulates stochastic gene expression in steady-state or differentiating cells
Simulations of RNA splicing enable RNA velocity estimation from generated data
Simulations show technical noise to greatly impact accuracy of network inference
Simulations recapitulate key regulators of T-Cell differentiation program
Acknowledgments
This work was supported by the National Institute of Health (grant R35 GM131819A and R01 GM114341A, to SS).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Declaration of Interests
The authors declare no competing interests.
Supplemental Information
Supplemental information (PDF) includes the supplemental figures and tables.
References
- Aibar S, González-Blas CB, Moerman T, Huynh-Thu VA, Imrichova H, Hulselmans G, Rambow F, Marine JC, Geurts P, Aerts J, et al. (2017). SCENIC: Single-cell regulatory network inference and clustering. Nat. Methods 14, 1083–1086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Albert Basson M (2012). Signaling in cell differentiation and morphogenesis. Cold Spring Harb. Perspect. Biol 4, 1–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrews TS, and Hemberg M (2019). M3Drop: dropout-based feature selection for scRNASeq. Bioinformatics 35, 2865–2867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balázsi G, Van Oudenaarden A, and Collins JJ (2011). Cellular decision making and biological noise: From microbes to mammals. Cell 144, 910–925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Becht E, McInnes L, Healy J, Dutertre CA, Kwok IWH, Ng LG, Ginhoux F, and Newell EW (2019). Dimensionality reduction for visualizing single-cell data using UMAP. Nat. Biotechnol 37, 38–47. [DOI] [PubMed] [Google Scholar]
- Bellot P, Olsen C, Salembier P, Oliveras-Vergés A, and Meyer PE (2015). NetBenchmark: A bioconductor package for reproducible benchmarks of gene regulatory network inference. BMC Bioinformatics 16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van den Berge K, Perraudeau F, Soneson C, Love MI, Risso D, Vert JP, Robinson MD, Dudoit S, and Clement L (2018). Observation weights unlock bulk RNA-seq tools for zero inflation and single-cell applications. Genome Biol 19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonneau R, Reiss DJ, Shannon P, Facciotti M, Hood L, Baliga NS, and Thorsson V (2006). The inferelator: An algorithn for learning parsimonious regulatory networks from systems-biology data sets de novo. Genome Biol 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buettner F, Natarajan KN, Casale FP, Proserpio V, Scialdone A, Theis FJ, Teichmann SA, Marioni JC, and Stegle O (2015). Computational analysis of cell-to-cell heterogeneity in single-cell RNA-sequencing data reveals hidden subpopulations of cells. Nat. Biotechnol 33, 155–160. [DOI] [PubMed] [Google Scholar]
- Butler A, Hoffman P, Smibert P, Papalexi E, and Satija R (2018). Integrating single-cell transcriptomic data across different conditions, technologies, and species. Nat. Biotechnol 36, 411–420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campbell KR, and Yau C (2018). Uncovering pseudotemporal trajectories with covariates from single cell and bulk expression data. Nat. Commun 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan TE, Stumpf MPH, and Babtie AC (2017). Gene Regulatory Network Inference from Single-Cell Data Using Multivariate Information Measures. Cell Syst 5, 251–267. e3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen S, and Mar JC (2018). Evaluating methods of inferring gene regulatory networks highlights their lack of performance for single cell gene expression data. BMC Bioinformatics 19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen C, Wu C, Wu L, Wang X, Deng M, and Xi R (2020). scRMD: imputation for single cell RNA-seq data via robust matrix decomposition. Bioinformatics 36, 3156–3161. [DOI] [PubMed] [Google Scholar]
- Chu D, Zabet NR, and Mitavskiy B (2009). Models of transcription factor binding: Sensitivity of activation functions to model assumptions. J. Theor. Biol 257, 419–429. [DOI] [PubMed] [Google Scholar]
- Dar RD, Shaffer SM, Singh A, Razooky BS, Simpson ML, Raj A, and Weinberger LS (2016). Transcriptional bursting explains the noise-versus-mean relationship in mRNA and protein levels. PLoS One 11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deshpande A, Chu L-F, Stewart R, and Gitter A (2019). Network Inference with Granger Causality Ensembles on Single-Cell Transcriptomic Data. BioRxiv 534834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Dijk D, Sharma R, Nainys J, Yim K, Kathail P, Carr AJ, Burdziak C, Moon KR, Chaffer CL, Pattabiraman D, et al. (2018). Recovering Gene Interactions from Single-Cell Data Using Data Diffusion. Cell 174, 716–729. e27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eraslan G, Simon LM, Mircea M, Mueller NS, and Theis FJ (2019). Single-cell RNA-seq denoising using a deep count autoencoder. Nat. Commun 10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franz K, Singh A, and Weinberger LS (2011). Lentiviral vectors to study stochastic noise in gene expression. Methods Enzymol 497, 603–622. [DOI] [PubMed] [Google Scholar]
- Gillespie DT (1976). A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys 22, 403–434. [Google Scholar]
- Gillespie DT (1977). Exact Stochastic Simulation of Coupled Chemical Reactions. J. Phys. Chem 81, 2340–2361. [Google Scholar]
- Gillespie DT (1992). A rigorous derivation of the chemical master equation
- Gillespie DT (2000). Chemical Langevin equation. J. Chem. Phys 113, 297–306. [Google Scholar]
- Gong W, Singh BN, Shah P, Das S, Theisen J, Chan S, Kyba M, Garry MG, Yannopoulos D, Pan W, et al. (2019). A novel algorithm for the collective integration of single cell RNA-seq during embryogenesis. BioRxiv 543314. [Google Scholar]
- Hedlund E, and Deng Q (2018). Single-cell RNA sequencing: Technical advancements and biological applications. Mol. Aspects Med 59, 36–46. [DOI] [PubMed] [Google Scholar]
- Herring CA, Banerjee A, McKinley ET, Simmons AJ, Ping J, Roland JT, Franklin JL, Liu Q, Gerdes MJ, Coffey RJ, et al. (2018). Unsupervised Trajectory Analysis of Single-Cell RNA-Seq and Imaging Data Reveals Alternative Tuft Cell Origins in the Gut. Cell Syst 6, 37–51. e9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hochgerner H, Zeisel A, Lönnerberg P, and Linnarsson S (2018). Conserved properties of dentate gyrus neurogenesis across postnatal development revealed by single-cell RNA sequencing. Nat. Neurosci 21, 290–299. [DOI] [PubMed] [Google Scholar]
- Holm L (2019). Benchmarking fold detection by DaliLite v.5. Bioinformatics 35, 5326–5327. [DOI] [PubMed] [Google Scholar]
- Hou R, Denisenko E, Forrest ARR, and Kelso J (2019). ScMatch: A single-cell gene expression profile annotation tool using reference datasets. Bioinformatics 35, 4688–4695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang S, Eichler G, Bar-Yam Y, and Ingber DE (2005). Cell fates as high-dimensional attractor states of a complex gene regulatory network. Phys. Rev. Lett 94. [DOI] [PubMed] [Google Scholar]
- Huynh-Thu VA, Irrthum A, Wehenkel L, and Geurts P (2010). Inferring regulatory networks from expression data using tree-based methods. PLoS One 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Intosalmi J, Mannerstrom H, Hiltunen S, and Lahdesmaki H (2018). SCHiRM: Single Cell Hierarchical Regression Model to detect dependencies in read count data. BioRxiv 335695. [Google Scholar]
- Karlebach G, and Shamir R (2008). Modelling and analysis of gene regulatory networks. Nat. Rev. Mol. Cell Biol 9, 770–780. [DOI] [PubMed] [Google Scholar]
- Kelsey G, Stegle O, and Reik W (2017). Single-cell epigenomics: Recording the past and predicting the future. Science 358, 69–75. [DOI] [PubMed] [Google Scholar]
- Kepler TB, and Elston TC (2001). Stochasticity in transcriptional regulation: Origins, consequences, and mathematical representations. Biophys. J 81, 3116–3136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khanin R, and Higham DJ (2008). Chemical Master Equation and Langevin regimes for a gene transcription model. Theor. Comput. Sci 408, 31–40. [Google Scholar]
- Kiselev VY, Kirschner K, Schaub MT, Andrews T, Yiu A, Chandra T, Natarajan KN, Reik W, Barahona M, Green AR, et al. (2017). SC3: Consensus clustering of single-cell RNA-seq data. Nat. Methods 14, 483–486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolodziejczyk AA, Kim JK, Svensson V, Marioni JC, and Teichmann SA (2015). The Technology and Biology of Single-Cell RNA Sequencing. Mol. Cell 58, 610–620. [DOI] [PubMed] [Google Scholar]
- Korthauer KD, Chu LF, Newton MA, Li Y, Thomson J, Stewart R, and Kendziorski C (2016). A statistical approach for identifying differential distributions in single-cell RNA-seq experiments. Genome Biol 17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li WV, and Li JJ (2018). An accurate and robust imputation method scImpute for single-cell RNA-seq data. Nat. Commun 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindström NO, Guo J, Kim AD, Tran T, Guo Q, De Sena Brandine G, Ransick A, Parvez RK, Thornton ME, Basking L, et al. (2018). Conserved and divergent features of mesenchymal progenitor cell types within the cortical nephrogenic niche of the human and mouse kidney. J. Am. Soc. Nephrol 29, 806–824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu ZP, Wu C, Miao H, and Wu H (2015). RegNetwork: An integrated database of transcriptional and post-transcriptional regulatory networks in human and mouse. Database 2015, 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Longabaugh WJR, Zeng W, Zhang JA, Hosokawa H, Jansen CS, Li L, Romero-Wolf M, Liu P, Kueh HY, Mortazavi A, et al. (2017). Bcl11b and combinatorial resolution of cell fate in the T-cell gene regulatory network. Proc. Natl. Acad. Sci. U. S. A 114, 5800–5807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Der Maaten L, and Hinton G (2008). Visualizing data using t-SNE. J. Mach. Learn. Res 9, 2579–2625. [Google Scholar]
- La Manno G, Soldatov R, Zeisel A, Braun E, Hochgerner H, Petukhov V, Lidschreiber K, Kastriti ME, Lönnerberg P, Furlan A, et al. (2018). RNA velocity of single cells. Nature 560, 494–498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marbach D, Prill RJ, Schaffter T, Mattiussi C, Floreano D, and Stolovitzky G (2010). Revealing strengths and weaknesses of methods for gene network inference. Proc. Natl. Acad. Sci 107, 6286–6291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marouf M, Machart P, Bansal V, Kilian C, Magruder DS, Krebs CF, and Bonn S (2020). Realistic in silico generation and augmentation of single-cell RNA-seq data using generative adversarial networks. Nat. Commun 11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsumoto H, Kiryu H, Furusawa C, Ko MSH, Ko SBH, Gouda N, Hayashi T, and Nikaido I (2017). SCODE: An efficient regulatory network inference algorithm from single-cell RNA-Seq during differentiation. Bioinformatics 33, 2314–2321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayer C, Hafemeister C, Bandler RC, Machold R, Batista Brito R, Jaglin X, Allaway K, Butler A, Fishell G, and Satija R (2018). Developmental diversification of cortical inhibitory interneurons. Nature 555, 457–462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCarthy DJ, Chen Y, and Smyth GK (2012). Differential expression analysis of multifactor RNA-Seq experiments with respect to biological variation. Nucleic Acids Res 40, 4288–4297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McInnes L, Healy J, Saul N, and Großberger L (2018). UMAP: Uniform Manifold Approximation and Projection. J. Open Source Softw 3, 861. [Google Scholar]
- Mohammadi S, Ravindra V, Gleich DF, and Grama A (2018). A geometric approach to characterize the functional identity of single cells. Nat. Commun 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Papadopoulos N, Gonzalo PR, and Söding J (2019). PROSSTT: probabilistic simulation of single-cell RNA-seq data for complex differentiation processes. Bioinformatics 35, 3517–3519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Papalexi E, and Satija R (2018). Single-cell RNA sequencing to explore immune cell heterogeneity. Nat. Rev. Immunol 18, 35–45. [DOI] [PubMed] [Google Scholar]
- Papili Gao N, Ud-Dean SMM, Gandrillon O, and Gunawan R (2018). SINCERITIES: Inferring gene regulatory networks from time-stamped single cell transcriptional expression profiles. Bioinformatics 34, 258–266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park J, Shrestha R, Qiu C, Kondo A, Huang S, Werth M, Li M, Barasch J, and Suszták K (2018). Single-cell transcriptomics of the mouse kidney reveals potential cellular targets of kidney disease. Science 360, 758–763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paulson KG, Voillet V, McAfee MS, Hunter DS, Wagener FD, Perdicchio M, Valente WJ, Koelle SJ, Church CD, Vandeven N, et al. (2018). Acquired cancer resistance to combination immunotherapy from transcriptional loss of class I HLA. Nat. Commun 9, 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng T, Zhu Q, Yin P, and Tan K (2019). SCRABBLE: single-cell RNA-seq imputation constrained by bulk RNA-seq data. Genome Biol 20, 88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pierson E, and Yau C (2015). ZIFA: Dimensionality reduction for zero-inflated single-cell gene expression analysis. Genome Biol 16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pratapa A, Jalihal AP, Law JN, Bharadwaj A, and Murali TM (2020). Benchmarking algorithms for gene regulatory network inference from single-cell transcriptomic data. Nat. Methods 17, 147–154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prill RJ, Vogel R, Cecchi GA, Altan-Bonnet G, and Stolovitzky G (2015). Noise-driven causal inference in biomolecular networks. PLoS One 10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Risso D, Perraudeau F, Gribkova S, Dudoit S, and Vert JP (2018). A general and flexible method for signal extraction from single-cell RNA-seq data. Nat. Commun 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saelens W, Cannoodt R, and Saeys Y (2018). A comprehensive evaluation of module detection methods for gene expression data. Nat. Commun 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- El Samad H, Khammash M, Petzold L, and Gillespie D (2005). Stochastic modelling of gene regulatory networks. Int. J. Robust Nonlinear Control 15, 691–711. [Google Scholar]
- Satija R, Farrell JA, Gennert D, Schier AF, and Regev A (2015). Spatial reconstruction of single-cell gene expression data. Nat. Biotechnol 33, 495–502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaffter T (2010). Numerical integration of SDEs: a short tutorial. Swiss Fed. Inst. Technol. Lausanne [Google Scholar]
- Schaffter T, Marbach D, and Floreano D (2011). GeneNetWeaver: In silico benchmark generation and performance profiling of network inference methods. Bioinformatics 27, 2263–2270. [DOI] [PubMed] [Google Scholar]
- Schaum N, Karkanias J, Neff NF, May AP, Quake SR, Wyss-Coray T, Darmanis S, Batson J, Botvinnik O, Chen MB, et al. (2018a). Single-cell transcriptomics of 20 mouse organs creates a Tabula Muris. Nature 562, 367–372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaum N, Karkanias J, Neff NF, May AP, Quake SR, Wyss-Coray T, Darmanis S, Batson J, Botvinnik O, Chen MB, et al. (2018b). Single-cell transcriptomics of 20 mouse organs creates a Tabula Muris. Nature 562, 367–372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siahpirani AF, and Roy S (2017). A prior-based integrative framework for functional transcriptional regulatory network inference. Nucleic Acids Res 45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siegenthaler C, and Gunawan R (2014). Assessment of network inference methods: How to cope with an underdetermined problem. PLoS One 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stegle O, Teichmann SA, and Marioni JC (2015). Computational and analytical challenges in single-cell transcriptomics. Nat. Rev. Genet 16, 133–145. [DOI] [PubMed] [Google Scholar]
- Street K, Risso D, Fletcher RB, Das D, Ngai J, Yosef N, Purdom E, and Dudoit S (2018). Slingshot: Cell lineage and pseudotime inference for single-cell transcriptomics. BMC Genomics 19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Svensson V, and Pachter L (2018). RNA Velocity: Molecular Kinetics from Single-Cell RNA-Seq. Mol. Cell 72, 7–9. [DOI] [PubMed] [Google Scholar]
- Swain PS, Elowitz MB, and Siggia ED (2002). Intrinsic and extrinsic contributions to stochasticity in gene expression. Proc. Natl. Acad. Sci 99, 12795–12800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trapnell C, Cacchiarelli D, Grimsby J, Pokharel P, Li S, Morse M, Lennon NJ, Livak KJ, Mikkelsen TS, and Rinn JL (2014). The dynamics and regulators of cell fate decisions are revealed by pseudotemporal ordering of single cells. Nat. Biotechnol 32, 381–386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vieira Braga FA, Kar G, Berg M, Carpaij OA, Polanski K, Simon LM, Brouwer S, Gomes T, Hesse L, Jiang J, et al. (2019). A cellular census of human lungs identifies novel cell states in health and in asthma. Nat. Med 25, 1153–1163. [DOI] [PubMed] [Google Scholar]
- Vieth B, Ziegenhain C, Parekh S, Enard W, and Hellmann I (2017). powsimR: power analysis for bulk and single cell RNA-seq experiments. Bioinformatics 33, 3486–3488. [DOI] [PubMed] [Google Scholar]
- Wilkinson DJ (2009). Stochastic modelling for quantitative description of heterogeneous biological systems. Nat. Rev. Genet 10, 122–133. [DOI] [PubMed] [Google Scholar]
- Wolf FA, Angerer P, and Theis FJ (2018). SCANPY: Large-scale single-cell gene expression data analysis. Genome Biol 19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zappia L, Phipson B, and Oshlack A (2017). Splatter: Simulation of single-cell RNA sequencing data. Genome Biol 18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeisel A, Moz-Manchado AB, Codeluppi S, Lönnerberg P, Manno G La, Juréus A, Marques S, Munguba H, He L, Betsholtz C, et al. (2015). Cell types in the mouse cortex and hippocampus revealed by single-cell RNA-seq. Science 347, 1138–1142. [DOI] [PubMed] [Google Scholar]
- Zhang L, and Zhang S (2018). Comparison of computational methods for imputing single-cell RNA-sequencing data. IEEE/ACM Trans. Comput. Biol. Bioinforma [DOI] [PubMed] [Google Scholar]
- Zhang X, Xu C, and Yosef N (2019). Simulating multiple faceted variability in single cell RNA sequencing. Nat. Commun 10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou W, Yui MA, Williams BA, Yun J, Wold BJ, Cai L, and Rothenberg EV (2019). Single-Cell Analysis Reveals Regulatory Gene Expression Dynamics Leading to Lineage Commitment in Early T Cell Development. Cell Syst 9, 321–337. e9. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
This study used several published and publicly available data sets. We obtained the raw mouse cortex data set (Zeisel et al., 2015) from Gene Expression Omnibus (GEO) with accession GSE60361. The raw 10X genomics expression for mouse MGE, CGE, and cortical regions (Mayer et al., 2018) obtained from GEO with accession GSE104156. The raw 10X genomics expressions for human kidney (Lindström et al., 2018) and human PBMC cells (Paulson et al., 2018) obtained from GEO with accession GSE102596 and GSE117988, respectively. The raw Drop-seq expression for human lung (Vieira Braga et al., 2019) obtained from GEO with accession GSE130148. The raw Smart-seq2 expression for mouse heart (Schaum et al., 2018a) obtained from GEO with accession GSE109774. Also, we obtained raw 10X genomics expression data for dentate gyrus of mouse hippocampus from GEO with accession GSE104323 (Hochgerner et al., 2018).
SERGIO v1.0.0 used to generate synthetic data sets in this study is available as a python package on GitHub: (https://github.com/PayamDiba/SERGIO).


