A Likelihood Approach for Uncovering Selective Sweep Signatures from Haplotype Data

Abstract

Selective sweeps are frequent and varied signatures in the genomes of natural populations, and detecting them is consequently important in understanding mechanisms of adaptation by natural selection. Following a selective sweep, haplotypic diversity surrounding the site under selection decreases, and this deviation from the background pattern of variation can be applied to identify sweeps. Multiple methods exist to locate selective sweeps in the genome from haplotype data, but none leverages the power of a model-based approach to make their inference. Here, we propose a likelihood ratio test statistic T to probe whole-genome polymorphism data sets for selective sweep signatures. Our framework uses a simple but powerful model of haplotype frequency spectrum distortion to find sweeps and additionally make an inference on the number of presently sweeping haplotypes in a population. We found that the T statistic is suitable for detecting both hard and soft sweeps across a variety of demographic models, selection strengths, and ages of the beneficial allele. Accordingly, we applied the T statistic to variant calls from European and sub-Saharan African human populations, yielding primarily literature-supported candidates, including LCT, RSPH3, and ZNF211 in CEU, SYT1, RGS18, and NNT in YRI, and HLA genes in both populations. We also searched for sweep signatures in Drosophila melanogaster, finding expected candidates at Ace, Uhg1, and Pimet. Finally, we provide open-source software to compute the T statistic and the inferred number of presently sweeping haplotypes from whole-genome data.

Introduction

A selective sweep is a genomic signature resulting from positive selection in which the linked variants surrounding the site under selection rise to high frequency together in a population, thereby yielding a footprint of reduced diversity that can span across megabases (Przeworski 2002; Gillespie 2004; Kim and Nielsen 2004; Garud et al. 2015; Hermisson and Pennings 2017). Thus, a recent selective event is identifiable in polymorphism data from a region of extended haplotype homozygosity, and the signal of a selective sweep accordingly decays over time as mutation and recombination break up long haplotypes (Sabeti et al. 2002; Schweinsberg and Durrett 2005; Voight et al. 2006). Selective sweeps can arise from multiple processes, including the de novo emergence of a selectively advantageous allele, selection on standing population haplotypic variation, and recurrent mutation to a selectively advantageous allele (Hermisson and Pennings 2005; Pennings and Hermisson 2006a, 2006b). The former scenario is a hard sweep, in which a single haplotype rises to high population frequency, gradually replacing all other haplotypes as the sweep proceeds to fixation. The latter two scenarios are soft sweeps, in which multiple haplotypes simultaneously rise to high population frequency, and a greater haplotypic diversity underlies the sweep.

Identifying selective sweeps is important because sweeps serve as indicators of recent rapid adaptation in a population, providing insight into the pressures that shaped its present-day levels of genetic diversity (Vatsiou et al. 2016; Librado et al. 2017). These pressures can vary considerably in their intensity and duration, resulting in selection signals of varying magnitude ranging from prominent, such as LCT in Europeans (Bersaglieri et al. 2004), to the more subtle ASPM, implicated in the development of human brain size (Kouprina et al. 2004; Peter et al. 2012). Whereas strong sweeps are typically easy to detect, weaker sweeps typically require a large sample size for detection (Jensen et al. 2007; Pavlidis et al. 2013) and may only be identifiable through sophisticated approaches (Chen et al. 2010). Selective sweeps, although not the only signature of adaptation in natural populations, are likely to occur at loci where mutations have a large effect size, little negative pleiotropic effects, and contribute to phenotypes that are either monogenic or controlled by few genes (Pritchard and Di Rienzo 2010). In addition, identifying selective sweeps is important to make inferences about the relative contributions of hard and soft sweeps to adaptive events in study organisms (Garud et al. 2015; Schrider and Kern 2016; Harris et al. 2018), which is a topic of continued debate (Hernandez et al. 2011; Jensen 2014; Schrider and Kern 2017; Harris, Sackman, et al. 2018; Mughal and DeGiorgio 2019).

Multiple powerful methods have been proposed to characterize selective sweeps, and well established among these are composite likelihood ratio (CLR) methods (Kim and Stephan 2002; Kim and Nielsen 2004; Nielsen et al. 2005; Chen et al. 2010; Pavlidis et al. 2013; Vy and Kim 2015; DeGiorgio et al. 2016; Huber et al. 2016; Racimo 2016) and haplotype homozygosity-based methods (Voight et al. 2006; Ferrer-Admetlla et al. 2014; Garud et al. 2015; Harris et al. 2018). The former category of methods represents approaches in which the probability of neutrality in a genomic region under analysis is compared with the probability of a selective sweep in that region, based on a model of distortion in the site frequency spectrum (SFS) expected under a sweep. A CLR statistic quantifies support for the alternative hypothesis of selection, with larger values indicating greater support. Although CLR methods make simplifying assumptions in their models (Beaumont et al. 2010; Pavlidis and Alachiotis 2017), they have demonstrated a powerful capacity for identifying multiple different signatures of selection without the need for computationally intense calculations of full likelihood functions (Kim and Stephan 2002; DeGiorgio et al. 2014; Huber et al. 2016). However, because they are typically allele frequency-based approaches, the CLR methods may lack in power to detect soft sweeps in comparison to haplotype-based methods, which can generally detect both (Pennings and Hermisson 2006b; Ferrer-Admetlla et al. 2014). Accordingly, the need exists for methods that leverage the power and efficiency of CLR approaches, while providing the sensitivity of haplotype-based approaches.

We introduce an approach for identifying selective sweep signatures using a likelihood ratio framework T that is the first haplotype-based method of its kind, intended to address the limitations of previous methods. Our T statistic (see Definition of Statistic) has high power to detect recent sweeps from genome-wide polymorphism data and additionally infers the number of presently sweeping haplotypes as a model parameter, providing an additional layer of insight not shared with other CLR methods. This attribute is especially important because it eliminates the need for time- and computation-heavy alternatives, such as training a machine-learning classifier (Lin et al. 2011; Kern and Schrider 2018; Mughal and DeGiorgio 2019), or drawing inferences from a posterior distribution by approximate Bayesian computation (Garud et al. 2015; Harris et al. 2018; Harris and DeGiorgio 2020). We demonstrate with simulated data that the T statistic identifies recent hard and soft sweeps and performs especially well for population size expansion models. As such, our application of the T statistic to human and Drosophila melanogaster data sets recovered multiple previously characterized candidate sweeps in both organisms, allowing us to corroborate and enhance our understanding of adaptation in each of their histories. We implement the T statistic in an open-source software package termed LASSI (Likelihood-based Approach for Selective Sweep Inference), which can be downloaded at http://degiorgiogroup.fau.edu/LASSI.html (last accessed May 25, 2020).

Definition of Statistic

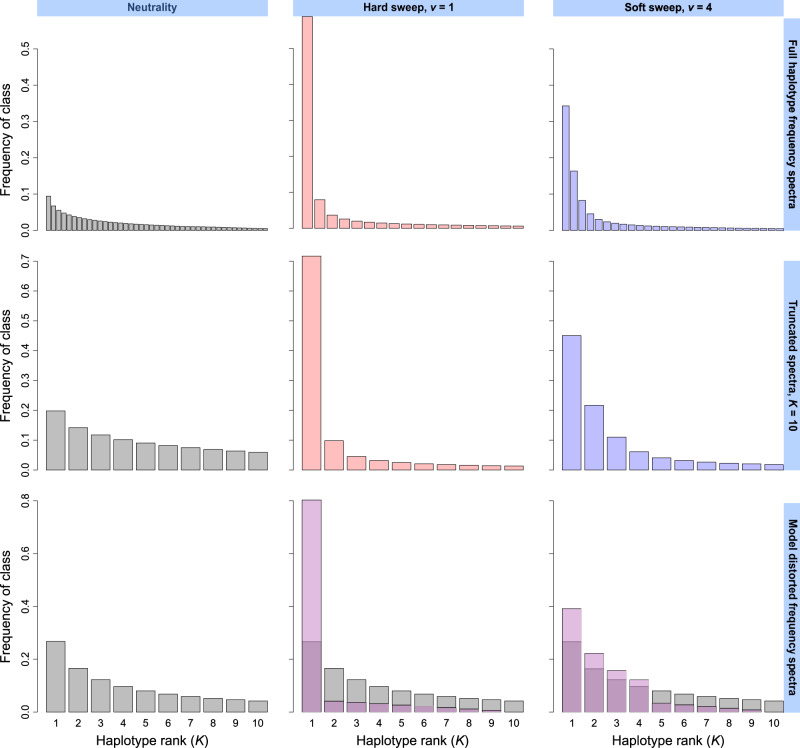
The goal of our approach is to identify genomic signatures of selective sweeps. We achieve this by assigning a T statistic to each single-nucleotide polymorphism (SNP)-delimited window of analysis in the genome. The T statistic is a measure of the likelihood that an analysis window is consistent with a selective sweep rather than neutrality. We base this inference on the sample haplotype frequency spectrum, reasoning that a spectrum with few high-frequency haplotypes indicates a sweep, and a spectrum with no moderate- or high-frequency haplotypes indicates neutrality. For this reason, genomic regions with low mutation and recombination rates can resemble selective sweep regions owing to their reduced nucleotide and haplotypic diversity (Pollinger et al. 2005; Wiehe et al. 2007; O’Reilly et al. 2008; Pavlidis and Alachiotis 2017), and so caution is warranted as with any approach. The T statistic is a likelihood ratio test in which the model of neutrality, based on the genome-wide haplotype frequency spectrum, is nested within the model of selection, based on a distortion of the genome-wide haplotype frequency spectrum toward few moderate- or high-frequency haplotypes. We illustrate examples of haplotype frequency spectra for neutrality and sweeps in figure 1 and also provide a schematic showing how key model parameters relate to distortions in the haplotype frequency spectrum.

Fig. 1.

Example simulated haplotype frequency spectra for neutrality, hard sweeps (ν = 1), and soft sweeps (ν = 4). Under neutrality, all sampled haplotypes in an analysis window exist at low frequency, and there are many haplotypes. In contrast, selective sweeps yield high-frequency haplotypes and fewer total haplotypes (top). Truncated spectra (K = 10) preserve their overall shape relative to untruncated spectra above (middle). We distort the truncated neutral spectrum computed from sampled haplotypes to yield spectra corresponding to alternative models (purple), in which the mass of nonsweeping classes is transferred to sweeping classes, resembling the expected pattern under a true selection event (bottom). Spectra represent the mean frequencies of each distinct haplotype across 10³ simulated replicates in a sample of n = 100 diploids under a constant-size simulated demographic history. Selective sweeps were simulated as one or more strongly selected (s = 0.1) haplotypes rising to high frequency starting at the time of selection t = 400 generations before sampling.

To begin, we must first define the haplotype spectrum on which we will base our neutral expectation. That is, the spectrum that we will assign as representative for a genomic window under neutrality. For all genomic windows in the sample, we extract the haplotype frequency spectrum, arrange frequencies in descending order, and truncate the spectrum at an arbitrary value K most frequent haplotypes (compare top and middle panels of fig. 1, first column). Thus, for each window $\ell ,\hspace{0.17em}\ell =1,2,\dots ,L$ for L windows, we have a truncated spectrum ${\mathbf{p}}^{(\ell )}=(p_1^{(\ell )},p_2^{(\ell )},\dots ,p_K^{(\ell )})$, where $p_1^{(\ell )}\ge p_2^{(\ell )}\ge \cdots \ge p_K^{(\ell )}$, and normalized such that ${\sum }_{i=1}^K{p}_i^{(\ell )}=1$. Next, we define the vector $\mathbf{p}=(p_1,p_2,\dots ,p_K)$, such that $p_i=(1/L){\sum }_{\ell =1}^L{p}_i^{(\ell )}$ for $i=1,2,\dots ,K$. We now use p as our neutral expectation for likelihood computations.

From the vector p, we define the vector ${\mathbf{q}}^{(m)}=(q_1^{(m)},q_2^{(m)},\dots ,q_K^{(m)})$, which represents a hypothetical distorted frequency spectrum consistent with a model of m sweeping haplotypes in an analysis window, with $q_1^{(m)}\ge q_2^{(m)}\ge \cdots \ge q_K^{(m)}$. Accordingly, the choice of K, although flexible for any analysis, most directly affects the resolution with which we can classify soft sweeps. For example, identifying a sweep on nine distinct, presently sweeping haplotypes requires at minimum a K = 10 truncation, whereas a sweep on 14 haplotypes requires K = 15 and would likely appear as neutral under smaller truncations. We generate ${\mathbf{q}}^{(m)}$ by increasing the frequency of sweeping haplotype classes $\{q_1^{(m)},q_2^{(m)},\dots ,q_m^{(m)}\}$ at the expense of nonsweeping haplotype classes $\{q_{m+1}^{(m)},q_{m+2}^{(m)},\dots ,q_K^{(m)}\}$ in a heuristic manner. We note therefore that our approach is purely statistical and does not feature an underlying population-genetic model but is an attempt to capture the features in the haplotype frequency spectrum consistent with those expected from a sweep. The vector ${\mathbf{q}}^{(m)}$ is related to p by

$$q_i^{(m)}=\{\begin{array}{c}{p}_i+f_i\sum _{j=m+1}^K(p_j-q_j^{(m)})i=1,2,\dots ,m\hfill \\ U-\frac{i-m-1}{K-m-1}(U-\epsilon )i=m+1,m+2,\dots ,K\hfill \end{array},$$ (1)

where f_i, with ${\sum }_{i=1}^m{f}_i=1$ and $f_i\ge 0$ for $i=1,2,\dots ,m$, is a term defining the manner in which the mass associated with haplotype frequencies $\{p_{m+1},p_{m+2},\dots ,p_K\}$ in the neutral frequency spectrum is distributed among $\{p_1,p_2,\dots ,p_m\}$ to generate the sweep frequency spectrum of the alternative model; U and ε are respectively the frequencies of the most and least frequent nonsweeping haplotype classes, $q_{m+1}^{(m)}$ and $q_K^{(m)}$.

We can define f_i in multiple ways. Choosing $f_i=1/m$ (model A) generates an alternative model in which value is uniformly added to each of $p_1,\dots ,p_m$. We can also specify a distortion in which value is added proportionally to each sweeping haplotype frequency, where $f_1>f_2>\cdots >f_m$, such as $f_i=(1/i)/{\sum }_{j=1}^{m}1/j$ (model B), $f_i=(1/i^2)/{\sum }_{j=1}^{m}1/j^2$ (model C), $f_i=e^{-i}/{\sum }_{j=1}^m{e}^{-j}$ (model D), or $f_i=e^{-i^2}/{\sum }_{j=1}^m{e}^{-j^2}$ (model E). The latter nonuniform models may provide a more accurate representation of the haplotype frequency spectrum following a sweep, as sweeping haplotypes, in contrast to neutral haplotypes, may not exist at similar frequencies to one another (see fig. 1, right column). As such, we primarily use model D for inferences in the Results. The choices of U and ε determine the frequency of the nonsweeping haplotype classes in the alternative model. For $U>\epsilon$, we make the simplifying assumption that the value of $q_i^{(m)}$ decreases linearly for $i=m+1,m+2,\dots ,K$, whereas $U=\epsilon$ constrains all $q_i^{(m)}$ to equal ε for $i=m+1,m+2,\dots ,K$. Regardless of the choice of U and ε, their relationship with each other and $p_{m+1}$ is necessarily $p_{m+1}\ge U\ge \epsilon$. We also note that ${\mathbf{q}}^{(K)}=\mathbf{p}$ by definition, illustrating that the null (neutral) model is nested within the alternative (sweep distortion) model.

For each analysis window, we must finally obtain a vector of counts x, observed for the most frequent K haplotypes. We define $\mathbf{x}=(x_1,x_2,\dots ,x_K)$, where elements are once again arranged in descending order, with $x_1\ge x_2\ge \cdots \ge x_K$. We normalize each x_i to satisfy the constraint ${\sum }_{i=1}^K{x}_i=n$, where n is the number of haplotypes in the sample.

Using the model haplotype frequency spectra p and ${\mathbf{q}}^{(m)}$ in conjunction with the observed vector of counts x for the most frequent K haplotypes in a particular genomic window, we define likelihood functions, which are based on the multinomial distribution. Our use of the multinomial distribution is reasonable as it describes the probability of observing the vector of haplotype counts (x) across K haplotype categories given the vector of respective haplotype frequencies (p or ${\mathbf{q}}^{(m)}$). The likelihood of the model parameters under the null hypothesis (neutrality) given the haplotype counts in an analysis window, equivalent to the probability of obtaining the observed haplotype counts x given p and K, is

$${ℒ}_0(\mathbf{p},K;\mathbf{x})=\prod _{i=1}^K{p}_i^{x_i},$$ (2)

whereas the likelihood under the alternative hypothesis (sweep distortion) is

$${ℒ}_1(\mathbf{p},K,\epsilon ,m;\mathbf{x})=\prod _{i=1}^K[q_i^{(m)}{]}^{x_i}.$$ (3)

Therefore, the log-likelihoods are

$${\ell }_0(\mathbf{p},K;\mathbf{x})=\sum _{i=1}^K{x}_i\hspace{0.17em}\text{log}(p_i)$$ (4)

and

$${\ell }_1(\mathbf{p},K,\epsilon ,m;\mathbf{x})=\sum _{i=1}^K{x}_i\hspace{0.17em}\text{log}(q_i^{(m)}).$$ (5)

We optimize ${\ell }_1(\mathbf{p},K,\epsilon ,m;\mathbf{x})$ over $m\in \{1,2,\dots ,K\}$ and $\epsilon \in [1/(100K),U]$, keeping U fixed, to find

$$(\widehat{m},\widehat{\epsilon })=\underset{(m,\epsilon )}{\text{argmax}}{\ell }_1(\mathbf{p},K,\epsilon ,m;\mathbf{x}).$$

Thus, our test statistic is defined as

$$T=2\{{\ell }_1(\mathbf{p},K,\widehat{\epsilon },\widehat{m};\mathbf{x})-{\ell }_0(\mathbf{p},K;\mathbf{x})\}.$$ (6)

Each analysis window in the genome is assigned a test statistic in this manner, and larger test statistics indicate greater support for a sweep in the window (i.e., greater distortion toward few moderate- or high-frequency haplotypes). Because in the process we also infer the most likely number of presently sweeping haplotypes $\widehat{m}$ to yield the underlying distorted haplotype spectrum, our approach can also be used to quantify the softness of an identified sweep.

Results

We first performed experiments with simulated data in which we generated populations based on nonequilibrium human demographic models inferred with smc++ (Terhorst et al. 2017), covering a variety of neutral and selection scenarios. These demographic models consisted of a history based on that of the CEU European population, featuring a prominent bottleneck about 2,000 generations prior to sampling, and a sub-Saharan African history resembling that of the YRI population, characterized by large population size with a recent expansion; these attributes of both models are consistent with previous estimates (Gravel et al. 2011; Gronau et al. 2011). Using these simulations, we measured the power of the T statistic and contextualized our results by comparing T to other popular methods, comprising (in order of increasing sophistication) H12 (Garud et al. 2015), nS_L (Ferrer-Admetlla et al. 2014), SweepFinder2 (Nielsen et al. 2005; DeGiorgio et al. 2016; Huber et al. 2016), and Trendsetter (Mughal and DeGiorgio 2019), across hard and soft sweep scenarios. We applied Trendsetter, a machine-learning method that uses information on the spatial autocorrelation of statistics, using both its standard six-statistic approach—incorporating pairwise sequence difference $\widehat{\pi }$, squared correlation coefficient r², number of distinct haplotypes $N_{\text{haps}}$, and the expected haplotype homozygosity statistics H1, H12, and H2/H1—and using contiguous T statistic analysis windows as input (“T-Trendsetter”).

To test the versatility of the T statistic, we probed the effects of various confounding factors on T statistic inferences. Foremost among these was admixture, which can mimic the signature of a sweep when a donor population of small effective size contributes ancestry to the sampled population (Lohmueller et al. 2009; Harris et al. 2018). We also computed the value of the T statistic in regions of low mutation and recombination rates to evaluate whether their associated reductions in haplotypic diversity could be mistaken for sweeps. Due to its pervasiveness in genomes, we then generated models of background selection to determine whether it can affect the value of the T statistic, as background selection has been implicated as a confounding factor when searching for selective sweeps (Charlesworth et al. 1993, 1995; Seger et al. 2010; Cutter and Payseur 2013; Nicolaisen and Desai 2013; Huber et al. 2016). Additionally, we evaluated the effects of data set confounding factors, exploring the impact of missing data and small sample size on power. Complementing the power analyses, we evaluated the performance of our method in terms of its ability to infer the number of sweeping haplotypes at the time of sampling ($\widehat{m}$). We use $\widehat{m}$ as a proxy for the number of distinct presently sweeping haplotypes in the population (model parameter m), which itself is a proxy for the true number of initially sweeping haplotypes (ν), an unknown parameter. Finally, we applied our method to data from the 1000 Genomes Project (1000 Genomes Project Consortium et al. 2015) and the Drosophila Genetic Reference Panel (DGRP; Mackay et al. 2012) to measure our ability to properly identify and classify selective sweep candidates.

Detection and Characterization of Selective Sweeps

We measured the power of our likelihood ratio test statistic (T) to differentiate selective sweeps from neutrality across diverse simulated scenarios using a sliding analysis window approach. For hard sweeps, as well as soft sweeps on ν = 4 initially sweeping haplotypes, we compare the power of T with that of the four alternate methods. Larger values of the T statistic for an analysis window indicate a greater departure from the neutral haplotype frequency spectrum, and therefore a greater probability of a sweep within that genomic region. To measure power, we first simulated 1,000 neutral replicates of 1-Mb chromosomes under the CEU and YRI demographic models. From these simulations, we obtained each model’s expected truncated neutral haplotype frequency spectrum $\mathbf{p}=(p_1,p_2,\dots ,p_K)$, which was the basis of our likelihood computations (see Definition of Statistic). The spectrum p for a model represents the mean across all genomic windows of all replicates, truncated at a particular value of K. Thus, K = 10 indicates the spectrum of the most frequent ten haplotypes in a genomic window, whose frequencies are labeled p₁–p₁₀. To assess power, we computed the T statistic for each 117-SNP (see Materials and Methods) genomic window of each simulated neutral replicate. We solely retained the maximum value of the T statistic across all windows for each neutral replicate, and similarly retained the maximum T statistic across each replicate of each selection scenario we tested. In our experiments, we assessed power at the 1% and 5% false positive rates (FPRs), meaning that we measured the proportion of selection replicates respectively exceeding the top 1% or 5% of T statistics within the neutral distribution.

The T statistic has high power to detect a recent hard sweep (ν = 1 sweeping haplotype) affecting the CEU-based demographic history, provided that the selection coefficient is at least s = 0.005 (fig. 2, top). At both the 1% and 5% (supplementary fig. S1, Supplementary Material online) FPRs, the T statistic reliably detects hard sweeps beginning between 1,000 and 1,500 generations before sampling, with the strongest sweeps extending the lower bound of this range to 200 generations (fig. 2, rightmost column). The power of the T statistic attenuates for more ancient sweep events because haplotype identity surrounding the selected site decays over time in the population as mutation and recombination generate new haplotypes. Additionally, power to detect the most recent and weakest sweeps is low because sufficient time has not elapsed for the selected haplotype to reach high frequency. Sweeps on s < 0.005 are specifically difficult to detect due to their smaller footprint and shorter time over which elevated haplotype homozygosity persists as selection proceeds. For these reasons, there is no point in time at which the T statistic can detect these sweeps (supplementary fig. S3, Supplementary Material online).

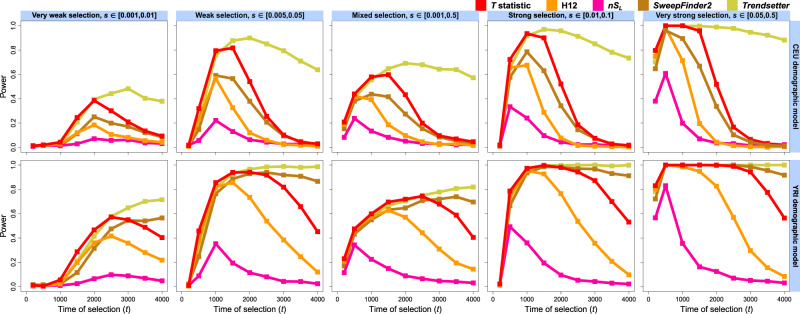
Fig. 2.

Powers of the T statistic and sweep detection methods—H12, nS_L, SweepFinder2, and Trendsetter—at the 1% FPR to detect hard selective sweeps originating from a single beneficial de novo mutation arising at times $t\in \{200,500,1,000,1,500,2,000,2,500,3,000,3,500,4,000\}$ generations prior to sampling, for the European CEU (top) and sub-Saharan African YRI (bottom) human demographic models inferred with smc++. Analysis data consisted of phased haplotypes of length 1 Mb, with 1,000 replicates for each distinct scenario. Selective sweeps were simulated for five ranges of selection coefficients (s) spanning very weak to very strong, with s for each replicate drawn uniformly at random (from a log scale for s drawn across orders of magnitude). All inferences used a spectrum of K = 10 for likelihood computations.

Across simulated CEU selection scenarios, each of the alternate methods we examined was subject to the same power limitations as the T statistic, which outperformed all except for the more sophisticated Trendsetter. The relative performance of all methods indicates that pairwise sequence identity tract length, which nS_L measures, is the most volatile sweep signal, decaying more rapidly than others. nS_L consistently had the lowest power of all tested methods and reached high power only for the most recent strong hard sweeps (fig. 2 and supplementary fig. S1, top-right, Supplementary Material online), quickly losing power as the sweep footprint eroded. Likewise, H12 never matched the power of the T statistic except in detecting the strongest sweeps, but in using a fixed window size retained somewhat more power than did nS_L. SweepFinder2 displayed greater power than H12, with higher maxima and longer signal duration. Despite not using haplotype information, SweepFinder2 incorporates a population-genetic model of a recent hard sweep, which results in more power than methods which do not. Finally, Trendsetter had easily the greatest power to detect hard sweeps under the CEU model, losing little resolution for sweeps up to 4,000 generations old. Using evidence from multiple signals may therefore be necessary to maximize power, as the strengths of each component statistic can complement the others’ weaknesses across different parameter configurations.

The T statistic achieves greater power for hard sweeps on simulated YRI demographic models than for CEU models across all tested scenarios (fig. 2 and supplementary fig. S1, bottom, Supplementary Material online). This increased power is due to the greater effective size of African relative to European human populations, which results in greater background haplotype diversity and therefore increased prominence of selective sweeps. Furthermore, because the size of the YRI population is an order of magnitude greater than that of the CEU for hundreds of generations, the population-scaled selection coefficient $\sigma =4Ns$ for YRI remains much larger, resulting in a stronger sweep. Accordingly, power declines more slowly for older sweeps and remains for sweeps as old as 4,000 generations before sampling. All methods therefore show greater power when applied to simulated YRI data. Notably, although Trendsetter and the T statistic display excellent performance once again, SweepFinder2 demonstrates consistently superior power for older sweeps under the YRI model, and this power scarcely decays. This suggests that SweepFinder2 may be more susceptible to demographic history than other methods, losing considerable power under the CEU bottleneck (Jensen et al. 2005; Huber et al. 2016). Meanwhile, the choice of K truncation—15, 20, or 25 (supplementary fig. S5, Supplementary Material online)—yielded little change in power to detect simulated sweeps from $s\in [0.01,0.1]$ relative to our highlighted value of K = 10 for either population model (fig. 2 and supplementary fig. S1, fourth column, Supplementary Material online). However, we note that power is slightly greater as K decreases, and so we recommend the use of smaller K truncations where possible.

For soft sweeps from selection on standing genetic variation ($\nu \in \{2,4,8,16,32\}$; supplementary fig. S4, Supplementary Material online), the power of the T statistic attenuates more rapidly than for hard sweeps, and T rarely reaches values as large, especially for weaker sweeps. Under both CEU (supplementary fig. S4, top, Supplementary Material online) and YRI (supplementary fig. S4, bottom, Supplementary Material online) demographic histories, trends in power remain consistent regardless of the number of sweeping haplotypes, with maximum power of T achieved once again for sweeps between 1,000 and 1,500 generations old (or up to 3,000 for YRI); however, power declines as the number of sweeping haplotypes increases. Assessing power at the 5% FPR indicates that we nonetheless maintain sufficient differentiation between sweeps and neutrality for up to ν = 4 distinct initially sweeping haplotypes for CEU models, or up to ν = 8 for YRI models. To better understand the relationship between power and ν, we tracked the mean number of distinct sweeping haplotypes through time for simulated soft sweeps across each selection strength range and choice of ν using an in silico barcoding approach (see Materials and Methods). We found that weak soft sweeps frequently lose most of their sweeping haplotypes by the time of sampling, undergoing a hardening (Wilson et al. 2014) during the early stages of the sweep when the beneficial allele’s frequency is low, and still subject to genetic drift (supplementary figs. S13 and S14, Supplementary Material online). After the beneficial allele becomes established in the population, the number of sweeping haplotypes remains generally stable. Because weaker sweeps require more time to establish, this provides more time for haplotypes to be lost, and for fewer sweeping haplotypes to be sampled, relative to stronger sweeps. Thus, the T statistic can have greater power for our weaker simulated soft sweeps from larger ν than for stronger soft sweeps because the former case ultimately yields a more distinct sweep signal with fewer high-frequency haplotypes, whereas the latter often results in scenarios of high haplotypic diversity that are difficult to distinguish from neutrality.

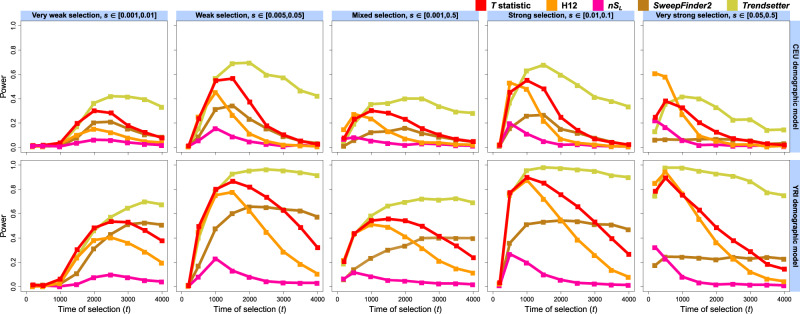
The power of each alternative method responded to soft sweep (ν = 4) scenarios in the same manner as that of T. Methods generally had poor to middling performance at the 1% FPR for the CEU history (fig. 3, top), but decent power at the 5% FPR, especially for sweep strengths between 0.005 and 0.1 (supplementary fig. S2, top, Supplementary Material online), whereas the power of all methods was improved for the YRI model (fig. 3 and supplementary fig. S2, bottom, Supplementary Material online). However, SweepFinder2 retains little power to detect soft sweeps, and lost power proportionally to the number of sweeping haplotypes at the time of sampling, as it is specifically formulated to detect hard sweeps through distortions in the SFS, and soft sweeps do not dramatically alter the SFS (Pennings and Hermisson 2006b). Expectedly, Trendsetter was still the most powerful method, with T and H12 following closely behind for recent sweeps, and nS_L lagging once again. Thus, the demographic and selective histories of the sampled population play an important role in the power of the T statistic and other sweep detection methods. Our results nonetheless indicate that the T statistic is flexible as to the selection scenarios it can distinguish from neutrality and detects recent sweeps especially well for the relatively little computation time it requires.

Fig. 3.

Powers of the T statistic and other sweep detection methods—H12, nS_L, SweepFinder2, and Trendsetter—at the 1% FPR to detect soft selective sweeps from selection on standing variation on ν = 4 distinct sweeping haplotypes beginning at times $t\in \{200,500,1,000,1,500,2,000,2,500,3,000,3,500,4,000\}$ generations prior to sampling, for the European CEU (top) and sub-Saharan African YRI (bottom) human demographic models inferred with smc++. Analysis data consisted of phased haplotypes of length 1 Mb, with 1,000 replicates for each distinct scenario. Selective sweeps were simulated for five ranges of selection coefficients (s) spanning very weak to very strong, with s for each replicate drawn uniformly at random (from a log scale for s drawn across orders of magnitude). All inferences used a spectrum of K = 10 for likelihood computations.

Selective sweeps produce elevated values of the T statistic along the simulated chromosome that on average peaks in the region surrounding the site under selection (supplementary figs. S6 and S7, first and third rows, Supplementary Material online). Furthermore, T remains elevated beyond the 900-kb bounds that we examined, indicating that on average, the shape of its distribution in a genomic region, as well as its overall elevated value, may be used to distinguish selection from neutrality. A signal peak often exists even for scenarios in which we do not have high power, though its maximum associated value remains small on average. Because neutral regions are likely to feature plateaus rather than peaks in the value of the T statistic, our observations illustrate the potential importance of considering the correlation in signal between windows to identify more subtle selection signatures. This is especially important for soft sweeps, which lose prominence proportionally to the number of sweeping haplotypes but still produce a peak-like distortion of local T statistic values.

To motivate this point, we reevaluated the power of our T statistic for sweeps on ν = 1 and ν = 4 haplotypes with the penalized multinomial regression method, Trendsetter (Mughal and DeGiorgio 2019), as it directly incorporates the genomic spatial distribution of sweep (summary) statistics in its inferences (supplementary figs. S8 and S9, Supplementary Material online). Using T as the sole statistic in the statistical learning protocol across 201 11-SNP windows (Trendsetter’s standard approach; see Materials and Methods), we considerably improved our ability to detect more ancient sweep signatures than in our standard application of T, especially under the CEU model, yielding power comparable to the full six-statistic approach. Moreover, we saw little change in power to detect recent sweeps, and power was improved overall for soft sweeps. When we instead used our typical 117-SNP windows for T, and 75 windows total, the T-Trendsetter approach yielded a uniformly enhanced power profile whose trends matched our original results with the standard T statistic, but with greater overall power, especially for soft sweeps (supplementary fig. S9, Supplementary Material online). Thus, the spatial distribution of the T statistic provides an informative sweep signature that can be used to isolate sweep regions from neutrality. By learning this spatial distribution, we can enhance the power of T to detect sweeps that may be overlooked using an isolated per-window approach.

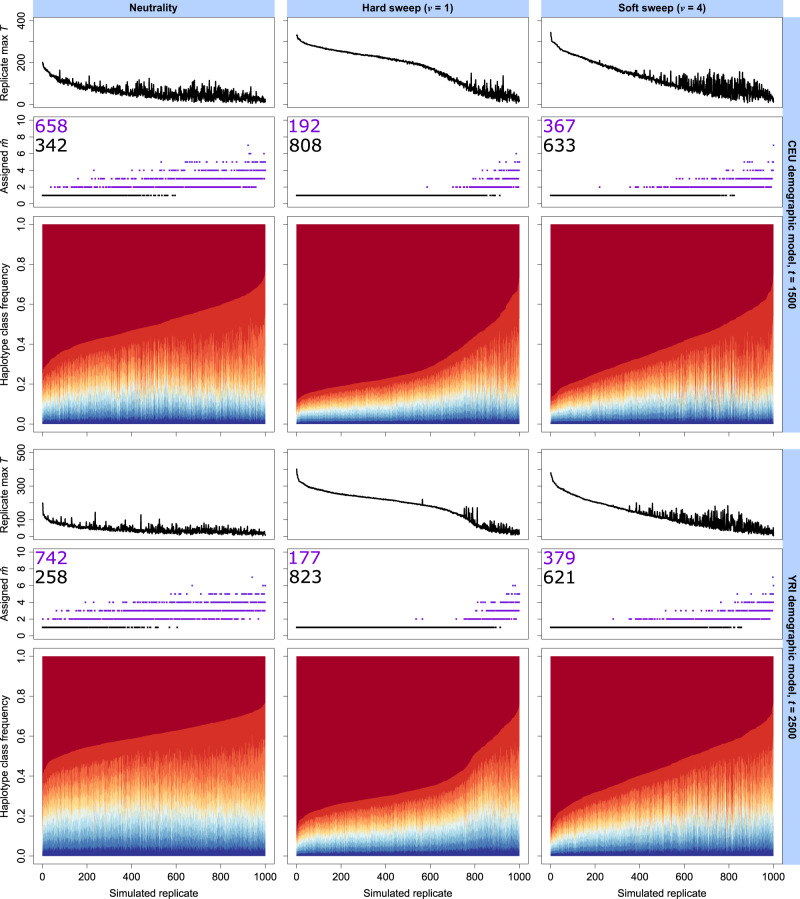
In addition to evaluating the power of the T statistic, we measured the ability of our approach to infer the number of presently sweeping haplotypes ($\widehat{m}$) at the site under selection. The ability to infer $\widehat{m}$ is a result of optimizing the likelihood function ${\ell }_1$ over all possible m distortion models for the chosen truncation K (see Definition of Statistic). In figure 4, we show the distribution of T statistics with their associated haplotype frequency spectra and $\widehat{m}$, for each of 1,000 neutral, mixed hard sweep ($s\in [0.001,0.5]$, ν = 1), and mixed soft sweep (ν = 4) replicates, under both the CEU and YRI models (same data as figs. 2 and 3; t = 1,500 for CEU and t = 2,500 for YRI, representing points of maximum power). Relative to neutrality (fig. 4, left), we more often assign smaller $\widehat{m}$ to sweep simulations (fig. 4, center and right). This result fits with the expectation that under a sweep, the first few haplotype classes exist at elevated frequency relative to the remaining classes, and this also translates to larger values of T for those replicates. Accordingly, sweeps that have weaker signatures due to their age or selection coefficient are not only difficult to distinguish from neutrality but also difficult to accurately classify with $\widehat{m}$, yielding patterns that fit within the neutral distribution. We found that trends were highly congruent between the CEU and YRI sweep models, but the large neutral background diversity for YRI made it less likely that we would infer a small $\widehat{m}$ in the absence of a sweep.

Fig. 4.

Truncated haplotype frequency spectra (K = 10) across 10³ simulated replicates for analysis window of maximum replicate-wide T statistic under neutral (left), hard sweep (center), and soft sweep (right) scenarios, for European CEU (top) and sub-Saharan African YRI (bottom) human demographic models. Each simulated replicate is one vertical slice within the lower panel, and replicate spectra are arranged in decreasing order of most frequent haplotype frequency. Replicates are associated with their T statistic (upper panel) and their inferred $\widehat{m}$ (middle panel). Inferred hard sweeps ($\widehat{m}=1$) are indicated with black dots, whereas inferred soft sweeps ($\widehat{m}\ge 2$) are indicated in purple. We indicate within the $\widehat{m}$ panel the number of replicates classified as hard (black text) or soft (purple text). Sweep replicates were drawn from mixed selection coefficients $s\in [0.001,0.5]$ uniformly at random on a log scale and are identical to those in figures 2 and 3.

To further understand the sweep classification properties of the T statistic, we generated box plots summarizing the distribution of $\widehat{m}$ across the more prominent strong sweep scenarios ($s\in [0.01,0.1]$) we previously analyzed (figs. 2 and 3 and supplementary fig. S4, Supplementary Material online). In this way, we were able to better understand our ability to correctly classify sweeps as hard or soft, especially because our trajectory results (supplementary figs. S13 and S14, Supplementary Material online) provided us with an expectation of the number of remaining sweeping haplotypes at the time of sampling for prominent sweep scenarios. We found that sweeps initiated from larger ν were more likely to be classified as soft using our K = 10 truncated spectra, but frequently we found that the median inferred $\widehat{m}$ for prominent soft sweeps was one, consistent with a hard sweep (supplementary figs. S10 and S11, Supplementary Material online). Regardless of ν, the spatial signature of $\widehat{m}$ along the chromosome forms a valley surrounding the site of selection that mirrors the signal peak when a sweep is detectable (supplementary figs. S6 and S7, Supplementary Material online). These results suggest that our present approach may therefore be more accurate as a binary classifier (hard versus soft), though we still assign soft sweeps on a continuum.

Because phasing haplotypes may not be possible in all cases, such as in the study of nonmodel organisms, we sought to expand our application of the T statistic to unphased multilocus genotype (MLG) data. To evaluate power for MLGs, we used the previous simulated human demographic model replicates of prior experiments (represented in figs. 2 and 3), merging each individual’s two haplotypes. Whereas haplotypes are character strings indicating the state of a biallelic SNP as either reference or alternate along a region of one copy of an individual’s genome, MLGs have three possible states for each biallelic SNP—homozygous reference, homozygous alternate, or heterozygous—and half the sample size of phased haplotypes. We found that, as with the transition between phased and unphased data for haplotype homozygosity statistics (Harris et al. 2018; Harris and DeGiorgio 2020), trends in power for the unphased application of the T statistic were wholly consistent with those of the phased application, for both hard and soft sweeps (supplementary fig. S15, Supplementary Material online). The smaller size of the MLG samples resulted in slight decreases in power for each sweep scenario, as well as smaller values of the T statistic relative to the phased application, but our results indicate that selective sweeps may be reliably identified nonetheless without the need to phase haplotypes. Likewise, we found that the T statistic applied to MLGs could generate inferences of sweep softness from $\widehat{m}$ that matched those of haplotype data, further underscoring the parallel performance of our approach on unphased data (supplementary fig. S16, Supplementary Material online).

Effects of Confounding Factors of the T Statistic

There are multiple genetic and nongenetic factors that may affect the ability of sweep statistics to properly localize a selection signature. Though these factors are varied in origin, they may each reduce genetic diversity locally and spuriously generate patterns similar to those of selective sweeps. Accordingly, we examined the effects of introducing these confounding factors to our simulated data, allowing us to understand the scenarios for which T is robust and susceptible to misclassifying sweeps. Among genomic factors, we observed the impact of admixture into the sampled population, reductions in mutation and recombination rates, and background selection. Common nongenomic factors that can change the interpretation of sweep statistics are missing data, small sample sizes, and reliance on a misspecified demographic model.

We begin with admixture, which can be pervasive in natural populations (Hudjashov et al. 2017; Kopatz et al. 2017; Browning et al. 2018; Barría et al. 2019). Previous work has shown that under certain scenarios, admixture from an unsampled donor population can lead to reductions in haplotypic diversity across the genome of a study population (Harris et al. 2018). Specifically, admixture from a diverged donor population of small effective size into the sampled study population may introduce large tracts of homozygous sequences that methods may interpret as a selection signal. To assess the extent to which the T statistic—which makes use of the study genome’s background haplotypic patterns—is affected by admixture, we simulated neutral replicates under the CEU and YRI models receiving pulse admixture from a highly diverged donor ($\tau =2N=2\times {10}^4$ generations prior to sampling). Our tested admixture proportions were $\alpha \in \{0.05,0.1,\dots ,0.4\}$ at $t_{\text{adm}}=200$ generations prior to sampling, and we examined donor population effective sizes of $N_{\text{adm}}\in \{{10}^3,{10}^4,{10}^5\}$ diploids (roughly 1/10, equal to, and 10-fold the effective size of the sampled populations).

We found that admixture had a considerable effect on the haplotype frequency spectrum of the target population and assessed this effect in two ways. First, we computed the T statistic for each admixture scenario, but using an unadmixed background p spectrum (supplementary figs. S17 and S19, Supplementary Material online). Our results demonstrate that admixture from a donor with small effective size yields the expected haplotypic diversity reduction in the sampled population, producing inflated T statistics. In contrast, gene flow from medium- and large-sized donors rarely produced large values of T, except for large-donor admixture at $\alpha \le 0.1$. We attempted to address the confounding effects of admixture by computing T from an appropriately matched admixed background ${\mathbf{p}}^{\alpha }$ spectrum for each tested value of α (supplementary figs. S18 and S20, Supplementary Material online). Using a matched ${\mathbf{p}}^{\alpha }$ resulted in T statistic distributions under admixture that more closely resembled unadmixed distributions. Regardless of scenario, the T distribution deriving from a ${\mathbf{p}}^{\alpha }$ spectrum informed by admixture resulted in median values of T for admixed scenarios closer to the median for unadmixed replicates, especially for small-donor admixture. Although this was uniformly beneficial for the CEU model, ${\mathbf{p}}^{\alpha }$ overcorrected for large-donor scenarios under the YRI model. The susceptibility of our T statistic to confounding admixture is a consequence of using a model that does not account for mixed ancestry in the target population. Instead, the reliance of our approach on an average neutral background spectrum means that we are not capturing the higher moment effects of admixture on the admixed T statistic distribution, such as its variance. Even so, we expect that in human populations, admixture is unlikely to be as extreme as in our simulated examples and is likely to feature populations that are less diverged from one another, and of closer effective size to one another, reducing its overall detrimental impact when searching for sweeps.

Because natural genomes may feature wide variation in recombination and mutation rates, we sought to determine the effect of such variation on the value of T in the absence of selection in order to quantify its potential misleading effect on T. In comparison to standard simulations featuring $\mu =1.25\times {10}^{-8}$ and mean $r={10}^{-8}$ drawn from an exponential distribution, we generated simulated replicates with $\mu =1.25\times {10}^{-9}$ and mean $r={10}^{-9}$, reduced by one order of magnitude (see Materials and Methods). Reducing the mean recombination rate had the anticipated effect of slightly inflating the distribution of T relative to normal values of r, a result of the reduction in genetic diversity in regions where new haplotypes rarely arise (supplementary fig. S21, Supplementary Material online). In contrast, reducing the mutation rate by an order of magnitude resulted in a deflation of T statistic values relative to the original rate. This is because our SNP-delimited windows become physically wider when SNP density is reduced, leading to the incorporation of SNPs in lower mean linkage disequilibrium (LD), and therefore more haplotypic diversity. Reducing both μ and mean r led to an intermediately deflated T statistic distribution. This result may suggest that mutation rate variation is more important than recombination rate variation in determining the T statistic value under SNP-delimited windows (supplementary fig. S21, Supplementary Material online). However, because we already draw recombination rates from a distribution in our default protocol, it is possible that we observed a greater effect by changing μ because our reduced-μ scenarios represent a greater departure from standard simulations. Thus, we caution that recombination rate variation should not be ignored as a source of false signals in analyses with any sweep statistic.

We next examined background selection scenarios for both haplotype and MLG data to determine whether the loss of genetic diversity associated with linked purifying selection could spuriously yield elevated values of the T statistic. Simulating 1-Mb chromosomes as previously under both human demographic models, we found that background selection had no discernible effect on the distribution of T relative to neutrality, even as we reduced mean r by two orders of magnitude to ${10}^{-10}$ across the central gene. We determined this by observing the receiver operating characteristic curves comparing neutral scenarios to those in which a central gene experiences strong ($s=-0.1$) background selection for the duration of the simulation (see Materials and Methods). For both the CEU (supplementary fig. S22, top, Supplementary Material online) and YRI (supplementary fig. S22, bottom, Supplementary Material online) populations, across central genes of size 11 kb (supplementary fig. S22, left, Supplementary Material online), 55 kb (supplementary fig. S22, center, Supplementary Material online), and 110 kb (supplementary fig. S22, right, Supplementary Material online), we see that all curves fit tightly along the diagonal, indicating no difference between compared replicate sets. Therefore, we expect that the presence of background selection, for which we do not explicitly account in our model, should not affect inferences with the T statistic.

Among the most common nongenomic confounders that may be encountered in analyses of natural populations is the presence of missing data. That is, sites for which the allelic state is indeterminate. We evaluated the performance of the T statistic for sequences with missing data at polymorphic sites by randomly removing alleles from our existing neutral replicates (see Materials and Methods). To address missingness in our data, we modified our scan using two corrective approaches. First, we removed polymorphic sites with >5% missing data, and second, we incorporated all remaining missing alleles as a new character “N,” thereby conservatively diversifying the remaining set of haplotypes relative to no missing data. Following this approach, we compared the distributions of T with and without missing data. We found that introducing missing data had little effect on the distribution of T statistic values under neutrality (supplementary fig. S23, Supplementary Material online). We expect that as long as sufficient polymorphism remains in the sample, that missing data are unlikely to yield false sweep inferences, and in extreme cases, are likely to resemble the effect of decreased mutation rate due to the depletion of allelic information.

A limitation of haplotype-based approaches is that their power derives from sample size (n). That is, sufficient diversity must be captured in a sample in order to distinguish between the unique signals of neutrality and selection. As sample size decreases, subtle signatures of selection recede into the genomic background and become imperceptible. To determine the minimum sample size to which the T statistic should be confidently applied, we resampled our existing hard sweep replicates (see fig. 2) for reduced sample sizes $n\prime \in \{20,50,100\}$ haplotypes, corresponding to 1/10, 1/4, and 1/2 the original sample size of n = 200. Reducing sample sizes led to a reduction in the minimum detectable range of selection coefficients s, and in the range of sweep ages t over which the T statistic had power (supplementary fig. S24, Supplementary Material online). Although power scarcely changed for larger samples of size $n\prime =100$ relative to n = 200 (as in our application to MLG data), we are unable to reliably detect even strong sweeps older than t = 500 generations for the CEU model when only $n\prime =20$ haplotypes are sampled (supplementary fig. S24, top-right, Supplementary Material online). Analysis of the YRI model was more accommodating to sample size reduction owing to the preexisting greater ease of detecting sweeps for populations with large effective sizes, but power quickly drops when small selection coefficients (s < 0.005) are included (supplementary fig. S24, Supplementary Material online).

A practical consideration when applying sweep statistics is inferring an accurate demographic model. A proper model can be used to generate simulated replicates from which P value cutoffs and false discovery rate (FDR) thresholds may be assigned. We subsequently demonstrate this in our own Application to Empirical Data Sets. To motivate the selection of an appropriate model, we show the effect on the neutral T statistic distribution of using nonideal demographic models. First, we generated T statistic distributions for CEU and YRI under constant-size models. Here, the constant sizes were equal to the effective size of the populations under each model (see Materials and Methods). Because these models included no population size fluctuations, they provided uniformly deflated T statistic distributions relative to smc++ models, with the constant-size CEU model especially underestimating values relative to its more accurate counterpart (supplementary fig. S25, Supplementary Material online). We also examined T statistic distributions resulting from the popular Gravel et al. (2011) model, which is based on the SFS. Relative to the smc++ model, the T statistic distribution for the Gravel et al. (2011) CEU model was comparable, but the YRI model, consisting of only two phases (constant size followed by 2-fold expansion), resulted in much smaller values of T (supplementary fig. S26, Supplementary Material online). Choosing a demographic model that captures both recent and ancient history is therefore important (Beichman et al. 2017), and model choice should be approached with caution.

Application to Empirical Data Sets

We searched for candidate selective sweeps in human and D. melanogaster data sets using the T statistic, choosing these data sets because of their high quality, size, and availability of phased haplotypes. Specifically, the 1000 Genomes Project (1000 Genomes Project Consortium et al. 2015) data set contains no missing data, as all allelic states have been imputed. Meanwhile, the DGRP data set (Mackay et al. 2012) provides a classic invertebrate model whose properties deviate considerably in history and genomic architecture from the mammalian model of humans. For each protein- and RNA-coding gene in each study population, we obtained values of T using inferences from a K = 10 truncation and assigned a P value to each of the top 40 candidate genes based on the window of maximum T overlapping that gene (supplementary tables S1–S3, Supplementary Material online). For windows to be associated with a gene, their central SNP must lie between the transcription start and stop sites of the gene. Additionally, we assigned an $\widehat{m}$ value to each gene using both K = 10 and K = 20 truncations. Analysis windows for scans of human data were of size 117 SNPs, advancing by 12-SNP increments, whereas windows for D. melanogaster analysis were 400 SNPs in size (as in the analyses of Garud et al. [2015] and Harris, Sackman, et al. [2018]) with a step size of 40 SNPs. To eliminate the effect of background LD on inferences, window sizes were based on the minimum physical interval across which LD decayed beyond one-third of its value between SNPs separated by 1 kb (see Materials and Methods). Following our successful application of T to simulated unphased MLG data, we analyzed the human 1000 Genomes Project data as MLGs by manually merging individuals’ two haplotypes. This was unnecessary for the DGRP data, as individuals are inbred. For haplotype data, we also determined FDR thresholds for each population based on simulated replicates, inferring T statistic cutoffs at a 5% FDR for all study populations (supplementary table S4, Supplementary Material online).

For human data, we examined the CEU and YRI populations (supplementary tables S1 and S2, Supplementary Material online), matching the demographic models used in our simulations. Though few of our top 40 sweep candidates produced a significant P value, all easily exceeded their population’s 5% FDR (supplementary table S4, Supplementary Material online). Among these candidates, hard sweeps predominated within either population, and we found that this depended somewhat on our K truncation. For K = 20, hard sweeps comprised all but two top candidates among the CEU, and 67.5% of top candidates among the YRI, whereas for K = 10, we did not classify any top CEU or YRI candidates as soft from phased haplotypes. Additionally, K = 20 candidate soft sweeps, except for BTNL2 in YRI ($\widehat{m}=6$), featured only three or fewer sweeping haplotypes. These results indicate that the T statistic is more sensitive to harder sweeps than to softer ones, which is a consequence of the greater distortion in the haplotype frequency spectrum of hard sweeps relative to soft sweeps. This finding matches our simulated results, in which the value of T was proportional to the number of sweeping haplotypes in the population. Moreover, we find that our choice of K truncation impacts our ability to classify sweeps as soft, with a greater distortion of haplotype classes two through m required for a sweep in a K = 10 truncated spectrum to be classified as soft relative to K = 20. Regardless of truncation, the increased presence of candidate soft sweeps in YRI relative to CEU mirrors our observation from simulated data that the T statistic has greater power to detect softer sweeps for populations that have not experienced a bottleneck in their history. Furthermore, these patterns corroborate results from the H12 analysis of this data set (Harris et al. 2018), which found more hard sweeps than soft in the CEU population, and among top candidates generally.

Across both the CEU and YRI populations, we were able to recover most of the top 40 candidates from the haplotype data within the MLG data, indicating the reliability of using MLGs for inference with the T statistic in natural populations when phased data are unavailable. The MLG results primarily deviated from the haplotype results when classifying candidates as hard or soft. Multiple candidates that were inferred to be hard sweeps from the haplotype data were classified as soft from their MLG spectra, particularly for the K = 20 truncation. These candidates include XIRP2 and BCAS3 in the CEU population, as well as ITGAE, SUGCT, NNT, and HLA-DPB2 in the YRI population. We examine the latter candidate more closely in figure 5 and supplementary figure S30, Supplementary Material online. These differing inferences may arise from the slightly different interpretation of $\widehat{m}$ between phased and unphased data. For phased data, $\widehat{m}$ refers to the number of sweeping haplotypes, whereas for unphased, it measures the number of MLGs involved in the sweep, which may be different for the same genomic window between the different data types if MLG frequencies are at or near their expected proportions under Hardy–Weinberg equilibrium. We also note that multiple top candidates in the MLG data inferred as soft are simply not present among top haplotype candidates, indicated by the absence of a turquoise-colored background in supplementary tables S1 and S2, Supplementary Material online. We consider the application of the T statistic to MLGs further in the Discussion.

Fig. 5.

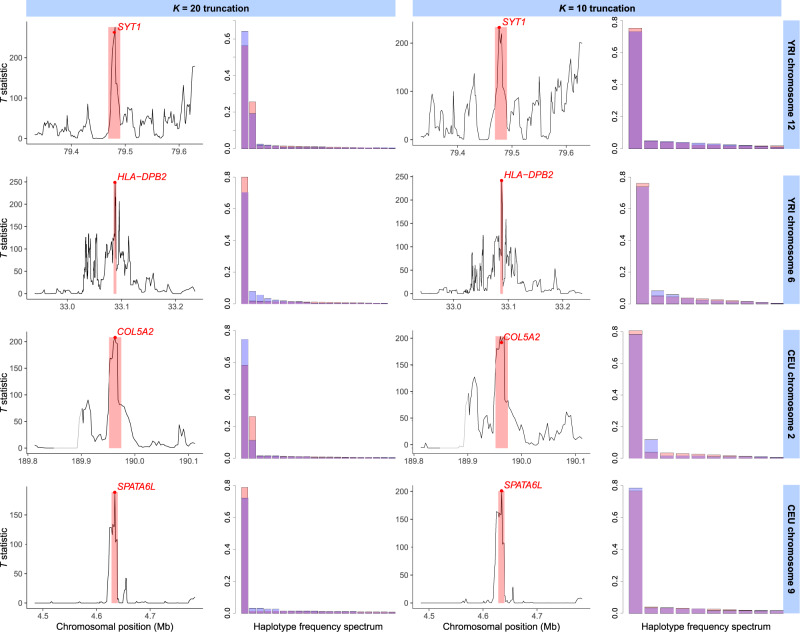
Selective sweep candidates detected with the T statistic from the 1000 Genomes Project data set (1000 Genomes Project Consortium et al. 2015) as for scans with a K = 20 (left) and K = 10 (right) truncation. For each of four sweep candidates in the human YRI (top two rows) and CEU (bottom two rows) populations, we show the T statistic across the 300-kb interval surrounding the candidate peak, as well as the frequency spectra for the most likely sweep model corresponding to the candidate at the 117-SNP analysis window of maximum T. The window of maximum T is shaded in red, with the position of the window center (median SNP) as a red dot. The frequency spectrum of the most likely model is also shown in red, whereas the observed frequency spectrum at the point of maximum T is overlaid in blue. The displayed candidates are a putative soft sweep ($\widehat{m}=2$) at SYT1 in YRI (top row), hard sweep ($\widehat{m}=1$) at HLA-DPB2 in YRI (second row), soft sweep ($\widehat{m}=2$ when analyzed with K = 20; hard for K = 10) at COL5A2 in CEU (third row), and hard sweep at SPATA6L in CEU (bottom row). We note that the window of maximum signal for K = 10 and K = 20 differed for SYT1 (top row). The gray segment upstream of COL5A2 (third row) indicates a portion of the genome that was filtered out (see Materials and Methods).

Among top sweep candidates in human data were expected results, including a hard sweep ($\widehat{m}=1$) at the cluster of genes on CEU chromosome 2 comprising LCT, MCM6, DARS, and ZRANB3 (minimum P value $3\times {10}^{-6}$), related to a well-documented adaptation to milk-based diets in European populations (Bersaglieri et al. 2004). Additionally, we found two noteworthy top candidates in CEU that have not been explicitly described as sweeps previously, RSPH3 and ZNF211 (both $\widehat{m}=1$). RSPH3 encodes a radial spoke protein that is integral in the structure of 9 + 2 motile cilia across diverse cell types, including flagellated cells (Teves et al. 2016), and so we speculate that selection here could be related to ancient sperm competition in humans (Leivers et al. 2014). ZNF211 is among a diverse set of zinc-finger genes whose products are believed to participate in the inactivation of endogenous retroviruses, parasitic mobile DNA whose effects can be deleterious to their hosts (Lukic et al. 2014). We recovered SYT1 ($\widehat{m}=2$ for K = 20, $\widehat{m}=1$ for K = 10; $P=3\times {10}^{-6}$), NNT ($\widehat{m}=1$), HEMGN ($\widehat{m}=1$), and RGS18 ($\widehat{m}=2$ for K = 20, $\widehat{m}=1$ for K = 10) in YRI, which have all received attention as potential adaptive targets (Voight et al. 2006; Pickrell et al. 2009; Fagny et al. 2014; Harris et al. 2018). Our significant candidates, SPRED3 and ITGAE have also been previously identified (Granka et al. 2012; Ayub et al. 2013; Grossman et al. 2013), though the effect of selection at these genes has not yet been elucidated. Both populations yielded HLA genes as top sweep candidates, overlapping at HLA-DRB5 ($\widehat{m}=1$), whereas HLA-DPB1 ($\widehat{m}=1$) was exclusive to CEU and HLA-DPB2 ($\widehat{m}=1$) was exclusive to YRI. This shared signal supports the recent evidence (Albrechtsen et al. 2010; Goeury et al. 2018) that sweeps at HLA loci, including those which we describe here, were important in the development of modern genetic diversity in human immune-related genes.

In figure 5 and supplementary figure S30, Supplementary Material online, we take a closer look at top candidate sweeps uncovered in our scan of the 1000 Genomes data set (1000 Genomes Project Consortium et al. 2015) for both K = 10 and K = 20 truncations, across both haplotypes and MLGs. Each top candidate fell within a well-defined T statistic peak region surrounded by regions of low signal, and T statistic spatial signatures were consistent between all data types. First, we found SYT1 as a near-significant ($P=3\times {10}^{-6}$) top sweep candidate in the YRI population, featuring both $\widehat{m}=2$ sweeping haplotypes and $\widehat{m}=2$ MLGs involved in the sweep at the window of maximum signal for K = 20 (fig. 5 and supplementary fig. S30, first row of first column, Supplementary Material online). For the K = 10 truncation, the window of maximum signal contains only a single sweeping haplotype and is located within an adjacent, upstream subpeak. SYT1 is the cell surface receptor through which the type B botulinum neurotoxin of Clostridium botulinum bacteria enters human neurons (Connan et al. 2017), and so a sweep here may be involved in resistance to this infection (Harris et al. 2018). Next, we identified HLA-DPB2 as an outlying hard sweep in YRI ($\widehat{m}=1$) based on haplotypes and K = 10 data, but featuring three elevated MLGs within the window of maximum signal for K = 20 (fig. 5 and supplementary fig. S30, second row, Supplementary Material online). Looking at the K = 20 haplotype frequency spectrum, it is clear that one haplotype predominates, and equivalently, only one MLG predominates, but individuals heterozygous for the first haplotype and either the second or third comprise just under 20% of the population, leading to an inference of $\widehat{m}=3$. COL5A2 was the most outlying soft sweep candidate we identified in CEU using the K = 20 truncation, harboring $\widehat{m}=2$ inferred sweeping haplotypes, but with a 7-fold disparity between their frequencies, which could occur due to a recombination event during the sweep, or a recurrent selected mutation (Hermisson and Pennings 2017). This gene has received little attention but is located within a significantly overrepresented run of homozygosity associated with schizophrenia (Lencz et al. 2007). Additionally, selection on collagen-related genes has been implicated in cold adaptations in European populations (Yudin et al. 2017). Finally, we propose the spermatogenesis-associated protein SPATA6L as a hard sweep candidate in CEU. Our finding here of an isolated T peak fits with existing evidence of selection at other spermatogenesis proteins (Schrider and Kern 2017), and with the result that European and sub-Saharan African populations are diverged at this locus, with selection in the hunter-gatherer Batwa population inferred here (Bergey et al. 2018).

We contextualize our results for outlying sweep candidates by illustrating the background haplotype frequency spectrum patterns we observed in regions of low T. In supplementary figure S31, Supplementary Material online, we highlight four regions each in the CEU and YRI populations with $T\approx 0$, 10, 20, or 30. In accordance with the expectation that classic selective sweep patterns are rare in the human genome (Hernandez et al. 2011), we observe that the majority of analysis windows had a small associated T, and accordingly resembled our example windows. We see from these examples that small peaks in the T statistic are common, and associated with haplotype frequency spectra that are distinct from those under selection, containing no high-frequency classes and an abundance of low-frequency classes of similar size. As we increase from $T\approx 0$ to $T\approx 30$, we see the spectra begin to distort and contain higher frequency classes, but this distortion is far from what we expect under a sweep.

Our scan of the North American DGRP population of D. melanogaster also identified expected sweep candidates among the top genic T statistic peaks. We note that although we were unable to establish statistical significance against a neutral model based on the DGRP demographic history of Duchen et al. (2013) (see Materials and Methods), and only our top candidate, CG11902, exceeded the 5% FDR threshold (supplementary table S4, Supplementary Material online), our top candidates have literature support as potential adaptive targets. Foremost among functionally characterized candidates was Ace, which encodes the acetylcholinesterase enzyme and has long been implicated in the development of resistance to organophosphate and carbamate insecticides within D. melanogaster (Menozzi et al. 2004; Karasov et al. 2010; Garud et al. 2015). Contrary to previous studies alleging a soft sweep at Ace (Karasov et al. 2010; Garud et al. 2015), we found the greatest support for a model of only one sweeping haplotype. We identified another candidate hard sweep of similar magnitude at Uhg1, which also contributes to insecticide resistance, but to the organochlorine dichlorodiphenyltrichloroethane (Pedra et al. 2004). The methyltransferase-encoding gene Pimet emerged as the most prominent candidate soft sweep ($\widehat{m}=3$) in our search using K = 20 ($\widehat{m}=1$ for K = 10) and is central to the viral RNA degradation pathway that is subject to ongoing coevolution against pathogen incursion and deleterious transposable element activity (Kolaczkowski et al. 2011; Lee and Langley 2012). We finally highlight ana3 as a candidate for adaptation in D. melanogaster. This prospective hard sweep affects a highly conserved gene encoding a centriole protein fundamental to the structural integrity of basal bodies within cells (Stevens et al. 2009). A sweep here may contribute to enhanced success in sperm competition and fits with the expectation that sperm gene evolution is an ongoing and central part of positive selection in D. melanogaster (Nurminsky et al. 1998; Dorus et al. 2008; Wong et al. 2008; Yeh et al. 2012).

Discussion

We have proposed a likelihood-based approach to detect selective sweeps in whole-genome polymorphism data that is applicable to a variety of different demographic scenarios, classifies detected sweeps as hard or soft without relying on additional analyses or statistics, and is the first likelihood-based method to leverage distortions in the haplotype frequency spectrum to make these inferences. Each of these attributes is important because selective sweeps are multifaceted genomic signatures that are not always characterized by the presence of a single high-frequency haplotype (Jones et al. 2013; Wilson et al. 2017), may be ongoing or incomplete at the time of sampling (Vy and Kim 2015; Vy et al. 2017), and may range in strength across multiple orders of magnitude (Messer and Neher 2012; Nam et al. 2017). Thus, our simulation experiments probed a realistically diverse complement of sweep scenarios likely to be relevant in a variety of study systems. Most importantly, the T statistic demonstrated high and consistent power and classification ability across examined parameters, highlighting its suitability to make inferences within variable contexts.

Expectedly, the T statistic achieved its maximum power for recent selective sweeps on fewer haplotypes and lost power proportional to the extent of departure from these ideal conditions (figs. 2 and 3 and supplementary fig. S4, Supplementary Material online). Because it is haplotype based, the T statistic captures distortions in the haplotype frequency spectrum relative to neutral expectations. These distortions require time to establish and decay over time as well. Thus, we found that for human demographic models, the T statistic could reliably identify sweeps that initiated between 500 and 2,000 generations before sampling. For stronger sweeps ($s\ge 0.05$), power was consistently elevated across this range, but because weaker sweeps require more time to establish, this range narrows and power peaks for older sweeps as s decreases. Additionally, we uniformly had more power to detect sweeps under the YRI demographic model than the CEU. This is due to the severe bottleneck underlying the history of the CEU, as well as all non-African human populations. Bottlenecks may reduce the diversity of haplotypes within a population, reducing the distinctiveness of sweeps relative to neutrality, whereas population expansions have the opposite effect (Jensen et al. 2005; Campbell and Tishkoff 2008). Nonetheless, the T statistic could generally detect sweep strengths across all but our weakest selection coefficient range for sweeps aged between 1,000 and 2,000 generations under either demographic model, comprising events that in humans cover the period from 25,000 to 58,000 years ago, between the out-of-Africa event and the spread of agriculture (Lukić and Hey 2012; Nakagome et al. 2016; Haber et al. 2019).

Importantly, ours is a powerful single-statistic approach that provides an ideal balance of detection capability and computational efficiency. Compared with popular recent methods, we found that the T statistic is generally more powerful than other single-statistic approaches and is also sensitive to the same range of sweep times as they are (figs. 2 and 3 and supplementary figs. S1 and S2, Supplementary Material online). This highlights the usefulness of T as a substitute for other single-statistic approaches, which may miss sweeps that the T statistic can detect. Although T is likely to be underpowered relative to machine-learning methods, such as Trendsetter, analyses with T have no need to train a classifier, which may be computationally intensive when training a composite of multiple signals, and must be undertaken for each study scenario. However, using the T statistic within a machine-learning framework can greatly enhance its performance. By learning the spatial distribution of T statistic signals within our T-Trendsetter construct, we were able to enhance the performance of our method considerably. Using a large number of small windows, we could extend our range of sweep detection to identify simulated selective events up to 4,000 generations in age, reflecting ancient sweeps far older than the out-of-Africa expansion. In contrast, training a classifier from a smaller amount of standard 117-SNP windows greatly improved performance for recent soft sweeps relative to the unassisted T statistic (supplementary figs. S8 and S9, Supplementary Material online). Our results suggest that optimizing the power of a machine-learning approach relies not only on the choice of input statistics but also on the manner in which those statistics are applied to make inferences.

The choice of simulated human demographic history did not impact our inferences on the number of currently sweeping haplotypes ($\widehat{m}$) in a population. Under equivalent sweep scenarios (s, t, and ν), our analyses yielded similar distributions of $\widehat{m}$ for both the CEU and YRI models and could accurately identify soft sweeps, provided that at least two sweeping haplotypes remained in the population at the time of sampling (fig. 4 and supplementary figs. S10 and S11, Supplementary Material online). We found that simulated soft sweeps were frequently assigned an inferred $\widehat{m}$ that was smaller than the ν with which we initiated the sweep. Furthermore, we observed that T statistic signal peaks were on average associated with valleys in $\widehat{m}$ regardless of ν (supplementary figs. S6 and S7, Supplementary Material online). To better understand these results, we devised an in silico barcoding approach to complement our existing simulations. We found that soft sweeps from selection on standing variation frequently lose the majority of their selected haplotypes within generations of selection start time t, meaning that many soft sweeps, especially for smaller s, appear hard at the time of sampling (supplementary figs. S13 and S14, Supplementary Material online). This hardening effect (Wilson et al. 2014), due to genetic drift at the early stage of selection, affected both simulated CEU and YRI populations equally, corroborating our consistently similar $\widehat{m}$ observations between the two populations. This means that even if soft sweeps are the dominant mode of adaptation in human history (Schrider and Kern 2017), there may be considerably more that can never be identified as soft.

As an attempt to improve the performance of the T statistic, we sought to examine whether the choice of sweep distortion model, based on the choice of f_i (see Definition of Statistic), would affect our inferences. Ultimately, using our YRI simulations as a basis, we found that all of our tested models yielded little difference in the power of T to identify sweeps (supplementary fig. S28, Supplementary Material online). The five models we examined, consisting of (A) $f_i=1/m$, (B) $f_i=(1/i)/{\sum }_{j=1}^{m}1/j$, (C) $f_i=(1/i^2)/{\sum }_{j=1}^{m}1/j^2$, (D, our primary model for analyses) $f_i=e^{-i}/{\sum }_{j=1}^m{e}^{-j}$, and (E) $f_i=e^{-i^2}/{\sum }_{j=1}^m{e}^{-j^2}$, differ in the amount of weight allocated to the secondary sweeping haplotypes $q_i^{(m)}$ for $i\in \{2,3,\dots ,m\}$ relative to $q_1^{(m)}$ when distorting p. In model A, each sweeping haplotype gains the same amount of weight after distortion, ensuring that each is prominent within spectrum ${\mathbf{q}}^{(m)}$. Models B–E represent increasingly uneven weight distributions that favor frequency $q_1^{(m)}$ at the expense of $q_2^{(m)},q_3^{(m)},\dots , \text{and} q_m^{(m)}$. We believe this is reasonable based on the observation in simulated data that soft sweeps do not affect each sweeping haplotype evenly, and one sweeping haplotype may still be considerably more prominent than the rest (fig. 1; see also, fig. 3 of Garud et al. [2015]). Furthermore, the different T statistic variants demonstrated little difference in sweep classification with $\widehat{m}$ (supplementary fig. S29, Supplementary Material online), suggesting that the most important consideration in constructing our sweep models lies in simply distinguishing sweeping from nonsweeping haplotype classes, and not the manner in which they sweep.

An important feature of the T statistic is its ability to detect sweeps from unphased MLG data. Our ability to extend the power of our approach to MLGs is meaningful because it provides the ability to interrogate polymorphism data from nonmodel organisms for which phased haplotypes are unavailable, difficult to obtain, or unreliable (Browning SR and Browning BL 2011; O’Connell et al. 2014; Castel et al. 2016; Laver et al. 2016; Zhang et al. 2017; Harris et al. 2018). Overall, we found no difference in power trends between the two data types, such that scenarios under which we have high power with phased data are scenarios of high power with unphased data (compare figs. 2 and 3 with supplementary fig. S15, Supplementary Material online). However, we find that the T statistic applied to haplotypes always matched or exceeded power for MLG data. This is to be expected because MLGs are a more diverse data type drawn from a smaller sample size. Under a random mating assumption, the presence of a single high-frequency haplotype implies that only one MLG should exist at high frequency, but in the case of two high-frequency haplotypes, both homozygotes, as well as their heterozygote, will be prominent in the population. In this way, a sweep on two haplotypes can appear as a sweep on three MLGs, and sweeps on larger numbers of haplotypes will result in even larger numbers of elevated MLGs, which may be more difficult to separate from neutrality proportional to their $\widehat{m}$. Likewise, one high-frequency haplotype and one medium frequency haplotype can yield two high-frequency MLGs, meaning that an inferred $\widehat{m}=2$ in MLG data could underlie a true hard sweep. Our results indicate that this may be a common occurrence (compare fig. 4 and supplementary fig. S16, Supplementary Material online), and so we recommend scrutinizing $\widehat{m}$ results obtained from MLG data more carefully.

Our extensive testing revealed that T is overall robust to the most common confounding scenarios that affect sweep statistics. Making use of the sample average background haplotype frequency spectrum for inference allows T to account for the effects of mutation rate, recombination rate, and sample size on inferences by creating an expectation specific to the study data (supplementary figs. S21 and S24, Supplementary Material online). Using haplotype information provides complete resistance to the effect of background selection on nucleotide diversity (supplementary fig. S22, Supplementary Material online), as background selection does not cause haplotypes to rise to high frequency (Enard et al. 2014). The choice of a SNP-delimited window, meanwhile, is ideal for analyzing data sets with missing sites (supplementary fig. S23, Supplementary Material online) or low polymorphism density because by fixing the number of SNPs included in a window, we avoid generating windows that have low diversity simply because they contain few SNPs. SNP-delimited windows may also be more robust to the effect of population bottlenecks on inferences (Harris et al. 2018). Despite these strengths, we found that T may be misled by certain admixture scenarios (supplementary figs. S17–S20, Supplementary Material online). Although the admixture we simulated was extreme, our results are still informative as to the limits of our model. We found that, as expected, admixture from a donor of small size could inflate the neutral T statistic distribution because small-sized donors have a smaller haplotypic diversity, but we also found that low-level admixture from a large-sized donor also had this effect. We attribute this to the lack of admixture parameter in our model and expect that models directly incorporating admixture could overcome the confounding effects that we have observed.

The results from our empirical analyses with T served as a validation of our method, yielding expected sweep candidate genes in agreement with previous investigations (supplementary tables S1–S3, Supplementary Material online). More specifically, our top candidates matched extensively with those inferred with H12 and G123 (Garud et al. 2015; Harris et al. 2018). Our top candidates in the European-descent CEU population were centered on the LCT locus, associated with adaptation to dairy consumption (Bersaglieri et al. 2004). In the sub-Saharan African YRI population, we saw commonly recurring candidates at SYT1, NNT, LONP2, and HEMGN (Voight et al. 2006; Pickrell et al. 2009; Fagny et al. 2014; Pierron et al. 2014). The largest discrepancy between the H12 and T statistic analyses of the 1000 Genomes Project data we observed was the absence of SLC12A1 from the top 40 candidates in CEU haplotype data. SLC12A1 is a proxy for SLC24A5 (which was filtered out), a solute transporter has been implicated in the shift toward lighter skin pigmentation among Indo-Europeans (Lamason et al. 2005), and still yields an outlying value of T = 163.35, but there are dozens of genes with larger T, whereas only ten genes produced a larger H12 (Harris et al. 2018). Even so, SLC12A1 easily passes our 5% FDR threshold, and even our more stringent 1% threshold (supplementary table S4, Supplementary Material online; all top YRI candidates also pass a 1% threshold). Though our simulation experiments show that T has greater power than H12 for the same data, each method prioritizes sweep signatures differently. H12 is most sensitive to the sum of the two most frequent haplotypes in the frequency spectrum, whereas T places high emphasis on the relative values of all haplotypes in a truncated spectrum. Similarly, SweepFinder2 is unlikely to find any soft sweeps but will find older hard sweeps than what H12 and T could find, particularly for the YRI population (fig. 2).

All of our top candidates for the DGRP scan overlapped with one of the top 10 H12 peaks that Garud et al. (2015) identified, except for Uhg1, CG8552, Skeletor/CG14681 (which were in lower-ranked peaks), and corn. However, none of our top candidates was statistically significant when compared against the neutral distribution we generated under the Duchen et al. (2013) model of North American D. melanogaster population history, and only our top candidate, CG11902 (located within the second-largest signal peak of Garud et al. [2015]), passed the 5% FDR threshold. This result matches that of Harris, Sackman, et al. (2018), who also found that they could not reject neutrality when using a model that incorporates uncertainty in key parameters (supplementary fig. S27, Supplementary Material online). In contrast, the original interpretation of Garud et al. (2015) found the top signal peaks to be significant but used fixed model parameters rather than drawing them from a posterior distribution. Even so, the top D. melanogaster candidates uncovered in recent analyses show literature support for selection, especially in response to pressure from pesticide application (Menozzi et al. 2004; Pedra et al. 2004; Karasov et al. 2010). Furthermore, future analyses with more certain demographic parameter estimates may aid in ultimately rejecting neutrality for these genes.

Finally, empirical analysis allowed us to understand the practical effect of using different K truncations to generate inferences. The most apparent difference between scans with K = 10 and K = 20 truncations was each configuration’s inference on $\widehat{m}$. Using a larger K truncation had the effect of classifying a greater number of candidate sweeps as soft ($\widehat{m}\ge 2$), and we observed this for both phased and unphased data, and all study populations. Without exception, $\widehat{m}$ for K = 10 truncations was less than or identical to $\widehat{m}$ for K = 20. We find that when $\widehat{m}$ changes, it is for borderline cases, such as that of COL5A2 in CEU. For this candidate, one high-frequency haplotype predominates, but there is clearly a second haplotype at an elevated frequency as well. In the K = 20 spectrum, the contrast in size between the second haplotype frequency and the others is sufficient to assign an inference of $\widehat{m}=2$, whereas this is not the case for the K = 10 truncation, where haplotype frequencies 3–10 are relatively large enough to the second that a hard sweep serves as a better explanation of the data (fig. 5). The MLG spectrum underlying COL5A2, in contrast, reflects $\widehat{m}=2$ regardless of truncation, and that is because we no longer have a borderline case, and two high-frequency MLGs are evident. Ultimately, T is more sensitive to hard sweeps, and any scan with T is likely to yield a greater number of hard sweeps, especially when choosing a smaller K. This is not to say that soft sweeps are uncommon or rarer than hard sweeps (Hernandez et al. 2011; Jensen 2014; Schrider and Kern 2017), but that we may simply be overlooking these more often due to the nature of our approach.

We believe that our T statistic will serve as an important contribution to the field of selective sweep detection methods, providing the first maximum-likelihood approach that exploits a haplotype and MLG frequency spectrum distortion model. As such, the T statistic offers high power for recent selective sweeps with little computation time and can additionally assign an $\widehat{m}$ value to candidates with no additional analysis required. This makes it an appropriate complement to methods such as the singleton density score (Field et al. 2016), which detects sweeps occurring within the past 100 generations of human history (outside the range of detection of T). The T statistic also complements machine-learning methods (Lin et al. 2011; Schrider and Kern 2016; Sheehan and Song 2016; Kern and Schrider 2018; Sugden et al. 2018; Mughal and DeGiorgio 2019; Mughal et al. 2019), which are more powerful in exchange for more computation time (and can also incorporate T into their algorithms). Our lack of dependence on phased data provides the opportunity to search for sweep signatures in any nonmodel organism for which whole-genome polymorphism data exist. We expect that our simple yet powerful statistical model of selective sweeps will yield novel insights into the adaptive histories of diverse populations. Even in well-studied species such as humans, there are yet understudied populations for which future analyses of selection signatures will provide important insights about population history that is missing from the current literature. To motivate this point, we highlight that insights into local adaptation within human populations continue to emerge (Buckley et al. 2017; Hu et al. 2017; Fan et al. 2019), more than a decade after the first investigations began (Bustamante et al. 2005; Ronald and Akey 2005; Sabeti et al. 2006). Finally, we make available the open-source software package LASSI, which implements the T statistic protocol in a single efficient pipeline.

Materials and Methods

General Simulation Protocol

We applied the T statistic to simulated data based on demographic models consistent with recent estimates of human (Terhorst et al. 2017) and D. melanogaster (Duchen et al. 2013) population history. For some experiments evaluating power under human models, we also applied the T statistic to unphased MLG data, which we produced by manually merging each simulated individual’s two haplotypes. We generated these data using the population-genetic simulation software SLiM (Haller and Messer 2017), as well as with the coalescent simulator ms (Hudson 2002). For power experiments based on human models, we exclusively performed simulations forward in time using a Wright–Fisher model implemented in SLiM (Fisher 1930; Wright 1931; Hartl and Clark 2007). These simulations lasted for a total of 200,000 generations, of which the former 100,000 (equivalent to 10N, where $N={10}^4$ is the diploid effective population size of the simulated population) was a burn-in period to achieve equilibrium values of neutral variation, and the latter 100,000 was the period over which population size variation occurred. To speed up run time, human-modeled simulations were scaled by a factor of λ = 20, whereas D. melanogaster simulations, which featured larger population sizes, were scaled by λ = 100. In order to scale, we multiplied mutation rates, recombination rates, and selection coefficients by λ, whereas the size of the simulated population and the duration of the simulation in generations were divided by λ. Thus, simulation duration was reduced by a factor of 400 (λ = 20) or 10⁴ ($\lambda =100)$.

For all simulations other than for the above human-model power experiments, we generated data for each replicate population using ms, either for use as input into SLiM (burn-in), or to simulate neutrality. We used the former approach to generate FDR thresholds under the human and D. melanogaster models (see Results and Selection Protocols below). Here, we used ms to run the majority of each simulation. For the D. melanogaster model, we ran ms up to the earliest point in time that selection could occur, which was the time of admixture between the African and European populations (supplementary fig. S27, Supplementary Material online; see also below). For human models, we simulated the first 10N generations prior to sampling. Simulations then proceeded forward in time with SLiM, and selection was allowed to take place. Meanwhile, we outputted neutral simulations to compute P values (see below) for both human and D. melanogaster models directly from ms. For human simulations, we chose a mutation rate of $1.25\times {10}^{-8}$ per site per generation (Narasimhan et al. 2017), and an exponentially distributed recombination rate with mean ${10}^{-8}$ per site per generation, with maximum value truncated at $3\times {10}^{-8}$, as in Schrider and Kern (2017) and Mughal and DeGiorgio (2019). For D. melanogaster, our recombination rate was a uniform $5\times {10}^{-9}$ per site per generation (equivalent to $5\times {10}^{-7}$ cM per base), and our mutation rate was ${10}^{-9}$ per site per generation, specifically chosen to match Garud et al. (2015) and Harris, Sackman, et al. (2018), but smaller than the value inferred by Keightley et al. (2009).

Our simulated human demographic histories consisted of a European-descended CEU model (individuals of northern and western European descent sampled in Utah, USA) and a sub-Saharan African YRI model (Yoruba individuals from Ibadan, Nigeria). Both models were inferred by Terhorst et al. (2017) using smc++. The CEU model features a severe bottleneck reducing population effective size by an order of magnitude ∼2,000 generations before sampling, followed by a population expansion over two orders of magnitude leading to present day. The YRI model contains population size fluctuations, but with no severe bottlenecks, and also includes an expansion similarly to the CEU model (see fig. 5 of Terhorst et al. [2017]). Thus, the simulated CEU population has an ∼2-fold reduction in its level of background genetic diversity relative to the YRI. For every replicate within each simulated human-model selection scenario (see below), we outputted a simulated chromosome in SLiM of length 1 megabase (Mb) and scanned it with a sliding analysis window of size 117 SNPs, advancing by 12 SNPs per iteration. A window of 117 SNPs roughly corresponds to the number of SNPs expected in a physical window of size 40 kb for our sample size of 100 European diploid individuals, or 20 kb for 100 sub-Saharan African diploid individuals (Watterson 1975). We selected this window size because it is over this interval that pairwise LD between SNPs decays by more than one-third on average in the human genome (Jakobsson et al. 2008). This makes it unlikely that elevated values of the T statistic are due to background LD.

We simulated the DGRP (Mackay et al. 2012) D. melanogaster demographic history following the protocol of Harris, Sackman, et al. (2018), adapting the model of Duchen et al. (2013) (supplementary fig. S27, Supplementary Material online). Here, an ancestral African population (effective size N₁) experiences a bottleneck at time $T_{\mathrm{B}}$, contracting to size $N_{\mathrm{B}}$ for 1,000 generations before expanding to size $N_1^{\prime }$. After the bottleneck, the ancestral European population diverges from the ancestral African population at time τ₁ and begins with an effective size N₂. The European population grows exponentially to its modern size, $N_2^{\prime }$. At time τ₂, the North American population ancestral to the modern DGRP sample is generated with initial size N₃ from the admixture of the European and African populations, modeled as a single event, with a proportion α of North American genomes deriving from African ancestors, and a proportion $1-\alpha$ deriving from European ancestors, where $\alpha <1/2$. The North American population grows exponentially to its final size, $N_3^{\prime }$. We draw each of the aforementioned model parameters according to their posterior probability density (Harris, Sackman, et al. 2018; supplementary table S1, Supplementary Material online), thereby incorporating uncertainty into the demographic model. We only output data from the North American population, and selection only occurs in that population. We used analysis windows of size 400 SNPs and a step size of 40 SNPs for D. melanogaster simulations. This represents the expected number of SNPs in a 10-kb window, over which a pairwise LD decay of greater than one-third occurs for the DGRP data set (Garud et al. 2015).

Across all experiments, we primarily used a haplotype frequency spectrum truncation of K = 10, but for human-model analyses, we also examined $K\in \{15,20,25\}$. As described in the Definition of Statistic section, we generate an averaged truncated haplotype frequency spectrum from each neutral replicate analysis window and use this as an estimate of the baseline variation in the absence of a selective sweep. Except where otherwise mentioned, we used weight allocation scheme (D) from the Definition of Statistic section, with $f_i=e^{-i}/{\sum }_{j=1}^m{e}^{-j}$, favoring a greater increase in the frequency of the first sweeping haplotype class relative to the neutral baseline. In practice, all schemes showed similar power, however (supplementary fig. S28, Supplementary Material online). Additionally, we only optimized models with U = p_K and did so over a grid of $\epsilon \in [1/(100K),U]$ (with intervals of $(U-\epsilon )/100$), providing us with a range of different U and ε combinations. Fixing U = p_K ensured that we would under all circumstances have frequencies $\{q_{m+1}^{(m)},q_{m+2}^{(m)},\dots ,q_K^{(m)}\}$ smaller than their equivalents in the p spectrum, though in doing so we often underestimate the empirically observed putatively nonsweeping classes. We emphasize, however, that due to the structure of our likelihood equations, the value of the T statistic depends more on the fit of the model’s sweeping classes than its nonsweeping classes and thus did not include an optimization of U because it would be unlikely to provide additional power to T but could potentially require considerably more computational burden.

Selection Protocols

To assess the power of the T statistic to differentiate between neutrality and sweeps, we simulated a variety of human selective sweep scenarios, defined primarily by their combination of selection time t, selection strength s, and simulated number of initially sweeping haplotypes ν. We simulated selection on de novo mutations arising at times $t\in \{200,500,1,000,1,500,2,000,2,500,3,000,3,500,4,000\}$ generations prior to sampling. We chose this range of t because the T statistic is suited to detecting recent sweeps that have established in a population, and so this range spans sweeps that are too recent to detect (as they are unlikely to have established), too ancient to detect (as their footprints have likely eroded), and optimal to detect. We simulated sweeps on $\nu \in \{1,2,4,8,16,32\}$ distinct sweeping haplotypes, drawn uniformly at random across the set of haplotypes in the population at time t, and conditioned that at least one copy of the selected allele would remain in the population for the duration of the simulation. We chose selection coefficients uniformly at random following five schemes to illustrate the effect of the selection coefficient on sweep detection. Weak selection protocols covered $s\in [0.001,0.01]$ and $s\in [0.005,0.05]$. Strong selection comprised $s\in [0.01,0.1]$ and $s\in [0.05,0.5]$. We drew mixed selection coefficients as a combination of the weak and strong ranges, with $s\in [0.001,0.5]$ drawn uniformly at random specifically from a log scale. We computed the T statistic for each simulated genomic analysis window using its truncated counts spectrum as input for the likelihood functions ${\ell }_0$ (eq. 4) and ${\ell }_1$ (eq. 5) and retained the largest T for a replicate as its score. We also computed the score in this manner for each existing neutral replicate. We assessed the power of our approach for each parameter set at 1% and 5% FPRs as the proportion of sweep replicates whose scores exceeded the top 1% or 5% of scores under neutrality, respectively.

For experiments to identify FDR thresholds, selection parameters were drawn at random from distributions of all parameters described above. Sweeps under the human model were initiated uniformly at random across $t\in [200,4,000]$ generations prior to sampling, and selection coefficients uniformly at random from $s\in [0.005,0.5]$ on a log scale. We raised the lower bound on s relative to power experiments because we found that the T statistic has little ability to identify sweeps on s < 0.005. Likewise, we drew $\nu \in \{1,2,\dots ,8\}$ to account for the range over which T has the most power. For the D. melanogaster model, we simulated hard and soft sweeps once again from $\nu \in \{1,2,\dots ,8\}$ but chose $t\in [500,7,000]$ and $s\in [0.001,0.5]$. The constraint on selection time here derives from the requirement that sweeps must occur in the North American D. melanogaster population, which we have fixed to arise 7,943 unscaled generations before sampling (this is the sole parameter that we do not draw from the posterior distribution of Duchen et al. [2013]), whereas we expect that the larger size of the D. melanogaster population should allow us to detect sweeps from smaller s due to the larger population-scaled selection coefficient $\sigma =4N_{\mathrm{e}}s$.

Because we were interested in tracking the number of haplotypes carrying the selected allele in a soft sweep over the course of a sweep, we implemented an in silico barcoding protocol in SLiM. This approach allowed us to observe the effect of hardening on soft sweeps due to genetic drift (Wilson et al. 2014), as well as the relationship among selection coefficient, $\widehat{m}$, and method power. We augmented the simulation procedure of previous power experiments by additionally introducing a unique neutral mutation adjacent to the site of selection for each selected haplotype at time t. Thus, no two selected haplotypes could be identical at time t. Then, at the end of each generation, we measured the frequency of both the selected allele and the count of each unique mutation, which served as a proxy for each unique haplotype’s count in the population. We quantified selected allele frequency and selected haplotype count trajectories by taking the mean of 1,000 replicates for each scenario. Supplementary figure S12, Supplementary Material online, summarizes our in silico barcoding protocol for ν = 4 initially selected haplotypes. For haplotype tracking experiments, we focused specifically on human scenarios across our five selection strength schemes and $\nu \in \{2,4,8,16,32\}$ but only studied the selection times for which we had the greatest power. For CEU, these were t = 2,000 ($s\in [0.001,0.01]$), t = 1,500 ($s\in [0.005,0.05]$ and $s\in [0.001,0.05]$), t = 1,000 ($s\in [0.01,0.1]$), and t = 500 ($s\in [0.05,0.5]$). Across the same s ranges for YRI, we respectively used t = 2,500, 2,000, 2,500, 1,500, and 500.

Scans of Simulated Data with Multiple Methods

In addition to the T statistic, we also applied other popular and powerful methods to our simulated data in order to thoroughly contextualize the power of our approach. Here, we reused the data generated for power experiments across all ranges of s for hard (ν = 1) and soft (ν = 4) sweeps. We elected to compare H12 (Garud et al. 2015), nS_L (Ferrer-Admetlla et al. 2014), SweepFinder2 (Nielsen et al. 2005; DeGiorgio et al. 2016; Huber et al. 2016), and Trendsetter (Mughal and DeGiorgio 2019), as each presents a unique approach in identifying signatures of selective sweeps. H12 and nS_L represent perhaps the most similar alternatives to T, as they are summary statistics that also leverage measures of haplotype frequency to make inferences. H12 is a haplotype homozygosity-based method that detects sweeps based on their reduced haplotypic diversity, whereas nS_L identifies sweeps based on their large tracts of sequence identity. Both approaches also have power to detect soft sweeps in addition to hard sweeps (this being the primary purpose of H12). SweepFinder is a likelihood method that detects sweeps from distortions in the SFS and has high power to detect hard sweeps but is underpowered for soft sweeps because it does not use haplotype information. Finally, Trendsetter is a sophisticated machine-learning approach that leverages the spatial autocorrelation of summary statistic signals along the chromosome to identify and classify sweeps and is therefore likely to outperform any single-statistic approach.

We applied these statistics in ways that allowed us to most directly compare their performance with that of T. For H12, we used the same SNP-based window and step sizes as with the T statistic, meaning that we computed H12 using the exact data as for T. Next, we implemented unstandardized nS_L with selscan (Szpiech and Hernandez 2014) running default options and obtained a value of the statistic for each SNP within a replicate. For SweepFinder2, we scanned with a step size of 1,000 nucleotides to ensure a dense grid of analysis windows. We generated a helper file from our neutral replicates, which served a similar purpose to our neutral haplotype frequency spectrum p, and only included polymorphic sites in computations (Huber et al. 2016). Finally, we implemented two versions of Trendsetter, each trained on simulated data across three classes—neutrality, hard sweeps, and soft sweeps ($\nu \in \{2,3,\dots ,8\}$ drawn uniformly at random)—and 5,000 replicates per training class, with $s\in [0.001,0.5]$ and $t\in [200,4,000]$ as previously. First, we used the standard approach, which studies the spatial signatures of six statistics—mean pairwise sequence difference $\widehat{\pi }$, squared correlation coefficient of LD r², the number of distinct haplotypes $N_{\text{haps}}$, and expected haplotype homozygosity H1, H12, and H2/H1 (Garud et al. 2015). Second, we applied Trendsetter to employ the spatial signature of only the T statistic (“T-Trendsetter”). This experiment served to highlight the power gain from incorporating spatial autocorrelation of T signals across genomic sequence tracts. In both applications, we used the default behavior of Trendsetter, drawing inferences across 201 windows of size 11 SNPs spaced apart by 5 SNPs for a total of 1,010 SNPs. For T-Trendsetter, we also trained a classifier on 75 117-SNP windows to better recapitulate our approach with the unaided solitary T statistic. To measure power, we retained the maximum value of each summary statistic (or for Trendsetter, the probability of assigning the replicate as a sweep, which is the sum of the hard and soft sweep class probabilities) as the score.

Modeling Confounding Scenarios

We considered admixture as a confounding scenario because its effect can mimic that of a selective sweep under certain circumstances (Harris et al. 2018). To determine the impact of admixture on the T statistic, we implemented contrived models overlaid onto our existing CEU and YRI models in which a distantly related donor population (diverged $\tau =2N=2\times {10}^4$ generations before sampling) unidirectionally admixes into the sampled CEU or YRI population as a single pulse 200 generations before sampling. We varied the size of the admixture pulse from 0.05 to 0.4, meaning between 5% and 40% of the subsequent generation derive their ancestry from the admixing donor population, at increments of 0.05, and tested admixing population sizes of $N={10}^3$, 10⁴, and 10⁵. For all scenarios, we generated neutral background haplotype frequency spectra ${\mathbf{p}}^{\mathbf{\alpha }}$ matching the admixture scenario but additionally computed the T statistic using the unadmixed p spectra to demonstrate the effect of not accounting for admixture. For these experiments, all scenarios included no selection in order to highlight the range of T statistics emerging from admixture in the absence of a sweep.

To evaluate background selection as a potential confounding factor that may also produce spurious sweep signals, we performed simulations in which we allowed for deleterious mutations to arise within the simulated chromosome throughout the simulation while maintaining all other parameters identical to neutrality. Our protocol was similar to that of Harris et al. (2018) and covered the human CEU and YRI models. As with our previous simulations, we generated a genomic region of length 500 kb with identical mutation rate and population sizes as previously, evolving once again for a duration of 20N generations ($N={10}^4$ diploids, the effective size during the burn-in period). At the center of the simulated sequence, we introduced a gene of length either 11 kb (small), 55 kb (medium), or 110 kb (large) consisting of a 5′ untranslated region (UTR, length 200 bases), either 10 kb (small), 50 kb (medium), or 100 kb (large) exons (100 bases each) and 9 kb (small), 49 kb (medium), or 99 kb (large) introns (1 kb each) alternating for 10 kb (small), 54 kb (medium), or 109 kb (large), and a 3′ UTR (800 bases). We based the sizes of genetic elements on human genome-wide mean values (Mignone et al. 2002; Sakharkar et al. 2004). Within the gene, strongly deleterious mutations ($s=-0.1$; gamma distribution of fitness effects with shape parameter 0.2) arose at rates of 50% within the UTRs, 75% within the exons, and 10% within the introns, whereas all other mutations within the gene and across the rest of the chromosome were selectively neutral. To enhance the effect of background selection under this scenario, we reduced the mean recombination rate from $r={10}^{-8}$ to $r={10}^{-10}$ per site per generation within the central gene.

Within natural genomes, and across different study systems, there can be considerable variability in mutation and recombination rates, which ultimately affects the density of SNPs and number of distinct haplotypes within a genomic analysis window. To understand this effect with respect to the value of the T statistic, we performed neutral simulations under both of our human models in which we reduced the mutation and mean recombination rates by an order of magnitude, both separately and simultaneously. Thus, altered mutation rates were lowered to $\mu =1.25\times {10}^{-9}$, and recombination rates were drawn as previously but centered on a mean of $r={10}^{-9}$. We performed 1,000 simulations of 1-Mb sequences once again, recorded the value of the T statistic to generate a distribution, and measured the proportion of false signals deriving from the above scenarios as a function of the true positive rate.

Similarly, analyses of data sets with missing sites can also reduce the number of SNPs and therefore haplotypes within an analysis window relative to ideal data, and so we performed a similar analysis measuring the distribution of the T statistic under neutrality after removing polymorphic sites with >5% missing data. To generate a data set with missing sites, we followed two types of approaches. First, we selected a number of SNPs, drawn uniformly at random for each existing replicate, and removed data from these SNPs in 5–20 diploid individuals (both haplotypes were treated identically). Second, we performed five iterations of data removal, with SNPs from between one and four individuals removed per iteration. For each approach, we performed three different intensities of data removal. The lowest intensity involved the removal of between 200 and 500 SNPs for the single-iteration approach or between 40 and 100 SNPs per iteration for the five-iteration approach. The middle intensity approach removed $[400,1,000]$ or $[80,200]$ SNPs, and the most intense approach removed $[600,1,500]$ or $[120,300]$. The single-iteration approach is more likely to force the removal of sites with missing data, since the possibility is greater that enough missing alleles will be present at an affected site. The five-iteration approach results in a scattering of missing alleles but a lower chance of any SNP having >5% missing data. Sites with ≤5% missing data were incorporated into haplotypes, encoded as a third character state “N” (in contrast to the binary 0/1 for nonmissing sites). Doing so allowed us to conservatively lower the value of the T statistic in such cases by introducing greater haplotypic diversity to samples with missing data.

An important component of analysis with the T statistic is the computation of statistical thresholds, such as P value and FDR cutoffs for determining candidate significance. In order to compute these thresholds, it is necessary to perform simulations under an appropriate demographic history and compare the T statistics of sweep candidates with the distribution of T statistics under simulated replicates. If the demographic history is improperly inferred, then P values and FDR cutoffs will also be incorrect, and may result in unwarranted emphasis on nonadaptive regions, or spurious disregard for true selective events. To demonstrate the effect of misspecifying the demographic history of a study population, we show the impact of generating neutral replicates from CEU and YRI demographic histories wherein population size remains constant and equal to the effective size of smc++-derived models, computed as the harmonic mean of the population size through the simulation. We also compared distributions of the T statistic generated under the Gravel et al. (2011) CEU and YRI models, which were inferred solely from SFS information in contrast to the potentially more accurate hybrid approach of smc++, which uses the SFS and whole-genome sequence information (Beichman et al. 2017).

Finally, we also examined the power of the T statistic for variably small sample sizes. Haplotype-based methods are sensitive to the number of sampled individuals because sufficient variation needs to be captured in a sample for the difference between neutral and sweep haplotypic diversity to become apparent (Harris et al. 2018). That is, reductions in diversity following a sweep become more apparent as more individuals are sampled, and more subtle signatures of sweeps can be elucidated. Accordingly, we resampled all of our existing sweep replicates used in the previous power analysis by drawing n = 100, 50, or 20 haplotypes uniformly at random and applying the T statistic as previously. We note that we computed a size-adjusted neutral background haplotype frequency spectrum p for each reduced-size sample as well.

Application of T Statistic to Empirical Data

We applied the T statistic to human empirical data from the 1000 Genomes Project (1000 Genomes Project Consortium et al. 2015), as well as to the DGRP inbred D. melanogaster data set (Mackay et al. 2012). The former application served primarily as a validation of our approach, as positive selection in the human genome has been widely explored. The latter application represented a typical insect model system that has also been well studied and diverges in size, genome architecture, and population history from humans. The complete outputs for our scans of these data sets are available at http://degiorgiogroup.fau.edu/LASSI.html. Our protocols for analyzing either data set were identical in approach. For each, we searched for candidate peaks by applying a sliding window to all autosomes in the subject genome, basing window size on the interval over which LD, measured as r², decayed below one-third of its original value relative to pairs of loci separated by 1 kb. This matched the prior approaches of Garud et al. (2015) and Harris et al. (2018). A candidate peak simply refers to an elevated instance of T within an RNA- or protein-coding region, and we retained the most prominent peak for each gene. For humans, our window size was 117 SNPs, and for D. melanogaster, it was 400 SNPs, both matching our values for simulation experiments.

After performing each scan of the CEU and YRI data sets, we filtered windows overlapping chromosomal regions of low alignability and mappability, removing windows overlapping with chromosomal regions of mean CRG100 score <0.9. For D. melanogaster, we removed strains 49, 85, 101, 109, 136, 153, 237, 309, 317, 325, 338, 352, 377, 386, 426, 563, and 802 from our analysis due to their high number of heterozygous sites and treated remaining heterozygous sites as missing data, as in Garud et al. (2015). We also only used SNPs that had a quality score (reported in the DGRP data) between 1 and 30. We computed T statistic for the K = 10 truncation and assigned $\widehat{m}$ values based on both K = 10 and K = 20 to examine the practical effect of truncation on candidate classifications.

We intersected the locations of computed T statistic values with the coordinates for protein- and RNA-coding genes based on hg19 and Dmel 5.13 annotations for humans and D. melanogaster, respectively. We assigned P values based on K = 10 truncations to the 40 genes with the largest associated values of T by generating 10⁶ neutral replicates simulated in ms (Hudson 2002). For humans, we generated neutral replicates under demographic models inferred with smc++ (Terhorst et al. 2017), and for D. melanogaster, neutral replicates were based on the Duchen et al. (2013) model, drawing parameters as previously. For each replicate, we simulated a sequence of length drawn uniformly at random from the set of all gene lengths, appended with the minimum number of nucleotides necessary to allow the application of full analysis windows centered across the entire length of the simulated gene. As an example, for a simulated human gene of length L nucleotides, we appended additional sequence length guaranteeing that 117-SNP windows centered at the first SNP and the last SNP of the simulated gene could be constructed. This allowed us to obtain a T statistic for at least one whole analysis window centered on the simulated gene during each replicate.

The P value for a selection candidate is the proportion of T statistics across all neutral replicates (using the maximum value for a replicate if there was more than one analysis window) that exceeded the maximum T associated with the candidate. All P values were Bonferroni corrected for multiple testing (Neyman and Pearson 1928), where a significant P value was $P<0.05/G$ and where G is the number of genes for which we assigned a score in the organism. Accordingly, we have for humans $G_{\text{human},\text{CEU}}=18,785,\hspace{0.17em}{G}_{\text{human},\text{YRI}}=19,379,\hspace{0.17em}{p}_{\text{human},\text{CEU}}=2.6617\times {10}^{-6}$, and $p_{\text{human},\text{YRI}}=2.5801\times {10}^{-6}$, whereas $G_{\text{Dm}}=10,000$ and $p_{\text{Dm}}=5\times {10}^{-6}$ for D. melanogaster. We ultimately examined fewer than the total number of genes for each study system as a consequence of our filtering and sliding window step size. Filtering had the effect of removing SNPs, which can lead to genes losing representation in the final data set, whereas the choice of window step size may result in genes being skipped over. The total number of protein- and RNA-coding autosomal genes in hg19 is 23,735, of which ∼20% were uncounted, whereas the total number of autosomal genes in Dmel 5.13 is 12,215, meaning that once again ∼20% were omitted. Finally, we computed FDR cutoffs for each population by generating simulated 10⁶ neutral and sweep replicates as described in Selection Protocols, generating a sample of size $2\times {10}^6$. The 5% FDR cutoff, which we assigned to all populations, was the T statistic value for which 5% of the replicates exceeding that value were neutral, and 95% were sweeps. There was no value of T which served as a 1% cutoff for the D. melanogaster model (i.e., there was no T value for which only 1% of replicates were neutral), but we did assign a 1% FDR cutoff to human populations (supplementary table S4, Supplementary Material online).