Abstract
Biomolecular condensates are emerging as an important organizational principle within living cells. These condensed states are formed by phase separation, yet little is known about how material properties are encoded within the constituent molecules and how the specificity for being in different phases is established. Here we use analytic theory to explain the phase behavior of the cancer-related protein SPOP and its substrate DAXX. Binary mixtures of these molecules have a phase diagram that contains dilute liquid, dense liquid, and gel states. We show that these discrete phases appear due to a competition between SPOP-DAXX and DAXX-DAXX interactions. The stronger SPOP-DAXX interactions dominate at sub-stoichiometric DAXX concentrations leading to the formation of crosslinked gels. The theory shows that the driving force for gel formation is not the binding energy, but rather the entropy of distributing DAXX molecules on the binding sites. At high DAXX concentrations the SPOP-DAXX interactions saturate, which leads to the dissolution of the gel and the appearance of a liquid phase driven by weaker DAXX-DAXX interactions. This competition between interactions allows multiple dense phases to form in a narrow region of parameter space. We propose that the molecular architecture of phase-separating proteins governs the internal structure of dense phases, their material properties and their functions. Analytical theory can reveal these properties on the long length and time scales relevant to biomolecular condensates.
Graphical Abstract
Introduction
Many biomolecules have been shown to spontaneously form condensed states that serve organizational or functional roles in living cells.1,2 Often these condensates are responsive to changes in environmental conditions, cell cycle, or stress.3–6 While many simple globular proteins undergo phase separation, their phase boundaries are usually in non-physiological, or even inaccessible, regions of phase space due to the weak intermolecular interactions.7,8 In contrast, multi-valent proteins have evolved to drive biologically relevant phase transitions; a higher valence means that a lower total protein concentration is sufficient to achieve phase separation.9 Many proteins that drive phase separation are intrinsically disordered with attractive moieties separated by long flexible linkers. This has inspired polymer theory-based models to describe the effects of the attractive “stickers” 10 and the flexible, inert “spacers” 11 to describe the condensation of these molecules into a polymer fluid. However, there is considerable heterogeneity in the protein architectures that have evolved to form condensates. Phase separation can be driven by discrete folded domains that specifically recognize linear motifs in binding partners9 and the linkers between domains/motifs can be long, short, or nonexistent. In other cases the driving force is weak contacts between sidechains or backbones of disordered regions.5,10,12 The existence of these different modes of interactions is thought to provide the specificity to facilitate the coexistence of multiple different biomolecular condensates and the conversion between different condensed states.
In this paper we study phase transitions involving the speckle-type POZ protein (SPOP). SPOP is the substrate adaptor of a ubiquitin ligase13,14 and recruits substrates such as the androgen receptor (AR),15 bromodomain-containing proteins (BRD2, BRD3 and BRD4),16,17 and the death-domain-associated protein (DAXX)18 for ubiquitination and subsequent degradation. SPOP is the most frequently mutated gene in prostate cancer and the cancer-associated mutations affect the interaction between SPOP and these substrates.19–22 We recently showed that SPOP can undergo phase separation with cDAXX, the intrinsically disordered C-terminal tail of DAXX. SPOP/DAXX phase separation leads to the colocalization of SPOP with its substrate DAXX. SPOP typically localizes to nuclear speckles and DAXX to PML bodies. Upon their co-expression, they colocalize in liquid-like SPOP/DAXX bodies. Importantly, the recruitment of additional ubiquitin ligase subunits, including the scaffold Cullin3 and the catalytic RING protein RBX1 to DAXX, depends on phase separation with SPOP. The SPOP/DAXX bodies show a signature of active SPOP-mediated DAXX ubiquitination, and in vitro ubiquitination experiments confirmed the activity of the assemblies. Importantly, colocalization of DAXX and SPOP in cells seems to be required for optimal function.
The phase behavior of SPOP with DAXX is complex.23 In isolation cDAXX forms liquid droplets, likely due to the association of oppositely charged amino acid blocks,24 while SPOP polymerizes into linear assemblies.25 When small amounts of DAXX are added to SPOP solutions the result is a crosslinked gel, indicative of a kinetically arrested state. However, the addition of more cDAXX (but less than the amount required to form cDAXX droplets) dissolves the gel, resulting in liquid droplets that contain both SPOP and cDAXX.23 This behavior contrasts with the standard progression of vapor to liquid to gel found in single component systems.26,27 This distinctive behavior motivates the present theoretical treatment.
Protein condensates are disordered and, therefore, it is difficult to probe the internal structure by experiments. Furthermore, the dense phases form on timescales of seconds to hours, which presents a severe challenge for simulation-based approaches. Here we obtain structural insight by developing a theory that captures the phase boundaries and condensate densities. We show that the gel phase is not driven by the binding energy of DAXX crosslinks, but rather by the entropy of multivalent DAXX binding. We also show that the liquid-gel transition is caused by a competition between SPOP-DAXX and DAXX-DAXX interactions, with the former giving way to the latter as the binding sites on SPOP become saturated. As a result, the addition of more DAXX simultaneously lubricates the kinetically trapped gel and introduces the liquid state as the free energy minimum.
Results
SPOP-SPOP interactions cause the formation of linear rods
SPOP is a three-domain protein, which binds substrates through the MATH domain (green in Fig. 1) and self-associates via two dimerization domains (red and blue in Fig. 1).25,28,29 The strong binding interface (BTB-BTB) leads to the formation of dimers with nanomolar affinity. Since the concentrations leading to dimers are considerably lower than the micromolar concentrations explored by Bouchard et al.,23 we neglect the presence of monomers and consider the assembly of a solution of dimers at concentration cs/2, via the BACK domain which has a micromolar affinity in the absence of crowding agents. Each dimer has two identical dimerization interfaces that can self-associate with an association constant ks = cn+2/(cnc2), where ci is the concentration of SPOP assemblies containing i monomers. Since these assemblies are linear and rigid on the lengthscale set by the DAXX binding sites, we refer to SPOP assemblies as rods throughout the paper. The concentration of SPOP rods of all lengths is
| (1) |
The total concentration of SPOP in the system is cs = 2c2∂cr/∂c2, which can be inverted to give the free dimer concentration as a function of the total concentration
| (2) |
The average assembly length, measured in dimer units, is
| (3) |
This function is plotted in Fig. 1 showing that the average length of SPOP assemblies ranges from 20-100 dimer units over the experimental concentration range.25
Figure 1:
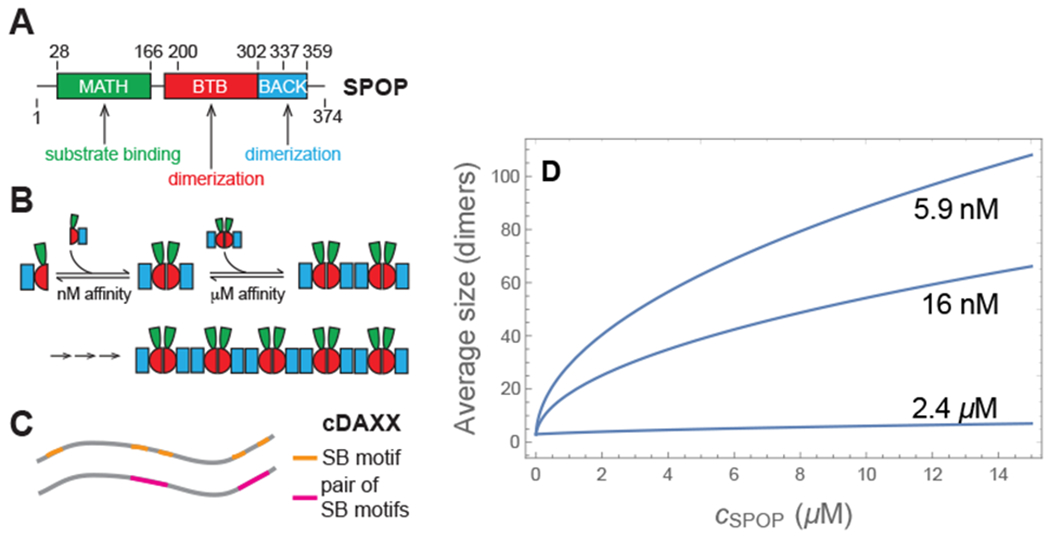
(A) The three domains of SPOP determine its assembly behavior. (B) BTB-BTB interactions lead to the formation of dimers with a nM affinity. BACK-BACK interactions allow for the polymerization of dimers to form linear rods. The MATH domain binds to substrates such as DAXX. (C) cDAXX, which is the intrinsically disordered C-terminus of DAXX and encompasses residues 495-740 of DAXX, has five SPOP binding (SB) motifs. Four of these are arranged in pairs that bind cooperatively to pairs of MAT14 domains. The remaining SB motif is weak and is neglected in our model. (D) Average length of SPOP assemblies (measured in dimer units) for three values of the polymerization constant, as calculated from Eq. 3. In the absence of ficoll the polymerization constant is . The other two curves represent the range of values consistent with the phase diagram observed in 4% ficoll.
In the absence of DAXX these rods remain dispersed in dilute solution. We refer to this state as the vapor phase, since the large separation between the rods enables a treatment that is mathematically equivalent to an ideal gas. Similarly, the liquid state will be used to refer exclusively to the dense fluid that coexists with the vapor phase.
Entropy of SPOP-DAXX binding depends on the aggregation state
Since our theory is expected to apply equally to DAXX and cDAXX (DAXX495–740), in the remainder of the paper we will use the term DAXX unless specihcally referring to cDAXX. DAXX has five appreciable SPOP recognition motifs that can bind to the MATH domain on a SPOP monomer;23 four of these are located in pairs separated by 9 and 17 amino acids, respectively (Fig. 1C). Given the small separation, we assume that these pairs will bind cooperatively to both sites on a SPOP dimer giving DAXX an effective valence of two (neglecting the weak fifth binding motif). In the remainder of the paper, references to DAXX binding sites will refer to a pair of SPOP recognition motifs and a binding event will occupy both sites on a SPOP dimer.
We compute the free energy of a solution of M SPOP dimers. We divide these into three groups. N0 dimers are unbound, N1 are bound to a DAXX molecule that has a free second site, and 2N2 are bound to a DAXX molecule that binds a second SPOP dimer with its other binding site. Therefore M = N0 + N1 + 2N2 and the total number of DAXX molecules that are bound to SPOP is N1 + N2. The free energy of the system is
| (4) |
where ϵ > 0 is the free energy of a SPOP dimer binding to a DAXX binding site and μD is the chemical potential of DAXX (both scaled by kBT to make them dimensionless). Eq. 4 neglects DAXX-DAXX interactions. These can be included using a term proportional to (N1 + N2)2, which can be treated using a self-consistent mean-field approximation. However, this adds considerable complexity with minimal additional insight.
The difficulty in FM is calculating Ω, which is the number of ways to arrange the DAXX molecules on the binding sites. To do this, we use a method inspired by the Flory-Huggins lattice model,30,31 which yields (see Methods)
| (5) |
where z is a parameter describing the number of SPOP dimers within reach of a DAXX molecule bound with one site. Minimizing the free energy with respect to the site occupancies (see Methods) yields
| (6) |
and the site occupancies
| (7) |
| (8) |
| (9) |
where f = FM/kBT, ni = Ni/M, and c1D is the concentration of unbound DAXX. This treatment assumes that the DAXX chemical potential can be related to the translational entropy in the dilute state μD = ln c1D.
Double bound DAXX molecules are of particular interest because these are the molecules that crosslink the rods into a gel. n2 is a non-monotonic function of the DAXX concentration (Fig. 2a). At low DAXX concentrations nearly all bound DAXX molecules bind with both sites. However, as the number of free binding sites n0 vanishes, only single bound molecules fit. This puts a limit on the concentration range where crosslinking can occur.
Figure 2:
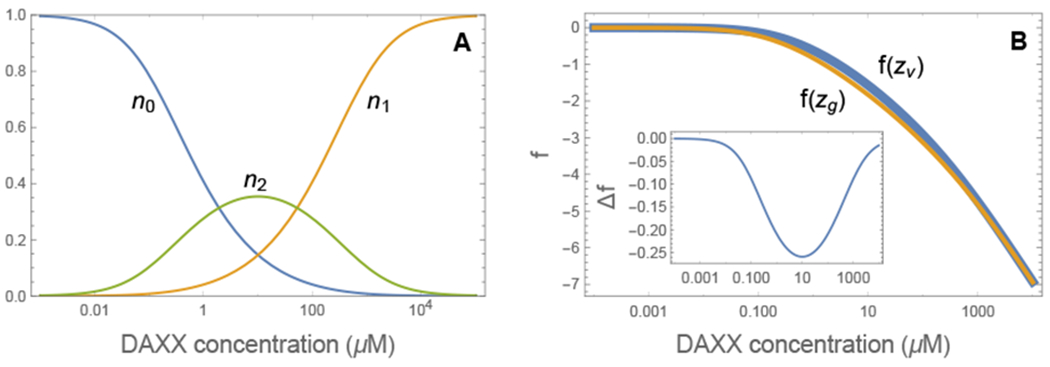
(A) Double bound DAXX molecules are only found in a limited concentration behavior of n2. At low DAXX concentration there is an abundance of free binding sites and most DAXX molecules are double bound. However, as the number of binding sites saturates, it becomes progressively harder to find a nearby second binding site. Eventually, all binding sites are filled with single bound DAXX. (B) Comparison of the free energy for two different binding site densities (zg = 2zv). The high density system is lower in free energy for values of c1D where DAXX is double bound. (inset) Free energy difference between the gel phase and the vapor phase.
The binding energy in the gel and vapor states is nearly identical since, in both cases, there are enough free sites for both binding sites on the DAXX molecules to bind. Instead, the free energy difference between the gel and vapor states arises from the increased entropy of arranging double bound DAXX on the SPOP sites, which is determined from the parameter z. From Eq. 6, the free energy change from the increased entropy is
| (10) |
where zg is the number of nearby binding sites in the gel state and zv ≃ 2Rg/DS is the number of nearby sites for a SPOP rod in the vapor phase, where Rg is the radius of gyration of the disordered region between DAXX binding sites and DS is the diameter of a SPOP dimer. The free energy difference (plotted in the inset of Fig. 2B) is small, on the order of 0.1 kBT per site. The contribution arising from the binding entropy is n2 ln(zg/zv), which accounts for nearly all of the free energy change. Δf vanishes at low and high DAXX concentrations where n2 is small. This limited range of attraction allows for re-entrant behavior similar to that seen for RNA condensation due to charge-charge interactions.32
Favorable DAXX-DAXX interactions lead to a liquid state
At high concentration DAXX condenses into a liquid state. This condensation is driven by a favorable interaction per molecule that we denote ϵD. When DAXX is mixed with SPOP, a rod of length L will acquire a layer of adsorbed DAXX. If we assume the double bound molecules are too constrained to participate in intermolecular interactions, ND = Ln1 DAXX molecules are available for liquid contacts. When this assembly enters a DAXX fluid, the attractive energy will be approximately NDϵD. This additive approximation is justified by the similar concentrations of the DAXX fluid and the DAXX condensed on SPOP (see density calculation below). This mechanism lowers the saturation concentration of the DAXX because SPOP scaffolds the formation of high molecular weight DAXX assemblies. Once again, this mechanism is not unique to the SPOP system as it has similarities to the condensation of RNA coated by intrinsically disordered proteins.33
Phase diagram can be computed using dilute solution affinity measurements
To compute the phase behavior of the system, we write down the chemical potentials for SPOP rods of length L (given by Eq. 3) in the vapor, liquid, and gel states
| (11) |
| (12) |
| (13) |
where cV and cL are the SPOP rod concentrations in the vapor and liquid phases, respectively. Each expression contains a term Lf accounting for the free energy of SPOP-DAXX binding. The vapor and liquid phases have terms for rotational entropy Frot, and translational entropy (scaled by a reference concentration c0). These contributions are neglected for the gel phase, which we expect to have solid-like ordering locally, even if it is disordered on longer length scales.23 Finally, the expression for the liquid contains a term for DAXX-DAXX interactions.
To mimic the crowded conditions of the cell, our experiments are conducted with added ficoll. This will enhance binding interactions, which is captured by the affinity parameters. It also introduces non-specific depletion interactions because the 5 nm equivalent radius of ficoll PM 70 is of the same order as the SPOP size.34 These specific and non-specific effects are difficult to disentangle under highly crowded conditions, so we employ a moderate ficoll concentration of 4% to promote phase separation without unduely enhancing non-specific effects. Eq. 13 neglects non-specific SPOP-SPOP interactions which can be added using a term proportional to L and the ficoll concentration. This omission results in minor qualitative shifts to the phase boundaries at 4% ficoll, but the depletion term is necessary to capture the larger changes at ~ 10% ficoll.
Eq. 11–Eq. 13 assume the average length of the rods follows Eq. 3 in all phases. While this is likely to be a safe assumption for the liquid and vapor phases, it is less clear that it is appropriate for the gel phase. In polymerizing systems the onset of a nematic phase, similar to the orientational ordering in the gel phase, results in a dramatic increase in the mean length.35,36 However, this is not expected to be a significant contribution to the phase behavior because the necessary correction to Eq. 13 due to end-to-end binding is an additive term on the order of ln cs. This is insignificant compared to the lateral binding term which scales with L. Furthermore, it is unclear that the arrested dynamics in the gel state would allow for the length distribution to substantially change on the experimental time scale. The equilibrium assumption underlying Eq. 13 should be valid for SPOP/DAXX binding (described by f(z)), but the reconfiguration of SPOP within the gel will be very slow due to the large number of DAXX crosslinkers limiting movement. We account for the arrest of SPOP dynamics by treating zg as an empirical parameter, rather than an equilibrium value.
We identify the quantity k2 = e2ϵ+ln(z) as the association constant for divalent SPOP-DAXX binding. This is the reciprocal of the dissociation constants reported in Fig. 3A (in the vapor phase) so k2v = (1.0 μM)−1. In the gel phase we have k2g = e2ϵ+ln(zg) or k2g = k2vzg/zv. Similarly, we identify the quantity with the association constant for DAXX bound to a single SPOP dimer. This was measured by deleting the BACK domain so that SPOP assembly is arrested at the dimer. From these measurements we find k1 = (10 μM)−1 in the presence of ficoll (Fig. 3B). Note that the use of experimental binding affinities ensures that contributions to SPOP/DAXX binding that are not explicitly included in the model, such as the conformational entropy of DAXX, are still accounted for. The SPOP polymerization affinity is in the absence of ficoll.25 The SPOP-SPOP interfaces exclude a larger volume to ficoll than the SPOP-DAXX interface, so it will be more strongly affected by ficoll. The latter affinity is enhanced by ln(17μM/10μM) ≃ 0.5kBT in the presence of ficoll. We find the best agreement with the experimental phase diagram when the SPOP-SPOP affinity is enhanced by 5-6 kBT, corresponding to . The other free parameters in the model are zg/zv and B, which have the effect of expanding and contracting the gel phase, respectively. Fig. 4 shows the phase diagram for zg = 2zv, B = 0.8 μM, and (equivalent to a 5.5 kBT ficoll effect).
Figure 3:
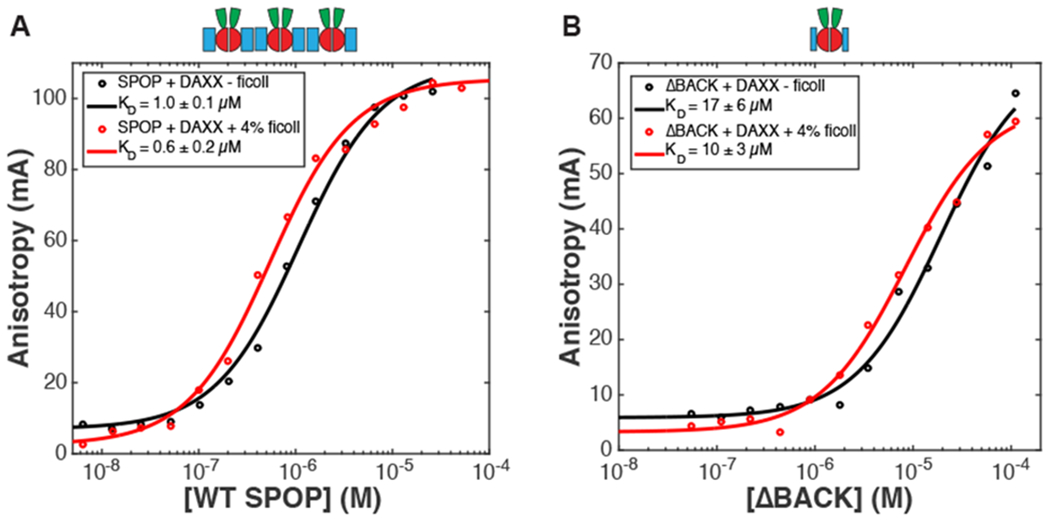
Binding curves in the presence and absence of ficoll. Representative fluorescence anisotropy direct binding curves of A) WT SPOP28–359 and B) SPOP ΔBACK28–337 from triplicate measurements with rhodamine-labeled His-cDAXX ±4% ficoll. Experimental data points are shown as circles, and non-linear least squares fits are shown as lines. Average KD values from triplicate experiments are reported in the legends, the errors represent standard deviations.
Figure 4:
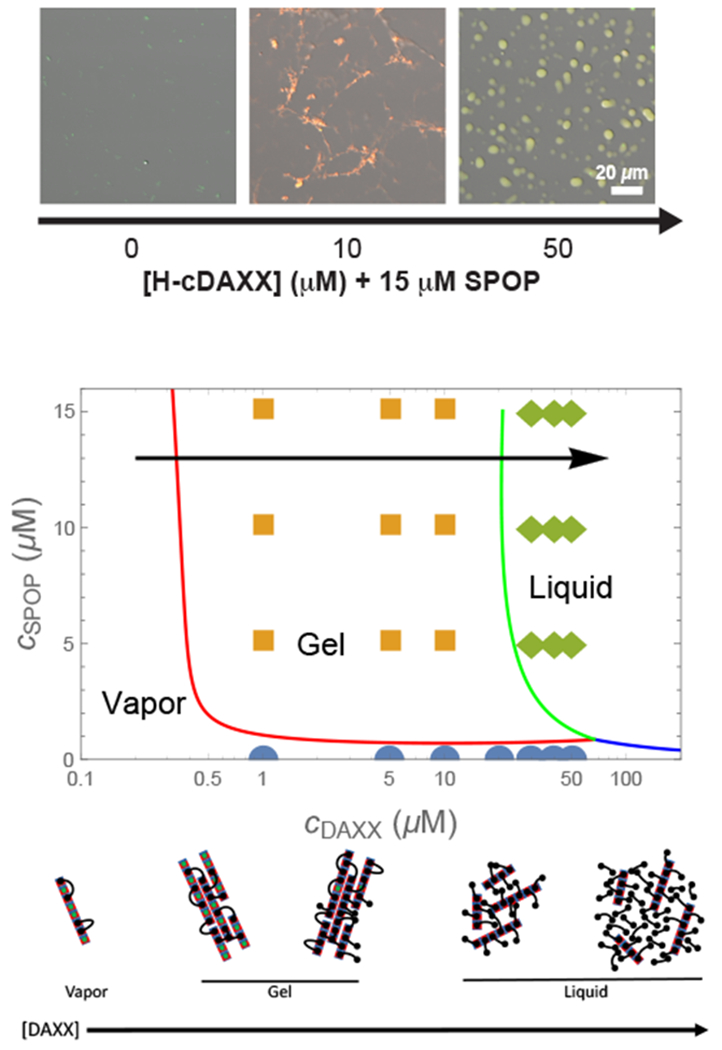
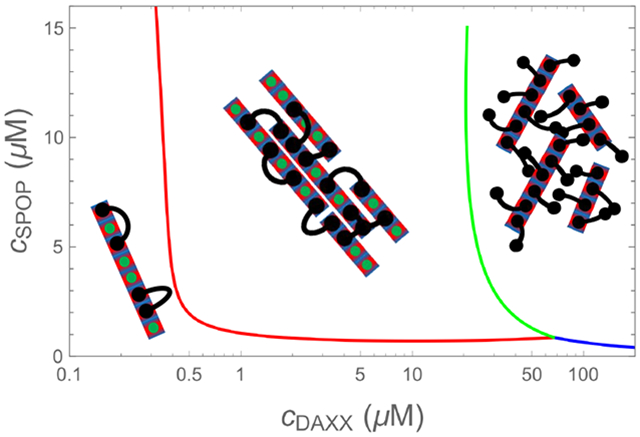
(top) Micrographs (fluorescence overlaid with DIG) of 15 μM SPOP solutions with increasing concentrations of cDAXX showing the vapor, gel, and liquid phases in 4% ficoll. (middle) Phase diagram calculated from Eq. 25, Eq. 26, and Eq. 28. Circles, squares, and diamonds indicate vapor, gel, and liquid phases observed experimentally.23 The calculation shows the behavior of SPOP assemblies and does not account for the pure DAXX fluid, (bottom) Cartoon of the progression of structures along the arrow in the phase diagram. At low DAXX concentration there are insufficient crosslinks to drive condensation and the SPOP assemblies are in the vapor phase. The gel is formed when the excess entropy of arranging the DAXX molecules is enough to offset the translational entropy of condensation. When the binding sites become saturated, double bound DAXX molecules become rare, however, the SPOP assemblies are still held together in the liquid phase by weak DAXX-DAXX interactions. Finally, at very high concentrations, DAXX monomers condense into a liquid that dissolves the SPOP assemblies.
Phase diagram shows a range of concentrations with a crosslinked gel state
The observed behavior is explained by the cartoons in the bottom panel of Fig. 4. At low DAXX concentrations the small enhancement in binding entropy is not sufficient to overcome the translational entropy loss of condensation, so the rods remain in the vapor phase. The gel appears when the increase in binding entropy is able to overcome this penalty. Although the benefit per molecule is small (Fig. 2B), the net gain can be substantial due to the large number of binding sites on the SPOP assemblies. Note that the high density of binding sites in the gel phase is possible because the rigid SPOP assemblies have a minimal conformational entropy penalty for stacking. This would not be the case for a molecule connected by flexible linkers instead of rigid polymerization interfaces.
As the SPOP sites saturate, the number of double bound DAXX molecules is insufficient to maintain the condensed state. This would lead to a return to the vapor state if not for the favorable DAXX-DAXX interaction. While these interactions are weaker than the SPOP-DAXX interactions, the SPOP assemblies are nearly saturated with DAXX and the collective effect of the DAXX interactions is enough to maintain a condensed, albeit liquid, state. At very high DAXX concentrations there is enough free DAXX to condense into droplets and the SPOP-DAXX assemblies will dissolve in the pure DAXX liquid.
This mechanism shows how the system can switch from a phase driven by the stronger SPOP-DAXX interactions to the weaker DAXX-DAXX interactions by altering the stoichiometry. The small difference in the binding affinities for binding to one vs. two SPOP dimers leads to a narrow range of parameter space where the crosslinked phase is possible (Fig. 2B), which allows for multiple phases to appear over accessible regions of parameter space.
Binding to SPOP increases the DAXX fluid density
To obtain an independent check that does not depend on free parameters, our model can be used to compute the protein concentrations in the dense phases. These concentrations can be compared to the experimental measurements at cs = 15 μM.23 At this concentration, the average length of SPOP rods is 50-100 dimers (Fig. 1). This implies a situation where the gel phase has a large number of crosslinks between adjacent rods that will relax very slowly to the equilibrium state of parallel aligned rods. Accordingly, microscope images of the gel phase show a disordered network with locally clustered filaments (Fig. 4 top panel). This is indicative that the SPOP concentration is determined by kinetic arrest. Using the measured SPOP concentration in the gel, csg as an input parameter, we can compute the expected concentration of DAXX within the gel. This is given by
| (14) |
where the factor of two comes from our assumption of cooperative binding to the dimer. Eq. 14 does an excellent job of predicting the DAXX concentration in the gel phase (Fig. 5, left of dashed line), which provides support for our assumption that pairs of SPOP recognition motifs bind cooperatively to SPOP dimers.
Figure 5:
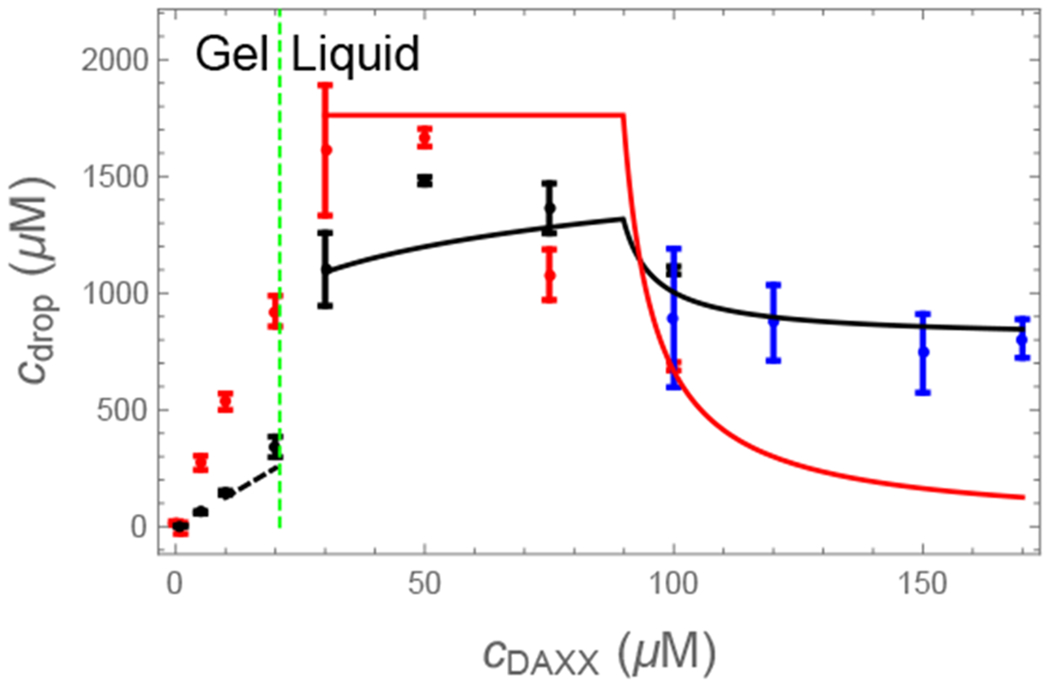
Experimental23 (points) and computed (lines) protein concentrations in the condensed phases. In the gel phase (left of the dashed line) the SPOP concentration is determined by a kinetic arrest of the network condensation. The cDAXX concentration (black) is given by the binding of cDAXX to this network (Eq. 14). In the liquid phase the SPOP (red) and cDAXX (black) concentrations (Eq. 32 and Eq. 33) are initially given by the excluded volume of the cylindrical SPOP-cDAXX assemblies (plateau region), before relaxing toward the values expected for a pure cDAXX solution (blue points).
As the DAXX concentration increases, the number of crosslinks declines and the system transitions to the liquid state. In the fluid state both SPOP and DAXX concentrations relax to their equilibrium values. These concentrations can be computed from the fraction of SPOP dimers occupied by DAXX molecules and the volume occupied by the brush-like SPOP-DAXX assembly as follows. At the onset of the liquid phase, there is very little free DAXX in the droplets so the SPOP concentration is given by , where Vb is the effective volume occupied by a SPOP dimer and the DAXX molecule bound to it. For a long SPOP rod, this volume is a disk with a thickness equal to the dimer diameter and a radius equal to the radius of gyration of DAXX. For the radius of gyration we use ~ 5 nm based on SAXS measurements (Fig. 6) and random coil estimates for the cDAXX length of 245 amino acids. If a SPOP monomer has a radius ~ 3 nm, this gives , in good agreement with the maximum SPOP concentration in the droplet (Fig. 5). The cDAXX concentration at the fluid onset is , also in good agreement with experiments. This is greater than the 800 μM concentration of pure cDAXX droplets.23 At greater DAXX concentrations, free DAXX will mix with the droplets. This will dilute the SPOP-DAXX assemblies, causing the SPOP concentration to drop steeply, while the DAXX concentration relaxes toward that of a pure DAXX fluid.
Figure 6:
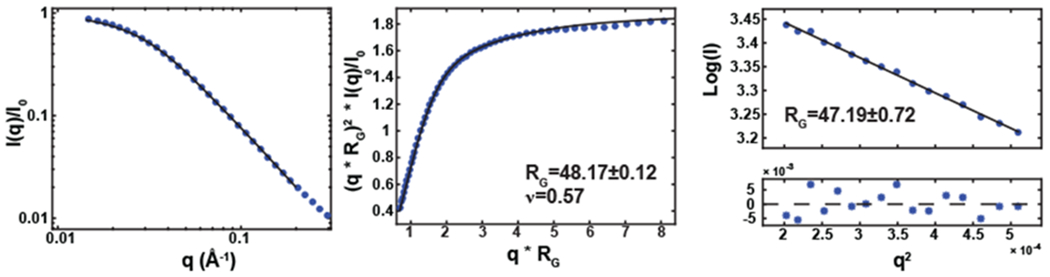
SAXS characterization of cDAXX. (A) Raw SAXS data of cDAXX, where I(q) normalized by the forward scattering, is plotted versus q, defined as q = 4π sin(2θ)/λ. Here, θ is the scattering angle and λ is the X-ray wavelength (~ 0.1 nm). Experimental data were logarithmically smoothed. Calculated scattering profiles from the empirically derived molecular form factor (MFF)37 (bottom) are overlaid as a solid line. (B) Raw SAXS data in normalized Kratky representation, logarithmically smoothed. Rg and n are a result from the fit to the empirical MFF (solid line). (C) Guinier transformation of the SAXS data. The black line is a linear fit to the Guinier equation with resulting Rg value; the residuals are shown below.
In the Methods section we derive formulas for the relative contributions of the pure DAXX fluid and the SPOP-DAXX brushes. These are compared to the experimental concentrations in Fig. 5. In the liquid phase (right of the dashed line) Eq. 32 and Eq. 33 describe a brush-dominated regime followed by a relaxation toward a pure DAXX fluid as more DAXX is added. This transition is somewhat more gradual than described by the theory indicating the recruitment of additional DAXX molecules to the droplet. This discrepancy is expected due to our neglect of DAXX-DAXX interactions in the assembly free energy (Eq. 4).
Discussion
We have developed an analytical theory that describes phase separation of the ubiquitin ligase component SPOP with its substrate DAXX. The SPOP-DAXX system has qualitative similarities to FUS condensates10 in that both systems form liquid droplets driven by interactions between intrinsically disordered proteins. However, the addition of the second component (SPOP) creates important differences in the phase behavior. First, SPOP provides a backbone that allows DAXX to effectively polymerize into a higher molecular weight entity. This increases the number of favorable contacts that can be formed and shifts the phase boundaries to lower DAXX concentrations. Secondly, the lack of a flexible linker between SPOP dimerization domains permits the formation of solid-like structures in which the movement of the rigid SPOP rods is very slow due to the large number of crosslinkers connecting them. The competing liquid and gel states serve as a kinetic switch, in which the system can toggle between slow and fast dynamics as a function of the molecule concentrations. This theory is transferable to other substrates. We have previously shown that, not only DAXX, but also AR undergoes phase separation via homotypic interactions and that binding to SPOP decreases its saturation concentration. The AR/SPOP system has similar behavior in that it forms a gel phase at lower AR concentrations and a dense liquid phase at higher AR concentrations. We speculate that our theory is applicable to additional SPOP substrates and potentially to other multivalent systems as well. The two condensed states may have implications for decisions to either sequester substrates in gel-like assemblies or turn them over in dense liquids.
Homeostasis requirements place severe restrictions on how living cells can control phase behavior. The system studied here shows several mechanisms that can be used instead of adjusting conditions like temperature, salt concentration, or the protein sequence. First, the effective valency can be controlled by the concentration of the molecules. Increasing the SPOP concentration leads to the assembly of larger scaffolds, while changing the DAXX concentration adjusts the number of crosslinking interactions. Secondly, the gel phase is only possible at intermediate DAXX concentrations, which makes it possible to select the phase assembled by the weaker DAXX-DAXX interactions by saturating the stronger SPOP-DAXX binding. Both phases leverage the effects of multivalency so that relatively weak interactions are sufficient to drive phase separation. However, this can leave the system prone to mutational effects because small perturbations are similarly amplified.
In conclusion, our results highlight the power of analytical theory to provide insight into the network structures of biomolecular condensates. Our work suggests that not all multivalent interactions result in the same network structures but that different protein architectures can encode different network structures and therefore likely different material properties and functions. Furthermore, switches between different types of assemblies are possible from changes in protein expression levels. We anticipate that network structures contribute to the specificity of condensate assembly and partitioning in cells. Different protein architectures require different analytical theories but once they have been devised they provide a powerful link between molecular descriptions and the long time and length scales that are characteristic of material properties.
Methods
Calculation of DAXX entropy
To calculate the number of ways to arrange SPOP-DAXX bonds, we start by placing the first site for each of the double-bound DAXX molecules. The number of ways to do this is M!/(N2!(M − N2)!). Next, we place the second binding site for each of these molecules. These sites are more restricted because they are constrained by the first bond. There are z possible sites within reach of each DAXX, however, we need to account for the probability that these sites are already occupied. For the placement of the first double attachment, N2 out of M sites are already occupied, so the probability that each of the z sites is available is (M − N2)/M. For the placement of the second free tail the probability the neighboring sites are free is (M − (N2 + 1))/M. Therefore, the number of ways of placing the second binding sites is
| (15) |
Finally, we need to place the N1 singly bound DAXX molecules among the remaining M − 2N2 sites leaving N0 sites unbound. The number of ways to do this is (M − 2N2)!/(N0!N1!). So the total number of ways to arrange the DAXX molecules is
| (16) |
which simplifies to Eq. 5.
Minimization of the gel free energy
With the above expression for the DAXX placement combinatorics and application of Stirling’s approximation, the free energy ( Eq. 4) can be written
| (17) |
where λ is a Lagrange multiplier that will be used to constrain the total number of sites. This can be re-written as
| (18) |
Where ni = Ni/M and
| (19) |
Minimizing the free energy with respect to the site occupancies yields ni = e−Ai, or
| (20) |
| (21) |
| (22) |
which can be expressed in terms of the concentration of unbound DAXX using the relation μD = ln c1D
Inserting Eq. 20–Eq. 22 back into Eq. 18 yields Eq. 6. Using Eq. 8 and Eq. 9 with the condition for the total number of sites, 1 = n0 + n1 + 2n2, gives a quadratic equation for n0 which yields Eq. 7 after selecting the root that gives n0 → 1 as c1D → 0.
Calculation of phase boundaries
The vapor-liquid phase boundary is determined from μℓ = μv. The quantities cV and cL appearing in Eq. 11 and Eq. 12 refer to the concentration of SPOP filaments in the vapor and liquid states. We would like to relate these quantities to experiments reporting the concentration of DAXX in the liquid phase. To do this we introduce the quantities cDV and cDℓ representing the concentration of bound DAXX in the vapor and liquid phases, respectively. These are related to the assembly concentrations by cDV = NDcV and cDL = NDcL, where ND = n1L is the number of single-bound DAXX attached to a SPOP rod. Equating the chemical potentials we have ln(cDV /c0ND) = ln(cDℓ/c0ND) + ϵDND or
| (23) |
The quantity in parentheses can be estimated from the phase separation of pure DAXX, in which case ND = 1. In the presence of ficoll the saturation concentration, , can be constrained by the absence of droplets at 75 μM and their appearance at 100 μM. The resulting droplets have a concentration cDL = 800 μM,23 therefore, eϵD ≃ 0.1. Using Eq. 1 for cV, the phase boundary is given by
| (24) |
| (25) |
The vapor-gel boundary is given by μv = μg which yields
| (26) |
The reference concentration and rotational entropy can be combined into a single parameter, B = c0e−Frot, which gives
| (27) |
The final phase boundary is obtained from μℓ = μg. Equating these chemical potentials we have
| (28) |
Equations Eq. 25, Eq. 27, and Eq. 28 are solved numerically to determine the phase boundaries. To do this, we require the concentrations of unbound SPOP and DAXX, which are obtained from Eq. 2 and c1D = cD − cs(n1 + n2), respectively.
Experimental Methods
Protein Purification
His-SUMO-SPOP28–359 (WT) and His-MBP-SPOP28–337 (ΔBACK) were expressed in auto-induction media38 and purified by Ni NTA affinity chromatography, TEV cleavage, another Ni NTA affinity chromatography (ion exchange for ΔBACK), and SEC chromatography as described before.25,28 His-cDAXX495–740 was expressed in LB medium and purified by Ni, ion exchange, and SEC chromatography as previously described.23 For SAXS measurements, the His-tag was cleaved with TEV protease at 4°C overnight before SEC. WT SPOP28–359 was labeled with Oregon Green 488 Carboxylic Acid, Succinimidyl Ester, and His-cDAXX495–740 was labeled with Rhodamine Red C2 maleimide, as previously described.23
Micrograph images
Samples were prepared with the designated concentrations of proteins, spiked with 0.5 μM fluorescently labeled protein as indicated, and 4% Ficoll 70. Coverslips were prepared and imaged as described before23 with a Nikon C2 laser scanning confocal microscope at 20x magnification on a (0.8NA) Plan Apo objective, using the same camera settings. Images were processed using Nikon NIS Elements software.
Measurement of binding affinities
All direct binding fluorescence anisotropy experiments were performed in 20 mM Tris pH = 7.6, 150 mM NaCl, 5 mM DTT, and 0.01% Triton X-100. Each SPOP construct was serial diluted 10-15 times (from 100 μM to 0.05 μM) into a 384-well plate containing 40 nM Rhodamine labeled His-cDAXX, and 4% Ficoll 70 when indicated. Anisotropy was measured using a CLARIOstar plate reader (BMG LABTECH). KD values were determined by fitting data points to the fraction bound equation for direct binding given by Roehrl et al. 2004,39 as described previously.23
SAXS
DAXX samples were prepared for SAXS measurements in a buffer containing 50mM Tris pH 8, 100 mM NaCl, 10 mM DTT and 2 mM TCEP. The buffer was exchanged over a Superdex 75 16/600 column (GE Life Sciences). Buffer was collected 1 column volume after elution for use as a buffer blank. Data was recorded in high-throughput via the mail-in program at the SIBYLS beamline 12.3.1 at the Advanced Light Source at Lawrence Berkeley National Laboratory.40 Data was recorded on a series of three dilutions (450, 225, 112.5 M) with matched buffer recorded before and after the dilution series. Data included 33 1 second exposures for each sample. All data that was determined to be statistically similar to the first exposure was averaged. For buffer, all 33 exposures were used. For DAXX samples, 12 exposures were used at the highest concentration and 20 exposures were used for the two lower concentrations. Buffer samples before and after the dilution series were identical and were averaged before subtraction. The peak at ~ 0.39 Å−1 associated with the Kapton window was used as a subtraction control. The two lower concentration samples perfectly overlaid and the data was merged to create the final scattering profile. Buffer subtraction, Guinier analysis and Kratky transformation was performed in Matlab (Mathworks). Final data was also fit to an empirically derived molecular form factor for unfolded proteins.37
Calculation of fluid density
We model the system as having three components, i) a fluid of brush-like SPOP-DAXX assemblies occupying a volume fraction ϕbrush, ii) a pure DAXX fluid occupying ϕDAXX, and iii) a vapor phase occupying ϕvapor = 1 − ϕbrush − ϕDAXX. The DAXX and brush phases are miscible but we treat them as separate for the moment.
Since the liquid phase is well removed from the vapor phase by the intervening gel phase, it is a good approximation to neglect the SPOP remaining in the vapor phase. Therefore the volume fraction occupied by the SPOP brushes is
| (29) |
The DAXX liquid volume fraction will be zero as long as the unbound DAXX concentration c1D is less than the saturation concentration for droplet formation . Once the unbound DAXX concentration exceeds this value, it will begin to accumulate in droplets with concentration cDL such that the remaining solution remains at a fixed concentration . This means that the unbound DAXX must satisfy which gives
| (30) |
The amount of unbound DAXX is given by
| (31) |
Since the brush liquid and the DAXX liquid are miscible, the protein concentration in the droplets is the weighted average of the two liquids
| (32) |
| (33) |
Table 1:
Association constants used in the calculations.
| Description | Symbol | no ficoll | 4% ficoll | Comment |
|---|---|---|---|---|
| SPOP polymerization | ks | (2.4 μM)−125 | 9.8 nM (6-16 nM) | (range consistent with expts) |
| Monovalent DAXX | eϵ | (17 μM)−1 | (10 μM)−1 | Measured using SPOP ΔBACK |
| Divalent DAXX (vapor) | e2ϵ+ln zv | (1.0 μM)−1 | (0.6 μM)−1 | Measured using WT SPOP |
| Divalent DAXX (gel) | e2ϵ+ln zg | (0.5 μM)−1 | (0.3 μM)−1 | Assumes zg/zv ≃ 2 |
Acknowledgements
JDS was supported by NIH Grant R01GM107487. T.M. acknowledges funding by NIH grant R01GM112846, by the St. Jude Childrens Research Hospital Research Collaborative on Membrane-less Organelles in Health and Disease, and the American Lebanese Syrian Associated Charities. We thank Melissa Marzahn for purifying SPOP mutants. Microscopy images were acquired at the St. Jude Cell & Tissue Imaging Center, which is supported by SJCRH and NCI (grant P30 CA021765). We also thank Victoria Frohlich and Jennifer Peters for technical help with microscopy. SAXS work was conducted at the Advanced Light Source (ALS), a national user facility operated by Lawrence Berkeley National Laboratory on behalf of the Department of Energy, Office of Basic Energy Sciences, through the Integrated Diffraction Analysis Technologies (IDAT) program, supported by DOE Office of Biological and Environmental Research. Additional support comes from the National Institute of Health project ALS-ENABLE (P30 GM124169) and a High-End Instrumentation Grant S10OD018483.
References
- (1).Shin Y; Brangwynne CP Liquid phase condensation in cell physiology and disease. Science. 2017, 357, eaaf4382. [DOI] [PubMed] [Google Scholar]
- (2).Banani SF; Lee HO; Hyman AA; Rosen MK Biomolecular condensates: organizers of cellular biochemistry. Nat. Rev. Mol. Cell Biol 2017, 18, 285–298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (3).Franzmann TM; Jahnel M; Pozniakovsky A; Mahamid J; Holehouse AS; Nüske E; Richter D; Baumeister W; Grill SW; Pappu RV; Hyman AA; Alberti S Phase separation of a yeast prion protein promotes cellular fitness. Science. 2018, 359, eaao5654. [DOI] [PubMed] [Google Scholar]
- (4).Rai AK; Chen JX; Selbach M; Pelkmans L Kinase-controlled phase transition of membraneless organelles in mitosis. Nature 2018, 559, 211–216. [DOI] [PubMed] [Google Scholar]
- (5).Nott TJ; Petsalaki E; Farber P; Jervis D; Fussner E; Plochowietz A; Craggs TD; Bazett-Jones DP; Pawson T; Forman-Kay JD; Baldwin AJ Phase Transition of a Disordered Nuage Protein Generates Environmentally Responsive Membraneless Organelles. Mol. Cell 2015, 57, 936–947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Riback JA; Katanski CD; Kear-Scott JL; Pilipenko EV; Rojek AE; Sosnick TR; Drummond DA Stress-Triggered Phase Separation Is an Adaptive, Evolutionarily Tuned Response. Cell 2017, 168, 1028–1040.e19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Muschol M; Rosenberger F Liquid-liquid phase separation in supersaturated lysozyme solutions and associated precipitate formation/crystallization. J. Chem. Phys 1997, 107, 1953–1962. [Google Scholar]
- (8).Wang Y; Lomakin A; Latypov RF; Laubach JP; Hideshima T; Richardson PG; Munshi NC; Anderson KC; Benedek GB Phase transitions in human IgG solutions. J. Chem. Phys 2013, 139, 121904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Li P; Banjade S; Cheng H-C; Kim S; Chen B; Guo L; Llaguno M; Hollingsworth JV; King DS; Banani SF; Russo PS; Jiang Q-X; Nixon BT; Rosen MK Phase transitions in the assembly of multivalent signalling proteins. Nature 2012, 483, 336–340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Wang J; Choi J-M; Holehouse AS; Lee HO; Zhang X; Jahnel M; Maharana S; Lemaitre R; Pozniakovsky A; Drechsel D; Drechsel D; Poser I; Pappu RV; Alberti S; Hyman AA A Molecular Grammar Governing the Driving Forces for Phase Separation of Prion-like RNA Binding Proteins. Cell 2018, 174, 688–699.e16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).Harmon TS; Holehouse AS; Rosen MK; Pappu RV Intrinsically disordered linkers determine the interplay between phase separation and gelation in multivalent proteins. Elife 2017, 6, e30294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (12).Vernon RM; Chong PA; Tsang B; Kim TH; Bah A; Farber P; Lin H; Forman-Kay JD Pi-Pi contacts are an overlooked protein feature relevant to phase separation. Elife 2018, 7, e31486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Hernández-Muñoz I; Lund AH; Van Der Stoop P; Boutsma E; Muijrers I; Verhoeven E; Nusinow DA; Panning B; Marahrens Y; Van Lohuizen M Stable X chromosome inactivation involves the PRC1 Polycomb complex and requires histone MACROH2A1 and the CULLIN3/SPOP ubiquitin E3 ligase. Proc. Natl. Acad. Sci. U. S. A 2005, 102, 7635–7640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Kent D; Bush EW; Hooper JE Roadkill attenuates Hedgehog responses through degradation of Cubitus interruptus. Development 2006, 133, 2001–2010. [DOI] [PubMed] [Google Scholar]
- (15).An J; Wang C; Deng Y; Yu L; Huang H Destruction of Full-Length Androgen Receptor by Wild-Type SPOP, but Not Prostate-Cancer-Associated Mutants. Cell Rep. 2014, 6, 657–669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (16).Janouskova H; El Tekle G; Bellini E; Udeshi ND; Rinaldi A; Ulbricht A; Bernasocchi T; Civenni G; Losa M; Svinkina T; Bielski CM; Kryukov GV; Cascione L; Napoli S; Enchev RI; Mutch DG; Carney ME; Berchuck A; Winterhoff BJN; Broaddus RR; Schraml P; Moch H; Bertoni F; Catapano CV; Peter M; Carr SA; Garraway LA; Wild PJ; Theurillat JPP Opposing effects of cancer-Type-specific SPOP mutants on BET protein degradation and sensitivity to BET inhibitors. Nat. Med 2017, 23, 1046–1054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Dai X; Gan W; Li X; Wang S; Zhang W; Huang L; Liu S; Zhong Q; Guo J; Zhang J et al. Prostate cancer-Associated SPOP mutations confer resistance to BET inhibitors through stabilization of BRD4. Nat. Med 2017, 23, 1063–1071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (18).Kwon JE; La M; Oh KH; Oh YM; Kim GR; Seol JH; Baek SH; Chiba T; Tanaka K; Bang OS; Joe CO; Chung CH BTB Domain-containing Speckle-type POZ Protein (SPOP) Serves as an Adaptor of Daxx for Ubiquitination by Cul3-based Ubiquitin Ligase. J. Biol. Chem 2006, 281, 12664–12672. [DOI] [PubMed] [Google Scholar]
- (19).Gan W; Dai X; Lunardi A; Li Z; Inuzuka H; Liu P; Varmeh S; Zhang J; Cheng L; Sun Y; Asara JM; Beck AH; Huang J; Pandolfi PP; Wei W SPOP Promotes Ubiquitination and Degradation of the ERG Oncoprotein to Suppress Prostate Cancer Progression. Mol. Cell 2015, 59, 917–930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Geng C; He B; Xu L; Barbieri CE; Eedunuri VK; Chew SA; Zimmermann M; Bond R; Shou J; Li C; Blattner M; Lonard DM; Demichelis F; Coarfa C; Rubin MA; Zhou P; O’Malley BW,; Mitsiades N Prostate cancer-associated mutations in speckle-type POZ protein (SPOP) regulate steroid receptor coactivator 3 protein turnover. Proc. Natl. Acad. Sci. U. S. A 2013, 110, 6997–7002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (21).Geng C; Kaochar S; Li M; Rajapakshe K; Fiskus W; Dong J; Foley C; Dong B; Zhang L; Kwon O-J; Shah SS; Bolaki M; Xin L; Ittmann M O’Malley BW; Coarfa C; Mitsiades N SPOP regulates prostate epithelial cell proliferation and promotes ubiquitination and turnover of c-MYC oncoprotein. Oncogene 2017, 36, 4767–4777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (22).Theurillat JPP; Udeshi ND; Errington WJ; Svinkina T; Baca SC; Pop M; Wild PJ; Blattner M; Groner AC; Rubin MA; Moch H; Priv GG; Carr SA; Garraway LA Ubiquitylome analysis identifies dysregulation of effector substrates in SPOP-mutant prostate cancer. Science. 2014, 346, 85–89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Bouchard JJ; Otero JH; Scott DC; Szulc E; Martin EW; Sabri N; Granata D; Marzahn MR; Lindorff-Larsen K; Salvatella X; Schulman BA; Mittag T Cancer Mutations of the Tumor Suppressor SPOP Disrupt the Formation of Active, Phase-Separated Compartments. Mol. Cell 2018. , 72, 19–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (24).Lin YH; Forman-Kay JD; Chan HS Sequence-Specific Polyampholyte Phase Separation in Membraneless Organelles. Phys. Rev. Lett 2016, 117. [DOI] [PubMed] [Google Scholar]
- (25).Marzahn MR; Marada S; Lee J; Nourse A; Kenrick S; Zhao H; Ben-Nissan G; Kolaitis R; Peters JL; Pounds S; Errington WJ; Priv GG; Taylor JP; Sharon M; Schuck P; Ogden SK; Mittag T Higher-order oligomerization promotes localization of SPOP to liquid nuclear speckles. EMBO J. 2016, 35, 1254–1275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (26).Semenov AN; Rubinstein M Thermoreversible gelation in solutions of associative polymers. 1. Statics. Macromolecules 1998, 31, 1373–1385. [Google Scholar]
- (27).Lin Y-H; Forman-Kay JD; Sun Chan H; Forman-Kay JD; Chan HS Theories for Sequence-Dependent Phase Behaviors of Biomolecular Condensates. Biochemistry 2018, 57, 2499–2508. [DOI] [PubMed] [Google Scholar]
- (28).Zhuang M; Calabrese MF; Liu J; Waddell MB; Nourse A; Hammel M; Miller DJ; Walden H; Duda DM; Seyedin SN; Hoggard T; Harper JW; White KP; Schulman BA Structures of SPOP-Substrate Complexes: Insights into Molecular Architectures of BTB-Cul3 Ubiquitin Ligases. Mol. Cell 2009, 36, 39–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (29).Errington W; Khan M; Bueler S; Rubinstein J; Chakrabartty A; Privé G Adaptor Protein Self-Assembly Drives the Control of a Cullin-RING Ubiquitin Ligase. Structure 2012, 20, 1141–1153. [DOI] [PubMed] [Google Scholar]
- (30).Flory PJ Principles of polymer chemistry; Cornell University Press, 1953; p 672. [Google Scholar]
- (31).Dill KA; Bromberg S Molecular Driving Forces: Statistical Thermodynamics in Chemistry & Biology; Garland Science, 2002; p 686. [Google Scholar]
- (32).Banerjee PR; Milin AN; Moosa MM; Onuchic PL; Deniz AA Reentrant Phase Transition Drives Dynamic Substructure Formation in Ribonucleoprotein Droplets. Angew. Chemie Int. Ed 2017, 56, 11354–11359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (33).Lin Y; Protter DS; Rosen MK; Parker R Formation and Maturation of Phase-Separated Liquid Droplets by RNA-Binding Proteins. Mol. Cell 2015, 60, 208–219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (34).Venturoli D; Rippe B Ficoll and dextran vs. globular proteins as probes for testing glomerular permselectivity: Effects of molecular size, shape, charge, and deformability. 2005. [DOI] [PubMed]
- (35).Kuriabova T; Betterton MD; Glaser MA Linear aggregation and liquid-crystalline order: Comparison of Monte Carlo simulation and analytic theory. J. Mater. Chem 2010, 20, 10366–10383. [Google Scholar]
- (36).Wensink HH Polymeric Nematics of Associating Rods: Phase Behavior, Chiral Propagation, and Elasticity. Macromolecules 2019, 52, 7994–8005. [Google Scholar]
- (37).Riback JA; Bowman MA; Zmyslowski AM; Knoverek CR; Jumper JM; Hinshaw JR; Kaye EB; Freed KF; Clark PL; Sosnick TR Innovative scattering analysis shows that hydrophobic disordered proteins are expanded in water. Science 2017, 358, 238–241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (38).Studier FW Protein production by auto-induction in high-density shaking cultures. Protein Expr. Purif 2005, 41, 207–234. [DOI] [PubMed] [Google Scholar]
- (39).Roehrl MHA; Wang JY; Wagner G A General Framework for Development and Data Analysis of Competitive High-Throughput Screens for Small-Molecule Inhibitors of Protein-Protein Interactions by Fluorescence Polarization . Biochemistry 2004, 43, 16056–16066. [DOI] [PubMed] [Google Scholar]
- (40).Hura GL; Menon AL; Hammel M; Rambo RP; Poole FL II; Tsutakawa SE; Jenney FE Jr; Classen S; Frankel KA; Hopkins RC; Yang S-J; Scott JW; Dillard BD; Adams MWW; Tainer JA Robust, high-throughput solution structural analyses by small angle X-ray scattering (SAXS). Nat. Methods 2009, 6, 606–612. [DOI] [PMC free article] [PubMed] [Google Scholar]


