Possibilities in the Application of Machine Learning on Bioimpedance Time-series

Abstract

The relation between a biological process and the changes in passive electrical properties of the tissue is often non-linear, in which developing prediction models based on bioimpedance spectra is not trivial. Relevant information on tissue status may also lie in characteristic developments in the bioimpedance spectra over time, often neglected by conventional methods. The aim of this study was to explore possibilities in machine learning methods for time series of bioimpedance spectra, where we used organ ischemia as an example. Based on published data on the development of the bioimpedance spectrum during liver ischemia, a simulation model was made and used to generate sets of synthetic data with different levels of organ-to-organ variation, measurement noise and drift. Three types of artificial neural networks were employed in learning to predict the ischemic duration, based on the simulated datasets. The simulated prediction performance was very dependent on the amount of training examples, the organ-to-organ variation and the selection of input variables from the bioimpedance spectrum. The performance was also affected by noise and drift in the measurement, but a recurrent neural network with long short-term memory units could obtain good predictions even on noisy and drifting measurements. This approach may be relevant for further exploration on several applications of bioimpedance having the purpose of predicting a biological state based on spectra measured over time.

Introduction

Analysis of the passive electrical properties of tissue (bioimpedance) can be challenging as the data is complex, the data amount can be large, methods of interpretation are vast, and the electrical properties often have a non-linear relation to the biological property of interest. Raw immittance data from bioimpedance measurements are typically presented as admittance, impedance or dielectric parameters, represented by real and imaginary components.

As the electrical properties of tissue always are frequency dependent (1), bioimpedance will typically be measured over more than one frequency, resulting in a set of a real and imaginary components for each frequency. Bioimpedance measurements are typically used to characterize the passive electrical properties of tissue and/or to investigate how the passive electrical properties of tissue change when influenced by biological processes. The overall aim can typically be to assess tissue state or level of pathological change related to situations where there is a clinical need for improvement (2-4).

The origin of the passive electrical properties of the tissue is the combination of structures and liquids that form the tissue. Ionic conduction in the tissue liquids contribute to the resistivity, while membrane structures contribute to the reactive properties (capacitive) (1). The relationship between the biological processes and changes in the passive electrical properties are rarely completely stationary and linear, reaching either a saturation level or changing in direction as the process evolves (4-8). This non-linearity and “change-in-direction” lead to the possibility that the value of electrical parameters changes at different rates and overlap at different time durations of biological processes, making the ability to discern the state of the tissue dependent on memory and the historical development of the parameters.

For example, during ischemia, there are a series of factors that individually contribute to either decreasing or increasing impedance at a frequency range. The sum of these effects typically results in a time development of electrical parameters during ischemia where there is in an early increase in impedance, before the impedance starts to decrease well beyond the initial values (7, 9, 10).

Reperfusion of tissue and the associated changes in electrical properties adds further complexity with respect to the time-development of bioimpedance and ischemia. The changes in bioimpedance related to reperfusion can be overlapping or larger than the changes caused by ischemia (11), dependent on the previous duration of ischemia and the ischemic tolerance of the organ.

Over the years a variety of approaches have been used with respect to presentation, modelling, and analysis of time series of bioimpedance data (figure 1). Modeling approaches such as fitting the data to electrically equivalent circuits and interpreting the data in this context are preferred approaches in gaining understanding of the reflection of tissue processes through bioimpedance. Machine learning methods also generate models, but they are generally very complex having the so-called “black-box” disadvantage, where the interpretation of the relation between variables becomes difficult.

Figure 1.

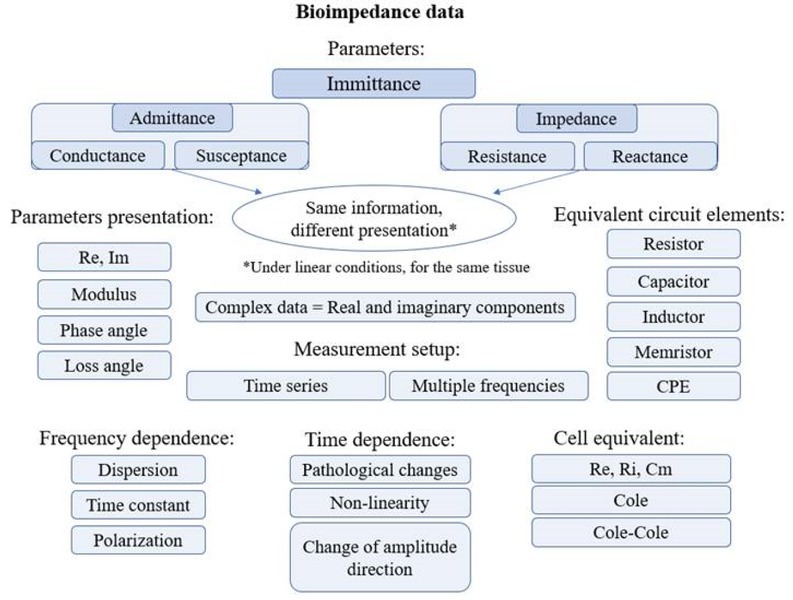
An overview over typical ways to present bioimpedance data, showing the level of complexity within the realm of presenting and analyzing bioimpedance data.

The advantage in machine learning methods is the possibility of learning generalizable predictive patterns in combining variables in a non-linear fashion, possibly increasing the predictive performance compared to simpler models. In addition, machine learning can be used to perform automatic feature extraction, useful when there is a lot of variables (e.g. different immittance parameters over many frequencies) and the important ones are not known. In some cases, such as clinical monitoring, the prediction performance is more important than drawing inference from the data or could be the next focus in technological development following statistical modeling and interpretation.

We believe that for bioimpedance, the possibilities in methods of analyzing non-linear dependencies could be further explored. To quote Gheorgihu et al. “a breakthrough might be provided by (non)linear analysis of the evolution of dispersion amplitudes and related time constants of distinct experiments…” (12).

A recent study from our group demonstrated promising results using a machine learning approach for classification of the grading of ischemic damage to the small intestine based on bioimpedance measurement (13). In particular, a recurrent neural network (RNN) with long short-term memory (LSTM) units obtained high classification accuracies using repeated measurements over several hours, suggesting that this type of machine learning approach may be useful in a wider sense for bioimpedance time series problems.

In this study we investigate the use of methods in machine learning for analysis of bioimpedance measurements with characteristic time-dependencies, with the aim of assessing the potential in predicting a biological event under conditions where conventional methods would be inadequate. This approach may advance the possibilities in fully utilizing the information within the bioimpedance spectra recorded over time.

Materials and methods

In order to assess the aim in a controlled way, and to investigate how the performance of these machine learning methods depend on different conditions such as the amount of training data, noise in the measurement and hyperparameter settings for the neural network training, we used a simulation approach based on the time development of bioimpedance data from ischemic liver (12). The simulations were implemented in the following way (overview shown in Figure 2):

Figure 2.

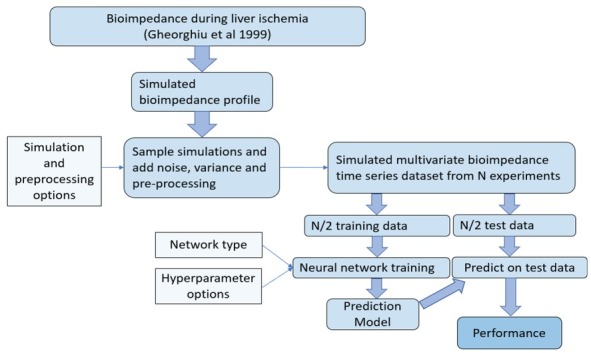
Overview of the methodology used for investigating the performance of different neural networks for predicting duration of ischemia based on bioimpedance using simulated measurements.

• Simulate the bioimpedance profile during ischemia based on the literature (12)

• Use the simulations to generate synthetic bioimpedance time-series datasets with different degrees of noise, drift and organ-to-organ variation

• Use half of each dataset to train machine learning models to predict the duration of ischemia based on bioimpedance, using different learning options

• Predict ischemic duration on the other half of each dataset and calculate the prediction error for all simulated cases and learning options

• Assess the performance of machine learning for predicting ischemia duration based on different datasets of bioimpedance time-series and how this performance depends on selected learning options.

Details on the simulations of bioimpedance profiles, generation of datasets and the neural network training and prediction are given in the following chapters.

Simulation of bioimpedance spectra during liver ischemia

Gheorgiou et al. described the evolution of bioimpedance spectra during the course of ischemia in heart and liver tissue (12). Based on this publication, we employed a two-compartment Cole model and approximated the Cole parameters and their changes over time according to the published data, creating synthetic data resembling the reported measurements.

This was used as a simulation model for the bioimpedance profile during liver ischemia in order to generate example data for this study. We selected to model the evolution of bioimpedance spectra during the course of ischemia in liver tissue (12), as the data follows a typical time development with both non-linear and “change-in-direction” effects (7). These typical changes present challenges for more traditional methods of data analysis.

Figure 3 shows an example of changes in resistance and reactance during liver ischemia based on the approximated model. Using the simulation model, larger amounts of data could be generated for the evolution of bioimpedance during up to 7 hours of ischemia at a selected range of frequencies. In order to produce interindividual differences among livers, an adjustable degree of randomness was included in the Cole parameter baselines and their change over time (adding a selectable percentage of the parameter value times a random Gaussian value).

Figure 3.

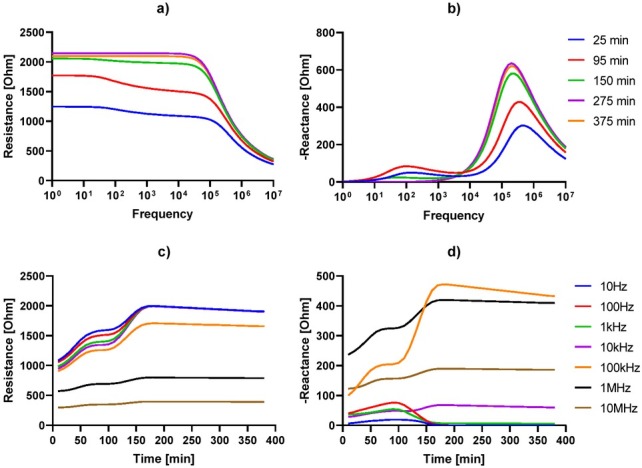
Simulated liver resistance and reactance profiles during ischemia.

As bioimpedance measurements often contain both noise and drift in the realistic environment, this was also added to the simulations at adjustable levels. Noise was simulated by adding white Gaussian noise at selected power levels to the measurement, while drift was simulated by adding a constant linear change over time, by a random magnitude with an adjustable maximum, simulating e.g. changes in a series resistance (such as electrode polarization impedance) over time.

In order to make the dataset more realistic with respect to continuous monitoring, the simulations were done with a random onset of ischemia for each liver, also including pre-ischemia measurements with baseline differences, noise and drift in the data. Control livers without ischemia were simulated with the same noise, drift and liver-to-liver variation, but without an onset of ischemia. Figure 4 shows an example simulation of the resistance and reactance from five ischemic livers and five control livers at one frequency, including noise in the measurement.

Figure 4.

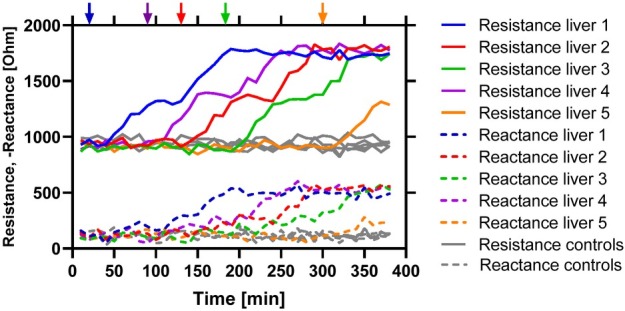
Example of simulated resistance and reactance data at 100kHz for five livers (in colors) having random onsets of ischemia (marked with arrows). Five non-ischemic control livers are added in gray. The data are simulated with a 5% liver variation, no drift, and a noise level of 30 dBW.

Training of artificial neural networks

Two different types of ANN were tested and compared in the study: Feedforward neural network (FNN) and a recurrent neural network (RNN) with short-term memory (LSTM) units. FNN is the first type of ANN invented and has no feedback connection and does not keep memory of previous time steps in a controlled way. The LSTM network on the other hand has a particular architecture that allows learning with memory over arbitrary time intervals.

For the FNN, we used a simple architecture of an input layer, a fully connected layer and an output regression layer. The LSTM network was composed of a sequence input layer, one or two LSTM layers, a fully connected layer of equal layer size as the LSTM layer(s), and a regression output layer. The hyperbolic tangent (tanh) function was used as activation function for the nodes in the hidden layers. See e.g. (14) for a thorough introduction to neural networks and their architectures.

Using the simulation model, different datasets were generated for different simulation parameters (i.e. noise, drift and liver-to-liver variation). In addition to the options in simulating the bioimpedance measurement, options for the input variable selection and machine learning hyperparameters were included. Different sizes of the dataset were generated (N=20 and N=100 training examples), having an equal amount of ischemic and control examples. Datasets were generated for different selections of frequencies from the impedance spectra, from 3 up to 70 frequencies ranging from 10 Hz to 10 MHz.

In training neural networks, the learning process can be very dependent on the selection of hyperparameters (adjustable meta-parameters not learned in the training process). As hyperparameters assessed in this study, we included the regularization (controlling shrinkage of model coefficients towards zero in order to prevent overfitting), the hidden layer size (number of nodes) of the neural network (i.e. the complexity of the model) for both the FNN and LSTM networks. Being a more complex type of network, two additional hyperparameters were assessed for the LSTM networks: the minibatch size (controlling a split in the training dataset used in error calculation and updating of model coefficients during training of the LSTM network) and the number of epochs (i.e. iterations) used in the model training. The learning rate parameter (degree of network weight adjustment with respect to estimated error during training) was set constant to 0.01. For more on hyperparameters in machine learning, see e.g. (15). Table 1 shows a complete list of all cases compared in the study. Ten replications of each case were run in order to better estimate the typical performance and its variability. A total of 1080 datasets were generated, using 24 different hyperparameter setting in two/three different ANN architectures, totaling 77760 ANN models that was trained using a supercomputer (Abel) at the University of Oslo (see acknowledgements).

Table 1.

List of all variables used for comparing different varieties of the bioimpedance input data and hyperparameters in the machine learning for prediction of ischemic duration.

Variable	Description	Tested levels	Values
Measurement noise	Setting for simulated input data	3	0, 10, 30
Liver variance	Setting for simulated input data	2	5, 20
Drift	Setting for simulated input data	3	0 ±50 +100
Frequencies	Selection of input variables	3	{102 104 106}, 101:7, 101:0.1:7
Sample size	Training and testing data size	2	20, 100
Regularization	Neural network hyperparameter	3	10-1, 10-2, 10-3
Hidden layer size	Neural network hyperparameter	3	2, 5, 25
Minibatch size	Neural network hyperparameter	2	16, 32
Epochs	Neural network hyperparameter	2	250, 500

Each dataset was split half-half into a training set and test set. No preprocessing was done on the data except for mean centering and standardization of the bioimpedance predictors using the total means and standard deviations of the training data partition (means and standard deviations of the training data was also used to center and standardize the test data). Applying the trained model on the test data, predictions of ischemic duration were made for each test data sequence. Performance for each case was assessed by calculating the root mean square error of prediction (RMSEP) for each liver and taking the mean RMSEP over all livers in the test dataset.

Ethical approval

The conducted research is not related to either human or animals use.

Results

The simulation results show that accurate predictions of ischemic duration was possible to obtain using the recurrent neural networks with one and two LSTM layers, outperforming the FNN network. As shown in Figure 5, the prediction performance was strongly dependent on the conditions for the simulated datasets, such as the number of training examples and the liver-to-liver variance, and to a lesser degree the drift and noise in the measurement.

Figure 5.

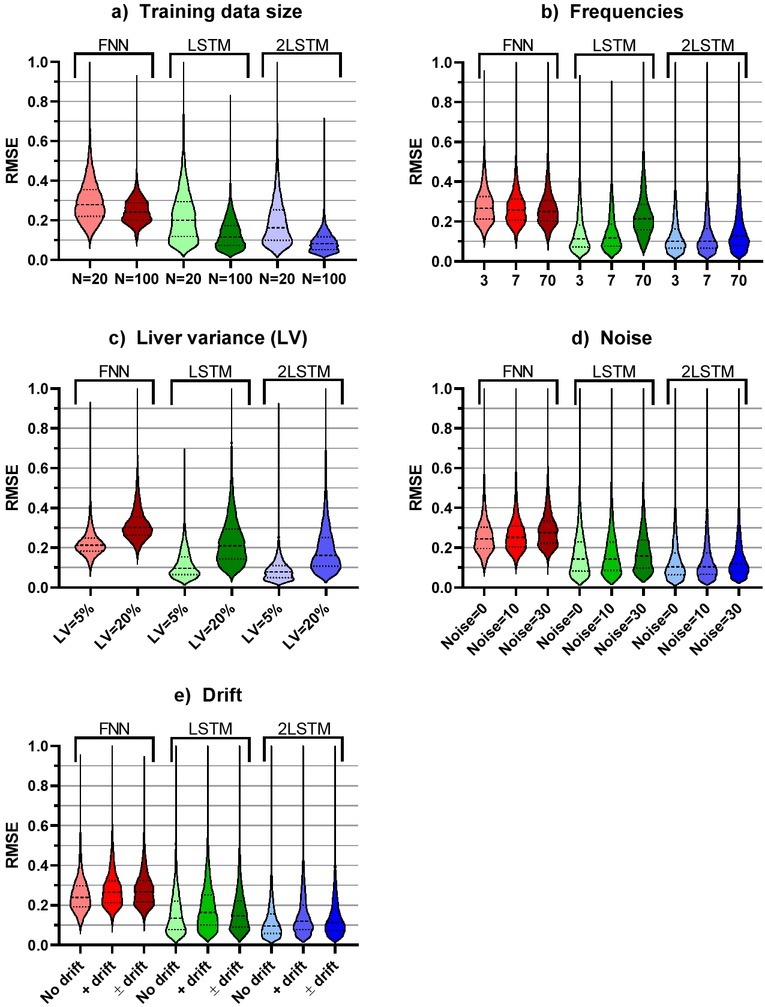
The distribution of prediction accuracies according to the different levels of cases included in the simulated data. The distributions are shown as violin plots with medium smoothing, where the dashed and dotted lines show the median and quartiles respectively.

As expected, the lowest prediction error for FNN, LSTM and 2LSTM was obtained for simulated datasets with a large number of training examples, a small liver-to-liver variance and no noise or drift in the measurement. Table 2 gives an overview of the best prediction performance that was obtained for the three ANN architectures, according to selected combinations of simulation variables representing three levels of difficulty in the dataset.

Table 2.

Comparison of prediction performance for the different ANN architectures in three different cases of difficulty based on the liver-to-liver variance, noise and drift in the measurement. The selection of input frequencies and hyperparameters for the best prediction performance of the different ANN architectures is provided in the rows below the prediction performances. The last row presents the best prediction performance when all 70 frequencies are used as input to the ANN. RMSEP=root mean square error of prediction, RMSEC=root mean square error of calibration, both having units of ischemia duration in hours.

Case	Easy			Medium			Hard
Liver variance	5 %			5 %			20 %
Noise	0			10			30
Drift	0			100			100
Drift direction	None			Increasing			Both
Training examples	100			100			100
Best performance	FNN	LSTM	2LSTM	FNN	LSTM	2LSTM	FNN	LSTM	2LSTM
Mean RMSEP	0.124	0.016	0.017	0.173	0.029	0.026	0.256	0.079	0.066
Std RMSEP	0.025	0.003	0.009	0.044	0.003	0.012	0.044	0.013	0.015
Mean RMSEC	0.112	0.014	0.015	0.175	0.026	0.021	0.256	0.037	0.038
Std RMSEC	0.029	0.005	0.007	0.029	0.006	0.009	0.029	0.006	0.018
Frequencies	70	3	7	70	7	3	70	3	3
Hidden layer size	25	25	5	5	5	25	2	25	25
l2 regularization	0.1	0.001	0.001	0.001	0.001	0.001	0.001	0.001	0.001
Training epochs	NA	500	500	NA	500	500	NA	500	500
Minibatch size	NA	32	32	NA	32	32	NA	32	16
Mean RMSEP (freq=70)	0.124	0.056	0.022	0.173	0.073	0.035	0.256	0.142	0.106

Scatterplots of these cases are shown in Figure 6. For data with low liver-to-liver variation and without noise and drift, predictions of useful performance could be obtained for FNN, and very accurate predictions were obtained for the LSTM networks. Adding noise and drift to the simulated data, the FNN was struggling to follow the ischemic duration after 2-3 hours, while the LSTM networks were able to provide a linear increase very close to the identity line. Increasing the liver-to-liver variance to 20%, the noise to 30 dBW and allowing drift in both directions, the prediction error was substantially larger for all ANN types, but both the LSTM predictions were still well within a useful accuracy level up to 6 hours of ischemia.

Figure 6.

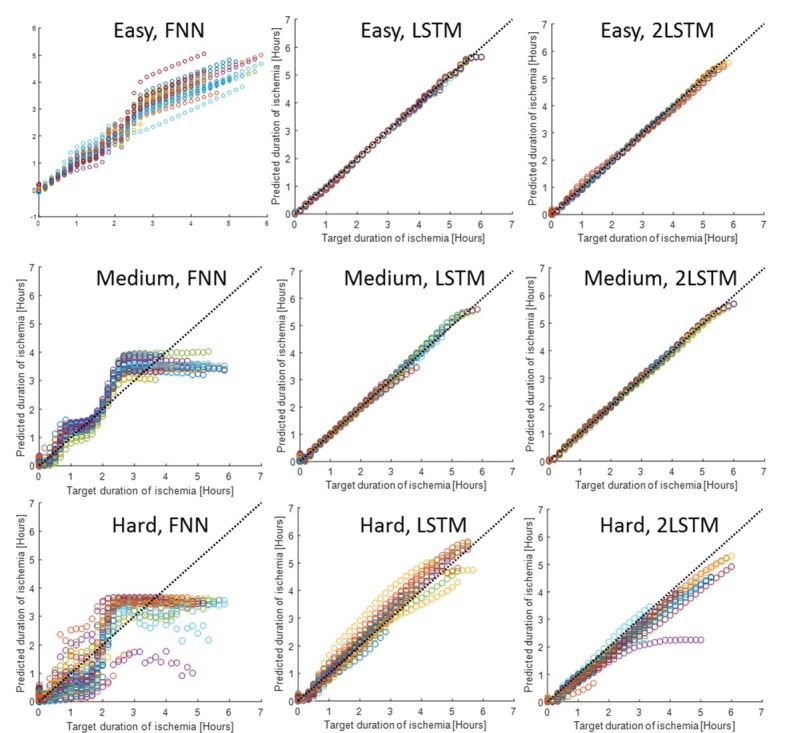
Predictions on 50 examples of liver ischemia and 50 controls from the test data for the different cases presented in table 2. Colors indicate different livers.

With respect to the selection of input variables, the results in table 2 show that including all available frequencies as variables might not always provide the best learning of the prediction model. The FNN provided best prediction performance with all 70 frequencies as input, while the LSTM provided superior prediction using only three or seven frequencies. The number of input variables should be considered in context with the hyperparameters of model training, as they all relate to model complexity. The best performing FNN models use 70 input frequencies, but the complexity is reduced by either a low hidden layer size or increased l2 regularization. The LSTM network seems to favor a much-reduced selection of frequencies for optimal model training, but with a more complex hidden layer model configuration (i.e. 25 nodes in the hard case). Models with higher complexity by using all frequencies as inputs, using 25 nodes in the hidden layer(s) and without increasing l2 would increase overfitting (0.027, 0.088 and 0.076 mean RMSEP minus mean RMSEC for the hard case of FNN, LSTM and 2LSTM respectively). With fewer training examples (N=20 instead of 100), these overfitting values would increase to 0.195, 0.262 and 0.259.

For the case of fewer training examples (N=20, 10 ischemic + 10 controls), good predictions (RMSEP<0.1) were not attainable for the hard case by any model. For the medium case, the single- and double layer LSTM models could obtain predictions with an RMSEP of 0.076 and 0.067 respectively, of comparable performance to the hard case predictions of these models. Good prediction was not obtainable for the FNN even in the easy case (best RMSEP=0.162) with N=20. The best performing model on the medium case data with N=20 (the double layer LSTM), used three input frequencies, 25 nodes in the hidden layers and was trained with l2=0.001, a minibatch size of 32 and over 250 epochs.

Discussion

The results indicate that LSTM-RNN is a relevant tool for analysis of bioimpedance time series. LSTM-RNN outperformed the FNN with the “easy” data category and excels even more when comparing performance with reduced data quality. The performance of FNN was inferior to the LSTM-RNN for these time-series data, and the difference in performance between the single and double-layer LSTM-RNN was small. Even for cases with high degrees of noise, drift and liver-to-liver variation, LSTM-RNN models could predict the duration of ischemia accurately, given that enough training examples were used.

The LSTM networks outperformed the FNN even in the cases free from noise and drift. The likely explanation for this difference lies in the memory property of the LSTM network, allowing information from previous observations to be included in predicting the current state.

The simple FNN deals well with nonlinearities in the relation between predictors (i.e. the bioimpedance spectrum) and target (i.e. a tissue status marker) but has no means to deal with nonlinear dependencies over time, such as overlapping predictor values at different targets of ischemic duration.

It can be seen from figures 3c and 3d that both the resistance and reactance had overlapping values at different times, e.g. resistance at around 150 and 350 minutes, and low-frequency reactance at around 50 and 120 minutes. Unless the bioimpedance at other frequencies offers information that can be used to differentiate between these time targets, the FNN will struggle to discriminate between them.

This is in agreement with the FNN predictions flattening out after around 2.5 hours in the scatter-plots shown in Figure , and also explains why the most predictive FNN models include a large selection of input frequencies. Inspecting Figure further, the prediction at around the 2h point seems to be most accurate, in particular for the FNN. Comparing with the bioimpedance profile in Figure 3, this is not surprising, as this is the point when most changes are occurring for all frequencies. The FNN would perform well in classifying livers before versus past this point in ischemic development.

It is important to note that this study is not a technical comparison between the FNN and LSTM network architectures, but rather an investigation on the possibilities in machine learning methods on time series of bioimpedance spectra. What our results mean is that learning of time-dependencies (by the LSTM recurrent neural network) provides good predictions of a biological event in our example, where machine learning without taking into account the changes over time (the FNN) were inadequate.

In this study, the ischemic liver was used as an example for investigating possibilities in applying new methods in machine learning on bioimpedance time-series. Nevertheless, this example might have some relevance for clinical application. Liver transplantation is a very successful treatment for a series of liver diseases, but the demand is higher than the supply (16). As per the “British Transplantation Society UK Guidelines for donors after circulatory death”, livers from donors are classified according to a set of criteria, among them “functional warm ischemic time” (FWIT) and “cold ischemic time” (CIT).

The classification of marginal donors includes the criterion of FWIT 20-30 min and CIT 8-12 hours (17). While the time-development of the passive electrical properties in tissue during CIT are different than during FWIT, when employing bioimpedance measurement with online implementation of such a method, there is a possibility of predicting ischemic duration with high accuracy, reducing the uncertainty with respect to donor liver quality.

Based on the conditions included in the simulations, the sets of frequency selections and the range of hyperparameters assessed, the LSTM-RNN stands out as the most suitable network for this problem in general. The difference between one and two LSTM layers is small, and the most important consideration seems to be the reduction in input frequencies. As bioimpedance spectra are highly correlated between close frequencies, a large degree of variable redundancy is indicated for the set of 70 frequencies. Inspecting figure 5b, the one-layer LSTM network performance is more affected by this variable redundancy than the two-layer LSTM network. The prediction performance of the LSTM network is worse when using all 70 frequencies as input variables (see Table 2), but interestingly, the performance of the two-layered LSTM network is not changed nearly as much when all 70 frequencies are used as input. This could be due to a filtering effect of the first LSTM layer in the stacked LSTM configuration working as an automatic feature extractor, which could be a favorable property in this application, in particular if the most informative frequencies are not known. The two-layer LSTM network therefore seems to be best suited for this problem in general, ideally using bioimpedance at a few selected frequencies as predictors. In addition, good performance was obtained from this network when trained on fewer examples. With respect to the hyperparameters, they should be tuned through validation strategies as part of the model development (see e.g. (18) for recommendations on hyperparameter tuning). Only a few selected simulation cases, ANN architectures and hyperparameters were assessed in this study in order to get an idea of their influence, but the options for further refinement under different conditions are limitless.

To our knowledge, this is the first study to investigate the general application of recurrent neural networks on bioimpedance time-series. While we do not aim to exhaustively assess the myriad of possibilities and methods within the realm of machine learning, we do intend to cast light on possibilities with neural network architectures for time-series data of bioimpedance. A recent study in our group compared the accuracy of using FNN, versus the accuracy when using LSTM-RNN with classification of intestinal viability following ischemia/reperfusion and found that accuracies in the range of what has been reported clinically can be achieved using FNN’s on a single bioimpedance measurement, and higher accuracies can be achieved when employing LSTM-RNN on a sequence of data history (13).

With respect to the input parameters used to model the bioimpedance data, there are a total of 3888 cases when including all combinations of parameters. In order to represent how the quality of the datasets affect prediction and what models and parameters can improve the accuracy, we chose to present 3 scenarios (easy, medium, hard), where easy represents a dataset with very clean measurements (no noise, drift and small variation between livers).

There are a series of causes that can reduce the quality of bioimpedance measurements causing drift and/or noise. Among these are stray properties of the instrumentation and electrode setup (1), electrode polarization impedance (19), geometric effects including compression/movement of tissue (20). While efforts typically are made to reduce or compensate for error sources, they can be hard to avoid completely. The levels of drift and noise that were included in the model are not meant to be exhaustive but are meant to represent what can be experienced in real-life measurements, with the main purpose of studying how measurement drift and noise influences the performance in ANN learning of patterns in bioimpedance time series.

The simulated data are obviously not accurately representing true measurements, including simplifications and assumptions on modeling, measurement and stochasticity. However, this approach allowed us to generate synthetic datasets with control of specific settings, which we could use to study the performance of machine learning approaches under different conditions in order to gain an idea of limits and possibilities of the method applied to bioimpedance time-series, and an indication of the most suitable machine-learning algorithm.

The obtained prediction performance values are also very dependent on the simulation conditions, which could differ from real measurements during ischemia on the true population of livers. The simulation is based on published data representing only one liver, and the variation between livers could be different from the simple assumptions made in this study. The level of prediction performance (i.e. the RMSEP values) should therefore not be regarded as an indication of e.g. clinical performance level, but rather offer a suggestion of methods having potential for use in studies on real data.

The “black-box” problem is a drawback of most machine-learning approaches, often making such approaches unattractive when we want to understand all variable associations. In such cases, using modeling approaches such as Cole parameterization and statistically studying the time-course of their development is more appropriate. However, if the goal is to try to develop the best possible prediction model, then this machine-learning approach may offer advantages. In addition to the possibility of a better prediction performance, this approach requires no preprocessing of the raw measurement data except for centering and scaling for optimal model training.

This approach may be relevant to several types of bioimpedance measurement with the purpose of predicting a biological state. In many cases, the temporal information from continuous measurements over time might not be fully utilized by conventional methods. In addition to organ ischemia, examples of a few other bioimpedance applications where this method could be relevant is cell culture monitoring (21), wound healing (22), meat quality assessment (23), needle guidance (24) and analysis of periodical bioimpedance signals related to respiration (25) or pulsation (26) or their morphology.

While the example in this study has been on a regression problem, this method is easy to convert into a classification problem. In the case of the LSTM-RNN, the final layer (regression layer) is replaced by a softmax layer followed by a classification layer.

In conclusion, this study has demonstrated new possibilities in predicting biological states or events based on bioimpedance time series, by employing a recurrent neural network with LSTM units. On simulated data of bioimpedance during liver ischemia, the duration of ischemia could be accurately predicted by this method, even in cases of large liver-to-liver variation, measurement noise and drift. The performance of the method is very dependent on the number of examples used in training of the prediction model, and the proper selection of input variables from the bioimpedance frequency spectrum. This approach is particularly relevant for non-linear time dependencies in the relation between bioimpedance and the biological process of interest.