MAXIMUM LIKELIHOOD ESTIMATION OF GAUSSIAN COPULA MODELS FOR GEOSTATISTICAL COUNT DATA

Abstract

This work investigates the computation of maximum likelihood estimators in Gaussian copula models for geostatistical count data. This is a computationally challenging task because the likelihood function is only expressible as a high dimensional multivariate normal integral. Two previously proposed Monte Carlo methods are reviewed, the Genz–Bretz and Geweke–Hajivassiliou–Keane simulators, and a new method is investigated. The new method is based on the so–called data cloning algorithm, which uses Markov chain Monte Carlo algorithms to approximate maximum likelihood estimators and their (asymptotic) variances in models with computationally challenging likelihoods. A simulation study is carried out to compare the statistical and computational efficiencies of the three methods. It is found that the three methods have similar statistical properties, but the Geweke–Hajivassiliou–Keane simulator requires the least computational effort. Hence, this is the method we recommend. A data analysis of Lansing Woods tree counts is used to illustrate the methods.

1. Introduction

Geostatistical data are a kind of spatial data collected in many earth and social sciences such as ecology, demography and geology. The literature offers a large number of models for the analysis of continuous geostatistical data but, in comparison, the number of models for the analysis of count geostatistical data is rather limited. Two main classes of models have been proposed for the analysis of the latter, both of which use Gaussian random fields as building blocks. The first is the class of hierarchical models proposed by Diggle et al. (1998), which can also be viewed as a class of generalized linear mixed models. De Oliveira (2013) proposed a class of hierarchical Poisson models that generalize the Poisson–lognormal model used by Diggle et al. (1998), and studied the second–order properties of these models. It was shown in De Oliveira (2013) that these models lack the flexibility to describe moderate or strong correlation in datasets that consist mostly of small counts or have small overdispersion. The second is the class of Gaussian copula models proposed by Madsen (2009), Kazianka and Pilz (2010) and Kazianka (2013). Han and De Oliveira (2016) studied the correlation structure of geostatistical Gaussian copula models with two types of marginal distributions, and found that their correlation structure is more flexible than that of hierarchical Poisson models. The latter is the class of models to be considered in this work.

Likelihood–based inference for Gaussian copula models with discrete marginals is computationally challenging, because evaluation of the likelihood functions require approximating high dimensional multivariate normal integrals. To avoid this computational challenge, Kazianka and Pilz (2010), Kazianka (2013) and Bai et al. (2014) proposed basing inference on some form of pseudo–likelihood that has similar properties as a true likelihood, but takes less time to compute. These works proposed the use of pairwise likelihoods and generalized quantile transforms. The former uses bivariate copulas, which is an example of the composite likelihood approach (see Varin et al. (2011) for a thorough review), while the latter uses a continuous approximation of the discrete distribution, which is based on copula densities. The statistical efficiencies of these approaches were numerically explored by Kazianka (2013) and Nikoloulopoulos (2013, 2016). These authors found that, compared to maximum likelihood estimators, the time savings in the computation of these pseudo–likelihood based estimators are obtained at the expense of a substantial increase of their biases and variances. Hence maximum likelihood estimators are preferable in situations in which they can be computed in a reasonable amount of time. In this work we study methods for efficient evaluation of likelihood functions of Gaussian copula models with count marginal distributions.

The goals of this work are threefold. First, we review two simulated likelihood methods that have been proposed in the literature for the approximation of high dimensional multivariate normal integrals using Monte Carlo methods. One of them is the quasi–Monte Carlo method proposed by Genz (1992) and Genz and Bretz (2002), while the other is the Geweke–Hajivassiliou–Keane simulator proposed by Geweke (1991), Hajivassiliou et al. (1996) and Keane (1994). Nikoloulopoulos (2013, 2016) and Masarotto and Varin (2012) used these methods to approximate likelihoods of Gaussian copula models with count marginals, which were then used to numerically compute the maximum simulated likelihood estimators. Second, we investigate the use of data cloning to compute maximum likelihood estimators (MLE). Data cloning is a method proposed by Lele et al. (2007) to approximate MLE and their (asymptotic) variances using Markov chain Monte Carlo methods. Finally, we carry out a simulation study to compare the statistical and computational efficiencies of these three methods, and compare the behavior of three types of confidence intervals for the model parameters. The simulated likelihood methods are implemented in the R packages mvtnorm (Genz and Bretz, 2009), gcmr (Masarotto and Varin, 2017) and gcKrig (Han and De Oliveira, 2018), while the data cloning method was coded and implemented by us in R and C++.

Similar simulation studies were carried out by Nikoloulopoulos (2013, 2016), in which the quasi–Monte Carlo, simple Monte Carlo and the pseudo–likelihood methods were compared. In those, the quasi–Monte Carlo method was the most effective regarding bias and variance, but the computational effort was not considered. Our study, tailored to the geostatistical context, compares methods not considered by Nikoloulopoulos, includes larger dimensional settings and compares both statistical and computational efficiency. The results of this simulation study indicate that, on the one hand, the three methods to approximate MLE have similar statistical properties. On the other hand, the quasi–Monte Carlo and data cloning methods require the most computational effort, while the Geweke–Hajivassiliou–Keane simulator requires substantially least computational effort. So the latter provides the best balance between statistical and computational efficiency. An analysis of the Lansing Woods tree counts dataset is used to illustrate the application of the methods for several inferential tasks.

2. Gaussian Copula Models with Discrete Marginals

2.1. Model Description

Let $\{Y(\mathbf{s}):\mathbf{s}\in D\},D\subset {\mathbb{R}}^2$, be a random field taking values on ${\mathbb{N}}_0=\{0,1,2,\dots \}$, and let {F_s(· ; ψ) : s ∈ D} be a family of marginal cdfs with support contained in ${\mathbb{N}}_0$ and corresponding pmfs f_s(· ; ψ), where ψ are marginal parameters. It is assumed that F_s(· ; ψ) is parameterized by ψ = (β^⊤, σ²), in a way that

$$\mathrm{E}(Y(\mathbf{s}))=t(\mathbf{s})\text{exp}({\beta }^{⊺}\mathbf{f}(\mathrm{s})),$$

where β = (β₁, …, β_p)^⊤ are regression parameters, f(s) = (f₁(s), …, f_p(s))^⊤ are known location–dependent covariates, and t(s) is a known ‘sampling effort’. The parameter σ² > 0 controls dispersion (usually overdispersion). For instance, when the support of the cdfs is ${\mathbb{N}}_0$, σ² may control the departure of F_s(· ; ψ) from the Poisson distribution with the same mean. The negative binomial and zero–inflated Poisson distributions are two common examples.

The Gaussian copula model for Y(·) is the random field defined by the property that for every $m\in \mathbb{N}$ and s₁, …, s_m ∈ D, the joint cdf of (Y(s₁), …, Y(s_m)) is

$$\mathrm{P}\left(Y({\mathbf{s}}_1)\le y_1,\dots ,Y({\mathbf{s}}_m)\le y_m\right)={\mathrm{\Phi }}_m\left({\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_1}(y_1;\psi )),\dots ,{\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_m}(y_m;\psi ));{\mathrm{\Psi }}_{\vartheta }\right),$$ (1)

where Φ(·) is the cdf of the standard normal distribution and Φ_m(· ; Ψ_ϑ) is the cdf of the N_m(0, Ψ_ϑ) distribution. The (i, j)^th entry of the m × m correlation matrix Ψ_ϑ is assumed to be

$$K_{\vartheta }({\mathbf{s}}_i,{\mathbf{s}}_j)=(1-{\tau }^2){\overline{K}}_{\theta }({\mathbf{s}}_i,{\mathbf{s}}_j)+{\tau }^{2}1\{{\mathbf{s}}_i={\mathbf{s}}_j\},$$ (2)

where ${\overline{K}}_{\theta }({\mathbf{s}}_i,{\mathbf{s}}_j)\ge 0$ is a correlation function in ${\mathbb{R}}^2$ that is continuous everywhere, ϑ = (θ^⊤, τ²) are correlation parameters, with τ² ∈ [0, 1], and 1{A} is the indicator function of A. This includes both correlation functions that are continuous everywhere and correlation functions that are discontinuous along the ‘diagonal’ s_i = s_j.

2.2. Likelihood

The computation of the likelihood function of Gaussian copulas with discrete marginals is challenging because it lacks a closed–form expression (unlike the case with continuous marginals), so numerical computation is required. Here we review several representations of this likelihood that have appeared in the literature.

Suppose that Y(·) is observed at n distinct sampling locations s₁, …, s_n ∈ D, resulting in the counts y = (y₁, …, y_n), where y_i is the realization of Y(s_i). Then the likelihood function of η = (ψ^⊤, ϑ^⊤) based on the data y is given by

$$\begin{array}{cc}\hfill L(\eta ;\mathit{y})& ={\mathrm{P}}_{\eta }(Y({\mathbf{s}}_1)=y_1,\dots ,Y({\mathbf{s}}_n)=y_n)\hfill \\ \hfill & =\sum _{j_1=1}^2\cdots \sum _{j_n=1}^2{(-1)}^{\sum _{i=1}^n{j}_i}{\mathrm{\Phi }}_n\left({\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_1}(t_1;\psi )),\dots ,{\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_n}(t_n;\psi ));{\mathrm{\Psi }}_{\vartheta }\right),\hfill \end{array}$$ (3)

with t_i = y_i + 1 – j_i, where the latter equality follows by taking the Radon–Nikodym derivative of (1) with respect to the counting measure on ${\mathbb{N}}_0^{\mathrm{n}}$ (Song, 2000). Evaluation of (3) is computationally intractable, even for moderate n, since it requires computing 2ⁿ terms, each involving an n–dimensional integral.

Alternatively, note that

$$Y(\mathbf{s})\stackrel{d}{=}{F}_{\mathbf{s}}^{-1}\left(\mathrm{\Phi }(Z(\mathbf{s}));\psi \right),$$ (4)

where $F_{\mathbf{s}}^{-1}(u;\psi )=\text{inf}\{x\in \mathbb{R}:F_{\mathbf{s}}(x;\psi )\ge u\}$, u ∈ (0, 1), is the quantile function of F_s(· ; ψ), and Z(·) is the Gaussian random field with mean 0 and covariance function (2) (Han and De Oliveira, 2016). For count cdfs, $F_{\mathbf{s}}^{-1}(\cdot ;\psi )$ is a step function so for any s ∈ D and $y\in {\mathbb{N}}_0$ it holds that Y(s) = y if and only of F_s(y – 1; ψ) < Φ(Z(s)) ≤ F_s(y; ψ). Then the likelihood function can also be written as

$$\begin{array}{cc}\hfill L(\eta ;\mathit{y})& ={\mathrm{P}}_{\eta }({\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_i}(y_i-1;\psi ))<Z({\mathbf{s}}_i)\le {\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_i}(y_i;\psi )):i=1,\dots ,n)\hfill \\ \hfill & ={\int }_{{\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_1}(y_1-1;\psi ))}^{{\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_1}(y_1;\psi ))}\cdots {\int }_{{\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_n}(y_n-1;\psi ))}^{{\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_n}(y_n-1;\psi ))}{\varphi }_n(z_1,\dots ,z_n;{\mathrm{\Psi }}_{\vartheta }){\mathit{dz}}_1,\dots {\mathit{dz}}_n,\hfill \end{array}$$ (5)

where φ_n(· ; Ψ_ϑ) is the pdf of the N_n(0, Ψ_ϑ) distribution. The latter expression is much more amenable for numerical computation, and will be used in the next section as the starting point for likelihood approximation.

Yet another likelihood representation is given in Masarotto and Varin (2012). Consider the change of variables (z₁, …, z_n) → (u₁, …, u_n) given by

$$u_i=\frac{F_{{\mathbf{s}}_i}(y_i;\psi )-\mathrm{\Phi }(z_i)}{f_{{\mathbf{s}}_i}(y_i;\psi )},i=1,\dots ,n,$$ (6)

with inverse z_i = z_i(u_i) = Φ⁻¹ (F_si(y_i; ψ)–u_if_si(y_i; ψ)). Then the integral (5) can be rewritten as

$$L(\eta ;\mathit{y})=\prod _{i=1}^n{f}_{{\mathbf{s}}_i}(y_i;\psi )\cdot {\int }_0^1\cdots {\int }_0^1{\mid {\mathrm{\Psi }}_{\vartheta }\mid }^{-\frac{1}{2}}\text{exp}\left(-\frac{1}{2}\mathit{z}{(\mathbf{u})}^{⊺}({\mathrm{\Psi }}_{\vartheta }^{-1}-I_n)\mathit{z}(\mathbf{u})\right)d\mathbf{u},$$ (7)

where z(u) = (z₁(u₁), …, z_n(u_n))^⊤; see Appendix A for the proof. It is also shown in Appendix A that the right-hand side of (7) agrees with the likelihood representation obtained by Madsen and Fang (2011) using a ‘continuous extension’ argument.

Madsen and Fang (2011) approximated the right–hand side of (7) using simple Monte Carlo based on independent draws from the unif(0, 1) distribution, but this results in an inefficient algorithm, even when the dimension n is small (Nikoloulopoulos, 2013). Approximating the right–hand side of (5) using the simple Monte Carlo algorithm based on independent draws from the N_n(0, Ψ_ϑ) distribution would also be inefficient, so more efficient algorithms are described in the next section.

Remark 1. In the statistical literature about copulas it is well known the lack of uniqueness of copula representations for multivariate distributions with discrete marginals. We do not view this as a weakness of copulas models for discrete spatial data though, as long as the copula model that is used is flexible and fits well the data under study; this is illustrated in Section 7. In addition, it is worth noting that the aforementioned lack of uniqueness does not arise within the class of Gaussian copula models because for any n and u₁, …, u_n, the copula Φ_n(Φ⁻¹(u₁), …, Φ⁻¹(u_n); Ψ_ϑ) is a one–to–one function of Ψ_ϑ.

3. Simulated Likelihood Methods

Approximating the n–dimensional integral in (5) by (deterministic) quadrature methods is not practical for moderate or large n, due to the high computational cost and large errors involved, so Monte Carlo or quasi–Monte Carlo methods are preferable. We describe in this section two such methods that have been proposed in the literature. Then the (simulated) maximum likelihood estimates would be computed by (numerically) maximizing an approximation to the likelihood that is obtained by simulation.

3.1. Genz–Bretz Method

We briefly summarize the method proposed by Genz (1992) and Genz and Bretz (2002) to compute n–dimensional integrals of normal densities over bounded hyper–rectangles; it will be called here the GB method. First, a three–step transformation (change of variable) is applied to the integrand, aimed at transforming (5) into an integral where the integration region is the hypercube [0, 1]^n–1. To simplify the expressions that follow, let a_i = Φ⁻¹(F_si(y_i – 1; ψ)) and b_i = Φ⁻¹(F_si (y_i; ψ)). After such transformation the likelihood (5) is rewritten as

$$L(\eta ;\mathit{y})={\int }_0^1\cdots {\int }_0^1\prod _{i=1}^n(e_i-d_i){\mathit{dw}}_1\dots {\mathit{dw}}_{n-1},$$ (8)

where $e_i=\mathrm{\Phi }((b_i-{\sum }_{j=1}^{i-1}{c}_{\mathit{ij}}{\mathrm{\Phi }}^{-1}(d_j+w_j(e_j-d_j)))∕c_{\mathit{ii}})$, $d_i=\mathrm{\Phi }((a_i-{\sum }_{j=1}^{i-1}{c}_{\mathit{ij}}{\mathrm{\Phi }}^{-1}(d_j+w_j(e_j-d_j)))∕c_{\mathit{ii}})$ and¹ (c_jk)_{1≤k≤j≤n} are the entries of the lower triangular matrix in the Cholesky decomposition of Ψ_ϑ. Note that the dimension of the integral was reduced by one. Second, a randomized quasi–Monte Carlo method with antithetic variables is used. Given the Monte Carlo size M and number of quasi–random points P, the GB method approximates (8) by

$${\widehat{L}}^{\text{GB}}(\eta ;\mathit{y})=\frac{1}{M}\sum _{k=1}^M\frac{1}{2P}\sum _{j=1}^P(f(\mid 2\{{\mathit{p}}_j+{\mathit{W}}_k\}-1_{n-1}\mid )+f(1_{n-1}-\mid 2\{{\mathit{p}}_j+{\mathit{W}}_k\}-1_{n-1}\mid )),$$

where f(·) is the integrand in (8), {t} and ∣t∣ denote, respectively, the vectors obtained by taking the fractional part and absolute value of each component of t, and 1_n–1 is the vector of ones. For k = 1, …, M and j = 1, …, P, W_k is an (n – 1)–vector whose components are independent draws from the unif(0, 1) distribution, and p_j is an (n – 1)–vector whose components are quasi–random numbers in (0, 1). Genz and Bretz (2002) recommended the use of quasi–random points as good lattice points; see Sloan and Kachoyan (1987) and Hickernell (1998). The GB method is implemented in the R package mvtnorm (Genz and Bretz, 2009).

Nikoloulopoulos (2013) compared the GB method with the simple Monte Carlo approximation proposed by Madsen and Fang (2011), and Nikoloulopoulos (2016) compared the GB method with generalized quantile transform proposed by Kazianka and Pilz (2010) and Kazianka (2013). Both comparisons found the GB method to be more efficient than the competing methods, but these comparisons did not involve the alternative simulated likelihood method described next.

3.2. Geweke–Hajivassiliou–Keane Method

Masarotto and Varin (2012) noticed the similarity between the likelihood function (5) and that of multivariate probit models, and adapted the algorithm proposed by Geweke (1991), Hajivassiliou et al. (1996) and Keane (1994) to compute multivariate normal rectangle probabilities. This is known as the Geweke–Hajivassiliou–Keane simulator, and will be called here the GHK method.

The integral (5) can be approximated by importance sampling, using the importance sampling density with support

$$\left({\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_1}(y_1-1;\psi )),{\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_1}(y_1;\psi ))\right)\times \cdots \times \left({\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_n}(y_n-1;\psi )),{\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_n}(y_n;\psi ))\right),$$

given by

$$g_{\eta }(\mathit{z})=\prod _{i=1}^n{p}_{\eta }(z_i\mid z_{i-1},\dots ,z_1,y_i),$$

where p_η(z_i ∣ z_i–1, …, z₁, y_i) is the conditional density of Z(s_i) given Z(s_i–1), …, Z(s₁), and Y(s_i) = y_i, and Z(·) is the Gaussian random field defined after (4). Since $Z({\mathbf{s}}_i)\mid Z({\mathbf{s}}_{i-1}),\dots ,Z({\mathbf{s}}_1)\sim \mathrm{N}(m_i,v_i^2)$, with m_i = E_ϑ(Z(s_i) ∣ Z(s_i–1), …, Z(s₁)) = mi(Z(s_i–1), …, Z(s₁);ϑ) and $v_i^2={\text{var}}_{\vartheta }(Z({\mathbf{s}}_i)\mid Z({\mathbf{s}}_{i-1}),\dots ,Z({\mathbf{s}}_1))=v_i^2(\vartheta )$, it follows from (4) that p_η(z_i ∣ Z_i–1, …, Z₁, y_i) is the density of the $\mathrm{N}(m_i,v_i^2)$ distribution truncated to (Φ⁻¹(F_Si(y_i – 1; ψ)), Φ⁻¹(F_si(y_i; ψ))). Then the GHK method approximates (5) by

$$\begin{array}{cc}\hfill {\widehat{L}}^{\text{GHK}}(\eta ;\mathit{y})& =\frac{1}{M}\sum _{k=1}^M\frac{{\varphi }_n({\mathit{Z}}^{(k)};{\mathrm{\Psi }}_{\vartheta })}{g_{\eta }({\mathit{Z}}^{(k)})}\hfill \\ \hfill & =\frac{1}{M}\sum _{k=1}^M\left\{\prod _{i=1}^n\frac{p_{\vartheta }(Z_i^{(k)}\mid Z_{i-1}^{(k)},\dots ,Z_1^{(k)})}{p_{\eta }(Z_i^{(k)}\mid Z_{i-1}^{(k)},\dots ,Z_1^{(k)},y_i)}\right\}\hfill \\ \hfill & =\frac{1}{M}\sum _{k=1}^M\left\{\prod _{i=1}^n\left[\mathrm{\Phi }\left(\frac{{\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_i}(y_i;\psi ))-m_{\mathit{ki}}}{v_{\mathit{ki}}}\right)-\mathrm{\Phi }\left(\frac{{\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_i}(y_i-1;\psi ))-m_{\mathit{ki}}}{v_{\mathit{ki}}}\right)\right]\right\},\hfill \end{array}$$

where Z⁽¹⁾, …, Z^(M) are i.i.d. draws from g_η(z), with ${\mathit{Z}}^{(k)}=(Z_1^{(k)},\dots ,Z_n^{(k)}),m_{\mathit{ki}}=m_i(Z_{i-1}^{(k)},\dots ,Z_1^{(k)};\vartheta )$ and $v_{\mathit{ki}}^2=v_i^2(\vartheta )$. The simulation of each Z^(k) is done sequentially, $Z_1^{(k)},Z_2^{(k)},\dots ,Z_n^{(k)}$, using the standard algorithm for simulating from truncated normal distributions: For k = 1, …, M and i = 1, …, n, set

$$Z_i^{(k)}=m_{\mathit{ki}}+v_{\mathit{ki}}{\mathrm{\Phi }}^{-1}\left\{(1-U_{\mathit{ki}})\mathrm{\Phi }\left(\frac{{\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_i}(y_i-1;\psi )))-m_{\mathit{ki}}}{v_{\mathit{ki}}}\right)+U_{\mathit{ki}}\mathrm{\Phi }\left(\frac{{\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_i}(y_i;\psi )))-m_{\mathit{ki}}}{v_{\mathit{ki}}}\right)\right\},$$

where the U_ki are i.i.d. with unif(0, 1) distribution. The GHK method is implemented in the R packages gcmr (Masarotto and Varin, 2017) and gcKrig (Han and De Oliveira, 2018).

Hajivassiliou et al. (1996) compared the GHK method with several other competing methods for the approximation of multivariate normal rectangle probabilities. They found that the GHK method was the most efficient, but this comparison did not involve the GB method nor the method to be described next.

Remark 2. The GHK method requires specifying an ordering of the sampling locations. Although there is a natural ordering in the case of time series data, no natural ordering exists in the case of spatial data, so any choice is somewhat arbitrary. In numerical explorations, we found that when the sampling locations are on a regular grid, the parameter estimates displayed little sensitivity to the chosen ordering. On the other hand, when the sampling locations are on an irregular grid, a common situation with geostatistical data, the parameter estimates displayed a bit more sensitivity for some of the chosen orderings, but not all, especially regarding the covariance parameter estimates. Based on our limited experience we conjecture that the sensitivity of the parameter estimates to the chosen ordering of the sampling locations is minor and will decrease as the sample size grows.

4. Data Cloning

Data cloning is a method proposed by Lele et al. (2007), and later studied further by Lele et al. (2010), to compute maximum likelihood estimators (MLE) and their asymptotic standard errors in statistical models with difficulty to compute likelihoods; this is the case for most hierarchical models. The method consists of using a Markov chain Monte Carlo (MCMC) algorithm to carry out an apparent Bayesian calculation. Instead of the likelihood based on the observed data, it uses the likelihood that results in the hypothetical scenario that K > 1 independent copies (clones) of the data had been observed, together with an arbitrary prior on the parameter space. The resulting posterior in the so–called DC–based distribution with the parameter space as its support. The idea is that when K is large, the DC–based distribution becomes highly concentrated at the MLE, regardless of the prior distribution. Then, the MLE can be approximated by the sample mean of draws from the DC–based distribution, and the asymptotic variance of the MLE can be approximated by K times the sample variance of these draws; this will be called the DC method. In spite of its Bayesian motivation, the DC method follows the classical frequentist inferential approach, and uses the MCMC machinery only as a computational device. The DC method was used by Baghishani and Mohammadzadeh (2011) and Torabi (2015) to fit spatial generalized linear mixed models.

4.1. Hierarchical Formulation of Gaussian Copula Models

We show here that the Gaussian copula model (4) can be written as a hierarchical model when the correlation function (2) has a ‘nugget effect’, i.e., when τ² > 0. The Gaussian random field Z(·) admits the representation $Z(\mathbf{s})\stackrel{d}{=}\Gamma (\mathbf{s})+ϵ(\mathbf{s})$, where Γ(·) is a Gaussian random field with mean 0 and covariance function $(1-{\tau }^2){\overline{K}}_{\theta }(\mathbf{s},\mathbf{u})$, ϵ(·) is Gaussian white noise with N(0, τ²) distribution, and Γ(·) and ϵ(·) are independent random fields. Let Γ = (Γ(s₁), …, Γ(s_n)). Then, the Gaussian copula model for Y(·) is equivalent to the following hierarchical model:

1. For any set of distinct locations {s₁, …, s_n} ⊂ D, the counts Y(s₁), …, Y(s_n) are conditionally independent given Γ, and

   $$\begin{array}{cc}\hfill Y({\mathbf{s}}_i)\mid \Gamma & \stackrel{d}{=}Y({\mathbf{s}}_i)\mid \Gamma ({\mathbf{s}}_i),i=1,\dots ,n\hfill \\ \hfill & \sim h_i(y\mid {\gamma }_i;\psi ,{\tau }^2),\hfill \end{array}$$

   where for any $y\in {\mathbb{N}}_0$

   $$h_i(y\mid {\gamma }_i;\psi ,{\tau }^2)=\mathrm{\Phi }\left(\frac{{\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_i}(y;\psi ))-{\gamma }_i}{\tau }\right)-\mathrm{\Phi }\left(\frac{{\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_i}(y-1;\psi ))-{\gamma }_i}{\tau }\right);$$ (9)

   see Appendix A.

2. Γ(·) is Gaussian random field with mean 0 and covariance function $(1-{\tau }^2){\overline{K}}_{\theta }(\mathbf{s},\mathbf{u})$, so Γ ~ N_n(0, (1 – τ²)R_θ), with ${(R_{\theta })}_{\mathit{ij}}={\overline{K}}_{\theta }({\mathbf{s}}_i,{\mathbf{s}}_j)$.

4.2. Algorithm

Let y = (y₁, …, y_n) be the data observed at the n sampling locations, γ = (γ₁, …, γ_n) an (unobservable) realization of Γ, which correspond to ‘random effects’ at the sampling locations, and π(η) = π(β, σ², θ, τ²) the prior distribution of the model parameters, assumed proper. Then, the posterior distribution of (η, γ) based on y is

$$\pi (\eta ,\gamma \mid \mathit{y})\propto \pi (\eta ){\varphi }_n(\gamma ;(1-{\tau }^2)R_{\theta })\prod _{i=1}^n{h}_i(y_i\mid {\gamma }_i;\psi ,{\tau }^2),$$

where h_i(· ∣ γ_i; ψ, τ²) is given in (9). Now, let y_(K) = (y, …, y) be the vector of ‘cloned data’, formed by concatenating K independent copies of the observed counts, and γ_(K) = (γ₁, …, γ_K), where ${\gamma }_1,\dots ,{\gamma }_K\stackrel{\text{iid}}{\sim }{\mathrm{N}}_n(0,(1-{\tau }^2)R_{\theta })$, with γ_k = (γ_k1, …, γ_kn), so γ_ki is the random effect at the i^th sampling location from the k^th replicate of Γ. Then the ‘posterior distribution’ of (η, γ_(K)) based on y_(K) is

$$\begin{array}{cc}\hfill {\pi }_{(K)}(\eta ,{\gamma }_{(K)}\mid {\mathit{y}}_{(K)})& \propto \pi (\eta )\pi ({\gamma }_{(K)}\mid \eta )p({\mathit{y}}_{(K)}\mid {\gamma }_{(K)},\eta )\hfill \\ \hfill & =\pi (\eta )\prod _{k=1}^K{\varphi }_n({\gamma }_k;(1-{\tau }^2)R_{\theta })\prod _{k=1}^K\prod _{i=1}^n{h}_i(y_i\mid {\gamma }_{\mathit{ki}};\psi ,{\tau }^2).\hfill \end{array}$$ (10)

Let $\widehat{\eta }$ be the MLE of η based on the observed data y. If $\{({\eta }^{(l)},{\gamma }_{(K)}^{(l)}):l=1,\dots ,M\}$ is a large sample from the distribution (10), it follows from results in Lele et al. (2010) that, under suitable conditions, for K large and regardless of the prior π(η)

$$\widehat{\eta }\approx \frac{1}{M}\sum _{l=1}^M{\eta }^{(l)}\text{and}\mathrm{var}(\widehat{\eta })\approx \frac{K}{M-1}\sum _{l=1}^M({\eta }^{(l)}-\widehat{\eta }){({\eta }^{(l)}-\widehat{\eta })}^{⊺},$$

where these approximations improve as K → ∞; see also Walker (1969) and Baghishani and Mohammadzadeh (2011) for similar results. Unlike simulated likelihood methods, the DC method approximates $\widehat{\eta }$ and its (asymptotic) variance directly, without approximating the likelihood function.

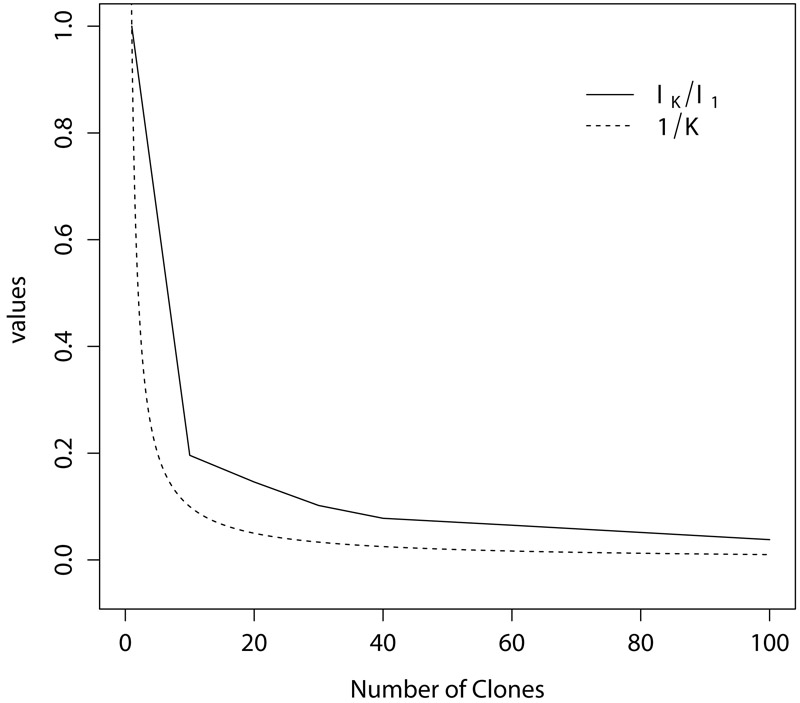
The number of clones K is chosen to strike a balance between computational accuracy and effort. Lele et al. (2010) proposed a simple rule to diagnose whether the DC–based distribution is close to ‘degenerate’, based on the fact that as K → ∞ the largest eigenvalue of the variance matrix of the DC–based distribution converges to zero at the same rate as 1/K. They proposed plotting λ_K/λ₁ versus K, K = 1, 2, …, where λ_K is the largest eigenvalue of the variance matrix of the DC–based distribution based on K clones, and comparing this plot with the plot of 1/K. The number of clones is chosen as the smallest K for which λ_K/λ₁ falls below a small positive threshold, say 0.1.

We use priors of the form π(β, σ², θ, τ²) = π(β)π(σ²)π(θ)π(τ²), where the marginal priors are chosen to be informative, as such priors require fewer clones than non–informative priors to achieve a desired accuracy; the MLE obtained by the DC method is insensitive to the chosen prior. Any Monte Carlo algorithm that produces samples from (10) would work. We found, after some experimentation, that the following ‘Metropolis–within–Gibbs’ sampler algorithm works well. The state variables (β, σ², θ, τ², γ_(K)) are updated by separately updating two blocks, (β, σ²) and (θ, τ², γ_(K)), where each block is updated using a Metropolis–Hastings algorithm. The details of the algorithm are given in Appendix B.

The requirement that the covariance function of the latent process Z(·) includes a nugget effect is a limitation of the above MCMC algorithm for implementing the DC method, arguably a moderate one since geostatistical data often contain measurement error. Although a model with a fixed small nugget effect could be used to approximately fit data with no measurement error, this is likely to produce computational instabilities in the evaluation of h_i(· ∣ γ_i; ψ, τ²).

5. Initial Values

All of the previously described methods require good initial values for the parameters for an efficient implementation. Good initial values would produce fast convergence of the iterative algorithm used for likelihood optimization in the GB and GHK methods, and good initial values allow the use of informative priors in the DC method.

We use a simple two–stage estimation method to obtain initial values, which shares some similarities with one of the methods proposed by Zhao and Joe (2005). The first stage consists of estimating the marginal parameters by maximizing the pseudo–likelihood obtained under the working assumption of independence, resulting in

$$\widehat{\psi }≔{\text{arg max}}_{\psi }\prod _{i=1}^n{f}_{{\mathbf{s}}_i}(y_i;\psi ).$$

Next, note from (4) that for any s ∈ D and $k\in {\mathbb{N}}_0$

$$Z(\mathbf{s})\mid Y(\mathbf{s})=k\sim \mathrm{N}(0,1)\text{truncated to}({\mathrm{\Phi }}^{-1}(F_{\mathbf{s}}(k-1;\psi )),{\mathrm{\Phi }}^{-1}(F_{\mathbf{s}}(k;\psi ))),$$

so a kind of ‘residuals’ can be defined as

$${\widehat{Z}}_i≔{\mathrm{E}}_{\widehat{\psi }}\{Z({\mathbf{s}}_i)\mid Y({\mathbf{s}}_i)=y_i\}=\frac{\varphi ({\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_i}(y_i-1;\widehat{\psi })))-\varphi ({\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_i}(y_i;\widehat{\psi })))}{F_{{\mathbf{s}}_i}(y_i;\widehat{\psi })-F_{{\mathbf{s}}_i}(y_i-1;\widehat{\psi })},i=1,\dots ,n,$$

where φ(·) is the pdf of the standard normal distribution. The second stage consists of estimating the covariance parameters by maximizing the pseudo–likelihood obtained under the working assumption that the joint distribution of $\widehat{\mathit{Z}}={({\widehat{Z}}_1,\dots ,{\widehat{Z}}_n)}^{⊺}$ is Gaussian with mean vector 0 and covariance matrix Ψ_ϑ, resulting in

$$\widehat{\vartheta }≔{\text{arg max}}_{\vartheta }{\mid {\mathrm{\Psi }}_{\vartheta }\mid }^{-1∕2}\text{exp}\{-\frac{1}{2}{\widehat{Z}}^{⊺}{\mathrm{\Psi }}_{\vartheta }^{-1}\widehat{\mathit{Z}}\}.$$

Remark 3. The GB and GHK methods provide approximations to likelihood functions at the MLEs (or any other parameter values), so they can be used for likelihood–based inferential tasks such as model selection, testing of nested hypotheses and computation of likelihood–based confidence intervals. Although the DC method does not approximate likelihood functions directly, likelihoods and likelihood ratios can be approximated using Monte Carlo techniques described in Thompson (1994), as long as the models under study are hierarchical. Ponciano et al. (2009) described how to perform the aforementioned likelihood–based inferential tasks using MLEs obtained from the DC method and a sample from the conditional distribution of the random effects given the data and parameter estimates. An application of some of these inferential tasks will be illustrated in Section 7.

6. Simulation Study

We conduct a simulation study to compare the three methods described above, GB, GHK and DC, to approximate the MLEs of the model parameters, and investigate some of their statistical properties. The properties to be investigated are absolute relative bias and mean absolute error, as well as coverage and length of different types of confidence intervals. In addition, we also compare the required computational effort to implement these methods. The results for the GB and GHK methods were obtained using, respectively, the R packages mvtnorm (Genz and Bretz, 2009) and gcKrig (Han and De Oliveira, 2018), while the DC method was coded and implemented by us in R and C++.

6.1. Design

Below we describe the factors of the simulation design, where some are fixed and others vary, as well as the MCMC settings required for the DC method.

• The study region is D = [0, 1] × [0, 1]. The sampling locations form an 11 × 11 regular lattice within D, so n = 121 and the minimum distance between sampling locations is 0.1.

• As marginals we use the family of negative binomial distributions parameterized in terms of their mean and a ‘size’ parameter (the so–called NB2 distribution; Cameron and Trivedi (2013)), where the pmf of Y(s) is given by

  $$f_{\mathbf{s}}^{\text{NB}}(y;\psi )=\frac{\mathrm{\Gamma }(y+1∕{\sigma }^2)}{\mathrm{\Gamma }(1∕{\sigma }^2)y!}{\left(\frac{1}{1+{\sigma }^2\mu (\mathbf{s})}\right)}^{1∕{\sigma }^2}{\left(1-\frac{1}{1+{\sigma }^2\mu (\mathbf{s})}\right)}^y,y=0,1,2,\dots$$ (11)

  With this parameterization it holds that E(Y(s)) = μ(s) and var(Y(s)) = μ(s)(1 + σ²μ(s)).

• The mean function μ(s) is exp(0.5 + 0.5x + y), so (β₁, β₂, β₃) = (0.5, 0.5, 1). The marginal priors for β used in the DC method is N₃((0.5, 0.5,1)^⊤, 30I₃).

• The dispersion parameter σ² is either 0.2 (small overdispersion) or 2 (large overdispersion). The marginal priors for σ² used in the DC method are IG(0.2,0.4) (inverse Gaussian) and IG(2, 4), respectively.

• The continuous correlation function ${\overline{K}}_{\theta }(\mathbf{s},\mathbf{u})$ in (2) is either exp(−d/0.1) or exp(−d/0.3), with d = ∥s – u∥ being Euclidean distance, so θ = 0.1 (weak dependence) or θ = 0.3 (strong dependence). The marginal priors for θ used in the DC method are LN(−2, 1) (lognormal) and LN(−1, 0.5), respectively.

• The nugget effect τ² in the correlation function (2) is 0.25, and its marginal prior used in the DC method is unif(0, 1).

• The number of clones for the DC method is K = 40. This choice was made based on plots of λ_K/λ₁ versus K obtained from a few pilot runs; see Section 4.2 and Figure 1.

• For the MCMC algorithm in the DC method, η⁽⁰⁾ were set at the initial values described in Section 5. The tuning constants c₁, c₂, c₃, c₄ > 0 were updated every 1000 iterations with memory parameter equal to 1000, while the tuning constant c₅ was fixed at 0.03; see Appendix B for details. The length of each MCMC run is 15000, with the first 5000 iterations as ‘burn–in’. These choices ensure the automaticity and robustness of the simulations.

Figure 1:

Plots of standardized eigenvalues of the posterior variance matrix based on the number of clones K (solid line), and the function 1/K (dashed line).

For each of the four simulation scenarios (two values of σ² and two values of θ) we simulated 1000 datasets, each of size n = 121, and computed the approximate MLE using the three methods. The approximate MLEs will be compared in terms of absolute relative bias (ARB) and mean absolute error (MAE). These are defined, for each simulation scenario, method and parameter ‘a’, as

$$\text{ARB}=\mid \frac{\text{MLE}-a_{\text{true}}}{a_{\text{true}}}\mid \text{and}\text{MAE}=\frac{1}{1000}\sum _{i=1}^{1000}\mid {\widehat{a}}_i-a_{\text{true}}\mid ,$$

where a_ture is the true value of a, ${\widehat{a}}_i$ is the estimate of a_ture based on the i^th simulated dataset, 1000 and $\text{MLE}=\frac{1}{1000}{\sum }_{i=1}^{1000}{\widehat{a}}_i$. In addition, for each simulation scenario we also compare the coverage and length of three types of (approximate) 95% confidence intervals (see below), defined as

$$\text{coverage}=\frac{1}{1000}\sum _{i=1}^{1000}1\{{\text{LB}}_i<a_{\text{true}}<{\text{UB}}_i\},\text{length}=\text{median}\{{\text{UB}}_i-{\text{LB}}_i:i=1,\dots ,1000\},$$

where LB_i, UB_i are the endpoints of a confidence interval based on the i^th simulated dataset. The 95% confidence intervals to be considered are:

• Wald: The Wald–type confidence interval has endpoints $({\text{LB}}_i,{\text{UB}}_i)={\widehat{a}}_i\mp 1.96{(\mathrm{v}\widehat{\mathrm{a}}\mathrm{r}({\widehat{a}}_i))}^{1∕2}$, where $\mathrm{v}\widehat{\mathrm{a}}\mathrm{r}({\widehat{a}}_i)$ is an estimate of the (asymptotic) variance of ${\widehat{a}}_i$ based on the ith simulated dataset. For the GHK method the variance estimates are obtained from the diagonal elements of the (estimated) inverse Hessian matrix obtained at the end of the optimization process.

• Wald–Tran: This is a Wald–type confidence interval obtained using the reparametrization of the likelihood in terms of the original regression parameters (β₁, β₂, β₃) and the transformed parameters (ξ₂, ξ₃, ξ₄) = (log(σ²), log(θ), logit(τ²)). The confidence intervals for the original parameters are obtained by back–transforming the endpoints of the Wald–type confidence intervals for the transformed parameters.

• PL: This is the confidence interval obtained by evaluating the profile likelihood and inverting a likelihood ratio test (Meeker and Escobar, 1995). LB_i and UB_i can be computed either by evaluating the profile likelihood on a selected grid of parameter values or by evaluating the profile likelihood over parameter values selected by an iterative algorithm; gcmr uses the former while gcKrig uses the latter.

6.2. Results

Table 1 displays the ARB and MAE results. Overall, the three methods to approximate the maximum likelihood estimators are comparable, in the sense that they produce similar ARB and MAE. In regard to the regression parameters, all methods produce MLEs for β₂ and β₃ that are close to being unbiased, but the MLEs of β₁ are (downward) biased when the dependence is strong. All the methods produce MLEs for σ², θ and τ² that are (downward) biased, with the ARB tending to increase when either the overdispersion or strength of dependence increase. Also, except for τ², the MAE of the MLEs of all parameters increase with overdispersion and strength of dependence.

Table 1:

Absolute relative bias (ARB) and mean absolute errors (MAE) for the three methods (GB, GHK and DC) and four simulation scenarios. The summaries are based on 1000 simulated datasets.

True parameters	ARB			MAE
	GB	GHK	DC	GB	GHK	DC
β1 = 0.5	0.06	0.06	0.14	0.25	0.24	0.26
β2 = 0.5	0.00	0.00	0.02	0.28	0.28	0.29
β3 = 1.0	0.02	0.01	0.00	0.28	0.28	0.29
σ2 = 0.2	0.15	0.15	0.10	0.07	0.07	0.08
θ = 0.1	0.10	0.20	0.20	0.04	0.04	0.04
τ2 = 0.25	0.40	0.36	0.32	0.22	0.21	0.20
β1 = 0.5	0.30	0.26	0.30	0.44	0.43	0.44
β2 = 0.5	0.10	0.10	0.04	0.44	0.45	0.45
β3 = 1.0	0.07	0.05	0.02	0.44	0.44	0.47
σ2 = 0.2	0.50	0.55	0.35	0.13	0.14	0.15
θ = 0.3	0.40	0.43	0.33	0.15	0.15	0.13
τ2 = 0.25	0.28	0.24	0.24	0.16	0.15	0.15
β1 = 0.5	0.18	0.16	0.12	0.46	0.45	0.46
β2 = 0.5	0.02	0.02	0.06	0.54	0.54	0.58
β3 = 1.0	0.03	0.03	0.08	0.55	0.55	0.60
σ2 = 2.0	0.06	0.05	0.04	0.37	0.38	0.40
θ = 0.1	0.10	0.10	0.10	0.04	0.04	0.04
τ2 = 0.25	0.32	0.32	0.28	0.21	0.22	0.22
β1 = 0.5	0.64	0.56	0.58	0.75	0.74	0.73
β2 = 0.5	0.10	0.06	0.02	0.78	0.77	0.80
β3 = 1.0	0.06	0.05	0.12	0.76	0.77	0.82
σ2 = 2.0	0.14	0.14	0.09	0.71	0.71	0.70
θ = 0.3	0.33	0.33	0.30	0.17	0.16	0.16
τ2 = 0.25	0.24	0.24	0.20	0.17	0.17	0.18

Next, for each simulation scenario and parameter we computed the three types of (approximate) 95% confidence intervals described above, and compare them in terms of their coverage and length. This is done only for the GHK method since the other methods produce very similar results.

Table 2 displays the confidence intervals results. For the regression parameters, all the confidence intervals display undercoverage, and this undercoverage becomes more substantial as the strength of dependence increases. Among all the confidence intervals the profile likelihood confidence intervals have coverage that are closest to nominal, while that of the other two are similar. The profile likelihood confidence intervals are in general wider, which partly explain their better coverage.

Table 2:

Empirical coverage probability and median length of different nominal 95% confidence intervals using the GHK method. The summaries are based on 1000 simulated datasets.

True parameters	Coverage			Length
	Wald	Wald–Tran	PL	Wald	Wald–Tran	PL
β1 = 0.5	0.902	0.900	0.927	0.977	0.974	1.076
β2 = 0.5	0.904	0.901	0.918	1.135	1.131	1.232
β3 = 1.0	0.908	0.907	0.929	1.142	1.140	1.243
σ2 = 0.2	0.875	0.979	0.972	0.268	0.500	0.355
θ = 0.1	0.971	0.767	0.941	0.291	0.318	0.348
τ2 = 0.25	0.968	0.954	0.952	0.901	0.912	0.735
β1 = 0.5	0.765	0.759	0.831	1.238	1.221	1.439
β2 = 0.5	0.787	0.782	0.842	1.349	1.335	1.521
β3 = 1.0	0.789	0.788	0.839	1.383	1.362	1.542
σ2 = 0.2	0.504	0.822	0.796	0.228	0.502	0.353
θ = 0.3	0.677	0.701	0.929	0.360	0.435	0.678
τ2 = 0.25	0.953	0.948	0.957	0.675	0.726	0.612
β1 = 0.5	0.901	0.899	0.928	1.866	1.859	2.001
β2 = 0.5	0.906	0.904	0.941	2.309	2.300	2.432
β3 = 1.0	0.912	0.912	0.939	2.329	2.321	2.446
σ2 = 2.0	0.859	0.897	0.868	1.651	1.678	1.592
θ = 0.1	0.986	0.785	0.956	0.318	0.385	0.427
τ2 = 0.25	0.971	0.956	0.961	0.886	0.891	0.769
β1 = 0.5	0.782	0.776	0.881	2.293	2.284	2.597
β2 = 0.5	0.846	0.839	0.896	2.711	2.689	2.869
β3 = 1.0	0.847	0.844	0.894	2.694	2.685	2.834
σ2 = 2.0	0.696	0.807	0.804	2.001	2.140	1.964
θ = 0.3	0.698	0.763	0.962	0.414	0.572	0.809
τ2 = 0.25	0.949	0.971	0.973	0.690	0.715	0.633

For the overdispersion parameter, all confidence intervals tend to display undercoverage, except when both dependence and overdispersion are small. The undercoverage of the Wald–Tran and profile likelihood confidence intervals are smaller than that of the Wald confidence interval, an the length of the all confidence intervals are similar, with Wald–Tran being slightly larger sometimes. For the range parameter, the Wald confidence interval displays overcoverage when the strength of dependence is small, and undercoverage when the strength of dependence is large. The Wald–Tran confidence interval always displays undercoverage. The profile likelihood confidence interval has coverage that is closest to nominal, and is wider than the other two confidence intervals. Finally for the nugget parameter, all three confidence intervals have similar coverages that are close to nominal, and the Wald confidence interval is wider than the profile likelihood confidence interval. Overall, profile likelihood confidence intervals seem to perform better than the other two, in agreement with what has been observed in other models and settings; see Meeker and Escobar (1995).

Although the above properties of point and interval estimators are somewhat unsatisfactory, they are in agreement with properties of maximum likelihood parameter inferences in Gaussian random fields; see Irvine et al. (2007) and the references therein. We expect the above properties of point and interval estimators to improve as the sample size grows in an increasing domain asymptotic regime (but not necessarily so in an infill asymptotic regime). To investigate this conjecture, we ran a second simulation study with the same design as before, except for the factor in the first bullet. Now we consider the larger study region D = [0, 2] × [0, 2], where the sampling locations form a 21 × 21 regular lattice so n = 441 and the minimum distance between sampling locations is still 0.1.

Table 3 displays the combined results for point and interval estimators using the GHK method (results for Wald confidence intervals are not reported since they are similar to or inferior than the results for Wald–Tran confidence intervals.) The MLEs for this larger sample size are, for most parameters and scenarios, approximately unbiased and the MAE are substantially reduced. The coverage probabilities of both confidence intervals are, for most parameters and scenarios, closer to nominal than those for the smaller sample size. The exception occurs for the Wald–Tran confidence interval for the range parameter that displays severe undercoverage for some scenarios. For most parameters and scenarios, the profile likelihood confidence intervals have coverages that are similar or better than those of the Wald–Tran confidence intervals, and theirs lengths are similar. Again, the profile likelihood confidence intervals are preferable. We end by pointing out that we did not include the GB and DC methods in this larger simulation study because their required computational effort is substantially much larger than that of the GHK method; see the next subsection.

Table 3:

ARB, MAE, empirical coverage probability and median length of nominal 95% confidence intervals using the GHK method for the second simulation study. The summaries are based on 1000 simulated datasets.

True parameters	GHK Estimate		Coverage		Length
	ARB	MAE	Wald–Tran	PL	Wald–Tran	PL
β1 = 0.5	0.02	0.12	0.933	0.938	0.556	0.562
β2 = 0.5	0.00	0.07	0.930	0.935	0.317	0.323
β3 = 1.0	0.01	0.07	0.918	0.932	0.325	0.348
σ2 = 0.2	0.05	0.02	0.950	0.951	0.107	0.108
θ = 0.1	0.10	0.02	0.784	0.967	0.120	0.126
τ2 = 0.25	0.24	0.16	0.944	0.980	0.798	0.539
β1 = 0.5	0.14	0.24	0.882	0.903	0.953	1.019
β2 = 0.5	0.02	0.12	0.897	0.915	0.504	0.534
β3 = 1.0	0.03	0.13	0.880	0.923	0.525	0.584
σ2 = 0.2	0.10	0.05	0.844	0.893	0.173	0.175
θ = 0.3	0.13	0.09	0.849	0.924	0.323	0.384
τ2 = 0.25	0.00	0.08	0.964	0.976	0.296	0.310
β1 = 0.5	0.06	0.23	0.931	0.940	1.082	1.103
β2 = 0.5	0.00	0.14	0.928	0.934	0.662	0.676
β3 = 1.0	0.00	0.14	0.945	0.951	0.666	0.672
σ2 = 2.0	0.01	0.17	0.941	0.929	1.531	1.417
θ = 0.1	0.00	0.02	0.789	0.974	0.123	0.125
τ2 = 0.25	0.16	0.17	0.934	0.972	0.722	0.552
β1 = 0.5	0.12	0.36	0.931	0.938	1.541	1.610
β2 = 0.5	0.00	0.17	0.944	0.948	0.817	0.855
β3 = 1.0	0.00	0.18	0.941	0.945	0.828	0.878
σ2 = 2.0	0.02	0.37	0.937	0.918	1.124	1.093
θ = 0.3	0.07	0.09	0.893	0.936	0.360	0.433
τ2 = 0.25	0.00	0.07	0.966	0.946	0.315	0.312

6.3. Computational Time

We now compare the three methods to approximate the MLE in terms of computational effort. The conclusions derived from such comparisons are arguably tentative, since computational times depend heavily on many implementation factors that are bound to change (evolve), such as programming environment and language, the method of optimization and even starting points in the optimization. Nevertheless, the following comparison provides information about the relative computational efforts required for the three methods under their current implementations, and how these efforts increase with sample size.

For the GB method the maximum number of function evaluations (maxpts) in mvtnorm was set to 25000, while the choices of M and P are selected (optimized) automatically by the package. For the GHK method the Monte Carlo size was set at M = 1000. For both simulated likelihood methods the R function optim was used with box constrained quasi-Newton method for optimization method = "L-BFGS-B" using same initial values. For the DC method the heavy-duty number crunching, like generation of proposal distributions, was coded in C++ with interface to R using the packages Rcpp and RcppArmadillo (Eddelbuettel and Sanderson, 2014), and the MCMC iterations were coded in R. We controlled other factors so the computational environment under different methods is the same. All computations were carried out on a Macbook Pro computer with a 2.8 GHz Intel Core i7 processor, 16 GB RAM and 6 MB L3 Cache using 4 cores working in parallel. To speed up the computations we used the R package snowfall (Knaus, 2015) to parallelize the computations in the three methods.

Table 4 displays the times (in seconds) that took for each of the three methods to compute the average of the MLE from 100 simulations with different sample sizes. Clearly, the GHK simulator is substantially faster than its competitors, more than ten times faster on average. It is faster than the GB method due to the generation of quasi–random points required for the latter, at least for the tested sample sizes (the maximum allowed dimension in the current version of mvtnorm is n = 1000). On the other hand, the DC method is the most computationally intensive due to its use of MCMC and clones of data. Given these findings and the results in Table 1, we conclude that the GHK method provides the best balance between statistical and computational efficiency.

Table 4:

Computational time (in seconds) needed to compute the average MLE for the three methods from 100 simulations with different sample sizes using 4 cores.

n	25	64	121	256	441	961
GB	10.05	18.37	62.23	116.21	286.81	1060.21
GHK	0.38	0.50	1.80	7.88	35.87	108.60
DC	28.20	37.38	69.47	200.17	367.62	1748.41

7. Example: Lansing Woods Dataset

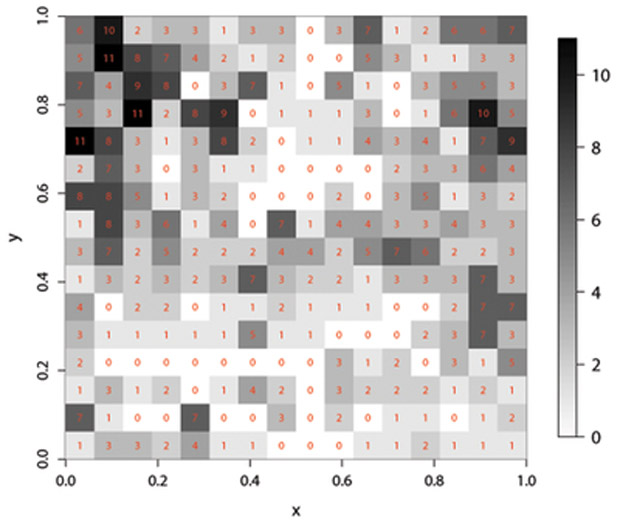
In this section we illustrate the application of the proposed methods for the analysis of a dataset previously analyzed by Kazianka (2013) using other methods. For comparison we follow and extend his analyses. The original dataset consists of the locations of 2251 trees and their botanical classification as hickories, maples, red oaks, white oaks, black oaks or miscellaneous trees, within a plot of 924 × 924 feet in Lansing Woods, Michigan, USA; it is available in the R package spatstat. The question of interest is to determine whether the presence of hickory trees tend to discourage the presence of maple trees nearby. These data were summarized by rescaling the original plot into the unit square and dividing the latter into 256 square quadrats of equal area. Let Y(s_i) denote the number of maple trees and f₂(s_i) the number of hickory trees in the quadrat with center s_i, i = 1,…, 256. Figure 2 displays the spatial distribution of these variables.

Figure 2:

Lansing wood dataset: spatial distribution of hickory counts (left) and maple counts (right).

As in Kazianka (2013), we first fit the Gaussian copula model with Poi(exp(β₁ + β₂f₂(s))) marginals and correlation function K_ϑ(s, u) = (1 – τ²)exp(−d/θ) + τ²1{s = u}. This model is fit using two methods, GHK and DC, where for the latter we used 40 clones and the priors $\beta \sim {\mathrm{N}}_2({\widehat{\beta }}_{\text{INI}},30I_2)$, θ ~ LN(−2, 1) and τ² ~ unif(0,1), with ${\widehat{\beta }}_{\text{INI}}$ the initial value of β whose computation is described in Section 5. The GHK implementation is carried out using the R package gcKrig. Table 5 displays the MLE and their standard errors (in parentheses) for each method, as well as the estimates obtained by Kazianka (2013) using two other estimation methods (generalized quantile transform (GQT) and composite likelihood (CL)). The estimates from both methods are quite similar for all parameters, and the standard errors display small discrepancies. For both methods the Wald–type 99% confidence interval for β₂ is made out entirely of negative numbers, suggesting the counts of hickory and maple trees in the quadrats are negatively associated. These findings agree with those in Kazianka (2013).

Table 5:

MLE and their estimated asymptotic standard deviations (in parentheses) of the GHK and DC methods from the Lansing Woods dataset, assuming Poisson marginals. GQT and CL estimates are from Kazianka (2013).

Method	${\widehat{\beta }}_1$	${\widehat{\beta }}_2$	$\widehat{\theta }$	${\widehat{\tau }}^2$
GHK	1.124 (0.097)	−0.152 (0.027)	0.084 (0.023)	0.504 (0.127)
DC	1.123 (0.113)	−0.150 (0.025)	0.083 (0.018)	0.494 (0.101)
GQT	1.057	−0.181	0.063	0.470
CL	1.227	−0.253	0.060	0.421

To investigate the adequacy of the Poisson family of marginal distributions, we also fit Gaussian copula models with negative binomial distributions, as in (11), and zero–inflated Poisson (ZIP) distributions as marginals, the latter having pmf given by

$$f_{\mathbf{s}}^{\text{ZIP}}(y;\psi )=\{\begin{array}{cc}\frac{{\sigma }^2}{{\sigma }^2+1}+\frac{1}{{\sigma }^2+1}\text{exp}(-(1+{\sigma }^2)\mu (\mathbf{s}))\hfill & \text{if}y=0\hfill \\ \frac{1}{{\sigma }^2+1}\frac{\text{exp}(-(1+{\sigma }^2)\mu (\mathbf{s})){((1+{\sigma }^2)\mu (\mathbf{s}))}^y}{y!}\hfill & \text{if}y=1,2,\dots \hfill \end{array}\phantom{\}};$$

see Han and De Oliveira (2016). Both families are parameterized in terms of the mean function μ(s) = exp(β₁ + β₂f₂(s)) and a ‘size’ parameter σ² ≥ 0 that controls overdispersion, and both include the aforementioned family of Poisson distributions (that results when σ² = 0). We continue using the aforementioned exponential correlation function with nugget τ² ∈ [0, 1].

Table 6 displays the MLE and asymptotic standard errors (in parenthesis) using the GHK and DC methods under both families of marginals. To fit the models with negative binomial and zero-inflated Poisson family of marginals using the DC method we used the same priors as in the fit with Poisson marginals, plus σ² ~ IG(1,1). The parameter estimates under Poisson and zero–inflated Poisson marginals are similar, while some differences are apparent under the negative binomial marginals. Under these families of marginals the Wald–type 99% confidence interval for β₂ are also made out entirely of negative numbers, supporting again the conclusion that there exist negative association between the number of hickory and maple trees in the quadrats. In addition, the estimates of σ² are positive and away from zero for both methods and both families of marginals, supporting the presence of overdispersion.

Table 6:

MLE and their asymptotic standard errors (in parentheses) for the Lansing Woods dataset, obtained from the GHK and DC methods, assuming ZIP and NB2 marginals.

	Method	${\widehat{\beta }}_1$	${\widehat{\beta }}_2$	${\widehat{\sigma }}^2$	$\widehat{\theta }$	${\widehat{\tau }}^2$
ZIP	GHK	0.905 (0.146)	−0.155 (0.030)	0.357 (0.119)	0.084 (0.024)	0.414 (0.149)
	DC	0.895 (0.131)	−0.155 (0.026)	0.355 (0.108)	0.082 (0.021)	0.408 (0.116)
NB2	GHK	0.747 (0.319)	−0.112 (0.037)	1.278 (0.484)	0.172 (0.081)	0.208 (0.097)
	DC	0.742 (0.292)	−0.113 (0.038)	1.264 (0.439)	0.178 (0.076)	0.212 (0.101)

As indicated in Remark 3, the GHK method approximates the likelihood function evaluated at the MLE, so information criteria can be used for selecting among candidate models. Table 7 reports the log–likelihood, AIC_c and BIC values for the fitted Gaussian copula models with families of Poisson, ZIP and NB2 marginals. The model with NB2 marginal is the one selected for both the AIC_c and BIC criteria. Based on the DC method, Ponciano et al. (2009) described a Monte Carlo method to approximate likelihood ratios which can be used to compute the difference in information criteria between two competing models, say BIC^model₁ – BIC^model₂, which reaches the same conclusion. Neither the models with Poisson or ZIP marginals are competitive, so the model with negative binomial marginals seems the more appropriate for this dataset.

Table 7:

Model comparison summaries from the Lansing Woods dataset for Gaussian copula models with different marginals.

Model	Number of Parameters	Log–likelihood	AICc	BIC
Poisson	4	−477.16	962.48	976.50
ZIP	5	−454.71	919.66	937.15
NB2	5	−422.96	856.16	873.65

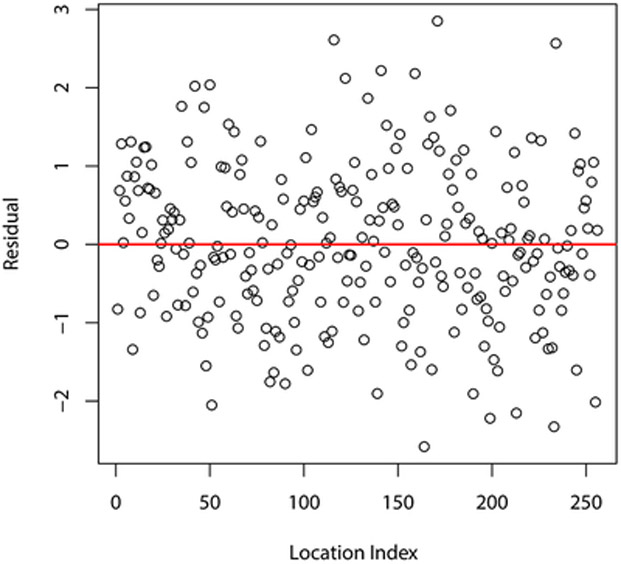
To assess the adequacy of the fitted Gaussian copula model with negative binomial marginals selected above we use the kind of residuals advocated by Masarotto and Varin (2012). Specifically, we use the randomized quantile residuals defined as

$$r_i={\mathrm{\Phi }}^{-1}\{U_i{F}_{{\mathbf{s}}_i}(y_i\mid y_{i-1},\dots ,y_1;\widehat{\eta })+(1-U_i)F_{{\mathbf{s}}_i}(y_i-1\mid y_{i-1},\dots ,y_1;\widehat{\eta })\},$$

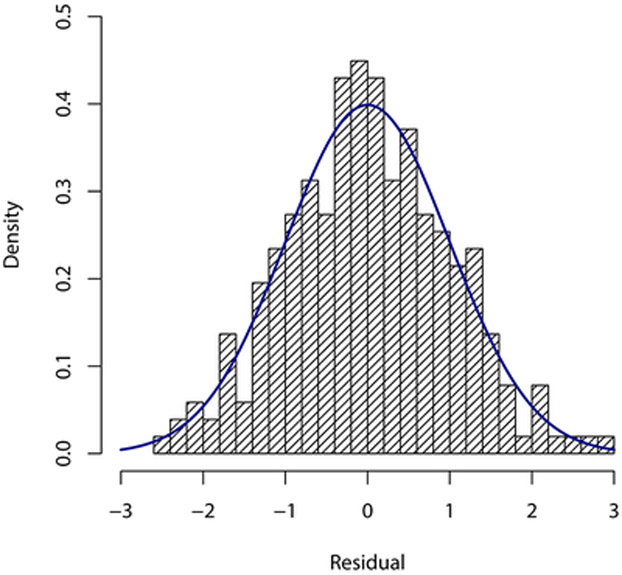
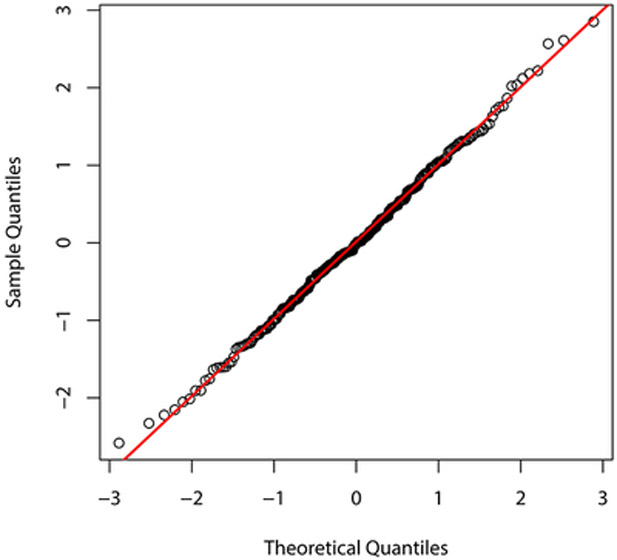
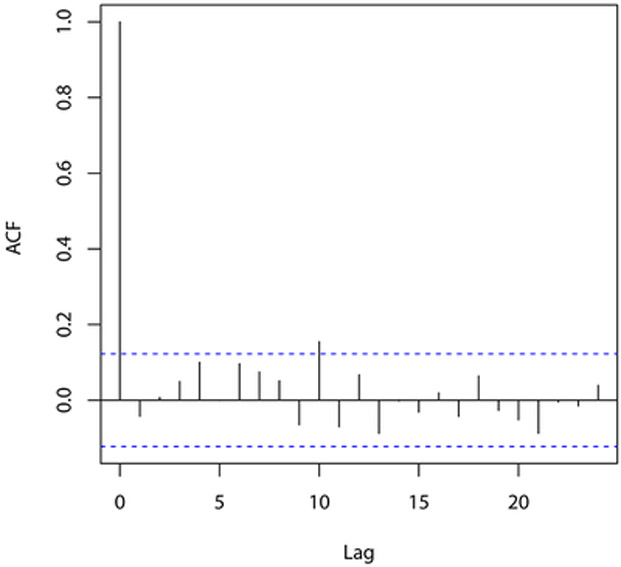
for i = 1, …, n, where $\widehat{\eta }=({\widehat{\beta }}_1,{\widehat{\beta }}_2,{\widehat{\sigma }}^2,\widehat{\theta },{\widehat{\tau }}^2)$, F_si(· ∣ y_i–1, …, y₁; η) is the conditional cdf of Y(s_i) given Y(s_i–1),…, Y(s₁) and U₁,…,U_n is an independent random sample from the unif(0,1) distribution; these are computed using the R package gcmr. If the model is correctly specified, then r₁,…,r_n behave (approximately) as a random sample from the standard normal distribution. Figure 3 displays different graphical summaries of these residuals. All of them support the normality assumption, and consequently the adequacy of the fitted model.

Figure 3:

Graphical summaries of residuals from the fitted Gaussian copula model with negative binomial marginals.

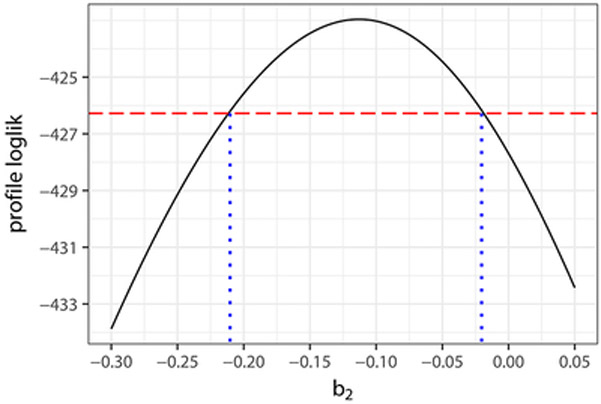
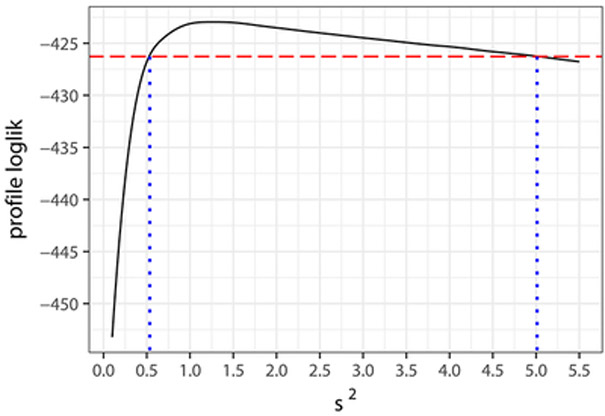
Finally, likelihood–based inferences are possible using the GHK method. Figure 4 displays the profile log–likelihoods of β₂ and σ² under the NB2 model, from which follow that (approximate) 99% confidence intervals for these parameters are (−0.210, −0.019) and (0.534, 5.012), respectively; the corresponding Wald–type 99% confidence intervals are (−0.206, −0.018) and (0.031, 2.524). These support even more strongly the above conclusions regarding the presence of a negative association between the number of hickory and maple trees in the quadrats, and the existence of overdispersion in the marginal distributions of the counts.

Figure 4:

Profile likelihoods of the parameter β₂ and σ² under the NB2 marginal and their corresponding 99% confidence intervals.

A script with code to replicate the data analysis of this section can be obtained from https://github.com/hanzifei/Code_GC_MLE.

8. Conclusions

In this work we considered the computationally challenging task of (numerically) computing MLE of parameters in Gaussian copula models for geostatistical count data. We reviewed two previously proposed Monte Carlo methods to approximate the likelihood function, the GB and GHK methods, and investigated the implementation for this model of the DC method. We also proposed a simple and fast way to obtain initial values that are needed for all the methods.

Based on our simulation study, the statistical properties of the MLE approximated by the three methods are similar. Of the three types of confidence intervals we explored, the profile likelihood confidence intervals displayed the best coverage, at the price of being on average wider, while the Wald–type confidence intervals displayed the worst coverage. Overall, we recommend using the former. The estimation bias of MLE and undercoverage of confidence intervals can be substantial when the sample size is small, but these become better as the sample size grows following an increasing domain asymptotic regime.

In terms of computational effort, the GHK method is the least computationally intensive of the three methods, while the GB and DC methods are much more computationally intensive, about ten times more on average. Because of all of the above, the GHK method provides the best balance between statistical efficiency and computational efficiency, so it is the method we recommend. Nevertheless, it is worth noting the ‘hybrid’ method proposed by Baghishani et al. (2012) that blends the DC method and integrated nested Laplace approximations. That article showed that the computational effort of this hybrid method is substantially smaller than that of the DC methods when fitting some simple hierarchical models, so investigating the properties of this hybrid method for fitting Gaussian copula models to geostatistical count data seems a worthwhile research problem.

Finally, note that spatial prediction/interpolation is often the end goal of many geostatistical analyses. For parameter estimates $\widehat{\eta }$ and prediction location s0, the (plug–in) predictive distribution ${\mathrm{P}}_{\widehat{\eta }}(Y({\mathbf{s}}_0)=y_0\mid \mathit{Y}=\mathit{y})$ is the ratio of two multivariate integrals like that in (5), so these can also be approximated using the GHK method. Details on this prediction method are given in Han and De Oliveira (2018).

Appendix A

Proof of Identity (7)

For the inverse of the map (6) we have

$$\frac{d}{{\mathit{du}}_i}{z}_i(u_i)=\frac{-f_{{\mathbf{s}}_i}(y_i;\psi )}{\varphi ({\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_i}(y_i;\psi )-u_i{f}_{{\mathbf{s}}_i}(y_i;\psi ))}=\frac{-f_{{\mathbf{s}}_i}(y_i;\psi )}{\varphi (z_i(u_i))},i=1,\dots ,n.$$

Since z_i is a function of u_i alone, the Jacobian matrix J = ∂(z₁(u₁), … , z_n(u_n))/∂(u₁, … , u_n) of the inverse mapping is diagonal, so

$$\mid \text{det}(J)\mid =\prod _{i=1}^n\frac{f_{{\mathbf{s}}_i}(y_i;\psi )}{\varphi (z_i(u_i))}.$$

Since (6) maps (Φ⁻¹(F_s1(y₁–1; ψ)), Φ⁻¹(F_s1(y₁; ψ))) ×⋯× (Φ⁻¹(F_sn(y_n–1; ψ)), Φ⁻¹(F_sn(y_n; ψ))) into (0, 1)ⁿ, by the change of variable formula for multivariate integrals, (5) becomes

$$\begin{array}{cc}\hfill L(\eta ;\mathit{y})& ={\int }_0^1\cdots {\int }_0^1{\varphi }_n(z_1(u_1),\dots ,z_n(u_n);{\mathrm{\Psi }}_{\vartheta })\mid \text{det}(J)\mid {\mathit{du}}_1\dots {\mathit{du}}_n\hfill \\ \hfill & =\prod _{i=1}^n{f}_{{\mathbf{s}}_i}(y_i;\psi )\cdot {\int }_0^1\cdots {\int }_0^1\frac{{\varphi }_n(z_1(u_1),\dots ,z_n(u_n);{\mathrm{\Psi }}_{\vartheta })}{\prod _{i=1}^n\varphi (z_i(u_i))}{\mathit{du}}_1\dots {\mathit{du}}_n\hfill \\ \hfill & =\prod _{i=1}^n{f}_{{\mathbf{s}}_i}(y_i;\psi )\cdot {\int }_0^1\cdots {\int }_0^1{\mid {\mathrm{\Psi }}_{\vartheta }\mid }^{-1∕2}\text{exp}\left(-\frac{1}{2}{\mathit{z}}^{⊺}(\mathbf{u})({\mathrm{\Psi }}_{\vartheta }^{-1}-{\mathit{I}}_n)\mathit{z}(\mathbf{u})\right)d\mathbf{u}.\hfill \end{array}$$

Equivalence Between (7) and Madsen and Fang Likelihood Representation

Madsen and Fang (2011) showed that the likelihood in (5) can be written as

$$L(\eta ;\mathit{y})={\mathrm{E}}_{\mathit{U}}\left\{{\mid {\mathrm{\Psi }}_{\vartheta }\mid }^{-1∕2}\text{exp}\left(-\frac{1}{2}{\mathit{z}}^{\ast ⊺}(\mathit{U})({\mathrm{\Psi }}_{\vartheta }^{-1}-{\mathit{I}}_n){\mathit{z}}^{\ast }(\mathit{U})\right)\cdot \prod _{i=1}^n{f}_{{\mathbf{s}}_i}^{\ast }(y_i-U_i;\psi )\right\},$$ (12)

where

$${\mathit{z}}^{\ast }(\mathit{U})={\left({\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_1}^{\ast }(y_1-U_1;\psi )),\dots ,{\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_n}^{\ast }(y_n-U_n;\psi ))\right)}^{⊺},$$

U = (U₁,…,U_n) ~ unif((0, 1)ⁿ), and $f_{{\mathbf{s}}_i}^{\ast }(\cdot ;\psi )$ and $F_{{\mathbf{s}}_i}^{\ast }(\cdot ;\psi )$ are, respectively, the pdf and cdf of the ‘continuously extended’ random variable $Y_i^{\ast }=Y({\mathbf{s}}_i)-U_i$. Now, it can be shown that for every s ∈ D and $y\in \mathbb{R}$, $F_{\mathbf{s}}^{\ast }(y;\psi )=F_{\mathbf{s}}(\lfloor y\rfloor ;\psi )+(y-\lfloor y\rfloor )f_{\mathbf{s}}(\lfloor y+1\rfloor ;\psi )$ and $f_{\mathbf{s}}^{\ast }(y;\psi )=f_{\mathbf{s}}(\lfloor y+1\rfloor ;\psi )$, where [y] is the largest integer not greater than y. Hence for any $y\in {\mathbb{N}}_0$ and u ∈ (0, 1), we have $f_{\mathbf{s}}^{\ast }(y-u;\psi )=f_{\mathbf{s}}(y;\psi )$ and $F_{\mathbf{s}}^{\ast }(y-u;\psi )=F_{\mathbf{s}}(y-1;\psi )+(1-u)f_{\mathbf{s}}(y;\psi )=F_{\mathbf{s}}(y;\psi )-{\mathit{uf}}_{\mathbf{s}}(y;\psi )$. Substituting these into(12) shows that the right–hand sides of (12) and (7) are the same.

Proof of Identity (9)

As indicated in Section 2.2, the events {Y(s) = y} and {F_s(y – 1; ψ) < Φ(Z(s)) ≤ F_s(y; ψ)} are equivalent, so for $y\in {\mathbb{N}}_0$ and i = 1,…,n we have

$$\begin{array}{cc}\hfill & \mathrm{P}(Y({\mathbf{s}}_i)=y\mid \Gamma ({\mathbf{s}}_i)={\gamma }_i;\psi ,{\tau }^2)\hfill \\ \hfill =& \mathrm{P}({\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_i}(y-1;\psi ))<Z({\mathbf{s}}_i)\le {\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_i}(y;\psi ))\mid \Gamma ({\mathbf{s}}_i)={\gamma }_i;\psi ,{\tau }^2)\hfill \\ \hfill =& \mathrm{P}\left(\phantom{\mid }\frac{{\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_i}(y-1;\psi ))-{\gamma }_i}{\tau }<\frac{ϵ({\mathbf{s}}_i)}{\tau }\le \frac{{\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_i}(y;\psi ))-{\gamma }_i}{\tau }\mid \Gamma ({\mathbf{s}}_i)={\gamma }_i;\psi ,{\tau }^2\right)\hfill \\ \hfill =& \mathrm{\Phi }\left(\frac{{\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_i}(y;\psi ))-{\gamma }_i}{\tau }\right)-\mathrm{\Phi }\left(\frac{{\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_i}(y-1;\psi ))-{\gamma }_i}{\tau }\right).\hfill \end{array}$$

Appendix B

MCMC Algorithm for the DC Method

In the Gaussian copula model, $\beta \in {\mathbb{R}}^p$, θ, σ² > 0 and τ² ∈ [0, 1]. To ease updating the parameters using a random–walk Metropolis–Hastings algorithm with Gaussian proposals, we transform each parameter to the real line. Specifically, let ξ₁ = β, ξ₂ = log(σ²), ξ₃ = log(θ) and ξ₄ = logit(τ²). As customary in the statistical literature, q_a(· ∣ a^old) would denote the proposal distribution for the state component ‘a’ in the current iteration, given its value in the previous iteration is a^old. The algorithm proceeds as follows:

Step 0: Choose the initial values for the parameters η⁽⁰⁾; simulate ${\gamma }_1^{(0)},\dots ,{\gamma }_K^{(0)}\stackrel{\text{iid}}{\sim }{\mathrm{N}}_n(0,R_{\theta (0)})$ and set the initial values for the replicated latent process as ${\gamma }_{(K)}^{(0)}=({\gamma }_1^{(0)},\dots ,{\gamma }_K^{(0)})$; set the tuning constants c₁, c₂, c₃, c₄, c₅ > 0; set l = 0.

Step 1: Simulate independently ${\beta }^{\ast }\sim {\mathrm{N}}_p({\beta }^{(l)},c_1{I}_p),{\xi }_2^{\ast }\sim \mathrm{N}({\xi }_2^{(l)},c_2)$ and U₁ ~ unif(0, 1).

Step 2: Compute the acceptance probability α₁ = min{1, t₁}, where

$$\begin{array}{cc}\hfill t_1=& \frac{{\pi }_{(K)}({\beta }^{\ast },{\sigma }^{2\ast }\mid {\theta }^{(l)},{\tau }^{2(l)},{\gamma }_{(K)}^{(l)},{\mathit{y}}_{(K)})q_{\beta }({\beta }^{(l)}\mid {\beta }^{\ast })q_{{\sigma }^2}({\sigma }^{2(l)}\mid {\sigma }^{2\ast })}{{\pi }_{(K)}({\beta }^{(l)},{\sigma }^{2(l)}\mid {\theta }^{(l)},{\tau }^{2(l)},{\gamma }_{(K)}^{(l)},{\mathit{y}}_{(K)})q_{\beta }({\beta }^{\ast }\mid {\beta }^{(l)})q_{{\sigma }^2}({\sigma }^{2\ast }\mid {\sigma }^{2(l)})}\hfill \\ \hfill =& \frac{\pi ({\beta }^{\ast })\pi ({\sigma }^{2\ast })\prod _{k=1}^K\prod _{i=1}^n{h}_i(y_i\mid {\gamma }_{\mathit{ki}}^{(l)};{\beta }^{\ast },{\sigma }^{2\ast },{\tau }^{2(l)}){\sigma }^{2\ast }}{\pi ({\beta }^{(l)})\pi ({\sigma }^{2(l)})\prod _{k=1}^K\prod _{i=1}^n{h}_i(y_i\mid {\gamma }_{\mathit{ki}}^{(l)};{\beta }^{(l)},{\sigma }^{2(l)},{\tau }^{2(l)}){\sigma }^{2(l)}},\hfill \end{array}$$

where it was used that $\frac{q_{\beta }({\beta }^{(l)}\mid {\beta }^{\ast })}{q_{\beta }({\beta }^{\ast }\mid {\beta }^{(l)})}=1$ and $\frac{q_{{\sigma }^2}({\sigma }^{2(l)}\mid {\sigma }^{2\ast })}{q_{{\sigma }^2}({\sigma }^{2\ast }\mid {\sigma }^{2(l)})}=\frac{{\sigma }^{2\ast }}{{\sigma }^{2(l)}}$. Then set

$$({\beta }^{(l+1)},{\sigma }^{2(l+1)})=\{\begin{array}{cc}({\beta }^{\ast },{\sigma }^{2\ast })\hfill & \text{if}{U}_1<{\alpha }_1\hfill \\ ({\beta }^{(l)},{\sigma }^{2(l)})\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}.$$

Step 3: Simulate independently ${\xi }_3^{\ast }\sim \mathrm{N}({\xi }_3^{(l)},c_3)$, ${\xi }_4^{\ast }\sim \mathrm{N}({\xi }_4^{(l)},c_4)$ and U₂ ~ unif(0, 1). The latent process is updated via the Langevin–Hastings algorithm which uses gradient information of the target density (Christensen et al., 2006). For k, k′ = 1,…, K, the proposed k^th set of random effects is simulated independently of the k′^th set (k ≠ k′) as then set ${\gamma }_{(K)}^{\ast }=({\gamma }_1^{\ast },\dots ,{\gamma }_K^{\ast })$.

$${\gamma }_k^{\ast }\sim {\mathrm{N}}_n\left({\gamma }_k^{(l)}+\frac{c_5}{2}\nabla \log \pi ({\gamma }_k^{(l)}\mid \mathit{y},{\beta }^{(l+1)},{\sigma }^{2(l+1)},{\theta }^{(l)},{\tau }^{2(l)}),c_5{I}_n\right);$$

Step 4: Compute the acceptance probability α₂ = min{1, t₂}, where

$$\begin{array}{cc}\hfill t_2=& \frac{{\pi }_{(K)}({\theta }^{\ast },{\tau }^{2\ast },{\gamma }_{(K)}^{\ast }\mid {\beta }^{(l)},{\sigma }^{2(l)},{\mathit{y}}_{(K)})q_{\theta }({\theta }^{(l)}\mid {\theta }^{\ast })q_{{\tau }^2}({\tau }^{2(l)}\mid {\tau }^{2\ast })q_{{\gamma }_{(K)}}({\gamma }_{(K)}^{(l)}\mid {\gamma }_{(K)}^{\ast })}{{\pi }_{(K)}({\theta }^{(l)},{\tau }^{2(l)},{\gamma }_{(K)}^{(l)}\mid {\beta }^{(l)},{\sigma }^{2(l)},{\mathit{y}}_{(K)})q_{\theta }({\theta }^{\ast }\mid {\theta }^{(l)})q_{{\tau }^2}({\tau }^{2\ast }\mid {\tau }^{2(l)})q_{{\gamma }_{(K)}}({\gamma }_{(K)}^{\ast }\mid {\gamma }_{(K)}^{(l)})}\hfill \\ \hfill =& \frac{\pi ({\theta }^{\ast })\pi ({\tau }^{2\ast })\prod _{k=1}^K{\varphi }_n({\gamma }_k^{\ast };(1-{\tau }^{2\ast })R_{{\theta }^{\ast }})\prod _{k=1}^K\prod _{i=1}^n{h}_i(y_i\mid {\gamma }_{\mathit{ki}}^{\ast };{\beta }^{(l)},{\sigma }^{2(l)},{\tau }^{2\ast })q_{{\gamma }_{(K)}}({\gamma }_{(K)}^{(l)}\mid {\gamma }_{(K)}^{\ast }){\theta }^{\ast }{\tau }^{2\ast }(1-{\tau }^{2\ast })}{\pi ({\theta }^{(l)})\pi ({\tau }^{2(l)})\prod _{k=1}^K{\varphi }_n({\gamma }_k^{\ast };(1-{\tau }^{2(l)})R_{{\theta }^{(l)}})\prod _{k=1}^K\prod _{i=1}^n{h}_i(y_i\mid {\gamma }_{\mathit{ki}}^{(l)};{\beta }^{(l)},{\sigma }^{2(l)},{\tau }^{2(l)})q_{{\gamma }_{(K)}}({\gamma }_{(K)}^{\ast }\mid {\gamma }_{(K)}^{(l)}){\theta }^{(l)}{\tau }^{2(l)}(1-{\tau }^{2(l)})}\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill q_{{\gamma }_{(K)}}({\gamma }_{(K)}^{\ast }\mid {\gamma }_{(K)}^{(l)})=& \prod _{k=1}^K{q}_{{\gamma }_k}({\gamma }_k^{\ast }\mid {\gamma }_k^{(l)})\hfill \\ \hfill =& \prod _{k=1}^K{\varphi }_n\left({\gamma }_k^{\ast }-{\gamma }_k^{(l)}-\frac{c_5}{2}\nabla \log \pi ({\gamma }_k^{(l)}\mid \mathit{y},{\beta }^{(l+1)},{\sigma }^{2(l+1)},{\theta }^{(l)},{\tau }^{2(l)});c_5{I}_n\right),\hfill \end{array}$$

$q_{{\gamma }_{(K)}}({\gamma }_{(K)}^{(l)}\mid {\gamma }_{(K)}^{\ast })$ is similarly defined, and it was used that $\frac{q_{\theta }({\theta }^{(l)}\mid {\theta }^{\ast })}{q_{\theta }({\theta }^{\ast }\mid {\theta }^{(l)})}=\frac{{\theta }^{\ast }}{{\theta }^{(l)}}$ and $\frac{q_{{\tau }^2}({\tau }^{2(l)}\mid {\tau }^{2\ast })}{q_{{\tau }^2}({\tau }^{2\ast }\mid {\tau }^{2(l)})}=\frac{{\tau }^{2\ast }(1-{\tau }^{2\ast })}{{\tau }^{2(l)}(1-{\tau }^{2(l)})}$. Then set

$$({\theta }^{(l+1)},{\tau }^{2(l+1)},{\gamma }_{(K)}^{(l+1)})=\{\begin{array}{cc}({\theta }^{\ast },{\tau }^{2\ast },{\gamma }_{(K)}^{\ast })\hfill & \text{if}{U}_2<{\alpha }_2\hfill \\ ({\theta }^{(l)},{\tau }^{2(l)},{\gamma }_{(K)}^{(l)})\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}.$$

Step 5: Increase l by 1, and repeat steps 1–4 until the states have reached the equilibrium distribution of the Markov chain.

Posterior Calculation of the Gradient of the Latent Process

The log of the full conditional distribution of the latent field γ is given by

$$\log (\pi (\gamma \mid \mathit{y},\psi ,\theta ,{\tau }^2))=\log ({\varphi }_n(\gamma ;(1-{\tau }^2)R_{\theta }))+\sum _{i=1}^n\log (h_i(y_i\mid {\gamma }_i;\psi ,{\tau }^2))+\text{const}.$$

For i = 1,…,n we have

$$\frac{\partial }{{\partial }_{{\gamma }_i}}\log (h_i(y_i\mid {\gamma }_i;\psi ,{\tau }^2))=\frac{\varphi \left(\frac{{\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_i}(y_i-1;\psi ))-{\gamma }_i}{\tau }\right)-\varphi \left(\frac{{\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_i}(y_i;\psi ))-{\gamma }_i}{\tau }\right)}{\tau \left[\mathrm{\Phi }\left(\frac{{\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_i}(y_i;\psi ))-{\gamma }_i}{\tau }\right)-\mathrm{\Phi }\left(\frac{{\mathrm{\Phi }}^{-1}(F_{{\mathbf{s}}_i}(y_i-1;\psi ))-{\gamma }_i}{\tau }\right)\right]},$$ (13)

and since $\log ({\varphi }_n(\gamma ;(1-{\tau }^2)R_{\theta }))=-\frac{1}{2}(\log \mid (1-{\tau }^2)R_{\theta }\mid +{(1-{\tau }^2)}^{-1}{\gamma }^{⊺}{R}_{\theta }^{-1}\gamma +n\log (2\pi )),$

$$\frac{\partial }{\partial \gamma }\log ({\varphi }_n(\gamma ;(1-{\tau }^2)R_{\theta }))=-\frac{R_{\theta }^{-1}\gamma }{1-{\tau }^2}.$$ (14)

Combining (13) and (14) we get ∇ log (π(γ ∣ γ, ∣ y, ψ, θ, τ²)).

Remark 4. The tuning constants c₁,…,c₄ could be selected by trial and error until both Metropolis–Hastings steps have good acceptance probabilities (in the range 0.25–0.5, say). Instead, in the simulation we used the algorithm in Haario et al. (1999) that automatically adjusts these constants every so often. Let ${\xi }_1^{(l)}$, ${\xi }_2^{(l)}$, ${\xi }_3^{(l)}$, ${\xi }_4^{(l)}$ be the transformed parameters at the 1^th iteration. The variances of their proposal distributions are adjusted every 1000 iterations, at iterations l ∈ {1001, 2001, …}, as $q_{{\xi }_1}(\cdot \mid {\xi }_1^{(l-1000)},\dots ,{\xi }_1^{(l-1)})\sim \mathrm{N}({\xi }_1^{(l-1)},r_{d_1}^2\mathrm{v}\widehat{\mathrm{a}}\mathrm{r}({\xi }_1^{(l)}))$, $q_{{\xi }_2}(\cdot \mid {\xi }_2^{(l-1000)},\dots ,{\xi }_2^{(l-1)})\sim \mathrm{N}({\xi }_2^{(l-1)},r_{d_1}^2\mathrm{v}\widehat{\mathrm{a}}\mathrm{r}({\xi }_2^{(l)}))$, $q_{{\xi }_3}(\cdot \mid {\xi }_3^{(l-1000)},\dots ,{\xi }_3^{(l-1)})\sim \mathrm{N}({\xi }_3^{(l-1)},r_{d_2}^2\mathrm{v}\widehat{\mathrm{a}}\mathrm{r}({\xi }_3^{(l)}))$ and $q_{{\xi }_4}(\cdot \mid {\xi }_4^{(l-1000)},\dots ,{\xi }_4^{(l-1)})\sim \mathrm{N}({\xi }_4^{(l-1)},r_{d_2}^2\mathrm{v}\widehat{\mathrm{a}}\mathrm{r}({\xi }_4^{(l)}))$, where $\mathrm{v}\widehat{\mathrm{a}}\mathrm{r}({\xi }_1^{(l)})$, $\mathrm{v}\widehat{\mathrm{a}}\mathrm{r}({\xi }_2^{(l)})$, $\mathrm{v}\widehat{\mathrm{a}}\mathrm{r}({\xi }_3^{(l)})$ and $\mathrm{v}\widehat{\mathrm{a}}\mathrm{r}({\xi }_4^{(l)})$ are the sample variance matrices computed from their previous 1000 iterations, $r_{d_1}=2.38∕\sqrt{d_1}$ and $r_{d_2}=2.38∕\sqrt{d_2}$, with d₁ and d₂ the dimensions of $({\xi }_1^{(l)},{\xi }_2^{(l)})$ and $({\xi }_3^{(l)},{\xi }_4^{(l)})$.