A Semiparametric Bayesian Approach to Dropout in Longitudinal Studies with Auxiliary Covariates

Abstract

We develop a semiparametric Bayesian approach to missing outcome data in longitudinal studies in the presence of auxiliary covariates. We consider a joint model for the full data response, missingness and auxiliary covariates. We include auxiliary covariates to “move” the missingness “closer” to missing at random (MAR). In particular, we specify a semiparametric Bayesian model for the observed data via Gaussian process priors and Bayesian additive regression trees. These model specifications allow us to capture non-linear and non-additive effects, in contrast to existing parametric methods. We then separately specify the conditional distribution of the missing data response given the observed data response, missingness and auxiliary covariates (i.e. the extrapolation distribution) using identifying restrictions. We introduce meaningful sensitivity parameters that allow for a simple sensitivity analysis. Informative priors on those sensitivity parameters can be elicited from subject-matter experts. We use Monte Carlo integration to compute the full data estimands. Performance of our approach is assessed using simulated datasets. Our methodology is motivated by, and applied to, data from a clinical trial on treatments for schizophrenia.

1. Introduction

In longitudinal clinical studies, the research objective is often to make inference on a subject’s full data response conditional on covariates that are of primary interest; for example, to calculate the treatment effect of a test drug at the end of a study. However, the vector of responses for a research subject is often incomplete due to dropout. Dropout is typically non-ignorable (Rubin, 1976; Daniels and Hogan, 2008) and in such cases the joint distribution of the full data response and missingness needs to be modeled. In addition to the covariates that are of primary interest, we would often have access to some auxiliary covariates (often collected at baseline) that are not desired in the model for the primary research question. Such variables can often provide information about the missing responses and missing data mechanism. For example, missing at random (MAR) (Rubin, 1976) might only hold conditionally on auxiliary covariates (Daniels and Hogan, 2008). In this setting, auxiliary covariates should be incorporated in the joint model as well, but we should proceed with inference unconditional on these auxiliary covariates.

The full data distribution can be factored into the observed data distribution and the extrapolation distribution (Daniels and Hogan, 2008). The observed data distribution can be identified by the observed data, while the extrapolation distribution cannot. Identifying the extrapolation distribution relies on untestable assumptions such as parametric models for the full data distribution or identifying restrictions (Linero and Daniels, 2018). Such assumptions can be indexed by unidentified parameters called sensitivity parameters (Daniels and Hogan, 2008). The observed data do not provide any information to estimate the sensitivity parameters. Under the Bayesian paradigm, informative priors can be elicited from subject-matter experts and be placed on those sensitivity parameters. Finally, it is desirable to conduct a sensitivity analysis (Daniels and Hogan, 2008; National Research Council, 2011) to assess the sensitivity of inferences to such assumptions. The inclusion of auxiliary covariates can ideally reduce the extent of sensitivity analysis that is needed for drawing accurate inferences.

In this paper, we propose a Bayesian semiparametric model for the joint distribution of the full data response, missingness and auxiliary covariates. We use identifying restrictions to identify the extrapolation distribution and introduce sensitivity parameters that are meaningful to subject-matter experts and allow for a simple sensitivity analysis.

1.1. Missing Data in Longitudinal Studies

Literature about longitudinal missing data with non-ignorable dropout can be mainly divided into two categories: likelihood-based and moment-based (semiparametric). Likelihood-based approaches include selection models (e.g. Heckman, 1979; Diggle and Kenward, 1994; Molenberghs et al., 1997), pattern mixture models (e.g. Little, 1993, 1994; Hogan and Laird, 1997) and shared-parameter models (e.g. Wu and Carroll, 1988; Follmann and Wu, 1995; Pulkstenis et al., 1998; Henderson et al., 2000). These three types of models differ from how the joint distribution of the response and missingness is factorized. Likelihood-based approaches often make strong parametric model assumptions to identify the full data distribution. For a comprehensive review see, for example, Daniels and Hogan (2008) or Little and Rubin (2014). Moment-based approaches, on the other hand, typically specify a semiparametric model for the marginal distribution of the response, and a semiparametric or parametric model for the missingness conditional on the response. Moment-based approaches are in general more robust to model misspecification since they make minimal distributional assumptions. See, for example, Robins et al. (1995); Rotnitzky et al. (1998); Scharfstein et al. (1999); Tsiatis (2007); Tsiatis et al. (2011).

There are several recent papers under the likelihood-based paradigm that are relevant to our approach, such as Wang et al. (2010); Linero and Daniels (2015); Linero (2017); Linero and Daniels (2018). These papers specify Bayesian semiparametric or nonparametric models for the observed data distribution, and thus have similar robustness to moment-based approaches. However, existing approaches do not utilize information from auxiliary covariates. We will highlight more of our contribution and distinction compared to existing methods, in particular Linero and Daniels (2015) and Linero (2017), after we have introduced the required notation. In the presence of auxiliary covariates, Daniels et al. (2014) model longitudinal binary responses using a parametric model under ignorable missingness. Our goal is to develop a flexible Bayesian approach to longitudinal missing data with non-ignorable dropout that also allows for incorporating auxiliary covariates. As mentioned earlier, the reason to include auxiliary covariates is that we anticipate it will make the missingness “closer” to MAR.

1.2. Notation and Terminology

We introduce some notation and terminology as follows. Consider the responses for a subject i at J time points. Let ${\mathit{Y}}_i=(Y_{i1},\hspace{0.17em}\dots \hspace{0.17em},Y_{iJ})$ be the vector of longitudinal outcomes that was planned to be collected, ${\overline{\mathit{Y}}}_{ij}=(Y_{i1},\hspace{0.17em}\dots \hspace{0.17em},Y_{ij})$ be the history of outcomes through the first j times, and ${\tilde{\mathit{Y}}}_{ij}=(Y_{i,j+1},\hspace{0.17em}\dots \hspace{0.17em},Y_{iJ})$ be the future outcomes after time j. Let Si denote the dropout time or dropout pattern, which is defined as the last time a subject’s response is recorded, i.e. S_i = max{j : Y_ij is observed}. Missingness is called monotone if Y_ij is observed for all j ≤ S_i, and missingness is called intermittent if Y_ij is missing for some j < S_i. For monotone missingness, S_i captures all the information about missingness. In the following discussion, we will concern ourselves with monotone missingness. Dropout is called random (Diggle and Kenward, 1994) if the dropout process only depends on the observed responses, i.e. the missing data are MAR; dropout is called informative if the dropout process also depends on the unobserved responses, i.e. the missing data are missing not at random (MNAR). We denote by X_i the covariates that are of primary interest, and V_i = (V_i1,…,V_iQ) the Q auxiliary covariates that are not of primary interest. Those auxiliary covariates should be related to the outcome and missingness. The observed data for subject i is (${\overline{\mathit{Y}}}_{i{S}_i}$, S_i, V_i, X_i), and the full data is (Y_i, S_i,V_i, X_i). In general, we are interested in expectation of the form E[t (Y_i) | X_i], where t denotes some functional of Y_i. Finally, denote by p (y, s, v | x, ω) the joint model for the full data response, missingness and auxiliary covariates conditional on the covariates that are of primary interest, where ω represents the parameter vector.

1.3. The Schizophrenia Clinical Trial

Our work is motivated by a multicenter, randomized, double-blind clinical trial on treatments for schizophrenia. The trial data were previously analyzed in Linero and Daniels (2015), which took a Bayesian nonparametric approach, but did not utilize information from the auxiliary covariates. For this clinical trial, the longitudinal outcomes are the positive and negative syndrome scale (PANSS) scores, which measure the severity of symptoms for patients with schizophrenia (Kay et al., 1987). The outcomes are collected at J = 6 time points corresponding to baseline, day 4 after baseline, and weeks 1, 2, 3 and 4 after baseline. The possible dropout patterns are S_i = 2, 3, 4, 5, 6. The covariate of primary interest is treatment, with X_i = T, A or P corresponding to test drug, active control or placebo, respectively. In addition, we have access to Q = 7 auxiliary covariates including age, onset (of schizophrenia) age, height, weight, country, sex and education level.

The dataset consists of N = 204 subjects, with 45 subjects for the active control arm, 78 subjects for the placebo arm, and 81 subjects for the test drug arm. Detailed individual trajectories and mean responses over time for the three treatment arms can be found in Appendix Figure A.1. The dropout rates are 33.3%, 20.0% and 25.6% for the test drug, active control and placebo arms, respectively. Subjects drop out for a variety of reasons. Some reasons including adverse events (e.g. occurrence of side effects), pregnancy and protocol violation are thought to be random dropouts, while the other reasons such as disease progression, lack of efficacy, physician decision and withdraw by patient are thought to be informative dropouts. It is ideal to treat those reasons differently while making inference. The informative dropout rates are 29.6%, 15.6% and 25.6% for the test drug, active control and placebo arms, respectively. Detailed dropout rates for each dropout pattern can be found in Appendix Table A.1. The dataset has a few intermittent missing outcomes (1 for the test drug arm, 1 for the active control arm, and 2 for the placebo arm). We focus our study on monotone missingness and assume partial ignorability (Harel and Schafer, 2009) for the few intermittent missing outcomes.

The goal of this study is to estimate the change from baseline treatment effect,

$$r_x=\text{E}[Y_{i6}-Y_{i1}|X_i=x].$$

In particular, the treatment effect improvements over placebo, i.e. r_T – r_P and r_A – r_P, are of interest.

1.4. Overview and Contribution

We stratify the model by treatment, and suppress the treatment variable x to simplify notation hereafter. The extrapolation factorization (Daniels and Hogan, 2008) is

$$p(\mathit{y},s,\mathit{v}|\mathit{\omega })=p({\mathit{y}}_s|{\overline{\mathit{y}}}_s,s,\mathit{v},{\mathit{\omega }}_E)p({\overline{\mathit{y}}}_s,s,\mathit{v}|{\mathit{\omega }}_o),$$

where the extrapolation distribution, $p({\mathit{y}}_s|{\overline{\mathit{y}}}_s,s,\mathit{v},{\mathit{\omega }}_E)$, is not identified by the data in the absence of uncheckable assumptions or constraints on the parameter space. The observed data distribution $p({\overline{\mathit{y}}}_s,s,\mathit{v}|{\mathit{\omega }}_o)$ is identified and can be estimated semiparametrically or nonparametrically. We factorize the observed data distribution based on pattern-mixture modeling (Little, 1993),

$$p({\overline{\mathit{y}}}_s,s,\mathit{v}|{\mathit{\omega }}_o)=p({\overline{\mathit{y}}}_s|s,\mathit{v},\mathit{\pi })p(s|\mathit{v},\mathit{\phi })p(\mathit{v}|\mathit{\eta }),$$ (1)

where we assume distinct parameters ω_o = (π, φ, η) parameterizing the response model, the missingness and the distribution of the auxiliary covariates, respectively.

The model specification (1) brings two challenges:

1. For the models $p({\overline{\mathit{y}}}_s|s,\mathit{v},\mathit{\pi })$ and p (s | v, φ), it is unclear how the auxiliary covariates are related to the responses and dropout patterns. For example, the auxiliary covariates contain height and weight, which might not have a linear and additive effect on the responses. For example, the responses might have a linear relationship with the body mass index, which is calculated by weight / height².

2. For the model $p({\overline{\mathit{y}}}_s|s,\mathit{v},\mathit{\pi })$, the observed patterns are sparse. For example the dropout pattern, S_i = 2 for the active control arm has only 1 observation.

To mitigate challenge 1, we specify semiparametric models for $p({\overline{\mathit{y}}}_s|s,\mathit{v},\mathit{\pi })$ and p (s | v, φ) via Gaussian process (GP) priors and Bayesian additive regression trees (BART), respectively. Such models, although still making some parametric assumptions, are highly flexible and robust to model misspecification. To address challenge 2, we utilize informative priors such as autoregressive (AR) and conditional autoregressive (CAR) priors to share information across neighboring patterns. Detailed model specifications will be described in Section 2.

We would like to emphasize the distinction between our approach and the approaches proposed in Linero and Daniels (2015) and Linero (2017). The earlier works by Linero and Daniels and Linero specified the observed data distribution (1) based on a working model for the full data constructed as a Dirichlet process mixture of selection models, i.e., $p^{\ast }(\mathit{y},s|\mathit{\omega })=\int p(\mathit{y}|{\mathit{\theta }}_1)p(s|\mathit{y},{\mathit{\theta }}_2)F(d\mathit{\theta })$ with F following a Dirichlet process; the approaches did not consider covariates but they could be added in a very simple way by introducing them independently (from y and s and from each other in the Dirichlet process mixture) as mentioned in the discussion of Linero (2017). These approaches can thus accommodate (auxiliary) covariates but they were not constructed to include them in a careful, efficient way. In contrast, the proposed approach was design specifically to allow (auxiliary) covariates and to estimate an average (mean) treatment effect. To address the former, we use a pattern-mixture model parameterization, and exploit the expected structure including sparse patterns and similar covariate effects across patterns and over time via GP, AR/CAR priors, and shrinkage priors. Later we will show through simulation studies that our approach indeed performs better than the approaches proposed in Linero and Daniels (2015) and Linero (2017) with a simple extension that accommodates auxiliary covariates.

The remainder of this article is structured as follows. In Section 2 we specify Bayesian (semiparametric) models for (1). In Section 3, we use identifying restrictions to identify the extrapolation distribution. In Section 4, we describe our posterior inference and computation approaches. In Section 5, we present simulation studies to validate our model and compare with results using other methods. In Section 6, we apply our method to a clinical trial on treatments for schizophrenia. We conclude with a discussion in Section 7.

2. Probability Model for the Observed Data

2.1. Model for the Observed Data Responses Conditional on Pattern and Auxiliary Covariates

We define the model for observed data responses conditional on drop out time and auxiliary covariates, i.e.$p({\overline{\mathit{y}}}_s|s,\mathit{v},\mathit{\pi })$, as follows. The distribution $p({\overline{\mathit{y}}}_s|s,\mathit{v},\mathit{\pi })$ can be factorized as

$$p_s\left({\overline{\mathit{y}}}_s|\mathit{v},\mathit{\pi }\right)=p_s(y_s|{\overline{\mathit{y}}}_{s-1},\mathit{v},\mathit{\pi })\cdots p_s(y_2|y_1,\mathit{v},\mathit{\pi })p_s(y_1|\mathit{v},\mathit{\pi }),$$ (2)

where the subscript s corresponds to conditioning on dropping out pattern S = s.

We assume

$$\left(Y_j|{\overline{\mathit{Y}}}_{j-1}={\overline{\mathit{y}}}_{j-1},S=s,\mathit{V}=\mathit{v},a_0,a,\mathit{\pi }\right)=\{\begin{array}{ll}{a}_0(\mathit{v},s)+{\epsilon }_{1s},\hfill & j=1;\hfill \\ a(y_{j-1},\mathit{v},j,s)+{\overline{\mathit{y}}}_{j-2}^T{\mathit{\varphi }}_{js}+{\epsilon }_{js},\hfill & j\ge 2,\hfill \end{array}$$ (3)

where j = 1,…, s; s = 2,…, J. Here a₀ and a are stochastic processes indexed by ${\mathcal{U}}_0=\mathcal{V}\times {\mathcal{J}}_0$ and $\mathcal{U}=\mathcal{Y}\times \mathcal{V}\times \mathcal{J}$ respectively, where $\mathcal{V}$ is the state space of v, ${\mathcal{J}}_0=\{2,\hspace{0.17em}\dots \hspace{0.17em},J\}$ is the state space of s, $\mathcal{J}\subset {\{1,\hspace{0.17em}\dots \hspace{0.17em},J\}}^2$ is the state space of (j, s), and $\mathcal{Y}$ is the state space of y_j−1. Furthermore, is the vector of lag ϕ_js coefficients (of order 2 and above) for each time/pattern, and ε_js ‘s are independent Gaussian errors,

$${\epsilon }_{js}~N(0,{\sigma }_{js}^2).$$

In order to have a flexible mean model for Y_j as a function of previous response and covariates, we place Gaussian process priors (Rasmussen and Williams, 2006) on a0 and a,

$$a_0(\mathit{v},s)~\mathcal{G}\mathcal{P}\left[{\mu }_0(\mathit{v},s),C_0(\mathit{v},s;\mathit{v}\prime ,s\prime )\right];$$

$$a(y_{j-1},\mathit{v},j,s)~\mathcal{G}\mathcal{P}\left[\mu (y_{j-1},\mathit{v},j,s),C(y_{j-1},\mathit{v},j,s;{y_{j\prime -1}}^{\prime },\mathit{v}\prime ,j\prime ,s\prime )\right],$$

with mean functions ${\mu }_0:{\mathcal{U}}_0\to ℝ$ and $\mu :\mathcal{U}\to ℝ$ and covariance functions $C_0:{\mathcal{U}}_0\times {\mathcal{U}}_0\to {ℝ}^{+}$ and $C:\mathcal{U}\times \mathcal{U}\to {ℝ}^{+}$, respectively. Specifically,

$$\begin{gathered} {\mu }_0(\mathit{v},s)\hspace{1em}\hspace{1em}\hspace{1em} ={\mathit{v}}^T{\mathit{\beta }}_{0s}+b_{1s}; \\ \mu (y_{j-1},\mathit{v},j,s)\hspace{1em}={\psi }_{js}{y}_{j-1}+{\mathit{v}}^T{\mathit{\beta }}_s+b_{js}, \end{gathered}$$ (4)

and

$$\begin{gathered} C_0(\mathit{v},s;\mathit{v}\prime ,s\prime )=\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\kappa }_0^2{D}_0(\mathit{v},s;\mathit{v}\prime ,s\prime )+{\tilde{\kappa }}_0^{2}I(\mathit{v},s;\mathit{v}\prime ,s\prime ); \\ \begin{array}{l}C(y_{j-1},\mathit{v},j,s;y_{j\prime -1}\prime ,\mathit{v}\prime ,j\prime ,s\prime )=\hspace{1em}\hspace{0.17em}{\kappa }^{2}D(y_{j-1},\mathit{v},j,s;y_{j\prime -1}\prime ,\mathit{v}\prime ,j\prime ,s\prime )+\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}{\tilde{\kappa }}^{2}I(y_{j-1},\mathit{v},j,s;y_{j\prime -1}\prime ,\mathit{v}\prime ,j\prime ,s\prime ).\end{array} \end{gathered}$$ (5)

We use two different stochastic processes a₀ and a for j = 1 and j ≥ 2. The reason is that for j = 1, a₀ represent the mean initial response with no past; for j ≥ 2, a represents the mean at subsequent thus with a measured past. In the mean functions (4), β_0s and β_s are the vectors of regression coefficients of the auxiliary covariates, ψ_js is the lag-1 coefficient, and b_js is the time/pattern specific intercepts. In the covariance functions (5), D₀(a; b) and D( a; b) are the exponential distances between a and b, defined by

$$\begin{gathered} D_0(\mathit{v},s;\mathit{v}\prime ,s\prime )=\exp \left[-\frac{{\Vert \underset{\_}{\mathit{v}}-\underset{\_}{\mathit{v}}\prime \Vert }_2^2}{2{\gamma }_{v0}^2}-\frac{\left|\underset{\_}{s}-\underset{\_}{s}\prime \right|}{{\gamma }_{s0}}\right], \\ D(y_{j-1},\mathit{v},j,s;y_{j\prime -1}\prime ,\mathit{v}\prime ,j\prime ,s\prime )=\exp [-\frac{{\Vert {\underset{\_}{y}}_{j-1}{\underset{\_}{y}}_{j\prime -1}\prime \Vert }_2^2}{2{\gamma }_y^2}-\frac{{\Vert \underset{\_}{\mathit{v}}-\underset{\_}{\mathit{v}}\prime \Vert }_2^2}{2{\gamma }_v^2}-\frac{\left|\underset{\_}{j}-\underset{\_}{j}\prime \right|}{{\gamma }_j}-\frac{\left|\underset{\_}{s}-\underset{\_}{s}\prime \right|}{{\gamma }_s}]. \end{gathered}$$

Here ${\kappa }_0^2$, ${\gamma }_{v0}$, ${\gamma }_{s0}$, ${\tilde{\kappa }}_0^2$, ${\kappa }^2$, $Y_y$, $Y_v$, $Y_j$, $Y_s$, ${\tilde{\kappa }}^2$ are the hyperparameters. Details about the hyper-priors or choices of these hyperparameters are described in Appendix A.2. The values $\underset{\_}{\mathit{v}}$, ${\underset{\_}{y}}_{j-1}$, $\underset{\_}{j}$ and $\underset{\_}{s}$ are standardized values for v, y_j−1, j and s (details in Appendix A.2). For categorical covariates, the distance between v and v′ is calculated by counting the number of different values. In addition, in (5), I(a; b) is the Kronecker delta function that takes the value 1 if a = b and 0 otherwise. The function I(a; b) is used to introduce a small nugget for the diagonal covariances, which overcomes near-singularity of the covariance matrices and improves numerical stability. The Gaussian processes flexibly model the relationship between auxiliary covariates and the previous response with the current response (Yj) and accounts for possibly non-linear and non-additive effects in the auxiliary covariates and previous response.

For the noise variance ${\sigma }_{js}^2$, we assume an inverse Gamma shrinkage prior,

$${\sigma }_{js}^2|{\nu }_{\sigma }\stackrel{iid}{~}\text{IG}({\lambda }_{\sigma },{\lambda }_{\sigma }{\nu }_{\sigma }),\hspace{1em}j=1,\dots ,s,s=2,\dots ,J,$$

With $\text{E}(1/{\sigma }_{js}^2)=1/\hspace{0.17em}{\nu }_{\sigma }$ and $\text{Var}(1/{\sigma }_{js}^2)=1/{\lambda }_{\sigma }\hspace{0.17em}{\nu }_{\sigma }^2$. This prior prior shrinks the time/pattern specific variances to a common value,${\nu }_{\sigma }$. We put hyper-priors on ${\lambda }_{\sigma }$ and ${\nu }_{\sigma }$.

$${\lambda }_{\sigma }-2\sim IG({\lambda }_1^{{\lambda }_{\sigma }},{\lambda }_2^{{\lambda }_{\sigma }}),\hspace{1em}{\nu }_{\sigma }\sim Gamma({\lambda }_1^{{\nu }_{\sigma }},{\lambda }_2^{{\nu }_{\sigma }}),$$

where we assume ${\lambda }_{\sigma }>2$ to impose more shrinkage and borrowing of information.

Next, we consider the parameters in the mean functions (4). We allow the regression coefficients of the auxiliary covariates to vary by pattern. However, it is typical to have sparse patterns. As a result, we consider an informative prior that assumes regression coefficients for neighboring patterns to be similar. In particular, we specify AR(1) type priors on β_0s and β_s. Let ${\mathit{\beta }}_0=({\mathit{\beta }}_{02},{\mathit{\beta }}_{03},\dots ,{\mathit{\beta }}_{0J})$ and $\mathit{\beta }=({\mathit{\beta }}_2,{\mathit{\beta }}_3,\dots ,{\mathit{\beta }}_J)$ denote the coefficient vectors for the auxiliary covariates in Equation (4). We assume

$${\mathbf{\beta }}_0\sim N\left[X_{\beta }{\mathbf{\beta }}_0,{\sigma }_{{\beta }_0}^2{\sum }_{\beta }({\rho }_0)\right],\hspace{1em}\mathbf{\beta }\sim N\left[X_{\beta }\mathbf{\beta },{\sigma }_{\beta }^2{\sum }_{\beta }(\rho )\right],$$

where $X_{\beta }^T=(I,I,\dots ,I)$, β₀ and β are the prior means for β_0s and β_s, respectively, and ${\sigma }_{{\beta }_0}^2{\sum }_{\beta }({\rho }_0)$ and ${\sigma }_{\beta }^2{\sum }_{\beta }(\rho )$ are the AR(1) type covariance matrices. Details and hyper-priors on the hyperparameters are described in Appendix A.2. The time/pattern specific intercepts are given conditional autoregressive (CAR) type priors (De Oliveira, 2012; Banerjee et al., 2014) as we expect them to be similar for neighboring patterns/times. Let b₀ = (b₁₂, b13, …, b_1J) and b = (b₂₂; b₂₃, b₃₃; …; b_2J, …, b_JJ) denote the time/pattern-specific intercepts in Equation (4). We assume

$${\mathit{b}}_0\sim N\left(1{\tilde{b}}_0,{\sigma }_{b_0}^2{(I-{\gamma }_{b_0}{W}_{b_0})}^{-1}{\mathcal{N}}_{b_0}\right),\hspace{1em}\mathit{b}\sim N\left(1\tilde{b},{\sigma }_b^2{(I-{\gamma }_b{W}_b)}^{-1}{\mathcal{N}}_b\right),$$

where ${\tilde{b}}_0$ and $\tilde{b}$ are the prior means for b₀ and b, respectively, and ${\sigma }_{b_0}^2{(I-{\gamma }_{b_0}{W}_{b_0})}^{-1}{\mathcal{N}}_{b_0}$ and ${\sigma }_b^2{(I-{\gamma }_b{W}_b)}^{-1}{\mathcal{N}}_b$ are the CAR type covariance matrices. Details in Appendix A.2. The time/pattern specific lag-1 coefficients are given CAR type priors similar to the priors on b_js for the same reason. Let $\psi =({\psi }_{22};{\psi }_{23},{\psi }_{33};\dots ;{\psi }_{2J},\dots ,{\psi }_{JJ})$ denote the time/pattern-specific coefficient vector for the lag-1 responses in Equation (4). We assume

$$\psi \sim N\left(1\tilde{\psi },{\sigma }_{\psi }^2{(I-{\gamma }_{\psi }{W}_{\psi })}^{-1}{\mathcal{N}}_{\psi }\right),$$

where $\tilde{\psi }$ is the prior mean for ψ, and ${\sigma }_{\psi }^2{(I-{\gamma }_{\psi }{W}_{\psi })}^{-1}{\mathcal{N}}_{\psi }$ is the CAR type covariance matrix. Again, more details in Appendix A.2. We complete the model with a prior for the higher-order (≥2) lag coefficients ϕ_js. Note that we assume the effect of higher-order lag responses on current response is linear. We do not include ${\overline{Y}}_{j-2}$ in a(·) as the dimension of ${\overline{Y}}_{j-2}$ varies for different time j. We expect to capture most of the non-linear and non-additive effects from lagged responses by including Y_j−1 in a(·) since we expect most of the temporal effects come from lag-1 response. We simply put normal priors with more prior mass around 0 to indicate the prior belief that higher-order lags have less impact on current response. Specifically,

$${\mathit{\varphi }}_{js}\sim N(0,{\sigma }_{\varphi }^{2}I),\hspace{1em}{\sigma }_{\varphi }^2\sim IG({\lambda }_1^{\varphi },{\lambda }_2^{\varphi }),$$

with ${\lambda }_1^{\varphi }>{\lambda }_2^{\varphi }$.

2.2. Model for the Pattern Conditional on Auxiliary Covariates

We model the hazard of dropout at time j with Bayesian additive regression trees (BART) (Chipman et al., 2010),

$$p(S=j|S\ge j,\mathit{v},\mathit{\phi })=F_N(f_j(\mathit{v})),$$

where F_N denotes the standard normal cdf (probit link), and f_j(v) is the sum of tree models from BART. The BART model captures complex relationships between auxiliary covariates and dropout including interactions and nonlinearities. We use the default priors for f_j(·) given in Chipman et al. (2010).

2.3. Model for the Auxiliary Covariates

We use a Bayesian bootstrap (Rubin, 1981) prior for the distribution for v. Suppose v can only take the N discrete values that we observed,$\mathit{V}\in \left\{{\mathit{v}}_1,\dots ,{\mathit{v}}_N\right\}$. The probability for each is

$$p(\mathit{V}={\mathit{v}}_i|\mathit{\eta })={\eta }_i,$$ (6)

where $\sum _{i=1}^N{\eta }_i=1$. We place a Dirichlet distribution prior on η,

$$({\eta }_1,\dots ,{\eta }_N)\sim Dir({\delta }_{\eta },\dots ,{\delta }_{\eta }).$$

3. The Extrapolation distribution

The extrapolation distribution for our setting can be sequentially factorized as

$$\begin{gathered} p_s({\mathit{y}}_s|{\overline{\mathit{y}}}_s,\mathit{v},{\mathit{\omega }}_E)=p_s(y_{s+1}|{\overline{\mathit{y}}}_s,\mathit{v},{\mathit{\omega }}_E)\cdot \\ {p}_s(y_{s+2}|{\overline{\mathit{y}}}_{s+1},\mathit{v},{\mathit{\omega }}_E)\cdots p_s(y_J|{\overline{\mathit{y}}}_{J-1},\mathit{v},{\mathit{\omega }}_E). \end{gathered}$$ (7)

The extrapolation distribution is not identified by the observed data. To identify the extrapolation distribution, we use identifying restrictions that express the extrapolation distribution as a function of the observed data distribution; see Linero and Daniels (2018) for a comprehensive discussion. For example, missing at random (MAR) (Rubin, 1976) is a joint identifying restriction that completely identifies the extrapolation distribution. It is shown in Molenberghs et al. (1998) that MAR is equivalent to the available case missing value (ACMV) restriction in the pattern mixture model framework. The same statement is true when conditional on V, in which case MAR is referred to as auxiliary variable MAR (A-MAR) (Daniels and Hogan, 2008). ACMV sets

$$p_k({\mathit{y}}_j|{\overline{y}}_{j-1},\mathit{v},{\mathit{\omega }}_E)=p_{\ge j}(y_j|{\overline{\mathit{y}}}_{j-1},\mathit{v},\mathit{\pi }),$$

for k < j and 2 ≤ j < J, where the subscript ≥ j indicates conditioning on S ≥ j. The latter involves averaging p_s(·) with respect to the missingness prior on s.

When the missingness is not at random, a partial identifying restriction (Linero and Daniels, 2018) is the missing non-future dependence (NFD) assumption (Kenward et al., 2003). NFD states that the probability of dropout at time j depends only on ${\overline{y}}_{j+1}$. Similarly, when conditional on V, auxiliary variable NFD (A-NFD) assumes

$$p(S=j|\hspace{0.17em}{\overline{\mathit{y}}}_J,\mathit{v},\mathit{\omega })=p(S=j|\hspace{0.17em}{\overline{\mathit{y}}}_{j+1},\mathit{v},\mathit{\omega }).$$

Within the pattern-mixture framework, NFD is equivalent to the non-future missing value (NFMV) restriction (Kenward et al., 2003). Under A-NFD, we have

$$p_k(y_j|{\overline{\mathit{y}}}_{j-1},\mathit{v},{\mathit{\omega }}_E)=p_{\ge j-1}(y_j|{\overline{\mathit{y}}}_{j-1},\mathit{v},\mathit{\pi }),$$ (8)

for k < j–1 and 2 < j ≤ J. NFMV leaves one conditional distribution per incomplete pattern unidentified:$p_s(y_{s+1}|{\overline{\mathit{y}}}_s,\mathit{v})$. To identify $p_s(y_{s+1}|{\overline{y}}_s,v)$, we assume a location shift ${\tau }_{s+1}$ (Daniels and Hogan, 2000),

$$\left[Y_{s+1}|{\overline{Y}}_s,S=s,V,\omega \right]\stackrel{d}{=}\left[Y_{s+1}+{\tau }_{s+1}|{\overline{Y}}_s,S\ge s+1,V,\omega \right],$$ (9)

where $\stackrel{d}{=}$ denotes equality in distribution, and ${\tau }_{s+1}$ measures the deviation of the unidentified distribution $p_s(y_{s+1}|{\overline{y}}_s,v)$ from ACMV. In particular, ACMV holds when ${\tau }_{s+1}=0$; ${\tau }_{s+1}$ is a sensitivity parameter (Daniels and Hogan, 2008). To help calibrate the magnitude of ${\tau }_{s+1}$, we set

$$\left[{\tau }_{s+1}|{\overline{Y}}_s={\overline{y}}_s,V=v\right]=\tilde{\tau }\text{}\hspace{0.17em}\text{}\cdot {\Delta }_{s+1}({\overline{y}}_s,v),$$ (10)

where ${\Delta }_{s+1}({\overline{y}}_s,v)$ is the standard deviation of $(Y_{s+1}|{\overline{y}}_s,s,v)$ under ACMV, and $\tilde{\tau }$ represents the number of standard deviations that $p_s(Y_{s+1}|{\overline{y}}_s,v)$ is deviated from ACMV. Similar strategies to calibrate sensitivity parameters based on the observed data can be found in Daniels and Hogan (2008) and Kim et al. (2017). Importantly, note that, based on this calibration, for a fixed $\tilde{\tau }$ we would have a smaller Δ using auxiliary covariates and thus a smaller deviation from ACMV, in comparison to unconditional on V.

4. Posterior Inference and Computation

4.1. Posterior Sampling for Observed Data Model Parameters

We use a Markov chain Monte Carlo (MCMC) algorithm to draw samples from the posterior $w_O^{(l)}\stackrel{iid}{\sim }p(w_O|{\{{\overline{y}}_{i{s}_i},s_i,v_i\}}_{i=1}^N)$, l = 1, …, L. Note that we use distinct parameters π, φ, η for $p({\overline{y}}_s|s,v,\pi )$, $p(s|v,\phi )$ and $p(v|\eta )$, and the parameter are also a prior independent,$p(\pi ,\phi ,\eta )=p(\pi )p(\phi )p(\eta )$. Therefore, the posterior distribution of w_O can be factored as

$$p\left(w_O|{\{{\overline{y}}_{i{s}_i},s_i,v_i\}}_{i=1}^N\right)=p\left(\pi |{\{{\overline{y}}_{i{s}_i},s_i,v_i\}}_{i=1}^N\right)p\left(\phi |{\{s_i,v_i\}}_{i=1}^N\right)p\left(\eta |{\left\{v_i\right\}}_{i=1}^N\right),$$ (11)

and posterior simulation can be conducted independently for π, φ and η. Gibbs transition probabilities are used to update π (details in Appendix A.2), the R packages bartMachine (Kapelner and Bleich, 2016) and BayesTree (Chipman and McCulloch, 2016) are used to update φ, and η is updated by directly sampling from its posterior $\eta |{\left\{v_i\right\}}_{i=1}^N\sim Dir(1+{\delta }_{\eta },\dots ,1+{\delta }_{\eta })$.

4.2. Computation of Expectation of Functionals of Full-data Responses

Our interest lies in the expectation of functionals of y, given by

$$E[t(y)]={\int }_{y}t(y)p(y)dy={\int }_{y}t(y)\left[\sum _s{\int }_v{p}_s(y_s|{\overline{y}}_s,v)p_s({\overline{y}}_s|v)p(s|v)p(v)dv\right]dy.$$ (12)

Once we have obtained posterior samples $\{w_O^{(l)},l=1,\dots ,L\}$, the expression (12) can be computed by Monte Carlo integration. Since the desired functionals are functionals of y, computing (12) involves sampling pseudo-data based on the posterior samples. We note that this is an application of G-computation (Robins, 1986; Scharfstein et al., 2014; Linero and Daniels, 2015) within the Bayesian paradigm (see Appendix Algorithm A.1).

In detail, at step 1, we draw V* = v_i with probability $p(V=v_i|{\eta }^{(l)})={\eta }_i^{(l)}$. At step 2, we draw S* by sequentially sampling from $R\sim Bernoulli[p(S^{\ast }=j|S^{\ast }\ge j,v)]$. If R = 1, take S* = j; otherwise proceed with $p(S^{\ast }=j+1|S^{\ast }\ge j+1,v)$, j = 2, …, J. At step 3, we first draw $y_1^{*}\sim N\left(a_0(v^{*},s^{*}),{\sigma }_{1s^{*}}^2\right)$ and then sequentially draw $y_j^{*}\sim N\left(a(y_{j-1}^{*},v^{*},j,s^{*})+{\overline{y}}_{j-2}^{*T}{\varphi }_{j{s}^{*}},{\sigma }_{J{s}^{*}}^2\right)$, $j=2,\dots ,s^{*}$ as in (2), where $a_0(v^{*},s^{*})$ and $a(y_{j-1}^{*},v^{*},j,s^{*})$ are generated by GP prediction rule (Rasmussen and Williams, 2006). At step 4, we sequentially draw $y_j^{*}$ for $j=s^{*}+1,\dots ,J$ as in (7) from the unidentified distributions, now identified using identifying restrictions. When the ACMV restriction is specified, step 4 involves generating the random $p_{\ge j}(y_j|{\overline{\mathit{y}}}_{j-1},\mathit{v})$, which is defined as

$$p_{\ge j}(y_j|{\overline{\mathit{y}}}_{j-1},\mathit{v})=\sum _{k=j}^J{\alpha }_{kj}({\overline{\mathit{y}}}_{j-1},\mathit{v})p_k({\mathit{y}}_j|{\overline{y}}_{j-1},\mathit{v}),$$ (13)

and

$$\begin{gathered} {\alpha }_{kj}({\overline{y}}_{j-1},v)=p(S=k|{\overline{y}}_{j-1},S\ge j,v) \\ =\frac{p({\overline{y}}_{j-1}|S=k,v)p(S=k|S\ge j,v)}{\sum _{k=j}^{J}p({\overline{y}}_{j-1}|S=k,v)p(S=k|S\ge j,v)}. \end{gathered}$$

The distribution in (13) is a mixture distribution over patterns. We sample from (13) by first drawing K = k with probability α_kj, k = j, …, J, then drawing a sample from $p_k(y_j|{\overline{y}}_{j-1},v)$. When the NFMV restriction is specified, step 4 also involves generating the random $p_{\ge j-1}(y_j|{\overline{y}}_{j-1},v)$, where

$$\begin{gathered} p_{\ge j-1}(y_j|{\overline{\mathit{y}}}_{j-1},\mathit{v})={\alpha }_{j-1,j-1}({\overline{\mathit{y}}}_{j-1},\mathit{v})p_{j-1}(y_j|{\overline{\mathit{y}}}_{j-1},\mathit{v})+ \\ [1-{\alpha }_{j-1,j-1}({\overline{\mathit{y}}}_{j-1},\mathit{v})]p_{\ge j}({\mathit{y}}_j|{\overline{y}}_{j-1},\mathit{v}). \end{gathered}$$

Sampling from $p_{\ge j-1}(y_j|{\overline{\mathit{y}}}_{j-1},\mathit{v})$ is done by first samplings $Y_j^{*}\sim p_{\ge j}({\mathit{y}}_j|{\overline{y}}_{j-1},\mathit{v})$ as in (13). Then draw $R\sim Bernoulli[{\alpha }_{j-1,j-1}]$. If R = 1, apply the location shift (9), otherwise, retain $Y_j^{*}$. See Appendix A.4 for more details of steps 3 and 4.

5. Simulation Studies

We conduct several simulation studies similar to the data example to assess the operating characteristic of our proposed model (denoted as GP hereafter). We simulate responses for J = 6 time points and fit our model to estimate the change from baseline treatment effect, i.e. E[Y_J –Y₁]. We set the prior and hyper-prior parameters at standard noninformative choices. See Appendix A.5 for exact values. For comparison, we consider four alternatives:

(1, LM) a linear pattern-mixture model that consists of a linear regression model for $p_s(y_j|{\overline{y}}_{j-1},v)$, a sequential logit model for p(s | v), and a Bayesian bootstrap model for p(v), as in Equations (16), (15) and (6), respectively;

(2, LM–) a linear pattern-mixture model without V that consists of a linear regression model for $p_s(y_j|{\overline{y}}_{j-1})$ and a Bayesian bootstrap model for p(s);

(3, DPM) a working model for the full data, constructed as a Dirichlet process mixture of selection models, $p^{*}(\mathit{y},s,\mathit{v}|\mathit{\omega })=\int p(\mathit{y}|\mathit{v},{\mathit{\theta }}_1)p(s|\mathit{y},\mathit{v},{\mathit{\theta }}_2)p(\mathit{v}|{\mathit{\theta }}_3)F(d\mathit{\theta })$ with F following a Dirichlet process. As suggested in Linero (2017), we use a linear regression model for p(y | v, θ₁) and a sequential logit model for p(s | y, v, θ₂). For p(v | θ₃), similar to Shahbaba and Neal (2009), we assume independent normal distributions for continuous V’s, Bernoulli distributions for binary V ‘s and multinomial distributions for categorical V’s; and

(4, DPM–) a working model for the full data without $\mathit{V},p^{*}(\mathit{y},s|\mathit{\omega })=\int p(\mathit{y}|{\mathit{\theta }}_1)p(s|\mathit{y},{\mathit{\theta }}_2)F(d\mathit{\theta })$, which was proposed by Linero and Daniels (2015) and Linero (2017).

We use noninformative priors for the two parametric models (1) and (2), and use the default prior choices in Linero and Daniels (2015) and Linero (2017) for the Dirichlet process mixture models (3) and (4). For each simulation scenario below, we generate 500 datasets with N = 200 subjects per dataset. See Appendix Section A.7 for further details on computing times.

5.1. Performance Under MAR

We first evaluate the performance of our model under the ACMV restriction (MAR). Since this restriction completely identifies the extrapolation distribution, this simulation study validates the appropriateness of our observed data model specification. We consider the following three simulation scenarios.

Scenario 1.

We test the performance of our approach when the data are generated from a simple linear pattern-mixture model to assess loss of efficiency from using an unnecessary complex modeling approach. For each subject, we first simulate Q = 4 auxiliary covariates from a multivariate normal distribution

$$\mathit{V}\stackrel{iid}{\sim }N(\mathbf{0},{\Sigma }_{vv}).$$ (14)

We then generate dropout time using a sequential logit model

$$logit P(S=s|S\ge s,\mathit{V})={\zeta }_s+{\mathit{V}}^T{\mathit{\xi }}_s.$$ (15)

Next, we generate ${\overline{\mathit{Y}}}_s$ from

$$\begin{gathered} \left(Y_j|{\overline{\mathit{Y}}}_{j-1},S=s,\mathit{V}\right)\sim N\left({\mu }_{js}({\overline{\mathit{Y}}}_{j-1},\mathit{V}),{\sigma }_{js}^2\right),\hspace{1em}for j=1,\dots ,s \\ \text{where}\hspace{1em}{\mu }_{js}({\overline{\mathit{Y}}}_{j-1},\mathit{V})=\{\begin{array}{ll}{\mathit{V}}^T{\mathit{\beta }}_{0s}+b_{1s}\hfill & \text{if}j=1\hfill \\ Y_{j-1}{\psi }_{js}+{\mathit{V}}^T{\mathit{\beta }}_s+b_{js}+{\overline{\mathit{Y}}}_{j-2}^T{\mathit{\varphi }}_{js}\hfill & \text{if}j\ge 2\hfill \end{array} \end{gathered}$$ (16)

Finally, the distribution of Y_s is specified under the ACMV restriction (for calculating the simulation truth of the mean estimate).

The parameters in (14), (15) and (16) are chosen by fitting the model to the test drug arm of the schizophrenia clinical trial (after standardizing the responses and the auxiliary covariates with mean 0 and standard deviation 1). See Appendix A.5 for details.

Scenario 2.

We consider a scenario where the covariates and the responses have more complicated structures in order to test the performance of our model when linearity does not hold. For simplicity, for each subject, we simulate Q = 3 auxiliary covariates from $\mathit{V}\stackrel{iid}{\sim }N(\mathbf{0},{\Sigma }_{vv})$. The responses and drop out times are generated in the same way as in scenario 1, but we include interactions and nonlinearities by replacing V in Equations (15) and (16) (case j = 1) with $\dot{\mathit{V}}=(V_1,V_2,V_3,V_1\times V_2,V_1\times V_3,V_2\times V_3,V_1^2,V_2^2,V_3^2)$ and replacing V in Equation (16) (case j ≥ 2) with $\ddot{\mathit{V}}=(V_1,V_2,V_3,V_1\times V_2,V_1\times V_3,V_2\times V_3,V_1^2,V_2^2,V_3^2,V_1\times Y_{j-1},V_2\times Y_{j-1},V_3\times Y_{j-1},\sqrt{\left|Y_{j-1}\right|})$. The regression coefficients ξ_s, β_0s and β_s change accordingly. See Appendix A.5 for further details.

Scenario 3.

We consider a scenario with a very different structure from our model formulation. In particular, we consider a lag-1 selection model with a mixture model for the joint distribution of Y and V. We generate

$$\begin{gathered} K\sim Categorical(\pi ), \\ {\Omega }^{(K)}\sim {\mathcal{W}}^{-1}\left((v-J-Q-1){\Omega }_0^{(K)},v\right), \\ \left(\begin{array}{l}\mathit{Y}\\ \mathit{V}\end{array}\right)|K\sim N\left[{\mathit{\mu }}^{(K)},{\Omega }^{(K)}\right], \\ logit P(S=s|S\ge s,\mathit{Y},\mathit{V})={\zeta }_s+{\psi }_s{Y}_s+{\mathit{V}}^T{\mathit{\xi }}_s \end{gathered}$$ (17)

where ${\mathcal{W}}^{-1}\left((v-J-Q-1){\mathrm{\Omega }}_0,v\right)$ is an inverse-Wishart distribution with precision parameter ν and mean Ω₀. See Linero and Daniels (2015) for further details on this type of model. Formulating a joint distribution as in (17) allows us to impose complicated relationships between Y and V (Müller et al., 1996). We consider Q = 3 auxiliary covariates and 5 mixture components. We assume µ^(K) and ${\Omega }_0^{(K)}$ correspond to a linear model of (Y | V) and have the form

$${\mathit{\mu }}^{(K)}=\left(\begin{array}{c}{\mathit{\mu }}_y^{(K)}\\ \mathbf{0}\end{array}\right),\hspace{1em}{\mathrm{\Omega }}_0^{(K)}=\left(\begin{array}{cc}{\Sigma }_{yy}^{(K)}& {\Sigma }_{yv}^{(K)}\\ {\Sigma }_{vy}^{(K)}& {\Sigma }_{vv}\end{array}\right).$$

In particular, we generate μ^(K) and ${\Omega }_0^{(K)}$ according to Linero and Daniels (2015) by fitting the mixture model to the active control arm of the schizophrenia clinical trial. See Appendix A.5 for further details.

The simulation results are summarized in Table 1. For scenario 1, the true data generating model is the linear regression model with V, i.e. the LM model. The five models have similar performance in terms of MSE. The 95% credible interval of the GP model has a frequentist coverage rate less than 95% due to the prior information, i.e., the Gaussian process priors and the AR/CAR priors, being quite strong and the sample size (N = 200) being relatively small. Therefore, the Bayesian credible interval is unlikely to have the expected frequentist coverage. The LM– and DPM– models (which ignore V) do not perform worse than the LM and DPM models. The reason is probably that the (linear) effects of different V’s on t(Y) cancel out in the integration (12). For scenario 2, the true data generating model does not match any of the five models used for inference. The GP model significantly outperforms the other models in all aspects. The result suggests that when the model is misspecified, the GP model has much more robust performance. We note that the DPM and DPM–models, although being nonparametric, perform worse than the GP model. The reason is that the GP model is designed specifically to incorporate auxiliary covariates. It better exploits the structure of the data, which allows it to more readily capture non-linear and non-additive effects and handle sparse patterns, in particular with small sample sizes. We also note that when Y and S do not have a linear relationship with V, ignoring V results in more significant bias than including V (even mistakenly). For scenario 3, the true data generating model is a mixture of linear regression models, similar to the specification of the DPM model. The five models again have similar performance. For a pattern-mixture model, the marginal distribution of the responses Y is a mixture distribution over patterns, which explains the good performance of the GP, LM and LM–models. For all the three scenarios, the GP model always gives narrower credible intervals and has lower bias, in particular versus the models without auxiliary covariates.

Table 1.

Summary of simulation results under MAR. Values shown are averages over repeat sampling, with numerical Monte Carlo standard errors in parentheses. GP, LM, LM–, DPM, DPM– represent the proposed semiparametric model, the linear regression model with covariates, the linear regression model without covariates, the Dirichlet process mixture model with covariates and the Dirichlet process mixture model without covariates, respectively. CI width and coverage are based on 95% credible intervals.

Model	Bias	CI width	CI coverage	MSE
	Scenario 1
GP	−0.013(0.004)	0.294(0.002)	0.909(0.012)	0.014(0.000)
LM	−0.005(0.004)	0.379(0.001)	0.969(0.007)	0.017(0.000)
LM–	0.004(0.004)	0.385(0.002)	0.969(0.007)	0.018(0.001)
DPM	−0.013(0.004)	0.355(0.002)	0.954(0.009)	0.018(0.001)
DPM–	−0.009(0.004)	0.343(0.001)	0.947(0.009)	0.016(0.001)
	Scenario 2
GP	0.037(0.010)	0.967(0.005)	0.943(0.010)	0.122(0.004)
LM	0.247(0.010)	1.021(0.004)	0.819(0.017)	0.189(0.006)
LM–	0.330(0.010)	1.094(0.005)	0.783(0.018)	0.243(0.007)
DPM	0.183(0.011)	1.188(0.006)	0.924(0.012)	0.192(0.005)
DPM–	0.302(0.011)	1.054(0.006)	0.781(0.019)	0.228(0.008)
	Scenario 3
GP	−0.005(0.007)	0.666(0.002)	0.958(0.009)	0.057(0.002)
LM	0.008(0.007)	0.705(0.002)	0.968(0.008)	0.061(0.002)
LM–	0.026(0.007)	0.707(0.002)	0.964(0.008)	0.061(0.002)
DPM	−0.008(0.008)	0.778(0.002)	0.984(0.006)	0.070(0.002)
DPM–	−0.001(0.007)	0.669(0.002)	0.953(0.010)	0.058(0.002)

In summary, the semiparametric approach (GP) loses little when a simple parametric alternative holds, and it significantly outperforms the other approaches when the model used for inference is misspecified. The simulation results suggest that the semiparametric approach accommodates complex mean models and is more favorable compared with the parametric approaches and even simple nonparametric alternatives.

5.2. Performance Under MNAR

To assess the sensitivity of our model to untestable assumptions for the extrapolation distribution, we fit our model to simulated data under an NFD restriction (8). We consider simulation scenarios 2 and 3 as in Section 5.1, where the simulation truth is still generated under MAR. We complete our model with a location shift (Equations (9) and (10)). Recall that the sensitivity parameter $\tilde{\tau }$ measures the deviation of our model from MAR, and the simulation truth corresponds to $\tilde{\tau }=0$. The sensitivity parameter $\tilde{\tau }$ is given four different priors:

Unif(−0.75, 0.25), Unif(−0.5, 0.5), Unif(−0.25, 0.75), Unif(0,1). All the four priors contain the simulation truth. Compared to fixing the value of $\tilde{\tau }$, using a uniform prior conveys uncertainty about the identifying restriction. For example, using a point mass prior $\tilde{\tau }=0$ implies MAR with no uncertainty, while using a prior such that $\text{E}[\tilde{\tau }]=0$ and $\text{Var}[\tilde{\tau }]>0$ implies MAR with uncertainty.

The simulation results for scenarios 2 and 3 are summarized in Table 2 and Appendix Table A.3, respectively. When the sensitivity parameter $\tilde{\tau }$ is centered at the correct value 0, the GP model significantly outperforms the alternatives under scenario 2 and performs as well as the alternatives under scenario 3. Comparing with the simulation results under MAR (Table 1), the use of a uniform prior for $\tilde{\tau }$ induces more uncertainty on inference resulting in the wider credible intervals. We also note that, when $\tilde{\tau }$ is not centered at 0, the models using V still perform better than the model not using V. This is due to the calibration of the location shift (Equations (9) and (10)). For the same $\tilde{\tau }$ we would have a smaller deviation from ACMV using V compared to not using V. This property makes the missingness “closer” to MAR and reduces the extent of sensitivity analysis with the inclusion of V.

Table 2.

Summary of simulation results for Scenario 2 under MNAR. Values shown are averages over repeat sampling, with numerical Monte Carlo standard errors in parentheses. CI width and coverage are based on 95% credible intervals. The values of $E(\tilde{\tau })$, –0.25, 0, 0.25 and 0.5, correspond to prior specifications Unif(−0.75, 0.25), Unif(−0.5, 0.5), Unif(−0.25, 0.75) and Unif(0,1), respectively.

Model	$\text{E}(\tilde{\tau })$	Bias	CI width	CI coverage	MSE
GP	−0.25	−0.024(0.011)	1.032(0.005)	0.957(0.009)	0.133(0.004)
	0	0.065(0.011)	1.050(0.005)	0.949(0.010)	0.140(0.004)
	0.25	0.157(0.011)	1.069(0.005)	0.909(0.012)	0.165(0.005)
	0.5	0.256(0.011)	1.091(0.005)	0.851(0.015)	0.210(0.007)
LM	−0.25	0.156(0.011)	1.122(0.005)	0.918(0.012)	0.170(0.005)
	0	0.271(0.011)	1.146(0.005)	0.866(0.015)	0.223(0.007)
	0.25	0.389(0.011)	1.170(0.005)	0.755(0.019)	0.307(0.009)
	0.5	0.513(0.011)	1.199(0.005)	0.626(0.021)	0.424(0.012)
LM–	−0.25	0.222(0.010)	1.215(0.005)	0.909(0.012)	0.204(0.006)
	0	0.352(0.010)	1.237(0.005)	0.842(0.016)	0.284(0.008)
	0.25	0.487(0.010)	1.266(0.006)	0.710(0.020)	0.403(0.011)
	0.5	0.626(0.011)	1.300(0.005)	0.528(0.022)	0.567(0.014)
DPM	−0.25	0.077(0.011)	1.275(0.006)	0.979(0.006)	0.178(0.004)
	0	0.185(0.011)	1.289(0.006)	0.954(0.009)	0.210(0.005)
	0.25	0.298(0.011)	1.308(0.007)	0.884(0.014)	0.269(0.008)
	0.5	0.415(0.012)	1.332(0.007)	0.795(0.018)	0.358(0.010)
DPM–	−0.25	0.179(0.011)	1.167(0.006)	0.932(0.011)	0.184(0.005)
	0	0.304(0.011)	1.197(0.006)	0.851(0.016)	0.252(0.008)
	0.25	0.435(0.011)	1.234(0.006)	0.712(0.020)	0.357(0.011)
	0.5	0.571(0.012)	1.278(0.006)	0.579(0.022)	0.504(0.014)

6. Application to the Schizophrenia Clinical Trial

We implement inference under the proposed model for data from the schizophrenia clinical trial described in Section 1.3. The dataset was first used in Linero and Daniels (2015). Recall the quantity of interest is the change from baseline treatment effect, $r_x=E[Y_{i6}-Y_{i1}|X_i=x]$, where x = T, A or P correspond to treatments under test drug, active control or placebo, respectively. We are particularly interested in the treatment effect improvements over placebo, i.e. r_T – r_P and r_A – r_P. Also, recall that we have Q = 7 auxiliary covariates including age, onset (of schizophrenia) age, height, weight, country, sex and education level. Details of computing specifications and times, as well as convergence diagnostics, are summarized in Appendix Section A.7.

6.1. Comparison to Alternatives and Assessment of Model Fit

We first compare the fit among the proposed model and alternatives. We consider the linear pattern-mixture models and Dirichlet process mixture of selection models with and without auxiliary covariates, as we have used in the simulation studies. We use the log-pseudo marginal likelihood (LPML) as the model selection criteria, where $LPML=\left[\sum _{i=1}^N\log (CP{O}_i)\right]/N,CP{O}_i$ is the conditional predictive ordinate (Geisser and Eddy, 1979) for observation i and $CP{O}_i=p\left({\overline{\mathit{Y}}}_{i{S}_i},S_i,V_i|{\{{\overline{\mathit{Y}}}_{i\prime S_{i\prime }},S_{i\prime },V_{i\prime }\}}_{i\prime =1,i\prime \ne i}^N\right)$. LPML can be straightforwardly estimated using posterior samples $\{{\omega }_o^{(l)},l=1,\dots ,L\}$ (Gelfand and Dey, 1994), without the need to refit the model N times. A model with higher LPML is more favorable compared to models with lower LPMLs. We fit the five models to the data and calculate the LPML by taking the summation of the LPML under each treatment arm. The results are summarized in Table 3. The proposed semiparametric model (GP) has the largest LPML over the alternatives. In particular, the LPML improvement over the linear pattern-mixture model without covariates (LM–) for the GP model is much higher than the LM and DPM– models. This is not surprising in light of the earlier simulation results. We also compare inferences on treatment effect improvements over placebo under the MAR assumption using the five models, as well as a complete case analysis (CCA) based on the empirical distribution of the subjects who have complete outcomes. The results are summarized in Table 3. We point out the two plus points shifts between the GP model and the other models for the test drug vs. placebo comparison and for the active drug vs. placebo. The DPM model has the lowest LPML and the widest credible intervals. The poorer performance of the DPM model is probably due to the small sample size of each treatment arm (e.g. 45 subjects for the active control arm) and the relatively large number of covariates (Q = 7). Inference under the DPM model has large variability with small sample sizes, and the covariates can dominate the partition structure (Wade, 2013). Further interpretation of the results of the GP model can be found in Section 6.2. The complete case analysis (which implicitly assumes missing completely at random) is inefficient and is generally very unrealistic for longitudinal data.

Table 3.

Comparison of LPML (the second column) and inference results (the third and fourth columns) under MAR (the first five rows) and CCA (the last row). For the inference results under MAR and CCA, values shown are posterior means, with 95% credible intervals in parentheses.

Model	LPML	rT – rP	rA – rP
GP	−31.93	0.60(−5.07, 7.01)	−6.08(−13.90, 1.72)
LM	−32.61	−1.26(−8.59, 5.74)	−7.24(−15.00, 0.05)
LM–	−32.71	−1.94(−9.00, 5.07)	−8.13(−15.30, −1.00)
DPM	−39.25	0.44(−10.14, 10.42)	−7.66(−25.27, 9.67)
DPM–	−32.58	−1.69(−8.03, 4.78)	−5.44(−12.61, 2.27)
CCA	–	−3.23(−8.63, 2.18)	−3.82(−10.18, 2.55)

Next, we assess the “absolute” goodness of fit of the proposed model. We estimate the cumulative dropout rates and observed-data means at each time point and under each treatment using the proposed model by

$$\begin{gathered} p(S\le j|x)=\int p(S\le j|v,x)p(\mathit{v}|x)d\mathit{v},\hspace{1em}\text{and} \\ \text{E}(Y_j|S\ge j,x)=\int E(Y_j|S\ge j,\mathit{v},x)p(\mathit{v}|S\ge j,x)d\mathit{v}. \end{gathered}$$

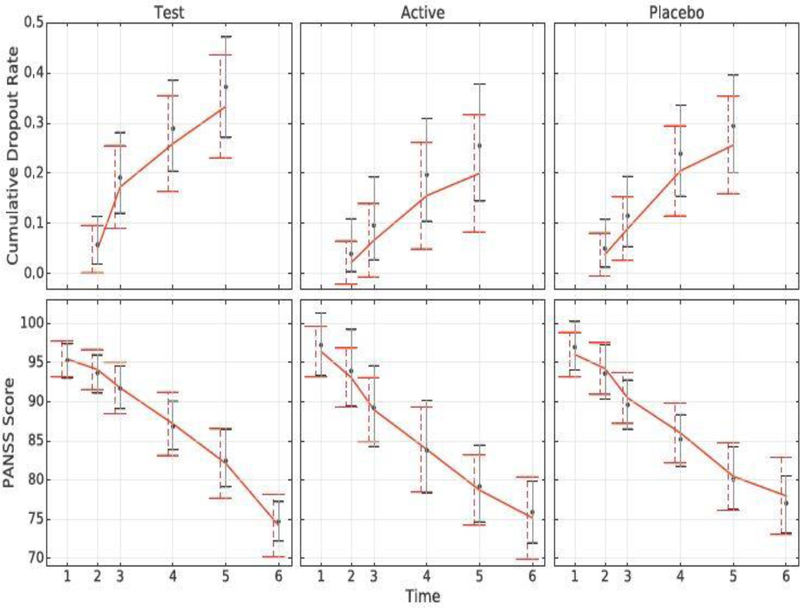
We then compare those estimates with results obtained from the empirical distribution of the observed data (that implicitly averages over the empirical distribution of the auxiliary covariates). Despite some small differences, there is no evidence for lack of fit. The comparison is shown in Figure 1.

Fig. 1.

Cumulative dropout rates (top) and means of the observed data (bottom) over time obtained from the model versus the ones obtained from the empirical distribution of the observed data. The solid line represents the empirical values, dots represent the posterior means, dashed error bars represent frequentist 95% confidence intervals, and solid error bars represent the model’s 95% credible intervals.

6.2. Inference

A large portion of subjects dropout for reasons that suggest the missing data are MNAR (see Section 1.3). To identify the extrapolation distribution, we make the NFD assumption (8). Recall that the NFD assumption leaves one conditional distribution per incomplete pattern unidentified:$p_s(y_{s+1}|{\overline{y}}_s,v,x)$. To better identify $p_s(y_{s+1}|{\overline{y}}_s,v,x)$, rather than simply assuming a location shift (9), we make use of information regarding the type of dropout. Let Z_i = 1 or 0 denote subject i drops out for informative or noninformative reasons, respectively. We model Z conditional on observed data responses, pattern, auxiliary covariates and treatment with BART,

$$P(Z=1|{\overline{\mathit{Y}}}_s,S=s,\mathit{V},X=x)=F_N(f_{sx}({\overline{\mathit{Y}}}_s,\mathit{V})).$$

Recall F_N is the standard normal cdf, and $f_{sx}({\overline{\mathit{Y}}}_s,\mathit{V})$ is the sum of tree models from BART.

The indicator Z is used to help identify $p_s({\mathit{y}}_{s+1}|{\overline{y}}_s,\mathit{v},x)$. We assume

$$\begin{gathered} \left[Y_{s+1}|{\overline{\mathit{Y}}}_s,S=s,\mathit{V},X,\omega \right]\stackrel{d}{=} \\ P(Z=1|{\overline{\mathit{Y}}}_s,S=s,\mathit{V},X)\cdot \left[Y_{s+1}+{\tau }_{s+1}|{\overline{\mathit{Y}}}_s,S\ge s+1,\mathit{V},X,\mathit{\omega }\right]+ \\ P(Z=0|{\overline{\mathit{Y}}}_s,S=s,\mathit{V},X)\cdot \left[Y_{s+1}|{\overline{\mathit{Y}}}_s,S\ge s+1,\mathit{V},X,\mathit{\omega }\right], \end{gathered}$$ (18)

which is a mixture of an ACMV assumption and a location shift. We refer to Equation (18) as a MAR/MNAR mixture assumption. The idea is that, if a subject drops out for a reason associated with MAR, we impute the next missing value under ACMV; otherwise, we impute the next missing value by applying a location shift. The sensitivity parameter ${\tau }_{s+1}$ is interpretable to subject-matter experts, thus prior on ${\tau }_{s+1}$ can be created. Suppose two hypothetical subjects A and B have the same auxiliary covariates and histories up to time s, and suppose subject B drops out for an informative reason at time s while subject A remains on study. Then, the response of subject B at time (s + 1) is stochastically identical to the response of subject A at time (s + 1) after applying the location shift ${\tau }_{s+1}$. As the prior for ${\tau }_{s+1}$, we assume ${\tau }_{s+1}\ge 0$ as we expect subject B would have a higher PANSS score at time (s + 1) than subject A. The magnitude of ${\tau }_{s+1}$ is calibrated as in Equation (10),

$$\left[{\tau }_{s+1}|{\overline{Y}}_s={\overline{\mathit{y}}}_s,\mathit{V}=\mathit{v},X=x\right]={\tilde{\tau }}_x\cdot {\mathrm{\Delta }}_{s+1,x}({\overline{\mathit{y}}}_s,\mathit{v}).$$ (19)

We assume a uniform prior on ${\tilde{\tau }}_x,{\tilde{\tau }}_x\sim Unif(0,1)$, as it is thought unlikely that the deviation from ACMV would exceed a standard deviation (Linero and Daniels, 2015).

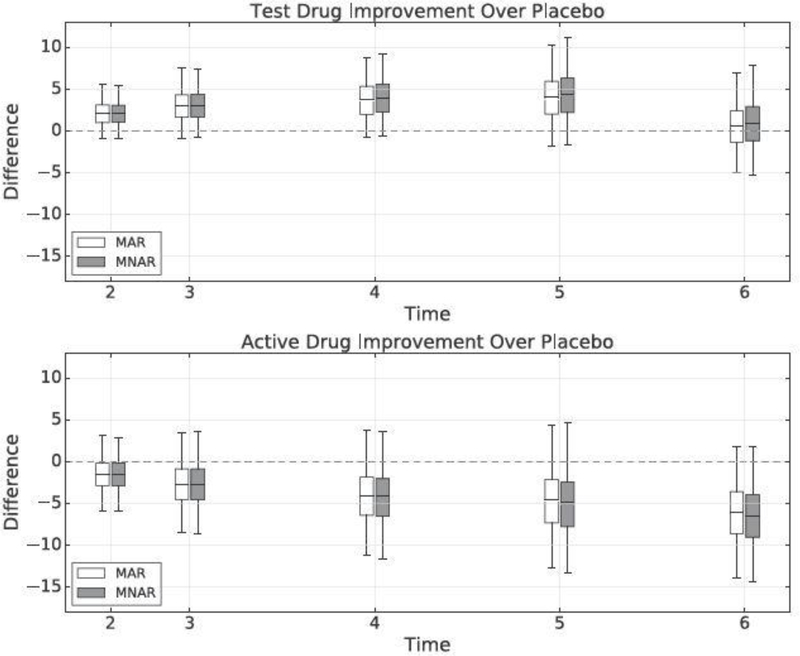
Figure 2 summarizes change from baseline treatment effect improvements of the test drug and active drug over placebo. We implement inference under both the MAR and the mixture of MAR/MNAR (Equations (18) and (19)) assumptions. For the test drug arm, the treatment effect improvement r_T – r_P has posterior mean 0.60 and 95% credible interval (−5.07,7.01) under MAR, and posterior mean 0.91 and 95% credible interval (−5.29,7.81) under MAR/MNAR mixture. There is no evidence that the test drug has better performance than placebo. The MAR/MNAR mixture assumption slightly increases the posterior mean of r_T – r_P as the test drug arm has a slightly higher informative dropout rate than the placebo arm (Appendix Table A.1). For the active drug arm, the treatment effect improvement r_A – r_P has posterior mean –6.08 and 95% credible interval (−13.90,1.72) under MAR, and posterior mean –6.45 and 95% credible interval (−14.34,1.75) under MAR/MNAR mixture. There appears to be some evidence that the active drug has better effect than placebo. The MAR/MNAR mixture assumption slightly decreases the posterior mean of r_A – r_P as the active drug arm has a slightly lower informative dropout rate than the placebo arm (Appendix Table A.1). Also, in both scenarios, the MAR/MNAR mixture assumption induces more uncertainty on the inferences (wider credible intervals), as we have discussed in Section 5.2.

Fig. 2.

Change from baseline treatment effect improvements of the test drug (top) and active drug (bottom) over placebo over time. Smaller values indicate more improvement compared to placebo. The dividing line within the boxes represents the posterior mean, the bottom and top of the boxes are the first and third quartiles, and the ends of the whiskers show the 0.025 and 0.975 quantiles.

The same dataset was previously analyzed in Linero and Daniels (2015), which concluded that there is little evidence that the test drug is superior to the placebo and some evidence of an effect of the active control. Our analysis is consistent with the previous analyses. See Appendix Table A.4 for a detailed comparison.

6.3. Sensitivity Analysis

To assess the sensitivity of inferences on treatment effect improvements (r_T – r_P and r_A – r_P ) to the informative priors on the sensitivity parameters (${\tilde{\tau }}_T$, ${\tilde{\tau }}_A$ and ${\tilde{\tau }}_P$), we consider a set of point-mass priors for each ${\tilde{\tau }}_x$ along the [0,1] grid. The detailed figure showing how inferences on r_T – r_P and r_A – r_P change for different choices of ${\tilde{\tau }}_T$, ${\tilde{\tau }}_A$ and ${\tilde{\tau }}_P$ is in Appendix Figure A.2. The sensitivity analysis corroborates our conclusion that there is no evidence that the test drug has better performance than placebo. For all the choices of ${\tilde{\tau }}_T$ and ${\tilde{\tau }}_P$, the posterior probability of r_T – r_P < 0 does not reach the 0.95 posterior probability cutoff. On the other hand, the sensitivity analysis shows that there is some evidence that the active drug is superior than placebo. For all the combinations of ${\tilde{\tau }}_A$ and $\hspace{0.17em}{\tilde{\tau }}_P$, the posterior probability of r_A – r_P < 0 is greater than 0.79. For most favorable values of ${\tilde{\tau }}_A$ and $\hspace{0.17em}{\tilde{\tau }}_P$, the posterior probability of r_A – r_P < 0 is greater than 0.95, although it only occurs when ${\tilde{\tau }}_A$ is substantially smaller than $\hspace{0.17em}{\tilde{\tau }}_P$. In summary, for all the choices of ${\tilde{\tau }}_x$, we do not reach substantially different results, which improves our confidence on the previous conclusions.

7. Discussion

In this work, we have developed a semiparametric Bayesian approach to monotone missing data with non-ignorable missingness in the presence of auxiliary covariates. Under the extrapolation factorization, we flexibly model the observed data distribution and specify the extrapolation distribution using identifying restrictions. We have shown the inclusion of auxiliary covariates in the model could in general improve the accuracy of inferences and reduce the extent of sensitivity analysis. We have also shown more accurate inferences can be obtained by using the proposed semiparametric Bayesian approach compared to using more restrictive parametric approaches and simple Bayesian nonparametric approaches.

The computational complexity in our application is manageable since the schizophrenia clinical trial dataset contains only 204 subjects. With much larger data sets computation becomes challenging. However, posterior simulation can be conducted in parallel for fitting the models of the observed responses, patterns and auxiliary covariates (see Equation 11). For each individual component, see Banerjee et al. (2013); Hensman et al. (2013) and Datta et al. (2016) for a scalable Gaussian process implementation and Pratola et al. (2014) for a scalable BART implementation. G-computation is easily scalable because it requires drawing independent hypothetical datapoint using each posterior sample.

When the number of auxiliary variables grows, it might be desirable to perform variable selection. Variable selection can be done through exploratory analysis, e.g. fitting linear regression or spline regression models. Alternatively, it can be done more formally for each component of Equation (1). See Savitsky et al. (2011) for variable selection for Gaussian process priors and Linero (2018) for variable selection for Bayesian additive regression trees.

A possible extension of our work is to consider continuous time dropout. The Gaussian process is naturally suitable for the continuous case. Another extension would be more flexible incorporation of auxiliary covariates beyond the mean. Extending our method to non-monotone missing data without imposing the partial ignorability assumption could be done with alternative identifying restrictions described in Linero and Daniels (2018) and possibly, a slightly modified semiparametric model. In the setting of binary outcomes, our method can be naturally extended by using a probit link. To identify the extrapolation distribution under NFD, we assume a location shift. Alternatively, we can consider exponential tilting (Rotnitzky et al., 1998; Birmingham et al., 2003).

Supplementary Material

Supp 1

Appendix: Appendix showing more details of the schizophrenia clinical trial dataset, prior specification, MCMC implementation, G-computation, simulation studies, real data analysis, convergence diagnostics and computing times.

Python package: Python package bspmis (with an R interface) containing code to perform the simulation studies and real data analysis described in the article. (GNU zipped tar file)