SVM-CART for Disease Classification

Abstract

Classification and regression trees (CART) and support vector machines (SVM) have become very popular statistical learning tools for analyzing complex data that often arise in biomedical research. While both CART and SVM serve as powerful classifiers in many clinical settings, there are some common scenarios in which each fails to meet the performance and interpretability needed for use as a clinical decision-making tool. In this paper, we propose a new classification method, SVM-CART, that combines features of SVM and CART to produce a more flexible classifier that has the potential to outperform either method in terms of interpretability and prediction accuracy. Further-more, to enhance prediction accuracy we provide extensions of a single SVM-CART to an ensemble, and methods to extract a representative classifier from the SVM-CART ensemble. The goal is to produce a decision-making tool that can be used in the clinical setting, while still harnessing the stability and predictive improvements gained through developing the SVM-CART ensemble. An extensive simulation study is conducted to asses the performance of the methods in various settings. Finally, we illustrate our methods using a clinical neuropathy dataset.

1. Introduction

Statistical learning methods such as decision trees and support vector machines have become very popular tools for analyzing complex data that of-ten arise in biomedical research [1–9]. Classification and Regression Trees (CART) are useful statistical learning tools because they allow for intuitive and simple disease classification by recursively partitioning the covariate space [1–5]. Support vector machines (SVMs) are non-probabilistic supervised learning procedures that create a multi-dimensional hyperplane to partition the covariate space into two groups allowing for classification [3,6–9].

While both CART and SVM serve as powerful classifiers in many clinical settings, there are some common scenarios in which both fail to meet the performance and interpretability needed for application as a decision-making tool. These scenarios often occur when there are different disease-exposure mechanisms in subgroups of the population. The following scenarios describe some pathological examples where SVM and CART fail to meet the above criteria.

1.1. Scenario 1: Disease Outcome, Patient Gender and two Continuous Exposure Variables

In Figure 1a, the exposure-disease mechanism is very different between males and females. The gender-outcome subgroups are represented by shape and the continuous exposure variables are in the x and y axis of the plot. The continuous exposure variables represent covariates that have different patterns of association with the disease outcome based on a third categorical covariate (e.g. gender). Examples include systolic blood pressure and HDL levels (continuous exposures).

Figure 1:

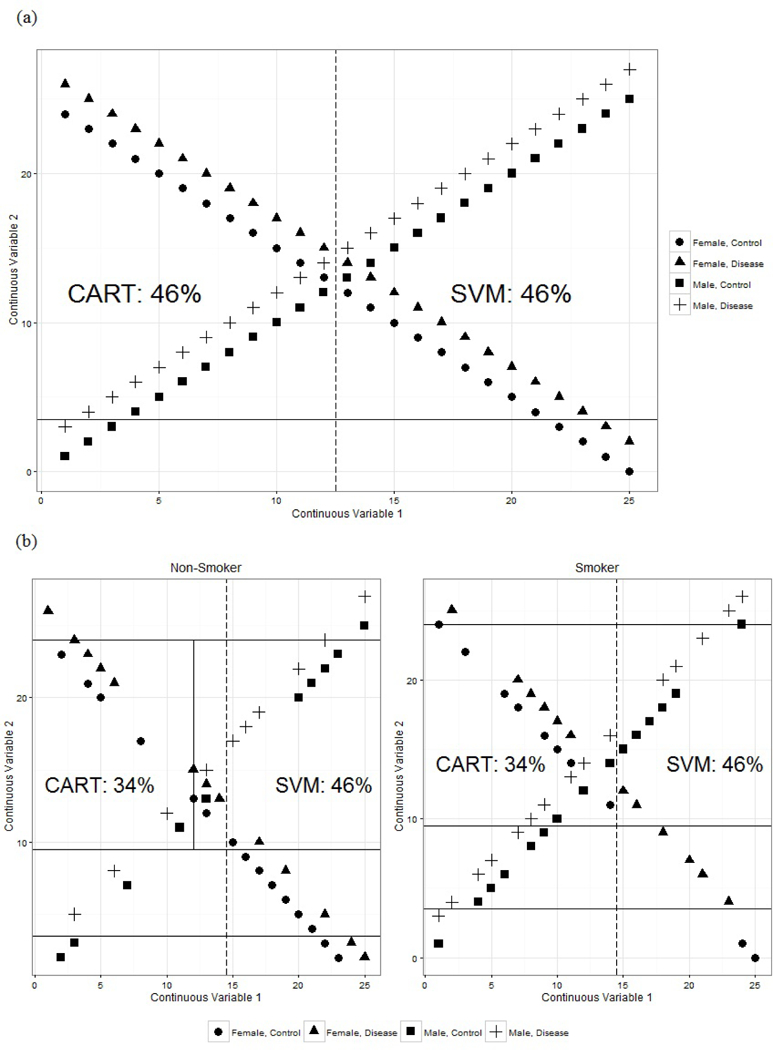
Results from SVM and CART for Simulated Scenarios

The dashed line in Figure 1a represents the split from a linear SVM and the solid line represents the single split from CART. The SVM splits the data down the middle of continuous covariate 1 and has a 46% misclassification rate. CART performs the same with a 46% misclassification rate. Visually, it is simple to classify the patients into disease and control groups, but both methods fail to perform this simple task.

1.2. Scenario 2: Disease Outcome, Patient Gender, Smoking Status and two Continuous Exposure Variables

In the second example, in addition to the gender groups and two continuous covariates, we have the additional binary covariate: smoking status. Figure 1b shows the CART and SVM classifiers: the solid lines represent the CART splits in the two-dimensional continuous exposure covariate space and the dashed line represent the hyperplane from the SVM classifier.

The CART splits perform slightly better this time with a misclassification rate of 34%. SVM still has a misclassification rate of 46%. We also see that the CART tree becomes quite complicated quickly, but in the end, still produces a relatively poor performing classifier.

Classification scenarios such as the two presented above provide motivation for our research. In this paper, we propose a new classification method that combines features of SVM and CART to allow a more flexible classifier that has the potential to outperform either method in terms of interpretability and prediction accuracy. Ultimately our goal is to develop a tool that can be used in the clinical setting for decision-making.

The literature on combination classifiers is somewhat sparse. Xu et. al (1992) described methods of combining classifiers to improve handwriting recognition. These authors propose a combination classifier that aggregates predictions across many different types of classifiers [10–12]. Our proposed method differs from Xu et al. in that we exploit specific aspects of each classifier in tandem to create a new single classifier [10–12]. While many different classifiers could be considered for use in tandem, the choice of CART and SVM was motivated by the clinical study in our context. In neurology, the mechanistic pathway towards the disease polyneuropathy can be different amongst gender/glycemic subgroups of the population. CART was chosen as the first classifier because it offers a very natural way of subgrouping patients and SVM was specifically chosen since it is non-probabilistic and complements CART by overcoming issues with rectangular splits that often plague tree based methods. Additionally, because CART and SVM are two of the most well known non-parametric approaches in the clinical setting, the methods will be more approachable by clinicians who will ultimately use this method to make clinical decisions. The binary decision rule generated by CART is attractive to clinicians; This is how clinicians ”think” and it is therefore easy for them to bin patients in the fashion that CART works.

There is a growing literature for combining classification trees with parametric models, often implemented at the terminal nodes. Additionally, methods have been developed for growing trees to find treatment-subgroup interactions. Examples include GUIDE (Loh), CRUISE (Kim and Loh), LOTUS (Chan and Loh), MOB (Zeileis), STIMA (Dusseldorp), PALM (Seibold), PPTree (Lee) and Interaction Trees (Su) [13–20]. In certain scenarios, these methods take a significant step to improve prediction accuracy compared to a typical classification tree by overcoming issues with perpendicular splits, finding important interaction subgroups and applying parametric models for inference. Our proposed method differs from the earlier works in that we use a fully non-parametric approach combining two classifiers to capture likely different disease-exposure mechanisms amongst subgroups of the population. In our proposed method, we elicit clinical information for covariate inputs into the CART portion of the classifier, without having to evaluate every pairwise interaction. By focusing on apriori knowledge-driven interactions, our resulting classifier is more nuanced in its application. The overall goal of the proposed method is to develop a valid, interpretable, and easily usable tool for prediction in the clinical setting.

Previous literature by De Leon et. al describe an approach for classification using general mixed-data models (GMDMs) [21]. Leon et. al take a parametric approach to classification that takes into account the measurement scale of the variables involved [21]. In our approach, we carefully distinguish variables based on measurement scales (continuous vs. categorical) to determine when to use them in the proposed classifier.

This paper is organized as follows. Section 2 describes the proposed methodology, SVM-CART. Section 3 describes ensemble methods for SVM-CART. In Section 4, we perform an extensive simulation to asses the prediction performance of our proposed SVM-CART classifier under various scenarios. Section 5 illustrates an application of our methodology to create a classifier for neuropathy. Last, concluding remarks and discussion are provided in Section 6.

2. Methodology

2.1. Classification and Regression Trees

First, we introduce some terminology that will be used to describe a classification tree. A classification tree T has multiple nodes where observations are passed down the tree. The tree starts with a root node at the top and continues to be recursively split to yield the terminal nodes at which stage no further split is prescribed. The intermediate nodes in the tree between the root node and terminal nodes are referred to as internal nodes. We specifically denote the set of terminal nodes as $\tilde{T}$ and the number of terminal nodes is denoted as $\left|\tilde{T}\right|$. In CART, a class prediction is given to each observation based on which terminal node it falls into.

In growing a tree, the natural question that arises is how and why a parent node is split into daughter nodes. Trees use binary splits, phrased in terms of the covariates, that partition the covariate space recursively. Each split depends upon the value of a single covariate. The partitioning is intended to increase within-node homogeneity. Goodness of a split must therefore weigh the homogeneities in the two daughter nodes. The extent of node homogeneity is measured using an ‘impurity’ function. Potential splits for each of the covariates are evaluated, and the covariate and split value resulting in the greatest reduction in impurity is chosen.

The impurity at proposed node h is denoted as i(h) and the probability that a subject falls into node h is P (h), where P (h) is estimated from the sample proportions in the training data. Specifically, for a split sϵS at node h, the left and right daughter nodes are denoted as h_L and h_R respectively. Where S is the set of all possible splits. The reduction in impurity is calculated as follows: ∆I(s, h) = i(h) – P(h_L)i(h_L) – P(h_R)i(h_R). For binary outcomes, i(h) is measured in terms of entropy or Gini impurity [1,2]. The splitting rule that maximizes ∆I(s, h) over the set S of all possible splits is chosen as the best splitter for node h.

2.2. Support Vector Machines

Support Vector Machines create separating hyperplanes to give class-level predictions. The SVM hyperplane takes a small or large number of covariates to create a hyperplane that can be used to classify patients into outcome groups [6–9].

Let y_i be the binary outcome for patient i, and x_i the p × 1 vector of covariates for the ith patient. Then we denote x as the p × n matrix of continuous covariates.

SVMs create a hyperplane of the form:

$$ℍ=\mathit{x}:{\mathit{w}}^{\prime }x+b=\text{0}$$

where $\mathit{w}ϵ{ℝ}^p$ and $bϵR$ are the set of optimal weights corresponding to each continuous covariate that construct the hyperplane. SVMs create the separating hyperplane by maximizing the margin between the nearest p-dimensional data points on each side of the hyperplane. In clinical data, we often do not have linearly separable data. To deal with non-separable data we use the optimal soft-margin hyperplane which introduces slack variables to penalize classification errors based on some predetermined weights [3,6,7]. The optimal soft-margin hyperplane is found by minimizing the following objective function:

$$\begin{gathered} \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\min }_{\mathit{w},b,\psi }\frac{1}{2}{\Vert \mathit{w}\Vert }^2+\frac{C}{n}{\sum }_{i=1}^n{\psi }_i \\ \text{subject to}:y_i\left({\mathit{w}}^{\prime }{\mathit{x}}_i+b\right)\ge 1-{\psi }_i\forall i \text{and} {\psi }_i\ge 0\forall i \end{gathered}$$

The solution to the above minimization problem represents the optimal hyperplane. C represents the cost penalty assigned for a misclassified subject and ψ_i are the slack variables that allow for this misclassification. Using Lagrangian multipliers, α_i ≥ 0, the optimal hyperplane is obtained as [3,6,7]:

$$\begin{gathered} \widehat{\mathit{w}}={\sum }_{i=1}^n{\widehat{\mathit{\alpha }}}_i{\mathit{y}}_i{\mathit{x}}_i \\ \hspace{1em}\widehat{b}=y_i-{\widehat{\mathit{w}}}^{\prime }{\mathit{x}}_i \end{gathered}$$

2.3. SVM-CART

In the traditional CART method, all covariates of interest are considered for tree building. For SVM-CART, we propose to employ CART to split based on only the categorical covariates. The terminal nodes from CART are used to pass along patients to subgroups. Support Vector Machines are developed on each of the subgroups using the continuous covariates, thereby generating $\left|\tilde{T}\right|$ separating hyperplanes.

The optimal hyperplane solution can now be written within the SVM-CART framework as follows:

$$\begin{gathered} {\widehat{\mathit{w}}}_{{\tilde{T}}_j}={\sum }_{i=1}^{n_j}{\widehat{\mathit{\alpha }}}_i{\mathit{y}}_i{\mathit{x}}_i \\ \hspace{1em}\widehat{b}=y_i-{\widehat{\mathit{w}}}_{{\tilde{T}}_j}{ }^{\prime }{\mathit{x}}_i \end{gathered}$$

where we have a unique solution for each of the ${\tilde{T}}_j$ terminal nodes created from CART. For each patient i in terminal node ${\tilde{T}}_j$, the classifier evaluates hyperplane j to determine classification: if ${\widehat{\mathit{w}}}_{{\tilde{T}}_j}{ }^{\prime }{\mathit{x}}_i+b>0$ we assign patient i to group 1. Alternatively, if ${\widehat{\mathit{w}}}_{{\tilde{T}}_j}{ }^{\prime }{\mathit{x}}_i+b<0$ we assign patient i to group 0. With a strong subgroup selection by CART, the terminal nodes may not be well mixed. If any of the terminal nodes are pure and contain only patients from one outcome group, no SVM is generated. For future prediction, patients that fall into these nodes are given the same predicted outcome.

Results from the single SVM-CART classifier offer a clinician friendly and easy to use tool by first distributing patients into different subgroups and then assigning an outcome class prediction based on an array of continuous data features.

2.4. Hyperparameter Tuning

2.4.1. Class Weights for CART

The proposed SVM-CART allows for implementation of class weights within the CART part of the method. For a rare disease, a user can put higher weight to the disease cases to assist in the most useful classification. Using inverse proportions of the cases and controls is a simple way to include weight for the CART part of the SVM-CART classifier.

2.4.2. SVM Cost Parameter

The cost parameter C allows the user to control how costly misclassification is in the creation of the SVM hyperplane. Large values of C generally result in a smaller and harder margin hyperplane and conversely smaller cost results in a larger, softer margin hyperplane. The cost parameter is chosen through a data-driven search. We select the cost parameter by examining the test error using a cross validation procedure or by examining the out-of-bag error estimates from a bootstrapped sample. In either case, a reasonable grid search over the range 10⁻⁵ to 10⁴ allows the user to select the proper cost parameter for building the SVM within the SVM-CART procedure.

2.4.3. Class Weights for SVM

There exist many scenarios in which we want to assign different misclassification costs to each outcome group. We propose assigning an outcome-class specific cost parameter by assigning weights to each of the outcome groups. Assigning weights to the two outcome classes allows us to re-write the hyperplane minimization problem as:

$${\min }_{{\mathit{w}}_{{\tilde{T}}_j},b,\psi }\frac{1}{2}{\Vert {\mathit{w}}_{{\tilde{T}}_j}\Vert }^2+\frac{C_{+}}{n_{j+}}{\sum }_{i=1}^{n_{j+}}{\psi }_i+\frac{C_{-}}{n_{j-}}{\sum }_{i=1}^{n_{j-}}{\psi }_i$$

where $C_{+}=r_{+}*C$ and $C_{-}=r_{-}*C$. In other words, to assign a higher cost to the misclassification of the disease outcomes, we do so by using the weights r₋ and r₊.

In SVM-CART, the inverse proportion of the cases and controls in each of CART’s terminal nodes is chosen to be that node’s SVM class weights. Then, a data driven search is performed to determine a weight multiplier, m, for the inverse proportion weights (r₋, r₊). The final chosen weights for the SVM-CART are: $C_{+}=m*r_{+}*C$ and $C_{-}=r_{-}*C$. The multiplier allows more flexibility in the class weights for the support vector machines in each terminal node.

2.5. SVM-CART as a Clinical Tool

Clinical applicability is an important goal of our proposed method. For certain data applications, our methodology is expected to provide a better performing yet simpler classifier due to the ability to create non-rectangular splits.

Using the SVM-CART classifier is very straightforward. First a patient is passed down the CART tree based on his/her characteristics until they are placed in one of the CART terminal nodes. Then, a linear equation is evaluated to classify patients into the final terminal classification nodes. For a SVM-CART with k continuous covariates, we evaluate an equation of the form:

$$I_{{\tilde{T}}_j}\left(x_1*w_1+\dots +x_k*w_k+b>0\right)$$

where the indicator function $I_{{\tilde{T}}_j}$ assigns patients to outcome 1 if $x_1*w_1+.+x_k*w_k+b>0$ in terminal node j and to outcome 0 otherwise. There is a terminal node classification equation for each of the subgroup terminal nodes ${\tilde{T}}_j$ created by the initial CART. The exception would be the scenario where terminal node ${\tilde{T}}_j$ is pure; in that case, we have a class prediction without a SVM classifier.

2.6. SVM-CART for Simulated Scenarios

For both simulated examples in Section 1, SVM-CART yields a perfect classifier. The CART portion in the first scenario splits on gender allowing us to create a perfect linear SVM based on the two continuous covariates. In Scenario two, we first split on smoking status and then by gender. Each of the four node groups from CART then yields itself to a linear SVM classifier that produces perfect classification. The results from the SVM-CART classifier in Scenario 2 are displayed in Figure 2.

Figure 2:

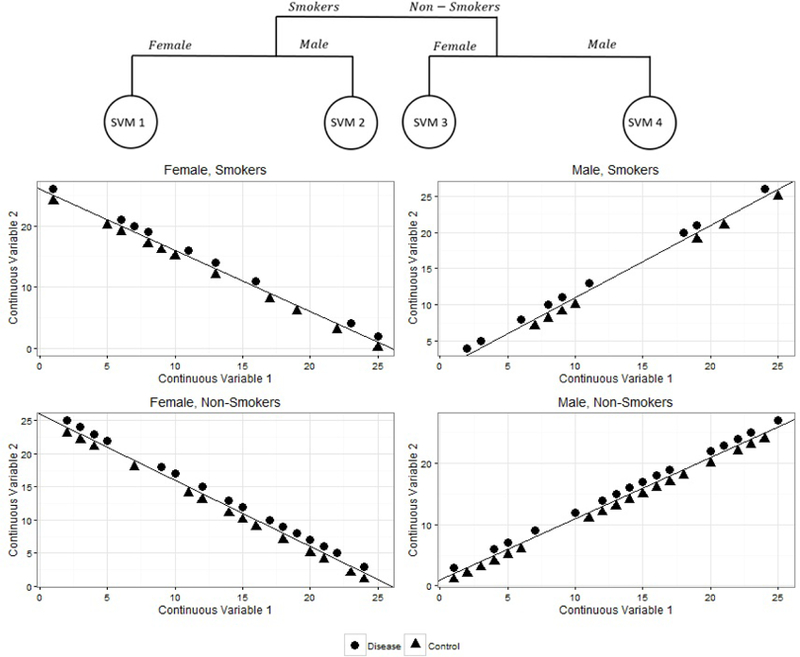
SVM-CART for Simulated Scenarios

3. SVM-CART Ensemble

3.1. Creating the SVM-CART Ensemble

Ensemble methods have become very popular in tree based applications, allowing for creation of more stable trees that often lead to improved predictions [22–25]. An ensemble method proposed in 1994 by Breiman involved bootstrap aggregating or Bagging [22]. The premise of this method is to generate many bootstrap samples of the data and create an individual classification tree from each of the bootstrap samples. A final classification is determined by voting across all trees in the ensemble [22–25].

We develop an SVM-CART ensemble to enhance prediction accuracy. Specifically, we generate b bootstrap samples by sampling uniformly n observations with replacement from the entire data of size n. On each of the b samples, we generate a SVM-CART classifier. For each patient, the most common class prediction across the b classifiers is the predicted outcome.

To obtain honest estimates of prediction accuracy, we derive error rates based on the out-of-bag sample. For the jth SVM-CART classifier, the out-of-bag sample consists of patients that were not included in the specific boot-strap sample used to create the jth classifier. For each SVM-CART classifier in the ensemble, we make a class prediction for only the patients in the out-of-bag sample. Finally, the out-of-bag prediction for each patient is the most common predicted class across all c ≤ b samples for which that patient was out-of-bag. The out-of-bag error rate for a single bootstrap sample is calculated as the percentage of misclassified patients in the out-of-bag sample. The out-of-bag error rate for the ensemble is calculated as the percentage of misclassified patients based on the out-of-bag prediction.

3.2. Selecting the Most Representative Classifier from the Ensemble

Bagging the SVM-CART improves stability and prediction ability; however, we lose the interpretability of a single classifier. This is a significant loss from a clinical standpoint because ultimately, we want to produce a decision-making tool that can be used in the clinic setting.

This section describes how to harness the stability and predictive improvements gained through the SVM-CART ensemble while still producing a clinician friendly tool. To obtain a usable prediction tool for the clinical setting, we attempt to extract the single most representative classifier from the ensemble. We think of each SVM-CART classifier as a point in a high-dimensional space and cluster the classifiers according to some measure of proximity. Note that this space is much more complex than the Euclidean space, and distances between the classifiers can be quantified in several ways. Any classifier in the above space can be identified by a finite set of parameters, and these parameters could include the partition of the covariate space and the predictions from each terminal classification node. We propose two such metrics that are extensions of Banerjee et al. [26].

The first metric focuses on prediction proximity (i.e. similarity). Two classifiers are similar if the predictions from them are the same for all subjects. Without loss of generality, the distance between SVM-CART 1 and SVM-CART 2 is measured using the metric:

$$d_1\left(T_1,T_2\right)=\frac{1}{n}{\sum }_{i=1}^n{\left({\widehat{y}}_{1i}-{\widehat{y}}_{2i}\right)}^2$$

where ${\widehat{y}}_{1i}$ is the class prediction for patient i from SVM-CART classifier 1.

The second metric focuses on how closely (i.e. similarly) the covariate space is partitioned by two classifiers. Classifiers that are similar will place the same subjects together in a terminal classification node and separate the same subjects in different terminal classification nodes (i.e. SVM-CART 1 and 2 are similar if two patients that are placed in the same terminal node by classifier 1 are also placed in the same terminal node by classifier 2). Towards that end, we define a metric that captures how subjects are clustered in the terminal classification nodes from SVM-CART. For all $\left(\begin{array}{l}n\\ 2\end{array}\right)$ pairs of subjects, let I(T₁(i, j)) be the indicator that patient i and patient j are in the same terminal classification node from SVM-CART 1.

The distance metric is then defined as:

$$d_2\left(T_1,T_2\right)=\frac{{\sum }_{i>j}{\sum }_j\left|I_{T_1}\left(i,j\right)-I_{T_2}\left(i,j\right)\right|}{\left(\begin{array}{l}n\\ 2\end{array}\right)}$$

The factor $\left(\begin{array}{l}n\\ 2\end{array}\right)$ scales the metric to the range (0, 1) such that 0 indicates perfect agreement. A pair of subjects contributes a positive amount to d₂ if and only if one SVM-CART classifier places the subjects together and the other SVM-CART classifier places them apart. Thus d₂ is 0 if the two classifiers partition the covariate space in exactly the same way.

The score D(T) for a SVM-CART classifier T is computed by averaging the individual distance metrics between the classifier T and all other classifiers in the ensemble. This is the average distance between T and all other classifiers in the ensemble. So, a low score for a classifier indicates its similarity to all other classifiers in the ensemble. The score D(T) is computed for each of the distance metrics (i.e. d₁, d₂ giving rise to scores D₁(T) and D₂(T)) and the representative classifiers in the ensemble are chosen based on the smallest D(T) values.

4. Simulation Study

We compare performance of the SVM-CART classifier using several criteria over a variety of simulation scenarios. We generated a binary outcome y based on a logistic regression model with two categorical covariates: x₁ ∼ bernoulli (0.3) and x₂ ∼ multinomial (0.45, 0.15, 0.4), and four continuous covariates: x₃ ~ uniform(0, 5), x₄ ~ N (7, 5), x₅ ~ weibull(0.5) and x₆ ~ N (1, 5).

Several tuning parameters were used to assess prediction performance under the various simulation scenarios. First, we varied the sample size: n = {100, 500, 1000}. Next, we assessed the impact that different levels of continuous-categorical covariate interactions may have on prediction performance. Specifically, we assess prediction performance under small to large interaction effect sizes as well as in the absence of any interaction between the categorical and continuous covariates. Lastly, we examine how varying degrees of the main effects of the categorical covariates influence prediction performance.

Specifically, we generate data using the following underlying model: logit(p) = Xα + Wβ, where p = P (y = 1|X, W), where X is the design matrix for the main effects and W is the matrix of interactions. The fixed α and β values are listed in Table 1. These give rise to varying main and interaction effects as described above. The binary outcome is generated as y ~ bernoulli(p).

Table 1:

Beta Coefficients for the Data Generated from Logistic Regression Models Under Various Scenarios

		Interaction Effect
		None		Low		Moderate		High
		Main Effects of Categorical Covariates
Beta Values	Covariate	High	Low	High	Low	High	Low	High	Low
α0	Intercept*	α0	α0	α0	α0	α0	α0	α0	α0
α1	x1	4.7	2.7	4.7	2.7	4.7	2.8	4.7	2.7
α2	$x_{2_1}$	8.05	4.05	8.05	4.05	8.05	−4.05	8.05	4.05
α3	$x_{2_2}$	−8.35	−4.35	−8.36	−4.36	−8.05	−4.36	−8.36	−4.36
α4	x3	−1	−1	−0.7184	−0.7184	−1	−1	8	8
α5	x4	−.5	−.5	0.317	0.317	0.5	0.5	2	2
α6	x5	2	2	0.215	0.215	2	2	5	5
α7	x6	4	4	0.695	0.695	4	4	−7	−7
β1	$x_1*x_{2_1}$	0	0	−2.2	−2.2	−2.2	−2.2	−2.2	−2.2
β2	$x_1*x_{2_2}$	0	0	−2.9	−2.9	−2.9	−2.9	−2.9	−2.9
β3	x3 * x1	0	0	0.4934	0.4934	6	6	−9	−9
β4	$x_3*x_{2_1}$	0	0	1.5764	1.5764	−4	−4	−16	−16
β5	$x_3*x_{2_2}$	0	0	0.6203	0.6203	−2	−2	−4	−4
β6	$x_3*x_1*x_{2_1}$	0	0	−1.21143	−1.21143	0	0	24	24
β7	$x_3*x_1*x_{2_2}$	0	0	−1.1303	−1.1303	0	0	14	14
β8	x4 * x1	0	0	0.229	0.229	−2	−2	−4	−4
β9	$x_4*x_{2_1}$	0	0	−0.591	−0.591	1	1	−1	−1
β10	$x_4*x_{2_2}$	0	0	−0.215	−0.215	0.5	0.5	−1	−1
β11	$x_4*x_1*x_{2_1}$	0	0	−0.909	−0.909	0	0	1	1
β12	$x_4*x_1*x_{2_2}$	0	0	0.0572	0.0572	0	0	1	1
β13	x5 * x1	0	0	0.772	0.772	−3	−3	−8	−8
β14	$x_5*x_{2_1}$	0	0	−0.318	−0.318	1	1	−4	−4
β15	$x_5*x_{2_2}$	0	0	−1.189	−1.189	−5	−5	−5	−5
β16	$x_5*x_1*x_{2_1}$	0	0	−0.658	−0.658	−2	−2	9	9
β17	$x_5*x_1*x_{2_2}$	0	0	0.5689	0.5689	7	7	14	14
β18	x6 * x1	0	0	−1.423	−1.423	−5	−5	11	11
β19	$x_6*x_{2_1}$	0	0	−0.15	−0.15	−3	−3	15	15
β20	$x_6*x_{2_2}$	0	0	−0.895	−0.895	−8	−8	10	10
β21	$x_6*x_1*x_{2_1}$	0	0	0.974	0.974	1	1	−14	−14
β22	$x_6*x_1*x_{2_2}$	0	0	1.652	1.652	12	12	−19	−19

^*Where α₀ centers the data at 0 to ensure a well mixed sample

In a separate simulation, we generated data from a true underlying SVM-CART type structure. In this set-up, the tree first splits patients by x₁. Patients with x₁ = 1 were further split by x₂ (1 vs. 2,3). For patients with x₁ = 0, those with x₂ = 3 were split from x₂ = 1 or x₂ = 2. For each of these four terminal nodes created by the true underlying tree, we generate data from node-specific logistic regression models. The data generating structure is displayed in Figure 3. We examine scenarios where the β coefficients were different across the four terminal nodes (Figure 3a) and similar across the four terminal nodes (Figure 3b).

Figure 3:

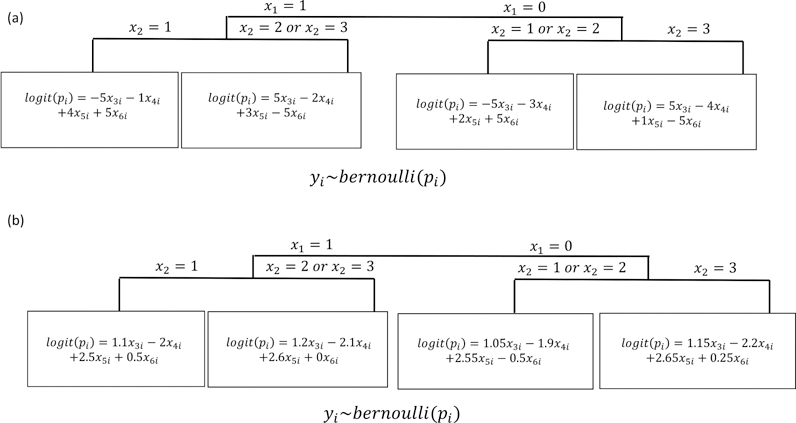
Data Simulated from Underlying SVM-CART Like Structure

For each of the above scenarios, we generated 1,000 simulated datasets. We split each dataset into a training and testing set by randomly assigning 70% of the sample for training and 30% for testing. To assess predictive performance, we calculated overall prediction accuracy (ACC), sensitivity (TPR), specificity (TNR), positive predictive value (PPV) and negative predictive value (NPV) based on the testing set. Lastly, we obtained average size of the classifiers based on the number of terminal nodes for CART, and the number of non-orthogonal dimensions of the hyperplane for SVM. For SVM-CART, we obtained both the number of terminal nodes created by the CART part of the classifier, and total number of SVM dimensions created for each of the CART terminal nodes.

4.1. Simulation Results

Simulation results for data generated from logistic regression models (Table 1 coefficients) are displayed in Table 2. As sample size increases, each of the three methods show improvement in prediction performance. CART and SVM-CART demonstrate significant prediction gains (SVM-CART: 6.9% and CART: 8.9% average ACC increase from n = 100 to n = 1000) while SVM has only modest gains (3.9% average ACC increase from n = 100 to n = 1000). Additionally, the largest improvements in prediction performance for SVM-CART occurred when sample sizes increased from n = 100 to n = 500, with only minor improvements occurring when sample size increased from n = 500 to n = 1000. SVM-CART and CART classifiers also increased in size as n increased.

Table 2:

Results Based on Data Generated from a Logistic Regression Model

			Main Effects of the Categorical Covariates
			Low						High
Interaction Effect	Sample Size (N)	Classifier	ACC	PPV	NPV	TPR	TNR	Size	ACC	PPV	NPV	TPR	TNR	Size
High	100	CART	0.72	0.69	0.74	0.70	0.73	3.5	0.70	0.70	0.69	0.70	0.70	3.6
	100	SVM	0.75	0.75	0.74	0.72	0.77	7.0	0.75	0.76	0.74	0.75	0.76	7.0
	100	SVM-CART	0.75	0.76	0.74	0.71	0.79	11.6,2.9	0.75	0.77	0.73	0.72	0.77	12.1,3.0
	500	CART	0.82	0.83	0.81	0.80	0.84	4.0	0.82	0.83	0.82	0.82	0.83	10.5
	500	SVM	0.78	0.79	0.78	0.76	0.81	7	0.80	0.79	0.81	0.81	0.80	7.0
	500	SVM-CART	0.87	0.89	0.86	0.84	0.90	16.1,4.0	0.82	0.85	0.79	0.78	0.86	17.0,4.3
	1000	CART	0.84	0.85	0.83	0.82	0.86	13.0	0.85	0.85	0.85	0.85	0.85	13.1
	1000	SVM	0.84	0.84	0.83	0.81	0.86	7.0	0.79	0.80	0.78	0.78	0.80	7.0
	1000	SVM-CART	0.90	0.92	0.88	0.87	0.92	16.6,4.2	0.82	0.85	0.80	0.78	0.86	18.4,4.6
Moderate	100	CART	0.72	0.71	0.73	0.65	0.78	3.3	0.73	0.81	0.63	0.74	0.72	3.3
	100	SVM	0.82	0.80	0.83	0.79	0.84	7.0	0.82	0.85	0.80	0.84	0.80	7.0
	100	SVM-CART	0.80	0.78	0.81	0.77	0.82	9.4,2.4	0.82	0.85	0.77	0.83	0.80	8.7,2.1
	500	CART	0.80	0.79	0.80	0.75	0.84	9.8	0.80	0.85	0.74	0.81	0.80	9.6
	500	SVM	0.84	0.83	0.85	0.82	0.86	7.0	0.84	0.87	0.80	0.86	0.82	7.0
	500	SVM-CART	0.84	0.84	0.84	0.81	0.87	11.9,3.0	0.86	0.89	0.82	0.87	0.85	10.0,2.5
	1000	CART	0.82	0.82	0.82	0.77	0.86	13.2	0.83	0.88	0.76	0.83	0.83	13.4
	1000	SVM	0.84	0.83	0.86	0.83	0.86	7.0	0.85	0.87	0.82	0.86	0.84	7.0
	1000	SVM-CART	0.86	0.85	0.86	0.83	0.88	12.0,3.0	0.87	0.90	0.84	0.88	0.86	10.1,2.5
Low	100	CART	0.69	0.69	0.70	0.70	0.69	3.8	0.68	0.68	0.67	0.69	0.66	3.8
	100	SVM	0.79	0.79	0.79	0.79	0.79	7.0	0.78	0.78	0.78	0.79	0.77	7.0
	100	SVM-CART	0.61	0.60	0.61	0.61	0.60	11.5,3.0	0.7	0.7	0.7	0.72	0.68	10.7,3.2
	500	CART	0.81	0.81	0.82	0.82	0.81	11.4	0.81	0.81	0.81	0.82	0.8	10.8
	500	SVM	0.81	0.81	0.82	0.82	0.81	7.0	0.81	0.8	0.81	0.83	0.79	7.0
	500	SVM-CART	0.73	0.74	0.72	0.70	0.75	14.9,4.0	0.71	0.7	0.72	0.76	0.66	15.2,3.9
	1000	CART	0.84	0.84	0.85	0.85	0.84	14.1	0.84	0.83	0.84	0.85	0.82	12.8
	1000	SVM	0.83	0.83	0.82	0.82	0.83	7.0	0.81	0.8	0.82	0.83	0.79	7.0
	1000	SVM-CART	0.74	0.74	0.73	0.72	0.75	15.7,4.0	0.71	0.66	0.77	0.81	0.61	16.0,4.0
None	100	CART	0.85	0.85	0.84	0.86	0.83	2.4	0.88	0.88	0.88	0.87	0.9	2.3
	100	SVM	0.94	0.94	0.94	0.94	0.93	7.0	0.94	0.93	0.94	0.94	0.93	7.0
	100	SVM-CART	0.85	0.88	0.83	0.84	0.87	9.8,2.5	0.9	0.9	0.9	0.88	0.91	9.0,2.3
	500	CART	0.90	0.89	0.90	0.91	0.87	6.8	0.91	0.9	0.91	0.9	0.92	5.5
	500	SVM	0.97	0.97	0.97	0.97	0.96	7.0	0.97	0.96	0.97	0.97	0.97	7.0
	500	SVM-CART	0.87	0.90	0.84	0.85	0.90	11.5,2.9	0.94	0.94	0.95	0.94	0.95	7.6,1.9
	1000	CART	0.91	0.91	0.91	0.92	0.89	8.6	0.92	0.92	0.92	0.9	0.93	6.9
	1000	SVM	0.97	0.97	0.97	0.97	0.97	7.0	0.97	0.97	0.97	0.97	0.97	7.0
	1000	SVM-CART	0.87	0.90	0.84	0.85	0.90	11.5,2.9	0.95	0.95	0.95	0.94	0.95	7.1,1.8

SVM-CART generally had better prediction performance when the main effects of the categorical covariates were large. When the main effects of the categorical covariates were large, the CART part of the SVM-CART classifier builds slightly larger trees. SVM performed similarly in the scenarios with high/low main effects of the categorical covariates and CART had somewhat modest improvement in the setting with high main effects.

There was generally a small, positive correlation between the SVM-CART prediction accuracy and the CART portion terminal node size. When the main effects of the categorical covariates were small, the Spearman correlations were 0.06, 0.00, 0.01, 0.11 for the simulation scenarios with no, low, moderate and high interaction effects. In contrast, when the main effects were large were large, the Spearman correlations were 0.02, −0.07, 0.12 and 0.04.

In the presence of interactions, the SVM-CART classifier outperforms SVM or CART alone. The prediction gains increase as the interaction effect sizes increase. When there were no interactions, SVM-CART performs similar to CART but worse than SVM alone in terms of prediction ability.

When there are distinctly different disease-exposure mechanisms in different subgroups of the population (Figure 3 setting), SVM-CART demonstrates the best prediction performance. This was consistently true across all sample sizes when the the disease-exposure effects varied substantially between the 4 subgroups (generated from Figure 3a), where SVM-CART outperformed CART or SVM alone in terms of ACC, PPV, NPV, TPR and TNR. When the continuous disease-exposure effects did not vary much between the 4 sub-groups (generated from Figure 3b): SVM-CART still performed better than CART but almost identically to SVM alone.

In conclusion, there are clinical scenarios in which SVM or CART alone may have low predictive performance. These typically arise when there are large and complex interactions that exist in the data, specifically, when there are different disease-continuous exposure mechanisms amongst subgroups of the population. In simulations, we observed that as these interaction effects increase, SVM-CART may have modest to substantial prediction gains compared to SVM or CART alone.

While prediction performance is an important aspect to consider when assessing the performance of SVM-CART, with the ultimate goal of aiding in clinical decision support: interpretability and clinical validity are also important considerations. In scenarios with complex interactions, SVM-CART may provide enhanced interpretability compared to SVM or CART alone. The improved interpretability is demonstrated in our application to build a classifier for polyneuropathy in the following section.

5. Polyneuropathy Classification in an Obese Cohort

5.1. Data Collection and Background Information

Polyneuropathy is a painful condition affecting 2–7% of the adult population [27,28]. The most common etiology of the disease is diabetes. However, it is hypothesized that other components of metabolic syndrome can play a role in the etiology of polyneuropathy [29,30]. In this section, we take an in-depth look at the classification of neuropathy using patient measures from the metabolic syndrome.

Data were collected from obese patients recruited to the University of Michigan Investigational Weight Management Cohort. There were 115 patients recruited between November 2010 and December 2014. Inclusion criteria included age 18 years or older and a body mass index of at least (BMI) 35kg/m² or 32kg/m² if they had one or more medical conditions in addition to obesity.

Five components make up the metabolic syndrome: glycemic status, waist circumference, high-density lipoprotein (HDL), triglycerides and systolic blood pressure (SBP). These five components along with patient’s gender were used to create a classification tool for polyneuropathy in these obese patients.

Previous research has found that many of the relationships between metabolic syndrome factors vary depending on patient glycemic status. The varying disease mechanisms within different glycemic subgroups make SVM-CART an ideal methodology in this setting. SVM-CART learns the distinct sub-groups that may exist within the metabolic syndrome-neuropathy mechanism to build a predictive tool.

Creating a strong clinician friendly classifier of polyneuropathy allows for greater detection of neuropathy in certain patient subgroups and subsequently may improve patient care. A neurologist has the greatest expertise to diagnose neuropathy. However, most patients with neuropathy are followed by their primary care physician who may not have specific expertise in making this diagnosis. In contrast, the metabolic syndrome components are easily measured by a wide range of clinicians. A good classification tool based on the metabolic syndrome could target certain patient subgroups that are highly likely to have neuropathy based on their demographics and metabolic profile. These patients could be referred for additional testing or consultation with a neurologist.

The following section compares SVM-CART, SVM alone and CART alone (single classifier as well as ensemble). The methods were compared based on both prediction accuracy and interpretability.

Covariates in the study were gender (binary: male/female), glycemic status (categorical: normoglycemic, pre-diabetes, diabetes), and four continuous variables: systolic blood pressure (SBP, units=mmHg), triglyceride levels (TRIG, unit=mg/dL), high-density lipoprotein levels (HDL, unit=mg/dL) and waist circumference (WC, unit=cm). The primary outcome measure was the Toronto consensus definition of probable polyneuropathy (two or all of the following: neuropathy symptoms, abnormal sensory examination, and abnormal reflexes) as determined by a neuromuscular specialist [29]. In this cohort, 27 patients were diagnosed with neuropathy while 88 patients were determined not to have neuropathy.

5.2. Determining Optimal Tuning Parameters

In this application, careful examination of the tuning parameters is especially important because neuropathy is a rare event, even in this at risk, obese cohort. For the CART part of the methodology we implemented inverse weights for the neuropathy cases. Implementing these inverse weights gave proportionally higher importance to the correct classification of the neuropathy cases in the dataset.

An empirical grid search was used to determine the optimal hyperparameters for the SVM part of the SVM-CART classifier. Cost parameters ranging from 10⁻⁵ to 10⁴ were considered. Within each terminal node created from the CART part, the SVM cost parameter weights were chosen as the inverse proportion within that terminal node subgroup. The cost weights were further extended by considering cost weight multipliers from 0.1 to 10 by 0.1 to either amplify or reduce the class weights on the cost parameters.

The optimal tuning parameters were selected by comparing prediction accuracy for the out-of-bag estimates across 1,000 bootstrapped samples for the 900 different cost/cost-weight multiplier scenarios. The classifiers were compared based on two statistics: % correct case classification and % correct control classification. Based on these statistics, the optimal cost parameter for SVM-CART was 100 and the class weight multiplier was 1.9. For SVM alone, the weight multiplier of 1.5 and the cost parameter of 100 were chosen as the optimal tuning parameters (figure not shown). Figure 4 shows the % correct classification for neuropathy and non-neuropathy based on SVM-CART.

Figure 4:

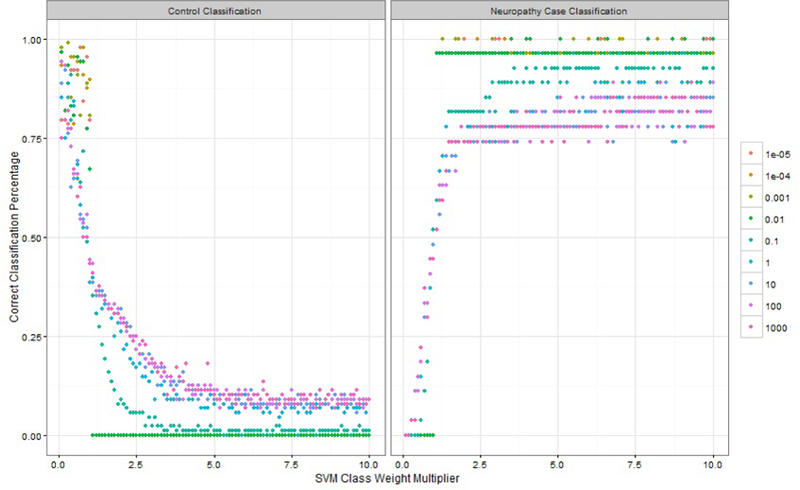
% Correct Classification Percentage for Tuning Parameter Selection

5.3. Comparison of SVM-CART, SVM and CART Single Classifiers

In this section, we compare the SVM-CART, SVM and CART classifiers based on prediction accuracy, interpretability and simplicity. Previous research lead us to believe that there are distinct subgroups based on glycemic status in this obese population. In the SVM-CART methodology, we first create a tree based on the patient gender and glycemic status. The resulting classifier is displayed in Figure 5.

Figure 5:

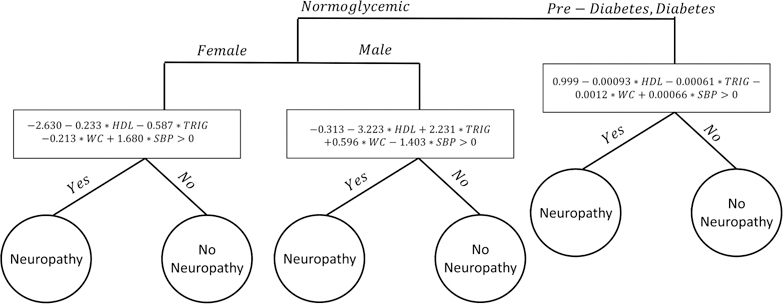
Single SVM-CART Classifier for Neuropathy

The first split was by glycemic status: normoglycemic patients were separated from the pre-diabetes/diabetes patients. The normoglycemic patients were then split based on gender, resulting in three distinct subgroups: normoglycemic male, normoglycemic female and pre-diabetes/diabetes. These three groups of patients were then passed along to create three distinct four dimensional hyperplanes based on a linear soft margin SVM. The hyperplane was generated using each patient’s waist circumference size, HDL, triglyceride and SBP levels.

CART-alone considered all five metabolic components and gender as a categorical variable, and produced a complicated tree with 10 terminal nodes. We determined the prediction accuracy of each method using a 10-fold cross validation.

The results are presented in Table 4. In terms of clinical relevance, the CART tree misses the most important predictor of neuropathy: glycemic status. In the tree created by CART alone, glycemic status only enters the tree at a deep tree split (figure not shown). Neuropathy case prediction accuracy (66.7% vs 70.4%) and overall prediction accuracy (53.9% vs 48.7%) were similar between SVM-CART and SVM alone respectively. SVM correctly classifies 19 of the 27 neuropathy patients while SVM-CART correctly classifies 18. SVM-CART correctly classifies 62/115 patients overall compared to SVM which only correctly classifies 56/115.

Table 4:

Prediction Accuracy Comparison of Various Classifiers

Method	% Correct Neuropathy Classification	% Correct Overall Classification
CART	51.9	59.1
SVM	70.4	48.7
SVM-CART Single Classifier	66.7	53.9
SVM-CART Ensemble	77.8	42.6

Though the prediction accuracy was similar between SVM and SVM-CART, SVM-CART was able to identify clinically meaningful subgroups which SVM alone was not able to create. For the neuropathy classifier demonstrated in this application, there are different mechanistic pathways to the disease within different subgroups of the population. Specifically, it was hypothesized that the neuropathy-metabolic syndrome relationship was different across glycemic subgroups. SVM-CART’s ability to identify these subgroups give it enhanced interpretability compared to SVM alone.

5.4. Ensemble Classifier

Next, we attempt to improve prediction ability by creating an ensemble of classifiers. To compare the three methods, we examined the out-of-bag error rates. Ensembles of the classifiers were built using 1,000 bootstrap samples from the entire data.

Each of the three methods experience a boost in neuropathy classification performance when predictions were averaged over the 1,000 classifiers in the ensemble. SVM-CART gains 11.1% improvement in correct case classification, however there is a 11.3% decrease in overall correct classification. In conclusion, the SVM-CART ensemble outperforms the CART ensemble (77.8% vs 44.4% correct neuropathy classification) but is comparable to boot-strapped SVM correct neuropathy classification (77.8% for both).

5.5. Representative Classifier

The ensemble of SVM-CART classifiers allows for a significant gain in neuropathy prediction accuracy compared to a single SVM-CART classifier, but we lose some of the interpretability. In this section, we select the most representative classifier from the ensemble based on two similarity metrics. The representative classifier can be used as a clinical decision-making tool. The first metric is based on the similarity in class prediction. The SVM-CART classifier that was most representative in this respect, is depicted in Figure 6. It is slightly different than the single classifier; we split first by all three glycemic categories and then further divide the pre-diabetes group by gender. We have four terminal nodes but only create three linear SVMs because the normoglycemic group is pure with a class prediction of no neuropathy.

Figure 6:

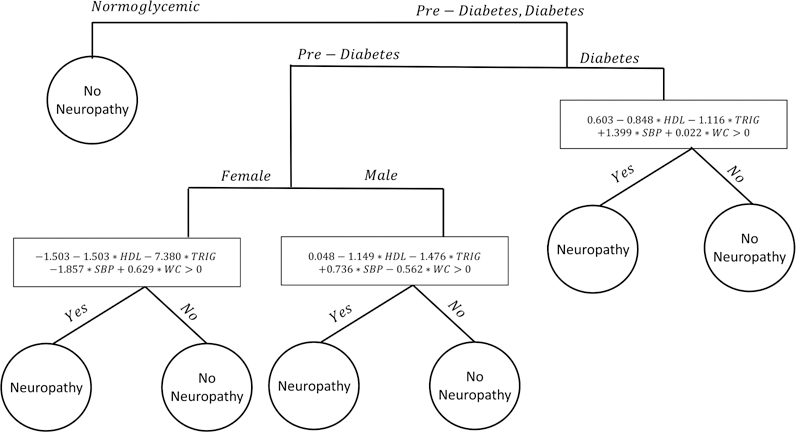
Most Representative SVM-CART Classifier from the Ensemble

The second similarity metric focuses on how patients are clustered within terminal nodes. The most representative classifier in this respect (figure not shown) creates six subgroups based on each gender by glycemic status subgroup.

5.6. Neuropathy Study Conclusions

In conclusion, a strong classifier for neuropathy using patient metabolic measures has the potential to improve patient care. SVM-CART produces an ideal classifier that identifies different neuropathy-metabolic relationships across different gender/glycemic subgroups.

SVM-CART outperforms CART and performs similarly to SVM in terms of prediction accuracy both for the single classifier and ensemble. Using two similarity metrics, we selected the two most representative classifiers from the SVM-CART ensemble. The representative classifier provides a useful clinical tool while harnessing the improved predictive ability of the ensemble.

6. Discussion

Classification of disease continues to be an important aspect of analyzing human health data. Classification trees and support vector machines have both become popular tools for classifying patients into different disease groups. There are many clinical scenarios where each of these two methods fail to meet standards in terms of performance and applicability. Some of these common scenarios were highlighted in Figure 1 and in the simulation study. We propose a new classifier SVM-CART, that combines features of SVM and CART to allow for a more flexible classifier that has the potential to improve prediction accuracy and model interpretability.

CART offers an intuitive and interpretable method for classification. However, one significant drawback of CART is that it only allows rectangular splits that are perpendicular to the covariate space. There are many clinical scenarios where a non-rectangular split is more appropriate. In such scenarios, CART must create a very complicated tree in order to achieve reasonable prediction accuracy. SVM-CART can achieve similar or improved prediction performance with generally a more parsimonious structure. The more parsimonious structure created with SVM-CART provides a more interpretable decision making tool for clinicians.

The flexibility of SVM-CART allow it to uncover complex interactions among the covariates. In simulations, in the presence of interaction, SVM-CART outperforms SVM or CART alone. The structure created by SVM-CART makes it a very intuitive predictive tool in clinical scenarios where the disease-exposure mechanism may be very different across patient subgroups. This was the case in our neuropathy application, where it made clinical sense to create distinct classifiers based on gender and glycemic status subgroups. SVM-CART’s potential ability to find clinically meaningful subgroups can lead to enhanced interpretability compared to SVM alone. When there is a priori clinical evidence to believe there are unique disease-exposure relationships between subgroups of the population, SVM-CART will likely have enhanced performance.

In settings where there is weak interaction, results from the simulation study were mixed. Therefore, we do not recommend using SVM-CART as a complete replacement for SVM or CART alone. In practice it will be important to utilize the expertise of clinicians to determine if complex interactions likely exist amongst subgroups of the population for the clinical problem of interest. In such scenarios, SVM-CART will improve prediction ability and interpretability.

One important goal of our methodology was to develop a practical and usable tool for clinical decision making. We developed SVM-CART ensemble to improve prediction accuracy and stability of the classifiers. Though the ensemble method improved prediction accuracy, we lost the interpretability of a single SVM-CART classifier. We proposed two metrics that were used to identify the most representative classifier from the ensemble of SVM-CART classifiers. The resultant representative SVM-CART provide an interpretable, easy to use and flexible classification tool.

While linear SVMs provided a simple extension in our case, using more intricate kernel function SVM classifiers at each node has the potential to provide a powerful boost in certain scenarios. These kernelized extensions of support vector machines may allow for more flexible implementation of the SVM-CART method in non-linear problems that often exist with high dimensional feature space. Due to the small sample size of our neuropathy dataset, the kernel extensions did not perform as well as the linear SVM splits in the presented application. The methodology presented here can also be easily extended to multi-class outcomes.

In Section 3, we detailed methods to extend the single SVM-CART classifier to an ensemble to improve predictive ability. While there is variation across the bootstrapped samples, we chose to give a final class prediction based on voting across all classifiers in the ensemble. This approach was originally proposed in the context of Bagging, and later used in Random Forest [22,23]. An alternative method for prediction involves using the predicted class probabilities obtained from each SVM-CART classifier in the ensemble [22]. In this alternative approach, the predicted disease outcome is given as the outcome with the highest average predicted probability. This prediction method would give higher preference to SVM-CART classifiers with large predicted probabilities and thus, could result in a different predicted outcome from the majority voting approach. Since the large predicted probabilities would stem from SVM-CART classifiers with very pure terminal nodes, the alternative method could potentially give preference to classifiers with lower empirical variance at the terminal nodes.

In this paper, we make a distinction between categorical vs. continuous covariates in terms of how they are used in the SVM-CART classifier. In practice, a continuous covariate may behave like a categorical variable or could be categorized into an ordinal variable. If there is a priori evidence in the literature that different levels of a continuous covariate result in sub-groups where the disease-exposure mechanism is different, then it should be added to the CART part of the classifier. One example of this might be age; as different age groups might lead to very different exposure mechanisms for various diseases.

The SVM-CART methodology presented here is one example of a composite classifier. In various clinical scenarios such as the ones presented in this research, using a wide range of classifiers in tandem might achieve better performance. In this research, CART was chosen as the first member of the composite classifier as it provided the most intuitive and flexible tool to separate patients into subgroups. Since CART is non-probabilistic, we decided to combine CART with another member of the general class of non-probabilistic classifiers. SVMs complement the rectangular splits created by CART and are arguably the most popular method within the class of non-probabilistic classifiers. Hence, we chose SVMs as the second member of the composite classifier. Extending the general approach to include other classifiers is an area of future research.

Table 3:

Results Based on Data Generated from an Underlying SVM-CART Like Structure

		Disease-Exposure Effects
		Vary Across Subgroups						Similar Across Subgroups
Sample Size (N)		ACC	PPV	NPV	TPR	TNR	Size	ACC	PPV	NPV	TPR	TNR	Size
100	CART	0.83	0.81	0.85	0.75	0.89	2.8	0.64	0.64	0.65	0.61	0.67	4.2
100	SVM	0.89	0.86	0.91	0.86	0.91	7.0	0.69	0.68	0.70	0.69	0.70	7.0
100	SVM-CART	0.88	0.85	0.90	0.84	0.91	6.6,1.7	0.75	0.74	0.75	0.73	0.76	10.8,2.7
500	CART	0.88	0.88	0.88	0.81	0.93	6.8	0.81	0.81	0.80	0.78	0.83	10.9
500	SVM	0.92	0.90	0.93	0.89	0.94	7.0	0.73	0.72	0.74	0.73	0.73	7.0
500	SVM-CART	0.91	0.89	0.92	0.88	0.93	4.9,1.2	0.84	0.86	0.83	0.80	0.88	12.0,3.0
1000	CART	0.89	0.90	0.89	0.82	0.94	9.1	0.84	0.86	0.83	0.81	0.87	13.3
1000	SVM	0.92	0.90	0.93	0.89	0.94	7.0	0.74	0.72	0.75	0.74	0.74	7.0
1000	SVM-CART	0.91	0.90	0.92	0.88	0.93	4.3,1.1	0.87	0.91	0.84	0.82	0.92	12.1,3.0