Broadband quadrature-squeezed vacuum and nonclassical photon number correlations from a nanophotonic device

Nanophotonic resonators can generate broadband quadrature squeezing and single temporal mode photon number difference squeezing.

Abstract

We report demonstrations of both quadrature-squeezed vacuum and photon number difference squeezing generated in an integrated nanophotonic device. Squeezed light is generated via strongly driven spontaneous four-wave mixing below threshold in silicon nitride microring resonators. The generated light is characterized with both homodyne detection and direct measurements of photon statistics using photon number–resolving transition-edge sensors. We measure 1.0(1) decibels of broadband quadrature squeezing (~4 decibels inferred on-chip) and 1.5(3) decibels of photon number difference squeezing (~7 decibels inferred on-chip). Nearly single temporal mode operation is achieved, with measured raw unheralded second-order correlations g⁽²⁾ as high as 1.95(1). Multiphoton events of over 10 photons are directly detected with rates exceeding any previous quantum optical demonstration using integrated nanophotonics. These results will have an enabling impact on scaling continuous variable quantum technology.

INTRODUCTION

Squeezed light is an essential resource for quantum optical information processing. Continuous variable (CV) photonic architectures for quantum computation and simulation (1) demand high-quality scalable devices for generating squeezed light, which is the fundamental building block for many photonic quantum information processing applications. These include CV quantum computation (2) and Gaussian boson sampling (3). The latter is one of the most promising avenues to the achievement of near-term quantum advantage and accommodates a host of intriguing use cases, including molecular vibronic spectrum simulations (4), and quantum embeddings of graph problems such as the identification of dense subgraphs (5), perfect matchings (6), graph isomorphism (7), and graph similarity (8). Gaussian boson sampling can also be used to predict molecular docking configurations (9). A scalable source of squeezed light is needed to implement all of these and could also be used to enhance optical sensing near the quantum limit (10). A natural platform to explore for these scalable squeezed light sources is integrated photonics: The stability and repeatable manufacturability offered by modern lithographic techniques hold much promise for realizing useful quantum technologies at scale. The integration of quantum light sources is especially important in variants of quantum computation based on CVs. This is due to the acute phase sensitivity of squeezed states, which serve as the basic resource for nonclassicality in these variants.

Progress to date on chip-integrated squeezing has been limited. Lenzini et al. (11), Mondain et al. (12), and Stefszky et al. (13) have demonstrated devices based on low index contrast lithium niobate waveguides with large cross sections, using periodically poled waveguide segments for squeezed light generation, in combination with linear optics on a monolithic chip. While this platform is attractive for its high second-order nonlinearity and electro-optic response, as well as its ease of integration with fiber components, currently, it lacks the scalability offered by nanophotonic systems: The low transverse confinement prohibits the monolithic integration of high-depth circuits with hundreds of optical elements. Dutt et al. (14) made the first forays into high-index contrast nanophotonic systems for squeezing by demonstrating intensity difference squeezing from a silicon nitride microring optical parametric oscillator (OPO) driven above threshold. However, quadrature squeezing was not achieved, and the demonstrated bright “twin beam”–type squeezing above threshold is necessarily accompanied by large classical mean fields and very high levels of excess noise, rendering it incompatible with experiments or architectures that require photon counting.

Among these architectures, quantum sampling (which includes the applications of Gaussian boson sampling) (4–9) places even more stringent demands on the nature of the squeezed light source used: In addition to being scalable, such a source must be capable of producing squeezed states in a single temporal mode (15). This requirement is often overlooked, since it can often be avoided in single photon–based quantum protocols by adequate spectral filtering or by postselecting on detection events that occur within a common, narrow temporal window. Unfortunately, these strategies cannot be used for CV quantum sampling: Spectral filtering imposes unacceptable losses on the system, the effects of which cannot be circumvented by postselecting on successful detection events; and temporal windowing cannot be applied on detection events in which many-photon contributions are present, owing to the low timing resolution of available photon number–resolving systems (16). Since many-photon events are, in general, important throughout the application space of CV quantum sampling and losses have significant deleterious effects on both fidelities and count rates (17), it becomes vital to engineer a source, which itself natively produces squeezed states in a single temporal mode. This feature has proven challenging across all platforms and has been most thoroughly investigated in periodically poled crystalline χ₂ waveguides (18–20) wherein approaching single temporal mode operation requires very careful dispersion engineering. These considerations make the temporal mode structure a key metric to assess when qualifying squeezed light sources for practical use.

Here, we report the demonstration of quadrature-squeezed vacuum and photon number difference squeezing generated with an integrated nanophotonic device. We use spontaneous four-wave mixing (SFWM) in silicon nitride microring resonators (21), a readily accessible and mature technology available on commercial fabrication platforms. We measure the variance of all quadratures of the squeezed modes with balanced homodyne detection and also verify the compatibility of this source with photon counting experiments and sampling applications by directly measuring the photon statistics of the output using photon number–resolving transition-edge sensors (TESs) (16). Raw photon number correlations are assessed, and close attention is paid to the temporal mode structure of the generated light: Unheralded second-order correlation measurements are performed to ensure that our device can approach single temporal mode operation (22).

The device itself is simple: Both quadrature and photon number difference squeezing are generated in silicon nitride microring resonators point coupled to channel waveguides, with microheaters overlaid for resonance wavelength tuning and stabilization. Fabrication was carried out by a commercial foundry (LIGENTEC SA). The waveguide geometry consists of a stoichiometric Si₃N₄ wire fully clad in SiO₂. The cross sections used were 800 nm by 1000 nm for quadrature squeezing and 800 nm by 1650 nm for photon number correlation measurements. This platform was selected for its low linear propagation loss, lack of two-photon absorption, and high third-order nonlinear parameter of approximately 1 (Wm)⁻¹. To generate squeezing, we used SFWM: A single strong pump (but weak enough to stay below any OPO thresholds), resonant with one of the ring resonances, generates multimode squeezed vacuum in a comb of neighboring resonances (Fig. 1). The nonlinear Hamiltonian H_NL describing the interaction between the pump mode and a particular pair of signal and idler resonances is given by (23)

$$\begin{array}{cc}\hfill H_{\text{NL}}& =-ħ\mathrm{\Lambda }((b_{\mathrm{P}}{b}_{\mathrm{P}}{b}_{\mathrm{S}}^{\mathrm{†}}{b}_{\mathrm{I}}^{\mathrm{†}}+\mathrm{H}.\mathrm{c})\hfill \\ & +\frac{1}{2}{b}_{\mathrm{P}}^{\mathrm{†}}{b}_{\mathrm{P}}^{\mathrm{†}}{b}_{\mathrm{P}}{b}_{\mathrm{P}}+2b_{\mathrm{P}}^{\mathrm{†}}{b}_{\mathrm{P}}(b_{\mathrm{S}}^{\mathrm{†}}{b}_{\mathrm{S}}+b_{\mathrm{I}}^{\mathrm{†}}{b}_{\mathrm{I}}))\hfill \end{array}$$ (1)

where b_x is the annihilation operator associated with the resonator mode x ∈ {P, S, I}, representing the pump, signal, and idler modes, respectively. Here, Λ is a coefficient representing the nonlinear coupling strength between the modes and is well approximated by $\mathrm{\Lambda }\approx \mathit{ħ}\overline{\mathrm{\omega }}{v}_{\mathrm{g}}^2{\mathrm{\gamma }}_{\text{NL}}/L$, where $\overline{\mathrm{\omega }}={({\mathrm{\omega }}_{\mathrm{P}}^2{\mathrm{\omega }}_{\mathrm{S}}{\mathrm{\omega }}_{\mathrm{I}})}^{1/4}$, v_g is the group velocity, γ_NL the waveguide nonlinear parameter, and L the resonator round trip length.

Fig. 1. Overview of device.

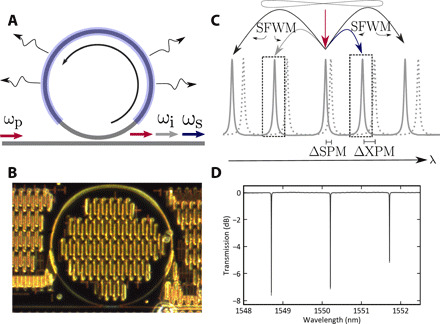
(A) Schematic of microring device showing resonator, side channel, microheater (blue), and scattering modes. (B) Optical microscope image of device. (C) Illustration of intraresonator SFWM process, showing frequency shifts ΔSPM and ΔXPM associated with self- and cross-phase modulation (SPM and XPM, respectively). (D) Representative transmission spectrum of microring device, showing three overcoupled resonances near 1550 nm.

The first term in Eq. 1 leads to SFWM, in which two pump photons are annihilated and a pair of signal and idler photons are generated; taken to higher order, this process generates a squeezed state involving the signal and idler (15, 24). For a strong coherent and continuous wave (CW) input pump field, we may treat the intraresonator pump classically and replace b_P by its classical expectation value ${\mathrm{\beta }}_{\mathrm{P}}={\overline{\mathrm{\beta }}}_{\mathrm{P}}{e}^{-i({\mathrm{\omega }}_{\mathrm{P}}+{\mathrm{\Delta }}_{\mathrm{P}})t}$, where ${\overline{\mathrm{\beta }}}_{\mathrm{P}}$ is a constant and Δ_P is the input pump field detuning from resonance. The effects of self- and cross-phase modulation (SPM and XPM, respectively), represented by the last two terms in Eq. 1, then manifest as pump power–dependent frequency shifts of the pump, signal, and idler resonances (Fig. 1C). Note that, in Eq. 1, we neglect the effects of SPM on the signal and idler modes, since these effects are negligible in our regime of interest well below the OPO threshold. Since the waveguides used in our devices for quadrature squeezing operate in the normal dispersion regime, these frequency shifts are detrimental for a single pump configuration, as they lead to an increased energy mismatch of the resonance frequencies away from the ideal operational point for SFWM of 2ω_P = ω_S + ω_I. Despite this, significant quadrature squeezing at modest input power levels was still achieved without dispersion engineering.

The statistics of the output signal and idler fields can be calculated using cavity input-output theory; full details are available in the Supplementary Materials. In the subsequent sections, we report the measured quadrature and photon number statistics from the device and then compare our results with the predictions based on this theory.

RESULTS

Quadrature squeezing

Since the SFWM interaction is of the form $b_{\mathrm{S}}^{†}{b}_{\mathrm{I}}^{†}$, the quantum state of the resonator output can (in the absence of nonparametric effects that could contribute noise) be characterized as a two-mode squeezed vacuum state subjected to loss; this loss arises both from the imperfect escape efficiency of the cavity and “downstream” losses that are incurred at the chip outcoupling point, post-chip fiber components, and those due to detector inefficiency. This state can also be understood as a product of two single-mode squeezed states, each having frequency support at both the signal and idler resonances, i.e., in modes described by annihilation operators ${\tilde{b}}_{\pm }=(b_{\mathrm{S}}\pm b_{\mathrm{I}})/\sqrt{2}$. In what follows, we adopt this perspective and study the quadrature statistics of these composite bichromatic modes (25, 26).

Normalizing the quadrature variance of the vacuum state to unity, the maximum and minimum quadrature variances V_± associated with a bichromatic mode in the output channel of the resonator having equal support at the signal and idler frequencies can be expressed as

$$V_{\pm }=1+4\mathrm{\eta }g(2g\pm \sqrt{1+4g^2})$$ (2)

where η is the net collection efficiency (including the ring escape efficiency and all collection and detection losses) and g is a dimensionless gain parameter defined as $g=\mathrm{\Lambda }{\mid {\overline{\mathrm{\beta }}}_{\mathrm{P}}\mid }^2/\overline{\mathrm{\Gamma }}$, with $\overline{\mathrm{\Gamma }}$ as the dissipation rate of the signal and idler cavity modes (assumed for simplicity to be equal). This dissipation rate can be estimated from the full loaded quality factor Q associated with a resonance at frequency ω via $\overline{\mathrm{\Gamma }}\approx \mathrm{\omega }/(2Q)$. Note that, here, we assumed that the pump frequency is adjusted at each fixed input power to follow the pump resonance, as its frequency shifts due to SPM and thermal effects. Doing so avoids crossing the OPO threshold at any power and maintains the linear scaling of intraresonator circulating power with pump input power (27).

To measure the quadrature variances V_± of the modes of interest, we performed balanced homodyne detection on the device output. The experimental setup is illustrated in Fig. 2A: A CW pump is coupled into the chip (and light extracted) via low-loss edge couplers. In the chip, the pump excites a single resonance of the microring and generates squeezed light across multiple signal and idler pairs. One such pair of signal and idler modes is selected by off-chip wavelength filters for analysis, while the remaining pump light after the chip is monitored and used for feedback to stabilize the microring resonance frequency. Since the signal and idler resonances are separated in frequency from the pump by ~190 GHz, beyond the capabilities of photoreceiver electronics, it was necessary to generate a bichromatic local oscillator (26) with frequency support at both ω_S and ω_I, coherent and phase stable with respect to the pump. To do so, two separate CW lasers were tuned to the signal and idler frequencies and phase-locked to each other, as well as to the pump, by beating them independently against the teeth of an optical frequency comb derived from a portion of the pump using a fast electro-optic modulator. This produced a bichromatic local oscillator that is phase stable relative to the pump, with approximately 4° root mean square phase noise between the pump and each local oscillator wavelength. The bichromatic local oscillator was then combined with the signal and idler light on a tunable fiber beam splitter set to 50:50 splitting ratio, with the outputs incident on a commercial fast balanced amplified differential photoreceiver with 1-GHz bandwidth. The difference photocurrent fluctuations were monitored on an electrical spectrum analyzer. As the local oscillator phase is ramped, the variance of different quadratures (Fig. 2B) can be identified relative to the shot noise level, which is measured by disconnecting the chip output. This process was repeated for a range of input pump powers, yielding the curves shown in Fig. 2C. Approximately 1.0(1) dB of squeezing is observed at the maximum input power at a sideband frequency of 20 MHz. Considering the estimated collection and detection losses and assuming that there is no appreciable excess noise, we estimate that about 4 dB of squeezing is available at the microring output on-chip, although this inference is affected significantly by the uncertainty in the loss estimate. The squeezing is limited both by available pump power and by the finite escape efficiency of the resonator (~75%). We also note that the squeezing is broadband, limited by the resonance linewidths; appreciable squeezing was observed at sideband frequencies as high as 1 GHz (limited by the detector bandwidth), as shown on the squeezing spectra illustrated in Fig. 3.

Fig. 2. Quadrature squeezing.

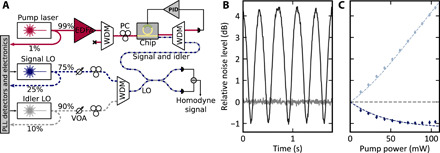
(A) Overview of experimental setup. Details in the main text and the Supplementary Materials. WDMs, wavelength division multiplexing components. LO, local oscillator; EDFA, erbium-doped fiber amplifier; PLL,phase-locked loop; VOA, variable optical attenuator; PC, polarization controller; PID, proportional-integral-derivative. (B) Quadrature variance (black line) relative to shot noise (gray line) as a function of time, while the local oscillator phase is ramped, exhibiting 1.0(1) dB of squeezing. Traces are obtained from the homodyne detector photocurrent fluctuations monitored on an electrical spectrum analyzer in zero-span mode at 20-MHz sideband frequency, with a resolution bandwidth of 1 MHz and a video bandwidth of 300 Hz. (C) Maximum and minimum quadrature variances as a function of pump power for the 20-MHz sideband, showing the power scaling of the squeezed and antisqueezed quadratures. The top and bottom dashed lines are obtained by fitting to Eq. 2; the shot noise level is shown (dashed line at 0 db)..

Fig. 3. Squeezing and antisqueezing frequency spectrum from 20 MHz to 1 GHz at different pump power levels.

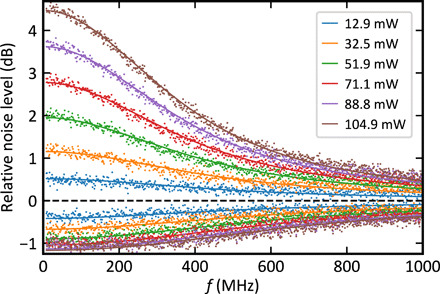
Powers listed are inferred values on-chip in the input waveguide. Dashed line is shot noise level; solid lines exhibit fits to the theoretical model (details in the Supplementary Materials), showing strong agreement with the measured data.

Apart from losses and limited pump power, another factor that can limit squeezing is the presence of excess noise added by processes other than parametric fluorescence. This is especially a concern for squeezing generated by third-order nonlinear optical interactions, in which the pump frequency is much closer to the measurement bands than in the case with more conventional downconversion-based squeezers. Our initial attempts to measure squeezing from similar devices within the pump resonance itself using fully degenerate four-wave mixing, based on the proposal of Hoff et al. (28), were hampered by strong excess noise contributions even at sideband frequencies exceeding 500 MHz. We attribute this to thermorefractive fluctuations: Although these contributions are usually only analyzed within a few megahertz of the pump frequency, for the pump powers required to generate squeezing, thermorefractive fluctuations can scatter a non-negligible amount of light to much higher sideband frequencies. Recent work (29, 30) suggests that this noise can be measurable even at terahertz offsets from the pump. This attribution is corroborated by the results of a recent experiment carried out by Cernansky and Politi (31), who attempted the Hoff et al. (28) scheme in a Sagnac loop configuration to suppress the bright pump. While a small amount of quadrature squeezing at high sideband frequencies was reported, most of the mode was contaminated by excess noise that eliminated squeezing on all quadratures. Aside from thermorefractive contributions, spontaneous Raman scattering (either in the microring device, channel waveguide, or fiber components used in the experiment) could also be present. Considering this “mine field” of nonparametric effects that can corrupt squeezing in devices based on third-order nonlinearities, it is important to assess the presence of excess noise in our system generated inside the squeezing band.

To gauge whether excess noise processes contribute to the measured variance, as shown in Fig. 2C, we fit the measured behavior of the variances V_± to a theoretical model that assumes only SFWM and loss and no nonparametric sources of excess noise. The same is performed for the squeezing spectra exhibited in Fig. 3. From the agreement of the fits with the data, we conclude that, within our measurement precision and at the pump power levels used, a model with no excess noise is adequate to account for the measured quadrature variances; our results can be explained very well by a squeezed vacuum state subjected to loss. Furthermore, the degree of loss inferred from the data is consistent with estimates based on direct loss measurements. We note that, at the highest powers used, a very slight drop in the squeezing was observed; however, this is expected from the rapid growth of the noise in the antisqueezed quadrature, which, at finite phase precision, negatively affects the observed squeezing levels. More study is needed with improved phase precision to better assess this effect.

Photon number correlations

While homodyne measurements are vital to assess quadrature squeezing, for many applications, it is also important to verify the compatibility of a squeezed light source with photon counting. Homodyne detection provides exquisite mode selectivity of the probed quantum state, whereas most photon counting schemes are limited in their ability to extract information from only a single well-defined field mode without incurring unacceptably high losses. For example, at the powers required to generate squeezing, one might be concerned that broadband spontaneous Raman scattering of the bright pump (32) (either in the chip or in the various fiber components through which the pump must propagate) might place unreasonable spectral filtering requirements on the signal and idler paths, adding losses that would destroy quantum correlations. In addition, as discussed in Introduction, any multimodedness of the light measured by a photon counting detection system will alter the measured statistics and corrupt the corresponding performance. An affirmative statement regarding the compatibility of a squeezed light source with photon counting therefore relates both to the greater experimental context and to the dynamics of the process that leads to squeezing.

To verify the compatibility of our squeezed light source with photon counting, we performed photon number–resolving detection on the device output. For this experiment, a microring resonator with a wider cross section of 800 nm by 1650 nm was used, which resulted in a higher loaded quality factor of approximately 8 × 10⁵ for the three resonances (escape efficiency of 80%). The device used for the quadrature squeezing experiment was selected to emphasize the broadband squeezing that can be generated in these microring devices; larger resonance linewidths (and thus lower quality factors) are required for that demonstration. While some photon number squeezing could be observed in the device used for quadrature squeezing, which displayed lower quality factors, results were much improved for the higher quality factor device. This is due to the higher sensitivity of photon number squeezing to the effects of broadband Raman noise generated in fiber components: Our photon detectors no longer benefit from the extremely narrowband mode selectivity of homodyne detection and, instead, must accept all the noise present within the 100-GHz passband of the filtering system used. Higher quality factors permit weaker pumps to be used, thereby increasing the overall signal-to-noise ratio.

As illustrated in Fig. 4A, the generated signal and idler were first separated and filtered by wavelength division multiplexing components, yielding a total extinction of above 120 dB at the pump wavelength, while incurring less than 2 dB of loss on the signal and idler. The output was then coupled to superconducting TES (16), which provide photon number resolution to about 10 photons per channel. The number of signal and idler photons detected in each pulse window was recorded for a range of pump powers, and the photon statistics were analyzed.

Fig. 4. Photon number difference squeezing.

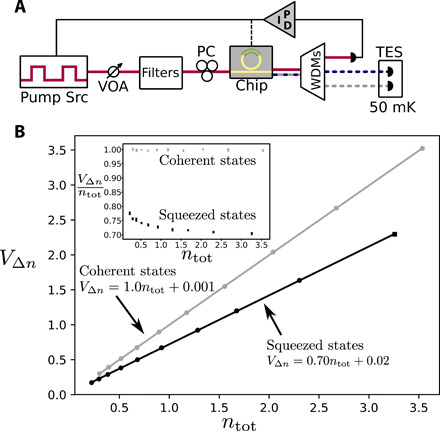
(A) Overview of experimental setup. Details in the main text and the Supplementary Materials. (B) Measured photon number difference variance V_Δn as a function of mean photon number n_tot, obtained by varying pump power, for coherent states (gray) and squeezed states (black) with linear fits (solid lines). The reduced slope for the squeezed state represents photon number difference squeezing. Inset: Ratio between number difference variance and mean photon number as a function of mean photon number for coherent states (gray) and squeezed states (black).

For a lossy parametric fluorescence process without excess noise, we expect the variance of the photon number difference V_Δn per pulse between the signal and idler to satisfy

$$V_{\mathrm{\Delta }n}=(1-\mathrm{\eta })n_{\text{tot},}$$ (3)

where η is the total collection efficiency and n_tot = 〈n_S + n_I〉 is the total average photon number detected in the signal and idler. For a coherent state, this variance is precisely equal to n_tot; thus, a reduction in the slope of V_Δn as a function of n_tot from unity is associated with a quantum-correlated signal and idler, which we refer to as photon number difference squeezing. In Fig. 4B, the measured behavior of V_Δn as a function of n_tot is plotted for both coherent state inputs and for the generated signal and idler from the microring device. A reduction in the slope to ~0.70 is observed, representing clearly evident photon number difference squeezing. At the highest powers (i.e., for measurements with the best signal-to-noise ratio), the ratio V_Δn/n_tot is suppressed to 0.704(5), representing 1.5(3) dB of number difference squeezing. This ratio, sometimes referred to as the “noise reduction factor” (20), is a metric for nonclassicality (33), with a value below unity indicating a nonclassical state. For lower powers resulting in n_tot ≪ 1, the signal-to-noise ratio (likely limited by pump light leakage and broadband linear scattering processes) worsens, and the squeezing degrades slightly (inset in Fig. 4B), although a significant subunity noise reduction factor is still observed even for the lowest powers used. This degradation effect at low powers was much more strongly pronounced in the samples with lower quality factor, consistent with our interpretation. The results exhibited in Fig. 3 are therefore primarily limited by losses; as with the quadrature squeezing results, our directly measured system efficiency estimates are consistent with the amount of photon number squeezing observed. Unlike quadrature squeezing, in principle, the magnitude of photon number difference squeezing is not gain limited: For an ideal lossless and noiseless SFWM process, V_Δn = 0 for all pump powers (assuming perfect detection efficiency), as signal and idler photons are always created in pairs. Thus, the degree of number correlations on the chip is limited only by the finite escape efficiency of the resonator, and from this, we infer that ~7 dB of these correlations are available on-chip. This can be improved by designing a ring-channel coupler that facilitates higher escape efficiency, albeit at the expense of generation efficiency (34).

A notable feature of this experiment is the high rate at which correlated multiphoton events are detected: At the maximum power used, coincidence events with 10 detected photons were recorded at rates of 9.6(3) × 10² counts/s. In contrast, quantum photonic technologies based on chip-integrated parametric single-photon sources must operate in the weakly driven regime, in which the probability of generating a photon pair is quite low, often well below 1%. Hence, applications requiring multiple photons typically suffer from extremely low count rates. Our results demonstrate that many-photon states can be generated in a nanophotonic platform at much higher rates, motivating progress on applications that demand squeezed light sources, rather than single photons.

Temporal mode structure

As discussed in Introduction, another crucial feature of squeezed light sources for quantum sampling applications—and most experiments using photon counting on CV states—is the temporal mode structure of the generated squeezed states. Squeezed states in a single temporal mode must be sought to yield the correct desired statistics and enable sampling applications to generate outputs that are faithfully sampled from the desired probability distribution. Sources, which generate squeezing in multiple modes that cannot be easily separated, will yield statistics that do not reflect the desired single mode features. A simple example of this is as follows: Considered independently, the signal and idler modes in an ideal two-mode squeezed state are each individually described by a thermal state and therefore should display an unheralded second-order correlation value of g⁽²⁾ = 2. If, however, the state contains the product of many such two-mode squeezed states, each of which populates a different temporal mode, and the measurement of the state cannot distinguish between photons that were detected from different temporal modes, then the second-order correlation will exhibit g⁽²⁾ < 2; in the limit of very many equally populated modes, the photon number statistics become Poissonian and g⁽²⁾ → 1. In quantum sampling applications using squeezed light, all relevant information is extracted directly from the photon statistics of the output (4–6, 8, 9); thus, using a squeezed light source with a highly multimode temporal structure would destroy the utility of such a machine. It is therefore important to assess the temporal mode structure of the generated squeezed states from our source (22).

In microresonator systems, the temporal mode structure of generated parametric fluorescence can be tuned by driving the device with pump pulses having varying pulse duration (35). This is a feature common to many parametric fluorescence sources: The use of broadband (i.e., temporally short) pump pulses, having less well-defined photon energies, leads to a weaker degree of spectral correlations between the generated signal and idler photons. Since the presence of spectral correlations is equivalent to the presence of multiple populated temporal modes in the generated beams, short pulses are therefore required to achieve single temporal mode operation. Here, the relevant bandwidth scale is the parametric gain bandwidth, i.e., the resonator linewidth or inverse dwelling time. Previously, this has been experimentally explored primarily in the context of weakly driven SFWM for photon pair generation (36). In that context and also in our regime of more strongly driven fluorescence for squeezing, pumping with a pulse that is comparable to or shorter than the resonator dwelling time ${\mathrm{\tau }}_{\text{dwell}}=2Q/\overline{\mathrm{\omega }}$ will result in nearly single temporal mode operation. However, unlike in the weakly driven context, here, the pump is sufficiently strong that SPM and XPM also play a role in modifying the temporal mode structure of the generated light. Detailed modeling and simulations to identify the optimal point in parameter space will be left for a future report; here, we merely demonstrate that our device approaches the desired operational point with g⁽²⁾ nearly 2, without any special engineering of the device (37) or intricate tailoring of the pump pulse shape (38) beyond simple tuning of the pulse duration.

To assess the temporal mode features of our source, we used the same measured photon number data as that used to extract the degree of photon number difference correlations and instead calculated the independent second-order correlation statistic $g_{\mathrm{S}(\mathrm{I})}^{(2)}$ for the signal (idler), defined as

$$g_{\mathrm{S}(\mathrm{I})}^{(2)}=\frac{\langle n_{\mathrm{S}(\mathrm{I})}^2\rangle -\langle n_{\mathrm{S}(\mathrm{I})}\rangle }{{\langle n_{\mathrm{S}(\mathrm{I})}\rangle }^2}$$ (4)

For two-mode squeezed vacuum states, this statistic provides a direct measure of the multimode character of the measured light; ideally, $g_{\mathrm{S}(\mathrm{I})}^{(2)}=2$ for both the signal and idler, which would indicate perfect single temporal mode operation. The results are plotted in Fig. 5 (green and orange points) for data collected with a range of pump pulse energies, leading to a range of generated photon numbers n in the signal and idler; also plotted are the measured g⁽²⁾ values for attenuated laser pulses, i.e., coherent states (gray points). The pulses used had approximately rectangular intensity profile and a duration of 1.5 ns, which is about 1.2 × τ_dwell. The highest measured second-order correlations for the signal and idler are $g_{\mathrm{S}}^{(2)}=1.95(1)$ and $g_{\mathrm{I}}^{(2)}=1.87(1)$. This raw measured g⁽²⁾ for the signal is comparable to previous demonstrations using specially engineered waveguide sources.

Fig. 5. Measured second-order correlation g⁽²⁾ (Eq. 4) for the signal and idler (green and orange points, respectively) and for coherent states (gray points) for different values of photon number n.

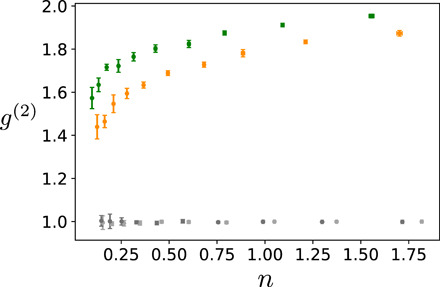
Data are collected over a range of pump pulse energies corresponding approximately to 0.1- to 1-nJ on-chip. Coherent state data were acquired using attenuated laser pulses and show excellent agreement with the predicted g⁽²⁾ = 1 for coherent states.

(18–20). The idler exhibited a consistently slightly lower second-order correlation value than that of the signal; we attribute this mismatch to an imbalance in the quantity of noise on each channel and estimate this noise to be between 0.02 and 0.07 measured photons per pulse for each channel, primarily from Raman scattering in the fiber components used.

DISCUSSION

That our source can generate nearly single temporal squeezed states without special engineering of dispersion or phase matching is primarily due to its resonant nature. Resonators provide an intrinsic narrow confinement of the nonlinear gain spectrum, owing to the narrow linewidths associated with their resonances, making it easier to avoid populating unwanted temporal modes with photons. The measured g⁽²⁾ quantities are not upper bounds: By selectively engineering the quality factors of the pump, signal, and idler resonances (37), or engineering the pump pulse more carefully (38), squeezed states with g⁽²⁾ arbitrarily close to 2 could be generated.

As with most integrated quantum optical devices, losses are the primary factor that limits performance. In our case, the ~1.5 dB of coupling losses associated with extracting the squeezed light to a fiber limits the squeezing obtainable off-chip (assuming a new device with perfect ring escape efficiency and assuming perfect collection and detection efficiencies) to about 5 dB for both quadrature and photon number measurement contexts. Lowering the outcoupling loss to 0.5 dB—a challenging but not unrealistic goal—would immediately improve this bound to nearly 10 dB, at which point the resonator escape efficiency would become the dominant factor limiting the available squeezing. Improving on-chip propagation loss would result in higher resonator quality factors, enabling higher escape efficiencies to be realized while maintaining or improving power efficiency, leading to better squeezing. We estimate that best reported microring resonator devices are capable of generating more than 10 dB of on-chip quadrature squeezing with under 100 mW of pump power (15). Improving the generation efficiency would also improve the signal-to-noise ratio by reducing the amount of power needed to operate at the desired level of squeezing, thereby reducing the quantity of photons generated from spontaneous Raman scattering in fiber components.

For some applications, including the most general CV quantum sampling architectures, it is convenient or necessary to generate squeezing in a single “degenerate” mode confined to a small frequency range, rather than distributed over a pair of signal and idler modes. This can be accomplished in our device using a dual pump scheme, which has already been used for degenerate photon pair sources (39) and OPOs (40). However, care must be taken with such a device to suppress spurious SFWM processes involving the squeezed resonance and unwanted resonances; without such a suppression scheme, an appreciable amount of excess noise is predicted to contaminate the output. This has been theoretically discussed (15) and is a natural next step for engineering chip-integrated squeezed light sources (41, 42).

MATERIALS AND METHODS

For all experiments, light was coupled into the chip using ultrahigh numerical aperture (UHNA7) optical fibers manually aligned to the chip facets. Index matching gel was used to reduce reflections at the interface. The chip was temperature stabilized using a thermoelectric cooler with a slow proportional-integral-derivative feedback loop, and electrical probes were used to access the microheater elements. The radii of the microring resonators used were 120 and 200 μm for the quadrature squeezing and photon number difference squeezing experiments, respectively.

Quadrature squeezing measurements were performed using a commercial balanced receiver (Wieserlabs, BPD1GA), which has approximately 80% quantum efficiency at 1550 nm. Balancing was performed using a tunable fiber-coupled beam splitter (Newport). Linearity of the detector was assessed by varying the local oscillator level while monitoring the difference photocurrent fluctuations on an electrical spectrum analyzer; the local oscillator was then set to provide 13 dB of dark noise clearance, well into the linear regime but far short of saturation, at an optical power of 6 mW. The quality factors of the resonances used in this experiment were approximately 2 × 10⁵, with escape efficiencies of approximately 75%. The pump, signal, and idler wavelengths were approximately 1550.2, 1548.7, and 1551.7 nm, respectively. The free spectral range of the resonator was approximately 190 GHz.

Photon number resolving measurements were carried out using TES, readout by inductive coupling to a cryogenic preamplifier based on low-noise coherent superconducting quantum interference device arrays; this system was provided by the National Institute of Standards and Technology. Traces from the detection system output were further amplified and then digitized by an analog-to-digital converter (AlazarTech, ATS9440), which was triggered by an electronic pulse synchronized to the optical pulses. The traces were then analyzed in software to assign each one an integer corresponding to its most probable photon number, using a technique based on principal components analysis (43). We estimate the photon miscategorization probability to be on the order of 10⁻³ in the regime studied. Coherent state calibration data were obtained by heavily attenuating a pulsed laser source incident on the detectors and measuring the corresponding statistics to verify they conform to a Poissonian distribution that agrees with the mean photon number. To avoid saturating the detectors, the photon number experiments were carried out with a pump pulse train with 62.5-kHZ repetition rate. The quality factors of the resonances used in this experiment were approximately 8 × 10⁵, with escape efficiencies of approximately 80%. The pump, signal, and idler wavelengths were approximately 1554.2, 1551.4, and 1557.0 nm, respectively. The free spectral range of the resonator was approximately 175 GHz.

Photon number data were taken in sets of 800,000 samples for each data point. Each set was used to develop a template for assigning integer photon numbers to the electrical pulses that are sampled from the TES detectors. The resultant 800,000 integer photon numbers were divided into eight subsets of 100,000 samples. Quantities such as noise reduction factor, number difference variance, and second-order correlation statistics were calculated for each of these subsets; the resultant means and SDs were used for the points and error bars on Figs. 4 and 5. Further detail on these and other aspects of the experimental apparatus and technique is available in the Supplementary Materials.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/39/eaba9186/DC1