Abstract
Global warming, extreme climate events, earthquakes and their accompanying socioeconomic disasters pose significant risks to humanity. Yet due to the nonlinear feedbacks, multiple interactions and complex structures of the Earth system, the understanding and, in particular, the prediction of such disruptive events represent formidable challenges to both scientific and policy communities. During the past years, the emergence and evolution of Earth system science has attracted much attention and produced new concepts and frameworks. Especially, novel statistical physics and complex networks-based techniques have been developed and implemented to substantially advance our knowledge of the Earth system, including climate extreme events, earthquakes and geological relief features, leading to substantially improved predictive performances. We present here a comprehensive review on the recent scientific progress in the development and application of how combined statistical physics and complex systems science approaches such as critical phenomena, network theory, percolation, tipping points analysis, and entropy can be applied to complex Earth systems. Notably, these integrating tools and approaches provide new insights and perspectives for understanding the dynamics of the Earth systems. The overall aim of this review is to offer readers the knowledge on how statistical physics concepts and theories can be useful in the field of Earth system science.
Keywords: Statistical physics, Complex Earth systems, Complex network, Climate change, Earthquake
1. Introduction
1.1. The Earth as a complex system
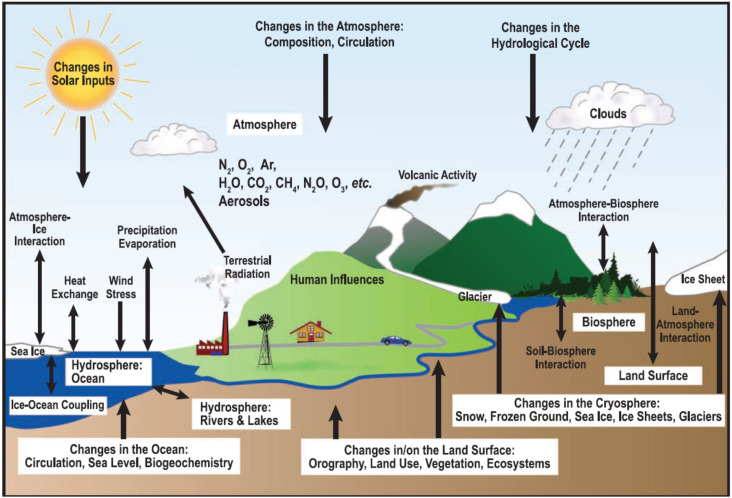
The Earth behaves as an integrated system comprised of geosphere, atmosphere, hydrosphere, cryosphere as well as biosphere components, with nonlinear interactions and feedback loops between and within them [1]. These components can be also regarded as self-regulating systems in their own right, and further broken down into more specialized subsystems. Nevertheless, the growing understanding of the multi-component interactions between physical, chemical, biological and human processes suggests that one should bring different disciplines together and take into account the Earth system as a whole. Such studies and results initiate the emergence of a new ‘science of the Earth’–Earth System Science (ESS) [2]. The ESS framework has already demonstrated its potential as a powerful tool for exploring the dynamical and structural properties of how the Earth operates as a complex system.
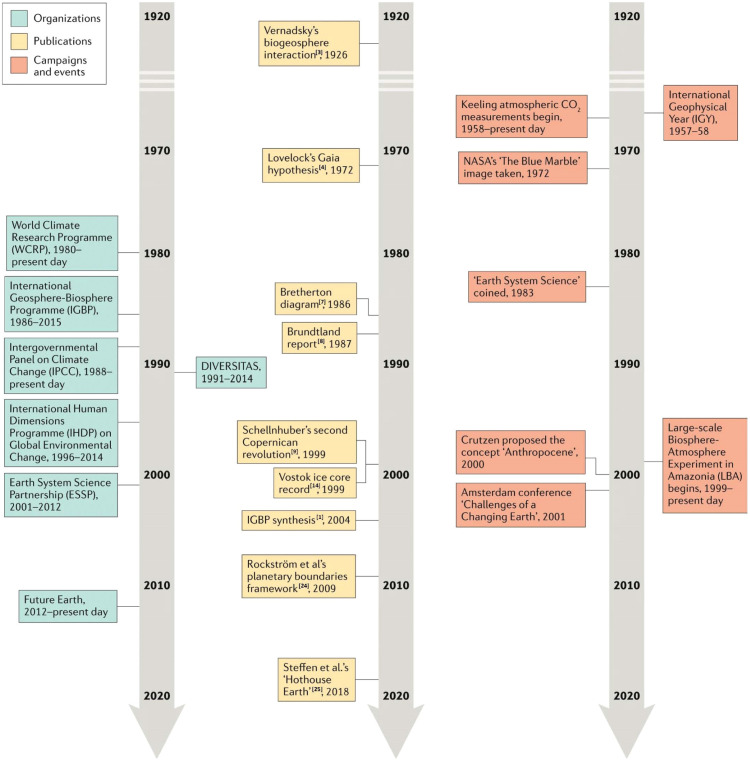
The ESS has emerged in the early to mid-20th century, and has developed rapidly during the last decades. Its historical evolution can be briefly outlined into four phases [2]: (i) Precursors and beginnings (pre-1970s). The systemic nature of Earth was mainly described and emphasized by some conceptualizations, such as Vernadsky’s biosphere concept that life has a strong influence on the physical and chemical properties of Earth [3], and Lovelock’s Gaia hypothesis that Earth is a synergistic and self-regulating, complex system [4]. These conceptualizations play vital roles in the contemporary understanding of the Earth system. In particular, the International Geophysical Year (IGY) 1957–1958 promoted the development of international science and led to the emergence of two contemporary paradigms, modern climatology and plate tectonics [5], [6]. (ii) Founding a new science (1980s). In the 1980s, the newly emerging recognition of Earth as an integrated entity: the Earth system, was called for by a series of workshops and conference reports. In particular, the Bretherton diagram developed by the National Aeronautics and Space Administration (NASA) [7] was the first systems-dynamics representation of the Earth System to couple the physical climate system and biogeochemical cycle. The Brundtland report published by the World Commission on Environment and Development in 1987 [8] developed guiding principles for a sustainable development and recognized the importance of the environmental problems for the Earth system. Some international organizations were also established in this stage, for example, the World Climate Research Programme (WCRP) aims to determine the predictability of the climate and the effects of human activities on the climate. The International Geosphere–Biosphere Programme (IGBP) was launched in 1987 in order to coordinate international research on global-scale and regional-scale interactions between Earth’s biological, chemical and physical processes and their interactions with human systems. The Intergovernmental Panel on Climate Change (IPCC) was created in 1988 to provide policymakers with scientific assessments on climate change, its implications and potential future risks, as well as to put forward adaptation and mitigation options. (iii) Going global (1990s–2015). Due to great research efforts of international programmes such as the IGBP, and the widespread use of the Bretherton diagram, ESS then developed rapidly, from the ‘new science of the Earth’ movement to a global one. In particular, the International Human Dimensions Programme (IHDP) on Global Environmental Change was founded with the aim to frame, develop and integrate social science research on global change. (iv) Contemporary ESS (beyond 2015). In the 21st century, the ESS framework was well established, and initiated a new programme, Future Earth, which was integrated by several international organizations or programmes, such as the IGBP and IHDP. Future Earth’s mission is to accelerate transformations to global sustainability through research and innovation. Following Ref. [1], we highlight the key organizations, publications, campaigns and events that characterize well the evolution of ESS in Fig. 1.
Fig. 1.
Timeline illustration of the development of Earth System Science (ESS). The figure shows the key organizations, publications, campaigns, events and concepts that have helped to define and develop the ESS.
Reprinted figure from Ref. [2].
Among the pioneering publications for the evolution of ESS, Hans Joachim Schellnhuber introduced and developed a fundamental concept for ESS: the dynamic, co-evolutionary relationship between nature and human factors at the planetary scale [9]. He proposed that the Earth system can be conceptually represented by the following mathematical form:
| (1) |
where ; . This model suggests that the overall Earth system contains two main components: stands the ecosphere and is interpreted as the human drivers. is composed of an alphabet of intricately interacting planetary sub-spheres (atmosphere), (biosphere), (cryosphere), etc. The human factor is much more subtle: means the ‘physical’ sub-component and the ‘metaphysical’ sub-component reflects the emergence of a ‘global subject’. This work provided the conceptual framework for fully integrating human dynamics into an Earth system and built a unified understanding of the Earth.
There exist numerous tools and approaches that support the evolutionary development of the ESS. However, it is worth noting that they can be integrated into three interrelated foci: observations, modeling and computer simulations, assessments and syntheses [2]. The Earth observations are usually referring to the instrumental data, for example, that are collected by the meteorological stations or polar orbiting and geostationary satellites. However, such datasets only extend, at best, for about one-to-two centuries into the past. In order to extend our reach beyond thousands or even millions of years ago, climate proxies fill this gap. There are multiple proxy records, including coral records [10], marine-sediment [11], stalagmite time series [12], tree rings [13] as well as the Vostok [14] and EPICA [15] ice core record that help us to better understand the past Earth system. Mathematical models are currently key methods for the understanding and projecting of climate and Earth systems. These models include different variants from conceptual climate models–Energy Balance Models (EBMs) [16] to more complex Earth models, the General Circulation Models (GCMs) [17]. In addition, the integrated assessment models (IAMs) were designed to take human dynamics as an integral component into account and aim to understand how human development and societal choices affect each other and the natural world, including climate change [18], [19]. Based on the GCMs, the Earth systems Models of Intermediate Complexity (EMICs) were developed to investigate the Earth’s systems on long timescales or at reduced computational cost [20]. These models provide knowledge-integration to explore the dynamic properties and basic mechanisms of the Earth system across multiple space and time scales. The assessments and syntheses also played crucial roles in building new scientific knowledge, linking the scientific and political communities, and facilitating new research fields based on the feedback from the political sector.
Some new concepts and theory have indeed arisen from the evolution of ESS, including the emerging concept of sustainability [21], Anthropocene [22], tipping elements [23], planetary boundaries framework [24], such as planetary thresholds and state shifts [25], etc. Taken together, they create powerful ways to better understand and project the future trajectory of the Earth system.
1.2. Why Statistical Physics?
Yet, despite the rapid development of the ESS, the nature and statistical properties of extreme climate events and earthquakes remain elusive and debated, and furthermore, the existence of early warning signals of these phenomena is still a major open question. As a consequence, in this review, we will present several novel approaches based on or stemmed from statistical physics, that could enhance our understanding of how the Earth system could evolve. In particular, the interdisciplinary perspective on statistical physics and the Earth system yields to an improvement of the prediction skill of high-impact disruptive events within the climate and earthquake systems.
Statistical Physics is a branch of physics that draws heavily on the laws of probability and the statistics of many interacting components. It can describe a wide variety of systems with an inherently stochastic nature, aiming to predict and explain measurable properties and behaviors of macroscopic systems. It has been applied to many problems including fields of physics, biology, chemistry, engineering and also social sciences. Note that statistical physics does not focus on the dynamic of every individual particle but on the macroscopic behavior of a large number of particles. The basic theory and ideas of statistical physics are depicted in many textbooks, such as [26], [27], [28].
Sethna motivated the relationship between statistical physics and complex systems in his book [29] as follows: ”Many systems in nature are far too complex to analyze directly. Solving for the motion of all the atoms in a block of ice – or the boulders in an earthquake fault, or the nodes on the Internet – is simply infeasible. Despite this, such systems often show simple, striking behavior. We use statistical mechanics to explain the simple behavior of complex systems”. A complex system is usually defined as a system composed of many components which interact with each other. Regarding the large variety of components and interrelations, the Earth system thus can be interpreted as an evolving complex system. The concepts and methods of statistical physics can infiltrate into ESS, in particular, (i) critical phenomena are analogous to tipping elements: a system will collapse and follow a breakdown [30], if it is close to a phase transition or tipping point. Critical phenomena and transitions exist widely in the Earth system [31], such as in atmospheric precipitation [32] and percolation phase transition in sea ice [33]. (ii) The concept of fractal was used to describe the Earth’s relief, shape, coastlines and islands [34]. (iii) The earthquake process is regarded as a complex spatio-temporal phenomenon, and has been viewed as a self-organized criticality (SOC) paradigm [35]. Moreover, the seismic activity exhibits scaling properties in both temporal and spatial dimensions [36].
Complex network theory provides a powerful tool to study the structure, dynamics and function of complex systems [37], [38], [39], [40]. Meanwhile, statistical physics is a fundamental framework and has brought theoretical insights for understanding many properties of complex networks. From an applied perspective, statistical physics has led to the definition of null models for real-world networks that reproduce global and local features [41]. Complex network theory is an emerging multidisciplinary discipline that has been applied to many fields including mathematics, physics, biology, computer science, sociology, epidemiology and others [42]. Ideas from network science have also been successfully applied to the climate system and revealed interesting mechanisms underlying its functions, and leading to the emergence of a new concept, Climate Network (CN) [43]. The nodes in a CN represent the available, geographically localized, time series, in particular, regular latitude–longitude grids, while the level of similarity and causality between the nonlinear climate records of different grid points represents the CN’s links [44], [45]. The development of this data-based approach is providing radical new ways to investigate the patterns and the dynamics of climate variability [46].
In this review, we will introduce how to apply statistical physics methods in Earth system science. Particularly, we focus largely on the surface of the Earth system, including the climate system, Earth’s relief as well as the earthquakes system, but not including the whole planetary interior.
1.3. Outline of the report
Apart from this introductory preamble, the report is organized along 3 Sections.
In the next Section, we start by offering the overall methodology that will accompany the rest of our discussion. Section 2 contains several topics that are essential but rather formal, including the CN approach, percolation theory, tipping points analysis, entropy theory and complexity. The reader will find there the attempt to define an overall theoretical framework encompassing the different situations and systems that will be later extensively treated.
Section 3 gives a comprehensive review of applications, especially those that were studied in climate systems, the Earth geometric surface relief and earthquake systems.
Finally, Section 4 presents our conclusive remarks and perspective ideas.
2. Methodology
2.1. Climate networks
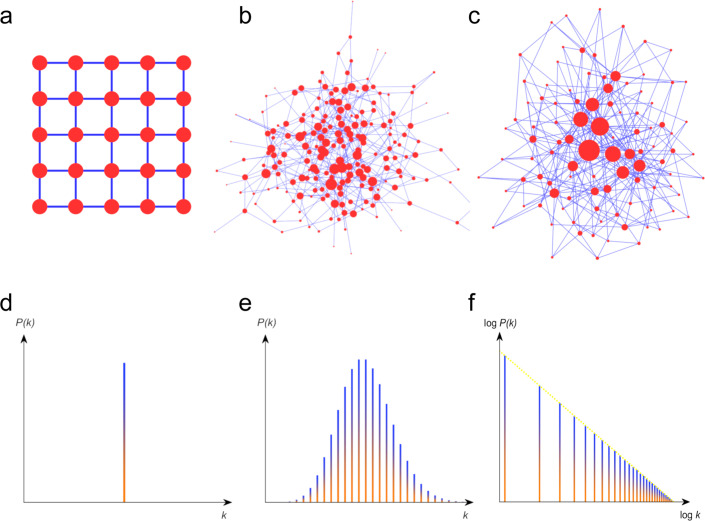
For more than two decades, the complex network paradigm has demonstrated its great potential as a versatile tool for exploring dynamical and structural properties of complex systems, from a wide variety of disciplines in physics, biology, social science, economics, and many other fields [37], [40], [47], [48], [49], [50], [51], [52]. In the context of network theory, a complex network is a graph with non-trivial topological features which do not occur in simple networks such as regular lattices (Fig. 2a) or random Erdős–Rényi graphs (Fig. 2b). One of the novelties of complex network theory is that it can relate the topological characteristics to the function and dynamics of the system. Complex network theory has been successfully applied to many real world systems and revealed fundamental mechanisms underlying their functions. It has been also found that many real world networks are scale-free networks (Fig. 2c) [38], [53].
Fig. 2.
Characteristics of the basic explored model networks. (a) A regular 2D square lattice, is the most degree-homogeneous network. (b) An Erdős–Rényi (ER) network, has a Poisson degree distribution and its degree heterogeneity is determined by the average degree . (c) A scale–free (SF) network, has a power-law degree distribution, yielding large degree heterogeneity. The degree distributions are shown for (d) the 2D square lattice, (e) the ER network and (f) the SF network.
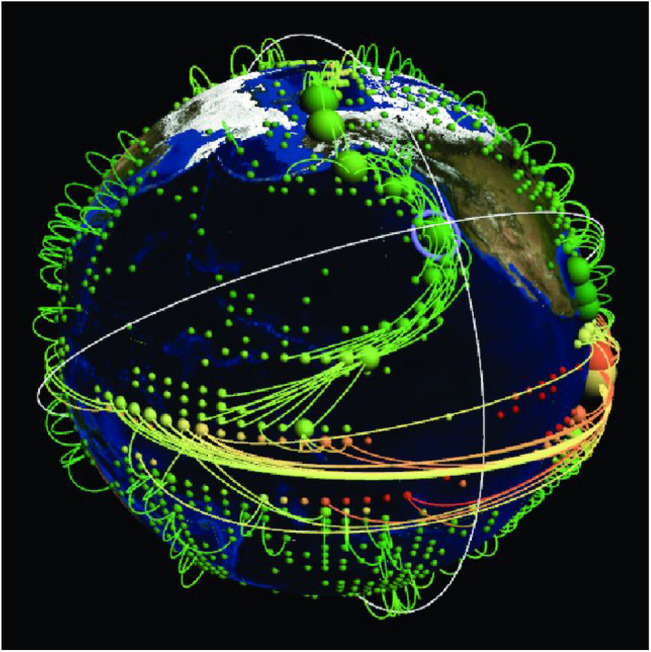
In recent years, the ideas of network theory have also been implemented in climate sciences to construct CN [43], [44], [54]. In CNs the geographical locations (or grid points) are regarded as the nodes of the networks and the level of similarity (causality) between the records (time series) of two grid points represents the links and their strength. Various climate data such as temperature, pressure, wind and precipitation can be used to construct a network. The climate networks approach allows to study the interrelationship between the different locations on the globe and thus represent the global behavior of the climate system, e.g., how energy and matter are transferred from on location to another. These networks have been used successfully to analyze, model, understand, and even predict various climate phenomena [44], [45], [46], [55], [56], [57], [58], [59], [60], [61], [62], [63], [64], [65], [66], [67], [68], [69], [70]. A visualization of a climate network is shown in Fig. 3 as an example.
Fig. 3.
Visualization of a climate network with surface air temperature taking into account the spatial embedding of vertices on the Earth’s surface.
Figure from Ref. [71].
We first provide an introduction of definitions, notations and basic quantities used to describe the topology of a network, and then present an overview on how to construct a climate network.
2.1.1. Network characteristics
In this Section we review basic characteristics and metrics used to describe and analyze networks, most of them come from graph theory [72]. Graph theory is a large field containing many branches but we present only a small fraction of those results here, focusing on the ones most relevant to the study of the complex Earth system. A network, also called a graph in the mathematical literature, is a collection of vertices connected by edges. Vertices and edges are also called nodes and links in computer science, sites and bonds in physics, and actors and ties in sociology [40]. Throughout this review we will denote the number of vertices by and the number of edges by , which is also a common notation in the mathematical and physics literature.
The adjacency matrix
Most of the networks we will study in this review have at most a single edge between any pair of vertices, i.e., self-edges or self-loops not allowed. A simple representation of a network for many purposes is the adjacency matrix , with elements such that
| (2) |
We should notice that the diagonal matrix elements are all zero in the adjacency matrix. In some situations it is useful to represent edges as having a strength, weight, or value to them, usually a real number. Such weighted or valued networks can be represented by giving the elements of the adjacency matrix values equal to the weights of the corresponding connections. A directed network or directed graph, also called a digraph for short, is a network in which each edge has a direction, pointing from one vertex to another. Such edges are themselves called directed edges. For this case, the adjacency matrix is usually not symmetric, and becomes
| (3) |
Degree
The degree of a vertex in a network is the number of edges connected to it. We denote the degree of vertex by . For an undirected network of vertices the degree can be written in terms of the adjacency matrix (Eq. (3)) as
| (4) |
The number of edges is equal to the sum of the degrees of all the vertices divided by 2, so
| (5) |
The mean degree of the node in an undirected graph is .
The concept of degree is more complicated in directed networks. In a directed network each vertex or node has two degrees. The in-degree is the number of in-going edges connected to a node and the out-degree is the number of out-going edges. From the adjacency matrix of a directed network Eq. (3), they can be written
| (6) |
Bearing in mind that the number of edges in a directed network is equal to the total number of in-going ends of edges at all vertices, or equivalently to the total number of out-going ends of edges.
Degree distributions
One of the most fundamental properties of a network that can be measured directly is the degree distribution, or the fraction of nodes having connections (degree ). A well-known result for the Erdős–Rényi [73] network is that its degree distribution follows a Poissonian,
| (7) |
where is the average degree. As shown in Fig. 2e, despite the fact that the position of the edges is random, a typical random graph is rather homogeneous, the maximum number of the nodes having the same number of edges.
However, direct measurements of the degree distribution for real networks, such as the Internet [74], WWW [38], email network [75], metabolic networks [76], airline networks [77], neuronal networks [78], and many more, show that the Poisson law does not apply. But they exhibit an approximate power-law degree distribution
| (8) |
where is a normalization factor. The constant is known as the exponent of the power law. Values in the range are typical, although values slightly outside this range are possible and are observed occasionally [79]. Networks with power-law degree distributions are called scale-free networks. The simplest strategy to determine the scale-free properties is to look at a histogram of the degree distribution on a log–log plot, as we did in Fig. 2f, to see if we have a straight line. Several models have been proposed for the evolution of scale-free networks, each of which may lead to a different ensemble. The first proposal was the preferential attachment model of Barabási and Albert, which is known as the Barabási–Albert model [38]. Several variants of this model have been suggested, see, e.g., in Ref. [80].
Clustering coefficient
The extent to which nodes cluster together on very short scales in a network is measured by the clustering coefficient. The definition of clustering is related to the number of triangles in the network. The clustering is high if two nodes sharing a neighbor have a high probability of being connected to each other. The most common way of defining the clustering coefficient is:
| (9) |
Here a “connected triple” means three nodes with edges and . The factor of three in the numerator arises because each triangle is counted three times when the connected triples in the network are counted.
We can also get a local clustering coefficient for a single vertex by defining
| (10) |
That is, to calculate , we go through all distinct pairs of vertices that are neighbors of , count the number of such pairs that are connected to each other, and divide by the total number of pairs. represents the average probability that a pair of ’s friends are friends of one another. For vertices with degree or , for which both numerator and denominator are zero, we assume . Then the clustering coefficient for the whole network [37] is the average . In both cases, the clustering is in the range .
Subgraphs
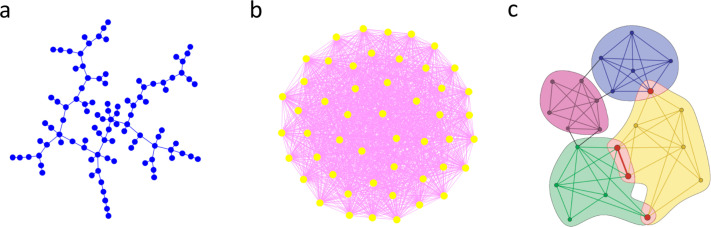
A graph consisting of a set of nodes and a set of edges is a subgraph of a graph if all nodes in are also nodes of and all edges in are also edges of . The simplest examples of subgraphs are cycles, trees, and complete subgraphs [81]. A cycle of order is a closed loop of edges such that every two consecutive edges and only those have a common node. That is, graphically a triangle is a cycle of order 3, while a rectangle is a cycle of order 4. The average degree of a cycle is equal to 2, since every node has two edges. A tree, as shown in Fig. 4a, is a connected, undirected network that contains no closed loops. Here, by “connected” we mean that every node in the network is reachable from every other via some path through the network. A river network is an example of a naturally occurring tree with directed links [82]. The most important property of trees is that, since they have no closed loops, there is exactly one path between any pair of nodes. Thus the number of edges in a tree is always exactly edges. Complete subgraphs of order , also called -clique, contain nodes and all the possible edges—in other words, they are completely connected [see Fig. 4b].
Fig. 4.
Illustration of the concept of subgraphs. Examples of (a) a tree network, (b) a fully completed network, (c) overlapping -clique communities at .
(c): Reprinted figure from Ref. [84].
Let us consider the ER model, in which we start from isolated nodes, then connect every pair of nodes with a probability . Most generally, we can ask whether there is a critical probability that marks the appearance of arbitrary subgraphs consisting of nodes and edges. A few important special cases that directly give an answer to this question [81] are: (i) The threshold probability of having a tree of order is ; (ii) The threshold probability of having a cycle of order is ; (iii) The critical probability of having a complete subgraph of order is .
Generally, a network is always composed of many separate subgraphs or components, i.e., groups of nodes connected internally, but disconnected from others. In each such component there exists a path between any two nodes, but there is no path between nodes in different components. A network component with size proportional to that of the entire network, , is called a giant component.
Similar to component, the concept of community is also one of the most fundamental properties in complex networks [83]. The nodes of the network might be joined together into tightly connected groups, whereas between them there are still links but less connections. A single node of the network may belong to more than one community, and most of the actual networks are made of highly overlapping communities of nodes [84]. Since community structures are quite common in real networks, community finding and detection are thus of great importance for better understanding the function of a network. An example of overlapping -clique communities is shown in Fig. 4c. A good review on the community detection in graphs can be found in Ref. [85].
Network models
Erdős–Rényi model: It can be interpreted by the following two well-studied graph ensembles, the ensemble of all graphs having vertices and edges, and the ensemble consisting of graphs with vertices, where each possible edge is realized/connected with probability . These two families, initially studied by Erdős and Rényi [73], are known to be similar if . They are referred to as Erdős–Rényi (ER) model. These descriptions are quite similar to the microcanonical and canonical ensembles studied in statistical physics [86]. The ER model has traditionally been the dominant subject of study in the field of random graphs [81], with Poissonian degree distributions, see Eq. (7).
Barabási–Albert model: It is based on two simple assumptions regarding network evolution [38]. (i) Growth: Starting with a small number of nodes, at every time step, a new node with edges that link the new node to different nodes already present in the system is added. (ii) Preferential attachment: This is the heart of the model. When choosing the nodes to which the new node will be connected, the probability that the new node will be connected to node depends on the degree of node , such that . In this process, after time steps this results in a network with nodes and edges. Theoretical and numerical results show that this network model evolves into a power-law degree distribution, see Eq. (8).
Watts–Strogatz model:
In 1998, Watts and Strogatz [37] proposed a one-parameter model that interpolates between a regular lattice and a random graph. The details behind the model are the following: (i) Start with order: Start with a ring lattice with nodes in which every node is connected to its closest neighbors. In order to have a sparse but connected network at all times, consider . (ii) Randomize: Randomly rewire each edge of the lattice with probability such that self-connections and duplicate edges are excluded. This process introduces long-range edges. The resulting network properties of this model are small-world and high clustering coefficient. Specifically, a small-world network is referring to a network where the characteristic path length grows proportionally to the logarithm of the number of nodes, [37].
2.1.2. Pearson correlation climate network
Our climate system is made up of an enormous number of nonlinear sub-systems having mutual nonlinear interactions and feedback loops active on a wide-range of temporal and spatial scales. Therefore, modeling the Earth climate system from the point of view of complex networks can clearly provide critical insights into the underlying dynamics of the evolving climate system. As discussed above, in CNs, geographical regions of Earth are regarded as nodes, and the bivariate statistical analysis of similarities between pairs of climatological variables time series represent the links.
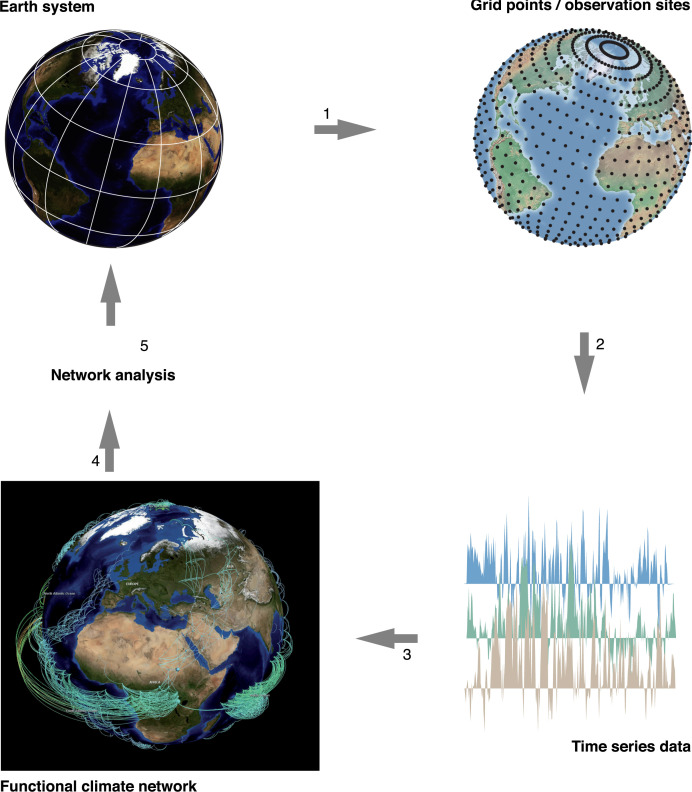
In general, there are five steps for the CNs construction and analysis [46], the procedure is displayed in Fig. 5, adapted from [87]. Step (i): Nodes, the nodes in CNs are usually defined as locations in a longitude–latitude spatial grid at various resolutions. (ii): Climatological variable, we select the suitable climatological time series to be analyzed, e.g., surface air temperature, sea surface temperature, precipitation, wind, etc. Some pre-processing is also often needed. For example, to avoid the strong effect of seasonality, we usually subtract the mean seasonal cycle and divide by the seasonal standard deviations for each grid point time series. (iii): Edges, in this step we compute the statistical similarity that quantifies the interdependencies between pairs of time series. The strength of each edge is correlation based. There are many measures for quantifying the interdependencies of time series, here we mention the types of CNs by correlation measures. For example, a Pearson correlation climate network, where we use Pearson correlation to quantify the cross-correlations between time series; while an event synchronization climate network uses the event synchronization method; and a mutual information climate network is based on mutual information. (iv): Construction, in this step we construct the CN which typically involves some thresholding criterion to select only statistically significant edges. Considering, for example, that the significant links have values above a given threshold, , then the adjacency matrix is determined as
| (11) |
where is the Heaviside function. We then investigate the obtained network by using various network characteristics. Finally, in step (v): Climatological interpretation, the results of this analysis are interpreted in terms of dynamical processes of the climate system (e.g., atmospheric circulation, ocean currents, plenty of waves, etc.).
Fig. 5.
Methodology used to construct a climate network from climatic time series.
Reprinted figure from Ref. [87].
In the following, we will demonstrate how to construct a Pearson correlation climate network. Suppose that the climatic variable is the daily surface air temperature, either from observations, proxy reconstructions, reanalyses, or simulations, gathered at static measurement stations, or provided at grid cells. At each node of the network, we calculate the daily atmospheric temperature anomalies (actual temperature value minus the climatological average which is then divided by the climatological standard deviation) for each calendar day.
For obtaining the time evolution of the weight of the link between a pair of nodes and , we follow [66] and compute, for each time windowing (such as month or year) over the whole time span, the time-delayed cross-correlation function defined as
| (12) |
and
| (13) |
where the brackets denote an average over the past days, according to
| (14) |
Here, is the time lag spanning from days. The reliable estimate of the background noise level, i.e., the values of the were discussed in [88], [89]. Based on the correlation functions, Eqs. (12), (13), a weighted and directed link between nodes and was defined in Refs. [59], [61], [64]. This is done by identifying the value of the highest peak (or lowest valley) of the cross-correlation function and denote the corresponding time lag of this peak (valley) as . The sign of indicates the direction of each link; i.e., when the time lag is positive (), the direction of the link is from to [64]. The positive and negative links and their weights are determined via , and are defined as
| (15) |
and
| (16) |
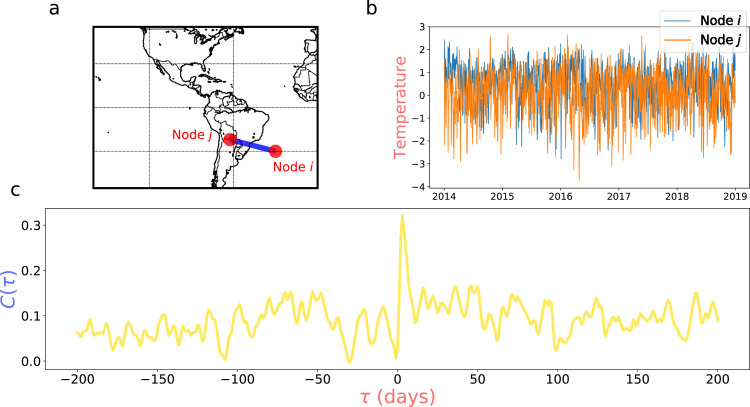
where “max” and “min” are the maximum and minimum values of the cross-correlation function, “mean” and “std” are the mean and standard deviation. Typical time series and their cross-correlation functions are shown in Fig. 6. For demonstration, two nodes are selected, a node is located in the Southwest Atlantic and a node is in the South American continent (Fig. 6a). The near surface daily air temperature anomalies are shown in Fig. 6b for the time period between 2014 to 2018. The cross-correlation function between the time series is shown in Fig. 6c, where the absolute value of a maximum cross-correlation function is much larger than the level of noise and the minimum value. Since , then the direction of the link is from to . According to Eq. (15), we calculate its weight to be . This value represents 5.71 standard deviations above the noise level, i.e., highly significant.
Fig. 6.
Typical weighted and directed link in a Pearson Correlation Climate Network. (a) Node is located on the Southwest Atlantic and node is in the South American continent. (b) The near surface daily air temperature anomalies for the period [2014,2018]. (c) The cross-correlation function between the time series shown in (b). The direction of this link is from to with weight .
Finally, networks can be constructed by establishing links between pairs of nodes with weights larger than some significant threshold. The advantage of this method is that it overcomes the problem of strong auto-correlation values in the data [88].
2.1.3. Event synchronization climate network
The event synchronization method provides an alternative way to construct a network from climate observations: event synchronization CN. It was originally proposed by Quian Quiroga et al. [90], where they measured synchronization and inferred time delays between signals in neuroscience. Event synchronization is based on the relative timings of events, such as rainfall, in a time series and is defined, e.g., by the crossing of a threshold or by local maxima or minima, etc. For instance, an extreme rainfall event is defined as the day where its precipitation is above the 99th percentiles of all days. Event synchronization is especially appropriate for studying extreme events. The degree of synchronization is obtained from the number of quasi-simultaneous events and the delay is calculated from the precedence of events in one time series (signal) with respect to the other.
Event synchronization starts by constructing two event series from two discrete univariate time series, and . An event that occurs at at time is considered to be synchronized with an event that occurs at at time within a time , if , where
| (17) |
Here, , and . and are the number of events in the and respectively. The number of times an event appears in shortly after it occurs in is counted:
| (18) |
with
| (19) |
and analogously to Eq. (18) we can define . Finally, the symmetrical and anti-symmetrical combinations
| (20) |
are used to measure the synchronization of the events and their delay behavior, respectively. They are normalized to and . It should be noted that if several extreme events are very close in one record, then only the first one is considered. Particularly, if and only if the events of the signals are fully synchronized. In addition, if the events in always precede those in , then we get .
The event synchronization method has been found useful for the study of electroencephalogram signals [90], neurophysiological signals [91], and the patterns of extreme rainfall events [92], [93], [94], [95], [96].
2.1.4. Mutual information climate network
The mutual information method is also one of the common tools for quantifying the interdependencies between time series and for constructing climate networks. The mutual information of two random variables is a measure of the mutual dependence between the two variables. The concept of mutual information is intricately linked to that of entropy of a random variable [97]. Let and be a pair of random variables with values over the space . If their joint distribution is , and their associated marginal probability distribution functions are and , then the mutual information is defined as
| (21) |
States with zero probability of occurrence are ignored.
Intuitively, is a measure of the inherent dependence expressed in the joint distribution of and relative to their corresponding joint distribution under the assumption of independence. Mutual information, therefore, measures dependence and nonlinearity, in fact: if and only if and are independent random variables, i.e., . Moreover, mutual information is non-negative, symmetric and can also be computed with a time lag [98]. After we get the mutual information coefficient, Eq. (21), for each pair of nodes, we can construct a mutual information climate network. It has been shown that the mutual information CN can well capture the westward propagation of sea surface temperature (SST) anomalies that occur in the Atlantic multidecadal oscillation [99].
To summarize, in this chapter we have described different network characteristics and presented various linear and nonlinear tools of time series analysis, which can be used to construct, define and characterize CNs. Linear and nonlinear methods include Pearson correlation, event synchronization, and information-theory measures such as entropy and mutual information. There are also some other powerful tools, such as, spectral analysis, empirical orthogonal function analysis and symbolic ordinal analysis that can be used to reconstruct CNs [46].
2.2. Percolation theory
Percolation originally has been used to describe the movement and filtering of fluids through porous materials [100]. The idea of percolation was also considered by Flory and Stockmayer on polymerization and the sol–gel transition [101]. In recent years, it has been a cornerstone in the theory of spatial stochastic processes with broad applications to diverse problems in fields such as statistical physics [102], [103], [104], [105], phase transitions [106], [107], materials [108], [109], epidemiology [110], [111], [112], [113], networks [30], [38], [40], [114], [115], [116], [117], [118], [119], [120], [121], colloids [122], [123], semiconductors [124], traffic [125], turbulence [126], as well as Earth systems [33], [65], [67], [127], [128], [129], [130]. Percolation theory also plays a pivotal role in studying the structure, robustness and functions of complex systems [131].
It is well known that in lattices and other ordered networks [106], [107], [132], for dimensions greater than one, a percolation phase transition occurs. The percolation process is a simple model in which the nodes (sites) or edges (bonds) are occupied with some probability and unoccupied with probability . Take a regular lattice as an example (see Fig. 2a). A system is regraded as percolating if there is a path from one side to the other parallel one, passing only through occupied bonds and sites. When such a path exists, the component or cluster of sites that spans the lattice is called the spanning cluster or the infinite percolation cluster. At low concentration , the sites are either isolated or form small clusters of nearest-neighbor sites. Two sites belong to the same cluster if they are connected by a path of nearest-neighbor sites. At large values, on the other hand, at least one path between opposite sides exists (see Fig. 7). The percolation phase transition occurs at some critical density that depends on the type and dimensionality of the lattice.
Fig. 7.
Bond percolation clusters on a 512 × 512 2D square lattice for(a) 0.3, (b) 0.5 and (c) 0.55, respectively. Different cluster sizes have different colors. The color of the larger clusters depends on their size and varies from blue (small clusters) to red (infinite cluster). The percolation threshold is .
For many complex networks, the notion of side does not exist. However, the ideas and tools of percolation theory can still be applied [51]. The main difference is that the condition for percolation is no longer the existence of spanning cluster, but rather having a cluster containing nodes. If such a component exists, we call it giant component, that was discussed in Section 2.1. Indeed, the condition of the existence of a giant component applies also to lattice networks, and therefore it can be used as a more general condition than the spanning property.
There exist two types of percolation, site percolation, where all sites are with probability occupied and empty. In bond percolation, however, it is the bonds which are occupied with probability and above they form a giant component of connected sites. In this review, we will focus on the critical phenomena of percolation near the percolation threshold , where for the first time a giant component is formed or the system collapses [133]. These aspects are called critical phenomena, and the fundamental theory to describe them is the scaling theory from phase transitions.
2.2.1. Phase transition
The concept of phase transition is usually used to describe transitions between solid, liquid, and gaseous states of matter for thermodynamic physical systems, where an ordered phase (e.g., solid) changes into a disordered phase (e.g., liquid) at some critical temperature [26]. Another classical example of a phase transition is the magnetic phase transition, explained by the Ising model, where a spontaneous magnetization appears, at low temperature without any external field. While increasing temperature, the spontaneous magnetization decreases and vanishes at .
Percolation is indeed a simple geometrical phase transition, where the percolation threshold distinguishes a phase of finite clusters (disordered phase) from a phase of an infinite cluster (ordered phase). The occupied probability of sites or bonds plays the same role as the temperature in the thermal phase transition. They are usually called control parameters in statistical physics.
Percolation order parameter
The percolation order parameter in the relative size of the infinite cluster which is defined as the fraction of the sites belonging to the infinite cluster. For , there exist only finite clusters, thus, ; For the case , however, is analogous to the magnetization below and behaves near as a power law
| (22) |
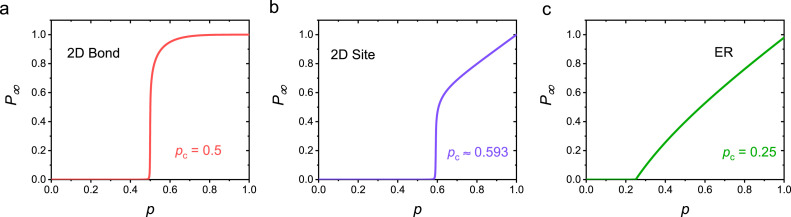
It describes the order in the percolation system and is therefore called the order parameter. We show in Fig. 8, how behaves as a function of , for both bond and site percolation in the 2D square lattice model, as well as, for site percolation in the ER network, respectively. It is worth noting that we adopt as the control parameter in Fig. 8, which results being a monotonic increasing function. When is gradually decreased (from 1), it can be regarded as removal (or attack) of nodes or links and the system collapses after removing a fraction of . Thus, can be a measure of the resilience of the system, i.e., how close it is to collapse.
Fig. 8.
Percolation phase transitions in lattice and network systems. The percolation order parameter as a function of occupied probability for (a) 2D bond percolation with , (b) 2D site percolation with and (c) ER network with . Here the average degree for ER network.
Cluster size distribution
The finite components distribution near criticality follows the scaling form [106], [107]
| (23) |
Where is the component size, and represents the number of components of size . At the percolation threshold diverges and the tail of the distribution behaves as a power law with the critical exponent .
Average cluster size
For any given site, the probability that it belongs to a cluster of size is . Let us define as the probability that any given site is part of a finite cluster,
| (24) |
which is the first moment of the cluster size distribution. Hence, for any given site of any given finite cluster, the probability that the cluster is of size is
| (25) |
with . For any given site of any given finite cluster, the average size of the cluster is
| (26) |
Note that, the average size , excluding the infinite cluster, diverges near the critical point as,
| (27) |
Correlation length
The correlation function is the probability that a site at position from an occupied site in a finite cluster belongs to the same cluster.
Typically, for large , there is an exponential cutoff, i.e., , at the correlation length . The correlation length is defined as
| (28) |
measures the mean distance between two sites on the same finite cluster. When approaches , increases as
| (29) |
The quantities and are analogous to the magnetization and the susceptibility in magnetic systems. , and are called the critical exponents and describe the critical behavior of the percolation phase transition.
2.2.2. Structural properties
Next, we will briefly introduce some fundamental measurements that are used to characterize the structural properties of a percolation cluster. For more details, the readers can refer to Ref. [106].
Fractal dimension
The fractal concept was introduced into the physical world by Mandelbrot [134] and applied to percolation by Stanley [135] to describe the cluster shapes at the percolation threshold . The infinite cluster is self-similar on all length scales, and can be regarded as a fractal. The fractal dimension is defined as how, on average, the mass of the cluster within a sphere of radius from a site of the cluster changes with ,
| (30) |
For length scales smaller than the correlation length , a fractal structure exists. For length scales larger than , the cluster becomes homogeneous. This can be summarized as
| (31) |
The relative size of the giant component, can also be expressed as
| (32) |
The fractal dimension of percolation clusters can be related to the critical exponents and . Substituting Eqs. (22), (29) into Eq. (32), yields .
Fractal analysis was also applied in the study of complex networks [136]. Generally, there are two basic methods to calculate the fractal dimensions of a given system, i.e., using either the box counting method [137] or the cluster growing method [138]. (i) The box counting method: Let be the number of boxes of linear size that are needed to cover the object, the fractal dimension is then given by . It means that the average number of nodes within a box of size is,
| (33) |
The fractal dimension can be obtained by a power law fit. (ii) The cluster growing method: Similar to Eq. (30), the dimension can be calculated by
| (34) |
where is the average mass of the cluster, defined as the average number of nodes within linear size in the cluster. Note that, the above methods are difficult to apply directly to networks, since networks are generally not embedded in space. In order to measure the fractal dimension of networks one usually combines the concept of renormalization [136], i.e., for each chemical size , boxes are placed until the network is covered. Then each box is replaced by a node (renormalization), and the renormalized nodes are connected if there is at least one link between the no-renormalized boxes. This procedure is repeated and the number of boxes scale with as .
Graph dimensions and
The fractal dimension has been used to describe the structural properties of the shortest path between two arbitrary sites in the same cluster. Let be the path length, which is often called the ”chemical distance” [139], it scales with as
| (35) |
and the number of sites within is
| (36) |
where is often called the “graph dimension” or “chemical” dimension. Combining Eqs. (30), (35), (36), we obtain the relation between , and , .
Besides the fractal dimension exponents , and discussed above, there are also some other exponents such as the backbone exponent and the red bonds exponents to describe the fractal dimensions of the substructures composing percolation clusters [26], [107].
2.2.3. Scaling theory
The scaling hypotheses of phase transitions were developed by Kenneth G. Wilson during the last century and honored by the 1982 Nobel prize. The scaling theory of percolation clusters relates the critical exponents of the percolation transition to the cluster size distribution, . According to the scaling hypotheses, it is possible to state the following relation for ,
| (37) |
where is the Fisher exponent [102], and is scaling function following , which rapidly decays to zero.
The correlation length is defined as the root mean square distance between occupied sites on the same finite cluster for all clusters, see Eq. (28). For clusters with sites, the root mean square distance between all pairs of sites on each cluster, is
| (38) |
and thus,
| (39) |
Close to the percolation threshold , , and we obtain from the above equation
| (40) |
To calculate the sums in Eq. (40), we transform them into integrals, and obtain
| (41) |
which yields the scaling relations between and
| (42) |
where is the system’s dimension.
Consider the th moment of the cluster size distribution
| (43) |
which scales in the critical region as,
| (44) |
Next we consider the percolation order parameter , which behaves as [106],
| (45) |
Combining with Eq. (22), we have,
| (46) |
Similarly, we obtain for , the relation , yielding
| (47) |
Thus, the critical exponents are not independent of each other but satisfy two sets of scaling and hyperscaling relations. The scaling relations can be easily expressed by Eqs. (42), (46), (47).
2.2.4. Universal gap scaling
An interesting property of percolation is universality, which is a fundamental principle of behavior at or near a phase transition critical point. As a result, the critical exponents depend only on the dimensionality of the system, and are independent of the microscopic interaction details of the system. The behavior of a system is characterized by a set of critical exponents, as discussed in the last section. If two systems have the same values of critical exponents, they belong to the same universality class. The universality property is a general feature of phase transitions. A phase transition is also characterized by scaling functions that govern the finite-size behaviors [140]. The concept of finite-size scaling provides a versatile tool to study the percolation transition.
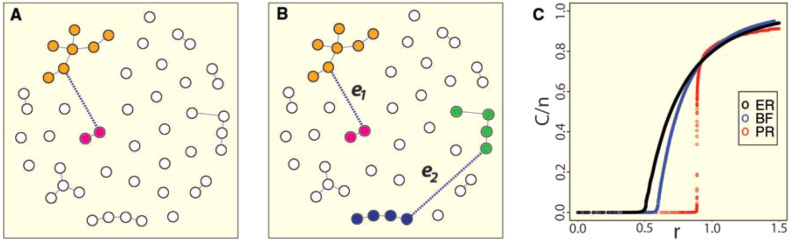
Usually, a lattice or network is expected to undergo a continuous percolation phase transition during a random occupation or failure process [81]. Explosive, hybrid and genuinely discontinuous percolation for processes that are not random but competitive link-addition processes has attracted much attention in recent years [116], [141], [142], [143], [144], [145], [146], [147], [148], [149], [150], [151], [152]. The description of the explosive percolation model is shown in Fig. 9.
Fig. 9.
Schematic of the explosive percolation model. (A) For each step two vertices are chosen randomly and connected by an edge. (B) At each time step of the Product Rule (PR) process, two edges, and , compete for addition. The selected edge is the one minimizing the product of the sizes of the components it merges. Here is accepted and is rejected. (C) Typical evolution of an ER, Bohman Frieze (BF), and PR process on a system of size .
Figure from Ref. [116].
Instead of performing a finite-size scaling analysis at the critical phase transition point, the finite-size scaling analysis on the percolation properties and critical scaling of the size of the largest gap in the order parameter is considered. For instance, Fan et al. [153] developed a new universal gap scaling theory and propose six gap critical exponents to describe the universality of percolation phase transitions. This theoretical framework can be applied for both continuous and discontinuous percolation in various lattice and network models by using finite-size scaling functions.
Gap exponents
Starting with an empty lattice, or network system with isolated nodes, bonds or links are added randomly or by competitive link-addition processes one by one. The control parameter is denoted as , which represents the link density , with being the maximal number of edges. The order parameter is the size of the largest cluster, given by the largest connected component in the entire system. During the evolution of the system, we record the size of the largest cluster at time step , and calculate its largest one-step gap
| (48) |
The step with the largest jump defines and its relative transition point as . Moreover, the percolation strength is defined as the size of the largest connected component at , i.e., .
Critical phenomena such as percolation exhibit scale-free behaviors that are quantified by scaling relations, see discussions in previous sections. Similarly, the averages , and are anticipated to exhibit the following power-law relations [153], as a function of ,2
| (49) |
| (50) |
| (51) |
where , and are three critical exponents describing the universal class of the percolation, and is the percolation threshold in the thermodynamic infinity limit, . Their corresponding fluctuations , and , are also investigated,
| (52) |
| (53) |
| (54) |
where is the number of independent realizations. We expect that , and decay algebraically with with the following scaling relations
| (55) |
| (56) |
| (57) |
where , and constitute another set of critical exponents. The universality class of the percolation is characterized by the new six gap critical exponents. Note that they are highly related to the standard percolation exponents, and not fully independent from each other. The relationships between the gap exponents and the standard percolation critical exponents are derived as [153],
| (58) |
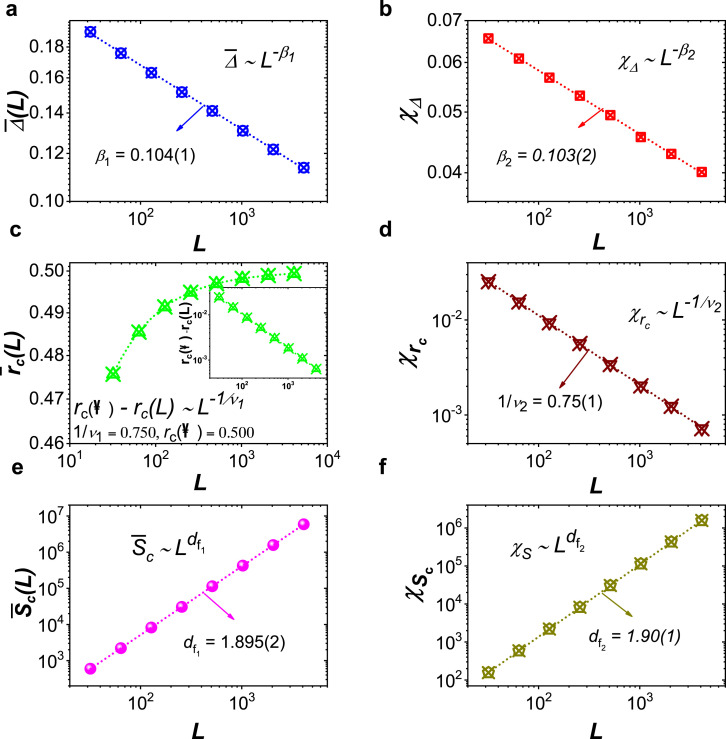
In particular, the values of can imply the order of the percolation. That is, indicates the percolation is a first order transition; whereas models with are continuous [120], [147]. We present the numerical results for bond percolation on a 2D square lattice in Fig. 10, where we obtain , , and , and . All results are in agreement with the known theoretical values [103].
Fig. 10.
Gap critical exponents for bond percolation on 2D square lattice systems. (a) and (b), and as functions of . (c) and (d), log–log plot of the percolation threshold and versus . (e) and (f). The power-law relations of and with . Inset in (c) shows the log–log plot of as a function of .
Reprinted figure from Ref. [153].
2.3. Tipping points analysis
The notion of tipping point: “little things can make a big difference”, was first published by Malcolm Gladwell in his book [154]. It means, at a particular moment in time, a small change can result a large and long-term consequences in a complex system. Tipping points are usually associated with bifurcations [155]. A tipping point is defined as “the moment of critical mass, the threshold, the boiling point”. Many complex systems experience sudden shifts in behavior, often referred to as tipping points or critical transitions, ranging from climate [23], [156], [157], [158], [159], [160], [161], ecosystems [158], [162], [163], [164], [165], [166], [167], to social science [168], [169], financial markets [170], [171], medicine [172], [173], [174] and event macroeconomic agent-based models [175].
Complex systems can shift abruptly from one state to another at tipping points, which may imply growing a threat and risk of abrupt and irreversible changes [161]. It is thus of great practical importance to understand the theoretical mechanisms and predict the tipping phenomena. Although predicting such critical points before they occur is notoriously difficult. Theory proposes the existence of generic early-warning signals (EWS) that may indicate for a wide class of systems if a critical threshold is approaching [176], [177], [178]. EWS is currently one of the most powerful tools for predicting critical transitions. The tipping point analysis technique provides a vital tool to anticipate, detect and predict tipping points in complex dynamical systems. The methodology usually combines monitoring memory in time series, includes dynamically derived lag-1 autocorrelation [179], power-law scaling exponent of detrended fluctuation analysis (DFA) [180], [181], and power-spectrum-based analysis [182].
2.3.1. Basic concepts
Defining tipping points: Following Ref. [177], a tipping point is the corresponding critical point at which the future state of the system is qualitatively changed. A single control parameter is identified as , for which there exists a threshold , from which a small perturbation leads to a qualitative change in a crucial feature of the system , after some time . The actual change is defined as:
| (59) |
In this definition, the critical threshold is considered as the tipping point, beyond which a qualitative change occurs. Note that such changes may occur immediately or even much later after the cause.
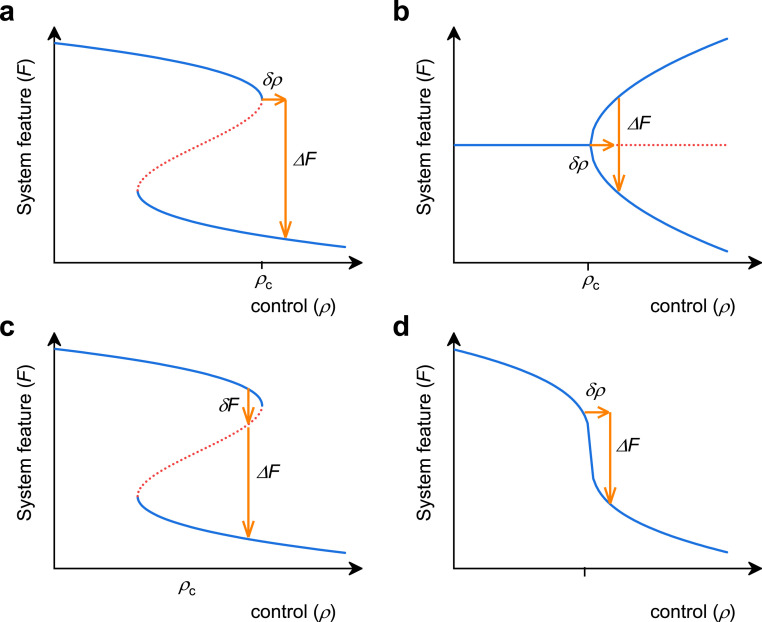
Types of tipping points: The theoretical mechanisms behind tipping phenomena in a complex system can be effectively divided into three distinct categories: bifurcation-induced, noise-induced and rate-dependent tipping [183].
Bifurcation, means that a small change in forcing past a critical threshold causes a large, nonlinear change in the system state, thus meeting the tipping point definition in Eq. (59). Given a conceptualized open system [184],
| (60) |
where is in general a time-varying input. In the case that is constant, we refer Eq. (60) as the parameterized system with parameter and to its stable solution as the quasi-static attractor. If passes through a bifurcation point of the system where a quasi-static attractor loses stability, it is intuitively clear that a system may ‘tip’ directly as a result of varying that parameter. We present two bifurcation-induced tipping point examples in Fig. 11. Where the system’s states are described by
| (61) |
and
| (62) |
for Fig. 11 a and b, respectively. In general, as a system approaches a bifurcation tipping point, where its current state becomes unstable, it leads to a shift to an alternative attractor.
Fig. 11.
Different sources of cascading tipping point types. (a) and (b) Bifurcation-induced, (c) noised-induced transitions, (d) reversible tipping points. Solid lines are stable steady states, dashed lines are unstable steady states.
Noise-induced, noise-induced transitions between existing stable states of a complex system (Fig. 11c), can also be regarded as tipping points [185], however, they do not meet the definition of forced changes, as in Eq. (59). Noise-induced tipping points mean that noisy fluctuations result in the system departing from a neighborhood of a quasi-static attractor. For example, Pikovsky and Kurths studied the coherence resonance in a noise-driven excitable Fitz Hugh–Nagumo system and uncovered that the effect of coherence resonance is explained by different noise dependencies of the activation and the excursion times [186]. The abrupt warming events during the last ice age, known as Dansgaard–Oeschger events, provide a noise-induced tipping real-world example [185]. In addition, Sutera [187] studied noise-induced tipping points in a simple global zero-dimensional energy balance model with ice-albedo and greenhouse feedback [188]. Their results indicate a characteristic time of 100,000 years for random transitions between ‘warm’ and ‘cold’ climate states, which match very well with the observed data. The noise-induced tipping points approach has also successfully been used for modeling changes in other climate models and phenomena [189]. In contrast to approaching bifurcations, it was found that noise-induced transitions are fundamentally unpredictable and show none of the EWS [177].
Rate-dependent, in which the system fails to track a continuously changing quasi-static attractor. To better understand the phenomenon of rate-dependent tipping, Ashwin et al. introduced a linear model with a tipping radius and discussed three examples where rate-dependent tipping appears [183]. Given a system for and the parameter has a quasi-static equilibrium with a tipping radius , then for some initial with , the evolution of with time is given by
| (63) |
where is a fixed stable linear operator (i.e. as ). is a time-varying parameter, that represents the input to the subsystem. The tipping radius may be related to the basin of attraction boundary for the nonlinear problem. This model shows only rate-dependent tipping—because is fixed and there is no bifurcation in the system and no noise is present. In particular, the model can be generalized to include and that vary with . Eq. (63) can be solved with the initial condition to give
| (64) |
Note that the rate-dependent tipping was also observed in the zero-dimensional global energy balance model [188].
Besides the above three tipping types, there is potentially another type, a reversible tipping point. In Fig. 11d, we show an example of a reversible tipping point, in which a mono-stable system exhibits non-linear but reversible change [159].
2.3.2. Tipping elements in the Earth’s climate system
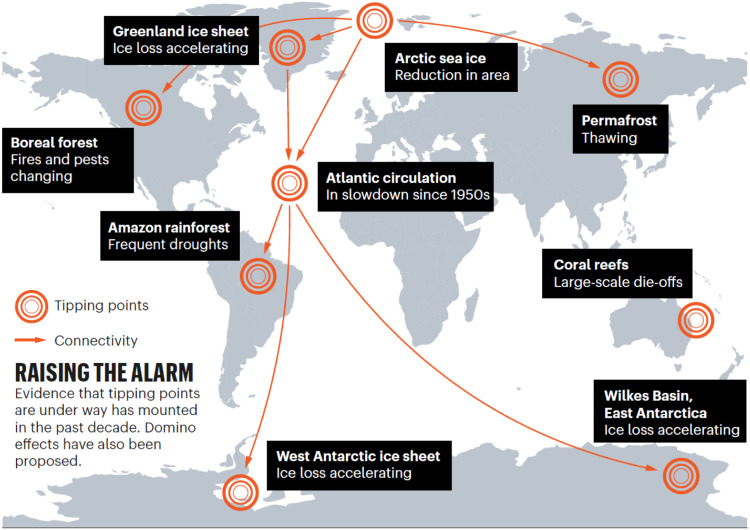
In Ref. [23] Lenton et al. introduced the term tipping elements to describe large-scale components of the Earth system that may pass a tipping point, and assessed where their tipping points lie. They emphasized that the human activities may play a vital role to push the components of the Earth system past their tipping points, resulting in profound impacts on our social and natural systems. They also defined the subset of policy-relevant tipping elements having the following conditions: (i) The first condition is described in Eq. (59); (ii) the second one is related to the “political time horizon” ; (iii) the third one is called “ethical time horizon” ; (iv) the last one is that a qualitative change should correspondingly be defined in terms of impacts. According to these four aforementioned conditions, we review here some policy-relevant potential tipping elements in the climate system, as shown in Fig. 12. For each tipping element, we consider its (1) feature of the system (see Eq. (59)) or direction of change, (2) control parameter(s) , (3) critical value(s) , (4) transition timescale as well as (5) key impacts.
Fig. 12.
Some basic main tipping elements in the Earth’s climate system.
Figure from Ref. [161].
Arctic Sea-Ice. For both summer and winter Arctic sea-ice, the area coverage is declining and the ice has thinned significantly over a large area [190]. In the IPCC projections with ocean–atmosphere GCMs, half of them will become ice-free in September during this century [191], at a polar temperature C [192]. The decline in the areal extent can be regarded as the feature of the system, denoted by ; the local air temperature and ocean heat transport can be regarded as control parameters; a numerical value of the critical threshold is still lacking in literature; the transition timescale is about years; the declining of the Arctic Sea-Ice can amplify warming and cause ecosystem changes.
Greenland ice sheet. It has been reported that the Greenland ice sheet is melting at an accelerating rate [193], which could add additional 7 meters to sea level over thousands of years if it passes a particular threshold. The decrease of the ice volume can be regarded as , a feature of system; the local air temperature is a control parameter; the critical value °; the transition timescale can reach about 300 years.
West Antarctic ice sheet. According to the IPCC report [193], the Amundsen Sea embayment of West Antarctica might have already passed a tipping point, i.e., the ‘grounding line’ (where ice, ocean and bedrock meet) is retreating irreversibly. This could also destabilize the rest of the West Antarctic ice sheet [194]. It has been found, using paleoclimatology data, that such widespread collapse of the West Antarctic ice sheet occurred repeatedly in the past. Similar to the Greenland ice sheet, the decrease of the Ice volume can be regarded as ; the local air temperature is the control parameter; the critical value °; the transition timescale can reach 300 years. The collapse of the West Antarctic ice sheet may lead to about 5 meters of sea-level rise on a timescale of centuries to millennia [23].
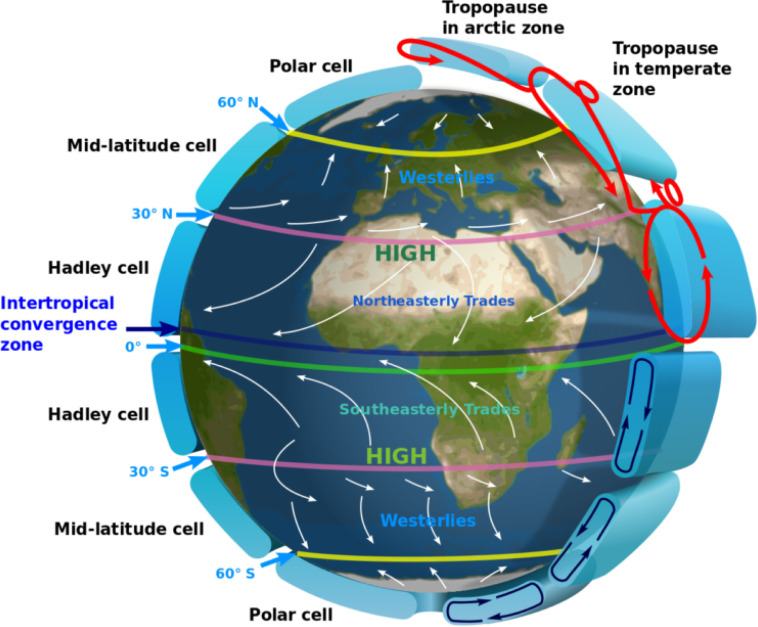
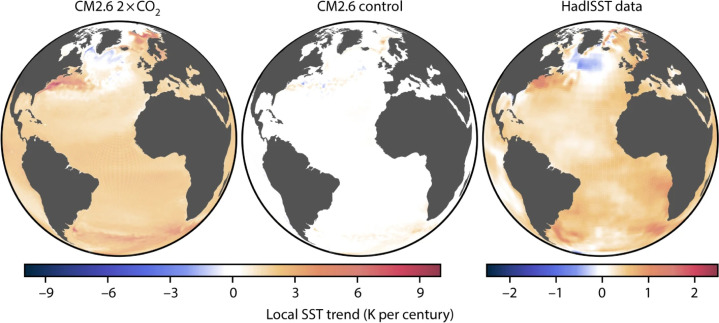
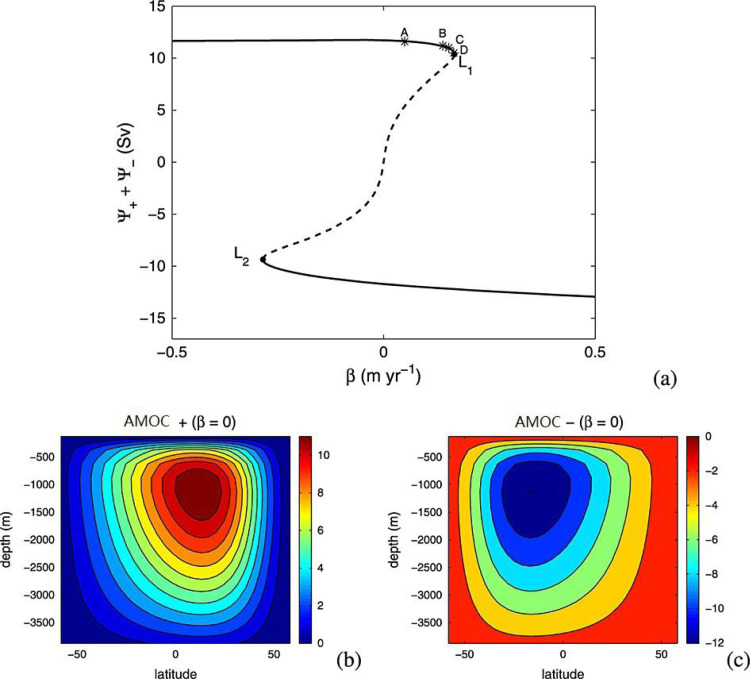
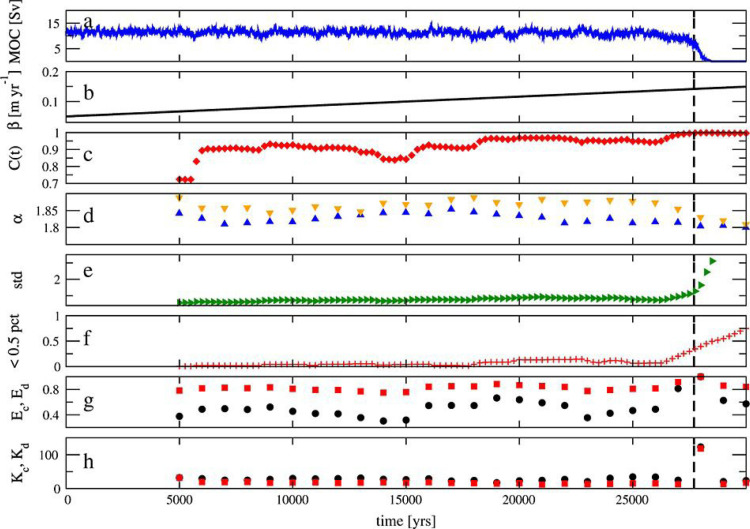
Atlantic circulation. The Atlantic meridional overturning circulation (AMOC) is one of Earth’s major ocean circulation systems, redistributing heat and affecting the climate. Research has provided evidence for a weakening of the AMOC by about sverdrups (around 15 per cent)3 since the mid-twentieth century [160]. The AMOC is also considered as one of the main tipping elements of the Earth system [23], [156]. The overturning of the Atlantic circulation can be regarded as ; the additional North Atlantic freshwater input is the control parameter; the critical value Sv; the transition timescale can reach 100 years. A slowdown of the AMOC is associated with a southward shift of the tropical rainfall belt by influencing the Intertropical Convergence Zone, and a warming of the Southern Ocean and Antarctica [17].
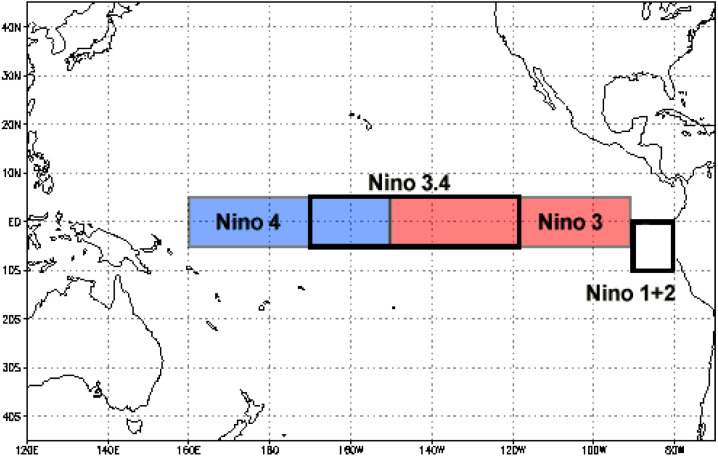
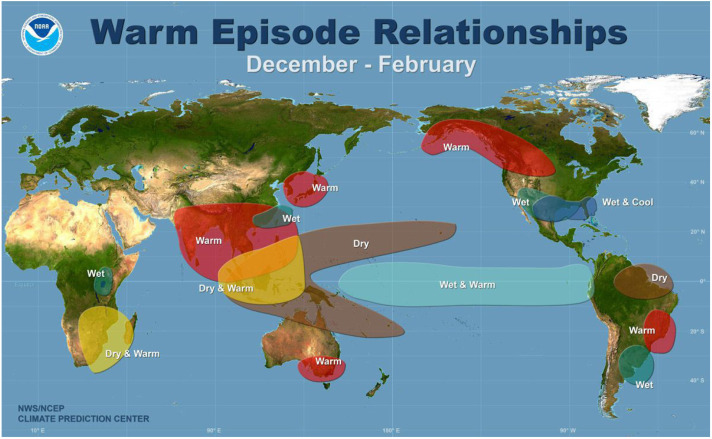
El Niño–Southern Oscillation (ENSO). ENSO, the interannual fluctuation between anomalous warm and cold conditions in the tropical Pacific, is one of the most influential coupled ocean–atmosphere climate phenomena on Earth [195], [196], [197]. It has been reported that extreme El Niño events are projected to likely increase in frequency in the 21st century [198]. The tipping point behavior of ENSO in a warming world was discussed in Ref. [199]. The amplitude of ENSO is regarded as ; the zonal mean thermocline depth, thermocline sharpness in the east equatorial Pacific, and the strength of the annual cycle are the control parameters; the transition timescale can reach 100 years. A stronger El Niño usually causes more extreme events (e.g., floods, droughts, or severe storms), which have serious consequences for economies, societies, agriculture and ecosystems.
Indian summer monsoon. The Indian summer monsoon rainfall (ISMR) has a decisive influence on India’s agricultural output and economy. The monsoon season (from June to September) can bring drought and food shortages or severe flooding, depending on how much rain falls. The land-to-ocean pressure gradient drives the monsoon circulation, related to the moisture-advection feedback [200]. The ISMR shows a declining trend since 1953 [201]. It has been reported that under some plausible decadal-scale scenarios of land use, greenhouse gas and aerosol forcing, the Indian summer monsoon switches between two metastable regimes corresponding to the “active” and “weak” monsoon phases [23]. Thus, the Indian summer monsoon can be also regarded as a tipping element. In particular, the ISMR is regarded as ; the planetary albedo over India is the control parameter; the critical value Sv; and the transition timescale is 1 years.
Amazon rainforest. Tropical forests play a vital role in the global carbon cycle [202] and are the home of more than half of the known species worldwide [203]. Deforestation and climate change are destabilizing the tropical forests with annual deforestation rates of around 0.5% since the 1990s, with a strong increase in recent years [204]. An empirical finding suggests that the observed tropical forest fragmentation is near to the critical point in three continents, including the Americas, Africa and Asia–Australia [205]. In particular, we focus on the Amazon rainforest, since it is the world’s largest rainforest and is home to one in ten known species [161]. If forests are close to tipping points, the Amazon dieback could release 90 gigatonnes Carbon dioxide. Finding the tipping point of the Amazon rainforest is thus essential for us to stay within the emissions budget. Here the rainforest in the Amazon is regarded as ; the precipitation and dry season length are the control parameters; the critical value mm/year; its transition timescale is about 50 years.
Besides the seven above mentioned tipping elements, there are also some potential policy-relevant tipping elements in the climate system, such as, Sahara/Sahel and West African monsoon, boreal forest, Antarctic bottom water, tundra, permafrost, marine methane hydrates, ocean anoxia and Arctic ozone. The readers who are interested can find them in Ref. [23]. Strong evidence indicates that “tipping points are under way has mounted in the past decade. Domino effects have also been proposed” [161].
2.3.3. Early warning of tipping points
As discussed above, many complex dynamical systems, in particular climate systems, can have tipping points and imply risks of unwanted collapse. Although predicting such tipping points before they are reached is a big challenge, the existence of generic EWS provide useful indicators for anticipating such critical transitions [176], [178]. Hence, if an early warning of a tipping point can be identified, then it could help broader society, scientists and policymakers to perform early actions to reduce system collapsed related damages. Thus, numerous studies have been dedicated to detecting and predicting these critical transitions, often making use of the EWS. In this review, we will highlight the tipping point analysis techniques that are used to anticipate, detect and forecast critical transitions in a dynamical system.
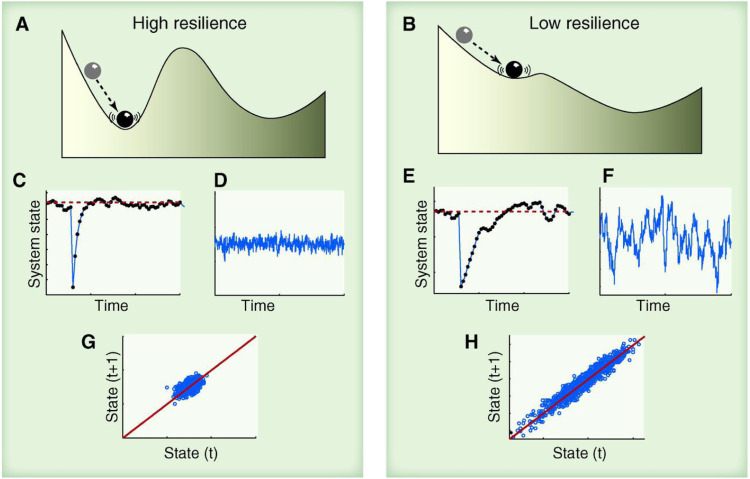
Critical slowing down near tipping points
The “critical slowing down” phenomenon has been suggested as indicators of whether a dynamical system is getting close to a critical threshold [206]. This happens, for instance, at the fold bifurcation (Fig. 11), often associated with tipping points. This indicates that the rate at which a system recovers from small perturbations becomes slow, and the slowness can be inferred from rising “memory” in small fluctuations in the state of a system. For example, Fig. 13 demonstrates that the critical slowing down has an indicator that the system has lost resilience and may be tipped more easily into an alternative state (as reflected by lag-1 autocorrelation) [178].
Fig. 13.
Critical slowing down as an indicator for foreseeing tipping points.
Figure from Ref. [178].
In order to illustrate the relation between the critical slowing down phenomenon, increased autocorrelation and increased variance, here we show a simple example that reveals the underlying mechanism. We consider a simple autoregressive model of first order,
| (65) |
where is the stable equilibrium of the model, is the period and is the recovery speed. Here is the deviation of the state variable from the equilibrium, is a random number obtained from a standard normal distribution and is the standard deviation. If and are independent of , Eq. (65) can be written as:
| (66) |
The lag-1 autocorrelation is zero for white noise and close to one for red noise. The expectation value of a first-order autoregressive process is
| (67) |
Let us consider , then the expectation value equals zero and the variance to be
| (68) |
The return speed to equilibrium decreases, when the system is close to the critical point. This implies that tends to zero and approaches to one. According to Eq. (68), the variance tends to infinity. In summary, the critical slowing down leads to an increase in lag-1 autocorrelation () and in the resulting pattern of fluctuations (variance).
Slowing down causes the intrinsic rates of change to decrease, and thus the state of the system becomes more like its past state, i.e., the autocorrelation increases. The resulting increase in “memory” can be measured in a variety of ways from the frequency spectrum of the system.
Autocorrelation function. The lag-1 autocorrelation function (ACF(1)) indicator is a simple way to provide an EWS for an impending tipping event. For instance, Held and Kleinen have shown that the autocorrelation increases in the vicinity of a bifurcation in a model of the thermohaline circulation [179]; Dakos et al. found that the autocorrelation increases before eight well-known climate transitions in the past data [157].
The coefficient of the correlation between two values in a time series is called the ACF. For example the ACF for a time series , see Eq. (66) in the autoregressive model, is given by: where is the time gap and is called the lag. In particular, a lag-1 autocorrelation is the correlation between values that are one time step apart. More generally, a lag autocorrelation is the correlation between values that are time steps apart.
The ACF scaling exponent, , is the power-law decay of the autocorrelation function with increasing lag [207]. Let us denote as the autocorrelation with lag of time series, then the scaling is defined as
| (69) |
for long-range correlations. Notably, for short-range correlated records, decays exponentially and only is indicative of a data variability close to a tipping point.
Detrended fluctuation analysis. Slowing down causes an increase in memory, which can also be measured using detrended fluctuation analysis (DFA) [180]. See [180] for the detailed method. DFA is often used to detect long-range correlations or the persistence of diverse time series including DNA sequences [208], heart rate [209], [210], [211], earthquakes [212], and also climate records [213]. If the time series is long-range correlated, the fluctuation function, , increases according to a power-law relation:
| (70) |
where is the window size and the DFA scaling exponent. Here, , where is the cumulative sum or the “profile” of a time series , and is the fitting polynomial, stands for the (polynomial) order of the DFA. The DFA exponent is calculated as the slope of a linear fit to the log–log graph of vs. . It has been found that the DFA exponent in the temporal range is sensitive to changes in a dynamical system, which is similar to [181].
Power spectrum. Recently, Prettyman et al. introduced a novel scaling indicator based on the decay rate of the power spectrum (PS) [214]. PS analysis partitions the amount of variation in a time series into different frequencies. When a system is close to a critical transition, it tends to show spectral reddening, i.e., higher variation at low frequencies [215]. The PS scaling exponent is calculated by estimating the slope of the power spectrum of the data, from the scaling relationship
| (71) |
Analytically, the three scaling exponents have the linear relationship: . It has been reported that the PS-indicator is a useful technique which behaves similarly to the related ACF(1)- and DFA-indicators. In addition, it also shows signs of providing an EWS for a real geophysical system, tropical cyclones, whereas the ACF(1)- indicator fails [214].
Besides the slower recovery from perturbations, increased autocorrelation and memory [see Eq. (67)], increased variance [measured as standard deviation, see Eq. (68)] is another possible indicator of a critical slowing down as a critical transition is approached. For example, Carpenter and Brock have shown that the variance increases in the vicinity of a bifurcation in a lake model [216].
Flickering before transitions. Another notable EWS is a system’s back and forth oscillation between two stable states in the vicinity of a critical transition. This oscillation has been called flickering and was observed on the model of lake eutrophication [217] and trophic cascades [218].
Skewness and Kurtosis. In addition to the aforementioned EWS before a catastrophic bifurcation, two further precursors, observed when approaching a critical transition and thus suggested as EWS, are changes in the skewness and kurtosis of the distribution of states [219], [220], [221]. While skewness indicates asymmetry in the distribution—with a negative skew indicating a right-sided concentration and a positive skew indicating the opposite. Skewness is the standardized third moment around the mean of a distribution,
| (72) |
Similarly, kurtosis is a measure of the “peakedness” of the distribution—with positive kurtosis indicating a peak higher than the one of a normal distribution and negative kurtosis indicating a lower peak. Kurtosis is the standardized fourth moment around the mean of a distribution estimated as,
| (73) |
2.3.4. Precursors of transitions in real systems
In the last section, we first highlighted the theoretical background of tipping points that may occur in non-equilibrium dynamics before critical transitions. Nonetheless, it poses much of a challenge to detect EWS in real complex systems such as, climate, social and ecological systems. Developing reliable predictive systems based on these generic properties can strengthen our capacity to navigate systemic failure and guide us for designing more resilient systems.
We will briefly review emerging precursors of transitions in different real systems, including climate, ecosystems, medicine and finance. An abrupt climate change occurs when the Earth system is forced to cross a threshold to a new climate state [222]. Large, abrupt, and widespread climate changes include the Carboniferous Rainforest Collapse [223], Younger Dryas [224], greenhouse–icehouse transition [225], Dansgaard–Oeschger events, Heinrich events and Paleocene–Eocene Thermal Maximum [226]. All these rapid climate changes could be explained as critical transitions [176]. For instance, a significant increase in autocorrelation is regarded as a precursor of eight well-known climate transitions [157]. A flickering phenomenon was found to precede the abrupt end of the Younger Dryas cold period, which can be also regarded as a precursor [227].
In ecology, tipping point analysis has also become a major focus of research. For example, an EWS was found in the destabilization of exploited fish stocks, where harvesting leads to increased fluctuations in fish populations [228]. The emerging of EWS has been demonstrated in lake and marine systems [229], [230]. In physiology, abrupt transitions were found in epileptic seizures and asthma attacks [174]. For example, flickering may occur before epileptic seizures. In finance, market dynamics may contain information indicating an abrupt change. For example, increased trade volatility may occur before a main shock [231]. For other precursors of transitions in real systems, the reader is referred to Ref. [176].
2.4. Entropy and complexity
2.4.1. Introduction
Entropy is an important concept arising from statistical mechanics. It is a characteristic that describes the state of a system composed of smaller components, and it has been used to be a general measure of complexity, with widespread applications. In classical thermodynamics, entropy is related to the loss of energy during an irreversible process, developed by Rudolf Clausius in the early 1850s. The thermodynamic entropy is derived from the heat flow at a fixed temperature ,
| (74) |
Note that the entropy of a system is defined only if it is in a thermodynamic equilibrium. The statistical mechanics definition of entropy was developed by Ludwig Boltzmann in 1870s via analyzing the statistical behavior of the microscopic components of a system as
| (75) |
Here is the entropy of the macrostate, is the Boltzmann’s constant, and standing the total number of possible microstates that yields the macrostate. When viewed in terms of information theory, Claude Shannon developed the very general concept of information entropy, a fundamental cornerstone of information theory, to describe an analogous loss of information [232]. It is a measure of the amount of information that is missing before reception. The definition of the information entropy is,
| (76) |
where (in bits), is the probability of each state. In quantum statistical mechanics, the concept of entropy has been developed by John von Neumann and is generally referred to as “von Neumann entropy”. For a quantum-mechanical system described by a density matrix , the von Neumann entropy is,
| (77) |
where denotes the trace operator.
There exist also many other types of entropy, such as Gibbs, Residual, Approximate, Sinai–Kolmogorov, Sample, Multiscale. Entropy has been proven useful in many real-world systems, including analysis of DNA sequences [233], cosmology and astrophysics [234], [235], [236], economics [237], [238], and climate systems [239], [240], [241]. Each definition of entropy could give better results for some systems but fails for others. We will discuss in the following that entropy has three related interpretations [29] as a measure (i) irreversible changes, (ii) disorder and (iii) uncertainty.
2.4.2. Entropy as irreversibility
The idea of irreversibility is central to the understanding of entropy. A process that is not reversible is usually called irreversible. This concept arises in thermodynamics. It has been reported that all complex dynamic natural processes are irreversible [242]. For an isolated system with an irreversible process, the entropy never decreases. This is known as the second law of thermodynamics.
In order to better understand the behavior of entropy in an irreversible process, we consider the Carnot heat engine and the corresponding Carnot cycle. As shown in Fig. 14a, given by a piston with pressure (external), and two heat baths, one at a hot temperature and the other at a cold temperature with some material (a monatomic ideal gas) inside the piston. During one Carnot cycle, heat flows out of the hot bath, heat flows into the cold bath, resulting in a net work . Carnot imagined a fully reversible heat engine, and the Carnot cycle moves the piston in and out with the following four steps (see, Fig. 14 b, the Carnot cycle P–V diagram). (1) : The gas is connected to the hot bath, and the piston moves outward at a varying pressure and a fixed temperature . In this step, heat flows into the piston. (2) : The piston expands at varying pressure . (3) : The expanded gas is then connected to the cold bath and compressed at a fixed temperature at . In this step, the heat flows out. (4) : The piston is compressed and returns to the original state. In this step, there is no heat transfer.
Fig. 14.
Entropy as Irreversibility. a. Prototype of Heat Engine. b. Carnot Cycle P–V Diagram.
The net work done by the piston is the area inside P–V Loop (integration) in Fig. 14b,
| (78) |
According to the ideal gas law,
| (79) |
where is the number of particles, the total energy of the ideal gas inside the piston is given by the equipartition theorem
| (80) |
where stands for the kinetic energy. During the first step, we get
| (81) |
Similarly, for the third step, we have
| (82) |
For the other two steps, there is no any heat flow, based on , and we have
| (83) |
The above equation gives and . Thus and hence
| (84) |
Substituting Eq. (84) into the heat flow, Eqs. (81), (81), we yield Carnot’s fundamental result,
| (85) |
Let us define the heat flow at a fixed temperature . Then the entropy change is
| (86) |
Note that the above is equivalent to Eq. (74). This means that for a reversible Carnot engine, the entropy flows from the hot bath equals the entropy flows from the piston , i.e., no entropy is created or destroyed. However, for any irreversible real engines, entropy will increase.
2.4.3. Entropy as disorder
Traditionally, another interpretation of entropy is described as a measurement of the disorder or randomness of a system. In thermodynamics, the entropy of mixing is the increase of entropy when two or more different types of particles are mixed without chemical reactions. Consider that molecules of an ideal gas are separated in a vessel with two equal volumes . The total unmixed entropy is [29]
| (87) |
Here we assume that the two separated ideal gases have the same masses and the same total energy. Let the partition between the gases be removed and they are allowed to mix. Then the mixed entropy becomes
| (88) |
According to Eqs. (87), (88), we obtain the increased entropy,
| (89) |
The above equation means that there will be a gain in entropy per molecule during the mixing process. This is since the temperatures and pressures are equal, and removing the partition of the vessel does not involve any heat transfer, thus mixing of gases (e.g., by diffusion), always results in an increasing entropy. The mixing is spontaneous! The diffusion of initially separated gases results in an increase in entropy. The process has increased the random distribution of molecules. Therefore, it is appropriate to suggest a relationship between entropy and complexity (disorder).
2.4.4. Entropy as uncertainty
The third interpretation of entropy is as a measure of the uncertainty or ignorance of a complex system. This interpretation is more general and strongly related to the information and memory. In this interpretation, the entropy is not an intrinsic property but representing our knowledge about the system.
Next, we will focus on the non-equilibrium entropy and the information entropy to insulate how entropy can be interpreted as uncertainty. The second law of thermodynamics states that the entropy of an isolated system never decreases, and is unchanged if and only if all processes are reversible. What we are interested in is how to define the entropy for non-equilibrium systems. Generally, for both non-equilibrium and equilibrium systems, we use a probability distribution , to define an ensemble of states. Given a probability distribution of a discrete set of states, the entropy is
| (90) |
where is the probability of state. In the case of continuum distributions, the entropy becomes
| (91) |
We consider a microcanonical ensemble, in which , the non-equilibrium of the entropy is shifted from the equilibrium (Eq. (75)), and the entropy is
| (92) |
For quantum systems, the non-equilibrium entropy can be described by the density matrix , as in Eq. (77).
For non-thermodynamic systems, the temperature variable does not exist. Therefore we do not need to use Boltzmann’s constant , but the constant . Then Eq. (76) becomes
| (93) |
here the entropy is measured in bits. This is called information entropy, which was introduced by Shannon [232]. Information entropy represents an ensemble of possible messages or images, and has important implications in communication technologies (message passing) and computer science (data compression). Note that the non-equilibrium Shannon entropy satisfies the following properties: (1) it is maximum for equal probabilities; (2) it is unaffected by extra states of zero probability; and (3) it changes for conditional probabilities. For more details, we refer the reader to Ref. [29].
2.4.5. Approximate entropy, sample entropy and system sample entropy
In the following, we will highlight several types of entropy, including Approximate Entropy (), Sample entropy () and System Sample Entropy (), which have been developed to quantify the complexity in non-linear time-series.
ApEn
The was introduced by Pincus in 1991 [243] motivated by the exact regularity statistics, Kolmogorov–Sinai (KS) entropy [244] and the entropy [245]. It is used as a quantification of regularity in time-series data, in particular for relatively short and noisy datasets. has a wide range of applications in areas from medical data, such as heart rate [243], to finance system [246], psychology [247] and human factors engineering [248].
Definition of : Given a time series of data . There are raw data equidistant in time. It forms a sequence of vectors through defined by . Here, is an integer representing the length of the data. Define the embedding distance [249] between vectors and as the maximum difference in their respective scalar components. Then use to construct, for each , (number of . Here,
| (94) |
where is a positive real number which specifies a filtering level. Based on the , the is defined as
| (95) |
For fixed and , Eq. (95) becomes
| (96) |
In particular, given data points, the statistic formula is implemented
| (97) |
One should note that a similar entropy, called Eckmann–Ruelle (E-R) entropy [244], has been defined as,
| (98) |
Despite their algorithms being very similar, is not intended to be an approximate value of the – entropy. Compared to the –, – and entropy, has the following advantages [250]: (i) Less affected by noise; (ii) It is robust to outliers; (iii) Lower computational demand, with good confidence; (iv) is finite for stochastic, noisy deterministic and composite processes; (v) Increasing corresponds to intuitively increasing process complexity. has been applied to classify the electroencephalogram (EEG) in psychiatric diseases, such as schizophrenia [251], epilepsy [252], and addiction [253].
SampEn
Motivated by the concept of , Richman and Moorman developed the sample entropy () to assess the complexity of physiological time-series signals, diagnosing diseased states [254]. is a modification of , but has three advantages: (i) agrees much better than statistics with the theory for random numbers having known probabilistic character over a broad range of operating conditions; (ii) maintains relative consistency and (iii) has a residual bias for very short record lengths.
Definition of : Similar to the definition of : given a time series of points, forms the vectors for , where is the vector of data points from to . The distance between two vectors is , the maximum difference of their corresponding scalar components. Let be the number of vectors within of and let be the number of vectors within of . Here represents the tolerance for accepting matches. It is convenient to set the tolerance as , the standard deviation of the dataset. Then the sample entropy is defined as:
| (99) |
It is clear that will always be smaller or equal to . Therefore, will be always either zero or positive. A smaller value of indicates more self-similarity in the dataset or less noise [254]. Note that the parameters , , and must be fixed for each calculation.
SysSampEn
One limitation of the aforementioned entropy is that it can only be applied to univariate or bivariate time series (cross-ApEn) [254]. For a complex system with multivariate time series and spatial–temporal structures, Meng et al. proposed the so called and applied it to study the climate system. Based on the , they could measure the complexity (disorder) of a system composed of temperature anomaly time series and forecast the magnitude of an El Niño event with a prediction horizon of year and high accuracy [241].
Definition of : Given interdependent time series of length composing the system:
-
1.
We select sub-records of length , starting at each th data point, i.e., starting at , as long as . Thus a specific sub-sequence is denoted as . Then we select sub-sequences from each time series and construct a set of template vectors from the system, i.e., . We assume that two vectors are close (similar) if their Euclidean distance (if , then ), where and are the standard deviations of the time series and respectively. defines the similarity criterion and is a nonzero constant.
-
2.
To examine the probability that two time series, which are close at data points, still will be close at the next data points, we construct analogously another set by selecting sub-records of length . To make the number of template vectors of length equal to that of length , we choose . In order to reduce the parameter degrees of freedom and save calculation time, we take , then . We assume that two template vectors from the set are close if (if , then ).
-
3.The of the system is defined as
where is the number of close vector pairs from the set , is the number of close vector pairs from the set , and , is the number of days that is used in the calculation of the .(100)
Note that, when , , and , the is equivalent to the classical [254]. Appropriate parameter values have to be identified since only certain value combinations can be used to estimate a system’s complexity with considerable accuracy. In order to achieve this, Meng et al. introduced two tests [241]: Spatial asynchrony test and temporal disorder test. The was calculated for the climate system composed of the near surface air or sea surface temperature anomaly time series in the Niño 3.4 region. It was found that a strong positive correlation between the El Niño magnitudes and the values of its previous calendar year exists (Fig. 15A,B). Fig. 15C demonstrates the calculation of the accuracy level, which allows to choose effective parameter combinations.
Fig. 15.
Correlation between SysSampEn and El Niño magnitude.
Reprinted figure from Ref. [241].
In addition, to reveal the mathematical meaning of the , Fig. 16 shows the logistic map as an example of applying the to estimate the system complexity and compare it with the Lyapunov exponents. It is found that higher (lower) values of the are strongly associated with higher (lower) Lyapunov exponents, which indicates that the can well capture the complexity of the system.
Fig. 16.
One logistic map example ofthat gives accurate estimation of the system complexity, i.e., higher values of theindicate higher complexity of the system. For each system, time series are generated from the logistic equation with the same value of , but for different initial conditions .
Reprinted figure from Ref. [241].
3. Applications
3.1. Climate system
The Earth’s Climate System is a highly complex and interactive system as defined by the Global Atmospheric Research Programme (GARP) of the World Meteorological Organization (WMO) in 1975, as being composed of five major components: the atmosphere, the hydrosphere, the cryosphere, the land surface and the biosphere. And in 1992, the United Nations’ Framework Convention on Climate Change (FCCC) defined the climate system as ‘the totality of the atmosphere, hydrosphere, biosphere and geosphere and their interactions’. Fig. 17 shows a schematic representation of the most important components of the climate system and their potential changes. The atmosphere is the gaseous envelope surrounding the solid planet and provides oxygen to most animal life at the Earth’s surface. It is the most unstable and rapidly changing component. Currently, the atmosphere is made up primarily of nitrogen (78.1%) and oxygen (20.9%). There are also a number of trace gases that cause of great concern for the future of the planet, including carbon dioxide (), methane () and ozone (). They are referred to as greenhouse gases (GHGs) and, along with water vapor, provide the Earth with the greenhouse effect. Their effect is to keep our Earth warm, but not too warm. The hydrosphere is the water on a planet, including oceans, seas, rivers, lakes and underground water. The cryosphere is the portion of the Earth’s surface where water is in solid form, consisting of land ice (including ice shelves and glaciers), snow and sea ice. It impacts the climate system greatly through its high albedo. Variations in the volume of the ice sheets are regarded as one of the major factors for sea level rise. Land Surface, i.e., the “solid” Earth, creates the distribution of continents, ocean basins, mountain ranges, etc. It influences the transformation of short-wave to long-wave radiation, reflectivity of the Earth’s surface, reservoir of dust, transfer of momentum and energy of the land surface. The biosphere is the total sum of all living things on the planet, including the organic cover of the land masses (vegetation, soil) and marine organisms. It plays a vital role in exchanging of carbon between the different reservoirs, such as the concentration of in the atmosphere, as well as the balances of other gases [255]. There are numerous interactions between the components, by exchanging mass, heat and momentum. For instance, the ocean–atmosphere interaction is a strongly-coupled system exchanging water vapor and heat through evaporation, among others. Each climate system component operates on a rather broad of characteristic temporal and spatial scales. Note that the climate system itself is often considered as part of the broader Earth System [2].
Fig. 17.
Schematic view of the most important components and associated processes of the climate system on a global scale .
Figure is from the IPCC’s Fourth Assessment Report (AR4) [255].
© 2020 IPCC. Reproduced with permission.
A fundamental factor in climate science analyses is the climate data, which provides information on changes in the Earth’s ecosystem and supplies decision makers with a reliable knowledge base on the climate crisis and its impact. In general, there are two data collection methods to gather quantitative and qualitative climate data (also briefly discussed in Section 1.1): observations (instrumental, proxies and reanalysis) and climate models simulations. Observational data of the climate system are based on direct measurements and remote sensing from satellites, radar and other platforms. The first meteorological stations were established in Europe and North America. Global-scale observations in the instrumental era began in the mid-19th century for temperature and other climatic variables. The increase and quality of the network of observations and the technology supporting the collection and storage of data have rapidly evolved form 1950 onwards. Paleoclimate reconstructions extend some proxy records back hundreds to millions of years, including coral records [10], [256], tree rings records [13] for the last few millennia, as well as stalagmite time series [12], Central-Mediterranean sediment [11] and ice-core records [257].
Climate studies require data of consistent spatial resolution and accuracy over long time intervals. To satisfy this goal, some numerical weather prediction centers have started to produce so-called reanalyses that are obtained by subtle data assimilation techniques which efficiently combine observational and numerical data. For example, the European Centre for Medium-range Weather Forecasts (ECMWF) [258] provides the following reanalysis datasets: ERA5, ERA-Interim, CERA-SAT, CERA-20C, ERA-20CM, ERA-40, ERA-20C and so on.4 The NCEP-NCAR Reanalysis I/II, 20th Century Reanalysis and North American Regional Reanalysis (NARR)5 are produced in collaboration by the U.S. National Centers for Environmental Prediction (NCEP) and the National Center for Atmospheric Research (NCAR) [259]. The JRA-25 and JRA-55 reanalysis6 are produced by the Japan Meteorological Agency (JMA) [260], [261]. Note that most climatic variables or fields in these reanalysis data agree very well with observed data, such as the geopotential fields over the continents of the Northern Hemisphere. However, substantial differences persist in some fields over the Southern Hemisphere or those that are poorly observed [262], [263], [264], [265], [266]. More details are summarized in Ref. [267].
Climate models are considered as the primary tools available for investigating the response of the climate system to various forcings, for making climate predictions on seasonal to decadal time scales and for making projections of future climate over the coming century and beyond. Climate models could be defined as a mathematical representation of the climate system based on physical, chemical and biological principles. The models used in climate research range from simple energy balance models to complex Earth System Models (ESMs), which can be slow and costly to use, even on high-performance computers, and the results can only be approximations [17]. Here, we provide a brief overview of the basic types of climate models: (i) Energy balance models propose a highly simplified version of the dynamic of the climate system. They are zero- or one-dimensional models describing the surface temperature as a function of the energy balance of the Earth, where the number of dimensions, from zero to three, refers to the number of independent space variables used in the model domain. For instance, the global mean surface temperature can be expressed as:
| (101) |
Here and are the absorbed shortwave radiation and outgoing longwave radiation. is the heat capacity of Earth system, in units of , is the planetary albedo, is the transmissivity of the atmosphere, a number less than 1 that represents the greenhouse effect of the Earth’s atmosphere, is the Stefan–Boltzmann constant, is an insolation parameter equal to unity for present-day conditions. (ii) Atmosphere–Ocean General Circulation Models (AOGCMs) are the most comprehensive standard climate models that are assessed in the IPCC Fourth Assessment Report (AR). They are used to understand the dynamics of the physical components of the climate system (such as, atmosphere, ocean, land and sea ice), and for making projections based on future GHGs and aerosol forcing. (iii) Earth System Models (ESMs) are the current state-of-the-art models, and they expand on AOGCMs by including representation of various biogeochemical cycles such as those involved in the carbon cycle, the sulfur cycle, or ozone. These models provide the most comprehensive tools available for simulating the past and future response of the climate system to external forcing, in which biogeochemical feedbacks play an important role. (iv) Regional Climate Models RCMs are limited-area models with representations of climate processes comparable to those in the atmospheric and land surface components of AOGCMs, though typically run without interactive ocean and sea ice. RCMs are often used to dynamically ‘downscale’ global model simulations for some particular geographical region to provide more detailed information. In addition, based on the GCMs, the Intermediate Complexity models were developed to investigate the Earth systems on long timescales or at a reduced computational cost [20]. A special application is to achieve reliable predictions of extreme events on a sub-seasonal scale.
Taken together, climate models provide a comprehensive view of the variability and long-term changes in the climate systems. However, assessing and forecasting climate extreme events, such as El Niño events and extreme rainfall, still poses challenges. The difficulties are mainly due to the intrinsically rare and disruptive natural conditions. They are strongly influenced by weather patterns, modes of variability, thermodynamic processes and various feedbacks. In the following, we will provide an in-depth and detailed description of how the statistical physics methodologies introduced in Section 2 can be applied to investigate and (or) predict various climate phenomena, such as El Niño–Southern Oscillation (ENSO), Indian Summer Monsoon (ISM), Extreme Rainfall, Atmospheric Circulation and Atlantic Meridional Overturning Circulation (AMOC).
3.1.1. El Niño–Southern Oscillation
One of the most important climate phenomena on year-to-year time scales is the El Niño Southern Oscillation (ENSO). As mentioned in Section 2.3, ENSO can be regarded as a tipping element of the Earth system. El Niño is the warm phase of the ENSO and is associated with a band of warm ocean water that develops in the central and east-central equatorial Pacific, sometimes called El Niño basin [44]. The cool phase of ENSO is called La Niña, with SSTs in the eastern Pacific below average. ENSO significantly impacts Earth’s ecosystems and human societies, by influencing temperatures and precipitation around the globe, including the Americas, India and surrounding tropical continents [268], [269], [270]. These remote effects are known as teleconnections [271].
Definition of El Niño: In this review, we use the Oceanic Niño Index (ONI) to define and distinguish the El Niñoand La Niña events. The ONI is one of the primary indices used to monitor the ONI. It is calculated by 3-month running mean SST anomalies (based on centered 30-year base periods updated every 5 years) in an area of the east-central equatorial Pacific Ocean, which is called the Niño 3.4 region (5°S to 5°N; 170°W to 120°W), see the Niño regions presented in Fig. 18. If the ONI °C for at least five consecutive months, then the event is defined as an El Niño; whereas, when ONI is °C for at least five consecutive months, the corresponding event is regarded as a La Niña. The ONI is use for the operational definition of the ENSO phase by NOAA.7 There are also some other indices to measure the El Niño events, such as, Niño 1+ 2, 3, 3.4, 4 and Trans-Niño indexes.8 Besides the SST, ENSO also influences other climate variables like atmospheric pressure gradients, upper ocean currents and the thermocline depth [272].
Fig. 18.
Niño Regions. The Niño 3.4 region (5°S to 5°N; 170°W to 120°W); The Niño 4 region (5°S to 5°N; 160°E to 150°W); The Niño 3 region (5°S to 5°N; 150°W to 90°W); The Niño 1+ 2 region (10°S to 0 °; 90°W to 80°W).
Figure is from NOAA.
ENSO transition mechanism in brief: In the following, we will describe the physical mechanism of ENSO. Bjerknes first postulated that the ocean–atmosphere interaction is essential for ENSO and is now referred to as the Bjerknes feedback [273]. This positive feedback mechanism is understood to be a prominent mechanism necessary for the development of ENSO. Consider an initial SST anomaly in the central/eastern tropical Pacific. This anomaly reduces the east–west SST gradient and hence weakens the Walker circulation [274], resulting in a westerly wind anomaly. The westerly wind anomaly, in turn, drives the ocean circulation change (easterly winds shoal the equatorial thermocline and induce upwelling in the eastern Pacific, keeping the east cool) that further reinforces the SST anomaly. As a result of the positive feedback, the tropical Pacific reaches a warm state, i.e., El Niño. Tziperman and Yu pointed out that the westerly wind bursts, while partially stochastic, seem an inherent part of the large-scale deterministic ENSO dynamics [275].
Besides the positive Bjerknes feedback, the oscillatory nature of ENSO requires a negative feedback to turn the coupled ocean–atmosphere system from a warm (El Niño) phase to a cold (La Niña) phase. Different negative feedbacks have been proposed since the 1980s associated with the delayed oscillator, the western Pacific oscillator, the recharge–discharge oscillator, and the advective–reflectiveoscillator. The delayed oscillator is a mechanism for the oscillatory nature of ENSO, which was proposed by McCreary based on the Rossby wave reflection at the ocean western boundary [276]. Suarez and Schopf introduced the delayed oscillator explaining the oscillatory feature of ENSO to emphasize the delayed effects of oceanic wave reflection at the ocean western boundary [277]. Cane and Zebiak developed the first coupled ocean–atmosphere model, and used it to predict ENSO [278], [279]. The conceptual delayed oscillator model is represented as follows:
| (102) |
where represents the SST anomaly in the equatorial eastern Pacific, and are constants. The first term on the right hand side of Eq. (102) stands for the Bjerknes positive feedback between the ocean and the atmosphere. The second term represents the delayed negative feedback of wave reflection at the ocean western boundary. The last term is a cubic damping term. It has been found that the delayed oscillator overlooks the role of the ocean–atmosphere interaction in the western Pacific and also assumes that wave reflection at the ocean eastern boundary is not important [280].
Since the delayed oscillator does not consider the western-Pacific anomaly pattern, Weisberg and Wang [281] developed a western-Pacific oscillator model for ENSO. This model stresses that the equatorial wind anomalies in the far western Pacific play an important role in the evolution of ENSO. The western-Pacific oscillator model is represented as:
| (103) |
| (104) |
| (105) |
| (106) |
| (107) |
where is the SST anomaly in the equatorial eastern Pacific, is the thermocline-depth anomaly in the off-equatorial western Pacific, and and are the equatorial zonal wind-stress anomalies in the central Pacific and the western Pacific, respectively. All model parameters are constants.
It has been found that the growth and decrease in sea level over the western Pacific Ocean are related to ENSO [282]. Based on these ideas Jin [283], [284] developed a recharge–discharge oscillator model for ENSO that is represented by:
| (108) |
| (109) |
where is the SST anomaly in the equatorial eastern Pacific and is the thermocline-depth anomaly in the equatorial western Pacific. The model parameters and are constants. In particular, Eqs. (108), (109) represent the discharge and recharge of tropical Pacific Ocean heat content.
Picaut et al. [285] proposed a conceptual model of the advective–reflective oscillator for ENSO. They found that the positive feedback results from ocean zonal currents that advect the western-Pacific warm pool (WPWP) towards the east. There are three negative feedbacks that tend to push the WPWP back to the western Pacific, include: (i) anomalous zonal current associated with wave reflection at the ocean western boundary, (ii) anomalous zonal current associated with wave reflection at the ocean eastern boundary and (iii) mean zonal current converging at the WPWP’s eastern edge. Unlike the other three oscillator models, the advective–reflective oscillator model does not have a set of simple and heuristic equations. Instead, they used a linear wind-forced ocean numerical model forced by wind anomalies, which were associated with the zonal current of the first baroclinic Kelvin and first meridional Rossby waves [195].
Moreover, based on the dynamics and thermodynamics of Zebiak and Cane’s coupled model, as well as all previous ENSO oscillator models, Wang [286] developed a unified ENSO oscillator ocean–atmosphere model with the hypothesis that ENSO may be a multi-mechanism phenomenon and their relative importance may depend on time. The unified ENSO oscillator model is formulated as:
| (110) |
| (111) |
| (112) |
| (113) |
where and are variables that stand for the SST anomalies in the equatorial eastern Pacific, the thermocline-depth anomalies in the off-equatorial western Pacific, the zonal wind-stress anomalies in the equatorial central Pacific and the zonal wind-stress anomalies in the equatorial western Pacific, respectively. For a given set of parameters, Eqs. (110)–(113) can oscillate on interannual time scales.
El Niño forecasting:
Since the 1990s, both dynamical and statistical models have been used to model and forecast El Niño events, providing the society the opportunity to prepare for associated hazards such as heavy rains, floods and droughts [287], [288]. Although there are about 17 dynamic and 8 statistical models in CPC/IRI currently providing ENSO forecasts routinely, high prediction skill is generally limited to about six months ahead, see the description in Fig. 19. The reason is the presence of the so-called “spring predictability barrier” (SPB), where errors are greatly amplified due to the coupled feedbacks in the equatorial ocean–atmosphere system [289], [290]. After the spring, the ability of the models to predict successfully becomes increasingly better.
Fig. 19.
Spring Predictability Barrier. The El Niño forecasting skill of models based on February–October observations to predict the November–January average value in the El Niño-3.4 region (see Fig. 18). Results are an average correlation coefficient from 20 models between 2002–2011.
Figure is from NOAA.
In general, a poor skill in forecasts can be divided into two categories: imperfections in the forecast system (including, error in model parameterization of sub-grid-scale motions, the relative scarcity of points with data, errors in the measurement of the data), and fundamental limits of predictability [272]. The fundamental limits are usually coming from the complex and chaotic nature of a system.
To overcome the limits of the SPB in El Niño forecasting, several CN-based approached were developed. For example, by analyzing the CN, Ludescher et al. found that a large-scale cooperative mode exists one calendar year before the warming event, linking the El Niño region and the rest of the ocean [291]. This mode is probably due to the emergence of El Niño acting as an autonomous component in the CN [61]. All nodes used in the CN are shown in Fig. 20a, where the 14 grid points in the El Niño basin [61] are in red and outside this domain there are 193 grid point in blue. The data is the daily surface air temperature (SAT) from NCEP/NCAR reanalysis I. As described in Section 2, the first step is to remove the seasonal trend by minus climatological average for each calendar day. And then, the links between the El Niño basin and outside (see Fig. 20a) are considered. The strength of each link is computed according to Eq. (15). The mean strength of the dynamical links in the CN is obtained by simply averaging over all individual link strengths. Fig. 20b, shows the time evolution of for the learning (top) and forecasting (bottom) phases. They found that before an El Niño event, tends to increase. They marked an alarm when crosses a threshold (see Fig. 20b). The prediction accuracy, through Receiver Operating Characteristic (ROC)-type analysis (explained later), is much better than the 12-months forecasts based on climate models. Based on these findings regarding the temporal evolution of the CN, Ludescher et al. successfully predicted the onset of the 2014–2016 El Niño event [292].
Fig. 20.
Climate Network and El Niño forecasting algorithm. a. The nodes in CN. Each node inside the El Niño basin (solid red symbols) is linked to each node outside the basin (open blue symbols). The red rectangle denotes the Niño 3.4 region. b. The red curve is the average link weight of the CN, the horizontal line indicates the decision threshold , and the blue areas show the El Niño events. When crosses the threshold from below, an alarm is given that an El Niño event will start in the following calendar year.
Reprinted figure from Ref. [291].
Motivated by this work, Meng et al. developed a multidisciplinary approach combining climate, network, and percolation theory to predict the onset of El Niño [65]. Their method can forecast El Niño events 1 year-ahead, with a high prediction accuracy of 70%, and a low false alarm of only 4%. Different from [291], they consider the global CN with initially isolated nodes. Links are added one by one according to the link strength, i.e., first adding the link with the highest weight, and continue selecting links ordered by decreasing weight. During the evolution of the CN, they found that the structure of the network changes violently approximately one year ahead of El Niño events, and thus suggest to use the largest size change of the largest cluster (percolation cluster) [see Eq. (48)] as a percolation-based precursor, to forecast El Niño events. In addition, based on finite size scaling analysis, they found that the percolation process is discontinuous.
To forecast both the onset and magnitude of El Niño events, another sophisticated network-based approach was developed by Meng et al. [66]. They proposed a new forecasting index based on CN links representing the similarity of low frequency temporal temperature anomaly variations between different sites in the Niño 3.4 region. They found that significant upward trends in the index forecast the onset of El Niño approximately 1 year ahead, and the highest peak since the end of last El Niño forecasts the magnitude of the following event. Their index was also tested on several datasets, including ERA-Interim, NCEP Reanalysis I, PCMDI-AMIP 1.1.3 and ERSST.v5. They defined the degree of coherence/disorder of the Niño 3.4 region as,
| (114) |
where is the number of nodes in the Niño 3.4 region and stands for the max value of the time-delayed cross-correlation function, see Eqs. (12), (13). The forecasting index (FI) was proposed as a function of time (months),
| (115) |
where indicates that the average of includes the current month, while is the total number of months preceding since Jan. 1981. We show the time evolution of the FI and ONI in Fig. 21 by using the ERA-Interim dataset. Based on the temporal evolution of the FI, they successfully predicted the onset of the 2018–2019 El Niño event, see the purple star above the purple arrow in Fig. 21b.
Fig. 21.
The El Niño forecasting algorithm. a. The red curve is the forecasting index defined in Eq. (115), the blue line stands for the ONI. The horizontal black dashed line indicates , and the blue shades under the ONI curve indicate the El Niño periods. True positive forecasts are marked by the green arrows, while false alarms are marked in black dashed arrows. The purple arrow is the alarm for 2018–2019 El Niño event. b. A detailed view of and the ONI since May 2012.
Reprinted figure from Ref. [66].
Note that one can use the peak of the FI to predict the magnitude of the following El Niño event. This peak value is determined from the end of the last event to the start of a new event, which means that we should wait until the new event begins to occur. To further improve the forecasting skill, in particular, the magnitude forecasting with a long lead time. Meng et al. [241] developed the SysSampEn method, see more details in Section 2.4.5. It is defined in Eq. (100) and shown in Fig. 15a. The correlation between the magnitude of the El Niño events and the SysSampEn can reach to [see Fig. 15b]. They further used this correlation to forecast the magnitude of an El Niño with a prediction horizon of 1 year and high accuracy (i.e., Root Mean Square Error C for the average of the individual datasets forecasts). In particular, for the 2018–2019 El Niño event, they forecasted a weak El Niño with a magnitude of C, compared to the observed value C.
Recently, Feng et al. combined machine learning techniques and climate networks to apply to El Niño predictions, especially for the occurrence of El Niño events and the development of the NINO 3.4 index over time [293]. In Ref. [294], Petersik and Dijkstra applied Gaussian density neural network and quantile regression neural network ensembles to predict ENSO. Classical machine learning models for prediction usually only predict a point value, e.g., the ONI. In contrast, their models forecast directly a probability distribution for the ONI. In particular, they found that their machine learning models have a high-correlation skill () for long lead times (12 months ahead) for an evaluation period between 1963 and 2017. In Ref. [295], Ham, Kim and Luo used transfer learning to train a convolutional neural network on historical simulations and reanalysis, and developed the heat map analyses. They found that a statistical forecast model employing a deep-learning approach produces skillful ENSO forecasts for lead times of up to one and a half years. A review of ENSO prediction based on modern machine learning and artificial neural networks was reported in Ref. [296].
ENSO remote impacts: teleconnections
As introduced above, the ENSO phenomenon mainly lies in the Pacific ocean. However, its effects are felt over a large part of the Earth. These remote effects are usually called teleconnections, emphasizing that changing climatic conditions in one place can affect areas far from the source [271], [297]. A teleconnection is usually indicated by the correlation between the values observed at two separate locations or regions. It is related to a pattern of variability, associated with atmospheric wave propagation, the presence of ocean currents, etc. For example, the teleconnections associated with the North Atlantic Oscillation (NAO) and ENSO are main examples of long-range correlations that can be found in the atmosphere. Because of those global teleconnections, El Niño leads to higher precipitation in the central Pacific and dry conditions over Indonesia and Northern Australia, much drier and warmer conditions in Mozambique, while the western USA tends to be wetter. Fig. 22 shows weather patterns statistically associated with El Niño conditions during the boreal winter months December–January–February. The regions that have been shown with some degree of reliability to be affected by warm ENSO phases are highlighted, for example, warm-vs.-cold and wet-vs.-dry anomalies. The effects for cold phases of ENSO, La Niña, are in approximately the same regions, but with the opposite sign.
Fig. 22.
El Niño remote impacts: teleconnections, during the boreal winter months December–January–February. Regions with statistically reliable relation of precipitation and surface air temperature to a warm ENSO episode.
Figure is reproduced with permission from NOAA.
The basic mechanism of ENSO remote influences are produced in the atmosphere via large-scale atmospheric waves, such as Rossby waves. Rossby waves are fundamental for the understanding of weather systems in the atmosphere and the large-scale circulation in the ocean. They depend fundamentally upon the variation of the Coriolis parameter with latitude. In the so called -plain approximation, the Coriolis parameter varies linearly with latitude where
| (116) |
where is the latitude, is the angular speed of the Earth’s rotation, and is the mean radius of the Earth. The wavelength of atmospheric Rossby wave is about km. The atmospheric wave dynamics are akin to those observed in the ocean for ENSO in that they involve a transfer of atmospheric mass by anomalous winds, which in turn affect pressure and winds.
In order to assess if a region has an ENSO connection, Fan et al. applied the Pearson correlation CNs approach to investigate the global remote impacts of El Niño and La Niña [64]. They refer to the Niño 3.4 region as the El Niño Basin (ENB). The CNs were constructed by using only directed links from the ENB to regions outside the ENB (“in”-links) based on the global daily SAT fields of the NCEP/NCAR reanalysis and EAR-Interim datasets. The links’ strengths are computed according to Eqs. (12), (13), (15). They identified the value of the highest peak of the absolute value of the cross-correlation function and denote the corresponding time lag as . The adjacency matrix of a CN became
| (117) |
where is the Heaviside step function for which and . The “in” and “out” degrees of each node are defined as , respectively, quantifying the number of links into a node or out from a node. The total “in” weights for each node outside the ENB using are defined as
| (118) |
The values of and reflect the impacts of the ENB. Specifically, if there are no “in” links for a node, both the “in” degree and “in” weights are zero, indicating no impact of ENB. Based on the ONI, the time is divided into El Niño , La Niña and normal years. The “in”-weighted degree fields for El Niño and La Niña are calculated by taking the average of the same type of events
| (119) |
where , and “EY” and “LY” refer to the years in which El Niño and La Niña start. The number of nodes with zero in-degree is defined as and the average in-weights per node is
| (120) |
Fig. 23(a–d) shows that, the affected regions by El Niño and La Niña, are characterized by relatively high in-weights (using and ). For comparison, mean winter (Dec–Feb) temperature anomalies during El Niño and La Niña years are shown in Fig. 23 (e–f). A quantitative analysis of the area that is affected/unaffected during El Niño and La Niña years is shown in Fig. 24, where El Niño and La Niña years are respectively emphasized by the red and blue shading. The network analysis reveals strongly (high ) localized (low ) impacts of ENSO, i.e., these stronger in-weighted activities are found to be concentrated in very localized areas, whereas a large fraction of the globe is not influenced by the events (low means that fewer nodes are influenced).
Fig. 23.
El Niño remote impacts: Climate Networks. (a), (c) “In”-weight maps (using and ) for El Niño events. (b),(d), “In”-weight maps (using and ) for La Niña events. (e), (f) Mean winter (Dec–Feb) temperature anomalies during El Niño and La Niña.
Reprinted figure from Ref. [64].
Fig. 24.
Strongly localized impacts of ENSO. (a) The ONI as a function of time. (b) The evolution of the number of nodes that have in-links with time. (c) The evolution of the average in-weights per node with time. El Niño and La Niña periods are respectively emphasized by the red and blue shading.
Reprinted figure from Ref. [64].
Diversity of El Niño
It has been reported that there are different types of El Niño events, such as the canonical eastern Pacific (EP) and the Modoki central Pacific (CP) types [298], [299]. They are classified based on spatial patterns of the SST anomaly. For instance, the strongest SST anomalies associated with the EP types are located off the coast of South America. However, for CP types, the strongest SST anomalies are located near the International Date Line. In Ref. [300], Wiedermann et al. proposed an index based on evolving CNs to objectively discriminate different types of El Niño and La Niña episodes. In particular, they find that their network index displays a sharp peak during EP events, whereas during CP events it remains close to the observed values during normal years. Based on the CNs analysis, Lu et al. developed a new approach to estimate the impacts of El Niño events in advance, as well as predicted the types of El Niño events [301].
3.1.2. Indian summer monsoon
The Indian Summer Monsoon (ISM) is the most prominent among the world’s monsoon systems and has a decisive influence on India’s agricultural output and economy. The ISM delivers more than 70% of the country’s annual rainfall. The prediction of the ISM timing (onset date and withdrawal date) as well as the ISM rainfall is a vital issue for the Indian subcontinent and strongly affects the gross domestic product of the country, up to 22% of which is determined by agriculture [302]. A slight deviation of the timing manifested as delay (or early arrival) may lead to drastic droughts (floods). Also, swings in the amount of rainfall, even with variations of only 10%, can cause severe flooding or drought, causing damages to infrastructure and loss of crops and livelihoods of the population [303]. The onset of the ISM takes place abruptly and the long lead-time operational forecasts for the onset, withdrawal and rainfall amount have shown little skill in the recent decades.
ISM onset and withdrawal forecasting
Several statistical climate models have been developed for ISM onset and withdrawal dates forecasting with different timescales from short-range (up to 4 days), medium-range (4–10 days) [304], [305] to extended-range (10–30 days) and long-range (more than 30 days) forecasts [306]. In particular, the Indian Meteorological Department (IMD) provides a forecast of the monsoon onset 21 days in advance, with an accuracy of 4 days. Note that most of the ISM forecasting models are based on the input values, including SST, mean sea level pressure, tropospheric moisture, moist static energy, outgoing longwave radiation, wind fields, etc [307], [308], [309], [310], [311]. However, there are still impending challenges in the existing forecasting methods: (i) The false monsoon onsets mostly related to non-monsoonal atmospheric circulation systems [312]; (ii) the limitations in predicting a withdrawal data earlier than 1st September.
To overcome these challenges, Stolbova et al. proposed a novel tipping elements approach to accurately forecast the ISM onset and withdrawal dates [95]. This approach relies on the combination of two methodologies: the climate network analysis and the nonlinear dynamics. First, the analysis of the network of extreme rainfall events allows to identify and reveal the teleconnection between the most active hubs, the Eastern Ghats (EG) and North Pakistan (NP). Second, the application of the nonlinear dynamics through the analysis of fluctuations allows to detect the critical transitions, which are used to define the tipping elements of the ISM. Later, the EG and NP were chosen as optimal observation locations or reference points (RPs) to predict the ISM monsoon onset and withdrawal. It was discovered that there is a tipping point between these RPs for the SAT and relative humidity, which yields a very successful prediction scheme.
The ISM CN is focused on the monsoon region (62.5–97.5°E, 5.0–40.0°N) with a spatial resolution of 2.5 degrees, which results in grid points, see Fig. 25. The near SAT () at 1000 hPa, relative humidity () at 1000 hPa, and wind fields at 700 hPa were used. The variance of and for each grid point are firstly calculated as [95]
| (121) |
where stands for a time series, is the length of the time window, is the number of days before the onset of the ISM, is a given year, and is the onset date for the given year . The time average value of is simply expressed as
| (122) |
where stands for the total number of years. The results are shown in Fig. 25. It has been confirmed that the EG and NP regions experience the highest growth of for both and , when approaching the monsoon onset date. It has been further discovered that there exist two intersections in the RPs for the average time series during the period from 1951 to 2014. At both intersections, it coincides with the mean values of the onset and withdraw as determined by the IMD with a standard deviation of days for the EG region, see Fig. 26. Thus, this allows to derive a prediction scheme for forecasting the onset and withdrawal of the ISM in the EG, based on the trends of and in the RPs.
Fig. 25.
Pre-monsoon growth of the variance of fluctuationsdefined in Eq. (121)of the weekly mean values of near SAT. (a) 21 days, (b) 7 days, and (c) 1 day before the ISM onset in the Eastern Ghats (EG), . Composites are for the period 1958–2001 and were calculated from the ERA40 reanalysis dataset, 700 hPa winds are indicated by the blue lines. Two boxes refer to the RPs: North Pakistan, NP (blue) and EG (pink). (e) Growth of the variance of fluctuations in NP (blue), EG (pink), and averaged over the Indian subcontinent (IS) at approaching the onset date of the monsoon.
Figure from Ref. [95].
Fig. 26.
Prediction of onset date (OD) and withdrawal date (WD) of the ISM: case study 2012. Left column: prediction of the ; right column: in the Eastern Ghats (EG). (a), (c): air temperature at 1000 hPa; (b), (d) relative humidity at 1000 hPa. Time series from the reference points: 14-year mean (black) and 2012 values for North Pakistan (NP) (blue) and the EG (red). Gray lines show the time series from NP and EG for the training period of 14 years. Saturation temperature and saturation humidity are marked by horizontal black solid lines ( and calculated as the intersection of mean time series for the training period from the EG and ), and the day of the saturation (when the temperature in the EG in 2012 reaches ) by vertical dark blue lines. The orange lines indicate trends to the mean time series in and EG for the training period, light blue are the trends for 2012. Black solid lines indicate mean values of the and for the training period. Vertical dotted gray lines correspond to the predicted onset and withdrawal dates , while vertical solid gray lines are the actual onset and withdrawal dates for .
Figure from Ref. [95].
Next, a linear trend estimation for the two RPs is performed and compared with the trends of the mean time series of the training period (1951–1965). The slopes of the trends for the RPs provided an estimation of an early, normal, or late monsoon arrival: a greater than average slope of will lead to an earlier than usual onset, and vice versa. Trends of in the RPs in comparison with the average trends for the training period add up to the predictability of the onset: higher than average values of the relative humidity lead to a late onset, and vice versa.
It has also been found that the ISM onset coincides with the date when in the EG and in NP become equal (see Fig. 26a). Therefore, for the forecasting of the onset, one should predict when for the EG will abruptly decrease and intersect for NP. Finally, the prediction scheme of the withdrawal is based on the symmetry of changes in NP during the year. The withdrawal is estimated as the intersection of the projected decrease in NP and the in the EG during the monsoon season (see Fig. 26c).
The prediction is regarded as successful if the time difference between the predicted onset and the real one is days for the onset and days for the withdrawal [95]. The proposed scheme using results in 74% successful predictions of the onset when made on day 125 of the year (April 10). The prediction scheme for the withdrawal succeeds in 84% of the years when made on day 205 (July 25). Based on this prediction scheme, they successfully predicted both the onset and withdrawal since 2016 in the EG region.9
ISM rainfall forecasting
The ISM is one of the most prominent monsoon systems. It affects the Indian subcontinent, where it is one of the oldest and most anticipated weather phenomena. Several theories have been proposed to explain the underlying mechanism of the monsoon. For example, the sea breeze theory: because of the differences in the specific heat capacity of land and water, continents heat up faster than seas. Consequently, the air above coastal lands heats up faster than the air above seas. These create areas of low air pressure above coastal lands compared with pressure over the seas, resulting moisture-laden winds to flow from the seas onto the lands. On reaching land, these winds rise because of the geographical relief, cooling adiabatically and leading to orographic rains. However, the understanding and predictability of ISM are still evolving.
The All India Rainfall Index (AIRI) is the total amount of ISM June-to-September rainfall averaged over the entire Indian subcontinent. It is the IMD’s primary indicator for monitoring the ISM rainfall [313]. An accurate long-term prediction of the ISMR is crucial for taking timely actions and mitigation activities. Over the last few decades, great efforts have been undertaken to understand the basic physics of the monsoon, and to improve the prediction skill for the AIRI [314], [315], [316], [317], [318], [319], [320]. However, both methods have the challenge of unstable relationships with the predictors over time, as observed during the recent years due to a weakened coupling between the boundary forcing and the Indian monsoon [321], [322]. In particular, the forecasting skill (cross correlation) of the official operational forecasts made by IMD statistical models is −0.12 for 1989–2012, for the five ENSEMBLE models’ multi-model ensemble is 0.09 and the four APCC/CliPAS models’ MME skill is 0.24 after 1989. It was discovered that the recent failure is largely due to the models’ inability to capture new predictability sources emerging during the recent global warming [303].
Traditionally, the April–May SST anomaly in the Niño 3 or Niño 3.4 region was used as a predictor for the ISMR prediction. This is since the ISMR variations are primarily driven by the EP-ENSO through tropical teleconnections [314], [315]. This inverse relationship between the AIRI and EP-ENSO, however, has weakened in recent decades [270]. It has been found that the CP-ENSO has also distinct teleconnections and affects on the ISMR [324]. Based on this physical mechanism, Wang et al. [303] proposed four physical–empirical AIRI predictors, EP-ENSO predictor (EPT), CP-ENSO predictor (CPT), mega-ENSO predictor (PSH) and Anomalous Asian Low (NAT). The EPT is defined as: May minus March east–west SST dipole tendency: (20°S-5°N, 150°E–170°E) minus DSST (10°S–10°N, 110°W–80°W); the CPT is defined as: May minus April SST north–south dipole tendency: (10 °–25°S, 170°E–160°W) minus DSST (5°–20°N, 180 °–150°W); the PSH is defined as: April–May mean SLP averaged over (40 °S–10°S, 160°W–90°W) and (10°N–30°N, 180°–130°W); the NAT is defined as: May minus March SLP averaged over (45°N–60°N, 95°E–125°E). means the difference of the SST between May and March (May minus March). means the difference of SST between May and April (May minus April). These predictors (EPT) produce an independent forecast skill of 0.51 for 1989–2012 and a 92-year retrospective forecast skill of 0.64 for 1921–2012. However, the forecasting lead-time for this model is quite short, i.e., starting from May (one month lead-time) or June (IMD’s operational model).
In order to achieve the goal of a long-term and reliable prediction of the ISM rainfall, Fan et al. constructed a series of dynamical and physical CNs based on the global near SAT field [323]. It was uncovered that some characteristics of the directed and weighted CNs can serve as efficient long-term predictors for ISM rainfall forecasting. The developed prediction method produces a forecast skill of 0.5 with a 5-month lead-time in advance by using the previous calendar year’s data. The skill of the forecasting, is comparable to the current state-of-the-art models, however, with quite a short (i.e., within one month) lead-time. The new network-based prediction approach is described as follows.
CN construction: Based on the NCEP/NCAR reanalysis daily SAT anomalies data, a CN is constructed for each calendar year from 1948 to the present. In the work, 726 nodes are selected, such that the globe is covered approximately homogeneously [61]. The link strength and direction are determined based on a similarity measure between the temperature anomaly time series of the nodes [see Eqs. (12)–(16)]. A pair of nodes is defined to be connected only if their link is within the top 5% positive strength, which is also corresponding to a statistical significance of above the 95% confidence level.
Network Predictors Mining: To mine the dynamic network predictors for the AIRI, the cross correlation between the observed AIRI and the time series of network in-degree [see Eq. (6)] for each node on the globe is calculated. Because the forecasting skill of the AIRI became very poor in the IMD operational forecasts and other models since the year 1989 [303], the record is divided into two consecutive periods, i.e., (i) 1950–1988, as the training period and (ii) 1989–2018, as the retrospective forecast period. For the training period, the correlation coefficients are shown in Fig. 27a. It was found that the in-degree index for some nodes captures well the behavior of the AIRI. Particularly, the node (in the region marked by a yellow box in Fig. 27a) having the maximal correlation is located in the South Atlantic ocean [(30°S, 30°W)]. Fig. 27b shows that the value of this maximal correlation is , with a student t-test significance of . Therefore, the in-degree index of this key node is regarded as the optimized network predictor for the AIRI.
Fig. 27.
Schematic of ISM rainfall forecasting based on climate networks. (a) The correlation coefficients between observed AIRI and in-degree time series during the training period for all nodes. (b) Scatter plots of the observed AIRI versus the optimized network predictor (i.e., the in-degree time series of the key node in the yellow box) in the training period. (c) Scatter plots of the observed AIRI versus the predicted AIRI during the forecast period 1989–2018. (d) Teleconnection path between the key node in South Atlantic and Indian subcontinent. Black in panel (a) represent the regions with correlations significant at the 95% confidence level (Student’s t-test). The recent five years are highlighted in red in panel (c). The colors and gray arrows depict the magnitudes and directions of the 850 hPa winds on 12th August 2014 during the Indian summer monsoon season in panel (d).
Reprinted figure from Ref. [323].
AIRI Forecasting: Next, the forecasting capability of the network predictor during the period 1989–2018 is tested. To obtain the forecasted value of the AIRI for one specific year, the forecasted year’s predictor value (i.e., the previous year’s network in-degree of the key node) is substituted into the least square linear regression equation. This equation used for prediction is derived using only the past information. The independent forecast skill for the period 1989–2018 becomes then , which is significantly higher than the IMD operational forecast skill [see Fig. 27c]. The result indicates the good accuracy of the network-based predictor with the long lead-time of 5 months. Finally, based on 2018’s data, the AIRI for 2019 is forecasted as 949.87 mm, a 7% departure percentage compared to10 the long-term average, which is 887.5 mm. The actual value of the AIRI for 2019 was 968.3 mm.
In the following, a potential physical mechanism is discussed. From a meteorological perspective, the teleconnection between the key node’s location in the mid-latitude of the South West Atlantic Ocean and the Indian subcontinent is no coincidence. The orography of the Eastern coast of the South American continent is prone to the formation of an anticyclone at mid-latitude due to the interaction with mid-latitude Westerlies (winds that blow from the west at the surface level between 30°and 60°S). Moreover, there is the influence of the South polar jet stream, which appears within the upper air Westerlies. The acceleration/deceleration of the South polar jet stream induces areas of low/high pressure, respectively, which links to the formation of cyclones and anticyclones. Because the South polar jet stream strengthens and weakens seasonally, and from year to year, it synchronizes with the variability in the strength of the circulation centered around the location of the key node. One of the possible data-based teleconnection paths is shown in Fig. 27d. Hence, the key node location is sort of the nexus of the South Atlantic circulation, the south polar jet stream and the main atmospheric circulations patterns over the Indian Ocean. It explains why we observe a significant correlation between the network characteristics of the key node and the AIRI.
Further analyses are performed and reveal that the physical mechanisms are related to (i) the network delayed ENSO teleconnection, i.e., the in-degree index is locally minimized in the previous calendar year of the El Niño onset. (ii) The ENSO-Monsoon teleconnection [270], [325], [326], i.e., the AIRI anomaly and the Niño 3.4 SST anomaly index are negatively correlated. The spatial correlation maps between the Niño 3.4 SST anomaly index with both the SST as well as the rainfall index for all nodes are presented in Fig. 28. These results indicate that the Niño 3.4 SST anomaly index is significantly anti-correlated with the SST in the equatorial Indian ocean and also heavily influences the rainfall pattern over the Indian land region.
Fig. 28.
Physical mechanisms of ISM rainfall forecasting. Correlation between the seasonal mean (Jun–Sep) Niño 3.4 SST and (a) SSTs (b) rainfall at each grid point. Statistically significant (95% confidence level) correlations are stippled.
Reprinted figure from Ref. [323].
Moreover, the network-based approach can be also successfully applied to forecast the Indian homogeneous region rainfall as a prediction scheme, including two specific homogeneous regions [323]: (1) the Central India Rainfall Index; (2) the East & Northeast India Rainfall Index.
In addition, there is solid evidence which reveals that climate change affects the forecast skills. The considerable warming trend in the last 70 years – the 850 hPa temperature in the key node area has risen 2.5 °C – substantially impacted the key node region. An increase of the in-degree index and a change in the structure of the network itself are observed. Concurrently with these changes, the prediction skill of this forecasting method for the ISM rainfall amount is improving substantially [323].
3.1.3. Extreme rainfall
Extreme precipitation events have produced more rain and have become more common since the 1950s in many regions of the world. Heavy precipitation may pose threats to our society. The most immediate impact is the threat of flooding. This risk can be heightened in urban and agricultural areas. In addition to flooding, extreme precipitation also increases the risk of landslides. Excessive precipitation can also degrade water quality, harming human health and ecosystems. Thus is crucial to predict extreme rainfall events and to establish an early warning system for them. However, the analysis of spatial patterns of co-variability of such events is challenging because traditional techniques based on principal component analysis of the covariance matrix only capture the first two statistical moments of the data distribution and are not suitable to analyze the behavior in the tails of the respective distributions [327].
Extreme Rainfall over India
To overcome these challenges, Malik et al. applied the CNs approach to analyze the spatial and temporal patterns of extreme rainfall during the ISM [92], [328]. This approach is based on the event synchronization method (see Section 2.1.3). In Ref. [328], the dataset is a daily precipitation gridded set for 1961–2004 developed as part of the project—Asian Precipitation Highly Resolved Observational Data Integration Towards the Evaluation of Water Resources.11 Then they extracted the data for the South Asian region at a 0.5 degree resolution. For calculating the event synchronization, two different thresholds of th percentile and th percentile were chosen to obtain the extreme event time series, referring to very heavy and heavy rainfall events, respectively. Next, they computed the strength of synchronization and the delay behavior between each pair of the grid sites and [see Eq. (20)]. After normalizing it holds, that and , where means complete synchronization, and stands for the absence of synchronization; and means that events at precede events in . The CN is then constructed by selecting only pairs of sites that show strong correlations, and the time lags between the events are used to define the direction of the links.
The spatial structures, organization, and scales of the extreme rainfall over India during the ISM period were investigated. Fig. 29 exhibits that the degree centrality [see Eq. (4)] of the CNs reveals well-defined spatial structures in the monsoonal extreme precipitation [92]. Based on the median of the geographical length of the links, calculated using the formula for the spherical Earth projected onto a plane, it has been uncovered that extreme rainfall events are synchronized up to 250 km for most of the region. They further found that such a spatial organization opens the possibility for predictions of a probable spatial extent of monsoonal rainfall activity without delay, e.g., for most of the subcontinent, the accuracy of the prediction is above 70% and even reaches up to 100% in certain places [92].
Fig. 29.
Degree centrality of the event synchronization CN for extreme rainfall over the Indian subcontinent. The extreme events threshold is (a) and (b) .
Figure from Ref. [92].
Extreme Rainfall over South America
This event synchronization CN approach was also applied to predict extreme rainfall events in the Central Andes of South America [94]. Based on the real-time satellite-derived rainfall data, TRMM 3B42V7 [329], Boers et al. were able to predict more than 60% of the rainfall events above the 99th percentile in the Central Andes, and even 90% during El Niño conditions. The interplay of northward migrating frontal systems and a low-level wind channel from the western Amazon to the subtropics are considered as the responsible mechanism.
Extreme rainfall events are defined as times with threshold for all Dec–Jan–Feb seasons in the spatial domain (85°W, 30°W) and (40°S, 15°N), at a resolution of , and 3-hourly temporal resolution for the time period from 1998 to 2012. After the construction of the event synchronization CN (see Section 2.1.3), the network divergence is defined as
| (123) |
where and stand for the in-strength and out-strength respectively at each node. Positive values of indicate sinks of the network; negative values indicate sources. The strength out of and into a region is
| (124) |
| (125) |
where denotes the number of grid points contained in .
Fig. 30a shows the network divergence (defined in Eq. (123)), which estimates the dynamics and temporal order of extreme rainfall in South America. The boxes labeled 1 to 7 are used for the tracking of extreme events. It was found that the most pronounced source region of the rainfall network is South Eastern South America (SESA), defined as the box ranging from (60°W, 53°W) to (35°S, 30°S). Fig. 30b depicts where synchronized extreme events occur within 2 days after extreme events occurred in SESA, measured by . For comparison, is shown in Fig. 30c. This analysis reveals that extreme events in SESA are followed by extreme events along a narrow band following the eastern Andean slopes up to western Bolivia, while they are only preceded by extreme events to the southwest. Based on the propagation of extreme rainfall from SESA to the eastern Central Andes (ECA), see Fig. 30d, a prediction for the extreme rainfall for the ECA within 2 days is made after they occurred in SESA. It should be noted that these extreme rainfall events could not be forecasted by using other methods.
Fig. 30.
Event synchronization CN for extreme rainfall over South America. (a) Network divergence, , is defined as the difference of in-strength and out-strength at each node (see Eq. (123)). The boxes labeled 1 to 7 are used for the tracking of extreme events. (b) Strength out of SESA, , which is the average out-Strength restricted to SESA ((see Eq. (124))). (c) Strength in of SESA, , which is the average in-Strength restricted to SESA ((see Eq. (125))). (d) Temporal evolution of extreme rainfall events from SESA to ECA along the sequence of boxes indicated in (a).
Figure from Ref. [94].
Extreme Rainfall over the Globe
The event synchronization CN method was also applied to investigate the global pattern of extreme-rainfall by Boers et al. [96]. The gauge-calibrated, satellite-derived rainfall dataset TRMM 3B42 V731, with daily temporal resolution, from °N to °S for the period 1998–2016 is used. The extreme rainfall event thresholds are of the wet days (¿1 mm) for the Jun–Jul–Aug season. Note that consecutive days with rainfall above the threshold are considered as single events and placed on the first day of the occurrence. To study the robustness of the method, Global Precipitation Climatology Project32 and NCEP/NCAR Reanalysis 1 data were also tested.
First, the synchronization of extreme events for each pair of nodes is computed (see Section 2.1.3). Network links are added between two nodes if the corresponding synchronization values are significant, . The global distribution of the spatial distances for which significant synchronizations occur was studied. This distribution decays as a power law , with an exponent very close to 1 for distances , but exhibits a super-power-law behavior for longer distances. The scale-break indicates that the significant links can be divided into two distinct classes: (i) links associated with regional weather systems with distances up to , which include mesoscale convective systems and tropical cyclones; and (ii) links associated with global-scale teleconnections. Such teleconnections are generally understood to be caused either by direct signal transport due to large-scale atmospheric circulations or by propagating waves triggered by disturbances of these circulations [96]. In Fig. 31, the teleconnection pattern for south-central Asia (SCA) for events above the 95th percentile is presented. Pronounced link bundles connecting SCA with eastern Asia, the African tropics, large parts of Europe and the eastern coast of North America, as well as the Southern Hemisphere extratropics are apparent. Further analysis reveals that the Rossby waves can be regarded as the physical mechanism underlying these global teleconnection patterns.
Fig. 31.
Event synchronization CN for extreme rainfall over globe. Teleconnection pattern for south-central Asia (SCA) for events above the 95th percentile. (a) Links connected to SCA, before correcting for the multiple-comparison bias. (b) Link bundles attached to SCA, after correcting for the multiple-comparison bias.
Figure from Ref. [96].
3.1.4. Atmospheric circulation and global warming
Earth’s atmosphere, made up essentially of the gases that surround our planet, consists of circulation patterns that move air from one location to another and from the surface to top elevations. The atmospheric circulation is controlled by Earth’s rotation, barometric pressure, topography, ocean currents, and differences in temperature, salinity, etc.
Latitude structure of the circulation
Since latitudinal gradients in solar energy input are dominant drivers of the atmospheric circulation, its primary features depend on the latitude. We show an idealized depiction of the large-scale atmospheric circulation on Earth in Fig. 32, which schematizes the main features of the circulation, both in a latitude–height plane and in the horizontal, without yet considering longitudinal variations due to continents, oceans, etc. This represents the circulation in an average over all longitudes, known as a zonal average. As we see, there are three large-scale convection cells in both hemisphere.
Fig. 32.
Schematic of major features of the atmospheric circulation. The average circulation is idealized as being independent of longitude and symmetric about the equator.
The figure is from https://courses.lumenlearning.com/geophysical/chapter/global-atmospheric-circulations/.
(i) The Hadley cell is a thermally driven, overturning circulation that tends to rise in the tropics and sink at slightly higher latitudes. Warming from the surface near the equator is transferred upward through a deep layer by convection clouds. The rising air spreads poleward and cools slowly, returning to the surface and then moves towards the equator. Roughly speaking, the Hadley circulation transports heat to about 30°latitude, and the average effect of the transient weather disturbances transports the heat further poleward.
(ii) The Ferrel cell is also called mid-latitude cell. In the Ferrel cell, air flows poleward and eastward near the surface and equatorward and westward at higher altitudes; this movement is the reverse of the airflow in the Hadley cell. It was the first to account for the westerly winds between latitudes 35° and 60° in both hemispheres.
(iii) The Polar cell is the smallest and weakest cell, which extends from between 60°and 70°north and south to the poles. Air in these cells sinks over the highest latitudes and flows out towards the lower latitudes at the surface. Note that the idealized picture of the atmospheric circulation based on latitude is a reasonable first approximation, but land–ocean contrasts and other variations in longitude are also important.
Climate Change Effects on Atmospheric Circulations
Climate change strongly affects the mode of atmospheric circulations, especially, the Hadley cell, which plays a pivotal role in the Earth’s climate by transporting energy and heat poleward [330], [331], [332]. An analysis of satellite observations indicates a poleward expansion of the Hadley cell by 2°latitude from 1979 to 2005 [330]. A possible mechanism for the changes in the Hadley cell and its relation to global warming has been reported [331]. Also, a possible mechanism for the changes in the Hadley cell’s strength and its relation to global warming was developed in [332]. Both aforementioned observations and theories suggest a weakening and poleward expansion of the Hadley cell under global warming.
As is well known, the locations of the subtropical dry zones and the major tropical/subtropical deserts are associated with the subsiding branches of the Hadley cell [333]. Therefore, the poleward expansion of the Hadley cell may result in a drier future in some tropical/subtropical regions [331]. In addition, the poleward migration of the location of the tropical cyclone maximum intensity is also considered as a consequence of the expansion of the Hadley cell [334].
The strength of the Hadley cell is calculated using the observed zonal-mean meridional wind in the stream function [335],
| (126) |
where is the meridional velocity in pressure coordinates, is the mean radius of the Earth, and is the pressure. The operators and stand for temporal and zonal averaging, respectively. When computing the field, we usually assume at the top of the atmosphere and integrating Eq. (126) downward to the surface. The intensity of the Hadley cell is much stronger in winter than in summer. To quantify the edges of the Hadley cell, the maximum of the absolute value of at 500 hPa is first determined (), and then the edges are identified as the first latitude poleward of the maximum at which becomes zero [331]. Theories of the Hadley cell suggest that the meridional extent should scale with the height of the tropopause [336],
| (127) |
where was computed from temperature data as the lowest pressure level at which the lapse rate decreases to 2 °C/km [337], is the tropospheric mean meridional potential temperature gradient, and is the angular velocity of the earth. From the thermodynamic equation and the mass continuity equation [335], the meridional overturning stream function of the circulation scales as,
| (128) |
where is the dry static stability of the tropical troposphere and is the characteristic overturning time scale of the circulation.
Although the conventional analysis of satellite observations and the climate change simulations suggests a poleward expansion of the Hadley cell, there are still two challenges. (i) The latitude–longitude structure of this expansion is not fully resolved. (ii) In contrast to models and theoretical considerations, which predict a decreasing intensity, an increasing trend was found in the intensity of the Hadley cell in reanalysis datasets [338]. To overcome these unsolved issues, Fanet al. developed an approach based on network and percolation frameworks to study the impacts of climate changes on the atmospheric circulations [67]. They found an abrupt transition during the evolution of the climate network, indicating a consistent poleward expansion of the largest cluster that corresponds to the tropical area, as well as a weakening of the strength of link in the tropics. This was found in both the reanalysis data and the CMIP5 simulations. The underlying mechanism for the observed expansion of the tropical cluster was linked to the weakening and expansion of the Hadley cell.
In Ref. [67], the CNs were embedded into a two-dimensional lattice, where only nearest neighbor links are considered. The strength of each link are calculated based on Eq. (15), with the month-to-month temperature difference. The links are sorted in decreasing order of strength and then added one by one according to the decreasing strength. More specifically, the nodes that are more similar are connected first. Existing clusters grow when a new link connects one cluster to another one. Then the CN undergoes an abrupt and statistically significant phase transition, i.e., exhibiting a significant discontinuity in the order parameter , the relative size of the largest cluster. Due to the Earth’s spherical shape, the largest component in the climate networks is redefined as
| (129) |
where is the latitude of node . The percolation threshold is determined according to Eq. (48), i.e., the step with the largest jump is regarded as the phase transition point. Fig. 33(a) shows the CN component structure in the global map at the percolation threshold. Just before this jump, the CN is characterized by three major communities; the largest one is located in the tropical region; the second and third largest are located in the high latitudes of the southern and northern hemispheres. Fig. 33(b) depicts the relative size of the largest cluster, , as a function of the link occupation probability in the evolution of the CN. It has been found that exhibits an abrupt jump at the percolation threshold . The probability density function (PDF) of the weight of links is shown in Fig. 33(d).
Fig. 33.
The network-percolation approach to the atmospheric circulation. Snapshots of the component structures of the CN. (a) Just before the percolation threshold. (b) The giant cluster relative size versus the fraction of total number of links , for real (red), spatially shuffled (blue) and temporally shuffled (purple) records. (c) Just before the formation of the spanning cluster (at the second largest jump at ). (d) The PDF of the weight of links around the globe, in real (solid line) and shuffled (dashed lines) data. The vertical line (orange) indicates the strength of the critical link, , at the percolation threshold .
Reprinted figure from Ref. [67].
To determine the temporal evolution of the largest component , and its intensity (the weight of the critical link that leads to the largest transition), a sequence of networks based on successive and non-overlapping temporal windows with lengths of years each was constructed. The results suggested that the tropical cluster is expanding poleward, meanwhile, its intensity decreases significantly with time. The robust weakening and poleward expansion of the tropical component have been observed both in the reanalysis data and in 31 CMIP5 models. The network-percolation approach was also used to identify the climate change response, by comparing the topology of the tropical component for the first and last twenty years of the 21st century, i.e., 2080–2100 vs. 2006–2026. It was found that some regions, for example, northern India, southern Africa, and western Australia have a higher probability to be influenced by the tropical component, whereas the impacts in other regions, e.g., the Northeast Pacific, will become weaker in the future.
3.1.5. Atlantic meridional overturning circulation
The Atlantic Meridional Overturning Circulation (AMOC) is a crucial part of the climate system in the North Atlantic. It has a major impact on climate because of its redistributing meridional heat transport [339], [340]. The AMOC has been identified as one of the important tipping elements of the Earth system [23]. Changes in the AMOC have not only affected the North Atlantic and surrounding landmasses, but have also had global impacts [156]. For example, negative change leads to increasing storminess in southern Europe [341], connects to above average sea-level rise at the US east coast [342], and associates with increasing drought in the Sahel (for both frequency and intensity) [343]. Recently, Caesar et al. provided solid evidence for a weakening of the AMOC by about (around 15%) sverdrups since the mid-twentieth century [160]. This weakening is revealed by the consisting of a pattern of cooling in the subpolar Atlantic Ocean and warming in the Gulf Stream region (see Fig. 34). The slowdown of the AMOC was found in both in a high-resolution climate model (CM2.6) in response to increasing atmospheric carbon dioxide concentrations, and in the observed HadISST data since the late 19th century. An improved SST-based AMOC index (the subpolar cold patch) was developed, which is optimized in its regional and seasonal coverage to reconstruct AMOC changes. In particular, it was found that the AMOC decline since the 1950s is very likely to be largely anthropogenic. This slowdown of the AMOC is mainly caused by the gradually varying freshwater forcing in the northern North Atlantic.
Fig. 34.
Slowdown of the Atlantic Meridional Overturning Circulation (AMOC). Comparison of SST trends in model and observations. Linear SST trends for the CM2.6 climate model of the Geophysical Fluid Dynamics Laboratory during a -doubling experiment (left) and in a control run with fixed concentrations (middle). Right, Linear SST trends for the observed HadISST data from 1870 to 2016. The data is shown from the November–May season.
Figure from Ref. [160].
The AMOC is the zonally averaged volume transport and its strength at 26°N in the Atlantic and is now routinely monitored by the RAPID-MOCHA array [344]. Mean patterns of the meridional overturning circulation in the Atlantic are determined from the Community Earth System Model (CESM) simulation [345], [346]. The AMOC has its maximum at about 1000 m depth around the separation latitude of the Gulf Stream with a strength of about 20 Sv. Since a future collapse of the AMOC has been identified as a tipping element, it is therefore crucial to develop early warning indicators for such a potential collapse. As we discussed in Section 2.3, various techniques have been developed and successfully applied to detect early warning indicators in single time series used based on the concepts of critical slowing down [177]. In particular, early warning indicators for the tipping point of the AMOC have been discussed in [179], [181].
Recently, several CN-based warning-signals have been proposed by analyzing the correlations for the AMOC collapse that efficiently monitor spatial changes in deep ocean circulation. Specifically, the values of the mean degree, its kurtosis, assortativity, and clustering increase when approaching a tipping point [69], [70]. The CN methodology is applied to temperature time series from an idealized ocean model of the AMOC, as well as to AMOC strength time series from a coupled atmosphere–ocean GCM. In addition, the optimal locations of measurement of the AMOC are formulated to provide early warning signals of a collapse through the analysis of the performance of this indicator. Next, we will provide an overview of these CN-based early warning indicators for the collapse of the AMOC.
Mheen et al. [69] used a dimensional (meridional-depth) idealized ocean model of the AMOC, where tipping points can be explicitly computed. In this model, there are two active tracers: temperature and salinity , which are related to the density by a linear equation of state [347]
| (130) |
where and are the thermal expansion and saline contraction coefficients, respectively, and , and are reference quantities. The surface freshwater forcing , which can be applied as a virtual salt flux, is
| (131) |
where indicates latitude, is the northern boundary of the equatorially symmetric domain, is the strength of the background freshwater forcing, and is a white noise term. is the strength of an anomalous freshwater flux which is only applied over the area , and is a constant used to normalize the surface-integrated salt flux from 0 to 1 for all parameter values. As shown in Fig. 35, the bifurcation diagram of the AMOC in the idealized ocean model indicates the existence of tipping points at and . The model was discretized on a 32 16 spatial grid, with four values of close to , labeled A, B, C and D. The output of this model is the temperature field time series.
Fig. 35.
Tipping points of the AMOC in the idealized ocean model. (a) Bifurcation diagram with the sum of the maximum () meridional overturning stream function and minimum () meridional overturning stream function vs. the anomalous freshwater flux strength . (b) Pattern of the meridional overturning stream function () at the upper stable branch. (c) Pattern of at the lower stable branch.
Reprinted figure from Ref. [69].
Next, an undirected and unweighted CN is constructed based on the Pearson correlation method (see Section 2.1) with no time lags and a threshold [69], i.e, if the correlation , the corresponding two nodes and are connected. Four network-based indicators , , and were developed to study the dynamic evolution of the AMOC. Here is defined as the expectation value of the normalized degree distribution ; is defined as the expectation value of the normalized clustering coefficients ; is the kurtosis of the degree distribution; and is the kurtosis of the clustering coefficients distribution. These four network indicators are presented in Fig. 36. It was found that increases steeply and smoothly when the tipping point is approached. The explanation for this increase is based on the increased dominance of the first EOF in the variance of the solution in a large part of the domain. The same holds for the indicator (Fig. 36g). The kurtosis distributions and (Fig. 36h) show even more clearly a strong increase when the tipping point is approached before the collapse. Note that the CNs were constructed from the full spatial temperature field using a sliding window of 5000 years with a shift of 1000 years. The results were not sensitive to the sliding window length. For comparison, previously suggested early warning indicators of the transition in the same AMOC time series, such as, lag-1 autocorrelation, DFA, standard deviation (see our discussion in Section 2.3) are also plotted in Fig. 36 and tend to exhibit a rapid increase/decrease when approaching the tipping point. In particular, the coefficient of the lag-1 autocorrelation (Fig. 36c) reaches its maximum near the tipping point indicating a critical slowdown of the AMOC. However, it has been found that the indicator is not monotonic and also increases when the AMOC is still far from the transition. The DFA analysis shown in Fig. 36d does not indicate early warnings of a transition. Fig. 36e depicts the standard deviation of the AMOC record. It shows a steady increase towards the transition but it is difficult to set a threshold for an alarm. In Fig. 36f, the fraction of the time spent below the 0.5 percentile (estimated based on the first 5000 years) of the AMOC strength is shown. This indicator displays a much sharper increase, but it is a rather ad-hoc measure which depends on a calibration in the far past [69].
Fig. 36.
Early warning signals of the AMOC. (a) Time series of the maximum value of the AMOC. (b) Transient change of versus time from 0.05 to 0.17 myr during 35,000 years. (c) Th lag-1 autocorrelation of the projection of the time series onto the first EOF. (d) The DFA exponent, using linear (up) and quadratic (down) detrending. (e) Standard deviation of the AMOC. (f) Fraction of the time spent below the 0.5 percentile of the AMOC strength. (g) The network-based indicators (circles) and (squares). (h) Same as (g) but for the kurtosis ( (circles) and (squares). The vertical dashed line indicates the value of at the tipping point.
Figure from Ref. [69].
The same CNs-based analysis was also performed in a more realistic Fast Met Office/UK Universities Simulator (FAMOUS) model by Feng et al. [70]. The FAMOUS model is a reduction for Hadley Centre Coupled Model with a lower resolution ocean and atmosphere component. The annual mean of AMOC strength data were obtained from a control simulation and from a freshwater-perturbed (referred to as “hosing”) simulation of the FAMOUS model. In the hosing simulation, the freshwater flux over the extratropical North Atlantic was increased linearly from zero to 1.0 Sv over 2000 years [70]. The complete AMOC streamfunction field for each of the six 100-year equilibrium simulations has been considered. It was found that when the freshwater forcing is increased, a high degree in the network – indicating high spatial AMOC correlations – first appears at nodes in the South Atlantic at about 1000 m depth. The kurtosis of the CN was introduced as an effective indicator to capture the changes in the topology of the degree field. For the hosing simulation, there is a strong increase of to values far extending those for the control simulation significantly before the collapse time. However, the critical slowdown indicators variance and lag-1 autocorrelation do not show any early warning signal. Moreover, the kurtosis can also be used to determine the optimal observation locations of the AMOC, which provides a strong anomalous signal at least 100 years before the transition.
3.2. Earth geometric surface relief
The topography or bathymetry of the Earth shows complex multifractal structures and scaling properties [34], [348], [349], [350], which can be regarded as a consequence of plate tectonic processes. Revealing the relations between geometrical features of terrestrial surfaces and their internal geological processes has long been a fundamental challenge in the Earth sciences. The plate tectonic theory is usually used to study most of the major surface topographic features of the Earth [351]. It has been reported that there exist strong connections between the ocean bottom topography and the Earth’s climate [352]. Moreover, the surface topography of the Earth plays a remarkable role in the dynamical evolution of oceans, especially, in regard to global climate change and sea level rising. Sea level rise is one of the major consequences of global climate warming [353] and the effects in combination with storm surges and other extreme events have been observed [354]. Decreasing global CO2 emissions is crucial for limiting the risks of sea-level rise. It is estimated that the median sea-level rise will be between 0.7 and 1.2 m until the year 2300 even within the constraints of the Paris Agreement [355]. The world’s large ice sheets in Greenland and Antarctica are considered to be the largest possible contributors to sea level rise. If these ice sheets melt completely, the sea level would rise about 7 m, 5 m and 53 m from the Greenland ice sheet, the West Antarctic ice sheet, and the East Antarctic ice sheet, respectively. There is thus a great interest in clarifying/predicting the influenced areas in response to sea level rise.
Recently, the ETOPO1 Global Relief Model was released and provided new opportunities for a better understanding of Earth’s surface processes based on geomorphic signatures [356]. ETOPO1 is a 1 arc-minute global relief model of the Earth’s surface that integrates land topography and ocean bathymetry and was developed by NOAA. It was built from global and regional datasets and used to calculate the volumes of the world’s oceans and to derive a hypsographic curve of Earth’s surface (see Fig. 37).
Fig. 37.
ETOPO1 Global Relief Model. ETOPO1 is a 1 arc-minute global relief model of the Earth’s surface that integrates land topography and ocean bathymetry. The present mean sea level (zero height) is assumed as a vertical datum of the height relief.
Figure is from NOAA https://www.ngdc.noaa.gov/mgg/global/.
In this Section, we will review statistical properties of the Earth geometric surface relief using percolation theory. Their fractal structure and scaling will also be discussed. In particular, the present mean sea level on Earth will be shown to coincide with the critical threshold in a percolation description of the global topography; strong evidence reveals abrupt transitions that occurred during the evolution of the Earth’s relief network, indicative of a continental/cluster aggregation. This could help us to identify the critical nodes or locations that will be more exposed to global climate change.
3.2.1. Self-similarity and long-range correlations
Self-similarity and long-range correlations are remarkable features of the Earth’s surface topography [34]. Starting about 30 years ago, new ideas in nonlinear dynamics, particularly fractals and scaling, provoked an explosive growth of research both in modeling and in experimentally characterizing the solid earth geophysics including the topography, for a review see Ref. [357]. The power spectrum of linear transects of Earth’s topography follows the scaling relation , where stands for the wave number [34]. Such a scaling relation was used to measure the self-similarity of the Earth’s surface topography. Moreover, similar scaling relations have been identified in Earth’s sea-floor topography [358], the topology of river networks [359], as well as natural rock surfaces [360].
The long-range correlation features of the Earth’s surface topography can be described in the following way. The exponent in the power-law spectrum is related to the Hurst exponent in fractional Brownian motion (fBm) via , which results in for the Earth’s topography. Whereas further universal multifractal parameters estimated for specific parts have resulted in a much more complex structure, i.e., for bathymetry, continents and continental margins, respectively [348].
The third characteristic of the Earth’s surface topography is the well known bimodal distribution, as a consequence of plate tectonic processes [361]. It indicates the topographic dichotomy of continents and ocean basins.
3.2.2. Landmass and oceanic clusters
Although the classical pate tectonic theory provided a framework that might explain most of the major surface topographic features of the Earth, a percolation-based description as discussed in Section 2.2 was developed to study the geometrical features of the Earth from a statistical physics perspective [127], [130]. The analysis is based on high-resolution ETOPO1 global relief records. The resolution is 1 arc-minute, i.e., grid points. The present mean sea level (zero height) is assumed as a vertical datum of the height relief , where , are the corresponding latitude and longitude of grid point .
In Ref. [127], the hypothetical water level was considered as the percolation control parameter. When it is decreased from the highest to lowest available heights on Earth, there occurs a geometrical percolation phase transition at a critical level around which most parts of landmass join together. Fig. 38 illustrates the landmass cluster aggregation by decreasing the sea level from (top) to (bottom). To determine the percolation threshold, the probability of any nodes to be part of the largest island was defined as the order parameter; the mean island size (analogous to the susceptibility of the system) was defined as, , where denotes the average number of islands of size at level and the prime on the sums stands for the exclusion of the largest island; the correlation length is defined as the average distance of nodes belonging to the same island cluster, , where is the radius of gyration of a given cluster. It has been found that the order parameter for islands has an abrupt jump around the zero height level , i.e., right at the present mean sea level (Fig. 39a). It was furthermore found, that both quantities and become divergent at the present mean sea level, see Fig. 39b. From these results, the most remarkable observation is that the critical level coincides with the present mean sea level on Earth. This may suggest the important role of water on Earth and shed new light on the tectonic plate motion [127].
Fig. 38.
Schematic illustration of the landmass cluster aggregation by decreasing the sea level. The nodes are occupied if its corresponding height is above the given threshold . Different colors stand for different clusters.
Figure from Ref. [127].
Fig. 39.
Percolation analysis of the Earth’s topography. (a) Relative surface area of the largest island (circles) and the largest sea (triangles) as a function of the sea level. The landmass critical level is close to the current sea level , whereas, the oceanic critical level is close to the level m at which the total island and oceanic surface areas are equal. (b) The correlation length and mean island size as a function of the sea level. The dashed line marks a geometrical percolation phase transition at the present mean sea level.
Reprinted figure from Ref. [127].
The same percolation analysis was also performed for the oceanic clusters, i.e., the hypothetical water level was increased from the lowest to highest. Fig. 39b gives rise to a discontinuous jump in the oceanic order parameter at around m. Further investigation in the lunar topography reveals various characteristic features of the Moon. It was found that the critical level for the Moon has the same amount of land and oceans at the threshold, indicating a purely geometrical phase transition [127].
3.2.3. Origin of the discontinuity
It has been reported that a random network or lattice system always undergoes a continuous percolation phase transition and shows standard scaling features [81]. Yet, the order of the percolation transition for the Earth’s topography is still an open question. To answer this, Fan et al. developed a more sophisticated percolation-based method [130]. The percolation model was defined as follows: starting from an unoccupied lattice, the sites are occupied one by one according to their ranking, i.e., first choosing the site with the largest height, then the second, etc. At each step, the fraction of occupied sites increases by the inverse of the total number of sites in the Earth’s relief landscape. By this procedure, a configuration of occupied sites is continually obtained at every . Here all the grid points in the ETOPO1 Global Relief Model were ranked according to their height , from the largest to the smallest value.
In the following, the size of the percolation landmass (oceanic) clusters was calculated based on Eq. (129) due to the Earth’s spherical nature. The size of the th gap at each fraction is defined as follows:
| (132) |
Specifically, here denotes the largest gap, indicates the second largest gap, etc. The larger the gap is, the larger are the two clusters before merging. The dynamical evolution of the largest landmass cluster as a function of the fraction of occupied nodes is shown in Fig. 40a. It was found that Earth’s relief network undergoes several abrupt and statistically significant phase transitions, i.e., exhibiting a discontinuity in the order parameter . Fig. 40b shows the network clusters landmass structure at the percolation threshold (just before the largest gap ). The results reveal that the network, just before this jump, is characterized by four major communities: the largest one being the Afro-Eurasia continental landmass, the second largest cluster is the Americas, the third is located in Antarctica, and the fourth is Oceania. Notably, there exists a critical node that connects the largest and second largest clusters at the percolation threshold , with altitude level m, under the current sea level.
Fig. 40.
Percolation analysis of the Earth’s topography. (a) The largest landmass cluster relative size as a function of the fraction of the total landmass for real (green) and shuffled (red) Earth relief records. – indicate the five largest gaps, defined in Eq. (132). (b) Snapshots of the landmass clusters of the Earth’s surface topography network at the percolation threshold, . The star indicates the critical node.
Reprinted figure from Ref. [130].
The same analysis has also been applied for the oceanic clusters, i.e., the nodes are occupied one by one according to their height level in increasing order. It also has given rise to a discontinuous jump in the oceanic order parameter at the percolation threshold with an altitude level m. This is very close to the result m reported in Ref. [127]. Note that the critical node, , connects the Atlantic+Indian Ocean Plate to the Pacific Plate. It is worth noting that the role of the largest cluster on the landmass structures is different from that on the oceanic one. These differences reveal the complex and different structure of the Earth’s topography (continents) and bathymetry (oceans). This dichotomy is manifested in the well-known bimodal distribution of the Earth’s topography [361].
To demonstrate the order of the percolation phase transition in Earth’s relief network, a finite-size effects analysis was performed by altering the resolution of the nodes. The largest gap was calculated for a given system size . Here, is defined as the number of nodes in the zonal direction. According to Eq. (49), if as , the corresponding giant cluster is assumed to undergo a continuous percolation; otherwise, the corresponding percolation is assumed to be discontinuous [147], [153]. In addition, the size of the order parameter at the percolation threshold [just before the largest jump ], , was also studied [see Eq. (51)]. The results are shown in Fig. 41a and b, which indicate a discontinuous percolation since (1) tends to be a non-zero constant; (2) , also indicates a discontinuous percolation. For comparison, a randomized topography obtained from the shuffling (spatial randomizing the height profile) of the original data was also considered (see Fig. 41a and b). The numerical results for the shuffled case, suggest a continuous percolation transition with known critical exponents and [106], [107], as expected when the long-range correlations were destroyed.
Fig. 41.
Finite size analysis of the percolation in Earth’s relief network. (a) Log–log plot of the largest gap vs. the network system size for original real data (red) and shuffled data (blue). (b) Log–log plot of the largest landmass cluster relative size at the percolation threshold vs. for real data (red) and shuffled data (blue). (c) The average of the largest jump as a function of system size ; (d) the corresponding percolation threshold as a function of for percolation on 2D fractional Brownian motion surfaces with the Hurst exponent .
Reprinted figure from Ref. [130].
In order to reveal the origin of the discontinuity, Fan et al. [130] further studied the percolation on 2D fBm surfaces with Hurst exponent [362], [363]. The parameter is usually between 0 and 1, where 0 is very noisy, and 1 is smoother. The Earth’s rough surfaces can be modeled via a fBm [364], and the estimation for the Earth continents topography is [348]. Next, the percolation analysis on fBm surfaces with was performed. Similar to the real network, the largest cluster also exhibited abrupt transitions around . The largest gap (average) as a function of system size is shown in Fig. 41c. It was found that the percolation on fBm surfaces with is discontinuous, since tends to be a non-zero constant when . The percolation threshold corresponding to the largest gap during the evolution of site percolation is shown in Fig. 41d. The values are robust and agree well with the real data where [see Fig. 38]. This indicates that the combined percolation and fBm methods can be used as an efficient tool to investigate the Earth’s surface topography.
3.3. Earthquake systems
Earthquakes are one of the most devastating natural disasters that plague society. Thus, reliable and skillful earthquake forecasts over different time scales (from days to decades) are essential for establishing rational seismic risk reduction strategies and to enhance preparedness and resilience. The earthquake process is a complex spatio-temporal phenomenon, and has been thought to be an example of self-organized criticality systems, in which events occur as cascades on a wide range of sizes, each determined by fine details of the rupture process. Despite rapid progress in the latter part of the 20th century, the study of earthquakes, like the science of many other complex natural systems, is still in its juvenile stages of exploration and discovery. The scientific challenge is how to understand the earthquake phenomena that are both profound and practical, in particular, the deterministic prediction of specific event sizes, their locations, and times. Recently, probabilistic forecasting, based on statistical patterns of earthquake occurrence, became a much more realistic goal, and has been actively explored and tested in global initiatives [36].
In this section, we will first present a description of the phenomenological laws of earthquake occurrence, and scale invariance and the intertime distribution is also briefly discussed. Then we will review how the statistical mechanics approach (memory analysis) can be applied to improve the forecasting skill for real earthquake catalogs.
3.3.1. Scale invariance and the inter-event distribution
First, we introduce some fundamental quantities that characterize earthquake occurrence. This information, such as occurrence time, hypocentral location, earthquake magnitude and depth, is usually reported in seismic catalogs available online for different geographic areas, for instance, the United States Geological Survey (USGS) earthquake catalog.12 We present here the main phenomenological laws for the statistical distribution of these quantities.
The most common method of describing the size of an earthquake is the Richter magnitude scale , which takes the logarithm of the ground displacement as measured by a seismograph, and applies a correction which varies with the distance from the earthquake to the seismograph [365]. The characteristic size of the fractured area , as well as the faulting duration , can be both expressed in terms of the magnitude as .
Next, we will give some well established empirical basic laws of earthquakes. In seismology, the Gutenberg–Richter (GR) law expresses the relationship between the magnitude and cumulative number of earthquakes in any given region and time period with magnitude larger or equal to , which exhibits an exponential decay [366]
| (133) |
where and are fitting parameters. We show the Gutenberg–Richter law for the Israeli earthquake catalog as an example, in Fig. 42. The -value of the Gutenberg and Richter law has been calculated using the approach described by Marzocchi and Sandri [367]. The value was found to be equal to . The intercept of the fit line defines the -value that explains the earthquake rate for the region selected. In our case . As expected, different catalogs exhibit different seismicity levels quantified by the magnitude range and by the total number of events, corresponding to different values of the constant . Conversely, the parameter appears to be quite independent of the geographical region and the temporal interval. Typical experimental results provide for tectonic earthquakes.
Fig. 42.
Gutenberg–Richter law for the Israeli earthquake catalog. (a) Map of the events present in the selected area. (b) Cumulative number as a function of magnitude. The orange line is the fit of the distribution based on Eq. (133), with and .
The second empirical law, the Omori law, was first described by the seismologist Omori in 1894 [368],
| (134) |
where is the aftershock rate, is the time elapsed from the mainshock occurrence; and are empirical constants controlling, respectively, the total number of aftershocks and the onset of the power law decay. is a third constant, which modifies the decay rate and typically falls in the range 0.7–1.5.
The magnitude of an event understandably influences the number of aftershocks triggered by it, i.e., the larger the mainshock magnitude, the larger is the total number of triggered aftershocks. This property is known as the productivity law, stating that the number of aftershocks [integral of Eq. (134)] belonging to a sequence increases exponentially with the mainshock magnitude ,
| (135) |
The parameter is typically small for swarm-type activity, and large for clear primary aftershock sequences [369].
The distribution of waiting times between seismic events has generated much attention and discussion over the last decades, since it was considered to have a universal scaling form [370]. Bak et al. proposed, for the first time, a unified scaling law for the waiting times between earthquakes, expressing a hierarchical organization in time, space, and magnitude. They considered the California earthquake catalog and covered the region with a grid of cells of size . Then they analyzed the inter-event times for each cell and calculated a histogram of the inter-event times whose magnitudes are greater than ; this was repeated for different values of and minimum magnitudes (see Fig. 43a). It was found that if they rescaled the inter-event times by (where is the Gutenberg–Richter -value and is the spatial fractal dimension), and rescaled by , where is some exponent, the distribution of waiting times all appeared to collapse onto a single curve (Fig. 43b). The scaling hypothesis was thus expressed as
| (136) |
where can be identified as the Omori-law exponent for aftershocks, is the value in the Gutenberg–Richter law, and describes the fractal dimension of the location of epicenters projected onto the surface of the Earth [370].
Fig. 43.
Unified Scaling Law for Earthquakes. (a) The distribution of interoccurrence time between earthquakes with magnitude greater than within an area of linear size for the California catalog. (b) The scaling function, see Eq. (136), for the data in (a) with s rescaled with as a function of the variable , with . The data collapse implies a unified law for earthquakes. The solid circles, squares, and triangles correspond to magnitude cutoffs , , and , respectively. The color coding represents the linear size (black), (red), (green), (blue), and (orange) of the cells.
Reprinted figure from Ref. [370].
Subsequently, Corral [371] has discovered that the probability density function of the inter-occurrence time can be simplified to the scaling form
| (137) |
where stands for the mean seismic rate that refers to the region. The scaling function can be expressed by a generalized Gamma distribution,
| (138) |
with the parameters , and . Corral verified the above scaling hypothesis by considering data from the global worldwide catalog from the National Earthquake Information Center (NEIC)13 and several local catalogs: The Southern California Earthquake Center (SCEC),14 the Japan University Network Earthquake Catalog (JUNEC),15 the Bulletins of the IGN (the Iberian Peninsula and the North of Africa),16 and the BGS catalog (the British Islands and the North Sea).17 The inter-event time distributions for the different geographic areas and for different values of the lower magnitude can be collapsed into a universal scaling function, as shown in Fig. 44.
Fig. 44.
Recurrence-time distributions without and with re-scaling. (a) Probability densities from the NEIC worldwide catalog. (b) Previous data, after re-scaling, with a fit of the scaling function , see Eq. (138).
Reprinted figure from Ref. [371].
Bak et al. and Corral are the main two proponents of the idea of a universal scaling law. The validity of the scaling relation Eq. (138) has attracted much interest. For example, Saichev and Sornette [372] carried out an extensive analysis to determine the distribution of the inter-event time based on the Epidemic-Type Aftershock Sequences (ETAS) model (see more details in the following section), and they found that it is only approximately universal and of a gamma form, assuming that in Eq. (134) has a value close to 1, and the branching ratio of seismicity, the average number of events each event triggers, is around 0.7–1. Then Molchan [373] published a rigorous mathematical study on the earthquake inter-event time, and proved that if the scaling distribution would be universal, the functional form must follow an exponential function. Touati et al. analyzed the variation of the distribution for both real data (SCEC catalog) and ETAS simulation data, and suggested that it is not universal [374]. They have shown that the distribution is a bimodal mixture distribution dominated by correlated aftershocks at short waiting times and independent events at longer times.
3.3.2. Modeling seismic time series by the point process approach
There are various statistical earthquake models for describing the occurrences process of earthquakes that can be used for real-time earthquake forecasts [375]. The principle of these models is to evaluate the probabilities of earthquake occurrence by using a point process approach. Among the different models, the ETAS model, which describes the features of earthquake clustering of mainshocks, foreshocks and aftershocks, has become a standard model for testing hypotheses and a starting point for short-term earthquake forecasts [376], [377], [378], [379].
Here we will focus on the ETAS model, which is used to generate synthetic earthquake catalogs. The ETAS model was developed by Ogata [369], [380], [381] who observed that seismic activity can be well described by the Gutenberg–Richter law Eq. (133), and the Omori law Eq. (134). The conditional rate in the ETAS model is given by,
| (139) |
where are the times of the past events and are their magnitudes; is the history of occurrence. provides the probability to have an earthquake above a threshold magnitude at time , given the earthquake history. Here, is the occurrence rate of earthquakes in the Omori law at zero lag [374], and is called the productivity parameter defined in Eq. (135). The ETAS model can also be written in terms of a stochastic integral [382],
| (140) |
where if an infinitesimal element would include an event for some , otherwise . The five parameters represent some characteristics of seismic activity of the region. Therefore, they vary spatially, and also temporally in some cases.
Then the ETAS model was extended to a space–time phase with the conditional intensity function [383],
| (141) |
where still is the background intensity, which is a function of space, but not of time; is the expected number of events triggered from an event of a magnitude in the form
| (142) |
is the probability density function of the occurrence times of the triggered events,
| (143) |
is the spatial distribution of the triggered events, which can be expressed in the following two ways: a short-range Gaussian decay,
| (144) |
or a long-range inverse power decay,
| (145) |
The ETAS model has been successfully used for operational earthquake forecasting, e.g., the complex Amatrice–Norcia seismic sequence [384], next-day earthquake forecasts for the Japan region [385] and California region [386]. More general discussions on modeling seismic time series by the point process approach are given in Ref. [387].
3.3.3. Memory analysis
In this subsection, we will review the memory analysis that has been applied to seismic records. The first method is the so-called detrended fluctuation analysis (DFA), which is used to detect long-range correlations or long-term memory of diverse time series, such as DNA sequences and climate records [180]. Details of the DFA are presented in Section 2.3.3. According to Eq. (70), if the time series has a long-term memory, the fluctuation function increases according to a power-law relation with a exponent . The DFA has been applied to earthquake interoccurrence times for the first time by Lennartz et al. [388]. They tested the real and the synthetic records for long-term correlations by employing the first two orders of the detrended fluctuation analysis DFA0 and DFA1 on the SCEC catalog (1995–1998) and the NCSN catalog (1995–1998). They found that there exists a long-term memory between seismic events in the Californian catalogs, which show up in characteristic fluctuations in both magnitudes and interoccurrence times. Both DFA0 and DFA1 have resulted in a DFA exponent , independently of the threshold and the catalog, see Fig. 45.
Fig. 45.
Detrended fluctuation analysis of the interoccurrence times from the Californian catalogs. (a) For all earthquakes with magnitude , and (b) . Black circles indicate the SCEC catalog (1995–1998) and red squares stand for the NCSN catalog (1995–1998), blue triangles represent an artificial Gutenberg–Richter distributed correlated dataset with . The open symbols show the DFA0 results and the filled symbols the DFA1 results. The corresponding slopes are represented by straight lines with .
Figure from Ref. [388].
A similar analysis, DFA2, has been applied to the real Israeli and Italian catalogs by Fan et al. [212]. They found that the exponent was also very close to 0.75 for the inter-occurrence time series between earthquake events with different magnitude threshold . Figs. 46a–d show the DFA2 results. They also performed DFA on other seismic variables, such as the number of earthquake events and the released energy within a coarse time window . The energy of earthquakes was defined as , where denotes the number of events that occurred between and , and denotes the magnitude of the event. To deal with more homogeneous time series, Fan et al. switched to for and zero for and for and zero for [212]. Next, applying the DFA analysis for the time series and in the Israeli and Italian catalogs, with different time windows , were tested. It was found that for both regions and for all studied magnitudes, the value of the scaling exponent is quite robust , i.e., the size of does not affect the memory exponent . Thus, the return intervals, the number of events and the released energy are significantly long-term correlated and have a very similar scaling exponent. The memory analysis has also been applied on the ETAS model. The DFA2 of the inter-occurrence times, with the parameters , , , and , see Eq. (139), yields and is shown in Fig. 46e.
Fig. 46.
Interoccurrence time series and DFA from the Israeli, Italian and ETAS catalogs. (a) Interoccurrence time series between earthquake events from the Israeli (a) and Italian (b) catalogs using magnitude threshold . DFA of the interoccurrence times from the (c) Israeli and (d) Italian catalogs with different values. (d) DFA of the interoccurrence times from the ETAS model, with parameters , , , and , see Eq. (139). The solid line is the best fitting line with slope , R-square . For comparison, the shuffled data with slope , indicating no memory, are presented in (d).
Reprinted figure from Ref. [212].
Another common method for studying memory in the occurrence of earthquakes is called conditional probability (CP), which was introduced by Livina et al. [389]. Considering a time series of recurrence intervals, they sorted it in ascending order and divided it into four 25% quantiles; i.e., the first quantile, , represents the shortest 25% of waiting times, etc. The distribution of recurrence times , that follow a prior recurrence time , , was studied, where belongs to either one of the quantiles at the extremes, or . Note that for records without memory, should be independent of and should be identical to . For the real data, Livina et al. found that depends strongly on the previous recurrence time , such that short recurrence times lead to short ones, and long recurrence times follow long ones (see Figs. 47a, c for the Israeli and Italian catalogs). To quantify and measure the level of memory, Fan et al. analyzed the cumulative distribution function (CDF) of the recurrence times and denoted the CDF for , and as , and , respectively. The strength of the memory for is defined as
| (146) |
and similarly, the level of memory for is
| (147) |
Thus, and , and higher (or ), imply stronger memory and (or ), implies no memory [212]. The results are shown in Fig. 47b and d for the Israeli and Italian earthquake catalogs. They found for and of the Israeli catalog, whereas for and of the Italian catalog [212]. Further study suggests that the values of are robust and do not depend on . To study the dependence of the correlations (, , and ) on the geographical location (tectonic setting), they performed the DFA and CP analysis for other earthquake catalogs, including New Zealand, Southern California Earthquake Center, Japan unified hIgh-resolution relocated catalog for earthquakes and Preliminary Determination of Epicenters global earthquake catalogs. It has been found that for all catalogs and for all studied magnitudes the values of , , and are quite robust.
Fig. 47.
Memory analyses for the Israeli, Italian and ETAS catalogs. (a, c, e) Conditional PDF and (b, d, f) CDF of the recurrence times for the (a, b) Israeli catalog above the threshold = 2.0, for the (c, d) Italian catalog above the threshold = 3.0 and for the (e, f) ETAS catalog above the threshold = 2.0.
Reprinted figure from Ref. [212].
Finally, the memory analyses DFA2 and CP, were performed in ETAS models, by measuring the coefficients , and , as shown in Fig. 46, Fig. 47. The results indicate that the empirically observed earthquake memory (for Israeli catalog) can be reproduced only for a narrow range of the model’s parameters. Moreover, the origin of memory in the ETAS model is influenced by: (i) the model’s background (noise) rate parameter which, affects the memory through the interference of temporally overlapping aftershock subsequences, i.e., smaller leads to stronger memory, and (ii) the branching ratio : the exponent relating the production of aftershocks as a function of magnitude, , and the power of Omori’s law can also affect the memory through the branching ratio of the ETAS model, i.e., smaller and larger result in a stronger memory (see Figures. 11 and 12 in Ref. [212]).
More recently, a lagged CP method was introduced by Zhang et al. to study a possible long-term memory in both the interevent times and distances of earthquakes [390]. The CP of times and distances were defined as and , respectively, where belongs to the or group. is the lagged th inter-event time that follows . In order to quantify the level of memory, was introduced, where is the common area of the PDF between and . Here . Similarly, represents the level of memory for the inter-event distances. Interestingly, it has been shown that can be expressed by the following scaling form,
| (148) |
where and are constants, as for the Gutenberg–Richter law. The distribution of , and their corresponding scaling functions for the Italian catalog are presented in Fig. 48, where and for the inter-event times ; and for the inter-event distances . The scaling functions shown in Fig. 48c and d suggest a crossover between two distinct power-law relations with . Both scaling functions exhibit a significant crossover at . These results indicate that the memory measure of different grid sizes and different magnitude thresholds can be rescaled into a single function. However, it was found that the memory function in the ETAS model is very different from that of real earthquake catalogs, i.e., the model’s memory is weaker (stronger) on short (long) timescale compared to the real catalogs. Moreover, the model does not exhibit a clear crossover observed in the real catalogs.
Fig. 48.
The lagged CP memory analysis for the inter-event times and distances from the Italian catalog. The memory measures (a) and (b) as a function of the lag index . Rescaled memory measure (c) for inter-event times and (d) distances. Colors represent different grid sizes . The shapes of the symbols represent different magnitude thresholds .
Reprinted figure from Ref. [390].
3.3.4. Earthquake forecasting
Earthquakes are one of the most destructive natural disasters in the world. Skilled and reliable earthquake forecasting remains an ultimate goal. The term earthquake prediction is usually referring to the specification of the occurrence time, location or magnitude of a future earthquake. However, “the term earthquake forecasting usually refers to the evaluation of the occurrence probability of an earthquake inside a hypercell of volume centered in the point . Therefore, the fundamental quantity is the occurrence probability conditioned on the whole set of information available at time ” [36]. The probability of having an earthquake at time , in the th interval conditioned to the previous history is
| (149) |
where is the local conditional rate as defined in Eqs. (139) or (141), denotes the center of the th cell. The forecasting probability, the integral over of the occurrence rate , depends on the volume of the hypercell , i.e., the smaller , the more accurate is the evaluation of . Secondly, the temporal extension of also influences the forecasting accuracy. According to the time scale of , one can separate arbitrarily Long-Term from Short-Term forecasting [391]: earthquake Long-Term forecasting, for in the interval of decades to centuries; Intermediate-Term forecasting, for of the order of months and Short-Term forecasting, for in the interval from few seconds up to several weeks. Short-Term forecasting is usually subdivided into post-seismic and pre-seismic forecasting, referring to the aftershock and foreshock of a mainshock. It is notable that the post seismic forecasting is still very important from the point of view of risk management, since aftershocks can have sizes comparable or even larger than their triggering mainshock. Long-Term forecasting, however, is probably the most relevant from the engineering point of view, such as urban planning risk assessment. Based on the early warning foreshock observations, one could successfully predict some big earthquakes, such as the 1975 Haicheng, China earthquake [392] and the 1995 Kozani–Grevena, Greece earthquake [393]. Nevertheless, most earthquakes do not present significant precursory patterns, e.g., the 2004 Parkfield (California) earthquake [394]. Thus the evaluation of foreshocks or precursory patterns is still an open question. Since most earthquake models are based on the well-established empirical laws, aftershock spatio-temporal occurrence clustering, as the ETAS model, they are able, in some degree, to provide reliable risk assessment only for the Long-Term and the post-seismic Short-Term forecasting but not for the foreshocks. Nevertheless, how to validate a forecasting model is still of great importance. In the following, we will review various methods for evaluating earthquake predictions and earthquake forecasts.
Receiver operating characteristic diagram
The receiver operating characteristic (ROC) diagram is a graphical plot that illustrates the prediction quality of a binary classifier system as its discrimination threshold is varied. For evaluating earthquake predictions, if an earthquake is expected (“YES”) with a probability , where is a threshold, we call it a hit, if an event has occurred; if earthquakes are not expected (“NO”) in the cell, we call it a , if an event has occurred. Each “YES” prediction in which no corresponding earthquake is observed is a false alarm, and each “NO” prediction in which no earthquake occurred is acorrect rejections. In this representation, there are four possible combinations of alarm declaration and event observation, see Table 1 for the number of each of these contingencies. Here we define as the number of hits, as the number of false alarms, as the number of misses and as the number of correct rejections, respectively. We define a true positive rate () as
| (150) |
and false positive rate () as
| (151) |
When and are plotted together on the square [0,1] [0,1], the resulting metric is called the ROC, whereas the perfect prediction corresponds to the point with coordinates and , the diagonal line represents the long-term behavior of random guessing. One can obtain the full ROC curve by changing continuously. Here we show an aftershock forecasting ROC curve by using a deep learning method in Fig. 49 as an example.
Table 1.
Contingency table for a binary event.
| Observation |
|||
|---|---|---|---|
| YES | NO | ||
| Forecast | YES | a number of hits | b number of false alarms |
| NO | c number of misses | d number of correct rejections | |
Fig. 49.
An example of ROC curves based on the neural network. (a) The true positive rate is plotted versus the false alarm rate. (b) For a synthetic case of a 60-km-long, right-lateral strike-slip fault (red lines) at a depth of 10 km. The dashed diagonal represents random prediction (the null-hypothesis).
Reprinted figure from Ref. [395].
The Molchan diagram
Closely related to the ROC is the Molchan diagram, which is an error diagram that allows to compare the prediction of the test model and another generic reference model [396]. It is a plot of the miss rate, , and the fraction of experiment space–time volume, , occupied by alarms or YES predictions. The best prediction in the Molchan diagram is the point (). In particular, the probability of obtaining or more hits by chance, given that there have been observed target earthquakes, is described by the binomial distribution
| (152) |
where stands for the binomial coefficient. One can obtain a confidence level curve in the Molchan diagram by fixing and changing continuously. Therefore, a very small value suggests that the alarm set has high skill.
The Number test (N-test)
The N-test is used to access how well the total number of forecasted earthquakes matches the number of events observed [397]. The target earthquakes are assumed to follow a generalized Poisson distribution, and the mass function of the negative binomial distribution (NBD) can be expressed as [384]
| (153) |
where is the gamma function, is the number of target earthquakes, and are the two parameters of the distribution. Then NBD can be derived as
| (154) |
where is the Poisson distribution and is assumed to follow a gamma distribution
| (155) |
where are the parameters of the gamma distribution with and . Next, we calculate the parameters and of the gamma distribution. To interpret the N-test results, one can use a one-sided test with an effective significance value , which is half of the intended significance value . Fig. 50c shows an example of the N-test.
Fig. 50.
The statistical tests for earthquake forecasting for the complex Amatrice–Norcia seismic sequence. (a) The Space test (S-test). The red dashed horizontal line is the critical value for rejection. (b) Expected number of target earthquakes for each forecast. (c) The Space test (S-test): probability distribution of the expected number of target earthquakes with a 95% confidence interval (marked by red) and the observed number of target earthquakes (vertical dashed blue line). (d) The CDF of the forecast and observed frequency–magnitude distribution.
Figure from Ref. [384].
The Space test (S-test)
The S-test is a likelihood test where only the spatial distributions of the forecast and the observation are considered [398]. The -test can be summarized by a
| (156) |
where is the th simulated spatial likelihood, is the set of simulated spatial likelihoods, is the likelihood of the spatial forecast relative to the observed, is the number of elements in a set . If is less than critical significance value , the observed spatial distribution is inconsistent with the forecast. However, values close to 1 indicate optimal spatial forecasts. We show an example of the S-test in Fig. 50a.
Besides the aforementioned methods, there are still various other methods that have been developed to evaluate the accuracy of a forecasting model, such as, the Likelihood test (L-test), the Likelihood Ratio test (R-test) and the Magnitude test (M-test). An instructive review on the evaluation of earthquake predictions and earthquake forecasts can be found in Ref. [399].
As discussed in the last section, we studied the possible origin of memory in earthquakes for both real catalogs and ETAS models. Here, we will show that the memory analysis can significantly improve the short-term forecasting rate for the real earthquake catalog. In estimating the ETAS model parameters for a given earthquake catalog, the ETAS parameters are commonly inverted from the data based on the point-process maximum likelihood (ML) method, by the Davidon–Fletcher–Powell algorithm [380] or by simulated annealing [400]. For example, by using the ML method, one can obtain , , , and , see Eq. (139), for the Italian catalog [400]. When considering the memory, however, the ETAS model can reproduce the same memory as in real catalogs, only for a small range of parameter values, i.e., , , , and [212]. As a test case the cumulative number of events, , after the Capitignano 5.7 main shock that happened on 18 January 2017 [401], was forecasted by using the ETAS model. The cumulative number at time is calculated by integrating Eq. (139) from 0 to . This way the forecasting accuracy within 14 days after the main shock can be improved by more than 20% by considering the memory. Moreover, a revised and generalized ETAS model was proposed recently by Zhang et al. in which the short- and long-term/distance memory was reproduced accurately [402]. The new ETAS model is also found to significantly improve earthquake forecasting for the Italian and South California earthquake catalogs.
4. Conclusions and perspectives
In this article, we have reviewed statistical physics and complex networks-based techniques that advance our knowledge on the complex Earth system, a relatively novel branch of geophysics. These techniques can help to address the understanding as well as the prediction of climate variability, Earth geometric relief features and earthquakes. In this section we try to draw a few concluding remarks and address the perspectives that remain still open for future research. We believe that these novel approaches will attract the attention of scientists in the related fields.
In Section 2 we started by describing the overall methodology based on statistical physics for analyzing important aspects of complex Earth subsystems. It includes complex networks, percolation theory, tipping points analysis, entropy theory and complexity. Although it was shown that the aforementioned approaches can be successfully applied to Earth systems individually or in a combination, there is still a lot of work ahead in order to develop a proper and comprehensive framework. Among the different open problems to be solved, we highlight the following four: (i) The need of gathering a better knowledge and understanding on the underlying physical mechanisms; (ii) The need of extending concepts of CNs to a more comprehensive description, such as multilayer climate networks [403]. This is since the climate is a coupled and multilayered system; (iii) The need of developing a universal theory of critical phenomena (percolation) in climate systems, in particular for out-of-equilibrium systems; (iv) The need of proposing a principle on how to anticipate the tipping points and entropy of the Earth system by means of time series of multiple spatio-temporal variables.
In Section 3, we have continued by reviewing the applications of statistical physics approaches to different Earth subsystems. Specifically, five weather and climate dynamical scenarios were highlighted in Section 3.1, including, El Niño-Southern Oscillation, Indian summer monsoon, extreme rainfall, atmospheric circulation and Atlantic meridional overturning circulation. We suggested that the evolving CNs (and other combined approaches) interactions and patterns can serve as novel predictors which significantly improve the predictions. Beside the above mentioned scenarios, the CNs method was also widely applied to other high-impact phenomena, such as the westward propagation of the Atlantic multidecadal oscillation [99], the detection of teleconnection paths [62], the identifying of causal gateways and mediators [404], the early prediction of extreme stratospheric polar vortex states [405], the impacts of carbon dioxide (CO2) on global SAT [406], etc. In spite of the great achievements, there are still many unexplored problems related to climate systems that merit further attention. Therefore, further topics are needed to be investigated, for example, (i) how human activities have changed and continue to change the Earth’s oceanic and atmospheric composition, some of these changes have a direct or indirect impact on the energy balance of the Earth and are thus drivers of climate change; (ii) The statistical mechanics and CNs behaviors in Earth System Models, ranging from simple energy balance models to general circulation models; (iii) The projected short-term and long-term abrupt phase transitions in paleoclimate, in particular, the role of sea ice and Snowball-Earth initiations [407], [408], [409]; (iv) Improving the predictability of severe convective weather processes including thunderstorms, hail and tornadoes by using the CNs approach.
In Section 3.2, we have reviewed the current literature on the statistical features and the percolation framework of the Earth’s surface topography. We have pointed out the evidence for abrupt transitions that occurred during the evolution of the Earth’s relief network, indicative of a continental/cluster aggregation. A further analysis via fractional Brownian motion models suggests that long-range correlations may play a key role in the observed discontinuity on Earth. This research may facilitate the understanding of the geometrical phase transition on Earth, but also can be used to identify the critical nodes for future global change in Earth’s relief network. In particular, (i) the future movement of tectonic plates, as well as (ii) the dynamic evolution of these critical nodes are of key importance and thus need to be further addressed.
In Section 3.3, we first presented a description of the well established empirical basic laws of earthquakes, including the Gutenberg–Richter, Omori and productivity laws. We then discussed the scaling hypothesis of the inter-event distributions. An epidemic-type aftershock sequence model (ETAS) and various methods for evaluating earthquake predictions and earthquake forecasts have been also reviewed. At last, we have shown that the two proposed memory analysis approaches, DFA and CP, can significantly improve the short-term forecasting rate for real earthquake catalogs. Nevertheless, earthquake prediction research has been plagued by controversy, and it remains an outstanding challenge. Besides the improvement of short-term aftershock forecasting, we also emphasize the potential of new directions. (i) The wide applications of tipping points and memory analysis in theoretical earthquake models which account for accelerated moment release and foreshock occurrence together with other precursory patterns, where mainshocks were treated as characteristic earthquakes within a seismic cycle [410]. (ii) The development of an earthquake forecasting model which is implemented for describing foreshock organization and memory behaviors. (iii) Motivated by the successful applications of network theory to the prediction of climate phenomena, the proposing of an earthquake network framework based on the occurrence time series [411], or in particular the seismic waves (elastic body and shear waves) and elastogravity signals preceding direct seismic waves [412].
One of the key features of statistical physics-based approaches reviewed here is the ability to better and reliably forecast the complex Earth phenomena, such as El Niño events, extreme rainfall in the Eastern Central Andes, Indian summer monsoon, the collapse of the Atlantic multidecadal oscillation and the occurrence of earthquakes. Moreover, we observed that artificial intelligence and deep learning techniques [413] have achieved great success during recent years in many fields, such as phase transitions in statistical physics [414], [415], [416], data-driven Earth system science [417], ENSO forecasts [294], [295], Indian monsoon rainfall [418], as well as the forecasting aftershock patterns [395] and detecting earthquakes [419] in seismic systems. In fact, we are confident that the combination and complement of network-based and artificial intelligence-based skills will boost each other. For instance, an application of machine learning to network attribute vectors (products similarity) can predict successful and failing firms with much better accuracy than current state of the art techniques for market forecasting [420]. In addition, deep learning systems can be regarded as complex networks, which thus gain some insights into the structural and functional properties of the computational graph resulting from the learning process [421].
As a final remark, there is still room for many approaches considering the analysis of climate resilience of societies, ecosystems and economies by using the complex network theory. We currently lack appropriate models to better understand or predict the effects of cascading failures [30] triggered by the increasing adverse effect of extreme climate/weather events on interdependent critical infrastructures. Closing this knowledge gap is crucial for developing means to achieve both climate and infrastructure resilience. Another very relevant subject of investigation that will certainly attract huge attention is the assessing and quantifying of the complex climate–health relationships. There is an overwhelming consensus that climate conditions, including temperatures and spatial–temporal distribution of precipitation, has key implications for human health [422]. Moreover, the morbidity and outbreak of some disease, such as the vector-borne (malaria and dengue fever) disease, the ongoing COVID-19 pandemic [423], and influenza are strongly affected by the climate change or the environment [424], [425], [426], [427], [428]. However, the climatic influences are often excluded from consideration in the traditional epidemiologic models [113], e.g., the SIR, SIRS and SEIR models. What we need to emphasize is that traditional epidemiologic models with taking into account the climate factor could be a very promising road towards a deeper understanding of epidemic processes and assess the health consequences of climate change both regionally and globally.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
We would like to acknowledge gratefully all colleagues with whom we maintained interactions and discussions on the topic in our report.
In particular, we would like to thank A. Agarwala, N. Boers, A. Bunde, D. Chen, R. Cohen, H. A. Dijkstra, G. Falcone, L. Da, N. B. George, G. Dong, J. F. Donges, Z. Fu, J. Gao, A. Gozolchiani, H. Hof, R. Hofstetter, H. Inoue, V. Livina, T. M. Lenton, Y. Liu, W. Lucht, N. Marwan, W. Marzocchi, M. McPhaden, J. Nagler, P. Nooteboom, A. A. Saberi, L. M. Shekhtman, H. E. Stanley, V. Stolbova, Y. Sun, E. Surovyatkina, K. Yamasaki, N. Yuan, Y. Zhang, D. Zhou.
This work was partly supported by the ‘East Africa Peru India Climate Capacities — EPICC’ project, which is part of the International Climate Initiative (IKI), Germany. The Federal Ministry for the Environment, Nature Conservation and Nuclear Safety (BMU), Germany supports this initiative on the basis of a decision adopted by the German Bundestag. The Potsdam Institute for Climate Impact Research (PIK), Germany is leading the execution of the project together with its project partners The Energy and Resources Institute (TERI) and the Deutscher Wetterdienst (DWD). S.H. thanks the Italian Ministry of Foreign Affairs and International Cooperation jointly with the Israel Ministry of Science, Technology, and Space (MOST); the Israel Science Foundation, and the EU H2020 project RISE, Europe for financial support. J.K. was supported by the Russian Ministry of Science and Education Agreement No. 075-15-2020-808.
Editor: I. Procaccia
Footnotes
The size of the system is .
In oceanography, a sverdrup (symbol: Sv) is a non-SI metric unit of flow, with 1 Sv equal to 1 million cubic meters per second.
The values of ONI are here: https://origin.cpc.ncep.noaa.gov/products/analysis_monitoring/ensostuff/ONI_v5.php.
For more details: https://climatedataguide.ucar.edu/climate-data/nino-sst-indices-nino-12-3-34-4-oni-and-tni.
For more detailed and updated information have a look at PIK’s information page on the Indian Summer Monsoon Forecast: https://www.pik-potsdam.de/services/infodesk/forecasting-indian-monsoon.
The observed AIRI data can be found in https://mausam.imd.gov.in/imd_latest/contents/rainfall_time_series.php.
It is freely downloadable from: https://www.chikyu.ac.jp/precip/.
Appendix. Acronyms
This Appendix contains two tables of acronyms used throughout the paper: Table A.2 contains the scientific acronyms and Table A.3 the institutional ones.
Table A.3.
Institutional acronyms.
| Acronym | Meaning |
|---|---|
| Assessment Report | |
| Climate Model Intercomparison Project | |
| European Center for | |
| Mid-range Weather Forecast | |
| Japan University Network Earthquake Catalog | |
| Indian Meteorological Department | |
| Intergovernmental Panel on Climate Change | |
| National Center for Atmospheric Research | |
| National Center for Environmental Prediction | |
| National Earthquake Information Center | |
| Program for Climate Model | |
| Southern California Earthquake Center |
Table A.2.
Scientific acronyms.
| Acronym | Meaning |
|---|---|
| Autocorrelation function | |
| All India Rainfall Index | |
| Atlantic Meridional Overturning Circulation | |
| Approximate Entropy | |
| s | Climate networks |
| Detrended fluctuation analysis | |
| Energy Balance Model | |
| Electroencephalogram | |
| El Niño Basin (ENB) | |
| El Niño-Southern Oscillation | |
| Earth System Models | |
| Earth System Science | |
| Epidemic Type Aftershock Sequence | |
| Early warning signals | |
| Fast Met Office/UK Universities Simulator (FAMOUS) | |
| fractional Brownian motion | |
| General Circulation Model | |
| Greenhouse Gases | |
| Indian Summer Monsoon | |
| North Atlantic Oscillation | |
| Onset date | |
| Oceanic Niño Index (ONI) | |
| Receiver Operating Characteristic | |
| Sample entropy | |
| Sea Level Pressure | |
| Sea Surface Temperature | |
| Spring Predictability Barrier | |
| System Sample Entropy | |
| Withdrawal date |
References
- 1.Steffen W., Sanderson R.A., Tyson P.D., Jäger J., Matson P.A., III B.M., Oldfield F., Richardson K., Schellnhuber H.J., Turner B.L., Wasson R.J. Global Change and the Earth System: A Planet Under Pressure. Springer-Verlag; Berlin Heidelberg: 2005. (Global Change - The IGBP Series). https://www.springer.com/gp/book/9783540265948. [DOI] [Google Scholar]
- 2.Steffen W., Richardson K., Rockström J., Schellnhuber H.J., Dube O.P., Dutreuil S., Lenton T.M., Lubchenco J. The emergence and evolution of earth system science. Nat. Rev. Earth Environ. 2020;1(1):54–63. doi: 10.1038/s43017-019-0005-6. https://www.nature.com/articles/s43017-019-0005-6. [DOI] [Google Scholar]
- 3.Vernadsky V.I. Springer Science & Business Media; 1998. The Biosphere. [Google Scholar]
- 4.Lovelock J.E., Margulis L. Atmospheric homeostasis by and for the biosphere: the gaia hypothesis. Tellus. 1974;26(1–2):2–10. doi: 10.1111/j.2153-3490.1974.tb01946.x. https://onlinelibrary.wiley.com/doi/abs/10.1111/j.2153-3490.1974.tb01946.x. [DOI] [Google Scholar]
- 5.Edwards P.N. MIT Press; 2010. A Vast Machine: Computer Models, Climate Data, and the Politics of Global Warming. [Google Scholar]
- 6.Oreskes N. Oxford University Press; 1999. The Rejection of Continental Drift: Theory and Method in American Earth Science. [Google Scholar]
- 7.N.A.C.E.S.S. Committee . National Aeronautics and Space Administration; 1986. Earth System Science Overview: A Program for Global Change. [Google Scholar]
- 8.Brundtland G.H., Khalid M., Agnelli S., Al-Athel S., Chidzero B. Oxford University Press; 1987. Our Common Future: Report of the World Commission on Environment and Development. [Google Scholar]
- 9.Schellnhuber H.J. ‘Earth system’ analysis and the second copernican revolution. Nature. 1999;402(6761):C19–C23. doi: 10.1038/35011515. https://www.nature.com/articles/35011515. [DOI] [Google Scholar]
- 10.Boiseau M., Ghil M., Juillet-Leclerc A. Climatic trends and interdecadal variability from south-central Pacific coral records. Geophys. Res. Lett. 1999;26(18):2881–2884. doi: 10.1029/1999GL900595. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/1999GL900595. [DOI] [Google Scholar]
- 11.Taricco C., Ghil M., Alessio S., Vivaldo G. Two millennia of climate variability in the central mediterranean. Clim. Past. 2009;5(2):171–181. doi: 10.5194/cp-5-171-2009. https://www.clim-past.net/5/171/2009/ [DOI] [Google Scholar]
- 12.Cheng H., Edwards R.L., Sinha A., Spötl C., Yi L., Chen S., Kelly M., Kathayat G., Wang X., Li X., Kong X., Wang Y., Ning Y., Zhang H. The asian monsoon over the past 640,000 years and ice age terminations. Nature. 2016;534(7609):640–646. doi: 10.1038/nature18591. Number: 7609 Publisher: Nature Publishing Group, https://www.nature.com/articles/nature18591. [DOI] [PubMed] [Google Scholar]
- 13.Esper J., Cook E.R., Schweingruber F.H. Low-frequency signals in long tree-ring chronologies for reconstructing past temperature variability. Science. 2002;295(5563):2250–2253. doi: 10.1126/science.1066208. https://science.sciencemag.org/content/295/5563/2250. [DOI] [PubMed] [Google Scholar]
- 14.Petit J.R., Jouzel J., Raynaud D., Barkov N.I., Barnola J.-M., Basile I., Bender M., Chappellaz J., Davis M., Delaygue G., Delmotte M., Kotlyakov V.M., Legrand M., Lipenkov V.Y., Lorius C., PÉpin L., Ritz C., Saltzman E., Stievenard M. Climate and atmospheric history of the past 420,000 years from the Vostok ice core, Antarctica. Nature. 1999;399(6735):429–436. doi: 10.1038/20859. https://www.nature.com/articles/20859. [DOI] [Google Scholar]
- 15.Jouzel J., Masson-Delmotte V., Cattani O., Dreyfus G., Falourd S., Hoffmann G., Minster B., Nouet J., Barnola J.M., Chappellaz J., Fischer H., Gallet J.C., Johnsen S., Leuenberger M., Loulergue L., Luethi D., Oerter H., Parrenin F., Raisbeck G., Raynaud D., Schilt A., Schwander J., Selmo E., Souchez R., Spahni R., Stauffer B., Steffensen J.P., Stenni B., Stocker T.F., Tison J.L., Werner M., Wolff E.W. Orbital and millennial antarctic climate variability over the past 800,000 years. Science. 2007;317(5839):793–796. doi: 10.1126/science.1141038. https://science.sciencemag.org/content/317/5839/793. [DOI] [PubMed] [Google Scholar]
- 16.North G.R., Cahalan R.F., Coakley J.A. Energy balance climate models. Rev. Geophys. 1981;19(1):91–121. doi: 10.1029/RG019i001p00091. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/RG019i001p00091. [DOI] [Google Scholar]
- 17.Stocker T.F., Qin D., Plattner G.-K., Tignor M., Allen S.K., Boschung J., Nauels A., Xia Y., Bex V., Midgley P.M. Cambridge university press; Cambridge New York: 2013. Climate change 2013: The physical science basis. [Google Scholar]
- 18.Parson E.A., Fisher-Vanden D., Karen G.-K. Integrated assessment models of global climate change. Annu. Rev. Energy Environ. 1997;22(1):589–628. doi: 10.1146/annurev.energy.22.1.589. [DOI] [Google Scholar]
- 19.van Vuuren D.P., Lowe J., Stehfest E., Gohar L., Hof A.F., Hope C., Warren R., Meinshausen M., Plattner G.-K. How well do integrated assessment models simulate climate change? Clim. Change. 2011;104(2):255–285. doi: 10.1007/s10584-009-9764-2. [DOI] [Google Scholar]
- 20.Flato G.M. Earth system models: an overview. WIREs Clim. Change. 2011;2(6):783–800. doi: 10.1002/wcc.148. https://onlinelibrary.wiley.com/doi/abs/10.1002/wcc.148. [DOI] [Google Scholar]
- 21.Clark W.C., Munn R.E. Cambridge University Press; 1986. Sustainable Development of the Biosphere. [Google Scholar]
- 22.Crutzen P.J. Geology of mankind. Nature. 2002;415(6867):23. doi: 10.1038/415023a. https://www.nature.com/articles/415023a. [DOI] [PubMed] [Google Scholar]
- 23.Lenton T.M., Held H., Kriegler E., Hall J.W., Lucht W., Rahmstorf S., Schellnhuber H.J. Tipping elements in the Earth’s climate system. Proc. Natl. Acad. Sci. 2008;105(6):1786–1793. doi: 10.1073/pnas.0705414105. http://www.pnas.org/content/105/6/1786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Rockström J., Steffen W., Noone K., Persson A., Chapin F.S., Lambin E.F., Lenton T.M., Scheffer M., Folke C., Schellnhuber H.J., Nykvist B., de Wit C.A., Hughes T., van der Leeuw S., Rodhe H., Sörlin S., Snyder P.K., Costanza R., Svedin U., Falkenmark M., Karlberg L., Corell R.W., Fabry V.J., Hansen J., Walker B., Liverman D., Richardson K., Crutzen P., Foley J.A. A safe operating space for humanity. Nature. 2009;461(7263):472–475. doi: 10.1038/461472a. https://www.nature.com/articles/461472a. [DOI] [PubMed] [Google Scholar]
- 25.Steffen W., Rockström J., Richardson K., Lenton T.M., Folke C., Liverman D., Summerhayes C.P., Barnosky A.D., Cornell S.E., Crucifix M., Donges J.F., Fetzer I., Lade S.J., Scheffer M., Winkelmann R., Schellnhuber H.J. Trajectories of the earth system in the anthropocene. Proc. Natl. Acad. Sci. 2018;115(33):8252–8259. doi: 10.1073/pnas.1810141115. https://www.pnas.org/content/115/33/8252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Stanley H. Clarendon, Oxford; 1971. Phase Transitions and Critical Phenomena. [Google Scholar]
- 27.Chandler D. Oxford University Press; 1987. Introduction to Modern Statistical Mechanics; p. 288. [Google Scholar]
- 28.Huang K. CRC press; 2009. Introduction to Statistical Physics. [Google Scholar]
- 29.Sethna J. Oxford University Press; 2006. Statistical Mechanics: Entropy, Order Parameters, and Complexity, vol. 14. [Google Scholar]
- 30.Buldyrev S.V., Parshani R., Paul G., Stanley H.E., Havlin S. Catastrophic cascade of failures in interdependent networks. Nature. 2010;464(7291):1025–1028. doi: 10.1038/nature08932. http://www.nature.com/nature/journal/v464/n7291/full/nature08932.html. [DOI] [PubMed] [Google Scholar]
- 31.Scheffer M. Princeton University Press; 2009. Critical Transitions in Nature and Society. [Google Scholar]
- 32.Peters O., Neelin J.D. Critical phenomena in atmospheric precipitation. Nat. Phys. 2006;2(6):393–396. doi: 10.1038/nphys314. http://arxiv.org/abs/cond-mat/0606076. [DOI] [Google Scholar]
- 33.Golden K.M., Ackley S.F., Lytle V.I. The percolation phase transition in sea ice. Science. 1998;282(5397):2238–2241. doi: 10.1126/science.282.5397.2238. https://science.sciencemag.org/content/282/5397/2238. [DOI] [PubMed] [Google Scholar]
- 34.Mandelbrot B.B. Stochastic models for the earth’s relief, the shape and the fractal dimension of the coastlines, and the number-area rule for islands. Proc. Natl. Acad. Sci. 1975;72(10):3825–3828. doi: 10.1073/pnas.72.10.3825. http://www.pnas.org/content/72/10/3825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Sornette A., Sornette D. Self-organized criticality and earthquakes. Europhys. Lett. 1989;9(3):197–202. doi: 10.1209/0295-5075/9/3/002. [DOI] [Google Scholar]
- 36.de Arcangelis L., Godano C., Grasso J.R., Lippiello E. Statistical physics approach to earthquake occurrence and forecasting. Phys. Rep. 2016;628:1–91. doi: 10.1016/j.physrep.2016.03.002. http://www.sciencedirect.com/science/article/pii/S0370157316300011. [DOI] [Google Scholar]
- 37.Watts D.J., Strogatz S.H. Collective dynamics of ‘small-world’ networks. Nature. 1998;393(6684):440–442. doi: 10.1038/30918. http://www.nature.com/nature/journal/v393/n6684/full/393440a0.html. [DOI] [PubMed] [Google Scholar]
- 38.Barabási A.-L., Albert R. Emergence of scaling in random networks. Science. 1999;286(5439):509–512. doi: 10.1126/science.286.5439.509. http://science.sciencemag.org/content/286/5439/509. [DOI] [PubMed] [Google Scholar]
- 39.Boccaletti S., Latora V., Moreno Y., Chavez M., Hwang D.U. Complex networks: Structure and dynamics. Phys. Rep. 2006;424(4–5):175–308. doi: 10.1016/j.physrep.2005.10.009. http://www.sciencedirect.com/science/article/pii/S037015730500462X. [DOI] [Google Scholar]
- 40.Newman M. Oxford university press; 2010. Networks: An Introduction. [Google Scholar]
- 41.Cimini G., Squartini T., Saracco F., Garlaschelli D., Gabrielli A., Caldarelli G. The statistical physics of real-world networks. Nat. Rev. Phys. 2019;1(1):58–71. doi: 10.1038/s42254-018-0002-6. https://www.nature.com/articles/s42254-018-0002-6. [DOI] [Google Scholar]
- 42.Barabási A.-L., Pósfai M. Cambridge University Press; 2016. Network Science. [Google Scholar]
- 43.Tsonis A.A., Roebber P.J. The architecture of the climate network. Physica A. 2004;333:497–504. doi: 10.1016/j.physa.2003.10.045. http://www.sciencedirect.com/science/article/pii/S0378437103009646. [DOI] [Google Scholar]
- 44.Yamasaki K., Gozolchiani A., Havlin S. Climate Networks around the Globe are Significantly Affected by El Niño. Phys. Rev. Lett. 2008;100(22) doi: 10.1103/PhysRevLett.100.228501. http://link.aps.org/doi/10.1103/PhysRevLett.100.228501. [DOI] [PubMed] [Google Scholar]
- 45.Donges J.F., Zou Y., Marwan N., Kurths J. Complex networks in climate dynamics. Eur. Phys. J. Spec. Top. 2009;174(1):157–179. doi: 10.1140/epjst/e2009-01098-2. http://link.springer.com/article/10.1140/epjst/e2009-01098-2. [DOI] [Google Scholar]
- 46.Dijkstra H.A., Hernández-García E., Masoller C., Barreiro M. Cambridge University Press; 2019. Networks in Climate. [DOI] [Google Scholar]
- 47.Eubank S., Guclu H., Kumar V.S.A., Marathe M.V., Srinivasan A., Toroczkai Z., Wang N. Modelling disease outbreaks in realistic urban social networks. Nature. 2004;429(6988):180. doi: 10.1038/nature02541. https://www.nature.com/articles/nature02541. [DOI] [PubMed] [Google Scholar]
- 48.Caldarelli G. Oxford University Press; 2007. Scale-Free Networks: Complex Webs in Nature and Technology. http://www.oxfordscholarship.com/view/10.1093/acprof:oso/9780199211517.001.0001/acprof-9780199211517. [Google Scholar]
- 49.Barrat A., Barthélemy M., Vespignani A. Cambridge University Press; 2008. Dynamical Processes on Complex Networks. [Google Scholar]
- 50.Kitsak M., Gallos L.K., Havlin S., Liljeros F., Muchnik L., Stanley H.E., Makse H.A. Identification of influential spreaders in complex networks. Nat. Phys. 2010;6(11):888–893. doi: 10.1038/nphys1746. https://www.nature.com/articles/nphys1746. [DOI] [Google Scholar]
- 51.Cohen R., Havlin S. Cambridge University Press; New York: 2010. Complex Networks: Structure, Robustness and Function. [Google Scholar]
- 52.Barabási A.-L. Cambridge university press; 2016. Network Science. [Google Scholar]
- 53.Albert R., Barabási A.L. Statistical mechanics of complex networks. Rev. Modern Phys. 2002;74(1):47. [Google Scholar]
- 54.Tsonis A.A., Swanson K.L., Roebber P.J. What do networks have to do with climate? Bull. Am. Meteorol. Soc. 2006;87(5):585–595. doi: 10.1175/BAMS-87-5-585. http://journals.ametsoc.org/doi/abs/10.1175/BAMS-87-5-585. [DOI] [Google Scholar]
- 55.Tsonis A.A., Swanson K.L. Topology and predictability of El Niño and La Nina networks. Phys. Rev. Lett. 2008;100(22) doi: 10.1103/PhysRevLett.100.228502. http://link.aps.org/doi/10.1103/PhysRevLett.100.228502. [DOI] [PubMed] [Google Scholar]
- 56.Gozolchiani A., Yamasaki K., Gazit O., Havlin S. Pattern of climate network blinking links follows El Niño events. Europhys. Lett. 2008;83(2):28005. doi: 10.1209/0295-5075/83/28005. http://stacks.iop.org/0295-5075/83/i=2/a=28005. [DOI] [Google Scholar]
- 57.Donges J.F., Zou Y., Marwan N., Kurths J. The backbone of the climate network. Europhys. Lett. 2009;87(4):48007. doi: 10.1209/0295-5075/87/48007. http://stacks.iop.org/0295-5075/87/i=4/a=48007. [DOI] [Google Scholar]
- 58.Steinhaeuser K., Chawla N.V., Ganguly A.R. An exploration of climate data using complex networks. SIGKDD Explor. Newsl. 2010;12(1):25–32. doi: 10.1145/1882471.1882476. http://doi.acm.org/10.1145/1882471.1882476. [DOI] [Google Scholar]
- 59.Wang Y., Gozolchiani A., Ashkenazy Y., Berezin Y., Guez O., Havlin S. Dominant imprint of Rossby waves in the climate network. Phys. Rev. Lett. 2013;111(13) doi: 10.1103/PhysRevLett.111.138501. http://link.aps.org/doi/10.1103/PhysRevLett.111.138501. [DOI] [PubMed] [Google Scholar]
- 60.Guez O., Gozolchiani A., Berezin Y., Wang Y., Havlin S. Global climate network evolves with North Atlantic oscillation phases: Coupling to southern Pacific ocean. Europhys. Lett. 2013;103(6):68006. doi: 10.1209/0295-5075/103/68006. http://stacks.iop.org/0295-5075/103/i=6/a=68006. [DOI] [Google Scholar]
- 61.Gozolchiani A., Havlin S., Yamasaki K. Emergence of El Niño as an autonomous component in the climate network. Phys. Rev. Lett. 2011;107(14) doi: 10.1103/PhysRevLett.107.148501. http://link.aps.org/doi/10.1103/PhysRevLett.107.148501. [DOI] [PubMed] [Google Scholar]
- 62.Zhou D., Gozolchiani A., Ashkenazy Y., Havlin S. Teleconnection paths via climate network direct link detection. Phys. Rev. Lett. 2015;115(26) doi: 10.1103/PhysRevLett.115.268501. http://link.aps.org/doi/10.1103/PhysRevLett.115.268501. [DOI] [PubMed] [Google Scholar]
- 63.Fan J., Meng J., Chen X., Ashkenazy Y., Havlin S. Network approaches to climate science. Sci. China Phys. Mech. Astron. 2017;60(1) doi: 10.1007/s11433-016-0362-2. http://link.springer.com/article/10.1007/s11433-016-0362-2. [DOI] [Google Scholar]
- 64.Fan J., Meng J., Ashkenazy Y., Havlin S., Schellnhuber H.J. Network analysis reveals strongly localized impacts of El Niño. Proc. Natl. Acad. Sci. 2017;114(29):7543–7548. doi: 10.1073/pnas.1701214114. http://www.pnas.org/content/114/29/7543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Meng J., Fan J., Ashkenazy Y., Havlin S. Percolation framework to describe El Niño conditions. Chaos. 2017;27(3) doi: 10.1063/1.4975766. http://aip.scitation.org/doi/abs/10.1063/1.4975766. [DOI] [PubMed] [Google Scholar]
- 66.Meng J., Fan J., Ashkenazy Y., Bunde A., Havlin S. Forecasting the magnitude and onset of El Niño based on climate network. New J. Phys. 2018;20(4) doi: 10.1088/1367-2630/aabb25. http://stacks.iop.org/1367-2630/20/i=4/a=043036. [DOI] [Google Scholar]
- 67.Fan J., Meng J., Ashkenazy Y., Havlin S., Schellnhuber H.J. Climate network percolation reveals the expansion and weakening of the tropical component under global warming. Proc. Natl. Acad. Sci. 2018;115(52):E12128–E12134. doi: 10.1073/pnas.1811068115. https://www.pnas.org/content/115/52/E12128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Ludescher J., Gozolchiani A., Bogachev M.I., Bunde A., Havlin S., Schellnhuber H.J. Improved El Niño forecasting by cooperativity detection. Proc. Natl. Acad. Sci. 2013;110(29):11742–11745. doi: 10.1073/pnas.1309353110. http://www.pnas.org/content/110/29/11742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Mheen M.v.d., Dijkstra H.A., Gozolchiani A., Toom M.d., Feng Q., Kurths J., Hernandez-Garcia E. Interaction network based early warning indicators for the atlantic MOC collapse. Geophys. Res. Lett. 2013;40(11):2714–2719. doi: 10.1002/grl.50515. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1002/grl.50515. [DOI] [Google Scholar]
- 70.Feng Q.Y., Viebahn J.P., Dijkstra H.A. Deep ocean early warning signals of an atlantic MOC collapse. Geophys. Res. Lett. 2014;41(16):6009–6015. doi: 10.1002/2014GL061019. http://onlinelibrary.wiley.com/doi/10.1002/2014GL061019/abstract. [DOI] [Google Scholar]
- 71.Nocke T., Buschmann S., Donges J.F., Marwan N., Schulz H.-J., Tominski C. Review: visual analytics of climate networks. Nonlinear Process. Geophys. 2015;22(5):545–570. doi: 10.5194/npg-22-545-2015. https://www.nonlin-processes-geophys.net/22/545/2015/ [DOI] [Google Scholar]
- 72.West D.B. Prentice hall Upper Saddle River; 2001. Introduction to Graph Theory, vol. 2. [Google Scholar]
- 73.Erdős P., Rényi A. On the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci. 1960;5(1):17–60. [Google Scholar]
- 74.Faloutsos M., Faloutsos P., Faloutsos C. On power-law relationships of the internet topology. ACM SIGCOMM Comput. Commun. Rev. 1999;29(4):251–262. doi: 10.1145/316194.316229. [DOI] [Google Scholar]
- 75.Ebel H., Mielsch L.-I., Bornholdt S. Scale-free topology of e-mail networks. Phys. Rev. E. 2002;66(3) doi: 10.1103/PhysRevE.66.035103. https://link.aps.org/doi/10.1103/PhysRevE.66.035103. [DOI] [PubMed] [Google Scholar]
- 76.Jeong H., Mason S.P., Barabási A.-L., Oltvai Z.N. Lethality and centrality in protein networks. Nature. 2001;411(6833):41–42. doi: 10.1038/35075138. https://www.nature.com/articles/35075138. [DOI] [PubMed] [Google Scholar]
- 77.Barrat A., Barthélemy M., Pastor-Satorras R., Vespignani A. The architecture of complex weighted networks. Proc. Natl. Acad. Sci. USA. 2004;101(11):3747–3752. doi: 10.1073/pnas.0400087101. http://www.pnas.org/content/101/11/3747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Eguíluz V.M., Chialvo D.R., Cecchi G.A., Baliki M., Apkarian A.V. Scale-free brain functional networks. Phys. Rev. Lett. 2005;94(1) doi: 10.1103/PhysRevLett.94.018102. https://link.aps.org/doi/10.1103/PhysRevLett.94.018102. [DOI] [PubMed] [Google Scholar]
- 79.Broido A.D., Clauset A. Scale-free networks are rare. Nature Commun. 2019;10(1):1017. doi: 10.1038/s41467-019-08746-5. https://www.nature.com/articles/s41467-019-08746-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Krapivsky P.L., Redner S., Leyvraz F. Connectivity of growing random networks. Phys. Rev. Lett. 2000;85(21):4629–4632. doi: 10.1103/PhysRevLett.85.4629. http://link.aps.org/doi/10.1103/PhysRevLett.85.4629. [DOI] [PubMed] [Google Scholar]
- 81.Bollobás B. Cambridge University Press; 2001. Random Graphs. [Google Scholar]
- 82.Fagan W.F. Connectivity, fragmentation, and extinction risk in dendritic metapopulations. Ecology. 2002;83(12):3243–3249. doi: 10.2307/3072074. https://www.jstor.org/stable/3072074. [DOI] [Google Scholar]
- 83.Girvan M., Newman M.E.J. Community structure in social and biological networks. Proc. Natl. Acad. Sci. 2002;99(12):7821–7826. doi: 10.1073/pnas.122653799. https://www.pnas.org/content/99/12/7821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Palla G., Derényi I., Farkas I., Vicsek T. Uncovering the overlapping community structure of complex networks in nature and society. Nature. 2005;435(7043):814–818. doi: 10.1038/nature03607. http://www.nature.com/nature/journal/v435/n7043/full/nature03607.html. [DOI] [PubMed] [Google Scholar]
- 85.Fortunato S. Community detection in graphs. Phys. Rep. 2010;486(3):75–174. doi: 10.1016/j.physrep.2009.11.002. http://www.sciencedirect.com/science/article/pii/S0370157309002841. [DOI] [Google Scholar]
- 86.Newman M.E.J., Ziff R.M. Fast Monte Carlo algorithm for site or bond percolation. Phys. Rev. E. 2001;64(1) doi: 10.1103/PhysRevE.64.016706. http://link.aps.org/doi/10.1103/PhysRevE.64.016706. [DOI] [PubMed] [Google Scholar]
- 87.Donges J.F., Heitzig J., Beronov B., Wiedermann M., Runge J., Feng Q.Y., Tupikina L., Stolbova V., Donner R.V., Marwan N., Dijkstra H.A., Kurths J. Unified functional network and nonlinear time series analysis for complex systems science: The pyunicorn package. Chaos. 2015;25(11) doi: 10.1063/1.4934554. https://aip.scitation.org/doi/abs/10.1063/1.4934554. [DOI] [PubMed] [Google Scholar]
- 88.Guez O.C., Gozolchiani A., Havlin S. Influence of autocorrelation on the topology of the climate network. Phys. Rev. E. 2014;90(6) doi: 10.1103/PhysRevE.90.062814. http://link.aps.org/doi/10.1103/PhysRevE.90.062814. [DOI] [PubMed] [Google Scholar]
- 89.Martin E.A., Paczuski M., Davidsen J. Interpretation of link fluctuations in climate networks during El Niño periods. Europhys. Lett. 2013;102(4):48003. doi: 10.1209/0295-5075/102/48003. http://stacks.iop.org/0295-5075/102/i=4/a=48003. [DOI] [Google Scholar]
- 90.Quian Quiroga R., Kreuz T., Grassberger P. Event synchronization: A simple and fast method to measure synchronicity and time delay patterns. Phys. Rev. E. 2002;66(4) doi: 10.1103/PhysRevE.66.041904. http://link.aps.org/doi/10.1103/PhysRevE.66.041904. [DOI] [PubMed] [Google Scholar]
- 91.Pereda E., Quiroga R.Q., Bhattacharya J. Nonlinear multivariate analysis of neurophysiological signals. Prog. Neurobiol. 2005;77(1):1–37. doi: 10.1016/j.pneurobio.2005.10.003. http://www.sciencedirect.com/science/article/pii/S030100820500119X. [DOI] [PubMed] [Google Scholar]
- 92.Malik N., Bookhagen B., Marwan N., Kurths J. Analysis of spatial and temporal extreme monsoonal rainfall over South Asia using complex networks. Clim. Dynam. 2012;39(3):971–987. doi: 10.1007/s00382-011-1156-4. doi: 10.1007/s00382-011-1156-4. [DOI] [Google Scholar]
- 93.Boers N., Bookhagen B., Marwan N., Kurths J., Marengo J. Complex networks identify spatial patterns of extreme rainfall events of the South American monsoon system. Geophys. Res. Lett. 2013;40(16):4386–4392. doi: 10.1002/grl.50681. http://onlinelibrary.wiley.com/doi/10.1002/grl.50681/abstract. [DOI] [Google Scholar]
- 94.Boers N., Bookhagen B., Barbosa H.M.J., Marwan N., Kurths J., Marengo J.A. Prediction of extreme floods in the eastern Central Andes based on a complex networks approach. Nature Commun. 2014;5:5199. doi: 10.1038/ncomms6199. http://www.nature.com/doifinder/10.1038/ncomms6199. [DOI] [PubMed] [Google Scholar]
- 95.Stolbova V., Surovyatkina E., Bookhagen B., Kurths J. Tipping elements of the Indian monsoon: Prediction of onset and withdrawal. Geophys. Res. Lett. 2016;43(8):3982–3990. doi: 10.1002/2016GL068392. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1002/2016GL068392. [DOI] [Google Scholar]
- 96.Boers N., Goswami B., Rheinwalt A., Bookhagen B., Hoskins B., Kurths J. Complex networks reveal global pattern of extreme-rainfall teleconnections. Nature. 2019;566(7744):373–377. doi: 10.1038/s41586-018-0872-x. https://www.nature.com/articles/s41586-018-0872-x. [DOI] [PubMed] [Google Scholar]
- 97.Cover T.M., Thomas J.A. John Wiley & Sons; 2012. Elements of Information Theory. [Google Scholar]
- 98.Deza J.I., Barreiro M., Masoller C. Assessing the direction of climate interactions by means of complex networks and information theoretic tools. Chaos. 2015;25(3) doi: 10.1063/1.4914101. https://aip.scitation.org/doi/abs/10.1063/1.4914101. [DOI] [PubMed] [Google Scholar]
- 99.Feng Q.Y., Dijkstra H. Are North Atlantic multidecadal SST anomalies westward propagating? Geophys. Res. Lett. 2014;41(2):541–546. doi: 10.1002/2013GL058687. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1002/2013GL058687. [DOI] [Google Scholar]
- 100.Kirkpatrick S. Percolation and conduction. Rev. Modern Phys. 1973;45(4):574–588. doi: 10.1103/RevModPhys.45.574. https://link.aps.org/doi/10.1103/RevModPhys.45.574. [DOI] [Google Scholar]
- 101.Flory P.J. Molecular size distribution in three dimensional polymers. I. Gelation1. J. Am. Chem. Soc. 1941;63(11):3083–3090. doi: 10.1021/ja01856a061. [DOI] [Google Scholar]
- 102.Fisher M.E. Statistical mechanics of dimers on a plane lattice. Phys. Rev. 1961;124(6):1664–1672. doi: 10.1103/PhysRev.124.1664. https://link.aps.org/doi/10.1103/PhysRev.124.1664. [DOI] [Google Scholar]
- 103.Essam I.W., Gaunt D.S., Guttmann A.J. Percolation theory at the critical dimension. J. Phys. A: Math. Gen. 1978;11(10):1983–1990. doi: 10.1088/0305-4470/11/10/016. [DOI] [Google Scholar]
- 104.Isichenko M.B. Percolation, statistical topography, and transport in random media. Rev. Modern Phys. 1992;64(4):961–1043. doi: 10.1103/RevModPhys.64.961. https://link.aps.org/doi/10.1103/RevModPhys.64.961. [DOI] [Google Scholar]
- 105.Sahimi M. Flow phenomena in rocks: from continuum models to fractals, percolation, cellular automata, and simulated annealing. Rev. Modern Phys. 1993;65(4):1393–1534. doi: 10.1103/RevModPhys.65.1393. https://link.aps.org/doi/10.1103/RevModPhys.65.1393. [DOI] [Google Scholar]
- 106.Stauffer D., Aharony A. Taylor & Francis; 2003. Introduction to Percolation Theory. [Google Scholar]
- 107.Springer; 1996. Fractals and Disordered Systems. [Google Scholar]
- 108.Vigolo B., Coulon C., Maugey M., Zakri C., Poulin P. An experimental approach to the percolation of sticky nanotubes. Science. 2005;309(5736):920–923. doi: 10.1126/science.1112835. https://science.sciencemag.org/content/309/5736/920. [DOI] [PubMed] [Google Scholar]
- 109.Grimaldi C., Balberg I. Tunneling and nonuniversality in continuum percolation systems. Phys. Rev. Lett. 2006;96(6) doi: 10.1103/PhysRevLett.96.066602. https://link.aps.org/doi/10.1103/PhysRevLett.96.066602. [DOI] [PubMed] [Google Scholar]
- 110.Newman M.E.J., Strogatz S.H., Watts D.J. Random graphs with arbitrary degree distributions and their applications. Phys. Rev. E. 2001;64(2) doi: 10.1103/PhysRevE.64.026118. http://link.aps.org/doi/10.1103/PhysRevE.64.026118. [DOI] [PubMed] [Google Scholar]
- 111.Sander L., Warren C., Sokolov I., Simon C., Koopman J. Percolation on heterogeneous networks as a model for epidemics. Math. Biosci. 2002;180(1–2):293–305. doi: 10.1016/s0025-5564(02)00117-7. [DOI] [PubMed] [Google Scholar]
- 112.Meyers L. Contact network epidemiology: Bond percolation applied to infectious disease prediction and control. Bull. Amer. Math. Soc. 2007;44(1):63–86. [Google Scholar]
- 113.Romualdo Pastor-Satorras L., Castellano C., Van Mieghem P., Vespignani A. Epidemic processes in complex networks. Rev. Modern Phys. 2015;87(3):925–979. doi: 10.1103/RevModPhys.87.925. http://link.aps.org/doi/10.1103/RevModPhys.87.925. [DOI] [Google Scholar]
- 114.Callaway D.S., Newman M.E.J., Strogatz S.H., Watts D.J. Network robustness and fragility: Percolation on random graphs. Phys. Rev. Lett. 2000;85(25):5468–5471. doi: 10.1103/PhysRevLett.85.5468. https://link.aps.org/doi/10.1103/PhysRevLett.85.5468. [DOI] [PubMed] [Google Scholar]
- 115.Derényi I., Palla G., Vicsek T. Clique percolation in random networks. Phys. Rev. Lett. 2005;94(16) doi: 10.1103/PhysRevLett.94.160202. https://link.aps.org/doi/10.1103/PhysRevLett.94.160202. [DOI] [PubMed] [Google Scholar]
- 116.Achlioptas D., D’Souza R.M., Spencer J. Explosive percolation in random networks. Science. 2009;323(5920):1453–1455. doi: 10.1126/science.1167782. https://science.sciencemag.org/content/323/5920/1453. [DOI] [PubMed] [Google Scholar]
- 117.Baxter G.J., Dorogovtsev S.N., Goltsev A.V., Mendes J.F.F. Bootstrap percolation on complex networks. Phys. Rev. E. 2010;82(1) doi: 10.1103/PhysRevE.82.011103. https://link.aps.org/doi/10.1103/PhysRevE.82.011103. [DOI] [PubMed] [Google Scholar]
- 118.Liu Y.-Y., Csóka E., Zhou H., Pósfai M. Core percolation on complex networks. Phys. Rev. Lett. 2012;109(20) doi: 10.1103/PhysRevLett.109.205703. http://link.aps.org/doi/10.1103/PhysRevLett.109.205703. [DOI] [PubMed] [Google Scholar]
- 119.Gao J., Buldyrev S.V., Stanley H.E., Havlin S. Networks formed from interdependent networks. Nat. Phys. 2012;8(1):40–48. doi: 10.1038/nphys2180. http://www.nature.com/nphys/journal/v8/n1/full/nphys2180.html. [DOI] [PubMed] [Google Scholar]
- 120.Fan J., Chen X. General clique percolation in random networks. Europhys. Lett. 2014;107(2):28005. doi: 10.1209/0295-5075/107/28005. http://stacks.iop.org/0295-5075/107/i=2/a=28005. [DOI] [Google Scholar]
- 121.Morone F., Makse H.A. Influence maximization in complex networks through optimal percolation. Nature. 2015;524(7563):65–68. doi: 10.1038/nature14604. http://www.nature.com/nature/journal/v524/n7563/full/nature14604.html. [DOI] [PubMed] [Google Scholar]
- 122.Safran S.A., Webman I., Grest G.S. Percolation in interacting colloids. Phys. Rev. A. 1985;32(1):506–511. doi: 10.1103/PhysRevA.32.506. https://link.aps.org/doi/10.1103/PhysRevA.32.506. [DOI] [PubMed] [Google Scholar]
- 123.Gnan N., Zaccarelli E., Sciortino F. Casimir-like forces at the percolation transition. Nature Commun. 2014;5(1):1–7. doi: 10.1038/ncomms4267. https://www.nature.com/articles/ncomms4267. [DOI] [PubMed] [Google Scholar]
- 124.Shklovskii B.I., Efros A.L. Springer Science & Business Media; 2013. Electronic Properties of Doped Semiconductors, vol. 45. [Google Scholar]
- 125.Li D., Fu B., Wang Y., Lu G., Berezin Y., Stanley H.E., Havlin S. Percolation transition in dynamical traffic network with evolving critical bottlenecks. Proc. Natl. Acad. Sci. 2015;112(3):669–672. doi: 10.1073/pnas.1419185112. http://www.pnas.org/content/112/3/669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126.Bernard D., Boffetta G., Celani A., Falkovich G. Conformal invariance in two-dimensional turbulence. Nat. Phys. 2006;2(2):124–128. doi: 10.1038/nphys217. https://www.nature.com/articles/nphys217. [DOI] [Google Scholar]
- 127.Ali Saberi A. Percolation description of the global topography of earth and the moon. Phys. Rev. Lett. 2013;110(17) doi: 10.1103/PhysRevLett.110.178501. http://link.aps.org/doi/10.1103/PhysRevLett.110.178501. [DOI] [PubMed] [Google Scholar]
- 128.Rodríguez-Méndez V., Eguíluz M V.M., Hernández-García E., Ramasco J.J. Percolation-based precursors of transitions in extended systems. Sci. Rep. 2016;6:29552. doi: 10.1038/srep29552. http://www.nature.com/articles/srep29552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Lu Z., Yuan N., Fu Z. Percolation phase transition of surface air temperature networks under attacks of El Niño/LaNiña. Sci. Rep. 2016;6(1):1–9. doi: 10.1038/srep26779. https://www.nature.com/articles/srep26779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130.Fan J., Meng J., Saberi A.A. Percolation framework of the earth’s topography. Phys. Rev. E. 2019;99(2) doi: 10.1103/PhysRevE.99.022304. https://link.aps.org/doi/10.1103/PhysRevE.99.022304. [DOI] [PubMed] [Google Scholar]
- 131.Saberi A.A. Recent advances in percolation theory and its applications. Phys. Rep. 2015;578:1–32. doi: 10.1016/j.physrep.2015.03.003. http://www.sciencedirect.com/science/article/pii/S0370157315002008. [DOI] [Google Scholar]
- 132.Essam J.W. Percolation theory. Rep. Progr. Phys. 1980;43(7):833. doi: 10.1088/0034-4885/43/7/001. http://iopscience.iop.org/0034-4885/43/7/001. [DOI] [Google Scholar]
- 133.Cohen R., Erez K., ben Avraham D., Havlin S. Resilience of the internet to random breakdowns. Phys. Rev. Lett. 2000;85(21):4626–4628. doi: 10.1103/PhysRevLett.85.4626. http://link.aps.org/doi/10.1103/PhysRevLett.85.4626. [DOI] [PubMed] [Google Scholar]
- 134.Mandelbrot B.B. 2nd ed. Times Books; San Francisco: 1982. The Fractal Geometry of Nature. [Google Scholar]
- 135.Stanley H.E. Cluster shapes at the percolation threshold: and effective cluster dimensionality and its connection with critical-point exponents. J. Phys. A: Math. Gen. 1977;10(11):L211–L220. doi: 10.1088/0305-4470/10/11/008. [DOI] [Google Scholar]
- 136.Song C., Havlin S., Makse H.A. Self-similarity of complex networks. Nature. 2005;433(7024):392–395. doi: 10.1038/nature03248. doi: 10.1038/nature03248. [DOI] [PubMed] [Google Scholar]
- 137.Song C., Havlin S., Makse H.A. Origins of fractality in the growth of complex networks. Nat. Phys. 2006;2(4):275–281. doi: 10.1038/nphys266. [DOI] [Google Scholar]
- 138.Daqing L., Kosmidis K., Bunde A., Havlin S. Dimension of spatially embedded networks. Nat. Phys. 2011;7(6):481–484. doi: 10.1038/nphys1932. https://www.nature.com/articles/nphys1932. [DOI] [Google Scholar]
- 139.Havlin S., Trus B., Weiss G.H., Ben-Avraham D. The chemical distance distribution in percolation clusters. J. Phys. A: Math. Gen. 1985;18(5):L247–L249. doi: 10.1088/0305-4470/18/5/004. [DOI] [Google Scholar]
- 140.Privman V., Fisher M.E. Universal critical amplitudes in finite-size scaling. Phys. Rev. B. 1984;30(1):322–327. doi: 10.1103/PhysRevB.30.322. http://link.aps.org/doi/10.1103/PhysRevB.30.322. [DOI] [Google Scholar]
- 141.Friedman E.J., Landsberg A.S. Construction and analysis of random networks with explosive percolation. Phys. Rev. Lett. 2009;103(25) doi: 10.1103/PhysRevLett.103.255701. http://link.aps.org/doi/10.1103/PhysRevLett.103.255701. [DOI] [PubMed] [Google Scholar]
- 142.Radicchi F., Fortunato S. Explosive percolation in scale-free networks. Phys. Rev. Lett. 2009;103(16) doi: 10.1103/PhysRevLett.103.168701. http://link.aps.org/doi/10.1103/PhysRevLett.103.168701. [DOI] [PubMed] [Google Scholar]
- 143.Ziff R.M. Explosive growth in biased dynamic percolation on two-dimensional regular lattice networks. Phys. Rev. Lett. 2009;103(4) doi: 10.1103/PhysRevLett.103.045701. http://link.aps.org/doi/10.1103/PhysRevLett.103.045701. [DOI] [PubMed] [Google Scholar]
- 144.Cho Y.S., Kahng B., Kim D. Cluster aggregation model for discontinuous percolation transitions. Phys. Rev. E. 2010;81(3) doi: 10.1103/PhysRevE.81.030103. http://link.aps.org/doi/10.1103/PhysRevE.81.030103. [DOI] [PubMed] [Google Scholar]
- 145.da Costa R.A., Dorogovtsev S.N., Goltsev A.V., Mendes J.F.F. Explosive percolation transition is actually continuous. Phys. Rev. Lett. 2010;105(25) doi: 10.1103/PhysRevLett.105.255701. http://link.aps.org/doi/10.1103/PhysRevLett.105.255701. [DOI] [PubMed] [Google Scholar]
- 146.Riordan O., Warnke L. Explosive percolation is continuous. Science. 2011;333(6040):322–324. doi: 10.1126/science.1206241. [DOI] [PubMed] [Google Scholar]
- 147.Nagler J., Levina A., Timme M. Impact of single links in competitive percolation. Nat. Phys. 2011;7(3):265–270. doi: 10.1038/nphys1860. http://www.nature.com/nphys/journal/v7/n3/full/nphys1860.html. [DOI] [Google Scholar]
- 148.Grassberger P., Christensen C., Bizhani G., Son S.-W., Paczuski M. Explosive percolation is continuous, but with unusual finite size behavior. Phys. Rev. Lett. 2011;106(22) doi: 10.1103/PhysRevLett.106.225701. https://link.aps.org/doi/10.1103/PhysRevLett.106.225701. [DOI] [PubMed] [Google Scholar]
- 149.Fan J., Liu M., Li L., Chen X. Continuous percolation phase transitions of random networks under a generalized Achlioptas process. Phys. Rev. E. 2012;85(6) doi: 10.1103/PhysRevE.85.061110. http://link.aps.org/doi/10.1103/PhysRevE.85.061110. [DOI] [PubMed] [Google Scholar]
- 150.Cho Y.S., Hwang S., Herrmann H.J., Kahng B. Avoiding a spanning cluster in percolation models. Science. 2013;339(6124):1185–1187. doi: 10.1126/science.1230813. [DOI] [PubMed] [Google Scholar]
- 151.D’Souza R.M., Nagler J. Anomalous critical and supercritical phenomena in explosive percolation. Nat. Phys. 2015;11(7):531. doi: 10.1038/nphys3378. https://www.nature.com/articles/nphys3378. [DOI] [Google Scholar]
- 152.D’Souza R.M., Gómez-Gardeñes J., Nagler J., Arenas A. Explosive phenomena in complex networks. Adv. Phys. 2019;68(3):123–223. doi: 10.1080/00018732.2019.1650450. [DOI] [Google Scholar]
- 153.Fan J., Meng J., Liu Y., Saberi A.A., Kurths J., Nagler J. Universal gap scaling in percolation. Nat. Phys. 2020;16(4):455–461. doi: 10.1038/s41567-019-0783-2. https://www.nature.com/articles/s41567-019-0783-2. [DOI] [Google Scholar]
- 154.Gladwell M. Little, Brown; 2006. The Tipping Point: How Little Things Can Make a Big Difference. [Google Scholar]
- 155.Strogatz S.H. second ed. Westview Press; Boulder, CO: 2015. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering. [Google Scholar]
- 156.Rahmstorf S. Ocean circulation and climate during the past 120,000 years. Nature. 2002;419(6903):207–214. doi: 10.1038/nature01090. https://www.nature.com/articles/nature01090. [DOI] [PubMed] [Google Scholar]
- 157.Dakos V., Scheffer M., Nes E.H.v., Brovkin V., Petoukhov V., Held H. Slowing down as an early warning signal for abrupt climate change. Proc. Natl. Acad. Sci. 2008;105(38):14308–14312. doi: 10.1073/pnas.0802430105. https://www.pnas.org/content/105/38/14308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 158.Hirota M., Holmgren M., Nes E.H.V., Scheffer M. Global resilience of tropical forest and savanna to critical transitions. Science. 2011;334(6053):232–235. doi: 10.1126/science.1210657. https://science.sciencemag.org/content/334/6053/232. [DOI] [PubMed] [Google Scholar]
- 159.Lenton T.M. Arctic climate tipping points. AMBIO. 2011 doi: 10.1007/s13280-011-0221-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 160.Caesar L., Rahmstorf S., Robinson A., Feulner G., Saba V. Observed fingerprint of a weakening atlantic ocean overturning circulation. Nature. 2018;556(7700):191–196. doi: 10.1038/s41586-018-0006-5. https://www.nature.com/articles/s41586-018-0006-5. [DOI] [PubMed] [Google Scholar]
- 161.Lenton T.M., Rockström J., Gaffney O., Rahmstorf S., Richardson K., Steffen W., Schellnhuber H.J. Climate tipping points — too risky to bet against. Nature. 2019;575(7784):592–595. doi: 10.1038/d41586-019-03595-0. https://www.nature.com/articles/d41586-019-03595-0. [DOI] [PubMed] [Google Scholar]
- 162.Scheffer M., Carpenter S., Foley J.A., Folke C., Walker B. Catastrophic shifts in ecosystems. Nature. 2001;413(6856):591–596. doi: 10.1038/35098000. https://www.nature.com/articles/35098000. [DOI] [PubMed] [Google Scholar]
- 163.Kéfi S., Rietkerk M., Alados C.L., Pueyo Y., Papanastasis V.P., ElAich A., Ruiter P.C.d. Spatial vegetation patterns and imminent desertification in mediterranean arid ecosystems. Nature. 2007;449(7159):213–217. doi: 10.1038/nature06111. https://www.nature.com/articles/nature06111. [DOI] [PubMed] [Google Scholar]
- 164.Drake J.M., Griffen B.D. Early warning signals of extinction in deteriorating environments. Nature. 2010;467(7314):456–459. doi: 10.1038/nature09389. https://www.nature.com/articles/nature09389. [DOI] [PubMed] [Google Scholar]
- 165.Dai L., Vorselen D., Korolev K.S., Gore J. Generic indicators for loss of resilience before a tipping point leading to population collapse. Science. 2012;336(6085):1175–1177. doi: 10.1126/science.1219805. https://science.sciencemag.org/content/336/6085/1175. [DOI] [PubMed] [Google Scholar]
- 166.Lever J.J., Nes E.H.v., Scheffer M., Bascompte J. The sudden collapse of pollinator communities. Ecol. Lett. 2014;17(3):350–359. doi: 10.1111/ele.12236. https://onlinelibrary.wiley.com/doi/abs/10.1111/ele.12236. [DOI] [PubMed] [Google Scholar]
- 167.Jiang J., Huang Z.-G., Seager T.P., Lin W., Grebogi C., Hastings A., Lai Y.-C. Predicting tipping points in mutualistic networks through dimension reduction. Proc. Natl. Acad. Sci. 2018 doi: 10.1073/pnas.1714958115. http://www.pnas.org/content/early/2018/01/03/1714958115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 168.Centola D., Becker J., Brackbill D., Baronchelli A. Experimental evidence for tipping points in social convention. Science. 2018;360(6393):1116–1119. doi: 10.1126/science.aas8827. http://science.sciencemag.org/content/360/6393/1116. [DOI] [PubMed] [Google Scholar]
- 169.Otto I.M., Donges J.F., Cremades R., Bhowmik A., Hewitt R.J., Lucht W., Rockström J., Allerberger F., McCaffrey M., Doe S.S.P., Lenferna A., Morán N., Vuuren D.P.v., Schellnhuber H.J. Social tipping dynamics for stabilizing earth’s climate by 2050. Proc. Natl. Acad. Sci. 2020;117(5):2354–2365. doi: 10.1073/pnas.1900577117. https://www.pnas.org/content/117/5/2354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 170.Haldane A.G., May R.M. Systemic risk in banking ecosystems. Nature. 2011;469(7330):351–355. doi: 10.1038/nature09659. https://www.nature.com/articles/nature09659. [DOI] [PubMed] [Google Scholar]
- 171.Majdandzic A., Braunstein L.a., Curme C., Vodenska I., Levy-Carciente S., Stanley H.E., Havlin S. Multiple tipping points and optimal repairing in interacting networks. Nature Commun. 2016;7:10850. doi: 10.1038/ncomms10850. http://www.nature.com/ncomms/2016/160301/ncomms10850/full/ncomms10850.html. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 172.Litt B., Esteller R., Echauz J., D’Alessandro M., Shor R., Henry T., Pennell P., Epstein C., Bakay R., Dichter M., Vachtsevanos G. Epileptic seizures may begin hours in advance of clinical onset: A report of five patients. Neuron. 2001;30(1):51–64. doi: 10.1016/S0896-6273(01)00262-8. http://www.sciencedirect.com/science/article/pii/S0896627301002628. [DOI] [PubMed] [Google Scholar]
- 173.McSharry P.E., Smith L.A., Tarassenko L. Prediction of epileptic seizures: are nonlinear methods relevant? Nature Med. 2003;9(3):241–242. doi: 10.1038/nm0303-241. https://www.nature.com/articles/nm0303-241. [DOI] [PubMed] [Google Scholar]
- 174.Venegas J.G., Winkler T., Musch G., Melo M.F.V., Layfield D., Tgavalekos N., Fischman A.J., Callahan R.J., Bellani G., Harris R.S. Self-organized patchiness in asthma as a prelude to catastrophic shifts. Nature. 2005;434(7034):777–782. doi: 10.1038/nature03490. https://www.nature.com/articles/nature03490. [DOI] [PubMed] [Google Scholar]
- 175.Gualdi S., Tarzia M., Zamponi F., Bouchaud J.-P. Tipping points in macroeconomic agent-based models. J. Econom. Dynam. Control. 2015;50:29–61. doi: 10.1016/j.jedc.2014.08.003. http://www.sciencedirect.com/science/article/pii/S0165188914001924. [DOI] [Google Scholar]
- 176.Scheffer M., Bascompte J., Brock W.A., Brovkin V., Carpenter S.R., Dakos V., Held H., van Nes E.H., Rietkerk M., Sugihara G. Early-warning signals for critical transitions. Nature. 2009;461(7260):53–59. doi: 10.1038/nature08227. http://www.nature.com/nature/journal/v461/n7260/full/nature08227.html. [DOI] [PubMed] [Google Scholar]
- 177.Lenton T.M. Early warning of climate tipping points. Nature Clim. Change. 2011;1(4):201–209. doi: 10.1038/nclimate1143. https://www.nature.com/articles/nclimate1143. [DOI] [Google Scholar]
- 178.Scheffer M., Carpenter S.R., Lenton T.M., Bascompte J., Brock W., Dakos V., Koppel J.v.d., Leemput I.A.v.d., Levin S.A., Nes E.H.v., Pascual M., Vandermeer J. Anticipating critical transitions. Science. 2012;338(6105):344–348. doi: 10.1126/science.1225244. http://science.sciencemag.org/content/338/6105/344. [DOI] [PubMed] [Google Scholar]
- 179.Held H., Kleinen T. Detection of climate system bifurcations by degenerate fingerprinting. Geophys. Res. Lett. 2004;31(23) doi: 10.1029/2004GL020972. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2004GL020972. [DOI] [Google Scholar]
- 180.Peng C.-K., Buldyrev S.V., Havlin S., Simons M., Stanley H.E., Goldberger A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E. 1994;49(2):1685–1689. doi: 10.1103/PhysRevE.49.1685. http://link.aps.org/doi/10.1103/PhysRevE.49.1685. [DOI] [PubMed] [Google Scholar]
- 181.Livina V.N., Lenton T.M. A modified method for detecting incipient bifurcations in a dynamical system. Geophys. Res. Lett. 2007;34(3) doi: 10.1029/2006GL028672. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2006GL028672. [DOI] [Google Scholar]
- 182.Prettyman J., Kuna T., Livina V. Generalized early warning signals in multivariate and gridded data with an application to tropical cyclones. Chaos. 2019;29(7) doi: 10.1063/1.5093495. https://aip.scitation.org/doi/abs/10.1063/1.5093495. [DOI] [PubMed] [Google Scholar]
- 183.Ashwin P., Wieczorek S., Vitolo R., Cox P. Tipping points in open systems: bifurcation, noise-induced and rate-dependent examples in the climate system. Phil. Trans. R. Soc. A. 2012;370(1962):1166–1184. doi: 10.1098/rsta.2011.0306. https://royalsocietypublishing.org/doi/10.1098/rsta.2011.0306. [DOI] [PubMed] [Google Scholar]
- 184.Lenton T.M., Livina V.N., Dakos V., van Nes E.H., Scheffer M. Early warning of climate tipping points from critical slowing down: comparing methods to improve robustness. Philos. Trans. Math. Phys. Eng. Sci. 2012;370(1962):1185–1204. doi: 10.1098/rsta.2011.0304. https://www.jstor.org/stable/41348438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 185.Ditlevsen P.D., Johnsen S.J. Tipping points: Early warning and wishful thinking. Geophys. Res. Lett. 2010;37(19) doi: 10.1029/2010GL044486. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2010GL044486. [DOI] [Google Scholar]
- 186.Pikovsky A.S., Kurths J. Coherence resonance in a noise-driven excitable system. Phys. Rev. Lett. 1997;78(5):775–778. doi: 10.1103/PhysRevLett.78.775. https://link.aps.org/doi/10.1103/PhysRevLett.78.775. [DOI] [Google Scholar]
- 187.Sutera A. On stochastic perturbation and long-term climate behaviour. Q. J. R. Meteorol. Soc. 1981;107(451):137–151. doi: 10.1002/qj.49710745109. https://rmets.onlinelibrary.wiley.com/doi/abs/10.1002/qj.49710745109. [DOI] [Google Scholar]
- 188.Fraedrich K. Catastrophes and resilience of a zero-dimensional climate system with ice-albedo and greenhouse feedback. Q. J. R. Meteorol. Soc. 1979;105(443):147–167. doi: 10.1002/qj.49710544310. https://rmets.onlinelibrary.wiley.com/doi/abs/10.1002/qj.49710544310. [DOI] [Google Scholar]
- 189.Sura P. Noise-induced transitions in a barotropic -plane channel. J. Atmos. Sci. 2002;59(1):97–110. doi: 10.1175/1520-0469(2002)059<0097:NITIAB>2.0.CO;2. https://journals.ametsoc.org/doi/full/10.1175/1520-0469(2002)059<0097:NITIAB>2.0.CO;2. [DOI] [Google Scholar]
- 190.Stroeve J., Holland M.M., Meier W., Scambos T., Serreze M. Arctic sea ice decline: Faster than forecast. Geophys. Res. Lett. 2007;34(9) doi: 10.1029/2007GL029703. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2007GL029703. [DOI] [Google Scholar]
- 191.Holland M.M., Bitz C.M., Tremblay B. Future abrupt reductions in the summer arctic sea ice. Geophys. Res. Lett. 2006;33(23) doi: 10.1029/2006GL028024. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2006GL028024. [DOI] [Google Scholar]
- 192.Winton M. Does the arctic sea ice have a tipping point? Geophys. Res. Lett. 2006;33(23) doi: 10.1029/2006GL028017. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2006GL028017. [DOI] [Google Scholar]
- 193.Pörtner H., Roberts D., Masson-Delmotte V., Zhai P., Tignor M., Poloczanska E., Mintenbeck K., Nicolai M., Okem A., Petzold J. IPCC Intergovernmental Panel on Climate Change; Geneva, Switzerland: 2019. IPCC Special Report on the Ocean and Cryosphere in a Changing Climate. [Google Scholar]
- 194.Feldmann J., Levermann A. Collapse of the west antarctic ice sheet after local destabilization of the amundsen basin. Proc. Natl. Acad. Sci. 2015;112(46):14191–14196. doi: 10.1073/pnas.1512482112. https://www.pnas.org/content/112/46/14191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 195.Dijkstra H.A. Springer Science & Business Media; 2005. Nonlinear Physical Oceanography: A Dynamical Systems Approach to the Large Scale Ocean Circulation and El Niño. [Google Scholar]
- 196.Clarke A.J. Elsevier; 2008. An Introduction to the Dynamics of El Niño and the Southern Oscillation. [Google Scholar]
- 197.Sarachik E.S., Cane M.A. Cambridge University Press; 2010. The El Niño-southern Oscillation Phenomenon. [Google Scholar]
- 198.Cai W., Borlace S., Lengaigne M., Rensch P.v., Collins M., Vecchi G., Timmermann A., Santoso A., McPhaden M.J., Wu L., England M.H., Wang G., Guilyardi E., Jin F.-F. Increasing frequency of extreme El Niño events due to greenhouse warming. Nature Clim. Change. 2014;4(2):111–116. doi: 10.1038/nclimate2100. https://www.nature.com/articles/nclimate2100. [DOI] [Google Scholar]
- 199.Latif M., Keenlyside N.S. El Niño/Southern Oscillation response to global warming. Proc. Natl. Acad. Sci. USA. 2009;106(49):20578–20583. doi: 10.1073/pnas.0710860105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 200.Zickfeld K., Knopf B., Petoukhov V., Schellnhuber H.J. Is the Indian summer monsoon stable against global change? Geophys. Res. Lett. 2005;32(15) doi: 10.1029/2005GL022771. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2005GL022771. [DOI] [Google Scholar]
- 201.Kumar P.V., Naidu C.V., Prasanna K. Recent unprecedented weakening of Indian summer monsoon in warming environment. Theor. Appl. Climatol. 2020;140(1):467–486. doi: 10.1007/s00704-019-03087-1. [DOI] [Google Scholar]
- 202.Quéré C.L., Moriarty R., Andrew R.M., Peters G.P., Ciais P., Friedlingstein P., Jones S.D., Sitch S., Tans P., Arneth A., Boden T.A., Bopp L., Bozec Y., Canadell J.G., Chini L.P., Chevallier F., Cosca C.E., Harris I., Hoppema M., Houghton R.A., House J.I., Jain A.K., Johannessen T., Kato E., Keeling R.F., Kitidis V., Klein Goldewijk K., Koven C., Landa C.S., Landschützer P., Lenton A., Lima I.D., Marland G., Mathis J.T., Metzl N., Nojiri Y., Olsen A., Ono T., Peng S., Peters W., Pfeil B., Poulter B., Raupach M.R., Regnier P., Rödenbeck C., Saito S., Salisbury J.E., Schuster U., Schwinger J., Séférian R., Segschneider J., Steinhoff T., Stocker B.D., Sutton A.J., Takahashi T., Tilbrook B., Werf G.R.v.d., Viovy N., Wang Y.-P., Wanninkhof R., Wiltshire A., Zeng N. Global carbon budget 2014. Earth Syst. Sci. Data. 2015;7(1):47–85. doi: 10.5194/essd-7-47-2015. https://www.earth-syst-sci-data.net/7/47/2015/ [DOI] [Google Scholar]
- 203.Wright S.J. Tropical forests in a changing environment. Trends Ecol. Evol. 2005;20(10):553–560. doi: 10.1016/j.tree.2005.07.009. http://www.sciencedirect.com/science/article/pii/S016953470500251X. [DOI] [PubMed] [Google Scholar]
- 204.Achard F., Beuchle R., Mayaux P., Stibig H.-J., Bodart C., Brink A., Carboni S., Desclée B., Donnay F., Eva H.D., Lupi A., Raši R., Seliger R., Simonetti D. Determination of tropical deforestation rates and related carbon losses from 1990 to 2010. Global Change Biol. 2014;20(8):2540–2554. doi: 10.1111/gcb.12605. https://onlinelibrary.wiley.com/doi/abs/10.1111/gcb.12605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 205.Taubert F., Fischer R., Groeneveld J., Lehmann S., Müller M.S., Rödig E., Wiegand T., Huth A. Global patterns of tropical forest fragmentation. Nature. 2018 doi: 10.1038/nature25508. https://www.nature.com/articles/nature25508. [DOI] [PubMed] [Google Scholar]
- 206.Wissel C. A universal law of the characteristic return time near thresholds. Oecologia. 1984;65(1):101–107. doi: 10.1007/BF00384470. [DOI] [PubMed] [Google Scholar]
- 207.Kantelhardt J.W., Koscielny-Bunde E., Rego H.H.A., Havlin S., Bunde A. Detecting long-range correlations with detrended fluctuation analysis. Physica A. 2001;295(3–4):441–454. doi: 10.1016/S0378-4371(01)00144-3. http://www.sciencedirect.com/science/article/pii/S0378437101001443. [DOI] [Google Scholar]
- 208.Buldyrev S.V., Goldberger A.L., Havlin S., Mantegna R.N., Matsa M.E., Peng C.-K., Simons M., Stanley H.E. Long-range correlation properties of coding and noncoding DNA sequences: Genbank analysis. Phys. Rev. E. 1995;51(5):5084–5091. doi: 10.1103/PhysRevE.51.5084. https://link.aps.org/doi/10.1103/PhysRevE.51.5084. [DOI] [PubMed] [Google Scholar]
- 209.Peng C.-K., Mietus J., Hausdorff J.M., Havlin S., Stanley H.E., Goldberger A.L. Long-range anticorrelations and non-Gaussian behavior of the heartbeat. Phys. Rev. Lett. 1993;70(9):1343–1346. doi: 10.1103/PhysRevLett.70.1343. https://link.aps.org/doi/10.1103/PhysRevLett.70.1343. [DOI] [PubMed] [Google Scholar]
- 210.Ashkenazy Y., Lewkowicz M., Levitan J., Moelgaard H., Thomsen P.E.B., Saermark K. Discrimination of the healthy and sick cardiac autonomic nervous system by a new wavelet analysis of heartbeat intervals. Fractals. 1998;06(03):197–203. doi: 10.1142/S0218348X98000249. https://www.worldscientific.com/doi/abs/10.1142/S0218348X98000249. [DOI] [Google Scholar]
- 211.Bunde A., Havlin S., Kantelhardt J.W., Penzel T., Peter J.-H., Voigt K. Correlated and uncorrelated regions in heart-rate fluctuations during sleep. Phys. Rev. Lett. 2000;85(17):3736–3739. doi: 10.1103/PhysRevLett.85.3736. https://link.aps.org/doi/10.1103/PhysRevLett.85.3736. [DOI] [PubMed] [Google Scholar]
- 212.Fan J., Zhou D., Shekhtman L.M., Shapira A., Hofstetter R., Marzocchi W., Ashkenazy Y., Havlin S. Possible origin of memory in earthquakes: Real catalogs and an epidemic-type aftershock sequence model. Phys. Rev. E. 2019;99(4) doi: 10.1103/PhysRevE.99.042210. https://link.aps.org/doi/10.1103/PhysRevE.99.042210. [DOI] [PubMed] [Google Scholar]
- 213.Koscielny-Bunde E., Bunde A., Havlin S., Roman H.E., Goldreich Y., Schellnhuber H.-J. Indication of a universal persistence law governing atmospheric variability. Phys. Rev. Lett. 1998;81(3):729–732. doi: 10.1103/PhysRevLett.81.729. https://link.aps.org/doi/10.1103/PhysRevLett.81.729. [DOI] [Google Scholar]
- 214.Prettyman J., Kuna T., Livina V. A novel scaling indicator of early warning signals helps anticipate tropical cyclones. Europhys. Lett. 2018;121(1):10002. doi: 10.1209/0295-5075/121/10002. [DOI] [Google Scholar]
- 215.Kleinen T., Held H., Petschel-Held G. The potential role of spectral properties in detecting thresholds in the earth system: application to the thermohaline circulation. Ocean Dyn. 2003;53(2):53–63. doi: 10.1007/s10236-002-0023-6. doi: 10.1007/s10236-002-0023-6. [DOI] [Google Scholar]
- 216.Carpenter S.R., Brock W.A. Rising variance: a leading indicator of ecological transition. Ecol. Lett. 2006;9(3):311–318. doi: 10.1111/j.1461-0248.2005.00877.x. https://onlinelibrary.wiley.com/doi/abs/10.1111/j.1461-0248.2005.00877.x. [DOI] [PubMed] [Google Scholar]
- 217.Wang R., Dearing J.A., Langdon P.G., Zhang E., Yang X., Dakos V., Scheffer M. Flickering gives early warning signals of a critical transition to a eutrophic lake state. Nature. 2012;492(7429):419–422. doi: 10.1038/nature11655. https://www.nature.com/articles/nature11655. [DOI] [PubMed] [Google Scholar]
- 218.Carpenter S.R., Brock W.A., Cole J.J., Kitchell J.F., Pace M.L. Leading indicators of trophic cascades. Ecol. Lett. 2008;11(2):128–138. doi: 10.1111/j.1461-0248.2007.01131.x. https://onlinelibrary.wiley.com/doi/abs/10.1111/j.1461-0248.2007.01131.x. [DOI] [PubMed] [Google Scholar]
- 219.Guttal V., Jayaprakash C. Changing skewness: an early warning signal of regime shifts in ecosystems. Ecol. Lett. 2008;11(5):450–460. doi: 10.1111/j.1461-0248.2008.01160.x. https://onlinelibrary.wiley.com/doi/abs/10.1111/j.1461-0248.2008.01160.x. [DOI] [PubMed] [Google Scholar]
- 220.Biggs R., Carpenter S.R., Brock W.A. Turning back from the brink: Detecting an impending regime shift in time to avert it. Proc. Natl. Acad. Sci. 2009;106(3):826–831. doi: 10.1073/pnas.0811729106. https://www.pnas.org/content/106/3/826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 221.Dakos V., Carpenter S.R., Brock W.A., Ellison A.M., Guttal V., Ives A.R., Kéfi S., Livina V., Seekell D.A., van Nes E.H., Scheffer M. Methods for detecting early warnings of critical transitions in time series illustrated using simulated ecological data. PLoS ONE. 2012;7(7) doi: 10.1371/journal.pone.0041010. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3398887/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- 222.Alley R.B., Marotzke J., Nordhaus W.D., Overpeck J.T., Peteet D.M., Pielke R.A., Pierrehumbert R.T., Rhines P.B., Stocker T.F., Talley L.D., Wallace J.M. Abrupt climate change. Science. 2003;299(5615):2005–2010. doi: 10.1126/science.1081056. https://science.sciencemag.org/content/299/5615/2005. [DOI] [PubMed] [Google Scholar]
- 223.Sahney S., Benton M.J., Falcon-Lang H.J. Rainforest collapse triggered carboniferous tetrapod diversification in euramerica. Geology. 2010;38(12):1079–1082. doi: 10.1130/G31182.1. https://pubs.geoscienceworld.org/geology/article-abstract/38/12/1079/130093/Rainforest-collapse-triggered-Carboniferous. [DOI] [Google Scholar]
- 224.Broecker W.S. Was the younger Dryas triggered by a flood? Science. 2006;312(5777):1146–1148. doi: 10.1126/science.1123253. https://science.sciencemag.org/content/312/5777/1146. [DOI] [PubMed] [Google Scholar]
- 225.Liu Z., Pagani M., Zinniker D., DeConto R., Huber M., Brinkhuis H., Shah S.R., Leckie R.M., Pearson A. Global cooling during the eocene-oligocene climate transition. Science. 2009;323(5918):1187–1190. doi: 10.1126/science.1166368. https://science.sciencemag.org/content/323/5918/1187. [DOI] [PubMed] [Google Scholar]
- 226.Board O.S., Council N.R. National Academies Press; 2002. Abrupt Climate Change: Inevitable Surprises. [Google Scholar]
- 227.Bakke J., Lie O., Heegaard E., Dokken T., Haug G.H., Birks H.H., Dulski P., Nilsen T. Rapid oceanic and atmospheric changes during the Younger dryas cold period. Nat. Geosci. 2009;2(3):202–205. doi: 10.1038/ngeo439. https://www.nature.com/articles/ngeo439. [DOI] [Google Scholar]
- 228.Hsieh C.-h., Reiss C.S., Hunter J.R., Beddington J.R., May R.M., Sugihara G. Fishing elevates variability in the abundance of exploited species. Nature. 2006;443(7113):859–862. doi: 10.1038/nature05232. https://www.nature.com/articles/nature05232. [DOI] [PubMed] [Google Scholar]
- 229.Scheffer M., Carpenter S.R. Catastrophic regime shifts in ecosystems: linking theory to observation. Trends Ecol. Evol. 2003;18(12):648–656. doi: 10.1016/j.tree.2003.09.002. http://www.sciencedirect.com/science/article/pii/S0169534703002787. [DOI] [Google Scholar]
- 230.Scheffer M., van Nes E.H. Shallow lakes theory revisited: various alternative regimes driven by climate, nutrients, depth and lake size. Hydrobiologia. 2007;584(1):455–466. doi: 10.1007/s10750-007-0616-7. doi: 10.1007/s10750-007-0616-7. [DOI] [Google Scholar]
- 231.Bates D.S. The crash of ’87: Was it expected? The evidence from options markets. J. Finance. 1991;46(3):1009–1044. doi: 10.2307/2328552. https://www.jstor.org/stable/2328552. [DOI] [Google Scholar]
- 232.Shannon C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948;27(3):379–423. doi: 10.1002/j.1538-7305.1948.tb01338.x. https://onlinelibrary.wiley.com/doi/abs/10.1002/j.1538-7305.1948.tb01338.x. [DOI] [Google Scholar]
- 233.Thanos D., Li W., Provata A. Entropic fluctuations in DNA sequences. Physica A. 2018;493:444–457. doi: 10.1016/j.physa.2017.11.119. http://www.sciencedirect.com/science/article/pii/S0378437117312037. [DOI] [Google Scholar]
- 234.Bekenstein J.D. Black holes and entropy. Phys. Rev. D. 1973;7(8):2333–2346. doi: 10.1103/PhysRevD.7.2333. https://link.aps.org/doi/10.1103/PhysRevD.7.2333. [DOI] [Google Scholar]
- 235.Hawking S.W. Particle creation by black holes. Comm. Math. Phys. 1975;43(3):199–220. doi: 10.1007/BF02345020. [DOI] [Google Scholar]
- 236.Srednicki M. Entropy and area. Phys. Rev. Lett. 1993;71(5):666–669. doi: 10.1103/PhysRevLett.71.666. https://link.aps.org/doi/10.1103/PhysRevLett.71.666. [DOI] [PubMed] [Google Scholar]
- 237.Georgescu-Roegen N. Valuing the Earth: Economics, Ecology, Ethics. MIT Press Cambridge, MA; 1993. The entropy law and the economic problem; pp. 75–88. [Google Scholar]
- 238.Ayres R.U. On the practical limits to substitution. Ecol. Econom. 2007;61(1):115–128. doi: 10.1016/j.ecolecon.2006.02.011. http://www.sciencedirect.com/science/article/pii/S0921800906000838. [DOI] [Google Scholar]
- 239.Stephens G.L., O’Brien D.M. Entropy and climate. I: ERBE observations of the entropy production of the earth. Q. J. R. Meteorol. Soc. 1993;119(509):121–152. doi: 10.1002/qj.49711950906. https://rmets.onlinelibrary.wiley.com/doi/abs/10.1002/qj.49711950906. [DOI] [Google Scholar]
- 240.O’brien D.M., Stephens G.L. Entropy and climate. II: Simple models. Q. J. R. Meteorol. Soc. 1995;121(527):1773–1796. doi: 10.1002/qj.49712152712. https://rmets.onlinelibrary.wiley.com/doi/abs/10.1002/qj.49712152712. [DOI] [Google Scholar]
- 241.Meng J., Fan J., Ludescher J., Agarwal A., Chen X., Bunde A., Kurths J., Schellnhuber H.J. Complexity-based approach for El Niño magnitude forecasting before the spring predictability barrier. Proc. Natl. Acad. Sci. 2020;117(1):177–183. doi: 10.1073/pnas.1917007117. https://www.pnas.org/content/117/1/177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 242.Lucia U. Probability, ergodicity, irreversibility and dynamical systems. Proc. R. Soc. A Math. Phys. Eng. Sci. 2008;464(2093):1089–1104. doi: 10.1098/rspa.2007.0304. https://royalsocietypublishing.org/doi/full/10.1098/rspa.2007.0304. [DOI] [Google Scholar]
- 243.Pincus S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. 1991;88(6):2297–2301. doi: 10.1073/pnas.88.6.2297. https://www.pnas.org/content/88/6/2297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 244.Eckmann J.P., Ruelle D. Ergodic theory of chaos and strange attractors. Rev. Modern Phys. 1985;57(3):617–656. doi: 10.1103/RevModPhys.57.617. https://link.aps.org/doi/10.1103/RevModPhys.57.617. [DOI] [Google Scholar]
- 245.Grassberger P., Procaccia I. Estimation of the Kolmogorov entropy from a chaotic signal. Phys. Rev. A. 1983;28(4):2591–2593. doi: 10.1103/PhysRevA.28.2591. https://link.aps.org/doi/10.1103/PhysRevA.28.2591. [DOI] [Google Scholar]
- 246.Pincus S., Kalman R.E. Irregularity, volatility, risk, and financial market time series. Proc. Natl. Acad. Sci. 2004;101(38):13709–13714. doi: 10.1073/pnas.0405168101. https://www.pnas.org/content/101/38/13709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 247.Pincus S.M., Goldberger A.L. Physiological time-series analysis: what does regularity quantify? American Journal of Physiology-Heart and Circulatory Physiology. 1994;266(4):H1643–H1656. doi: 10.1152/ajpheart.1994.266.4.H1643. https://journals.physiology.org/doi/abs/10.1152/ajpheart.1994.266.4.H1643. [DOI] [PubMed] [Google Scholar]
- 248.McKinley R.A., McIntire L.K., Schmidt R., Repperger D.W., Caldwell J.A. Evaluation of eye metrics as a detector of fatigue: Human Factors. 2011 doi: 10.1177/0018720811411297. https://journals.sagepub.com/doi/10.1177/0018720811411297. [DOI] [PubMed] [Google Scholar]
- 249.Takens F. Detecting strange attractors in turbulence. In: Rand D., Young L.-S., editors. Dynamical Systems and Turbulence, Warwick 1980. Springer; Berlin, Heidelberg: 1981. pp. 366–381. (Lecture Notes in Mathematics). [DOI] [Google Scholar]
- 250.Pincus S. Approximate entropy (apen) as a complexity measure. Chaos. 1995;5(1):110–117. doi: 10.1063/1.166092. http://aip.scitation.org/doi/10.1063/1.166092. [DOI] [PubMed] [Google Scholar]
- 251.Sabeti M., Katebi S., Boostani R. Entropy and complexity measures for EEG signal classification of schizophrenic and control participants. Artif. Intell. Med. 2009;47(3):263–274. doi: 10.1016/j.artmed.2009.03.003. http://www.sciencedirect.com/science/article/pii/S0933365709000530. [DOI] [PubMed] [Google Scholar]
- 252.Yuan Q., Zhou W., Li S., Cai D. Epileptic EEG classification based on extreme learning machine and nonlinear features. Epilepsy Res. 2011;96(1):29–38. doi: 10.1016/j.eplepsyres.2011.04.013. http://www.sciencedirect.com/science/article/pii/S0920121111001185. [DOI] [PubMed] [Google Scholar]
- 253.Yun K., Park H.-K., Kwon D.-H., Kim Y.-T., Cho S.-N., Cho H.-J., Peterson B.S., Jeong J. Decreased cortical complexity in methamphetamine abusers. Psychiatry Res. Neuroimaging. 2012;201(3):226–232. doi: 10.1016/j.pscychresns.2011.07.009. http://www.sciencedirect.com/science/article/pii/S0925492711002496. [DOI] [PubMed] [Google Scholar]
- 254.Richman J.S., Moorman J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000;278(6):H2039–H2049. doi: 10.1152/ajpheart.2000.278.6.H2039. https://journals.physiology.org/doi/full/10.1152/ajpheart.2000.278.6.H2039. [DOI] [PubMed] [Google Scholar]
- 255.Cambridge University Press; Cambridge ; New York: 2007. Climate change 2007: the physical science basis: contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. [Google Scholar]
- 256.Karamperidou C., Nezio P.N.D., Timmermann A., Jin F.-F., Cobb K.M. The response of ENSO flavors to mid-holocene climate: implications for proxy interpretation. Paleoceanography. 2015;30(5):527–547. doi: 10.1002/2014PA002742. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1002/2014PA002742. [DOI] [Google Scholar]
- 257.members N.G.I.C.P. High-resolution record of northern hemisphere climate extending into the last interglacial period. Nature. 2004;431(7005):147–151. doi: 10.1038/nature02805. https://www.nature.com/articles/nature02805. [DOI] [PubMed] [Google Scholar]
- 258.Dee D.P., Uppala S., Simmons A., Berrisford P., Poli P., Kobayashi S., Andrae U., Balmaseda M., Balsamo G., Bauer P. The ERA-interim reanalysis: Configuration and performance of the data assimilation system. Q.J.R. Meteorol. Soc. 2011;137(656):553–597. [Google Scholar]
- 259.Kalnay E., Kanamitsu M., Kistler R., Collins W., Deaven D., Gandin L., Iredell M., Saha S., White G., Woollen J., Zhu Y., Chelliah M., Ebisuzaki W., Higgins W., Janowiak J., Mo K.C., Ropelewski C., Wang J., Leetmaa A., Reynolds R., Jenne R., Joseph D. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996;77(3):437–472. doi: 10.1175/1520-0477(1996)077<0437:TNYRP>2.0.CO;2. https://journals.ametsoc.org/doi/abs/10.1175/1520-0477(1996)077<0437:TNYRP>2.0.CO;2. [DOI] [Google Scholar]
- 260.Onogi K., Tsutsui J., Koide H., Sakamoto M., Kobayashi S., Hatsushika H., Matsumoto T., Yamazaki N., Kamahori H., Takahashi K., Kadokura S., Wada K., Kato K., Oyama R., Ose T., Mannoji N., Taira R. The JRA-25 reanalysis. J. Meteorol. Soc. Jpn. Ser. II. 2007;85(3):369–432. doi: 10.2151/jmsj.85.369. [DOI] [Google Scholar]
- 261.Kobayashi S., Ota Y., Harada Y., Ebita A., Moriya M., Onoda H., Onogi K., Kamahori H., Kobayashi C., Endo H., Miyaoka K., Takahashi K. The JRA-55 reanalysis: General specifications and basic characteristics. J. Meteorol. Soc. Jpn. Ser. II. 2015;93(1):5–48. doi: 10.2151/jmsj.2015-001. [DOI] [Google Scholar]
- 262.Dell’Aquila A., Lucarini V., Ruti P.M., Calmanti S. Hayashi spectra of the northern hemisphere mid-latitude atmospheric variability in the NCEP–NCAR and ECMWF reanalyses. Clim. Dynam. 2005;25(6):639–652. doi: 10.1007/s00382-005-0048-x. [DOI] [Google Scholar]
- 263.Kharin V.V., Zwiers F.W., Zhang X. Intercomparison of near-surface temperature and precipitation extremes in AMIP-2 simulations, reanalyses, and observations. J. Clim. 2005;18(24):5201–5223. doi: 10.1175/JCLI3597.1. https://journals.ametsoc.org/doi/10.1175/JCLI3597.1. [DOI] [Google Scholar]
- 264.Dell’Aquila A., Ruti P.M., Calmanti S., Lucarini V. Southern hemisphere midlatitude atmospheric variability of the NCEP-NCAR and ECMWF reanalyses. J. Geophys. Res.: Atmos. 2007;112(D8) doi: 10.1029/2006JD007376. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2006JD007376. [DOI] [Google Scholar]
- 265.Marques C.A.F., Rocha A., Corte-Real J. Comparative energetics of ERA-40, JRA-25 and NCEP-r2 reanalysis, in the wave number domain. Dyn. Atmos. Oceans. 2010;50(3):375–399. doi: 10.1016/j.dynatmoce.2010.03.003. http://www.sciencedirect.com/science/article/pii/S0377026510000126. [DOI] [Google Scholar]
- 266.Kim Y.-H., Kim M.-K. Examination of the global lorenz energy cycle using MERRA and NCEP-reanalysis 2. Clim. Dynam. 2013;40(5):1499–1513. doi: 10.1007/s00382-012-1358-4. doi: 10.1007/s00382-012-1358-4. [DOI] [Google Scholar]
- 267.Ghil M., Lucarini V. The physics of climate variability and climate change. Rev. Modern Phys. 2020;92(3) doi: 10.1103/RevModPhys.92.035002. https://link.aps.org/doi/10.1103/RevModPhys.92.035002. [DOI] [Google Scholar]
- 268.Ropelewski C.F., Halpert M.S. North American precipitation and temperature patterns associated with the El Niño/southern oscillation (ENSO) Mon. Weather Rev. 1986;114(12):2352–2362. doi: 10.1175/1520-0493(1986)114<2352:NAPATP>2.0.CO;2. http://journals.ametsoc.org/doi/abs/10.1175/1520-0493(1986)114<2352:NAPATP>2.0.CO;2. [DOI] [Google Scholar]
- 269.Power S., Casey T., Folland C., Colman A., Mehta V. Inter-decadal modulation of the impact of ENSO on Australia. Clim. Dynam. 1999;15(5):319–324. doi: 10.1007/s003820050284. http://link.springer.com/article/10.1007/s003820050284. [DOI] [Google Scholar]
- 270.Kumar K.K., Rajagopalan B., Cane M.A. On the weakening relationship between the Indian monsoon and ENSO. Science. 1999;284(5423):2156–2159. doi: 10.1126/science.284.5423.2156. https://science.sciencemag.org/content/284/5423/2156. [DOI] [PubMed] [Google Scholar]
- 271.Gershunov A., Barnett T.P. Interdecadal modulation of ENSO teleconnections. Bull. Am. Meteorol. Soc. 1998;79(12):2715–2726. doi: 10.1175/1520-0477(1998)079<2715:IMOET>2.0.CO;2. https://journals.ametsoc.org/doi/abs/10.1175/1520-0477(1998)079079<2715:IMOET>2.0.CO;2. [DOI] [Google Scholar]
- 272.J. David Neelin A. first ed. Cambridge University Press; Cambridge, New York: 2011. Climate Change and Climate Modeling. [Google Scholar]
- 273.Bjerknes J. Atmospheric teleconnections from the equatorial Pacific. Mon. Wea. Rev. 1969;97(3):163–172. [Google Scholar]
- 274.Gill A.E. Some simple solutions for heat-induced tropical circulation. Q. J. R. Meteorol. Soc. 1980;106(449):447–462. doi: 10.1002/qj.49710644905. https://rmets.onlinelibrary.wiley.com/doi/abs/10.1002/qj.49710644905, eprint: https://rmets.onlinelibrary.wiley.com/doi/pdf/10.1002/qj.49710644905. [DOI] [Google Scholar]
- 275.Tziperman E., Yu L. Quantifying the dependence of westerly wind bursts on the large-scale tropical Pacific SST. J. Clim. 2007;20(12):2760–2768. doi: 10.1175/JCLI4138a.1. https://journals.ametsoc.org/jcli/article/20/12/2760/31543/Quantifying-the-Dependence-of-Westerly-Wind-Bursts. [DOI] [Google Scholar]
- 276.McCreary J.P. A model of tropical ocean-atmosphere interaction. Mon. Weather Rev. 1983;111(2):370–387. doi: 10.1175/1520-0493(1983)111<0370:AMOTOA>2.0.CO;2. https://journals.ametsoc.org/mwr/article/111/2/370/62626/A-Model-of-Tropical-Ocean-Atmosphere-Interaction. [DOI] [Google Scholar]
- 277.Suarez M.J., Schopf P.S. A delayed action oscillator for ENSO. J. Atmos. Sci. 1988;45(21):3283–3287. doi: 10.1175/1520-0469(1988)045<3283:ADAOFE>2.0.CO;2. https://journals.ametsoc.org/jas/article/45/21/3283/22200/A-Delayed-Action-Oscillator-for-ENSO. [DOI] [Google Scholar]
- 278.Zebiak S.E., Cane M.A. A model El Niño–southern oscillation. Mon. Weather Rev. 1987;115(10):2262–2278. [Google Scholar]
- 279.Cane M.A., Zebiak S.E., Dolan S.C. Experimental forecasts of El Niño. Nature. 1986;321(6073):827–832. doi: 10.1038/321827a0. https://www.nature.com/articles/321827a0. [DOI] [Google Scholar]
- 280.Wang C. A review of ENSO theories. Natl. Sci. Rev. 2018;5(6):813–825. doi: 10.1093/nsr/nwy104. https://academic.oup.com/nsr/article/5/6/813/5126370. [DOI] [Google Scholar]
- 281.Weisberg R.H., Wang C. A western Pacific oscillator paradigm for the El Niño-southern oscillation. Geophys. Res. Lett. 1997;24(7):779–782. doi: 10.1029/97GL00689. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/97GL00689, _eprint: https://agupubs.onlinelibrary.wiley.com/doi/pdf/10.1029/97GL00689. [DOI] [Google Scholar]
- 282.Wyrtki K. El Niño—The Dynamic response of the equatorial Pacific oceanto atmospheric forcing. J. Phys. Oceanogr. 1975;5(4):572–584. doi: 10.1175/1520-0485(1975)005<0572:ENTDRO>2.0.CO;2. https://journals.ametsoc.org/jpo/article/5/4/572/11672/El-Nino-The-Dynamic-Response-of-the-Equatorial. [DOI] [Google Scholar]
- 283.Jin F.-F. An equatorial ocean recharge paradigm for ENSO. part I: conceptual model. J. Atmos. Sci. 1997;54(7):811–829. doi: 10.1175/1520-0469(1997)054<0811:AEORPF>2.0.CO;2. https://journals.ametsoc.org/jas/article/54/7/811/24364/An-Equatorial-Ocean-Recharge-Paradigm-for-ENSO. [DOI] [Google Scholar]
- 284.Jin F.-F. An equatorial ocean recharge paradigm for ENSO. Part II: a stripped-down coupled model. J. Atmos. Sci. 1997;54(7):830–847. doi: 10.1175/1520-0469(1997)054<0830:AEORPF>2.0.CO;2. https://journals.ametsoc.org/jas/article/54/7/830/24365/An-Equatorial-Ocean-Recharge-Paradigm-for-ENSO. [DOI] [Google Scholar]
- 285.Picaut J., Masia F., Penhoat Y.d. An advective-reflective conceptual model for the oscillatory nature of the ENSO. Science. 1997;277(5326):663–666. doi: 10.1126/science.277.5326.663. https://science.sciencemag.org/content/277/5326/663. [DOI] [Google Scholar]
- 286.Wang C. A unified oscillator model for the El Niño–southern oscillation. J. Clim. 2001;14(1):98–115. doi: 10.1175/1520-0442(2001)014<0098:AUOMFT>2.0.CO;2. https://journals.ametsoc.org/jcli/article/14/1/98/28568/A-Unified-Oscillator-Model-for-the-El-Nino. [DOI] [Google Scholar]
- 287.Chen D., Cane M.A., Kaplan A., Zebiak S.E., Huang D. Predictability of El Niño over the past 148 years. Nature. 2004;428(6984):733–736. doi: 10.1038/nature02439. http://www.nature.com/nature/journal/v428/n6984/full/nature02439.html. [DOI] [PubMed] [Google Scholar]
- 288.Yeh S.-W., Kug J.-S., Dewitte B., Kwon M.-H., Kirtman B.P., Jin F.-F. El Niño in a changing climate. Nature. 2009;461(7263):511–514. doi: 10.1038/nature08316. http://www.nature.com/nature/journal/v461/n7263/full/nature08316.html. [DOI] [PubMed] [Google Scholar]
- 289.Goddard L., Mason S.J., Zebiak S.E., Ropelewski C.F., Basher R., Cane M.A. Current approaches to seasonal to interannual climate predictions. Int. J. Climatol. 2001;21(9):1111–1152. doi: 10.1002/joc.636. https://rmets.onlinelibrary.wiley.com/doi/abs/10.1002/joc.636. [DOI] [Google Scholar]
- 290.Duan W., Wei C. The ‘spring predictability barrier’ for ENSO predictions and its possible mechanism: results from a fully coupled model. Int. J. Climatol. 2013;33(5):1280–1292. doi: 10.1002/joc.3513. https://rmets.onlinelibrary.wiley.com/doi/abs/10.1002/joc.3513. [DOI] [Google Scholar]
- 291.Ludescher J., Gozolchiani A., Bogachev M.I., Bunde A., Havlin S., Schellnhuber H.J. Improved El Niño forecasting by cooperativity detection. Proc. Natl. Acad. Sci. 2013;110(29):11742–11745. doi: 10.1073/pnas.1309353110. http://www.pnas.org/content/110/29/11742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 292.Ludescher J., Gozolchiani A., Bogachev M.I., Bunde A., Havlin S., Schellnhuber H.J. Very early warning of next El Niño. Proc. Natl. Acad. Sci. 2014;111(6):2064–2066. doi: 10.1073/pnas.1323058111. http://www.pnas.org/content/111/6/2064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 293.Feng Q.Y., Vasile R., Segond M., Gozolchiani A., Wang Y., Abel M., Havlin S., Bunde A., Dijkstra H.A. Climatelearn: A machine-learning approach for climate prediction using network measures. Geosci. Model Dev. Discuss. 2016:1–18. doi: 10.5194/gmd-2015-273. http://www.geosci-model-dev-discuss.net/gmd-2015-273/ [DOI] [Google Scholar]
- 294.Petersik P.J., Dijkstra H.A. Probabilistic forecasting of El Niño using neural network models. Geophys. Res. Lett. 2020;47(6) doi: 10.1029/2019GL086423. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2019GL086423. [DOI] [Google Scholar]
- 295.Ham Y.-G., Kim J.-H., Luo J.-J. Deep learning for multi-year ENSO forecasts. Nature. 2019;573(7775):568–572. doi: 10.1038/s41586-019-1559-7. https://www.nature.com/articles/s41586-019-1559-7. [DOI] [PubMed] [Google Scholar]
- 296.Dijkstra H.A., Petersik P., Hernández-García E., López C. The application of machine learning techniques to improve El Niño prediction skill. Front. Phys. 2019;7 doi: 10.3389/fphy.2019.00153. https://www.frontiersin.org/articles/10.3389/fphy.2019.00153/full. [DOI] [Google Scholar]
- 297.Alexander M.A., Bladé I., Newman M., Lanzante J.R., Lau N.-C., Scott J.D. The atmospheric bridge: The influence of ENSO teleconnections on air–sea interaction over the global oceans. J. Clim. 2002;15(16):2205–2231. doi: 10.1175/1520-0442(2002)015<2205:TABTIO>2.0.CO;2. https://journals.ametsoc.org/doi/full/10.1175/1520-0442. [DOI] [Google Scholar]
- 298.Ashok K., Behera S.K., Rao S.A., Weng H., Yamagata T. El Niño Modoki and its possible teleconnection. J. Geophys. Res. Oceans. 2007;112(C11) doi: 10.1029/2006JC003798. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2006JC003798. [DOI] [Google Scholar]
- 299.Kao H.-Y., Yu J.-Y. Contrasting eastern-Pacific and central-Pacific types of ENSO. J. Clim. 2009;22(3):615–632. doi: 10.1175/2008JCLI2309.1. https://journals.ametsoc.org/doi/10.1175/2008JCLI2309.1. [DOI] [Google Scholar]
- 300.Wiedermann M., Radebach A., Donges J.F., Kurths J., Donner R.V. A climate network-based index to discriminate different types of El Niño and La Niña. Geophys. Res. Lett. 2016;43(13):7176–7185. doi: 10.1002/2016GL069119. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1002/2016GL069119. [DOI] [Google Scholar]
- 301.Lu Z., Yuan N., Chen L., Gong Z. On the impacts of El Niño events: A new monitoring approach using complex network analysis. Geophys. Res. Lett. 2020;47(6) doi: 10.1029/2019GL086533. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2019GL086533. [DOI] [Google Scholar]
- 302.Subash N., Gangwar B. Statistical analysis of Indian rainfall and rice productivity anomalies over the last decades. Int. J. Climatol. 2014;34(7):2378–2392. doi: 10.1002/joc.3845. https://rmets.onlinelibrary.wiley.com/doi/abs/10.1002/joc.3845. [DOI] [Google Scholar]
- 303.Wang B., Xiang B., Li J., Webster P.J., Rajeevan M.N., Liu J., Ha K.-J. Rethinking Indian monsoon rainfall prediction in the context of recent global warming. Nature Commun. 2015;6:7154. doi: 10.1038/ncomms8154. http://www.nature.com/ncomms/2015/150518/ncomms8154/full/ncomms8154.html. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 304.Das S., Mitra A.K., Iyengar G.R., Singh J. Skill of medium-range forecasts over the Indian monsoon region using different parameterizations of deep convection. Weather Forecast. 2002;17(6):1194–1210. doi: 10.1175/1520-0434(2002)017<1194:SOMRFO>2.0.CO;2. https://journals.ametsoc.org/doi/full/10.1175/1520-0434(2002)017<1194:SOMRFO>2.0.CO;2. [DOI] [Google Scholar]
- 305.Durai V.R., Roy Bhowmik S.K. Prediction of Indian summer monsoon in short to medium range time scale with high resolution global forecast system (GFS) T574 and T382. Clim. Dynam. 2014;42(5):1527–1551. doi: 10.1007/s00382-013-1895-5. doi: 10.1007/s00382-013-1895-5. [DOI] [Google Scholar]
- 306.Alessandri A., Borrelli A., Cherchi A., Materia S., Navarra A., Lee J.-Y., Wang B. Prediction of Indian summer monsoon onset using dynamical subseasonal forecasts: Effects of realistic initialization of the atmosphere. Mon. Weather Rev. 2014;143(3):778–793. doi: 10.1175/MWR-D-14-00187.1. https://journals.ametsoc.org/doi/full/10.1175/MWR-D-14-00187.1. [DOI] [Google Scholar]
- 307.Prasad V.S., Hayashi T. Onset and withdrawal of Indian summer monsoon. Geophys. Res. Lett. 2005;32(20) doi: 10.1029/2005GL023269. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2005GL023269. [DOI] [Google Scholar]
- 308.Wang B., Ding Q., Joseph P.V. Objective definition of the Indian summer monsoon onset. J. Clim. 2009;22(12):3303–3316. doi: 10.1175/2008JCLI2675.1. https://journals.ametsoc.org/doi/full/10.1175/2008JCLI2675.1. [DOI] [Google Scholar]
- 309.Taniguchi K., Koike T. Comparison of definitions of Indian summer monsoon onset: Better representation of rapid transitions of atmospheric conditions. Geophys. Res. Lett. 2006;33(2) doi: 10.1029/2005GL024526. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2005GL024526. [DOI] [Google Scholar]
- 310.Rajagopalan B., Molnar P. Combining regional moist static energy and ENSO for forecasting of early and late season Indian monsoon rainfall and its extremes. Geophys. Res. Lett. 2014;41(12):4323–4331. doi: 10.1002/2014GL060429. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1002/2014GL060429. [DOI] [Google Scholar]
- 311.Puranik S.S., Ray K.C.S., Sen P.N., Kumar P.P. An index for predicting the onset of monsoon over Kerala. Current Sci. 2013;105(7):954–961. https://www.jstor.org/stable/24098515. [Google Scholar]
- 312.Flatau M.K., Flatau P.J., Rudnick D. The dynamics of double monsoon onsets. J. Clim. 2001;14(21):4130–4146. doi: 10.1175/1520-0442(2001)014<4130:TDODMO>2.0.CO;2. https://journals.ametsoc.org/doi/full/10.1175/1520-0442(2001)014<4130:TDODMO>2.0.CO;2. [DOI] [Google Scholar]
- 313.Rajeevan M., Pai D.S., Anil Kumar R., Lal B. New statistical models for long-range forecasting of southwest monsoon rainfall over India. Clim. Dynam. 2007;28(7):813–828. doi: 10.1007/s00382-006-0197-6. [DOI] [Google Scholar]
- 314.Shukla J., Mooley D.A. Empirical prediction of the summer monsoon rainfall over India. Mon. Weather Rev. 1987;115(3):695–704. doi: 10.1175/1520-0493(1987)115<0695:EPOTSM>2.0.CO;2. https://journals.ametsoc.org/doi/abs/10.1175/1520-0493(1987)115<0695:EPOTSM>2.0.CO;2. [DOI] [Google Scholar]
- 315.Webster P.J., Magaña V.O., Palmer T.N., Shukla J., Tomas R.A., Yanai M., Yasunari T. Monsoons: Processes, predictability, and the prospects for prediction. J. Geophys. Res. Oceans. 1998;103(C7):14451–14510. doi: 10.1029/97JC02719. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/97JC02719. [DOI] [Google Scholar]
- 316.Di Capua G., Kretschmer M., Runge J., Alessandri A., Donner R.V., van den Hurk B., Vellore R., Krishnan R., Coumou D. Long-lead statistical forecasts of the Indian summer monsoon rainfall based on causal precursors. Weather Forecast. 2019;34(5):1377–1394. doi: 10.1175/WAF-D-19-0002.1. https://journals.ametsoc.org/doi/10.1175/WAF-D-19-0002.1. [DOI] [Google Scholar]
- 317.Gadgil S., Srinivasan J. Seasonal prediction of the Indian monsoon. Curr. Sci. 2011;100(3):343–353. [Google Scholar]
- 318.Rajeevan M., Unnikrishnan C.K., Preethi B. Evaluation of the ENSEMBLES multi-model seasonal forecasts of Indian summer monsoon variability. Clim. Dynam. 2012;38(11):2257–2274. doi: 10.1007/s00382-011-1061-x. doi: 10.1007/s00382-011-1061-x. [DOI] [Google Scholar]
- 319.Ramu D.A., Sabeerali C.T., Chattopadhyay R., Rao D.N., George G., Dhakate A.R., Salunke K., Srivastava A., Rao S.A. Indian summer monsoon rainfall simulation and prediction skill in the CFSv2 coupled model: Impact of atmospheric horizontal resolution. J. Geophys. Res.: Atmos. 2016;121(5) doi: 10.1002/2015JD024629. http://onlinelibrary.wiley.com/doi/10.1002/2015JD024629/abstract. [DOI] [Google Scholar]
- 320.DelSole T., Shukla J. Climate models produce skillful predictions of Indian summer monsoon rainfall. Geophys. Res. Lett. 2012;39(9) doi: 10.1029/2012GL051279. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2012GL051279. [DOI] [Google Scholar]
- 321.Rajeevan M. Prediction of Indian summer monsoon: Status, problems and prospects. Curr. Sci. 2001;81(11):1451–1458. [Google Scholar]
- 322.Gadgil S., Rajeevan M., Nanjundiah R. Monsoon prediction - why yet another failure? Current Sci. 2005;88(9):1389–1400. http://eprints.iisc.ernet.in/3309/ [Google Scholar]
- 323.Fan J., Meng J., Ludescher J., Li Z., Surovyatkina E., Chen X., Kurths J., Schellnhuber H.J. 2020. Network-based approach and climate change benefits for forecasting the amount of Indian monsoon rainfall. cond-mat, physics:physics, http://arxiv.org/abs/2004.06628. [Google Scholar]
- 324.Kumar K.K., Rajagopalan B., Hoerling M., Bates G., Cane M. Unraveling the mystery of Indian monsoon failure during El Niño. Science. 2006;314(5796):115–119. doi: 10.1126/science.1131152. http://science.sciencemag.org/content/314/5796/115. [DOI] [PubMed] [Google Scholar]
- 325.Webster P.J., Yang S. Monsoon and enso: Selectively interactive systems. Q. J. R. Meteorol. Soc. 1992;118(507):877–926. doi: 10.1002/qj.49711850705. http://onlinelibrary.wiley.com/doi/10.1002/qj.49711850705/abstract. [DOI] [Google Scholar]
- 326.Rajeevan M., Pai D.S. On the El Niño-Indian monsoon predictive relationships. Geophys. Res. Lett. 2007;34(4) doi: 10.1029/2006GL028916. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2006GL028916. [DOI] [Google Scholar]
- 327.Springer International Publishing; 2015. Machine Learning and Data Mining Approaches to Climate Science: Proceedings of the 4th International Workshop on Climate Informatics. https://www.springer.com/gp/book/9783319172194. [DOI] [Google Scholar]
- 328.Malik N., Marwan N., Kurths J. Spatial structures and directionalities in monsoonal precipitation over south asia. Nonlinear Process. Geophys. 2010;17(5):371–381. doi: 10.5194/npg-17-371-2010. http://www.nonlin-processes-geophys.net/17/371/2010/ [DOI] [Google Scholar]
- 329.Huffman G.J., Bolvin D.T., Nelkin E.J., Wolff D.B., Adler R.F., Gu G., Hong Y., Bowman K.P., Stocker E.F. The TRMM multisatellite precipitation analysis (TMPA): quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007;8(1):38–55. doi: 10.1175/JHM560.1. https://journals.ametsoc.org/doi/full/10.1175/JHM560.1. [DOI] [Google Scholar]
- 330.Fu Q., Johanson C.M., Wallace J.M., Reichler T. Enhanced mid-latitude tropospheric warming in satellite measurements. Science. 2006;312(5777):1179. doi: 10.1126/science.1125566. http://science.sciencemag.org/content/312/5777/1179. [DOI] [PubMed] [Google Scholar]
- 331.Lu J., Vecchi G.A., Reichler T. Expansion of the hadley cell under global warming. Geophys. Res. Lett. 2007;34(6):L06805. doi: 10.1029/2006GL028443. http://onlinelibrary.wiley.com/doi/10.1029/2006GL028443/abstract. [DOI] [Google Scholar]
- 332.Seo K.-H., Frierson D.M.W., Son J.-H. A mechanism for future changes in hadley circulation strength in CMIP5 climate change simulations. Geophys. Res. Lett. 2014;41(14) doi: 10.1002/2014GL060868. http://onlinelibrary.wiley.com/doi/10.1002/2014GL060868/abstract. [DOI] [Google Scholar]
- 333.Held I.M., Soden B.J. Robust responses of the hydrological cycle to global warming. J. Clim. 2006;19(21):5686–5699. doi: 10.1175/JCLI3990.1. http://journals.ametsoc.org/doi/abs/10.1175/JCLI3990.1. [DOI] [Google Scholar]
- 334.Kossin J.P., Emanuel K.A., Vecchi G.A. The poleward migration of the location of tropical cyclone maximum intensity. Nature. 2014;509(7500):349–352. doi: 10.1038/nature13278. http://www.nature.com/nature/journal/v509/n7500/full/nature13278.html. [DOI] [PubMed] [Google Scholar]
- 335.Vallis G.K. Cambridge University Press; 2017. Atmospheric and Oceanic Fluid Dynamics. [Google Scholar]
- 336.Held I.M., Hou A.Y. Nonlinear axially symmetric circulations in a nearly inviscid atmosphere. J. Atmos. Sci. 1980;37(3):515–533. doi: 10.1175/1520-0469(1980)037<0515:NASCIA>2.0.CO;2. http://journals.ametsoc.org/doi/abs/10.1175/1520-0469(1980)037<0515:NASCIA>2.0.CO;2. [DOI] [Google Scholar]
- 337.Reichler T., Dameris M., Sausen R. Determining the tropopause height from gridded data. Geophys. Res. Lett. 2003;30(20) doi: 10.1029/2003GL018240. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2003GL018240. [DOI] [Google Scholar]
- 338.Mitas C.M., Clement A. Has the Hadley cell been strengthening in recent decades? Geophys. Res. Lett. 2005;32(3):L03809. doi: 10.1029/2004GL021765. http://onlinelibrary.wiley.com/doi/10.1029/2004GL021765/abstract. [DOI] [Google Scholar]
- 339.Ganachaud A., Wunsch C. Improved estimates of global ocean circulation, heat transport and mixing from hydrographic data. Nature. 2000;408(6811):453–457. doi: 10.1038/35044048. https://www.nature.com/articles/35044048. [DOI] [PubMed] [Google Scholar]
- 340.Johns W.E., Baringer M.O., Beal L.M., Cunningham S.A., Kanzow T., Bryden H.L., Hirschi J.J.M., Marotzke J., Meinen C.S., Shaw B., Curry R. Continuous, array-based estimates of atlantic ocean heat transport at N. J. Clim. 2010;24(10):2429–2449. doi: 10.1175/2010JCLI3997.1. https://journals.ametsoc.org/doi/full/10.1175/2010JCLI3997.1. [DOI] [Google Scholar]
- 341.Jackson L.C., Kahana R., Graham T., Ringer M.A., Woollings T., Mecking J.V., Wood R.A. Global and european climate impacts of a slowdown of the AMOC in a high resolution GCM. Clim. Dynam. 2015;45(11):3299–3316. doi: 10.1007/s00382-015-2540-2. [DOI] [Google Scholar]
- 342.Sallenger A.H., Doran K.S., Howd P.A. Hotspot of accelerated sea-level rise on the Atlantic coast of North America. Nature Clim. Change. 2012;2(12):884–888. doi: 10.1038/nclimate1597. https://www.nature.com/articles/nclimate1597. [DOI] [Google Scholar]
- 343.Defrance D., Ramstein G., Charbit S., Vrac M., Famien A.M.s., Sultan B., Swingedouw D., Dumas C., Gemenne F., Alvarez-Solas J., Vanderlinden J.-P. Consequences of rapid ice sheet melting on the Sahelian population vulnerability. Proc. Natl. Acad. Sci. 2017;114(25):6533–6538. doi: 10.1073/pnas.1619358114. https://www.pnas.org/content/114/25/6533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 344.Cunningham S.A., Kanzow T., Rayner D., Baringer M.O., Johns W.E., Marotzke J., Longworth H.R., Grant E.M., Hirschi J.-M., Beal L.M., Meinen C.S., Bryden H.L. Temporal variability of the atlantic meridional overturning circulation at N. Science. 2007;317(5840):935–938. doi: 10.1126/science.1141304. https://science.sciencemag.org/content/317/5840/935. [DOI] [PubMed] [Google Scholar]
- 345.Hurrell J.W., Holland M.M., Gent P.R., Ghan S., Kay J.E., Kushner P.J., Lamarque J.-F., Large W.G., Lawrence D., Lindsay K., Lipscomb W.H., Long M.C., Mahowald N., Marsh D.R., Neale R.B., Rasch P., Vavrus S., Vertenstein M., Bader D., Collins W.D., Hack J.J., Kiehl J., Marshall S. The community earth system model: A framework for collaborative research. Bull. Am. Meteorol. Soc. 2013;94(9):1339–1360. doi: 10.1175/BAMS-D-12-00121.1. https://journals.ametsoc.org/doi/full/10.1175/BAMS-D-12-00121.1. [DOI] [Google Scholar]
- 346.Danabasoglu G., Lamarque J.-F., Bacmeister J., Bailey D.A., DuVivier A.K., Edwards J., Emmons L.K., Fasullo J., Garcia R., Gettelman A., Hannay C., Holland M.M., Large W.G., Lauritzen P.H., Lawrence D.M., Lenaerts J.T.M., Lindsay K., Lipscomb W.H., Mills M.J., Neale R., Oleson K.W., Otto-Bliesner B., Phillips A.S., Sacks W., Tilmes S., Kampenhout L.v., Vertenstein M., Bertini A., Dennis J., Deser C., Fischer C., Fox-Kemper B., Kay J.E., Kinnison D., Kushner P.J., Larson V.E., Long M.C., Mickelson S., Moore J.K., Nienhouse E., Polvani L., Rasch P.J., Strand W.G. The community earth system model version 2 (CESM2) J. Adv. Modelling Earth Syst. 2020;12(2) doi: 10.1029/2019MS001916. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2019MS001916. [DOI] [Google Scholar]
- 347.den Toom M., Dijkstra H.A., Wubs F.W. Spurious multiple equilibria introduced by convective adjustment. Ocean Model. 2011;38(1):126–137. doi: 10.1016/j.ocemod.2011.02.009. http://www.sciencedirect.com/science/article/pii/S1463500311000448. [DOI] [Google Scholar]
- 348.Gagnon J.-S., Lovejoy S., Schertzer D. Multifractal earth topography. Nonlinear Processes Geophys. 2006;13(5):541–570. doi: 10.5194/npg-13-541-2006. https://www.nonlin-processes-geophys.net/13/541/2006/ [DOI] [Google Scholar]
- 349.Sapoval B., Baldassarri A., Gabrielli A. Self-stabilized fractality of seacoasts through damped erosion. Phys. Rev. Lett. 2004;93(9) doi: 10.1103/PhysRevLett.93.098501. https://link.aps.org/doi/10.1103/PhysRevLett.93.098501. [DOI] [PubMed] [Google Scholar]
- 350.Maritan A., Colaiori F., Flammini A., Cieplak M., Banavar J.R. Universality classes of optimal channel networks. Science. 1996;272(5264):984–986. doi: 10.1126/science.272.5264.984. http://science.sciencemag.org/content/272/5264/984. [DOI] [PubMed] [Google Scholar]
- 351.Gill J.B. Springer Science & Business Media; 2012. Orogenic Andesites and Plate Tectonics. [Google Scholar]
- 352.Jayne S.R., Laurent L.C.S., Gille S.T. Connections between ocean bottom topography and earth’s climate. Oceanography. 2004;17(1):65–74. [Google Scholar]
- 353.Slangen A.B.A., Church J.A., Agosta C., Fettweis X., Marzeion B., Richter K. Anthropogenic forcing dominates global mean sea-level rise since 1970. Nature Clim. Change. 2016;6(7):701–705. doi: 10.1038/nclimate2991. https://www.nature.com/articles/nclimate2991. [DOI] [Google Scholar]
- 354.Sweet W.V., Park J. From the extreme to the mean: Acceleration and tipping points of coastal inundation from sea level rise. Earth’s Future. 2014;2(12):579–600. doi: 10.1002/2014EF000272. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1002/2014EF000272. [DOI] [Google Scholar]
- 355.Mengel M., Nauels A., Rogelj J., Schleussner C.-F. Committed sea-level rise under the Paris agreement and the legacy of delayed mitigation action. Nature Commun. 2018;9(1):601. doi: 10.1038/s41467-018-02985-8. https://www.nature.com/articles/s41467-018-02985-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 356.C. Amante, B. Eakins, NOAA Technical Memorandum NESDIS NGDC-24, 2009.
- 357.Lovejoy S., Schertzer D. Scaling and multifractal fields in the solid earth and topography. Nonlinear Process. Geophys. 2007;14(4):465–502. https://hal.archives-ouvertes.fr/hal-00331103. [Google Scholar]
- 358.Bell T.H. Statistical features of sea-floor topography. Deep Sea Res. Oceanogr. Abstr. 1975;22(12):883–892. doi: 10.1016/0011-7471(75)90090-X. http://www.sciencedirect.com/science/article/pii/001174717590090X. [DOI] [Google Scholar]
- 359.Mantilla R., Troutman B.M., Gupta V.K. Testing statistical self-similarity in the topology of river networks. J. Geophys. Res. Earth Surf. 2010;115(F3) doi: 10.1029/2009JF001609. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2009JF001609. [DOI] [Google Scholar]
- 360.Brown S.R., Scholz C.H. Broad bandwidth study of the topography of natural rock surfaces. J. Geophys. Res. Solid Earth. 1985;90(B14):12575–12582. doi: 10.1029/JB090iB14p12575. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/JB090iB14p12575. [DOI] [Google Scholar]
- 361.Wegener A. Courier Corporation; 1966. The Origin of Continents and Oceans. [Google Scholar]
- 362.Du C., Satik C., Yortsos Y.C. Percolation in a fractional Brownian motion lattice. AIChE J. 1996;42(8):2392–2395. doi: 10.1002/aic.690420831. https://onlinelibrary.wiley.com/doi/abs/10.1002/aic.690420831. [DOI] [Google Scholar]
- 363.Vicsek T. World scientific; 1992. Fractal Growth Phenomena. [Google Scholar]
- 364.Family F., Vicsek T. World Scientific; 1991. Dynamics of Fractal Surfaces. [Google Scholar]
- 365.Wells D.L., Coppersmith K.J. New empirical relationships among magnitude, rupture length, rupture width, rupture area, and surface displacement. Bull. Seismol. Soc. Am. 1994;84(4):974–1002. https://pubs.geoscienceworld.org/bssa/article-abstract/84/4/974/119792/New-empirical-relationships-among-magnitude. [Google Scholar]
- 366.Gutenberg B., Richter C.F. Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 1944;34(4):185–188. https://pubs.geoscienceworld.org/ssa/bssa/article-abstract/34/4/185/101140/frequency-of-earthquakes-in-california. [Google Scholar]
- 367.Marzocchi W., Sandri L. A review and new insights on the estimation of the b-valueand its uncertainty. Ann. Geophys. 2009;46(6) doi: 10.4401/ag-3472. https://www.annalsofgeophysics.eu/index.php/annals/article/view/3472. [DOI] [Google Scholar]
- 368.Omori F. On the after-shocks of earthquakes. J. Coll. Sci. 1894;7:111–120. [Google Scholar]
- 369.Ogata Y. Detection of precursory relative quiescence before great earthquakes through a statistical model. J. Geophys. Res. Solid Earth. 1992;97(B13):19845–19871. doi: 10.1029/92JB00708. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/92JB00708. [DOI] [Google Scholar]
- 370.Bak P., Christensen K., Danon L., Scanlon T. Unified scaling law for earthquakes. Phys. Rev. Lett. 2002;88(17) doi: 10.1103/PhysRevLett.88.178501. http://link.aps.org/doi/10.1103/PhysRevLett.88.178501. [DOI] [PubMed] [Google Scholar]
- 371.Corral A. Long-term clustering, scaling, and universality in the temporal occurrence of earthquakes. Phys. Rev. Lett. 2004;92(10) doi: 10.1103/PhysRevLett.92.108501. http://link.aps.org/doi/10.1103/PhysRevLett.92.108501. [DOI] [PubMed] [Google Scholar]
- 372.Saichev A., Sornette D. “Universal” distribution of interearthquake times explained. Phys. Rev. Lett. 2006;97(7) doi: 10.1103/PhysRevLett.97.078501. https://link.aps.org/doi/10.1103/PhysRevLett.97.078501. [DOI] [PubMed] [Google Scholar]
- 373.Molchan G. Interevent time distribution in seismicity: A theoretical approach. Pure Appl. Geophys. 2005;162(6):1135–1150. doi: 10.1007/s00024-004-2664-5. [DOI] [Google Scholar]
- 374.Touati S., Naylor M., Main I.G. Origin and nonuniversality of the earthquake interevent time distribution. Phys. Rev. Lett. 2009;102(16) doi: 10.1103/PhysRevLett.102.168501. https://link.aps.org/doi/10.1103/PhysRevLett.102.168501. [DOI] [PubMed] [Google Scholar]
- 375.Vere-Jones D. Stochastic models for earthquake occurrence. J. R. Stat. Soc. Ser. B Stat. Methodol. 1970;32(1):1–45. doi: 10.1111/j.2517-6161.1970.tb00814.x. https://rss.onlinelibrary.wiley.com/doi/abs/10.1111/j.2517-6161.1970.tb00814.x. [DOI] [Google Scholar]
- 376.Helmstetter A., Sornette D. Foreshocks explained by cascades of triggered seismicity. J. Geophys. Res. Solid Earth. 2003;108(B10) doi: 10.1029/2003JB002409. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2003JB002409. [DOI] [Google Scholar]
- 377.Zhuang J., Ogata Y., Vere-Jones D. Analyzing earthquake clustering features by using stochastic reconstruction. J. Geophys. Res. Solid Earth. 2004;109(B5) doi: 10.1029/2003JB002879. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2003JB002879. [DOI] [Google Scholar]
- 378.Hainzl S., Ogata Y. Detecting fluid signals in seismicity data through statistical earthquake modeling. J. Geophys. Res. Solid Earth. 2005;110(B5) doi: 10.1029/2004JB003247. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2004JB003247. [DOI] [Google Scholar]
- 379.Lombardi A.M., Cocco M., Marzocchi W. On the increase of background seismicity rate during the 1997–1998 umbria-marche, central Italy, sequence: Apparent variation or fluid-driven triggering?on the increase of background seismicity rate during the 1997–1998 umbria-marche sequence. Bull. Seismol. Soc. Am. 2010;100(3):1138–1152. doi: 10.1785/0120090077. https://pubs.geoscienceworld.org/bssa/article-abstract/100/3/1138/349415/On-the-Increase-of-Background-Seismicity-Rate. [DOI] [Google Scholar]
- 380.Ogata Y. Statistical models for earthquake occurrences and residual analysis for point processes. J. Amer. Statist. Assoc. 1988;83(401):9–27. doi: 10.1080/01621459.1988.10478560. https://www.tandfonline.com/doi/abs/10.1080/01621459.1988.10478560. [DOI] [Google Scholar]
- 381.Ogata Y. Statistical model for standard seismicity and detection of anomalies by residual analysis. Tectonophysics. 1989;169(1):159–174. doi: 10.1016/0040-1951(89)90191-1. http://www.sciencedirect.com/science/article/pii/0040195189901911. [DOI] [Google Scholar]
- 382.Daley D.J., Vere-Jones D. Probability and Its Applications, An Introduction to the Theory of Point Processes. second ed. Springer-Verlag; New York: 2003. An Introduction to the Theory of Point Processes: Volume I: Elementary Theory and Methods. https://www.springer.com/gp/book/9780387955414. [DOI] [Google Scholar]
- 383.Ogata Y. Space-time point-process models for earthquake occurrences. Ann. Inst. Statist. Math. 1998;50(2):379–402. doi: 10.1023/A:1003403601725. https://link.springer.com/article/10.1023/A:1003403601725. [DOI] [Google Scholar]
- 384.Marzocchi W., Taroni M., Falcone G. Earthquake forecasting during the complex amatrice-norcia seismic sequence. Sci. Adv. 2017;3(9) doi: 10.1126/sciadv.1701239. http://advances.sciencemag.org/content/3/9/e1701239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 385.Zhuang J. Next-day earthquake forecasts for the Japan region generated by the ETAS model. Earth Planets Space. 2011;63(3):5. doi: 10.5047/eps.2010.12.010. https://link.springer.com/article/10.5047/eps.2010.12.010. [DOI] [Google Scholar]
- 386.Field E.H., Milner K.R., Hardebeck J.L., Page M.T., Elst N.v.d., Jordan T.H., Michael A.J., Shaw B.E., Werner M.J. A spatiotemporal clustering model for the third uniform California earthquake rupture forecast (UCERF3-ETAS): Toward an operational earthquake forecasta spatiotemporal clustering model for the UCERF3-ETAS. Bull. Seismol. Soc. Am. 2017;107(3):1049–1081. doi: 10.1785/0120160173. https://pubs.geoscienceworld.org/bssa/article-abstract/107/3/1049/354189/A-Spatiotemporal-Clustering-Model-for-the-Third. [DOI] [Google Scholar]
- 387.Ogata Y. Seismicity analysis through point-process modeling: A review. Pure Appl. Geophys. 1999;155(2):471–507. doi: 10.1007/s000240050275. [DOI] [Google Scholar]
- 388.Lennartz S., Livina V.N., Bunde A., Havlin S. Long-term memory in earthquakes and the distribution of interoccurrence times. Europhys. Lett. 2008;81(6):69001. doi: 10.1209/0295-5075/81/69001. http://stacks.iop.org/0295-5075/81/i=6/a=69001. [DOI] [Google Scholar]
- 389.Livina V.N., Havlin S., Bunde A. Memory in the occurrence of earthquakes. Phys. Rev. Lett. 2005;95(20) doi: 10.1103/PhysRevLett.95.208501. http://link.aps.org/doi/10.1103/PhysRevLett.95.208501. [DOI] [PubMed] [Google Scholar]
- 390.Zhang Y., Fan J., Marzocchi W., Shapira A., Hofstetter R., Havlin S., Ashkenazy Y. Scaling laws in earthquake memory for interevent times and distances. Phys. Rev. Res. 2020;2(1) doi: 10.1103/PhysRevResearch.2.013264. https://link.aps.org/doi/10.1103/PhysRevResearch.2.013264. [DOI] [Google Scholar]
- 391.Kagan Y.Y., Knopoff L. Statistical short-term earthquake prediction. Science. 1987;236(4808):1563–1567. doi: 10.1126/science.236.4808.1563. http://science.sciencemag.org/content/236/4808/1563. [DOI] [PubMed] [Google Scholar]
- 392.Wang K., Chen Q.-F., Sun S., Wang A. Predicting the 1975 Haicheng earthquake. Bull. Seismol. Soc. Am. 2006;96(3):757–795. doi: 10.1785/0120050191. [DOI] [Google Scholar]
- 393.Bernard P., Pinettes P., Hatzidimitriou P.M., Scordilis E.M., Veis G., Milas P. From precursors to prediction: a few recent cases from Greece. Geophys. J. Int. 1997;131(3):467–477. doi: 10.1111/j.1365-246X.1997.tb06590.x. https://onlinelibrary.wiley.com/doi/abs/10.1111/j.1365-246X.1997.tb06590.x. [DOI] [Google Scholar]
- 394.Bakun W.H., Aagaard B., Dost B., Ellsworth W.L., Hardebeck J.L., Harris R.A., Ji C., Johnston M.J.S., Langbein J., Lienkaemper J.J., Michael A.J., Murray J.R., Nadeau R.M., Reasenberg P.A., Reichle M.S., Roeloffs E.A., Shakal A., Simpson R.W., Waldhauser F. Implications for prediction and hazard assessment from the 2004 parkfield earthquake. Nature. 2005;437(7061):969–974. doi: 10.1038/nature04067. https://www.nature.com/articles/nature04067. [DOI] [PubMed] [Google Scholar]
- 395.DeVries P.M.R., Viégas F., Wattenberg M., Meade B.J. Deep learning of aftershock patterns following large earthquakes. Nature. 2018;560(7720):632–634. doi: 10.1038/s41586-018-0438-y. https://www.nature.com/articles/s41586-018-0438-y. [DOI] [PubMed] [Google Scholar]
- 396.Molchan G.M. Strategies in strong earthquake prediction. Phys. Earth Planet. Inter. 1990;61(1):84–98. doi: 10.1016/0031-9201(90)90097-H. http://www.sciencedirect.com/science/article/pii/003192019090097H. [DOI] [Google Scholar]
- 397.Schorlemmer D., Gerstenberger M.C., Wiemer S., Jackson D.D., Rhoades D.A. Earthquake likelihood model testing. Seismol. Res. Lett. 2007;78(1):17–29. doi: 10.1785/gssrl.78.1.17. https://pubs.geoscienceworld.org/srl/article-abstract/78/1/17/143320/Earthquake-Likelihood-Model-Testing. [DOI] [Google Scholar]
- 398.Zechar J.D., Gerstenberger M.C., Rhoades D.A. Likelihood-based tests for evaluating space–rate–magnitude earthquake forecastslikelihood-based tests for evaluating space-rate-magnitude earthquake forecasts. Bull. Seismol. Soc. Am. 2010;100(3):1184–1195. doi: 10.1785/0120090192. https://pubs.geoscienceworld.org/bssa/article-abstract/100/3/1184/349446/Likelihood-Based-Tests-for-Evaluating-Space-Rate. [DOI] [Google Scholar]
- 399.Zechar J.D. Evaluating earthquake predictions and earthquake forecasts: A guide for students and new researchers. Community Online Resour. Stat. Seism. Anal. 2010;126 [Google Scholar]
- 400.Lombardi A.M. Estimation of the parameters of ETAS models by simulated annealing. Sci. Rep. 2015;5:8417. doi: 10.1038/srep08417. https://www.nature.com/articles/srep08417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 401.Falcucci E., Gori S., Bignami C., Pietrantonio G., Melini D., Moro M., Saroli M., Galadini F. The campotosto seismic gap in between the 2009 and 2016–2017 seismic sequences of central Italy and the role of inherited lithospheric faults in regional seismotectonic settings. Tectonics. 2018;37(8):2425–2445. doi: 10.1029/2017TC004844. https://agupubs.onlinelibrary.wiley.com/doi/full/10.1029/2017TC004844. [DOI] [Google Scholar]
- 402.Zhang Y., Zhou D., Fan J., Marzocchi W., Ashkenazy Y., Havlin S. 2020. Improved earthquake forecasting model based on long-term memory in earthquake. physics, http://arxiv.org/abs/2003.12539. [Google Scholar]
- 403.Boccaletti S., Bianconi G., Criado R., del Genio C.I., Gómez-Gardeñes J., Romance M., Sendiña Nadal I., Wang Z., Zanin M. The structure and dynamics of multilayer networks. Phys. Rep. 2014;544(1):1–122. doi: 10.1016/j.physrep.2014.07.001. http://www.sciencedirect.com/science/article/pii/S0370157314002105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 404.Runge J., Petoukhov V., Donges J.F., Hlinka J., Jajcay N., Vejmelka M., Hartman D., Marwan N., Paluš M., Kurths J. Identifying causal gateways and mediators in complex spatio-temporal systems. Nature Commun. 2015;6:8502. doi: 10.1038/ncomms9502. http://www.nature.com/ncomms/2015/151007/ncomms9502/full/ncomms9502.html. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 405.Kretschmer M., Runge J., Coumou D. Early prediction of extreme stratospheric polar vortex states based on causal precursors. Geophys. Res. Lett. 2017;44(16):8592–8600. doi: 10.1002/2017GL074696. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1002/2017GL074696. [DOI] [Google Scholar]
- 406.Ying N., Zhou D., Han Z.G., Chen Q.H., Ye Q., Xue Z.G. Rossby waves detection in the CO2 and temperature multilayer climate network. Geophys. Res. Lett. 2020;47(2) doi: 10.1029/2019GL086507. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2019GL086507. [DOI] [Google Scholar]
- 407.Ashkenazy Y., Gildor H., Losch M., Macdonald F.A., Schrag D.P., Tziperman E. Dynamics of a snowball earth ocean. Nature. 2013;495(7439):90–93. doi: 10.1038/nature11894. https://www.nature.com/articles/nature11894. [DOI] [PubMed] [Google Scholar]
- 408.Hoffman P.F., Abbot D.S., Ashkenazy Y., Benn D.I., Brocks J.J., Cohen P.A., Cox G.M., Creveling J.R., Donnadieu Y., Erwin D.H., Fairchild I.J., Ferreira D., Goodman J.C., Halverson G.P., Jansen M.F., Hir G.L., Love G.D., Macdonald F.A., Maloof A.C., Partin C.A., Ramstein G., Rose B.E.J., Rose C.V., Sadler P.M., Tziperman E., Voigt A., Warren S.G. Snowball earth climate dynamics and cryogenian geology-geobiology. Sci. Adv. 2017;3(11) doi: 10.1126/sciadv.1600983. https://advances.sciencemag.org/content/3/11/e1600983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 409.Lucarini V., Bódai T. Transitions across melancholia states in a climate model: reconciling the deterministic and stochastic points of view. Phys. Rev. Lett. 2019;122(15) doi: 10.1103/PhysRevLett.122.158701. https://link.aps.org/doi/10.1103/PhysRevLett.122.158701. [DOI] [PubMed] [Google Scholar]
- 410.Mignan A. Functional shape of the earthquake frequency-magnitude distribution and completeness magnitude. J. Geophys. Res. Solid Earth. 2012;117(B8) doi: 10.1029/2012JB009347. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2012JB009347. [DOI] [Google Scholar]
- 411.Chorozoglou D., Iliopoulos A., Kourouklas C., Mangira O., Papadimitriou E. Earthquake networks as a tool for seismicity investigation: a review. Pure Appl. Geophys. 2019 doi: 10.1007/s00024-019-02253-w. [DOI] [Google Scholar]
- 412.Vallée M., Ampuero J.P., Juhel K., Bernard P., Montagner J.-P., Barsuglia M. Observations and modeling of the elastogravity signals preceding direct seismic waves. Science. 2017;358(6367):1164–1168. doi: 10.1126/science.aao0746. http://science.sciencemag.org/content/358/6367/1164. [DOI] [PubMed] [Google Scholar]
- 413.LeCun Y., Bengio Y., Hinton G. Deep learning. Nature. 2015;521(7553):436–444. doi: 10.1038/nature14539. https://www.nature.com/articles/nature14539. [DOI] [PubMed] [Google Scholar]
- 414.Carrasquilla J., Melko R.G. Machine learning phases of matter. Nat. Phys. 2017;advance online publication doi: 10.1038/nphys4035. http://www.nature.com/nphys/journal/vaop/ncurrent/full/nphys4035.html. [DOI] [Google Scholar]
- 415.Nieuwenburg E.P.L.v., Liu Y.-H., Huber S.D. Learning phase transitions by confusion. Nat. Phys. 2017;13(5):nphys4037. doi: 10.1038/nphys4037. https://www.nature.com/articles/nphys4037. [DOI] [Google Scholar]
- 416.Bapst V., Keck T., Grabska-Barwińska A., Donner C., Cubuk E.D., Schoenholz S.S., Obika A., Nelson A.W.R., Back T., Hassabis D., Kohli P. Unveiling the predictive power of static structure in glassy systems. Nat. Phys. 2020;16(4):448–454. doi: 10.1038/s41567-020-0842-8. https://www.nature.com/articles/s41567-020-0842-8. [DOI] [Google Scholar]
- 417.Reichstein M., Camps-Valls G., Stevens B., Jung M., Denzler J., Carvalhais N., Prabhat A. Deep learning and process understanding for data-driven earth system science. Nature. 2019;566(7743):195. doi: 10.1038/s41586-019-0912-1. https://www.nature.com/articles/s41586-019-0912-1. [DOI] [PubMed] [Google Scholar]
- 418.Saha M., Mitra P., Nanjundiah R.S. Deep learning for predicting the monsoon over the homogeneous regions of India. J. Earth Syst. Sci. 2017;126(4):54. doi: 10.1007/s12040-017-0838-7. doi: 10.1007/s12040-017-0838-7. [DOI] [Google Scholar]
- 419.Perol T., Gharbi M., Denolle M. Convolutional neural network for earthquake detection and location. Sci. Adv. 2018;4(2) doi: 10.1126/sciadv.1700578. http://advances.sciencemag.org/content/4/2/e1700578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 420.Fan J., Cohen K., Shekhtman L.M., Liu S., Meng J., Louzoun Y., Havlin S. Topology of products similarity network for market forecasting. Appl. Netw. Sci. 2019;4(1):1–15. doi: 10.1007/s41109-019-0171-y. https://appliednetsci.springeropen.com/articles/10.1007/s41109-019-0171-y. [DOI] [Google Scholar]
- 421.Testolin A., Piccolini M., Suweis S. Deep learning systems as complex networks. J. Complex Netw. 2020;8(1) doi: 10.1093/comnet/cnz018. https://academic.oup.com/comnet/article/8/1/cnz018/5512542. [DOI] [Google Scholar]
- 422.Carleton T.A., Hsiang S.M. Social and economic impacts of climate. Science. 2016;353(6304):aad9837. doi: 10.1126/science.aad9837. http://science.sciencemag.org/content/353/6304/aad9837. [DOI] [PubMed] [Google Scholar]
- 423.Mehta P., McAuley D.F., Brown M., Sanchez E., Tattersall R.S., Manson J.J. COVID-19: consider cytokine storm syndromes and immunosuppression. Lancet. 2020;395(10229):1033–1034. doi: 10.1016/S0140-6736(20)30628-0. https://www.thelancet.com/journals/lancet/article/PIIS0140-6736(20)30628-0/abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 424.Li R., Xu L., Bjørnstad O.N., Liu K., Song T., Chen A., Xu B., Liu Q., Stenseth N.C. Climate-driven variation in mosquito density predicts the spatiotemporal dynamics of dengue. Proc. Natl. Acad. Sci. 2019;116(9):3624–3629. doi: 10.1073/pnas.1806094116. https://www.pnas.org/content/116/9/3624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 425.Towers S., Chowell G., Hameed R., Jastrebski M., Khan M., Meeks J., Mubayi A., Harris G. Climate change and influenza: the likelihood of early and severe influenza seasons following warmer than average winters. PLoS Curr. 2013;5 doi: 10.1371/currents.flu.3679b56a3a5313dc7c043fb944c6f138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 426.Deyle E.R., Maher M.C., Hernandez R.D., Basu S., Sugihara G. Global environmental drivers of influenza. Proc. Natl. Acad. Sci. 2016 doi: 10.1073/pnas.1607747113. http://www.pnas.org/content/early/2016/10/25/1607747113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 427.Pei S., Kandula S., Yang W., Shaman J. Forecasting the spatial transmission of influenza in the United States. Proc. Natl. Acad. Sci. 2018;115(11):2752–2757. doi: 10.1073/pnas.1708856115. http://www.pnas.org/content/115/11/2752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 428.Wu X., Nethery R.C., Sabath B.M., Braun D., Dominici F. 2020. Exposure to air pollution and COVID-19 mortality in the united states: A nationwide cross-sectional study. medRxiv, https://www.medrxiv.org/content/10.1101/2020.04.05.20054502v2. [DOI] [PMC free article] [PubMed] [Google Scholar]