Introduction to dynamical systems analysis in quantitative systems pharmacology: basic concepts and applications

Abstract

Quantitative systems pharmacology (QSP) can be regarded as a hybrid of pharmacometrics and systems biology. Here, we introduce the basic concepts related to dynamical systems theory that are fundamental to the analysis of systems biology models. Determination of the fixed points and their local stabilities constitute the most important step. Illustration of a phase portrait further helps investigate multistability and bifurcation behavior. As a motivating example, we examine a cell circuit model that deals with tissue inflammation and fibrosis. We show how increasing the severity and duration of inflammatory stimuli divert the system trajectories towards pathological fibrosis. Simulations that involve different parameter values offer important insights into the potential bifurcations and the development of efficient therapeutic strategies. We expect that this tutorial serves as a good starting point for pharmacometricians striving to widen their scope to QSP and physiologically-oriented modeling.

INTRODUCTION

Pharmacometrics is a relatively young field that applies computational modeling and simulation to clinical pharmacology. In the narrowest sense, it denotes population pharmacokinetic-pharmacodynamic (PopPKPD) modeling using one of the standard nonlinear mixed-effects modeling software, such as NONMEM. In a wider sense, pharmacometrics is the science of “mathematical models of biology, pharmacology, disease, and physiology used to describe and quantify interactions between xenobiotics and patients, including beneficial effects and side effects resultant from such interfaces [1].”

There are two main approaches to pharmacometrics modeling. A “top-down” approach [2] primarily aims to construct a model that provides reasonable approximations to the observed data. Biological details are often omitted for the sake of simplicity. A “bottom-up” approach, on the other hand, aims to construct a model that faithfully reflects the underlying biology. Less effort is taken to curve-fit the model or acquire precise parameter estimates, although limited tuning of parameter values is done as needed.

Each of the two approaches has its advantages and disadvantages. The former is often easier to implement and analyze. Its major drawback is its poor extrapolative capability. The latter effectively solves this problem but is generally more complex and difficult to construct. The physiologically based pharmacokinetic (PBPK) approach rapidly established itself as an improved methodology to implement inter-species scaling [3]. Quantitative systems pharmacology (QSP) [4] applies a similar philosophy to modeling pharmacodynamics and disease progression.

QSP can be regarded as a hybrid of pharmacometrics and systems biology. Systems biology applies mathematical models to biological networks in order to understand and predict the complex interactions among their components. While pharmacometrics models can also be considered as comprising of small networks linking different compartments, systems biology models tend to deal with networks that are both larger and more densely connected. Hence, systems biology models generally require a more sophisticated method of analysis than is often needed for analyzing typical PKPD models.

In this tutorial, we will introduce the basic concepts related to a mathematical field called dynamical systems theory that plays a prominent role in the analysis of systems biology models. In fact, the concepts of dynamical systems theory also implicitly form the groundwork of pharmacometrics. The tutorial aims to demonstrate how they apply to both pharmacometrics and QSP by taking a ‘learning-by-doing’ approach. Important concepts are introduced through examples, and towards the end, we examine a cell circuit model proposed by Adler et al. [5] that deals with tissue inflammation and fibrosis.

BASIC CONCEPTS

Formulation of a dynamical systems model

Central to both pharmacometrics and systems biology modeling is the formulation of a system of ordinary differential equations (ODEs). The general structure of the system of ODEs involving n dynamic variables, x₁, x₂, …, x_n, is as follows:

$$\frac{d{x}_1}{dt}{\mathrm{ }=\mathrm{ }f}_1(x_1,x_2,\dots ,x_n,t)$$

$$\frac{d{x}_2}{dt}\mathrm{ }=\mathrm{ }{f}_2(x_1,x_2,\dots ,x_n,t)$$

…

$$\frac{d{x}_n}{dt}{\mathrm{ }=\mathrm{ }f}_n(x_1,x_2,\dots ,x_n,t)$$

A specific function, f_k (x₁,x₂,…,x_n,t) (k = 1, 2, …, n), relates the time derivative of the kth variable to the values of all other variables. When there is an explicit dependence of $\frac{d{x}_k}{dt}$ on time (= t), the ODE is called non-autonomous; otherwise, it is called autonomous. All non-autonomous systems can be converted to an autonomous system by introducing a dummy variable u to represent time, where $\frac{du}{dt}$ = 1 and u(0) = 0.

If all f_k (x₁,x₂,…,x_n) (k = 1, 2, …, n) are linear combinations of x_k (k = 1, 2, …, n), the system is called a linear system of ODEs with constant coefficients:

$$\frac{d{x}_1}{dt}\mathrm{ }=\mathrm{ }{\beta }_{10}\mathrm{ }+\mathrm{ }{\beta }_{11}{x}_1 +\mathrm{ }{\beta }_{12}{x}_2 +\mathrm{ }\dots \mathrm{ }+\mathrm{ }{\beta }_{1n}{x}_n$$

$$\frac{d{x}_2}{dt}\mathrm{ }=\mathrm{ }{\beta }_{20}\mathrm{ }+\mathrm{ }{\beta }_{21}{x}_1 +\mathrm{ }{\beta }_{22}{x}_2 +\mathrm{ }\mathrm{ }\dots \mathrm{ }+\mathrm{ }{\beta }_{2n}{x}_n$$

…

$$\frac{d{x}_n}{dt}\mathrm{ }=\mathrm{ }{\beta }_{n0}\mathrm{ }+\mathrm{ }{\beta }_{n1}{x}_1 +\mathrm{ }{\beta }_{n2}{x}_2 +\mathrm{ }\mathrm{ }\dots \mathrm{ }+\mathrm{ }{\beta }_{nn}{x}_n$$

When β₁₀ = β₂₀ = … = β_n0 = 0, the system is said to be homogeneous; otherwise, it is non-homogeneous.

In matrix notation,

$$\frac{dX}{dt}\mathrm{ }=\mathrm{ }BX$$

where X = [1,x₁,x₂,…,x_n]^T and $B\mathrm{ }=\mathrm{ }\left[\begin{array}{c}{\beta }_{10}\\ ⋮\\ {\beta }_{n0}\end{array} \begin{array}{ccc}{\beta }_{11}& \cdots & {\beta }_{1n}\\ ⋮& \ddots & ⋮\\ {\beta }_{n1}& \cdots & {\beta }_{nn}\end{array}\right]$.

A continuous dynamical system is a system that can be described using the above formalisms. A set of values x₁, x₂, …, x_n constituting X = [x₁,x₂,…,x_n]^T is called the system state. A state-space encompasses all possible values of X. The time evolution of the system state in state-space defines a particular trajectory, which is a unique curve that depends on both the initial state and the parameters, β_ij (i,j = 1, 2, …, n), constituting the function f_k (x₁,x₂,…,x_n). The matrix B that maps the current state to its rate of change is called the coefficient matrix.

Fixed point(s)

While an ideal method to investigate the behavior of the system is to derive an analytic solution of the ODEs, most systems of ODEs cannot be solved analytically. An alternative method is to focus on the long-term behavior of the system. Rather than trying to acquire x(t) for all possible values of t, one could instead ask where x(t) ultimately ends up as t → ∞. To this end, we usually try to find the value of x associated with $\frac{dx}{dt} = 0$. Such a value is called the fixed point (or the steady-state) of the system.

Stability of the fixed point(s)

In the realm of pharmacokinetic models, there is usually a single fixed point that is stable. Given a particular set of model parameters, the system approaches a unique steady state regardless of the initial values. For example, given a particular choice of the infusion rate, R_in, and drug clearance, CL, the drug concentration will always approach $\frac{R_{in}}{CL}$.

Not all fixed points are stable, however. To understand this, let us examine a simple differential equation with a single parameter r:

$$\frac{dX}{dt}\mathrm{ }=\mathrm{ }r·X$$

We will consider two cases based on the magnitude of r relative to zero.

Case 1. r < 0.

The rate, $\frac{dX}{dt}\mathrm{ }(=\mathrm{ }r·X)$, is less than 0 when X > 0, and greater than 0 when X < 0. Hence, X increases when X is negative and decreases when X is positive. In both cases, X will converge to X = 0, making it a stable fixed point.

Case 2. r > 0.

The rate, $\frac{dX}{dt}\mathrm{ }(=\mathrm{ }r·X)$, is greater than 0 when X > 0, and less than 0 when X < 0. This means that X decreases when X is negative and increases when X is positive. Therefore, X moves away from zero regardless of whether X is positive or negative. The only condition under which X remains at rest is when X is initially zero. This shows that X = 0 is an unstable fixed point.

From the above analysis, we can propose the following method of stability assessment:

X_fixed is a stable fixed point if:

• i) $\frac{dX}{dt} = 0$ when X = X_fixed.

• ii) $\frac{dX}{dt} > 0$ when X < X_fixed.

• iii) $\frac{dX}{dt} < 0$ when X > X_fixed.

X_fixed is an unstable fixed point if:

• i) $\frac{dX}{dt} = 0$ when X = X_fixed.

• ii) $\frac{dX}{dt} > 0$ when X > X_fixed.

• iii) $\frac{dX}{dt} < 0$ when X < X_fixed.

Alternatively, given that $\frac{dX}{dt} = 0$ when X = X_fixed, X_fixed is stable if $\frac{\partial }{\partial X}\left(\frac{\partial X}{\partial t}\right)\mathrm{ }<\mathrm{ }0$ and unstable if $\frac{\partial }{\partial X}\left(\frac{\partial X}{\partial t}\right)\mathrm{ }>\mathrm{ }0$. Hence, the sign of the second derivative $\frac{{\partial }^{2}X}{\partial X\partial t}$ can be used to determine the stability of the system. This is a straightforward method of stability assessment when X is a one-dimensional variable.

Phase portrait

When dealing with multiple variables, a graphical approach of plotting one variable against another often turns out to be useful. For a two-variable case, the resultant plot is called a phase portrait drawn on a phase plane. The phase portrait represents the trajectories of two variables, x and y, whose state at time t is represented by the coordinate (x(t), y(t)) on the Cartesian plane.

To investigate the long-term trajectories of the system given different initial conditions, a frequently used approach involves sketching a direction field. This is done by calculating $(\frac{\mathrm{d}\mathrm{x}}{\mathrm{d}\mathrm{t}},\mathrm{ }\frac{\mathrm{d}\mathrm{y}}{\mathrm{d}\mathrm{t}})$ for a set of xy coordinates and then placing an arrow on each of the coordinate points in the direction of the vector, $\frac{\mathrm{d}\mathrm{x}}{\mathrm{d}\mathrm{t}}i +\mathrm{ }\frac{\mathrm{d}\mathrm{y}}{\mathrm{d}\mathrm{t}}j$, where i and j are standard basis vectors of (1, 0) and (0, 1), respectively.

While direction fields are useful in assessing the fixed point(s) of the system, one can use a more direct method based on the system nullclines. For example, given a system of two variables, x and y, the x-nullcline(s) is (are) the set of points satisfying $\frac{\mathrm{d}\mathrm{x}}{\mathrm{d}\mathrm{t}} = 0$ while the y-nullcline(s) is (are) that satisfying $\frac{\mathrm{d}\mathrm{y}}{\mathrm{d}\mathrm{t}}\mathrm{ }=\mathrm{ }0$. The point of intersection of the two nullclines constitutes the fixed point.

Multiple fixed points

Multiple fixed points occur when there are more than one nullclines for each variable or when the nullclines are highly nonlinear such that they meet at more than one point. Hence, multiple fixed points occur only when the underlying system of ODEs is nonlinear. However, the converse is not true: nonlinear systems can either have single or multiple fixed points. The contrapositive statement also holds: a linear system of ODEs with constant coefficients always has a single fixed point. This is easy to understand since two straight lines cannot intersect at more than one point.

A systematic method for the assessment of stability exists for linear systems. For non-linear systems, linearization around the fixed point enables applying this method for stability analysis. Before we go into that, an illustrative example is presented to demonstrate how multiple fixed points can arise.

Example 1. Cell growth dynamics

The simplest model dealing with cellular growth is an exponential growth model:

$$\frac{dX}{dt}\mathrm{ }=\mathrm{ }g·X$$

(X: Number of cells, g: per capita growth rate)

While this equation roughly captures the cellular growth in its early stages, it becomes unrealistic in the long-term since X diverges to infinity. Two popular models that impose an upper limit to cellular growth are the logistic growth model and Gompertzian growth model:

$$\frac{dX}{dt}\mathrm{ }=\mathrm{ }g·X · (1-\frac{X}{K})$$ [Logistic growth model]

$$\frac{dX}{dt}\mathrm{ }=\mathrm{ }g·X ·\mathrm{l}\mathrm{o}\mathrm{g}\left(\frac{K}{X}\right)$$ [Gompertzian growth model]

In both these models, as t → ∞, X → K. The additional parameter, K, is often called the carrying capacity.

Equipped with the above background, suppose that there are two types of cells –tumor cells, X, and normal cells, Y. We could model the competition between X and Y for common resources using the logistic growth equation, as follows:

$$\frac{dX}{dt}\mathrm{ }=\mathrm{ }X · (1\mathrm{ }-\mathrm{ }X -\mathrm{ }u·Y)$$

$$\frac{dY}{dt}\mathrm{ }=\mathrm{ }Y · (1\mathrm{ }-\mathrm{ }Y -\mathrm{ }v·X)$$

The X-nullclines are X = 0 and X = 1 − u·Y while the Y-nullclines are Y = 0 and Y = 1 − v·X. Let u = 0.1 and v = 1. The phase portrait is shown in Fig. 1.

Figure 1. Phase portrait of the tumor-normal cell competition model. The fixed points are (X, Y) = (0, 0), (0, 1), and (1, 0). The fixed point at (0, 0) represents the state of no cells, which is unstable. So long as there are no tumor cells, the trajectory starting from (0, 0) converges to (0, 1), consisting of only normal cells. With the emergence of a single tumor cell, however, the state shifts towards (1, 0), which is the only stable fixed point characterized by 100% tumor cells.

Linear stability analysis

To assess the stability of fixed points associated with multiple ODEs, we need to evaluate the eigenvalues of the coefficient matrix. For readers unfamiliar with these concepts, refer to Appendix 1 for a brief introduction.

Let us look at the following matrix differential equation,

$$\frac{dX}{dt}\mathrm{ }=\mathrm{ }AX\mathrm{ }\to$$

where X is a k-dimensional vector representing the states of k variables and A is a (k×k) coefficient matrix, $\left[\begin{array}{ccc}{a}_{11}& \cdots & a_{1k}\\ ⋮& \ddots & ⋮\\ a_{k1}& \cdots & a_{kk}\end{array}\right]$ (i = 1, 2, …, k and j = 1, 2, …, k),

To solve the equation, we first need to calculate the eigenvectors and the eigenvalues of the matrix A. We then define a (k×k) matrix P by stacking the k-dimensional eigenvectors, v_i (i = 1, 2, …, k), horizontally and a diagonal matrix D whose elements are the eigenvalues, λ_i (i = 1, 2, …, k).

P = [v₁ … v_k],

$$D\mathrm{ }=\mathrm{ }\left[\begin{array}{ccc}{\lambda }_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\lambda }_k\end{array}\right]$$

The series of equations, Av₁ = λ₁v₁, Av₂ = λ₂v₂, …, and Av_k = λ_kv_k, is then compressed into a single matrix equation, as follows:

AP = A[v₁ … v_k] = [λ₁v₁ … λ_kv_k]

The right-hand side can be expressed as a product of P and D:

$$\left[\begin{array}{ccc}{{\lambda }_{1}v}_1& \dots & {\lambda }_k{v}_k\end{array}\right]\mathrm{ }=\mathrm{ }\left[\begin{array}{ccc}{v}_1& \dots & v_k\end{array}\right]\left[\begin{array}{ccc}{\lambda }_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\lambda }_k\end{array}\right]\mathrm{ }=\mathrm{ }PD$$

Since P is invertible, the following holds:

A = PDP⁻¹

The above decomposition of a matrix A is called diagonalization.

Now, define a new variable Y = P⁻¹X and let y_i (i = 1, 2, …, k) denote the ith element of Y.

Differentiating both sides with respect to t,

$$\frac{dY}{dt}{\mathrm{ }=\mathrm{ }P}^{-1}\frac{dX}{dt}\mathrm{ }=\mathrm{ }{P}^{-1} AX\mathrm{ }=\mathrm{ }{P}^{-1}\left(PD{P}^{-1}\right)X\mathrm{ }=\mathrm{ }D{P}^{-1}X\mathrm{ }=\mathrm{ }DY$$

Hence,

$$\frac{dY}{dt}\mathrm{ }=\mathrm{ }\left[\begin{array}{c}\frac{d{y}_1}{dt}\\ \dots \\ \frac{d{y}_k}{dt}\end{array}\right]\mathrm{ }=\mathrm{ }DY\mathrm{ }=\mathrm{ }\left[\begin{array}{ccc}{\lambda }_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\lambda }_k\end{array}\right]\mathrm{ }\left[\begin{array}{c}{y}_1\\ \dots \\ y_k\end{array}\right]$$

Therefore,

y₁ = C₁e^λ₁t, …, y_k = C_ke^λ_kt

where C_i (i = 1, 2, …, k) are the initial values of y_i.

Finally,

$$X\mathrm{ }=\mathrm{ }PY\mathrm{ }=\mathrm{ }\left[\begin{array}{ccc}{v}_1& \dots & v_k\end{array}\right]\mathrm{ }\left[\begin{array}{c}{y}_1\\ \dots \\ y_k\end{array}\right]$$

= C₁e^λ₁tv₁ + … + C_ke^λ_ktv_k

This shows that all solutions of X can be expressed as a linear combination of e^λtv where λ denotes the eigenvalues and v the eigenvectors.

Returning to our original discussion of stability assessment, if any of the exponential terms, C_ie^λ_itv_i (i = 1, 2, …, k), is associated with a positive λ_i, the solution will diverge as t → ∞. On the other hand, if all of the eigenvalues are negative, the system converges to a stable fixed point.

For non-linear systems, we must first acquire all possible fixed points and then linearize the system around each of them. The resultant linear system of ODEs can then be used to assess the stability of each fixed point. This technique is called linear stability analysis.

Caution is needed at this point. An astute reader might have noticed that eigenvalues can also be complex numbers. Complex eigenvalues lead to an interesting phenomenon of oscillations. The following example looks at a prototypical nonlinear system with complex eigenvalues.

Example 2. Lotka-Volterra equation

The following model describes the interaction between predators, X, and preys, Y. The birth rate of predators depends on the number of preys at any given time. On the other hand, the death rate of preys depends on the number of predators.

$$\frac{dX}{dt}\mathrm{ }=\mathrm{ }\mathrm{\alpha }·X·Y\mathrm{ }-\mathrm{ }\mathrm{\beta }·X$$

$$\frac{dY}{dt}\mathrm{ }=\mathrm{ }\mathrm{\gamma }·Y\mathrm{ }-\mathrm{ }\mathrm{\delta }·X·Y$$

(α: Growth rate of predators, β: Death rate of predators, γ: Growth rate of preys, δ: Death rate of preys)

Let α = β = γ = δ = 1.

Draw a phase portrait of the above system, identify the fixed points, and assess its local stability.

Answer)

Linearization of the system at (1, 1) results in the following system of ODEs.

Defining ΔX = X − 1, ΔY = Y − 1,

$$\frac{d\Delta X}{dt}\mathrm{ }=\mathrm{ }\frac{dX}{dt}\mathrm{ }\approx \mathrm{ }{\frac{\partial }{\partial X}(X·Y\mathrm{ }-\mathrm{ }X)\mathrm{ }|}_{X=1,Y=1}\Delta X\mathrm{ }+\mathrm{ }{\frac{\partial }{\partial Y}(X·Y\mathrm{ }-\mathrm{ }X)|}_{X=1, Y=1}\Delta Y\mathrm{ }=\mathrm{ }0\mathrm{ }+\mathrm{ }\Delta Y$$

$$\frac{d\Delta Y}{dt}\mathrm{ }=\mathrm{ }\frac{dY}{dt}\mathrm{ }\approx \mathrm{ }{\frac{\partial }{\partial X}(Y\mathrm{ }-\mathrm{ }X·Y)\mathrm{ }|}_{X=1,Y=1}\Delta X\mathrm{ }+\mathrm{ }{\frac{\partial }{\partial Y}(Y\mathrm{ }-\mathrm{ }X·Y)|}_{X=1, Y=1}\Delta Y\mathrm{ }=\mathrm{ }\Delta X\mathrm{ }+\mathrm{ }0$$

Hence,

$$\frac{d\Delta X}{dt}\mathrm{ }\approx \mathrm{ }\Delta Y$$

$$\frac{d\Delta Y}{dt}\mathrm{ }\approx \mathrm{ }\Delta X$$

The coefficient matrix of the above system is $\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]$, whose eigenvalues are ± i.

Fig. 2 shows the phase portrait of the given system.

Figure 2. Phase portrait of the predator-prey equation. The 2 nullclines meet at (0, 0) and (1, 1), respectively. The direction field suggests that the trajectories do not converge to (1, 1) but rather circle around it with a constant radius.

Cell circuit for tissue repair and fibrosis

We finally embark on dealing with a real systems biology model with therapeutic implications.

Tissue injury leads to inflammation that gives rises to two different processes – healing and fibrosis. A model was proposed to understand how a single process leads to two such different outcomes [5]. It is known that inflammatory processes recruit blood monocytes into the injured tissue and transforms them to tissue macrophages. Macrophages secrete platelet derived growth factor (PDGF) that activates fibroblasts and promote their differentiation into myofibroblasts. Myofibroblasts, in turn, secrete colony stimulating factor (CSF) that promotes the growth of macrophages. In addition, myofibroblasts secrete PDGF in an autocrine loop to activate their own growth. Macrophages and myofibroblasts thus reciprocally interact through paracrine signaling. However, the proteins secreted by each perform opposite functions: myofibroblasts secrete extracellular matrix (ECM) that promote fibrotic changes while macrophages secrete proteases that resolve it.

We will hereafter denote the tissue macrophages and myofibroblasts using the symbols M and mF, respectively. The model consists of the following system of ODEs.

$$\frac{d\left[mF\right]}{dt}\mathrm{ }=\mathrm{ }\left[mF\right]·({\lambda }_1·[PDGF]·(1\mathrm{ }-\mathrm{ }\frac{\left[mF\right]}{K})\mathrm{ }-{\mu }_1)$$ (1)

$$\frac{d\left[PDGF\right]}{dt}\mathrm{ }=\mathrm{ }{\beta }_2·\left[M\right]\mathrm{ }+\mathrm{ }{\beta }_3·\left[mF\right]\mathrm{ }-\mathrm{ }{\alpha }_2·\left[mF\right]·\left[PDGF\right]\mathrm{ }-\gamma ·\left[PDGF\right]$$ (2)

$$\frac{d\left[M\right]}{dt}\mathrm{ }=\mathrm{ }\left[M\right]·({\lambda }_2·\left[CSF\right]\mathrm{ }-\mathrm{ }{\mu }_2)$$ (3)

$$\frac{d\left[CSF\right]}{dt}\mathrm{ }=\mathrm{ }{\beta }_1·\left[mF\right]\mathrm{ }-{\alpha }_1·\left[M\right]·\left[CSF\right]\mathrm{ }-\mathrm{ }\gamma ·\left[CSF\right]$$ (4)

where λ₁, µ₁, λ₂, µ₂ are the proliferation and removal rates of mF and M, respectively. A logistic growth model was used to impose an upper limit to mF, where K represents the carrying capacity. No growth restriction was imposed on M.

CSF is produced by mF at rate β₁, and endocytosed by macrophages at rate α₁. PDGF is secreted by both M and mF at rates β₂ and β₃, respectively and endocytosed by mF at rate α₂. Both growth factors are degraded at rate γ.

We employ the principle of separation of timescales and apply a quasi-steady state approximation to Eq. (2) since the production and removal of PDGF take minutes to hours while cell division and death take about a day or so. (Refer to Appendix 2 for further explanations of the concepts.) We treat mF as a constant and derive an algebraic expression for PDGF. To this end, we solve $\frac{d\left[PDGF\right]}{dt}\mathrm{ }=\mathrm{ }0$:

$$\left[PDGF\right]\mathrm{ }=\mathrm{ }\frac{{\beta }_2·\left[M\right] + {\beta }_3·\left[mF\right]}{{\alpha }_2·\left[mF\right]+\gamma }$$ (5)

Plugging Eq. (5) into Eq. (1),

$$\frac{d\left[mF\right]}{dt}\mathrm{ }=\mathrm{ }\left[mF\right] ·({\lambda }_1·\frac{{\beta }_2·\left[M\right] + {\beta }_3·\left[mF\right]}{{\alpha }_2·\left[mF\right]+\gamma }·(1\mathrm{ }-\mathrm{ }\frac{\left[mF\right]}{K})\mathrm{ }-\mathrm{ }{\mu }_1)$$ (6)

Similarly, we solve $\frac{d\left[CSF\right]}{dt}\mathrm{ }=\mathrm{ }0$ to acquire the following equation:

$$\left[CSF\right]\mathrm{ }=\mathrm{ }\frac{{\beta }_1·\left[mF\right]}{{\alpha }_1·\left[M\right] + \gamma }$$ (7)

Plugging Eq. (7) into Eq. (3) yields:

$$\frac{d\left[M\right]}{dt}\mathrm{ }=\mathrm{ }\left[M\right]·({\lambda }_2·\frac{{\beta }_1·\left[mF\right]\mathrm{ }}{{\alpha }_1·\left[M\right]+\gamma }\mathrm{ }-\mathrm{ }{\mu }_2)$$ (8)

We now incorporate the effect of inflammation by modifying Eq. (8) as follows:

$$\frac{d\left[M\right]}{dt}\mathrm{ }=\mathrm{ }I·(t<Dur)\mathrm{ }+\mathrm{ }\left[M\right]·({\lambda }_2·\frac{{\beta }_1·\left[mF\right]\mathrm{ }}{{\alpha }_1·\left[M\right]+\gamma }\mathrm{ }-\mathrm{ }{\mu }_2)$$ (9)

I and Dur denote the severity and duration of inflammation, respectively. The expression within the parentheses represents a logical function that returns 1 when true and 0 otherwise.

We will sketch the phase portraits consisting of direction fields, nullclines, and three specific trajectories of the system assuming four different clinical scenarios (see Figure 6). We arbitrarily set the model parameters as follows:

Figure 6. Decreasing the growth rate (λ₁) or increasing the death rate of mF (μ₁) lead to similar effects on the phase portrait.

• i) λ₁ = λ₂ = µ₁ = µ₂ = K = β₁ = β₂ = β₃ = 1

• ii) α₁ = 1, α₂ = 0

• iii) γ = 0.25

For parameters that reflect physiological reality, refer to the original article [5].

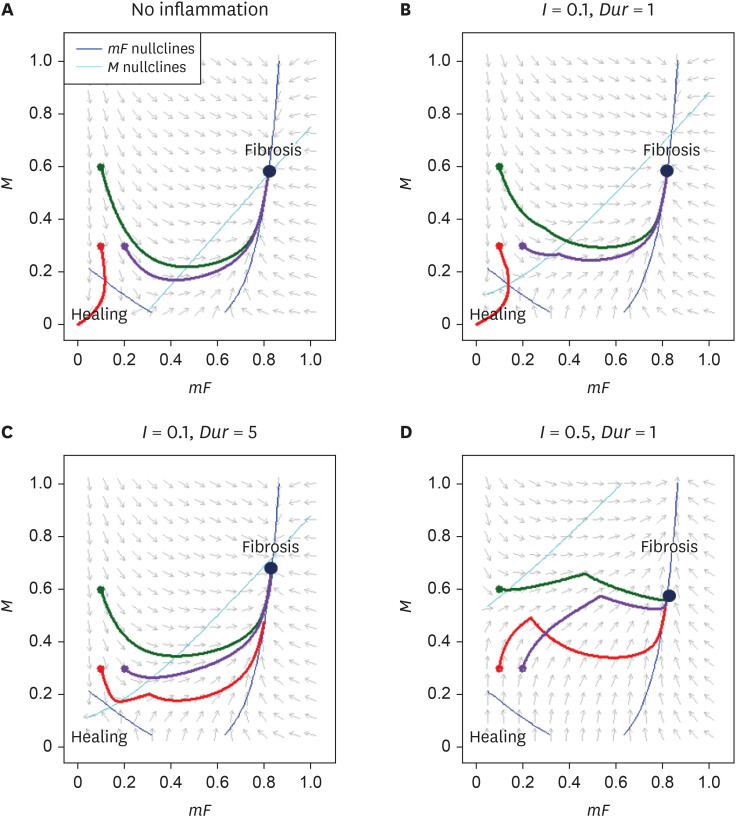
The initial states of the three trajectories are (mF, M) = (0.1, 0.3), (0.1, 0.6), and (0.2, 0.3). mF and M nullclines are depicted using dark and light blue curves, respectively. The direction fields and nullclines are drawn for t = 0.

Fig. 3A illustrates the bistability of the system. When mF = 0.1 and M = 0.3, the system converges to mF = 0 and M = 0, corresponding to the state of complete wound healing. The moment we push either mF or M slightly higher (M = 0.3 to 0.6 or mF = 0.1 to 0.2), the system converges to a new fixed point corresponding to the fibrotic state.

Figure 3. Phase portraits illustrating direction fields, nullclines, and three different trajectories under four different scenarios of (A) no inflammation, (B) I = 0.1, Dur = 1, (C) I = 0.1, Dur = 5, and (D) I = 0.5, Dur = 1.

Fig. 3B-D inspects how the severity and duration of inflammation affect the system. With minimal inflammation of I = 0.1 and Dur = 1, the fates of the three trajectories remain undeterred. However, when we either increase the duration (Dur = 1 to 5) or the severity (I = 0.1 to 0.5) of inflammation, the trajectory that previously led to complete wound healing (the red curve in Figure 3) alters its course and converges to the fibrotic state.

Exploration of therapeutic strategies

We have analyzed the system behavior under differing severity and duration of the extrinsic inflammatory stimulus. This obviously suggests that reducing the severity and duration of such inflammatory stimulus would help promote wound healing. Apart from this uninteresting strategy, what are the other potential therapeutic options? The authors propose that altering β₃, α₂, λ₁, and µ₁ would constitute efficient therapeutic strategies.

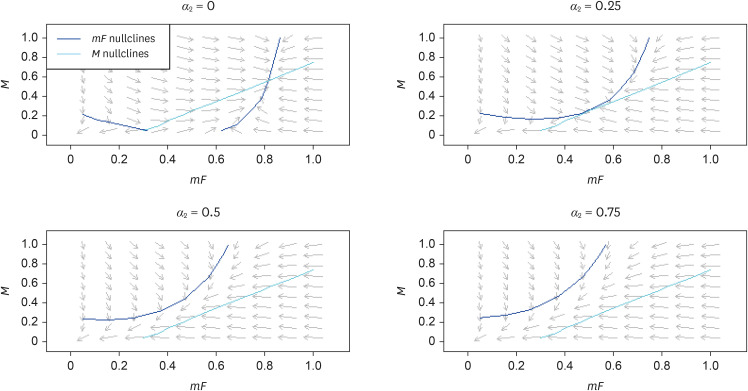
Fig. 4 demonstrates the effect of inhibiting the autocrine secretion rate of PDGF by mF (β₃). Fig. 5 shows how increasing PDGF's rate of endocytosis by mF (α₂) has a similar effect as inhibiting β₃. Once β₃ < 0.5 or α₂ > 0.5, a bifurcation occurs whereby the fibrotic fixed point disappears altogether. Fig. 6 demonstrates that either reducing the growth rate (λ₁) or increasing the death rate of mF (µ₁) lead to a vertical upward shift of the mF-nullcline. Altering the parameters related to M, on the other hand, would change the M-nullcline, which would not be as efficient as modulating the mF-nullcline.

Figure 4. The effect of reducing the autocrine secretion rate of platelet derived growth factor by mF (β₃). The curvature of mF-nullcline decreases, expanding the basin of attraction towards the healing state.

Figure 5. The effect of increasing platelet derived growth factor's rate of endocytosis by mF (α₂), which is similar to that of decreasing β₃.

In summary, drugs should target mF instead of M, and aim at either reducing its net proliferation or PDGF concentration around it through either lower autocrine secretion rate or enhanced endocytosis.

CONCLUSION

In this tutorial, we learned the basic concepts of dynamical systems theory frequently applied to QSP model analysis. Determination of the fixed points and their local stabilities often constitute the most important step in analyzing the system. Illustration of a phase portrait helps investigate the overall system behavior. Simulations that involve different parameter values offer important insights into the potential bifurcations and the development of efficient therapeutic strategies.

The author hopes that this tutorial serves as a good starting point for pharmacometricians striving to widen their scope to QSP and physiologically-oriented modeling.

SUGGESTED READINGS

1. Brian P. Ingalls mathematical modeling in systems biology: an introduction. Cambridge (MA): The MIT Press; 2013.

2. Alon U. An introduction to systems biology. Design principles of biological circuits. 2nd ed. Boca Raton (FL): CRC Press; 2020.

3. Strogatz SH. Nonlinear dynamics and chaos. 2nd ed. Boca Raton (FL): CRC Press; 2015.

4. Hirsch MW, Smale S, Devaney RL. Differential equations, dynamical systems, and an introduction to chaos. 3rd ed. Cambridge (MA): Academic Press; 2013.

5. Mager DE, Kimko H. Systems pharmacology and pharmacodynamics. Arlington (VA): American Association of Pharmaceutical Scientists; 2016.

Appendix 1

Eigenvalues and eigenvectors

Given a (n×n) matrix A, a non-zero n-dimensional vector v that satisfies

A_v = λv … (a)

is called the eigenvector of A, and the scalar variable λ is called the eigenvalue.

For the equation

(A − λI)·v = 0 … (b)

(I: (n×n) identity matrix, 0: n-dimensional zero vector)

to have a non-trivial solution (i.e. v ≠ 0), (A − λI) must be singular. Otherwise, we could multiply its inverse to both sides of the equation (a) to yield v = 0, which contradicts our assumption.

We define p(λ) = A − λI as the characteristic polynomial.

Solving det (p(λ)) = 0 yields λ, the eigenvalues, and solving Av = λv yields v, the eigenvectors.

Appendix 2

Separation of timescales

Oftentimes in modeling, the rates of two processes differ so drastically such that from the point of view of one of the processes, the other seems as if occurring almost instantaneously. The two most widely used techniques for model reduction are:

• (i) Rapid equilibrium (RE) approximation

• (ii) Quasi-steady state (QSS) approximation

We will examine a prototypical system of equations describing the dynamics of ligand-receptor binding.

$$\frac{dL}{dt}\mathrm{ }=\mathrm{ }-k_{on}L·R\mathrm{ }+\mathrm{ }{k}_{off}C\mathrm{ }- k_{el}L$$

$$\frac{dR}{dt}\mathrm{ }=\mathrm{ }{k}_{syn}\mathrm{ }-\mathrm{ }{k}_{out}R\mathrm{ }-\mathrm{ }{k}_{on}L·R\mathrm{ }+\mathrm{ }{k}_{off}C$$

$$\frac{dC}{dt}\mathrm{ }=\mathrm{ }{k}_{on}L·R\mathrm{ }-\mathrm{ }{k}_{off}C\mathrm{ }-\mathrm{ }{k}_{int}C$$

L, R, and C denote concentrations of ligands, receptors, and ligand-receptor complexes, respectively.

The first technique of RE approximation can be thought of as lumping compartments. We assume that ligand-receptor binding reaches equilibrium instantly (i.e. k_on R·L = k_offC). Denoting the total ligand and receptor concentration as L_tot(= L + C) and R_tot (= R + C),

$$C\mathrm{ }=\mathrm{ }{R}_{tot}\mathrm{ }-\mathrm{ }R\mathrm{ }=\mathrm{ }{R}_{tot}\mathrm{ }-\mathrm{ }\frac{k_{off}}{k_{on}·L}C\mathrm{ }=\mathrm{ }\frac{R_{tot}·L}{\frac{k_{off}}{k_{on}} + L}\mathrm{ }=\mathrm{ }\frac{R_{tot}·L}{K_D + L}\mathrm{ }(K_D\mathrm{ }=\mathrm{ }\frac{k_{off}}{k_{on}})$$

We then formulate ODEs of L_tot and R_tot as follows:

$$\frac{d{L}_{tot}}{dt}\mathrm{ }=\mathrm{ }\frac{dL}{dt}\mathrm{ }+\mathrm{ }\frac{dC}{dt}\mathrm{ }=\mathrm{ }-k_{int}C\mathrm{ }- k_{el}L\mathrm{ }=\mathrm{ }-k_{int}\frac{R_{tot}·L}{K_D + L}\mathrm{ }- k_{el}L$$

$$\frac{d{R}_{tot}}{dt}\mathrm{ }=\mathrm{ }\frac{dR}{dt}\mathrm{ }+\mathrm{ }\frac{dC}{dt}\mathrm{ }=\mathrm{ }{k}_{syn}\mathrm{ }-\mathrm{ }{k}_{out}R\mathrm{ }-\mathrm{ }{k}_{int}C\mathrm{ }=\mathrm{ }{k}_{syn}\mathrm{ }-\mathrm{ }{k}_{out}R\mathrm{ }-\mathrm{ }{k}_{int}\frac{R_{tot}·L}{K_D + L}$$

Since L = L_tot − C = L_tot − $\frac{R_{tot}·L}{K_D + L}$, we can solve the following quadratic equation to express L as a function of L_tot and R_tot.

L² + (K_D + R_tot − L_tot)·L − L_tot·K_D = 0

$$\to \mathrm{ }L\mathrm{ }=\mathrm{ }0.5\mathrm{ }\left[\right(L_{tot}\mathrm{ }-\mathrm{ }{K}_D\mathrm{ }-\mathrm{ }{R}_{tot})\mathrm{ }+\mathrm{ }\sqrt{{(L_{tot}\mathrm{ }-\mathrm{ }{K}_D\mathrm{ }-\mathrm{ }{R}_{tot})}^2+4L_{tot}·K_D}]$$

We have thus reduced the system of three ODEs to a system of two ODEs.

Using a QSS approximation, we assume that changes associated with C are significantly faster than those of L and R. Hence, we treat L and R as constants. Given this assumption, C would soon approach a quasi-steady state.

$$\frac{dC}{dt}\mathrm{ }=\mathrm{ }{k}_{on}L·R\mathrm{ }-\mathrm{ }{k}_{off}C\mathrm{ }-\mathrm{ }{k}_{int}C\mathrm{ }\approx \mathrm{ }0$$

Hence, $C\mathrm{ }=\mathrm{ }\frac{k_{on}L·R}{k_{off} + k_{int}}$

Defining $K_{SS}\mathrm{ }=\mathrm{ }\frac{k_{off} + k_{int}}{k_{on}}$, $C\mathrm{ }=\mathrm{ }\frac{L·R}{K_{SS}}\mathrm{ }=\mathrm{ }\frac{L·(R_{tot}\mathrm{ }- C)}{K_{SS}}$ and solving for C yields the following result:

$$C\mathrm{ }=\mathrm{ }\frac{R_{tot}·L}{K_{SS} + L}$$

We now substitute $C\mathrm{ }=\mathrm{ }\frac{k_{on}L·R}{k_{off} + k_{int}}$ into the original equation.

$$\frac{dL}{dt}\mathrm{ }=\mathrm{ }-k_{on}L·R\mathrm{ }+\mathrm{ }{k}_{off}\frac{k_{on}L·R}{k_{off}+ k_{int}}\mathrm{ }- k_{el}L\mathrm{ }=\mathrm{ }-\frac{k_{on}·k_{int}}{k_{off} + k_{int}} L·R\mathrm{ }- k_{el}L$$

$$\frac{dR}{dt}\mathrm{ }=\mathrm{ }{k}_{syn}\mathrm{ }-\mathrm{ }{k}_{out}R\mathrm{ }-\mathrm{ }{k}_{on}L·R\mathrm{ }+\mathrm{ }{k}_{off}\frac{k_{on}L·R}{k_{off}+ k_{int}}\mathrm{ }=\mathrm{ }{k}_{syn}\mathrm{ }-\mathrm{ }{k}_{out}R\mathrm{ }- \frac{k_{on}·k_{int}}{k_{off} + k_{int}} L·R$$

While both RE and QSS approximations reduce the number of ODEs, the former creates new lumped variables to replace the original variables while the latter formulates an algebraic function linking the slowly changing variables (e.g. L and R) to the rapidly changing variable (e.g. C). When applying either of the two approximations, one must make sure that the assumptions are reasonable.