Significance
During the Paleocene–Eocene Thermal Maximum (PETM) (56 Mya), the planet warmed by 5 to 8 °C, deep-sea organisms went extinct, and the oceans rapidly acidified. Geochemical records from fossil shells of a group of plankton called foraminifera record how much ocean pH decreased during the PETM. Here, we apply a geochemical indicator, the B/Ca content of foraminifera, to reconstruct the amount and makeup of the carbon added to the ocean. Our reconstruction invokes volcanic emissions as a driver of PETM warming and suggests that the buffering capacity of the ocean increased, which helped to remove carbon dioxide from the atmosphere. However, our estimates confirm that modern CO2 release is occurring much faster than PETM carbon release.
Keywords: ocean acidification, foraminifera, Paleocene–Eocene Thermal Maximum, boron proxies, dissolved inorganic carbon
Abstract
The Paleocene–Eocene Thermal Maximum (PETM) (55.6 Mya) was a geologically rapid carbon-release event that is considered the closest natural analog to anthropogenic CO2 emissions. Recent work has used boron-based proxies in planktic foraminifera to characterize the extent of surface-ocean acidification that occurred during the event. However, seawater acidity alone provides an incomplete constraint on the nature and source of carbon release. Here, we apply previously undescribed culture calibrations for the B/Ca proxy in planktic foraminifera and use them to calculate relative changes in seawater-dissolved inorganic carbon (DIC) concentration, surmising that Pacific surface-ocean DIC increased by µmol/kg during the peak-PETM. Making reasonable assumptions for the pre-PETM oceanic DIC inventory, we provide a fully data-driven estimate of the PETM carbon source. Our reconstruction yields a mean source carbon δ13C of −10‰ and a mean increase in the oceanic C inventory of +14,900 petagrams of carbon (PgC), pointing to volcanic CO2 emissions as the main carbon source responsible for PETM warming.
The Paleocene–Eocene Thermal Maximum (PETM) (55.6 Ma) remains the closest geologic analog for anthropogenic carbon release and associated climate changes. During the event, isotopically depleted carbon was released into the surface ocean–atmosphere system, causing a decrease in terrestrial and marine δ13C records, prolonged warming, ocean acidification, and changes to ocean circulation (1–4). It has been suggested that the PETM carbon release was a response to internal carbon-cycle instabilities in a warmer world, such as the release of methane clathrates from the deep ocean (5) or the oxidation of organic carbon in melting permafrost (6), possibly triggered by orbital forcing (7). However, past data-driven reconstructions of the PETM’s carbon source have led to nonunique solutions. For example, interpretations of the carbon-isotope excursion (CIE) have been based on simple mixing models, constraining the possible size(s) of carbon release by assuming the δ13C of the source carbon (δ13Csource) (8). Given that the potential sources of PETM carbon—such as methane clathrates, oxidized organic matter, and volcanic emissions—all have distinct δ13C signatures (−60, −25, and −6‰, respectively), the respective choice of source δ13C leads to large differences in the amount of carbon released (8).
Reconstructions of the magnitude of ocean acidification using boron-isotope (δ11B) measurements of fossil planktic foraminifera shells have added a crucial constraint on the marine carbon system across the PETM (3, 9, 10). Experiments using the Grid Enabled Integrated Earth System Model (cGENIE) have paired these surface seawater-pH records with planktic foraminiferal δ13C to infer the carbon source and amount (10). These estimates suggest that 10,000 petagrams of carbon (PgC) were released with a source δ13C of −11 to −17‰, invoking large contributions from volcanism, likely caused by the emplacement of the North Atlantic Igneous Province (NAIP) (11, 12). However, quantitative inferences on the surface-ocean carbon reservoir and surface-ocean pCO2 require a second parameter of the ocean carbon system (13), which has not been available before now.
New opportunities to constrain a second parameter of the surface-ocean carbonate system arise with recent advances in our understanding of B/Ca ratios in planktic foraminifera shells. Laboratory culture studies first established that planktic foraminiferal B/Ca is controlled by the seawater borate concentration ([B(OH)4−]), which depends directly on pH (14). Planktic foraminiferal B/Ca records from geographically disparate locations display a large decrease in B/Ca across the PETM (3, 9), which is expected as seawater pH declined. However, these records have escaped quantitative interpretation because the use of culture calibrations from modern foraminifera cannot reasonably explain the data assuming only a pH control on the proxy (15). Barring other information, it could not be excluded that these B/Ca excursions may have been amplified by reduced photosymbiont activity or biased by diagenesis (3).
Recent culture studies show that instead of simple [B(OH)4−] control, B/Ca in planktic foraminifera is controlled by the [B(OH)4−]/dissolved inorganic-carbon (DIC) ratio of seawater (15–17). Following this discovery, increased DIC across the event may have amplified the B/Ca excursion (3, 15, 16). Furthermore, the culture studies show that, in two modern foraminifera species, Trilobatus sacculifer and Orbulina universa, the sensitivity of B/Ca to [B(OH)4−]/DIC increases under simulated “Paleocene” seawater chemistry with lower seawater Mg/Ca and lower total-boron concentration ([B]T) (15, 16). Importantly, B/Ca in both foraminifera species responds to [B(OH)4−]/DIC with the same normalized sensitivity (Methods and SI Appendix, Fig. S1), enabling and increasing confidence in applying these calibrations to records from now-extinct species (15). In contrast to Pleistocene B/Ca downcore records, which show little consistency across glacial/interglacial cycles and between sites, PETM B/Ca data have been replicated at five sites (9) and display consistent results, suggesting that a strong environmental parameter unifies the records. Combining reconstructed [B(OH)4−] from δ11B-derived pH with B/Ca records, these calibrations present an opportunity to deconvolve pH and DIC contributions to B/Ca and quantitatively reconstruct the PETM DIC excursion.
Here, we apply this calibration framework to a previously published B/Ca record from the now-extinct symbiont-bearing Paleocene foraminifer species Morozovella velascoensis (3). To do this, we normalize PETM B/Ca data to the average pre-PETM B/Ca value of M. velascoensis (i.e., B/CaPETM/B/CaPre-PETM) and combine this normalized B/Ca excursion with [B(OH)4−] estimates from δ11B3. Following Gutjahr et al. (10), we assume pre-PETM surface-ocean DIC was 1,760 µmol/kg, which allows us to translate the [B(OH)4−]/DIC excursion to a relative DIC change across the event (Methods):
| [1] |
Surface-ocean DIC across the PETM would have been influenced by the size and duration of carbon release, the amount of CaCO3 dissolved from sediments, and the strength and timescale of the chemical-weathering feedback, which increases DIC by adding HCO3− (18). Reconstructions of the magnitude and timing of DIC change can therefore provide a new constraint on the amount, source, and fate of carbon released during this event.
Results
Reconstructed DIC Change across the PETM.
For our DIC reconstruction, we use previously published B/Ca and δ11B data from Ocean Drilling Program (ODP) Site 1209, situated in the North Pacific (3) (Fig. 1 A and B). The CIE onset at this this site is expressed as a millimeter-scale clay layer, reflecting an unknown but possibly modest duration of missing time due to sedimentary dissolution (3). Whereas further B/Ca and δ11B records have been published in recent years and support the earlier data in magnitude and timing (9, 10, 19), we have chosen the paired B/Ca–δ11B data from Site 1209 for this analysis as this record provides the highest resolution for both proxies published to date, avoiding age-model biases between cores.
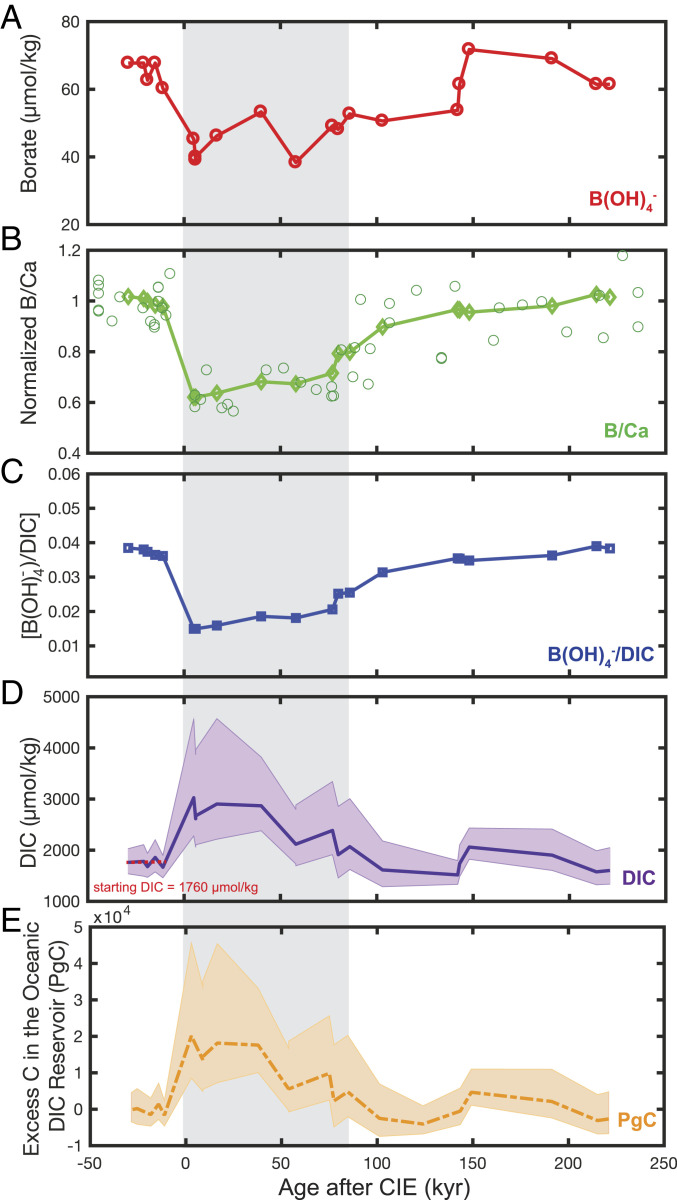
Fig. 1.
Input records and reconstructed seawater DIC from ODP Site 1209. The shaded gray region in A–E denotes the peak-PETM interval (as defined by ref. 3). (A) [B(OH)4−] was calculated using the δ11B-derived pH record of ref. 3, assuming a pre-PETM pH of 7.8 (ref. 20). (B) Measured B/Ca from ODP Site 1209 (ref. 3) has been normalized to the pre-PETM baseline B/Ca (69.5 µmol/mol) and is shown in open circles, whereas the five-point running mean of normalized B/Ca is shown in diamonds. (C) Culture calibrations (ref. 15) were used to calculate B(OH)4-/DIC. (D) Reconstructed DIC given calculated B(OH)4-/DIC (C) and B(OH)4- (A). Shaded purple regions on reconstructed DIC denote 95% CIs, derived from uncertainties on calculated [B(OH)4−] (C), normalized B/Ca (B), and the calibration slope. (E) Associated increase in the size of the oceanic DIC reservoir, assuming that the DIC excursion in (D) applies to the whole ocean volume.
The resulting reconstructed DIC excursion (ΔDIC) is shown in Fig. 1D, including 95% confidence bounds based on propagated uncertainties on calibration slope, measured B/Ca, and δ11B-derived [B(OH)4−] estimates. Taking the age model at face value, our record suggests an immediate (5 to 6 ky post-CIE) Pacific surface-ocean DIC increase of µmol/kg above the imposed baseline of 1,760 µmol/kg (10) (Fig. 1D). DIC remains elevated for ∼40 ky and then decreases to preevent values 100,000 y after the onset, followed by a second smaller increase at around 150 ky post-CIE. Reasonable uncertainties of input parameters such as seawater [B], T, S, and starting-pH and -DIC do not significantly affect our conclusions within 95% uncertainty bounds (SI Appendix, Fig. S2). Our analysis suggests that the paired B/Ca–δ11B method will be useful in determining relative DIC changes across Paleogene climate perturbations despite large uncertainties on such input parameters.
Reconstructing the Oceanic DIC Inventory.
Although the reconstructed surface-ocean DIC anomaly is derived from only one core site, we argue it applies to the entire ocean volume. Firstly, elevated surface-ocean DIC was sustained for ∼40 ky (Fig. 1), which implies several full-ocean mixings equilibrated DIC between the surface and deep ocean over this timeframe. Similarly, modeled surface- and deep-ocean DIC excursions change in tandem in simulations using Earth system models cGENIE and Long-Term Ocean–Atmosphere–Sediment Carbon Cycle Reservoir (LOSCAR) across the 0- to 40-ky post-CIE timescale (10, 21) (SI Appendix, Fig. S3). Secondly, unlike pCO2 and [CO32−], surface-ocean DIC is a conservative quantity that, in a closed system, is independent of temperature, and other local influences at this open-ocean core site are unlikely to modify the large magnitude change that we observe.
To calculate the increase in the oceanic DIC inventory at the peak-PETM, we multiply our ΔDIC by the total Paleocene ocean volume (22) (Methods). We estimate the size of the oceanic C reservoir increased by PgC, equating to a minimum +6,300-PgC increase (Fig. 1E). However, these estimates do not necessarily reflect the total PgC released during the event. Firstly, some of the added DIC will have been derived from dissolution of carbonate sediments. We calculate that dissolution of the entire estimated available CaCO3 sediment reservoir (23) could have added a maximum of ∼1,300 PgC (in the form of CO32−) to the total ocean C inventory (Methods). If we include this conservatively high value for CaCO3 dissolution, our estimates reduce to a minimum 5,000-PgC input to the oceanic C reservoir from exogenic sources, with a mean estimated increase of 14,900 PgC at the peak-PETM. Finally, sedimentation and organic carbon burial would have removed some C from the oceanic reservoir at each time point. Based on these possible C removal processes, we therefore suggest that our estimate of a +14,900-PgC increase reflects a minimum estimate of the total amount of C released during the PETM onset.
Although we concentrate our reconstruction on ODP 1209, globally distributed PETM B/Ca records yield a DIC increase of similar magnitude. Paired B/Ca and δ11B records also exist from Deep Sea Drilling Project Site 401, but we do not interpret these results given the poor drilling recovery of the PETM at this site (9). Instead, we investigate the peak-PETM DIC increase implied by all other existing B/Ca records from symbiont-bearing, surface-dwelling foraminifers across the PETM, including two sites from the New Jersey (NJ) Margin, ODP Sites 689 and 690, and an additional foraminifer species, Acarinina soldadoensis, from ODP Site 1209 (3, 9, 19). These four additional records show a similar decrease in B/Ca across the event as M. velascoensis at ODP Site 1209 (37%), ranging from 31 to 40%. Because the −0.3-unit pH decrease recorded at ODP Site 1209 has been replicated at globally distributed core sites (9), the B/Ca decrease translates to DIC increases of 1,164 µmol/kg (ODP 1209, Acarinina), 1,338 µmol/kg (ODP 689), 1,199 µmol/kg (Bass River), and 489 µmol/kg (ODP 690; Dataset S5). These values fall well within the uncertainty range of our main analysis (µmol/kg DIC). Given that each of these sites has different depositional and diagenetic histories, we believe that these consistent results support the notions that 1) planktic foraminiferal B/Ca is not significantly biased by diagenesis at the PETM (9) and 2) the surface-ocean DIC signal from Site 1209 is applicable to the global surface ocean.
Constraints on δ13CSource.
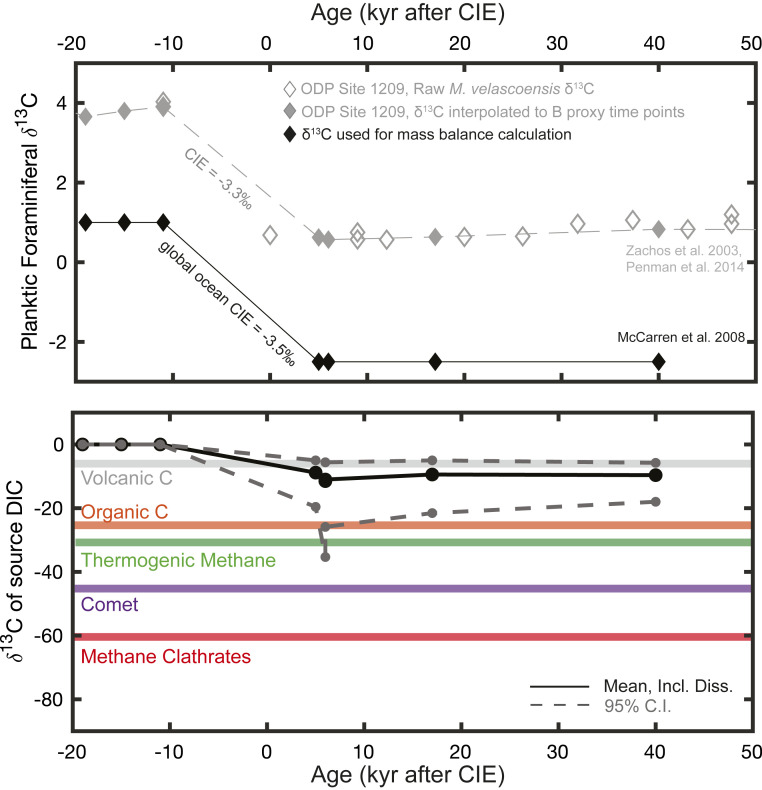
Building on our reconstructed DIC excursion and estimated change in the ocean DIC reservoir, we follow Kirtland-Turner and Ridgwell (24) and use the average estimated global ocean CIE magnitude of −3.5‰ (25) to constrain the δ13C of added DIC (δ13Csource) using a simple mass-balance approach (Methods). Our analysis estimates the mean δ13Csource at −9.3‰ at the peak-PETM, with a maximum of −5.1‰ and a minimum of −19.9‰ (95% CIs and including 2 SE uncertainties of our DIC reconstruction; Dataset S2). As already noted, surface-ocean DIC at this time inevitably comprised a mixture of carbon from the external carbon source as well as dissolved seafloor CaCO3 (δ13C = +2‰) (22), causing an overestimate of δ13Csource. To account for this effect, we calculate the maximum influence of seafloor CaCO3 dissolution on δ13Cpeak-PETM based on total dissolution of the available CaCO3 reservoir as above (23). Assuming a 1,300-PgC addition of DIC from CaCO3 (Methods), our mean reconstructed δ13Csource is decreased by only −0.81‰. Including this maximum contribution from dissolved seafloor carbonate, our analysis yields a revised mean source δ13C estimate of −10.1‰ (maximum, −5.3‰; minimum, −24.37‰; Fig. 2B).
Fig. 2.
Reconstructed δ13C of source DIC across the peak-PETM interval. (Top) We show the input δ13C data used as the CIE (black diamonds). Initial (pre-PETM) seawater δ13C was estimated at 1‰ based on carbon-isotope records of N. truempyi (26); pre-PETM δ13C makes a negligible influence on reconstructed δ13Csource. A CIE magnitude of −3.5‰ was then assumed for the global ocean after McCarren et al. (25). For reference, the raw M. velascoensis planktic δ13C data from ODP Site 1209 are shown in open diamonds (1, 3), and the same data interpolated to δ11B time points are shown in filled gray diamonds. (Bottom) We show calculated δ13Csource given the DIC excursion shown in Fig. 1D and the estimated seawater δ13C excursion shown in Top (black diamonds); 95% confidence bounds are shown in dashed gray lines. Our plotted δ13Csource reconstruction includes maximum possible contributions from seafloor carbonate dissolution (Dataset S4).
Solving the Carbon System at the PETM.
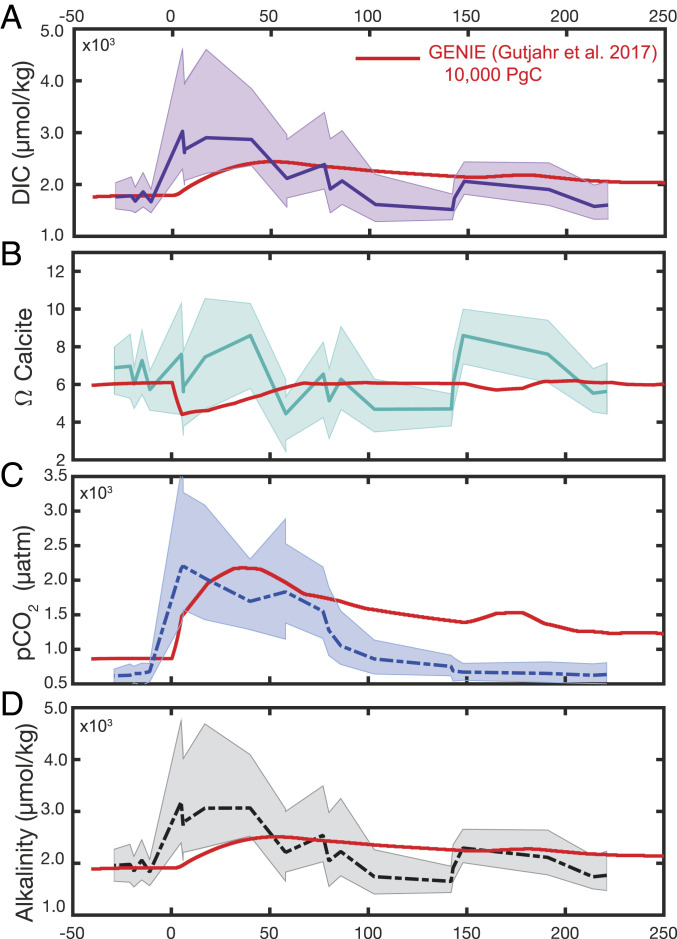
Combining our B/Ca–DIC reconstruction with pH from δ11B, we now command two parameters that can be used to calculate the full carbon-system solution, including surface-ocean pCO2 and surface-ocean calcite saturation (Ωcalcite). It should be noted, however, that these calculations are somewhat circular because pH enters the calculation twice, once as a stand-alone carbon-system parameter and once to estimate [B(OH)4−] in the B/Ca-to-DIC translation (SI Appendix, Fig. S6). The following carbonate-system calculations therefore need to be evaluated with caution, and we do not recommend using our reconstructed pCO2 trajectory to infer climate sensitivity. Instead, our estimates serve to gauge the general magnitude of the carbon-system changes implied by our DIC reconstruction.
The degree of Ωcalcite change that occurs due to ocean acidification will ultimately depend on the timescale over which carbon is released. On these short geologic timescales (i.e., assuming no changes to seawater [Ca2+] = 20 mmol/kg) (23), Ωcalcite will be controlled by seawater [CO32−]. If carbon is released slowly, and dissolution and weathering feedbacks have time to restore [CO32−], then surface-ocean saturation changes will be lessened. Conversely, given a more rapid injection of CO2, [CO32−] restoration feedbacks will not act quickly enough and surface-ocean saturation will sharply decrease, as is projected for 21st century carbon release (27, 28).
Reconstructed mean Ωcalcite from pairing pH and DIC does not show a systematic pattern of increase or decrease across the peak-PETM, although we note the variability and uncertainty on Ωcalcite is quite large (Fig. 3B). Concurrently, our reconstruction implies a large immediate increase in surface-ocean alkalinity across the PETM onset of ∼1,000 µmol/kg. Surface-ocean pCO2 increased from an imposed baseline of 660 to microatmospheres (µatm), equating to doublings of pCO2. At the upper bound of uncertainty, the average δ11B-derived pH trajectory paired with extremely high DIC predicts a large increase in surface-ocean saturation. This upper reconstruction is at odds with modeling projections that surface-ocean saturation should not immediately increase upon carbon injection (e.g., ref. 24), unless alkalinity feedbacks occurred with a much greater strength and rapidity than previously estimated. While theoretically possible, we instead highlight that these high upper error estimates are likely due to the compounding of errors at very low [B(OH)4−]/DIC, as the calculation is a reciprocal function that begins to approach the asymptote at normalized B/Ca = 0.40 (SI Appendix, Fig. S7).
Fig. 3.
Calculated carbon-system parameters and comparison with Earth system model results for the PETM. Pairing pH and DIC (A) with records of temperature, salinity, and surface pressure, we calculate surface-ocean calcium carbonate-saturation state (Ω calcite) (B), pCO2 (C), and alkalinity (D). Presented runs of the Earth system model cGENIE (10) (red) include enhanced organic carbon burial during the recovery period in order to better match the more rapid recovery of δ13C.
Discussion
Implications for Carbon Release and Earth System Recovery.
A mean δ13Csource of −10‰ and a mean reconstructed increase in the oceanic DIC reservoir of +14,900 PgC imply a substantial contribution of magma-derived CO2 emissions to the peak-PETM oceanic CIE (δ13Csource = −6‰), with smaller C addition from other sources with more negative δ13C. Mechanisms for carbon release associated with NAIP volcanism span a significant isotopic range, including magma-derived CO2 (−6‰) (29), organic carbon from shales proximal to sill intrusions (−25‰), and thermogenic methane (−30‰) (30, 31). Assuming that magma-derived CO2 mixed with thermogenic methane, our reconstruction allows a mean contribution of 17%, with an upper bound of 77%. In comparison, recent modeling of sill intrusion associated with NAIP concluded that thermogenic methane contributed 80 to 90% of PETM carbon, with mantle-derived CO2 providing a much smaller amount (32). Boron proxy-derived DIC records therefore allow for a lesser, but still significant, role for thermogenic methane in PETM carbon release.
It is additionally possible to invoke organic carbon sources from either direct contact with sill intrusions or other carbon-system feedback mechanisms. A recent study implicated up to 10,000 PgC could have been released from oxidation of remobilized fossil carbon during the peak-PETM interval, contributing to the temporal extension of the CIE (33). Given organic carbon δ13C is −25‰ (34), a peak-PETM δ13Csource of −10‰ allows a mean organic carbon contribution of 22% by mass (Fig. 2C and SI Appendix, Fig. S5), which is easily consistent with the sedimentary oxidation of organic matter (33). In contrast, a recent suggestion that the PETM may have been catalyzed by impact of a 12C-rich comet (−45‰) (20, 35) is less consistent with our DIC estimates. Assuming the potential cooccurrence of a comet impact and severe volcanism during the PETM onset, comet-derived carbon could only supply 10% of the carbon added to the ocean reservoir at the PETM. Similarly, our analysis supports the notion that methane clathrate thawing (with δ13C = −60‰) catalyzed by PETM warming could have only contributed a small portion (8%) of the total carbon added to the oceanic reservoir (10, 36). While it is possible that more than two sources contributed to the carbon release, reconciling the large DIC increase estimated herein with the whole-ocean CIE of −3.5‰ requires a dominant contribution of an isotopically heavy carbon source such as magmatic CO2.
Earth system models such as cGENIE and LOSCAR are vital tools for testing the feasibility and maximum likelihood of PETM carbon-release scenarios (10, 21, 22, 37) and therefore serve as a useful comparison for understanding the processes controlling the timing and magnitude of reconstructed ocean DIC change. Particularly illuminating is the comparison with a recent cGENIE model scenario that used δ11B-derived pH and planktic δ13C reconstructions as constraints for the size and duration of PETM carbon release (10). The study estimated 10,200 PgC were released over 50 ky, implying a δ13C source of −11‰. Our paired pH–DIC estimates are more stringently constrained than the modeling approach but support the earlier estimates in that volcanic emissions likely significantly contributed to the PETM carbon release (10).
Despite a similar δ13Csource estimate (−10‰ versus −11‰), our reconstruction suggests an even larger DIC increase. In addition, the reconstructed DIC addition also has a much faster onset time (Fig. 3A). The maximum oceanic DIC content is manifested at the first peak-PETM time points (5 to 6 ky post-CIE; Fig. 1), and this DIC increase is paired with an immediate increase in alkalinity (Fig. 3D). Following our estimate of maximum possible contribution of seafloor CaCO3 dissolution to DIC as 1,300 PgC, the alkalinity increase should be no larger than 154 µmol/kg, as opposed to the large increase of 1,000 µmol/kg that we observe. One possibility for this discrepancy is that alkalinity feedbacks in addition to oceanic carbonate dissolution reacted to PETM warming more quickly than the Earth system model estimate, causing a more rapid DIC and alkalinity input from weathering sources and the muted saturation-state changes that we observe (Fig. 3). Given the long timescales over which silicate weathering occurs (28), terrestrial CaCO3 weathering is the most likely secondary alkalinity source. Reduced pelagic calcification caused by environmental changes may also have played a role in increasing alkalinity during peak acidification (38).
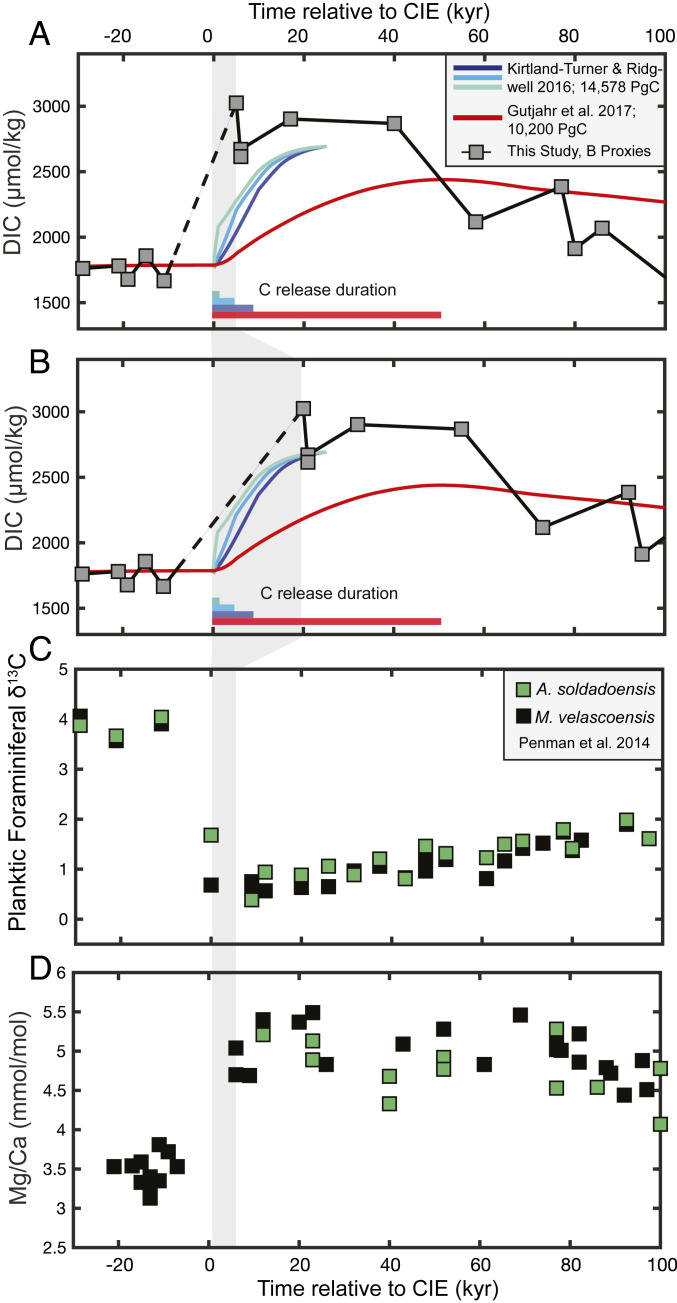
In comparison with our data, the delayed DIC maximum projected by modeling is significant and not only a feature of this one scenario, in which carbon was released over a long timescale of 50 ky (10). Instead, it appears to be a consistent feature in Earth system models regardless of the duration of C release. Kirtland-Turner and Ridgwell (24) undertook model experiments with a similar total C release to our scenario (14,578 PgC, compared with our mean estimate of 14,900 PgC) with varying carbon-release durations of 1, 5, and 10 ky. In each scenario, DIC and alkalinity increase quasilinearly after the carbon injection but do not reach their maximum until ∼20 ky after the PETM onset (Fig. 4 A and B and SI Appendix, Fig. S8).
Fig. 4.
Proxy records from ODP Site 1209 and comparison with the timing of modeled DIC change from cGENIE. In A and B, we compare our calculated DIC trajectory (blue squares) with a suite of cGENIE modeling experiments where the carbon-release duration was systematically varied from 1 to 10 ky (24) (blue, teal, and green lines). In each of these three simulations, the total amount of carbon released was 14,578 PgC. The red line shows the DIC trajectory of the C-release simulation of ref. 10, with 10,200 PgC released over an ∼50-ky duration. C and D show planktic foraminiferal δ13C and Mg/Ca records from ODP Site 1209 for context (refs. 1, 3). In A, C, and D, proxy records are plotted according to the age model of ref. 3, where DIC reaches its maximum value at 5 to 6 ky post-CIE. In B, proxy-derived DIC is plotted assuming that the first PETM time point at Site 1209 is instead at 20 ky, implying that ∼20 ky of the PETM onset is missing from the record. For illustration of this theoretical gap, all post-PETM time points in B have simply been shifted by +15 ky post-CIE. The shaded gray bar highlights the two different assumed time points for the first post-CIE data point from ODP Site 1209 (5 to 6 ky versus 20 ky).
Given these model scenarios, a perhaps more likely possibility is that the Site 1209 sedimentary record is more truncated than previously estimated (3). While all open-ocean sites are affected by some degree of sediment dissolution during the peak-PETM, recent work further suggests that peak-PETM M. velascoensis specimens from Site 1209 may in fact be younger in age, winnowed, and mixed down from younger sediments (34). It is therefore feasible that the first peak-PETM samples from Site 1209 are younger than the 5 to 6 ky post-CIE previously estimated (3). In order for our DIC (and alkalinity) reconstructions to match the timing of modeled carbon-injection scenarios, we estimate that ∼20 ky of time including the PETM onset and peak acidification may be missing from this sedimentary record (Fig. 4D). If this is correct, then the large alkalinity spike that we observe post-CIE is a combination of rapid sedimentary CaCO3 dissolution and slower terrestrial weathering feedbacks, similar to that projected by the model scenarios (SI Appendix, Fig. S8).
If the Site 1209 sedimentary record is indeed more truncated than previously estimated, then what are the consequences for other paleoenvironmental interpretations of the PETM from this location? δ13C records from the planktic species M. velascoensis and A. soldadoensis reveal a CIE magnitude of −3.3‰ (1, 3) (Fig. 4). This is smaller than the global value of −3.5‰ estimated by Kirtland Turner and Ridgwell (24) and is well below the maximum recorded by planktic foraminifera (−4.4‰) (10), leaving open the possibility that the full CIE magnitude is missing. Peak-PETM pH may have therefore been even lower than boron-isotope records at Site 1209 suggest (3), yielding a peak excursion larger than −0.3 pH units and a higher maximum pCO2 than we report here. In this case, the ODP Site 1209 record misses peak-PETM acidification and the immediate decline in saturation state, which our record implies would have largely recovered by ∼20 ky post-CIE (Fig. 3). Finally, Mg/Ca-temperature reconstructions from Site 1209 yield a temperature increase of 4 to 5 °C (3), which is consistent with a synthesis of model and data estimates of global sea-surface temperature change (39). However, we note that profound uncertainties exist on the paleosensitivity of the Mg/Ca proxy due to low Mg/Casw and possible amplifying factors (e.g., seawater pH and DIC) (40). Given the available proxy evidence from ODP Site 1209, we thus conclude that this larger than previously estimated amount of time is missing from the planktic foraminiferal proxy records.
While the onset of this record may have been lost to dissolution, it is crucial to note that our DIC reconstruction still yields a valid estimate of the amount of carbon added to the ocean as well as its source. Because modeling simulations indicate that DIC and alkalinity reach their maximum values after ∼20 ky, our reconstruction is able to yield estimates of the size of the PETM C release without recovery of the onset. If we are missing the true maximum of the DIC peak, then our estimates serve as a minimum bound on the amount of carbon released and imply that an even larger proportion of volcanic carbon contributed to PETM warming. Further boron-proxy work on high-resolution sedimentary records, such as those found on the NJ Margin, will be crucial in helping to disentangle the timing of C release, the immediate surface-ocean saturation state response, and how these changes related to the observed changes in plankton communities (41).
Because dissolution apparently truncated this open-ocean record and maximum oceanic DIC was delayed (Fig. 4), we cannot constrain the time-varying rate of DIC input during the PETM onset. However, a recent study of the relative phasing of surface and benthic δ18O records suggests that the PETM carbon release occurred over at least 4 ky (42). If we assume that the entire increase in the oceanic carbon inventory we reconstruct here (+5,000 to 14,900 PgC) occurred over this 4-ky time window, this would suggest a maximum DIC input rate of ∼1.3 to 3.7 PgC/y. Taking the amount of carbon added to the DIC reservoir as an approximation to the total amount of carbon released during the event, this equates to C-release rates that are much slower than the modern anthropogenic carbon release (10 PgC/y). Recent estimates of reasonable carbon-release rates from sill complexes in the NAIP are even lower at 0.2 to 0.5 PgC/y (32). Whereas our reconstruction therefore supports the consensus that the PETM is not a perfect analog for anthropogenic climate change, studying biotic and environmental responses to PETM carbon input provide a reference for minimum changes to be expected from anthropogenic emissions; the actual changes will likely be much more extreme.
Methods
Normalized B/Ca–[B(OH)4−]/DIC Calibration.
The calibration framework for B/Ca versus [B(OH)4−]/DIC laid out by Haynes et al. (15) shows that when B/Ca data from two modern foraminifer species—O. universa and T. sacculifer—are normalized to each species’ B/Ca value at the same corresponding [B(OH)4−]/DIC, both species show the same relative sensitivity to [B(OH)4−]/DIC (SI Appendix, Fig. S1 A and B). We use this dual-species calibration to calculate relative changes in [B(OH)4−]/DIC across the PETM, deviating from a set preevent value, by using the fractional change in B/Ca that is recorded across this event. Pre-PETM [B(OH)4−]/DIC =0.037 is set by making reasonable assumptions about preevent [B(OH)4−]—65 ± 7 µmol/kg (2 SE), calculated from pH 7.8 (26); [B]sw = 90% of Modern (43)—and DIC = 1,760 µmol/kg (10). The B/Ca record from ODP Site 1209 (3) is then normalized by dividing each B/Ca value by the preevent B/Ca value (69.5 µmol/mol). At the peak-PETM, B/Ca decreases by 40% (Fig. 1B). In order to scale the B/Ca culture calibrations to the ODP Site 1209 M. velascoensis record of ref. 3, the B/Ca culture data from O. universa and T. sacculifer (15, 16) are normalized to PETM M. velascoensis B/Ca by dividing by each modern species’ B/Ca value at [B(OH)4−]/DIC = 0.037 (SI Appendix, Fig. S1 B and C). Because there is no B/Ca culture data point at [B(OH)4−]/DIC = 0.037 in the calibration dataset, we interpolate between the existing culture data points to define this normalization value for each species (SI Appendix, Fig. S1A, gray boxes; after ref. 15):
| [2] |
DIC Reconstruction and Associated 2σ Uncertainties.
All data analyses were conducted in MATLAB. To calculate relative DIC changes from B/Ca records, we need to constrain B/Ca and [B(OH)4−] from δ11B-derived pH reconstructions at the same time points. To compare the B/Ca record with the much lower-resolved δ11B record, we decided to smooth the B/Ca record and avoid any noise. To do so, we first created a five-point running mean of measured B/Ca values in M. velascoensis (3) (Fig. 1B and Dataset S1). Where multiple measurements were made at a single time point, measurements from that time point were averaged before creating the running mean. To prevent the PETM onset itself from averaging, we created two sections of the running mean, before and after the onset of the CIE. The SE (2SE) on each five-point running mean B/Ca value was estimated as:
| [3] |
where σ represents the SD of the five measurements used in each mean point and n = 5. However, B/Ca and δ11B were rarely measured on the same samples. To find the B/Ca value corresponding to δ11B time points, we linearly interpolated between the two nearest values on our running mean B/Ca curve (Fig. 1B). The resultant SE (2 SE) on this value was calculated by averaging the SEs of the interpolated values. The errors on interpolated B/Ca values range from 3 to 9 μmol/mol (Dataset S1). We note that B/Ca smoothing has the greatest influence and therefore results in the largest B/Ca uncertainties during the recovery period, where the spread in measured B/Ca is much larger than either the pre- or peak-PETM time intervals (Fig. 1B and Dataset S1).
In order to calculate relative DIC changes, multiple input parameters in addition to δ11B and B/Ca records are needed. To solve Eq. 1, we must firstly calculate seawater [B(OH)4−]. In the original study (3), boron-isotope measurements from Site 1209 have been translated into seawater pH by assuming modeled pre-PETM pH values (7.8 or 7.67) (21, 42). We use here the pre-PETM case of pH 7.8, noting that choosing a lower pH of 7.67 does not significantly affect our reconstruction (SI Appendix, Fig. S2). Other inputs into this calculation include the estimated T and S excursions of ref. 3, where T increases from 30 to 35 °C during peak-PETM warming and S increases from 37 to 38.5‰ (Dataset S1). In addition, major seawater ionic composition is defined as [Ca] = 2.0×, [Mg] = 0.6×, and [B]T = 0.9× the modern concentration (43–45) (where modern values are 10.3 mmol/kg, 52.8 mmol/kg, and 432.6 µmol/kg, respectively, at S = 35). [B(OH)4−] is then calculated using the CO2SYS.m program (16) (Fig. 1A and Dataset S1).
In order to find the relative DIC change, we also need to assume a pre-PETM DIC value. We use DIC = 1,760 µmol/kg, the value estimated by Earth system modeling in cGENIE (10), which compares with ∼2,000 µmol/kg in the modern ocean. To estimate the relative size of the B/Ca excursion, we normalize the B/Ca record (B/Cat = n) to the pre-PETM B/Ca value (B/Cat = 0, 69.5 µmol/mol; Fig. 1B):
| [4] |
Finally, we solve for DIC at each data point using Eq. 1.
Uncertainty on reconstructed DIC includes contributions from calibration slope, B/Ca analytical uncertainty, and [B(OH)4−] (see uncertainties on each parameter in Dataset S1). Uncertainties on [B(OH)4−] were determined by running pH ± 2σ uncertainties through the CO2sys.m script, noting these uncertainties are asymmetrical (3) with the lower pH error being larger and propagating to give a larger uncertainty on the lower bound of reconstructed DIC. Uncertainty arising from the calibration slope was determined by generating least-squares linear fits of our normalized B/Ca calibration with uncertainty in x and y using the Yorkfit function in MATLAB (SI Appendix, Fig. S1). For each simulated slope value, we scale the intercept to pass through the determined pre-PETM condition (i.e., normalized B/Ca = 1, [B(OH)4−]/DIC = 0.037; SI Appendix, Fig. S1C). To find the uncertainty on the normalized B/Ca change across the PETM, we conducted an error propagation including the 2 SE on measured M. velascoensis pre-PETM B/Ca (i.e., ±2.8 µmol/mol; n = 17) and the uncertainty on each data point in the running mean of measured B/Ca (Dataset S1).
Resultant uncertainty on reconstructed DIC was determined by Monte Carlo error propagation based on 10,000 simulations of DIC using normally distributed variables of input [B(OH)4−], calibration slope, and normalized B/Ca. Because [B(OH)4−] errors are asymmetrical, we conducted two simulations using vectors of [B(OH)4−] that were normally distributed with a SD corresponding to either the upper or lower [B(OH)4−] uncertainty. Calculated DIC from each Monte Carlo simulation has a nonnormal distribution that is skewed toward higher values because our DIC calculation is a reciprocal function (SI Appendix, Fig. S7). In order to find upper and lower 95% uncertainty bounds, we calculated the 2.5 and 97.5 percentiles of DIC values from the Monte Carlo simulations including the lower and upper pH-derived [B(OH)4−] uncertainties, respectively.
Calculating δ13Csource and the Oceanic C Inventory.
We use our reconstructed surface-ocean DIC concentrations (in micromoles per kilogram) to find the total pre- and peak-PETM oceanic DIC reservoir size. Pre-PETM surface-ocean DIC is estimated at 1,760 µmol/kg, whereas deep-sea DIC is set at 2,020 µmol/kg, according to the cGENIE model parameterization of ref. 10. We assume a mixed layer depth of 100 m, a whole-ocean surface area of 3.49 × 1014 m2, and a volume of 1.29 × 1018 m (3, 22). We calculate the corresponding mass of the surface and deep-ocean DIC reservoirs in grams assuming the respective DIC concentrations noted above as well as the density of seawater (1.02 × 106 g/m3):
| [5] |
| [6] |
| [7] |
| [8] |
| [9] |
In order to calculate the increase in the size of the whole oceanic carbon reservoir, we assume our reconstructed surface-ocean DIC excursion applies to the entire ocean volume (Reconstructing the Oceanic DIC Inventory). According to our PETM DIC reconstruction, we calculate the %mass of DIC composed of C based on the percentages of [CO32−], [HCO3−], and [CO2] that make up DIC at each time step. Our analysis suggests that DIC under these conditions is composed of 20% C by mass, which does not vary across our reconstruction (Dataset S1). We use this wt% to translate the increase in the DIC reservoir (in moles) into PgC.
To calculate the δ13C of the carbon that was added to the ocean as DIC, we utilize the whole-ocean CIE estimate of −3.5‰ (25) using a simple mass-balance approach:
| [10] |
Pre-PETM δ13C from the benthic species Nutallides truempyi range between 0 and 2‰ (e.g., ref. 40). Because benthic species are not influenced by vital effects associated with symbiont photosynthesis, we therefore make a reasonable assumption of preevent δ13C of DIC (δ13Cinitial) of 1‰. Subsequently, δ13C decreases to −2.5‰ at the peak-PETM (Dataset S2). Pre-PETM δ13C asserts only a minor influence on the reconstruction in comparison with the potential C sources (i.e., −5‰ for volcanic CO2, −25‰ for organic carbon, or −60‰ for methane; SI Appendix, Fig. S4). In addition, assuming a much larger CIE value of −4.6‰ (44) does not change our primary conclusion that volcanic emissions were the main contributor to PETM carbon release (SI Appendix, Text). Finally, we determine the preevent size of the ocean’s DIC inventory (DICinitial) by utilizing a starting surface-ocean DIC of 1,760 µmol/kg (as in our reconstructions above) and a surface-to-deep DIC gradient of 260 µmol/kg (10). Total ocean surface area, mixed-layer depth, and total ocean volume are accounted for as described previously.
We utilize the sedimentary CaCO3 inventory estimate of ref. 23 to determine the maximum contribution of CaCO3 dissolution to seawater δ13C and the carbon inventory during the peak-PETM (1.1 × 1019 g of CaCO3). This estimate assumes a sedimentary mixed-layer depth of 10 cm and variable porosities of CaCO3 and clay. Given CaCO3 is 12% C by weight, this corresponds to a maximum possible 1,300-PgC contribution from CaCO3 dissolution, compared with a much larger predicted total mean increase of 16,000 PgC from our DIC reconstruction. The corresponding possible contribution of CO32− from dissolved CaCO3 to DIC has a mass of 3.36 × 1018 g. Assuming the sedimentary CaCO3 reservoir has a carbon-isotopic composition of +2‰ (22), we calculate that CaCO3 dissolution can produce a 0.75‰ increase in estimated δ13Csource at the peak-CIE.
Surface-Ocean Ωcalcite, pCO2, Alkalinity, and Resultant Uncertainties.
We paired δ11B-derived pH estimates with our DIC reconstruction to calculate the full carbon system, including Ωcalcite, alkalinity, and pCO2, using the CO2sys.m script. We assume the same T and S excursions and the same [Ca], [Mg], and [B]T as above. Given a pre-PETM pH of 7.8 and a DIC of 1,760 µmol/kg, pre-PETM pCO2 is 660 µatm (Fig. 3C), which is similar to the absolute pCO2 value suggested by Eocene terrestrial stomatal proxy-derived estimates ( µatm) (46) but lower than estimates commonly used in Earth system models (750 to 1,000 µatm) (10, 21, 24).
For the calculation of carbon-system parameters, we tested the influence of using the methods of both Zeebe and Tyrrell (26) and Hain et al. (47, 48) to take into account the influence of seawater [Ca] and [Mg] on the carbon-system dissociation constants K1 and K2 and the calcite-solubility product KSp. Using the Zeebe and Tyrrell (49) constants yields overall lower Ωcalcite but does not influence the magnitude of Ωcalcite change across the event (SI Appendix, Fig. S9). There is no appreciable difference between the two methodologies on reconstructed carbonate alkalinity (SI Appendix, Fig. S9). To find 95% confidence bounds on Ωcalcite, alkalinity, and pCO2, we conduct a Monte Carlo simulation of errors from input DIC and pH (n = 1,000; Dataset S1). Because the errors on reconstructed DIC are asymmetrical, we conducted one simulation for each the upper and lower bound of DIC uncertainty to find the respective 97.5 and 2.5% uncertainty bounds.
Supplementary Material
Acknowledgments
We are grateful for comments from Sandra Kirtland-Turner and one anonymous reviewer that significantly improved this manuscript. We further thank Stephen Eggins, Yair Rosenthal, and Andy Ridgwell for helpful feedback on previous drafts of this manuscript and Sidney Hemming, Maureen Raymo, Kate Holland, Don Penman, Joji Uchikawa, Kelsey Dyez, and Jesse Farmer for helpful discussion of the data. Previously published LOSCAR DIC output was helpfully provided by Richard Zeebe and Don Penman, and cGENIE output was provided by Andy Ridgwell and Sandra Kirtland-Turner. This research was funded by NSF Grant OCE12-32987 (to B.H.).
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2003197117/-/DCSupplemental.
Data Availability.
All study data are in the article and Supporting Information.
References
- 1.Zachos J. C. et al., A transient rise in tropical sea surface temperature during the Paleocene-Eocene thermal maximum. Science 302, 1551–1554 (2003). [DOI] [PubMed] [Google Scholar]
- 2.Zachos J. C. et al., Rapid acidification of the ocean during the Paleocene-Eocene thermal maximum. Science 308, 1611–1615 (2005). [DOI] [PubMed] [Google Scholar]
- 3.Penman D., Hönisch B., Zeebe R., Thomas E., Zachos J., Rapid and sustained surface ocean acidification during the paleocene‐eocene thermal maximum. Paleoceanography 29, 1–13 (2014). [Google Scholar]
- 4.Thomas D. J., Bralower T. J., Jones C. E., Neodymium isotopic reconstruction of late Paleocene - early Eocene thermohaline circulation. Earth Planet. Sci. Lett. 209, 309–322 (2003). [Google Scholar]
- 5.Dickens G., O’Neil J. R., Rea D. K., Owen R. M., Dissociation of oceanic methane hydrate as a cause of the carbon isotope excrusion at the end of the Paleocene. Paleoceanography 10, 965–971 (1995). [Google Scholar]
- 6.DeConto R. M. et al., Past extreme warming events linked to massive carbon release from thawing permafrost. Nature 484, 87–91 (2012). [DOI] [PubMed] [Google Scholar]
- 7.Zeebe R. E., Lourens L. J., Solar System chaos and the Paleocene-Eocene boundary age constrained by geology and astronomy. Science 365, 926–929 (2019). [DOI] [PubMed] [Google Scholar]
- 8.McInerney F. a., Wing S. L., The paleocene-eocene thermal maximum: A perturbation of carbon cycle, climate, and biosphere with implications for the future. Annu. Rev. Earth Planet. Sci. 39, 489–516 (2011). [Google Scholar]
- 9.Babila T. L. et al., Capturing the global signature of surface ocean acidification during the Palaeocene-Eocene Thermal Maximum. Philos. Trans.- Royal Soc., Math. Phys. Eng. Sci. 376, 20170072 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Gutjahr M. et al., Very large release of mostly volcanic carbon during the Palaeocene-Eocene Thermal Maximum. Nature 548, 573–577 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Dickson A. J. et al., Evidence for weathering and volcanism during the PETM from Arctic Ocean and Peri-Tethys osmium isotope records. Palaeogeogr. Palaeoclimatol. Palaeoecol. 438, 300–307 (2015). [Google Scholar]
- 12.Storey M., Duncan R. A., Swisher C. C. 3rd, Paleocene-Eocene thermal maximum and the opening of the Northeast Atlantic. Science 316, 587–589 (2007). [DOI] [PubMed] [Google Scholar]
- 13.Zeebe R. E., Wolf-Gladrow D. A., CO2 in Seawater: Equilibrium, Kinetics, Isotopes, (Elsevier, Amsterdam, 2001). [Google Scholar]
- 14.Allen K. A. et al., Controls on boron incorporation in cultured tests of the planktic foraminifer Orbulina universa. Earth Planet. Sci. Lett. 309, 291–301 (2011). [Google Scholar]
- 15.Haynes L. L., Hönisch B., Holland K., Rosenthal Y., Eggins S. M., Evaluating the planktic foraminiferal B/Ca proxy for application to deep time paleoceanography. Earth Planet. Sci. Lett. 528, 115824 (2019). [Google Scholar]
- 16.Haynes L. L. et al., Calibration of the B/Ca proxy in the planktic foraminifer Orbulina universa to Paleocene seawater conditions. Paleoceanography 32, 580–599 (2017). [Google Scholar]
- 17.Allen K. A., Honisch B., Eggins S. M., Rosenthal Y., Environmental controls on B/Ca in calcite tests of the tropical planktic foraminifer species Globigerinoides ruber and Globigerinoides sacculifer. Earth Planet. Sci. Lett. 351, 270–280 (2012). [Google Scholar]
- 18.Penman D. E. et al., An abyssal carbonate compensation depth overshoot in the aftermath of the Palaeocene–Eocene Thermal Maximum. Nat. Geosci. 9, 575–580 (2016). [Google Scholar]
- 19.Babila T. L., Rosenthal Y., Wright J. D., Miller K. G., A continental shelf perspective of ocean acidification and temperature evolution during the Paleocene-Eocene Thermal Maximum. Geology 44, 1–4 (2016). [Google Scholar]
- 20.Schaller M. F., Fung M. K., Wright J. D., Katz M. E., Kent D. V., Impact ejecta at the Paleocene-Eocene boundary. Science 354, 225–229 (2016). [DOI] [PubMed] [Google Scholar]
- 21.Zeebe R. E., Zachos J. C., Dickens G. R., Carbon dioxide forcing alone insufficient to explain Palaeocene – Eocene Thermal Maximum warming. Nat. Geosci. 2, 1–5 (2009). [Google Scholar]
- 22.Zeebe R. E., LOSCAR: Long-term Ocean-atmosphere-Sediment CArbon cycle Reservoir model v2.0.4. Geosci. Model Dev. 5, 149–166 (2012). [Google Scholar]
- 23.Komar N., Zeebe R. E., Oceanic calcium changes from enhanced weathering during the paleocene-eocene thermal maximum: No effect on calcium-based proxies. Paleoceanography 26, 1–13 (2011). [Google Scholar]
- 24.Kirtland-Turner S., Ridgwell A., Development of a novel empirical framework for interpreting geological carbon isotope excursions, with implications for the rate of carbon injection across the PETM. Earth Planet. Sci. Lett. 435, 1–13 (2016). [Google Scholar]
- 25.McCarren H. K., Thomas E., Hasegawa T., Röhl U., Zachos J. C., Depth dependency of the Paleocene-Eocene carbon isotope excursion: Paired benthic and terrestrial biomarker records (Ocean drilling program Leg 208, Walvis Ridge). Geochem. Geophys. Geosyst. 9, 1–10 (2008). [Google Scholar]
- 26.Panchuk K., Ridgwell A., Kump L. R., Sedimentary response to paleocene-eocene thermal maximum carbon release: A model-data comparison. Geology 36, 315–318 (2008). [Google Scholar]
- 27.Hönisch B. et al., The geological record of ocean acidification. Science 335, 1058–1063 (2012). [DOI] [PubMed] [Google Scholar]
- 28.Zeebe R., History of seawater carbonate chemistry, atmospheric CO2, and ocean acidification. Annu. Rev. Earth Planet. Sci. 40, 141–165 (2012). [Google Scholar]
- 29.Eldholm O., Thomas E., Environmental impact of volcanic margin formation. Earth Planet. Sci. Lett. 117, 319–329 (1993). [Google Scholar]
- 30.Svensen H. et al., Release of methane from a volcanic basin as a mechanism for initial Eocene global warming. Nature 429, 542–545 (2004). [DOI] [PubMed] [Google Scholar]
- 31.Frieling J. et al., Thermogenic methane release as a cause for the long duration of the PETM. Proc. Natl. Acad. Sci. U.S.A. 113, 12059–12064 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Jones S. M., Hoggett M., Greene S. E., Dunkley Jones T., Large Igneous Province thermogenic greenhouse gas flux could have initiated Paleocene-Eocene Thermal Maximum climate change. Nat. Commun. 10, 5547 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lyons S. L. et al., Palaeocene – Eocene Thermal Maximum prolonged by fossil carbon oxidation. Nat. Geosci. 12, 54–60 (2019). [Google Scholar]
- 34.Higgins J., Schrag D., Beyond methane: Towards a theory for the paleocene-eocene thermal maximum. Earth Planet. Sci. Lett. 245, 523–537 (2006). [Google Scholar]
- 35.Cramer B. S., Kent D. V., Bolide summer: The Paleocene/Eocene Thermal maximum as a response to an extraterrestrial trigger. Palaeogeogr. Palaeoclimatol. Palaeoecol. 224, 144–166 (2005). [Google Scholar]
- 36.Cui Y., Schubert B., Towards determination of the source and magnitude of atmospheric pCO2 change across the early Paleogene hyperthermals. Global Planet. Change 170, 120–125 (2018). [Google Scholar]
- 37.Bralower T. J. et al., Impact of dissolution on the sedimentary record of the Paleocene-Eocene thermal maximum. Earth Planet. Sci. Lett. 401, 70–82 (2014). [Google Scholar]
- 38.Dunkley-Jones T. et al., Earth-science reviews climate model and proxy data constraints on ocean warming across the paleocene – eocene thermal maximum. Earth Sci. Rev. 125, 123–145 (2013). [Google Scholar]
- 39.Gibbs S. J. et al., Ocean warming, not acidification, controlled coccolithophore response during past greenhouse climate change. Geology 44, 59–62 (2016). [Google Scholar]
- 40.Holland K. et al., Constraining multiple controls on planktic foraminiferal Mg/Ca. Geochim. Cosmochim. Acta 273, 116–136 (2020). [Google Scholar]
- 41.Boudreau B., Middleburg J., Luo Y., The role of calcification in carbonate compensation. Nat. Geosci. 11, 894–900 (2018). [Google Scholar]
- 42.Zeebe R. E., Ridgwell A., Zachos J. C., Anthropogenic carbon release rate unprecedented during the past 66 million years. Nat. Geosci. 9, 1–5 (2016). [Google Scholar]
- 43.Lemarchand D., Gaillardet J., Lewin E., Allègre C. J., The influence of rivers on marine boron isotopes and implications for reconstructing past ocean pH. Nature 408, 951–954 (2000). [DOI] [PubMed] [Google Scholar]
- 44.Kozdon R., Kelly D. C., Valley J. W., Diagenetic attenuation of carbon isotope excursion recorded by planktic foraminifers during the Paleocene-Eocene Thermal Maximum. Paleoceanogr. Paleoclimatol. 33, 367–380 (2018). [Google Scholar]
- 45.Lowenstein T. K., Kendall B., Anbar A. D., “The geologic history of seawater” in Treatise on Geochemistry, Turekian K., Holland H., Eds. (Elsevier, 2nd Ed., 2014). [Google Scholar]
- 46.Kowalczyk J. B. et al., Multiple proxy estimates of atmospheric CO2 from an early Paleocene rainforest. Paleoceanogr. Paleoclimatol. 33, 1427–1438 (2018). [Google Scholar]
- 47.Hain M., Sigman D. M., Higgins J. A., Haug G. H., The effects of secular calcium and magnesium concentration changes on the thermodynamics of seawater acid/base chemistry: Implications for Eocene and Cretaceous ocean carbon chemistry and buffering. Global Biogeochem. Cycles 29, 517–533 (2015). [Google Scholar]
- 48.Hain M., Sigman D. M., Higgins J. A., Haug G. H., Response to comment from Zeebe and Tyrrell on “The effects of secular calcium and magnesium concentration changes on the thermodynamics of seawater acid/base chemistry: Implications for Eocene and Cretaceous ocean carbon chemistry and buffering”. Global Biogeochem. Cycles 32, 898–901 (2018). [Google Scholar]
- 49.Zeebe R. E., Tyrrell T., History of carbonate ion concentration over the last 100 million years II: Revised calculations and new data. Geochim. Cosmochim. Acta 257, 373–392 (2019). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All study data are in the article and Supporting Information.