Visualizing conical intersection passages via vibronic coherence maps generated by stimulated ultrafast X-ray Raman signals

Significance

The capabilities of modern X-ray sources have substantially increased the temporal and spectral resolutions for the observation of elementary molecular events. Theoretically, it has been shown that these unique features can be exploited to probe vibronic coherences that emerge when molecules pass through conical intersections. Here, we demonstrate this technique for the photorelaxation of the RNA-nucleobase uracil after UV excitation. The generated coherence maps reveal the path of the nuclear wavepacket on the excited-state surface in the vicinity of the conical intersection. This information is directly accessible from the spectroscopically recorded signal. Being transferrable to other molecules, these coherence maps will provide detailed visualizations of other nonadiabatic passages in the future.

Abstract

The rates and outcomes of virtually all photophysical and photochemical processes are determined by conical intersections. These are regions of degeneracy between electronic states on the nuclear landscape of molecules where electrons and nuclei evolve on comparable timescales and thus become strongly coupled, enabling radiationless relaxation channels upon optical excitation. Due to their ultrafast nature and vast complexity, monitoring conical intersections experimentally is an open challenge. We present a simulation study on the ultrafast photorelaxation of uracil, based on a quantum description of the nuclei. We demonstrate an additional window into conical intersections obtained by recording the transient wavepacket coherence during this passage with an X-ray free-electron laser pulse. Two major findings are reported. First, we find that the vibronic coherence at the conical intersection lives for several hundred femtoseconds and can be measured during this entire time. Second, the time-dependent energy-splitting landscape of the participating vibrational and electronic states is directly extracted from Wigner spectrograms of the signal. These offer a physical picture of the quantum conical intersection pathways through visualizing their transient vibronic coherence distributions. The path of a nuclear wavepacket in the vicinity of the conical intersection is directly mapped by the proposed experiment.

The absorption of visible or ultraviolet (UV) photons, be it naturally or through artificial light fields, brings molecules into an electronically excited state. Through a variety of mechanisms, the excess energy is either reemitted through fluorescence, dissipated to some environment, or processed in a photochemical reaction. Ultrafast and radiationless relaxation mechanisms back to the electronic ground state are enabled by conical intersections (CoIns) (1, 2). These are ubiquitous regions on the excited-state nuclear landscape of molecules, where the energies of two or more states become degenerate. The electronic and nuclear degrees of freedom are then strongly coupled, leading to the breakdown of the adiabatic Born–Oppenheimer picture. Upon optical excitation, an evolving nuclear wavepacket (WP) can cross into a lower electronic state, if CoIns are within reach. Prominent examples where this process principally determines the outcome of a photochemical process include the primary event of vision (3) and the ability of nucleobases as the building blocks of the genetic code to repair the damage of UV radiation (4).

The existence of CoIns is widely accepted based on simulations, yet has so far eluded direct experimental observation. Indirect experimental evidence for CoIns is usually based on the observation of ultrafast internal conversion rates via electronic-state population dynamics (3, 5, 6). Different approaches for visualizing CoIns introduced recently include Coulomb explosion imaging (7), multidimensional approaches (8, 9), or ultrafast electron diffraction (10). The decisive impact of CoIns on textbook examples of ultrafast dynamics, like the ring opening of 1,3-cyclohexadiene (11), has been revealed with unprecedented precision. An access to CoIn detection has been enabled recently by the emergence of coherent XUV and X-ray sources (12–18). Their unique temporal and spectral profiles can access faster timescales and wider energy windows for spectroscopic measurements (19).

Here, we show how free-electron lasers can be used to monitor CoIn dynamics of the RNA-nucleobase uracil in great detail. A hybrid combination of phase-controlled attosecond (as) and femtosecond X-ray pulses is used to probe the nonadiabatic passage via a stimulated Raman process. A vibronic coherence is generated at the CoIn, which shows up in the signal and its phase at specific Raman shifts and offers a window into the quantum dynamics at these points. The recorded signal reveals the time-resolved distribution of energy splittings of the vibronic states, which provides unique fingerprints of the CoIn pathway. The resulting ultrafast vibronic coherence maps reflect the exact electron/nuclear eigenstates and are independent of any basis set. Spatially localized nuclear WPs offer a sensitive probe for the energetic topology variation across the CoIn. This spectroscopic access to the WP coherence at the CoIn reveals surprising features, with implications for the observation and control of CoIn processes.

X-Ray TRUECARS Signal of the Uracil Conical Intersection

To spectroscopically monitor the uracil CoIn passage, we use the TRUECARS (transient redistribution of ultrafastelectronic coherences in attosecond Raman signals) technique (12) that employs a stimulated Raman process induced by a hybrid narrowband and a broadband X-ray pulse. Originally introduced for an ideal model system (12), here we use a realistic ab initio molecular Hamiltonian, which we describe in the following.

The two nuclear degrees of freedom that span the relevant coordinate space (Fig. 1A) have been constructed from structures that were found to be important in uracil S₂ photorelaxation (20, 21) and have originally been described in ref. 20. The first coordinate $q_1$ describes the motion from the Franck–Condon (FC) to the CoIn and is mainly an out-of-plain motion of the initially planar ring structure. The second coordinate $q_2$ represents the motion from the FC to a local energetic minimum in the S₂ state and describes the bending of one hydrogen atom out of the ring plane. The excited-state potential energy surfaces (PESs) in this two-dimensional (2D) nuclear space are displayed in Fig. 1D and have been shown to reproduce experimental kinetic rates following optical excitation (20, 21). This reduced-dimensional space has been verified by higher-dimensional treatments (20). The nonadiabatic couplings (NACs) that are necessary to simulate the passage of the nuclear WP through the CoIn are displayed in Fig 1B. They exhibit a smooth variation with nuclear coordinates, with the characteristic sign change due to the switching of electronic character of the adiabatic states. With the PESs and the NACs, nuclear WP simulations were launched by exactly solving the time-dependent Schrödinger equation (TDSE) for our effective Hamiltonian. The full protocol is given in Materials and Methods. The nuclear dynamics are launched using a 34-fs full width at half-maximum (FWHM) Gaussian laser pump in resonance with the S₀ $\to$ S₂ transition, as was done experimentally (21). The path of the WP is drawn in Fig. 1D. After excitation to the S₂ state, and following a free S₂ evolution period, the WP reaches the CoIn at around 100 fs. Here, a vibronic coherence between the S₂ and the S₁ electronic state is created due to the nuclear WP relaxing through the CoIn. Both electronic states are now populated, and the overlap integral of the S₂ and the S₁ nuclear WP becomes finite. This coherence is probed by the TRUECARS signal. The WP parts that reach the S₁ state evolve away from the CoIn toward the energetic minimum. There, it is absorbed by using a Butterworth filter (22), preventing the WP from oscillating through the S₁ minimum and evolving back to the CoIn region. Our coordinate space is tailored to describe the S₂ evolution and does not accurately capture WP evolution in the S₁ far from the CoIn, as other nuclear degrees of freedom start to become important. For example, the exit channel for the WP to further CoIns with the S₀ state is not included. Back evolution of the WP to the CoIn region should therefore lead to artifacts in the coherence, and absorbing the WP in the S₁ minimum should describe reality more accurately.

Fig. 1.

Wavepacket dynamics of uracil and key molecular quantities for the signal calculation. (A) Uracil structure at the ground-state minimum geometry, with the vectors indicating the molecular displacement according to the two nuclear degrees of freedom. (B) Nonadiabatic couplings between S₂ and S₁ at the CoIn seam versus the two nuclear coordinates of the molecules. The characteristic peaked switch of the sign is clearly visible. (C) S₂–S₁ transition polarizabilities (Eq. 3) at 354 eV. The change of electronic character at the conical intersection, where the nonadiabatic couplings have significant values (compare B), is clearly visible in the bottom right corners. (D) Potential energy surfaces of the three electronic states with the ground-state S₀, the dark $n\pi *$ S₁ state, and the bright $\pi \pi *$ state. The conical intersection seam is marked in black, and the wavepacket path is sketched in gray. 1) Optical excitation from S₀ to S₂ using a 34-fs UV pump. 2) Free evolution in the S₂ state through the local minimum, with subsequent barrier crossing toward the conical intersection. 3) Nonadiabatic passage through the conical intersection, creating a vibronic coherence. 4) Relaxation in the S₁ state toward the energetic minimum, where the wavepacket is absorbed.

The obtained $\psi \left(T\right)$ enters the expression for the frequency-dispersed TRUECARS signal (12) of the S₂ $\to$ S₁ transition

$$\begin{array}{cc}\hfill S\left({\omega }_r,T\right)& =2\mathcal{I}{\int }_{-\infty }^{\infty }dt{e}^{i{\omega }_r\left(t-T\right)}{\epsilon }_0^{*}\left({\omega }_r\right){\epsilon }_1\left(t-T\right)\hfill \\ \hfill & \hspace{1em}\times ⟨\psi \left(T\right)\left|\widehat{\alpha }\right|\psi \left(T\right)⟩.\hfill \end{array}$$ [1]

${\epsilon }_0$ and ${\epsilon }_1$ are the broadband 2-fs and narrowband 500-as X-ray fields, $\widehat{\alpha }$ is the electronic polarizability operator, $\mathcal{I}$ stands for the imaginary part, and $T$ is the delay between the optical pump and the X-ray probe fields. Applied to the S₂/S₁ intersection, the loop diagram and level scheme of the signal are drawn in Fig. 2. An optical UV pump pulse creates a population in the S₂ state. Following a free evolution period, a coherence between S₂ and S₁ (denoted $e$ and $e\prime$ in Fig. 2D) is created at the CoIn. This coherence is probed at the instantaneous time T by the hybrid X-ray pulse configuration. As sketched in Fig. 2E, they are tuned to be off-resonant with any valence-to-core transition, and their wavelength is at 354 eV between the carbon and nitrogen core absorption edges (resonant X-ray signatures of the dark S1 state were demonstrated in ref. 23).

Fig. 2.

TRUECARS signal of uracil. (A) The frequency-dispersed signal $S\left({\omega }_r,T\right)$ (Eq. 1), using ${\widehat{\alpha }}_{xx}$ at 354 eV (Fig. 1C). (B) Valence-state population dynamics after an optical pump and the dynamics sketched in Fig. 1D. (C) Expectation value of the polarizability operator ${\widehat{\alpha }}_{xx}$ (Eq. 2). $T=0$ is set to the maximum intensity of the 34-fs FWHM Gaussian pump. (D) Loop diagram for the signal. The Gaussian pump ${\epsilon }_p$ creates an electronic and nuclear population in the excited state. A coherence between e (S₂) and e′ (S₁) that emerges at the conical intersection is probed by the hybrid field ${\epsilon }_0$ (500 as) and ${\epsilon }_1$ (2 fs). For diagram rules, see ref. 26. (E) Energy-level scheme of the measurement. Electronic-state color code is according to B, where blue and red correspond to the states $i$ and $f$ in Eq. 4. The C, N, and O core edges at 291, 405, and 536 eV correspond to the states $c$ in Eq. 4. The green arrows represent the off-resonant Raman process.

The time-dependent polarizability in Eq. 1 is the relevant material quantity that results from the wavepacket dynamics. In matrix form, it reads

$$⟨\psi \left|\widehat{\alpha }\right|\psi ⟩=⟨\left(\begin{array}{c}\hfill {\psi }_2\hfill \\ \hfill {\psi }_1\hfill \end{array}\right)\left|\left(\begin{array}{cc}\hfill {\alpha }_{22}\hspace{1em}\hfill & \hfill {\alpha }_{21}\hfill \\ \hfill {\alpha }_{12}\hspace{1em}\hfill & \hfill {\alpha }_{11}\hfill \end{array}\right)\right|\left(\begin{array}{c}\hfill {\psi }_2\hfill \\ \hfill {\psi }_1\hfill \end{array}\right)⟩.$$ [2]

The diagonal elements ${\alpha }_{22}$ and ${\alpha }_{11}$ are the S₂ and S₁ electronic-state polarizabilities, and the off-diagonal elements are the transition polarizabilities between them. All elements are operators in the nuclear space. When taking the imaginary part in Eq. 1, population terms do not contribute to the signal, and ${\alpha }_{11}$ and ${\alpha }_{22}$ can be set to zero. This is an important feature of TRUECARS that makes it a background-free probe of vibronic coherences that in our model exist only in the CoIn vicinity. Since the electronic-state populations are larger than the coherence by around three orders of magnitude, the latter would be masked in more conventional transient Raman probing schemes. The hybrid narrowband/broadband X-ray pulse configuration used in TRUECARS provides the necessary temporal and spectral profiles to capture the energy splitting of the S₁ S₂ superposition and the time resolution to resolve the ultrafast coherences. This is not accessible with visible pulses.

Each element of $\widehat{\alpha }$ is a second-rank tensor with x, y, and z Cartesian components in the molecular frame:

$$\widehat{\alpha }\hspace{0.17em}=\left(\begin{array}{ccc}\hfill {\alpha }_{xx}\hspace{1em}\hfill & \hfill {\alpha }_{yx}\hspace{1em}\hfill & \hfill {\alpha }_{zx}\hfill \\ \hfill {\alpha }_{xy}\hspace{1em}\hfill & \hfill {\alpha }_{yy}\hspace{1em}\hfill & \hfill {\alpha }_{zy}\hfill \\ \hfill {\alpha }_{xz}\hspace{1em}\hfill & \hfill {\alpha }_{yz}\hspace{1em}\hfill & \hfill {\alpha }_{zz}\hfill \end{array}\right).$$ [3]

Depending on the orientation of the molecule and the pulse configuration, a certain component of Eq. 3 is selected. In general, each component of $\widehat{\alpha }$ can be calculated according to (24, 25)

$${\left[{\alpha }_{xy}\right]}_{fi}=\sum _c\left\{\frac{⟨f\left|{\widehat{\mu }}_y\right|c⟩⟨c\left|{\widehat{\mu }}_x\right|i⟩}{{\omega }_{cf}+{\omega }_0}+\frac{⟨f\left|{\widehat{\mu }}_x\right|c⟩⟨c\left|{\widehat{\mu }}_y\right|i⟩}{{\omega }_{ci}-{\omega }_0}\right\}.$$ [4]

Here, ${\widehat{\mu }}_x$ and ${\widehat{\mu }}_y$ are the Cartesian $x$ and $y$ components of the dipole operator in the molecular frame. The summation is over all core–hole states $c$, ${\omega }_{ci}$ is the energy difference between valence-state $i$ and the core-state $c$, and ${\omega }_0$ = 354 eV is the carrier frequency of the probe field taken between the carbon and nitrogen K edges (Fig. 1). Considering an off-resonant X-ray core process between valences states $i$ and $f$, the summation in Eq. 4 should be over all core–hole states $c$. The key quantities in this equation are the transition dipole moments $⟨f\left|{\widehat{\mu }}_y\right|r⟩$ between valence and core states, where ${\widehat{\mu }}_y$ is the $y$ component of the dipole operator. In this work, we calculated all Cartesian components of the dipole moments between the valence S₁ and S₂ states on the multireference level of quantum chemistry (Materials and Methods) by including 80 core–hole states. Uracil has 8 nonhydrogen atoms, and we included the first 10 core–hole states of each atom. Dipole moments were calculated at the 2D nuclear coordinate space on 270 grid points, with subsequent interpolation of the surfaces to the grid for WP simulations. Exemplary S₂/S₁ transition polarizability surfaces at ${\omega }_0=354\hspace{0.17em}\text{eV}$ are drawn in Fig. 1C. They show a pronounced structure along the nuclear coordinates, and the change of electronic character is clearly visible at the CoIn seam.

The TRUECARS signal of the S₂ $\to$ S₁ transition displayed in Fig. 2 exhibits some striking features. At the CoIn, a vibronic coherence is created and time-dependent material quantity, i.e., the polarizability expectation value according to Eq. 2, becomes finite as well. A signal shows up and remains visible for several hundred femtoseconds, until the vibronic coherence decays. This long-lived vibronic coherence is due to the delocalized nature of the quantum nuclear WP on the S₂ surface. Tails of the WP continue to reach the CoIn, and even with an instant exit channel for the WP in the S₁ state, the coherence survives for several hundred femtoseconds. This has profound implications for the observation and control of quantum events at CoIns. The vibronic coherence that determines the outcome of the photophysical process is long-lived and its monitoring will require longer temporal windows rather than precise timings for molecules like uracil. Note that Fig. 1 shows the signal with the $xx$ component of the polarizability, which would require oriented molecules. However, the signal can be measured for other orientations as well.

This is demonstrated in Fig. 3, where the TRUECARS signal is shown using the ${\alpha }_{xx}$, ${\alpha }_{yy}$, and ${\alpha }_{zz}$ in Fig. 1C. The signal is visible for all three possible molecular orientations. This is even the case for the isotropic signal in Fig. 3D, corresponding to a randomly oriented sample.

Fig. 3.

Comparison of molecular orientations in the TRUECARS signal. (A–C) Signal using $xx$, $yy$, and $zz$ components of the polarizability operator in Eq. 3. The $zz$ component, which is perpendicular to the molecular plane (Fig. 1A), exhibits the strongest signal, according to the magnitude of the polarizability surfaces in Fig. 1C. (D) Isotropic signal, corresponding to a randomly oriented molecular sample. The signal is visible due to the dominating $zz$ contribution.

The Time-Resolved Vibronic Frequency Map across the Conical Intersection

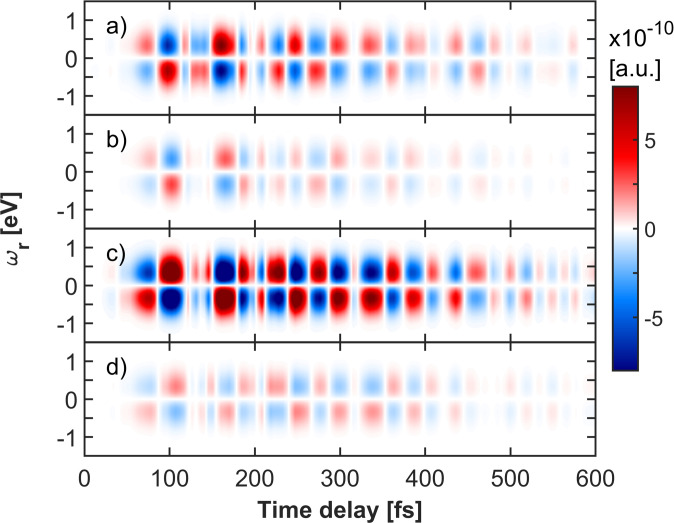
The signal depicted in Fig. 2A exhibits temporal Stokes and anti-Stokes oscillations between positive (red) and negative (blue) values. This is because the contributing vibronic states have different frequencies, and the dynamical phase evolution is contained in the signal. To display the time-dependent frequency map, we show in Fig. 4 the Wigner spectrogram of a temporal trace $S\left(T\right)$ of the signal (Fig. 4B) at a fixed Raman shift ${\omega }_r$:

$$W\left(T,{\omega }_{coh}\right)={\int }_{-\infty }^{\infty }d\tau S\left(T+\tau \right)S\left(T-\tau \right)e^{i{\omega }_{coh}\tau }.$$ [5]

The 0- to 0.2-eV frequency window spanned by $W\left(T,{\omega }_{coh}\right)$ represents the potential energy splitting of the CoIn where the vibronic coherence is located. The main feature at 0.1 eV (marked with the white arrow in Fig. 4E) exhibits no temporal variation of ${\omega }_{coh}$. The contributions visible in the Wigner spectrogram map the vibronic frequencies that contribute to the coherence. Unlike in classical simulations, the complete set of eigenstates is time independent in our effective Hamiltonian. At all times, the quantum nuclear WP can be expressed as a superposition of the vibronic eigenstates, where usually many of them contribute. The Wigner spectrogram reveals the dominating contributions to the coherence. Stated differently, when the nuclei are treated as classical, the system has a well-defined, time-dependent energy splitting which vanishes at the conical intersection. In the quantum treatment, this is replaced by a distribution of energy splittings given by the wavepacket frequencies. The average of that distribution serves as the effective splitting.

Fig. 4.

Wigner spectrogram (Eq. 5) of the TRUECARS signal. A, C, and E use a 34-fs Gaussian pump (delocalized wavepacket). (A) The signal $S\left({\omega }_r,T\right)$ (Eq. 1). (C) Signal trace $S\left(T\right)$ at ${\omega }_r$ = 0.33 eV (maximum signal intensity). (E) Wigner spectrogram $W\left(T,{\omega }_{coh}\right)$ of the signal trace $S\left(T\right)$ (Eq. 5). B, D, and F use a 20-fs Gaussian pump which produces a more localized wavepacket.

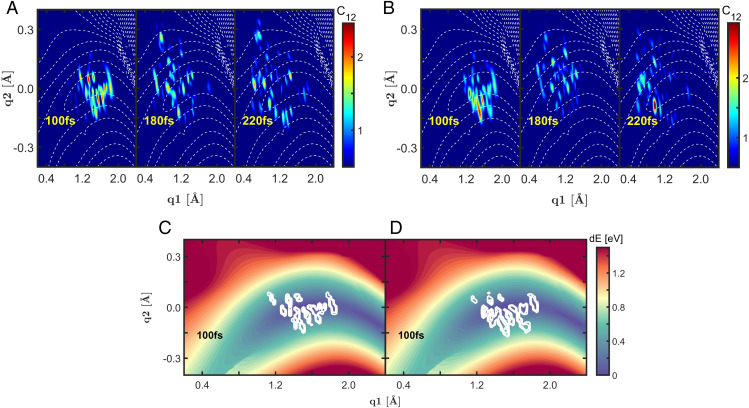
To extend this analysis even farther, we reduced the 34-fs FWHM optical Gaussian pump to 20 fs, as shown in Fig. 4 B, D, and F. The WP is now more localized in the S₂ PES, which strongly influences the coherence. While there is no change in the Raman shift ${\omega }_r$ of the signal, the temporal oscillations are now much faster, so that the frequency regime covered by the vibronic coherence is broader in Fig. 4F. More importantly, the energy position of the main feature (marked with the white arrow) does vary with time. Starting at around 0.2 eV at 100 fs, the coherence evolves to lower frequencies until around 250 fs, where it eventually decays. This spectrogram directly maps the distribution of vibronic excitations along the CoIn path, as revealed by the WP coherence and illustrated in Fig. 5. Representative snapshots of the normalized WP coherence at 100, 180, and 220 fs are shown in Fig. 5. For the 34-fs pump, the coherence is indeed initially mainly located at energy splittings between 0 and 0.2 eV and delocalizes with time. The position and spread of the coherence in the nuclear phase space are determined by the WPs in S₂ and S₁. A delocalized coherence does not mean it is lost or has dispersed; it is simply spread over a larger region on the PES. In this context, decoherence means that the coherence magnitude, integrated over the nuclear degrees of freedom, decays. This is independent of whether the coherence is local (e.g., at the CoIn) or spread over a larger region.

Fig. 5.

Vibronic coherence distribution along the conical intersection path. Similar to Fig. 4, a 34-fs Gaussian pump was used for A and C and a 20-fs Gaussian pump for B and D. (A and B) Vibronic coherence that makes the signal, shown as the normalized product between the S₂ and S₁ nuclear wavepacket at 100, 180, and 220 fs. The dashed isoline marks the energy difference surface between the adiabatic S₂ and S₁ states, with a spacing of 0.2 eV, and the conical intersection seam around $q_2=0$. Using the 20-fs pump, the vibronic coherence is more localized at 100 and 220 fs and explores a larger energy splitting. (C and D) Different visualizations of the 100-fs snapshots in A and B with the energy difference E(S₂) − E(S₁) as the contour plot. The product of the S₂ and S₁ nuclear wavepacket using both pulses is shown at 100 fs (compare A and B). In D, the coherence is located at higher splittings than in C. This is directly seen in the corresponding Wigner spectrogram.

Using the 20-fs pump (Fig. 4 B, D, and F), the main initial coherence at 100 fs is at higher frequencies. After a short delocalization period, the coherence again becomes localized at 220 fs and shows lower frequencies than at 100 fs. This again corresponds to the position of the vibronic coherence in the nuclear space, depicted in Fig. 5. In Fig. 5 A and B, the WP overlap is drawn as the colored contour plot, while the S₂ S₁ energy difference is represented by the isolines. This shows the more local coherence of the 20-fs pump WP in contrast to the 34-fs one at 100 and 220 fs propagation time. To better identify the range of energy splitting which is spanned by the coherence and that this corresponds to the main feature in the Wigner spectrograms in Fig. 4 E and F, the plotting scheme is inverted in Fig. 5 C and D. Here, the WP overlap is drawn in isolines, while the S₂ S₁ energy splitting is shown with a colored contour plot. The snapshots at 100 fs are shown for both probing schemes, and it can be seen that the WP overlap is located at higher-energy splittings in Fig. 5D (20-fs pump) than in Fig. 5C (34-fs pump). The transient pathway of the vibronic WP coherence is directly accessible from the recorded signal. While we used an adiabatic basis here, the WP simulations in the 2D nuclear space of our 2D model Hamiltonian are exact and therefore independent of the electronic basis. Due to the quantum treatment of the nuclei, the time-resolved frequency map in the Wigner spectrogram is an experimental observable, independent of the basis set used, and reveals the exact vibronic-state landscape across the CoIn path.

Summary

Our study offers a detailed picture of ultrafast nonadiabatic transitions at CoIns. The frequency, phase, and duration of the vibronic coherences, created by the quantum nuclear WP evolution, are monitored in real time. Contrary to the common picture of precisely timed CoIn events, the coherence remains visible for several hundred femtoseconds. This is due to the delocalized nature of the quantum nuclear WP in the S₂ state after photoexcitation, where small tails consecutively reach the CoIn. The coherence that is built decays due to the S₁ WP evolving away from the CoIn toward the minimum, but it is constantly rebuilt by other parts arriving at the CoIn in the S₂ state. Localized nuclear WPs provide a sensitive scan of the frequency landscape surrounding the CoIn. The magnitude and range of the energy splitting of the participating adiabatic vibronic states can be read directly from the signal. This measure is an intrinsic molecular property and does not depend on the choice of a particular basis set. No further theoretical input is necessary to access this information from the signal. Uracil photorelaxation is experimentally accessible, and all quantities are produced at the fully ab initio level. The presented Wigner spectrograms offer a physical picture of CoIn processes by viewing them through the complex coherence distributions rather than a change in absorption lines or a single vanishing energetic gap.

The off-resonant probing scheme employed here with respect to core excitations renders the signal ubiquitous and translatable to other molecules with a nonvanishing dipole transition between a CoIn valence state and other core–hole states. Monitoring the vibronic coherence provides a unique window into how the outcomes of ultrafast photophysical processes are decided. This insight is also beneficial for developing approaches for controlling photochemical reactions by modulating this coherence (27–29). An important step toward phase-controlled XUV/X-ray pulses that are necessary to record the stimulated Raman signal was made very recently (30), and our proposed experiment lies within the capabilities of state-of-the-art X-ray sources (31, 32). Altogether, the reported spectroscopic maps of CoIn passages provide direct access to the quantum WP pathways in CoIn passages, which paves the way for a deeper understanding and better control of these ubiquitous processes.

Materials and Methods

Quantum Chemistry.

The computation of the PESs and dipole moments for the adiabatic states was described in ref. 20. This was done on the complete active space self-consistent field (CASSCF) and the multi-reference configuration interaction singles level of theory, employing an active space of 12 electrons in 9 orbitals (5 $\pi$, one oxygen lone pair, and 3 ${\pi }^{*}$ orbitals). For the present study, we recalculated the NACs, taking into account the phase of the electronic wavefunction. This was done at the CASSCF level and the same (12/9) active space, using the program package MOLPRO (33). A wavefunction file was created containing the selected active space. Using a fine spacing around the CoIn, this wavefunction file was read in for all other NAC calculations, to guarantee that the sign of the electronic wavefunction remains the same in all structures. The resulting NACs are shown in Fig. 1B.

To compute the polarizabilities in Eq. 4, the same active space and level of theory were used with the 6-311G* basis set (34, 35) to calculate 80 core–hole states. Uracil has 8 nonhydrogen atoms, and we included the first 10 core–hole states of each atom. Dipole moments between the valence S₁ and S₂ states to these core states were calculated at the 2D nuclear coordinate space on 270 grid points, with subsequent interpolation of the surfaces to the 256 × 256 grid for WP simulations. Within one calculation, first the valence states were calculated using the (12/9) active space. Then, the lowest-energy orbital in the active space was rotated for an s-orbital of one of the C, N, or O cores. This orbital was then frozen, single occupation in this orbital was enforced, and the first 10 excited states were calculated. Afterward, the spatial components of the dipole operator were calculated between the 2 valence and 10 core states. This results in a total dataset of $270*8*10*2*3=\mathrm{129,600}$ dipole moments.

Wavepacket Simulations.

To model the photophysics of uracil, nuclear WP simulations were performed by solving the TDSE

$$\begin{array}{cc}\hfill i\hslash \frac{\partial }{\partial t}\psi & =Ĥ\psi \hfill \\ \hfill & =\left[{\widehat{T}}_q+\widehat{V}-\widehat{\mu }\epsilon \left(t\right)\right]\psi ,\hfill \end{array}$$ [6]

with the kinetic energy operator ${\widehat{T}}_q$ of the nuclei in internal coordinates $q$, the potential energy operator $\widehat{V}$, and the light–matter interaction in the dipole approximation with the dipole operator $\widehat{\mu }$ and the electric field $\epsilon \left(t\right)$. Our model Hamiltonian space has two nuclear degrees of freedom and three electronic states. The WP simulation setup has been described and used in ref. 20.

All quantities are represented on a 2D 256 × 256 spatial grid. The two nuclear coordinates $q_1$ and $q_2$ are selected from molecular structures that are known to play an important role in uracil S₂ photorelaxation: The FC, a local S₂ minimum, and the optimized conical intersection to the S₁ state. $q_1$ is the normalized displacement vector that points from the FC to the CoIn. $q_2$ is the displacement vector from FC to the local S₂ minimum, which is then orthonormalized to S₁ (20). Numerical propagation using the adiabatic PES basis and a nuclear grid is performed by integrating the TDSE according to

$$\psi \left(t+dt\right)=exp\left(-iĤdt\right)\psi \left(t\right)=Û\psi \left(t\right).$$ [7]

The evolution operator $Û$ is expanded in a Chebyshev series according to ref. 36, using a time step of 2 a.u. The kinetic energy operator in internal coordinates $q$ and $s$ is set up according to the G-matrix formalism (37) as described in ref. 38,

$${\widehat{T}}_q\simeq -\frac{{\hslash }^2}{2m}\sum _{r=1}^M\sum _{s=1}^M\frac{\partial }{\partial q_r}\left[G_{rs}\frac{\partial }{\partial q_s}\right]$$ [8]

with the G-matrix computed via its inverse elements

$${\left(G^{-1}\right)}_{rs}=\sum _{i=1}^{3N}{m}_i\frac{\partial x_i}{\partial q_r}\frac{\partial x_i}{\partial q_s},$$ [9]

i.e., via finite differences by displacement of the Cartesian molecular geometry along the internal coordinates. In the case of the uracil coordinates described above, the G-matrix elements are $G_{q_1{q}_1}=0.000167$ a.u., $G_{q_2{q}_2}=0.000139$ a.u., and the kinetic coupling $G_{q_1{q}_2}=-0.00007$ a.u.

A Butterworth filter (22) was employed in the electronic S₁ state, which absorbs the parts of the WP that reach the S₁ minimum. The filter was of “right-pass” type (absorbing all parts on the left side of the border) and placed at $q_1=0.5$ Å with an order of 100 (22). This was done to create an exit channel for the WP, which otherwise would move back to the CoIn region after being relaxed from there.

Data Availability.

All study data are included in this article.