Higher-order clinical risk factor interaction analysis for overall mortality in maintenance hemodialysis patients

Abstract

Background and Aims:

In Taiwan, approximately 90% of patients with end-stage renal disease receive maintenance hemodialysis. Although studies have reported the survival predictability of multiclinical factors, the higher-order interactions among these factors have rarely been discussed. Conventional statistical approaches such as regression analysis are inadequate for detecting higher-order interactions. Therefore, this study integrated receiver operating characteristic, logistic regression, and balancing functions for adjusting the ratio in risk classes and classification errors for imbalanced cases and controls using multifactor-dimensionality reduction (MDR-ER) analyses to examine the impact of interaction effects between multiclinical factors on overall mortality in patients on maintenance hemodialysis.

Meterials and Methods:

In total, 781 patients who received outpatient hemodialysis dialysis three times per week before 1 January 2009 were included; their baseline clinical factor and mortality outcome data were retrospectively collected using an approved data protocol (201800595B0).

Results:

Consistent with conventional statistical approaches, the higher-order interaction model could indicate the impact of potential risk combination unique to patients on maintenance hemodialysis on the survival outcome, as described previously. Moreover, the MDR-based higher-order interaction model facilitated higher-order interaction effect detection among multiclinical factors and could determine more detailed mortality risk characteristics combinations.

Conclusion:

Therefore, higher-order clinical risk interaction analysis is a reasonable strategy for detecting non-traditional risk factor interaction effects on survival outcome unique to patients on maintenance hemodialysis and thus clinically achieving whole-scale patient care.

Introduction

According to the 2005–2012 data in the Taiwan Renal Registry Data System, the incidence of end-stage renal disease (ESRD) increased from 376 to 426 people per million, and the prevalence increased from 2111 to 2926 people per million in the Taiwan population.¹ Hemodialysis is the most frequently prescribed treatment option for kidney failure worldwide. Approximately 90% of ESRD patients in Taiwan receive hemodialysis.²

In 2010, chronic kidney disease (CKD) was ranked 18th in global mortality causes by a systematic analysis for the Global Burden of Disease Study, with an annual death rate of 163 per 100,000 people.³ The increase in CKD-related mortality indicates that the burden of renal disease is increasing globally. Laboratory blood tests are major indicators for medical management in hemodialysis patients. The survival predictability of various patient characteristics, hemodialysis vintage, and laboratory tests in maintenance hemodialysis patients has been reported by several recent studies.^4,5 Overall survival is considered a long-term outcome of hemodialysis patients.^6–10 An acceptable level of overall survival in hemodialysis patients should be achieved to indicate that the quality of dialysis treatment is acceptable.

The interaction between risk factors is considered clinically relevant for survival outcome estimation, particularly in observational studies.¹¹ Conven-tional statistical approaches such as regression analysis can explain the association and statistical interaction of CKD with clinical or environmental risk factors or both; however, these approaches are inadequate for detecting higher-order interactions among clinical risk factors. The multifactor dimensionality reduction (MDR) method is a novel computational approach initially developed for detecting complex multifactor interactions.¹² Several new MDR-based methods, such as generalized MDR,¹³ classification based MDR,¹⁴ balanced MDR,¹⁵ multi-objective MDR,^6,17 and other approaches have been proposed for improving the performance and applicability of the general MDR method. Evenly distributed case–control data sets are required for general MDR-based analyses. Previous studies have commonly used resampling or undersampling approaches while using general MDR-based methods.¹⁸ A balancing function for adjusting the ratio in risk classes and classification errors for imbalanced cases and controls using MDR, named MDR-ER, improved the classification and error rate evaluation functions to fit imbalanced data sets without increasing the number of steps in the procedure and the number of parameters.¹⁹ These computational approaches have rarely been used for detecting the complex interactions among clinical risk factors in a hemodialysis population.

Compared with common clinical methods, including logistic and Cox regression analyses, MDR-ER uses the case–control proportion to determine the dichotomous threshold between multifactor higher-order interactions without increasing the computational difficulty. Notably, here, the robustness of interaction model was confirmed through cross validation. Moreover, the non-parametric nature of MDR-ER could alleviate the limitation of the small sampling size. In addition, the MDR-ER model could be used to efficiently investigate the higher-order marginal or non-marginal interaction effects of unique risk factor combinations and determine the impact on the survival outcome. Here, we used a combination of logistic regression and MDR-ER analyses for constructing an optimal clinical risk factor interaction detection model for overall mortality by using imbalanced data sets of patients on maintenance hemodialysis. The main purpose of this study was to examine the interaction of the indicated clinical factors and their contribution to overall mortality in patients on regular hemodialysis. Furthermore, we aimed to recognize the clinical significance in higher-order interaction of multi clinical factors to demonstrate mortality risk combinations that are unique to the study population and provide whole-scale patient care clinically.

Materials and methods

Study design and participants selection

The data of 909 patients were reviewed; however, 128 of these patients were excluded because of having incomplete data or being aged <18 years. The remaining 781 patients who received outpatient hemodialysis dialysis three times per week at Kaohsiung Chang Gung Memorial Hospital (CGMH), Taiwan before 1 January 2009 were included, and their mortality outcome was tracked from the date of initial study inclusion to 31 December 2013. Finally, the retrospective hemodialysis data set comprised 182 deceased (cases) and 599 surviving (controls) patients.

Ethics content

The present study was approved by the Committee on Human Research at Kaohsiung Chang Gung Memorial Hospital (201800595B0) and conducted in accordance with the Declaration of Helsinki with a waiver of patient consent. All patients were verbally informed that their medical information would be collected at the beginning of treatment, and all the medical information is maintained by the corresponding department. All data was retrospectively collected from the medical review database without involving any identifiable private information under the consent of the corresponding department. CGMH allowed a waiver of consent for the current study as the research involves no more than minimal risk to subjects, and the waiver did not adversely affect the rights and welfare of the subjects.

Variables and measurements

The age of patients is the age at entering hemodialysis. Other variables and measurements of the study population were collected at January 2009. All participants received three-session hemodialysis weekly with bicarbonate-containing dialysate and high-efficiency (cellulose acetate) and high-flux dialyzers (polysulfone, polymethyl methacrylate). All blood tests were examined mid-week (Wednesday and Thursday) in fasting status before hemodialysis. The corrected Ca levels were calculated using the following equation: measured total Ca (mg/dL) + 0.8 [4.0 – serum albumin (g/dL)]. Urea reduction ratio was calculated by using the following equation: [predialysis BUN – postdialysis BUN/predialysis BUN] × 100%. Kt/V urea was calculated by using the following equation: Kt/V urea = –Ln (R – 0.008 × t) + [4–(3.5 × R)] × UF/W, where R is the ratio of postdialysis and predialysis serum urea nitrogen, t (in hours) is the duration of dialysis, UF is the ultrafiltrate amount (L), and W is the postdialysis body weight (kg). All blood samples were measured using commercial kits and an autoanalyzer (Hitachi 7600-210, Hitachi Ltd., Tokyo, Japan). Albumin levels were measured using the bromocresol green method. The CT ratio was measured using chest radiographs obtained after hemodialysis: cardiac size was first measured by drawing parallel lines at the most lateral points of each side of the heart and then measuring the distance between them. Thoracic width was subsequently measured by drawing parallel lines down the inner aspect of the widest points of the rib cage and then measuring the distance between the lines. Finally, the CT ratio was calculated as the cardiac size divided by the thoracic width. All the introduced variables and measurements were included in ROC analysis.

ROC analysis

Conventional statistical approaches, such as logistic regression, and the innovative MDR-based methods are both non-linear. However, the clinical factors for maintenance hemodialysis patients are commonly measured in a continuous spectrum. Hence, a ROC analysis and the AUC were employed to dichotomize the continuous spectrums into categorical items.⁴² ROC analysis is commonly used to demonstrate the performance of diagnostic tests, relying on the true-positive rate (sensitivity) compared with the false-positive rate (1-specificity) at various threshold settings. The AUC can summarize the overall discriminant accuracy of the continuous spectrums. All clinical factors, the hemodialysis vintage, age, Hgb, albumin, Fe, blood urea nitrogen, serum creatinine, potassium, corrected serum calcium (Ca), phosphorus, urea reduction ratio, Kt/V urea-Daugirdas score, the CT ratio, and parathyroid hormone, were recorded as continuous variables.

The k-means is a method of vector quantization which aims to partition n observations into k clusters with the within-cluster variances. In this study, we used the k-means algorithm to determine within-cluster variances which could be used as a dichotomized reference level for later analysis. First, all clinical factors were dichotomized according to the cutoff points of k-means, mean, median, or clinical indicator or all, regardless of sex and DM status (Supplemental Table S2). ROC analyses were employed to estimate the distinguishing characteristic used for classifying participants from the overall mortality data set. The highest AUC was considered the appropriate cutoff point for clinical factor dichotomization for the subsequent non-linear analysis (Supplemental Table S3). Youden index (sensitivity + specificity − 1) is used for determining the performance of dichotomous test in single variables. The likelihood ratio was calculated through likelihood testing by comparing the results of the dichotomous test in single variables, in which an increased value (>1) indicates an increase in mortality in patients with score 1 conditions.

Logistic regression

Backward selection was used for final model selection for logistic regression with an elimination criterion of p > 0.02, and univariate logistic regression was used to demonstrate the effects of independent clinical factors for overall mortality. MDR and MDR-ER results were compared in the final model to determine the significance of the effects of risk factors were included rather than chance findings. ORs and 95% CIs were computed. The crude ORs were estimated using univariate analysis, and the adjusted ORs were estimated using multivariate logistic regression. Both ORs indicated the risk of clinical risk factors for overall mortality. A p value of < 0.05 was considered statistically significant. All statistical analyses were performed using STATA Version 11.0.

MDR

MDR is a novel computational method for detecting higher-order interactiocns in various diseases. MDR was designed to detect categorical independent variables and a dichotomous case–control status. In MDR, an exhaustive search is performed to evaluate all possible combinations of independent variable strata and finally select the most relevant combinations according to various parameters. CVC, the most critical parameter for evaluating MDR results, indicates the number of times a model is identified as the optimal model consistent to the cross validation (CV) sets. High CVC can avoid overfitting results for the existing data set, thereby increasing the predictive ability of the model produced. The MDR process includes the following six steps:

• Step 1. Randomly sort and divide the case–control data sets into 10 partitions for CV, as shown in (1).

$$\mathrm{K}=\{\mathrm{k}1,\mathrm{k}2,\mathrm{k}3,\dots ,\mathrm{kn}\}$$ (1)

• Step 2. Arrange n combinations in a contingency table with the all possible multifactor cell. The value of n is designated depending on the number of factors being considered. Subsequently, a set of n clinical factors is selected. The number of cases and controls for each strata combination is counted.

• Step 3. Calculate the case–control ratio compared with the threshold (T = 1). For MDR, the multifactor class count and ratio is calculated. The ratio in the multifactor cell that meets or exceeds the threshold is labeled high-risk (H), indicating the high-risk group. The multifactor cell under the threshold is labeled low-risk (L), indicating the low-risk group. The equation is shown in (2).

• Step 4. Repeat steps 1–3 to search for all possible combinations in each stratum of independent variables

$$f\left(K\right)=\frac{{\sum }_{j=1}^{P^{*}}u\left(K,P_j\right)}{{\sum }_{j=1}^{N^{*}}u\left(K,N_j\right)}$$ (2)

where

$$u\left(K,A\right)=\{\begin{array}{cc}1& \forall k\in A\\ 0& \forall k\notin A\end{array},\forall k\in K$$

where P is the case data set, N is the control data set, P* is the number of case groups in the training set, N* is the number of control groups in the training set, and K is a vector of variable combinations.

• Step 5. Compute the misclassification error for all possible interaction models. The function u(K,A) is a match if all parameters K in the vector K match their cases or controls and is scored as 1, whereas a misclassification error is scored as 0. The minimum classification error rate is chosen as the optimal model in each CV. The equation in (3) was used to estimate the error rate.

$$f\left(C\right)=\frac{FN+FP}{TP+FN+FP+TN}$$ (3)

where C is the evaluated model. TP is true positive, the total number of cells labeled high-risk (H) in the case data. FP is false positive, the total number of cells labeled high-risk (H) in the control data. FN is false negative, the total number of cells labeled low-risk (L) in the case data. TN is true negative, the total number of cells labeled low-risk (L) in the control data.

• Step 6. Repeat steps 1–5 for each partition CV until the last partition is met. Select the optimal model according to the minimized error rate and CVC.

MDR-ER

As mentioned, MDR has limited applications for the imbalanced data sets. Traditionally, undersampling and resampling approaches have been used to overcome this limitation. Conversely, the MDR-ER method estimates the classification error from the existing case–control proportion and uses the case–control ratio to weigh the outcome probability. Previous studies have proven the feasibility of MDR-ER in association analysis in gene–gene and gene–environment interactions for imbalanced data sets.¹⁹ The functions of MDR-ER modified to fit imbalanced data sets are as follows and the complete MDR-based MDR-ER procedure is illustrated in Supplemental files.

In the MDR-ER method, the case–control ratio (percentage) for each multifactor cell is calculated to enhance the ratio between the cases and controls in the ratio function of MDR. The ratio in the multifactor cell that meets or exceeds a threshold is labeled H, whereas others are labeled L. The equation is shown in (4).

$$f\left(K\right)=\frac{N^{*}\left[{\sum }_{j=1}^{P^{*}}u\left(K,P_j\right)\right]}{P^{*}[{\sum }_{j=1}^{N^{*}}u\left(K,N_j\right)]}$$ (4)

where

$$u\left(K,A\right)=\{\begin{array}{cc}1& \forall k\in A\\ 0& \forall k\notin A\end{array},\forall k\in K$$

where P is the case data set, N is the control data set, P* is the number of case groups in the training set, N* is the number of control groups in the training set, and K is a vector of variable combinations.

The adjusted misclassification error, based on the arithmetic mean of the sensitivity and specificity, is algebraically identical to the error rate if the data set is imbalanced. The adjusted equation is shown in (5).

$$f\left(C\right)=0.5\times \left(\frac{FN}{TP+FN}+\frac{FP}{FP+TN}\right)$$ (5)

where TP is true positive, the total number of cells labeled H in the case data. FP is false positive, the total number of cells labeled high-risk (H) in the control data. FN is false negative, the total number of cells labeled low-risk (L) in the case data. TN is true negative, the total number of cells labeled low-risk (L) in the control data.

Results

Receiver operating characteristic (ROC) approach

A total of 781 patients were analyzed. The ROC approach was used to dichotomize all variables into the categorical form to fit the non-linear analysis. Table 1 summarizes the dichotomous characteristics of 16 clinical factors according to the overall mortality status. The top three clinical factors according to the area under the ROC curve (AUC) values were albumin, age, and cardiothoracic (CT) ratio. Albumin had the highest AUC (0.676), with a sensitivity of 0.637, a specificity of 0.715, a Youden index of 0.352, and a positive likelihood ratio (LR+) of 2.233. Age showed an AUC of 0.653, with a sensitivity of 0.670, a specificity of 0.636, a Youden index of 0.306, and an LR+ of 1.842. The CT ratio exhibited an AUC of 0.619, with a sensitivity of 0.593, a specificity of 0.644, a Youden index of 0.237, and an LR+ of 1.669. Supplemental Material Table S1 online summarizes the clinical factor distribution among hemodialysis patients according to the overall mortality status. Compared with the survival (control) group, the death (case) group had a significantly higher proportion of the following characteristics: diabetes mellitus (DM), age ⩾61.59 years, Hgb levels <10.48 g/dL, albumin levels <3.76 g/dL, ferritin (Fe) levels ⩾415.48 ng/cc, creatinine levels <10.65 mg/dL, potassium levels ⩾5 meq/L, Kt/V urea-Daugirdas score ⩾1.70, and CT ratio ⩾0.51.

Table 1.

Dichotomous characteristics for clinical factors in hemodialysis patients.

Factors	Variable	AUC	Score 1	Score 0	Sensitivity	Specificity	Youden index	LR+
1	Sex	0.513	Female	Male	0.571	0.454	0.025	1.047
2	DM	0.586	Yes	No	0.368	0.803	0.171	1.869
3	Age, years	0.653	⩾61.59	<61.59	0.670	0.636	0.306	1.842
4	Hemodialysis vintage, years	0.495	⩾7.49	<7.49	0.357	0.633	0.010	0.972
5	Hemoglobin, g/dL	0.404	⩾10.48	<10.48	0.374	0.434	0.192	0.660
6	White blood cell, 103/µL	0.528	⩾6.19	<6.19	0.445	0.611	0.056	1.144
7	Platelet, 103/µL	0.510	⩾195	<195	0.451	0.569	0.020	1.046
8	Albumin, g/dL	0.676	<3.76	⩾3.76	0.637	0.715	0.352	2.233
9	Ferritin, ng/cc	0.571	⩾415.48	<415.48	0.610	0.533	0.143	1.305
10	Blood urea nitrogen, mg/dL	0.463	⩾68.77	<68.77	0.462	0.464	0.074	0.861
11	Creatinine, mg/dL	0.616	<10.65	⩾10.65	0.681	0.551	0.232	1.517
12	Potassium, meq/L	0.458	⩾5	<5	0.560	0.524	0.085	1.178
13	Corrected serum calcium, mg/dL	0.519	⩾9.53	<9.53	0.506	0.533	0.039	1.081
14	Phosphorus, mg/dL	0.470	⩾5	<5	0.544	0.516	0.060	1.124
15	Urea reduction ratio	0.453	⩾0.74	<0.74	0.511	0.409	0.080	0.865
16	Kt/V urea-Daugirdas score	0.560	⩾1.70	<1.70	0.643	0.478	0.121	1.230
17	Cardiothoracic ratio	0.619	⩾0.51	<0.51	0.593	0.644	0.237	1.669
18	Intact parathyroid hormone, pg/mL	0.469	⩾402.06	<402.06	0.319	0.619	0.062	0.837

AUC, area under the curve; DM, diabetes mellitus; LR+, positive likelihood ratio.

Logistic regression approach using backward selection

Backward selection in logistic regression was used for the final model selection (Table 2). The clinical factors that satisfied the statistical criteria (p < 0.2) were included in the multivariate analysis. In the final model analysis, the clinical factors significantly associated with overall mortality were DM status (yes versus no, adjusted odds ratio (OR) = 1.87, 95% confidence interval (CI) = 1.25–2.81, p < 0.001), age (⩾61.59 years versus <61.59 years, adjusted OR = 2.09, 95% CI = 1.41–3.10, p < 0.001), albumin levels (<3.76 g/dL versus ⩾3.76 g/dL, adjust-ed OR = 2.65, 95% CI = 1.81–3.88, p < 0.001), Kt/V urea-Daugirdas score (⩾1.70 versus <1.70, adjusted OR = 0.60, 95% CI = 0.40–0.89, p < 0.001), and CT ratio (⩾0.51 versus <0.51, adjusted OR = 1.64, 95% CI = 1.12–2.40, p < 0.001). Similar results were obtained in the univariate analysis (Table 2).

Table 2.

Logistic regression analysis using backward selection for overall mortality.

Variables	Comparison	Univariate		Multivariate
		Crude OR (95% CI)	p	Adjusted OR (95% CI)	p
Sex	Female versus male	1.11 (0.79–1.55)	0.544	–
DM	Yes versus no	2.37 (1.65–3.41)	<0.001	1.87 (1.25–2.81)	<0.001
Age, years	⩾61.59 versus <61.59	3.55 (2.50–5.05)	<0.001	2.09 (1.41–3.10)	<0.001
Hemodialysis vintage, years	⩾7.49 versus <7.49	0.84 (0.59–1.17)	0.300	–
Hemoglobin, g/dL	⩾10.48 versus <10.48	0.46 (0.33–0.64)	<0.001	0.62 (0.42–0.90)	0.643
White blood cell, 103/µL	⩾6.19 versus <6.19	1.26 (0.90–1.76)	0.177	–
Platelet, 103/µL	⩾195 versus <195	1.08 (0.78–1.51)	0.637	–
Albumin, g/dL	<3.76 versus ⩾3.76	4.40 (3.10–6.24)	<0.001	2.65 (1.81–3.88)	<0.001
Ferritin, Fe, ng/cc	⩾415.48 versus <415.48	1.78 (1.27–2.50)	0.001	–
Blood urea nitrogen, mg/dL	⩾68.77 versus <68.77	0.74 (0.53–1.04)	0.079	–
Creatinine, mg/dL	<10.65 versus ⩾10.65	2.62 (1.85–3.73)	<0.001	1.51 (0.98–2.31)	3.725
Potassium, meq/L	⩾5 versus <5	1.4 (1.01–1.96)	0.046	–
Corrected serum calcium, mg/dL	⩾9.53 versus <9.53	1.16 (0.84–1.62)	0.368	–
Phosphorus, mg/dL	⩾5 versus <5	1.27 (0.91–1.77)	0.158	–
Urea reduction ratio	⩾0.74 versus <0.74	0.72 (0.52–1.01)	0.057	–
Kt/V urea-Daugirdas score	⩾1.70 versus <1.70	1.64 (1.17–2.32)	0.004	0.60 (0.40–0.89)	<0.001
Cardiothoracic ratio	⩾0.51 versus <0.51	2.64 (1.88–3.72)	<0.001	1.64 (1.12–2.40)	<0.001
Intact parathyroid hormone, pg/mL	⩾402.06 versus <402.06	0.76 (0.53–1.08)	0.129	0.29 (0.18–0.47)	1.083

Bold font indicates statistically significant results with p-value less than 0.05.

Adjusted-OR, adjusted odds ratio estimated from multivariate logistic regression; CI, confidence interval; Crude-OR, crude odds ratio estimated from univariate analysis.

Interactions between multiclinical risk factors

Shown in Table 3, the two- and four-order interaction models had the highest cross validation consistency (CVC). The two-order interaction model exhibited a combination of DM and albumin levels (OR = 5.55, 95% CI = 3.73–8.24; risk ratio (RR) = 3.61, 95% CI = 2.62–4.88) with a satisfactory CVC (10/10, error rate = 0.31). The four-order interaction model exhibited a combination of risk factors, including DM, age, albumin level, and CT ratio, which could reduce patient survival (OR = 7.07, 95% CI = 4.86–10.30; RR = 4.05, 95% CI = 3.05–5.39) with a satisfactory CVC (10/10, error rate = 0.27). In addition, the results showed the three- and five-order interaction model have not reached the satisfactory CVC. The three-order interaction model (CVC = 4/10, error rate = 0.30) included a combination of DM, age, and albumin level (OR = 5.49, 95% CI = 3.79–7.95; RR = 3.70, 95% CI = 2.75–4.98), and the five-order interaction model (CVC = 3/10, error rate = 0.26) included a combination of DM, age, albumin, CT ratio, ferritin level (OR = 7.79, 95% CI = 5.31–11.42; RR = 4.17, 95% CI = 3.13–5.54).

Table 3.

MDR-ER analysis results for overall mortality.

Order	Best model	CVC	TN	TP	Error rate	OR	95% CI	RR	95% CI
Two-order	DM, albumin	10/10	354	142	0.31	5.55	3.73–8.24	3.61	2.62–4.88
Three-order	DM, age, albumin	4/10	397	134	0.30	5.49	3.79–7.95	3.70	2.75–4.98
Four-order	DM, age, albumin, CT ratio	10/10	435	129	0.27	7.07	4.86–10.30	4.05	3.05–5.39
Five-order	DM, age, albumin, CT ratio, ferritin	3/10	427	131	0.26	7.79	5.31–11.42	4.17	3.13–5.54

CI, confidence interval; CT, cardiothoracic; CVC, cross validation consistency; DM, diabetes mellitus; MDR-ER, balancing functions for adjusting the ratio in risk classes and classification errors for imbalanced cases and controls using multifactor-dimensionality reduction; OR, odds ratio; RR, risk ratio estimated from MDR-ER; TN, true negative; TP, true positive.

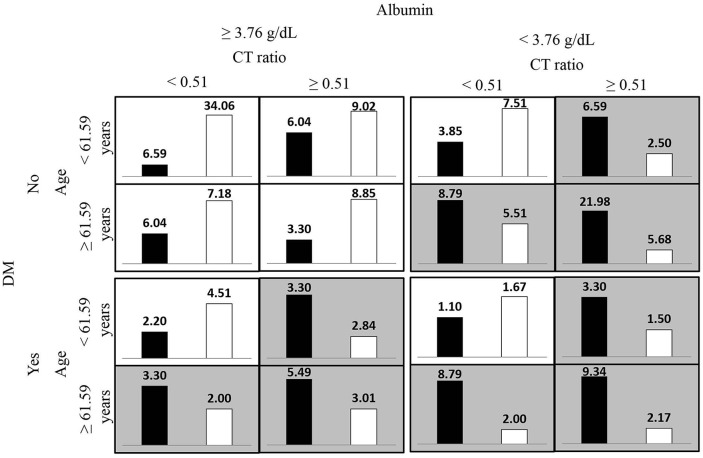
Figures 1 and 2 respectively present the most satisfactory two- and four-order models summarized according to the proportion of clinical risk factor combinations associated with high and low risks for overall mortality in the imbalanced hemodialysis data set. The high-risk pattern for overall mortality depended on the presence of DM and low albumin levels (<3.76 g/dL), old age (⩾61.59 years), and a high CT ratio (⩾0.51).

Figure 1.

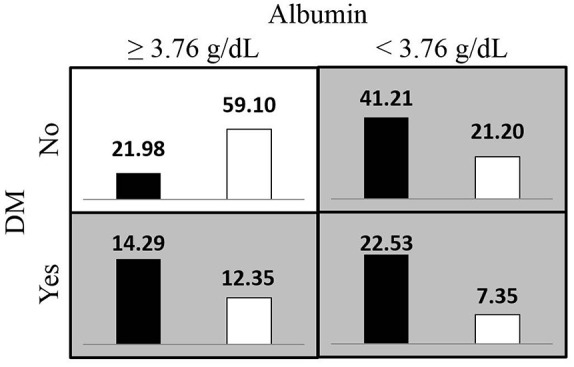
Proportion of the diabetes mellitus (DM) status and albumin level combinations associated with high and low risks for overall mortality in hemodialysis data sets from the MDR-ER two-order interaction model. The white bars indicate survivals proportion and the black bars indicate deaths proportion, the darker shading indicates the high-risk group.

MDR-ER, balancing functions for adjusting the ratio in risk classes and classification errors for imbalanced cases and controls using multifactor-dimensionality reduction.

Figure 2.

Proportion of age, the diabetes mellitus (DM) status, albumin level and cardiothoracic (CT) ratio combinations associated with high and low risks for overall mortality in hemodialysis data sets from the MDR-ER four-order interaction model. The white bars indicate survivals proportion and the black bars indicate deaths proportion, the darker shading indicates the high-risk group.

MDR-ER, balancing functions for adjusting the ratio in risk classes and classification errors for imbalanced cases and controls using multifactor-dimensionality reduction.

Discussion

With the combined use of ROC dichotomous methods, logistic regression, and a novel MDR-based method, our results demonstrated a systematic analysis of both main effects and interactions using an imbalanced data set for overall mortality in maintenance hemodialysis patients. Previous studies have reported that conventional statistical approaches, including logistic regression, are inadequate for detecting higher-order interactions.^20,21 The MDR method is a novel, non-parametric, non-linear method for detecting the complex effect of multifactor associations among risk factors.^22–25 The MDR-based MDR-ER method uses modified functions to overcome its limitations in imbalanced data sets. The interaction of a typical linear model such as generalized linear model or logistic regression was mainly dependent on the linear equation; however, an MDR-based algorithm could determine the high-order interaction using a non-linear model. In addition, the model-free and non-parametric nature of MDR-based approaches also avoids the sample size restriction compared with linear analysis approaches. The backward selection multivariate logistic regression was used to analyze associations among all dichotomous risk factors for overall mortality, and the MDR-ER was used to construct an optimal multiclinical risk factor interaction model for overall mortality in hemodialysis patients based on common clinical risk factors. Conventional regression-based analysis was useful to evaluate the association between overall mortality and clinical factors. On the other hand, the high-order interaction analysis was more complex than the regression-based analysis but was restricted because of sample distribution. The MDR-based algorithm was non-parametric and useful for interpreting multifactor risk interaction at a glance. Similarly, the MDR-ER obtained similar results with conventional logistic regression findings. The present study proposed a different strategy to detect the effects of complex interactions between multiclinical risk factors on overall mortality, and the implications on practice might need additional clinical prospective investigation.

For the backward selection logistic regression results, the mortality risk was associated with DM, old age, low Hgb levels, low albumin levels, low Kt/V urea-Daugirdas score, and a high CT ratio. The clinical risk factors detected in the two- to five-order interaction models for overall mortality were DM, age, albumin, ferritin levels, and CT ratio. According to the proportion of clinical risk factor combinations associated with high and low risks for overall mortality (Figures 1 and 2), both analysis approaches detected highly similar clinical risk factors for the high-risk groups for mortality. In addition, the overlapping clinical factors in the interaction models, DM, age, and albumin levels, and CT ratio, were associated with mortality in CKD, which has been reported by several studies.^26–30

DM and old age increased the mortality risk in hemodialysis patients.^27,31 Albumin levels were highly associated with overall mortality.³¹ Serum albumin level <4.0 g/L was considered a critical contributing factor to the mortality of hemodialysis patients. The CT ratio was computed as the ratio of the heart diameter to the transverse thoracic diameter. A high CT ratio indicated cardiac enlargement, which is associated with adverse outcomes in dialysis patients.³² Several continuous clinical variables, such as age, albumin levels, and CT ratio, were dichotomized according to the highest AUC value in ROC estimation from the cutoff points derived using various statistical inference (Supplemental Table S2). These cut-off points provide a possible tolerable range for the existing clinical indicator standard and may assist in clinical decision making. The impact of interaction between inflammation, malnutrition, and fluid status upon survival among patients who underwent hemodialysis has been demonstrated in prior studies.^33–35 Thence, analyzing interaction between clinical factors is more precise for mortality assessment among patients undergoing hemodialysis.

The retrospective design of this study limited the set of clinicopathological factors; hence, the number of potentially associated factors that can be included in our analysis was limited. Although we could not consider all potential covariates or confounding factors, we have included factors that are most commonly associated with overall mortality in hemodialysis patients. The CT ratio was used as a proxy of cardiovascular function despite the lack of cardiovascular disease history. The application data set restricted the possible association and interaction results in hemodialysis patients, including vascular access category, hemodialyzer category, ultrafiltration amount in hemodialysis session and components of dialysate in hemodialysis session. Furthermore, the time effects of the follow-up interval were not included in this study. Despite the aforementioned limitations, the determined high-order interaction results are beneficial in demonstrating the risk characteristics of overall mortality in hemodialysis patients. This study proposed a different strategy to detect the complex interaction between multiclinical risk factors on overall mortality, and the implication to practice might require additional clinical prospective investigation yet.

Overall, the study results suggested that a combination of the ROC, logistic regression, and MDR-ER methods suitably detects both main effects and interactions for overall mortality using an imbalanced case–control maintenance hemodialysis data set. We found that the albumin level exhibited the main effects on overall mortality in hemodialysis patients. Likewise, the albumin level, DM, age group, and CT ratio may have exhibited high-order interaction effects on overall mortality in hemodialysis patients. The main effect indicated that any effect could serve as a guide for determining the correct multiclinical factor interaction in overall mortality, and the interaction effect indicated that the least proper subset of risk factors interacted suitably. Consistent with the conventional statistical approaches, the higher-order interaction model could indicate the impact of potential risk combination unique to maintenance hemodialysis patients on the survival outcome. Moreover, the MDR-based higher-order interaction model contributed to higher-order interaction effect detection among multiclinical factors by using non-parametric strategies and provided more detailed risk characteristic combination for mortality risk. Therefore, higher-order clinical risk interaction analysis is a reasonable strategy for determining the non-traditional risk factors’ interaction effects unique to patients on maintenance hemodialysis on the survival outcome, such as the effects of inflammation, adipokines, appetite-related gut hormones, and oxidative stress on clinical outcomes.^36–41