A tutorial on frailty models

Abstract

The hazard function plays a central role in survival analysis. In a homogeneous population, the distribution of the time to event, described by the hazard, is the same for each individual. Heterogeneity in the distributions can be accounted for by including covariates in a model for the hazard, for instance a proportional hazards model. In this model, individuals with the same value of the covariates will have the same distribution. It is natural to think that not all covariates that are thought to influence the distribution of the survival outcome are included in the model. This implies that there is unobserved heterogeneity; individuals with the same value of the covariates may have different distributions. One way of accounting for this unobserved heterogeneity is to include random effects in the model. In the context of hazard models for time to event outcomes, such random effects are called frailties, and the resulting models are called frailty models. In this tutorial, we study frailty models for survival outcomes. We illustrate how frailties induce selection of healthier individuals among survivors, and show how shared frailties can be used to model positively dependent survival outcomes in clustered data. The Laplace transform of the frailty distribution plays a central role in relating the hazards, conditional on the frailty, to hazards and survival functions observed in a population. Available software, mainly in R, will be discussed, and the use of frailty models is illustrated in two different applications, one on center effects and the other on recurrent events.

1 Introduction

The central concept in survival analysis is the hazard function. It describes the instantaneous risk of the event of interest for an individual, given that the individual has not experienced the event previously. The hazard function indirectly also describes the distribution of the time to event; there is a one-to-one relation between the probability of being alive over time, the survival function, and the hazard function. Individuals may differ with respect to their survival probabilities, or, equivalently, with respect to their hazards. Females tend to live longer than males, or in terms of hazards, the mortality rate of males is higher than that of females; patients with more severe disease tend to die earlier and have a higher hazard than less severely diseased patients. Such characteristics can be accounted for in survival models by including them in models for the hazards. The most influential of such models is Cox’s proportional hazards model.¹ The proportional hazards assumption specifies that the ratio of the hazards between any two individuals is constant over time, and the shape of the hazard is given by a non-parametric “baseline hazard”. If a model is perfectly specified, so that all possible relevant covariates are accounted for, then the baseline hazard reflects the randomness of the event time, given the value of covariates.

In practice, however, it is rarely possible to account for all relevant covariates. Then the explanatory variables account for observed heterogeneity, and the unaccounted part is termed unobserved heterogeneity. If this is the case, then the estimated hazard for a specific set of covariates does not have an individual interpretation.² Rather, it represents an average hazard function, where the average is taken at each time point over the individuals still alive at that time point. The effects of unobserved heterogeneity on life times are collectively referred to as frailty in demographic research.³ The frailty is an unobserved individual random effect that acts multiplicatively on the hazard. The estimated spread of this random effect (e.g. variance) is an indication of the amount of unobserved heterogeneity. The frailty model quickly gained popularity in econometrics,⁴ demographics⁵ and biostatistics.⁶

Frailty models are useful for two purposes. First, univariate frailty models can be used to explain effects of selection of healthier subjects over time, and also to explain lack of fit, such as deviations from the proportional hazards model. Frailty models can be used in this context to offer alternative explanations for the behavior of the hazard and of hazard ratios over time. These alternative explanations are hypothetical to a large degree, because of identifiability issues, but useful nonetheless. Second, in shared frailty models, frailties can also be used to model dependence of survival times in clustered data or recurrent events. Here the frailty term is shared among individuals in the same cluster, or, in the case of recurrent events, among subsequent events of the same individual.

The aim of this tutorial is to provide an overview of theory and practice in the field of frailty models, while offering insight into the problems that are addressed by such models. We concentrate on the use of frailty models in survival analysis. Frailties have also been used in, for instance, infectious disease modeling,^7,8 but this is outside the scope of the present tutorial. For more detailed information, we recommend the books.^9–11 In section 2 we study the effects of unobserved heterogeneity in survival data, univariate frailty models, and we discuss different frailty distributions. In section 3, we analyze the effect of unobserved heterogeneity in shared frailty models, covering clustered survival data, recurrent events, and an overview of estimation methods. In section 4, we compare available software packages for frailty models and the representation of event history data in the R statistical software. In section 5 we examine different extensions to the frailty models. Finally, in section 6, we illustrate the application of frailty models in two common situations, the modeling of center effects and the analysis of recurrent events.

2 Univariate frailty models

2.1 Heterogeneity in the Cox model

Before we introduce the frailty model and start discussing the effects of unobserved heterogeneity, we illustrate here some of these effects in the more familiar setting of the Cox proportional hazards model.

2.1.1 Heterogeneity over time

The Cox model specifies the hazard of a time to event T as

$$\underset{\Delta t\to 0}{\lim }P(t<T\le t+\Delta t|T>t,\mathbf{x})/\Delta t=\lambda (t|\mathbf{x})={\lambda }_0(t)\exp ({\beta }^{\mathrm{\top }}\mathbf{x})$$ (1)

where β is a $p\times 1$ vector of regression coefficients, x is a $p\times 1$ vector of covariates and ${\lambda }_0(t)$ is an unspecified baseline hazard function. The hazard functions of two individuals with covariate vectors ${\mathbf{x}}^{*}$ and $\tilde{\mathbf{x}}$ are equal only when ${\beta }^{\mathrm{\top }}{\mathbf{x}}^{*}={\beta }^{\mathrm{\top }}\tilde{\mathbf{x}}$. The exponent $\exp ({\beta }_j)$ is the hazard ratio between an individual with x_j = 1 and an individual with x_j = 0 (the other covariates being the same for the two individuals). Time-dependent covariates are easily accommodated in equation (1) and are discussed in section 4. For the time being, we assume that x is time-constant.

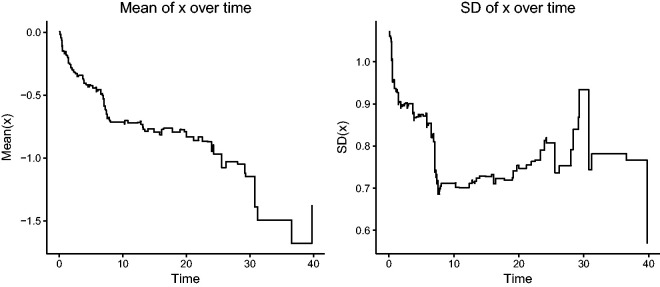
The risk set at time t is composed of individuals that have not yet experienced the event of interest and have not yet been removed for other reasons, such as censoring. The distribution of the covariates among the individuals in the risk set changes over time. We illustrate this by considering model (1) and a single covariate following a standard normal distribution $x\sim N(0,1)$ and $\beta >0$, so that individuals with larger values of x have a higher hazard. At time t = 0, the mean and variance of x are 0 and 1, respectively. Because individuals with higher hazards tend to be the first to die, as time passes, the risk set progressively comprises individuals with lower values of x. For this reason, the average value and the sample variance of x among the individuals at risk decreases over time.

This is illustrated by simulating a single sample of life times of size n = 100, according to equation (1), with a covariate $x\sim N(0,1)$, β = 1, ${\lambda }_0(t)\equiv 0.1$ and uniform censoring on (20, 50). In this simulated sample, at time 0, x had mean 0.007 and standard deviation 1.068. The estimated β was 0.943, with a standard error of 0.127. The mean and standard deviation of x among the individuals in the risk set are shown in Figure 1, as a function of time. The message is that, over time, the population of “survivors” (those still at risk) becomes more homogeneous and of lower risk than the original risk set at time 0.

Figure 1.

Changes in the mean and variance of a covariate x over time among survivors in a proportional hazards model.

2.1.2 Heterogeneity due to missing covariates

The proportional hazards assumption in the Cox model (1) specifies that the ratio $\lambda (t|{\mathbf{x}}^{*})$ divided by $\lambda (t|\tilde{\mathbf{x}})$ equals $\exp ({\beta }^{\mathrm{\top }}({\mathbf{x}}^{*}-\tilde{\mathbf{x}}))$, which does not depend on time. When this assumption is violated, the covariate effect β is time-dependent. The true model is then

$$\lambda (t|\mathbf{x})={\lambda }_0(t)\exp (\beta (t)\mathbf{x}),$$

with $\beta (t)$ not constant.

Assume that the model (1) is correct and $p\ge 2$. Then, if important covariates are omitted from the model, the proportional hazards assumption does not usually hold for the remaining covariates. This is illustrated by simulating a single large data set with sample size n = 10,000. Two independent covariates x₁ and x₂ are considered, both $\sim N(0,1)$, with ${\beta }_1={\beta }_2=1,{\lambda }_0\equiv 1$ and uniform censoring on (20, 50). The following output is shown from Cox models fitted with the standard survival package in R.¹² When both covariates are included into the model, the results are close to the simulation scenario, with both estimated regression coefficients close to 1:

## Call:

## c12 <- coxph(formula = Surv(time, status) ∼ x1 + x2, data = d)

##

## coef exp(coef) se(coef)   z    p

## x1 1.0016 2.7225  0.0138  72.7 <2e-16

## x2 1.0240 2.7843  0.0140  73.2 <2e-16

##

## Likelihood ratio test = 9014 on 2 df, p = 0

## n= 10000, number of events= 8240

No evidence of violation of the proportional hazards assumption is found, when a test based on Schoenfeld residuals is used¹³

## Call: cox.zph(c12, transform = “identity”)

## rho    chisq    p

## x1  0.00101  0.0081  0.928

## x2   -0.00357  0.1050  0.746

## GLOBAL NA     0.1510    0.927

However, when x₂ is omitted, the resulting estimate of the effect of x₁ is visibly smaller than 1:

## Call:

## c1 <- coxph(formula = Surv(time, status) ∼ x1, data = d)

##

## coef exp(coef)     se(coef)   z      p

## x1  0.7028  2.0195  0.0124  56.6   <2e-16

##

## Likelihood ratio test = 3271 on 1 df, p = 0

## n= 10000, number of events= 8240

Moreover, there is clear evidence against the proportional hazards assumption.

## Call: cox.zph(c1, transform = “identity”)

## rho   chisq      p

## x1  -0.0852  55.3  1.06e-13

This is also illustrated by the plot of scaled Schoenfeld residuals of $\beta (t)$ in Figure 2. It appears that the effect of x starts close to the true value 1, and then decreases over time. The result given by the Cox model only with x₁ is an “average” effect in this case. The attenuation of the estimated effect of x₁ when a covariate is omitted has been studied in detail in the literature.^14–16

Figure 2.

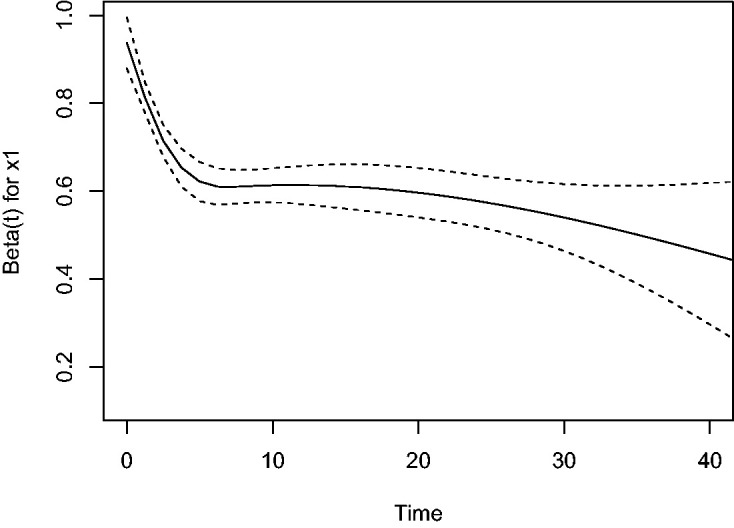
Plot of scaled Schoenfeld residuals-based $\beta (t)$ induced by omitting a covariate from a proportional hazards model.

The explanation for the phenomenon illustrated in the simulated example is that the individual hazard is determined by the combined effect of x₁ and x₂. Since β₁ and β₂ are both positive, the “high risk” individuals (high x₁, high x₂) are the first to experience the event, on average, followed by the “moderate risk” ones (high x₁ and low x₂, or low x₁ and high x₂), and eventually the “low risk” ones (low x₁ and low x₂). This causes the correlation between x₁ and x₂, which is initially around 0, to become negative, as can be seen in Figure 3, where the sample correlation between x₁ and x₂ over time, among the survivors at the time, is shown in the large simulated data set. This phenomenon is also known in epidemiology as the obesity paradox.¹⁷ The result of this negative correlation is that if x₂ is not accounted for, the individuals with high x₁ in the population of survivors artificially appear at lower risk than before, since they are likely to have a low value of x₂, if they are still alive. This induced loss of independence has profound consequences. Suppose that x₁ stands for a treatment in a randomized clinical trial. Since the treatment has been randomized, at randomization x₁ may be expected to be independent of any measured or unmeasured characteristics influencing the time to the event of interest. Putting it differently, the distribution of these characteristics is expected to be the same for the randomized treatment arms at baseline. The above shows that this independence between x₁ and the unmeasured characteristics can no longer be expected to hold at later points in time, ultimately implying that the hazard ratio is unsuited as a causal effect measure for survival data in the presence of unobserved heterogeneity.^18,19

Figure 3.

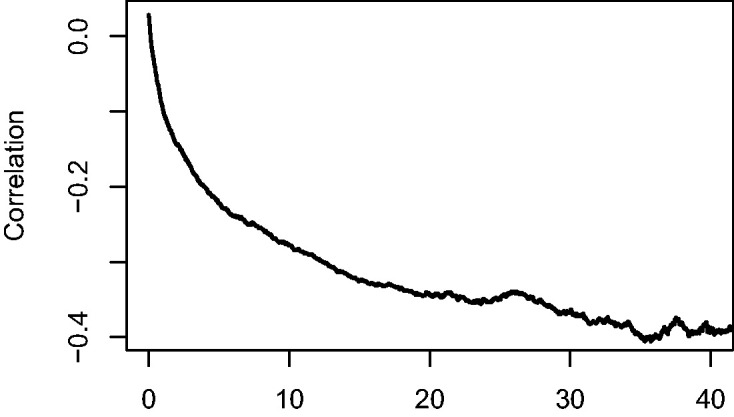
Correlation between x₁ and x₂ among survivors over time.

2.1.3 Conditional and marginal hazards

More generally, suppose that the proportional hazards model (1) holds for a covariate vector $\mathbf{x}=({\mathbf{x}}_{\text{incl}},{\mathbf{x}}_{\text{omit}})$ with covariate effects $\beta =({\beta }_{\text{incl}},{\beta }_{\text{omit}})$, so that the true model is

$$\lambda (t|\mathbf{x})={\lambda }_0(t)\exp ({\beta }_{\text{incl}}^{\mathrm{\top }}{\mathbf{x}}_{\text{incl}}+{\beta }_{\text{omit}}^{\mathrm{\top }}{\mathbf{x}}_{\text{omit}})$$ (2)

Imagine that a Cox model is fitted only including ${\mathbf{x}}_{\text{incl}}$. If we are aiming for ${\beta }_{\text{incl}}$, then this will result in an estimated effect that is attenuated towards 0 and, usually, a violation of the proportional hazards assumption. Thus, the proportional hazards model lacks an internal consistency, in the sense that, if equation (2) is the true proportional hazards model, then the model with only ${\mathbf{x}}_{\text{incl}}$ does not obey a proportional hazards structure.²⁰ In reality, it is possible that some relevant covariates are not measured (here represented by ${\mathbf{x}}_{\text{omit}}$). In this case, these omitted covariates are said to induce unobserved heterogeneity. The differences between individuals that are explained by ${\mathbf{x}}_{\text{incl}}$ are referred to as observed heterogeneity.

The $\lambda (t|\mathbf{x})$, as defined in model (2), is referred to as the conditional hazard, with ${\beta }_{\text{incl}}$ summarizing the conditional effect of ${\mathbf{x}}_{\text{incl}}$. When unobserved heterogeneity is present, the resulting $\lambda (t|{\mathbf{x}}_{\text{incl}})$ is referred to as the marginal hazard (although it is only marginal with respect to ${\mathbf{x}}_{\text{omit}}$ but still conditional on ${\mathbf{x}}_{\text{incl}}$). The estimated effect from the marginal model does not have an individual interpretation. Namely, $\lambda (t|{\mathbf{x}}_{\text{incl}})$ represents a weighted average of the individual hazards corresponding to those individuals in the risk set at time t, where the weighting is determined by the distribution of ${\mathbf{x}}_{\text{omit}}$ in this risk set.

Since the effect of ${\mathbf{x}}_{\text{omit}}$ cannot be directly observed, one can define the random variable $Z=\exp ({\beta }_{\text{omit}}^{\mathrm{\top }}{\mathbf{x}}_{\text{omit}})$, and write equation (2) as $\lambda (t|\mathbf{x})=Z{\lambda }_0(t)\exp ({\beta }_{\text{incl}}^{\mathrm{\top }}{\mathbf{x}}_{\text{incl}})$. Z is referred to as a “frailty” term that acts multiplicatively on the hazard.

2.2 The frailty model

A frailty model is a model for the hazards in which this unobserved heterogeneity is explicitly included as a multiplicative random effect, the frailty. In the univariate frailty model, the hazard of an individual with frailty Z is specified as

$$\lambda (t|Z)=Z\lambda (t)$$ (3)

The frailty Z is a latent random term, assumed to have a certain non-negative distribution. Individuals with a higher frailty can be thought of as being more frail, and therefore expected to die sooner than other individuals with the same measured covariates. If the event of interest is a positive outcome, like pregnancy or recovery, subjects with a higher “frailty” are expected to experience the positive outcome sooner than others with the same covariates. For identifiability, Z is assumed to be scaled so that $\text{E}Z=1$. The term $\lambda (t)\equiv \lambda (t|Z=1)$ in equation (3) is the conditional hazard for an individual with Z = 1. We refer to $\lambda (t)$ simply as the conditional hazard. This conditional hazard may include covariates, but for simplicity this is not expressed in the notation. The conditional cumulative hazard is defined as $\Lambda (t)={\int }_0^t\lambda (s)ds$. The conditional survival function for an individual with frailty Z is then given by

$$S(t|Z)=\exp (-Z\Lambda (t))$$ (4)

The survival function $S(t|Z=1)=\exp (-\Lambda (t))$ corresponds to the survival of an individual with average frailty value 1. The survival of the heterogenous population, consisting of individuals with different frailty values, is called the marginal survival curve associated with $\Lambda (t)$, and is obtained by taking the expectation of $S(t|Z)$ with respect to Z

$$\overline{S}(t)=\text{E}[\exp (-Z\Lambda (t))]$$ (5)

Unlike S(t), $\overline{S}(t)$ has a population averaged interpretation. If there are no covariates, $\overline{S}(t)$ may be seen as a weighted average of individual survival curves, where the weighing depends on the distribution of Z. The marginal hazard may be derived from the survival function as $\lambda (t)=d/\text{d}t[-\log S(t)]$. Therefore, the marginal hazard may be calculated as

$$\overline{\lambda }(t)=\frac{\text{E}\left[Z\exp (-Z\Lambda (t))\right]}{\text{E}\left[\exp (-Z\Lambda (t)\right]}\lambda (t)=\text{E}[Z|T\ge t]\lambda (t)$$ (6)

A population averaged interpretation may also be given here: $\overline{\lambda }(t)$ may be seen as a weighted average of individual hazards of individuals alive at time t, where the weighting depends on the distribution of Z among the individuals alive at time t.

The conditional and marginal hazards are equal only if $\text{E}[Z|T\ge t]=1$ for all t, in other words if all frailties Z are equal to 1. Otherwise, the frailty distribution among the survivors at time t behaves in a similar fashion as the distribution of an observed covariate among survivors, as shown in section 2.1.1.

If observed covariates are also present, then it is usually assumed that the proportional hazards assumption holds conditional on the frailty, with

$$\lambda (t|Z)=Z{\lambda }_0(t)\exp ({\beta }^{\mathrm{\top }}\mathbf{x})$$ (7)

Then, the population averaged interpretations of $\overline{S}(t)$ and $\overline{\lambda }(t)$ hold conditional on x. In other words, for a hypothetical population of individuals with given covariate values x. This is the same as the interpretation that is given to the marginal hazard in section 2.1.2.

Regardless of whether the differences between individuals come from observed covariates x or from the frailty, individuals with higher hazards die earlier. Therefore, the population of survivors is more homogeneous and at a lower risk for events than the general population at time 0. Before we further study the relation between marginal and conditional hazards in section 2.4, we first discuss different frailty distributions.

2.3 Frailty distributions

2.3.1 The Laplace transform

The Laplace transform turns out to be a very useful concept in describing relations between the conditional hazards and the marginal hazards and survival functions. The distribution of a non-negative random variable Z can be uniquely specified by its Laplace transform

$$\mathcal{L}(c)=\text{E}\left[\exp (-cZ)\right]$$

It is immediate that $\mathcal{L}(0)=1$. The expectation of Z may be obtained as minus the derivative of $\mathcal{L}$ evaluated at 0, $\text{E}Z=-\mathcal{L}\prime (0)$. Furthermore, $\mathcal{L}″(0)=\text{E}{Z}^2$, and, denoting ${\mathcal{L}}^{(k)}$ as the k-th derivative of the Laplace transform, in general we have ${\mathcal{L}}^{(k)}(0)={(-1)}^k\text{E}{Z}^k$. The squared coefficient of variation, defined as ${\text{CV}}^2[Z]=\text{var}[Z]/{(\text{E}[Z])}^2$, may be expressed as

$${\text{CV}}^2[Z]=\frac{\mathcal{L}″(0)}{{(\mathcal{L}\prime (0))}^2}-1$$

Let us return to the frailty model of the previous section, where we wrote the hazard as $\lambda (t|Z)=Z\lambda (t)$, with $\lambda (t)$ the conditional hazard, and $S(t|Z)=\exp (-Z\Lambda (t))$ the conditional survival function. In terms of the Laplace transform, the marginal survival function from equation (5) may be written as

$$\overline{S}(t)=\mathcal{L}(\Lambda (t))$$

and the marginal hazard as

$$\overline{\lambda }(t)=\frac{d}{\text{d}t}[-\log S(t)]=-\frac{\mathcal{L}\prime (\Lambda (t))}{\mathcal{L}(\Lambda (t))}\lambda (t)$$

The Laplace transform of the frailty distribution of survivors can be easily expressed in terms of the Laplace transform of Z. First, denote the density of Z as f(z) and the density of $Z|T\ge t$ as $f_{Z|T\ge t}(z)$. From Bayes’ theorem and the definition of the conditional survival function (4), it follows that

$$\begin{array}{l}{f}_{Z|T\ge t}(z)=\frac{P(T\ge t|Z=z)f(z)}{{\int }_{z}P(T\ge t|Z=z)f(z)\text{d}z}\hfill \\ \hspace{0.17em}=\frac{S(t|Z=zf(z))}{\int S(t|Z=z)f(z)\text{d}z}\hfill \\ \hspace{0.17em}=\frac{\exp (-z\Lambda (t))f(z)}{\int \exp (-z\Lambda (t))f(z)\text{d}z}\hfill \end{array}$$

The Laplace transform of $Z|T\ge t$ can then be written as

$$\begin{array}{l}{\mathcal{L}}_{Z|T\ge t}(c)=\text{E}\left[\exp (-Zc)|T\ge t\right]\hfill \\ \hspace{0.17em}={\displaystyle \int \exp }(-zc)f_{Z|T\ge t}(z)\text{d}z\hfill \\ \hspace{0.17em}=\frac{\int \exp (-zc)\exp (-z\Lambda (t))f(z)\text{d}z}{\int \exp (-z\Lambda (t))f(z)\text{d}z}\hfill \\ \hspace{0.17em}=\frac{\text{E}[\exp (-Z(c+\Lambda (t)))]}{\text{E}[\exp (-Z\Lambda (t))]}\hfill \\ \hspace{0.17em}=\frac{\mathcal{L}(c+\Lambda (t))}{\mathcal{L}(\Lambda (t))}\hfill \end{array}$$ (8)

The expectation, variance and squared coefficient of variation of $Z|T\ge t$ follow as

$$\begin{array}{l}\hspace{0.17em}\text{E}[Z|T\ge t]=-\frac{{\mathcal{L}}^{\prime }(\Lambda (t))}{\mathcal{L}(\Lambda (t))},\hfill \\ \hspace{0.17em}\text{var}[Z|T\ge t]=\frac{{\mathcal{L}}^{″}(\Lambda (t))}{\mathcal{L}(\Lambda (t))}-{\left(\frac{{\mathcal{L}}^{\prime }(\Lambda (t))}{\mathcal{L}(\Lambda (t))}\right)}^2,\hfill \\ \hspace{0.17em}{\text{CV}}^2[Z|T\ge t]=\frac{{\mathcal{L}}^{″}(\Lambda (t))\mathcal{L}(\Lambda (t))}{{({\mathcal{L}}^{\prime }(\Lambda (t)))}^2}-1\hfill \end{array}$$

2.3.2 Infinitely divisible distributions

A rich family of frailty distributions with tractable Laplace transform are formed by the infinitely divisible distributions with Laplace transform specified as $\mathcal{L}(c)=\exp (-\alpha \psi (c;\gamma ))$ with $\alpha >0$ and $\gamma >0$. They are called infinitely divisible because their distributions can be expressed as the probability distribution of a sum of an arbitrary number of independent and identically distributed random variables from that same family. For $\mathcal{L}(c)$ to be a proper Laplace transform, we require $\psi (0;\gamma )=0$. The expectation, variance and coefficient of variation of Z, conditional on survival until time t, can be expressed in terms of derivatives of ψ as

$$\begin{array}{l}\hspace{0.17em}\text{E}[Z|T\ge t]=\alpha {\psi }^{\prime }(\Lambda (t);\gamma ),\hfill \\ \hspace{0.17em}\text{var}[Z|T\ge t]=-\alpha {\psi }^{″}(\Lambda (t);\gamma ),\hfill \\ \hspace{0.17em}{\text{CV}}^2[Z|T\ge t]=-\frac{{\psi }^{″}(\Lambda (t);\gamma )}{\alpha {({\psi }^{\prime }(\Lambda (t;\gamma )))}^2}\hfill \end{array}$$ (9)

The unconditional expectation, variance and coefficient of variation of Z follow by replacing $\Lambda (t)$ by 0.

The gamma distribution is a prominent member of the infinitely divisible family. The density of the gamma distribution with parameters $\theta >0$ and $\eta >0$ is given by $f(t;\theta ,\eta )=\frac{{\theta }^{\eta }}{\Gamma (\eta )}{t}^{\eta -1}{e}^{-\theta t}$, where $\Gamma (\eta )={\int }_0^{\infty }{s}^{\eta -1}{e}^{-s}ds$ is the gamma function. Its Laplace transform is given by

$$\mathcal{L}(c)={\left(\frac{\theta }{\theta +c}\right)}^{\eta }$$

which, in terms of equation (9), can be expressed as $\alpha =\eta ,\gamma =\theta$, and $\psi (c;\gamma )=\log (\gamma +c)-\log (\gamma )$. By convention, the expectation of the frailty is fixed to 1, so the restriction $\theta =\eta$ is applied. In this parametrization, Z follows a $\text{gamma}(\theta ,\theta )$ distribution, with $\text{E}[Z]=1$ and $\text{var}[Z]={\theta }^{-1}=\xi$. The expectation and variance of the frailty distribution of the survivors is given through equation (9), resulting in

$$\begin{array}{cc}\hspace{0.17em}& \text{E}\left[Z|T\ge t\right]=\frac{\theta }{\theta +\Lambda (t)},\\ \hspace{0.17em}& \text{var}\left[Z|T\ge t\right]=\frac{\theta }{{(\theta +\Lambda (t))}^2}\end{array}$$

Both functions reach their maximum over $t\ge 0$ at t = 0, with expectation 1 and variance ${\theta }^{-1}$, and decrease over time. For the gamma frailty, it is immediate that $\overline{\lambda }(t)\le \lambda (t)$. In words, the marginal hazard is always smaller than the hazard of an individual with frailty 1.

A more general family of infinitely divisible distributions is the power-variance-function (PVF) family, with the Laplace transform $\mathcal{L}$ described by

$$\mathcal{L}(c;\alpha ,\gamma ,m)=\exp \left(-\alpha \text{sign}(m)\left\{1-{\left(\frac{\gamma }{\gamma +c}\right)}^m\right\}\right)$$

where $\text{sign}(m)$ is the sign of m, $\alpha >0,m>-1$ and $m\ne 0$. It was proposed in a series of papers^21–23 and is studied in detail in Hougaard.⁹ To obtain $\text{E}[Z]=1$ and $\text{var}[Z]={\theta }^{-1}$, one can set $\alpha =\theta (m+1)/\left|m\right|$ and $\gamma =\theta (m+1)$. Particular cases of the distributions in the PVF family include:

• The gamma frailty, obtained as a limiting case when $\alpha \to \infty$ and $m\to 0$ in such a way that $\alpha m\to \eta$;

• The inverse Gaussian distribution, when $m=-1/2$;

• The so-called Hougaard distributions, when m < 0;

• The compound Poisson distribution, when m > 0, which has probability mass $\exp (-\alpha )$ at 0. This is consistent with a scenario where a part of the population is not susceptible for the event of interest;

• The positive stable distribution, obtained as a limiting case when $-1<m<0,\gamma \to 0$, and $\alpha \to \infty$ in such a way that ${\gamma }^m\alpha \to \tilde{\alpha }$, for some positive constant $\tilde{\alpha }$. The resulting Laplace transform takes the simple form $\mathcal{L}(c)=\exp (-\tilde{\alpha }{c}^{\tilde{\gamma }})$, with $\tilde{\gamma }=-m\in (0,1)$. This distribution cannot be scaled to have $\text{E}[Z]=1$, so usually the restriction $\tilde{\alpha }=1$ is imposed. Its expectation is infinite and the variance is not defined (but they are finite for the conditional distribution $Z|T\ge t$, if $\Lambda (t)>0$).

2.3.3 Other frailty distributions

The log-normal distribution has often been used for frailty models, although it is not part of the PVF family. The normal distribution is infinitely divisible, but the log-normal distribution is not, and its Laplace transform and expressions for the distribution of survivors are not easily obtained in closed form. Its popularity stems from the normal random effects in linear models. The log-normal frailty is usually standardized with $\text{E}[\log Z]=0$ and $\text{var}[\log Z]={\sigma }^2$, corresponding to a normally distributed random effect on the scale of the covariates. If matched by mean and variance, it is virtually indistinguishable from the inverse Gaussian distribution. Other families of distributions, such as the Addams and Kummer families of distributions were also introduced in the context of frailty models.^24,25

2.4 Frailty effects

The different frailty distributions discussed in section 2.3 represent different ways of expressing unobserved heterogeneity. Different frailty distributions lead to different selection effects, such as the one illustrated in section 2.1.1. Moreover, they impact the marginal effect of the observed covariates in different ways, generalizing the phenomenon illustrated in section 2.1.2. An advantage of the PVF family of distributions and their closed form Laplace transforms is that it facilitates the study of these phenomenons.^5,6,26 An overview may be found in Aalen et al.,²⁴ Chapter 6.

2.4.1 The selection effect

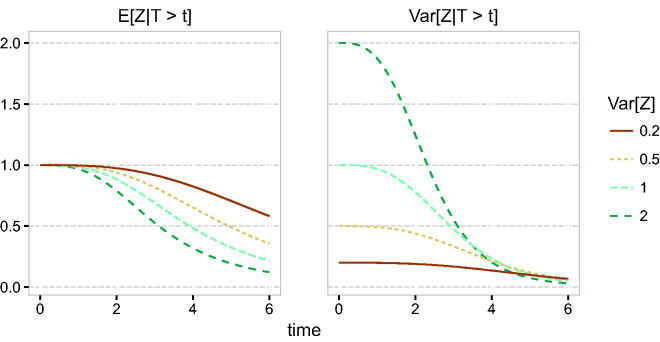
In section 2.3, it was shown that, for the gamma frailty model, the expectation and variance of the frailty distribution of the survivors decrease over time, in a similar way as illustrated in section 2.1.1. In Figure 4, we show the expectation and the variance of $\text{E}[Z|T\ge t]$, when the conditional hazard is given by $\lambda (t)=t^2/20$, for frailty variances 0.2, 0.5, 1 and 2. It follows that the marginal hazard appears as a “dragged down” version of the conditional hazard, similar to Figure 1. This selection effect is stronger if the frailty variance is larger. In particular, depending on the variance of the frailty, the marginal hazard may appear to grow, reach a peak and then decrease beyond a time point, even if the conditional hazard is increasing. As in section 2.1.1, the explanation is that individuals with a higher hazard die earlier, on average, than individuals with a lower hazard. In particular, this is true for all frailty distributions discussed in section 2.3. For example, for the compound Poisson distribution, when individuals with frailty 0 never experience the event of interest, the marginal hazard will eventually decrease towards 0 after some time.

Figure 4.

Frailty distribution of survivors, gamma frailty, $\lambda (t)=t^2/20$.

2.4.2 The marginal hazard ratio

In section 2.1.2, we illustrated that, when important covariates are omitted from a Cox model, the marginal effect of the remaining covariates is time-dependent. The same phenomenon happens with the marginal covariate effect in the case of frailty models. Suppose that only one observed covariate is present, $x\in \left\{0,1\right\}$, and that the frailty model (7) is true. Then, $e^{\beta }$ is the hazard ratio between two individuals with the same frailty, one with x = 1, the other with x = 0. The marginal hazards for the two subgroups defined by x are given by

$$\begin{array}{l}{\overline{\lambda }}_0(t)=\text{E}[Z|T\ge t,x=0]{\lambda }_0(t),\\ {\overline{\lambda }}_1(t)=\text{E}[Z|T\ge t,x=1]e^{\beta }{\lambda }_0(t)\end{array}$$

The marginal effect of x can be quantified by the ratio of these two marginal hazards. This results in

$$e^{\overline{\beta }(t)}=\frac{{\overline{\lambda }}_1(t)}{{\overline{\lambda }}_0(t)}=\frac{\text{E}[Z|T\ge t,x=1]}{\text{E}[Z|T\ge t,x=0]}{e}^{\beta }$$

It follows that the original hazard ratio $e^{\beta }$ is distorted over time by differential selection effects over time in the two subgroups, caused by the frailty. As a result, $\overline{\beta }(t)$ will generally not be constant over time. If Z is a gamma frailty with variance ${\theta }^{-1}$, for example, this is

$$e^{\overline{\beta }(t)}=\frac{\theta +{\Lambda }_0(t)}{\theta +e^{\beta }{\Lambda }_0(t)}{e}^{\beta }$$

If $\beta <0,\overline{\beta }(t)$ is an increasing function with a minimum of β and an asymptotic maximum of 0, if ${\Lambda }_0(t)\to \infty$. Conversely, if $\beta >0$, then $\overline{\beta }(t)$ is a decreasing function with a maximum of β and asymptotic minimum of 0. The conclusion is that, at the population level, the covariate effect appears to vanish over time. Therefore, the gamma frailty shows a similar behavior with the unobserved covariates scenario to that in the simulation in section 2.1.2.

Similar considerations apply for other frailty distributions. For example, for the inverse Gaussian distribution, the marginal hazard ratio is

$$e^{\overline{\beta }(t)}={\left(\frac{\theta +2{\Lambda }_0(t)}{\theta +2{\Lambda }_0(t)e^{\beta }}\right)}^{1/2}{e}^{\beta }$$

In this case, we see that $\overline{\beta }(t)\to \beta /2$ if ${\Lambda }_0(t)\to \infty$, as $t\to \infty$. A peculiar case is that of the positive stable distribution, for which

$$e^{\overline{\beta }(t)}=e^{\gamma \beta }$$

which does not depend on time, so we have $\overline{\beta }(t)\equiv \overline{\beta }=\gamma \beta$. Since $0<\gamma <1,\overline{\beta }$ is an “attenuated” version of β.

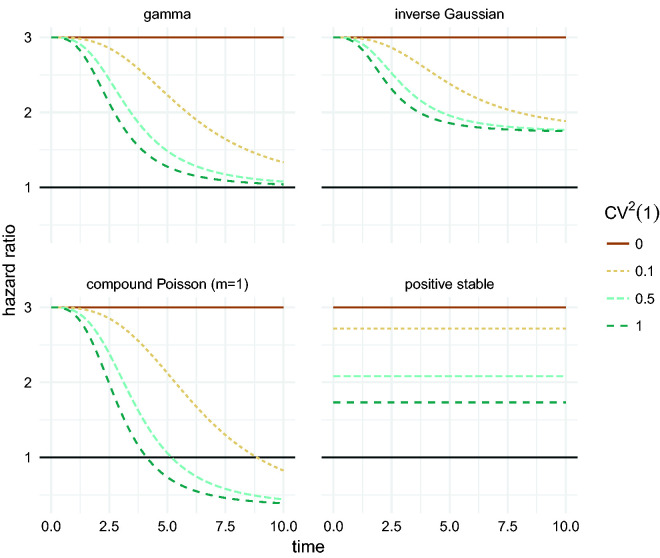
The effect of different frailty distributions on the hazard ratio is illustrated in Figure 5. For the gamma frailty distribution, the marginal hazard ratio approaches 1 with time, while for the inverse Gaussian it approaches $\exp (\beta /2)$. For the positive stable distribution, the attenuated marginal effect is observed. For the compound Poisson distribution, a “crossover” is present, where the marginal hazard ratio actually crosses 1. This is the effect of having non-susceptible individuals, represented by the mass at 0 of the distribution. As a result, in the risk set at sufficiently large time points, the proportion of non-susceptible individuals is higher in the high risk group than in the low risk group.

Figure 5.

Marginal hazard ratio between two groups of individuals: a low risk one with ${\lambda }_0(t)=t^2/20$, and a high risk one with ${\lambda }_1(t)=3{\lambda }_0(t)$. For comparability, the distributions are matched by the squared coefficient of variation of the distribution of survivors at time t = 1, with $C{V}^2(1)=\text{var}[Z|T\ge 1]/\text{E}{[Z|T\ge 1]}^2$.

2.5 Identifiability

In the frailty model, the marginal hazard equals $\overline{\lambda }(t)=\lambda (t)\text{E}[Z|T>t]$. If there are no covariates, then only $\overline{\lambda }(t)$ is observed. Without strong parametric assumptions on $\lambda (t)$, it is impossible to decide whether frailty is present or not. In other words, the frailty model is not identifiable in this case. The presence of covariates, together with the assumption of proportional hazards conditional on the frailty, makes the frailty model identifiable, as long as the frailty distribution has finite expectation. This is due to the marginal non-proportional effect of the observed covariates, as exemplified in Figure 5. This identifiability result has been studied in Elbers and Ridder.²⁷

Without further assumptions, observing a time-dependent covariate effect of the type shown in Figure 5 is equally compatible with (at least) two explanations. One is that the proportional hazards assumption holds in the conditional model, and this effect appears distorted at the marginal level as a result of unobserved heterogeneity. The second is that there is no unobserved heterogeneity, and the observed covariate has a time-dependent effect. In the first case, the frailty model is the natural choice. The frailty then explains heterogeneity due to unobserved covariates or other sources of natural variation. Even with an exhaustive set of covariates, the remaining natural between-subject variation can be explained by the frailty. In the second case, the modeling strategy would include a stratified analysis or an extended Cox model with interactions of covariates with time [Therneau and Grambsch,¹² Chapter 6.5]. Further explanations of violation of the proportional hazards assumption are discussed in Van Houwelingen and Putter,²⁸ Chapter 5.

In this context, the result of Elbers and Ridder,²⁷ while theoretically interesting, is of little practical use. Only a firm – and probably naïve – belief in the conditional proportional hazards assumption can substantiate a claim towards the presence of frailty. In principle, this situation changes in the case of clustered survival data, because positive correlation between the event times is induced by the frailty. This is discussed in section 3. The more information on the correlation structure, the easier it is to distinguish the presence of frailty from non-proportional hazards. However, when the cluster sizes are small, identifying the appropriate model remains a difficult problem because presence of frailty and violations of proportional hazards are confounded.²⁹

The positive stable distribution does not have finite expectation, and therefore it does not fall under the result of Elbers and Ridder.²⁷ As shown in Figure 5, it preserves the proportional hazards assumption at the marginal level. It is not identifiable with univariate survival data, even with covariates in a proportional hazards model. In some sense, this may be seen as an advantage, since it illustrates that the identifiability of univariate frailty models is based on a strong assumption about the mechanism that generated the data. The positive stable distribution does prove useful in the context of clustered failures or recurrent events in section 3.

Since the presence of frailty in a conditional proportional hazards model with univariate frailties is only identifiable through the distortion of the proportional hazards assumption in the marginal model, it follows that the frailty distribution is extremely hard to determine from such univariate data. Basically, it can be identified, assuming proportional hazards for the conditional model, only through the way in which the non-constant $\beta (t)$ behaves in the marginal model. As a result, quite different estimates of the conditional regression coefficients can result when (univariate) frailty models with different frailty distributions are fitted on the same data. This is illustrated in Keiding et al.,³⁰ where the authors argue for the use of the accelerated failure time model in this context.

3 Shared frailty models

In the previous section we used the familiar setting of the Cox model to illustrate some of the “odd effects of frailty”.²⁴ Also here, before introducing shared frailty models in clustered and recurrent events data, we will illustrate, again in the Cox model setting with shared covariates, some of the issues that turn out to play a role in shared frailty models.

3.1 Missing covariates in paired data

Consider the situation of paired event times, where covariate values are shared between individuals from the same pair. Assume that individuals from a given pair have the same distribution of the event time, denoted as T, with the hazard function $\lambda (t|x)={\lambda }_0(t)\exp (\beta x)$. Conditional on x, all the life times are assumed to be independent. Further, assume that x is a realization of a random variable X with density $f_X(x)$. We denote $f(t|x)$ and $S(t|x)$ as the density and survival function of T, given X = x. The marginal survival function of T (where the covariate x is integrated out) is given by $\overline{S}(t)=\int S(t|x)f_X(x)\text{d}x$.

Consider one pair, with event times T₁ and T₂. The marginal survival function of either T₁ or T₂ is given by $\overline{S}$. If T₁ = t₁ is observed, the shared covariate will cause the conditional survival function of T₂ to change. Heuristically, if a large life time t₁ is observed, then it is likely that the pair has a low hazard, which in turn makes it more likely that the value of x in that pair is low if $\beta >0$ (or high if $\beta <0$). Since x is shared by both individuals, a low hazard for T₁ means that the hazard for T₂ is also low, and that in turn makes it more likely that the corresponding life time t₂ is large as well.

All this leads to a positive marginal correlation of the two life times. More specifically, it is straightforward to show that the marginal survival function of T₂, given T₁ = t₁, is given by

$$S(t_2|T_1=t_1)={\displaystyle \int f}(x|t_1)S(t_2|x)\text{d}x$$

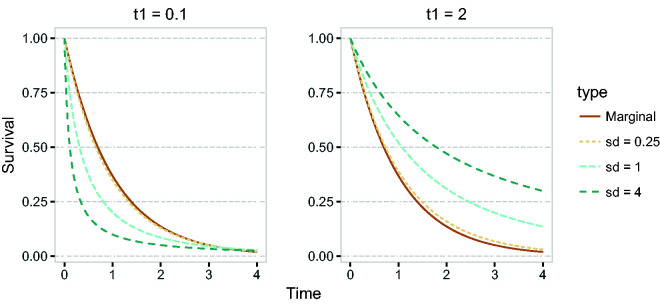
with $f(x|t_1)=f(t_1|x)f_X(x)/(\int f(t_1|x)f_X(x)\text{d}x)$, the conditional density of X, given T₁ = t₁. Figure 6 shows $S(t_2|T_1=t_1)$ for $t_1=0.1$ and $t_1=2$, for the case where the conditional distribution of T₁ and T₂, given x = 0, is exponential with mean 1, and β  =  1, and X has a normal distribution with mean 0 and standard deviation σ, for different values of σ.

Figure 6.

Conditional survival function of T₂, given $t_1=0.1$ and given $t_1=2$; the conditional distribution of T₁ and T₂ given X = x is exponential with rate $\lambda e^{\beta x}$, λ = 1 and β = 1, and X has a normal distribution with mean 0 and standard deviation ${\sigma }^2$, with different values of σ.

It can be seen that for $t_1=2$, the conditional survival curves are higher than the marginal survival curve, while for $t_1=0.1$ this is the other way around. For higher standard deviation of the distribution of X, the conditional survival curves are more distinct from the marginal survival function. That means that for higher standard deviation of X, the influence of knowing the value of T₁ is higher, and the correlation between T₁ and T₂ is higher. In fact, one can derive an explicit expression of the correlation between T₁ and T₂, when the baseline distribution of T₁ is exponential with rate λ. It is given by

$$\text{cor}(T_1,T_2)=\frac{e^{2{\beta }^2{\sigma }^2}-e^{{\beta }^2{\sigma }^2}}{2e^{2{\beta }^2{\sigma }^2}-e^{{\beta }^2{\sigma }^2}}$$

A plot of the correlation as a function of ${\sigma }^2$, for β = 1, is shown in Figure 7. The form of this correlation depends on several factors, such as the baseline distribution, the distribution of X and the effect of X on T₁ and T₂. However, the phenomenon may be observed by simulation in general scenarios: larger unexplained between-subject variation leads to larger marginal correlation between the two event times.

Figure 7.

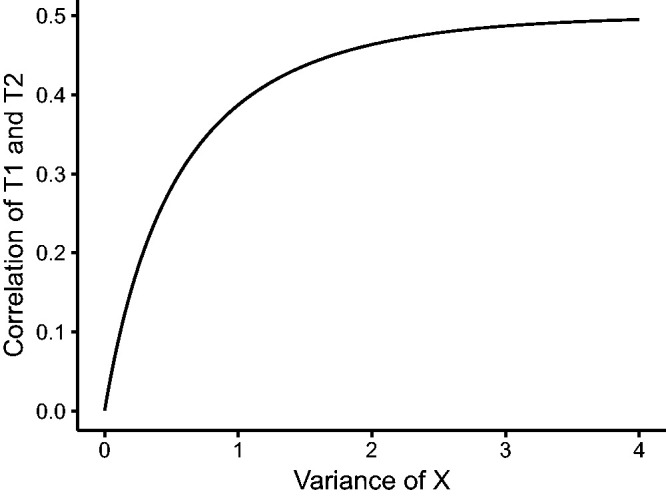
Correlation between T₁ and T₂ as a function of ${\sigma }^2$; the conditional distribution of T₁ and T₂ given X = x is exponential with rate $\lambda e^{\beta x}$ and β = 1, and X has a normal distribution with mean 0 and variance ${\sigma }^2$.

If the correlation of life times cannot be explained by observed covariates (for example, because x is omitted), then there are two practical approaches. One is marginal modeling, which is in the spirit of general estimating equation (GEE) models. For the Cox model, this involves adjusting the standard errors of the observed covariates.³¹ The second is to model the conditional hazard by introducing a “shared” frailty Z, that would take the place of $\exp (\beta x)$ in the previous example. The resulting “shared” frailty model is discussed in section 3.1. The advantage of this approach is that differences between clusters can be quantified, and that the covariate effects have an individual interpretation, as in the case of univariate frailty models.

3.2 Clustered failures

3.2.1 The shared frailty model

Assume that there are N clusters and n_i individuals are part of cluster i. The hazard of the jth individual from cluster i is specified as

$${\lambda }_{ij}(t|Z_i)=Z_i\exp ({\beta }^{\mathrm{\top }}{\mathbf{x}}_{ij}){\lambda }_0(t)$$ (10)

The individuals in cluster i share the frailty Z_i, and conditional on Z_i their lifetimes are assumed to be independent. While in the univariate case individuals are thought to be a random sample from a larger population of individuals, in the clustered failures case the clusters are thought to be an independent random sample from a population of clusters, and the individuals within a cluster are considered to be an independent random sample from a distribution specific to the cluster and further modified by covariates.

In the univariate case, the marginal survival function was derived, and also the marginal hazard. In the clustered failure case, we can derive the marginal joint survival function of a pair of individuals (or more), and it is useful to derive the posterior distribution of the frailty, given all information about the cluster, including observed events and censorings. This is studied in the next section.

3.2.2 Frailty distributions and clustered failures

Consider two individuals j = 1, 2 in the same cluster, with conditional hazards λ₁ and λ₂. The conditional cumulative hazards for these individuals are given by ${\Lambda }_j(t)={\int }_0^t{\lambda }_j(s)\text{d}s)$. Conditional on Z, the joint survival function of (T₁, T₂) is defined as

$$S(t_1,t_2|Z)=P(T_1>t_1,T_2>t_2|Z)=\exp (-Z({\Lambda }_1(t_1)+{\Lambda }_2(t_2)))$$

The last equation follows from the assumed conditional independence of T₁ and T₂, given the frailty. The marginal joint survival probability is obtained by taking the expectation with respect to Z, which results in

$$S(t_1,t_2)=\mathcal{L}({\Lambda }_1(t_1)+{\Lambda }_2(t_2))$$ (11)

There is a close connection with copulas, see for instance.¹⁰ The Laplace transform of Z, given that individual 1 and 2 are alive at t₁ and t₂, is obtained, with the same arguments as in equation (8), as

$${\mathcal{L}}_{Z|T_1>t_1,T_2>t_2}(c)=\frac{\mathcal{L}(c+{\Lambda }_1(t_1)+{\Lambda }_2(t_2))}{\mathcal{L}({\Lambda }_1(t_1)+{\Lambda }_2(t_2))}$$

The only difference from the univariate case is that $\Lambda (t)$ is now replaced by ${\Lambda }_1(t_1)+{\Lambda }_2(t_2)$.

Assume now that the event time T₁ of the first subject is observed at t₁, and subject 2 is still seen to be alive at t₂. Recall that the density of T_j is given by ${\lambda }_j(t)\exp (-{\Lambda }_j(t))$. We obtain

$$\begin{array}{l}\underset{\Delta t\downarrow 0}{\lim }\frac{\mathrm{P}(t_1\le T_1<t_1+\Delta t,T_2>t_2|Z)}{\Delta t}=Z{\lambda }_1(t_1)\exp (-Z({\Lambda }_1(t_1)+{\Lambda }_2(t_2)))\hfill \\ \hspace{0.17em}=-\frac{\partial }{\partial t_1}S(t_1,t_2|Z)\hfill \end{array}$$

The Laplace transform of Z, given $T_1=t_1,T_2>t_2$, defined as

$${\mathcal{L}}_{Z|T_1=t_1,T_2>t_2}(c)=\text{E}[\exp (-cZ)|T_1=t_1,T_2>t_2]$$

can be calculated from Bayes’ theorem

$$\begin{array}{l}{\mathcal{L}}_{Z|T_1=t_1,T_2>t_2}(c)=\frac{\text{E}[Z{\lambda }_1(t_1)\exp (-Z(c+{\Lambda }_1(t_1)+{\Lambda }_2(t_2)))]}{\text{E}[Z{\lambda }_1(t_1)\exp (-Z({\Lambda }_1(t_1)+{\Lambda }_2(t_2)))]}\hfill \\ \hspace{0.17em}=\frac{{\mathcal{L}}^{\prime }(c+{\Lambda }_1(t_1)+{\Lambda }_2(t_2))}{{\mathcal{L}}^{\prime }({\Lambda }_1(t_1)+{\Lambda }_2(t_2))}\hfill \end{array}$$

For a more detailed derivation, see equation (8). If both events are observed, the Laplace transform of Z given $T_1=t_1,T_2=t_2$ can be calculated similarly as

$${\mathcal{L}}_{Z|T_1=t_1,T_2=t_2}(c)=\frac{\mathcal{L}″(c+{\Lambda }_1(t_1)+{\Lambda }_2(t_2))}{\mathcal{L}″({\Lambda }_1(t_1)+{\Lambda }_2(t_2))}$$

where $\mathcal{L}″$ is the second derivative of the Laplace transform of Z. A general pattern can be observed, where for each event observed in the cluster a further derivative of the Laplace transform is involved.

So far the Laplace transforms of the conditional distribution of Z, given T₁ and T₂, have been expressed in terms of generic hazard rates. Let us now turn to the situation where we have observed data from a cluster of arbitrary size, in which all subjects share the same frailty. Some of these observations include right-censored observations, for others the event of interest has been observed. Suppose we have a model that, conditional on observed covariates x, specifies the hazard rate λ_j of each individual j in the cluster. We can use the relations derived above to derive the posterior distribution of the frailty, given the observed data in the cluster (rather its Laplace transform). We denote the observed data of the cluster (the event history of all its individuals up to some horizon τ) as ${\mathcal{F}}_{\tau }$. Assume that the data comprises $N(\tau )$ observed events, and let

$${\Lambda }_{•}(\tau )={\displaystyle \sum _j{\displaystyle {\int }_0^{\tau }{Y}_j}}(s){\lambda }_j(s)ds$$ (12)

where $Y_j(s)$ is the at risk indicator of subject j in the cluster, equal to 1 if subject j is at risk at time s, and 0 otherwise. Recall ${\mathcal{L}}^{(k)}$ as the k-th derivative of the Laplace transform. The Laplace transform of Z, given the event history ${\mathcal{F}}_{\tau }$ of the cluster, is given by

$${\mathcal{L}}_{Z|{\mathcal{F}}_{\tau }}(c)=\frac{{\mathcal{L}}^{(N(\tau ))}(c+{\Lambda }_{•}(\tau ))}{{\mathcal{L}}^{(N(\tau ))}({\Lambda }_{•}(\tau ))}$$ (13)

The expectation of this distribution follows as minus the derivative of its Laplace transform at c = 0

$$\text{E}[Z|{\mathcal{F}}_{\tau }]=-\frac{{\mathcal{L}}^{(N(\tau )+1)}({\Lambda }_{•}(\tau ))}{{\mathcal{L}}^{(N(\tau ))}({\Lambda }_{•}(\tau ))}$$ (14)

For the gamma frailty, we obtain that

$$\text{E}[Z|{\mathcal{F}}_{\tau }]=\frac{\theta +N(\tau )}{\theta +{\Lambda }_{•}(\tau )},\text{var}[Z|{\mathcal{F}}_{\tau }]=\frac{\theta +N(\tau )}{{(\theta +{\Lambda }_{•}(\tau ))}^2}$$

The class of infinitely divisible distributions, discussed in section 2.3.2, allows similar expressions to be derived.

3.2.3 Dependence and the cross-ratio

The estimated frailty variance offers an indication of unobserved heterogeneity between clusters, but it offers little information on the resulting marginal correlation of the event times. Even for paired data, the formulas for the bivariate survival function in equation (11) are difficult to interpret.

One measure of bivariate dependence is Kendall’s coefficient of concordance (Kendall’s tau). Denote two pairs of individuals as $\left\{(11),(12)\right\}$ and $\left\{(21),(22)\right\}$, where (ij) refers to individual j of cluster (pair) i. Denote T_ij as the event time of subject (ij). Kendall’s tau is defined as

$${\tau }_K=\text{E}[\text{sign}((T_{11}-T_{21})(T_{12}-T_{22}))]$$

where $\text{sign}$ is the sign function. This is proportional to the probability that the order of events is concordant between the two clusters. The median concordance is a similar measure that only involves one pair

$$\kappa =\text{E}[\text{sign}((T_1-\text{median}(T_1))(T_2-\text{median}(T_2)))]$$

This is proportional to the probability that the events within the same cluster are concordant, in the sense that they occur both before the median survival time or after. In frailty models, both τ_K and κ are positive quantities, since the specification (10) only allows for positive dependence. Under independence, both measures would be 0. However, the reverse statement is not usually true. Estimation of these coefficients in censored data is detailed in Hougaard,⁹ Chapter 4.

A more natural way of exploring the within-cluster dependence structure is via the cross-ratio,³² defined for pairs of subjects from the same cluster. It compares how the hazard of one subject in the pair would behave if an event would happen to the other subject, as opposed to an event not happening. Unlike τ_K and κ, it is a local measure of dependence. To illustrate this, we consider one cluster with individuals 1 and 2. Conditional on the frailty, their event times T₁ and T₂ are independent. Denote the hazard of individual 2 if individual 1 is alive at t₁ as

$${\lambda }_2(t|T_1>t_1)=\frac{\mathcal{L}\prime ({\Lambda }_1(t_1)+{\Lambda }_2(t))}{\mathcal{L}({\Lambda }_1(t_1)+{\Lambda }_2(t))}{\lambda }_2(t)$$

and the hazard of individual 2 if individual 1 had an event at time t₁ as

$${\lambda }_2(t|T_1=t_1)=\frac{\mathcal{L}″({\Lambda }_1(t_1)+{\Lambda }_2(t))}{\mathcal{L}\prime ({\Lambda }_1(t_1)+{\Lambda }_2(t))}{\lambda }_2(t)$$

These two hazards concern different hypothetical event histories of the other individual in the cluster. They are equal only if there is no dependence between the two individuals. The cross-ratio can be expressed as

$$\begin{array}{l}\text{CR}(t_1,t_2)=\frac{{\lambda }_2(t_2|T_1=t_1)}{{\lambda }_2(t_2|T_1>t_1)}\hfill \\ \hspace{0.17em}=\frac{{\mathcal{L}}^{″}({\Lambda }_1(t_1)+{\Lambda }_2(t_2))}{{\mathcal{L}}^{\prime }({\Lambda }_1(t_1)+{\Lambda }_2(t_2))}{\left(\frac{{\mathcal{L}}^{\prime }({\Lambda }_1(t_1)+{\Lambda }_2(t_2))}{\mathcal{L}({\Lambda }_1(t_1)+{\Lambda }_2(t_2))}\right)}^{-1}\hfill \end{array}$$

which is a function of ${\Lambda }_1(t_1)+{\Lambda }_2(t_2)$. Intuitively, if there is positive dependence between the two event times, we have $\text{CR}(t_1,t_2)\ge 1$. It was suggested in Hougaard⁹ that a more interpretable comparison would be to replace the denominator by ${\lambda }_2(t_2|T_1>t)$, to compare the hazard given that “individual 1 died at time t₁” with “individual 1 is alive now”. This “adjusted cross ratio” is defined as

$$\begin{array}{l}{\text{CR}}_a(t_1,t_2)=\frac{{\lambda }_2(t_2|T_1=t_1)}{{\lambda }_2(t_2|T_1>t)}\hfill \\ \hspace{0.17em}=\frac{{\mathcal{L}}^{″}({\Lambda }_1(t_1)+{\Lambda }_2(t_2))}{{\mathcal{L}}^{\prime }({\Lambda }_1(t_1)+{\Lambda }_2(t_2))}{\left(\frac{{\mathcal{L}}^{\prime }({\Lambda }_1(t)+{\Lambda }_2(t_2))}{\mathcal{L}({\Lambda }_1(t)+{\Lambda }_2(t_2))}\right)}^{-1}\hfill \end{array}$$

${\text{CR}}_a$ can be interpreted as the ratio between the hazard of individual 1 when individual 2 is dead and the hazard of individual 1 when individual 2 is alive.

In Figure 8, we illustrate the unadjusted and adjusted cross-ratio functions for the gamma, inverse Gaussian and positive stable distributions. For comparison purposes, the distributions are matched by Kendall’s tau rather than variance. Both unadjusted and adjusted cross-ratio functions show that the hazard of individual 2 is larger if individual 1 has an event. The unadjusted cross-ratio for the gamma frailty is constant, showing that the event of individual 1 affects the hazard in the same way over time. The shape of the unadjusted cross-ratio for the inverse Gaussian and positive stable frailties shows that there is a strong immediate dependence that vanishes over time.

Figure 8.

Cross-ratio (top row) and adjusted cross-ratio (bottom row, at $t_1=1$) for the gamma, inverse Gaussian and positive stable distributions, for different values of Kendall’s tau. The individual hazard, conditional on Z = 1, is taken as $\lambda (t)=t^2/20$.

The adjusted cross-ratio paints a slightly different picture. For the gamma, it implies that, if one member of the pair dies, the hazard for the survivor would appear increasingly larger as compared to the scenario where the partner would still be alive. For the positive stable distribution, the surviving individual is at a perceived high risk right after the partner died, but the differences quickly decreases. This can be interpreted as a large correlation between the life times on the short term. As before, the inverse Gaussian is somewhere in the middle.

The unadjusted cross-ratio may be interpreted as an “instantaneous odds ratio”,³³ and for bivariate survival data it may be used for selecting the frailty distribution (Duchateau and Janssen,¹⁰ Chapter 4). One disadvantage is that it depends on the conditional cumulative hazard; a scaled cross-ratio that overcomes this has been proposed by Paddy Farrington et al.²⁵

The gamma frailty is said to induce “late dependence” (a high probability of events occurring close by at later time points), the positive stable frailty induces “early dependence” (a high probability of event occurring close by early in the follow-up) and the inverse Gaussian is somewhere in the middle. The timing of the dependence can be studied by analyzing the joint distribution of T₁ and T_2.⁹ A disadvantage of this approach is that the marginal distributions of T₁ and T₂ must be known separately, which is usually not possible.

3.2.4 Frailty model for recurrent events

Recurrent events are most commonly defined in the framework of counting processes. Each individual is described by a process N(t) that “counts” the number of events experienced by the individual until time t.

The two common frameworks for modeling N are the Poisson process and the renewal process.³⁴ If unobserved individual heterogeneity is present, then there are two approaches that may be used in practice. One is the marginal approach, where the unobserved heterogeneity is treated as a nuisance.³⁵ In that case, the focus of analysis is the marginal rate of N, which is defined as the probability of observing an increase in N in the small interval $(t,t+\text{d}t)$.

The second approach is to model the intensity of N. While the hazard is defined as the instantaneous probability of an event given that the individual is alive, the intensity is defined as the instantaneous probability of an event given the whole previous event history of the individual. One way of incorporating the previous event history of the individual is to assume that the intensity at time t depends in some way on the number of events observed prior to time t. When the Poisson and renewal processes depend explicitly on the past, they result in so-called modulated Poisson and renewal processes. Another way is to implicitly model the dependence on the event history through a frailty Z. The conditional intensity of N, given Z, is then specified as

$$\lambda (t|Z)=Y(t)Z{\lambda }_0(t)\exp ({\beta }^{\mathrm{\top }}\mathbf{x})$$ (15)

where Y(t) is an indicator function that is 1 if the individual is under observation at time t and 0 otherwise. Similarly to the univariate frailty, the variance of Z describes between-individual unobserved heterogeneity.

The marginal intensity is obtained by replacing Z by $\text{E}[Z|{\mathcal{F}}_{t-}]$, with ${\mathcal{F}}_{t-}$ now representing the event history of the individual until just before time t. As in the case of univariate frailty in section 2.4, the effect of the covariates in the marginal intensity is usually time-dependent. Similar to the clustered failures scenario, $\text{E}[Z|{\mathcal{F}}_{t-}]$ includes information on previous event times.

The intensity in equation (15), with t referring to “time since origin of the recurrent event process”, is referred to as the calendar time or Andersen-Gill formulation. In the Andersen-Gill formulation, N is assumed to be a Poisson process, conditional on Z, meaning that its intensity conditional on Z does not depend on the history ${\mathcal{F}}_{t-}$. Alternatively, in the gap-time scale, t refers to “time since the previous event”. The intensity may then be expressed as $\lambda (t|Z)=\lambda (t-B(t)|Z)$, where B(t) is the time of the event before time t. From a practical point of view, the gap time scale has a very similar representation to (10), where ${\lambda }_{ij}(t|Z)$ is interpreted as the hazard of the j-th event, on the time scale since the last observed event. Conditional on Z, N is then a renewal process.

In the case of recurrent events, the frailty mainly expresses that, if two individuals with identical covariates were observed over the same period of time, the expected number of events is larger for the one with the higher frailty. The number of events carries the most information on the frailty⁹ (Chapter 9). Therefore, the measures of dependence discussed in subsection 3.2.3 are of little interest in this context.

Modeling recurrent events is a complex task and several types of models may be accommodated with counting processes (Therneau and Grambsch,¹² Section 8.5). Furthermore, time-dependent covariates representing, for example, the number of previous events, may also be added in the model (Aalen et al.,24 Chapter 8). A comprehensive reference on recurrent event modeling may be found in Cook and Lawless.³⁴

3.3 Estimation and inference for frailty models

Depending on the nature of the baseline hazard or intensity λ₀, the frailty models may be classified as semi-parametric or parametric. In semi-parametric models, no assumptions are made on the baseline hazard or intensity λ₀ and the maximum likelihood estimate of λ₀ has mass only at the event times, as is the case for the Breslow estimator.³⁶ In parametric models, λ₀ is determined by a small number of parameters, such as the exponential, Weibull or Gompertz models, or flexible parametric approaches employing spline-based estimators.

3.3.1 Likelihood and EM-based approaches

The likelihood construction for counting processes is detailed in most survival analysis textbooks.^24,37 To cover all the scenarios described previously, assume that i denotes the cluster, (i, j) the j-th individual within the cluster i and t_ijk denotes the k-th event or censoring time observed on individual (i, j). We define the event indicator δ_ijk as 1 if t_ijk is an event time and 0 otherwise. Suppose that the conditional hazard of subject (i, j), conditional on the frailty Z_i is given by ${\lambda }_{ij}(t|Z_i)=Z_i{\lambda }_{ij}(t)$ with ${\lambda }_{ij}(t)={\lambda }_0(t)\exp ({\beta }^{\mathrm{\top }}{\mathbf{x}}_{ij})$. Denote the at risk indicator of subject j in cluster i by $Y_{ij}(t)$ and let ${\Lambda }_{i•}(\tau )=\sum j{\int }_0^{\tau }{Y}_{ij}(t){\lambda }_{ij}(t)\text{d}t$, with τ the horizon, be the sum of conditional cumulative hazards of cluster i, as defined in equation (12).

Assuming that the frailties Z_i are observed, the conditional likelihood contribution of cluster i is given by

$$L_i(\beta ,{\lambda }_0|Z_i)={\displaystyle \prod _{jk}{\left({\lambda }_{ij}(t_{\mathit{ijk}}|Z_i)\right)}^{{\delta }_{\mathit{ijk}}}}\times \exp \left(-Z_i{\Lambda }_{i•}(\tau )\right)$$

and the likelihood for all the individuals is a product of all L_is. The clustered failure data is represented by having only one time point per individual ($k\equiv 1$), while the recurrent events case is represented by having only one individual per cluster ($j\equiv 1$). An implicit assumption here is that censoring is independent. In terms of counting processes, the at-risk process Y(t) is assumed to be independent of N(t), given the covariates and event history up to time t.

In the first part of this expression, Z_i appears to the power N_i•, the total number of events from the cluster i. The marginal likelihood contribution of cluster i is obtained by taking the expectation over Z_i

$$\begin{array}{c}{L}_i(\beta ,{\lambda }_0,\theta )={\displaystyle \prod _{j,k}{\lambda }_{ij}}{(t_{\mathit{ijk}})}^{{\delta }_{\mathit{ijk}}}\text{E}\left[Z_i^{N_{i•}}\exp \left(-Z_i{\Lambda }_{i•}(\tau )\right)\right]\end{array}$$ (16)

The parameters to be optimized are β, the vector of regression coefficients, λ₀, the baseline hazard, and θ, the parameters of the frailty distribution, usually the frailty variance. For valid inference based on $L(\beta ,{\lambda }_0,\theta )$, the censoring or at-risk process must also not involve the frailty, for reasons outlined in Nielsen et al.³⁸ This assumption is similar to that of regular Cox models, where dependent censoring arises, for example, if the censoring process depends on unobserved covariates. In models where the baseline hazard λ₀ is parametric, direct optimization of the likelihood is feasible. When the baseline hazard is non-parametric, as in a (conditional) Cox model, the dimension of λ₀ is usually equal to the number of total distinct event time points in the data. This prevents a direct maximization of the likelihood.

For semi-parametric gamma frailty models, the Expectation-Maximization (EM) algorithm³⁹ has been proposed.^38,40 It can be extended in a straightforward way to the class of infinitely divisible distributions described in section 2.3.2.^9,41 This involves iterating between two steps:

1. The “E” step, which involves calculating the expected log-likelihood

   $$\text{E}\ell (\beta ,{\lambda }_0,\theta )={\displaystyle \sum _i\text{E}}\left[\log L_i(\beta ,{\lambda }_0|Z)\right]$$

In practice, this involves calculating $\text{E}[Z_i|{\mathcal{F}}_{\tau }]$ and possibly $\text{E}[\log Z_i|{\mathcal{F}}_{\tau }]$.

• 2. The “M” step, where $\beta ,{\lambda }_0$ and θ are updated, by maximizing $\text{E}\ell (\beta ,{\lambda }_0,\theta )$.

The advantage of this approach is that the M step may be calculated via Cox’s partial likelihood,⁴² effectively eliminating the problem of the high-dimensional λ₀. For the E step, the “posterior” distribution of Z_i, given the event history ${\mathcal{F}}_{\tau }$ of cluster i, needs to be evaluated. It has the density kernel

$$f_{Z_i}(z|{\mathcal{F}}_{\tau })\propto z^{N_{i•}}\exp (-z{\Lambda }_{i•}(\tau ))f_{Z_i}(z)$$

This is available in closed form only for the gamma frailty, and is typically difficult to calculate for other frailty distributions. The expectation of this distribution, $\text{E}[Z_i|{\mathcal{F}}_{\tau }]$, is also known as the empirical Bayes frailty estimate. It can be calculated via the Laplace transform, as discussed in section 3.2.2, see equation (14). This may involve having to take many derivatives of the Laplace transform, if $N_{i•}$ is large. In principle, for the “E” step, also $\text{E}[\log Z_i|{\mathcal{F}}_{\tau }]$ is needed. Calculation of $\text{E}[\log Z_i|{\mathcal{F}}_{\tau }]$ can be avoided via a “profile EM” algorithm, which involves performing the EM algorithm described here for fixed values of θ, and maximizing over θ in an outer loop.³⁸ As an alternative for the EM algorithm, a Monte Carlo EM algorithm may be employed, which involves a stochastic approximation of the E step.⁴³

3.3.2 Alternative approaches

The penalized likelihood method^44,45 is a very popular way of estimating gamma and log-normal semi-parametric frailty models. The basic idea behind it is that, for fixed θ, the $\log Z_i$'s may be treated as regular parameters (on the same scale with the regression coefficients β). Afterwards, a penalization of a specific form is imposed upon them. Depending on the penalization, the results are equivalent to those of a gamma or a log-normal distributional assumption. This approach is typically the fastest for semi-parametric models, and is implemented in coxph in the survival package. A downside is that it is not immediately possible to extend the estimation to other frailty distributions.

Other approaches include a pseudo-likelihood method,⁴⁶ which leads to consistent estimators and may be employed for a larger number of frailty distributions, and the h-likelihood method.^47,48 This approach relies on maximizing the joint likelihood of the observed and unobserved data. It has been developed for the gamma and log-normal distributions.

3.3.3 Inference

For parametric models, the variance–covariance matrix is typically obtained directly, as the inverse of the numeric Hessian matrix. This is usually provided directly by optimization software. For models estimated with the EM algorithm, Louis’ formula may be used⁴⁹ to obtain standard errors of the estimates. It has been shown that the baseline hazard may be regarded, for practical purposes, as an ordinary finite dimensional parameter and the information matrix may be constructed from the matrix of second derivatives.⁵⁰

For the profile EM algorithm, the variance covariance matrix for $(\beta ,{\lambda }_0)$ is obtained under the assumption of fixed θ. Similarly to the penalized likelihood methods, the variance–covariance matrix for β, based on the partial likelihood, is also obtained under fixed θ. The complete variance–covariance matrix for $\beta ,{\lambda }_0$ or for β should then be adjusted for the variability of θ (Hougaard⁹ Chapter B3),⁵¹ although this is usually ignored in practice.

Inference regarding the frailty variance is more challenging. The limiting case, when the variance is 0, is a proportional hazards model without frailty. A likelihood ratio test based on a 50:50 mixture of ${\chi }^2$ distributions with 0 and 1 degree of freedom can be employed to test the difference between these two models.^52,53 Another issue is that, since the variance must be positive, symmetric confidence intervals are not very meaningful. An alternative is to calculate likelihood-based confidence intervals, as is illustrated in Therneau and Grambsch,¹² Chapter 9.

4 Frailty models in practice

4.1 Software

Support for frailty models exists in major statistical packages such as R,⁵⁴ SAS⁵⁵ and Stata.⁵⁶ The PHREG command in SAS implements the penalized likelihood method for the gamma and log-normal frailty models. The streg procedure in Stata implements parametric gamma and inverse Gaussian frailty models. In what follows, we will focus on packages for R.

Semi-parametric gamma and log-normal frailty models may be estimated via the penalized likelihood method in the survival package.^12,57 Semi-parametric frailty models with the infinitely divisible class of frailty distributions discussed in section 2.3.2 may be estimated via the profile EM algorithm with the frailtyEM package.⁵⁸ Log-normal frailty models (including correlated frailties, discussed in section 5) may be estimated with the coxme package.⁵⁹ Similar models may be fitted with the Monte Carlo EM algorithm with the phmm R package.⁶⁰ Log-normal and gamma frailty models can also be estimated via $h-$likelihood with the frailtyHL package.⁶¹ The pseudo-likelihood approach is implemented in the frailtySurv package,⁶² supporting some of the infinitely divisible distributions from the PVF family.

Parametric and flexible parametric frailty models for the gamma and log-normal distributions are supported by the frailtypack package^63,64 (including correlated random effects, nested random effects and numerous other scenarios). Parametric frailty models with support for some of the PVF family distributions are implemented in the parfm package.⁶⁵

4.2 Data representation

In R,⁵⁴ the canonical resources for survival analysis are found in the survival package.⁵⁷ Event histories corresponding to survival times or to recurrent events have a very similar representation, as described in detail in Therneau and Grambsch.¹²

An event history is represented by a collection of observations, which are vectors $(t_L,t_R,\delta ,\mathbf{x})$ where (t_L, t_R) are two time points that define an “at-risk” interval, δ is equal to 1 if the interval ended with an event and 0 otherwise, and x is a vector of covariate values that are constant on this interval. In R, the tuple $(t_L,t_R,\delta )$ is referred to as (tstart, tstop, status). Univariate survival times and clustered failures are usually represented by having t_L = 0 and a simplified (tstop, status) notation. Furthermore, the $(t_L,t_R,\delta )$ notation may also be used to express:

• Recurrent events in calendar time (or “Andersen-Gill” representation). In this case, for an individual, t_R are event times and t_L is usually 0 or the time of the previous event. Usually, the last observation is censored with the last t_R being the end of follow-up.

• Recurrent events in gap time. In this case, t_L = 0 and t_R are observed gap times. The last observation may be censored, indicating an incomplete gap time at the end of follow-up.

• Left truncated survival times, where t_L is the time point after which the individual enters the study.

• Time-dependent covariates. In this case, if the value x changes at time $\tilde{t}\in (t_L,t_R)$, this results in two observations corresponding to time intervals $(t_L,\tilde{t})$ and $(\tilde{t},t_R)$, with the first one being artificially censored.

In the presence of frailty, an observation is interpreted as a contribution to the conditional likelihood of the form

$$L(\beta ,{\lambda }_0|Z;t_L,t_R,\delta ,\mathbf{x})={\left\{Z{\lambda }_0(t_R)e^{{\beta }^{\mathrm{\top }}\mathbf{x}}\right\}}^{\delta }·\exp \left(-Z({\Lambda }_0(t_R)-{\Lambda }_0(t_L))e^{{\beta }^{\mathrm{\top }}\mathbf{x}}\right)$$

For a collection of observations sharing the same frailty Z, the software maximizes

$${\text{E}}_Z\left[{\displaystyle \prod _{\text{intervals}}L}(\beta ,{\lambda }_0|Z;t_L,t_R,\delta ,\mathbf{x})\right]$$

which is the contribution of one cluster to the marginal likelihood (16). This is appropriate in the case of recurrent events and time-dependent covariates, or for clustered survival times without left truncation.

For left truncated survival times, however, this is generally incorrect. In the univariate case, the frailty distribution of a left truncated individual is that of $Z|T\ge t_L$, referred to as the distribution of survivors (until time t_L) in section 2.4.

In the case of clustered survival times, the event of observing the whole cluster must be taken into account.^66–68 If the individuals from the same cluster have truncation times $t_{L,1},t_{L,2},\dots t_{L,J}$ that are independent given Z, then the frailty distribution of the cluster is that of $Z|T_1>t_{L,1},\dots T_J>t_{L,J}$.

More complicated selection schemes arise when the left truncation times are not independent, even conditional on the frailty.⁶⁹ In the case of recurrent events, such selection schemes may arise when individuals are included into the study only if they experience a certain number of events.⁷⁰ Such scenarios usually require ad-hoc estimation procedures and are not generally supported by the main software packages.

In R, one of the reasons why the same notation is used to denote both recurrent events and left truncation is because they lead to the same likelihood in frailty-less models. In the case of frailty models, the treatment depends on the package used. For example, the survival package calculates the correct likelihood for the recurrent events case, parfm calculates the correct likelihood for the left truncation case. In frailtypack and frailtyEM, both scenarios are supported.

5 Extensions

The standard shared frailty model assumes that the frailty is shared among all individuals in the same cluster. This assumption can be relaxed by assuming that the frailty terms of individuals in the same cluster are not shared, but correlated.^7,11,71,72 Correlated frailty models address the limitation that shared frailty models may only be employed for positively correlated event times.

Furthermore, so far the random effect Z has been assumed to be time-constant. This is consistent with the interpretation that Z accounts for individual specific or cluster specific characteristics that are fixed from the time origin, and have an effect that is constant over time. However, the unobserved heterogeneity might be time-dependent, thus better explained by an unobserved random process that unfolds over time. Several approaches based on this idea have been proposed. The frailty may be modeled with diffusion processes^73,74 or Levy processes.⁷⁵ More recently, an approach on birth-death Poisson processes has been proposed.⁵¹ Simpler, piecewise constant, frailty models have also been considered.^76,77 A limited implementation combining the birth-death processes and the piecewise constant frailty is implemented in the R package dynfrail.⁷⁸ Related approaches include the constructions of auto-regressive frailty processes based on log-normal frailties^79,80 or gamma frailties.⁸¹

Since the models presented in sections 2 and 3 are intended for the analysis of one stochastic event process, it has been assumed that the censoring does not depend on the frailty included in the time to event model. This assumption may be tested,⁸² and in case a violation of this independence assumption is detected, the event and censoring processes can be modeled jointly. An example is when the observation recurrent event process may be stopped by death⁸³ or when the frailty is also associated with the censoring.⁸⁴

Moreover, we assumed that in case of time-dependent covariates, the vector $\mathbf{x}(t)$ is “external” to the event process, in the sense of Kalbfleisch and Prentice.³⁷ If x contains internal time-dependent covariates, such as repeated individual measurements, the processes should be modeled jointly (Rizopoulos,⁸⁵ Chapter 2). In this case, the frailty is shared by the model for the time-dependent covariate (or biomarker) and the model for the event process. Software for estimating joint models is also available in R.⁸⁶

More advanced random effect structures may be, in theory, considered. For example, if individuals experience recurrent events and are nested within clusters, a hierarchical random effects model may be considered. This is, however, not easily done in practice, and there is no standard software that currently supports such models.

6 Illustration

We end by discussing two illustrations of the use of frailty models. The first is a study on center effects in a breast cancer study, the second on recurrent events in patients with chronic granulomatous disease. The R code for the analyses performed is available as Supplementary Material.

6.1 Frailty models for center comparisons

The data originate from a clinical trial in breast cancer patients, conducted by the European Organization for Research and Treatment of Cancer (EORTC-trial 10854). The objective of the trial was to study whether a short intensive course of perioperative chemotherapy yields better therapeutic results than surgery alone. The trial included patients with early breast cancer, who underwent either radical mastectomy or breast conserving therapy before being randomized. The trial consisted of 2795 patients, randomized to either perioperative chemotherapy or no perioperative chemotherapy. Results of the trial were reported in literature.^87,88 The data have been studied in a multi-state model in Putter et al.⁸⁹ and Van Houwelingen and Putter.²⁸ This data is based on a subset of all 2687 patients with complete information on all covariates used below. For descriptives on these covariates, see Van Houwelingen and Putter,²⁸ Appendix A.2.

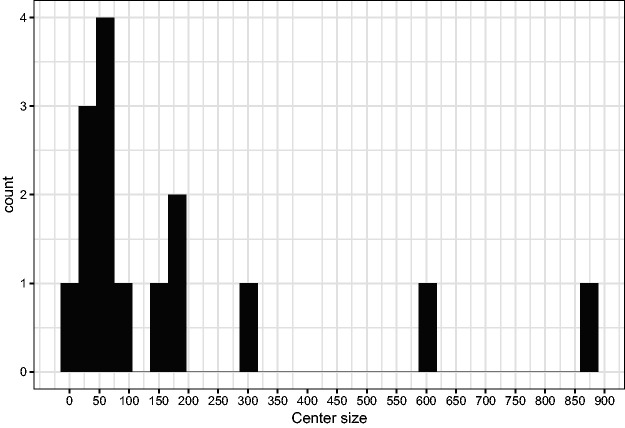
In the trial, patients have been included in 15 participating centers. The size of the centers varies between 6 patients (the smallest one) and 880 (the largest), as illustrated in Figure 9.

Figure 9.

Histogram of center sizes.

Figure 10.

Kaplan–Meier survival estimates, overall and by center.

For this illustration, the endpoint of interest is overall survival. In Figure 10, we show the Kaplan–Meier estimates corresponding to each center (gray) and the overall estimate (black). These survival curves do not make it easy to compare centers. One of the reasons is that the survival curves are not controlled for possible differences between the distribution of covariates across centers (so-called case-mix), another is that it is difficult to disentangle randomness from systematic differences between centers.

For the inclusion of covariates, we start with a proportional hazards model, where the hazard of subject j from center i, given its covariates ${\mathbf{x}}_{ij}$, is given by

$${\lambda }_{ij}(t)={\lambda }_0(t)\exp ({\beta }^{\mathrm{\top }}{\mathbf{x}}_{ij})$$

This model does not yet include any differences between centers. Estimating it is straightforward in principle, but for the standard maximum likelihood approach, the event times of the individuals are assumed to be independent. This assumption might not hold when observations come from the same center. Generalized estimating equations (GEE), with independent working covariance, may be used to obtain valid (sandwich) standard errors in this case. The results, with unadjusted and adjusted (robust) standard errors, are shown in Table 1, under “Cox model”. The hazard ratios $\exp (\beta )$ have a marginal interpretation, in the sense that they are averaged over all unmeasured covariates (such as, for example, center effects). Therefore, the estimated regression coefficients apply to an individual selected at random from the population.

Table 1.

Estimates from the Cox model, the fixed effects model, the gamma and log-normal frailty models.

		Cox model				Fixed Effects			Gamma frailty			Log-normal frailty
		Coef	SE	Robust SE		Coef	SE		Coef	SE		Coef	SE
Type of surgery	Mastectomy with RT
	Mastectomy without RT	0.25	0.11	0.17		0.16	0.13		0.16	0.12		0.16	0.12
	Breast conserving	−0.07	0.10	0.10		−0.09	0.10		−0.08	0.10		−0.08	0.10
Tumor size	<2 cm
	2–5 cm	0.35	0.10	0.10		0.35	0.10		0.35	0.10		0.35	0.10
	>5 cm	0.89	0.15	0.16		0.83	0.16		0.84	0.16		0.84	0.16
Nodal status	Node negative
	Node positive	0.97	0.11	0.26		0.77	0.11		0.79	0.11		0.78	0.11
Age	$\le$50
	>50	0.01	0.10	0.12		0.10	0.10		0.09	0.10		0.09	0.10
Adjuvant chemo	No
	Yes	−0.38	0.13	0.35		−0.15	0.14		−0.17	0.13		−0.17	0.14
Tamoxifen	No
	Yes	−0.17	0.12	0.31		0.12	0.13		0.08	0.12		0.08	0.12
Perioperative chemo	No
	Yes	−0.12	0.07	0.06		−0.13	0.07		−0.13	0.07		−0.13	0.07
Frailty variance									0.122			0.132

Note: Estimated center effects of the fixed effects model have been omitted from the table.

To explain more of the underlying heterogeneity, we account for center effects. The centers are included in a fixed effects model. The underlying model would be given by

$${\lambda }_{ij}(t)={\lambda }_0(t)\exp ({\gamma }_i+{\beta }^{\mathrm{\top }}{x}_{ij})$$

Such a model can be fitted using center as a factor variable, taking one of the centers, usually the first, as reference center. The resulting estimates of the regression coefficients are shown in Table 1, under Fixed Effects. We can visually assess the differences between centers via a caterpillar plot, shown in Figure 11. The error bars denoted with “fixed effects” correspond to the estimates and 95% confidence intervals of the fixed effects estimates. In the Cox model estimated above, the first center is taken as reference, with an implicit ${\gamma }_1=0$. Denote γ as the vector of regression coefficients of the remaining centers, and $\overline{\gamma }$ as their average. For this visual representation, we center the γ’s at 0, i.e. we set ${\tilde{\gamma }}_i={\gamma }_i-\overline{\gamma }$, and ${\tilde{\gamma }}_1=-\overline{\gamma }$, with $\overline{\gamma }$ the average of the original estimates of the γ’s. The standard errors are then also calculated accordingly. The confidence intervals suggest that there is a lot of variability in estimated center effects in this way. Most of the confidence intervals include 0, with the exception of center E, which shows a lower mortality, and centers M, N, and O, which show a higher mortality.

Figure 11.

Center effects from the fixed effects and frailty models, expressed in hazard ratios.

More naturally, we would think about the centers as being randomly drawn from a population of centers, and their effects as being realizations from a frailty distribution. The underlying model would be

$${\lambda }_{ij}(t)=Z_i{\lambda }_0(t)\exp ({\beta }^{\mathrm{\top }}{x}_{ij})$$

where Z_i is the (random) center effect corresponding to center i. The frailty variance can then be used to quantify the degree of between center variability. The result of fitting a gamma frailty model is shown in Table 1, under frailty model. The frailty variance is estimated as 0.122. The 95% confidence interval for the frailty variance, given by (0.048, 0.324), is based on the profile likelihood function (see section 3.3.1). This means that there is a one-to-one correspondence between the confidence interval for the frailty variance and the profile likelihood ratio test. Although the frailty variance is not really large, the likelihood ratio test deems the differences in mortality rates between centers, after adjustment for covariates, as statistically significant. Figure 11 shows a caterpillar plot of the center effects from the fixed effects model and from the frailty model. For the frailty model, for each center, the estimate shown is the empirical Bayes estimate, and the 95% interval is given by the 2.5% and 97.5% percentiles of the posterior frailty distribution, given the data in the center, as detailed in equation (13) in section 3.2.2.

It may be observed that, particularly for the extreme centers, the frailty estimates are shrunken towards the mean (1). In terms of interpretation of the frailty estimates, it is helpful to study the form of the empirical Bayes estimates. For the gamma frailty model, it may be shown that the empirical Bayes estimate for center i is given by

$${\widehat{z}}_i=\frac{\widehat{\theta }+N_i}{\widehat{\theta }+{\widehat{\Lambda }}_{i•}}$$

where $\widehat{\theta }$ is the estimate of the inverse variance parameter, N_i the number of events in center i and ${\widehat{\Lambda }}_{i•}$ the sum of the cumulative hazards of all individuals from center i, evaluated at the end of follow-up of each individual, cf. equation (12). While N_i is the “observed” number of events, ${\widehat{\Lambda }}_{i•}$ may be interpreted as the expected number of events in center i, based on the case-mix and the length of follow-up of the patients in the center. We can re-write ${\widehat{z}}_i$ as

$${\widehat{z}}_i=\lambda \frac{N_i}{{\widehat{\Lambda }}_{i•}}+(1-\lambda )$$

with

$$\lambda =\frac{{\widehat{\Lambda }}_{i•}}{\widehat{\theta }+{\widehat{\Lambda }}_{i•}}$$

Therefore, ${\widehat{z}}_i$ is a weighted average of the ratio between observed and expected number of events and the overall average (1). In particular, smaller centers (with smaller ${\widehat{\Lambda }}_{i•}$) will show more shrinking.

The proportional hazards assumption may be checked with, for example, with a test based on residuals.¹³ In the case of the Cox model, this tests shows evidence against non-proportionality for tumor size and nodal status. For the frailty model, the same test can be carried out on the same Cox model, but with the logarithm of the log-frailties as offset. In this case, the conclusions are unchanged and indicate that further modeling of these variables may be required. Note that this may not be the case if the clusters would be smaller in size; we discuss this in section 7.

For comparison, we also estimated the same model with log-normal instead of gamma frailty. The maximized likelihood of this model was −5449.4 versus −5450.9 for the gamma frailty, suggesting a better fit to the data. The estimates of the regression coefficients are also shown in Table 1. The results from the two models are virtually identical, except for the estimated frailty variance which is slightly larger than the one from the gamma frailty.

6.2 Frailty models for recurrent events

The data are from a placebo controlled trial of gamma interferon in chronic granulomatous disease (CGD) and are available in the survival package. It contains the time to recurrence of serious infections, observed from randomization until end of study for each patient. The follow-up and event history of each individual are visualized in Figure 12. Most individuals, in fact, have no events during their follow-up; see Figure 13 for a histogram of the number of recurrences per individual.

Figure 12.

Event history of the CGD data. The length of the line indicates the length of follow-up, and the dots indicate the infections.

Figure 13.

Histogram of number of events per individual.

A preliminary Cox model fit reveals that the treatment is highly significant, and that age, inherit and steroid usage are also significant. For the purpose of illustration, we will include these variables, plus sex, from now on. The results from the Cox model with these selected covariates are shown in Table 2. The covariates explain part of the differences between intensities in the occurrence of infections between the individuals. To quantify the unobserved heterogeneity in the intensities, we fit a shared gamma frailty model to the data. The frailties reflect the increase or decrease in infection rates of different individuals. The result is shown in Table 2. The frailty variance is estimated as 0.555, with (profile) likelihood ratio test-based 95% confidence interval $(0.067-1.449)$. A histogram of the empirical Bayes frailty estimates is shown in Figure 14.

Table 2.

Estimates of the regression coefficients and fit summary from the Cox model and shared frailty models, with gamma, inverse Gaussian, positive stable and compound Poisson (with parameters 0.5 and 1.1) distributions, fitted on the CGD data.

				Inverse	Positive	Compound Poisson
		Cox model	Gamma	Gaussian	Stable	(m = 0.5)	(m = 1.1)
Treatment	Placebo
	IFN-g	−1.10 (0.26)	−1.01 (0.30)	−1.03 (0.30)	−1.10 (0.30)	−1.00 (0.30)	−1.00 (0.31)
Sex	Male
	Female	−0.68 (0.39)	−0.70 (0.48)	−0.67 (0.47)	−0.63 (0.45)	−0.71 (0.48)	−0.72 (0.48)
Age (years)		−0.04 (0.01)	−0.04 (0.02)	−0.04 (0.02)	−0.04 (0.02)	−0.04 (0.02)	−0.04 (0.02)
Pattern of	X-linked
inheritance	Autosomal	0.64 (0.28)	0.60 (0.33)	0.59 (0.34)	0.61 (0.34)	0.60 (0.33)	0.61 (0.33)
Use of	No
corticosteroids	Yes	1.40 (0.56)	1.56 (0.78)	1.49 (0.73)	1.41 (0.62)	1.59 (0.80)	1.60 (0.82)
Log-likelihood		−324.939	−322.206	−322.431	−324.837	−322.160	−322.149
Frailty variance			0.555	0.557		0. 544	0.529
95% CI			(0.067, 1.449)	(0.049, 1.865)		(0.071, 1.328)	(0.072, 1.234)
LRT p-value			0.0085	0.0110	0.2568	0.0081	0.0080

Figure 14.

Histogram of the estimated frailties.

It is possible to question our choice for the gamma frailty. Partially due to software limitations, other distributions are rarely considered in practice. Table 2 also shows estimated frailty variances with 95% confidence intervals, as well as marginal log-likelihoods of fitted frailty models with other frailty distributions, including the inverse Gaussian, compound Poisson (m = 0.5), and positive stable distributions. Recall that the inverse Gaussian is a particular case of the PVF distributions. So is the compound Poisson distribution, where the parameter m, initially chosen as 0.5, determines the actual distribution. A grid search among possible values of the m parameter of the compound Poisson distribution (from 0.2 to 2.0 in steps of 0.1) identified m = 1.1 as optimal value, in terms of maximizing the log-likelihood. The small differences between the log-likelihoods for different values of m, however, indicate that no clear difference can be seen between any of the compound Poisson distributions. It is notoriously difficult to choose between frailty distributions; in practice this choice is usually made by convenience.

The positive stable distribution is interesting to note. As mentioned before it does not have finite mean or variance; in contrast to the other frailty models, the fit of the positive stable frailty model is not deemed significantly better than that of the Cox model without frailty, by the likelihood ratio test.

In a sense, a frailty model implies that the marginal intensity of the counting process, given the past, depends on the previous number of events, through $\text{E}[Z|{\mathcal{F}}_{t-}]$, with ${\mathcal{F}}_{t-}$ representing the event history of the individual until just before time t. The past can also be incorporated directly, by including the number of previous events, or a pre-specified function of it, as a covariate in a proportional hazards model. Including the number of previous events leads to a regression coefficient of 0.182 (SE = 0.101), p = 0.069, with a log-likelihood of −323.396. Including the logarithm of the number of previous events leads to a regression coefficient of 0.615 (SE = 0.252), p = 0.015, with a log-likelihood of −322.086, which is, interestingly, higher than the log-likelihoods of all frailty models considered here.

7 Practical modeling advice

In practice, one would fit the frailty model for clustered survival data or recurrent event modeling. For univariate survival data, estimating frailty models involves a large degree of speculation, and their practical value is therefore limited. Nevertheless, they are useful tools in situations where there is a strong a priori evidence for heterogeneity, as for example in modeling time to pregnancy,⁹⁰ or when the objective is to understand or provide alternative explanations of the shape of the hazard.⁹¹

In the context of clustered survival data, one would fit a frailty model for estimating covariate effects while adjusting for, and with the objective of quantifying the between-cluster heterogeneity. In the context of recurrent event data, one would fit a frailty model for estimating covariate effects without assuming that the recurrent event process is Poisson and quantifying the between-subject heterogeneity. The usage of random effects is particularly sensible when the clusters (or individuals, in the case of recurrent events) are considered to be a random sample from a larger population.

The starting point for modeling is typically a marginal model, using the GEE approach. The point estimates for covariate effects are obtained from a proportional hazards model, and the standard errors are calculated using a sandwich estimator. With coxph, for example, this may be obtained with the +cluster() option. In some cases, this explanation may suffice. The hazard ratios in such a marginal model quantify the effect of the covariates at the population level.

When the clusters are large in size, or when individuals have numerous recurrent events, one may consider including cluster-specific (or individual-specific, in the case of recurrent events) fixed effects. The variability of these fixed effects may be assessed informally, as illustrated in section 6.1. A meaningful variability would indicate the presence of unobserved heterogeneity. One issue with this is that the fixed effects estimates of the clusters with few subjects will have a large variability, and shrinkage towards the mean would be desirable. This was also illustrated in the same section. All frailty distributions will provide some degree of shrinkage, but only for the gamma and a limited set of other frailty distributions closed-form results are easily available. One way to formally evaluate the presence of unobserved heterogeneity is with the Commenges-Andersen score test. In practice, a frailty model may be useful to be estimated anyway, to be able to quantify the heterogeneity and formally evaluate the improvement in model fit via the likelihood ratio test.

In terms of choosing which frailty distribution is most appropriate, we start with the practical considerations. The gamma frailty model is the simplest and most well understood frailty model, and may be estimated by the base R survival package. Furthermore, theoretical results indicate that the gamma distribution is the limiting distribution of the frailty of long-time survivors,⁹² irrespective of the frailty distribution at baseline. The log-normal frailty model is conceptually simple as well, since it involves considering an additive random effect on the same scale as the other covariates. This can also be estimated by the survival and coxme packages. In both cases, a likelihood ratio test can be carried out to formally explore whether the frailty models provide significantly better fits to the data. This aspect is illustrated in section 6.2.

In principle, different frailty models may be compared via their log-likelihoods. Such a procedure might be useful for selecting a well-fitting frailty distribution from a larger class of frailty distributions, such as the power variance family, but since the frailties are latent, there typically is not a lot of information in the data to make a well informed choice, as could also be seen in section 6.2. Since the gamma frailty distribution is the most popular frailty distribution, a number of procedures for testing goodness-of-fit of the frailty distribution in the shared gamma frailty model have been proposed. Shih and Louis⁹³ suggest to visually assess the fit of the gamma frailty distribution by plotting the empirical Bayes estimators of the frailties given the observable data so far over time. For the gamma frailty model, these should be constant over time. This test was later extended by Glidden.⁹⁴ Geerdens et al.⁹⁵ developed a goodness-of-fit test by constructing a class of frailty model that extend the gamma frailty model using polynomial expansions that are orthogonal to the gamma density. The aforementioned tests focus on the goodness-of-fit of the gamma frailty distribution in the gamma frailty model. When evaluating the fit of a proportional hazards frailty model, another aspect is the validity of the (conditional) proportional hazards assumption. This assumption may be assessed in a similar way as in a regular survival model, by including the logarithm of the empirical Bayes frailty estimates as an offset in the proportional hazards model, and studying the Schoenfeld residuals.¹² This is most sensible when cluster sizes are relatively large (e.g. above 10 subjects). When this is not the case, the presence of frailty and the proportional hazards assumption may still be, to some extent, confounded.²⁹

Declaration of conflicting interests

The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Funding

The author(s) received no financial support for the research, authorship, and/or publication of this article.

ORCID iD

Hein Putter https://orcid.org/0000-0001-5395-1422